Open Access Article
Open Access ArticleLength-dependent symmetry in narrow chevron-like graphene nanoribbons†
R. S. Koen
Houtsma
 a,
Mihaela
Enache
a,
Remco W. A.
Havenith
a,
Mihaela
Enache
a,
Remco W. A.
Havenith
 abc and
Meike
Stöhr
abc and
Meike
Stöhr
 *a
*a
aZernike Institute for Advanced Materials, University of Groningen, 9747AG Groningen, The Netherlands. E-mail: m.a.stohr@rug.nl
bStratingh Institute for Chemistry, University of Groningen, 9747AG Groningen, The Netherlands
cGhent Quantum Chemistry Group, Department of Chemistry, Ghent University, Krijgslaan 281 (S3), B-9000 Gent, Belgium
First published on 3rd June 2022
Abstract
We report the structural and electronic properties of narrow chevron-like graphene nanoribbons (GNRs), which depending on their length are either mirror or inversion symmetric. Additionally, GNRs of different length can form molecular heterojunctions based on an unusual binding motif.
Introduction
Graphene nanoribbons are a promising candidate material for next-generation nanoelectronic devices as they may combine the excellent electronic properties of graphene with the opening of an electronic band gap. With a bottom-up approach, GNRs of different structures can be synthesized with atomic precision and both their electronic and structural properties have been well-characterized.1 These studies report, depending on the GNRs' width and edge structure (e.g. armchair or zigzag), semiconducting behavior,2 doping3 and more recently GNRs with topological phases.4 Length-dependent effects in GNRs have received increasing attention. For instance, seven atom wide armchair GNRs (7-AGNRs) have length-dependent band gaps5 and 5-AGNRs undergo a topological phase transition once they reach a certain critical length.6 Chevron GNRs, i.e., GNRs with meandering edge structure and a possible combination of zigzag and armchair edge terminations can be used to further tune the band gap of GNRs7 and are expected to be good candidates for optoelectronic and thermoelectric applications.8 In addition, chevron GNRs have the intriguing property that depending on the number of monomer units incorporated into the ribbon, not only their length, but also their symmetry changes.9 However, the effect of this symmetry on their electronic properties has not been investigated thus far. Here we investigate the electronic and structural properties of narrow chevron-like GNRs, also in dependence of their length and symmetry, using a combination of high-resolution scanning tunneling microscopy (STM), spectroscopy (STS) and density functional theory (DFT) calculations. We found that the ribbons have a strongly length-dependent band gap while their symmetry determines the spatial distribution of the electronic states, but does not influence the band gap. In addition, we identified a common ‘defective’ coupling motif which has a determining influence on the electronic properties of the ribbons and can even be used as a basis for the formation of molecular heterojunctions. We expect that our observations for the heterojunctions can be transferred to the formation and properties of heterojunctions made from structurally different GNRs.Methods
Sample preparation
All experiments were conducted under ultra-high vacuum conditions. The on-surface synthesis was performed on an Au(111) single crystal which was cleaned with repeated Ar + sputtering and annealing cycles. The commercially available monomers, 6,12-dibromochrysene (Sigma-Aldrich), were thermally evaporated at 170 °C from a four pocket Knudsen cell evaporator (Omnivac). The substrate was held at room temperature during deposition. Using resistive heating the monomers were converted to graphene nanoribbons following the procedure of Pham et al.9aScanning tunneling microscopy and spectroscopy
STM imaging was performed with a commercial low temperature STM (Scienta Omicron) operated at 4.5 K. The STM was operated in constant current mode and when using a CO functionalized PtIr tip in constant height mode. Before recording constant height images, the tip-sample distance was set by allowing the feedback loop to relax with parameters Iset = 200 pA and Vbias = 10 mV. All STM images were processed using the WSXM software package.10 Differential conductance (dI/dV) measurements were performed using a lock-in amplifier with modulation voltage Vrms = 12 mV and modulation frequency of 757 Hz. Differential conductance spectra were recorded in open feedback loop conditions and before each spectrum the tip was calibrated to the Au(111) Shockley surface state.11 dI/dV point spectra were normalized according to Feenstra et al. unless stated otherwise.12 Differential conductance mapping was performed in constant current mode.DFT calculations
The gas phase DFT calculations were carried out with the BAND2018 software package within the local-density approximation (LDA).13 The convergence criterion for changes in energy was <0.03 eV while for the (nuclear) gradients it was <0.0003 eV Å−1. The numerical integration was performed using the procedure developed by Becke et al.14 and its implementation in BAND is described in ref. 13c The integration grid quality was set to Becke Good.14 The triple-zeta with one polarization function (TZP) basis set was used. The core shells of all elements were treated by the frozen-(large)-core approximation.15Results
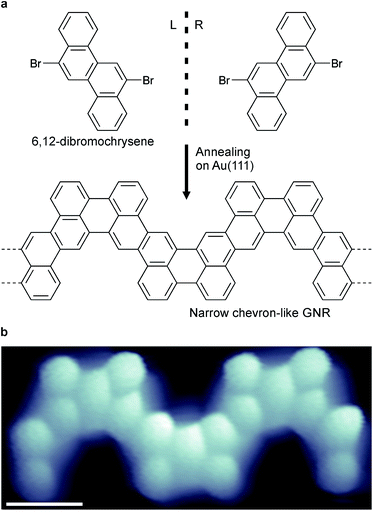
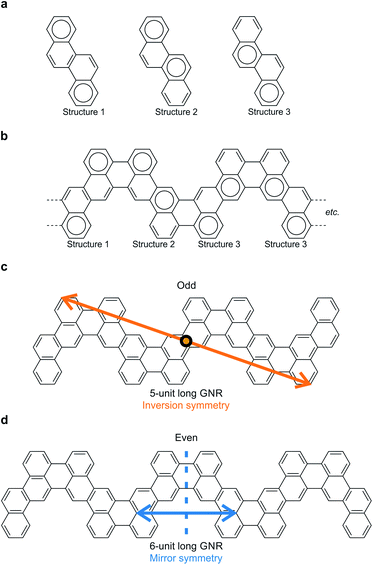
Narrow chevron-like graphene nanoribbons were fabricated according to the procedure of Pham et al.9a The prochiral monomer units, 6,12-dibromochrysene (Fig. 1a), were sublimed onto a clean Au(111) substrate held at room temperature in ultra-high vacuum. The monomers are adsorbed on the surface in either the left- or right-handed geometry (Fig. 1a), thus a racemic mixture of two enantiomers is available on the surface. Annealing activates enantioselective, surface-assisted Ullmann-type coupling followed by thermally induced cyclodehydrogenation, yielding achiral narrow chevron-like graphene nanoribbons (Fig. 1b). For a more detailed description of the synthesis process, we refer to the work of Pham et al.9aAfter synthesis of the GNRs, the sample was subsequently cooled to 4.5 K for characterization with scanning tunneling microscopy (STM) and spectroscopy (STS). A high-resolution STM image obtained with a CO-functionalized tip confirms the distinct, narrow chevron-like structure of the GNRs (Fig. 2b).16 The central carbon ring, i.e., the one that connects two monomer units, always appears larger in such images. This may be rationalized from the Clar structure of these ribbons, where two chrysene monomers are always linked by two single bonds (Fig. 2a and b).17 Interestingly, the symmetry of the GNRs is length-dependent, where GNRs consisting of an odd or even number of monomer units are inversion or mirror symmetric, respectively (Fig. 2c and d).
Large-scale STM images reveal in addition to straight GNRs the formation of a considerable number of bent ones, i.e., the formation of heterojunctions from GNRs with different length and symmetry (Fig. S1 in the ESI†). It is important to note that pristine or straight (i.e., without junctions) ribbons are a minority. Furthermore, the ribbons preferentially lie on the face-centered cubic (fcc) areas of the well-known Au(111) herringbone reconstruction.18 This suggests that the herringbone reconstruction may have a quasi-1D templating effect on the GNR growth.
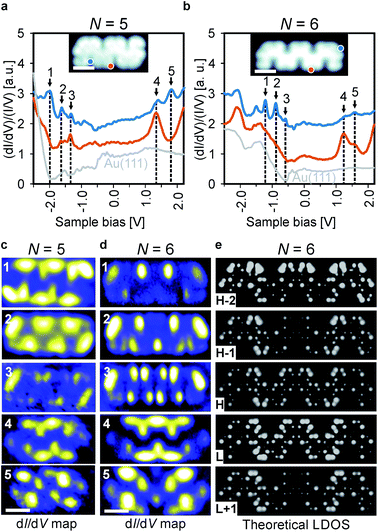
To investigate the effect of spatial symmetry on the electronic structure of the GNRs, we first focus on pristine ribbons consisting of 5 and 6 monomer units, which are inversion and mirror symmetric (Fig. 2c and d), respectively, using a combination of dI/dV spectroscopy and DFT calculations. The results for a selection of typical dI/dV point spectra for 5 and 6 unit long ribbons are shown in Fig. 3a and b, respectively (more spectra are provided in Fig. S2†). The electronic states of the GNRs are substantially localized giving rise to position-dependent electronic resonances in the dI/dV spectra, similar to results previously reported for other GNRs.2b,d,3b,19 Thus, probing multiple areas of the ribbons is necessary to reveal all electronic resonances. For the 5-unit long ribbon, we identify the electronic resonances corresponding to occupied states at −1.97 V, −1.63 V and −1.33 V and resonances corresponding to unoccupied states at 1.33 V and 1.79 V. We identify the band gap (measured from onset to onset) of the 5-unit long ribbons as 2.3 eV. The electronic state positions change substantially when investigating the 6-unit long ribbon. This time, we identify occupied states at −1.2 V, −0.88 V, −0.58 V and unoccupied states at 1.23 V and 1.57 V and the band gap narrows accordingly to 1.5 eV, a decrease of 0.8 eV in comparison to the 5-unit long ribbon. Length-dependent band gaps have been previously reported for other short GNRs, however a change in band gap of 0.8 eV by adding only a single monomer unit is exceptionally large.5 Further investigations of longer ribbons indicated that this is a length-dependent effect and not due to the differing symmetry of the 5- and 6-unit long GNRs (Fig. S3†). Comparison of a 6-unit long ribbon with a 9-unit long ribbon (Fig. S3†) shows that their electronic states are at similar positions with respect to the Fermi level, indicating that the electronic properties of a 6-unit long ribbon are close to that of an ideal, infinitely long ribbon. The band gap of the chevron-like GNRs is 0.5 eV larger than an 8-AGNR of equal width, likely due to the increased electronic confinement in chevron-like structures.20 It is also interesting to note that the most studied chevron GNR so far, derived from 6,11-dibromo-1,2,3,4-tetraphenyltriphenylene (DBTT), has a larger bandgap (∼2.4 eV) than the narrow chevron-like GNR investigated in this work, despite its greater width.3b,9b,21 This may be due to this chevron GNR (based on DBTT) being derived from a 15-wide AGNR, which belongs to the medium gap 3p family of GNRs, whereas the narrow chevron-like GNR is derived from an 8-wide AGNR from the small gap 3p + 2 family of GNRs.22
To investigate the spatial distribution of the frontier states, differential conductance maps were recorded at the peak positions determined from the dI/dV spectra and compared to DFT calculations. The results are summarized in Fig. 3c and d. It is obvious that the spatial symmetry of the electronic states is the same as that of the ribbons, i.e., the states for the 5-unit long ribbon are inversion symmetric, whereas the states for the 6-unit long ribbon are mirror symmetric. The overall electron distribution for each state is the same regardless of ribbon length. The distinct localized character of the states, which was also observed in dI/dV point spectroscopy experiments, is also apparent in the dI/dV maps.
In order to further validate these findings, gas-phase DFT calculations were carried out within the local-density approximation (LDA) and the resulting local density of states (LDOS) maps show excellent agreement with our experimentally obtained dI/dV maps (Fig. 3e). The similarity of the calculated LDOS maps of gas-phase GNRs and the experimentally obtained dI/dV maps on the metal-supported GNRs indicates that the substrate-GNR interaction is weak.
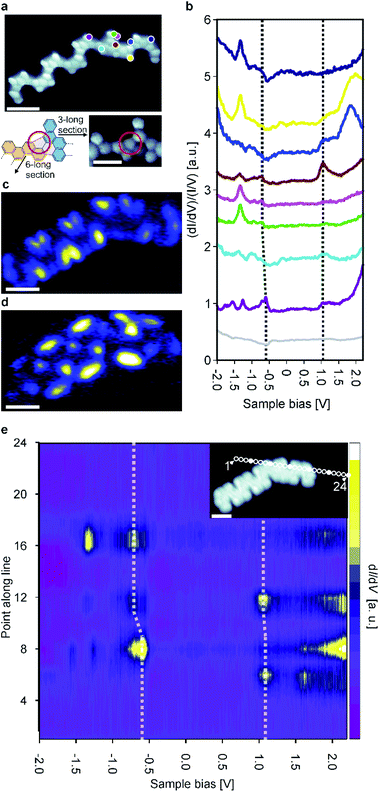
At this point it is interesting to compare pristine ribbons with bent ones exhibiting junctions of two or more ribbons. Such bent ribbons were more common on the sample than the pristine ones. As is confirmed by high-resolution STM images, these junctions are based on the formation of homochiral coupling as opposed to heterochiral coupling, which forms straight ribbons (Fig. 4a). The relative abundance of junctions found on our samples (Fig. S1†) compared to studies of other GNRs1,2b,23 may be due to a combination of factors: (i) there is no strong energetic preference for heterochiral compared to homochiral coupling9a and (ii) the templating effect of the Au(111) herringbone reconstruction.
Junctions in the chevron-like GNRs are based on the formation of both a 5- and 6-membered ring between two monomer units (Fig. 4a and S4†). Such a binding motif has not been observed thus far. Based on 55 junctions, the average angle was determined to 141 ± 8° (Fig. S5†). Since no other angles were observed and high resolution STM images always gave similar results, we conclude that the junctions are always formed through this same binding motif.
To study the electronic properties of the junctions in more detail, a junction of a 6-unit (mirror symmetric) and 3-unit (inversion symmetric) long GNR (a ‘6–3 junction’) was examined. To inspect the electronic properties of the 6–3 junction, we recorded multiple dI/dV point spectra on both sides of the 6–3 junction (Fig. 4b). Interestingly, the positions of the electronic resonances are slightly altered (in comparison to pristine ribbons) on either side of the junction area. We recorded a series of equidistant spectra across the junction area which corroborate this finding (Fig. 4e). Moreover, we identified a downshift of both the valence and conduction band in the 3-unit long section compared to the 6-unit long one. Thus, the 6–3 junction acts as a type II heterojunction, formed from a single precursor and in a single step. The formation of the heterojunction is ascribed to the length-dependent band gap of the chevron-like graphene nanoribbons, i.e., the 6 unit long section has a narrower band gap than the 3 unit long section. In addition, as was noted previously, the length dependence of the band gap is particularly pronounced for the chevron-like GNRs. The band gap difference between the 6 unit and 3 unit long sections is not as much as one might expect from the results for ‘isolated’ straight ribbons, indicating that there is electronic coupling between the two ribbons participating in the junction. It is interesting to note that the Clar structure of the junction is not different from the Clar structure of the two individual ribbons that constitute it, i.e., the Clar structure is unperturbed by the junction (Fig. S7†). This is in contrast with the case of 3, 1 chiral GNRs where junctions between two ribbons adopt an open shell structure and lead to single spin features.24
In addition, we performed dI/dV mapping for the 6–3 junction to investigate the spatial distribution of its frontier orbitals (Fig. 4c and d). At tip-sample bias of 1.1 V, the LUMO of both the 6- and 3-unit long sections are imaged simultaneously. Because the LUMO is (almost) aligned, this state ignores the junction area. However, the situation changes when we consider the state at −0.55 V: the HOMO of the 6-unit long section. This state is localized on the 6-unit long section of the 6–3 junction and only weakly penetrates into the 3-unit long section, typical for GNR heterojunctions.9c,23,25 This further corroborates that the 6–3 junction acts as a molecular heterojunction.
Lastly, we can now compare our results for the 5-, 6- and 9-unit long ribbon with an arbitrary ribbon with numerous junctions incorporated into it. Such a general ribbon was recently characterized by others in ref. 26 and by us in Fig. S6†.26 Our results are in excellent agreement with those in ref. 26. It is clear from these results that the electronic properties of such a ribbon are vastly altered, with an upshift of the HOMO by ∼0.5 eV and an upshift of the LUMO of ∼0.2 eV and a corresponding band gap decrease, with respect to the pristine ones without a junction. This may be due to a combination of factors: (i) the coupling defect made from a 5- and 6-membered ring locally alters the π-system of the GNR, (ii) numerous other defects (which appear as bright protrusions in Fig. S1†) have an unknown effect on the GNRs' electronic properties, (iii) the 5-membered ring introduces strain in the GNR structures and (iv) the 5-membered ring causes a frustration in the sublattices of the GNR.
Conclusion
Our results demonstrate that the narrow chevron-like GNRs from 6,12-dibromochrysene are semiconducting with a band gap of 1.5 eV, wider than that of an AGNR of equal width. We identified various edge-localized molecular states, which have symmetry reflecting the symmetry of the ribbons. The band gap of the chevron-like GNRs depends sensitively on their length: an increase in length of one monomer unit can lead to a change in band gap of almost 1 eV. The symmetry of the ribbons does not affect the band gap. In addition to short and straight ribbons, we investigated junctions of GNRs of different lengths. The junctions are formed through a homochiral coupling in combination with the formation of 5- and 6-membered ring. As a case study, we investigated the electronic properties of a 6–3 junction. It was found that the two sides of the junction are partially electronically decoupled, leading to a misalignment of the HOMO. Thus, it was found that junctions between two ribbons may act as molecular heterojunctions formed by a single molecular precursor. We expect that this may be a more general property of junctions between short GNRs, as length-dependent band gaps have been demonstrated for other GNRs as well.5Author contributions
R. S. K. H., M. E. and M. S. conceptualized the project. R. S. K. H. and M. E. performed the STM and STS measurements. M. E. and R. W. A. H. performed the DFT calculations. R. S. K. H. performed the data analysis with input from all authors. All authors contributed to discussing the results and writing the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by the Netherlands Organization for Scientific Research (NWO) (Vici grant 680-47-633) and the Zernike Institute for Advanced Materials of the University of Groningen. R. W. A. H. and M. E. acknowledge access to computational facilities at the Peregrine high-performance computing cluster (University of Groningen) and access to the national computing facilities provided by the Netherlands Organization for Scientific Research (contract no. 171977095).Notes and references
- (a) J. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Müllen and R. Fasel, Nature, 2010, 466, 470–473 CrossRef CAS PubMed; (b) L. Talirz, P. Ruffieux and R. Fasel, Adv. Mater., 2016, 28, 6222–6231 CrossRef CAS PubMed; (c) Z. Chen, A. Narita and K. Müllen, Adv. Mater., 2020, 32, 2001893 CrossRef CAS PubMed; (d) X. Zhou and G. Yu, Adv. Mater., 2020, 32, 1905957 CrossRef CAS PubMed; (e) R. S. K. Houtsma, J. De La Rie and M. Stöhr, Chem. Soc. Rev., 2021, 50, 6541–6568 RSC.
- (a) P. Ruffieux, J. Cai, N. C. Plumb, L. Patthey, D. Prezzi, A. Ferretti, E. Molinari, X. Feng, K. Müllen, C. A. Pignedoli and R. Fasel, ACS Nano, 2012, 6, 6930–6935 CrossRef CAS PubMed; (b) L. Talirz, H. Söde, T. Dumslaff, S. Wang, J. R. Sanchez-Valencia, J. Liu, P. Shinde, C. A. Pignedoli, L. Liang, V. Meunier, N. C. Plumb, M. Shi, X. Feng, A. Narita, K. Müllen, R. Fasel and P. Ruffieux, ACS Nano, 2017, 11, 1380–1388 CrossRef CAS PubMed; (c) Y.-C. Chen, D. G. de Oteyza, Z. Pedramrazi, C. Chen, F. R. Fischer and M. F. Crommie, ACS Nano, 2013, 7, 6123–6128 CrossRef CAS PubMed; (d) P. H. Jacobse, M. J. J. Mangnus, S. J. M. Zevenhuizen and I. Swart, ACS Nano, 2018, 12, 7048–7056 CrossRef CAS PubMed.
- (a) C. Bronner, S. Stremlau, M. Gille, F. Brauße, A. Haase, S. Hecht and P. Tegeder, Angew. Chem., Int. Ed., 2013, 125, 4518–4521 CrossRef; (b) R. A. Durr, D. Haberer, Y.-L. Lee, R. Blackwell, A. M. Kalayjian, T. Marangoni, J. Ihm, S. G. Louie and F. R. Fischer, J. Am. Chem. Soc., 2018, 140, 807–813 CrossRef CAS PubMed; (c) J. Li, P. Brandimarte, M. Vilas-Varela, N. Merino-Díez, C. Moreno, A. Mugarza, J. S. Mollejo, D. Sánchez-Portal, D. Garcia De Oteyza, M. Corso, A. Garcia-Lekue, D. Peña and J. I. Pascual, ACS Nano, 2020, 14, 1895–1901 CrossRef CAS PubMed; (d) S. Kawai, S. Saito, S. Osumi, S. Yamaguchi, A. S. Foster, P. Spijker and E. Meyer, Nat. Commun., 2015, 6, 8098 CrossRef CAS PubMed.
- (a) D. J. Rizzo, G. Veber, J. Jiang, R. Mccurdy, T. Cao, T. Chen, S. G. Louie, F. R. Fischer and M. F. Crommie, Science, 2020, 369, 1597–1603 CrossRef CAS PubMed; (b) D. J. Rizzo, G. Veber, T. Cao, C. Bronner, T. Chen, F. Zhao, H. Rodriguez, S. G. Louie, M. F. Crommie and F. R. Fischer, Nature, 2018, 560, 204–208 CrossRef CAS PubMed; (c) O. Gröning, S. Wang, X. Yao, C. A. Pignedoli, G. Borin Barin, C. Daniels, A. Cupo, V. Meunier, X. Feng, A. Narita, K. Müllen, P. Ruffieux and R. Fasel, Nature, 2018, 560, 209–213 CrossRef PubMed.
- (a) A. Kimouche, M. M. Ervasti, R. Drost, S. Halonen, A. Harju, P. M. Joensuu, J. Sainio and P. Liljeroth, Nat. Commun., 2015, 6, 10177 CrossRef CAS PubMed; (b) L. Talirz, H. Söde, S. Kawai, P. Ruffieux, E. Meyer, X. Feng, K. Müllen, R. Fasel, C. A. Pignedoli and D. Passerone, ChemPhysChem, 2019, 20, 2348–2553 CrossRef CAS PubMed.
- J. Lawrence, P. Brandimarte, A. Berdonces-Layunta, M. S. G. Mohammed, A. Grewal, C. C. Leon, D. Sánchez-Portal and D. G. De Oteyza, ACS Nano, 2020, 14, 4499–4508 CrossRef CAS PubMed.
- (a) E. Costa Girão, E. Cruz-Silva, L. Liang, A. G. S. Filho and V. Meunier, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235431 CrossRef; (b) L. Liang, E. C. Girão and V. Meunier, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 035420 CrossRef.
- (a) L. Liang and V. Meunier, Appl. Phys. Lett., 2013, 102, 143101 CrossRef; (b) S. Wang and J. Wang, J. Phys. Chem. C, 2012, 116, 10193–10197 CrossRef CAS; (c) W. Huang, J. S. Wang and G. Liang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045410 CrossRef.
- (a) T. A. Pham, B. V. Tran, M. T. Nguyen and M. Stöhr, Small, 2017, 13, 1603675 CrossRef PubMed; (b) O. Deniz, C. Sánchez-Sánchez, R. Jaafar, N. Kharche, L. Liang, V. Meunier, X. Feng, K. Müllen, R. Fasel and P. Ruffieux, Chem. Commun., 2018, 54, 1619–1622 RSC; (c) C. Bronner, R. A. Durr, D. J. Rizzo, Y.-L. Lee, T. Marangoni, A. M. Kalayjian, H. Rodriguez, W. Zhao, S. G. Louie, F. R. Fischer and M. F. Crommie, ACS Nano, 2018, 12, 2193–2200 CrossRef CAS PubMed.
- I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 013705 CrossRef CAS PubMed.
- W. Chen, V. Madhavan, T. Jamneala and M. F. Crommie, Phys. Rev. Lett., 1998, 80, 1469–1472 CrossRef CAS.
- J. A. Stroscio, R. M. Feenstra and A. P. Fein, Phys. Rev. Lett., 1986, 57, 2579–2582 CrossRef CAS PubMed.
- (a) G. Te Velde and E. J. Baerends, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 7888–7903 CrossRef CAS PubMed; (b) G. Wiesenekker and E. J. Baerends, J. Phys.: Condens. Matter, 1991, 3, 6721–6742 CrossRef; (c) M. Franchini, P. H. T. Philipsen and L. Visscher, J. Comput. Chem., 2013, 34, 1819–1827 CrossRef CAS PubMed; (d) M. Franchini, P. H. T. Philipsen, E. Van Lenthe and L. Visscher, J. Chem. Theory Comput., 2014, 10, 1994–2004 CrossRef CAS PubMed; (e) SCM, TheoreticalChemistry, BAND2018, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed; (f) F. Bloch, Zeitschrift für Phys., 1929, 57, 545–555 CrossRef CAS; (g) P. A. M. Dirac, Math. Proc. Cambridge Philos. Soc., 1930, 26, 376–385 CrossRef CAS; (h) S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1988, 88, 2547–2553 CrossRef CAS.
- E. J. Baerends, D. E. Ellis and P. Ros, Chem. Phys., 1973, 2, 41–51 CrossRef CAS.
- (a) L. Gross, F. Mohn, N. Moll, P. Liljeroth and G. Meyer, Science, 2009, 325, 1110–1114 CrossRef CAS PubMed; (b) G. Kichin, C. Weiss, C. Wagner, F. S. Tautz and R. Temirov, J. Am. Chem. Soc., 2011, 133, 16847–16851 CrossRef CAS PubMed.
- (a) L. Gross, F. Mohn, N. Moll, B. Schuler, A. Criado, E. Guitián, D. Peña, A. Gourdon and G. Meyer, Science, 2012, 337, 1326–1329 CrossRef CAS PubMed; (b) I. Pozo, Z. Majzik, N. Pavliček, M. Melle-Franco, E. Guitián, D. Peña, L. Gross and D. Pérez, J. Am. Chem. Soc., 2019, 141, 15488–15493 CrossRef CAS PubMed; (c) T. Wassmann, A. P. Seitsonen, A. M. Saitta, M. Lazzeri and F. Mauri, J. Am. Chem. Soc., 2010, 132, 3440–3451 CrossRef CAS PubMed; (d) P. Hapala, G. Kichin, C. Wagner, F. S. Tautz, R. Temirov and P. Jelínek, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085421 CrossRef CAS; (e) O. Krejčí, P. Hapala, M. Ondráček and P. Jelínek, Phys. Rev. B, 2017, 95, 045407 CrossRef; (f) P. Hapala, M. Švec, O. Stetsovych, N. J. Van Der Heijden, M. Ondráčk, J. Van Der Lit, P. Mutombo, I. Swart and P. Jelínek, Nat. Commun., 2016, 7, 11560 CrossRef CAS PubMed.
- J. V. Barth, H. Brune, G. Ertl and R. J. Behm, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9307 CrossRef CAS PubMed.
- J. D. Teeter, P. Zahl, M. Mehdi Pour, P. S. Costa, A. Enders and A. Sinitskii, ChemPhysChem, 2019, 20, 2281–2285 CrossRef CAS PubMed.
- K. Sun, P. Ji, J. Zhang, J. Wang, X. Li, X. Xu, H. Zhang and L. Chi, Small, 2019, 15, 1804526 CrossRef PubMed.
- G. D. Nguyen, H. Z. Tsai, A. A. Omrani, T. Marangoni, M. Wu, D. J. Rizzo, G. F. Rodgers, R. R. Cloke, R. A. Durr, Y. Sakai, F. Liou, A. S. Aikawa, J. R. Chelikowsky, S. G. Louie, F. R. Fischer and M. F. Crommie, Nat. Nanotechnol., 2017, 12, 1077–1082 CrossRef CAS PubMed.
- (a) Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef PubMed; (b) K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17954 CrossRef CAS PubMed.
- D. J. Rizzo, M. Wu, H.-Z. Tsai, T. Marangoni, R. A. Durr, A. A. Omrani, F. Liou, C. Bronner, T. Joshi, G. D. Nguyen, G. F. Rodgers, W.-W. Choi, J. H. Jørgensen, F. R. Fischer, S. G. Louie and M. F. Crommie, Nano Lett., 2019, 19, 3221–3228 CrossRef CAS PubMed.
- J. Li, S. Sanz, M. Corso, D. J. Choi, D. Peña, T. Frederiksen and J. I. Pascual, Nat. Commun., 2019, 10, 200 CrossRef PubMed.
- P. H. Jacobse, A. Kimouche, T. Gebraad, M. M. Ervasti, J. M. Thijssen, P. Liljeroth and I. Swart, Nat. Commun., 2017, 8, 119 CrossRef CAS PubMed.
- S. Sun, Y. Guan, Z. Hao, Z. Ruan, H. Zhang, J. Lu, L. Gao, X. Zuo and J. Cai, Nano Res., 2021, 15, 653–658 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00297c |
| This journal is © The Royal Society of Chemistry 2022 |