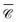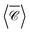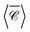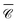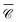Open Access Article
Open Access ArticleOrientation dependence of optical activity in light scattering by nanoparticle clusters†
Atefeh
Fazel-Najafabadi
 ab and
Baptiste
Auguié
ab and
Baptiste
Auguié
 *ab
*ab
aSchool of Chemical and Physical Sciences, Victoria University of Wellington, PO Box 600, Wellington, 6140, New Zealand. E-mail: baptiste.auguie@vuw.ac.nz
bThe MacDiarmid Institute for Advanced Materials and Nanotechnology, Wellington, New Zealand
First published on 14th December 2021
Abstract
The optical properties of nanoparticle clusters vary with the spatial arrangement of the constituent particles, but also the overall orientation of the cluster with respect to the incident light. This is particularly important in the context of nanoscale chirality and associated chiroptical responses, such as circular dichroism or differential scattering of circularly polarised light in the far-field, or local degree of optical chirality in the near-field. We explore the angular dependence of such quantities for a few archetypal geometries: a dimer of gold nanorods, a helix of gold nanospheres, and a linear chain of silicon particles. The examples serve to illustrate the possible variation of chiroptical responses with the direction of light incidence, but also, consequently, the importance of a robust orientation-averaging procedure when modelling general clusters of particles in random orientation. Our results are obtained with the rigorous superposition T-matrix method, which provides exact analytical formulas for fixed and orientation-averaged properties.
1 Introduction
Light scattering by assemblies of nanoparticles underpins many important applications of advanced nanomaterials, notably in the realm of optical sensing,1–4 spectroscopy,5–8 nano-optics,9–11 and light-harvesting technologies.12 It is also key to their characterisation.13 Bottom-up synthesis and assembly of nanoparticles enables fine-tuned optical properties, where the particles or clusters of particles are often fabricated, characterised, and used in colloidal form. In later characterisation or application, the particles may be attached on a substrate and assume preferential orientations. Nanoparticles are often used in combinations; in fact, the assembly of nanoparticles into clusters of well-defined geometry is a powerful means to realise optical properties that cannot be achieved with single particles. For instance, one of the best-performing configurations for surface-enhanced spectroscopies is to form a very small gap between two or more particles, strongly enhancing local electric fields in the gap region.5 In the context of nanoscale chirality, the assembly of nanoparticles into three-dimensional clusters has proven in recent years a very fruitful strategy,14–17 notably to overcome the intrinsic difficulty in synthesising individual chiral nanoparticles.14,15 Some of the first structures to be proposed were dissymmetric tetrahedra16,18 and helices of nanospheres.14,19–21 With nonspherical particles such as nanorods, only 2 particles are needed to produce a chiral “fingers crossed” assembly,22–26 which has been realised in a variety of ways,25–30 such as with DNA origami.25,28,29 The optical properties of nanoparticle clusters can differ dramatically from those of the constituent particles; this occurs when the presence of the neighbouring particles substantially modifies the net field exciting each particle. A typical example is a dimer, where the field scattered by one particle contributes to the net excitation of its neighbour, and vice versa.23,24 Such inter-particle coupling can occur cumulatively over several particles, provided the scattered fields add up with a well-defined phase relationship.31 This means that the precise geometrical arrangement of particles in a cluster and the direction and polarisation of the light wave exciting them lead to a delicate interaction,16,32,33 that is revealed in the overall optical properties. With chiral geometries, one is often concerned with the difference in optical response when the assembly is excited by circularly polarised light of either left or right handedness. In the far-field, this is measured as circular dichroism,34 for light extinction, or differential scattering or absorption.35,36 The recent surge of interest in polarised light's interaction with chiral nanostructures has also turned to near-field properties, following the proposal by Cohen et al.37 of locally-enhanced degree of optical chirality,![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , in the vicinity of suitably-engineered nanostructures. This quantity potentially leads to an enhancement of chiroptical spectroscopies of molecular species, of enormous practical importance for pharmaceutical and bio/chemical compounds.36,38,39
, in the vicinity of suitably-engineered nanostructures. This quantity potentially leads to an enhancement of chiroptical spectroscopies of molecular species, of enormous practical importance for pharmaceutical and bio/chemical compounds.36,38,39
The theoretical description of many experiments requires averaging the optical response over all possible particle cluster orientations, as they randomly move in solution.40–42 This averaging is often done numerically by simulating the optical response for several directions of incidence. For very small clusters, compared to the wavelength, it has been proposed that 3 directions of incidence (along 3 orthogonal axes, x, y, z) provide a good estimate of the orientation-averaged circular dichroism response.16,43 This approximation is expected to fail for larger clusters, but its range of validity has not been explored, leaving researchers to use their own numerical integration prescription in each particular study. Accurate orientation-averaging is particularly important for quantities relating to optical activity, i.e. the differential response to left and right circularly polarised light, such as far-field circular dichroism, and near-field local degree of optical chirality. Conversely, the chiroptical response along specific indicence directions can differ markedly from the orientation-averaged one. This can have important implications when the clusters assume a preferential orientation, such as in many dark-field spectroscopy experiments with particles immobilised on a substrate and illuminated over a restricted solid angle.
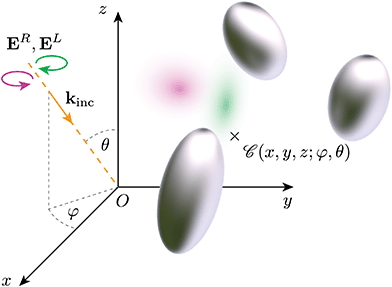
We illustrate here the dependency of chiroptical properties on cluster orientation, and the associated difficulty in obtaining an accurate orientation-averaged response. Fig. 1 depicts schematically the light scattering problem under consideration, with a rigid cluster of N particles (held together by a template, which is however neglected in the simulations) immersed in an infinite homogeneous medium (water or air), illuminated by a plane wave with left or right handed circular polarisation. The incidence direction is indexed by Euler angles (φ,θ) in a Cartesian frame attached to the cluster. Our simulations are performed using a rigorous solution of Maxwell's equations for multi-particle clusters, the superposition T-matrix method.40,44–46 In this framework, incident and scattered fields are expressed in bases of vector spherical waves; the scattering properties of the cluster are thereby captured in a way that is independent of the incident field, leading to efficient calculations for multiple independent incident fields, and to analytical formulas for orientation-averaged properties. These provide accurate benchmark results against which the performance of numerical methods can be tested.40,47
2 “Fingers crossed” dimer
The first structure under consideration is a “fingers crossed” dimer of gold nanorods22,26 (Fig. 2). This is arguably the simplest chiral nanostructure composed of achiral particles: with spherical particles, a minimum of 4 spheres is required.16,48 For computational convenience, we model the nanorods as prolate spheroids,49 using a fast and accurate T-matrix algorithm developed by our group;50 other elongated shapes would produce qualitatively similar results.51 Many studies have explored the strong chiroptical response displayed by such dimers,52–55 with a characteristic bisignate lineshape around the dominant plasmon resonance of the nanorods.22–25 This signature circular dichroism is reminiscent of exciton-coupling between chromophores,56 and is well-described in the coupled-dipole approximation.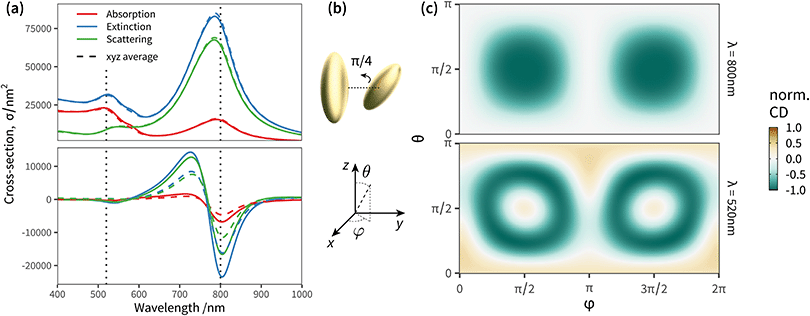 | ||
| Fig. 2 Angular response of a “fingers crossed” dimer of gold nanorods immersed in water (refractive index 1.33). (a) Orientation-averaged far-field extinction (blue), absorption (red), and scattering (green) cross-sections. Lower panel: Orientation averaged circular dichroism spectra. The solid lines correspond to analytical orientation-averaging (exact), while the dashed lines are for the numerical approximation using x, y, z incidence directions only. (b) Schematic representation of the dimer of gold nanorods. Each particle is modelled as a prolate spheroid with semi-axes a = b = 30 nm and c = 80 nm. The first particle is at (0, − 100, 0) with major axis along z, while the second particle is at (0, + 100, 0), and titled from the z axis by a polar angle θ = π/4. (c) Angular map of the extinction CD at λ = 800 nm (upper panel) and λ = 520 nm (lower panel). The values are normalised to unity in both panels to facilitate comparison of the patterns. See ESI† Fig. S2 for maps at other wavelengths. | ||
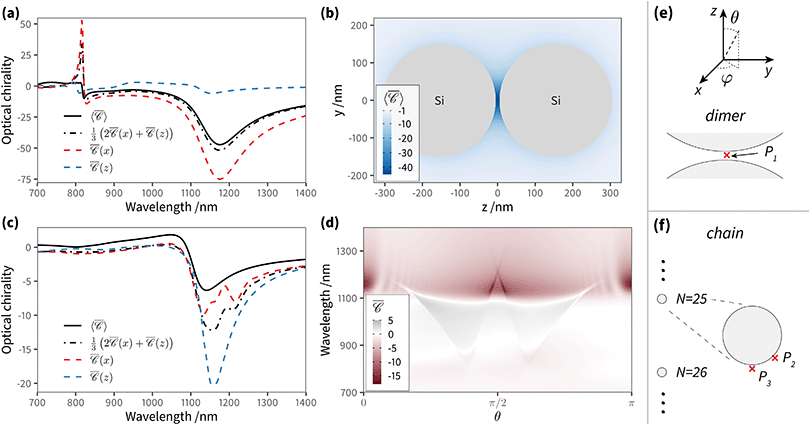
We can artificially scale the structure – both the size of the particles, and their separation – from a deep-subwavelength regime, dominated by absorption, to a scattering dominated lineshape with sizes approaching the wavelength, and observe the evolution of the circular dichroism response (additional simulations in ESI† Fig. S1). The plasmon resonances red-shift with increased size due to radiative damping, the relative contribution of scattering starts to dominate over absorption, but the lineshape remains very similar. As proposed by Govorov et al.,16 averaging the circular dichroism spectra over 3 orthogonal directions of incidence x, y, z suffices to obtain a good accuracy compared to the exact orientation-averaged spectrum, for clusters that are small compared to the wavelength. However, with larger particles and/or separation, light is able to excite non-negligible multipolar contributions to the far-field response of the cluster, which gradually increase the complexity of the angular excitation pattern particularly in the high-energy region, with a detrimental effect on the accuracy of a simple “x, y, z” angular averaging (Fig. S1 (ESI†), f > 0.8; Fig. 2 corresponds to the largest scale, f = 2).
We compare in Fig. 2c the angular maps at two wavelengths, 520 nm and 800 nm, corresponding to the vertical lines in the spectra of Fig. 2a. These maps correspond to extinction circular dichroism at fixed incidence, with the wave-vector spanning the full solid angle. For visualisation purposes the values are scaled to unity, helping the comparison between the two wavelengths. The circular dichroism is strongest in the spectral region of the main longitudinal plasmon resonance (800 nm), and when light is incident along the dimer axis. Interestingly, circular dichroism vanishes when the wave vector is orthogonal to the dimer axis. The map at 520 nm displays a richer pattern, due to the contribution of higher-order multipoles, beyond the dipolar term, needed to describe the light scattered by the dimer. This leads, in turn, to a less accurate orientation average when using three directions only.
To better quantify and contrast the relative complexity in the angular patterns of Fig. 2c, we perform a spherical harmonic (SH) decomposition of the two-dimensional angular profile (Fig. 3), using the Chebfun library.57 Specifically, we project the far-field differential cross-section σcd(φ,θ) onto spherical harmonics (SH) up to degree 20 as
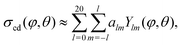 | (1) |
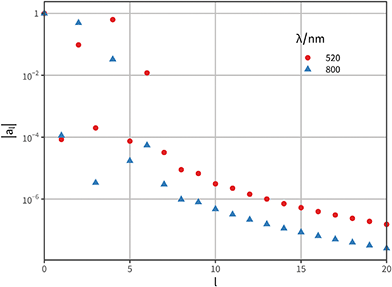 | ||
Fig. 3 Spherical harmonic analysis of the circular dichroism angular patterns shown in Fig. 2(c). We use the function sphharm from the Matlab library Chebfun57,58 to compute the decomposition of the angular map into spherical harmonics. For each harmonic degree l we collapse the corresponding 2l + 1 orders as 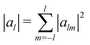 ; the result summarises the total weight of degree l in the pattern (higher degrees correspond to higher angular frequencies). For ease of comparison the scale is logarithmic, and we normalise the results such as |a0| = 1. The two cases considered correspond to λ = 520 nm (red dots) and λ = 800 nm (blue triangles). ; the result summarises the total weight of degree l in the pattern (higher degrees correspond to higher angular frequencies). For ease of comparison the scale is logarithmic, and we normalise the results such as |a0| = 1. The two cases considered correspond to λ = 520 nm (red dots) and λ = 800 nm (blue triangles). | ||
3 Helix of nanoparticles
The dimer example above is a very compact cluster, with only two particles. With more particles, the optical response becomes even richer, as the resonances hybridise in complex ways.17,32,62 This is particularly striking in the circular dichroism response of small helices of 5–10 nanospheres, where the addition of one particle can flip entirely the CD spectrum.15,63 This sensitivity to precise positioning can potentially be an asset, enabling very precise retrieval of geometrical information from far-field optical interrogation, or a drawback if the fabrication technique does not offer sufficient control to ensure precisely identical clusters. We note that helices with different parameters, or with more particles, can be more robust.63 Alternatively, replacing the spherical particles with elongated nanorods aligned with the helix, results in a robust CD lineshape.15 This is because the induced electric dipole for each particle is given a preferential orientation, unlike with nanospheres where its orientation is purely dictated by the self-consistent field originating from the incident light and the field scattered by its neighbours. This serves to illustrate the complex interplay of relative phase and direction of the vector fields, at the heart of chiroptical responses in nanoparticle assemblies. Helices appear commonly in natural systems presenting optical activity, and are indeed a prototypical structure to study the interaction of light with chiral matter. Early theoretical models based on coupled-dipole approximations have considered the response of helices, and notably the possibility to induce long-range interactions through the well-defined phase relationship between induced dipoles positioned in such geometries.64In the more recent context of chiral clusters of plasmonic particles, long helices have also been proposed,21,65,66 notably “GoldHelix”61 which comprise hundreds of gold nanospheres attached on a helical silica template. This structure provides an interesting example of a relatively large rigid cluster of nanoparticles, which is still free to move and rotate randomly when characterised, or used, in solution. We simulated a representative “GoldHelix” cluster of Au nanospheres 5 nm in radius, following the description in ref. 61, with 4 × 80 nanospheres arranged in a ∼470 nm long helix (Fig. 4; see ESI† for the list of particle positions we used). Coupled-dipole modelling described in ref. 61 indicated the need for 30 directions of incidence over an octant to accurately model the averaged circular dichroism spectra. We explore the reasons for this relatively challenging numerical averaging by simulating the differential CD response of the helix as a function of θ and φ angles. Note that we chose to orient the axis of the helix along z, for easier interpretation (Fig. 4g and h).
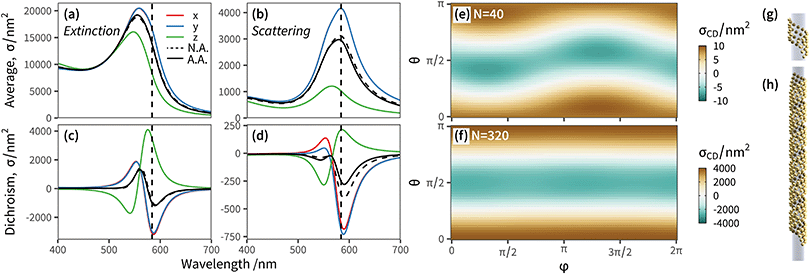 | ||
| Fig. 4 Far-field chiroptical response of a “GoldHelix” cluster described in ref. 61 consisting of a ribbon of 5 nm radius Au nanospheres wrapped in a helix and immersed in water. The list of particle positions we used is available in ESI.† (a and b) Extinction and scattering spectra for three perpendicular incident directions, x-axis (solid red line), y-axis (solid blue line), z-axis (solid green line), the average over the three (dashed black line), and the analytical orientation averaged result (solid black line). (c and d) The corresponding results for circular dichroism. (e and f) Angular map of circular dichroism (for extinction) for a GoldHelix with number of particles N = 40 (e) and N = 320 (f). (g and h) Schematic illustration of the GoldHelix geometry with N = 40 and N = 320, respectively. Note that cross-sections are normalised by the number of particles in each cluster, to facilitate comparisons. The simulations considered a maximum multipole order lmax = 4. | ||
To fully illustrate the influence of the cluster's spatial extent and anisotropy, we compare two structures: the full helix (Fig. 4f and h), and a truncated helix with identical parameters but only 4 × 10 particles (Fig. 4e and g). The optical response is qualitatively similar with a strong bisignate CD spectrum at the position of the localised plasmon resonance (λ ≈ 550 nm) of small Au nanospheres in water. The extinction spectrum is dominated by absorption, but we note that some characterisation techniques such as dark-field spectroscopy would measure a somewhat distinct lineshape (panel d). Both structures present an angular dependence with a strong pattern in the polar angle θ, but only a small variation along φ which becomes almost invisible for the longer helix. Circular dichroism is strongest for incidence with k vector along the helix axis, as would be expected since both the helix of the structure and of the circularly polarised light overlap. Perhaps less intuitively, incidence normal to the helix axis also yields intense circular dichroism, and reverses its sign. Interestingly, the circular dichroism vanishes at θ = ±π/4 for this helix; at such angles, the “ribbon” of nanospheres upon which the (idealised) structure is built appears locally as a square array, and the near-neighbour electromagnetic couplings are therefore achiral.
Because GoldHelix clusters are quite long (∼470 nm in this example) and have only few particles breaking the rotational symmetry at both ends, the variation with azimuth is much less pronounced, and the differential angular response is relatively independent of φ. We can perform the same spherical harmonic decomposition as described above for the dimer, with the results shown in ESI† Fig. S4. The spherical harmonic coefficients decay less rapidly, and the larger GoldHelix would typically require a degree l ≈ 10 to capture most of the angular pattern. In terms of numerical orientation-averaging, optimal cubature methods such as Lebedev cubature would require 40 to 50 points to integrate exactly spherical harmonics of degree 10,59 justifying the relative difficulty in estimating numerically the orientation average for the coupled-dipole simulations in ref. 61. We note that the T-matrix framework offers clear advantages for this type of situation, where access to the analytical result for orientation-averaged optical properties provides a rigorous benchmark to assess the accuracy of numerical cubature methods. A detailed comparison of the performance of different cubature methods for light scattering calculations is however beyond the scope of this work, and will be presented elsewhere.
4 Local degree of chirality: Si nanospheres
Our last example moves away from plasmonic nanoparticles and considers instead silicon dielectric spheres. With a relatively high refractive index,67 silicon nanoparticles have recently attracted attention for their ability to sustain intense electric and magnetic resonances in the visible-near-IR region.68,69 Of particular interest in the context of chiroptical properties is the recent realisation that such scatterers can conserve light's helicity31 in the vicinity of the Kerker condition (electric and magnetic dipole coefficients of equal magnitude). This property leads to locally-enhanced near-fields at resonance without change in handedness, that would otherwise compromise or lessen the amplification of signals for chiroptical spectroscopies of molecular adsorbates.70 We focus here on a near-field quantity, namely the local degree of optical chirality![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ∝ ℑ (E*·B), with E, B the complex electric and magnetic fields. In the plots below we display
∝ ℑ (E*·B), with E, B the complex electric and magnetic fields. In the plots below we display 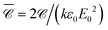 , normalised with respect to the value of circularly-polarised plane waves with incident field E0. The quantity
, normalised with respect to the value of circularly-polarised plane waves with incident field E0. The quantity 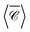 denotes the orientation-average of
denotes the orientation-average of 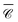 with respect to the direction of incident light.46
with respect to the direction of incident light.46
We assess the angular dependence of the local degree of optical chirality at small distances from a dimer of Si nanospheres (radius r = 150 nm and gap = 10 nm), where multipolar modes can play an important role in the optical spectrum. Fig. 5(a) presents the normalised optical chirality 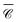 at position P1 in the gap. The results are shown for two perpendicular incident directions, kx
at position P1 in the gap. The results are shown for two perpendicular incident directions, kx![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ky and kz, from which we compute the numerical average over three perpendicular incident directions (dash-dotted black line), to contrast with the analytical orientation-averaged result
ky and kz, from which we compute the numerical average over three perpendicular incident directions (dash-dotted black line), to contrast with the analytical orientation-averaged result 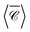 (solid black line). These calculations used a maximum multipolar order lmax = 12 in the T-matrix method, sufficient to capture the role of higher order modes. Although the average over three perpendicular incident directions is relatively similar to
(solid black line). These calculations used a maximum multipolar order lmax = 12 in the T-matrix method, sufficient to capture the role of higher order modes. Although the average over three perpendicular incident directions is relatively similar to 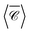 at lower energies, where the dimer's response is dominated by dipolar electric and magnetic resonances, at higher energies there is a noticeable difference. In fact, the sign of the averaged
at lower energies, where the dimer's response is dominated by dipolar electric and magnetic resonances, at higher energies there is a noticeable difference. In fact, the sign of the averaged 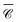 and
and 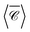 is different at the shorter wavelengths. The interaction between quadrupoles and other higher order modes in the Si nanospheres results in a distinct sharp peak with a Fano resonance lineshape at λ = 816 nm, excited when the incident wave vector is perpendicular to the main axis of the dimer (kx
is different at the shorter wavelengths. The interaction between quadrupoles and other higher order modes in the Si nanospheres results in a distinct sharp peak with a Fano resonance lineshape at λ = 816 nm, excited when the incident wave vector is perpendicular to the main axis of the dimer (kx![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ky). Although it is often the case that dielectric nanoparticles preserve the sign of the helicity of the incident wave, this is not observed here in this spectral region.
ky). Although it is often the case that dielectric nanoparticles preserve the sign of the helicity of the incident wave, this is not observed here in this spectral region.
It is the case, however, for a dimer or indeed any arrangement of such scatterers, that the helicity of incident light is preserved in the scattering process31,71 near the Kerker condition.72–74 This is apparent in the map of 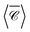 at λ = 1175 nm, where only negative values appear (Fig. 5b; the Kerker condition is at λ = 1208 nm, see ESI† Fig. S5). Molecules adsorbed anywhere on the surface of this particle cluster will experience an enhanced degree of local optical activity, compared to the value (−1) corresponding to the excitation in free-space by a right circularly-polarised plane wave. In contrast, a similar dimer with plasmonic particles would typically show a spatial distribution of peaks of positive and negative signs, weakening the spatial average for analytes uniformly adsorbed on the particle surfaces.46 Remarkably,
at λ = 1175 nm, where only negative values appear (Fig. 5b; the Kerker condition is at λ = 1208 nm, see ESI† Fig. S5). Molecules adsorbed anywhere on the surface of this particle cluster will experience an enhanced degree of local optical activity, compared to the value (−1) corresponding to the excitation in free-space by a right circularly-polarised plane wave. In contrast, a similar dimer with plasmonic particles would typically show a spatial distribution of peaks of positive and negative signs, weakening the spatial average for analytes uniformly adsorbed on the particle surfaces.46 Remarkably, 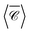 is enhanced by a factor ∼44 in the gap between nanospheres, compared to the incident plane wave. This enhancement reaches ∼75 times for the fixed incident direction along kx
is enhanced by a factor ∼44 in the gap between nanospheres, compared to the incident plane wave. This enhancement reaches ∼75 times for the fixed incident direction along kx![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ky. Si dimers are therefore a good candidate for producing superchiral fields of use in surface-enhanced spectroscopy of chiral molecules.31,37
ky. Si dimers are therefore a good candidate for producing superchiral fields of use in surface-enhanced spectroscopy of chiral molecules.31,37
The Si dimer, much like the Au dimer presented above, presents a relatively smooth angular dependence, due to its compactness. There is however a richer spectral signature due to the excitation of higher-order resonances. For our last example, we consider a recently-proposed variation on the dimer of dielectric resonators, in the form of a long chain of Si nanospheres (Fig. 5(c) with N = 50, in our case, but longer chains have been studied). This provides a realistic example of an extended, one-dimensional structure,31 bridging the regimes of compact, solution-based clusters, and of more extended structures obtained by top-down lithography. Periodic chains (or arrays) of resonant particles have received a lot of attention in the context of plasmonics and meta-surfaces, notably for their ability to support intense resonances when the periodicity of the chain is commensurate with the light wavelength. This occurs with the coherent superposition of scattering events at each particle along the chain, i.e. the condition for a grazing diffraction order. In this regime, the particles can be strongly coupled over very large distances despite their wide separation, and sustain a highly-delocalised mode. The inter-particle distance is here chosen to coincide with the Kerker condition (λ = 1208 nm), to combine the benefits of field enhancement and helicity preservation.31
The elongated GoldHelix structure already illustrated that as a cluster structure extends in an anisotropic way, along at least one direction, the collective optical response becomes more dependent on the incidence direction. This can be understood from the perspective of a multipolar expansion, as used in the superposition T-matrix framework.44,47 Placing the origin of coordinates somewhere near the centre of mass of the particle cluster, the description of the scattered field from the cluster as a whole requires higher multipole orders as the size parameter of the cluster increases, that is, the wavenumber times the radius of the cluster's circumscribed sphere. In turn, higher multipole orders are associated with higher frequencies in the angular pattern of the scattered field, and, by optical reciprocity, of the incident field causing the local enhancement 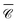 or the far-field response.
or the far-field response.
Fig. 5(f) depicts the chain with 50 Si nanospheres along the z axis, with separation d = 1208 nm; the degree of optical chirality 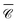 and
and 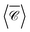 is calculated for an off-axis point P2 placed at θ = π/3 and 5 nm away of the middle particle's surface (Fig. 5(c)). The Si chain yields a maximum value of optical chirality
is calculated for an off-axis point P2 placed at θ = π/3 and 5 nm away of the middle particle's surface (Fig. 5(c)). The Si chain yields a maximum value of optical chirality ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) at λ = 1156 nm and λ = 1134 nm for incident directions along kz and kx
at λ = 1156 nm and λ = 1134 nm for incident directions along kz and kx![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ky. We note that for this chain, the peak of the
ky. We note that for this chain, the peak of the ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) spectrum is mainly a result of the interaction between electric and magnetic dipoles induced in the particles, with negligible influence of higher order modes. Remarkably, there is a clear difference between the maximum value of
spectrum is mainly a result of the interaction between electric and magnetic dipoles induced in the particles, with negligible influence of higher order modes. Remarkably, there is a clear difference between the maximum value of 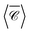 and the average over three perpendicular incident directions. One might have expected that the orientation-averaged spectrum should fall somewhere between the three perpendicular incident directions (x, y, z), yet here
and the average over three perpendicular incident directions. One might have expected that the orientation-averaged spectrum should fall somewhere between the three perpendicular incident directions (x, y, z), yet here 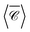 is in a different range altogether. To better understand this counter-intuitive result, we present in Fig. 5(d) a 2D map of
is in a different range altogether. To better understand this counter-intuitive result, we present in Fig. 5(d) a 2D map of 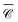 versus wavelength and polar angle θ, i.e. a dispersion plot. Note that for this map we chose a position P3 along the z axis so that
versus wavelength and polar angle θ, i.e. a dispersion plot. Note that for this map we chose a position P3 along the z axis so that 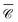 is independent of φ, for simplicity. Varying the incident direction θ near the normal θ ∼ π/2, the diffractive mode moves very rapidly with angle and the strong value of
is independent of φ, for simplicity. Varying the incident direction θ near the normal θ ∼ π/2, the diffractive mode moves very rapidly with angle and the strong value of 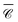 associated with it is not well captured in the three directions x, y, z.
associated with it is not well captured in the three directions x, y, z.
5 Conclusions
Although the angular dispersion of electromagnetic resonances is ubiquitous in the field of metamaterials, metasurfaces and photonics in general, it is much less often discussed or studied in compact clusters of nanoparticles, such as those self-assembled by chemical methods. Such clusters may be characterised in solution – in which case the optical properties are typically averaged over all possible orientations over the duration of a measurement –, or probed over a finite solid angle of illumination, if immobilised on a substrate, as in many microscopy techniques such as dark-field spectroscopy. For very small clusters, the common assumption that the orientation-averaged response can be obtained by averaging the response along x, y, z axes is generally valid, though the average may still hide some dramatic variation between the three cases. This is particularly clear for chiroptical properties such as circular dichroism, where the typically minute difference in scattering or absorption between left and right polarisations is very sensitive to the exact phase and polarisation relationships between the neighbouring particles and the incident field. As the cluster size grows, in comparison to the wavelength, a larger number of multipolar components is required to describe the optical response of the ensemble, seen as a single composite scatterer; in turn, these higher order components are associated with spherical harmonics of increasing degree and therefore angular frequencies. This leads to more complex angular patterns, as we illustrated for the case of a wavelength-sized helical structure. Finally, as the structure extends even further, the angular response can show sharply peaked angular features associated with electromagnetic modes of well-defined momentum. We illustrate this effect with a long chain of Si nanoparticles supporting a diffractive mode, where the excitation of the mode at specific phase-matching conditions leads to an enhanced optical response, here the local degree of optical chirality.This brief selection of examples should illustrate the importance of considering orientation dependence in the characterisation and modelling of clusters of nanoparticles, even those fabricated by bottom-up synthesis routes. Often, the numerical simulation methods can discourage the comprehensive study of this angular response, as the time-consuming calculations need to be repeated for many angles of incidence, but we hope our benchmark results on select configurations provide a useful guide for the study of similar geometries. Similarly, with experiments on immobilised clusters using a restricted angular range of illumination, the characterisation of chiroptical properties can easily become misleading due to extrinsic optical activity, i.e. a differential response to left and right polarisations induced by the specific direction of the incident wave vector. Unlike other optical properties such as field enhancement, scattering or absorption, with chiroptical properties the measured response in such situations may not only have a different magnitude, compared to the orientation-averaged response, it can even have the opposite sign altogether.
Author contributions
All authors contributed to the design of the study, to the numerical simulations, and to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Dmitri Schebarchov and Eric Le Ru for helpful discussions, the Royal Society Te Apārangi for support through a Rutherford Discovery Fellowship (B. A., Grant number RDF-VUW1603), and the MacDiarmid Institute for additional funding (A. F. N.).Notes and references
- A. D. McFarland and R. P. Van Duyne, Nano Lett., 2003, 3, 1057–1062 CrossRef CAS.
- Y. Saylan, S. Akgönüllü and A. Denizli, Biosensors, 2020, 10, 142 CrossRef CAS PubMed.
- S. Kasani, K. Curtin and N. Wu, Nanophotonics, 2019, 8, 2065–2089 CAS.
- F. Neubrech, M. Hentschel and N. Liu, Adv. Mater., 2020, 32, 1905640 CrossRef CAS PubMed.
- E. C. Le Ru and P. Etchegoin, Principles of Surface-Enhanced Raman Spectroscopy: and related plasmonic effects, Elsevier, 2009 Search PubMed.
- N. Maccaferri, G. Barbillon, A. N. Koya, G. Lu, G. P. Acuna and D. Garoli, Nanoscale Adv., 2021, 3, 633–642 RSC.
- K. G. Stamplecoskie, J. C. Scaiano, V. S. Tiwari and H. Anis, J. Phys. Chem. C, 2011, 115, 1403–1409 CrossRef CAS.
- A. J. Haes, C. L. Haynes, A. D. McFarland, G. C. Schatz, R. P. Van Duyne and S. Zou, MRS Bull., 2005, 30, 368–375 CrossRef CAS.
- L. Novotny and B. Hecht, Principles of nano-optics, Cambridge University Press, 2012 Search PubMed.
- S. Lal, S. Link and N. J. Halas, Nanosci. Technol., 2010, 213–220 Search PubMed.
- V. Sandoghdar, Nano Lett., 2020, 20, 4721–4723 CrossRef CAS PubMed.
- S. Carretero-Palacios, A. Jiménez-Solano and H. Mguez, ACS Energy Lett., 2016, 1, 323–331 CrossRef CAS PubMed.
- A. Djorovic, S. J. Oldenburg, J. Grand and E. C. Le Ru, ACS Nano, 2020, 14, 17597–17605 CrossRef CAS PubMed.
- A. O. Govorov, Y. K. Gun'ko, J. M. Slocik, V. A. Gérard, Z. Fan and R. R. Naik, J. Mater. Chem., 2011, 21, 16806–16818 RSC.
- A. Guerrero-Martínez, J. L. Alonso-Gómez, B. Auguié, M. M. Cid and L. M. Liz-Marzán, Nano Today, 2011, 6, 381–400 CrossRef.
- Z. Fan, H. Zhang and A. O. Govorov, J. Phys. Chem. C, 2013, 117, 14770–14777 CrossRef CAS.
- X. Lan, X. Lu, C. Shen, Y. Ke, W. Ni and Q. Wang, J. Am. Chem. Soc., 2015, 137, 457–462 CrossRef CAS PubMed.
- W. Yan, L. Xu, C. Xu, W. Ma, H. Kuang, L. Wang and N. A. Kotov, J. Am. Chem. Soc., 2012, 134, 15114–15121 CrossRef CAS PubMed.
- A. Kuzyk, R. Schreiber, Z. Fan, G. Pardatscher, E.-M. Roller, A. Högele, F. C. Simmel, A. O. Govorov and T. Liedl, Nature, 2012, 483, 311–314 CrossRef CAS PubMed.
- X. Shen, C. Song, J. Wang, D. Shi, Z. Wang, N. Liu and B. Ding, J. Am. Chem. Soc., 2012, 134, 146–149 CrossRef CAS PubMed.
- S. H. Jung, J. Jeon, H. Kim, J. Jaworski and J. H. Jung, J. Am. Chem. Soc., 2014, 136, 6446–6452 CrossRef CAS PubMed.
- B. Auguié, J. L. Alonso-Gómez, A. Guerrero-Martnez and L. M. Liz-Marzán, J. Phys. Chem. Lett., 2011, 2, 846–851 CrossRef PubMed.
- X. Yin, M. Schäferling, B. Metzger and H. Giessen, Nano Lett., 2013, 13, 6238–6243 CrossRef CAS PubMed.
- A. F. Najafabadi and T. Pakizeh, ACS Photonics, 2017, 4, 1447–1452 CrossRef CAS.
- X. Lan, Z. Chen, G. Dai, X. Lu, W. Ni and Q. Wang, J. Am. Chem. Soc., 2013, 135, 11441–11444 CrossRef CAS PubMed.
- Y. Zhao, A. N. Askarpour, L. Sun, J. Shi, X. Li and A. Alù, Nat. Commun., 2017, 8, 1–8 CrossRef CAS PubMed.
- X. Yin, M. Schäferling, A.-K. U. Michel, A. Tittl, M. Wuttig, T. Taubner and H. Giessen, Nano Lett., 2015, 15, 4255–4260 CrossRef CAS PubMed.
- Q. Jiang, Q. Liu, Y. Shi, Z.-G. Wang, P. Zhan, J. Liu, C. Liu, H. Wang, X. Shi and L. Zhang, et al. , Nano Lett., 2017, 17, 7125–7130 CrossRef CAS PubMed.
- C. Zhou, X. Duan and N. Liu, Nat. Commun., 2015, 6, 1–6 Search PubMed.
- W. Ma, H. Kuang, L. Wang, L. Xu, W.-S. Chang, H. Zhang, M. Sun, Y. Zhu, Y. Zhao and L. Liu, et al. , Sci. Rep., 2013, 3, 1–6 Search PubMed.
- J. Lasa-Alonso, D. R. Abujetas, Á. Nodar, J. A. Dionne, J. J. Sáenz, G. Molina-Terriza, J. Aizpurua and A. Garca-Etxarri, ACS Photonics, 2020, 7, 2978–2986 CrossRef CAS.
- M. Hentschel, M. Schäferling, T. Weiss, N. Liu and H. Giessen, Nano Lett., 2012, 12, 2542–2547 CrossRef CAS PubMed.
- J. A. Bordley, N. Hooshmand and M. A. El-Sayed, Nano Lett., 2015, 15, 3391–3397 CrossRef CAS PubMed.
- N. Berova, Comprehensive chiroptical spectroscopy, Wiley, 2012 Search PubMed.
- L.-Y. Wang, K. W. Smith, S. Dominguez-Medina, N. Moody, J. M. Olson, H. Zhang, W.-S. Chang, N. Kotov and S. Link, ACS Photonics, 2015, 2, 1602–1610 CrossRef CAS.
- W. Ma, H. Kuang, L. Xu, L. Ding, C. Xu, L. Wang and N. A. Kotov, Nat. Commun., 2013, 4, 1–8 Search PubMed.
- Y. Tang and A. E. Cohen, Phys. Rev. Lett., 2010, 104, 163901 CrossRef PubMed.
- E. Severoni, S. Maniappan, L. M. Liz-Marzan, J. Kumar, F. J. Garca de Abajo and L. Galantini, ACS Nano, 2020, 14, 16712–16722 CrossRef CAS PubMed.
- J. Garcia-Guirado, M. Svedendahl, J. Puigdollers and R. Quidant, Nano Lett., 2019, 20, 585–591 CrossRef PubMed.
- M. I. Mishchenko, L. D. Travis and A. A. Lacis, Scattering, absorption, and emission of light by small particles, Cambridge University Press, 2002 Search PubMed.
- O. Avalos-Ovando, L. V. Besteiro, A. Movsesyan, G. Markovich, T. Liedl, K. Martens, Z. Wang, M. A. Correa-Duarte and A. O. Govorov, Nano Lett., 2021, 21, 7298–7308 CrossRef CAS PubMed.
- Y.-l. Xu and N. G. Khlebtsov, J. Quant. Spectrosc. Radiat. Transfer, 2003, 79, 1121–1137 CrossRef.
- Z. Fan and A. O. Govorov, Nano Lett., 2012, 12, 3283–3289 CrossRef CAS PubMed.
- B. Stout, J.-C. Auger and J. Lafait, J. Mod. Opt., 2002, 49, 2129–2152 CrossRef.
- D. Schebarchov, E. C. Le Ru, J. Grand and B. Augui'e, Opt. Express, 2019, 27, 35750–35760 CrossRef CAS PubMed.
- A. Fazel-Najafabadi, S. Schuster and B. Auguié, Phys. Rev. B, 2021, 103, 115405 CrossRef CAS.
- D. W. Mackowski, J. Opt. Soc. Am. A, 1994, 11, 2851–2861 CrossRef.
- A. J. Mastroianni, S. A. Claridge and A. P. Alivisatos, J. Am. Chem. Soc., 2009, 131, 8455–8459 CrossRef CAS PubMed.
- J. Pérez-Juste, I. Pastoriza-Santos, L. M. Liz-Marzán and P. Mulvaney, Coord. Chem. Rev., 2005, 249, 1870–1901 CrossRef.
- W. R. C. Somerville, B. Augui’e and E. C. Le Ru, J. Quant. Spectrosc. Radiat. Transfer, 2016, 174, 39–55 CrossRef CAS.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, John Wiley & Sons, 2008 Search PubMed.
- C. de Dios, A. Jiménez, F. García, A. García-Martín, A. Cebollada and G. Armelles, Opt. Express, 2019, 27, 21142–21152 CrossRef CAS PubMed.
- M. A. Kuntman, E. Kuntman, J. Sancho-Parramon and O. Arteaga, Phys. Rev. B, 2018, 98, 045410 CrossRef CAS.
- L.-Y. Wang, K. W. Smith, S. Dominguez-Medina, N. Moody, J. M. Olson, H. Zhang, W.-S. Chang, N. Kotov and S. Link, ACS Photonics, 2015, 2, 1602–1610 CrossRef CAS.
- Y. Qu, Y. Zhang, F. Wang, H. Li, H. Ullah, T. Aba, Y. Wang, T. Fu and Z. Zhang, Ann. Phys., 2018, 530, 1800142 CrossRef.
- N. Harada, Y. Takuma and H. Uda, J. Am. Chem. Soc., 1978, 100, 4029–4036 CrossRef CAS.
- Chebfun Guide, ed. T. A. Driscoll, N. Hale and L. N. Trefethen, Pafnuty Publications, 2014 Search PubMed.
- 2019, https://www.chebfun.org/examples/sphere/SphericalHarmonics.html.
- A. Penttilä and K. Lumme, J. Quant. Spectrosc. Radiat. Transfer, 2011, 112, 1741–1746 CrossRef.
- V. I. Lebedev, USSR Computat. Mathemat. Mathemat. Phys., 1976, 16, 10–24 CrossRef.
- J. Cheng, G. Le Saux, J. Gao, T. Buffeteau, Y. Battie, P. Barois, V. Ponsinet, M.-H. Delville, O. Ersen and E. Pouget, et al. , ACS Nano, 2017, 11, 3806–3818 CrossRef CAS PubMed.
- M. Hentschel, D. Dregely, R. Vogelgesang, H. Giessen and N. Liu, ACS Nano, 2011, 5, 2042–2050 CrossRef CAS PubMed.
- Z. Fan and A. O. Govorov, J. Phys. Chem. C, 2011, 115, 13254–13261 CrossRef CAS.
- J. Applequist, K. R. Sundberg, M. L. Olson and L. C. Weiss, J. Chem. Phys., 1979, 70, 1240 CrossRef CAS.
- C. Song, M. G. Blaber, G. Zhao, P. Zhang, H. C. Fry, G. C. Schatz and N. L. Rosi, Nano Lett., 2013, 13, 3256–3261 CrossRef CAS PubMed.
- X. Lan, T. Liu, Z. Wang, A. O. Govorov, H. Yan and Y. Liu, J. Am. Chem. Soc., 2018, 140, 11763–11770 CrossRef CAS PubMed.
- E. D. Palik, Handbook of optical constants of solids, Academic Press, 1998, vol. 3 Search PubMed.
- A. B. Evlyukhin, S. M. Novikov, U. Zywietz, R. L. Eriksen, C. Reinhardt, S. I. Bozhevolnyi and B. N. Chichkov, Nano Lett., 2012, 12, 3749–3755 CrossRef CAS PubMed.
- A. B. Evlyukhin, C. Reinhardt and B. N. Chichkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235429 CrossRef.
- L. V. Poulikakos, J. A. Dionne and A. Garca-Etxarri, Symmetry, 2019, 11, 2073–8994 CrossRef.
- M. Hanifeh and F. Capolino, J. Appl. Phys., 2020, 127, 093104 CrossRef CAS.
- M. Kerker, D.-S. Wang and C. Giles, J. Opt. Soc. Am., 1983, 73, 765–767 CrossRef.
- M. Nieto-Vesperinas, R. Gomez-Medina and J. Saenz, J. Opt. Soc. Am. A, 2011, 28, 54–60 CrossRef CAS PubMed.
- X. Zambrana-Puyalto, I. Fernandez-Corbaton, M. Juan, X. Vidal and G. Molina-Terriza, Opt. Lett., 2013, 38, 1857–1859 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional numerical simulations. See DOI: 10.1039/d1ma00869b |
| This journal is © The Royal Society of Chemistry 2022 |