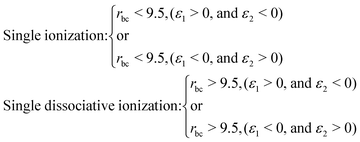Dissociative ionization of the H2 molecule under a strong elliptically polarized laser field: carrier-envelope phase and orientation effect
Gaurav
Pandey
 ,
Sandip
Ghosh
,
Sandip
Ghosh
 and
Ashwani K.
Tiwari
and
Ashwani K.
Tiwari
 *
*
Indian Institute of Science Education and Research Kolkata, Mohanpur 741246, India. E-mail: ashwani@iiserkol.ac.in
First published on 4th October 2022
Abstract
A coupled electron–nuclear dynamical study is performed to investigate the sub-cycle dissociation and ionization of the H2 molecule in a strong 750 nm 4.5 fs elliptically polarized laser pulse. A quasi-classical method is employed in which additional momentum-dependent potentials are added to the molecular Hamiltonian to account for the non-classical effects. The effect of molecular orientation with respect to the laser polarization plane on the probabilities of different dynamical channels and proton energy spectra has been examined. We demonstrate the 2D-control of proton anisotropy by manipulating the carrier-envelope phase of the pulse. We demonstrate that the quasi-classical method can capture the carrier-envelope phase effects in the dissociative ionization of the H2 molecule. Our results indicate that the classical models provide an efficient approach to study the mechanistic insights of strong-field molecular dynamics.
1 Introduction
Directly controlling electronic and nuclear motion on their natural timescales is the most fundamental way of manipulating the outcome of a chemical reaction. With the rapid advancement in optical technologies, it is now possible to generate ultrashort intense laser pulses, which are being used to guide the motion of electrons and nuclei in atomic and molecular systems.1–6 When an intense laser pulse interacts with a molecular system, the molecule experiences an external force comparable to the Coulombic force between a bound electron and the nuclear core. These laser pulses with enormous field strength change the electronic structure of the molecular system, which ultimately guides the nuclear dynamics. An ultrashort intense laser pulse initiates several non-linear strong-field processes, such as high-harmonic generation (HHG),7 above-threshold ionization (ATI),8 bond-softening (BS),9 bond-hardening (BH),10 above-threshold dissociation (ATD),11etc. Investigating such complex dynamics in molecules is challenging, both experimentally and theoretically, because of the inclusion of the various degrees of freedom of different timescales, viz., rotational, vibrational and electronic, which occur on picosecond (10−12 seconds), femtosecond (10−15 seconds) and attosecond (10−18 seconds) timescales, respectively. The hydrogen molecule and its ionic companion serve as benchmark molecular systems to understand the complex strong-field processes at the fundamental level.12–20 Various experimental parameters are used to control the electronic and nuclear dynamics in these simple molecular systems in real time, such as peak intensity of the laser pulse, polarization, relative phase between the two-color laser pulses, pulse duration, chirp, wavelength, etc.12,15,21,22 In molecules, the dynamics of the nuclei follow the slower-moving pulse envelope, whereas the electrons follow the rapidly oscillating electric field under the envelope. Therefore, by tuning the shape of the oscillatory electric field under the pulse envelope, it is possible to control the electronic motion with subfemtosecond temporal resolution. The shape of the electric field in a pulse is controlled by the phase offset between the maxima of the pulse envelope and the maxima of the carrier electric field. This phase offset is termed as the carrier-envelope phase (CEP) of the pulse, which determines the instantaneous field strength of the laser pulse. The CEP of the pulse has been widely used in the study of ionization and dissociation dynamics of molecules.12,23–26 CEP-controlled experiments allow steering of the attosecond electronic wavepacket in molecules because the CEP of the laser pulse controls the electric field with attosecond precision. For example, Kling and co-workers observed CEP-dependent asymmetry in the fragment (D+) ejection from the dissociative ionization of D2 exposed to a linearly polarized pulse.12 The effect of the CEP is strongly dependent on the peak intensity and pulse duration of the laser pulse and, therefore, these parameters should be optimized to achieve a high degree of control. Experiments performed on the neutral H2 molecule and on the molecular ion H2+ suggest that the first ionization step of neutral H2 is highly dependent on the CEP, which, in turn, affects the localization of the remaining electron.25 The orientation of the molecule is another important parameter in the observation of CEP-dependent control of the electronic wavepacket. In the linearly polarized laser pulse, the most suitable condition that demonstrates a large CEP dependency of the observable is when the H2 molecule is parallel to the laser polarization axis, which induces the 1sσ+g → 2pσ−u transition.24The majority of the CEP-controlled experiments are performed on the neutral hydrogen molecule, whereas theoretical studies take H2+ as the starting target. From the theoretical perspective, the challenge in treating the neutral hydrogen molecule is the first ionization step, which creates a H2+ nuclear wavepacket with coherent superposition of vibrational states in the 1sσ+g electronic state.25,27,28 Another intractable problem in directly treating the neutral H2 molecule is the electron correlation. Of course, to understand and simulate the strong-field non-perturbative processes of the laser-induced H2 molecule, a full quantum mechanical treatment is needed. When the H2 molecule is irradiated with a strong laser field, both the ionization and dissociation processes occur simultaneously. In such a case, the potential of the molecule gets highly perturbed, which results in the coupling of the electronic and nuclear dynamics. Because of the coupling, the Born–Oppenheimer approximation becomes invalid and, therefore, coupled evolution of the electronic and nuclear wavepackets becomes an absolute necessity. Progress has been made in this direction, however, solving the full-dimensional time-dependent Schrödinger equation for the H2 molecule is still very expensive from the computational point of view. In the past few years, classical methods have been widely used to study and interpret the strong-field photo-induced dynamics of atoms and molecules.29–35 Classical methods acquire several advantages over quantum mechanical methods, because taking electron correlation into account during the complete course of the reaction is easier with classical methods than with quantum mechanical methods. Additionally, solving the classical coupled Hamilton's equations of motion, which are ordinary differential equations, for a large number of interacting particles is easier than solving the partial differential equations found in the time-dependent Schrödinger equation. On the other hand, the interpretation and calculation of observables from the classical trajectories are more straightforward than from the quantum dynamical ones. Moreover, in the classical trajectories, different reaction channels can be easily identified by the back analysis of individual trajectories, where the probability of a reaction channel can be calculated by comparing the number of trajectories of a specific channel with the total number of trajectories evolved. It is noteworthy that in the classical methods, the individual trajectories are independent of each other, which allows easy parallelization of the large number of trajectories for many-particle systems.
Although there are some detailed experiments on the influence of an ultrashort elliptical laser pulse on the dynamics of the H2 molecule,36,37 there are no detailed theoretical calculations on the molecule. A quasi-classical model based on the Heisenberg’s model potentials has been employed to perform a full-dimensional coupled electron–nuclear dynamics study of the H2 molecule, where both the dissociation and ionization processes are treated on an equal footing. Different dynamical channels have been identified and the effect of molecular orientation on their probability with respect to the laser polarization plane has been elucidated. The effects of the CEP on the dissociative ionization probability and on the two-dimensional proton momentum distribution have been demonstrated. Since the CEP dependence is based on the interference of different quantum paths, we have addressed whether it is possible to capture an interference effect within the quasi-classical framework.
2 Theoretical model and simulation details
A well-established quasi-classical model38,39 has been employed to simulate the coupled electron–nuclear dynamics of the H2 molecule, where both the nuclei and the electrons are treated as point particles. All the particles are allowed to move freely in a three-dimensional phase space. Since the classical molecule is dynamically unstable against auto-ionization and pre-dissociation, additional momentum dependent auxiliary potentials are incorporated between the electrons and nuclei to stabilize the molecule. The present quasi-classical model differs from the conventional classical methods by the fact that, in the present model, the added potentials depend on the momentum of the particles, whereas, in other classical based methods, the potential energy of the system depends on the position of the particle. The auxiliary potentials were first introduced by Kirschbaum and Wilets40,41 and later, further developments were carried out by Cohen.42 The model has been used extensively to study laser-driven atomic and molecular processes,38,43–47 as well as atom–ion collision processes.48The field-free Hamiltonian of the H2 molecule in the quasi-classical model is given by eqn (1) (atomic units are used throughout unless stated otherwise):
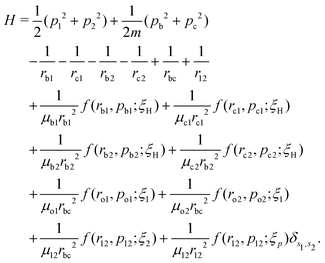 | (1) |
The labels b and c stand for the two protons, 1 and 2 stand for the first and second electron, respectively, and the mid-point between the two protons is represented by o. The positions and the canonical momenta of the particles are denoted by ri and pi, respectively, where i is any one of b, c, 1 and 2. For any pair of b, c, 1 and 2, the relative distance is
| rij = ri − rj, | (2) |
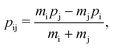 | (3) |
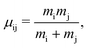 | (4) |
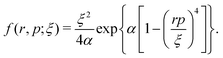 | (5) |
The dynamics of the system are performed by numerically solving the coupled Hamilton's equations of motion for all the four particles
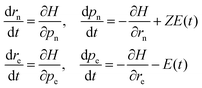 | (6) |
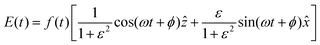 | (7) |
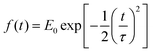 is the pulse envelope with
is the pulse envelope with 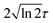 FWHM pulse duration. A laser pulse of 750 nm wavelength, 4.5 fs FWHM pulse duration and ellipticity of ε = 0.85 was chosen in the present study. The carrier-envelope phase of the pulse is denoted by ϕ. The same pulse was used in a previous experimental study.36
FWHM pulse duration. A laser pulse of 750 nm wavelength, 4.5 fs FWHM pulse duration and ellipticity of ε = 0.85 was chosen in the present study. The carrier-envelope phase of the pulse is denoted by ϕ. The same pulse was used in a previous experimental study.36
A field-free trajectory was evolved for a sufficiently long time to ensure the stability of the molecule and was found to be stable in the absence of the laser field. The time evolution of the field-free energy of the molecule has been reported in our previous article.43 Finally, an ensemble of ∼105 molecules was generated and, thereafter, evolved in the presence of the laser field. The detailed procedure for sampling the initial conditions can be found elsewhere.43 Finally, the probabilities of the different channels are calculated by
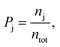 | (8) |
3 Results and discussion
Before moving to the results, it is important to point out the applicability of the current quasi-classical model. The model has been recently applied to study the double ionization of the H2 molecule under the influence of an ultrashort elliptically polarized laser pulse with the same laser parameters as used in the current study.43 The simulated results were compared with an experimental study.51 Suffice to say that the KER spectra of the double ionization channel, correlated photoelectron energy spectrum, position of the nuclear wavepacket, etc. were found to be in reasonably good agreement with the experimental measurements, which qualifies this model for its application in the present study.3.1 Identification of the dynamical channels
When an ultrashort intense laser pulse interacts with a molecule, various dynamical channels open up, including dissociation and ionization. In the quasi-classical picture, the H2 molecule is considered as a four-particle system, where, depending on such a four-particle picture, the following dynamical channels of the molecule are initiated during the interaction with the laser pulse,The definition of the dynamical channels in the quasi-classical model are given by:
| Survival: rbc < 9.5, ε1 < 0, and ε2 < 0 |
| Double ionization: rbc > 9.5, (ε1 > 0, and ε2 > 0) |
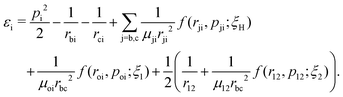 | (9) |
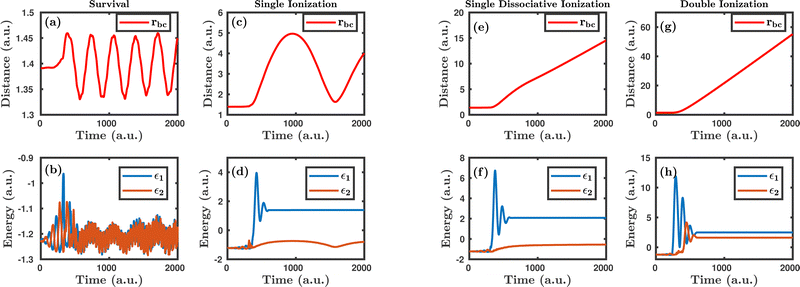
Fig. 1 shows the characteristic trajectories for the survival, single ionization, single dissociative ionization and double ionization channels. In the survival channel, the internuclear distance is oscillating about the equilibrium distance (1.4 a.u.) of the H2 molecule, which indicates that there is no dissociation (see Fig. 1a). On the other hand, the negative values of the corresponding single particle energy of both the electrons, as shown in Fig. 1b, suggest that both the electrons are bound and, thus, no ionization has occurred. Conversely, in the single ionization channel, the internuclear distance, as depicted in Fig. 1c, oscillates with a large amplitude, but does not reach the cut-off value of dissociation (∼9.5 a.u.), which clearly implies that the bond still survives. From Fig. 1d, it is noticeable that the corresponding single particle energy of one of the electrons (labeled 1) becomes positive, representing the ionization of the electron, but the other electron (labeled 2) is still bound to the molecule. It is also to be noted that the single particle energy profile of the bound electron (labeled 2) shows some fluctuation in between the time range of ∼0–500 a.u., possibly because of the shake-up excitation, where the ionization of the first electron leads to shaking up of the second electron to an excited bound state. Collectively, the trajectories in Fig. 1c and d dictate that one of the electrons in the H2 molecule ionizes in the presence of the laser field, creating a vibrationally excited H2+ molecular ion. In the single dissociative ionization channel, one of the electrons ionizes and the resulting H2+ molecular ion dissociates into H + H+. The trajectories shown in Fig. 1e and f represent the dissociation and the ionization of one electron, respectively. In the double ionization channel, both the electrons get ionized in the presence of the laser field, which is seemingly evident from Fig. 1h. Additionally, for this double ionization channel, the resulting H22+ ion undergoes a Coulomb explosion to form two protons, leading to the rapid increase of the internuclear distance, as displayed in Fig. 1g.
3.2 Intensity and orientation effect on the dynamical channels’ probabilities
First, we investigate the effect of the laser peak intensity on the temporal evolution of different dynamical channels. Two different orientations have been considered in our simulation. In the first case, the laser polarization plane is parallel to the molecular plane, and, in the other case, the laser polarization plane is perpendicular to the molecular plane. Fig. 2 shows the temporal evolution of the dynamical channels in the case of parallel orientation. The probability values shown in Fig. 2 are for CEP = 0° and demonstrate how different channels initiate during the interaction of the H2 molecule with the laser pulse. Firstly, the single ionization channel starts, in which an electron gets ionized by projecting the molecular wavepacket from the ground state of H2 to the ground electronic state of H2+. For the peak intensity of I = 1.0 × 1015 W cm−2, the ionization starts at ∼312 a.u., just after the peak of the pulse, which is at ∼300 a.u. (see Fig. 2a). As the peak intensity of the laser pulse increases (2.0 × 1015 W cm−2), the initiation of ionization shifts to an earlier time of ∼244 a.u., as expected (see Fig. 2b). The wavepacket associated with the molecular ion may possibly follow three pathways: (i) it remains in the potential well of H2+; (ii) it propagates in time along the 1sσ+g state of H2+, where, at larger internuclear separation, it can interfere with the first excited state 2pσ−u of H2+ and, as a result, initiates the single dissociative ionization channel (H++ H + e−); (iii) it absorbs more energy from the laser pulse and is excited to the Coulomb repulsive curve to initiate the double ionization channel (H++ H++ 2e−). At the lower peak intensity of the laser pulse (1.0 × 1015 W cm−2), only two channels, namely, single ionization and single dissociative ionization, exist at the end of the simulation, with probabilities of 0.26 and 0.30, respectively. As the peak intensity of the laser pulse increases (2.0 × 1015 W cm−2), the double ionization channel becomes a prominent dynamical channel. Note that double ionization of the molecule occurs by following the sequential double ionization mechanism. Qualitatively, it can be identified by observing the starting time of the single ionization (≈244 a.u.) and double ionization (≈588 a.u.) channels. After the first ionization channel, the second ionization channel starts with a delay of about 344 a.u. (8.3 fs), which points towards the sequential double ionization mechanism. Moreover, calculations have also been performed at the laser peak intensity of 0.8 × 1015 W cm−2 and the dissociation and ionization probabilities are found to be negligibly small and, therefore, not presented in the article.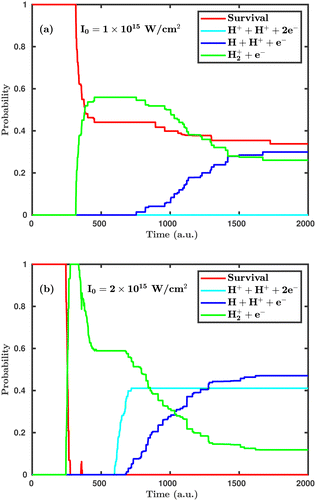 | ||
| Fig. 2 Temporal evolution of dynamical channels when the laser polarization plane is parallel to the molecular plane. (a) Peak intensity I = 1.0 × 1015 W cm−2, (b) I = 2.0 × 1015 W cm−2. | ||
Now, we turn to the perpendicular orientation, where the molecular plane is perpendicular to the laser polarization plane. Fig. 3 shows total probabilities for different dynamical channels in the case of perpendicular orientation, where the dissociation and ionization probabilities are highly enhanced. Even at the laser peak intensity of 0.8 × 1015 W cm−2, the double ionization channel is the dominant dynamical channel, which is found to be negligibly small in the case of parallel orientation. On increasing the laser peak intensity from 0.8 × 1015 to 1.0 × 1015 W cm−2, the final single dissociative ionization probability does not change, but the double ionization probability is increased by ∼10%. It may be noted that the average starting time of the single ionization channel is not much affected by the laser peak intensity, but the time delay between initiation of the single ionization and the double ionization channels is highly influenced. To be specific, at the laser peak intensity of 0.8 × 1015 W cm−2, the time delay between the initiation of the two channels is 158 a.u. (≈3.8 fs), whereas at the intensity of 1.0 × 1015 W cm−2, it remains only 62 a.u. (≈1.5 fs). This observation clearly indicates that, upon further increasing the laser peak intensity, such a time delay will gradually decrease and, thus, the ionization mechanism will change from sequential to instantaneous. A careful inspection of the channel probabilities for both parallel and perpendicular orientations seemingly reveals that the molecule responds more intensively in the case of the perpendicular orientation compared to the parallel orientation. Specifically, the ionization process is more sensitive to the orientation compared to the dissociation.
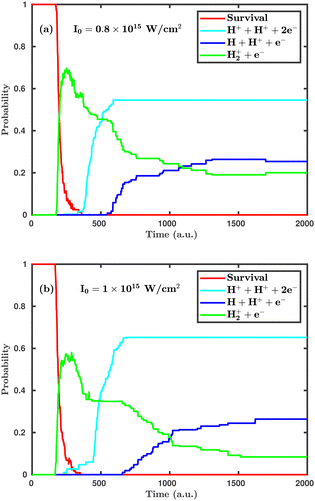 | ||
| Fig. 3 Temporal evolution of dynamical channels when the laser polarization plane is perpendicular to the molecular plane. (a) Peak intensity I = 0.8 × 1015 W cm−2, (b) I = 1.0 × 1015 W cm−2. | ||
3.3 The effect of carrier-envelope phase on single dissociative ionization probability
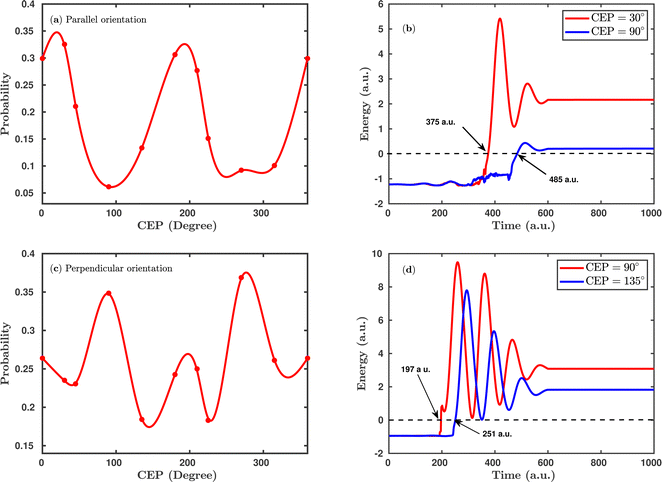
Since the carrier-envelope phase (CEP) of a laser pulse controls the instantaneous strength of the electric field under the pulse envelope, it significantly affects the outcome of the photo-induced process. Previous experimental and theoretical studies were mainly focused on the CEP effect on the proton ejection asymmetry for H2+ or H2 targets. The majority of the studies achieved a high degree of control over the asymmetry (∼30%) modulation, but a small degree of control is attained over the total dissociation probability by altering the CEP of the linearly polarized laser pulse.25 Here, we investigate the effect of the CEP on the single dissociative ionization (H2 + nħω → H + H+ + e−) probability using an elliptically polarized pulse, where such probabilities are calculated by the formula given in eqn (8).Fig. 4 shows the CEP-dependent probability of the single dissociative ionization channel at a laser peak intensity of 1 × 1015 W cm−2. In both the parallel and perpendicular orientations, the dissociation probability shows a strong dependence on the CEP of the elliptically polarized pulse. For the parallel orientation (see Fig. 4a), a four-fold enhancement of the dissociation probability is observed at the CEP values of ∼0°, 180° and 360° compared to that at CEP values of ∼90° and 270°. A similar CEP dependence on the dissociation probability has also been observed in a full quantum mechanical calculation.52 To understand the physical mechanism associated with the enhanced and suppressed dissociation probability at a specific range of CEP values, individual trajectories have been analyzed at some specific CEP values. After careful inspection of the trajectories, it has been found that the timing of the first ionization step (H2 + nħω → H2+) is responsible for the enhancement or suppression of the dissociation probability. Interestingly, at the CEP values where the dissociation probability is high, the ionization of H2 occurs significantly earlier compared to the CEP values where the dissociation probability is low. To validate this, the time evolution profiles of the single particle energy for the first ionized electron at the CEP values of 30° and 90°, one from the range where the dissociation probability is maximum (CEP = 30°) and the other from the range where the dissociation probability is minimum (CEP = 90°), are shown in Fig. 4b. For CEP = 30°, the first ionization step starts 2.66 fs earlier compared to the CEP = 90° case. Moreover, the final energy of the ionized electron is higher for the CEP value of 30°, which suggests that the molecular system is comparatively more perturbed at CEP = 30° than at 90° and, as a consequence, the dissociation probability is found to be enhanced at CEP = 30°. It is also noteworthy that the single particle energy of the ionized electron at CEP = 90° shows more fluctuations than that at CEP = 30°. It is known that the CEP of the laser pulse determines the shape of the electric field under the pulse envelope and thereby determines the instantaneous field strength of the pulse at the time of the N-photon transition from the ground state to the excited state. When the CEP of the laser pulse is 90°, the field strength along the molecular axis is smaller than that at CEP = 30°. Therefore, at CEP = 90°, the electron feels a lesser force from the laser pulse and does not ionize instantly, and this change in perturbation possibly leads to more fluctuations in the energy profile.
Interestingly, the CEP dependence on the dissociation probability gets reversed when the molecular plane is perpendicular to the laser polarization plane (see Fig. 4c). More precisely, for the perpendicular orientation at the CEP values of 90° and 270°, the dissociation probability is enhanced, whereas, in the parallel orientation, a suppressed dissociation probability is obtained at the same values of CEPs. On a similar note, a reverse trend is also observed around the CEP values of ∼0°, 180° and 360° for the perpendicular orientation compared to the parallel orientation. Similar to the parallel orientation case, for the CEP values corresponding to higher dissociation probabilities, the first ionization starts earlier than it does for the CEP values associated with low dissociation probabilities. For instance, at the CEP value of ∼90° for which the dissociation probability is high, the ionization of H2 occurs ∼54 a.u. (1.31 fs) earlier than for the CEP value of ∼135°, where the dissociation probability is low (see Fig. 4d). The results shown in Fig. 4 indicate that the CEP, as well as the orientation of the molecular plane with respect to the polarization plane, are both major controlling parameters for the dissociation probability of the H2 molecule in a few-cycle elliptically polarized laser pulse.
3.4 Proton kinetic energy release spectra in the single dissociative ionization channel
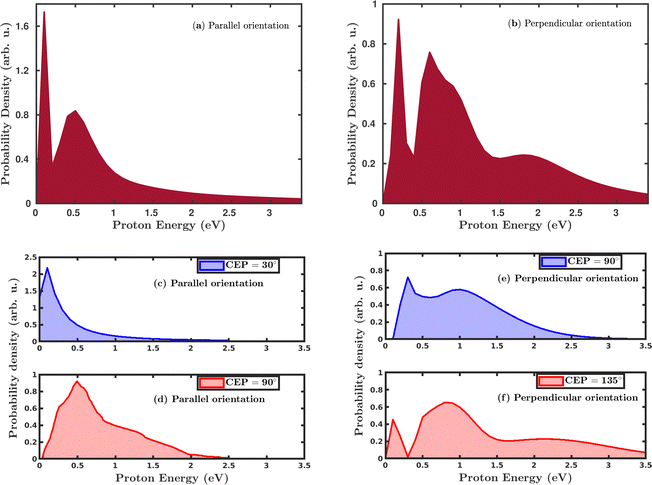
Quantum mechanically, in the single dissociative ionization channel, the H2 molecule gets ionized under the influence of the laser field and launches the H2+ wavepacket in the 1sσ+g state. Thereafter, the H2+ wavepacket propagates in time towards larger internuclear distances. At later times, the H2+ molecular ion dissociates due to the coupling between the 1sσ+g state and the repulsive 2pσ+u state, and produces H + H+ fragments. The kinetic energy of the produced proton is a readily measured quantity in the strong-field experiments and was used to investigate the dissociation mechanism of the H2+ molecular ion. We have calculated the proton kinetic energy in the single dissociative ionization channel to study the effects of molecular orientation and the CEP of the laser pulse. Fig. 5 shows the CEP-averaged proton kinetic energy spectra in the single dissociative ionization channel. In both the parallel and perpendicular orientation of the H2 molecule with respect to the polarization plane of the laser pulse, the proton kinetic energy spectra exhibit a double-peak structure, as shown in Fig. 5a and b, respectively. Indeed, the classically simulated proton kinetic energy spectra are in agreement with previous experimental studies.12,53 The double-peak structure of the proton kinetic energy spectra suggests that two different mechanisms are involved in the generation of the protons after the dissociation of H2+. The lower energy peak in both the parallel and perpendicular orientation cases is due to the well-known bond-softening (BS) mechanism of dissociation, whereas the broad peak at higher energy arises due to the above-threshold dissociation (ATD) mechanism. As discussed earlier, the molecules' response to the laser pulse is more intense when the molecular plane is perpendicular to the polarization plane of the laser pulse, which is also reflected in the ATD peak of the proton kinetic energy spectrum in Fig. 5b. Specifically, in the parallel orientation, the proton kinetic energy spectrum has one ATD peak at ∼0.5 eV, whereas, in the case of perpendicular orientation, a broad shoulder (∼2.0 eV) is also present along with the main ATD peak. The higher energy peaks mainly emerge due to either a re-collision-induced contribution or the higher-order ATD. Note that in the elliptically polarized laser pulses, the re-collision process is highly suppressed. In any case, we have analyzed the individual trajectories in the proton energy range of ∼2.0 eV and, as expected, no trajectory is found to support the re-collision mechanism. Therefore, the shoulder in Fig. 5b is quite possibly originating because of the higher-order ATD.Next, we investigated the influence of the CEP of the laser pulse on the proton kinetic energy spectra. In the parallel orientation, the proton kinetic energy spectra are calculated for the CEP values of 30° and 90°, as shown in Fig. 5c and d, respectively. For these values of CEPs, the proton kinetic energy spectra do not depict the double-peak structure. At the CEP value of 30°, where the dissociation probability is maximum (see Fig. 4a), only one peak appears at the lower energy value of ∼0.2 eV, which suggests that the dissociation of the created H2+ occurs through the BS mechanism, but not through the ATD mechanism. However, for the CEP value of 90°, from the region of minimum dissociation probability, a single broad peak is observed at ∼0.5 eV, suggesting that the ATD mechanism is responsible for the dissociation process. The results displayed in Fig. 5c and d dictate that the mechanism of the dissociation can be controlled by varying the CEP of the laser pulse. In the case where the molecule is perpendicular to the laser polarization plane, the control of the dissociation mechanism is not very precise. However, in contrast to the parallel orientation, it is clearly noticeable that the double-peak structure of the proton kinetic energy spectra persists at these values of the CEPs, as shown in Fig. 5e and f, which validates the contribution from both the mechanisms (BS and ATD) towards the single dissociative ionization of H2. The proton energy spectra after CEP averaging and for fixed CEP suggest that the dissociation of H2+ after the ionization of H2 can be more precisely controlled for the parallel orientation compared to the perpendicular orientation of the molecule.
It is to be noted that, in the present study, we have focused on the proton kinetic energy release spectra of the single dissociative ionization channel. However, it is worth pointing out that, in our previous study,43 we reported the proton kinetic energy release spectra of the double ionization channel and compared them to the experimental measurements.54 A very good agreement was obtained in contrast to other previous studies, where some disagreements were observed between theoretical and experimental results.6,13,27,28
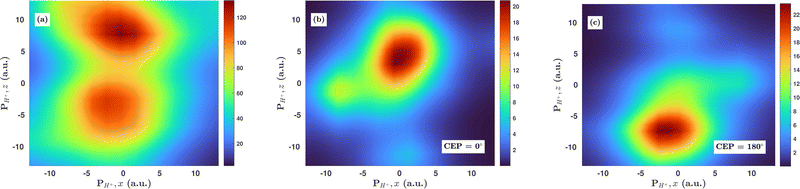
3.5 Effect of CEP on the proton momentum distribution
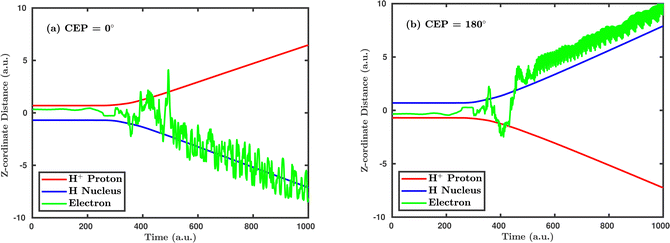
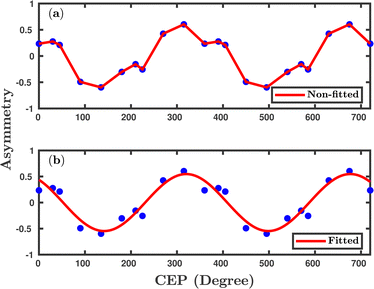
Inspired by the fact that more precise control of the dissociative ionization process is obtained for the parallel orientation (see Fig. 4 and 5), we have scrutinized the effect of the CEP on the proton momentum distribution with such a parallel orientation of the laser pulse. Indeed, by observing the proton momentum distribution for certain values of CEPs, the effect of the CEP on the directional bond-breaking in the molecule can be understood. For the single dissociative ionization channel, the CEP-averaged proton momentum distribution in the polarization plane is shown in Fig. 6a. It may be noted that, initially, in the polarization plane, the H2 molecule is taken to be randomly oriented with respect to the major axis of the polarization ellipse. Moreover, the proton momentum distribution encodes the instantaneous orientation of the molecule in the polarization plane. The two maxima along the z-axis in Fig. 6a indicate that the majority of the molecules are along the major axis (z-axis) of the polarization ellipse at the time of dissociation (H2+ → H + H+). When the CEP of the laser pulse is not stabilized, the proton has a nearly equal probability to be ejected in both the up (pH+, z > 0) and down (pH+, z < 0) directions. For the investigation of the CEP effect on the directional bond-breaking, the proton momentum distribution is calculated at the CEP values of 0° and 180°, as shown in Fig. 6b and c, respectively. At the CEP value of 0°, the protons have a greater tendency to be ejected in the up direction with positive momentum along the major axis of the polarization ellipse. Conversely, if the CEP of the laser pulse changes by 180°, the protons tend to be dislodged in the opposite direction with negative momentum. To the best of our knowledge, our results are probably the first theoretical demonstration of CEP-dependent two-dimensional proton anisotropy. However, from the experimental point of view, the first two-dimensional proton anisotropy control by the CEP of the laser pulse was recently achieved by Kangaparambil and co-workers.36 Controlling the proton ejection direction is directly related to the controlling of the electronic motion within the H2+ molecule formed subsequently after the first ionization of H2. After the first ionization step of H2, the remaining electron oscillates between the two nuclei under the influence of the laser field, where such oscillations of the electron are greatly affected by the laser electric field under the pulse envelope. As the internuclear separation increases, the electron gets localized on one of the nuclei because of the high intra-molecular potential barrier. The rapid directional motion of the remaining electron is controlled by the CEP of the laser pulse. At CEP = 0°, the proton is ejected in the up direction (pH+, z > 0), which essentially implies that the electron is localized on the other H nucleus being ejected in the down direction (pH+, z < 0). The choice of nucleus for the electron to localize on gets reversed when the CEP of the pulse changes to 180°. Trajectories to support the mechanism for the CEP control of electron localization and reversal of proton ejection direction are presented in Fig. 7. These trajectories show the evolution of both the nuclei and the electron, after the first ionization of the H2 molecule. Initially, both the nuclei are at the equilibrium distance (1.4 a.u.), whereas at the maxima of the laser pulse (≈300 a.u.), the internuclear distance rapidly increases and eventually the molecule breaks. The electronic motion is shown by the green curves in Fig. 7a and b for CEP = 0° and 180°, respectively. In the quantum mechanical picture, this localization control of the electron in the molecule could be understood in terms of the superposition of the 1sσ+g and 2pσ−u states, which are formed via the population transfer in the presence of the laser field. Because of this superposition, the parity of the electronic wavefunction breaks, which essentially guides the electron to localize on either the up or down nucleus.In order to illustrate the effect of the CEP of an elliptically polarized pulse on the proton ejection direction, we define an asymmetry parameter
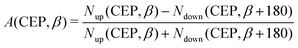 | (10) |
4 Conclusions
We have investigated the CEP effect and the orientation effect on the dissociative ionization of the H2 molecule exposed to an elliptically polarized few-cycle laser pulse. For the parallel orientation, more precise control is achieved in terms of the dissociative ionization probability with an almost four-fold enhancement at some specific CEPs. The dissociative ionization probability oscillates with π periodicity over the CEP of the laser pulse, which is in accordance with the experiments performed with linearly polarized pulses. At the specific CEP values having prominent CEP dependence, the single dissociative ionization process is also found to be strongly correlated with the first ionization step (H2 + nħω → H2+ + e−). The single dissociative ionization occurs via the BS and ATD mechanisms, as indicated by the double-peak structure of the CEP-averaged proton kinetic energy spectra, which is in agreement with the experimental observation.12 A strong CEP dependence is observed in the proton ejection direction, which is flipped when changing the CEP of the laser pulse by 180°. This could possibly be the first theoretical observation on 2D-control of the proton anisotropy by the CEP of the laser pulse and is in agreement with a recent experimental study.36 The oscillations in the total single dissociative ionization probability (π periodicity), as well as in the proton ejection asymmetry (2π periodicity), indicate that the Heisenberg's model potentials can capture the interference effects. Furthermore, the control of directional bond-breaking via regulating the electronic motion can be achieved in elliptical polarized pulses. Predictions made in our study, especially for the orientation-dependent CEP effect on the reaction probabilities of various channels, could be tested in future experiments. Moreover, the simulated proton kinetic energy release spectra for the dissociative ionization channel and their dependence on the CEP could also be another testing point for future experiments, which might essentially reveal some more physical insights into the identification of dissociation, as well as the ionization mechanism. Indeed, our theoretical investigation enhances the understanding and applicability of the presently employed classical model in the simulation and, at the same time, enables us to “accurately” predict the strong-field phenomenon in molecules. Although, in the present study, the quasi-classical method based on the Heisenberg's model potentials is applied to a 2e− molecular system, this model, in the near future, could further be extended to other multi-electron atoms and molecules by incorporating a greater number of Heisenberg's model potentials with suitable parameters.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. P. expresses his gratitude to IISER Kolkata for the financial aid, and the DIRAC supercomputing facility. S. G. acknowledges IISER Kolkata and A. K. T. for the financial aid through DST-SERB project number: CRG/2020/000040. A. K. T. thanks DST-SERB New Delhi, India, for funding through project number: CRG/2020/000040.Notes and references
- M. Garg, A. Martin-Jimenez, M. Pisarra, Y. Luo, F. Martín and K. Kern, Nat. Photonics, 2022, 16, 196–202 CrossRef CAS.
- H. Ahmadi, E. Plésiat, M. Moioli, F. Frassetto, L. Poletto, P. Decleva, C. D. Schröter, T. Pfeifer, R. Moshammer, A. Palacios, F. Martin and G. Sasone, Nat. Commun., 2022, 13, 1242 CrossRef CAS PubMed.
- M. Kübel, Z. Dube, A. Y. Naumov, D. M. Villeneuve, P. B. Corkum and A. Staudte, Nat. Commun., 2019, 10, 1042 CrossRef PubMed.
- M. Garg and K. Kern, Science, 2020, 367, 411–415 CrossRef CAS.
- D. Ayuso, A. Palacios, P. Decleva and F. Martín, Phys. Chem. Chem. Phys., 2017, 19, 19767–19776 RSC.
- R.-F. Lu, P.-Y. Zhang and K.-L. Han, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 066701 CrossRef PubMed.
- T. Zuo, S. Chelkowski and A. D. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 48, 3837–3844 CrossRef CAS PubMed.
- S. Pan, W. Zhang, H. Li, C. Lu, W. Zhang, Q. Ji, H. Li, F. Sun, J. Qiang, F. Chen, J. Tong, L. Zhou, W. Jiang, X. Gong, P. Lu and J. Wu, Phys. Rev. Lett., 2021, 126, 063201 CrossRef CAS PubMed.
- P. H. Bucksbaum, A. Zavriyev, H. G. Muller and D. W. Schumacher, Phys. Rev. Lett., 1990, 64, 1883–1886 CrossRef CAS.
- K. Dota, M. Garg, A. K. Tiwari, J. A. Dharmadhikari, A. K. Dharmadhikari and D. Mathur, Phys. Rev. Lett., 2012, 108, 073602 CrossRef CAS PubMed.
- W. Gao, B.-B. Wang, X.-J. Hu, S. Chai, Y.-C. Han and J. B. Greenwood, Phys. Rev. A, 2017, 96, 013426 CrossRef.
- M. Kling, C. Siedschlag, A. J. Verhoef, J. Khan, M. Schultze, T. Uphues, Y. Ni, M. Uiberacker, M. Drescher and F. Krausz, et al. , Science, 2006, 312, 246–248 CrossRef CAS.
- A. Staudte, D. Pavičić, S. Chelkowski, D. Zeidler, M. Meckel, H. Niikura, M. Schöffler, S. Schössler, B. Ulrich, P. P. Rajeev, T. Weber, T. Jahnke, D. M. Villeneuve, A. D. Bandrauk, C. L. Cocke, P. B. Corkum and R. Dörner, Phys. Rev. Lett., 2007, 98, 073003 CrossRef CAS PubMed.
- L. Cattaneo, J. Vos, R. Y. Bello, A. Palacios, S. Heuser, L. Pedrelli, M. Lucchini, C. Cirelli, F. Martn and U. Keller, Nat. Phys., 2018, 14, 733–738 Search PubMed.
- S. A. Bozpolat, P. Rosenberger, M. F. Ciappina, M. F. Kling and L. Yavuz, Phys. Rev. A, 2019, 100, 063409 CrossRef CAS.
- L. Xu and F. He, Phys. Rev. A, 2021, 103, 063108 CrossRef CAS.
- E. Khosravi, A. Abedi, A. Rubio and N. T. Maitra, Phys. Chem. Chem. Phys., 2017, 19, 8269–8281 RSC.
- L. Cattaneo, L. Pedrelli, R. Y. Bello, A. Palacios, P. D. Keathley, F. Martín and U. Keller, Phys. Rev. Lett., 2022, 128, 063001 CrossRef CAS PubMed.
- A. Sopena, H. Bachau, F. Catoire, F. Martín and A. Palacios, Phys. Chem. Chem. Phys., 2021, 23, 22395–22403 RSC.
- H. Ibrahim, C. Lefebvre, A. D. Bandrauk, A. Staudte and F. Légaré, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 042002 CrossRef.
- H. Xu, Z. Li, F. He, X. Wang, A. Atia-Tul-Noor, D. Kielpinski, R. T. Sang and I. V. Litvinyuk, Nat. Commun., 2017, 8, 15849 CrossRef CAS PubMed.
- H. Xu, H. Hu, X.-M. Tong, P. Liu, R. Li, R. T. Sang and I. V. Litvinyuk, Phys. Rev. A, 2016, 93, 063416 CrossRef.
- M. Kremer, B. Fischer, B. Feuerstein, V. L. B. de Jesus, V. Sharma, C. Hofrichter, A. Rudenko, U. Thumm, C. D. Schröter, R. Moshammer and J. Ullrich, Phys. Rev. Lett., 2009, 103, 213003 CrossRef.
- V. Roudnev and B. D. Esry, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 023403 CrossRef.
- T. Rathje, A. M. Sayler, S. Zeng, P. Wustelt, H. Figger, B. D. Esry and G. G. Paulus, Phys. Rev. Lett., 2013, 111, 093002 CrossRef CAS PubMed.
- N. G. Kling, K. J. Betsch, M. Zohrabi, S. Zeng, F. Anis, U. Ablikim, B. Jochim, Z. Wang, M. Kübel, M. F. Kling, K. D. Carnes, B. D. Esry and I. Ben-Itzhak, Phys. Rev. Lett., 2013, 111, 163004 CrossRef.
- H.-X. He, R.-F. Lu, P.-Y. Zhang, K.-L. Han and G.-Z. He, J. Chem. Phys., 2012, 136, 024311 CrossRef.
- S. Chelkowski, A. D. Bandrauk, A. Staudte and P. B. Corkum, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 013405 CrossRef.
- K. Sacha and B. Eckhardt, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 63, 043414 CrossRef.
- S. Haan, L. Breen, A. Karim and J. Eberly, Phys. Rev. Lett., 2006, 97, 103008 CrossRef CAS PubMed.
- P. J. Ho, R. Panfili, S. L. Haan and J. H. Eberly, Phys. Rev. Lett., 2005, 94, 093002 CrossRef PubMed.
- G. P. Katsoulis, R. Sarkar and A. Emmanouilidou, Phys. Rev. A, 2020, 101, 033403 CrossRef CAS.
- M. B. Peters, V. P. Majety and A. Emmanouilidou, Phys. Rev. A, 2021, 103, 043109 CrossRef CAS.
- L. Sarkadi, Phys. Rev. A, 2021, 103, 053113 CrossRef CAS.
- M. B. Peters, G. P. Katsoulis and A. Emmanouilidou, Phys. Rev. A, 2022, 105, 043102 CrossRef CAS.
- S. Kangaparambil, V. Hanus, M. Dorner-Kirchner, P. He, S. Larimian, G. Paulus, A. Baltuška, X. Xie, K. Yamanouchi, F. He, E. Lötstedt and M. Kitzler-Zeiler, Phys. Rev. Lett., 2020, 125, 023202 CrossRef CAS PubMed.
- J. Wu, M. Magrakvelidze, L. P. H. Schmidt, M. Kunitski, T. Pfeifer, M. Schöffler, M. Pitzer, M. Richter, S. Voss, H. Sann, H. Kim, J. Lower, T. Jahnke, A. Czasch, U. Thumm and R. Dörner, Nat. Commun., 2013, 4, 2177 CrossRef CAS.
- Y. Zhou, C. Huang, Q. Liao and P. Lu, Phys. Rev. Lett., 2012, 109, 053004 CrossRef.
- E. Lötstedt and K. Midorikawa, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 043415 CrossRef.
- C. L. Kirschbaum and L. Wilets, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 21, 834–841 CrossRef CAS.
- L. Wilets and J. S. Cohen, Contemp. Phys., 1998, 39, 163–175 CrossRef CAS.
- J. S. Cohen, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 51, 266–277 CrossRef CAS.
- G. Pandey and A. K. Tiwari, Eur. Phys. J. D, 2022, 76, 75 CrossRef CAS.
- E. Lötstedt, T. Kato and K. Yamanouchi, Phys. Rev. Lett., 2011, 106, 203001 CrossRef PubMed.
- G. Pandey, D. Dey and A. K. Tiwari, J. Phys. Chem. A, 2020, 124, 9710–9720 CrossRef CAS.
- D. Dey, D. Ray and A. K. Tiwari, J. Phys. Chem. A, 2019, 123, 4702–4707 CrossRef CAS PubMed.
- K. J. LaGattuta, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 043404 CrossRef.
- F. Frémont, Phys. Rev. A, 2017, 96, 032712 CrossRef.
- J. S. Cohen, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 56, 3583–3596 CrossRef CAS.
- W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical Recipes in Fortran 77: The Art of Scientific Computing, Cambridge University Press, 1992 Search PubMed.
- V. Hanus, S. Kangaparambil, S. Larimian, M. Dorner-Kirchner, X. Xie, M. S. Schöffler, G. G. Paulus, A. Baltuška, A. Staudte and M. Kitzler-Zeiler, Phys. Rev. Lett., 2019, 123, 263201 CrossRef CAS.
- G. K. Paramonov and O. Kuhn, J. Phys. Chem. A, 2012, 116, 11388–11397 CrossRef CAS PubMed.
- H. Sakai, J. J. Larsen, I. Wendt-Larsen, J. Olesen, P. B. Corkum and H. Stapelfeldt, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 063404 CrossRef.
- V. Hanus, S. Kangaparambil, S. Larimian, M. Dorner-Kirchner, X. Xie, M. S. Schöffler, G. G. Paulus, A. Baltuška, A. Staudte and M. Kitzler-Zeiler, et al. , Phys. Rev. Lett., 2019, 123, 263201 CrossRef CAS PubMed.
- V. Roudnev and B. D. Esry, Phys. Rev. Lett., 2007, 99, 220406 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |