Quantum materials with strong spin–orbit coupling: challenges and opportunities for materials chemists

Abstract

Spin–orbit coupling is a quantum effect that can give rise to exotic electronic and magnetic states in the compounds of the 4d and 5d transition metals. Exploratory synthesis, chemical tuning and structure–property characterisation of such compounds is an increasingly active area of research with both fundamental and application-related outlooks. However, these exotic states have an extremely sensitive dependence on the structure and bonding of the host materials, meaning that great care is required with regards to their chemistry, but this is not always considered sufficiently. This Perspective will give an accessible introduction to topical materials with strong spin–orbit coupling, their crystal chemistry, and challenges in their synthesis and characterisation that must be faced if their structure–property relationships are to be correctly determined. These are common to investigations of the same compounds in other fields and rely on the contributions of materials chemists.

---

Alexander J. Browne

Alex is a graduate of the University of Oxford and the University of Edinburgh, and completed his PhD in Chemistry at the latter in 2018 under the supervision of Prof. J. P. Attfield. He subsequently carried out postdoctoral research at Edinburgh, as a Visiting Researcher to the Institute for Solid State Physics at the University of Tokyo, and at the Department of Chemistry of Princeton University, before joining the School of Chemistry of the University of St Andrews as a Research Fellow in April 2021.

Aleksandra Krajewska

Aleks is an instrument scientist on the MAPS neutron spectrometer at the ISIS Neutron and Muon Source. She received her MChem from the University of Edinburgh in 2016 and her doctorate of natural sciences from the Max Planck Institute for Solid State Research in 2021. Her research interests focus on the discovery of novel correlated materials, in particular strongly spin–orbit coupled magnets and molecular orbital crystals.

Alexandra S. Gibbs

Alex completed her MPhys (arrived at via a transfer to a joint chemistry–physics degree from her original chemistry programme) at the University of St Andrews in 2008. She stayed there for her interdisciplinary PhD with Prof. P. Lightfoot and Prof. A. P. Mackenzie on emergent states in transition metal oxides. Following this she took up opportunities for research in Japan (at the University of Tokyo and RIKEN) and Germany (Max Planck Institute for Solid State Research in Stuttgart) with Prof. H. Takagi. She then moved to the ISIS Neutron and Muon Source in Oxfordshire to follow her continued interest in high resolution neutron diffraction. These research streams have now converged in her EPSRC Early Career Fellowship at St Andrews in association with the Crystallography Group at ISIS. Her research is at the chemistry–physics boundary, studying structure–property relationships in quantum and functional materials.

---

1 Introduction

Whilst the properties of all materials originate in one way or another from quantum mechanics, the term ‘quantum materials’ has recently come to be used to collectively categorise those materials – such as superconductors, Mott insulators, and those with topologically-protected states, amongst many others – that have macroscopic properties which cannot be described simply through their constituent atoms and electrons behaving as classical (or at least ‘semi-classical’) particles.^1–3 Materials exhibiting quantum magnetism (Fig. 1(a)), as a contrast to conventional magnetic materials, provide another – highly-topical – example. Atoms with unpaired electrons have a net magnetic moment, and in conventional magnets these can be considered to interact with one another according to the principles of standard ferromagnetic and antiferromagnetic exchange interactions to form ordered states. An increasing number of materials, however, are being discovered in which quantum-mechanical effects such as fluctuations, particle entanglement, wavefunction topology and spin–orbit coupling are significant enough that those conventional magnetic states are in competition with exotic ones that are now being revealed for the first time.^4–6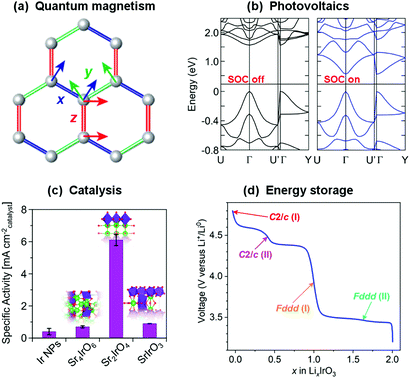

Fig. 1 Strong spin–orbit coupling underpins the electronic and magnetic properties of many topical materials, such as (a) the realisation of quantum spin liquids and other exotic states in compounds of the platinum group transition metals,⁷ and (b) determining the band gap of hybrid metal halide perovskites (shown are calculated band structures for MAPbI₃).⁸ These materials also have a variety of functional properties – for example, the same iridates that have been heavily studied with regards to quantum magnetism also have exceptional (c) catalytic⁹ and (d) electrochemical¹⁰ properties. All of these are rooted in the structure and bonding of the material, so there is great potential for different communities of materials chemists to benefit from each others' investigations. Figures reprinted/adapted with permission from (a) ref. 7 Nature, 2018; (b) ref. 8, (c) ref. 9 and (d) ref. 10 American Chemical Society, 2013, 2019, 2017.

The quantum effect of interest in the materials that we will focus on in this Perspective is spin–orbit coupling. This is the interaction between the spin angular momentum S and the orbital angular momentum L of the electrons, which is expressed in terms of a new quantum number J that redefines the energy levels of the electrons.¹¹ Spin–orbit coupling perturbs the wavefunctions of the electrons under its influence and the magnetic forces acting on them, affecting their spatial distributions and magnetic moments. We will discuss it in the context of its effect on the magnetic and electronic states of transition metal compounds, which strengthens on moving from 3d to 4d and 5d systems.

The magnetism of transition metal species is commonly described using the ‘spin-only’ model, which assumes that the orbital angular momentum of the d orbitals is quenched by their splitting by the crystal field and hence discounts any orbital effects. However, whilst spin-only predictions of the magnetic moment are often reasonably accurate for 3d systems, the assumption is only strictly true for some electron configurations – those with 1, 2, 4 or 5 t_2g electrons retain orbital angular momentum and this can have noticeable effects on their behaviour, even for 3d species such as V⁴⁺ and high-spin Co²⁺.^12,13 For 4d and 5d species, orbital effects are even more significant. The crystal field splitting Δ_O (the lifting of the degeneracy of the valence d orbitals of an ion in a perfect octahedral coordination environment) becomes larger, increasing from 1.5–2 eV in 3d oxides to 2.5–3 eV and 3–4 eV in 4d and 5d oxides, respectively,¹¹ hence the valence electrons in the latter two almost exclusively adopt a low-spin configuration. However, the spin–orbit coupling experienced by those electrons increases even more significantly, having a dependence on the atomic number Z between Z² and Z⁴,¹⁴ and the spin–orbit coupling constant λ_SO increases from 0.02–0.07 eV for 3d species to 0.1–0.2 eV for 4d species and 0.3–0.5 eV for 5d ones.¹¹ Consequently it can become large enough to be comparable to other energy scales, such as additional splitting of the t_2g orbitals induced by distortions of the coordination octahedron, and can therefore play a pivotal role in determining the electronic ground state.^11,15–17

As such, materials featuring 4d or 5d transition metal cations with t_2g¹, t_2g², t_2g⁴ or t_2g⁵ electron configurations, such as Ir⁴⁺ and Ru³⁺, are sought after as hosts for the exotic electronic states that can result from strong spin–orbit coupling. It is worth noting that many of the materials in which such states have been found have actually been known for decades,¹⁸ but the development of new theoretical frameworks and experimental probes was required before their electronic and magnetic properties could be properly described. Now that some have been proposed, studies of their intriguing phases have blossomed – not just for basic understanding of their electronic and magnetic properties,⁴ but also for applications such as spintronics^19,20 and energy harvesting.²¹ It is also important to consider that spin–orbit coupling will affect the behaviour of the electrons in any material containing high-Z elements, not just transition metal compounds. In fact an interesting parallel can be drawn between these materials and hybrid perovskites containing heavy main-group elements such as Pb and Bi. Although we will not elaborate on these materials in this Perspective their electronic structures, as in their transition metal counterparts that we focus on, are heavily affected by strong spin–orbit coupling (Fig. 1(b)). This is influential not only in determining the band gaps that underpin their photovoltaic properties,⁸ but may also give rise to exotic states that could be employed in spintronics and other applications similar to those proposed for the transition metal compounds we discuss.^22,23 The electronic and magnetic properties of f-electron systems are also heavily influenced by strong spin–orbit coupling.²⁴ We therefore hope that our discussion of the challenges faced in the accurate characterisation of transition metal systems may also be of use more broadly.

The discovery of a variety of exotic states in compounds of iridium, ruthenium and other platinum group metals in recent years has stimulated significant effort towards both the discovery of new materials with strong spin–orbit coupling and the tuning of known systems through chemical modification and physical means such as the application of pressure. However, the synthesis, characterisation and reproducibility of these materials can be challenging, and this has not always been sufficiently recognised. In this Perspective we aim to introduce these materials to a wider chemical audience and demonstrate the opportunities for materials chemists that these challenges provide. We will not repeat the detailed introductions to the physics of these materials available elsewhere,^{4–6,25–30} and instead focus on discussing the critical role of materials chemistry in this field and highlighting where some of the challenges and potential opportunities in this regard lie. Additionally, the materials we discuss have a relevance much broader than our own – perhaps rather narrow – horizons. The structural and physical chemistry of extended-structure compounds of the heavy transition metals, in particular the platinum group metals, is significantly under-studied in comparison to their 3d relatives. Fortunately this is being rectified because these compounds are of current interest not only to the quantum materials community but to others with a highly complementary range of experimental and theoretical approaches. Ruthenates and iridates have exciting potential in various catalytic applications (Fig. 1(c)), in part due to their resilience to extreme pH environments, and descriptions of their catalytic structure–property relationships that are centred on the geometry of (Ir/Ru)O₆ octahedra are highly analogous to those used in studies of quantum magnetism.^31–33 Ruthenates and iridates are also receiving considerable attention in the battery materials community (Fig. 1(d)), with the consequence that contemporary materials discovery and development is progressing along a strikingly similar path to that in the quantum materials field, for example through the use of soft-chemical and electrochemical methods to access and manipulate lithium-, sodium- and hydrogen-containing materials.^10,34–36 In fact, the exact same materials are often under study by the two communities at the same time.^10,37,38

At the outset it is also worth noting that, although materials such as iridates have so far been the most popular for studies of d electrons with strong spin–orbit coupling, it is not only oxides that host such states but also e.g. halides¹⁶ and intermetallics,³⁹ and in addition to compounds of the platinum group metals that we focus on there are a growing number of materials based on other 5d elements, such as rhenium and tantalum.^40,41 Developments in theory also continue to motivate efforts in this field.^42,43

2 Exotic electronic and magnetic states in materials with strong spin–orbit coupling

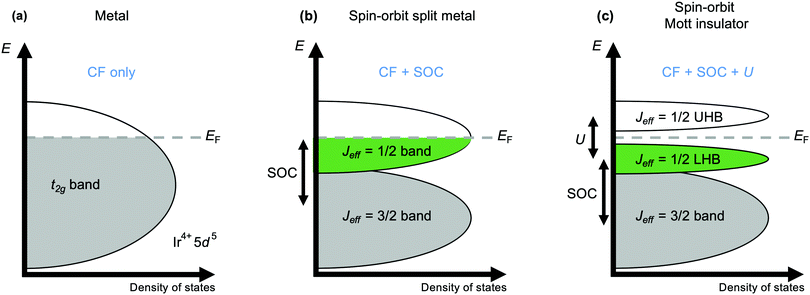
The current explosion of interest in the effects of strong spin–orbit coupling on the behaviour of d-electron systems was sparked by the discovery, in 2008, that the iridate Sr₂IrO₄ has an insulating ground state.⁴⁴ With its spatially extended 5d valence orbitals this material was expected to be metallic, like its 4d analogues Sr₂RuO₄ and Sr₂RhO₄. Initial tempering of surprise may have been sought by turning to the Mott-Hubbard model, which accounts for many 3d oxides expected to be metallic actually being insulating by considering the magnitude of the electrostatic repulsion U between electrons occupying orbitals of the same atom.⁴⁵ A larger U encourages the electrons to remain localised, and above a critical value manifests as the opening of a band gap at the Fermi energy E_F that is the cause of insulating behaviour in materials without otherwise filled bands. However, that critical value increases with the improvement of d–d orbital overlap from 3d to 4d and 5d systems that broadens the valence d band, and a sufficiently large value cannot normally be obtained for a Mott-insulating ground state to be realised. However, such a state is realised in Sr₂IrO₄ because the t_2g valence band is first split by strong spin–orbit coupling into two distinct ones defined by their different effective values J_eff of the total angular momentum quantum number J (Fig. 2).⁴⁶ The higher-energy J_eff = 1/2 band straddles E_F, and being now separate from the lower-energy J_eff = 3/2 band is sufficiently narrow to be susceptible to the Mott-Hubbard splitting that makes Sr₂IrO₄ an insulator.¹¹

Fig. 2 Schematic band structure diagram illustrating the origins of the Mott-insulating ground state of Sr₂IrO₄. (a) A simple metallic state should be expected for the wide, partially-filled t_2g band formed by the valence 5 d orbitals in an octahedral crystal field (CF). (b) Strong spin–orbit coupling (SOC; formally ζ = 2Sλ_SO, where ζ is the atomic spin–orbit coupling coefficient and λ_SO the spin–orbit coupling constant) splits the t_2g band into low-energy J_eff = 3/2 and high-energy J_eff = 1/2 bands. (c) The J_eff = 1/2 band is further split by electron–electron repulsion U into a lower Hubbard band (LHB) and an upper Hubbard band (UHB) on either side of the Fermi energy E_F to form the insulating state.

Mott behaviour and the effect of U has underpinned the rich physics of 3d transition metal oxides that has been revealed over the last decades. The realisation since 2008 that strong spin–orbit coupling can also provide access to novel states has led to the search for – and discovery of – unprecedented exotic behaviours in iridates and other 4d and 5d systems. A prominent contemporary example is Kitaev magnetism, including the Kitaev quantum spin liquid state. A spin liquid is a magnetic state in which the spins of different atoms are entangled with one another through space but don't establish long-range magnetic order. The Kitaev model is a fully-solvable model of S = 1/2 spins on a honeycomb lattice and describes the possibility of a spin liquid arising from ‘bond-dependent’ magnetic interactions (see Fig. 1(a)) that contrasts with the physics of ‘traditional’ Cu²⁺-based spin liquid candidates.^26,27 The realisation that certain iridates and ruthenates have structures that provide a template for realising Kitaev physics has spurred intense interest in these materials over the last decade.^4,5

Electronic phases with unusual band structure topologies, such as the topological semimetal phases found in some pyrochlore iridates and in SrIrO₃,^4,47–50 are also a feature of materials with strong spin–orbit coupling. Another recent development has been the exploration of potential excitonic magnetism in d⁴ compounds. The effects of spin–orbit coupling and U generally cause t_2g⁴ systems to have a non-magnetic J_eff = 0 ground state, but an exotic form of magnetism dubbed excitonic magnetism that is mediated by excitations to the J_eff = 1 state may be found.^42,43,51 This can also compete with the formation of orbital molecules, where a covalent-like sharing of electrons between cations forms M–M bonds.¹¹ This bonding does not solely originate from strong spin–orbit coupling – the essential requirement is simply for a structure in which the d orbitals of neighbouring cations can interact directly.⁵² However, as many of the materials being studied for the effects of strong spin–orbit coupling have such a structure, orbital molecule states are amongst those being found.^53–57

There are many other exotic electronic and magnetic states that have been found in materials with strong spin–orbit coupling which we will not discuss here (see e.g.ref. 58–60). We also confine ourselves to discussion of bulk materials, though thin films and heterostructures provide unique and exciting access to further tuning parameters and exotic phases.²¹ Many excellent reviews exist for the interested reader.^{4–6,11,20,25–29}

3 Crystal chemistry

In the majority of the materials with strong spin–orbit coupling that have been studied to date, the active transition metal cation M is octahedrally coordinated by oxide ligands. MO₆ octahedra therefore constitute the basic building block of their crystal structures, which are constructed by connecting these octahedra through different patterns of corner-, edge- and face-sharing. These connectivities define the M–M and M–O–M orbital interactions, which in turn determine the electronic band structure and magnetic exchange interactions for a given material. So that the relationship of the exciting properties arising from these interactions to the underlying structure of the host materials can be better understood, we now outline some common structure types and their relationships in terms of the connectivity of the MO₆ octahedra (Fig. 3). In general formulae we use M to indicate spin–orbit-coupling-active transition metal cations (commonly Ir or Os in the materials we discuss) and A to indicate non-active cations (typically Group 1, Group 2 and rare-earth elements). Furthermore, whilst we refer to these in general as oxides, many of these structure types can be realised with halide and chalcogenide anions too.^41,61,62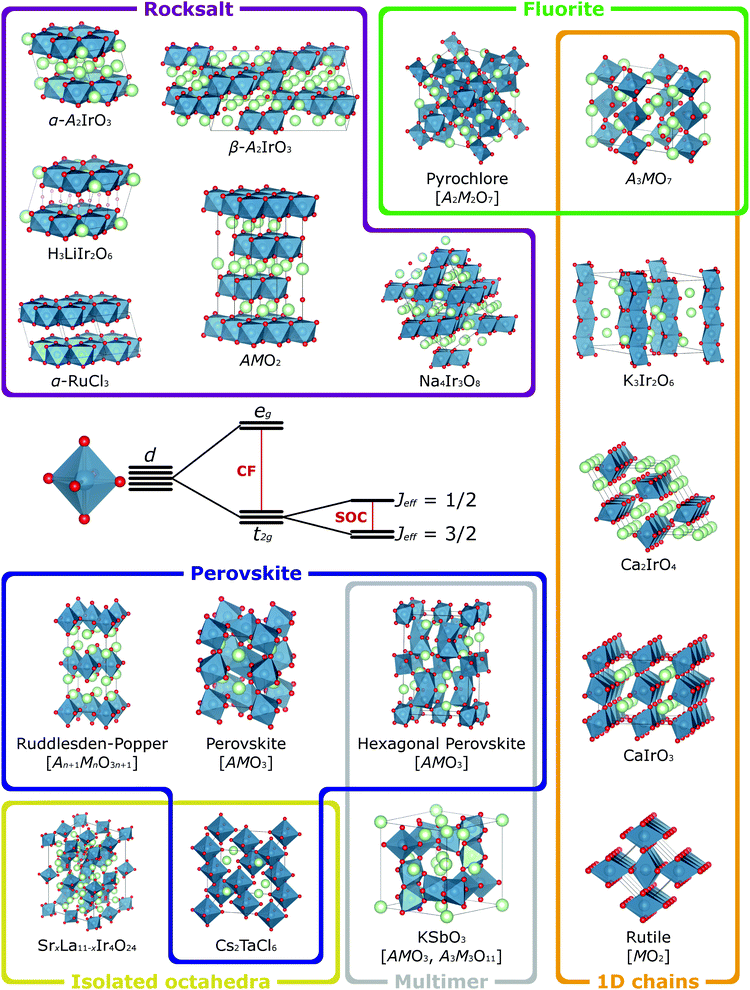

Fig. 3 When a transition metal cation is octahedrally coordinated, its five valence d orbitals are split into t_2g and e_g sets by the octahedral crystal field (CF). The t_2g orbitals retain orbital angular momentum, so for species with t_2g¹, t_2g², t_2g⁴ or t_2g⁵ electron configurations, these can be further split by spin–orbit coupling (SOC) into states defined by their effective total angular momentum J_eff. Many of the materials currently of interest for the effects that spin–orbit coupling has on their magnetic and electronic properties have structures built from such octahedra and a selection of more prominent examples are depicted here, categorised according to the different connectivities of the octahedra. The compositions of common structure types are given with a general formula, where M is the spin–orbit-coupling-active transition metal (blue atoms) and A is a different, non-active species (green atoms). For simplicity all such compositions are shown as oxides (red atoms), though many of these structure types are also adopted by chalcogenide and halide materials. Crystal structures visualised using VESTA.⁶⁵

This section is not intended to replicate comprehensive reviews of all known structure types and their possible variations.^63,64 In particular, the range of known polymorphs and superstructures, arising for example from perovskite rotation/tilting distortions, different stacking arrangements in layered rocksalt-type materials and hexagonal perovskites, or the (dis)order of vacancies in topochemically-tunable materials, is too great to be covered here. Instead, this section is intended to be an introduction to relevant crystal chemistry, upon which the nuances of the detailed structural characterisation that understanding quantum states requires will be developed in later sections.

3.1 Rocksalt-related structures

We start with a discussion of materials with structures derived from the rocksalt type, as a number of the most well-studied materials with interesting spin–orbit coupling effects fall into this category. The rocksalt structure comprises a face-centred cubic anion lattice within which cations occupy all the octahedral interstitial sites, giving a 1 : 1 ratio of cations to anions. Structurally, each edge of each MO₆ octahedron is shared with a neighbouring one. Derivative structures are realised when there are multiple cationic species that have an ordered distribution over these octahedral sites. In α-NaFeO₂-type materials the two cationic species, the transition metal M and a Group 1 cation A, order into alternating layers perpendicular to the 111 axis of the cubic rocksalt unit cell, generating a rhombohedral supercell. Within each layer the MO₆ octahedra share edges with six neighbours, forming a hexagonal lattice. However, changing the ratio of the cationic species from 1 : 1 forces one species to occupy sites in the layer of the other. In Na₂IrO₃ and α-Li₂IrO₃ (better described as e.g. Na₃[NaIr₂]O₆) that extra Na/Li cation occupies ordered sites such that they sit in the centre of the ‘cells’ of a honeycomb lattice formed by the remaining Ir. Thus, the 2D honeycomb structure that is the basis for the Kitaev spin liquid state is realised.⁵α-RuCl₃ (and IrCl₃, though being d⁶ it does not exhibit a magnetic ground state) are isostructural – they are effectively the same materials with all Na/Li removed.^66,67 Analogous α-OsCl₃ is not known, though substoichiometric Os_xCl₃ (in which honeycomb nanodomains may be realised through local ordering of the Os-site vacancies) and partially-lithiated Li_2.15Os_0.85O₃ have the same structural basis.^68,69 The layered motif of these materials facilitates topochemical removal/exchange of the interlayer species. In this way, A′₃AIr₂O₆ (A′ = H, Cu, Ag) have been prepared.^7,70–72 As these A′ cations favour the linear coordination of an O–A′–O dumbbell over the octahedral AO₆ coordination of Li/Na in the parent materials, these materials have a different stacking pattern of the honeycomb layers than in α-A₂IrO₃, though that structural motif is retained with the remaining Li cation in the cells of the honeycomb lattice.⁷⁰ The exchange of these in addition to those located between the honeycomb layers has been demonstrated with Cu₂IrO₃.⁷³

Li₂IrO₃ also has β and γ polymorphs in which the zigzag chains of edge-sharing IrO₆ that define the honeycomb lattice in the α phase propagate in three dimensions instead of two, generating 3D networks described as hyperhoneycomb and stripy honeycomb, respectively.⁷⁴ Despite these different long-range connectivities, the local environment in which each IrO₆ octahedron shares its three orthogonal edges with three neighbours is the same in all three polymorphs, so where α-Li₂IrO₃ provides a structural template for 2D Kitaev physics its β and γ polymorphs allow for the study of the same physics in 3D. The sodium analogue, β-Na_1.7IrO₃, is of interest for the same reason and was actually first synthesised by the battery community.³⁵

A face-centred cubic anion lattice is the basis not only of the rocksalt structure but many others, defined by their different fillings of the octahedral and tetrahedral interstices. In spinels, tetrahedrally coordinated cations A and octahedrally coordinated cations M are present as AM₂O₄. The MO₆ octahedra share edges with six neighbours, forming infinite chains that run along the six 110-type directions of the cubic structure. Only a few AM₂O₄ spinels with 4d/5d M-site cations are known, though the edge-sharing chains allow for interesting orbital effects.^55,75 However, spinel-type phases can be accessed by increasing the ratio of A to M cations, such that the former partially occupy the sublattice of the latter. If this occupation is spatially ordered the A cations can ‘block’ particular M–M interactions, defining for example a hyperkagome Ir sublattice in Na₄Ir₃O₈ and Na₃Ir₃O₈.^4,76 The kagome lattice is a 2D network in which each cation interacts with four nearest neighbours, and has become an important structural template for studying the effect of geometric frustration on magnetic ordering – due to competing interactions in vertex-sharing triangles of cations, more exotic ground states may realised.²⁶ The hyperkagome lattice is its 3D analogue, and as with the honeycomb and hyperhoneycomb lattices described previously, despite their different long-range connectivities the local environments of the octahedrally-coordinated M species are the same in both the kagome and hyperkagome networks, providing 2D and 3D templates upon on which exotic ground states can be realised.⁷⁷

3.2 Fluorite-related structures

The MO₂ fluorite structure is also derived from a face-centred cubic lattice, though here it is formed by the cations, whilst the anions occupy the tetrahedral interstices. The cations have eight-fold cubic coordination, though this coordination number is reduced in derivative structures when the anion-to-cation ratio is reduced. One such derivative is the A₃MO₇ family of osmates and iridates (A is a rare-earth cation), in which one-dimensional chains of corner-sharing MO₆ octahedra run in parallel to the c axis of the orthorhombic unit cell.^78–80 The cations M are also octahedrally coordinated in pyrochlores, A₂M₂O₇, though here the corner-sharing chains have 3D connectivity. It is notable that, although one is based on octahedra sharing corners and the other on them sharing edges, the spatial arrangement of the M cations in pyrochlores and spinels is the same – they themselves form a network of corner-sharing tetrahedra known as a pyrochlore lattice that is also a template for geometric frustration. Iridium and osmium both form pyrochlores with a range of A-site species such as Cd, Hg, main-group and rare-earth elements.^81–84 However, as one of the seven oxygens in the pyrochlore formula unit is crystallographically distinct from the other six and is not involved in the MO₆ coordination octahedra, pyrochlore materials are susceptible to oxygen non-stoichiometry, as in for example Pb₂Ir₂O_6.5.⁸⁵

3.3 Perovskite-related structures and isolated octahedra

The structure most commonly described in terms of its construction from octahedral MO₆ units is perhaps the perovskite type, adopted by materials with AMO₃ ideal stoichiometry, in which corner-sharing MO₆ octahedra surround a central cavity occupied by the A cation. The AMO₃ lattice with a vacant A site can by itself be stable, as demonstrated by the binary oxides ReO₃ and WO₃; however, the attractiveness of the perovskite structure to materials chemists derives from its flexibility to accommodate A-site cations (either single species or solid solutions) with a wide range of ionic radii relative to that of the chosen M. This allows careful control not only of the number of valence d electrons available to the M species, through variation of its oxidation state, but also of how these interact with one another, because this flexibility is achieved through cooperative rotations and tiltings of the MO₆ octahedra in their corner-sharing network. Judicious choice of the A-site species therefore allows sensitive manipulation of the O–M–O bond angles. The ideal perovskite structure, in which these angles are all 180 degrees, is in fact relatively rare – more commonly, the A-site species is smaller than ideal, and this manifests in a rich variety of distorted variants, such as the orthorhombic GdFeO₃-type adopted by SrIrO₃, NaOsO₃ and others.^86,87

The corner-sharing perovskite network is the basis for numerous derivative structures. Layered variants such as the Ruddlesden–Popper (A_n+1B_nO_3n+1) and Dion–Jacobson (A′A_n−1B_nO_3n+1) types separate the framework of MO₆ octahedra into 2D layers, though as in the 3D analogues the MO₆ octahedra are susceptible to tilting distortions that can dramatically affect quantum properties determined by orbital interactions. These can be further impacted by the reduced dimensionality, which reduces the width of the valence d band, leading to stronger Mott effects. A similar effect can also be achieved by introducing a second octahedrally-coordinated species M′ which, when M and M′ have very different ionic radii or charge states, is stabilised in a cation-ordered structure.⁸⁸ In these A₂MM′O₆ double perovskites, such as Ba₂MgReO₆ and Ba₂NaOsO₆, the M and M′ species order in a rocksalt-like pattern, and this provides a template upon which the magnetic M species are spatially separated by the non-magnetic M′ ones, reducing the width of the valence d band and allowing the electrons to experience both strong spin–orbit coupling and a large U.⁴⁰ This separation of the MO₆ octahedra is taken to its extreme in the halides Cs₂TaCl₆ and Rb₂TaCl₆, which effectively have a rocksalt-ordered double perovskite structure in which the M′ site is vacant.⁴¹ In other words, the TaCl₆ octahedra have no structural connections to one another. Isolated IrO₆ octahedra are also found in tetragonal Sr_xLa_11−xIr₄O₂₄.⁸⁹

3.4 Multimer-based structures

AMO₃ perovskites in which the A cation is too large adopt a different type of structure, forming a family of materials known as hexagonal perovskites. Here, instead of sharing corners the MO₆ octahedra share faces, forming dimer, trimer and larger multimer units oriented parallel to the axis of three/six-fold rotational symmetry of the unit cell. This symmetry element has made hexagonal perovskites of emerging interest because it again provides a structural basis for geometric frustration, whilst the face sharing allows for unusually short M–M distances and small M–O–M bond angles that can dramatically influence their quantum properties.⁹⁰ Hexagonal perovskites effectively have a stacked structure, formed by the face-sharing multimers sharing corners with neighbouring multimers (which can be of the same or different types), and this gives rise to extensive polymorphism derived from different stacking arrangements. AMO₃ materials can also show polymorphism between hexagonal and conventional perovskite structures – for example, the ambient pressure polymorph of SrIrO₃ is actually of the hexagonal 6H type, and the conventional GdFeO₃-type polymorph mentioned previously is a metastable phase accessed through high-pressure synthesis.^86,91

Dimers of MO₆ octahedra are also found in materials adopting the KSbO₃-type structure, though here the octahedra in each dimer are connected by a shared edge. The dimers themselves are linked by shared vertices and form a three-dimensional tunnel-like structure. As well as materials with AMO₃ stoichiometry such as KIrO₃,⁹² variants the same tunnel-like structural framework but different stoichiometries, such as A₃M₃O₁₁, A₂M₃O₉ and A₄M₆O₁₉, can be prepared through control of the synthesis method and the choice of A-site cation.⁹³

In both edge- and face-sharing multimers the M–M distances are relatively short, and this may allow for sufficient direct interaction between the valence orbitals of the cations of neighbouring octahedra that they form multi-site molecular orbitals over which the valence d electrons delocalise. In other words, the magnetic ‘units’ of the structure may no longer be the individual MO₆ octahedra but multimer ‘molecules’.^90,94,95

3.5 1D chain structures

The edge- and face-sharing connectivity of MO₆ octahedra is not limited to forming just small multimer units. We have already introduced a few structure types in which edge-sharing octahedra form infinite chains, such as α-NaFeO₂ layered rocksalt and AM₂O₄ spinel, though in these the octahedra share multiple orthogonal edges such that the chains intersect and form two- and three-dimensional networks respectively. One dimensional systems, in which infinite chains run parallel to one another without intersecting, are also known. In the rutile structure adopted by metal dioxides such as OsO₂ and IrO₂, chains of edge-sharing octahedra chains run along the short axis of the tetragonal unit cell. Corner-sharing of all six vertices of each octahedron connects each chain to four neighbours. Comparatively, in the structure adopted by CaIrO₃ and NaIrO₃ only the axial vertices of the octahedra are corner-sharing, whilst the equatorial ones are only involved in edge-sharing, giving an arrangement of 1D chains connected in 2D planes.⁹⁶ The Ca₂IrO₄ structure also features edge-sharing chains but with no corner-sharing, so the 1D chains are isolated from one another.⁶⁴ Isolated 1D chains are also found in structures with corner- and face-sharing connectivities of the MO₆ octahedra. The former are found in, for example, the fluorite-type A₃MO₇ materials mentioned previously, whilst the latter are found in recently-reported K₃Ir₂O₆.⁹⁷

4 Structure–property relationships

The determination of structure–property relationships is a key principle of materials chemistry, and in materials with strong spin–orbit coupling this can be exceptionally challenging. This challenge is the result of their often extreme sensitivity to subtle structural distortions, as the different forces acting on the electrons are finely balanced and exquisitely responsive to changes of M–M distances and M–O–M angles that perturb the band structure and magnetic exchange.⁹⁹ In honeycomb iridates, for example, minute distortions of the IrO₆ octahedral network or spacer ion configuration are sufficient to drive the material into a completely different phase (Fig. 4(a)), and many target phases occupy only a tiny volume of parameter space (Fig. 4(b)).^29,98,100 Furthermore, the positions and concentrations of light elements, which are particularly difficult to characterise, are often crucial to the exotic behaviour displayed. It has been estimated that the presence or absence of hydrogen at a particular site can change the magnitude of the Kitaev coupling in H₃LiIr₂O₆ by a factor of 3.¹⁰⁰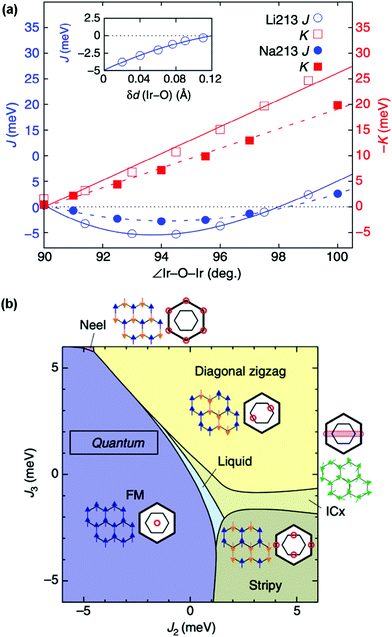

Fig. 4 (a) Dependence of the Heisenberg magnetic exchange coupling J and the Kitaev exchange coupling K on the Ir–O–Ir angle and Ir–O bond length within the honeycomb network for simplified structures of α-Li₂IrO₃ and Na₂IrO₃. The exchange couplings both have an extreme sensitivity to these two structural parameters, even in this simplified model. (b) Theoretical phase diagram for layered honeycomb Li₂IrO₃ for a range of second- and third-neighbour exchange coupling strengths J₂ and J₃. The extremely delicate balance of interactions can be seen in the phases occupying only tiny areas of the phase diagram. Adapted from ref. 98.

It is obvious in such cases that, if the structures and compositions of materials with strong spin–orbit coupling are not accurately known, the virtuous cycle between experiment and theory that is so essential for understanding these materials cannot be optimal. In addition, highly detailed (and often painstakingly collected) physical characterisation measurements cannot be correctly assigned to a stated material if the nuances that distinguish real-world materials from theoretical models have not been considered. In the following sections we will discuss some of the challenges that the study of quantum materials faces in this regard, and outline potential solutions that are coming to light – and which may even seem intuitive to materials chemists from other fields. We will also present some notable examples from the recent literature that illustrate the confusion that can result when these challenges have not been addressed, with the aim of motivating more detailed characterisation of new materials immediately upon their discovery and thorough reinvestigations of existing systems where necessary; such efforts have proven extremely fruitful to date.⁶⁶

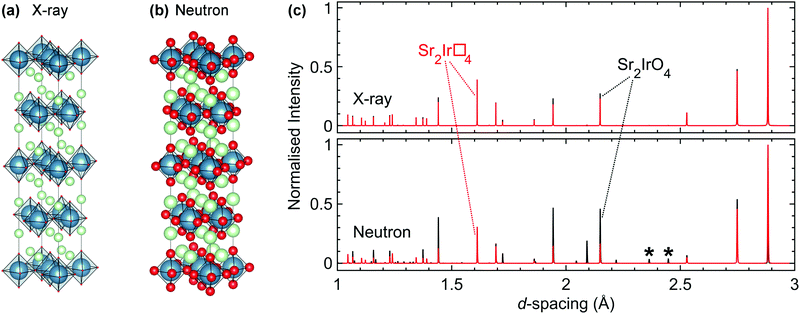
5 Materials chemistry challenges

5.1 Structure determination and refinement

As introduced in Section 3, materials with strong spin–orbit coupling almost always contain both very heavy metallic elements and very light elements such as oxygen, and perhaps even lithium or hydrogen. This poses a challenge for structural characterisation as the most common structural probe available in home laboratories is X-ray diffraction. In the presence of heavy 5d elements which scatter X-rays strongly the extremely weak signal from the oxygen positions, for example, is simply swamped. Absorption, particularly for diffractometers operating with a capillary/transmission geometry, is also a significant problem when 4d and 5d elements are present. Furthermore, techniques such as neutron diffraction that are often better suited to the characterisation of materials containing light elements such as oxygen alongside heavy transition metals (Fig. 5) have their own difficulties, such as the large absorption cross-section of natural Ir for neutron studies of iridates. The neutron scattering lengths and scattering/absorption cross-sections of different elements and isotopes are available in standard references,^101,102 and the values in the first of these are also available in an online database maintained by NIST.¹⁰³

Fig. 5 (a) The relative X-ray scattering strengths of different elements are dependent on their atomic numbers, represented graphically here for Sr₂IrO₄ by the size of the atoms (Sr in green, Ir in blue, O in red). (b) An analogous representation for neutron scattering. Neutron scattering lengths are not dependent on atomic number, facilitating the location of light elements such as oxygen. (c) Simulated X-ray (upper) and neutron (lower) powder diffraction patterns of Sr₂IrO₄, with the intensities of the reflections normalised to the most intense in each. For both the X-ray and neutron simulations, the black pattern is for stoichiometric Sr₂IrO₄ whilst the red pattern is for a hypothetical analogue, Sr₂Ir□₄, that has an identical unit cell but all oxygen sites vacant (indicated by □). The asterisks indicate two superstructure reflections that are the result of a rotation of the IrO₆ octahedra. This rotation is crucial in determining the physical properties of the material but is almost invisible to X-rays.

This particular problem has been previously tackled for absorbing compounds by e.g. using high-flux instruments and optimising experimental geometry.¹⁰⁴ More recently, we have achieved a significant breakthrough by developing the use of ¹⁹³Ir, the lower-absorption isotope of the two naturally-occurring ones (37.3% ¹⁹¹Ir, σ_abs = 954 barns; and 62.7% ¹⁹³Ir, σ_abs = 111 barns). Whilst ¹⁹³Ir is commercially available its use in neutron scattering had not been reported in the literature and no scattering length, which parameterises the scattering strength and is necessary for data analysis such as Rietveld refinement, was available. Using a novel total scattering-based technique we determined the scattering length of ¹⁹³Ir, allowing samples enriched in this isotope to be used in neutron scattering studies effectively.¹⁰⁵ As such, high-resolution structural data (including detailed studies at high pressures that were effectively impossible previously⁵⁶) can now be obtained for iridates as a matter of course, allowing unprecedented access to the structural and spectroscopic information that is crucial for unravelling the origin of the exotic ground states and properties of these materials.^77,105

5.2 Determining composition

Accurately determining the composition of many of the materials of interest is also a significant challenge, and if sufficient care is not taken with this it is easily possible to assign physical properties to a mis-identified compound. Commonly-available techniques such as energy-dispersive X-ray analysis (EDX), inductively-coupled plasma analysis (ICP) and X-ray fluorescence spectroscopy (XRF) may not be sufficiently sensitive to light elements that their concentrations can be reasonably determined. Oxygen content can be determined by structural refinements using neutron diffraction data, but this is only reliable when the data are not affected by other complications such as absorption, oxidation state variability and crystal structure uncertainties.

The difficulty in determining composition is exemplified by the cases of Na₄Ir₃O₈ and Na₃Ir₃O₈. These two compounds have closely related crystal structures that are almost indistinguishable in laboratory powder X-ray diffraction patterns. Although a continuous transition from one structure to the other is not possible,⁷⁶ Na₃Ir₃O₈ was discovered during experiments aimed at growing single crystals of Na₄Ir₃O₈ as they occupy similar synthetic parameter space.¹⁰⁶ Furthermore, Na₄Ir₃O₈ is amenable to Na-deficiency, allowing Na_4−xIr₃O₈ to be synthesised – deliberately or otherwise – for a range of x.¹⁰⁷ Therefore, a synthesis can easily produce a sample that is not of the expected composition but without that being realised.

Related to this is the characterisation of chemical (in)homogeneity, which is often not considered until late in the investigation cycle. Certain synthesis methods also present particular characterisation challenges. For example, it is difficult to determine if an ion-exchange reaction has progressed to completion if the starting content of the species to be exchanged has not been determined. Another challenge lies in ensuring that the target transition metal oxidation state is actually realised, or whether mixed valences and/or non-stoichiometry are present. Examples of this include the double perovskites Ba₂CaIrO₆ (for which the stoichiometric Ir⁶⁺ phase is only stabilised by high-pressure synthesis)¹⁰⁸ and Sr₂CoIrO₆ (in which only 10% of the iridium content is Ir⁶⁺),¹⁰⁹ and pyrochlores such as Bi₂Ir₂O_7−y.⁸⁵ One recent development that may be particularly helpful in many cases is muon elemental analysis, which is sensitive to oxygen, lithium and other problematic light elements.¹¹⁰

5.3 Oxidation states and mixed valence

When the spin–orbit-coupling-active species is of mixed valence, correct assignment of oxidation states to its different crystallographic sites is imperative if the interactions between sites are to be correctly understood. Osmates are a prime case as osmium has several stable oxidation states, which compounds the difficulties derived from the determination of composition. For example, Li_2.15Os_0.85O₃ is the first reported honeycomb osmate but, in contrast to its single-valence iridate analogue, samples of this material were found to be approximately 70% Os⁵⁺ and 30% Os⁴⁺.⁶⁸ This has a significant effect on the magnetism as the mixture of nominally J_eff = 3/2 and J_eff = 0 ions creates disorder on the honeycomb spin network. Another intriguing example is the Os⁵⁺/Os⁶⁺ mixed oxide Sr₅Os₃O₁₃, which shows complex temperature-dependent behaviour.¹¹¹ In this material, one of the three osmium sites remains Os⁵⁺ across a wide temperature range, but the other two sites seem to show charge-ordering that varies continuously down to the Néel temperature, at which point full charge-order locks in alongside antiferromagnetic ordering. Precisely determining the oxidation states present and whether they are ordered, clustered or disordered is key to understanding the structures and magnetism of these materials but is non-trivial, often requiring facility-based techniques such as X-ray absorption spectroscopy (XAS).⁶⁸ However, recent progress in oxidation state control by a variety of synthetic routes is showing that the effort can certainly be worthwhile.^112,113

5.4 Disorder

The effects of strong spin–orbit coupling are incredibly sensitive to structural perturbations, so if the virtuous cycle of experimental observations feeding into theoretical predictions and vice versa is to be maintained, all the real-world nuances of the materials under study must be accounted for. This includes the identification and characterisation of disorder. Disorder is commonly seen as a negative complication that drives materials away from desirable exotic ground states but it is ubiquitous, and in fact can sometimes stabilise states that would not otherwise be accessible – for example, the formation of the spin liquid state in H₃LiIr₂O₆ is thought to be closely linked to hydrogen disorder.^7,114 However, this can be compared to honeycomb Li₂RhO₃, in which the effect of structural disorder on the magnetic ground state is to drive the formation not of a dynamic spin liquid but of a static glassy phase.^115,116 Disorder is difficult to characterise structurally, particularly if diffraction alone is used as it only reveals the periodic structure of crystalline materials, meaning that disorder can be overlooked. Complementary local-structure probes such as muon spin relaxation (μSR),^7,117 solid-state NMR¹¹⁸ and total scattering^70,119,120 therefore have the ability to make significant contributions towards unravelling the complexities of real quantum materials.

5.5 Stacking faults

Stacking faults are a particular type of disorder that merit further elaboration. These microstructural defects are discontinuities in the stacking pattern of layered materials, and as such are relevant in the honeycomb and Ruddlesden–Popper materials that are of principal interest for strong spin–orbit coupling at this time. In fact, the presence of stacking faults in these materials provides a huge challenge for the determination of their structure–property relationships and the connecting of experiment and theory.

Firstly, even a low concentration of stacking faults complicates structure determination. As they affect both the shapes and intensities of the peaks in a diffraction pattern in a complex manner it can be difficult to disentangle the contribution of stacking faults from those of factors such as occupational disorder, hence data are often misinterpreted. Until recently simulation was the only way to easily quantify stacking faults in powder diffraction patterns (Fig. 6); however, recent developments in Rietveld refinement software are making the inclusion of stacking faults into structural models more feasible, thus allowing for improved refinements and the more accurate structure determination for significantly faulted materials.^121,122 A rare trio of examples in the quantum materials field are the TOPAS refinements of H₃LiIr₂O₆, Ag₃LiRu₂O₆ and Ag₃LiIr₂O₆.^70,120 Single crystal diffraction can also be used to identify and study stacking faults, through the rods and streaks of diffuse scattering they generate in single crystal diffraction patterns (see e.g.ref. 66 and 123–125 for a range of examples).

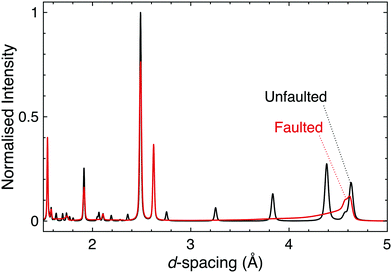Fig. 6 Simulated powder neutron diffraction patterns of D₃LiIr₂O₆ illustrate the challenge to characterisation caused by the presence of stacking faults. The black pattern is for a pristine, unfaulted structure, whilst the red is for a faulted structure modelled using DIFFaX.¹³⁰ Following experimental observations, a faulting parameter of x = 0.42 was used and the faults were evenly distributed between three different stacking types. The dramatic effect that introducing stacking faults has on the diffraction pattern, including the complete suppression of some reflections, demonstrates how the characterisation of layered materials can be significantly complicated by this microstructural phenomenon.

Stacking faults can also influence the behaviour of the electrons in a material. Early studies of α-RuCl₃ produced conflicting reports of physical properties that were shown to be largely due to high concentrations of stacking faults in certain samples. A comprehensive diffraction study was required before awareness of this issue became widespread.^66,126 Another clear example of the effect of stacking faults on physical properties may be found in the layered honeycomb iridates and ruthenates, a case in point being Ag₃LiIr₂O₆, for which samples show ordering or an absence of ordering depending on the level of faulting.^127,128

Complementary techniques such as electron microscopy have the potential to accelerate our understanding of, and ability to control, stacking fault disorder.⁷⁰ Furthermore, efforts to study and control stacking faults in α-Li₂IrO₃ and relatives are paralleled by current efforts in the energy materials field with regard to e.g. Li₂MnO₃,¹²⁹ another example of the generality of the materials science issues faced by quantum materials researchers.

5.6 Challenges related to synthesis

Not only is the progress of materials discovery hampered by the characterisation challenges outlined above, but the synthesis of materials with strong spin–orbit coupling is often non-trivial. Particular synthesis methods bring their own specific issues; for example, soft-chemistry techniques can be difficult to carry out reproducibly, and can also give products with very small particle sizes that complicate diffraction analysis through greater peak broadening. Single crystal growth is often very difficult and obtaining high quality crystals of large size is a particular issue, as techniques such as floating zone growth are often not suitable. Furthermore, single crystals often present different physical properties to polycrystalline samples that are nominally of the same material, and determining which form is displaying the intrinsic behaviour is not straightforward. The oft-made assumption that single crystals are ‘better’ than powders is not a reliable one.^131,132

One other major challenge is polymorphism. Syntheses of Li₂IrO₃, for example, often do not reliably produce the target polymorph, even when a previously-successful method is followed.^4,10,74 This can be related to reagent quality, as obtaining platinum group metal oxides of reliable composition may not be trivial – it is not unusual to find that batches of oxides contain fractions of the native element. Furthermore, when using isotopically enriched precursors for e.g. neutron scattering or NMR studies the range of available reagents may be reduced, forcing synthetic procedures to be re-designed. Control of stoichiometry is particularly difficult in soft-chemistry cases where the elemental composition makes chemical characterisation very difficult, and comparisons of the properties of samples prepared by different groups are limited if sufficient synthesis details and/or characterisation data are not included in publications. A further point of difficulty, particularly in the case of osmates but also not uncommon in iridates,¹³³ is the stabilisation of the nominal oxidation state. High-pressure (multi-GPa) or high-oxygen-pressure methods are two approaches that have been used to achieve this and access the higher oxidation states of osmium, such as Os⁸⁺ without significant production of volatile and highly toxic OsO₄ (which most osmates are unstable towards in an oxidising environment, and many even on storage in ambient air).^81,134,135 The stabilisation of single (or multiple controlled) oxidation states and further elucidating the chemistry of osmium in the solid state is a focus of current developments.⁸¹

6 Literature examples

The literature on iridates and other materials with strong spin–orbit coupling has focused on detailed explorations of the physics of their exotic electronic and magnetic states by property measurements, computation and the development of theory. In the understandable rush to discover and understand these exciting materials, detailed structural and chemical characterisation has often been neglected. This has led to conflicting reports of properties and ground states for particular materials, and theoretical models based on structures determined only by preliminary lab X-ray data. A prominent example is given by Na₂IrO₃. Four years after the properties of this material were first reported a detailed study demonstrated its air-sensitivity,¹³⁸ yet in reports to that point samples were routinely handled in air. Inspection of published diffraction patterns now allows the likely partial-decomposition to be identified. Studies of the ruthenium analogue of this material, Na₂RuO₃, have also been beset by issues of air sensitivity, with recent reports suggesting an entirely different ground state in samples that were handled in an air-free environment (Fig. 7).^132,137 Na₄Ir₃O₈ also degrades on storage under ambient conditions, with sodium gradually being lost and the physical properties changing substantially.^117,139,140 Such problems are not limited to materials containing volatile elements such as Na – in 2019 two groups reported property measurements of the KSbO₃-type iridate La₃Ir₃O₁₁, though as one found an anomaly at 3.5 K whilst the other did not, they cannot truly have been measuring the same material.^141,142 The tendency of pyrochlore iridates to oxygen non-stoichiometry underlies another example. A large literature generated on ‘pure’ A₂Ir₂O₇ materials claimed that these undergo a metal–insulator transition, but detailed investigations eventually showed that the stoichiometric materials do not undergo such a transition at all (Fig. 8).¹³³ Even more extremely, the compound Sr₅Ir₃O₁₁ was reported to exist in the Sr–Ir–O phase diagram but was later found to be simply the result of intergrowths of the n = 1 Ruddlesden–Popper phase Sr₂IrO₄ in the n = 2 phase Sr₃Ir₂O₇.¹⁴³ In other words, Sr₅Ir₃O₁₁ as a distinct compound does not in fact exist, although at the time of writing a search of the Inorganic Crystal Structure Database¹⁴⁴ suggests that it does, and the unwary user may inadvertently misidentify their material.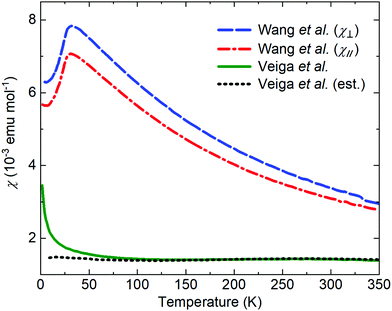

Fig. 7 The reported magnetic properties of Na₂RuO₃ provide an example of conflicting measurements of a quantum material. In 2014, Wang et al.¹³⁶ reported the susceptibility of a single-crystal sample oriented with the plane of the RuO₆ layers perpendicular to (blue) or parallel to (red) a 3 T applied field. In 2020, Veiga et al.¹³² reported the susceptibility of a polycrystalline sample in a 1 T applied field (green; the dotted line shows an estimated intrinsic susceptibility obtained by subtracting a Curie-like impurity contribution). Recent studies of polycrystalline samples have shown that Na₂RuO₃ is not stable in air at ambient conditions and that carefully handled samples do not display long-range magnetic order.^132,137

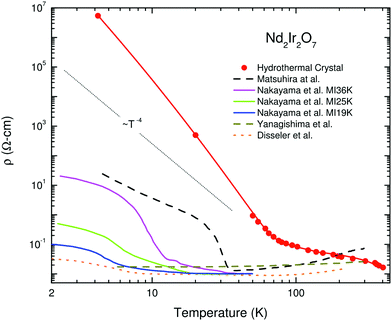Fig. 8 Variation in electrical resistivity for nominally pure samples of Nd₂Ir₂O₇ (note the logarithmic y-axis). Solid lines are measurements of single-crystal samples, whilst dashed lines are of polycrystalline ones. Rare-earth iridate pyrochlores are susceptible to non-stoichiometry of the form A_2−xIr₂O_7−y; the hydrothermally-prepared single crystal that has the highest resistivity also has a composition closest to stoichiometric, so its behaviour best represents that intrinsic to the material. Reprinted from ref. 133 with permission from Elsevier.

A final key difficulty in following the literature on these materials arises from the tendency to use physical property measurements for the characterisation of samples when chemical and structural methods are difficult. Whilst such measurements are essential for thorough characterisation, and in certain cases provide significantly more insight into sample quality than e.g. lab X-ray diffraction can,¹⁴⁵ it should not be used as a primary method unless the applicability of the technique has been rigorously determined. The reported physical properties of many compounds have often been shown later to be non-intrinsic, instead being due to decomposed samples, impurity phases or incorrect compositional assignment. Such problems have led to significant issues of reproducibility and held back our understanding of these important materials.

7 Conclusions

In this Perspective we have provided a brief introduction to the many challenges and opportunities that quantum materials with strong spin–orbit coupling afford to materials chemists. The often extreme sensitivity of their physical properties to disorder, distortions and other chemical factors makes the input of chemists all the more essential, with potential payoffs through more rigorous investigations and a significant strengthening of the virtuous cycle between theory and experiment that could pave the way for critical developments in a range of fundamental and applied fields. These challenges may well be familiar, and our hope is that by recognising the complementary efforts currently being pursued in a wide variety of materials chemistry communities interdisciplinary exchange will be promoted and our understanding of these fascinating materials advanced.

Author contributions

AJB: conceptualisation, investigation, visualisation, writing–original draft, writing–review & editing. AK: investigation, writing–original draft, writing–review & editing. ASG: conceptualisation, supervision, funding acquisition, project administration, investigation, visualisation, writing–original draft, writing–review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

ASG acknowledges funding through an EPSRC Early Career Fellowship EP/T011130/1. ASG and AK would like to acknowledge Dr T. Takayama and Prof. H. Takagi for their invaluable support, discussions and insights into materials with strong spin–orbit coupling (and many others) over the years. ASG acknowledges Dr K. S. Knight, Dr A. D. Fortes and Prof. W. I. F. David for insightful discussions.

Notes and references

1. Editorial, Nat. Phys., 2016, 12, 105.
2. Y. Tokura, M. Kawasaki and N. Nagaosa, Nat. Phys., 2017, 13, 1056–1068.
3. R. Cava, N. de Leon and W. Xie, Chem. Rev., 2021, 121, 2777–2779.
4. T. Takayama, J. Chaloupka, A. Smerald, G. Khaliullin and H. Takagi, J. Phys. Soc. Jpn., 2021, 90, 062001.
5. H. Takagi, T. Takayama, G. Jackeli, G. Khaliullin and S. E. Nagler, Nat. Rev. Phys., 2019, 1, 264–280.
6. G. Cao and P. Schlottmann, Rep. Prog. Phys., 2018, 81, 042502.
7. K. Kitagawa, T. Takayama, Y. Matsumoto, A. Kato, R. Takano, Y. Kishimoto, S. Bette, R. Dinnebier, G. Jackeli and H. Takagi, Nature, 2018, 554, 341–345.
8. J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005.
9. A. L. Strickler, D. Higgins and T. F. Jaramillo, ACS Appl. Energy Mater., 2019, 2, 5490–5498.
10. P. E. Pearce, A. J. Perez, G. Rousse, M. Saubanère, D. Batuk, D. Foix, E. McCalla, A. M. Abakumov, G. Van Tendeloo, M.-L. Doublet and J.-M. Tarascon, Nat. Mater., 2017, 16, 580–586.
11. D. I. Khomskii and S. V. Streltsov, Chem. Rev., 2021, 121, 2992–3030.
12. H. Kessler and M. Sienko, J. Solid State Chem., 1970, 1, 152–158.
13. P. M. Sarte, M. Songvilay, E. Pachoud, R. A. Ewings, C. D. Frost, D. Prabhakaran, K. H. Hong, A. J. Browne, Z. Yamani, J. P. Attfield, E. E. Rodriguez, S. D. Wilson and C. Stock, Phys. Rev. B, 2019, 100, 075143.
14. D. I. Khomskii, Transition Metal Compounds, Cambridge University Press, Cambridge, 2014.
15. N. Khan, D. Prishchenko, M. H. Upton, V. G. Mazurenko and A. A. Tsirlin, Phys. Rev. B, 2021, 103, 125158.
16. K. S. Pedersen, J. Bendix, A. Tressaud, E. Durand, H. Weihe, Z. Salman, T. J. Morsing, D. N. Woodruff, Y. Lan, W. Wernsdorfer, C. Mathonière, S. Piligkos, S. I. Klokishner, S. Ostrovsky, K. Ollefs, F. Wilhelm, A. Rogalev and R. Clérac, Nat. Commun., 2016, 7, 12195.
17. S. Calder, G.-X. Cao, S. Okamoto, J. W. Kim, V. R. Cooper, Z. Gai, B. C. Sales, M. D. Lumsden, D. Mandrus and A. D. Christianson, Phys. Rev. B, 2014, 89, 081104.
18. J. J. Randall, Jr., L. Katz and R. Ward, J. Am. Chem. Soc., 1957, 79, 266–267.
19. N. Lee, E. Ko, H. Y. Choi, Y. J. Hong, M. Nauman, W. Kang, H. J. Choi, Y. J. Choi and Y. Jo, Adv. Mater., 2018, 30, 1805564.
20. C. Lu and J.-M. Liu, Adv. Mater., 2019, 1904508.
21. J. Matsuno, J. Fujioka, T. Okuda, K. Ueno, T. Mizokawa and T. Katsufuji, Sci. Technol. Adv. Mater., 2018, 19, 899–908.
22. M. Kepenekian and J. Even, J. Phys. Chem. Lett., 2017, 8, 3362–3370.
23. K. Fujiwara, Y. Fukuma, J. Matsuno, H. Idzuchi, Y. Niimi, Y. Otani and H. Takagi, Nat. Commun., 2013, 4, 2893.
24. S. F. A. Kettle, Physical Inorganic Chemistry: A Coordination Chemistry Approach, 2013, Oxford University Press, Oxford.
25. J. Bertinshaw, Y. K. Kim, G. Khaliullin and B. J. Kim, Annu. Rev. Condens. Matter Phys., 2019, 10, 315–336.
26. J. R. Chamorro, T. M. McQueen and T. T. Tran, Chem. Rev., 2021, 121, 2898–2934.
27. C. Broholm, R. J. Cava, S. A. Kivelson, D. G. Nocera, M. R. Norman and T. Senthil, Science, 2020, 367, eaay0668.
28. A. A. Tsirlin and P. Gegenwart, 2021, arXiv:2103.14073.
29. S. M. Winter, Y. Li, H. O. Jeschke and R. Valentí, Phys. Rev. B, 2016, 93, 214431.
30. J. Knolle and R. Moessner, Annu. Rev. Condens. Matter Phys., 2019, 10, 451–472.
31. W. Sun, J.-Y. Liu, X.-Q. Gong, W.-Q. Zaman, L.-M. Cao and J. Yang, Sci. Rep., 2016, 6, 38429.
32. W. Sun, Z. Wang, Z. Zhou, Y. Wu, W. Q. Zaman, M. Tariq, L.-M. Cao, X.-Q. Gong and J. Yang, Chem. Commun., 2019, 55, 5801–5804.
33. C. W. Song, J. Lim, H. B. Bae and S.-Y. Chung, Energy Environ. Sci., 2020, 13, 4178–4188.
34. Y. Yu, P. Karayaylali, S. H. Nowak, L. Giordano, M. Gauthier, W. Hong, R. Kou, Q. Li, J. Vinson, T. Kroll, D. Sokaras, C.-J. Sun, N. Charles, F. Maglia, R. Jung and Y. Shao-Horn, Chem. Mater., 2019, 31, 7864–7876.
35. P. E. Pearce, G. Rousse, O. M. Karakulina, J. Hadermann, G. Van Tendeloo, D. Foix, F. Fauth, A. M. Abakumov and J.-M. Tarascon, Chem. Mater., 2018, 30, 3285–3293.
36. J. Yu, X. Wu, D. Guan, Z. Hu, S.-C. Weng, H. Sun, Y. Song, R. Ran, W. Zhou, M. Ni and Z. Shao, Chem. Mater., 2020, 32, 4509–4517.
37. T. Takayama, A. Kato, R. Dinnebier, J. Nuss, H. Kono, L. S. I. Veiga, G. Fabbris, D. Haskel and H. Takagi, Phys. Rev. Lett., 2015, 114, 077202.
38. S. Tepavcevic, H. Zheng, D. G. Hinks, B. Key, L. Ward, Z. Lu, C. Stoumpos, Y. Ren, J. W. Freeland, C. Wolverton, P. Phillips, R. Klie, J. F. Mitchell and N. M. Markovic, Adv. Energy Mater., 2020, 10, 1903128.
39. K. Górnicka, X. Gui, B. Wiendlocha, L. T. Nguyen, W. Xie, R. J. Cava and T. Klimczuk, Adv. Funct. Mater., 2021, 31, 2007960.
40. D. Hirai and Z. Hiroi, J. Phys.: Condens. Matter, 2021, 33, 135603.
41. H. Ishikawa, T. Takayama, R. K. Kremer, J. Nuss, R. Dinnebier, K. Kitagawa, K. Ishii and H. Takagi, Phys. Rev. B, 2019, 100, 045142.
42. G. Khaliullin, Phys. Rev. Lett., 2013, 111, 197201.
43. O. N. Meetei, W. S. Cole, M. Randeria and N. Trivedi, Phys. Rev. B, 2015, 91, 054412.
44. B. J. Kim, H. Jin, S. J. Moon, J.-Y. Kim, B.-G. Park, C. S. Leem, J. Yu, T. W. Noh, C. Kim, S.-J. Oh, J.-H. Park, V. Durairaj, G. Cao and E. Rotenberg, Phys. Rev. Lett., 2008, 101, 076402.
45. P. A. Cox, Transition metal oxides: an introduction to their electronic structure and properties, Oxford University Press, Oxford, 2010.
46. G. Jackeli and G. Khaliullin, Phys. Rev. Lett., 2009, 102, 017205.
47. N. Nagaosa, T. Morimoto and Y. Tokura, Nat. Rev. Mater., 2020, 5, 621–636.
48. K. Wang, B. Xu, C. W. Rischau, N. Bachar, B. Michon, J. Teyssier, Y. Qiu, T. Ohtsuki, B. Cheng, N. P. Armitage, S. Nakatsuji and D. van der Marel, Nat. Phys., 2020, 16, 1194–1198.
49. K. Ueda, T. Oh, B.-J. Yang, R. Kaneko, J. Fujioka, N. Nagaosa and Y. Tokura, Nat. Commun., 2017, 8, 15515.
50. T. Kondo, M. Nakayama, R. Chen, J. J. Ishikawa, E.-G. Moon, T. Yamamoto, Y. Ota, W. Malaeb, H. Kanai, Y. Nakashima, Y. Ishida, R. Yoshida, H. Yamamoto, M. Matsunami, S. Kimura, N. Inami, K. Ono, H. Kumigashira, S. Nakatsuji, L. Balents and S. Shin, Nat. Commun., 2015, 6, 10042.
51. B. H. Kim, D. V. Efremov and J. van den Brink, Phys. Rev. Mater., 2019, 3, 014414.
52. A. J. Browne and J. P. Attfield, Phys. Rev. B, 2020, 101, 024112.
53. K. R. Knox, A. M. M. Abeykoon, H. Zheng, W.-G. Yin, A. M. Tsvelik, J. F. Mitchell, S. J. L. Billinge and E. S. Bozin, Phys. Rev. B, 2013, 88, 174114.
54. S. A. J. Kimber, I. I. Mazin, J. Shen, H. O. Jeschke, S. V. Streltsov, D. N. Argyriou, R. Valentí and D. I. Khomskii, Phys. Rev. B, 2014, 89, 081408.
55. E. S. Bozin, W. G. Yin, R. J. Koch, M. Abeykoon, Y. S. Hor, H. Zheng, H. C. Lei, C. Petrovic, J. F. Mitchell and S. J. L. Billinge, Nat. Commun., 2019, 10, 3638.
56. T. Takayama, A. Krajewska, A. S. Gibbs, A. N. Yaresko, H. Ishii, H. Yamaoka, K. Ishii, N. Hiraoka, N. P. Funnell, C. L. Bull and H. Takagi, Phys. Rev. B, 2019, 99, 125127.
57. Y. Wang, R. Wang, J. Kim, M. H. Upton, D. Casa, T. Gog, G. Cao, G. Kotliar, M. P. M. Dean and X. Liu, Phys. Rev. Lett., 2019, 122, 106401.
58. Y. Shi, Y. Guo, X. Wang, A. J. Princep, D. Khalyavin, P. Manuel, Y. Michiue, A. Sato, K. Tsuda, S. Yu, M. Arai, Y. Shirako, M. Akaogi, N. Wang, K. Yamaura and A. T. Boothroyd, Nat. Mater., 2013, 12, 1024–1027.
59. A. J. Princep, H. L. Feng, Y. F. Guo, F. Lang, H. M. Weng, P. Manuel, D. Khalyavin, A. Senyshyn, M. C. Rahn, Y. H. Yuan, Y. Matsushita, S. J. Blundell, K. Yamaura and A. T. Boothroyd, Phys. Rev. B, 2020, 102, 104410.
60. D. Hirai, H. Sagayama, S. Gao, H. Ohsumi, G. Chen, T.-H. Arima and Z. Hiroi, Phys. Rev. Res., 2020, 2, 022063.
61. P. G. Radaelli, Y. Horibe, M. J. Gutmann, H. Ishibashi, C. H. Chen, R. M. Ibberson, Y. Koyama, Y.-S. Hor, V. Kiryukhin and S.-W. Cheong, Nature, 2002, 416, 155–158.
62. J. Nasu and Y. Motome, Phys. Rev. B, 2014, 90, 045102.
63. H. Müller-Buschbaum, Z. Anorg. Allg. Chem., 2005, 631, 1005–1028.
64. H. Müller-Buschbaum, Z. Anorg. Allg. Chem., 2008, 634, 2111–2124.
65. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
66. R. D. Johnson, S. C. Williams, A. A. Haghighirad, J. Singleton, V. Zapf, P. Manuel, I. I. Mazin, Y. Li, H. O. Jeschke, R. Valentí and R. Coldea, Phys. Rev. B, 2015, 92, 235119.
67. K. Brodersen, F. Moers and H. G. Schnering, Naturwissenschaften, 1965, 52, 205–206.
68. M. K. Wallace, P. G. LaBarre, J. Li, S.-T. Pi, W. E. Pickett, D. S. Dessau, D. Haskel, A. P. Ramirez and M. A. Subramanian, Sci. Rep., 2018, 8, 6605.
69. K. Kataoka, D. Hirai, T. Yajima, D. Nishio-Hamane, R. Ishii, K.-Y. Choi, D. Wulferding, P. Lemmens, S. Kittaka, T. Sakakibara, H. Ishikawa, A. Matsuo, K. Kindo and Z. Hiroi, J. Phys. Soc. Jpn., 2020, 89, 114709.
70. S. Bette, T. Takayama, V. Duppel, A. Poulain, H. Takagi and R. E. Dinnebier, Dalton Trans., 2019, 48, 9250–9259.
71. J. H. Roudebush, K. A. Ross and R. J. Cava, Dalton Trans., 2016, 45, 8783–8789.
72. F. Bahrami, W. Lafargue-Dit-Hauret, O. I. Lebedev, R. Movshovich, H.-Y. Yang, D. Broido, X. Rocquefelte and F. Tafti, Phys. Rev. Lett., 2019, 123, 237203.
73. M. Abramchuk, C. Ozsoy-Keskinbora, J. W. Krizan, K. R. Metz, D. C. Bell and F. Tafti, J. Am. Chem. Soc., 2017, 139, 15371–15376.
74. K. A. Modic, T. E. Smidt, I. Kimchi, N. P. Breznay, A. Biffin, S. Choi, R. D. Johnson, R. Coldea, P. Watkins-Curry, G. T. McCandless, J. Y. Chan, F. Gandara, Z. Islam, A. Vishwanath, A. Shekhter, R. D. McDonald and J. G. Analytis, Nat. Commun., 2014, 5, 4203.
75. H. Kuriyama, J. Matsuno, S. Niitaka, M. Uchida, D. Hashizume, A. Nakao, K. Sugimoto, H. Ohsumi, M. Takata and H. Takagi, Appl. Phys. Lett., 2010, 96, 182103.
76. M. V. Talanov, V. B. Shirokov and V. M. Talanov, Inorg. Mater., 2016, 52, 815–823.
77. T. Takayama, A. N. Yaresko, A. S. Gibbs, K. Ishii, D. Kukusta and H. Takagi, Phys. Rev. Mater., 2020, 4, 075002.
78. W. R. Gemmill, M. D. Smith, Y. A. Mozharivsky, G. J. Miller and H.-C. zur Loye, Inorg. Chem., 2005, 44, 7047–7055.
79. Y. Hinatsu and Y. Doi, J. Solid State Chem., 2013, 198, 176–185.
80. H. Nishimine, Y. Doi, Y. Hinatsu and M. Sato, J. Ceram. Soc. Jpn., 2007, 115, 577–581.
81. E. S. Converse, J. Li, D. Haskel, P. G. LaBarre, A. P. Ramirez and M. A. Subramanian, Inorg. Chem., 2020, 59, 1227–1233.
82. S. M. Disseler, C. Dhital, T. C. Hogan, A. Amato, S. R. Giblin, C. de la Cruz, A. Daoud-Aladine, S. D. Wilson and M. J. Graf, Phys. Rev. B, 2012, 85, 174441.
83. J. Reading, C. S. Knee and M. T. Weller, J. Mater. Chem., 2002, 12, 2376–2382.
84. J. S. Gardner, M. J. P. Gingras and J. E. Greedan, Rev. Mod. Phys., 2010, 82, 53–107.
85. B. J. Kennedy, J. Solid State Chem., 1996, 123, 14–20.
86. J. M. Longo, J. A. Kafalas and R. J. Arnott, J. Solid State Chem., 1971, 3, 174–179.
87. Y. G. Shi, Y. F. Guo, S. Yu, M. Arai, A. A. Belik, A. Sato, K. Yamaura, E. Takayama-Muromachi, H. F. Tian, H. X. Yang, J. Q. Li, T. Varga, J. F. Mitchell and S. Okamoto, Phys. Rev. B, 2009, 80, 161104(R).
88. G. King and P. M. Woodward, J. Mater. Chem., 2010, 20, 5785–5796.
89. B. F. Phelan, J. Krizan, W. Xie, Q. Gibson and R. J. Cava, Phys. Rev. B, 2015, 91, 155117.
90. L. T. Nguyen and R. J. Cava, Chem. Rev., 2021, 121, 2935–2965.
91. T. Takayama, A. N. Yaresko and H. Takagi, J. Phys.: Condens. Matter, 2019, 31, 074001.
92. S. Guo, K. M. Powderly and R. J. Cava, Dalton Trans., 2020, 49, 12018–12024.
93. Y. Yuan, H. L. Feng, Y. Shi, Y. Tsujimoto, A. A. Belik, Y. Matsushita, M. Arai, J. He, M. Tanaka and K. Yamaura, Sci. Technol. Adv. Mater., 2014, 15, 064901.
94. Y. Hinatsu, J. Ceram. Soc. Jpn., 2015, 123, 845–852.
95. S. V. Streltsov and D. I. Khomskii, JETP Lett., 2018, 108, 686–690.
96. M. Bremholm, S. E. Dutton, P. W. Stephens and R. J. Cava, J. Solid State Chem., 2011, 184, 601–607.
97. S. Guo, R. Zhong, W. Wang, J. Tao, D. Ni and R. J. Cava, J. Am. Chem. Soc., 2020, 142, 5389–5395.
98. S. Nishimoto, V. M. Katukuri, V. Yushankhai, H. Stoll, U. K. Rößler, L. Hozoi, I. Rousochatzakis and J. van den Brink, Nat. Commun., 2016, 7, 10273.
99. R. Morrow, J. Yan, M. A. McGuire, J. W. Freeland, D. Haskel and P. M. Woodward, Phys. Rev. B, 2015, 92, 094435.
100. R. Yadav, M. S. Eldeeb, R. Ray, S. Aswartham, M. I. Sturza, S. Nishimoto, J. van den Brink and L. Hozoi, Chem. Sci., 2019, 10, 1866–1872.
101. V. F. Sears, Neutron News, 1992, 3, 26–37.
102. H. Rauch and W. Waschkowski, Neutron Data Booklet, Old City Publishing, 2nd edn, 2003.
103. NIST, Neutron scattering lengths and cross sections, https://www.ncnr.nist.gov/resources/n-lengths/.
104. A. Biffin, R. D. Johnson, S. Choi, F. Freund, S. Manni, A. Bombardi, P. Manuel, P. Gegenwart and R. Coldea, Phys. Rev. B, 2014, 90, 205116.
105. A. C. Hannon, A. S. Gibbs and H. Takagi, J. Appl. Crystallogr., 2018, 51, 854–866.
106. T. Takayama, A. Yaresko, A. Matsumoto, J. Nuss, K. Ishii, M. Yoshida, J. Mizuki and H. Takagi, Sci. Rep., 2014, 4, 6818.
107. S. Yoon, S.-H. Baek, A. Balodhi, W.-J. Lee, K.-Y. Choi, I. Watanabe, J. S. Lord, B. Büchner, B. J. Suh and Y. Singh, J. Phys.: Condens. Matter, 2015, 27, 485603.
108. G. Demazeau, D. Y. Jung, L. Fournès, J. P. Sanchez, E. Colineau and A. Blaise, High Pressure Res., 1994, 12, 313–322.
109. S. Agrestini, K. Chen, C.-Y. Kuo, L. Zhao, H.-J. Lin, C.-T. Chen, A. Rogalev, P. Ohresser, T.-S. Chan, S.-C. Weng, G. Auffermann, A. Völzke, A. C. Komarek, K. Yamaura, M. W. Haverkort, Z. Hu and L. H. Tjeng, Phys. Rev. B, 2019, 100, 014443.
110. A. D. Hillier, D. McK. Paul and K. Ishida, Microchem. J., 2016, 125, 203–207.
111. S. A. Mohitkar, J. Nuss, H. A. Höppe, C. Felser and M. Jansen, Dalton Trans., 2018, 47, 5968–5976.
112. K. Sardar, J. Fisher, D. Thompsett, M. R. Lees, G. J. Clarkson, J. Sloan, R. J. Kashtiban and R. I. Walton, Chem. Sci., 2011, 2, 1573.
113. A. Talanov, W. A. Phelan, Z. A. Kelly, M. A. Siegler and T. M. McQueen, Inorg. Chem., 2014, 53, 4500–4507.
114. W.-H. Kao, J. Knolle, G. B. Halász, R. Moessner and N. B. Perkins, Phys. Rev. X, 2021, 11, 011034.
115. V. M. Katukuri, S. Nishimoto, I. Rousochatzakis, H. Stoll, J. van den Brink and L. Hozoi, Sci. Rep., 2015, 5, 14718.
116. I. I. Mazin, S. Manni, K. Foyevtsova, H. O. Jeschke, P. Gegenwart and R. Valentí, Phys. Rev. B, 2013, 88, 035115.
117. A. Shockley, F. Bert, J.-C. Orain, Y. Okamoto and P. Mendels, Phys. Rev. Lett., 2015, 115, 047201.
118. R. F. Moran, D. M. Dawson and S. E. Ashbrook, Int. Rev. Phys. Chem., 2017, 36, 39–115.
119. H. Playford, R. Singh, L. J. Chang, K. Sardar, A. Hannon, M. Tucker, M. Lees, G. Balakrishnan and R. Walton, Acta Crystallogr., Sect. A: Found. Crystallogr., 2014, 70, C869.
120. S. Bette, T. Takayama, K. Kitagawa, R. Takano, H. Takagi and R. E. Dinnebier, Dalton Trans., 2017, 46, 15216–15227.
121. C. M. Ainsworth, J. W. Lewis, C.-H. Wang, A. A. Coelho, H. E. Johnston, H. E. A. Brand and J. S. O. Evans, Chem. Mater., 2016, 28, 3184–3195.
122. A. A. Coelho, J. S. O. Evans and J. W. Lewis, J. Appl. Crystallogr., 2016, 49, 1740–1749.
123. H.-B. Bürgi, M. Hostettler, H. Birkedal and D. Schwarzenbach, Z. Kristallogr. - Cryst. Mater., 2005, 220, 1066–1075.
124. H. B. Cao, A. Banerjee, J.-Q. Yan, C. A. Bridges, M. D. Lumsden, D. G. Mandrus, D. A. Tennant, B. C. Chakoumakos and S. E. Nagler, Phys. Rev. B, 2016, 93, 134423.
125. J. E. Auckett, W. T. Lee, K. C. Rule, A. Bosak and C. D. Ling, Inorg. Chem., 2019, 58, 12317–12324.
126. A. Banerjee, C. A. Bridges, J.-Q. Yan, A. A. Aczel, L. Li, M. B. Stone, G. E. Granroth, M. D. Lumsden, Y. Yiu, J. Knolle, S. Bhattacharjee, D. L. Kovrizhin, R. Moessner, D. A. Tennant, D. G. Mandrus and S. E. Nagler, Nat. Mater., 2016, 15, 733–740.
127. F. Bahrami, E. M. Kenney, C. Wang, A. Berlie, O. I. Lebedev, M. J. Graf and F. Tafti, Phys. Rev. B, 2021, 103, 094427.
128. J. Wang, W. Yuan, T. Imai, P. M. Singer, F. Bahrami and F. Tafti, Phys. Rev. B, 2021, 103, 214405.
129. A. S. Menon, D. O. Ojwang, T. Willhammar, V. K. Peterson, K. Edström, C. P. Gomez and W. R. Brant, ACS Appl. Mater. Interfaces, 2020, 12, 5939–5950.
130. M. M. J. Treacy, J. M. Newsam and M. W. Deem, Proc. R. Soc. London, Ser. A, 1991, 433, 499–520.
131. N. H. Sung, H. Gretarsson, D. Proepper, J. Porras, M. Le Tacon, A. V. Boris, B. Keimer and B. J. Kim, Philos. Mag., 2016, 96, 413–426.
132. L. S. I. Veiga, M. Etter, E. Cappelli, H. Jacobsen, J. G. Vale, C. D. Dashwood, D. Le, F. Baumberger, D. F. McMorrow and R. S. Perry, Phys. Rev. Mater., 2020, 4, 094202.
133. A. W. Sleight and A. P. Ramirez, Solid State Commun., 2018, 275, 12–15.
134. K. M. Mogare, W. Klein and M. Jansen, Z. Anorg. Allg. Chem., 2005, 631, 468–471.
135. S. Injac, A. K. L. Yuen, M. Avdeev, F. Orlandi and B. J. Kennedy, Phys. Chem. Chem. Phys., 2019, 21, 7261–7264.
136. J. C. Wang, J. Terzic, T. F. Qi, F. Ye, S. J. Yuan, S. Aswartham, S. V. Streltsov, D. I. Khomskii, R. K. Kaul and G. Cao, Phys. Rev. B, 2014, 90, 161110.
137. T. Takayama, A. Mukundan, A. Krajewska, D. Le, A. Gibbs and H. Takagi, Magnetic excitations in honeycomb ruthenate Na2RuO3, 2019, https://data.isis.stfc.ac.uk/doi/STUDY/101225406/.
138. J. Krizan, J. Roudebush, G. Fox and R. Cava, Mater. Res. Bull., 2014, 52, 162–166.
139. A. Balodhi, A. Thamizhavel and Y. Singh, Phys. Rev. B, 2015, 91, 224409.
140. R. Dally, T. Hogan, A. Amato, H. Luetkens, C. Baines, J. Rodriguez-Rivera, M. J. Graf and S. D. Wilson, Phys. Rev. Lett., 2014, 113, 247601.
141. T. Aoyama, K. Emi, C. Tabata, Y. Nambu, H. Nakao, T. Yamauchi and K. Ohgushi, J. Phys. Soc. Jpn., 2019, 88, 093706.
142. J. Yang, J. R. Wang, W. L. Zhen, L. Ma, L. S. Ling, W. Tong, C. J. Zhang, L. Pi and W. K. Zhu, Phys. Rev. B, 2019, 100, 205107.
143. R. Harlow, Z. Li, W. Marshall, M. Crawford and M. Subramanian, Mater. Res. Bull., 1995, 30, 217–223.
144. M. Hellenbrandt, Crystallogr. Rev., 2004, 10, 17–22.
145. A. P. Mackenzie, R. K. W. Haselwimmer, A. W. Tyler, G. G. Lonzarich, Y. Mori, S. Nishizaki and Y. Maeno, Phys. Rev. Lett., 1998, 80, 161–164.

---