The efficacy of Lewis affinity scale metrics to represent solvent interactions with reagent salts in all-inorganic metal halide perovskite solutions

Abstract

Solvents employed in the solution processing of metal halide perovskites are known to play a key role in defining the morphology and properties of the resulting thin film, and thus the performance of perovskite solar cell devices. Accurate metrics are needed that are capable of differentiating among candidates, finding solvents that adequately solubilize the various precursor species in solution and facilitate the nucleation and growth of these materials. Existing metrics such as the unsaturated Mayer bond order (UMBO) and the Gutmann donor number (DN) have been tested for lead iodide perovskite systems; but there has yet to be a comprehensive study on their transferability to lead-free perovskite solutions. We use ab initio methods (density functional theory) and regression analysis tools to study the usefulness of DN and BF₃ affinity scales in this regard. We compared the relative effectiveness of these scales to describe interactions between solvents and BX_n perovskite salts of lead (Pb²⁺), tin (Sn²⁺ and Sn⁴⁺), germanium (Ge²⁺), bismuth (Bi³⁺), and antimony (Sb³⁺ and Sb⁵⁺). The DN proved to be a better representation than the BF₃ of such interactions, reflecting the closer similarity of these species to the “parent” SbCl₅ Lewis acid than to BF₃. In addition, we have uncovered the usefulness of the lithium cation affinity metric (LCA) to describe the strength of interactions between solvents and A-site cations (e.g. Na⁺, K⁺, Rb⁺ and Cs⁺) in all-inorganic metal halide perovskite solutions. We find that the coordination strengths of solvents towards species in all-inorganic metal halide perovskite solutions are best described by two different metrics with distinct modes of action: DN differentiates among BX_n salt complexes, and LCA among A-site cation species. This revelation can help guide the choice of solvent to optimize processing conditions. It also emphasizes the importance of selecting solvents whose DN and LCA optimize coordination to key Lewis acid species in all-inorganic perovskite solutions.

---

1 Introduction

Metal halide perovskites (hereafter shortened to “perovskites”) exhibit electronic and optical properties that have resulted in their consideration for use in photovoltaic (PV) devices,^1,2 light-emitting diodes (LED),^3–5 and X-ray detection.^6–8 Beyond their tunable band gap,⁹ perovskites also offer the ability to adjust the perovskite composition and processing protocol.^10,11 This has led to a commercially competitive solar cell efficiency of over 25%.¹² In addition, these materials have the advantage of being able to be processed in solution at room temperature using earth-abundant species.^13–18

Perovskites consist of a large class of materials that possess a general chemical formula of ABX₃, where A and B represent different site-specific cations, and X is an anion (most often, a halide ion in the case of metal halide perovskites).^9,19,20 This presents hundreds of candidate material options by altering the choice of the B-site cation (typically Pb and/or Sn), the A-site cation (methyl ammonium (MA), cesium (Cs), formamidinium (FA)), and three choices of anions/halides (chloride (Cl), bromide (Br), and iodide (I)).^9–11 But these materials are not limited to a single selection of A, B, or X species; mixed combinations of A-site cations (A⁺), halides, and even B-cations have also been studied.^21–26 In addition, the oxidation state of some B-site cations can be chosen to introduce different dimensional structures and classes, maintaining the charge neutrality of the final material.^20,27,28

These hundreds of ABX₃ combinations need to be coupled with all the possible blends of bath solvents and antisolvents that facilitate the dissolution and nucleation of the perovskite constituents in solution.²⁹ As a result, there are simply far too many options (at least 500 000) to investigate using current experimental methods. Clearly, an exploration of even a fraction of these options would benefit from the use of machine learning techniques.³⁰ One such study³¹ ranked better performing perovskite compositions in pure solvents, which was an encouraging first step towards a thorough exploration of a larger set of compositional and processing options.

Processing conditions and the composition of the reagent species exert a strong influence on the properties of the final film.³² One well-known influence is the choice of solvent^13–18 and its action in controlling the rate of homogeneous crystal nucleation and subsequent growth of the thin film via its affinity for Lewis acids in perovskite solution (A- and B-site cation species). The interactions between solvents and these perovskite-specific Lewis acids results in solvent–solute solvation structures and intermediate phases that precede the formation of the final perovskite structure.^{13,17,29,33–37}

In concert, there has been a long-standing quest for metrics that can evaluate solvent efficacy without the need for experimental (or indeed computational) investigations. The community's experiential knowledge has uncovered some “good” solvents (e.g., DMSO, DMF and GBL).^38–40 But whether there are better solvents, or solvent blends, remains unclear, let alone how to identify them without experimentation.^41,42

An experimental Lewis affinity metric like the Gutmann donor number (DN),^43,44 and a computational metric like the Unsaturated Mayer Bond Order (UMBO),⁴⁰ based on the Mayer bond order⁴⁵ and the tendency for Pb²⁺ to form dative bonds with the most polar atom in the solvent molecule, have proven useful for uncovering the efficacy of new solvent additives like dimethyl propylene urea (DMPU) and tetrahydrothiophene-1-oxide (THTO), respectively.^13,46 Both these uncommon solvents could be introduced as additives to achieve higher quality films by delaying the nucleation of the perovskite crystal from solution.^13,42,46,47 Earlier posited metrics, such as the Hansen solubility of the solvent, have fallen out of favor.^48,49 Electronic properties of solvents, such as the dipole moment, have been used to determine which solvents are better suited for coordinating with perovskite species. But, like the UMBO, such electronic properties may not always capture the strength of the solvent–salt interactions if the nature of the bonding comes from a different source.⁴⁴ For example, “covalent” bonding, as defined in the textbook by Gal et al., includes bonding between Lewis acids and bases that are governed by orbital overlaps between the bonding atoms. This type of orbital-controlled bonding is particularly significant between Lewis acids or bases that are considered “soft”. On the other hand, interactions between a “harder” Lewis acid and base are generally governed by electrostatic forces and are considered to be charge-controlled interactions.^44,50

The donor number, DN, was thought to be more effective in capturing both these bonding types (“covalent” – more commonly considered to be dative bonding – and electrostatic) but, by design, the DN specifically captures the interaction between solvents (bases) and the reference Lewis acid, antimony pentachloride (SbCl₅).^43,44 As a result, this has generated some skepticism towards use of this metric for the rather different perovskite-specific species.⁵¹ Nonetheless, several studies^52–59 have embraced this metric as a guide of solvent strength following the demonstration of its ability to trend reliably for a list of popular solvents.¹³ Probing the efficacy of the DN for perovskite species is worth exploring further in terms of its extensibility to a much larger ‘pool’ of solvents and also to determine its effectiveness in describing enthalpic interactions between solvents and perovskite salts^40,58 rather than using macroscopic observations like thin film morphology and solar cell efficiency.¹³ In addition, there exist other Lewis affinity scales that have not yet been explored for their appropriateness to perovskite building blocks in solution. One of these is the BF₃ affinity scale,^43,44 which captures the interaction between a solvent (Lewis base) and boron trifluoride (as the reference Lewis acid), that could potentially yield a stronger correlation between the solvent and perovskite-specific species.

In this paper, we explore which of the two Lewis affinity metrics (the (SbCl₅)-based DN or a BF₃-based one) is better suited to describe interactions between solvents and isolated units of a perovskite's B-site cation salt (BX_n salt complexes), which includes BX₂, BX₃, BX₄, and BX₅ species in solution. Here B represents the B-site cations of atoms which can exhibit different oxidation states (Pb(II), Sn(II/IV), Ge(II), Sb(III/V), Bi(III)), and X represents the halide ions (I⁻, Br⁻, Cl⁻) comprising the salt complexes. Further, it has been suggested that interactions between solvents and A-site cations (A⁺) like Na⁺, K⁺, Rb⁺ and Cs^+60–63 might also play a role in the evolution and growth of the perovskite film.^51,64,65 We have also studied the lithium cation affinity (LCA),^44,66–68 which captures the interaction strength between Li⁺ and a Lewis base, as a potential substitute for solvent–A⁺ interactions in a perovskite solution.

These three affinity scales, the DN, BF₃, and LCA, were studied to determine their transferability across a variety of perovskite species in solution, identifying which of the three are best suited to represent Lewis acid–base interactions that impact the quality of the final all-inorganic perovskite thin film.^51,69

2 Computational estimation of affinity scale metrics

Our objective was to study the suitability of the three affinity scales, outlined in the ESI,† to describe the interactions between solvents and Lewis acids in perovskite solutions (BX_n salt complexes and A-site cations). The first step involved predicting values for the three affinity scales for solvents that have been used in perovskite processing yet have no reported values in the literature, e.g., S-donor solvents, phosphoamide, methylamine and sulfoxide solvents.^{46,47,55,58,70}

In this study, our first task was to use linear regression with a least squares optimization approach^71,72 to fit our computed binding enthalpy data to experimental values from numerous sources.^{44,66,68,73–75} The enthalpy data were determined from density functional theory (DFT) calculations at 0 K using the ORCA-DFT package.⁷⁶ But, since experimental measurements for the DN and BF₃ are determined at a different temperature, 298 K, we assumed a linear fit to compensate for the temperature differences. Eqn (S1)–(S6) in the ESI† outline the procedure to calculate binding enthalpies for the three affinity scales and their subsequent fitting to linear models of the experimental results. Eqn (1) below presents the general form for calculations of the binding enthalpy (BE) between a Lewis base (LB) and a Lewis acid (LA) in terms of the energies for the bound acid–base species minus energies for the acid and the base:

−BE_LA:LB = E(LA:LB) − E(LB) − E(LA) (1)

For the BF₃ and DN scales, each of the constituent molecules was optimized in an implicit solvent medium using a conductor-like polarizable continuum model (CPCM),⁷⁷ which uses the dielectric constant of a solvent to replicate the solvent environment in which the DN and BF₃ scales are experimentally conducted, i.e., 1,2-dichloroethane (10.6) and dichloromethane (8.96), respectively.⁴⁴ The LCA calculations were determined in the gas phase,⁴⁴ so there was no need to include an implicit solvent medium in these simulations.

For each affinity scale, eighteen solvents were used to train our linear model, while five more were retained for independent testing (validation) of the resultant model. The different linear models are based on results from four DFT functionals: two generalized gradient approximation (GGA) functionals, namely B97 ⁷⁸ and PBE,⁷⁹ and two hybrid functionals (PW6B95 ⁸⁰ and B3LYP⁸¹). A triple zeta basis set (def2-TZVP⁸²) was used for all calculations. This basis set was chosen to minimize any superposition errors and provide an accurate estimate of these affinity values.⁸³ The models can also be further divided into functionals that either include or do not include a dispersion correction.^84,85 This correction provides an estimate for the contribution from longer-ranged van der Waals (vdW) interactions between atoms. For each of the functionals, we computed binding enthalpy results with, and without, dispersion correction terms added to the functionals. This study ascertained the importance of including vdW interactions in the estimation of Lewis affinity values.

The best models for each affinity scale were determined based on two criteria: (1) the extent of errors associated with the raw-DFT binding enthalpies and linear model estimations of the experimental Lewis affinity values (2) the coefficient of determination (R²) of the raw-DFT binding enthalpies and experimental training data and the R² value based on a 4-fold cross-validation. The raw-DFT binding enthalpies uncover the effectiveness of the DFT functional (to include or omit dispersion) to capture the underlying chemistry of the Lewis acid–base interactions without fitting to experimental data. The errors reported for these metrics include consideration of all the data (both training and test sets). On the other hand, the errors associated with the linear model assess the effectiveness of the model trained on experimental values at predicting affinity scale values in the test set alone. More information on these metrics and their results can be found in Tables S3–S5 and eqn (S8)–(S11) in the ESI.† Once the best DFT-methods for each affinity scale were determined using these criteria, they were used to predict affinity scale values for as yet unreported solvent values (see Table 1 below for solvent sets). We predicted affinity scale values for solvents in the thiourea, thioamide, phosphoamide, and sulfoxide solvent groups as well as methylamine. Our procedure is depicted in Fig. 1.

Table 1 Computational predictions of Lewis affinity metrics (rounded to the nearest kcal mol⁻¹) for nine solvents. The DN and BF₃ predictions were determined by linear models based on a PW6B95 functional with dispersion correction. The LCA predictions were determined by a linear model based on a B97 functional with dispersion correction

Solvents	DN	BF3	LCA
Diethyl sulfoxide (DESO)	34	27	55
N-Methyl-pyrrolidone-2-thione (NMPT)	32	16	48
Dimethylthioformamide (DMTF)	33	16	45
Tetrahydrothiophene-1-oxide (THTO)	32	26	55
Phosphoramide (PA)	34	29	58
Urea	28	27	55
Thiourea	32	16	45
1,3-Dimethyl-1,3-diazinane-2-thione (DMDT)	38	16	52
Methylamine	38	35	42

---

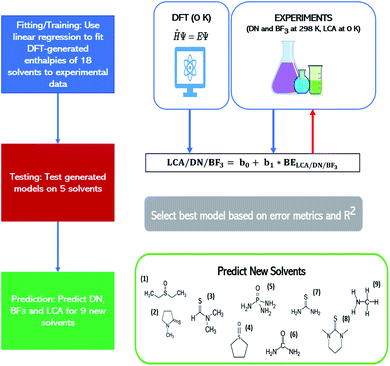Fig. 1 Work flow showing how linear models describing the affinity metrics are constructed to allow predictions of these metrics for nine solvents: (1) DESO (2) NMPT (3) DMTF (4) THTO (5) PA (6) urea (7) thiourea (8) DMDT and (9) methylamine. See Table 1 for the full names of the solvents. The lefthand column provides the workflow of the procedure. The righthand column provides more details on these steps. BE refers to the binding enthalpy between the solvent and the relevant Lewis acid.

2.1 Results of Lewis affinity training and validation against experimental data

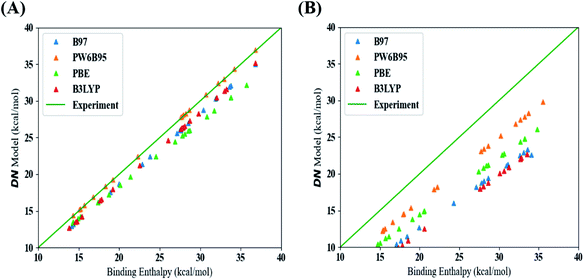
This section discusses our results from the aforementioned procedure outlined in Fig. 1. From this approach, we were able to identify the best methods (functionals and dispersion corrections) to estimate values for the DN, BF₃, and LCA. Fig. S7 and S8, in the ESI,† show the errors associated with the raw DFT binding enthalpy (all data) and linear model (test set) used for the DN. Table S3† shows that the DFT methods with the lowest error between the raw DFT binding enthalpy data (i.e., no linear fitting was performed) and experimental values were those that included a dispersion correction. Fig. 2 maps the raw DFT binding enthalpies of each DFT-method to their corresponding linear model estimations of the DN. The “best” methods should arise from data lying closest to the line (shown in green) at which the binding enthalpy estimated using DFT is the same as the experimental value. A comparison of Fig. 2A and B highlights the effect of including a dispersion term in the DFT method; methods that include dispersion terms lie significantly closer to the line of equality, by about 3 kcal mol⁻¹.

Fig. 2 Comparison of binding enthalpies estimated using DFT to predicted values of the DN for four DFT models, listed in the inset, which either included (A) or excluded (B) a dispersion correction. Color code as in the inset. Experimental values are shown as a green line which represents the line of equality (y = x) i.e. an ideal DFT method that yields DN values identical to the experimental data.

Considering the test error results based on linear model estimation from Fig. S8 and Table S3 in the ESI,† the lowest mean absolute error (MAE) and root mean squared error (RMSE) results were observed from a model that used a B97 (GGA) functional and one that used the PW6B95 (hybrid) functional (both including a dispersion correction). We elected to base the prediction of the new solvents on the PW6B95 functional with a dispersion correction because it also produced the lowest raw DFT binding enthalpy error and the highest R² value from the training data and from 4-fold cross-validation (see Table S3†).

In our estimation of BF₃ affinity values, binding enthalpy calculations reveal that dispersion corrections do not significantly improve the estimation of the BF₃ value compared to the improvements seen from the DN estimation (see Fig. S7 and S9 in the ESI†). Of the four DFT methods we tested, the methods based on a PW6B95 (hybrid) functional with/without dispersion provided more accurate estimations of this property. This result can also be observed when comparing Fig. S5a and b,† where there is no significant difference between data based on methods with or without a dispersion correction. Considering the errors for the test set (see Table S4†), the best DFT method to represent the BF₃ affinity scale was the hybrid functional PW6B95 with a dispersion correction. Predictions for new solvents will be based on the linear model of this method as it also had comparably high R² values for the training data and cross-validation (see Table S4†).

Similar to the BF₃ scale, binding enthalpy (BE) calculations reveal that dispersion corrections do not improve the estimation of the LCA, as seen in Fig. S6a and b.† This observation can also be garnered from Fig. S11, S12 and Table S5 in the ESI.† Considering the errors and R² of each method, the linear model based on the B97 functional with a dispersion correction was best suited to predict the LCA values for the solvents listed in Table 1.

2.2 Affinity scale predictions

Now that we have selected the best DFT methods to use for each of the three affinity scales, we used their corresponding linear models to predict affinity metrics for the nine unexplored solvents listed in Table 1 below (rounded up to the nearest unit). We estimated the error of DN predictions to be 1.7 kcal mol⁻¹, while the error associated with the BF₃ and LCA predictions were 0.6 and 0.7 kcal mol⁻¹, respectively; these estimates are based on the mean absolute error (MAE) of the selected linear model i.e. the model based on the best DFT method for that affinity scale (see Tables S3–S5 in the ESI†).

We now turn our attention to comparing affinity scale values for oxygen-donor (O-donor) solvents (DMF, NMP, DMPU, and urea) to their (sulfur) S-donor counterparts (DMTF, NMPT, DMDT, and thiourea). The latter can be visualized by replacing the electron-donating oxygen atom with sulfur, e.g., C=O becomes C=S. Hamil et al. explored differences in interaction strength between these groups in a solution containing hybrid organic–inorganic perovskite precursors.⁵⁸ Our results in Table 2 revealed that S-donor solvents have a stronger interaction with SbCl₅, indicative of the DN scale, than their O-donor counterparts. In contrast, for the BF₃ and LCA affinity scales, this trend is reversed. This observation is supported by trends in existing BF₃ data⁴⁴ and a LCA study.⁸⁶ To date, no experiments have looked into these trends for the DN scale. Our results reveal a key difference that would make certain affinity scales better suited than others to represent particular perovskite species.

Table 2 Comparison of predictions of the DN, BF₃, and LCA metrics for S-donor and O-donor solvent counterparts. S-donor solvent values and all LCA values were determined via linear model predictions. All values are rounded to the nearest kcal mol⁻¹

Solvents	Donor type	DN	BF3	LCA
NMP	O-donor	27	26	56
NMPT	S-donor	32	16	48
DMF	O-donor	27	25	53
DMTF	S-donor	33	16	45
UREA	O-donor	28	27	55
THIOUREA	S-donor	32	16	45
DMPU	O-donor	33	26	60
DMDT	S-donor	38	16	52

---

3 Application of Lewis affinity scales to perovskite species in solution

3.1 Estimating binding enthalpies of solvents towards perovskite Lewis acids

In Section 2.2 we predicted values for the DN, BF₃, and LCA for different solvents; in this section, we extend this study to identify which Lewis acid–base affinity scales best describe species in a metal halide perovskite solution. Specifically, we explored the correlation of values obtained using the three affinity scales with our computationally determined binding enthalpies of solvents to a number of representative A-site cations and BX_n salt complexes in perovskite solutions.⁸⁷ The species of interest differ in size and oxidation state of the central ion, as well as the number and type of halide atoms bound to this central ion. We use the term “perovskite acid” to refer to the Lewis acids present in perovskite solutions i.e. A-site cations and BX_n salt complexes (see Fig. 3 below). We also use the term “solvent” to refer to all the Lewis bases explored, which includes bath solvents, antisolvents and solvent additives.

Fig. 3 Schematic of the perovskite acids explored: (a) BX₂ salt complexes e.g. PbX₂, SnX₂ and GeX₂ (b) BX₃ salt complexes e.g. BiX₃ and SbX₃ (c) BX₄ salt complexes e.g. SnX₄ (d) BX₅ salt complexes e.g. SbX₅ (where X = Cl⁻, Br⁻, and I⁻) and (e) A-site cations e.g. Na⁺, K⁺, Rb⁺ and Cs⁺. Color code as in inset.

Our motivation here is that if a correlation can be found between the solvent–perovskite acid interactions in solution and the existing affinity scales (DN, BF₃, and LCA), it would allow users of such models to leverage much larger databases as a route to select more effective and greener solvent alternatives.⁸⁸ In addition, we have calculated binding enthalpies of halides (Cl⁻, Br⁻, and I⁻) towards BX_n salt complexes. These data will provide insight into the coordination preferences of mixed halide systems, such as APbI_3−xCl_x ^23,24 and the competition between solvent molecules and halides that leads to the formation of halo-cation complexes like iodoplumbates in perovskite solutions.^{32,39,57,89–94}

We were interested in solvents previously used in experimental studies of perovskite systems to evaluate whether either the DN or BF₃ scale can be extended to represent the binding of solvents to BX_n salt complexes, and whether the LCA can be used to describe interactions of A-site cation species in solution. Solvents from thirteen different functional groups were studied for their interaction with seven BX_n salt complexes incorporating three different halides and four choices of A-site cations. In all, our study covered 600 different combinations of species.

We calculated solvent interactions with the aforementioned perovskite acids as manifested through their binding enthalpy at 0 K using eqn (1), where the Lewis base (LB) represents the solvents explored and the Lewis acid (LA) represents the perovskite acids (BX_n salt complexes and A-site cations). Eqn (S7†) also describes how the binding enthalpy of these interactions were quantified, with the term “adduct” indicating the complexes formed between solvents and the perovskite acids explored in this study. Each component of the binding enthalpy was determined in DFT using a PW6B95 ⁸⁰ hybrid functional with a dispersion correction^84,85 and a B97 ⁹⁵ GGA functional with a dispersion correction for the solvent–BX_n and solvent–A⁺ interactions, respectively. These DFT methods were chosen because the former resulted in the best estimation for the DN/BF₃, while latter provided the best estimation for the LCA (see Tables S3–S5†). As in Section 2, an accurate triple zeta basis set, def2-TZVP,⁸² was used to avoid superposition issues.⁸³

In addition, each component is optimized in an implicit solvent medium of the coordinating solvent using the CPCM⁷⁷ represented by its dielectric constant (see Table S18 in the ESI†), with the exception of simulations involved in the A-site cation and solvent interactions (which was optimized in the gas-phase). This was done in order to mimic the solution environment in which the solvent and salts interact, while keeping the cost of the simulation to a reasonable level.⁹⁶ Regarding systems where the coordinating Lewis base is a halide ion, dielectric constants of 10.0, 25.0, 40.0, and 70.0 were explored to study these interactions in different solvent media. Calculated binding enthalpy values for the perovskite acids can be found in the ESI.†

Our results for “BX_n” salts (where n = 2, 3, 4, and 5) indicated that the DN correlates better than the BF₃ affinity scale in relation to solvent interactions with “BX_n” salt complexes. Specifically, the R² values of these solvent–perovskite acid interaction for the DN metric ranged from 0.91–0.99, while that for BF₃ ranged from 0.31 to 0.64, a weak correlation. The LCA metric correlated strongly with interactions between solvents and A-site cations, with R² results ranging from 0.94–0.98. Our correlation results can be found in Tables S31 and S32.† Based on these findings, we generated linear models that relate the DN to solvent–BX_n interactions, and that relate the LCA to solvent–A⁺ interactions; these models were determined by fitting the enthalpies of eighteen solvents (see Table S18†) to the DN and LCA, respectively. Table 3 describes these linear models.

Table 3 Perovskite adduct proxy equations. Assuming a linear equation relating DN and LCA metrics to solvent–Lewis acid interactions in a perovskite solution, we provide slope and intercept values that will allow the calculation of solvent–‘perovskite acid’ (PA) affinities from DN and LCA values; the mean absolute error (MAE) in kcal mol⁻¹ for each linear model is also provided. Binding strength values of halides I⁻, Br⁻ and Cl⁻ (in kcal mol⁻¹) towards these ‘perovskite acids' are also provided and can be compared to the solvent coordination values for predicting the likelihood of halo-cation formation^a

PA	Proxy	Slope	Y-intercept	MAE	I^−	Br^−	Cl^−
a NR – not reported.
PbI2	DN	0.53	+3.6	0.7	19.8	21.3	24.5
PbBr2		0.47	+4.8	0.7	19.3	21.1	24.4
PbCl2		0.48	+4.3	0.5	18.3	20.2	23.6
SnI2		0.56	+3.8	0.9	19.5	21.5	25.5
SnBr2		0.56	+3.7	0.9	18.7	21.0	25.2
SnCl2		0.54	+3.6	0.7	17.5	20.0	24.2
GeI2		0.73	+2.7	0.8	21.5	23.8	28.4
GeBr2		0.68	+3.6	0.6	20.4	23.1	27.8
GeCl2		0.65	+3.5	1.0	18.5	21.3	26.1
BiI3	DN	0.39	+0.8	0.8	13.5	14.6	17.5
BiBr3		0.40	+1.6	0.8	13.8	15.3	18.6
BiCl3		0.39	+1.8	0.9	12.8	14.6	18.0
SbI3		0.39	−1.2	0.7	10.2	11.4	14.7
SbBr3		0.41	−0.8	0.9	10.2	11.8	15.6
SbCl3		0.38	−0.1	1.1	9.1	10.9	14.7
SnI4	DN	0.55	−5.6	0.8	6.7	8.1	12.6
SnBr4		0.64	−3.8	1.1	11.7	14.3	18.9
SnCl4		0.66	−2.0	1.0	14.2	17.1	22.2
SbI5	DN	0.86	−4.9	1.3	20.0	21.1	25.7
SbBr5		0.94	−1.7	1.3	25.7	27.1	31.9
SbCl5		0.95	+1.9	0.5	29.0	30.7	35.8
Na^+	LCA	0.74	−0.2	0.6		NR
K^+		0.65	−4.8	0.6
Rb^+		0.59	−5.1	0.8
Cs^+		0.55	−5.3	0.8

---

The intrinsic value of these models is that they allow readers to use known DN or LCA values as inputs to the linear equations in Table 3 (described by their slope and intercept values) and hence predict the interaction strength of posited solvents to the listed perovskite acids without having to perform any computational simulations. Fig. 5 describes how enthalpies can be determined from DN/LCA values. The accuracy of these models is represented by the mean absolute error (MAE) of their estimations for six solvents not included in the fitting process against DFT-derived values. The MAE ranged from 0.5 to 1.3 kcal mol⁻¹ for the 25 perovskite acids studied (see Tables 3 and 4 below as well as Tables S34–S41 in the ESI†).

Fig. 4 Ranking of solvents by classes of functional groups as given by their DN and LCA scales. The DN is a proxy for the interactions of solvents towards BX_n salt complexes, and the LCA for A⁺ perovskite species, respectively. Classes of functional groups that are shown in green contribute to a higher DN or LCA values than those shown in red. They can be used to select solvents that would maximize BX_n salt complex or A-site cation coordination strength. Of the solvents we tested, gaps exist between 21–24 kcal mol⁻¹ for the DN kcal mol⁻¹ which formed the basis of the classification into red and green groups. For the LCA, formamide and propylene carbonate (PC) belonged to different functional groups (amide and carbonate, respectively) yet yielded similar LCA values (≈49 kcal mol⁻¹). However, formamide yielded the lowest LCA value amongst the amides, while PC yielded the highest amongst the carbonates, which resulted in amides being classified into green, while the carbonates were classified amongst the reds.

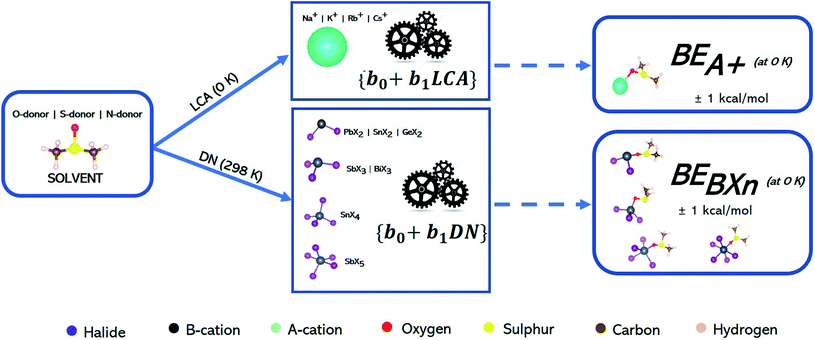Fig. 5 Work flow showing how linear models (b₀ + b₁DN/LCA) describing how the affinity metrics are used to estimate the binding enthalpies of S, N, and O-donor solvents towards BX_n and A⁺ ions using DN and LCA values as inputs. Color code as given below the schematic. See Table 3 for the accuracy determined for each model.

Table 4 Test cases of our linear models against DFT calculated binding enthalpies of solvents with unique functional groups (thioamide, sulfoxide, amide, nitrile, carbonate and ether) towards PbI₂ and Cs⁺ at 0 K resulting in an MAE of 0.7 and 0.8 kcal mol⁻¹, respectively. A full collection of test cases for the other BX_n salt complexes and A-site cations can be found in Tables S34–41 in the ESI

Solvent	DN/LCA (kcal mol^−1)	DFT (kcal mol^−1)	Model (kcal mol^−1)	|DFT-model| (kcal mol^−1)
PbI 2 : 0.53DN + 3.6
N-Methyl-pyrrolidone-2-thione (NMPT)	32.4	21.3	20.8	0.5
Diethyl sulfoxide (DESO)	33.5	20.1	21.4	1.3
Formamide	24.0	16.0	16.3	0.3
Propionitrile	16.1	11.0	12.1	1.1
Ethylene carbonate (EC)	15.0	11.3	11.6	0.3
Diethyl ether (DE)	19.0	14.4	13.6	0.8
				MAE error = 0.7 kcal mol ^−1
Cs ^+ : 0.55LCA − 5.3
N-Methyl-pyrrolidone-2-thione (NMPT)	47.8	21.7	21.0	0.7
Diethyl sulfoxide (DESO)	55.3	25.7	25.1	0.6
Formamide	51.7	21.6	21.4	0.2
Propionitrile	45.4	20.2	19.7	0.5
Ethylene carbonate (EC)	47.9	22.1	21.0	1.1
Diethyl ether (DE)	43.2	16.8	18.5	1.7
				MAE error = 0.8 kcal mol ^−1

---

We have also provided halide (Cl⁻, Br⁻, I⁻) coordination strengths towards each BX_n salt complex to compare with the derived solvent–perovskite acid affinity values. The halide–BX_n coordination results offer a guide for research groups studying systems that involve the competition between halide ions and solvents for coordination to perovskite acids. The values reported in Table 3 are for single halide–BX_n binding enthalpies in a dielectric medium of 40.0; results for other media are provided in the ESI.† We observed an inverse relationship between the dielectric constant of the solvent medium and the coordination strength of halides to BX_n salt complexes, which decays at higher dielectric values. The profiles shown in the ESI† mimic the electrostatic potential's dependence on a medium's dielectric constant, i.e., a lower dielectric constant increases the magnitude of the coulombic attraction between oppositely charged ions.⁹⁷ This increase in affinity of halide for BX_n salt complexes in a lower dielectric medium is also supported by a recent study by Sorenson et al. which showed that reducing the dielectric of the solution medium via the introduction of antisolvents increases the formation of halo-cation complexes.⁹⁸

In addition, explicit solvent interactions with the halides, which can be measured by the acceptor number (AN),^99,100 is likely to impact the apparent solvent–BX_n interaction strength in solution,¹⁰¹ an effect that cannot be ignored for high AN solvents like water and alcohols.^57,102 For this reason, we explored solvents with AN values less than 20 (or solvents without strong hydrogen-bond donor groups) with the exceptions of formamide and methylamine, the former having an AN of 39.8 and the latter having two hydrogen-bond donors (see Tables S18 and S33 in the ESI†). Also, when exploring the formation of higher-order halo-cation species, such as PbI₄²⁻ and PbI₅³⁻ iodoplumbates, we need to consider the enthalpically preferred configurations of the additional halides and solvents molecules bound to the Lewis acid.³⁹ Nonetheless, Fig. 6 provides DN thresholds for solvents that would yield a greater binding strength to the BX_n salt complexes than halides (Cl⁻, Br⁻ and I⁻) in a dielectric medium of 10 (typical of antisolvents) and 40 (typical of bath solvents and additives) at 0 K. The results from this figure show how halide binding strength is impacted by the dielectric of the medium and the Lewis acid to which it binds. For example, lower dielectric media resulted in a greater halide binding strength and BX₃ salt complexes had a greater enthalpic preference for halides over the solvents reported in Fig. 6 relative to the other salt groups we explored (BX₂, BX₄ and BX₅). Further, we observed a consistent electronegative trend (Cl⁻ > Br⁻ > I⁻) in strength.¹⁰¹Fig. 4 ranks different solvent functional groups by their DN and LCA values, the identified proxies for the solvent–BX_n and solvent–A⁺ interactions, respectively. This figure indicates the functional groups that contribute to a strong interaction between solvents and the perovskite acids explored. Details on the BX_n salt complexes and A-site cations are presented in ESI Section S6–S10.†

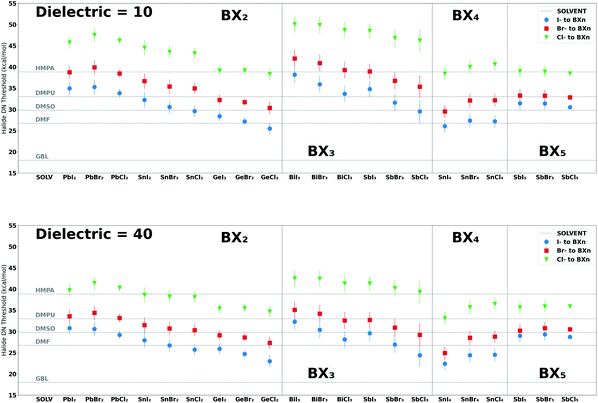Fig. 6 Threshold DN values for halides bound to BX_n salt complexes in a dielectric medium of 10 (upper curves) and 40 (lower curves). The DN values for each halide are indicative of the minimum DN of a solvent required to yield a binding enthalpy higher than the pertinent halides (Cl⁻, Br⁻ and I⁻) at 0 K and in different dielectric media. These values were determined by inputting the halide enthalpies for each BX_n salt complex reported in Table 3 to the inverse of the linear model for that system i.e. DN = (BE_Halide – b₀)/b₁; the error bars are associated with the MAE of each model i.e. MAE/b₁. We also included horizontal lines to represent the DN values of five solvents HMPA (DN = 38.8), DMPU (DN = 33.0), DMSO (DN = 29.8), DMF (DN = 26.7) and GBL (DN = 18.0) to compare with the halide values for each BX_n salt complex. Results show that the dielectric of the medium impacts the DN threshold values for each halide, which increases in lower dielectric media. See Fig. S24 in the ESI† for results in dielectric media of 25 and 70.

3.2 Experimental Cs- and Rb-NMR studies of S- and O-donor solvents

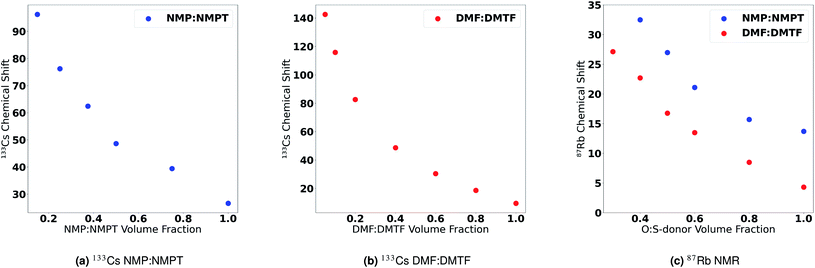
The computational results above showed that there is a strong correlation between the Gutmann DN and BX_n salt complexes. But the strongest correlation for A-site cations arose using the LCA metric. This brought us back to our original observation when comparing these two metrics in Section 2 of this paper, namely the apparent conflict of S-donor and O-donor solvent binding strengths: S-donor solvents have a stronger interaction with the BX_n salt complexes and have a higher predicted DN than their O-donor counterparts. But this trend is reversed when comparing the strength of these solvent groups to A-site cations, showing the best correlation to the LCA metric.

To test the coordination preference of O-donor and S-donor solvents towards Cs⁺, we first tested the solubility of CsI and RbI (cesium and rubidium iodide) in two pairs of processing solvent blends (NMP/NMPT and DMF/DMTF) where the difference between each pair is the identity of the donor atom. Table 5 shows that both CsI and RbI are highly soluble in O-donor solvents compared to S-donor solvents where they both have negligible solubility. This observation suggests that there is a difference in effectiveness between S-donor and O-donor solvents towards Cs⁺ and Rb⁺, though there are other factors influencing the solubility that cannot be overlooked.^64,103–106

Table 5 Solubility limits of CsI and RbI in O-donor perovskite processing solvents (NMP and DMF) and their S-donor counterparts (NMPT and DMTF), reported in mM, showing a clear difference in the effectiveness of both solvent groups in dissolving A-cation salts

Solvents	Solubility in CsI (mM)	Solubility in RbI (mM)
DMF	510	1670
DMTF	<20	<10
NMP	100	1430
NMPT	<10	<10

---

More definitive evidence for this hypothesis was provided by Cesium NMR. To test this hypothesis, we conducted ¹³³Cs NMR on solutions of CsI in mixtures of O-donor and S-donor solvents. Fig. 7a shows the change in ¹³³Cs chemical shift as a function of increasing O-donor volume fraction in the NMP and NMPT solvent pair. We observe a small change in the chemical shift of Cs⁺ when transitioning from a pure NMP solution to ones with increasing NMPT content. Conversely, we observe a larger change in the chemical shift of Cs⁺ when transitioning from a solution of high NMPT content to one with less NMPT and more NMP. This observation suggests that Cs⁺ is more stable in an O-donor-rich solvent environment. Thus, we observe that the effect of adding an O-donor solvent into a S-donor-rich solution is much stronger than adding a S-donor solvent into an O-donor-rich solution. This effect is also observed in mixtures of DMF and DMTF (Fig. 7b). ¹³³Cs NMR spectra are shown in Fig. S27 and S28.† Unsurprisingly, we observed the same coordination preference of O-donor S-donor solvents towards Rb⁺. Fig. 7c shows the change in the ⁸⁷Rb chemical shift as a function of increasing O-donor volume fraction in DMF/DMTF NMP/NMPT solvent pairs. Similar to the case with Cs⁺, the difference in chemical shift increases as the solution changes from O-donor rich to S-donor rich, suggesting that Rb⁺ is more stable in a O-donor rich solvent environment compared to a S-donor rich environment. ⁸⁷Rb NMR spectra are shown in Fig. S29 and S30.† These observations supports the LCA predictions of O-donor vs. S-donor and its correlation with solvent–A⁺ interactions, i.e., O-donor solvents have a greater preference to stay bound to the A-site cations than S-donor solvents. The opposite trend for the DN has been supported in a recent publication by Hamil et al.⁵⁸ that used extended X-ray absorption fine structure (EXAFS) measurements to determine that S-donor solvents preferentially coordinate to Pb²⁺ based complexes than their O-donor counterparts. In addition, earlier studies on S-donor solvent preferences for PbX₂ salts over O-donor solvents also support this trend.¹⁰⁷

Fig. 7 ¹³³Cs NMR chemical shifts as a function of the ratio of O-donor solvent to S-donor solvent in solution showing (a) results for various mixtures of NMP and NMPT and (b) results for mixtures of DMF and DMTF. (c) ⁸⁷Rb NMR chemical shifts as a function of the ratio of O-donor solvent to S-donor solvent in solution for mixtures of NMP : NMPT and DMF : DMTF.

4 Discussion

We have compared DFT-generated binding enthalpies of solvents to perovskite reagent salts and cations to those defined by three established affinity scales, the Gutmann DN, BF₃ and LCA. We observed that the DN (but not the BF₃ scale) correlates strongly with solvent–salt binding affinities for the perovskite reagents we studied. Similarly, the LCA scale correlated well with solvent–A⁺ interactions (but the DN did not). Table 3 provides simple linear equations which use the DN and LCA as inputs to predict binding enthalpies between solvents and halide perovskite species.

Results for the efficacy of the BF₃ scale for perovskite reagents were disappointing. We posit that the main reason behind the disparity between the effectiveness of the DN and BF₃ in describing solvent–BX_n interactions pertains to their inconsistent predictions for the binding affinity of S-donor solvents compared to O-donor counterparts. For instance, excluding S-donor solvents (DMTF and thiourea) from our fitting resulted in a substantial increase in the R² value of the BF₃ scale towards solvent–BX_n enthalpies (see Table S32†). These results can be attributed to the “hardness” or “softness” of the species involved, as described by hard and soft acid and base theory (HSAB).^108–110 For example, Lewis acids like SbCl₅ and other group 14 and 15 based acids are considered “softer” acids due to their lower charge-to-volume ratios,^50,111 whereas BF₃ and group 1 metal ions are considered “harder” acids. Moreover, S-donor solvents are considered “softer” bases, whereas O-donor solvents are considered “harder” bases.^{50,108,110,111} The hardness and softness of the associated perovskite acids and solvents were determined in DFT^112–114via their HOMO and LUMO levels (see Tables S42 and S43†). The hardness of the BF₃ molecule was determined to be 5.8 eV, while that of SbCl₅ was 2.4 eV (the hardness of BX_n salt complexes ranged from 1.8 to 3.4 eV), in agreement with our theorized ranking. The underlying theory of HSAB suggests that harder acids form stronger complexes with harder bases, while softer acids prefer to bind to softer bases.^50,108 This confirms that even if both the DN and BF₃ describe the affinity between Lewis acids and bases accurately, the reference Lewis acid of the affinity scale has an influence in the trends between the affinity of the acid to solvent types (S-donor, O-donor, and N-donor solvents).⁴⁴

As a result, we can attribute the strong correlation between the DN and perovskite salts to the extent of molecular similarity (hardness and softness) between SbCl₅ (the foundation of the DN) and salt complexes based on ions of Ge(II), Sn(II), Pb(II), Bi(III), Sb(III), Sn(IV), and Sb(V) – see Table S43.† In the same vein, the LCA (Li⁺-based) metric shares the same group as other “hard” alkali metals in this study¹¹⁵ and we calculated a hardness range of 7.6 to 29.6 eV for these ions. We believe this to be responsible for the strong correlation between the LCA scale and the binding enthalpies of solvents to A-site cations.

To enhance the coordination strength between solvents and all the perovskite acids (BX_n salt complexes and A-site cations) in an all-inorganic perovskite solution, we find that no single scale – whether the DN or the LCA – will adequately predict the effectiveness of a candidate solvent for this objective. Instead, a solvent that maximizes both the DN and LCA is required.

We have shown that the LCA values of S-donor solvents are lower than their O-donor counterparts, whereas the DN shows the reverse trend. These results create implications for optimal processing choices for all-inorganic perovskite thin films. For example, if a perovskite processing protocol was to swap out an O-donor solvent (DMF, say) for an analogous S-donor solvent (DMTF, say), there would be an increased coordination strength between the solvent and BX_n salt complexes like PbX₂;^58,107 but its coordination towards A-site cation species like Cs⁺ would be likely to weaken. As a result, in an inorganic solution, one could rely on the presence of a solvent blend of an S-donor and an O-donor to leverage the preferences of both solvents towards certain perovskite acids: the S-donor solvent for the BX_n salt complexes, and the O-donor solvent for the A-site cations.

Positing a different strategy, we have identified solvents like DMPU, THTO, and HMPA (with urea, sulfoxide, and phosphoamide functional groups, respectively) that have both a high DN and LCA value, covering preferences for A-site cations and BX_n salt complexes. However, not all solvents with high DNs, like pyridine and methylamine (33.5 and 37.5 kcal mol⁻¹), have comparably high LCA values (45.5 and 41.8 kcal mol⁻¹). The lack of a clear correlation between the LCA and the DN warrants the need to consider both scales when selecting solvents for all-inorganic perovskite processing.

5 Conclusions

We predicted values of three affinity metrics (the DN, BF₃ and LCA) for nine bases using density functional theory and simple linear regression tools. Our studies of the effect of changing the DFT functional revealed that the inclusion of long-ranged vdW interactions, captured via dispersion corrections, are more important in describing interactions associated with the DN than for the BF₃ and LCA scales. S-donor solvents generally have a higher DN than their O-donor counterparts, but this trend is reversed for the BF₃ and LCA affinity scales.

Extending these metrics to perovskite complexes, we find that the DN is better suited than the BF₃ scale at describing the interactions between solvents and BX_n salt complexes due to their difference in affinities for S-donor solvents. Conversely, we found that the LCA metric is the best metric to use to describe interactions between solvents and group 1 A-site cations (Na⁺, K⁺, Rb⁺ and Cs⁺) in all-inorganic metal halide perovskite solutions. The affinity of S-donor solvents towards the DN and BX_n salt complexes and their O-donor counterparts towards LCA and A-site cations were supported by previously published EXAFS results⁵⁸ and Cs-NMR/Rb-NMR results from this study, respectively.

We have provided linear models that relate the DN to solvent–BX_n interactions in an implicit solvent medium and the LCA to solvent–A⁺ interactions in the gas phase with a reported error of ≈1 kcal mol⁻¹ for the 25 perovskite acid models developed. This bypasses the need for density functional theory calculations to determine the direct affinity of processing solvents (bath solvent, antisolvent, and additives) towards Lewis acids in all-inorganic metal halide perovskite solutions (BX_n salt complexes and A⁺ ions).

We determined the affinities of halide ions towards BX_n salt complexes in different dielectric media to compare with the binding enthalpies of solvents garnered from our linear models. Our results showed that a decrease in dielectric constant increases the binding strength between halides and the associated perovskite acids in line with Coulomb's law; we also observed an electronegative trend (Cl⁻ > Br⁻ > I⁻) of halide binding strength towards these species. In addition, it may be necessary to consider the strength of solvent–halide interactions, particularly for high AN solvents, as it influences the effective coordination preferences of halides to Lewis acids. The community may benefit from future studies of these interactions. Nonetheless, these results could guide the selection of solvents that could bind more strongly to BX_n salt complexes than halides to potentially limit the formation of halo-cation complexes and delay the onset of nucleation in solution via solvent–halide competition.

Overall, when choosing an effective solvent for binding in an all-inorganic metal halide perovskite solution, our results suggest that a single metric or scale cannot represent all the interactions present in a perovskite solution. The preference of solvents towards perovskite specific Lewis acids is influenced by the chemical nature of the acid with which it is interacting.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Maryland Advanced Research Computing Center (MARCC) which is partially funded by the State of Maryland, for provision of the computational resources needed here. OR and PC acknowledge partial support from NSF DMR-1719875. The experimental results are based upon work supported by the U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy (EERE) under the Solar Energy Technologies Office (SETO) Award Number DE-EE0008560.

References

1. S. D. Stranks and H. J. Snaith, Nat. Nanotechnol., 2015, 10, 391.
2. J. Berry, T. Buonassisi, D. A. Egger, G. Hodes, L. Kronik, Y.-L. Loo, I. Lubomirsky, S. R. Marder, Y. Mastai and J. S. Miller, Adv. Mater., 2015, 27, 5102.
3. A. Sadhanala, S. Ahmad, B. Zhao, N. Giesbrecht, P. M. Pearce, F. Deschler, R. L. Z. Hoye, K. C. Go, T. Bein and P. Docampo, Nano Lett., 2015, 15, 6095.
4. Z. Xiao, R. A. Kerner, L. Zhao, N. L. Tran, K. M. Lee, T.-W. Koh, G. D. Scholes and B. P. Rand, Nat. Photonics, 2017, 11, 108.
5. D. Liang, Y. Peng, Y. Fu, M. J. Shearer, J. Zhang, J. Zhai, Y. Zhang, R. J. Hamers, T. L. Andrew and S. Jin, ACS Nano, 2016, 10, 6897.
6. S. Yakunin, M. Sytnyk, D. Kriegner, S. Shrestha, G. J. Matt, H. Azimi, C. J. Brabec, J. Stangl, V. Kovalenko and W. Heiss, Nat. Photonics, 2015, 9, 444.
7. Q. Chen, J. Wu, X. Ou, B. Huang, J. Almutlaq, A. A. Zhumekenov, X. Guan, S. Han, L. Liang and Z. Yi, Nature, 2018, 561, 88.
8. H. Wei, Y. Fang, P. Mulligan, W. Chuirazzi, H. H. Fang, C. Wang, B. R. Ecker, Y. Gao, M. A. Loi and L. Cao, Nat. Photonics, 2016, 10, 333.
9. S. C. Watthage, Z. Song, A. B. Phillips and M. J. Heben, in Perovskite Photovoltaics, ed. S. Thomas and A. Thankappan, Academic Press, 2018, pp. 43–88.
10. O. J. Weber, B. Charles and M. T. Weller, J. Mater. Chem. A, 2016, 4, 15375.
11. N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Nature, 2015, 517, 476.
12. T. N. R. E. Laboratory, The National Renewable Energy Laboratory Best Research-Cell Efficiency Chart, Accessed 2021-02-24.
13. J. C. Hamill, J. Schwartz and Y.-L. Loo, ACS Energy Lett., 2018, 3, 92.
14. X. B. Cao, C. L. Li, L. L. Zhi, Y. H. Li, X. Cui, Y. W. Yao, L. J. Ci and J. Q. Wei, J. Mater. Chem. A, 2017, 5, 8416.
15. J. W. Lee, H. S. Kim and N. G. Park, Acc. Chem. Res., 2016, 49, 311.
16. P. P. Khlyabich, J. C. Hamill and Y.-L. Loo, Adv. Funct. Mater., 2018, 28, 1801508.
17. A. G. Ortoll-Bloch, H. C. Herbol, B. A. Sorenson, M. Poloczek, L. A. Estroff and P. Clancy, Cryst. Growth Des., 2020, 20, 1162–1171.
18. M. Yang, Z. Li, M. O. Reese, O. G. Reid, D. H. Kim, S. Siol, T. R. Klein, Y. Yan, J. J. Berry and M. F. A. M. van Hest, Nat. Energy, 2017, 2, 17038.
19. S. K. Sahoo, B. Manoharan and N. Sivakumar, in Perovskite Photovoltaics, ed. S. Thomas and A. Thankappan, Academic Press, 2018, pp. 1–24.
20. P. Reshmi Varma, in Perovskite Photovoltaics, ed. S. Thomas and A. Thankappan, Academic Press, 2018, pp. 197–229.
21. M. Salado, R. K. Kokal, L. Calio, S. Kazim, M. Deepa and S. Ahmad, Phys. Chem. Chem. Phys., 2017, 19, 22905–22914.
22. Y. Sun, J. Peng, Y. Chen, Y. Yao and Z. Liang, Sci. Rep., 2017, 7, 46193.
23. M. S. G. Hamed and G. T. Mola, Crit. Rev. Solid State Mater. Sci., 2020, 45, 85–112.
24. F. H. Isikgor, B. Li, H. Zhu, Q. Xu and J. Ouyang, J. Mater. Chem. A, 2016, 4, 12543–12553.
25. S. Premkumar, K. Kundu and S. Umapathy, Nanoscale, 2019, 11, 10292–10305.
26. P. Selvarajan, K. Kundu, C. I. Sathish, S. Umapathy and A. Vinu, J. Phys. Chem. C, 2020, 124, 9611–9621.
27. K. Kundu, P. Acharyya, K. Maji, R. Sasmal, S. S. Agasti and K. Biswas, Angew. Chem., Int. Ed., 2020, 59, 13093–13100.
28. P. Acharyya, K. Kundu and K. Biswas, Nanoscale, 2020, 12, 21094–21117.
29. C. Liu, Y.-B. Cheng and Z. Ge, Chem. Soc. Rev., 2020, 49, 1653–1687.
30. Q. Tao, P. Xu, M. Li and W. Lu, npj Comput. Mater., 2021, 7, 23.
31. H. C. Herbol, W. Hu, P. Frazier, P. Clancy and M. Poloczek, npj Comput. Mater., 2018, 4, 51.
32. J. Kim, B.-w. Park, J. Baek, J. S. Yun, H.-W. Kwon, J. Seidel, H. Min, S. Coelho, S. Lim, S. Huang, K. Gaus, M. A. Green, T. J. Shin, A. W. Y. Ho-baillie, M. G. Kim and S. I. Seok, J. Am. Chem. Soc., 2020, 142, 6251–6260.
33. A. S. Tutantsev, N. N. Udalova, S. A. Fateev, A. A. Petrov, W. Chengyuan, E. G. Maksimov, E. A. Goodilin and A. B. Tarasov, J. Phys. Chem. C, 2020, 124, 11117–11123.
34. A. A. Petrov, S. A. Fateev, V. N. Khrustalev, Y. Li, P. V. Dorovatovskii, Y. V. Zubavichus, E. A. Goodilin and A. B. Tarasov, Chem. Mater., 2020, 32, 7739–7745.
35. X. Lian, J. Chen, Y. Zhang, M. Qin, T. R. Andersen, J. Ling, G. Wu, X. Lu, D. Yang and H. Chen, J. Mater. Chem. A, 2019, 7, 19423–19429.
36. D. Barrit, P. Cheng, M.-C. Tang, K. Wang, H. Dang, D.-M. Smilgies, S. F. Liu, T. D. Anthopoulos, K. Zhao and A. Amassian, Adv. Funct. Mater., 2019, 29, 1807544.
37. K. Chaisan, D. Wongratanaphisan, S. Choopun, T. Sagawa and P. Ruankham, J. Mater. Sci.: Mater. Electron., 2019, 30, 939–949.
38. M. Wang, F. Cao, K. Deng and L. Li, Nano Energy, 2019, 63, 103867.
39. E. Radicchi, E. Mosconi, F. Elisei, F. Nunzi and F. De Angelis, ACS Appl. Energy Mater., 2019, 2, 3400–3409.
40. J. Stevenson, B. Sorenson, V. H. Subramaniam, J. Raiford, P. P. Khlyabich, Y. L. Loo and P. Clancy, Chem. Mater., 2017, 29, 2435.
41. Y.-H. Seo, E.-C. Kim, S.-P. Cho, S.-S. Kim and S.-I. Na, Appl. Mater. Today, 2017, 9, 598–604.
42. O. Shargaieva, H. Näsström, J. A. Smith, D. Többens, R. Munir and E. Unger, Mater. Adv., 2020, 1, 3314–3321.
43. C. Laurence, J. Graton and J.-F. Gal, J. Chem. Educ., 2011, 88, 1651–1657.
44. C. Laurence and J.-F. Gal, Lewis Basicity and Affinity Scales: Data and Measurement, John Wiley Sons Ltd, Hoboken, NJ, 2009.
45. A. J. Bridgeman, G. Cavigliasso, L. R. Ireland and J. Rothery, Dalton Trans., 2001, 2095.
46. B. J. Foley, J. Girard, B. A. Sorenson, A. Z. Chen, J. Scott Niezgoda, M. R. Alpert, A. F. Harper, D. M. Smilgies, P. Clancy, W. A. Saidi and J. J. Choi, J. Mater. Chem. A, 2017, 5, 113.
47. C. Xu, Z. Zhang, S. Zhang, H. Si, S. Ma, W. Fan, Z. Xiong, Q. Liao, A. Sattar, Z. Kang and Y. Zhang, Adv. Funct. Mater., 2021, 2009425.
48. K. L. Gardner, J. G. Tait, T. Merckx, W. Qiu, U. W. Paetzold, L. Kootstra, M. Jaysankar, R. Gehlhaar, D. Cheyns and P. Heremans, Adv. Energy Mater., 2016, 6, 1600386.
49. C. Hansen, Hansen Solubility Parameters: A User's Handbook, CRC Press, 2nd edn, 2007.
50. R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539.
51. T. Moot, A. R. Marshall, L. M. Wheeler, S. N. Habisreutinger, T. H. Schloemer, C. C. Boyd, D. R. Dikova, G. F. Pach, A. Hazarika, M. D. McGehee, H. J. Snaith and J. M. Luther, Adv. Energy Mater., 2020, 10, 1903365.
52. A. Hadi, B. J. Ryan, R. D. Nelson, K. Santra, F.-Y. Lin, E. W. Cochran and M. Gs. Panthani, Chem. Mater., 2019, 31, 4990–4998.
53. X. Cao, L. Zhi, Y. Jia, Y. Li, K. Zhao, X. Cui, L. Ci, D. Zhuang and J. Wei, ACS Appl. Mater. Interfaces, 2019, 11, 7639–7654.
54. Y. Deng, C. H. Van Brackle, X. Dai, J. Zhao, B. Chen and J. Huang, Sci. Adv., 2019, 5, eaax7537.
55. S. Wang, Z. Ma, B. Liu, W. Wu, Y. Zhu, R. Ma and C. Wang, Sol. RRL, 2018, 2, 1800034.
56. T. Sekimoto, M. Suzuka, T. Yokoyama, Y. Miyamoto, R. Uchida, M. Hiraoka, K. Kawano, T. Sekiguchi and Y. Kaneko, Cryst. Growth Des., 2020, 20, 874–883.
57. E. Radicchi, F. Ambrosio, E. Mosconi, A. A. Alasmari, F. A. S. Alasmary and F. De Angelis, J. Phys. Chem. B, 2020, 124, 11481–11490.
58. J. C. Hamill, O. Romiluyi, S. A. Thomas, J. Cetola, J. Schwartz, M. F. Toney, P. Clancy and Y.-L. Loo, J. Phys. Chem. C, 2020, 124, 14496–14502.
59. D. Di Girolamo, J. Pascual, M. H. Aldamasy, Z. Iqbal, G. Li, E. Radicchi, M. Li, S.-H. Turren-Cruz, G. Nasti, A. Dallmann, F. De Angelis and A. Abate, ACS Energy Lett., 2021, 6, 959–968.
60. C. W. Myung, J. Yun, G. Lee and K. S. Kim, Adv. Energy Mater., 2018, 8, 1702898.
61. A. Suzuki, Y. Miyamoto and T. Oku, J. Mater. Sci., 2020, 55, 9728–9738.
62. Z. Tang, T. Bessho, F. Awai, T. Kinoshita, M. M. Maitani, R. Jono, T. N. Murakami, H. Wang, T. Kubo, S. Uchida and H. Segawa, Sci. Rep., 2017, 7, 12183.
63. J. Song, G. Zhou, W. Chen, Q. Zhang, J. Ali, Q. Hu, J. Wang, C. Wang, W. Feng, A. B. Djurišić, H. Zhu, Y. Zhang, T. Russell and F. Liu, Adv. Mater., 2020, 32, 2002784.
64. A. Kirakosyan, Y. Kim, M. R. Sihn, M.-G. Jeon, J.-R. Jeong and J. Choi, ChemNanoMat, 2020, 6, 1863–1869.
65. B. Sun, W. Wang, H. Lu, L. Chao, H. Gu, L. Tao, J. Hu, B. Li, X. Zong, W. Shi, X. Ran, H. Zhang, Y. Xia, P. Li and Y. Chen, J. Phys. Chem. C, 2021, 125, 6555–6563.
66. S. Bourcier, R. X. Chia, R. N. B. Bimbong and G. Bouchoux, Eur. J. Mass Spectrom., 2015, 21, 149–159.
67. W. Y. Feng, S. Gronert and C. Lebrilla, J. Phys. Chem. A, 2003, 107, 405–410.
68. J.-F. Gal, C. Mayeux, L. Massi, M. Major, L. Charles and T. Haljasorg, J. Chem. Educ., 2012, 89, 1476–1478.
69. J. Wang, J. Zhang, Y. Zhou, H. Liu, Q. Xue, X. Li, C.-C. Chueh, H.-L. Yip, Z. Zhu and A. K. Y. Jen, Nat. Commun., 2020, 11, 177.
70. J.-A. Yang, T. Qin, L. Xie, K. Liao, T. Li and F. Hao, J. Mater. Chem. C, 2019, 7, 10724–10742.
71. C. Kramer, C. S. Tautermann, D. J. Livingstone, D. W. Salt, D. C. Whitley, B. Beck and T. Clark, J. Chem. Inf. Model., 2009, 49, 28–34.
72. W. DeCoursey, Statistics and Probability for Engineering Applications, Elsevier, San Diego, CA, 2003.
73. Y. Valadbeigi, J. Theor. Comput. Chem., 2016, 1091, 169–175.
74. M. Rodgers and P. Armentrout, Int. J. Mass Spectrom., 2007, 267, 167–182.
75. F. Cataldo, Eur. Chem. Bull., 2015, 2015, 92–97.
76. F. Neese, WIREs Comput. Mol. Sci., 2018, 8, e1327.
77. Y. Takano and K. N. Houk, J. Chem. Theory Comput., 2005, 1, 70–77.
78. N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372.
79. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
80. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667.
81. R. H. Hertwig and W. Koch, Chem. Phys. Lett., 1997, 268, 345–351.
82. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
83. P. Salvador, B. Paizs, M. Duran and S. Suhai, J. Comput. Chem., 2001, 22, 765–786.
84. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
85. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
86. L. M. d. Costa, L. A.-l. W. C. Paes and J. A. W. d. M. Carneiro, J. Braz. Chem. Soc., 2012, 23, 648–655.
87. W. A. Dunlap-Shohl, Y. Zhou, N. P. Padture and D. B. Mitzi, Chem. Rev., 2019, 119, 3193.
88. Y. Cui, S. Wang, L. Ding and F. Hao, Adv. Energy Sustainability Res., 2020, 2, 2000047.
89. A. Sharenko, C. Mackeen, L. Jewell, F. Bridges and M. F. Toney, Chem. Mater., 2017, 29, 1315–1320.
90. G. S. Shin, S.-G. Kim, Y. Zhang and N.-G. Park, Small Methods, 2020, 4, 1900398.
91. K. Yan, M. Long, T. Zhang, Z. Wei, H. Chen, S. Yang and J. Xu, J. Am. Chem. Soc., 2015, 137, 4460–4468.
92. L.-M. Wu, X.-T. Wu and L. Chen, Coord. Chem. Rev., 2009, 253, 2787.
93. J. Kim, B.-w. Park, J. Baek, J. S. Yun, H.-W. Kwon, J. Seidel, H. Min, S. Coelho, S. Lim, S. Huang, K. Gaus, M. A. Green, T. J. Shin, A. W. Y. Ho-baillie, M. G. Kim and S. I. Seok, J. Am. Chem. Soc., 2020, 142, 6251–6260.
94. Z. Li, A. Johnston, M. Wei, M. I. Saidaminov, J. Martins de Pina, X. Zheng, J. Liu, Y. Liu, O. M. Bakr and E. H. Sargent, Joule, 2020, 4, 631–643.
95. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
96. B. A. Sorenson, S. S. Hong, H. C. Herbol and P. Clancy, Comput. Mater. Sci., 2019, 170, 109138.
97. J. Smiatek, Theoretical and Computational Insight into Solvent and Specific Ion Effects for Polyelectrolytes: The Importance of Local Molecular Interactions, 2020.
98. B. A. Sorenson, L. U. Yoon, E. Holmgren, J. J. Choi and P. Clancy, J. Mater. Chem. A, 2021, 9, 3668–3676.
99. U. Mayer, V. Gutmann and W. Gerger, Chem. Mon., 1975, 106, 1235–1257.
100. M. Schmeisser, P. Illner, R. Puchta, A. Zahl and R. van Eldik, Chem.–Eur. J., 2012, 18, 10969–10982.
101. W. Linert, R. F. Jameson and A. Taha, J. Chem. Soc., Dalton Trans., 1993, 3181–3186.
102. W. R. Fawcett, J. Phys. Chem., 1993, 97, 9540–9546.
103. B. G. Kim, W. Jang, J. S. Cho and D. H. Wang, Sol. Energy Mater. Sol. Cells, 2019, 192, 24–35.
104. M. Jung, S.-G. Ji, G. Kim and S. I. Seok, Chem. Soc. Rev., 2019, 48, 2011–2038.
105. X. Cao, G. Zhang, L. Jiang, Y. Cai, Y. Gao, W. Yang, X. He, Q. Zeng, G. Xing, Y. Jia and J. Wei, ACS Appl. Mater. Interfaces, 2020, 12, 5925–5931.
106. B. Zhou, D. Ding, Y. Wang, S. Fang, Z. Liu, J. Tang, H. Li, H. Zhong, B. Tian and Y. Shi, Adv. Optical Mater., 2021, 9, 2001435.
107. I. Wharf, T. Gramstad, R. Makhija and M. Onyszchuk, Can. J. Chem., 1976, 54, 3430–3438.
108. T.-L. Ho, Chem. Rev., 1975, 75, 1–20.
109. R. D. Hancock and A. E. Martell, J. Chem. Educ., 1996, 73, 654.
110. R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516.
111. R. G. Pearson, Inorg. Chem., 1988, 27, 734–740.
112. A. Avramopoulos, D. Catone and M. V. Putz, Sci. World J., 2013, 2013, 348415.
113. R. Shankar, K. Senthilkumar and P. Kolandaivel, Int. J. Quantum Chem., 2009, 109, 764–771.
114. R. G. Pearson, J. Chem. Sci., 2005, 117, 369–377.
115. H. Xu, D. C. Xu and Y. Wang, ACS Omega, 2017, 2, 7185–7193.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta03063a

---