Open Access Article
Open Access ArticleUnderstanding the different reactivity of (Z)- and (E)-β-nitrostyrenes in [3+2] cycloaddition reactions. An MEDT study†
Mar Ríos-Gutiérrez *a,
Luis R. Domingo
*a,
Luis R. Domingo a and
Radomir Jasiński
a and
Radomir Jasiński *b
*b
aDepartment of Organic Chemistry, University of Valencia, Dr Moliner 50, 46100 Burjassot, Valencia, Spain. E-mail: rios@utopia.uv.es
bFaculty of Chemical Engineering and Technology, Department of Organic Chemistry and Technology, Cracow University of Technology, Warszawska 24, 31-155 Cracow, Poland. E-mail: radomir@chemia.pk.edu.pl
First published on 4th March 2021
Abstract
The experimental reactivity of isomeric (Z)- and (E)-β-nitrostyrenes participating in [3+2] cycloaddition (32CA) reactions has been analysed on the basis of molecular electron density theory (MEDT) at the HF/6-311G(d,p), B3LYP/6-311G(d,p) and ωB97X-D/6-311G(d,p) computational levels. It was found that the polar zw-type 32CA reactions with 5,5-dimethylpyrroline-N-oxide proceed via a one-step mechanism, characterised by the attack of the nucleophilic oxygen centre of the nitrone on the electrophilically activated β-position of these nitrostyrenes. This behaviour is completely understood by means of the analysis of the conceptual DFT reactivity indices. These 32CA reactions present low activation enthalpies of 4.4 (Z) and 5.0 (E) kcal mol−1, and are exo (Z) and endo (E) stereoselective (B3LYP), as well as completely meta regioselective (ωB97X-D, B3LYP). The less stable (Z)-β-nitrostyrene is more reactive than the (E)-one (HF). ELF and AIM topological analyses of the reagents and TSs show the great similitude between their electronic structures. Finally, NCI allows explaining the exo stereoselectivity found in the reaction of (Z)-β-nitrostyrene. The present MEDT study explains the different reactivity, selectivity and competitiveness in the title reactions.
1. Introduction
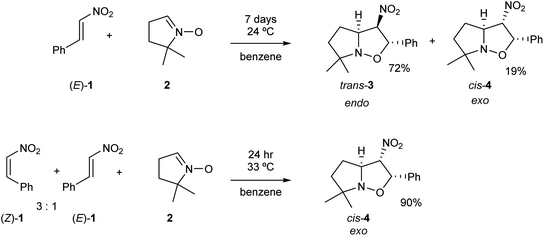
Nitroethylene derivatives are valuable precursors in organic synthesis.1–6 They allow the stereoselective preparation of oximes, amines, nitrile N-oxides and many other molecular systems. The electrophilic activation of the ethylene moiety as a consequence of the presence of the strong electron-withdrawing nitro group allows the easy synthesis of a wide range of functionalized four-, five- and six-membered carbo- and heterocycles.7 Most of the 2-substituted nitroethylenes only exist in the more stable (E) configuration.8 Only 2-(N,N-dimethylamine)-nitroethene is characterised by a stable (Z) configuration.9 Some nitroethylenes can exist as transitory unstable (Z)-isomeric form.10–16 These structures have shown to have some tendency to gradually transform into the (E)-isomers. Consequently, it appears that the physicochemical properties of (Z)-nitroethylenes are very poorly known. In particular, only some minor mentions regarding the participation of (Z)-nitroethylenes in [3+2] cycloaddition (32CA) reactions can be found in the literature.13,16Gandolfi and coworkers16 studied the course of 32CA reactions of (E)-β-nitrostyrene (E)-1 and (Z)-β-nitrostyrene (Z)-1 with 5,5-dimethylpyrroline-N-oxide 2, a five-membered cyclic nitrone, in benzene, under kinetic control conditions (see Scheme 1). They found that the 32CA reaction involving β-nitrostyrene (E)-1 gave isoxazolidine trans-3 in a 72% yield, together with isoxazolidine cis-4. Note that isoxazolidine cis-4 comes from a basic catalysed isomerisation of isoxazolidine trans-3.16 The cis and trans nomenclature refers to the relative position of the nitro and phenyl groups in the final isoxazolidines. On the other hand, the reaction involving a mixture of β-nitrostyrenes (Z)-1 and (E)-1 in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio mainly led to isoxazolidine cis-4, which was isolated with 90% yield (see Scheme 1). Interestingly, while the 32CA reaction of (E)-β-nitrostyrene (E)-1 was endo stereoselective, that of (Z)-β-nitrostyrene (Z)-1 was exo stereoselective. Both 32CA reactions presented a complete meta regioselectivity. Gandolfi and coworkers concluded that these 32CA reactions proceed via a “concerted” mechanism, but the determining factors controlling the reaction course were not examined.
1 ratio mainly led to isoxazolidine cis-4, which was isolated with 90% yield (see Scheme 1). Interestingly, while the 32CA reaction of (E)-β-nitrostyrene (E)-1 was endo stereoselective, that of (Z)-β-nitrostyrene (Z)-1 was exo stereoselective. Both 32CA reactions presented a complete meta regioselectivity. Gandolfi and coworkers concluded that these 32CA reactions proceed via a “concerted” mechanism, but the determining factors controlling the reaction course were not examined.
Recent Molecular Electron Density Theory17 (MEDT) studies on 32CA reactions of a wide diversity of three-atom-components (TACs) towards ethylene allowed establishing a good correlation between the electronic structure of TACs and their reactivity in 32CA reactions.18 Nitrones are zwitterionic TACs participation in zw-type 32CA reactions with high activation energies. Due to the nucleophilic character of nitrones, their zw-type 32CA reactions are accelerated by increasing the electrophilic character of the ethylene derivative.19 Nitroethylenes are strong electrophilic species participating in polar zw-type 32CA reactions with low activation energy and full regioselectivity. Usually, these type of 32CA reactions take place via a one-step mechanism; however, the use of non-symmetric, strongly electrophilic nitroethylenes can change the mechanism to a two-step one with the participation of a zwitterionic intermediate.20–24
Most of the theoretical studies of 32CA reactions of nitrones have been performed by using (E)-β-nitroethylenes yielding trans-isoxazolidines stereospecifically, but those using (Z)-β-nitroethylenes have not been theoretically studied so far. Hence, the corresponding 32CA reaction of nitrone 2 with (Z)-β-nitrostyrene (Z)-1 requires a deeper exploration. Herein, an MEDT study of the competitive stereospecific 32CA reactions of β-nitrostyrenes (E)-1 and (Z)-1 with nitrone 2, experimentally reported by Gandolfi and coworkers,16 is carried out in order to compare the reactivity of these isomers in 32CA reactions, and thus, to explain the experimental outcomes given in Scheme 1.
2. Results and discussion
The present MEDT study has been divided into five sections: (i) in Section 2.1, a topological analysis of the ELF of β-nitrostyrenes (E)-1 and (Z)-1, and nitrone 2 is performed in order to characterise their electronic structure; (ii) in Section 2.2, the Conceptual Density Functional Theory (CDFT) reactivity indices of the reagents are analysed in order to understand their reactivity; (iii) in Section 2.3, the energy profiles of the 32CA reactions of β-nitrostyrenes (E)-1 and (Z)-1 with nitrone 2 are studied in order to explain the experimental selectivities; (iv) in Section 2.4, a non-covalent interactions (NCI) analysis is performed in order to determine the origin of the exo stereoselectivity in the 32CA reaction of (Z)-β-nitrostyrene (Z)-1; and finally, (v) in Section 2.5, electron localisation function (ELF) and atoms-in-molecules (AIM) topological analyses of the endo TSs are carried out in order to characterise the bonding changes between the two pairs of (E) and (Z) TSs.2.1. Topological analysis of the ELF of β-nitrostyrenes (E)-1 and (Z)-1, and nitrone 2
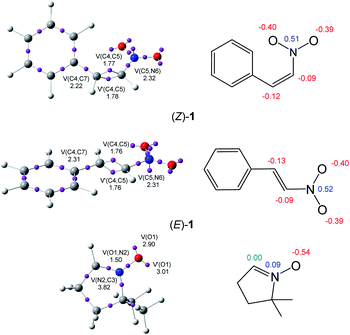
The topological analysis of the ELF25 allows a quantitative characterisation of chemical regions of molecules,26 thus being useful to classify TACs according to their electronic structure, and then, correlate them with their molecular reactivity within the MEDT framework. Proposed by Domingo in 2019,18 this standard classification of TACs into pseudodiradical, pseudo(mono)radical, carbenoid or zwitterionic TACs has allowed characterising 32CA reactions into pmr-type, pdr-type, cb-type and zw-type, respectively, based on the corresponding structure and reactivity of TACs.18 Herein, the ELF topology and charge distribution of β-nitrostyrenes (E)-1 and (Z)-1, and nitrone 2 are studied to assess their electronic structures. The ELF basin attractor positions and Lewis-like structures together with the most relevant ELF valence basin populations and atomic charges are shown in Fig. 1.The ELF topological analysis of nitrone 2 shows the presence of two monosynaptic basins, V(O1) and V′(O1), integrating a total population of 5.91 e, associated with the non-bonding electron density on the O1 oxygen, one V(O1,N2) disynaptic basin, integrating 1.50 e, associated with an underpopulated O1–N2 single bond, and one V(C3,N2) disynaptic basin, integrating 3.82 e, associated with the N2–C3 double bond. The absence of any V(C3) monosynaptic basin associated with a pseudoradical or carbenoid center allows the classification of the nitrone as a zwitterionic TAC.19
On the other hand, the ELF topological analysis of β-nitrostyrenes (E)-1 and (Z)-1 shows the presence of two disynaptic basins, V(C4,C5) and V′(C4,C5), integrating a total of 3.53 ((E)-1) and 3.55 ((Z)-1) e, associated to a somewhat depopulated C4–C5 double blond. The population of the V(C5,N6) and V(C4,C7) disynaptic basins associated to the C5–N6 and C4–C7 single bonds, higher than 2.2 e, emphasizes the delocalisation of the electron density of the C4–C5 bonding regions into the neighbouring nitro and phenyl groups. As expected, the population associated with the C4–C7 bond next to the phenyl substituent is slightly higher, i.e. by 0.09 e, at (E)-1 than at (Z)-1, denoting a higher delocalization at the former. Note, indeed, that (Z)-1 is more energetic than (E)-1 (see Table S1 and S2 in the ESI†).
Analysis of the natural atomic charges at the reactive ethylene framework of β-nitrostyrenes shows that they are very similar; both C4 and C5 ethylene carbons are negatively charged by ca. 0.1 e. Interestingly, the most electrophilic β-conjugated C4 carbon is slightly negatively charged, ca. −0.1 e, indicating that the electrophilic and nucleophilic properties cannot be related to positive and negative charges, respectively. On the other hand, the charge distribution at the O–N–C framework of nitrone 2 shows that while the O1 oxygen is negatively charged by 0.54 e, the N2 nitrogen is slightly positively charged by 0.09 e and the terminal C3 carbon is neutral. This charge distribution is a consequence of the polarisation of the O–N–C framework towards the more electronegative O1 oxygen, but not the result of any Lewis resonance structures.18 Thus, the topological analysis of the ELF and the charge distribution at both isomeric forms of the β-nitrostyrenes show no significant changes in their electronic structure.
2.2. Analysis of the CDFT reactivity indices of the reagents
On the basis of the CDFT reactivity indices,27,28 it is possible to shed valuable light on the nature of electronic interactions between the separated reagents. This approach has recently been successfully applied to the exploration of a great number of 32CA reactions. The CDFT indices were calculated at the B3LYP/6-31G(d) computational level since it was originally used to define the electrophilicity and nucleophilicity scales.28 The global reactivity indices, namely, electronic chemical potential μ, chemical hardness η, global electrophilicity ω and global nucleophilicity N, for β-nitrostyrenes (E)-1 and (Z)-1, and nitrone 2 are given in Table 1.| μ | η | ω | N | |
|---|---|---|---|---|
| (E)-1 | −4.79 | 4.31 | 2.66 | 2.17 |
| (Z)-1 | −4.78 | 4.24 | 2.70 | 2.22 |
| 2 | −2.85 | 5.51 | 0.74 | 3.52 |
The electronic chemical potential μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 of nitrone 2, μ = −2.85 eV, is higher than that of isomeric β-nitrostyrenes, μ = −4.79 ((E)-1) and −4.78 ((Z)-1) eV (see Table 1). This means that along a polar 32CA reaction, the flux of electron density will take place from nitrone 2 towards these β-nitrostyrenes, in complete agreement with the global electron density transfer30 (GEDT) calculated at the TSs (see later). Consequently, these 32CA reactions are classified as reactions of forward electron density flux (FEDF).31
29 of nitrone 2, μ = −2.85 eV, is higher than that of isomeric β-nitrostyrenes, μ = −4.79 ((E)-1) and −4.78 ((Z)-1) eV (see Table 1). This means that along a polar 32CA reaction, the flux of electron density will take place from nitrone 2 towards these β-nitrostyrenes, in complete agreement with the global electron density transfer30 (GEDT) calculated at the TSs (see later). Consequently, these 32CA reactions are classified as reactions of forward electron density flux (FEDF).31
The chemical hardness η of the β-nitrostyrenes is very similar, 4.24 ((Z)-1) and 4.31 ((E)-1) eV, being lower than that of nitrone 2, 5.51 eV. The β-nitrostyrenes are, therefore, softer species than nitrone 2, i.e. more sensitive to perturbations.
The electrophilicity ω indices32 of the two isomeric β-nitrostyrenes are 2.70 ((Z)-1) and 2.66 ((E)-1) eV, being classified as strong electrophiles within the electrophilicity scale.28 On the other hand, the nucleophilicity N indices33 of these β-nitrostyrenes are 2.22 ((Z)-1) and 2.17 ((E)-1) eV, being classified as moderate nucleophiles within the nucleophilicity scale.28 These reactivity indices indicate that the two isomeric β-nitrostyrenes will have a similar reactivity as strong electrophiles in polar reactions. It is worth mentioning, though, that the more energetic β-nitrostyrene (Z)-1 (see Table S1 in the ESI†) is slightly more electrophilic and more nucleophilic than (E)-1, thus expecting a higher reactivity of the former.
The electrophilicity ω and nucleophilicity N indices of nitrone 2 are 0.74 and 3.52 eV, respectively, being classified as a marginal electrophile and a strong nucleophile.
Analysis of global reactivity indices suggests, therefore, that these zw-type 32CA reactions will have a high polar character as a consequence of the strong electrophilic character of β-nitrostyrenes and the strong nucleophilic character of the nitrone, and as such, they will present low activation energies under normal conditions.18
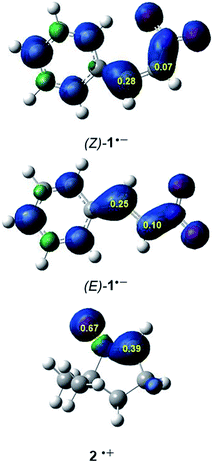
It is generally known that in polar cycloaddition reactions involving non-symmetric reagents, the preferred reaction course can be predicted by means of the nature of the most favourable two-center interaction between the nucleophilic–electrophilic reagents.34 In this context, the electrophilic P+k and nucleophilic P−k Parr functions35 derived from the excess of spin electron density reached via the GEDT process from the nucleophile towards the electrophile have shown to be the most accurate and insightful tools for the study of the local reactivity in polar and ionic processes. Hence, in order to characterise the most nucleophilic and electrophilic centers of the species involved in these 32CA reactions, the electrophilic P+k and nucleophilic P−k Parr functions were analysed (see Fig. 2).
Analysis of the electrophilic P+k Parr functions at the two isomeric β-nitrostyrenes indicates that the β-conjugated position, P+k = 0.28 ((Z)-1) and 0.25 ((E)-1), is more electrophilically activated than the α one, P+k = 0.07 ((Z)-1) and 0.10 ((E)-1). On the other hand, the oxygen atom of nitrone 2 is the most nucleophilic center of this species, P+k = 0.69. Note that the nitrone O1 oxygen is ca. twice as nucleophilically activated than the C3 carbon (see Fig. 1).
The analysis of the Parr functions at these compounds suggests that these 32CA reactions will be highly regioselective, the preferred interaction being that between the oxygen atom of nitrone 2, i.e. the O1 oxygen, and the β-conjugated carbon of the β-nitrostyrenes, i.e. the C4 carbon (see Scheme 2 for atom labels). Furthermore, analysis of global and local reactivity indices at both isomeric β-nitrostyrenes suggests that from an electronic point of view, both isomers will experience a similar reactivity.
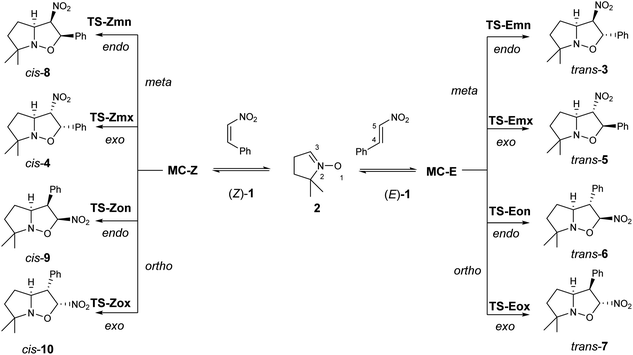 | ||
| Scheme 2 The four competitive reaction paths associated with the 32CA reactions of β-nitrostyrenes (Z)-1 and (E)-1 with nitrone 2. | ||
2.3. Analysis of the energy profiles of the 32CA reactions of β-nitrostyrenes (E)-1 and (Z)-1 with nitrone 2
Due to the non-symmetry of the reagents, the two 32CA reactions can take place along four competitive reaction paths. They are related to a pair of regioisomeric reaction paths, named ortho and meta, and a pair of stereoisomeric reaction paths, named as endo and exo (see Scheme 2). While the ortho reaction paths are associated with the O1–C5 single bond formation, the meta ones are associated with the expected most favourable O1–C4 interaction. Along the endo reaction paths, the nitro group is approached towards the nitrone framework. Analysis of the stationary points found along each reaction path in benzene and the thermodynamic data indicate that both 32CA reactions take place through a one-step mechanism (see Scheme 2). The relative energies in benzene of the stationary points involved in the two 32CA reactions are given in Table 2, while the absolute electronic energies are given in Tables S1 and S2 in the ESI.†| Structure | ΔE | Structure | ΔE |
|---|---|---|---|
| MC-Z | −11.7 | MC-E | −10.2 |
| TS-Zon | 13.9 | TS-Eon | 11.4 |
| TS-Zox | 8.6 | TS-Eox | 10.5 |
| TS-Zmn | 3.7 | TS-Emn | 4.2 |
| TS-Zmx | 4.3 | TS-Emx | 6.4 |
| cis-9 | −28.2 | trans-6 | −23.9 |
| cis-10 | −32.3 | trans-7 | −24.6 |
| cis-8 | −28.1 | trans-3 | −23.6 |
| cis-4 | −30.3 | trans-5 | −20.2 |
β-Nitrostyrene (Z)-1 is found 6.1 kcal mol−1 higher in energy than the (E)-1 isomer (see Tables S1 and S2 in the ESI†). The steric hindrance present between the NO2 and the phenyl groups at the (Z)-1 isomer breaks the planar geometry present at the (E)-1 isomer (see the geometries of β-nitrostyrenes (Z)-1 and (E)-1 in Fig. S1 in the ESI†). This behaviour causes a loss of the electron delocalisation present in the planar geometry of (E)-1 (see Section 2.1), justifying the higher electronic energy of the (Z)-1 isomer.
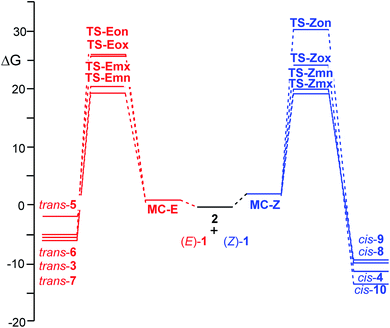
When the two reagents approach along the four competitive reaction paths, the formation of a series of molecular complexes (MCs) takes place; these species are more stable than the separated reagents in the PES. As the MCs are found in equilibrium, only the most stable MC for each 32CA reaction, which is the one associated with the meta/endo reaction path, is considered. Formation of these MCs is exothermic by 11.7 (MC-Z) and 10.2 (MC-E) kcal mol−1. The geometries of these MCs are given in Fig. S2 in the ESI.†
The activation energies associated to the two 32CA reactions in benzene are 3.7 (TS-Zmn) and 4.2 (TS-Emn) kcal mol−1, the reactions being strongly exothermic by 28.1 (cis-9) and 23.6 (trans-6) kcal mol−1. From the relative energies given in Table 2, some appealing conclusions can be drawn: (i) the activation energies associated with these 32CA reactions are very low, in agreement with the high electrophilic and nucleophilic character of the reagents (see Section 2.2) and the polar character of the reactions (see later). Note that the activation energy of the 32CA reactions between nitrone 2 and ethylene, a very poor electrophile, is 14.0 kcal mol−1; (ii) at the ωB97X-D/6-311G(d,p) level, the activation energy associated to the 32CA reaction of β-nitrostyrene (Z)-1 is only 0.5 kcal mol−1 lower than that of β-nitrostyrene (E)-1; (iii) by means of the relative electronic energies in benzene, these 32CA reactions present an endo stereoselectivity as TS-Zmn and TS-Emn are 0.6 and 2.2 kcal mol−1 lower in energy than TS-Zmx and TS-Emx, respectively. However, note that the 32CA reaction of (Z)-1 is completely exo stereoselective experimentally (see Scheme 1); (iv) these 32CA reactions are completely meta regioselective as TS-Zmn and TS-Emn are 4.9 and 6.3 kcal mol−1 lower in energy than TS-Zox and TS-Eox, respectively, in complete agreement with the experimental outcomes (see Scheme 1) and the analysis of the Parr functions (see Section 2.2); and (v) the ωB97X-D/6-311G(d,p) electronic energies in benzene seem to account only for the total meta regioselectivity experimentally found.
ωB97X-D/6-311G(d,p) calculations give a slightly higher reactivity to the β-nitrostyrene (Z)-1 than the β-nitrostyrene (E)-1, as the activation energy associated to TS-Zmx is only 0.1 kcal mol−1 lower than that associated to TS-Emn. A similar result was obtained at the B3LYP/6-311G(d,p) level, 0.6 kcal mol−1. Consequently, none of these DFT functionals account for the higher reactivity of (Z)-β-nitrostyrene (Z)-1 experimentally observed when a mixture of (Z)-1, (E)-1 and 2 led only to cis-4, coming from TS-Zmx, in 90% yield (see Scheme 1). Interestingly, when these TSs were optimised at the HF/6-311G(d,p) level in benzene, the activation energy associated to TS-Zmx, 23.2 kcal mol−1, was found 3.6 kcal mol−1 lower than that associated to TS-Emn (see Table S5 in the ESI†).
When the difference between the gas phase energies of the (Z)-1 and (E)-1 isomers was calculated at the HF, B3LYP and ωB97X-D theoretical levels, ΔEZ–E = 7.1, 6.0 and 6.0 kcal mol−1, respectively, the DFT calculations showed to underestimate the strain in β-nitrostyrene (Z)-1 by 1.1 kcal mol−1 with respect to the HF ones. Along the reaction path, β-nitrostyrene (Z)-1 loses the strain present at its ground state, and consequently, the DFT calculations might underestimate the relative energies associated to the (Z) TSs, yielding a lower activation energy for the 32CA reaction of (Z)-1, and consequently, a lower difference between the reactivities of β-nitrostyrenes (Z)-1 and (E)-1 than that experimentally observed.
The thermodynamic data of the 32CA reactions of β-nitrostyrenes (E)-1 and (Z)-1 with nitrone 2 were analysed. The relative enthalpies, entropies and Gibbs free energies are given in Table 3, while the absolute thermodynamic data are gathered in Tables S1 and S2 in the ESI.† The Gibbs free energy profiles associated with the four competitive reaction paths are represented in Fig. 3.
| ΔH | ΔS | ΔG | ΔH | ΔS | ΔG | ||
|---|---|---|---|---|---|---|---|
| MC-Z | −10.3 | −41.9 | 2.2 | MC-E | −8.7 | −33.4 | 1.2 |
| TS-Zon | 15.1 | −51.7 | 30.5 | TS-Eon | 12.3 | −48.4 | 26.7 |
| TS-Zox | 9.6 | −49.9 | 24.4 | TS-Eox | 11.5 | −50.0 | 26.4 |
| TS-Zmn | 4.4 | −53.5 | 20.4 | TS-Emn | 5.0 | −49.7 | 19.8 |
| TS-Zmx | 5.0 | −49.8 | 19.9 | TS-Emx | 7.2 | −48.9 | 21.8 |
| cis-9 | −25.3 | −54.8 | −9.0 | trans-6 | −20.8 | −53.0 | −5.0 |
| cis-10 | −29.4 | −53.2 | −13.5 | trans-7 | −21.6 | −51.8 | −6.2 |
| cis-8 | −25.1 | −53.5 | −9.2 | trans-3 | −20.7 | −50.3 | −5.7 |
| cis-4 | −27.4 | −53.5 | −11.5 | trans-5 | −17.3 | −51.2 | −2.1 |
Inclusion of thermal corrections to the electronic energies in benzene decreases the relative enthalpies by between 0.7 and 3.1 kcal mol−1 in both 32CA reactions. As the incidence at the TSs is the same, the relative enthalpies change neither the stereoselectivity nor the regioselectivity found by considering the electronic energies in benzene.
Inclusion of the temperature and entropies, found between −33.4 and −54.8 cal mol−1 K−1 (see Table 3), to the enthalpies increases the relative Gibbs free energies by between 12.5 and 16.4 kcal mol−1 for the 32CA reaction involving β-nitrostyrene (Z)-1, and by between 9.9 and 15.8 kcal mol−1 for the 32CA reaction involving β-nitrostyrene (E)-1, as a consequence of the unfavourable activation entropies associated to these bimolecular processes. The activation Gibbs free energies associated to these 32CA reactions rise to 19.9 (TS-Zmx) and 19.8 (TS-Emn) kcal mol−1, while formation of cycloadducts becomes exergonic by 11.5 (cis-10) and 5.7 (trans-6) kcal mol−1. On the other hand, considering the Gibbs free energies, the 32CA reaction of β-nitrostyrene (Z)-1 becomes slightly exo stereoselective, by 0.5 kcal mol−1, as a consequence of the more unfavourable activation entropy associated to TS-Zmn, −53.5 cal mol−1 K−1, than that associated to TS-Zmx, −49.8, cal mol−1 K−1. The exergonic character of the reactions under the experimental conditions makes them irreversible and the corresponding products are obtained by kinetic control.
As aforementioned, the ωB97X-D/6-311G(d,p) electronic energies and enthalpies in benzene yield an endo stereoselectivity along the more favourable meta reaction paths of the 32CA reaction involving β-nitrostyrene (Z)-1, in contrast with the complete exo stereoselectivity experimentally reported (see Scheme 1). Only the ωB97X-D/6-311G(d,p) activation Gibbs free energies gives a small exo stereoselectivity. Thus, in order to verify the dependency of the endo stereoselectivity on the computational level, the corresponding meta TSs were optimised at the B3LYP/6-311G(d,p) and M06-2X/6-311G(d,p) computational levels (see Tables S3, S4 and S6 in the ESI†). Interestingly, while the M06-2X/6-311G(d,p) calculations yield an even higher endo stereoselectivity, the B3LYP/6-311G(d,p) affords the complete exo stereoselectivity, ΔΔE = 2.1 kcal mol−1, in clear agreement with the experimental outcomes (see Scheme 1).
When the ωB97X-D/6-311G(d,p) absolute electronic energies of the eight TSs are compared with the B3LYP/6-311G(d,p) ones, a very good linear correlation can be established, R = 0.96 (see Fig. S3 in the ESI†). In general, the B3LYP TSs are stabilised by ca. 180 kcal mol−1 with respect the ωB97X-D ones. However, TS-Zmn is less stabilised, 177.3 kcal mol−1, indicating that at the ωB97X-D level there is a slightly higher electronic stabilisation of TS-Zmn, −2.7 kcal mol−1, with respect to the other TSs. This electronic stabilisation is in agreement with the lower entropy of TS-Zmn at ωB97X-D, thus favouring this pathway at that level (see Table 3).
Interestingly, when a correction factor of −2.7 kcal mol−1 is applied to the ωB97X-D/6-311G(d,p) electronic structure of TS-Zmn, now this TS is 2.1 kcal mol−1 higher in energy than TS-Zmx, in clear agreement with the exo stereoselectivity found experimentally (see Scheme 1). Note that the B3LYP/6-311G(d,p) thermodynamic calculations of the more favourable meta TS-Zmn and TS-Zmx afford a complete exo stereoselectivity, ΔΔG = 2.8 kcal mol−1, in complete agreement with the experimental outcomes (see Scheme 1).
The optimised geometries in benzene of the endo TSs involved in the 32CA reactions of β-nitrostyrenes (E)-1 and (Z)-1 with nitrone 2 are given in Fig. 4, while the distances between the four interacting centers at all TSs are given in Table 4. Some appealing conclusions can be obtained from the geometrical parameters given in Table 4: (i) no significant differences between the endo/exo TS pairs are observed; (ii) the geometries of the (E) and (Z) TSs are very similar; (iii) the distances involving the β-conjugated C4 carbon of β-nitrostyrenes are always shorter than those involving the α C5 carbon; (iv) at the more asynchronous meta TSs, the shorter O1–C4 distances correspond to the most favourable two-center interactions between the most nucleophilic center of nitrone 2, the O1 oxygen, and the most electrophilic center of β-nitrostyrenes (E)-1 and (Z)-1, the β-conjugated C4 carbon; and (v) considering that the C–C and C–O single bond formation takes place at the short distance range of 2.0–1.9 and 1.8–1.7 Å, respectively,18 these distances indicate that while at the more unfavourable ortho TSs only the O1–C5 single bond formation can be considered not started yet, at the most favorable meta TSs only the C3–C5 single bond formation can be considered not started yet, i.e. in both reactions the distance involving the more electrophilic C4 carbon might already be formed.
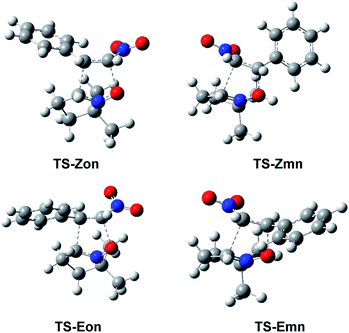 | ||
| Fig. 4 ωB97X-D/6-311G(d,p) optimised geometries in benzene of the endo TSs involved in the 32CA reactions of β-nitrostyrenes (E)-1 and (Z)-1 with nitrone 2. | ||
| O1–C5 | C3–C4 | GEDT | O1–C5 | C3–C4 | GEDT | ||
|---|---|---|---|---|---|---|---|
| TS-Zon | 1.998 | 1.994 | 0.15 | TS-Eon | 2.122 | 1.989 | 0.17 |
| TS-Zox | 2.166 | 1.988 | 0.17 | TS-Eox | 1.975 | 2.037 | 0.13 |
| O1–C4 | C3–C5 | GEDT | O1–C4 | C3–C5 | GEDT | ||
|---|---|---|---|---|---|---|---|
| TS-Zmn | 1.693 | 2.333 | 0.24 | TS-Emn | 1.776 | 2.270 | 0.19 |
| TS-Zmx | 1.747 | 2.380 | 0.23 | TS-Emx | 1.757 | 2.293 | 0.21 |
Finally, the GEDT at the TSs was calculated in order to assess the polarity of these zw-type 32CA reactions. Reactions with GEDT values lower than 0.05 e correspond to non-polar processes, while values higher than 0.20 e correspond to polar processes. From the GEDT values given in Table 4 some appealing conclusions can be obtained: (i) the high GEDT values found at the more favourable meta TSs, between 0.24 e (TS-Zmn) and 0.21 (TS-Emn), indicate that these zw-type 32CA reactions have a high polar character; (ii) the more favourable meta TSs are more polar that the ortho ones since the former are more advanced. Note that the GEDT depends not only on the electrophilic/nucleophilic behaviour of the reagents, but also on the distance between the two interacting frameworks;36 and (iii) this GEDT analysis suggests that these 32CA reactions are classified as reactions of FEDF,31 in clear agreement with the analysis of the CDFT global reactivity indices given in Section 3.2.
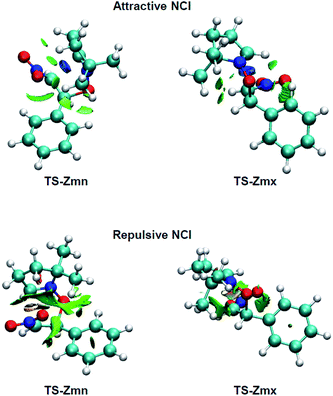
2.4. NCI analysis of the origin of the exo stereoselectivity in the 32CA reaction of (Z)-β-nitrostyrene (Z)-1 with nitrone 2
Many polar zw-type 32CA reactions of nitrones present an endo selectivity resulting from favourable electrostatic interactions taking place between the positively and negatively charged frameworks after the GEDT. Thus, TS-Emn is found 2.2 kcal mol−1 lower in energy than TS-Emx (see Table 1), in clear agreement with the experimental outcomes (see Scheme 1). However, the polar 32CA reaction involving β-nitrostyrene (Z)-1 presents an exo selectivity (see Scheme 1). Exo selectivity might result from repulsive NCI taking place between two hydrocarbon fragments that exceed the attractive electrostatic interactions present in the endo approach.Therefore, in order to understand the unexpected experimental exo stereoselectivity in the polar zw-type 32CA reaction between β-nitrostyrene (Z)-1 and nitrone 2, a topological analysis of the NCI37 taking place at the meta TS-Zmn and TS-Zmx was performed. The NCI isosurfaces are shown in Fig. 5.
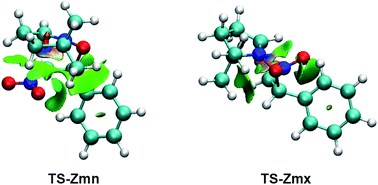 | ||
| Fig. 5 NCI isosurfaces associated with the density overlap at TS-Zmn and TS-Zmx. Isosurface value of 0.5 and blue-green-red color scale from −0.08 < sign(λ2)ρ(r) < 0.08 a.u. | ||
As can be observed, endo TS-Zmn presents more isosurfaces than the more favourable exo TS-Zmx (see Fig. 5). When these NCI are divided into their attractive, i.e. sign(λ2)ρ(r) < 0 a.u., and repulsive, i.e. sign(λ2)ρ(r) > 0 a.u., components, the most notable differences between both endo and exo stereoisomeric TSs are observed in the topology of the repulsive NCI (see Fig. 6). While endo TS-Zmn presents a larger green surface associated with repulsive interactions between the nitrone and β-nitrostyrene frameworks, the most relevant surface at exo TS-Zmx is only associated with punctual repulsive interactions between one of the nitrone methyl groups and the β-nitrostyrene hydrogen atoms. Consequently, it appears that the higher steric hindrance along the endo approach mode overcomes the favourable electrostatic interactions in the 32CA reaction involving β-nitrostyrene (Z)-1, thus leading to an exo stereoselectivity. It seems to be that, unlike the B3LYP functional, the ωB97X-D one underestimates the repulsive interactions present at the endo TS-Zmn, yielding an unexpected endo stereoselectivity, ΔΔExn = 0.6 kcal mol−1 (see Table 1). Note that at the B3LYP level, this energy difference becomes negative, ΔΔExn = −2.1 kcal mol−1, in clear agreement with the experimental outcomes (see Tables S2 and S4 in the ESI†).
2.5. ELF and AIM topological analyses of the endo TSs
In order to characterise the bonding changes between the two pairs of (E) and (Z) TSs of the 32CA reactions of β-nitrostyrenes (E)-1 and (Z)-1 with nitrone 2, ELF21 and AIM38,39 topological analyses of the four endo TSs was performed. As the TSs were optimised in benzene, the electronic structure of the reagents in benzene were also analysed as a reference. The ELF valence basin populations at the reagents and TSs in benzene are given in Table 5 while the basin attractor positions at the four TSs are shown in Fig. 7.| (Z)-1 | (E)-1 | 2 | TS-Zon | TS-Zmn | TS-Eon | TS-Emn | |
|---|---|---|---|---|---|---|---|
| V(O1,N2) | 1.47 | 1.29 | 1.19 | 1.29 | 1.21 | ||
| V(N2,C3) | 3.81 | 2.38 | 3.10 | 2.39 | 3.02 | ||
| V(C4,C5) | 1.78 | 1.76 | 2.94 | 2.58 | 2.94 | 2.62 | |
| V′(C4,C5) | 1.77 | 1.76 | |||||
| V(O1) | 2.91 | 2.87 | 2.60 | 2.83 | 2.82 | ||
| V′(O1) | 3.04 | 2.82 | 2.74 | 2.86 | 3.03 | ||
| V′′(O1) | 0.67 | ||||||
| V(N2) | 1.26 | 1.00 | 1.36 | 1.13 | |||
| V(C3) | 0.58 | 0.53 | |||||
| V(C4) | 0.53 | 0.51 | 0.09 | ||||
| V(C5) | 0.67 | 0.68 |
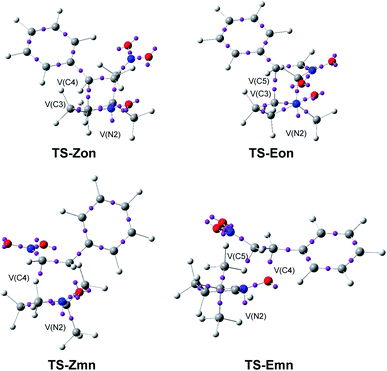 | ||
| Fig. 7 ELF basin attractor positions at the endo TSs, pointing out the new V(C) and V(N) monosynaptic basins created along the reaction paths. | ||
A great similitude is observed in the geometrical aspects between the pairs of the two ortho TSs and the two meta TSs (see Fig. 7). At both pairs of TSs, the O1–N2 and the N2–C3 bonding regions of the nitrone have been depopulated by ca. 0.18 (ortho) and 0.26 (meta) e, and 1.43 (ortho) and 0.71 (meta) e, respectively (see the populations of the V(O1,N2) and V(N2,C3) disynaptic basins in Table 5), while a new V(N2) monosynaptic basin, integrating between 1.00 and 1.36 e, has been created at the N2 nitrogen, associated with the N2 non-bonding electron density present at the final isoxazolidines.19 This data indicates that while the O1–N2 region of nitrone 2 is slightly more depopulated than the N2–C3 one along the more favourable meta reaction paths, the N2–C3 region is considerably more depopulated than the O1–N2 one along the ortho reaction paths. Indeed, at the ortho TSs, a new V(C3) monosynaptic basin, integrating ca. 0.5 e, is created, as a consequence of the strong depopulation of the V(N2,C3) disynaptic basins.
On the other hand, as a consequence of the significant depopulation of the C4–C5 bonding region of the ethylene framework at the TSs by ca. 0.6 (Z) and 0.9 (E) e, the two V(C4,C5) and V′(C4,C5) disynaptic basins present in nitrostyrenes have merged into one V(C4,C5) disynaptic basin. These bonding changes have provoked the creation of one V(C5) monosynaptic basin at the meta TSs, integrating ca. 0.5 (Z) and 0.7 (E) e. Note that at TS-Emn a V(C4) monosynaptic basin with a unappreciable population of 0.09 e is also created.
At TS-Zmn, the two V(O1) monosynaptic basins present in nitrone 2 have been split into three V(O1), V′(O1) and V′′(O1) monosynaptic basins, with a total population of 6.01 e. The new V′′(O1) monosynaptic basin, which has a population of 0.67 e, will participate in the formation of the O1–C5 single bond.
Neither V(O1,C5) nor V(C3,C4) disynaptic basins are observed at the four TSs, indicating that the formation of either O–C and C–C single bonds has not yet begun at any of them. In addition, it can be noticed that the C4–C5 double bond of the β-nitrostyrenes is depopulated, i.e. being broken, before the formation of any O–C and C–C single bond, thus indicating that although these zw-type 32CA reactions present a one-step mechanism, the bonding changes are non-concerted, ruling out the experimentalist's proposal.16
Finally, a comparison of the el ELF of two pairs of (E) and (Z) TSs shows a great similitude between them, indicating that the (E) or (Z) configuration of the β-nitrostyrene does no noticeable effect to the electronic structure of the TSs, in agreement with the similar activation Gibbs free energies of both reactions.
Bader and coworkers38,39 proposed the AIM concept to reveal the nature of interatomic interactions. Consequently, in order to confirm that none of the new O–C and C–C single bonds have been yet formed at the four TSs, an AIM topological analysis of the four electronic structures was also performed. The total electron density ρ and Laplacian of electron density ∇2ρ(rc) at the bond critical points (BCPs) CP1 and CP2 associated to the interatomic O–C and C–C regions, respectively, of the endo TSs are given in Table 6.
| CP1 | CP2 | |||
|---|---|---|---|---|
| ρ | ∇2ρ(rc) | ρ | ∇2ρ(rc) | |
| O1–C5 | C3–C4 | |||
| TS-Zon | 0.0767 | 0.1407 | 0.0918 | −0.0086 |
| TS-Eon | 0.0810 | 0.1373 | 0.0839 | 0.0058 |
| O1–C4 | C3–C5 | |||
| TS-Zmn | 0.1411 | 0.0040 | 0.0472 | 0.0530 |
| TS-Emn | 0.1175 | 0.0812 | 0.0536 | 0.0478 |
The total electron density accumulated at the BCPs is less than 0.14 a.u. in every TS and the Laplacian of electron density ∇2ρ(rc) shows small positive values at three TSs, suggesting rather non-covalent interactions. Only TS-Zon shows a small negative value of the Laplacian ∇2ρ(rc) associated with the C3–C4 bond path, suggesting a slight covalent nature for this interaction. However, note that the topological analysis of the ELF at this TS shows no disynaptic basin in this region.
Thus, AIM suggests that only the formation of the C3–C4 single bond has already started at TS-Zon. Interestingly, this AIM topological analysis allows establishing that at the more favourable meta TSs the O1–C4 bond formation is more advanced than the C3–C5 one (see the greater values of ρ at the meta TSs), while at the ortho TSs the C3–C4 looks more advanced (see the greater positive values of ∇2ρ(rc) at CP1). This finding indicates that the most electrophilic β-conjugated C4 atom of the β-nitroalkanes is controlling the regioselectivity.34
3. Conclusions
The 32CA reactions of the stereoisomeric β-nitrostyrenes (E)-1 and (Z)-1 with 3,4-dihydroisoquinoline-N-oxide 2, experimentally studied by Gandolfi and coworkers,16 have been studied within MEDT, using the HF, B3LYP and ωB97X-D functionals together with the 6-311G(d,p) basis set, in order to analyse the participation of stereoisomeric (E) and (Z) β-nitrostyrenes in 32CA reactions.Topological analysis of the ELF of nitrone 2 shows its zwitterionic structure, thus participating in zw-type 32CA reactions. On the other hand, topological analysis of the ELF of β-nitrostyrenes (E)-1 and (Z)-1 shows the great similitude between their electronic structures. Analysis of the CEDT indices indicates that β-nitrostyrenes (E)-1 and (Z)-1 are strong electrophiles and nitrone 2 a strong nucleophile participating in polar zw-type 32CA reactions, in agreement with the GEDT computed at the TSs. Analysis of the Parr functions indicates that the O1 oxygen atom of nitrone 2 is the most nucleophilic center, while the β-conjugated C4 position of the two β-nitrostyrenes is the most electrophilic center, accounting for the total meta regioselectivity experimentally found. Indeed, the most favourable meta TSs show highly asynchronous geometries in which the O1–C4 distance is much shorter.
These 32CA reactions take place through a one-step mechanism, with low activation Gibbs free energies, 19.9 (TS-Zmx) and 19.8 (TS-Emn) kcal mol−1, the processes being exergonic by between 11.5 (CA-Zmx) and 5.7 (CA-Emx) kcal mol−1. These 32CA reactions, which are completely meta regioselective, present an exo stereoselectivity for the (Z) isomer (B3LYP) and an endo stereoselectivity for the (E) isomer (ωB97X-D, B3LYP).
ELF and AIM topological analyses of the four endo TSs show the similitude between the electronic structures of the pairs of TSs involved in the 32CA reactions of E/Z stereoisomeric β-nitrostyrenes (E)-1 and (Z)-1. Both analyses establish that the formation of neither new C–O nor C–C single bonds has begun yet at the TSs in spite of the very advanced character of the meta TSs. NCI topological analysis of the meta/endo TS-Zmn allows characterising the steric interaction responsible for the exo stereoselectivity found in the 32CA reaction of β-nitrostyrene (Z)-1.
The present MEDT study provides a reliable answer to the determining factors controlling the reaction course of the 32CA reactions of isomeric E/Z β-nitrostyrenes with nitrones. The feasibility of these reactions at experimental mild conditions is the consequence of their high polar character resulting from the strong electrophilic and nucleophilic behaviour of the reagents. The reactions of both isomers present similar kinetics, and the Parr functions account for the full meta regioselectivity. The unexpected exo stereoselectivity of the reaction involving the Z isomer is due to the unfavourable steric hindrance taking place between the reagents along the endo approach mode, which overcomes the favourable electrostatic interactions. It is worth mentioning that while the ωB97X-D functional cannot account for the exo stereoselectivity of β-nitrostyrene (Z)-1, the B3LYP can, and while none of them account for the low competitiveness between both isomeric β-nitrostyrenes, only the HF functional can. Finally, the postulated “concerted” nature of title reactions in the light of our MEDT studies should be completely ruled out.
4. Computational methods
DFT calculations were performed using the HF,40 B3LYP41,42 and hybrid ωB97X-D functional43 which includes long range exchange (denoted by X) correction as well as the semiclassical London-dispersion correction (indicated by suffix-D). The standard 6-311G(d,p)40 basis set was used, which includes d-type polarization for second row elements and p-type polarization functions for hydrogen atoms. The Berny method was used in optimizations.44,45 Only one imaginary frequency characterised all studied TSs. The intrinsic reaction coordinate (IRC) paths46 were carried out to find the unique connection given between the TSs and the minimum stationary points.47,48 Solvent effects of benzene were considered by full optimization of the gas phase structures at the same computational level using the polarizable continuum model (PCM)49,50 in the framework of the self-consistent reaction field (SCRF).51–53 Values of B3LYP/6-311G(d,p) and ωB97X-D/6-311G(d,p) enthalpies, entropies and Gibbs free energies in benzene were calculated with standard statistical thermodynamics at 298.15 K and 1 atm.40The GEDT30 values were estimated by a natural population analysis (NPA)54,55 using the equation 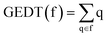 , were q are the atoms of a framework (f) at the TSs. CDFT reactivity indices27,28 were calculated through the equations given in ref. 28. All computations were carried out with the Gaussian 16 suite of programs.56
, were q are the atoms of a framework (f) at the TSs. CDFT reactivity indices27,28 were calculated through the equations given in ref. 28. All computations were carried out with the Gaussian 16 suite of programs.56
The topology of the ELF25 of the ωB97X-D/6-311G(d,p) monodeterminantal wavefunctions was carried out using the TopMod57 package with a cubical grid of step size of 0.1 bohr, while AIM38,39 analysis was performed using Multiwfn software.58 GaussView program59 was used to visualize molecular geometries of all the systems as well as the position of the ELF basin attractors. NCI analysis37 was performed with the NCIPLOT4 program.60
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Ministerio de Ciencias, Innovación y Universidades of the Spanish Government, project PID2019-110776GB-I00 (AEI/FEDER, UE), by PL-Grid Infrastructure in the regional computer center ‘Cyfronet’ in Cracow, and by the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 846181 (MRG).References
- V. V. Pelipko and R. I. Bajczurin, Chem. Heterocycl. Compd., 2020, 56, 1277–1279 CrossRef.
- N. Orlova, M. Vorona, V. Baskevics, M. Petrova, S. Belyakov, H. Kazoka, R. Muhamadejev and G. Veinberg, Chem. Heterocycl. Compd., 2020, 56, 997–1009 CrossRef CAS.
- A. Fryzlewicz, A. Łapczuk-Krygier, K. Kula, O. M. Demchuk, E. Dresler and R. Jasiński, Chem. Heterocycl. Compd., 2020, 56, 120–122 CrossRef CAS.
- A. Kącka-Zych and R. Jasiński, Theor. Chem. Acc., 2020, 139, 119 Search PubMed.
- K. Kula, J. Dobosz, R. Jasiński, A. Kącka-Zych, A. Łapczuk-Krygier, B. Mirosław and O. M. Demchuk, J. Mol. Struct., 2020, 1203, 127473 CrossRef CAS.
- G. Petrillo, A. Benzi, L. Bianchi, M. Maccagno, A. Pagano, C. Tavani and D. Spinelli, Tetrahedron Lett., 2020, 61, 152297 CrossRef CAS.
- A. Kącka-Zych, Organics, 2020, 1, 36–48 CrossRef.
- A. Boguszewska-Czubara, A. Łapczuk-Krygier, K. Rykała, A. Biernasiuk, A. Wnorowski, Ł. Popiołek, A. Maziarka, A. Hordyjewska and R. Jasiński, J. Enzyme Inhib. Med. Chem., 2016, 31, 900–907 CrossRef CAS PubMed.
- J. L. Chiara, A. Gómez-Sánchez and J. Bellanato, J. Chem. Soc., Perkin Trans. 2, 1992, 787–798 RSC.
- D. Seebach, A. K. Beck, J. Goliński, J. N. Hay and T. Laube, Helv. Chim. Acta, 1985, 68, 162–172 CrossRef CAS.
- Yu. V. Baskov, T. Urbański, M. Witanowski and L. Stefaniak, Tetrahedron, 1964, 20, 1519–1526 CrossRef CAS.
- G. Hesse and V. Jager, Liebigs Ann. Chem., 1970, 740, 79–84 CrossRef CAS.
- P. Cailleux, J. C. Piet, H. Benhaoua and R. Carrie, Bull. Soc. Chim. Belg., 1996, 105, 45–51 CrossRef CAS.
- E. Zandvoort, E. M. Geertsema, B.-J. Baas, W. J. Quax and G. J. Poelarends, ChemBioChem, 2012, 13, 1869–1873 CrossRef CAS PubMed.
- M. Z. Kassaee and E. Vessally, J. Photochem. Photobiol., A, 2005, 172, 331–336 CrossRef CAS.
- M. Burdisso, A. Gamba, R. Gandolfi and P. Pevarell, Tetrahedron, 1987, 43, 1835–1846 CrossRef CAS.
- L. R. Domingo, Molecules, 2016, 21, 1319 CrossRef PubMed.
- M. Ríos-Gutiérrez and L. R. Domingo, Eur. J. Org. Chem., 2019, 267–282 CrossRef.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, J. Org. Chem., 2018, 83, 2182–2197 CrossRef CAS PubMed.
- R. Jasiński and E. Dresler, Organics, 2020, 1, 49–69 CrossRef.
- R. Jasiński, Comput. Theor. Chem., 2018, 1125, 77–85 CrossRef.
- R. Jasiński, M. Zmigrodzka, E. Dresler and K. Kula, J. Heterocycl. Chem., 2017, 54, 3314–3320 CrossRef.
- R. Jasiński, RSC Adv., 2015, 5, 101045–101048 RSC.
- R. Jasiński, Tetrahedron Lett., 2015, 56, 532–535 CrossRef.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, NY, USA, 1989 Search PubMed.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Molecules, 2016, 21, 748 CrossRef PubMed.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- L. R. Domingo, RSC Adv., 2014, 4, 32415–32428 RSC.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, RSC Adv., 2020, 10, 15394–15405 RSC.
- R. G. Parr, L. v. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- L. R. Domingo, E. Chamorro and P. Pérez, J. Org. Chem., 2008, 73, 4615–4624 CrossRef CAS PubMed.
- M. J. Aurell, L. R. Domingo, P. Pérez and R. Contreras, Tetrahedron, 2004, 60, 11503–11509 CrossRef CAS.
- L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486–1494 RSC.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Molecules, 2020, 25, 2535 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, USA, 1994 Search PubMed.
- R. F. W. Bader and H. Essén, J. Chem. Phys., 1984, 80, 1943–1960 CrossRef CAS.
- M. J. Hehre, L. Radom, P. v. R. Schleyer and J. Pople, Ab initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218 CrossRef CAS.
- H. B. Schlegel, in Modern electronic structure theory, ed. D. R. Yarkony, World Scientific Publishing, Singapore, 1994 Search PubMed.
- K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS.
- C. González and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef.
- C. González and H. B. Schlegel, J. Chem. Phys., 1991, 95, 5853–5860 CrossRef.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 CrossRef CAS.
- B. Ya. Simkin and I. I. Sheikhet, Quantum chemical and statistical theory of solutions – computational approach, Ellis Horwood, London, 1995 Search PubMed.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS.
- E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS.
- V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16, Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- S. Noury, X. Krokidis, F. Fuster and B. Silvi, Comput. Chem., 1999, 23, 597–604 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView Version 6.0, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J. P. Piquemal, Y. Maday and J. Contreras-García, J. Chem. Theory Comput., 2020, 16, 4150–4158 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: ωB97X-D/6-311G(d,p) optimised geometries of β-nitrostyrenes (Z)-1 and (E)-1, and of MCs MC-Z and MC-E, plot of the B3LYP/6-311G(d,p) total energies vs. the ωB97X-D/6-311G(d,p) ones of the eight TSs involved in the 32CA reactions of β-nitrostyrenes (Z)-1 and (E)-1 with nitrone 2, ωB97X-D/6-311G(d,p) and B3LYP/6-311G(d,p) total energies, enthalpies, entropies and Gibbs free energies of all the stationary points, and HF/6-311G(d,p) and M06-2X/6-311G(d,p) total and relative energies of TS-Zmx and TS-Emn in benzene. See DOI: 10.1039/d1ra00891a |
| This journal is © The Royal Society of Chemistry 2021 |