Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrogen induced interface engineering in Fe2O3–TiO2 heterostructures for efficient charge separation for solar-driven water oxidation in photoelectrochemical cells†
Aadesh P. Singh *a,
Richard Baochang Wang
*a,
Richard Baochang Wang b,
Camilla Tossi
b,
Camilla Tossi a,
Ilkka Tittonen
a,
Ilkka Tittonen a,
Björn Wickman
a,
Björn Wickman b and
Anders Hellman
b and
Anders Hellman *b
*b
aDepartment of Electronics and Nanoengineering, School of Electrical Engineering, Aalto University, P.O. Box 13500, 00076 Aalto, Finland. E-mail: aadesh.singh@aalto.fi
bDivision of Chemical Physics, Department of Physics, Chalmers University of Technology, SE-412 96 Göteborg, Sweden. E-mail: anders.hellman@chalmers.se; Tel: +46 31 772 5611
First published on 21st January 2021
Abstract
Semiconductor heterostructure junctions are known to improve the water oxidation performance in photoelectrochemical (PEC) cells. Depending on the semiconductor materials involved, different kinds of junctions can appear, for instance, type II band alignment where the conduction and valence bands of the semiconductor materials are staggered with respect to each other. This band alignment allows for a charge separation of the photogenerated electron–hole pairs, where the holes will go from low-to-high valance band levels and vice versa for the electrons. For this reason, interface engineering has attracted intensive attention in recent years. In this work, a simplified model of the Fe2O3–TiO2 heterostructure was investigated via first-principles calculations. The results show that Fe2O3–TiO2 produces a type I band alignment in the heterojunction, which is detrimental to the water oxidation reaction. However, the results also show that interstitial hydrogens are energetically allowed in TiO2 and that they introduce states above the valance band, which can assist in the transfer of holes through the TiO2 layer. In response, well-defined planar Fe2O3–TiO2 heterostructures were manufactured, and measurements confirm the formation of a type I band alignment in the case of Fe2O3–TiO2, with very low photocurrent density as a result. However, once TiO2 was subjected to hydrogen treatment, there was a nine times higher photocurrent density at 1.50 V vs. the reversible hydrogen electrode under 1 sun illumination as compared to the original heterostructured photoanode. Via optical absorption, XPS analysis, and (photo)electrochemical measurements, it is clear that hydrogen treated TiO2 results in a type II band alignment in the Fe2O3–H:TiO2 heterostructure. This work is an example of how hydrogen doping in TiO2 can tailor the band alignment in TiO2–Fe2O3 heterostructures. As such, it provides valuable insights for the further development of similar material combinations.
1. Introduction
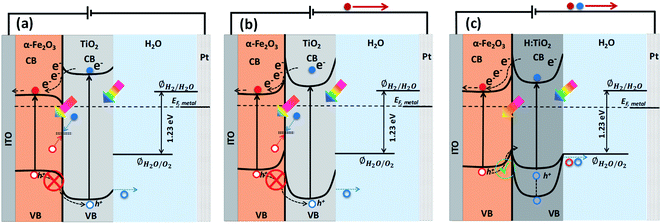
Solar energy-assisted splitting of water into its constituents, hydrogen and oxygen, in a photoelectrochemical (PEC) cell, represents a promising route to convert solar energy into more useful chemical fuels.1,2 The water reduction process can produce hydrogen, where the required electrons can be generated via the water oxidation reaction at the surface of a photoanode through PEC reactions. However, the water oxidation reaction is a demanding electrochemical process, requiring an oxidatively robust and yet inexpensive semiconducting material as the photoanode.3 Despite tremendous efforts, developing a highly active photoanode for water oxidation at low cost remains a significant challenge. After the first report on water splitting by Fujishima and Honda,4 titanium dioxide (TiO2) in its anatase phase has been extensively studied in solar-driven photocatalytic processes.5–7 However, for practical applications, the large bandgap of TiO2 (∼3.2 eV) requires solar radiation with wavelength below 388 nm to create an electron–hole pair; thereby, limiting the overall efficiency of TiO2 when illuminated under real Sun conditions.8,9 Another material of high interest for PEC water splitting is hematite (α-Fe2O3), due to its suitable band gap (2.1 eV), high stability over a wide range of pH and potentials, and low material cost.10,11 In spite of these various advantages, the solar-to-hydrogen conversion efficiency of α-Fe2O3 falls well below the theoretical maximum value (≈12.9%) due to a number of factors such as (i) bulk charge recombination, (ii) interfacial carrier trapping and recombination, (iii) surface trapping and recombination, and (iv) improper band positions for unassisted water splitting12 (see Fig. S1† for further information).To address the issues with solely α-Fe2O3 and TiO2 based oxide semiconductors and design a photoanode for PEC water oxidation with high solar-to-hydrogen conversion efficiency, the heterostructure of these two semiconductors has been recognized as an attractive candidate to enhance the photocurrents and lower the onset potential.13,14 The combined properties of α-Fe2O3 and TiO2 allow the heterostructures to absorb a wider range of photons, thanks to the relatively narrow band gap of α-Fe2O3.15 Also, the formation of heterostructures between α-Fe2O3 and TiO2 can allow band structure engineering to manipulate surface/interface properties for charge transfer/separation, thereby enhancing the water oxidation performance.16 In particular, the valence and conduction band alignment mechanisms at the interface are crucial for the separation of photogenerated charge carriers.17 In both oxide semiconductors, the Fermi levels depend on the concentrations of the conduction electrons and hence on the oxygen vacancy concentrations. By appropriate adjustments of the Fermi levels via defect concentration, the valence band edge in the bulk of the semiconductor may be brought to a common equilibrium. Using the available data18 of the electron affinities for Fe2O3 (4.71 eV) and TiO2 (4.33 eV), together with the generally accepted model of heterojunctions, the discontinuity at the conduction bands (CB) is estimated to be 0.38 eV while that for the valence bands (VB) is estimated to be 0.42 eV. Owing to the mutual positions of Fe2O3 and TiO2 conduction band edges, photogenerated electrons in TiO2 can be easily transferred to Fe2O3 and injected into the Indium Tin Oxide (ITO) substrate, and subsequently can migrate through the external electric circuit to reduce water at the cathode, thus suppressing detrimental recombination effects (Fig. 1a). On the other hand, the VB offset at the interface by 0.42 eV act as an energy barrier that blocks the hole transfer from the α-Fe2O3 to the TiO2 layer and prevents the water oxidation reaction on the surface of TiO2 (Fig. 1a). This means the heterostructure between α-Fe2O3 and TiO2 forms a type I band alignment at the semiconductors' interface, and the hole transport from α-Fe2O3 to TiO2 is energetically impeded, as depicted in Fig. 1a and b.
However, in the case of a thin pours TiO2 layer (<100 nm) over Fe2O3 and at applied anodic potential, the depletion region and upward band bending in TiO2 at Fe2O3–TiO2 nano-heterostructure in contact with the electrolyte may extend into the α-Fe2O3. This high band bending in the thin TiO2 overlayer, under the influence of anodic potential, can provide a channel to transfer the photogenerated holes from Fe2O3 to TiO2 where they participate in the water oxidation reaction, thereby improving the water oxidation performance of the Fe2O3–TiO2 photoanode. Barreca et al.15 reported that the use of external potential could transfer of photogenerated holes from porous hematite to TiO2 layers that can improve the PEC response under simulated light. However, in the case of thick and dense TiO2 layer over α-Fe2O3, the mismatched band alignment can hinder the charge transfer process at Fe2O3–TiO2 heterostructure, thereby constitute the limiting factor in PEC applications. Therefore, for swift transfer of photogenerated holes from VB of α-Fe2O3 to the VB of TiO2, band edge and band gap tailoring in TiO2 are required to form a type II band alignment at the Fe2O3–TiO2 heterostructure interface. In our previous study,8,9,17 we demonstrated that a high temperature hydrogen treatment in TiO2 under partial pressure can modify the structural, optical, and electrical properties and significantly improve the photocatalytic and photoelectrochemical performance. An upshift of the valence band of TiO2 was achieved after the high temperature hydrogen treatment at partial pressure that was useful for band edge engineering at TiO2–BiVO4 heterostructure. However, a downshift of valance band maximum (VBM) was also obtained when TiO2 thin films were grown in situ in hydrogen plasma.19
In this study, first-principles calculations on a model Fe2O3–TiO2 heterostructure show that the strain at the interface shifts the valance and conduction band positions and affects the bandgap of the TiO2 layer. Furthermore, the calculations show that neutral and positive charged H interstitials are energetically preferred under hydrogen treatment conditions. These interstitials introduce states in the bandgap of TiO2, which can assist in the transfer of holes through the TiO2 layer. To challenge the theoretical predictions, well-defined planar Fe2O3–TiO2 heterostructures were manufactured. The experimental results show that Fe2O3–TiO2 initially forms a type I band alignment, prohibiting the transfer of holes through TiO2. However, after hydrogen treatment, the Fe2O3–H:TiO2 heterostructure seems to form a type II band alignment; thus, hole transfer becomes possible, leading to an enhanced PEC response.
2. Experimental section
2.1 Preparation of α-Fe2O3 thin films
The ultra-thin hematite films were prepared onto indium-doped tin oxide (SnO2:In, ITO, PGO GmbH, sheet resistance < 20 Ω sq−1) substrate by using physical vapor deposition technique, followed by annealing of Fe coated ITO substrate in air atmosphere.20 Briefly, all the substrates were cleaned by using soap solution, acetone, and deionized water followed by ultra-sonication in isopropanol for 5 minutes and finally with oxygen plasma for two minutes. Before deposition, 1/3 area (5 mm × 10 mm) of the substrate was covered with a thermal tape for making the electrical contact later for PEC measurements. To fabricate the ultra-thin hematite film (approximately 25 nm), a 10 nm thick Fe films were deposited on ITO substrate by physical vapor deposition (PVD 225, Kurt J. Lesker, base pressure < 5 × 10−7 mbar) and annealed in air atmosphere at 350 °C for 8 h with a heating rate of 4 °C min−1. The thickness of the Fe film was measured in situ during deposition using a quartz-crystal microbalance monitor integrated in PVD system. After annealing, the samples were allowed to cool down to room temperature naturally.2.2 Preparation of Fe2O3–TiO2 and Fe2O3–H:TiO2 heterostructures
Thin films of TiO2 were deposited onto ITO substrates and also on hematite coated ITO substrate by sol–gel technique.6 In short, a transparent gel solution of titanium dioxide was prepared by mixing 3 ml titanium tetra-isopropoxide (TTIP, 97% pure) in 20 ml ethanol in the presence of diethanolamine. The solution was stirred for 4 h at room temperature to enhance the reaction rate between diethanolamine and TTIP, and finally, it was converted into a gel. This gel solution was applied on α-Fe2O3/ITO substrate and uniformly coated with the help of a spin coating unit at 3000 rpm for 1 minute. A thin layer of TiO2 was achieved by the deposition of prepared gel over the α-Fe2O3/ITO substrates. After deposition, the prepared TiO2–Fe2O3 heterostructure was allowed to dry for 10 min at 80 °C and further annealed at 350 °C for 4 h. The hydrogen treatment was carried out by annealing the Fe2O3–TiO2 heterostructures at 300 °C in 4% H2 in Ar at atmospheric pressure for 6 h. We also prepared a hydrogen doped TiO2 thin film photoanode under the same annealing conditions to see the effect of hydrogen doping individually on optical, electrical, and PEC properties.2.3 Material characterization
The chemical phase of the prepared samples was determined by using a confocal Raman microscope (alpha300 R; WITec) with a 488 nm laser pulse as an excitation source. The surface morphology of the bare and TiO2 coated α-Fe2O3 samples was examined by field emission scanning electron microscope (FE-SEM) using a Zeiss Supra 60 VP microscope operated at an acceleration voltage of 10 kV. The optical absorption of all the samples was measured with the help of a Cary 5000 spectrophotometer (Varian). X-ray photoelectron spectroscopy (XPS) spectra were acquired in a PerkinElmer Phi 5500 setup (base pressure < 10−10 mbar) using AlKα radiation of 1.4866 keV. The XPS spectra were shifted using the Fe(2p3/2) peak corresponding to 710.9 eV as a reference.2.4 Photoelectrochemical measurements
For electrochemical measurements, thin films of α-Fe2O3, TiO2, H:TiO2, Fe2O3–TiO2 and Fe2O3–H:TiO2 heterojunctions were converted into the photoelectrodes with an active surface area of about 0.50 cm2. All the (photo)electrochemical measurements, current–voltage (I–V), capacitance–voltage (C–V), and electrochemical impedance spectroscopy (EIS), were conducted in a three-electrode configuration using a H-type PEC cell made of glass and fitted with a flat optical quartz window containing 0.1 M NaOH as electrolyte (pH = 12.9). The PEC cell was controlled by using the Gamry Ref. 600 potentiostat and a solar simulator (SKU SS150, Sciencetech Inc.) with an output intensity of 100 mW cm−2 as an illumination source. Here, the prepared photoelectrodes were used as a working electrode, Pt wire as a counter electrode, and Ag/AgCl as a reference electrode. For better representation of our results, the Ag/AgCl reference potential was converted into the reversible hydrogen electrode (RHE) potential by using the following formula: VRHE = VAg/AgCl + 0.059pH + VoAg/AgCl, where VoAg/AgCl is the standard potential of Ag/AgCl at 25 °C (0.1976 V vs. the standard hydrogen electrode, SHE). The cyclic voltammetry sweep scans in the potential range between 0 and 2.0 VRHE at a scan rate of 10 mV s−1 were performed to obtain the I–V characteristics under dark and illumination. The photocurrent density (Jph) has been calculated by subtracting the dark current from the current measured under illumination and devised by the geometrical area of the photoanode. Electrochemical impedance spectroscopic (EIS) measurements under illumination were carried out in the frequency range 105 and 0.1 Hz at applied potentials between 1.23 VRHE. Nyquist plots obtained under illumination were fitted using the software EIS spectrum analyzer. Mott–Schottky analysis was performed at an applied frequency of 1 kHz in the dark condition in a potential window between 0 and 1.5 VRHE. The obtained Mott–Schottky curves (1/C2 versus VRHE) were used to determine the donor density (ND) and flat band potential (Vfb) by using the Mott–Schottky equation: C−2 = (2/qεoεsND)[V − Vfb − kT/q], where εo is the permittivity of the vacuum, εs is the dielectric constant of the hematite, q is the electronic charge, and kT/q is the thermal voltage (26 meV at room temperature). The donor density was calculated using the equation, ND = 2/(εoεsq)[d(1/C2)/dV]−1, from the slope of the linear region, between 0.6 and 1.0 VRHE, of Mott–Schottky plots.2.5 Computational methods
The first-principles calculations were performed using density functional theory (DFT) as implemented in the VASP package.21–23 The interaction between the valance electrons and the core follows the projector augmented wave (PAW) method.24 PAW potentials with the valence states 1s for H, 2s and 2p for O, 3d and 4s for Fe, and 3d and 4s for Ti have been employed. A plane wave basis with a kinetic energy cut-off 700 eV was used. To improve convergence, a Gaussian smearing broadening of the Fermi surface of 0.1 eV was employed. The exchange–correlation (XC) interaction was treated at the level of the generalized gradient approximation (GGA) using the XC-functional of Perdew, Burke, and Ernzerhof (PBE).25 In the DFT+U calculations, the rotationally-invariant scheme proposed by Dudarev et al.26 and a U − J = 4.3 eV on Fe atom and U − J = 5.2 eV on Ti atom are employed in all our calculations.27,28 The HSE06 method, as implemented in VASP, was employed to study H defects in anatase TiO2.29,30 A kinetic cut-off of 600 eV was applied in all calculations. The interface system is composed of a six-layer thick Fe2O3 with a (0001) termination of p(2 × 2), that is joined with a four-layer thick anatase TiO2 with a (101) termination of p(1 × 2). Owing to the lattice mismatch between Fe2O3 and TiO2, the interface will introduce strain to the system. Here the lattice cell (a = b = 10.17 Å, a = 120°) of Fe2O3 (0001) surface is kept fixed, which implies a strain to the original lattice cell (a = 11.35 Å, b = 10.23 Å, alpha = 111.69°) of the TiO2 (101) surface. The strain amounts to 10% compression strain on the a-axis and 0.6% compression strain to the b-axis, and an increase of the angle by 7.4%. During the relaxation of the interface system, the anatase TiO2 reconstructs to amorphous TiO2 (a-TiO2). Here, the term amorphous is used to indicate that the reconstructed TiO2 in the interface model can not be identified with any known phase (rutile, anatase, brookite, etc.) of TiO2. However, it should be noted that due to the periodic conditions, this phase should not be considered as genuinely amorphous TiO2. Defect calculations were carried out in a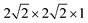 (96 atoms) supercell of anatase TiO2, with a Γ-centered 1 × 1 × 1 k-point sampling. The effect of higher concentrations of defects is modeled by a
(96 atoms) supercell of anatase TiO2, with a Γ-centered 1 × 1 × 1 k-point sampling. The effect of higher concentrations of defects is modeled by a 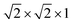 (24 atoms) supercell and a 1 × 1 × 1 (12 atoms) unit cell, using a 3 × 3 × 1 Monkhorst–Pack (MP) sampling.31 All geometries were relaxed until the maximum force was less than 0.05 eV Å−1. The relative stability of the various defects in charged and/or neutral states is determined by the formation energy,
(24 atoms) supercell and a 1 × 1 × 1 (12 atoms) unit cell, using a 3 × 3 × 1 Monkhorst–Pack (MP) sampling.31 All geometries were relaxed until the maximum force was less than 0.05 eV Å−1. The relative stability of the various defects in charged and/or neutral states is determined by the formation energy,| ΔEf = Et(Dq) − Et(TiO2) − ΔnOμO − ΔnHμH + qEF + Ecorr, | (1) |
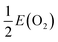 , where E(O2) is the calculated total energy of isolated O2 molecule. In the extreme O-poor limit, μO corresponds to the formation of Ti2O3, which has a relationship of μO(O-poor) = μO(O-rich) − 3.97 eV calculated by HSE06. μH is selected as one half of the total energy of isolated H2 molecule, ½E(H2).
, where E(O2) is the calculated total energy of isolated O2 molecule. In the extreme O-poor limit, μO corresponds to the formation of Ti2O3, which has a relationship of μO(O-poor) = μO(O-rich) − 3.97 eV calculated by HSE06. μH is selected as one half of the total energy of isolated H2 molecule, ½E(H2).
3. Results
3.1 Simulation results
The valence band offset (VBO) at the interface of Fe2O3 and a-TiO2 was calculated through the reference potential method originally introduced by Kleinman32,33 where the reference potential use the macroscopically averaged electrostatic potential.34 The calculated results are shown in Fig. 2. The VBO for the individual system, Fe2O3 (0001) and a-TiO2 thin film, were also calculated and are shown in the ESI (Fig. S2).† The blue curve in Fig. 2 refers to the electrostatic potential calculated using PBE+U method. The valence band edges of Fe2O3 and a-TiO2 were determined with respect to the macroscopically averaged electrostatic by performing calculations on the separated systems. The values of Fermi energy were calculated to 3.88 eV and 0.87 eV for Fe2O3 (0001) and a-TiO2 thin film, respectively. The macroscopically averaged electrostatic potential was calculated by,
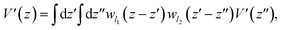 | (2) |
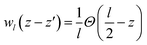 , Θ is the unit-step function, l1 and l2 are in the order of the (strained) thickness of hematite (0001) and amorphous TiO2 thin film along z, respectively.
, Θ is the unit-step function, l1 and l2 are in the order of the (strained) thickness of hematite (0001) and amorphous TiO2 thin film along z, respectively.
 | (3) |
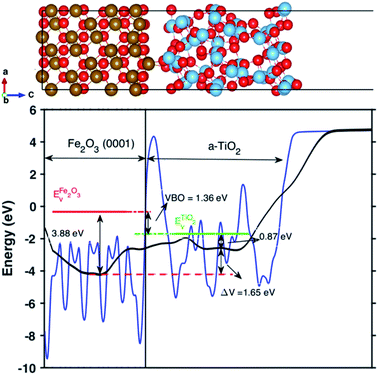 | ||
| Fig. 2 Up panel is the relaxed structures from the PEB + U calculation for the Fe2O3 and amorphous TiO2 interface. Bottom panel is the calculated valence band offset (VBO) of the interface with PBE+U methods. The black line is the calculated macroscopically averaged electrostatic potential and the blue line is the electrostatic potential at the interface averaged along the thickness (c-axis) of the interface. The red line is the position of VBM of Fe2O3 and the green line is the position of VBM of bulk TiO2 with respect to vacuum level. The electrostatic potential across the interface is ΔV = 1.65 eV and the calculated VBO at the interface is 1.36 eV. The VBO of the joint interface is slightly larger than that of separated systems by 0.18 eV that indicating the creation of an interface dipole or double layers.37 | ||
The calculated V′(z) is the black line in Fig. 2. The VBO was calculated via,
| VBO = ΔEv + ΔV. | (4) |
The calculated VBO for the individual system is −1.18 eV using DFT+U, which agrees well with the experimental observations (∼0.5 eV).38 However, the calculated VBO at the interface is around 1.36 eV, with the valence band edge of TiO2 sitting below the Fe2O3, which is 0.18 eV higher than the separated systems indicating an interface dipole or double layer were created at the interface. The electrostatic potential across the interface is ΔV = 1.65 eV.
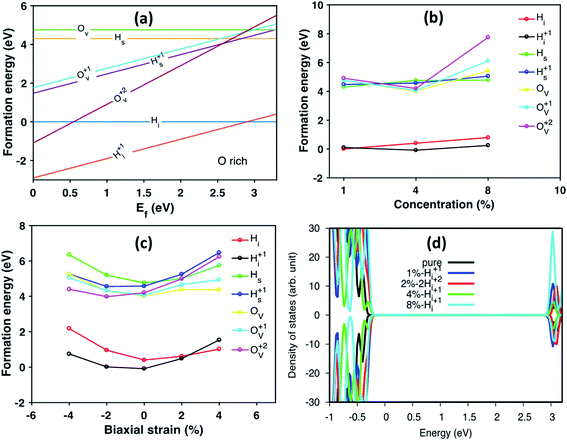
We further studied H defects and O vacancy in anatase TiO2, including their formation energy and electronic structure. The formation energy is calculated using eqn (1), and the results are shown in Fig. 3a, which corresponds to the results from the modeled supercell of 96 atoms. It is clearly shown that the positively charged H interstitial is the most favorable (with negative formation energy) defect when the Fermi energy is located above the valence band edge and below 2.9 eV, while the H interstitial becomes stable when Ef is larger than 2.9 eV (see Fig. 3). The formation energy of H interstitial is 0.04 eV. In contrast, O vacancies and substitutional H are less energetically favorable.
Next, we have studied the formation energies of different concentrations of defects in anatase TiO2 using different supercells, and the results are shown in Fig. 3b. Here, the formation energy plot is shown for O-rich conditions and the Fermi energy is set to 3.0 eV. As seen from Fig. 3b, the two most stable defect configurations are neutral and positively charged H interstitials, Hi, where the positively charged H interstitial is the most favorable defect at high concentrations. The neutral H interstitial is the second state configuration when H concentration larger than 4 at%. The other defects are less stable as their formation energies are very high (larger than 3 eV). At high concentration (8 at%), the substitutional Hs becomes more stable than O vacancies. Interestingly, under O-poor conditions, the Hs is as stable as the Hi (the formation energy plot is shown in Fig. S3†).
When constructing the interface, a strain is induced automatically due to the lattice mismatch. Therefore, we also studied the stain effects on defect configurations for defect concentration of 4 at%. The calculated formation energy of different defects under biaxial strain is shown in Fig. 3c. It is interesting to notice that under biaxial tensile strain, the stable defect configuration changes to Hi. Under compressive strain, positively charged Hi+ remains as the most stable defect configuration. As shown in Fig. 3c, when changing from compressive to tensile strain, the stable configurations of defects are changed from charged ones to neutral ones, e.g., Hs becomes more stable than Hs+ and Ov becomes more stable than Ov+ and Ov2+. Similarly, the formation energy of defects calculated under O-poor conditions is shown in Fig. S4.† At such conditions, the defect configuration is changing from Ov2+ to Ov as the strain changes from compression to expansion. However, Hi+ is still the preferable defect under ambient condition (Fig. S4†). The DOS of anatase with different concentration of Hi+ compared with pure anatase are shown in Fig. 3d. The energy of doped systems is aligned by shifting 1s state of O atom far away from the defect to that of pure anatase. It can be seen that doping with Hi+ shifts the valence band edge upwards (∼0.1 eV) without changing the position of the conduction band edge. More specifically, the change of the valence band edge can be explained as the hybridization of 2p states of O atom bonded with Hi+ and Ti 3d nearby (see Fig. S5†).
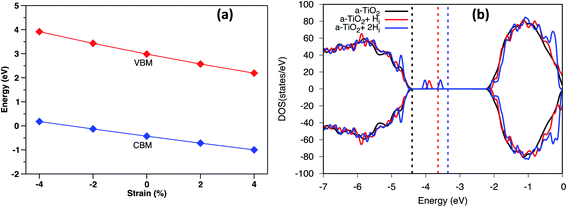
Under biaxial strain, due to lattice mismatch, the valence band maximum and conduction band minimum (CBM) of pure anatase (32 atoms supercell) under different strain are calculated and plotted in Fig. 4a. It is clear that both VBM and CBM decrease in energy as strain increases from compressive to tensile strain. When strain increases to 2%, the value of VBM decreases around 0.3 eV. Similarly, the CBM decreases around 0.4 eV. Therefore, the band gap is shrinking as strain increases. When doped with Hi+, the VBM position is located below the VBM of pure anatase under 2% tensile strain, while the VBM remains unchanged with doped with Hi (shown in Fig. S4†). Hydrogen doping also introduces distortions to anatase TiO2, which results in the formation of the amorphous TiO2 at the interface. To shed further light on this, H doped amorphous TiO2 was studied with the PBE+U method, keeping the same parameters used for the interface. Doping with Hi is energetically favorable (shown in Fig. S4†) with a formation energy of −0.4 eV for single Hi. The calculated DOS of H doped systems is shown in Fig. 4b. Compared with pure a-TiO2, single Hi introduces one occupied localized state on top of the valence band edge about 0.5 eV high in energy. The doping with H does not seem to change the averaged electrostatic potential, as can be seen from Fig. S5.† Adding two Hi introduce two localized states in the gap, but with slightly different energies. As more interstitial hydrogens are incorporated, we speculate that these states will eventually form energy levels in the range of up to ∼0.7 eV above the valence band edge. These energy levels work as the hole acceptance levels and help the transport of photo-excited holes generated from the Fe2O3 side to the H:TiO2 electrolyte side, where they can take part in the water oxidation reaction.
3.2 Experimental results
To test our hypothesis and to scrutinize the first-principles results experimentally, we have fabricated Fe2O3–TiO2 heterojunction electrodes in two steps. First, we deposited an ultra-thin α-Fe2O3 (25 nm) film on ITO substrate by thermal evaporation of Fe followed by air annealing at 350 °C. Further, the as-prepared α-Fe2O3 thin films were coated with TiO2 by sol–gel spin coating method followed by thermal annealing at 400 °C. In as-prepared Fe2O3–TiO2 heterostructure, the band edge engineering was achieved by hydrogen doping (Fe2O3–H:TiO2) by further annealing the Fe2O3–TiO2 heterostructure in 4% H2 in Ar at 300 °C at atmospheric pressure for 6 h.To determine the crystal structures of α-Fe2O3, TiO2, and Fe2O3–TiO2 heterostructure thin films and possible phase changes after hydrogen doping in TiO2, Raman spectroscopy was performed, and its results are shown in Fig. S7a.† In pristine α-Fe2O3, normally seven phonon modes are expected in the Raman spectrum: namely two A1g modes (225 and 498 cm−1) and five Eg modes (247, 293, 299, 412, and 613 cm−1), but the 293 and 299 cm−1 bands can only be resolved at temperatures ≤100 K. In the present case, six of the observed bands (A1g, 223 and 498 cm−1; Eg, 244, 294, 410, and 607 cm−1) are detected, which agrees with the formation of the hematite phase (α-Fe2O3). On the other hand, the Raman spectra of both pristine and hydrogen doped TiO2 samples exhibit well-resolved TiO2 Raman peaks at 144 cm−1 (Eg), 398 cm−1 (B1g), 515 cm−1 (Eg), and 640 cm−1 (Eg), indicating that anatase is the predominant species, except for 147 cm−1 (B1g), which is suppressed by a much stronger Eg peak at 144 cm−1. No phase change after hydrogen doping in TiO2 was observed (ESI Fig. S7b†). The Raman spectra of TiO2–Fe2O3 heterostructure shows the significant up-shift of Eg mode of TiO2 from 141 to 155 cm−1 and also other bands of TiO2. The shift of Raman bands by 14 cm−1 (inset of ESI Fig. S7b†) is probably due to the strain and defect states at the junction with α-Fe2O3 and lattice mismatch. Morphological characteristics were investigated by scanning electron microscopy (SEM) (ESI Fig. S8†) and transmission electron microscopy (TEM) (ESI Fig. S9†). SEM images of pristine α-Fe2O3 electrodes showed uniform deposition of a thin layer of a thickness of about 25 nm without any inter-particle pores, as shown in Fig. S8.† Optimized thickness of TiO2 layer (thickness < 10 nm) over the α-Fe2O3 layer on ITO clearly showed a smooth and dense coverage, as shown in Fig. S8c.†
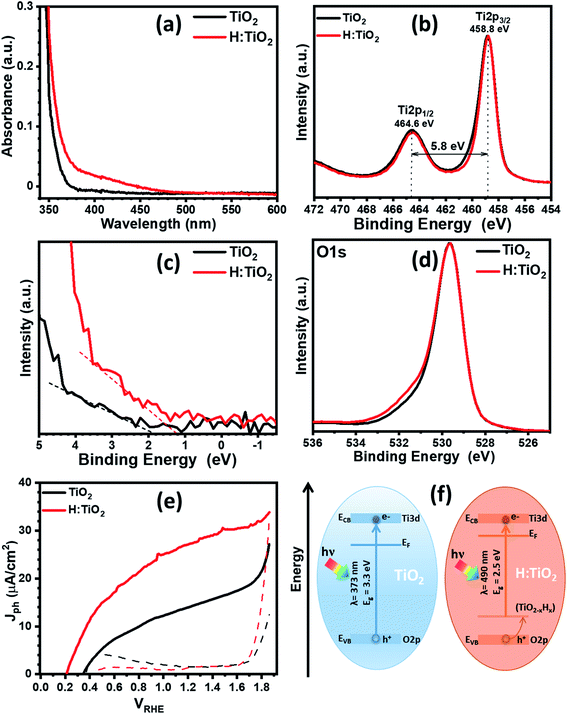
First, we optimized the temperature for optimized hydrogen doping with respect to the reduction in band gap and upshift of band edge position. Fig. 5a displays the optical absorption spectra of the TiO2, H:TiO2, samples in the wavelength range 340–600 nm measured by using the integrating sphere. Optical absorption spectra of all the samples, α-Fe2O3, TiO2, H:TiO2, Fe2O3–TiO2, and Fe2O3–H:TiO2, in the wavelength range 300–700 nm measured under the same experimental conditions are shown in the ESI (Fig. S10).† In pristine TiO2 samples, a steep increase in absorption at wavelengths shorter than ∼373 nm can be attributed to the intrinsic band gap of crystalline TiO2. The hydrogen doping of the TiO2 sample show a significant shift of absorption edge from higher wavelengths down to 490 nm in the visible light absorption. The calculated values of the band gap energy show that the band gap of the pristine TiO2 thin films is approximately 3.30 eV, slightly higher than that of bulk anatase TiO2. However, the onset of light absorption in hydrogen doped TiO2 thin film is lowered to about 2.5 eV.
To validate the reduction of band gap energy, we have carried out the XPS measurement on both pristine and hydrogen doped TiO2 thin films to understand the surface chemical bonds, chemical composition, peak position, and hence the electronic properties. Therefore, the Ti 2p, O 1s, and valance band spectra were measured and analyzed for pristine and hydrogen doped TiO2 thin films. The Ti 2p core level XPS spectrum, Fig. 5b, shows that the Ti 2p3/2 peak is at 458.8 ± 0.1 eV, which was attributed to Ti4+ states for both the samples. However, after hydrogen doping, a slight asymmetric narrowing in the Ti 2p3/2 peak can be seen. This narrowing in the peak upon hydrogen doping is likely due to a decrease in Ti3+ states, concurrent with the reduction in oxygen content, and to a disorder due to the thermal annealing of TiO2 in hydrogen environment.39 However, no reduction in the Ti4+ was observed in TiO2 after hydrogen doping. Fig. 5c shows the valence band spectra obtained for the pristine and hydrogen treated TiO2 thin films. The VBM were calculated by linearly extrapolating the peaks to the baselines. The VBM for pristine TiO2 thin film was observed at 1.93 eV below the zero potential energy point. However, in the case of hydrogen doped TiO2 films, VBM was obtained at 1.27 eV. Therefore, a valence band edge shift by ∼0.66 eV was observed towards the Fermi level. Moreover, small bands occurred above the VBM, and small bands existed close to the binding energy at zero. In light of the first-principles calculations, the up-shift of the VBM is suggested to be the result of defects states above the valance band induced by interstitial hydrogen in the TiO2 thin films. Fig. 5d represents the O 1s spectra of pristine and hydrogen doped TiO2 samples. The peak at a binding energy of 529.6 ± 0.1 eV corresponds to O–Ti bonds in TiO2 in both the samples. However, in hydrogen doped samples, an additional peak can be seen at 531.6 ± 0.1 eV, which is probably due to oxygen vacancies, formation of hydroxyl groups, and Ti–OH bonds.39,40 From Fig. S13b and c,† where the XPS spectra of all four samples are shown, it is further visible that Fe2O3–H:TiO2 displays the same narrowing of the Ti4+ peak as H:TiO2, and a more accentuate OH− peak in the oxygen 1s spectrum, correlating the formation of the iron oxide heterostructure with the generation of oxygen vacancies and/or hydroxyl groups.
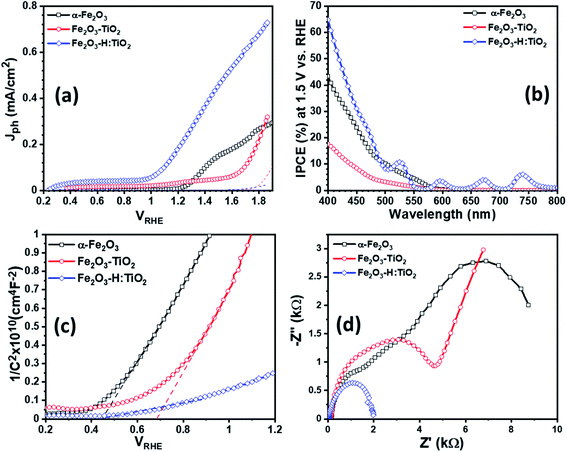
The PEC measurement in the form of photocurrent densities vs. applied potential (Jph vs. VRHE) curves are shown in Fig. 5e for pristine and hydrogen doped TiO2 samples under 1 sun illumination. The calculated value of Jph for pristine TiO2 photoanode was obtained ∼14 μA cm−2 at 1.23 VRHE. However, hydrogen doping in TiO2 enhanced the PEC response significantly and reached a Jph to ∼27.4 μA cm−2 at 1.23 VRHE. It is noticed that hydrogen doping in TiO2 thin films greatly enhanced the Jph and shifted the photocurrent onset potential to 0.2 VRHE. The relatively low value of photocurrent onset potential indicates that the charge separation and transportation in hydrogen doped TiO2 thin films are more efficient than the pristine TiO2 thin films. We have also calculated the flat-band potential (Vfb) and carrier concentration (Nd) for pristine and hydrogen doped TiO2 samples using Mott–Schottky plots. The value of Vfb was calculated from the intercept of the straight line to the x-axis in the linear region of the plot, as shown in Fig. S11.† The pristine TiO2 sample exhibit a Vfb value of 0.29 VRHE. However, a shift in Vfb to 0.15 VRHE was calculated for the H:TiO2 photoanode. This significant shift of Vfb by 0.14 V towards the cathodic side in H:TiO2 is likely because the hydrogen doping can enhance the carrier concentration due to increased oxygen vacancies, which could serve as shallow electron donor and upshift the Fermi level towards the conduction band of TiO2. Schematic positions of band edges of TiO2 and H:TiO2 are shown in Fig. 5f. The band alignment of H:TiO2 facilitates more efficient charge separation at the semiconductor/electrolyte interface as compared to pristine TiO2 by increasing the degree of band bending at the H:TiO2 surface. The experimental value of Vfb for H:TiO2 is more cathodic in comparison to the pristine TiO2, which favors the water splitting reaction. In summary, the enhancement in photocurrent density in the H:TiO2 sample is thanks to the combined effect of decreased bandgap energy, which allows absorption of a wide range of solar radiation, high donor density which is responsible for the shift in Fermi level towards the conduction band, and more negative flat band potential.
To examine the PEC performance of the targeted heterostructures photoanodes, Fe2O3–TiO2 and Fe2O3–H:TiO2, the Jph vs. VRHE characteristics under dark and illumination was measured in a three-electrode PEC cell. Fig. 6a depicts the PEC performance of the optimized Fe2O3–TiO2 and Fe2O3–H:TiO2 heterostructures compared with pristine α-Fe2O3 photoanode. The dark current densities, for the applied potential range up to 1.7 VRHE, are negligible for all samples. The Jph of the pure α-Fe2O3 photoanode is ∼10 μA cm−2 at 1.23 V vs. RHE, which is reasonable as compared to the previously reported values due to the difference in the film thickness and has an onset of photocurrent at 1.15 VRHE.20 A much lower onset potential of ∼0.35 VRHE and lower Jph of ∼35 μA cm−2 at 1.23 VRHE obtained for the Fe2O3–TiO2 heterostructure. However, the hydrogen doped TiO2 layer in the Fe2O3–H:TiO2 heterostructure substantially shifted the onset of photocurrent to 0.21 VRHE and the Jph at 1.23 VRHE increased to 215 μA cm−2. The value of Jph for Fe2O3–H:TiO2 heterostructure photoanode reached 450 μA cm−2 at 1.5 VRHE, which is three and nine times the Jph for α-Fe2O3 (153 μA cm−2) and Fe2O3–TiO2 (51 μA cm−2) photoanodes, respectively. The obtained value of Jph for Fe2O3–H:TiO2 heterostructured system is significantly high to that of a pristine α-Fe2O3 and Fe2O3–TiO2 systems. As the magnitude of Jph corresponds to the number of photogenerated holes that reach the electrode surface, the Fe2O3–TiO2 sample exhibits a high recombination of photogenerated electrode and holes at the junction due to the discontinuity of the mismatch of band edge positions, which hinders the water oxidation process at the surface of the Fe2O3–TiO2 photoanode. As we reported in our previous work on hydrogen treated TiO2 and predicted in our simulation for this work, hydrogen doping in TiO2 can upshift the valance band position and create the lattice defects in TiO2. Our simulation results on hydrogen doping in TiO2 indicate that heterojunctions of α-Fe2O3 and hydrogen doped TiO2 can lead to considerably enhanced hole transport from α-Fe2O3 to H:TiO2 and, thus, to a more efficient separation of photoexcited electron–hole pairs. Consequently, hydrogen treated Fe2O3–TiO2 photoanode exhibits a higher number of photogenerated holes that can participate in the oxidation process before recombining with excited electrons.
Further, to quantitatively investigate the PEC performance of the photoanodes, incident photon-to-current conversion efficiency (IPCE) measurements were performed at 1.5 V vs. RHE in 1.0 M KOH and shown in Fig. 6b. All the samples show photocurrent response to incident light in the wavelength region of 400–580 nm, which matches the bandgap of hematite (∼2.1 eV). The pristine α-Fe2O3 photoanode exhibits 42% IPCE at the excitation wavelength of 400 nm, which is comparable with the reported IPCE values of α-Fe2O3 photoanode. A significantly low IPCE, 18%, was recorded in the case of the Fe2O3–TiO2 photoanode. This Fe2O3–TiO2 photoanode also exhibits the low photocurrent density in PEC measurements. However, Fe2O3–H:TiO2 photoanode exhibits substantially high quantum efficiency as compared with pristine α-Fe2O3 and Fe2O3–TiO2 photoanodes in the wavelength range of 400–550 nm. The IPCE of the Fe2O3–H:TiO2 photoanode reaches to ∼65% at the excitation wavelength of 400 nm, which is 1.5 and 3.6 times that of α-Fe2O3 (42%) and Fe2O3–TiO2 (18%), respectively.
To gain even more insight into the enhancement of photocurrent density and IPCE values in Fe2O3–H:TiO2 heterostructure photoanodes, Mott–Schottky measurements were performed with applied potential at 1 kHz frequency in the dark. From the Mott–Schottky plots, which represent the changes in capacitance (C) against the applied potential, it can be seen that all the samples possess a positive slope (Fig. 6c), which is a characteristic of n-type semiconductors with electrons as majority carriers. The flat band potential (Vfb) and carrier density (Nd) were calculated from the slopes of Mott–Schottky plots. The value of Vfb was observed to shift towards the more cathodic side from 0.44 VRHE for α-Fe2O3 to 0.68 VRHE for the Fe2O3–TiO2 sample. However, after the hydrogen treatment of the TiO2 layer, the flat band potential remains at the same values to 0.28 VRHE as Fe2O3–TiO2.
Further, the charge transport properties of the Fe2O3–TiO2 and Fe2O3–H:TiO2 photoanodes were investigated by electrochemical impedance spectroscopic (EIS) measurements at 1.23 VRHE applied potential under one sun illumination conditions and compared with α-Fe2O3. Fig. 6d shows the EIS Nyquist plots for α-Fe2O3, Fe2O3–TiO2, and Fe2O3–H:TiO2 photoanodes. The series resistance (Rs) at the interface between the ITO substrate and α-Fe2O3 and Fe2O3–TiO2 layers display a substantial reduction from ca. 140 Ω cm−2 for the pristine α-Fe2O3 sample, to 120 Ω cm−2 for Fe2O3–TiO2, to ca. 40 Ω cm−2 for the Fe2O3–H:TiO2 photoanode surface. The radii of the semicircle in the EIS plots from the Fe2O3–H:TiO2 heterostructure is much smaller than that from Fe2O3–TiO2, which indicates that the hydrogen treatment of the TiO2 layer changes the charge distribution in Fe2O3–H:TiO2. The new charge distribution results in a lower magnitude of the equivalent series resistance in Fe2O3–H:TiO2 heterojunction photoanodes indicating strongly improved charge transport properties as compared to Fe2O3–H:TiO2.
Finally, in order to assess the durability of the photoanodes, chronoamperometry was performed on the Fe2O3–TiO2 and the Fe2O3–H:TiO2 electrodes (as presented in Fig. S12 in the ESI†): the resulting photocurrent density, under a bias voltage of 0.5 VRHE and an illumination of 1 sun, was found to be stable around a value of 0.4 mA cm−2 for up to 500 minutes for Fe2O3–H:TiO2, with no sign of decreasing, while the non-treated sample displayed a lower photocurrent (0.23 mA cm−2) at the start, which halved after less than 300 minutes of continuous use. This sustained stability of Fe2O3–H:TiO2 electrodes confirms the applicability of the device.
4. Conclusion
First-principles calculations predict that hydrogen treatment induce states above the valance band, which can transfer holes through the heterostructure junction. The predictions are validated with experimental observation obtained on sol–gel grown TiO2 thin films. Optical absorption, XPS analysis, and (photo)electrochemical measurements show that the tailoring in optical band gap, shift in valence band position, and change in electrical properties in hydrogen doped TiO2 results in a type II band alignment in the Fe2O3–H:TiO2 heterostructure. The Fe2O3–H:TiO2 heterostructure reduces the electron–hole recombination sharply at the junction and improves the water oxidation performance. This study shows that hydrogen treatment can enhance the photoelectrochemical response of the Fe2O3–TiO2 heterostructure, thanks to the formation of type II band alignment at the interface junction. The theoretical and experimental strategies can be applied to other oxides based heterostructures and might become important tools for engineering efficient and stable photoelectrodes.Author contributions
A. P. S., B. W. and A. H. conceived the idea and designed the experimental work. A. H. and R. B. W. supported the work through theoretical simulations. A. P. S. have prepared and characterized the samples for experimental work and R. B. W. preformed the thermotical simulation. A. P. S., B. W. and A. H. analyzed the experimental data for the manuscript. The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support provided by the Swedish Research Council, Formas and the Academy of Finland. This article is based upon work from COST Action 18234, supported by COST (European Cooperation in Science and Technology). C. T. acknowledges the financial support of the Vilho, Yrjö ja Kalle Väisälä Fund issued by the Finnish Academy of Sciences and Letters. A. P. S., C. T. and I. T. acknowledge the financial support of the Academy of Finland, projects 285972, 319018, and the Academy of Finland Flagship Programme PREIN (320167).References
- M. Grätzel, Nature, 2001, 414, 338–344 CrossRef.
- H. Ahmad, S. K. Kamarudin, L. J. Minggu and M. Kassim, Renewable Sustainable Energy Rev., 2015, 43, 599–610 CrossRef CAS.
- Y. Tachibana, L. Vayssieres and J. R. Durrant, Nat. Photonics, 2012, 6, 511–518 CrossRef CAS.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS.
- A. Fujishima, T. N. Rao and D. A. Tryk, J. Photochem. Photobiol., C, 2000, 1, 1–21 CrossRef CAS.
- A. P. Singh, S. Kumari, R. Shrivastav, S. Dass and V. R. Satsangi, Int. J. Hydrogen Energy, 2008, 33, 5363–5368 CrossRef CAS.
- M. R. Hoffmann, S. T. Martin, W. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69–96 CrossRef CAS.
- M. Mehta, N. Kodan, S. Kumar, A. Kaushal, L. Mayrhofer, M. Walter, M. Moseler, A. Dey, S. Krishnamurthy, S. Basu and A. P. Singh, J. Mater. Chem. A, 2016, 4, 2670–2681 RSC.
- A. P. Singh, N. Kodan and B. R. Mehta, Appl. Surf. Sci., 2016, 372, 63–69 CrossRef CAS.
- A. P. Singh, N. Saini and B. R. Mehta, ChemistrySelect, 2017, 2, 1413–1420 CrossRef CAS.
- A. P. Singh, A. Mettenbörger, P. Golus and S. Mathur, Int. J. Hydrogen Energy, 2012, 37, 13983–13988 CrossRef CAS.
- S. Shen, S. A. Lindley, X. Chena and J. Z. Zhang, Energy Environ. Sci., 2016, 9, 2744–2775 RSC.
- L. Pei, H. Wang, X. Wang, Z. Xu, S. Yan and Z. Zou, Dalton Trans., 2018, 47, 8949–8955 RSC.
- S. Choudhary, S. Upadhyay, P. Kumar, N. Singh, V. R. Satsangi, R. Shrivastav and S. Dass, Int. J. Hydrogen Energy, 2012, 37, 18713–18730 CrossRef CAS.
- D. Barreca, G. Carraro, A. Gasparotto, C. Maccato, M. E. A. Warwick, K. Kaunisto, C. Sada, S. Turner, Y. Gönüllü, T. -P. Ruoko, L. Borgese, E. Bontempi, G. V. Tendeloo, H. Lemmetyinen and S. Mathur, Adv. Mater. Interfaces, 2015, 2, 1500313 CrossRef.
- R. d. S. Santos, G. A. Faria, C. Giles, C. A. P. Leite, H. d. S. Barbosa, M. A. Z. Arruda and C. Longo, ACS Appl. Mater. Interfaces, 2012, 4, 5555–5561 CrossRef CAS.
- A. P. Singh, N. Kodan, B. R. Mehta, A. Held, L. Mayrhofer and M. Moseler, ACS Catal., 2016, 6, 5311–5318 CrossRef CAS.
- M. A. Butler and D. S. Ginley, J. Electrochem. Soc., 1978, 125, 228–232 CrossRef CAS.
- A. P. Singh, N. Kodan, B. R. Mehta, A. Dey and S. Krishnamurthy, Mater. Res. Bull., 2016, 76, 284–291 CrossRef CAS.
- A. P. Singh, A. Levinsson, B. Iandolo, J. Oksanen, A. Hellman and B. Wickman, J. Photochem. Photobiol., A, 2020, 401, 112781 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- B. J. Morgan and G. W. Watson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 144119 CrossRef.
- Z. Hu and H. Metiu, J. Phys. Chem. C, 2011, 115, 5841–5845 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187–1192 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 7412–7414 CrossRef CAS.
- D. M. Bylander and L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 3229–3236 CrossRef CAS.
- C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 1871–1883 CrossRef CAS.
- M. Peressi, N. Binggeli and A. Baldereschi, J. Phys. D: Appl. Phys., 1998, 31, 1273–1299 CrossRef CAS.
- A. Baldereschi, S. Baroni and R. Resta, Phys. Rev. Lett., 1988, 61, 734–737 CrossRef CAS.
- X. Luo, G. Bersuker and A. A. Demkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195309 CrossRef.
- B. Iandolo, B. Wickman, E. Svensson, D. Paulsson and A. Hellman, Nano Lett., 2016, 16, 2381–2386 CrossRef CAS.
- B. Bharti, S. Kumar, H.-N. Lee and R. Kumar, Sci. Rep., 2016, 6, 32355 CrossRef CAS.
- A. P. Singh, C. Tossi, I. Tittonen, A. Hellman and B. Wickman, RSC Adv., 2020, 10, 33307–33316 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra09655e |
| This journal is © The Royal Society of Chemistry 2021 |