Open Access Article
Open Access ArticleExtended enantiopure ortho-phenylene ethylene (o-OPE)-based helical systems as scaffolds for supramolecular architectures: a study of chiroptical response and its connection to the CISS effect†
Ana M.
Ortuño
a,
Pablo
Reiné
a,
Sandra
Resa
a,
Luis
Álvarez de Cienfuegos
 a,
Victor
Blanco
a,
Victor
Blanco
 a,
José Manuel
Paredes
b,
Antonio J.
Mota
a,
José Manuel
Paredes
b,
Antonio J.
Mota
 *c,
Giuseppe
Mazzeo
de,
Sergio
Abbate
*c,
Giuseppe
Mazzeo
de,
Sergio
Abbate
 de,
Jesus M.
Ugalde
f,
Vladimiro
Mujica
*fg,
Giovanna
Longhi
de,
Jesus M.
Ugalde
f,
Vladimiro
Mujica
*fg,
Giovanna
Longhi
 *de,
Delia
Miguel
*de,
Delia
Miguel
 *b and
Juan Manuel
Cuerva
*b and
Juan Manuel
Cuerva
 *a
*a
aDepartment of Organic Chemistry, Faculty of Science, Universidad de Granada (UGR), Unidad de Excelencia de Química (UEQ), E-18071 Granada, Spain. E-mail: jmcuerva@ugr.es
bDepartment of Physical Chemistry, Faculty of Pharmacy, UGR-UEQ. E-mail: dmalvarez@ugr.es
cDepartment of Inorganic Chemistry, Faculty of Science, UGR-UEQ. E-mail: mota@ugr.es
dDepartment of Molecular and Translational Medicine, Università di Brescia, Brescia, Italy
eIstituto Nazionale di Ottica – CNR, Brescia Research Unit, via Branze 45, 25123 Brescia, Italy. E-mail: giovanna.longhi@unibs.it
fKimika Fakultatea, Euskal Herriko Unibertsitatea and Donostia International Physics Center (DIPC), P. K. 1072, 20080 Donostia, Euskadi, Spain
gArizona State University, School of Molecular Sciences, Tempe, AZ 85287, USA. E-mail: vmujica@asu.edu
First published on 28th June 2021
Abstract
A novel synthetic strategy based on a bifunctional stapled chiral nucleus from which segments of different lengths can be added to both ends of o-phenylene ethynylenes (o-OPEs) has been developed to obtain a new type of foldamer and a novel chiral Pd2L2 metallacycle. For the first time, an enantiopure fully conjugated helical foldamer having 14 phenyl rings and 13 alkynes is reported. The folded structure has four complete loops and is able to host three Ag(I) cations in their cavity with high binding constants. The complete photophysical and chiroptical (ECD, CPL and VCD) characterization of these foldamers has shown that these molecules show intense chiroptical responses with dissymmetry ratios in the range of 10−2. Theoretical modeling of these systems reveals the origin of these remarkable responses and points out a potential connection with the chiral induced spin selectivity (CISS) effect. The magnetic dipole moment is proposed as a key physical variable connecting the chiroptical properties and CISS-based spin filtering properties observed in chiral compounds.
Introduction
Helical structures are widespread motifs in biomolecules and many efforts have been made to imitate such geometries using abiotic components.1 Thus for example, [n]-helicenes have attracted the attention of chemists for almost a century.2,3 Particularly appealing is the fact that they present a conjugated system arranged in a helical geometry, which is preserved beyond [6]-helicenes. Their chiroptical properties, derived from their intrinsic chirality, such as optical rotatory dispersion (ORD), electronic circular dichroism (ECD), vibrational circular dichroism (VCD), Raman optical activity (ROA) and more recently, circularly polarized luminescence (CPL),4,5 are in fact remarkable, and have been extensively studied. Moreover, the helical geometry is also relevant in other fields. It has been suggested that conductive helical arrangements are of importance in the context of the chiral induced spin selectivity (CISS) effect6 once they can be prepared as enantiopure entities. The CISS effect is based on the phenomenon of electron spin polarization in electron transfer, electron transport and bond polarization processes in chiral molecules. Although initial experiments were based on biomacromolecules,7 it is worth noting that it has also been observed in in fully conjugated [7]-helicene and in other helicene-like molecules.8 Consequently, fully conjugated helical molecules have been theoretically suggested as interesting candidates for spintronics, quantum sensing and quantum information applications.9–11Moreover, the remarkable geometry of [6]-helicenes has also been used in the context of chiral metallosupramolecular architectures12,13 as bidentate donors with an angle between the binding sites close to 0°.14 These systems have emerged as an unique research field owing to their electronic, optical and sensing capabilities. However, the main drawback in [n]-helicene chemistry is the challenging synthesis of members with increasing turns, even in their racemic form. In fact, the longest member of the series, [16]-helicene, composed of two and a half turns, represents an isolated example (Fig. 1, top).15
Although longer related helicene-like molecules (two and a half turns) have been described, easy access to fully conjugated helical systems continues to be a synthetic challenge.16,17 Therefore, easy-to-prepare extended and conjugated helical systems would be highly desirable for important applications like those mentioned above. Within this context, foldamers based on conjugated subunits constitute a privileged scaffold for a number of different reasons: (i) they can be easily prepared by iterative protocols using simple conjugated monomers with different geometries, (ii) the functionality present in such monomers can cooperatively act to strengthen their properties or even create new ones, and (iii) they can also interact dynamically with the environment. In fact, many aromatic foldamers can be switched between different states by different stimuli such as the presence of light,18–22 changes in temperature,23–26 solvent composition,27 anions,28–32 cations,33,34 or water35–38 binding, and redox processes.39,40 Moreover, foldamers are able to generate chirality in a dynamic way even using achiral monomers/repeating units. Therefore, the control of the P/M helicity41–46 yields systems that are able to act as chiroptical probes47,48 or even CPL emitters.49–53
In recent years, we have been working on conjugated helical structures based on o-OPEs54–58 as an alternative to [n]-helicenes exhibiting, in many cases, better chiroptical responses. Our approach relies on widening the inner cavity present in [n]-helicenes, which translates into an enhancement in the magnetic moment of optical transitions and the corresponding chiroptical response, especially at the longest wavelength. Thus, we have developed two strategies to obtain enantiopure folded fully conjugated helical systems: the first based on the use of chiral sulfoxides59,60 and, secondly, the use of chiral staples, demonstrating that enantiopure P/M helixes can be also prepared by efficient chirality transfer from a chiral staple to the o-OPE core, including even double staples to avoid racemization processes.61–64 However, the later systems could be synthesized with only one turn and a half.65
All the above approaches provide structures with remarkable chiroptical responses in ECD, CPL and VCD. It is worth noting that the response of ECD in terms of molar circular dichroism has been for some time correlated with the magnitude of the chiral-induced spin selectivity (CISS) effect.66 Actually, this phenomenon has been recently discovered, offering a promising change of paradigm for the discrimination and filtering of spin states. The spin of the electron, S = ½, yields two quantum states characterized by its projection on a given axis, ms = ±½. The two states are degenerate in the absence of either internal or external magnetic fields and, consequently, any electron current under such circumstances will consist of a half–half mixture of both states. The separation of the spin states of the electrons is a milestone of the greatest importance for the development of spintronics.
Although spin states of neutral particles67 can be selected passing through an in-homogeneous magnetic field, charged particles, like electrons, suffer from the Lorentz force arising from the interaction of the electric charge with the magnetic field, preventing a Zeeman's effect-based technique to be used for separating electron spin states. Although more complex architectures can be used,68 the (preferential) selection of the spin state of electrons travelling through chiral structures is highly appealing. The chemically relevant fact is that now it is the scattering of electrons through the molecular (helical) structure that induces the filtering of the electron spin states. Namely, depending on the helicity of the molecular structure, it preferentially allows the passage of one of the two spin states over the other, because helicity couples the spin of the electron with its own linear momentum, resulting in the selective transmission of electrons with the preferred spin state. This opens the way to great opportunities for “chemical control” in the selection and discrimination of the spin state of electric currents. The key concept resides in the achievement of precise chemical control on the factors affecting the molecular helical structure, i.e. length, diameter, pitch, chemical composition, chemical environment, either the solvent selection or its deposition on selected surfaces, including nanoparticles, etc. The absence of external electromagnetic fields avoids any interference with the spins in “uncontrollable” ways. The implications of the CISS effect for the control of the electronic spin state have already been documented.69 Nevertheless, a long-standing goal, not fully resolved at the time being, is to know beforehand which molecules are best for CISS spin-filtering. Within this context, remarkable effort has been made by Waldeck et al.,66 who showed conclusive experimental evidence for the direct correlation between CISS induced spin-filtering power and the magnitude of features of the molecule electronic circular dichroism (ECD) spectrum. A direct correlation of the dissymmetry of the electron-transfer rate for photoelectrons produced by circularly polarized light was found with both the sign and intensity of the ECD signal of electron acceptor chiral molecules. This suggests that the larger the ECD signal intensity the better the CISS spin-filtering a molecule can perform. The sign determines which spin is preferentially filtered.
Although the relationship between both phenomena seems plausible, it is not clear which factors are relevant for such a connection. One conceivable hypothesis is that the CISS effect may be associated with a transient magnetic moment in chiral molecules. Indeed, the intrinsic magnetic nature of the CISS effect suggests that induced magnetic transition moments (m) could be relevant to characterize the magnetic molecular response associated with the dynamic spin-polarized electron transport through a molecule. The optimal design of structures in which such a relationship could be validated is, therefore, essential.
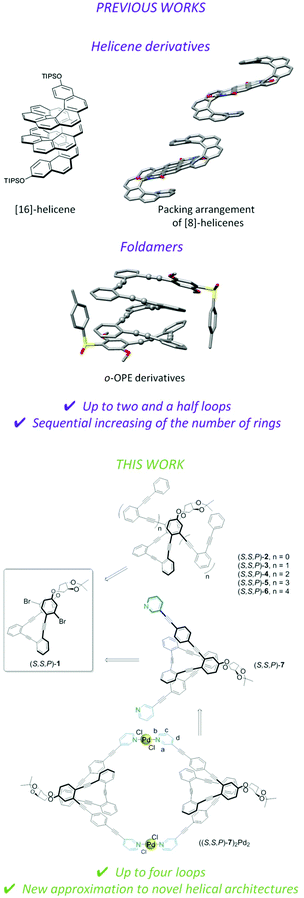
Here we report on a versatile scaffold to explore new helical architectures using simple derivatizations. Chiral stapled nucleus (S,S,P)-1 can be used as a chiral seed for the synthesis of highly extended enantiopure conjugated helical systems (S,S,P)-2–(S,S,P)-6 (Fig. 1, bottom) containing one up to four complete turns. In the presence of Ag(I) we have obtained the most extended enantiopure systems with a well-defined structure described to date.70–73 This situation is optimal to gain insight into the importance of the length of helical systems, the magnitude of the magnetic dipole transition moment (m) associated with the less energetic transition, and their potential use as a predictor of CISS capabilities for an organic architecture. We must emphasize that a comprehensive theoretical model coupling optical dichroism with the CISS effect is still missing, but the work reported here may be a step forward in this direction.
Moreover, the usefulness of (S,S,P)-1 is also demonstrated with the preparation of ligand (S,S,P)-7. This compound increases the toolbox of the supramolecular research area showing that simple helical foldamers can be also used as a building block for the Pd(II)-directed self-assembly of a chiral Pd2L2 metallacycle, thus expanding the scarce number of examples of chiral metallosupramolecular architectures reported to date.13
Results and discussion
Synthesis
The main objective of our approach is the synthesis of a chiral core able to be further functionalized. Taking into account our previous successful route to enantiopure stapled o-OPEs based on an etherification reaction of a simple o-OPE and a chiral bis-tosylate derivative,53 we decided to adopt this strategy to access compound (S,S,P)-1. Hence, this compound could be easily prepared following the route described in Scheme 1. (S,S,P)-1 presents two aromatic bromides suitable for symmetric extension of the conjugated system using different Sonogashira reactions. Enantiomeric (R,R,M)-1 was also prepared resulting in the expected and opposite chiroptical properties (see Fig. S118 and S134†). For simplicity, from now on the discussion is restricted to (S,S,P)-1 enantiomer. A simple coupling reaction affords enantiopure compounds (S,S,P)-2 to (S,S,P)-6 with increasing number of alkynes, enabling the study of systems from three alkynes/one turn, (S,S,P)-1, to thirteen alkynes, (S,S,P)-6, reaching in the latter case four complete turns, which has no precedent in the literature. The coupling reaction of the chiral nucleus (S,S,P)-1 with pyridine-containing dialkyne 19 yielded (S,S,P)-7. These reactions demonstrate that (S,S,P)-1 is in fact a versatile chiral building block that enables access to a variety of structures in a straightforward and modular way.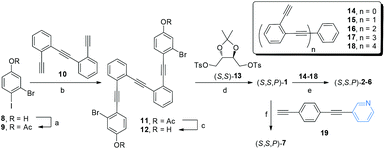 | ||
| Scheme 1 Synthesis of helical systems (S,S,P)-2–(S,S,P)-6 and ligand (S,S,P)-7. Reagents and conditions: (a) Ac2O (1.4 eq.), DMAP (2 eq.), CH2Cl2, rt, 5 min, 100%; (b) Pd(CH3CN)2Cl2 (0.03 eq.), PtBu3·HBF4 (0.06 eq.), CuI (0.03 eq.), iPr2NH, rt, 24 h, 70%; (c) K2CO3 (7 eq.), THF, MeOH, rt, 30 min, 88%; (d) CsCO3, CH3CN, reflux, 24 h, 56%; (e) Pd(CH3CN)2Cl2, CuI, PtBu3·HBF4, iPr2NH/THF, 60 °C, 24 h; (f) Pd(CH3CN)2Cl2, CuI, PtBu3·HBF4, iPr2NH/THF, 60 °C, 24 h; 81%. Yields of step e for each derivative are described in the ESI.† | ||
Photophysics of compounds (S,S,P)-1 to (S,S,P)-7
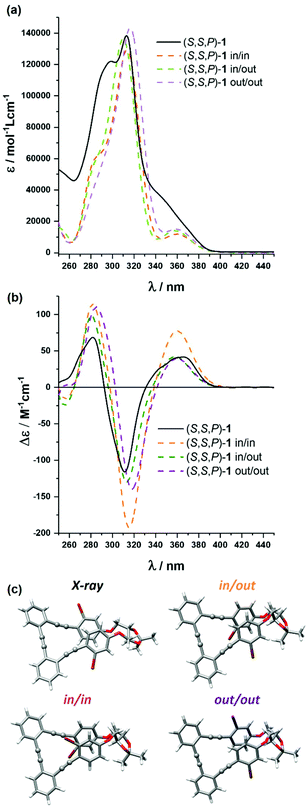
Compound (S,S,P)-1 was fully characterized by NMR and mass spectrometry (see the ESI†) but also by means of optical and chiroptical techniques. The absorption spectrum in CH2Cl2 exhibits two main bands centered at 305 nm and 290 nm with a smooth shoulder around 350 nm (Fig. 2a). On the other hand, the emission spectrum presents one band at 410 nm (Fig. S110†) with a fluorescence quantum yield of 4.6% (Table S1†).Circular dichroism of (S,S,P)-1 (CH2Cl2) showed a positive Cotton effect at the longest wavelength, Δε = +47 M−1 cm−1, which is characteristic of P helicity (Fig. 2b). We note that molar circular dichroism (Δε) depends on the intensity of absorption (that is, on electric transition dipole moment) and its magnitude cannot be always correlated with the intrinsic chirality of the sample. In that situation, a dimensionless gabs value, Δε/ε, is more representative and easy to compare with theoretical values. Nevertheless, extracting reliable experimental gabs values from ECD bands is tricky since calculations predict energetically close transitions with the opposite sign, such that the observed gabs value results from the algebraic sum of g-values for the individual transitions. Being interested in the first electronic transition, the best estimate can be obtained from the tail of the CD band. In that case, the experimental gabs value (+1 × 10−2) is comparable to previously described values for related systems.52,53
The origin of this helical chirality could be clarified using density functional theory (DFT) calculations. After a molecular mechanics (MM) conformational search, all structures within 5 kcal mol−1 have been optimized with both P and M helicities at the B3LYP/6-31G** level in CH2Cl2, treated with the polarizable continuum model (PCM). Only three conformers, corresponding to the relative spatial orientations of the bromine atoms (out–out, out–in and in–in), have been obtained with non-negligible populations (Fig. 2c and Table S10†). They all present P helicity and, considering the calculated energy, are nearly equally populated. As a consequence, the P epimer dominates the conformational equilibrium and makes possible a definite assignment of the (S,S,P)-1 absolute configuration in solution. This conclusion was strengthened by the similarity between the averaged simulated ECD and absorption spectra of the abovementioned P conformers (M06/6-31G** level) and the experimental ones (Fig. 2a and b). The calculated gabs value for the longest wavelength transition is in reasonable agreement with the experimental one.
Fortunately we could also obtain the single-crystal X-ray diffraction structure of (S,S,P)-1, which confirms its helical geometry with P preference in the solid state (Fig. 2c). This helical arrangement generates a dihedral angle between the central aromatic rings close to 40°. The outer aromatic rings adopt a parallel orientation, although displaced, with a distance between their main planes of 3.5 Å and a distance between centroids of 3.8 Å, suggesting the establishment of π-stacking interactions between them.
Being dynamic systems, foldamers are affected by the environment and, consequently, their properties are usually solvent dependent. In this case, we only observed a single set of signals in NMR, showing that any conformational equilibrium takes place faster than the NMR timescale. The absorbance and fluorescence of (S,S,P)-1 were analyzed in different solvents, including apolar, polar and protic ones. Although no significant differences were observed in the emission spectra, a slightly increment of the shoulder in the absorbance spectra was observed in some solvents (Fig. S109†). Fluorescence lifetimes were also measured at the emission maximum using an excitation source of 325 nm. In all tested solvents, decays were fit to a biexponential function where the shortest fluorescence lifetimes were around 0.5 ns in most cases, except in CH2Cl2 in which it presented a considerably lower value of 0.2 ns. However, we observed higher differences for the longest fluorescence lifetimes, which varied between 0.7 ns in CH2Cl2 to 4.1 ns in toluene (see Table S2† for more details). In view of these results we recorded the time-resolved emission spectra (TRES) of compound (S,S,P)-1 in CH2Cl2 covering all of the emission range, between 340 and 600 nm. This global analysis also afforded a biexponential decay showing, along the whole spectra, an exclusive contribution of the shortest lifetime species, the presence of the largest being almost negligible (see Fig. S106†). Regarding chiroptical properties and according to the abovementioned data, minor changes in the ECD of (S,S,P)-1 were observed. We noticed that the chiroptical response of (S,S,P)-1 is maximized in MeOH with an experimental gabs value of +1.3 × 10−2.
Since (S,S,P)-1 is fluorescent and chiral, CPL is a valuable tool to extract information of the dynamic system. Although the fluorescence was weak, reliable dissymmetry factors of the emission, glum values defined as 2(IL − IR)/(IL + IR), could be measured (CH2Cl2: glum = +1.1 × 10−2, MeOH: glum = +1.0 × 10−2, MeCN: glum = +1.0 × 10−2, n-hexane: glum = +0.9 × 10−2). These results suggest that the P helicity is preserved in the excited state. Consequently, the similarity of gabs and glum values also reveals that the structure is highly preserved in the excited state despite the apparent conformational flexibility.
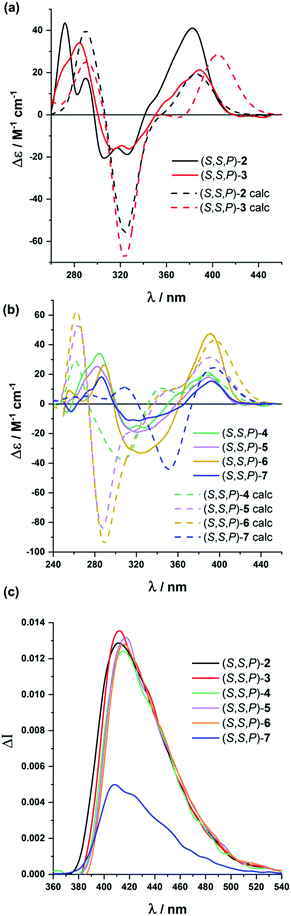
Analogous studies were carried out with compounds (S,S)-2 to (S,S)-7 (Fig. 3). Again, chiroptical properties, especially ECD and CPL, were highly informative and solvent dependent. The compound presenting five alkynes, (S,S,P)-2, showed remarkable molar circular dichroism in MeCN (Δε = +41 M−1 cm−1, gabs = +1.0 × 10−2), being compatible with a relatively ordered structure. Again, we found a correlation between the polarity of the solvent and the gabs value for the longest wavelength transition, with similar values in MeOH (Δε = +36 M−1 cm−1, gabs = +1.4 × 10−2) to those obtained in MeCN, but being weaker in CH2Cl2 (Δε = +20 M−1 cm−1, gabs = +0.8 × 10−2) and hexane (Δε = +20 M−1 cm−1, gabs = +1 × 10−2). If we assume gabs values as the representative parameter of the system helicity, polar solvents are apparently favoring the folding process. Although this is a well-known effect for m-OPEs,27 this is the first time it is clearly observed for o-OPEs.
Theoretical calculations support the prevalence of the fully folded conformations both considering CH2Cl2 and acetonitrile in the polarizable continuum model using the integral equation formalism variant (iefpcm) (see the ESI†), showing again a clear preference for the P conformation.74 The rotational barrier for the unfolding process was theoretically estimated by turning one arm of the folded structure in 100 steps (Fig. S156†), achieving a maximum at 8.1 kcal mol−1. Therefore, the partially disordered situation favored by less polar solvents might explain the observed differences (see Fig. S119, in the ESI†).
Compound (S,S,P)-2 is also fluorescent, with quantum yield values varying from 19% to 29% depending on the solvent (see Table S3 in the ESI†). The fluorescence lifetime at the emission maximum showed again two values around 4 and 2 ns in all solvents. Interestingly, time-resolved fluorescence allows the deconvolution of the emission spectra, providing the ratio of the different emitting species by using the areas of the species-associated emission spectra (SAEMS). In the four solvents we could detect two main contributions coming from two different species with around 4.6 and 2.6 ns, which cannot interconvert in that timescale. Although relative proportion depends on the solvent nature (see Fig. S107†), two limit situations are present in hexane and MeOH, in which the corresponding populations are reversed. The coexistence of fully folded and partially folded structures in the excited state may be a reasonable explanation, fully folded structures being maximized in MeOH.
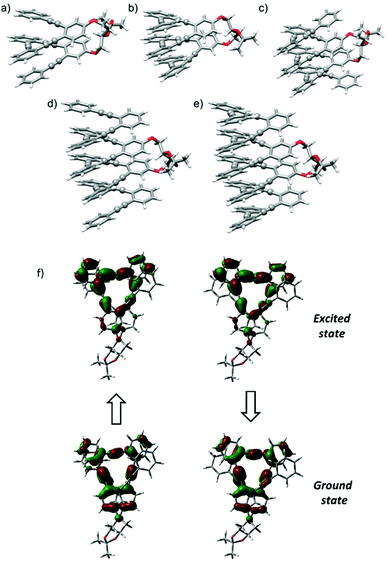
Since the chiroptical properties of the abovementioned species are expected to be different, CPL is once again a valuable tool to extract information on the dynamic system. Representative solvents as MeOH, MeCN, CH2Cl2 and hexane were evaluated using this technique, obtaining remarkably high glum values (MeOH: +1.3 × 10−2, MeCN: +1.3 × 10−2, CH2Cl2: +0.88 × 10−2, hexane: +1 × 10−2). Once more, a correlation with the polarity of the solvent was observed, the fully folded conformations with higher glum values being preferred in MeOH or MeCN. The positive sign of CPL is correlated with the positive sign of the ECD signal for the longest wavelength transition, P helicity being preserved in the excited state.4 The similarity of gabs and glum values also reveals that the geometrical structure of the ground state is preserved in the excited state. In fact, the optimized structure for the first excited state starting from the lowest-energy fully folded ground state structure resulted in a nearly superimposable helix in both ground and excited states, showing differences only in the bond length alteration (BLA) of the C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C groups (see Fig. 4f and Table S12†).
C–C groups (see Fig. 4f and Table S12†).
Similar conclusions were extracted for (S,S,P)-3–(S,S,P)-5 and (S,S,P)-7. Molar circular dichroism and gabs values remain high, especially in MeCN ((S,S,P)-3: Δε = +21 M−1 cm−1, gabs = +0.9 × 10−2; (S,S,P)-4: Δε = +18 M−1 cm−1, gabs = +0.5 × 10−2; (S,S,P)-5: Δε = +47 M−1 cm−1, gabs = +0.9 × 10−2; (S,S,P)-7: Δε = +19 M−1 cm−1, gabs = +0.8 × 10−2), compared to CH2Cl2 ((S,S,P)-3: Δε = +6 M−1 cm−1, gabs = +0.3 × 10−2; (S,S,P)-4: Δε = +8 M−1 cm−1, gabs = +0.3 × 10−2; (S,S,P)-5: Δε = +13 M−1 cm−1, gabs = +0.3 × 10−2; (S,S,P)-7: Δε = +19 M−1 cm−1, gabs = +0.3 × 10−2), although exceptions can be also observed (see the ESI†). These higher gabs in MeCN suggest a relatively ordered structure in more polar solvents, in accordance with the stability of the helical structure. Nevertheless, the increasing number of potential conformations did not allow a complete modeling of the conformational space as in previous cases. Even so, it seems reasonable to assume that in the absence of solvophobic interactions many more disordered structures in solution could be present. For compound (S,S,P)-6, we found some solubility issues in hexane and MeOH and reliable CD spectra could be obtained only in CH2Cl2 (Δε = +13 M−1 cm−1, gabs = +0.3 × 10−2) and MeCN (Δε = +15 M−1 cm−1, gabs = +0.3 × 10−2).
Fluorescence lifetimes and quantum yields for such longer oligomers (S,S,P)-3-(S,S,P)-7 were evaluated in MeOH, MeCN, CH2Cl2 and hexane and are summarized in Table S4.† Quantum yields depend on both the solvent and number of alkynes present in the molecule, but no sensible relationships could be obtained in any of the cases. However, it is remarkable that, except for compound (S,S,P)-3, the intensity-averaged lifetime of longer oligomers is always lower in hexane (around 3 ns) than in MeOH and CH3CN (around 4 ns), showing again a higher contribution of the shortest lifetime species in apolar solvents, in accordance with the results obtained for TRES of the first member of the series (S,S,P)-2.
All helical systems were also very efficient CPL emitters, especially in MeOH ((S,S,P)-3, glum = +1.3 × 10−2, (S,S,P)-4, glum = +1.1 × 10−2, (S,S,P)-5, glum = +1.3 × 10−2, (S,S,P)-6, glum = +1.3 × 10−2, (S,S,P)-7, glum = +0.54 × 10−2). Modeling CPL properties has been be carried out for compound (S,S,P)-2 in the most stable folded conformer. However, the analysis of larger systems is computationally too demanding. Despite this limitation, the structures were optimized by DFT calculations (Fig. 4b–e). Although, the similarity between gabs and glum values, which is also observed in experimental trends, is expected, the glum value is controlled by the S1 → S0 transition, which cannot be assumed to be identical to the S0 → S1 transition because the structural changes in the excited state may affect the ground state transition parameters.
(S,S,P)-1–(S,S,P)-7 Ag(I) complexes
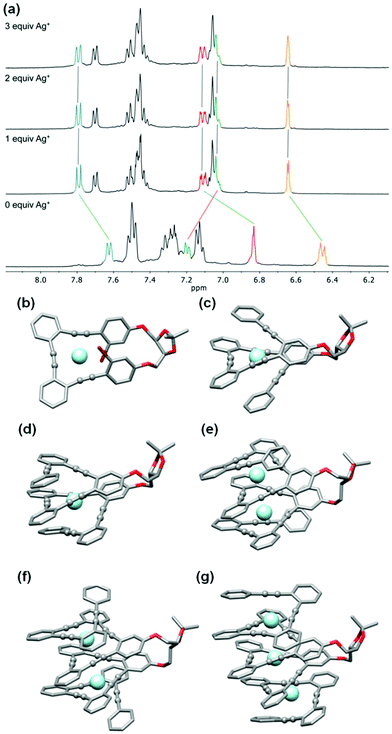
Stapled o-OPEs present a perfect arrangement for the coordination of Ag(I) cations (AgBF4) using carbophilic interactions. In this case, we restricted our study to CH2Cl2 owing to the incompatibility of such interactions and polar coordinating solvents.The first member of the series, (S,S,P)-1, presents evident structural changes after Ag(I) addition as we observed an increased resolution and downfield shielding of the aromatic protons (Fig. S49†). Regarding the 13C NMR spectra, alkyne carbons, which were initially located within 1 ppm to around 92 ppm, evolve to three different signals at 89, 92 and 94 ppm by coordination with the Ag(I) cation (Fig. S50†). The coordination process was also followed by ECD spectroscopy (Fig. S126†). In this particular case, we observed a decrease in the chiroptical response. This fact is in agreement with previous results in related o-OPEs with three alkynes owing to a planarization of the helical structure. ECD titration experiments resulted in a relatively strong single binding event, K1:Ag = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 ± 2% M−1. Theoretical calculations (M06/6-31G* plus LANL2DZ (valence + ECP) for silver in CH2Cl2) showed that the minimum energy structure corresponds to a distorted trigonal bipyramidal geometry (Fig. 6b) in which the bromine atoms participate in the coordination to the Ag(I) cation.
480 ± 2% M−1. Theoretical calculations (M06/6-31G* plus LANL2DZ (valence + ECP) for silver in CH2Cl2) showed that the minimum energy structure corresponds to a distorted trigonal bipyramidal geometry (Fig. 6b) in which the bromine atoms participate in the coordination to the Ag(I) cation.
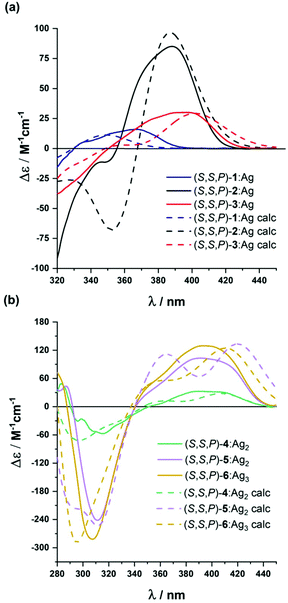 | ||
| Fig. 5 Experimental (solid line) and calculated (dashed line) ECD spectra of: (a) (S,S,P)-2-(S,S,P)-3 and (b) (S,S,P)-4–(S,S,P)-6 in CH2Cl2 in the presence of an excess of Ag(I). | ||
Compound (S,S,P)-2 is expected to behave as a ligand for only one Ag(I) cation taking into account the previous studies of related o-OPE systems.61 The binding process can be again properly followed by 1H NMR spectroscopy. NMR titrations showed that the original signals of ortho hydrogen atoms of the inner phenyl rings experience the characteristic deshielding (i.e. from 6.45 ppm to 6.64 ppm, Fig. 6a) attributed to Ag(I) coordination. In addition, significant changes in the chemical shift of alkyne carbons were observed in the 13C NMR spectrum (Fig. S52†). The ECD response at the longest wavelength is intense (Δε = +85 M−1 cm−1, gabs = +2.5 × 10−2) in agreement with a well-defined helical structure upon the formation of the complex (Fig. 6). It is worth noting that such a dissymmetry ratio is huge compared with usual values for organic molecules at the longest wavelength. The corresponding ECD titration showed a high binding constant K2:Ag = 3.67 × 105 ± 5% M−1. As expected, the DFT-based conformational analysis (see the ESI†) of complex (S,S,P)-2:Ag is in agreement with experimental findings, showing a stabilization of the fully folded structure. The calculated ECD is also in good agreement with the experimental one, thus confirming the folding process with Ag(I) (Fig. 5a and 6c). In this case, the distorted trigonal bipyramidal geometry is generated by coordination with five alkynes. Ag–alkyne bond distances are predicted to lay within 2.51–2.69 Å, with the Ag–C (alkyne) distances ranging from 2.57 to 2.76 Å. The distance between the terminal aromatic rings of the side arms and those on the corners on the central core of the helix, which display a quite displaced parallel arrangement, is ca. 3.5–3.6 Å, which suggests some extent of π-interactions between them.
On the other hand, the increase to seven potential binding sites for Ag(I) cations in compound (S,S,P)-3 did not result in a significant increase of the chiroptical properties (Δε = +21 M−1 cm−1, gabs = +1 × 10−2). In principle, a single Ag(I) cation does not need all the alkynes in the binding event, making the remaining ones useless to stabilize a second Ag(I) cation. In this situation the presence of loosely or non-bound side arms can result in a more disordered structure compared to (S,S,P)-2, even in the presence of Ag(I). Unfortunately, the complex conformational space makes it difficult to perform any theoretical prediction. As a consequence of the previous assumption, ECD titrations showed that the compound is only bound to one Ag(I) cation with a binding constant K3:Ag = 3.7 × 106 ± 15% M−1. Minimum energy calculated structures showed that Ag(I) interacts with five alkynes. Only two alkynes remain free to bind a new cation. Our previous studies60 indicated that two alkynes are unable to provide an efficient coordination to another Ag(I) cation. The different spatial arrangement for these two additional unbound side chains and even in-cavity Ag(I) displacements could explain the weaker ECD response.
The presence of two additional alkynes in (S,S,P)-4 should be in principle beneficial for the coordination process. Nevertheless, the ECD response remains weak and similar to the previous case (Δε = +24 M−1 cm−1, gabs = +0.6 × 10−2). This fact suggest that at the concentrations used for the ECD experiments there is only a relevant binding constant, although subsequent Ag(I) coordination processes can take place with a modest binding constant. Accordingly, in the titration experiments a higher overall binding constant, K4:Ag2 = 2.4 × 1010 ± 12% M−2, was obtained (se Fig. S129–S131†). It is worth noting that the corresponding NMR studies were carried out at much higher concentrations. Under such experimental conditions more than two equivalents of the Ag(I) cation are required to fully resolve the signals, suggesting the existence of a symmetric dimetallated structure.
Compound (S,S,P)-5, presenting eleven alkynes, is able to accept two Ag(I) cations, thus yielding a longer helical structure. The first evidence came from the ECD spectra, showing a remarkable molar circular dichroism (Δε) at the longest wavelength (Δε = +85 M−1 cm−1, gabs = +1.7 × 10−2) in the presence of an excess of Ag(I). ECD titrations also showed strong coordination of two Ag(I) cations (K5:Ag2 = 18 × 109 ± 1.6% M−2). This is the first example of a pure and well-defined o-OPE system presenting an enantiopure helical structure with three and a half turns. This fact shows that the chiral nucleus can be useful with the aid of Ag(I) cations in the preparation of long and conjugated helical systems. Although different situations are possible, DFT calculations showed that the energetically favored case is that in which the Ag(I) cations are separated by a distance of approximately 5.2 Å (Fig. 6f).
The best chiroptical response was observed for compound (S,S,P)-6, which showed an even higher molar circular dichroism (Δε = +130 M−1 cm−1, gabs = +2.2 × 10−2). Again, this result strongly suggests a fully folded helical structure. ECD titrations also showed three strong binding events with three Ag(I) cations (K6:Ag3 = 2.7 × 1017 ± 19% M−3). As it can be seen in Fig. 6g, DFT calculations predict a highly symmetric structure with four complete loops. The interatomic distances between consecutive Ag(I) cations are 4.4 and 4.5 Å. Interestingly, on the basis of the Ag–alkyne distances, calculations predict that the metal centers are coordinated to five alkynes. As a result, there are two alkynes that coordinate simultaneously to two Ag(I) centers, which results in longer Ag–alkyne distances (2.74–2.89 Å) in comparison with those involving triple bonds coordinated just to one metal center (Ag–alkyne distances: 2.44–2.65 Å).
VCD studies
The existence of the helical structures was also confirmed by VCD spectroscopy, particularly evident when considering longer oligomers (see the ESI†). Concerning IR measurements, the presence of the Ag(I) complex results in a band shift and broadening of the feature observed at 1500 cm−1 and in the appearance of a band at 1315 cm−1 (Fig. 7). In VCD an intensification of the triplet signal at 1445, 1482 and 1493 cm−1 (+,−,+) is also characteristic of the presence of interacting Ag(I) cations, particularly considering (S,S,P)-4 to 6 compounds. This hints at the possibility of designing good silver switches based on IR range measurements. This (+,−,+) triplet shows similar intensity in short and long chains in the absence of silver, suggesting that the central portion of the backbone rigidified by the staple is the one responsible for this signal in all compounds.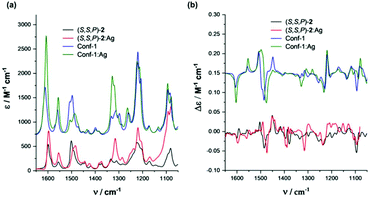 | ||
| Fig. 7 Comparison of theoretical and experimental (a) IR and (b) VCD spectra of compound (S,S,P)-2 in CH2Cl2 solvent. | ||
To better understand the origin of the spectroscopic changes upon silver addition, we examined two representative cases with the aid of DFT calculations: the shortest oligomer (S,S,P)-2 and a longer case, (S,S,P)-5. For the first case, we considered the possible conformers and compared the calculated spectra for the most stable structures in the absence or presence of silver. The details of this analysis are given in the ESI (conformer characteristics and spectra).† Due to the staple, the structure of the short oligomer is rigid enough to present a VCD signal typical of the ordered OPE structures already observed.60,61 In particular, the configuration of the staple dictates the prevalent helicity sense and the most stable conformer presents already the correct shape to host a silver ion; however, also partially unfolded structures of (S,S,P)-2 maintain the spectroscopic pattern. In the presence of Ag(I), the calculated spectrum reproduces the wavenumber shift of the two higher energy components of the previously cited triplet (+,−,+) and the 1315 cm−1 feature intensification (Fig. 7). Also the IR spectra differences are correctly predicted.
In the case of the longer oligomer, Ag(I) cations give rise to the enhancement of the triplet at 1450–1500 cm−1. The phenomenon can be attributed to normal modes delocalized along the whole molecule, consisting of in-plane bending of the phenyl CH bonds. Structures with various Ag contents have been optimized: one central Ag ion, two Ag ions symmetrically or non-symmetrically disposed and three Ag ions (see Fig. S150† for the optimized structures and Fig. S151† for the corresponding calculated spectra). Overall, there is a good correspondence between calculated and experimental data. In fact, compound (S,S,P)-5 revealed to be quite efficient in incorporating silver ions and has sufficient length to show an enhancement of VCD signals when it is guided to form a regular helix in the presence of silver. In conclusion, in the presence of silver, the longer backbone assumes an ordered structure able to show intensification of the triplet; the increase in intensity is more regular considering VCD, while ECD shows a non-monotonic dependence on the alkyne number. A complete theoretical representation of all the situations and of the two spectroscopic responses (ECD and VCD) is not easy due to the complexity of the conformational landscape and of the evident solvent effect (see Fig. 2) which is not simple to model.
Chiroptical properties and CISS effect for compounds (S,S,P)-2 to (S,S,P)-6 and their corresponding Ag(I)-complexes
In this vein, compounds denoted as (S,S,P)-2–6, appear to be ideal for examining the influence of the number of turns of helical molecules on their chiroptical properties and its eventual connection to the CISS effect-based spin selection power. The chiroptical properties are customarily quantified by the dissymmetry factor, gabs, of the electronic transitions. The latter quantity is expressed in terms of the extinction coefficients for left-, ε_, and right-polarized, ε+, incident exciting light and reads as, gabs = 2(ε_ − ε+)/(ε_ + ε+) = 4(|μ||m|)cos(θ)/(|μ|2 + |m|2) ≈ 4R/D, where R and D are the rotational and dipole strengths respectively for the corresponding S0 → Sn transition This equation expresses the dissymmetry factor in terms of the electric dipole transition moment, μ, and the magnetic dipole transition moment, m, and the angle subtended by these two vectors, θ. Since the magnetic dipole transition moment is normally much smaller than the corresponding electric one, one can expand (|μ|2 + |m|2)−1 in terms of powers of (|m|/|μ|) to obtain, at the first order approximation, gabs = 4(|m|/|μ|)cos(θ). On the other hand, the CISS effect translates into an additional component of the magnetic moment associated with a Rashba-like term: mCISS = α(E·(σ × p)), where a is a coupling constant, E the molecular electric field, σ the Pauli matrix vector and p the linear momentum of the electron involved in the transport. This additional term has to be included in the optical response, generating, in principle, a direct connection between ECD and the CISS effect Namely, as noted above, an electron moving along the electric field in a chiral structure defined by the fixed nuclei and not by an external field, will experience in its rest frame a magnetic field, which will interact equally as above with the electron magnetic moment. Hence, the electron magnetic moment appears to be directly connected to the CISS effect. Given the nature of the optical activity response, one could hypothesize the transition magnetic vector m as a descriptor for enhanced chiroptical properties, which could explain the observed relationship between the chiroptical properties and enhanced CISS spin selectivity power.75 Despite the fact that gabs values can be high when |m| and |μ| are similar in magnitude and aligned as possible, that fact does not guarantee the absolute value of |m| to be high. That is, compounds can present high gabs values simply by diminishing |μ|. We hypothesize that conductive helical structures, which supposedly are ideal candidates for relevant CISS the effect, must show a high |m|, higher than 1 × 10−20 cgs units,76 for transitions capturing the helical structure of the involved molecular orbitals. Moreover, the CISS effect is directional and must be analyzed in the direction of electron transport, which is difficult using scalar quantities like gabs or rotational strength (R = (|μ||m|)cos(θ)). The lower energy transitions are of special relevance since the most accessible orbitals for electron transport at low voltages are involved.We have analyzed the relevant chiroptical parameters, such as electric and magnetic dipole transition moments |m| and |μ|, dipole (D) and rotational strengths (R), and angle between electric dipole transition moment and magnetic dipole transition moment, obtained by TD-DFT calculations (M06/6-31G**) of molecules (S,S,P)-2 to (S,S,P)-6 and their corresponding Ag(I) complexes. It is important to note that the studied systems are quite large and cannot be fully modelled at a high level of theory. Consequently, only tendencies and not precise values can be provided by the calculations. It is worth noting that theoretical calculations overestimate the predicted gabs values.77 In this case, we use CH2Cl2 as the solvent for a better comparison with the parent compounds and Ag(I) complexes derived.
Inspection of the data of Table 1 shows that the magnetic dipole transition moment for the S0 → S1 transition increases monotonically with the number of windings for the whole set of helical molecules (S,S,P)-2 to (S,S,P)-6. This is in agreement with the naïve view that holds that increasing the helicity of the compound should translate into an increase of the magnetic moment. It had been suggested that when the magnetic dipole transition moment stands for the power absorbed from the exciting light magnetic field in a conductive helix, a linear relationship between the transition magnetic dipole moment and the number of loops n exists.78
| Compound | μ (10−20) | m (10−20) | D (10−40) length | R (10−40) length | E–M | g abs |
|---|---|---|---|---|---|---|
| (S,S,P)-2 | 204 | 3.74 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568 568 |
645 | 32 | 0.062 |
| (S,S,P)-3 | 382 | 3.97 | 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 279 279 |
1407 | 22 | 0.03 |
| (S,S,P)-4 | 426 | 4.19 | 181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 829 829 |
1606 | 26 | 0.03 |
| (S,S,P)-5 | 442 | 4.20 | 195![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208 208 |
1727 | 22 | 0.03 |
| (S,S,P)-6 | 524 | 4.42 | 275![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 017 017 |
2237 | 15 | 0.03 |
| (S,S,P)-2:Ag | 215 | 3.73 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231 231 |
705 | 29 | 0.06 |
| (S,S,P)-3:Ag | 249 | 3.45 | 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 283 283 |
811 | 20 | 0.05 |
| (S,S,P)-4:Ag2 | 216 | 3.84 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 991 991 |
815 | 12 | 0.06 |
| (S,S,P)-5:Ag2 | 185 | 3.94 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572 572 |
734 | 0 | 0.08 |
| (S,S,P)-6:Ag3 | 289 | 4.28 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 865 865 |
1190 | 17 | 0.05 |
In that case, the classical electromagnetic power dissipated by light absorption of intensity E02 and wavelength λ by the magnetic field alone in a helix of conductivity σ, cross section a, radius r, pitch length d, and pitch angle Φ, is dictated by P = aσ(E0r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ/4λ)2(d2 + 4π2r2)1/2n. Such a linear relationship is nicely paralleled by the plot in Fig. 8 of the magnetic dipole transition moment |m| versus N, where N, the number of alkynes displayed on the x-axis, is related to the number of loops (n) through n = N/3. This is in agreement with a seminal paper about the CISS effect by Zacharias et al.79 in which the spin polarization increases as a function of the number of turns in helical polypeptide molecules adsorbed on a gold surface, a result that runs parallel with the observed dependence of the transition magnetic moment.
Φ/4λ)2(d2 + 4π2r2)1/2n. Such a linear relationship is nicely paralleled by the plot in Fig. 8 of the magnetic dipole transition moment |m| versus N, where N, the number of alkynes displayed on the x-axis, is related to the number of loops (n) through n = N/3. This is in agreement with a seminal paper about the CISS effect by Zacharias et al.79 in which the spin polarization increases as a function of the number of turns in helical polypeptide molecules adsorbed on a gold surface, a result that runs parallel with the observed dependence of the transition magnetic moment.
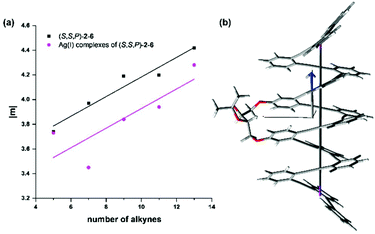 | ||
| Fig. 8 (a) Linear fitting of |m| with the number of alkynes of compounds (S,S,P)-2–6 in CH2Cl2 solutions in the absence of Ag(I) (black squares, y = 3.38 + 0.8x, R2 = 0.955) and silver complexes (S,S,P)-2:Ag, (S,S,P)-3:Ag, (S,S,P)-4:Ag2, (S,S,P)-5:Ag2 and (S,S,P)-6:Ag3 (pink circles, y = 3.13 + 0.08x, R2 = 0.69). (b) Calculated structure including helix axis and magnetic dipole transition moment of (S,S,P)-6 (for the rest of compounds see Fig. S157 and 158†). | ||
This nice result is based on the alignment of the magnetic transition vector and the helix axis for the S0 → S1 transition. At this point we hypothesized that the projection of the magnetic transition vector on the helix axis could be even a better predictor owing to the fact that spin filtering implies some sort of directionality, implicit in the idea that the scattered electron should pass through the helix. In this way, transitions with magnetic transition vectors misaligned with respect to the direction of the electron transport (helix axis) would not be relevant for the desired relationship between CISS and chiroptical properties. Although the helix axis is not fully conserved in all the structures (see Fig. S157 and 158†) we could observe again an almost perfect alignment between m and the defined helix axis. Consequently, the linear relationship is preserved (Fig. S159†).
A similar analysis can be carried out with the Ag(I) complexes, although in this case the geometrical variations along the series are higher resulting in a worse linearity (see Fig. 8, pink circles). In any case, a clear increase in the magnetic moment of the transition (m) can be observed for the Ag(I)-saturated structures (S,S,P)-2:Ag, (S,S,P)-3:Ag, (S,S,P)-4:Ag2, (S,S,P)-5:Ag2, (S,S,P)-6:Ag3.
As suggested above we speculate that the magnetic transition vector or its projection in the electron transport direction of a selected transition could be the missing link between the CISS effect and chiroptical properties. This can be supported by the interpretation of the CISS effect as an additional contribution to molecular magnetic response that is triggered in the presence of electron transport through a chiral (helical) structure. A simple theoretical explanation for this dependence of the spin polarization with molecular length in helices can be given in terms of a scattering model including both coherent and incoherent contributions to electron transport.80 All these assumptions, although promising, require further theoretical inquiries.
Metallosupramolecular complex ((S,S,P)-7)2Pd2
Finally, we have checked the coordination capabilities of homochiral ligand (S,S,P)-7 towards Ag(I) and Pd(II) cations. Despite the presence of five alkynes, this ligand has two additional pyridine rings that can coordinate to non-carbophilic metal centres as Pd(II). The meta substitution of these pyridine rings results in an almost parallel orientation of the binding sites (with an angle between them close to 0°). This geometry allows the assembly of well-defined metallosupramolecular entities with metal centres with coordination sites in a 180° orientation, resulting in either linear Ag(I) complexes or square planar Pd(II) complexes with two additional ligands in trans positions.12In the case of the Ag(I) cations, two different binding sites are possible, the alkynes and the pyridines. ECD spectroscopy was highly informative to discriminate between the two alternatives. As in the case of related compound (S,S,P)-3, intensification of the ECD signal at the longest wavelength (Δε = +41 M−1 cm−1, gabs = +0.45 × 10−2) is observed upon the addition of a Ag(I) salt to a solution 2.5 × 10−5 M of (S,S,P)-7, compatible with an increase of the helicity of the system (Fig. S121†). Moreover, titration experiments also showed that this increase was related to the coordination of the ligand to one Ag(I) cation (K7:Ag = 8.21 × 105 ± 13% M−1) (Fig. S132†). Therefore, the interaction of Ag(I) cations with the alkynes seems to be the most favorable interaction for the first added equivalent. Nevertheless, in the presence of an excess of Ag(I) cation the ECD signals drastically decrease suggesting the formation of insoluble material in CH2Cl2, probably by subsequent coordination of the cation with the available pyridine groups. All these results allow us to conclude that carbophilic metals cannot easily direct the self-assembly of metallosupramolecular structures for our systems.
On the other hand, the addition of a solution of trans-PdCl2(MeCN)2 (10 mM) to solutions of (S,S,P)-7 in CD2Cl2 or DMSO-d6 (10 mM) resulted in the appearance of new signals in the corresponding 1H NMR spectra. This fact indicates the presence of new species in solution and suggests the formation of a metallacycle as a result of the coordination of the pyridine rings to the Pd(II) centers (see ESI, Fig. S92–102†). The DOSY NMR spectrum in DMSO-d6 of this mixture (Fig. S103†) agrees with the presence of two species as two diffusion coefficients are observed for the 1H signals. Thus, the new set of signals that appeared after Pd(II) addition shows a lower diffusion coefficient, supporting the coordination of (S,S,P)-7 to the metal center and the self-assembly of the larger metallacycle. By increasing the amount of the added Pd(II) complex, this new set of signals became the main one in the mixture, being practically the only one present when 1–1.2 equiv. of trans-PdCl2(MeCN)2 were added (Fig. S93 and S98†). In this case, the DOSY NMR spectrum confirms that all signals correspond to a single species that diffuses as a whole, as expected, as only one diffusion coefficient is observed (Fig. S65 and S70†).
The clear solution obtained in DMSO-d6 was monitored over time by 1H NMR spectroscopy, showing no significant changes in the spectrum over 6 days (see ESI, Fig. S102†). In CD2Cl2 the evolution of the system was more complicated since a precipitate was formed soon after the addition of the metal when a final concentration of 5 mM was used. After filtration, the 1H NMR spectrum of the remaining solution showed two sets of signals, one corresponding to the free ligand and the other one to the newly formed species, postulated as the ((S,S,P)-7)2Pd2 complex. However, the ratio between species was not maintained over time, as a decrease of the proportion of the coordination complex was observed by 1H NMR monitoring. Better results were obtained when the concentration was lowered to 2.5 mM, as no precipitation was observed. In this case, the set of signals attributed to the coordinated species was present almost exclusively after 24 h and good stability was observed over time (Fig. S96†).
Comparison of the 1H NMR of (S,S,P)-7 before and after the addition of Pd(II) both in DMSO-d6 and CD2Cl2 shows a downfield shift (ΔδHa = 0.23 ppm; ΔδHb = 0.32 ppm in CD2Cl2 and ΔδHa = 0.22 ppm; ΔδHb = 0.23 ppm in DMSO-d6) of the H atoms of the pyridine ring at positions 2 and 6 (Fig. 9a). This is the expected behavior for the coordination of the pyridine ring to the Pd(II) center. To lend further support to the fact that the observed shift corresponds to the binding event, 3-(phenylethynyl)pyridine was prepared as a model ligand. The similarities between the chemical shift for the signals of the pyridine nuclei and their variation in the two complexes (ΔδHa = 0.23 ppm; ΔδHb = 0.25 ppm in CD2Cl2 and ΔδHa = 0.23 ppm; ΔδHb = 0.19 ppm in DMSO-d6, see Fig. S93 and 104†) support the same coordination pattern in both cases.
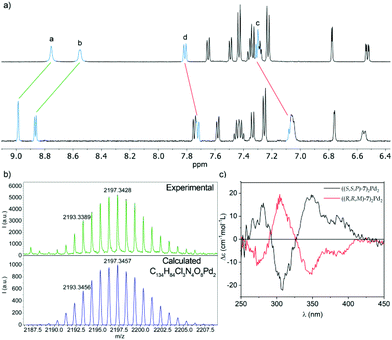 | ||
| Fig. 9 (a) Partial 1H NMR (500 MHz, CD2Cl2) spectra of ligand (S,S,P)-7 (top) and metallosupramolecular complex ((S,S,P)-7)2Pd2, (bottom). The lettering corresponds to that shown in Fig. 1; (b) observed (top) and calculated (bottom) HRMS (MALDI+) isotopic pattern for the [M − Cl]+ ion of metallacycle ((S,S,P)-7)2Pd2; (c) ECD spectra of complex ((S,S,P)-7)2Pd2 (black line) and its enantiomer ((R,R,M)-7)2Pd2 (red line). | ||
Dilution experiments down to 0.5 mM both in CD2Cl2 or DMSO-d6 show that the self-assembled complex is the only species at 2.5 mM in CD2Cl2 and in the 5–2.5 mM range in DMSO-d6 and the major one down to 1 mM in both solvents. This fact strongly suggests that the more entropically favored complex is being obtained. At 0.5 mM in CD2Cl2, the complex is still the major species in solution, although the free ligand is clearly observed. In contrast, a considerable amount of the bare (S,S,P)-7 ligand is observed in DMSO-d6 at the same concentration. This is not surprising taking into account the higher coordinating character of DMSO compared to CH2Cl2, which leads to a higher self-assembly concentration.33
The self-assembly of a ((S,S,P)-7)2Pd2 complex was further demonstrated by MALDI mass spectrometry of an evaporated sample of the complex. The high-resolution mass spectrum shows a signal at m/z = 2193.3, whose exact mass and isotopic distribution (Fig. 9b) nicely match those calculated for the [M − Cl]+ ion, resulting from the loss of one chloride ligand by one of the Pd centers.
Chiroptical properties were not particularly informative owing to just a moderate distortion of the electronic states after coordination. Therefore, very similar UV-Vis and almost identical ECD spectra to those of the free ligand were obtained (Fig. 9c and S122†). To confirm that we were really observing the signal associated with the complex, the 1H NMR spectra of the sample were recorded before and after the UV-CD measurements, performed at the NMR concentration (Fig. S123 and S124†).
Finally, the structures of metallosupramolecular complex ((S,S,P)-7)2Pd2 and its ((R,R,M)-7)2Pd2 enantiomer were investigated by means of DFT calculations at the ωB97XD/def2SVP level of theory both in DMSO and CD2Cl2 (Fig. 10 and Tables S25–28†). The optimized structures gave structural arrangements which were in good agreement with the experimental data. They showed the coordination of the pyridine rings to the Pd(II) metal centers and the generation of a chiral cavity defined by the helical cores.
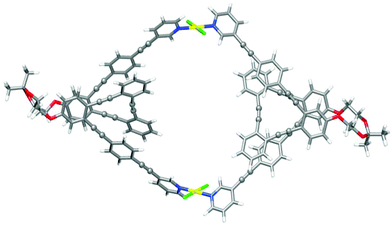 | ||
| Fig. 10 Optimized DFT (ωB97XD/def2SVP, DMSO) structure of ((S,S,P)-7)2Pd2. Color coding: C, grey; H, white; O, red, Pd, yellow; Cl, green. | ||
Conclusions
In this work, we have synthesized a new family of enantiopure helical foldamers with an increasing number of turns. Moreover, in the presence of the Ag(I) cation well defined structures containing up to three ions and four turns are formed. As a consequence of such a helical structure intense chiroptical properties associated with electron transitions both from the ground (ECD) and excited state (CPL) have been observed. The versatility of this approach has been further validated by preparing an enantiopure metallacyclic structure upon coordination with Pd(II), thus enriching this chemistry with a new class of chiral ligands. We have observed that gabs does not monotonically depend on the number of turns, in contrast to the trend observed in the 1Bb band in helicenes.81 While the magnetic dipole transition moment seems non progressive with increasing number of rings in helicenes, we have found a lineal dependence of this vector in these helical foldamers. This fact can also be related to the potential use of these systems as spin filters, the magnetic dipole transition moment being a potential predictor of the CISS-based spin filtering capabilities of these Ag(I)-complexes.Author contributions
A. M. O.: formal analysis, investigation, validation. P. R.: formal analysis, investigation, validation. S. R.: formal analysis, investigation. L. A. C.: conceptualization, formal analysis, writing-original draft. V. B.: investigation, formal analysis, writing-original draft. J. M. P.: investigation, formal analysis. A. J. M.: formal analysis, methodology, writing-original draft. G. M.: methodology, formal analysis. S. A.: formal analysis, investigation, validation. J. U.: methodology, conceptualization, formal analysis, writing-original draft. V. M.: methodology, conceptualization, formal analysis, writing-original draft. G. L.: conceptualization, formal analysis, writing-original draft. D. M.: funding acquisition, methodology, supervision, project administration, writing-original draft, writing – review. J. M. C.: conceptualization, funding acquisition, methodology, project administration, supervision, writing-original draft, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Ministerio de Economía y Competitividad (CTQ2017-85454-C2-1-P), Ministerio de Ciencia en Innovación (PID2020-113059GB-C21) and Junta de Andalucía (P20_00162) (Spain) for funding and P. R. and A. O. G. also for FPU contracts. We also thank the UGR CSIRC for access to computational facilities. We also thank Big&Open Data Innovation Laboratory (BODaI-Lab), University of Brescia, granted by Fondazione Cariplo and Regione Lombardia, for access to resources of Computing Center CINECA (Bologna), Italy. Support from the Italian MIUR (grant N. 2017A4XRCA) is also acknowledged. VM acknowledges a Fellowship from Ikerbasque, the Basque Foundation for Science.Notes and references
- S. Rinaldi, The Diverse World of Foldamers: Endless Possibilities of Self-Assembly, Molecules, 2020, 25, 3276 CrossRef CAS; H. Song, M. Postings, P. Scott and N. J. Rogers, Metallohelices emulate the properties of short cationic α-helical peptides, Chem. Sci., 2021, 12, 1620–1631 RSC.
- M. Rickhaus, M. Mayor and M. Jurıček, Strain-induced helical chirality in polyaromatic systems, Chem. Soc. Rev., 2016, 45, 1542–1556 RSC.
- K. Dhbaibi, L. Favereau and J. Crassous, Enantioenriched Helicenes and Helicenoids Containing Main-Group Elements (B, Si, N, P), Chem. Rev., 2019, 119, 8846–8953 CrossRef CAS PubMed.
- First papers in helicene CPL: O. E. Weigang Jr., J. A. Turner and P. A. Trouard, Emission Polarization and Circular Dichroism of Hexahelicene, J. Chem. Phys., 1966, 45, 1126–1134 CrossRef CAS; S. Abbate, G. Longhi, F. Lebon, E. Castiglioni, S. Superchi, L. Pisani, F. Fontana, F. Torricelli, T. Caronna, C. Villani, R. Sabia, M. Tommasini, A. Lucotti, D. Mendola, A. Mele and D. A. Lightner, Helical Sense-Responsive and Substituent-Sensitive Features in Vibrational and Electronic Circular Dichroism in Circularly Polarized Luminescence, and in Raman Spectra of Some Simple Optically Active Hexahelicenes, J. Phys. Chem. C, 2014, 118, 1682–1695 CrossRef.
- H. Tanaka, Y. Inoue and T. Mori, Circularly Polarized Luminescence and Circular Dichroisms in Small Organic Molecules: Correlation between Excitation and Emission Dissymmetry Factors, ChemPhotoChem, 2018, 2, 386–402 CrossRef CAS; W.-L. Zhao, M. Li, H.-Y. Lu and C.-F. Chen, Advances in helicene derivatives with circularly polarized luminescence, Chem. Commun., 2019, 55, 13793–13803 RSC.
- K. Ray, S. P. Ananthavel, D. H. Waldeck and R. Naaman, Asymmetric Scattering of Polarized Electrons by Organized Organic Films of Chiral Molecules, Science, 1999, 283, 814–816 CrossRef CAS PubMed; P. C. Mondal, C. Fontanesi, D. H. Waldeck and R. Naaman, Spin-Dependent Transport through Chiral Molecules Studied by Spin-Dependent Electrochemistry, Acc. Chem. Res., 2016, 49, 2560–2568 CrossRef PubMed.
- Z. Xie, T. Z. Markus, S. R. Cohen, Z. Vager, R. Gutierrez and R. Naaman, Spin Specific Electron Conduction through DNA Oligomers, Nano Lett., 2011, 11, 4652–4655 CrossRef CAS PubMed; B. Goehler, V. Hamelbeck, T. Z. Markus, M. Kettner, G. F. Hanne, Z. Vager, R. Naaman and H. Zacharias, Spin Selectivity in Electron Transmission Through Self-Assembled Monolayers of Double-Stranded DNA, Science, 2011, 331, 894–897 CrossRef PubMed; P.-J. Hu, S.-X. Wang, X.-H. Gao, Y.-Y. Zhang, T.-F. Fang, A.-M. Guo and Q.-F. Sun, Spin-dependent electron transport along hairpinlike DNA molecules, Phys. Rev. B, 2020, 102, 195406 CrossRef.
- For [7]helicene see: M. Kettner, V. V. Maslyuk, D. Nürenberg, J. Seibel, R. Gutierrez, G. Cuniberti, K.-H. Ernst and H. Zacharias, Chirality-Dependent Electron Spin Filtering by Molecular Monolayers of Helicenes, J. Phys. Chem. Lett., 2018, 9, 2025–2030 CrossRef CAS PubMed . For helicene-like molecules see: V. Kiran, S. P. Mathew, S. R. Cohen, I. Hernández Delgado, J. Lacour and R. Naaman, Helicenes—A New Class of Organic Spin Filter, Adv. Mater., 2016, 28, 1957–1962 CrossRef PubMed.
- M. Geyer, R. Gutierrez, V. Mujica and G. Cuniberti, Chirality-Induced Spin Selectivity in a Coarse-Grained Tight-Binding Model for Helicene, J. Phys. Chem. C, 2019, 123, 27230–27241 CrossRef CAS.
- J. M. Matxain, J. M. Ugalde, V. Mujica, S. I. Allec, B. M. Wong and D. Casanova, Chirality Induced Spin Selectivity of Photoexcited Electrons in Carbon-Sulfur [n]Helicenes, ChemPhotoChem, 2019, 3, 770–777 CrossRef CAS.
- T.-R. Pan, A.-M. Guo and Q.-F. Sun, Spin-polarized electron transport through helicene molecular junctions, Phys. Rev. B, 2016, 94, 235448 CrossRef.
- T. R. Schulte, J. J. Holstein and G. H. Clever, Chiral Self-Discrimination and Guest Recognition in Helicene-Based Coordination Cages, Angew. Chem., Int. Ed., 2019, 58, 5562–5566 CrossRef CAS PubMed.
- L.-J. Chen, H.-B. Yang and M. Shionoya, Chiral metallosupramolecular architectures, Chem. Soc. Rev., 2017, 46, 2555–2576 RSC.
- For a classification of the possible combinations of ligand and metal centre geometries that give access to 2D and 3D metallosupramolecular architectures see: R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Supramolecular Coordination: Self-Assembly of Finite Two- and Three-Dimensional Ensembles, Chem. Rev., 2011, 111, 6810–6918 CrossRef CAS PubMed.
- K. Mori, T. Murase and M. Fujita, One-Step Synthesis of [16]Helicene, Angew. Chem., Int. Ed., 2015, 54, 6847–6851 CrossRef CAS PubMed.
- J. Nejedlý, M. Šámal, J. Rybáček, I. Gay Sánchez, V. Houska, T. Warzecha, J. Vacek, L. Sieger, M. Buděšínský, L. Bednárová, P. Fiedler, I. Císařová, I. Starý and I. G. Stará, Synthesis of Racemic, Diastereopure, and Enantiopure Carba- or Oxa[5]-, [6]-, [7]-, and -[19]helicene (Di)thiol Derivatives, J. Org. Chem., 2020, 85, 248–276 CrossRef PubMed.
- B. Liu, M. Böckmann, W. Jiang, N. L. Doltsinis and Z. Wang, Perylene Diimide-Embedded Double [8]Helicenes, J. Am. Chem. Soc., 2020, 142, 7092–7099 CrossRef CAS PubMed.
- Z. Yu and S. Hecht, Remote control over folding by light, Chem. Commun., 2016, 52, 6639–6653 RSC.
- B. Gole, B. Kauffmann, V. Maurizot, I. Huc and Y. Ferrand, Light-Controlled Conformational Switch of an Aromatic Oligoamide Foldamer, Angew. Chem., Int. Ed., 2019, 58, 8063–8067 CrossRef CAS PubMed.
- S. Steinwand, Z. Yu, S. Hecht and J. Wachtveitl, Ultrafast Dynamics of Photoisomerization and Subsequent Unfolding of an Oligoazobenzene Foldamer, J. Am. Chem. Soc., 2016, 138, 12997–13005 CrossRef CAS PubMed.
- Z. Yu and S. Hecht, Control over Unfolding Pathways by Localizing Photoisomerization Events within Heterosequence Oligoazobenzene Foldamers, Angew. Chem., Int. Ed., 2013, 52, 13740–13744 CrossRef CAS PubMed.
- Z. Yu, S. Weidner, T. Risse and S. Hecht, The role of statistics and microenvironment for the photoresponse in multi-switch architectures: The case of photoswitchable oligoazobenzene foldamers, Chem. Sci., 2013, 4, 4156–4167 RSC.
- Y. Zhao, A. L. Connor, T. A. Sobiech and B. Gong, Effects of Oligomer Length, Solvents, and Temperature on the Self-Association of Aromatic Oligoamide Foldamers, Org. Lett., 2018, 20, 5486–5489 CrossRef CAS PubMed; Y. Zhao, A. L. Connor, T. A. Sobiech and B. Gong, Correction to Effects of Oligomer Length, Solvents, and Temperature on the Self-Association of Aromatic Oligoamide Foldamers, Org. Lett., 2020, 22, 2111 CrossRef PubMed.
- H. G. Jeon, H. K. Lee, S. Lee and K. S. Jeong, Foldamer-based helicate displaying reversible switching between two distinct conformers, Chem. Commun., 2018, 54, 5740–5743 RSC.
- B. Fimmel, M. Son, Y. M. Sung, M. Grüne, B. Engels, D. Kim and F. Würthner, Phenylene Ethynylene-Tethered Perylene Bisimide Folda-Dimer and Folda-Trimer: Investigations on Folding Features in Ground and Excited States, Chem. – Eur. J., 2015, 21, 615–630 CrossRef CAS PubMed.
- V. Berl, I. Huc, R. G. Khoury, M. J. Krische and J.-M. Lehn, Interconversion of single and double helices formed from synthetic molecular strands, Nature, 2000, 407, 720–723 CrossRef CAS PubMed.
- D. J. Hill and J. S. Moore, Helicogenicity of solvents in the conformational equilibrium of oligo(m-phenylene ethynylene)s: Implications for foldamer research, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5053–5057 CrossRef CAS PubMed.
- F. C. Parks, Y. Liu, S. Debnath, S. R. Stutsman, K. Raghavachari and A. H. Flood, Allosteric Control of Photofoldamers for Selecting between Anion Regulation and Double-to-Single Helix Switching, J. Am. Chem. Soc., 2018, 140, 17711–17723 CrossRef CAS PubMed.
- Y. Hua, Y. Liu, C. H. Chen and A. H. Flood, Hydrophobic Collapse of Foldamer Capsules Drives Picomolar-Level Chloride Binding in Aqueous Acetonitrile Solutions, J. Am. Chem. Soc., 2013, 135, 14401–14412 CrossRef CAS PubMed.
- J. M. Suk, V. R. Naidu, X. Liu, M. S. Lah and K. S. Jeong, A Foldamer-Based Chiroptical Molecular Switch That Displays Complete Inversion of the Helical Sense upon Anion Binding, J. Am. Chem. Soc., 2011, 133, 13938–13941 CrossRef CAS PubMed.
- Y. Liu, F. C. Parks, W. Zhao and A. H. Flood, Sequence-Controlled Stimuli-Responsive Single–Double Helix Conversion between 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Chloride-Foldamer Complexes, J. Am. Chem. Soc., 2018, 140, 15477–15486 CrossRef CAS PubMed.
2 Chloride-Foldamer Complexes, J. Am. Chem. Soc., 2018, 140, 15477–15486 CrossRef CAS PubMed. - S. B. Seo, S. Lee, H.-G. Jeon and K.-S. Jeong, Dramatic Enhancement of Binding Affinities Between Foldamer-Based Receptors and Anions by Intra-Receptor π-Stacking, Angew. Chem., Int. Ed., 2020, 59, 10441–10445 CrossRef CAS PubMed.
- S. Y. L. Leung, A. Y. Y. Tam, C. H. Tao, H. S. Chow and V. W. W. Yam, Single-Turn Helix–Coil Strands Stabilized by Metal⋯Metal and π–π Interactions of the Alkynylplatinum(II) Terpyridyl Moieties in meta-Phenylene Ethynylene Foldamers, J. Am. Chem. Soc., 2012, 134, 1047–1056 CrossRef CAS PubMed.
- M. H. Y. Chan, S. Y. L. Leung and V. W. W. Yam, Rational Design of Multi-Stimuli-Responsive Scaffolds: Synthesis of Luminescent Oligo(ethynylpyridine)-Containing Alkynylplatinum(II) Polypyridine Foldamers Stabilized by Pt⋯Pt Interactions, J. Am. Chem. Soc., 2019, 141, 12312–12321 CrossRef CAS PubMed.
- H.-G. Jeon, J. Y. Jung, P. Kang, M.-G. Choi and K.-S. Jeong, Folding-Generated Molecular Tubes Containing One-Dimensional Water Chains, J. Am. Chem. Soc., 2016, 138, 92–95 CrossRef CAS PubMed.
- H. Zhao, S. Sheng, Y. Hong and H. Zeng, Proton Gradient-Induced Water Transport Mediated by Water Wires Inside Narrow Aquapores of Aquafoldamer Molecules, J. Am. Chem. Soc., 2014, 136, 14270–14276 CrossRef CAS PubMed.
- J. Kim, H.-G. Jeon, P. Kang and K.-S. Jeong, Stereospecific control of the helical orientation of indolocarbazole–pyridine hybrid foldamers by rational modification of terminal chiral appendages, Chem. Commun., 2017, 53, 6508–6511 RSC.
- H. B. Jang, Y. R. Choi and K.-S. Jeong, Matched and Mismatched Phenomena in the Helix Orientation Bias Induced by Chiral Appendages at Multiple Positions of Indolocarbazole-Pyridine Hybrid Foldamers, J. Org. Chem., 2018, 83, 5123–5131 CrossRef CAS PubMed.
- M. Woźny, J. Pawłowska, A. Osior, P. Świder, R. Bilewicz and B. Korybut-Daszkiewicz, An electrochemically switchable foldamer – a surprising feature of a rotaxane with equivalent stations, Chem. Sci., 2014, 5, 2836–2842 RSC.
- F. Zhang, S. Bai, G. P. A. Yap, V. Tarwade and J. M. Fox, Abiotic metallofoldamers as electrochemically responsive molecules, J. Am. Chem. Soc., 2005, 127, 10590–10599 CrossRef CAS PubMed.
- M. S. Gin, T. Yokozawa, R. B. Prince and J. S. Moore, Helical Bias in Solvophobically Folded Oligo(Phenylene Ethynylene)s, J. Am. Chem. Soc., 1999, 121, 2643–2644 CrossRef CAS.
- M. T. Stone, J. M. Fox and J. S. Moore, A Helicene-Containing Foldamer Displaying Highly Solvent-Dependent CD Spectra, Org. Lett., 2004, 6, 3317–3320 CrossRef CAS PubMed.
- M. S. Gin and J. S. Moore, Helical Twist Sense Bias in Oligo(phenylene ethynylene)s Induced by an Optically Active Flexible Tether, Org. Lett., 2000, 2, 135–138 CrossRef CAS PubMed.
- K. Goto and J. S. Moore, Sequence-Specific Binding of m-Phenylene Ethynylene Foldamers to a Piperazinium Dihydrochloride Salt, Org. Lett., 2005, 7, 1683–1686 CrossRef CAS PubMed.
- B. A. F. Le Bailly and J. Clayden, Dynamic foldamer chemistry, Chem. Commun., 2016, 52, 4852–4863 RSC.
- S. M. Morrow, A. J. Bissette and S. P. Fletcher, Transmission of chirality through space and across length scales, Nat. Nanotechnol., 2017, 12, 410–419 CrossRef CAS PubMed.
- D. P. Iwaniuk and C. Wolf, A stereodynamic probe providing a chiroptical response to substrate-controlled induction of an axially chiral arylacetylene framework, J. Am. Chem. Soc., 2011, 133, 2414–2417 CrossRef CAS PubMed.
- Z. A. De los Santos, G. Yusin and C. Wolf, Enantioselective sensing of carboxylic acids with a bis (urea) oligo (phenylene) ethynylene foldamer, Tetrahedron, 2019, 75, 1504–1509 CrossRef CAS.
- Y. Shi, G. Yin, Z. Yan, P. Sang, M. Wang, R. Brzozowski, P. Eswara, L. Wojtas, Y. Zheng and X. Li, et al., Helical Sulfono-γ-AApeptides with Aggregation-Induced Emission and Circularly Polarized Luminescence, J. Am. Chem. Soc., 2019, 141, 12697–12706 CrossRef CAS PubMed.
- D. Zheng, L. Zheng, C. Yu, Y. Zhan, Y. Wang and H. Jiang, Significant enhancement of circularly polarized luminescence dissymmetry factors in quinoline oligoamide foldamers with absolute helicity, Org. Lett., 2019, 21, 2555–2559 CrossRef CAS PubMed.
- E. Merlet, K. Moreno, A. Tron, N. McClenaghan, B. Kauffmann, Y. Ferrand and C. Olivier, Aromatic oligoamide foldamers as versatile scaffolds for induced circularly polarized luminescence at adjustable wavelengths, Chem. Commun., 2019, 55, 9825–9828 RSC.
- P. Reiné, A. M. Ortuño, S. Resa, L. Álvarez de Cienfuegos, V. Blanco, M. J. Ruedas-Rama, G. Mazzeo, S. Abbate, A. Lucotti, M. Tommasini, S. Guisán-Ceinos, M. Ribagorda, A. G. Campaña, A. J. Mota, G. Longhi, D. Miguel and J. M. Cuerva, OFF/ON switching of circularly polarized luminescence by oxophilic interaction of homochiral sulfoxide-containing o-OPEs with metal cations, Chem. Commun., 2018, 54, 13985–13988 RSC.
- P. Reiné, J. Justicia, S. P. Morcillo, S. Abbate, B. Vaz, M. Ribagorda, A. Orte, L. Álvarez de Cienfuegos, G. Longhi, A. G. Campaña, D. Miguel and J. M. Cuerva, Pyrene-Containing ortho-Oligo(phenylene)ethynylene Foldamer as a Ratiometric Probe Based on Circularly Polarized Luminescence, J. Org. Chem., 2018, 83, 4455–4463 CrossRef PubMed.
- T. V. Jones, M. M. Slutsky, R. Laos, T. F. A. de Greef and G. N. Tew, Solution 1H NMR Confirmation of Folding in Short o-Phenylene Ethynylene Oligomers, J. Am. Chem. Soc., 2005, 127, 17235–17240 CrossRef CAS PubMed.
- R. A. Blatchly and G. N. Tew, Theoretical study of helix formation in substituted phenylene ethynylene oligomers, J. Org. Chem., 2003, 68, 8780–8785 CrossRef CAS PubMed.
- M. M. Slutsky, T. V. Jones and G. N. Tew, Spin System Assignment of Homo-o-Phenylene Ethynylene Oligomers, J. Org. Chem., 2007, 72, 342–347 CrossRef CAS PubMed.
- M.-X. Zhu, W. Lu, N. Zhu and C.-M. Che, Structures and Solvatochromic Phosphorescence of Dicationic Terpyridyl–Platinum(II) Complexes with Foldable Oligo(ortho–phenyleneethynylene) Bridging Ligands, Chem. – Eur. J., 2008, 14, 9736–9746 CrossRef CAS PubMed.
- Y.-T. Shen, N. Zhu, X.-M. Zhang, K. Deng, W. Feng, Q. Yan, S. Lei, D. Zhao, Q.-D. Zeng and C. A. Wang, A foldamer at the liquid/graphite interface: The effect of interfacial interactions, solvent, concentration, and temperature, Chem. – Eur. J., 2011, 17, 7061–7068 CrossRef CAS PubMed.
- S. Resa, D. Miguel, S. Guisán-Ceinos, G. Mazzeo, D. Choquesillo-Lazarte, S. Abbate, L. Crovetto, D. J. Cárdenas, M. C. Carreño, M. Ribagorda, G. Longhi, A. J. Mota, L. Álvarez de Cienfuegos and J. M. Cuerva, Sulfoxide–Induced Homochiral Folding of ortho–Phenylene Ethynylenes (o–OPEs) by Silver(I) Templating: Structure and Chiroptical Properties, Chem. – Eur. J., 2018, 24, 2653–2662 CrossRef CAS PubMed.
- S. Resa, P. Reiné, L. Álvarez de Cienfuegos, S. Guisán-Ceinos, M. Ribagorda, G. Longhi, G. Mazzeo, S. Abbate, A. J. Mota, D. Miguel and J. M. Cuerva, Optically active Ag (i): o-OPE helicates using a single homochiral sulfoxide as chiral inducer, Org. Biomol. Chem., 2019, 17, 8425–8434 RSC.
- S. P. Morcillo, D. Miguel, L. Álvarez de Cienfuegos, J. Justicia, S. Abbate, E. Castiglioni, C. Bour, M. Ribagorda, D. J. Cárdenas, J. M. Paredes, L. Crovetto, D. Choquesillo-Lazarte, A. J. Mota, M. C. Carreño, G. Longhi and J. M. Cuerva, Stapled helical o-OPE foldamers as new circularly polarized luminescence emitters based on carbophilic interactions with Ag(I)-sensitivity, Chem. Sci., 2016, 7, 5663–5670 RSC.
- N. Fuentes, A. Martin-Lasanta, L. Alvarez de Cienfuegos, R. Robles, D. Choquesillo-Lazarte, J. M. García-Ruiz, L. Martínez-Fernández, I. Corral, M. Ribagorda and A. J. Mota, et al., Versatile Bottom–up Approach to Stapled π–Conjugated Helical Scaffolds: Synthesis and Chiroptical Properties of Cyclic o–Phenylene Ethynylene Oligomers, Angew. Chem., Int. Ed., 2012, 51, 13036–13040 CrossRef CAS PubMed.
- P. Reiné, J. Justicia, S. P. Morcillo, G. Mazzeo, E. García-Fernández, A. Rodríguez-Diéguez, L. Álvarez de Cienfuegos, S. Abbate, J. M. Cuerva and G. Longhi, et al., Exploring potentialities and limitations of stapled o–oligo(phenyleneethynylene)s (o–OPEs) as efficient circularly polarized luminescence emitters, Chirality, 2018, 30, 43–54 CrossRef PubMed.
- P. Reiné, A. G. Campaña, L. Alvarez de Cienfuegos, V. Blanco, S. Abbate, A. J. Mota, G. Longhi, D. Miguel and J. M. Cuerva, Chiral double stapled o-OPEs with intense circularly polarized luminescence, Chem. Commun., 2019, 55, 10685–10688 RSC.
- For other extended aromatic systems with four loops/turns in a racemic form, see: C. Tie, J. C. Gallucci and J. R. Parquette, Helical Conformational Dynamics and Photoisomerism of Alternating Pyridinedicarboxamide/m-(Phenylazo)azobenzene Oligomers, J. Am. Chem. Soc., 2006, 128, 1162–1171 CrossRef CAS PubMed.
- B. P. Bloom, B. M. Graff, S. Ghosh, D. N. Beratan and D. H. Waldeck, Chirality control of electron transfer in quantum dot assemblies, J. Am. Chem. Soc., 2017, 139, 9038–9043 CrossRef CAS PubMed.
- W. Gerlach and O. Stern, Der experimentelle nachweis der richtungsquantelung im magnetfeld, Z. Phys., 1922, 9, 349–352 CrossRef CAS; W. Gerlach and O. Stern, Der experimentelle nachweis der richtungsquantelung im magnetfeld, Z. Phys., 1922, 9, 353–355 CrossRef.
- M. Kohda, S. Nakamura, Y. Nishihara, K. Kobayashi, T. Ono, J. Ohe, Y. Tokura, T. Mineno and J. Nitta, Spin–orbit induced electronic spin separation in semiconductor nanostructures, Nat. Commun., 2012, 3, 1082 CrossRef PubMed.
- R. Naaman, Y. Patiel and D. H. Waldeck, Chiral molecules and the electron spin, Nat. Rev. Chem., 2019, 3, 250–260 CrossRef CAS.
- M. Inouye, M. Waki and H. Abe, Saccharide-dependent induction of chiral helicity in achiral synthetic hydrogen-bonding oligomers, J. Am. Chem. Soc., 2004, 126, 2022–2027 CrossRef CAS PubMed.
- M. Ohkita, J.-M. Lehn, G. Baum and D. Fenske, Helicity Coding Programmed Molecular Self-Organization of Achiral Nonbiological Strands Into Multiturn Helical Superstructures: Synthesis and Characterization of Alternating Pyridine-Pyrimidine Oligomers, Chem. – Eur. J., 1999, 5, 3471–3481 CrossRef CAS.
- C. Zhang, J. Tian, S. Qi, B. Yang and Z. Dong, Highly Efficient Exclusion of Alkali Metal Ions via Electrostatic Repulsion Inside Positively Charged Channels, Nano Lett., 2020, 3627–3632 CrossRef CAS PubMed.
- Oxa[9]-helicene: M. Sako, Y. Takeuchi, T. Tsujihara, J. Kodera, T. Kawano, S. Takizawa and H. Sasai, Efficient enantioselective synthesis of oxahelicenes using redox/acid cooperative catalysts, J. Am. Chem. Soc., 2016, 138, 11481–11484 CrossRef CAS PubMed.
- In CH2Cl2 the folded structure is populated at 76%, in acetonitrile at 82% considering energy Boltzmann weights. Gibbs free energy gives a lower population for the folded structures; however, the flexibility of the diphenylacetylene moieties makes it difficult to correctly evaluate the entropic contribution.
- R. Naaman, Y. Patiel and D. H. Waldeck, Chiral molecules and the spin selectivity effect, J. Phys. Chem. Lett., 2020, 11, 3660–3666 CrossRef CAS PubMed.
- H. Kubo, T. Hirose, T. Nakashima, T. Kawai, J.-Y. Hasegawa and K. Matsuda, Tuning Transition Electric and Magnetic Dipole Moments:[7] Helicenes Showing Intense Circularly Polarized Luminescence, J. Phys. Chem. Lett., 2021, 12, 686–695 CrossRef CAS PubMed.
- H. Kubo, D. Shimizu, T. Hirose and K. Matsuda, Circularly Polarized Luminescence Designed from Molecular Orbitals: A Figure-Eight-Shaped [5]Helicene Dimer with D2 Symmetry, Org. Lett., 2020, 23, 9276–9281 CrossRef CAS PubMed; K. Dhbaibi, L. Abella, S. Meunier-Gatta, T. Roisnel, N. Vanthuyne, B. Jamoussi, G. Pieters, B. Racine, E. Quesnel, J. Ausschbach, J. Crassous and L. Favereau, Achieving high circularly polarized luminescence with push–pull helicenic systems: from rationalized design to top-emission CP-OLED applications, Chem. Sci., 2021, 12, 5522–5533 RSC; Y. Nojima, M. Hasegawa, N. Hara, Y. Imai and Y. Mazaki, Small Figure-Eight Luminophores: Double-Twisted Tethered Cyclic Binaphthyls Boost Circularly Polarized Luminescence, Chem. – Eur. J., 2021, 27, 5923–5929 CrossRef PubMed.
- S. S. Andrews and J. Tretton, Physical Principles of Circular Dichroism, J. Chem. Educ., 2020, 97, 4370–4376 CrossRef CAS.
- B. Göhler, V. Hamelbeck, T. Z. Markus, M. Kettner, G. F. Hanne, Z. Vager, R. Naaman and H. Zacharias, Spin Selectivity in Electron Transmission Through Self-Assembled Monolayers of Double-Stranded DNA, Science, 2011, 6019, 894–897 CrossRef PubMed.
- E. Medina, F. López, M. A. Ratner and V. Mujica, Chiral molecular films as electron polarizers and polarization modulators, EPL, 2012, 99, 17006 CrossRef.
- Y. Nakai, T. Mori and Y. Inoue, Theoretical and Experimental Studies on Circular Dichroism of Carbo[n]helicenes, J. Phys. Chem. A, 2012, 27, 7372–7385 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures and tables referred to in the main text, the experimental details for NMR, IR, ECD, CPL and VCD measurements, the details of the conformational analysis, the computational aspects of the spectral calculations and data treatment. CCDC 2073558. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1qo00822f |
| This journal is © the Partner Organisations 2021 |