Design principles of noble metal-free electrocatalysts for hydrogen production in alkaline media: combining theory and experiment

Abstract

Water electrolysis is a promising solution to convert renewable energy sources to hydrogen as a high-energy-density energy carrier. Although alkaline conditions extend the scope of electrocatalysts beyond precious metal-based materials to earth-abundant materials, the sluggish kinetics of cathodic and anodic reactions (hydrogen and oxygen evolution reactions, respectively) impede the development of practical electrocatalysts that do not use precious metals. This review discusses the rational design of efficient electrocatalysts by exploiting the understanding of alkaline hydrogen evolution reaction and oxygen evolution reaction mechanisms and of the electron structure–activity relationship, as achieved by combining experimental and computational approaches. The enhancement of water splitting not only deals with intrinsic catalytic activity but also includes the aspect of electrical conductivity and stability. Future perspectives to increase the synergy between theory and experiment are also proposed.

---

1. Introduction

Clean energy transitions to replace traditional carbon sources are being sought to mitigate fossil-fuel depletion, carbon emissions and environmental pollution.^1,2 Conversion and storage of sustainable energy such as wind or solar energy to hydrogen as an energy-dense carrier has been advocated as a promising solution.³ Electrochemical water splitting (2H₂O → 2H₂ + O₂) has been accepted as a potential hydrogen-production technology, due to the availability of water as a reactant, and stable output efficiency.^4–8 It avoids emission of huge amounts of carbon dioxide and does not exacerbate fossil-fuel depletion, which are two major objections to conventional steam reforming of natural gas to yield hydrogen.⁹

Water electrolysis consists of the hydrogen evolution reaction (HER; water reduction to hydrogen gas) as a cathodic half-reaction and the oxygen evolution reaction (OER; water oxidation to oxygen gas) as an anodic half-reaction. The thermodynamic potential requirement for splitting water into hydrogen and oxygen is theoretically 1.23 V vs. standard hydrogen electrode (SHE) under the standard conditions, but it always takes more energy (overpotential) than this in practice. To minimize the overpotential requirement and achieve efficient water electrolysis, it should be conducted in either a highly acidic medium or a highly alkaline medium.^10–12 Acid electrolysis is usually performed using a proton exchange membrane (PEM), and has the advantages of high energy efficiency and fast hydrogen production rate, but uses expensive noble-metal electrocatalysts. Promising and relatively inexpensive transition metal oxides (TMOs) for OER catalysts mostly suffer from serious instability such as decomposition and metal dissolution in acidic and strongly oxidative environments at high operation voltages.¹³ Alkaline electrolysis overcomes some of these instability problems and extends the scope of electrocatalysts to earth-abundant materials.^14,15 However, the alkaline medium of water splitting causes slow HER kinetics due to the low proton concentration.^16–19 Therefore, increase of both activity and stability in alkaline media for the OER and HER has been huge research topics in electrochemistry.

To obtain an economically viable alkaline electrolyzer, the first choice should be to replace noble metal-based catalysts (Pt/C, IrO₂) with inexpensive, earth-abundant metal-based catalysts, given that catalysts account for a large portion of the stack price.²⁰ Although water electrolysis is considered a promising hydrogen-production method, the sluggish OER kinetics at the anode and sluggish HER kinetics at the cathode under alkaline conditions remain primary impediments to the development of low-cost electrocatalysts.^21,22 Emerging materials based on earth-abundant transition metal (TM) elements have been evaluated for the alkaline HER and OER, and if applicable can solve the long-standing problem of low price efficiency. TMs and TM alloys have been widely studied theoretically and experimentally as HER catalysts.^23–25 Emerging TM materials with ligands such as sulfides,^26–32 phosphides,^33–37,43 carbides,^38–42 and hydroxides^44–47 have been extensively investigated owing to their high activity comparable to noble metal-based catalysts.

For the OER, substantial research efforts have been devoted to investigating the activity of TMO catalysts that use perovskites,^48–51 spinels,^52–56 layered oxides including hydr(oxy)oxides^44,57–60 and other types of oxides^61–65 owing to their low cost, easy synthesizability, rich selection of structural combinations, and environmentally benign nature. Furthermore, they are stable in alkaline solution and have moderate conductivities, which make them good candidates for the electrocatalytic OER. Non-oxide catalysts like metal chalcogenides that include sulfides,^66–69 selenides,^70–73 and carbides^74–77 have also been reported as promising electrocatalytic materials for the alkaline OER.

For these emerging materials to be widely accepted and further developed, the atomic-level mechanisms of catalysis must be understood and exploited. These mechanisms can be identified using interdisciplinary theoretical methods and high-resolution characterization and imaging techniques. Computational simulations that use density functional theory (DFT) have illuminated the intrinsic properties of catalysts by observing the properties of transition states and reaction intermediates, and have provided insights that enable rational design of catalysts.⁷⁸ The simulations provide the interaction energies of atoms or molecules on a catalytic surface with sufficient accuracy, and thereby provide thermodynamic data for the targeted reaction. The nudged elastic band (NEB) method enables identification of the minimum-energy path (MEP) for a given chemical process if both the initial and final states are known, and provides kinetic data.⁷⁹ DFT calculations can also investigate the charge distribution and electronic structure of catalyst systems, whereas such information is not easily obtained experimentally.⁸⁰ Finding the relationship between the thermodynamic properties of catalysts and their electronic structural properties is an important step in increasing the performance of catalysts. By exploiting a deep understanding of material properties at the atomic scale, a combination of theoretical approaches with experimental methods has been successfully implemented to study catalytic activity, search for new material combinations, and eliminate inefficient trial-and-error searches. In addition, computer speed and memory are being increased rapidly, so high-throughput screening of material search spaces is being performed extensively by considering the accumulated knowledge about activity descriptors.

The blooming of the massive ab initio calculation database has opened up a new possibility of exploring the limitless material search space by means of machine learning (ML) techniques. Recently, ML-based high-throughput screening studies have successfully discovered a large number of new catalysts for the HER¹¹⁴ and OER.¹⁴⁶ Furthermore, ML approaches have expanded our understanding on the physical nature of catalytic materials for water splitting, igniting the huge research interest of data-driven ML studies in the materials design field.

Several great review articles have covered the HER, OER, and overall water splitting catalysis, but a comprehensive theory-specialized perspective on the topic is missing. Two reviews^18,81 have considered only one side of the water-splitting electrode. Many other researchers focused on specific materials such as homogeneous Co catalysts,^82,83 heterogeneous Ni catalysts,⁸⁴ borides and sulfides,⁸⁵ specific morphology (low dimensional (1D/2D) and single/double atomic coordination),^86,87 precious metals,⁸⁸ photocatalysis,⁸⁹ or bifunctional catalysts.⁹⁰ Some other reviews have focused on specific design strategies such as support, interface and strain engineering.^91,92 Here, we will consider the specificity of alkaline media while addressing a universal strategy to develop cost-efficient catalysts.

This review looks at recent progress towards overcoming the slow kinetics of the HER and OER under alkaline conditions, by combining computation and experimentation. First, several powerful descriptors for the HER and OER are introduced, focusing on the strategies to which the descriptors are applied in rational design to increase intrinsic catalytic activity. For the HER, hydrogen-binding strength has been a widely applied descriptor that can be tuned by electronic structure engineering, various nano-structuring concepts, and new active materials identified using machine learning. Several influential papers regarding the water dissociation barrier descriptor are highlighted, as a result of their efforts to increase the understanding and ability to manipulate the descriptor. The function of promoter species in the electrolyte is highlighted with important theoretical and experimental findings. For the OER, the descriptors for determining the two major mechanisms, i.e., the adsorbate-evolution mechanism (AEM) and lattice-oxygen oxidation mechanism (LOM), are introduced; oxygen vacancy formation energy, electron donating ability of B cations in the ABO₃ perovskites, oxygen 2p-band center (O_p) and metal 3d-band center (M_d). In the AEM, several activity determining descriptors such as the Gibbs free energy difference of adsorbed O and OH intermediates (ΔG_O − ΔG_OH) and electronic structural descriptors including e_g orbital occupancy, metal–oxygen covalency, and number of excess electrons (NEE) are explored. In the case of LOM, metal–oxygen covalency, oxygen anion and vacancy diffusion are discussed experimentally and computationally, with practical examples. Although the alkaline environment generally provides better catalyst stability than the acidic environment, the stability issues still exist under alkaline conditions and have not yet been completely elucidated. The stability and electrical conductivity of the materials are summarized comprehensively. The relationships among stability, conductivity and activity are reviewed, considering several strategies to increase the stability and the electrical conductivity.

We hope our review broadens the design principles of inexpensive catalysts for alkaline water splitting reactions by combining theory and experiment, and that it extends insight into the hydrogen oxidation and oxygen reduction reactions (HOR/ORR), which share similar intermediates with the HER and OER, and CO₂ and NO_x reduction that involves water dissociation reactions similar to those in the alkaline HER. We will also cover important experimental and computational considerations of alkaline media, so our design principles may also be applicable to other alkaline environmental reactions.

2. Alkaline hydrogen evolution reaction

2.1. HER mechanism under alkaline conditions

The HER under alkaline conditions involves water dissociation and coupling of hydrogen atoms. The general consensus on the mechanism has been well established to occur in two sequential steps; first, the water dissociation step occurs:

H₂O + e⁻ → H* + OH⁻ (Volmer step, 120 mV dec⁻¹),

then the hydrogen evolution step occurs

H₂O + H* + e⁻ → H_2(g) + OH⁻ (Heyrovsky step, 40 mV dec⁻¹),

or

H* + H* → H_2(g) (Tafel step, 30 mV dec⁻¹)

The protons under the alkaline conditions are obtained by the Volmer reaction, which dissociates water molecules. These hydrogen atoms then recombine by either the Heyrovsky recombination reaction or the Tafel recombination reaction. For those two steps, hydrogen binding energy (HBE) is a determinant in predicting the reaction rate of the HER. Under acidic conditions, the H atom is the sole intermediate of the HER, so the HBE determines the HER activity, following the Sabatier principle that the key intermediate should have modest binding strength, neither strong nor weak. Strong binding of the catalyst to the H hinders the hydrogen desorption in the subsequent Tafel or Heyrovsky steps; weak binding hinders the Volmer step.

Despite the successful implementation of the HBE descriptor in acidic media, HBE could not solely explain the HER under alkaline conditions due to the complexity of the reaction environments. Long-standing debates have been conducted on the much lower HER activity in alkaline than in acidic media for the state-of-the-art Pt and Au catalysts (Fig. 1a).⁹³ Although the HER mechanism under alkaline conditions is still elusive, many researchers consider that the Volmer step is the activity-limiting reaction, in which excess energy is required to overcome the high water dissociation barrier. The Markovic group have reported a series of results which implied that the water dissociation is a key step which actually limits HER kinetics.⁴⁶ Oxophilic sites such as Ni(OH)₂ can accelerate the water dissociation, increasing the HER activity three to five times under alkaline conditions, so it may serve as the active site for the water dissociation step (Fig. 1b). Therefore, along with HBE, other important descriptors have been highlighted including hydroxyl binding energy (OHBE), water dissociation barrier, solvated electrolyte cations, chemical dynamics in the double layer and co-adsorbed spectator species.

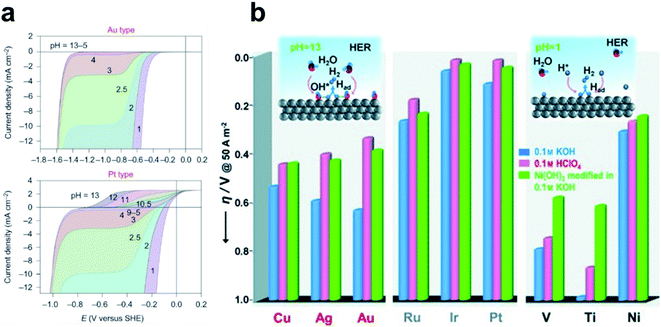Fig. 1 (a) pH-dependent current–potential polarization curves at rotation rates of 1600 rpm and sweep rate of 50 mV s⁻¹ for Au(111) and Pt(111). Reproduced from ref. 93 Copyright 2013, Springer Nature. (b) Overpotential η required for a 5 mA cm⁻² current density, in 0.1 M HClO₄ and 0.1 M KOH for bare metal surfaces (Cu, Ag, Au, Ru, Ir, Pt, V, Ti and Ni) and Ni(OH)₂-modified surfaces. Reproduced from ref. 46. Copyright 2012, Wiley.

First, HBE as a practical descriptor under alkaline conditions will be discussed in Section 2.2, focusing on four aspects: (1) the volcano relationship between HBE and alkaline HER activity, (2) the linear relationship between HBE and the electronic structure, (3) nano-structuring of materials towards the optimal HBE, and (4) machine learning approaches towards the optimal HBE. Then, the importance of the water dissociation barrier, OHBE, and ‘dual active site’ strategy in the alkaline HER will be covered in Section 2.3. Finally, the role of electrolyte species will be discussed in Section 2.4, and conductivity issues will be covered in Section 2.5.

2.2. Hydrogen binding

2.2.1. Volcano activity relationship. HBE has been widely accepted as the most important single descriptor to predict HER activity under acidic conditions, because the optimal HBE dictates the thermodynamics of hydrogen coupling and desorption reaction. Thus, classical efforts of theorists in the field mostly focused on the HBE to identify the HER activity. The Nørskov group has proposed a theoretical framework that a simple hydrogen adsorption calculation can be used to understand the trend in the acidic HER exchange current density.⁹⁴ They found that the Pt positioned near the apex of a volcano-like relationship under acidic conditions when the HBE was used as a descriptor.

Although many other influential factors such as OHBE, water dissociation barrier, and electrolyte dynamics should be considered to obtain a complete picture of HER kinetics under alkaline conditions, the HBE is still widely used as a HER activity descriptor under alkaline conditions due to its practicality. Sheng et al. provided important experimental evidence that the HER under alkaline conditions follows the HBE trend by performing the fundamental study of combining theoretical HBE calculation and the exchange current density measurement (Fig. 2a).⁹⁵ Their results also demonstrated that HBE and current density have the volcano relationship under both acidic and alkaline conditions. A follow-up study that also combined theory and experiment⁹⁶ showed that HBE was correlated well with current density, and overpotential in universal pH. Durst et al. reached a similar conclusion that the HBE serves as a powerful descriptor of the HER under alkaline conditions by conducting control experiments using platinum-group metals.⁹⁷ In addition, several reports have successfully described the high alkaline HER activity of carbides and selenides using HBE as a single descriptor. Vrubel et al. found that Mo₂C shows excellent activity and stability under both alkaline and acidic conditions comparable to that of the Pt/C catalyst, which was confirmed by the optimal HBE.¹⁰⁴ The HBEs of monometallic carbide surfaces have been evaluated by DFT calculations in low-coverage and high-coverage carbide systems, which showed a clear correlation between HBE and exchange current density under the alkaline conditions.¹⁰⁷ Zheng et al. synthesized a phase controlled CoSe₂ by modifying the d-electron states of the Co atoms via P doping, hence optimizing the HBE in alkaline solution.¹¹⁰

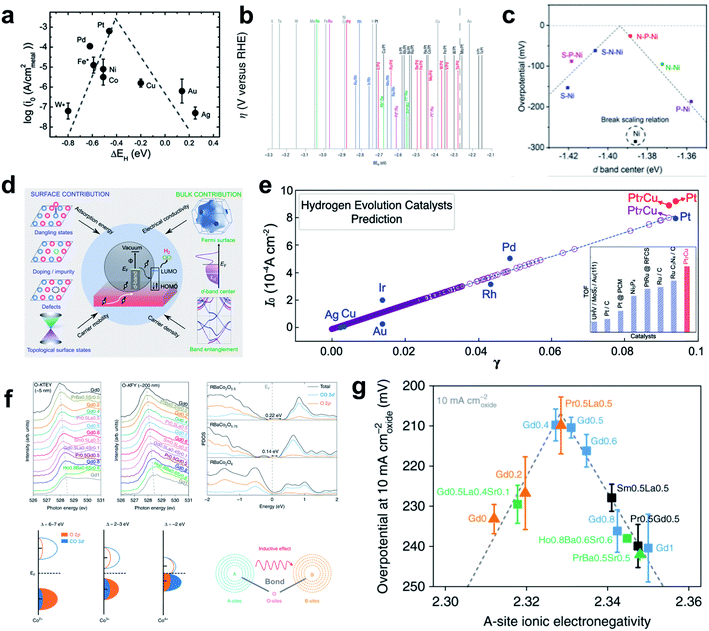Fig. 2 (a) Exchange current density as a function of HBE. Reproduced from ref. 95. Copyright 2013, Royal Society of Chemistry. (b) Overpotential as a function of HBE. Reproduced from ref. 100. Copyright 2004, Springer Nature. (c) Overpotential as a function of the d-band center of the heteroatom doped Ni catalyst. Reproduced from ref. 101. Copyright 2019, American Chemical Society. (d) Schematic of the electronic properties considered; electronic conductivity, carrier density, carrier mobility and adsorption energy. (e) Exchange-current density as a function of PBP. Reproduced from ref. 102. Copyright 2020, American Chemical Society. (f) Soft XAS spectra at the O–K edge collected in TEY mode, FY modes, PDOS calculations of Co 3d and O 2p orbitals for three perovskites, charge-transfer models of Co²⁺, Co³⁺, and Co⁴⁺ in covalent systems. (g) Inductive effects and electron exchange interactions between A-sites and B-sites in perovskite overpotential at 10 mA cm⁻² as a function of A-site ionic electronegativity. Reproduced from ref. 103. Copyright 2019, Springer Nature.

2.2.2. Electronic structure. The atomic binding energies are widely associated with the electronic structure of the surface atoms, as the electronic structure of the catalyst surface affects the binding strengths of the adsorbates.^98,99 As a result, adjusting the electrical structure by alloying, doping, and phase transition is a common strategy for the material design. Three descriptors for the electronic structure will be explored in this section: d-band center, projected berry phase, and electronegativity. The HBE is linearly correlated with the d-band level of the materials, which represents their bonding and anti-bonding occupancy. The antibonding orbitals would be less occupied if the antibonding band position is high, where the d-band center position is high. Therefore, the adsorbate binding strength increases as the surface's d-band center upshifts relative to the E_f. For a material with a high d-band position, such as Ru_hcp, the hydrogen binding is too strong to be thermodynamically favorable for the H* desorption process. On the other hand, a material with a low d-band position relative to E_f, such as Pt, generally has a weak hydrogen adsorption strength, and thus the HER could be limited by the hydrogen binding process. A series of studies conducted by Greeley et al. revealed principles to design metal-alloy catalysts for hydrogen production and hydrogen utilization (Fig. 2b);¹⁰⁰ the d-band center position relative to the Fermi level shows a strong correlation with hydrogen bonding, and this correlation suggests that the electronic structure of the materials dictates the HBE. A follow-up study²⁴ identified 15 candidates from 736 materials by considering stability factors such as segregation and islanding. These studies have provided a general guideline that theorists can use to design materials by considering the electronic structure, and suggested many candidates that experimental researchers can test. Heteroatom doping can be used to finely control the electronic structure of the surface, which can optimize the HBE of the materials. Jin et al. found that nitrogen and phosphorus dual doping on a nickel catalyst can induce a charge distribution in the metal and yield optimized HBE (Fig. 2c).¹⁰¹

Xu et al. found that the ‘projected berry phase’ (PBP) value, which depends solely on the topological structure and electronic structure, has a good linear relationship with HER exchange current density (Fig. 2d and e).¹⁰² They found that the PBP descriptor is linearly correlated with the HBE, electronic structure, work function, Fermi level and d-band center model. To test the idea, and to apply the strategy in practical search for an HER material, they considered the PBP to select Pt₇Cu model catalyst, and synthesized it. It showed superior HER activity, and thereby confirmed the relationship between the electronic structure and HBE.

Tuning the A site ionic electronegativity (AIE) of perovskite materials¹⁰³ is a good example of a rational strategy suggested by Shao and coworkers to design novel materials by optimizing the electronic structure. Comparison of cobalt-containing single perovskites ABO_3−δ and a double perovskite family AA′B₂O_6−δ. (A′  = lanthanide) showed a solid volcano relationship between AIE and the HER activity (Fig. 2f and g). They found that a material with AIE = ∼2.33 would have better catalytic activity than Pt/C; measurements using (Gd_0.5La_0.5)BaCo₂O_5.5+δ confirmed this prediction.

Despite some studies that questioned the ability of the electronic structure to serve as a universal descriptor,⁴⁴ this approach has been effective in providing an important physical background for materials design and enabling a direct correlation between catalytic activity and surface electronic properties.

2.2.3. Nano-structuring. Materials that have similar electronic structures to those of platinum and other noble metals may have comparable catalytic activity. Carbides have been spotlighted as they have a similar electronic structure to platinum. Vrubel et al. found that molybdenum carbides and borides show remarkable performance comparable to that of the Pt/C catalyst.¹⁰⁴ Mo₂C showed excellent activity and stability under both alkaline and acidic conditions. Doping and heterostructuring have arisen as general strategies to optimize the HBE by tuning the electronic structure of the materials. Liu et al. found that nitrogen atom doping in the Mo–C lattice induces a special electron transfer (Mo₂C → C → N), which helps the C atoms to act as both electron acceptor and donor.¹⁰⁵ The catalytic activity of the cobalt-doped Mo₂C catalyst was further increased by hetero-structuring with N doped CNTs, and achieved overpotential (η₁₀) = 170 mV, and stable current density.¹⁰⁶

Monometallic carbide surfaces have been evaluated by using DFT to investigate the HBE in low-coverage and high-coverage carbide systems.¹⁰⁷ Analysis results identified carbides that maximize the HER; when synthesized, they showed a clear correlation between the adsorption free energy of H (ΔG_H) and exchange current density concluding that HBE is a useful guideline for HER activity in predicting carbide activity under the alkaline conditions. In addition, the coverage dependent ΔG_H implied that the surface coverage effects are three times more sensitive on the carbide system than on the pure-metal system. This result may suggest a viable design strategy to optimize the HBE on carbide and similar systems (Fig. 3a and b).

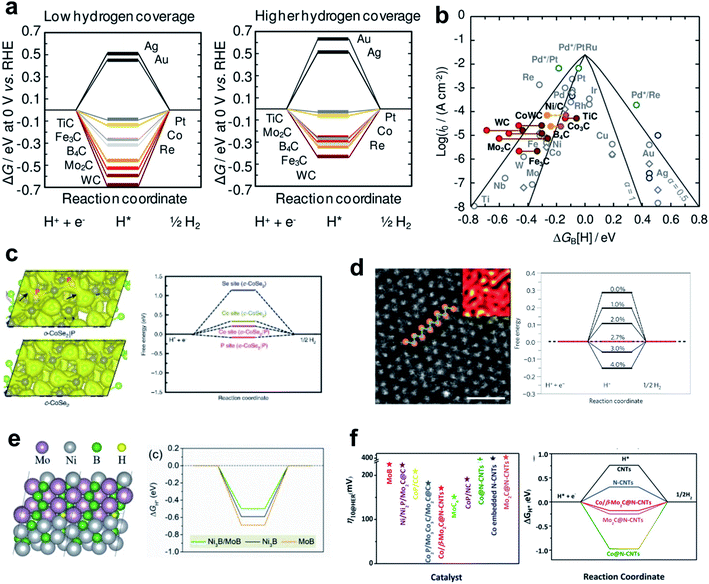Fig. 3 (a) Free-energy diagrams for the electrochemical reduction of H⁺ in 1/4 ML coverage and 1/2 ML coverage. (b) Volcano plot for the HER on polycrystalline (gray circles) or single-crystal (dark blue circles) TMs (1/4 ML H*). Reproduced from ref. 107. Copyright 2014, American Chemical Society. (c). Calculated charge density distribution for o-CoSe₂|P and free energy diagrams for hydrogen adsorption. Reproduced from ref. 110. Copyright 2018, Springer Nature. (d) High-resolution STEM images of an as-exfoliated WS₂ monolayer 1T superlattice and the free energy diagram of H⁺ adsorption. Reproduced from ref. 111. Copyright 2013, Springer Nature. (e) H* adsorbed on the Ni₃B/MoB heterosturcture; free-energy diagram (at U = 0 V) for the HER on the Ni₃B/MoB, Ni₃B and MoB structure. Reproduced from ref. 113. Copyright 2020, Elsevier. (f) η₁₀ of recently reported catalysts and calculated Gibbs free energy for H* adsorption on different catalysts. Reproduced from ref. 106. Copyright 2019, Wiley.

Nørskov and his coworkers conducted several pioneering studies that have broadened the material space of sulfides for HER materials.¹⁰⁸ They opened up the potential application of MoS₂ in the HER by showing the theoretical HBE of the material followed by in-depth characterizations. They found that the edge sites of the MoS₂ have similar adsorption behavior to Pt, whereas the MoS₂(0001) facet was inactive to the H binding. Subsequent studies maximized the fraction of active edge sites by nanostructuring.²⁷ Although MoS₂ showed poor activity under alkaline conditions, breakthrough results were obtained by introducing conductive elements such as Ni and Co, which can foster the water dissociation steps.¹⁰⁹

Active and stable phases of dichalcogenides also have been evaluated as HER catalysts. Zheng et al. developed o-CoSe₂ by phase transforming c-CoSe₂ with controllable P doping that provided weakened electronegative sites and thereby tuned the d-electron states of the Co atoms.¹¹⁰ Their nano-structuring strategy, phase transformation by hetero-atom doping, has achieved high HER activity and stability in alkaline solution. The active sites of o-CoSe₂ are always closer to the optimal HER activity than c-CoSe₂ (Fig. 3c).

WS₂ also shows phase-dependent reactivity. Voiry et al. found that the abundant 1T phase of WS₂ has high HER activity.¹¹¹ In the 1T WS₂ phase, the exfoliated nanosheet structure of WS₂ has a certain amount of tensile and compressive strain, which contribute to HER activity. DFT calculation revealed that the 1T phase is stable enough owing to a high phase transformation barrier. In addition, an ideally introduced tensile strain controlled the optimal free energy of atomic hydrogen adsorption (Fig. 3d). The applied tensile strain induces shift of the density of states near the Fermi level. Similar activity enhancement strategies by strain engineering can be applied generally under the alkaline conditions.¹¹²

Heterostructuring is another nano-structuring strategy that can tune catalyst activity. Huang et al. designed a grain boundary structure between Ni₃B and MoB which serves as the active center with induced strain.¹¹³ The grain boundary enriched with bimetallic borides created additional defects and large voids, which served as hydrogen-binding sites and yielded near-optimal HBE (Fig. 3e). Ouyang et al. developed an efficient heterostructure HER catalyst comprising Co/β-Mo₂C@N-CNTs. The heterointerface site enriched the active sites, resulting in much lower overpotential, which was confirmed by overpotential measurement and theoretical analysis (Fig. 3f).¹⁰⁶

2.2.4. Machine learning approaches. Based on the accumulated understanding of the HER catalytic descriptors and the increasing number of available open-source database, machine learning (ML) has been widely applied in the search for novel HER materials across the infinitely large search space. In this section, pioneering ML-based high-throughput studies will be discussed. Physical insights on the activity descriptors derived from ML will also be covered.

Tran et al. provided an automated machine learning scheme to seek materials, which can automatically identify the best candidates for the HER from millions of possible structures by using only the HBE descriptor.¹¹⁴ In this study, they obtained 1499 intermetallic bulk structures from the Materials Project database, and possible surfaces were cleaved from the bulk structures. The HBE on each surface was calculated using DFT to make a fingerprint-like input database combined with three atomic features. The surrogate ML model was then trained by the input database using the Tree-based Pipeline Optimization Tool (TPOT), and the trained ML model was used to predict the HBE of unknown candidate materials. They identified all possible surface structures and suggested that even for the same materials the HBE can vary depending on the coordination structure. The model identified 102 candidate HER alloys, and all have optimal HBE (Fig. 4a).

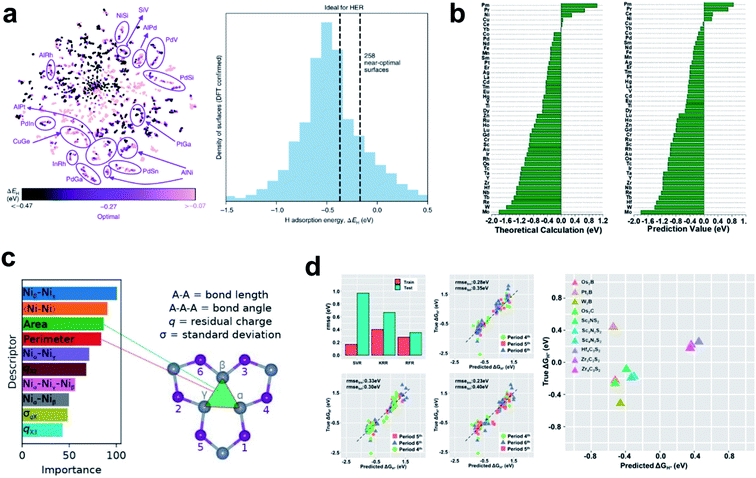Fig. 4 (a) t-SNE40 visualization of all the adsorption sites simulated using DFT, and normalized distribution of low-coverage ΔE_H values calculated using DFT. Reproduced from ref. 114. Copyright 2018, Wiley. (b) Comparison of DFT calculation and (b) machine-learning predictions of 2H adsorption energies. Reproduced from ref. 116. Copyright 2019, Wiley. (c) Relative importance of descriptors calculated from the RRF model. Reproduced from ref. 118. Copyright 2018, American Chemical Society. (d) Average root mean square error of SVR, KRR, and RFR obtained using the LOCO CV method. Predicted vs. DFT-calculated ΔG_H* of MXenes by using RFR. Reproduced from ref. 117. Copyright 2020, American Chemical Society.

Back et al. conducted a machine learning aided screening process of HER materials using available databases such as Materials Project and GASpy databases.¹¹⁵ A convolutional neural network called CGCNN was used to predict the HBE and CO poisoning tolerance. They discovered 18 promising alloy combinations and 4 cost-effective materials by considering the HBE descriptor, and confirmed that data-driven search for materials can be easily performed using a single powerful descriptor. Sun et al. performed DFT combined with ML for the high-throughput screening study of atomic transition and lanthanide metals anchored on graphdiyne.¹¹⁶ They first calculated the adsorption strengths of all possible HER intermediates on the catalyst surfaces, and then together with electronic structure features as the input data, they trained an ML model using bag-tree algorithm. The trained machine learning model predicted almost the same HBE as the result calculated by DFT, and the results were passed to experimentalists for further investigation (Fig. 4b). Zheng et al. combined DFT and machine learning models to identify 8 MXenes as promising HER candidates from 299 MXenes.¹¹⁷ In addition, they provided data-driven physical insights into the material that S groups are HER-regulating species due to the antibonding states (Fig. 4d).¹¹⁷

The emerging machine learning techniques provide new tools to help understand the most important factors in designing HER catalysts. Wexler et al. studied the theoretical activity of dopant-substituted Ni₂P using DFT and RRF ML model.¹¹⁸ By performing relative importance analysis, they found that structure-based descriptors such as Ni–Ni bond length in Ni₂P materials and existence of Ni₃-hollow structural motifs are the most influential factors (Fig. 4c).¹¹⁸

2.3. Water dissociation

While HBE has been widely accepted as the HER activity descriptor under a wide range of pH conditions due to its practicality in the rational design of electrocatalysts, it is increasingly accepted that the HBE Sabatier principle does not fully explain the significantly slower reaction kinetics under alkaline conditions than under acidic conditions. The sluggish kinetics of the HER in an alkaline environment is generally attributed to the huge potential required for the water dissociation step, known as the Volmer step (H₂O + e⁻ → OH⁻ + H*). Thus, enhancing the alkaline HER can be accomplished by overcoming the requirement for a high rate-limiting potential. The general consensus for improving the Volmer step is to introduce active sites suitable for easily cleaving the H–OH bond and moderately binding the resultant hydroxyl ion. Thus, OHBE as a second thermodynamic descriptor and the water dissociation energy barrier as an intrinsic kinetic parameter have been widely used in the rational design of next-generation alkaline HER catalysts. This section will explore the significance of the water dissociation barrier and OHBE in the design of alkaline HER catalysts, followed by ‘dual-active site’ strategies for accelerating the Volmer step.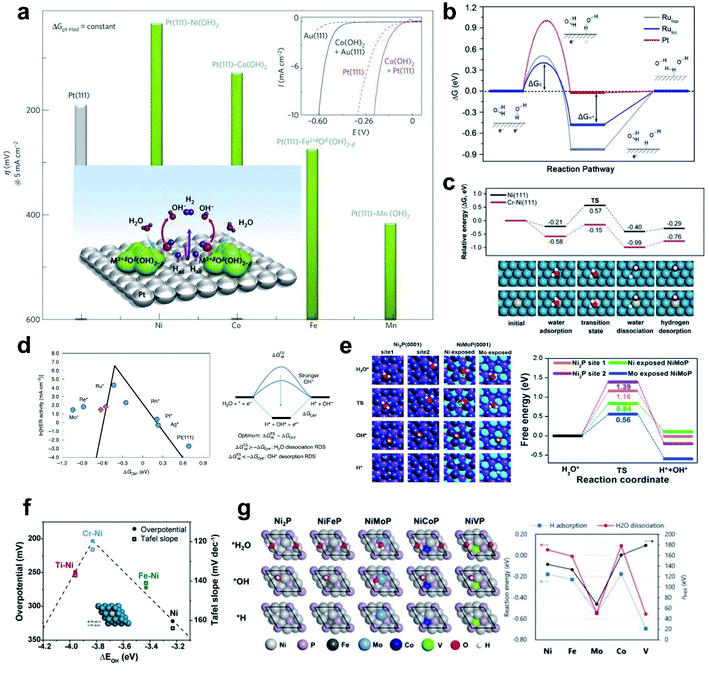

2.3.1. Water dissociation energy. Use of Ni(OH)₂, which is an active water dissociation material, can increase the HER rate by a factor of three to five fold under alkaline conditions.⁴⁴ This result is further evidence that the water dissociation reaction is the key reaction of the HER under alkaline conditions (Fig. 5a). The simplest and strongest computational analysis to identify the reaction barrier is to estimate the transition state energy of the water dissociation. Computational approaches have become available to exactly estimate the reaction barrier by using the NEB method, so collaborative work that combines in situ techniques and computation has been driving identifications of the mechanism, and the search for new materials.

Fig. 5 (a) Trend in overpotential for the HER as a function of 3d transition elements. Reproduced from ref. 44. Copyright 2012, Springer Nature. (b) Gibbs free energy diagram of the HER on different surfaces including reactant initial state, intermediate state, and final state. Reproduced from ref. 119. Copyright 2016, American Chemical Society. (c) Theoretical calculation of HER energy profile over Ni and Cr–Ni catalysts. (d) Simulated and experimentally measured HER activity and HER reaction mechanism. Reproduced from ref. 124. Copyright 2020, Springer Nature. (e) Free energy diagram for H₂O activation. Reproduced from ref. 43. Copyright 2018, Elsevier. (f) Volcano plot of overpotentials at 10 mA cm⁻², and Tafel slopes as a function of the ΔE_OH for M–Ni and Ni catalysts. (g) DFT calculation results of NiP and NiMPs (M = Fe, Mo, Co, V) for electrocatalytic activity analysis in the HER. Reproduced from ref. 120. Copyright 2020, American Chemical Society.

Zheng et al. recently provided a comprehensive study that revealed the importance of water dissociation in determining the HER kinetics in an alkaline environment by performing characterization and in-depth theoretical analysis using a well-defined model system.¹¹⁹ The Ru catalyst showed better H₂O dissociation ability than the Pt catalyst; theoretical analysis showed that the difference is a result of the high barrier to water dissociation on Pt, so the Ru catalyst has higher activity than the Pt catalyst, even though the Ru catalyst does not have an optimal HBE. This work showed that the kinetic barrier to H₂O dissociation is more important in the HER than hydrogen binding is (Fig. 5b).

Kim et al. developed Cr-incorporated nickel nano-helices which can accelerate the dissociative adsorption of H₂O. Oxophilic dopants such as Fe, Ti and Cr can provide active sites. Theoretical analysis of the reaction barrier by using the NEB method suggested that the Cr–Ni bimetallic system had a significantly lower reaction barrier (0.42 eV) than the bare Ni surface. The nano-helical morphology of the catalyst may also have enriched the active stepped structure of Ni and Cr (Fig. 5c).¹²⁰

Wu et al. elucidated that the diminished kinetic barrier of water dissociation on N-doped NiCo₂S₄ over NiCo₂S₄ is the key to the enhanced HER kinetics. DFT calculation revealed that the N incorporation on NiCo₂S₄ decreased the water dissociation barrier from 1.32 eV to 1.06 eV in the Volmer step, and also accelerated the H–H coupling (Heyrovsky) step.¹²¹ DFT analysis indicated that the barrier of the Heyrovsky step was higher on N-doped NiCo₂S₄ than on NiCo₂S₄; this result emphasizes the importance of considering the kinetic water dissociation descriptor.

Lee et al. developed a Co-doped NiFe phosphide which outperformed most of the alkaline HER catalysts. The HBE of NiFe–Co phosphide was the same as that of NiFe phosphide and the water dissociation thermodynamics were even worse on NiFe–Co phosphide (−0.10 eV) than on NiFe phosphide (−0.13 eV). However, the water dissociation kinetic barrier was effectively reduced, so HER kinetics was increased; these results imply that to understand the full reaction, kinetic analysis is necessary.¹²²

2.3.2. Hydroxyl and water binding. The water dissociation step can be favored by optimizing the thermodynamic adsorption strength of reaction intermediates on the materials. The simplest explanation regarding the need for optimized adsorption in the water dissociation step is that the strong adsorption of the final state of the reaction (OH* + H*) would lower the reaction barrier according to the Brønsted–Evans–Polanyi relationship.¹²³ Therefore, the best catalyst should bind water molecule and hydroxyl species strongly, although if hydroxyl binding is too strong, the HER can be slowed down.

Several reports suggested that the hydroxide binding energy (OHBE) can be useful as an HER descriptor. The Koper group extensively studied to reveal the correlation between HER activity and OHBE.¹²⁴ A well-defined catalyst surface is modeled to capture the atomic scale picture of the HER using DFT. Similar to the HBE descriptor, the OHBE formed a volcano activity relationship; if the OHBE is too strong, it hinders hydroxide desorption, but if it is too weak, it slows the water dissociation step (Fig. 5d). An overall volcano plot between HER activity and OHBE, considering all possible HER reaction paths, suggested that Ru incorporation will place Pt at the top of the volcano, owing to optimal OHBE and HBE; this conclusion is consistent with previous reports.⁹³ They concluded that both HBE and OHBE should be optimized simultaneously.

The Ni nano-helix system also shows a clear volcano-shaped relationship between OHBE and HER activity.¹²⁰ Oxophilic dopants like Fe, Ti and Cr can provide OH binding sites that have higher OHBE than pure Ni (Fig. 5f). Ni and Fe–Ni do not have strong enough OHBE, so water dissociation is not favored. However, Ti–Ni has a too-strong OHBE, which implies that adsorbed OH can block the active site limiting the water adsorption. Cr–Ni had an optimal OHBE, and therefore was likely to have an optimal water dissociation barrier; this suggestion was confirmed by theoretical calculation and experimental measurement.

The adsorption energy of a water molecule can explain the enhanced HER activity, given that water adsorption is the first step of the Volmer reaction. Yu et al. compared the water adsorption property of Ni₂P and NiMoP structures as well as HBE and water dissociation (Fig. 5e).⁴³ The results showed that the water dissociation barrier decreases as the strength of water binding increases. Water adsorption alone cannot explain HER activity, but can at least provide thermodynamic insights into the reaction and trend.

2.3.3. Design strategy: dual active sites. Combining the HBE and water dissociation barriers may give a better description of HER kinetics. A recent study conducted by Roh et al. provided an interesting insight on the (Fe, Mo, V, Co)-doped Ni₂P nanowire catalyst system. The measured overpotential followed the HBE and water dissociation barrier trend with a very high consistency (Fig. 5g).¹²⁵ The high consistency of the two main descriptors suggests that HBE and water dissociation act significantly together in the complex system, so to be comprehensive, the analysis should consider both of them.

Water dissociation and hydrogen binding occur together in the complex alkaline environment, so incorporating a water dissociation active site together with a hydrogen-binding active site to form a dual active site should synergistically increase the catalytic efficiency. The Marković group is one of the pioneers in designing a dual active site HER catalyst. By introducing water dissociation active materials such as Ni(OH)₂, CoO(OH), FeO(OH) and MnO(OH), they significantly increased the HER activity under alkaline conditions. This result implies that the water dissociation reaction occurs near the metal hydroxide species, and that the hydrogen binds to the optimal Pt site.⁴⁴ This finding stimulated many other studies of dual active sites to exploit their synergistic effect.

The idea of destabilizing the water molecule to facilitate the Volmer step was realized by the Sargent group.¹²⁶ They designed a Cu-based catalyst that had a surface that was doped with Ni atoms, and decorated with a CrO_x complex (Fig. 6a). They achieved an exceptional performance of 48 mV overpotential at a current density of 10 mA cm⁻² under neutral conditions. DFT calculation of the energies of water dissociation, and H and OH binding energy showed that the water dissociation was much lower when the CrO_x complex was present, and that the OHBE was significantly increased on the doped Ni atom. The conclusion was that dual active sites created by Ni atom and CrO_x dissociate H₂O much faster with smaller barriers than other model systems.

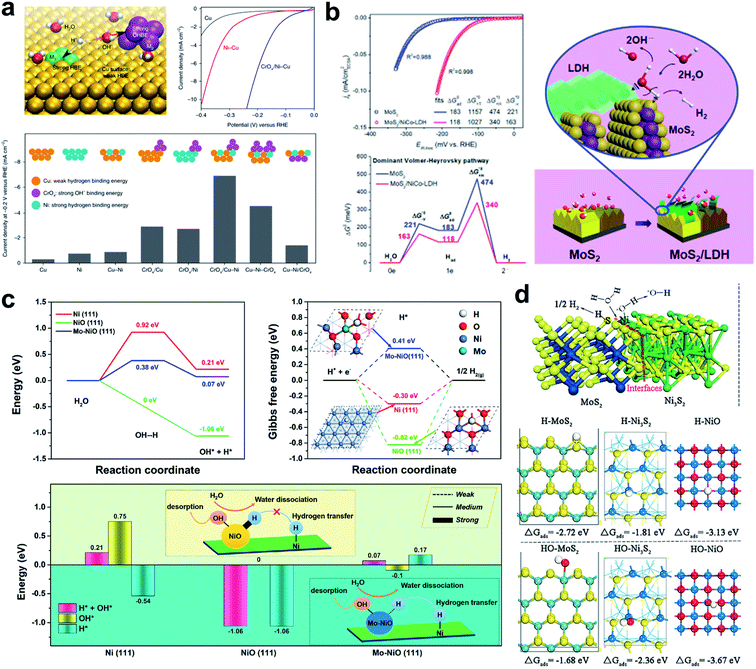Fig. 6 (a) Design principle of HER catalysts in neutral water by anisotropic surface doping to destabilize the water molecule on the catalyst surface; representative current density–voltage (J–V) curves before iR correction; comparison of HER activities on various Cu–Ni–CrO_x catalysts. Reproduced from ref. 126. Copyright 2019, Springer Nature. (b) CSA normalized polarization curves; free energy diagram of the dominant Volmer–Heyrovsky pathway for the HER in an alkaline electrolyte; schematic illustration of the HER in the MoS₂/LDH interface. Reproduced from ref. 32. Copyright 2017, Cell Press. (c) Calculated H₂O-dissociation barriers; calculated Gibbs free energies of H adsorption on Ni(111), NiO(111), and Mo–NiO(111); summary of adsorption energy of H* + OH*, OH*, and H* on the three surfaces. Reproduced from ref. 127. Copyright 2019, American Chemical Society. (d) Chemisorption models of H and OH intermediates on the surfaces of MoS₂, Ni₃S₂, NiO, and MoS₂/Ni₃S₂ heterostructures. Reproduced from ref. 128. Copyright 2016, Wiley.

Hu et al. developed a synergistic hybrid HER catalyst composed of MoS₂ and LDH which have a low HER overpotential of 78 mV at 10 mA cm²; the Heyrovsky step was rate limiting for both the MoS₂ and the MoS₂/NiCo-LDH system (Fig. 6b).³² However, every water dissociation step was facilitated by the NiCo-LDH, and the H species that formed then transfer to MoS₂ which has an optimal ΔG_H ∼ 0.08 eV.

Huang et al. developed a Mo–NiO and Ni dual active site catalyst which can dissociate the water molecule with ease on the Mo–NiO while transferring the hydrogen atom dissociated from H₂O on the Mo–NiO site to the Ni site easily for the next Tafel or Heyrovsky reaction (Fig. 6c).¹²⁷ A heterostructured MoS₂/Ni₃S₂ presented high activity toward both the HER and OER under alkaline conditions.¹²⁸ DFT analysis revealed that the outstanding HER activity is a result of dual active properties of the material. The H atom is preferentially adsorbed on the MoS₂, and the hydroxyl binds preferentially to the Ni₃S₂. The created interfacial sites therefore act as a water dissociation center and the formed H and OH species are partitioned among the materials (Fig. 6d).

2.4. The role of water and cations

In this section, the importance of water and solvated cation species in the HER process as a reactant and a carrier will be discussed. As pointed out by a recent perspective, “beyond adsorption” such as the solvation strength of electrolyte cations, chemical dynamics in the double layer and co-adsorbed spectator species can play important roles in the HER, and thus emphasis should be made on this.²⁴⁶ While the underlying role of these species is still unclear, pioneering studies have shed light on the role of cations and water molecules in the alkaline HER. The Marković group found that Li⁺ cation in Ni(OH)₂/Pt-islands/Pt(111) can contribute to HER reaction kinetics by controlling water molecules.⁴⁵ The metal hydroxide species provides an anchoring site that stabilizes an HO–Li–H₂O complex. The hydrated Li⁺ may act as a destabilizer of HO–H bonding and thereby increase the HER under alkaline conditions. Removing hydroxyl ions from the surface to prevent poisoning of the active site was highlighted since it would then facilitate further dissociative water adsorption.⁴⁴ In the following work, they proposed that S_ad^δ−–Cⁿ⁺–H₂O clusters may promote HER kinetics by activating water molecules in the double layer regions.¹²⁹ In-depth experiment was performed to reveal the elusive role of the cation in the electrolyte. Liu et al. proposed the role of a cation complex of hydroxyl and water which can promote the HER.¹³⁰ They found that increasing the amount of Li⁺ and Na⁺ caused increase in HER activity (Fig. 7a). Li⁺ alone did not increase the HER rate of Pt, so other species like Ni(OH)₂ must interact with Li⁺. A series of these studies indicated the importance of water and solvated cation species in the HER process as a reactant and a carrier.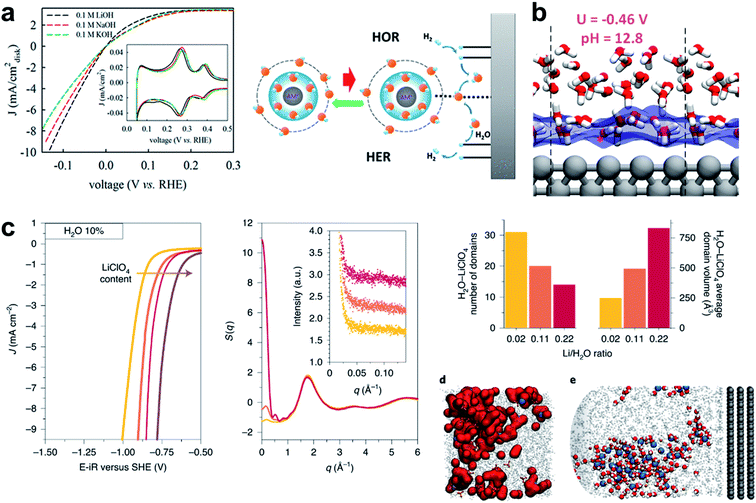

Fig. 7 (a) Cyclic voltammetry on Pt/C with various concentrations of Ni²⁺, and on the Pt₁Ni₁/C alloy. Reproduced from ref. 130. Copyright 2019, American Chemical Society. (b) Snapshots with atomic details of the interfaces at U = −0.46 V. Reproduced from ref. 131. Copyright 2018, American Chemical Society. (c) Linear sweep voltammograms recorded in ACN with 10% in mass of added H₂O in the presence of 100 mM (yellow), 500 mM (orange), 1 M (red), or 2 M (brown) LiClO₄ on a rotating disc (1600 rpm) Pt electrode with a 50 mV s⁻¹ sweeping rate and E–iR being the potential corrected for ohmic drop; total X-ray-weighted structure factor of the electrolytes containing 10% H₂O, 100 mM (yellow), 500 mM (orange), 1 M (red) LiClO₄ as computed from the MD simulations; number of LiClO⁴⁻–H₂O domains and their average volume depending on the LiClO₄/H₂O ratio at 10% in mass of water calculated from the MD simulations; (d) and (e) MD snapshots of the concentrated electrolyte (1 M LiClO₄ and 10% H₂O) showing the nanodomains in the bulk. Reproduced from ref. 133. Copyright 2020, Springer Nature.

To reveal the role of the cations in the solution, a study combining theory and experiment was conducted by the Grimaud group. They utilized organic solvents such as acetonitrile to decouple the H₂O–H₂O effect, and left H₂O as the only reactant. They also performed molecular dynamics simulation of bulk liquid and electric interface to investigate the long- and short-range cation–H₂O interaction. The aqueous-rich nano-domains were captured; their size and reactivity can be controlled by the electrolyte. The water molecules engaged in both short-range and long-range interaction (Fig. 7c),¹³¹ which is consistent with an earlier theoretical report for the function of the cation in the electrolyte.¹³²

Another theoretical study to identify the role of water in HBE was conducted using a Quantum Mechanics Molecular Dynamics (QMMD) study performed by the Goddard group. They concluded that the water adsorption preference depends largely on the pH, so the HBE can be manipulated by adjusting the pH.¹³³ They also proposed that the electrode tends to repel water when the applied voltage is negative, and thereby increases the HBE. They raised the possibility that the change of water adsorption is a key to the pH dependence (Fig. 7b).

Many enlightening theoretical studies have been performed to describe the realistic adsorption/desorption behaviors of the reaction intermediate at the electrolyte–electrode interface, which is one of the major issues in the DFT modeling of electrocatalysis. Including solvent molecules explicitly with excess protons has been used for an atomistic level picture of electrode potential and the solvation effect on the HER. Rossmeisl et al. constructed a realistic atomic model for the solid–liquid interface at electrode surfaces.²⁴⁷ They established a model with protons solvated in water layers to naturally distribute the electrons and control the electrode potential by protons. Their model accurately described interface capacitance, and the work function was related directly to the electrode potential. In addition, they suggested that a change in the configurational entropy of the proton upon approaching the electrode surface largely drives the pH-dependence of the electrochemical proton transmission.²⁴⁸ When a proton is carried from the bulk solution to the electrode surface, entropy is converted to enthalpy, and this conversion is greater in an alkaline environment. This work emphasized the critical role of a restructured interfacial water solvation environment in affecting the HBE in relation to pH. Chan and Nørskov proposed a capacitor-like model to precisely determine the HER energetics at a constant potential for the charge transfer reactions by explicitly including solvent molecules.²⁴⁹ Using a single water layer, they could develop a simple but realistic model to depict the HER.

2.5. Electronic conductivity

Sufficient electronic conductivity is highly demanding for an electrode material to effectively carry out an electrochemical reaction by transferring electrons from the electrode to the surface. However, the development of emerging HER materials such as TM oxides and TM chalcogenides has been largely hampered due to the semiconductive nature of those materials. Substantial efforts have been devoted to promote the intrinsic electronic conductivity using a variety of strategies such as chemical doping, strain control and phase transition. These strategies have been effectively implemented by the combination of the theoretical predictions and experimental validations.

The electronic structure of a material can be theoretically predicted by analyzing DFT calculated density of states where the band gap between the conduction band and the valence band of the electronic structure represents the conductive nature. By analyzing the electronic band structure of a material upon the modification such as doping and structural transformation, the conductivity of the material can be predicted in the atomic scale. For the experimental validations, the charge transfer resistance (R_ct) of the material can be evaluated by electrochemical impedance spectroscopy (EIS) and the resulting Nyquist plot. The following series of reports will provide a general guideline for the improvement of the electronic conductivity of semiconductive materials such as MoS₂. The Nørskov group found that MoS₂ nanoparticle supported on graphite is a promising HER catalyst, which was inspired by nitrogenase enzymes in nature that can effectively evolve hydrogen.¹⁰⁸ MoS₂ has a hexagonal layered crystal structure and the HER activity of MoS₂ is considered to originate from the edges rather than basal planes. However, intrinsically low conductivity through the in-plane S–Mo–S layers and deficient carrier as a prototype Mott-insulator still greatly impede wide applications. Therefore, various attempts to dope heteroatoms into MoS₂ have been made to improve the conductivity of the materials. The 2D graphene-like structure of MoS₂ transferred electrons between in-plane nanosheets, and avoided an inferior 3D transfer process between S–Mo–S layers in bulk MoS₂. The dopants introduced some new states in the band gap and narrowed it, which leads to improved electron transfer kinetics. Sun et al. doped vanadium in a MoS₂ interlayer and engineered its 2D structure to increase its electronic conductivity.¹³⁴ V element in the MoS₂ interlayer formed new states in the conduction band that were much closer to the valence band than in pure Mo₂S, so the V-doped MoS₂ behaved as a semimetal, in which valence electrons could be easily activated to the defect states (Fig. 8a and b).

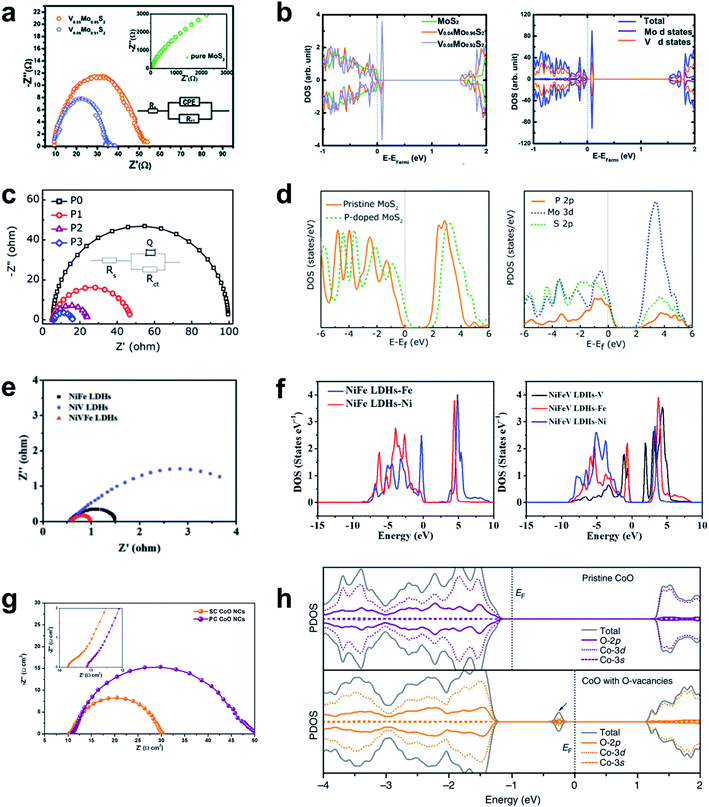Fig. 8 (a) Nyquist plot and (b) PDOS of pristine and V-doped MoS₂ nanosheets. Reproduced from ref. 134. Copyright 2014, Royal Society of Chemistry. (c) Nyquist plot and (d) PDOS of pristine and P-doped MoS₂ nanosheets. Reproduced from ref. 135. Copyright 2017, American Chemical Society. (e) Nyquist plot and (f) PDOS of NiFe LDHs and NiFeV LDHs. Reproduced from ref. 182. Copyright 2018, Wiley. (g) Nyquist plot and (h) PDOS of pristine and oxygen-defective CoO. Reproduced from ref. 183. Copyright 2016, Springer Nature.

P doping also increases the electronic conductivity and stability of MoS₂ nanosheet, and increases its alkaline HER activity compared to pure MoS₂.¹³⁵ The electrical resistivity decreased as the P doping ratio was increased to 5%; this trend indicates that the P is responsible for improving the electrical conductivity of the MoS₂ nanosheet (Fig. 8c). The P-doped MoS₂ monolayer has 0.3 eV narrower bandgap than the pristine MoS₂ monolayer, and the 2p-band of P atom strongly hybridized with the 3d orbital of its neighboring Mo atoms and to the 2p orbital of S atoms, and thereby promoted fast charge transfer in the basal plane (Fig. 8d). Other heteroatoms such as Se,¹³⁶ Nb,¹³⁷ N,¹³⁸ and TMs (Fe, Co, Ni, Cu, and Zn)^139,140 can also be doped into MoS₂ to increase its electronic conductivity. A different system consists of single-atomic Co supported on g-C₃N₄ (Co₁/CN). Doping the system with P increased its electrical conductivity.¹⁴¹ The P atom was well incorporated on the C₃N₄, and promoted HER kinetics by increasing its electronic conductivity.

3. Alkaline oxygen evolution reaction

3.1. OER mechanism

The adsorbate evolution mechanism (AEM) and the lattice oxygen oxidation mechanism (LOM) are widely accepted as possible OER mechanisms. In the AEM, the two oxygen atoms that constitute one oxygen molecule are supplied by an aqueous solution, whereas in LOM one oxygen comes from the lattice and leaves an oxygen vacancy. Lattice oxygen can be oxidized when the O₂/H₂O redox potential is aligned with the lattice oxygen 2p-band, so the LOM can show pH-dependent kinetics.^142–144

To predict whether AEM or LOM dominates in OER catalysts, the oxygen vacancy formation energy (ΔE^Vo_f) and the N–V descriptor have been applied to ABO₃ perovskites (A = La, La_0.5Sr_0.5, Sr and B = Mn, Fe, Co, Ni),¹⁴⁵ where N is the number of unpaired electrons on the isolated B atom, and V is the nominal charge of B in the stoichiometric bulk ABO₃. According to the reaction energy calculation of AEM and LOM, the OER mechanism of this system is determined by the free energy difference between the A₀-like intermediate (*O) of the AEM and the A₁-like intermediate (*OO with oxygen vacancy) of the LOM. The free energy difference decreases linearly with decreasing oxygen vacancy formation energy; this trend occurs because the B cation's electron-donating ability weakens, which is well explained by the N–V parameter (Fig. 9a).

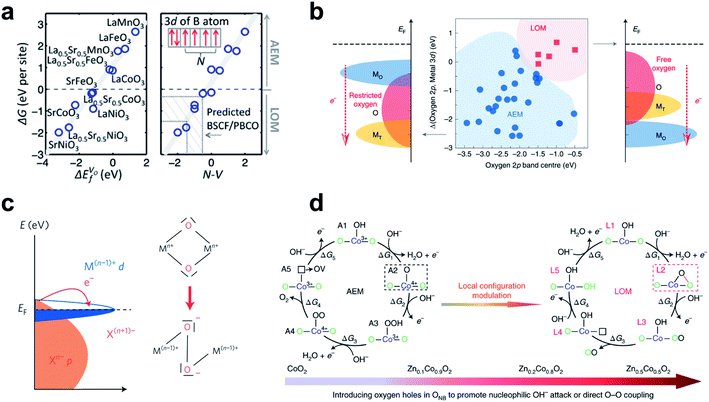Fig. 9 (a) Linear relationship of free-energy difference between A₁-like and A₀-like intermediates with ΔE^Vo_f and N–V. Reproduced from ref. 145. Copyright 2016, American Chemical Society. (b) Co-regulation of the OER mechanism on spinel oxides to O_p and the relative O_p to M_d. Reproduced from ref. 146. Copyright 2020, Springer Nature. (c) Schematic of the cationic d-band entering the ligand p-band, transferring electrons to the metal forming ligand holes. Reproduced from ref. 148. Copyright 2016, Springer Nature. (d) AEM and LOM on Zn_xCo_1−xO₂ slabs. Reproduced from ref. 147. Copyright 2019, Springer Nature.

The oxygen 2p-band center (O_p) and its relative value to the metal 3d-band center (M_d) have been proposed to determine the OER mechanism of spinels after analyzing the relationship between thirty experimental references and DFT-calculated band centers (Fig. 9b).¹⁴⁶ For the LOM, the lattice oxygen of the spinel should meet both the activity and priority criteria. The activity criterion is met when O_p is high enough (greater than −1.75 eV) to ensure escape from the lattice. The priority criterion is met when O_p is higher than M_d for intramolecular charge transfer from the oxygen to the cation. Therefore, to define the OER mechanism in spinels, both absolute O_p and O_p relative to M_d must be evaluated.

In transition metal oxyhydroxides (MOOH), the LOM occurs only if two neighboring oxidized oxygens can hybridize their oxygen holes without significantly sacrificing M–O hybridization.¹⁴⁷ Incorporation of catalytically inactive Zn²⁺ (d¹⁰) ion into CoOOH increased the Co–O covalency and formed an accessible oxygen non-bonding state, which was confirmed by Bader charge distribution and projected density of state (PDOS) analysis. As the zinc content of Zn_xCo_1−xO₂ increased (x = 0, 0.1, 0.2), the relative stability of A₂ (AEM intermediate) to L₂ (LOM intermediate) (Fig. 9d) and the activation energy from A₂ to L₂ all decreased. As a result, the Zn_0.2Co_0.8O₂ slab proceeded through the preferential LOM path, and the potential barrier was 0.60 V lower than that of the CoO₂ slab. However, the excess Zn component (Zn_0.5Co_0.5O₂ slab) impedes recharging of the remaining oxygen vacancies after O₂ gas formation (energy barrier ∼0.96 eV), so structural instability develops. This study showed that the OER of MOOH can undergo LOM with sufficiently high M–O covalency and smooth recovery of lattice oxygen. M–O covalency can be strengthened by the metal's high oxidation state, which has low M_d close to O_p, and thereby lattice oxygen can be activated in the presence of highly oxidized metal species (Fig. 9c).¹⁴⁸ For example, Ni⁴⁺ species derived by the Fe component of the (FeCoCrNi)OOH surface accompanied holes into the related oxygen 2p-band and facilitated lattice oxygen coupling, and thereby triggered lattice oxygen activation at the Fe–Ni dual-site center, which have high intrinsic OER activity.¹⁴⁴

3.2. Adsorbate evolution mechanism

This section presents the factors that determine the catalytic activity of TM alkaline OER catalysts, and strategies to control the factors. The four-electron pathway for AEM on metal surfaces was established first,¹⁴⁹ and the LOM was demonstrated in next section.^142,150,151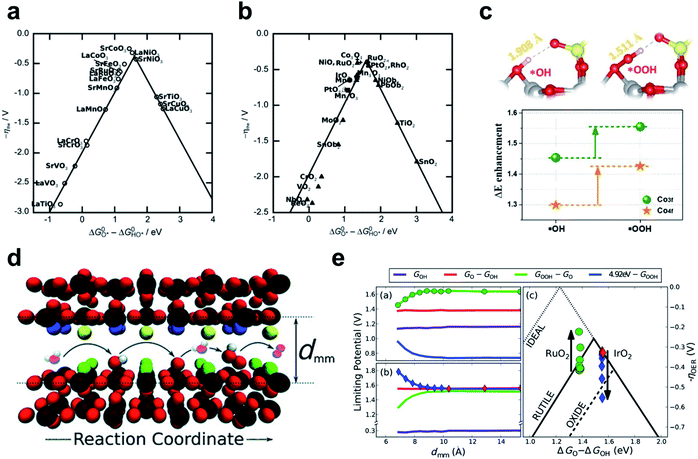

3.2.1. Scaling relationship: ΔG_O − ΔG_OH. The stabilities of oxygen containing intermediates (OCIs; *OH, *O, and *OOH in AEM) adsorbed on metal and metal oxide surfaces have linear relationships with each other.^152–154 ΔG_OOH − ΔG_OH has a constant value of ∼3.2 eV, so this scaling relationship in AEM provides ΔG_O − ΔG_OH as a conventional OER activity descriptor with an optimal value close to 1.6 eV (Fig. 10a and b). However, the scaling relationship limits the catalytic activity from improving to less than ∼0.4 V overpotential.

Fig. 10 The negative theoretical overpotential plotted against ΔG_O − ΔG_OH (a) for perovskites and (b) for rutile, anatase, Co₃O₄, Mn_xO_y oxides. Reproduced from ref. 154. Copyright 2011, Wiley. (c) The optimized *OH and *OOH structures on Co₃O₄–SO₄ surface and the stabilization of intermediate binding at the Co₃O₄–SO₄ surface compared to Co₃O₄. Reproduced from ref. 155. Copyright 2020, Elsevier. (d) Schematic of OER elementary steps in the microscopic channel with d_mm width. (e) Limiting potential change of each OER elementary step and corresponding overpotential change as d_mm decreases on RuO₂ (up) and IrO₂ (down). Reproduced from ref. 156. Copyright 2015, Wiley.

One attempt to circumvent this limitation is to use hydrogen bonding to separate the *OOH stability from the scaling relationship. SO₄²⁻ modification of the Co₃O₄ surface strengthens *OOH adsorption relatively more than *OH adsorption, so the OER overpotential decreases by 40 mV.¹⁵⁵ *OOH is longer and more flexible than *OH, so *OOH could form closer hydrogen bonds to the upper O atom of the adjacent SO₄²⁻ than *OH could (Fig. 10c).

Another way to design additional hydrogen bonding sites for *OOH is to use three-dimensional nanoscopic channels. Doyle and coworkers investigated the OCI stability with nanoscopic channel spacing by means of DFT calculation (Fig. 10e).¹⁵⁶ In this system, the second surface of the opposite site interacts with the *OOH intermediate, whereas *O and *OH remain unaffected (Fig. 10d). A channel width of about 7 Å increased the theoretical catalyst efficiency of RuO₂ (111) by 10%, and width less than this caused proton transfer from *OOH to the opposite surface. This strategy may be applicable to planar catalysts, such as γ-NiOOH, in which interlayer spacing can be controlled if sufficient catalytic durability is ensured. However, methods to stabilize *OOH are limited to improving the catalysts on the “left leg” (ΔG_O − ΔG_OH < 1.6 eV) of the activity volcano, which are hindered by the *OOH formation step.

The simplicity of the intermediate adsorption energy calculation and the universality of ΔG_O − ΔG_OH as a descriptor have made it applicable to many OER catalyst screening studies.^157–161 However, the ΔG_O − ΔG_OH descriptor does not much decrease calculation cost from the overall OER pathway investigation, and is consequential rather than fundamental. Rational design of catalysts with optimal ΔG_O − ΔG_OH is a difficult task, because we do not know which electronic properties directly determine ΔG_O − ΔG_OH. This difficulty raised the need for parameters related to electronic structure as essential OER activity descriptors.

3.2.2. e_g occupancy. The e_g orbital occupancy of TM cations has been demonstrated as an effective descriptor of OER activity in perovskites¹⁶² and spinels.¹⁶³ The former study covered various types of B metals (Cr, Mn, Fe, Co, and Ni), and estimated the oxidation state of surface metal cations by hard X-ray absorption and magnetometry. The latter dealt with Mn_xCo_3−xO₄ (x = 2, 2.5, 3), Li_xMn₂O₄ (x = 0.7, 1), XCo₂O₄ (X = Co, Ni, Zn), and XFe₂O₄ (X = Mn, Co, Ni) and estimated the oxidation state of octahedral metal cations by X-ray absorption spectroscopy (XAS). In both studies, OER activity showed a volcano plot against e_g occupancy, with an optimal point at ∼1.2 (Fig. 11a and d). The electronic structural basis comes from that the e_g orbitals mainly participate in σ-bonding with the adsorbate and that lower e_g leads to stronger oxygen adsorption. Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ perovskite and Mn₃O₄ spinel were located at the optimal points in these studies, respectively.

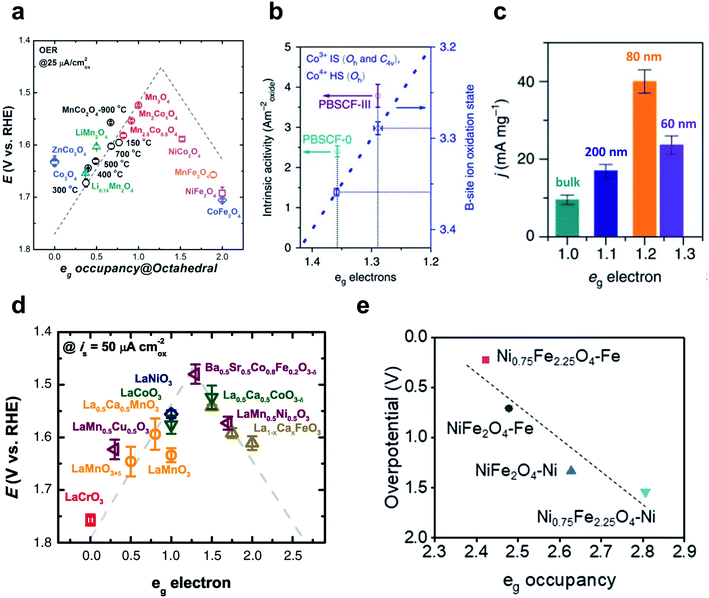Fig. 11 (a) Relationship between OER overpotentials and e_g occupancy of TMs in perovskites. Reproduced from ref. 163. Copyright 2017, Wiley. (b) Intrinsic activity versus e_g occupancy of PBSCF-0 and PBSCF-III. Reproduced from ref. 165. Copyright 2017, Springer Nature. (c) Mass activities for the bulk and nanosized LCO. Reproduced from ref. 164. Copyright 2016, Springer Nature. (d) Relationship between OER overpotentials and e_g occupancy of octahedral metals in spinels. Reproduced from ref. 162. Copyright 2011, AAAS. (e) Relationship between theoretical OER overpotentials and e_g occupancy of the octahedral TM in NiFe₂O₄ and Ni_0.75Fe_2.25O₄. Reproduced from ref. 167. Copyright 2021, Elsevier.

Zhao et al. have reported a perovskite nanostructure designing method to engineer e_g occupancy. Reducing the particle size of a single perovskite LaCoO₃ (LCO) to ∼80 nm increased the e_g occupancy of cobalt ions from 1 to ∼1.2 with optimal OER activity.¹⁶⁴ The e_g occupancy of the LCO nanoparticle was estimated assuming a core–shell model in which the spin states of Co³⁺ ions in the core were maintained at 50% high spin (HS: t⁴_2ge²_g) and 50% low spin (LS: t⁵_2ge⁰_g), while the spin states of the shell were in the 100% HS state. Starting from bulk LCO with only LS state Co³⁺ ions (e_g occupancy ∼1), decreasing LCO particle sizes to 200, 80, and 60 nm resulted in 1.09, 1.21, and 1.27 e_g occupancy, respectively. The OER activity, expressed as the current density of 10 mA cm⁻² per unit mass, showed a volcano curve as a function of e_g occupancy with an optimal point at ∼80 nm particle size (Fig. 11c). In summary, particle size reduction increased the ratio of core-to-shell composed of HS state Co³⁺ ions and e_g occupancy was successfully tuned to increase OER activity.

Their subsequent study tuned the e_g occupancy of B metals in the double perovskite PrBa_0.5Sr_0.5Co_1.5Fe_0.5O_5+δ (PBSCF) by synthesizing nanofiber morphology and controlling the diameter.¹⁶⁵ Reducing the diameter of PBSCF nanofibers from 196 to 20 nm increased the mass activity, and the thinnest (PBSCF-III) showed 1.6 times higher intrinsic activity than PBSCF powder (PBSCF-0), and was far superior to commercial IrO₂ catalyst and reported advanced perovskite catalysts. The e_g occupancy of PBSCF-0 and PBSCF-III was estimated using a first-order approximation to the B-metal oxidation state proposed by Grimaud and their coworkers.¹⁶⁶ Compared to PBSCF-0, PBSCF-III had a lower B-site cobalt ion oxidation state; this difference indicates a lower and closer e_g occupancy (∼1.29) to the optimal value than PBSCF-0 (∼1.36) (Fig. 11b).

The metal composition can also be adjusted to optimize e_g occupancy. Lee et al. have altered the Ni/Fe composition in NiFe₂O₄ through conventional corrosion of the Ni foam in the presence of exotic Fe³⁺ cations.¹⁶⁷ Ni_0.75Fe_2.25O₄ nanoparticles required 82 mV lower overpotential than NiFe₂O₄ to reach a current density of 10 mA cm⁻², and the Tafel slope showed a 14 mV dec⁻¹ faster OER rate than NiFe₂O₄. DFT calculation confirmed the increased intrinsic OER activity of Ni_0.75Fe_2.25O₄ than NiFe₂O₄, and the correlation of e_g occupancy and theoretical overpotential also revealed that Ni is the major active site for these nickel ferrites (Fig. 11e).

However, metal oxide may become amorphous under OER conditions, and the presence of two crystal fields, i.e., octahedral O_h and square pyramidal C_4v, causes ambiguity in e_g occupancy estimates.¹⁶⁶ In addition, e_g occupancy cannot represent electron sharing in M–O bonds, which specifically affects the LOM process. LaMnO₃, LaCoO₃, and LaNiO₃ have the same ∼1 e_g occupancy but contrasting OER activity; these are representative examples of the limitations of e_g occupancy as a descriptor.¹⁶⁸ Descriptors that consider M–O covalency avoid these limitations.

3.2.3. Metal–oxygen covalency. Lee et al. certified that the difference between M_d and O_p (ΔE_d–p) can be used as an OER activity descriptor of perovskite and introduced oxygen vacancy to tune Co–O covalency (Fig. 12a).¹⁶⁹ Duan et al. reported that substitution of 10 at% Fe in the B-site of LaCoO₃ perovskite increased its OER; the change might be a result of increased overlap between the cobalt 3d-band and the oxygen 2p-band covalency.¹⁷⁰ Statistical study also clarified that the charge-transfer energy is related linearly to the OER overpotential and specific activity of perovskites, in addition to e_g occupancy and O_p.¹⁷¹ The charge-transfer energy was calculated by subtracting the uncoupled M_d from O_p, to reveal the M–O covalency (Fig. 12b). Machine learning research on 101 intrinsic OER activities and 51 perovskites found that prediction of OER activity should consider M–O covalency as well as electron occupancy.¹⁷²

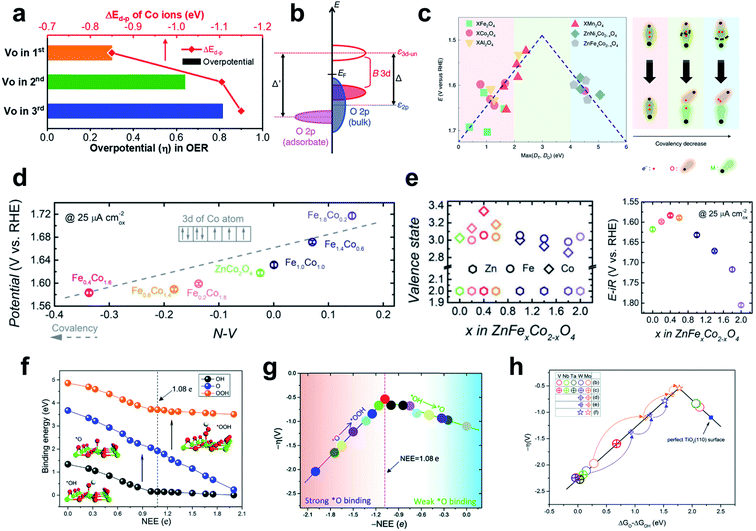Fig. 12 (a) Overpotential and ΔE_d–p values of the OER depending on the oxygen-vacancy position in Sm_0.5Sr_0.5CoO_3−δ. Reproduced from ref. 169. Copyright 2020, American Chemical Society. (b) Schematics of charge-transfer energies in bulk perovskites. Reproduced from ref. 171. Copyright 2018, American Chemical Society. (c) The experimentally measured OER overpotential plotted as a function of the calculated max (D_T, D_O) (eV). Reproduced from ref. 146. Copyright 2020, Springer Nature. (d) OER overpotential plotted as a function of the N–V parameter. (e) TM valence states (left) and OER operating potentials (right) as a function of composition x in ZnFe_xCo_2−xO₄ oxides. Reproduced from ref. 173. Copyright 2018, Wiley. (f) OCI binding energies and (g) OER overpotentials as a function of NEE. (h) Volcano plot of OER activities of V, Nb, Ta, Mo, and W atom doped TiO₂(110). Reproduced from ref. 174. Copyright 2019, Royal Society of Chemistry.

For spinels, the ΔE_d–p descriptor used for perovskites should be modified due to the covalency competition between octahedral and tetrahedral sites.¹⁴⁶ M–O breakage occurs from the weaker covalent bond in the M_O–O–M_T backbone, where M_O denotes an octahedral metal and M_T denotes a tetrahedral metal; thus one with a higher 3d-band center with lower bond durability should be the OER descriptor in spinels (Fig. 12c).

As mentioned in Section 3.1, N–V could predict the M–O covalency and dominant OER mechanism of perovskites. Zhou et al. used the same descriptor to explain the trend in AEM activity vs. B-metal composition in spinel ZnFe_xCo_2−xO₄ oxides (x = 0–2.0).¹⁷³ In this system the highly crystalline surface is well preserved over OER cycling, and O_p is lower than the Fermi level, so the LOM is not a favorable route. Among the series of ZnFe_xCo_2−xO₄ oxides, ZnFe_0.4Co_1.6O₄ catalyst showed the lowest overpotential (35 mV at 25 μA cm⁻²) and the highest valence state of cobalt (Fig. 12e). A higher valence state of Co cation (Co⁴⁺) compared with Co³⁺ indicates a lower energy 3d state and would produce higher hybridization with oxygens. Consequently, the experimentally measured OER overpotential was linearly related to N–V; this trend indicates M–O covalency (Fig. 12d).

3.2.4. Number of excess electrons. Excess electron number (NEE) has been proposed as another fundamental OER activity descriptor for reducible oxides.¹⁷⁴ Pseudo-hydrogen atoms with different numbers of valence electrons were used to tune the excess electrons in a TiO₂(110) model. The binding energies of *OH and *OOH species were strengthened linearly as NEE was increased from 0 to 1, whereas they were constant in the NEE range from 1 to 2 e (Fig. 12f). The binding energy of *O species linearly increased from NEE 0 to 2 e, and the slope was steeper than for *OH and *OOH. This different tendency may occur because *OH and *OOH require 1 e to satisfy the octet rule, whereas *O needs 2 e. As a result, with increase in NEE, the relative energy of *O with respect to *OH and *OOH was increased under ∼1.08 e NEE, and decreased at higher NEE. The potential determining step (PDS) clearly changes from *OH → *O to *O → *OOH at ∼1.08 e NEE (Fig. 12g). At NEE = ∼1.08 e, the *O state was midway between *OH and *OOH states; this condition resulted in optimal OER activity of the TiO₂(110) surface.

Replacing some Ti atoms with hetero-metal dopants (V, Nb, Ta, Mo, W) could tune the NEE and OER activity of the TiO₂(110) surface (Fig. 12h). This strategy can be extended to other reducible metal oxides such as SnO₂, NiO, WO₃, and ZnO. Quantitative NEE measurements are difficult both experimentally and computationally, but indirect analysis of NEE can be attempted using Bader charge analysis or calculation of valence electron configuration.

3.3. Lattice oxygen oxidation mechanism

Yoo et al. demonstrated the importance of considering lattice oxygen participation in understanding the trends in the OER on ABO₃ perovskites.¹⁵¹ Using DFT, they showed that LOM can lead to higher OER activity than the conventional AEM by bypassing the scaling relationships dictated in the AEM-based reaction process (Fig. 13a). They also showed that the OER activity volcano for AEM is universal for all perovskites, whereas that for LOM depends on the identity of the A cation in ABO₃. This observation explains experimental observations that perovskites such as Pr_0.5Ba_0.5CoO_3−δ and SrCoO_3−δ show higher OER activities than the conventionally predicted optimal compounds such as LaNiO₃ and SrCoO₃, and consequently emphasized the need for detailed evaluation of LOM activity.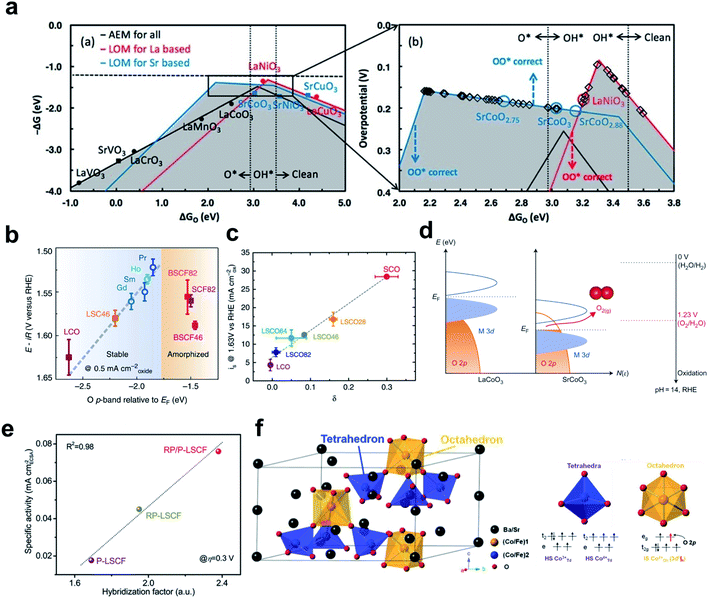

Fig. 13 (a) Overall OER activity volcano that considers AEM for all perovskites, LOM for lanthanum-bearing perovskites, and LOM for strontium-bearing perovskites. Reproduced from ref. 151. Copyright 2018, American Chemical Society. (b) OER potential versus the DFT computed Op of (Ln_0.5Ba_0.5)CoO_3−δ with Ln = Pr, Sm, Gd or Ho. Reproduced from ref. 166. Copyright 2013, Springer Nature. (c) Correlation of OER current density with the vacancy parameter δ of La_1−xSr_xCoO_3−δ. Reproduced from ref. 150. Copyright 2016, Springer Nature. (d) Schematic rigid band diagrams of LaCoO₃ and SrCoO₃. Reproduced from ref. 142. Copyright 2017, Springer Nature. (e) Correlation of intrinsic OER activity with the hybridization factor of P-LSCF, RP-LSCF, and RP/P-LSCF. Reproduced from ref. 176. Copyright 2020, Wiley. (f) Structural characterization of hex-BSCF (left) and the electronic structure of Co ion at the tetrahedral and octahedral sites in hex-BSCF (right). Reproduced from ref. 175. Copyright 2020, Wiley.

3.3.1. Metal–oxygen covalency. Grimaud et al. have demonstrated that the OER activity and catalytic stability of perovskites can be explained with O_p.¹⁶⁶ Increase in the oxidation state of Co in double perovskites (Ln_0.5Ba_0.5)CoO_3−δ (Ln = Pr, Sm, Gd, Ho) upshifted O_p toward the Fermi level and increased the Co–O covalency. Higher hybridization of the Co–O bond increased OER activity, but further increase in O_p degraded the oxide stability (Fig. 13b). Their subsequent study clarified that lattice oxygen participates in the OER process of LaCoO₃, La_0.5Sr_0.5CoO_3−δ, Pr_0.5Ba_0.5CoO_3−δ, and SrCoO_3−δ perovskites with in situ¹⁸O isotope labelling and that an increase in M–O covalency triggers LOM activation.¹⁴²

The correlation between LOM activity and M–O covalency occurs because oxygen vacancies form during the LOM process.¹⁵⁰ The degree of oxygen vacancy formation is affected by the relative positions of the TM 3d-band compared with the oxygen 2p-band of the crystal; a more covalent system exhibits a higher vacancy concentration. A high oxidation state of the TM increases the overlap of the metal 3d-band with the oxygen 2p-band, and downshifts the Fermi level. When the oxygen 2p-band states at the Fermi level lie above the redox energy of the O₂/H₂O couple, ligand holes are created in the oxygen 2p-band; this process indicates that the oxidation of lattice oxygen becomes thermodynamically favorable (Fig. 13d).¹⁴² Therefore, the charge transfer energy and oxidation state that represent M–O covalency in TMs can represent LOM activity and be tuned to increase OER activity.

Transforming the structure of perovskites is one way to use the highly oxidized TM for higher LOM activity. Mefford et al. adjusted A-site metal composition in the La_1−xSr_xCoO_3−δ perovskite to increase both the bulk oxidation state of Co and the concentration of oxygen vacancies; as a result the vacancy parameter increased and current density at 1.63 V vs. RHE also increased (Fig. 13c).¹⁵⁰ Zhu et al. have reported the unique hexagonal structure composed of one honeycomb-like network, Ba₄Sr₄(Co_0.8Fe_0.2)₄O₁₅ (hex-BSCF), as a highly active and durable OER electrocatalyst in alkaline solution.¹⁷⁵ Its unique structure ensures that both the high spin Co³⁺/Co⁴⁺ ions in the tetrahedral site and intermediate spin Co⁴⁺ ions in the octahedral site are active, which give rise to AEM and LOM, respectively. Increase in the oxidation state of Co ions increased the Co–O covalency, and the high-lying unoccupied e_g orbitals of Co⁴⁺ ions that have O_h symmetry have stronger covalency than the t_2g orbitals of Co⁴⁺ ions that have T_d symmetry (Fig. 13f). Therefore, the strong M–O covalency between the Co⁴⁺_Oh and the 2p ligand hole can trigger oxidation of lattice oxygen. The distinct OER mechanisms of the two active sites were further confirmed by combined XAS analysis and DFT calculations.

They also hybridized Ruddlesden–Popper phase LaSr₃Co_1.5Fe_1.5O_10−δ with perovskite phase La_0.25Sr_0.75Co_0.5Fe_0.5O_3−δ (RP/P-LCSF) which increased M–O covalency and oxygen ion diffusion (Fig. 13e).¹⁷⁶ RP/P-LSCF delivers a much lower OER overpotential and smaller Tafel slope than RP-LSCF, P-LSCF, and RuO₂. The strengthened M–O covalence of RP/P-LCSF was confirmed by O K-edge XAS spectra, considering the pre-edge peak below ∼530 eV in the O–K XAS spectra which correspond to the unoccupied O 2p orbitals hybridized with TM 3d orbitals.^166,177,178

3.3.2. Oxygen anion and vacancy diffusion. Fast oxygen-ion diffusion facilitates refilling of surface lattice oxygen that is consumed during LOM operation, and consequently the catalytic OER process. Increase in the freedom of access of lattice oxygen to metal ions increases surface exchange kinetics and facilitates the oxygen-ion diffusion, so similar OER activity trends were observed as a function of oxygen-ion diffusion rate (Fig. 14a and b) instead of the M–O covalence parameter (Fig. 13c and e). They measured oxygen-ion diffusion coefficients (D_O) by using a bounded 3D solid-state diffusion model with a rotating disk electrode.^150,179 According to isotope tracer studies, the diffusion rates decrease in the order ‘surface oxygen’ > ‘oxygen at grain boundaries’ > ‘bulk oxygen in perovskite systems’,¹⁸⁰ and the fast diffusion rates in this study may have been a result of movement of surface oxygen. Pan et al. have shown that the oxygen diffusion rate can be accelerated by doping silicon at the B-metal site of perovskite SrCoO_3−δ (SCO); the optimal OER activity (419 mV OER overpotential at 10 mA cm⁻²) was reached at 5% Si (Fig. 14c and d).¹⁸¹ At Si doping amount >5%, the OER activity decreased due to the formation of Sr₂SiO₄ impurity.

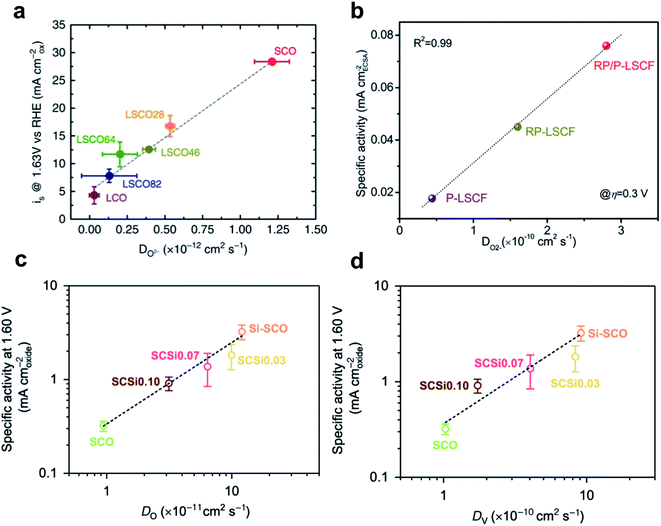Fig. 14 (a) Correlation of OER current density with the oxygen ion diffusion rate of La_1−xSr_xCoO_3−δ. Reproduced from ref. 150. Copyright 2016, Springer Nature. (b) Correlation of intrinsic OER activity with the oxygen-ion diffusion coefficient of P-LSCF, RP-LSCF, and RP/P-LSCF. Reproduced from ref. 176. Copyright 2020, Wiley. Correlation of intrinsic OER activity with (c) the oxygen anion diffusion rate and (d) the oxygen vacancy diffusion rate. Reproduced from ref. 181. Copyright 2020, Springer Nature.

3.4. Electronic conductivity

Attempts to accelerate the Faraday process have also been made in OER kinetics. V doping in NiFe LDHs reduces the onset potential and achieved efficient electrocatalysis for water oxidation.¹⁸² This doping significantly lowered the electron-transfer resistance (Fig. 8e) and the sheet resistance from (2.4 ± 0.3) × 10³ Ω sq⁻¹ to (1.3 ± 0.2) × 10³ Ω sq⁻¹; these changes are direct evidence of increased conductivity of NiFeV LDHs. The PDOS plot showed that V narrowed the bandgap, and thereby changed the conduction band state of NiFe LDHs (Fig. 8f).

Creation of oxygen vacancies on pyramidal facets can tune the atomic structure of one-dimensional single crystal (SC) CoO nanorods and increased their OER activity.¹⁸³ The SC nature and the oxygen vacancies increased the carrier concentration in SC CoO compared to polycrystalline (PS) CoO, and thereby lowered the electronic resistance of SC CoO (Fig. 8g). The PDOS analysis showed that oxygen vacancies created new electronic states in the bandgap by hybridization of O 2p, Co 3d and Co 3s bands for increased charge transfer (Fig. 8h).

4. Stability

The electrode material should be chosen by considering its stability for long operation and practical usages. Undesired oxidation and subsequent dissolution of the catalyst surface impede the development of TM based electrocatalysts, given that the surface properties of the materials often dictate the activity. The susceptibility of TMs to oxidation and corrosion can greatly reduce the catalyst efficiency by limiting the duration for which they are effective. Cheap TM elements have been introduced, but their poor stability gives them inferior catalytic activity compared to noble metal catalysts. Alkaline conditions generally increase the stability of TMs by forming passivation structures such as oxides and hydroxides, but the catalyst can corrode regardless of the environment (Fig. 15a).¹⁸⁴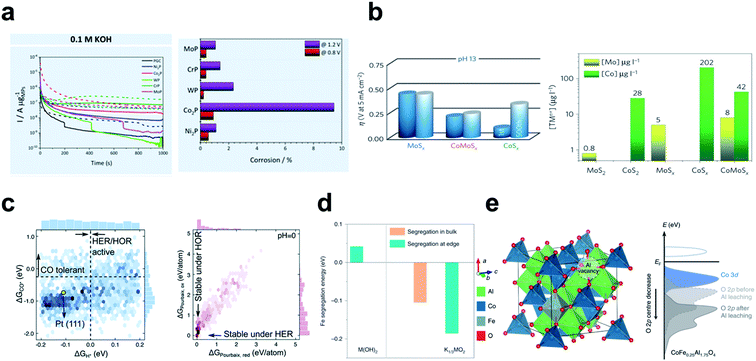

Fig. 15 (a) Corrosion of the M_xP_y in acidic and alkaline environments. Chronoamperometry at 0.8 V (solid line) and 1.2 V (dashed line) vs. RHE for 1000 s; corrosion percentages (wt%) calculated on the basis of the metal phosphides. Reproduced from ref. 184. Copyright 2019, American Chemical Society. (b) Activity–stability relationship of TMS_x for the HER in acid and alkaline environments. Reproduced from ref. 129. Copyright 2016, Springer Nature. (c) Two-dimensional histograms of ΔG_H* and ΔG_CO*; electrochemical stability ΔG_Pourbaix under reduction (−0.2 V_RHE) and oxidation conditions (+0.2 V_RHE) at pH = 0. Reproduced from ref. 115. Copyright 2020, Royal Society of Chemistry. (d) Fe segregation energies for pristine M(OH)₂ and the sample at the OER potential (K_1/3MO₂). Reproduced from ref. 199. Copyright 2020, Springer Nature. (e) Computational model for CoFe_0.25Al_1.75O₄ after Al³⁺ leaching and schematic band diagrams with and without Al³⁺ vacancies. Reproduced from ref. 188. Copyright 2019, Springer Nature.

4.1. Stability measurement

Several measurement techniques have been used to evaluate the stability of the catalyst. The long-term stability of the HER catalyst is often studied by monitoring the variation of current density or overpotential over time. For example, the electrochemical long-term stability of Cu/NiCu was assessed by monitoring the current density, overpotential, and charge transfer resistance over a 120 hour period.¹⁸⁵ Zadick et al. studied the large instability of Pt/C under alkaline conditions, and found that the degradation rate is three times worse than in acidic medium.¹⁸⁶ Accelerated stress tests (ASTs) were used to determine the deterioration of Pt/C samples under three different pH conditions. The degradation of the catalyst surface was then clearly identified by analyzing the electrochemical surface area (ECSA) measurements and identical location transmission electron microscopy (ILTEM) images. They suggested that the extreme carbon surface modification under alkaline operating conditions can dissolve up to 63% of the Pt nanoparticles, as demonstrated by Raman spectroscopy and X-ray photoelectron spectroscopy (XPS) measurements.

Another way to measure the stability of the materials is to analyze the dissolution concentration of the element. Hofmann et al. quantified the amount of cobalt and phosphorus dissolved in Co₂P both under acidic and alkaline conditions.¹⁸⁷ They determined the pH-dependent stability using linear sweep voltammetry (LSV). Using Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES) analysis, the amount of dissolved elements in the catalytic materials was then compared before and after the repeated LSV measurement. They found that Co₂P preferentially dissolves P atoms over Co atoms under alkaline conditions, which largely degrades the activity. In contrast, in an acidic environment, the dissolution occurred stoichiometrically (two Co per P), so the activity and ECSA were retained uniformly. The degraded Co₂P formed Co(OH)₂, then deactivated.

The direct detection of stability can be achieved before, after and even in real time, using state-of-the-art advanced operando spectroscopy and microscopic high-resolution imaging techniques. XAS,^{141,219–222} surface X-ray scattering,²²³ mass spectrometry,²²⁴ attenuated total reflectance Fourier transform infrared spectroscopy (ATR FT-IR),²²⁵ and Raman spectroscopy²²⁶ have been used for in-depth stability analysis and mechanistic studies, as we have discussed in Section 5.

In summary, electrochemical stability can be assessed by several stability evaluation criteria. To determine long-term stability, conventional electrochemical measurements such as linear/cyclic sweep voltammetry and amperometry have been extensively used. To detect degradation and dissolution of catalytic materials, high resolution spectroscopy and in situ techniques have been frequently employed in conjunction with ECSA. These state-of-the-art measurement techniques accelerate our understanding of the catalyst stability and aid in the development of stable materials.

4.2. Stability–activity relationship

Corrosion of a component in a multicomponent system often creates additional defect sites, which can act as active sites for the HER and OER. The Marković group demonstrated the stability and activity relationship in TMS that the dissolution of cations from Co–Mo–S_x chalcogens in strong alkaline media induces formation of active defects which serve as an active site. They confirmed that the activity–stability has strong correlation in that a less stable catalyst is more likely to have better activity.¹²⁹ They compared the amount of the dissolved cations (Mo and Co) to find that a moderately defective structure has the smallest overpotential after 500 hours of operation and decent stability (Fig. 15b).

Moderate instability of the catalyst surface promotes LOM in metal oxides, and increases their overall OER activity. Some studies have shown that descriptors for predicting the OER mechanism or activity can also be used to predict the stability of the catalyst.^{145,147,166,188} However, excessive destruction such as metal dissolution, structural reconstruction and oxidative decomposition decreases OER operation and remains a problem to be solved.

Recently, it has been found that many OER active materials suffer severe dissolution during the reaction;^189,190 this observation implies that high activity in the OER is always accompanied by elevated metal dissolution rates (thermodynamic material instability).^191,192 The traditional view that all components are ‘frozen’ in space (static active sites) and that only the reactants and products are mobile has been revised as dynamic phenomena have been observed during the OER on metal oxide^193,194 and perovskite^142,150,195 surfaces. These changes suggest that activity and stability can be increased simultaneously. To consider both activity and stability, the activity–stability factor (ASF) has been suggested as a metric; it is the ratio of the rate of O₂ production (activity) to the rate of metal dissolution (stability), measured simultaneously using in situ inductively coupled plasma mass spectrometry.¹⁹⁶

4.3. Predicting the stability

DFT can determine the stability of the electrochemical catalyst by calculating the thermodynamic energy of reactions that destroy it, such as metal dissolution,^197–199 lattice oxygen escape,^188,200 surface segregation^201,202 and thermodynamic phase stability.²⁰³ For example, Kuai et al. revealed that Fe segregation in mixed Ni–Fe hydroxide is energetically favorable at edge sites and at high potential in the alkaline OER (Fig. 15d).¹⁹⁹ Wu et al. theoretically showed that the surface reconstruction of CoFe_0.25Al_1.75O₄ can be self-terminated by Al³⁺ leaching (Fig. 15e).¹⁸⁸ Introduction of Al vacancies into the CoFe_0.25Al_1.75O₄ lattice downshifted O_p and blocked further formation of oxygen vacancies; the modulated surface reconstruction provided a highly active oxyhydroxide surface without disruption of bulk structures.

A data driven screening study conducted by Back et al. has performed phase stability analysis to filter out unstable materials.¹¹⁵ They constructed Pourbaix diagrams, which evaluate thermodynamic phase stability with respect to applied potential and pH. The Pourbaix Gibbs free energy (ΔG_Pourbaix) was calculated at between −0.2 and +0.2 V_RHE, at pH = 0, 7 and 14. ΔG_Pourbaix alone cannot capture the kinetic stability such as dissolution and segregation, but does provide a thermodynamic picture which serves as the least requirement for the materials. Structural stability represented by convex Hull energy was also used to filter out unstable materials. From a dataset of 23 050 DFT calculations, 573 candidates were identified by referring with respect to activity criteria (η_HER/HOR > 0.2 V), and the set was then reduced to 134 by considering electrochemical stability criteria (ΔG_Pourbaix < 0.1 eV) (Fig. 15c).

4.4. Strategies to enhance stability

To prevent the dissolution of metals in hydr(oxy)oxides, methods of adding metal cations to the electrolyte have been proposed. Chung et al. added Fe cations to the electrolyte for the increased stability of Fe–MO_xH_y hydr(oxy)oxide clusters (M = Ni, Co, Fe) in the alkaline OER.²⁰⁴ In pure KOH solutions, the activities of the Fe–MO_xH_y samples were deactivated and Fe was depleted after just 1 h of potential hold at 1.7 V (Fig. 16a). However, addition of 0.1 ppm Feⁿ⁺(aq.) to the electrolyte effectively prevented activity loss under the same test conditions, without decrease in the initial OER activity (Fig. 16c). Isotope experiment with ⁵⁶Fe in the initial electrode and ⁵⁷Fe in the initial electrolyte showed that two isotope Fe were switched during OER operation so the electrode maintained its total Fe content (Fig. 16b and d). The results indicate that Fe–MO_xH_y itself was not absolutely stable in 0.1 ppm Feⁿ⁺(aq.) electrolyte, but that OER activity could be sustained over time by enabling continuous Fe dynamic exchange at the interface. In the case of Ni–Co₃O₄, it was also reported that Fe impurities in KOH electrolyte suppressed the lattice-metal corrosion under OER conditions.²⁵⁰ Fe impurities replacing the lattice metal of the Ni (oxy)hydroxide catalyst not only improved the dynamic stability, but also provided the highly active site by themselves.^160,251

Fig. 16 Stability test of the Fe-NiO_xH_y electrode for 1 h (a) in Fe-free purified KOH and (b) in KOH solution containing 0.1 ppm Fe. Change of total Fe amount in the Fe-NiO_xH_y electrode over time (c) in Fe-free purified KOH and (d) in a KOH solution containing 0.1 ppm Fe. Reproduced from ref. 204. Copyright 2020, Springer Nature. (e) Schematic of the deposition of a permselective CeO_x layer on the OER catalyst. (f) Compositions of bare and CeO_x-coated NiFeO_x measured by ICP before and after the stability test for 96 h. (g) Electrocatalytic stability test by controlled current electrolysis. Reproduced from ref. 205. Copyright 2018, Wiley. (h) HER scheme for the Co-WSe₂/MWNT heterostructure catalyst. Reproduced from ref. 206. Copyright 2018, Royal Society of Chemistry. (i) HAADF image and calculated charge-density differences of different models. Reproduced from ref. 208. Copyright 2017, Springer Nature.

Fe impurities in alkaline electrolytes also help in the phase maintenance of the Ni- and Co-based OER catalysts. Ni(OH)₂ films aged in Fe-containing 1 M KOH exhibited a stable double (oxy)hydroxide (LDH) phase, inhibiting the phase transformation over aging or overcharging. In contrast, Ni(OH)₂ films aged in an Fe-containing electrolyte predominantly presented the β-Ni(OH)₂ phase, which undergoes phase transformation over aging (into β-Ni(OH)₂ and β-NiOOH) and overcharging (from β-NiOOH to γ-NiOOH).²⁵² The Pourbaix diagram of Ni–H₂O with/without Fe doping showed that Fe incorporation lowers the free energy of all compounds and expands the phase region of Ni(OH)₂, NiOOH, and NiO₂ under OER conditions (near 1.5 V vs. SHE). In the same study, ab initio molecular dynamics (AIMD) simulation showed that the intercalation and adsorption of the hydrated Fe cations are thermodynamically and kinetically stable in the layered γ-NiOOH system, and those adsorbed on the catalyst surface lower the OER overpotential of Ni active sites.²⁵³ On the other hand, Fe cations adsorbed on the oxygen-defective Co oxide catalyst (CoO_x) serve as main active sites of the alkaline OER.²⁵⁴

Leakage of metal cations from the OER electrode can also be prevented by coating the active surface with a layer that is permselective to reactants. Highly active NiFeO_x electrocatalysts for the OER gradually deactivate over time, owing to loss of Fe species from the active sites into solution during catalysis. Anodic deposition of a CeO_x layer prevented the loss of such Fe species from the OER catalysts (Fig. 16f), and yielded a highly stable activity (Fig. 16g).²⁰⁵ The CeO_x layer did not affect the OER activity or electronic conductivity of the catalyst underneath, but allowed the selective permeation of OH⁻ and O₂ while preventing diffusion of redox ions (Fig. 16e). The deposition of the CeO_x layer even retained Co species in CoO_x nanoparticles; this result suggests that CeO_x layer addition could increase the stability, without significant loss of the OER activity.

To prevent oxidation and dissolution of a material, strain engineering to induce phase transformation to a more stable phase is a feasible strategy. Jun et al. developed a synthetic technique for cobalt-doped tungsten selenide (Co-WSe₂) using multi-walled carbon nanotubes (MWNTs) as a topological template. The nucleation and growth occur on the carbon template, which induces curvature strain to the Co-WSe₂ and exposes the 1 T phase (Fig. 16h). The 1 T phase Co-WSe₂/MWNT heterostructure showed better HER activity and stability than other Co-WSe₂ which were degraded by oxidation of the surface. The improved stability is attributed to the stable curved 1T phase decreasing the oxidation degree.²⁰⁶

Encapsulation is widely applied to increase stability by increasing dissolution resistance and conductivity.²⁰⁷ Chen et al. have synthesized a cobalt based bimetallic alloy encapsulated by six to fifteen layers of nitrogen-doped graphene layers²⁰⁸ (Fig. 16i). They achieved perfect stability, with corrosion resistance even after 10 000 cycles of HER operation under alkaline conditions, and had superior activity to commercial Pt/C. DFT calculations reveal that a small number of Ru atoms helped to optimize the HBE, and charges were transferred well to the carbon sheets, so the HBE was optimized.

In summary, the oxidation and dissolution of metal components in a high potential environment can significantly degrade a material's electrochemical activity even under alkaline conditions. Many experimental and theoretical developments in recent years have led to significant stability improvements through various strategies. One potential strategy is to dynamically recover the dissolved metals by adding metal cations to the electrolyte. Impurity metal elements can be added to increase the inherent dissolution resistance by minimizing unwanted phase transformation. Furthermore, the phase of a material can be altered intentionally by strain engineering to increase its resistance to the oxidation and dissolution. Coating the active materials with a permselective CeO_x layer or graphene layers can also be applied to enhance the corrosion resistance.

5. Scope and future perspectives

DFT calculations that are used with suitable activity descriptors enable rational design of highly active catalysts by executing a theoretical screening process; they also explain the reason for activity, stability and conductivity increase observed in experiments. Despite the undeniable success of the theoretical approaches in the field, researchers should pay attention to the accuracy of the simulation and consistency with the experiments. Although descriptors based on the adsorption strength of the intermediates of the reaction, such as ΔG_H for the HER and ΔG_O − ΔG_OH for the OER, have guided the development of novel catalysts, these only give a thermodynamic picture of the reaction, and thus are used to rapidly capture the trends of electrochemical reactions. Although the activation barriers can be examined by various optimization methods, the results rely largely on the transition state pathways. To ensure reliability and reproducibility, the transition state should be carefully characterized by providing configurations and vibrational frequencies, and the key simulation details should be open to other researchers.

The solvent effect is also required for the adsorption energy calculation given that the reaction takes place in a solvation environment.^209,210 Inclusion of the solvent effect increases the computational complexity, but some compromises have been proposed, such as implicit solvation²¹¹ or microsolvation²¹² with just three water molecules. Those methods cannot capture the overall contribution of co-adsorbed water to the adsorbates, but can be a good compromise between calculation cost and the need to consider the solvation effect.

The effects of spectator species such as hydroxide anion or aqueous metal cations should also be considered. They can induce electrostatic interaction at the double layer region of the electrode surface. The double layer structures contain substrate and adsorbate interaction, which have important functions.²¹³ The full effect of the system should be considered when elucidating the atomic nature of the catalytic system by simulation. In addition, the electronic structure-based descriptors such as orbital occupancy or band center, must select an appropriate U parameter for TMs in oxides.^214–217

Accurate mechanistic studies can increase the understanding of HER and OER catalysis to guide the development of new materials. However, their reaction mechanisms are still in debate. Even from the same perovskite family, different LOM pathways^142,145 or further refined steps²¹⁸ have been proposed. Operando and in situ spectroscopies can be used to reveal the nature of the active sites, metal oxidation states and local coordination structure of the catalyst during the water splitting reaction. XAS,^{141,219–222} surface X-ray scattering,²²³ mass spectrometry,²²⁴ attenuated total reflectance Fourier transform infrared spectroscopy (ATR FT-IR)²²⁵ and Raman spectroscopy²²⁶ have been used for mechanistic studies of electrochemistry, coupled with DFT calculation. Thorough operando spectroscopy and computational identification of the active sites and structure-dependent activity origin also can extend the perspectives and considerations of each material.

Most in situ and theoretical efforts so far have been conducted only on well-defined surfaces of polycrystalline catalysts. However, the material search space has expanded to include hydroxides, phosphides, sulfides, and nitrides, so fundamental studies on those surfaces are necessary. The surface structure and reconstruction vary in the electrochemical environment, so these various structures must be considered when designing a surface-reaction simulation.^227,228 The Pourbaix diagram could give a simple and powerful description to help identify stable structures.²²⁹

Electronic structural characteristics differ among different types of catalysts, so setting a suitable descriptor for each catalyst could be a way to increase the accuracy of the OER activity descriptor. Various OER candidates (e.g., hydroxides, oxyhydroxides, phosphides, sulfides, carbides) do not have OER activity descriptors; their identification requires analysis of the electronic structure and water oxidation mechanism of these materials, although previous research mainly focused on perovskites and simple oxides. In oxyhydroxides, OER cycling of the low valence of Co can reduce the overpotential,^22,230 and the increased OER activity with V dopant in NiFe(OH)₂ could be explained by an increased overlap between M_d and O_p.²³¹ In nickel phosphides, the OER overpotential shows a volcano plot with change in the Ni 3d-band center, which could be decreased by Fe substitution.^125,232 Further analysis of OER mechanisms and activity descriptors must be expanded to diverse material groups.

Finally, recent research on water electrolysis has focused on applications on a real commercial scale. Such applications require reduction of prices, use of abundant water resources such as seawater, and must be validated experimentally on a commercial scale. For compatible integration of the catalyst to increase the cost efficiency of electrolyzers, the need to develop an HER-and-OER bifunctional catalyst has been emphasized. Several important findings have shown great opportunity in the field of bifunctional catalysts, such as NiFe-layered double hydroxides, CoMnO/CN, and N, S co-doped carbon nanotubes.^233–235 Compatibility with different operating conditions is also important to reduce the overall cost, so a pH-universal catalyst that can be effective both in acidic and alkaline environments has been sought.^{37,129,236,237} Abundant seawater is also being evaluated as a resource for water electrolysis,^238,239 and the alkaline media alleviates the OER selectivity problem, which is in competition with an accompanying chlorine evolution reaction (CER).²⁴⁰ Therefore, mechanistic study on the CER in alkaline seawater splitting is required, although recent CER research has been focused on noble metal oxide catalysts in acidic environments.^241–245 Consequently, commercial-scale activity and durability tests are also expected for both alkaline OER and HER.^233–235

6. Conclusion

Fundamental understanding on the nature of the catalytic reaction has advanced the development of the TM-based HER and OER catalysts in recent decades. In the case of the HER, substantial effort has been devoted both to find a catalyst that has optimal hydrogen binding thermodynamics, and to minimize the water dissociation energy barrier kinetics. These two important criteria have been proven to determine the HER activity of the materials. We have first explored from classical HBE dependent volcano relationships to the state-of-the-art design strategies such as electronic structure tuning, various nano-structuring concepts and machine learning-based expansion of search space. Thereafter, we discussed the Volmer reaction, with main focus on the water dissociation barrier, from the perspectives of kinetics and thermodynamics. Several studies have determined that fine tuning the adsorption strength of OH, H and H₂O provides huge room for increase in catalytic activity. From the kinetics perspective, introducing a water dissociation center to make a dual active site is the most powerful design strategy, and has proven to be viable. The functions of promoter species in the electrolyte have also been highlighted.

Two major mechanisms of the OER, i.e., AEM and LOM, and parameters for determining favorable paths, such as oxygen vacancy formation energy, N–V, O_p and M_d were introduced. In AEM, ΔG_O − ΔG_OH has been proposed as a conventional OER activity descriptor according to the scaling relationship between the adsorption strength of intermediates, and electronic structural descriptors including e_g occupancy, M–O covalency, and NEE could predict catalytic activity. In the LOM, in which lattice oxygen participates, M–O covalency, oxygen anion and vacancy diffusion are significantly involved in catalytic activity. The pros and cons of each descriptor and their suitability for specific material families should be considered when choosing an appropriate descriptor. We also discussed ways to tune that property to increase OER activity or investigate it experimentally and computationally.

High conductivity of the electrode material is an essential requirement when developing semiconductor materials as an electrode. Given that the electrical conductivity of a material is determined by the band gap of the electronic structure, the computationally obtained density of states is widely used to predict the conductivity. Several strategies are reviewed, including doping with conductive heteroatoms such as Co, Ni, V and P atoms, and introducing oxygen vacancies. The broadening of the material search space to TM-based materials is inevitably accompanied by deactivation of the catalyst, and this problem should be considered when evaluating catalysts for practical uses. The detection of the activity criteria by time dependent high-resolution spectroscopy and advanced operando spectroscopy revealed the origin of stability and activity trends. Several computational descriptors have been implemented to gain mechanistic insight towards the stability, and to filter out unstable materials. Successful synthesis methods were reviewed.

Focusing on the combination of theory and experiment, this review has described the design principles of inexpensive catalysts for alkaline water splitting reactions, by increasing the understanding of alkaline HER and OER mechanisms and the relationship between the electronic structure and catalytic activity. Electrical conductivity and instability problems were also mentioned, and future perspectives for increased synergy between theory and experiment were proposed. We hope that this review broadens the perspective of a design principle of inexpensive catalyst for alkaline water splitting reactions, and can provide insight into the field of electrochemistry such as hydrogen oxidation and oxygen reduction reactions (HOR/ORR), which share similar intermediates.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (MSIT) (NRF-2018M3A7B4062825, NRF-2021M3H7A1026173, and NRF-2021M3H4A1A01079300) and the Korea Institute of Energy Technology Evaluation and Planning (20193410100050) in the Ministry of Trade, Industry and Energy.

References

1. M. Dresselhaus and I. Thomas, Nature, 2001, 414, 332–337.
2. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
3. J. A. Turner, Science, 2004, 305, 972–974.
4. S. K. Sahoo, Y. Ye, S. Lee, J. Park, H. Lee, J. Lee and J. W. Han, ACS Energy Lett., 2018, 4, 126–132.
5. J. Park, S. Lee, H. E. Kim, A. Cho, S. Kim, Y. Ye, J. W. Han, H. Lee, J. H. Jang and J. Lee, Angew. Chem., Int. Ed., 2019, 58, 16038–16042.
6. J. Kim, Y. Yang, A. Seong, H.-J. Noh, C. Kim, S. Joo, A. Cho, L. Zhang, J. Zhou, J. Q. Wang, J. W. Han, J. Mahmood, J. B. Baek and G. Kim, J. Mater. Chem. A, 2020, 8, 14927–14934.
7. A. Cho, J. Ko, B.-K. Kim and J. W. Han, ACS Catal., 2018, 9, 967–976.
8. H. Zhao, Y. P. Zhu and Z. Y. Yuan, Eur. J. Inorg. Chem., 2016, 2016, 1916–1923.
9. A. Le Goff, V. Artero, B. Jousselme, P. D. Tran, N. Guillet, R. Métayé, A. Fihri, S. Palacin and M. Fontecave, Science, 2009, 326, 1384–1387.
10. J. Wang, W. Cui, Q. Liu, Z. Xing, A. M. Asiri and X. Sun, Adv. Mater., 2016, 28, 215–230.
11. J. Rossmeisl, K. Dimitrievski, P. Siegbahn and J. K. Nørskov, J. Phys. Chem. C, 2007, 111, 18821–18823.
12. S. Anantharaj, S. Ede, K. Karthick, S. S. Sankar, K. Sangeetha, P. Karthik and S. Kundu, Energy Environ. Sci., 2018, 11, 744–771.
13. H. Jin, J. Joo, N. K. Chaudhari, S. I. Choi and K. Lee, ChemElectroChem, 2019, 6, 3244–3253.
14. L. Chen, X. Dong, Y. Wang and Y. Xia, Nat. Commun., 2016, 7, 11741.
15. L. Han, S. Dong and E. Wang, Adv. Mater., 2016, 28, 9266–9291.
16. F. Safizadeh, E. Ghali and G. Houlachi, Int. J. Hydrogen Energy, 2015, 40, 256–274.
17. F. Lu, M. Zhou, Y. Zhou and X. Zeng, Small, 2017, 13, 1701931.
18. N. Mahmood, Y. Yao, J. W. Zhang, L. Pan, X. Zhang and J. J. Zou, Adv. Sci., 2018, 5, 1700464.
19. Y. Zheng, Y. Jiao, A. Vasileff and S. Z. Qiao, Angew. Chem., Int. Ed., 2018, 57, 7568–7579.
20. M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934.
21. G. Glenk and S. Reichelstein, Nat. Energy, 2019, 4, 216–222.
22. B. Zhang, L. Wang, Z. Cao, S. M. Kozlov, F. P. G. de Arquer, C. T. Dinh, J. Li, Z. Wang, X. Zheng, L. Zhang, Y. Wen, O. Voznyy, R. Comin, P. De Luna, T. Regier, W. Bi, E. E. Alp, C.-W. Pao, L. Zheng, Y. Hu, Y. Ji, Y. Li, Y. Zhang, L. Cavallo, H. Peng and E. H. Sargent, Nat. Catal., 2020, 3, 985–992.
23. L. Birry and A. Lasia, J. Appl. Electrochem., 2004, 34, 735–749.
24. J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913.
25. X. Mao, L. Wang, Y. Xu, P. Wang, Y. Li and J. Zhao, npj Comput. Mater., 2021, 7, 46.
26. T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102.
27. J. Kibsgaard, Z. Chen, B. N. Reinecke and T. F. Jaramillo, Nat. Mater., 2012, 11, 963–969.
28. J. Kibsgaard, T. F. Jaramillo and F. Besenbacher, Nat. Chem., 2014, 6, 248–253.
29. M. S. Faber, R. Dziedzic, M. A. Lukowski, N. S. Kaiser, Q. Ding and S. Jin, J. Am. Chem. Soc., 2014, 136, 10053–10061.
30. H. Li, C. Tsai, A. L. Koh, L. Cai, A. W. Contryman, A. H. Fragapane, J. Zhao, H. S. Han, H. C. Manoharan, F. Abild-Pedersen, J. K. Nørskov and X. Zheng, Nat. Mater., 2016, 15, 48–53.
31. P. Wang, X. Zhang, J. Zhang, S. Wan, S. Guo, G. Lu, J. Yao and X. Huang, Nat. Commun., 2017, 8, 14580.
32. J. Hu, C. Zhang, L. Jiang, H. Lin, Y. An, D. Zhou, M. K. Leung and S. Yang, Joule, 2017, 1, 383–393.
33. M. Caban-Acevedo, M. L. Stone, J. R. Schmidt, J. G. Thomas, Q. Ding, H. C. Chang, M. L. Tsai, J. H. He and S. Jin, Nat. Mater., 2015, 14, 1245–1251.
34. Y. Wen, J. Qi, D. Zhao, J. Liu, P. Wei, X. Kang and X. Li, Appl. Catal., B, 2021, 293, 120196.
35. K. Xu, Y. Sun, Y. Sun, Y. Zhang, G. Jia, Q. Zhang, L. Gu, S. Li, Y. Li and H. J. Fan, ACS Energy Lett., 2018, 3, 2750–2756.
36. X. Yang, A.-Y. Lu, Y. Zhu, M. N. Hedhili, S. Min, K.-W. Huang, Y. Han and L.-J. Li, Nano Energy, 2015, 15, 634–641.
37. Z. H. Xue, H. Su, Q. Y. Yu, B. Zhang, H. H. Wang, X. H. Li and J. S. Chen, Adv. Energy Mater., 2017, 7, 1602355.
38. Q. Gao, W. Zhang, Z. Shi, L. Yang and Y. Tang, Adv. Mater., 2019, 31, 1802880.
39. Y.-Y. Ma, Z.-L. Lang, L.-K. Yan, Y.-H. Wang, H.-Q. Tan, K. Feng, Y.-J. Xia, J. Zhong, Y. Liu, Z.-H. Kang and Y.-G. Li, Energy Environ. Sci., 2018, 11, 2114–2123.
40. Q. Hu, X. Liu, B. Zhu, L. Fan, X. Chai, Q. Zhang, J. Liu, C. He and Z. Lin, Nano Energy, 2018, 50, 212–219.
41. W. Xiong, Q. Guo, Z. Guo, H. Li, R. Zhao, Q. Chen, Z. Liu and X. Wang, J. Mater. Chem. A, 2018, 6, 4297–4304.
42. Y. Huang, Q. Gong, X. Song, K. Feng, K. Nie, F. Zhao, Y. Wang, M. Zeng, J. Zhong and Y. Li, ACS Nano, 2016, 10, 11337–11343.
43. L. Yu, I. K. Mishra, Y. Xie, H. Zhou, J. Sun, J. Zhou, Y. Ni, D. Luo, F. Yu and Y. Yu, Nano Energy, 2018, 53, 492–500.
44. R. Subbaraman, D. Tripkovic, K.-C. Chang, D. Strmcnik, A. P. Paulikas, P. Hirunsit, M. Chan, J. Greeley, V. Stamenkovic and N. M. Markovic, Nat. Mater., 2012, 11, 550–557.
45. R. Subbaraman, D. Tripkovic, D. Strmcnik, K.-C. Chang, M. Uchimura, A. P. Paulikas, V. Stamenkovic and N. M. Markovic, Science, 2011, 334, 1256–1260.
46. N. Danilovic, R. Subbaraman, D. Strmcnik, K. C. Chang, A. Paulikas, V. Stamenkovic and N. M. Markovic, Angew. Chem., Int. Ed., 2012, 51, 12495–12498.
47. G. Chen, T. Wang, J. Zhang, P. Liu, H. Sun, X. Zhuang, M. Chen and X. Feng, Adv. Mater., 2018, 30, 1706279.
48. Y. Matsumoto, S. Yamada, T. Nishida and E. Sato, J. Electrochem. Soc., 1980, 127, 2360.
49. J. O. M. Bockris and T. Otagawa, J. Electrochem. Soc., 1984, 131, 290.
50. A. Vojvodic and J. K. Nørskov, Science, 2011, 334, 1355–1356.
51. Y. Zhu, W. Zhou, J. Sunarso, Y. Zhong and Z. Shao, Adv. Funct. Mater., 2016, 26, 5862–5872.
52. B. Marsan, N. Fradette and G. Beaudoin, J. Electrochem. Soc., 1992, 139, 1889.
53. I. Nikolov, R. Darkaoui, E. Zhecheva, R. Stoyanova, N. Dimitrov and T. Vitanov, J. Electroanal. Chem., 1997, 429, 157–168.
54. M. Li, Y. Xiong, X. Liu, X. Bo, Y. Zhang, C. Han and L. Guo, Nanoscale, 2015, 7, 8920–8930.
55. R. Chen, H.-Y. Wang, J. Miao, H. Yang and B. Liu, Nano Energy, 2015, 11, 333–340.
56. Y. Wang, T. Zhou, K. Jiang, P. Da, Z. Peng, J. Tang, B. Kong, W. B. Cai, Z. Yang and G. Zheng, Adv. Energy Mater., 2014, 4, 1400696.
57. H. Liang, F. Meng, M. Cabán-Acevedo, L. Li, A. Forticaux, L. Xiu, Z. Wang and S. Jin, Nano Lett., 2015, 15, 1421–1427.
58. Z. Lu, H. Wang, D. Kong, K. Yan, P.-C. Hsu, G. Zheng, H. Yao, Z. Liang, X. Sun and Y. Cui, Nat. Commun., 2014, 5, 4345.
59. F. Song and X. Hu, Nat. Commun., 2014, 5, 4477.
60. J. X. Feng, S. H. Ye, H. Xu, Y. X. Tong and G. R. Li, Adv. Mater., 2016, 28, 4698–4703.
61. T. Gao, Z. Jin, M. Liao, J. Xiao, H. Yuan and D. Xiao, J. Mater. Chem. A, 2015, 3, 17763–17770.
62. Y. Liu, H. Wang, D. Lin, C. Liu, P.-C. Hsu, W. Liu, W. Chen and Y. Cui, Energy Environ. Sci., 2015, 8, 1719–1724.
63. M. Xing, L.-B. Kong, M.-C. Liu, L.-Y. Liu, L. Kang and Y.-C. Luo, J. Mater. Chem. A, 2014, 2, 18435–18443.
64. Y. Meng, W. Song, H. Huang, Z. Ren, S.-Y. Chen and S. L. Suib, J. Am. Chem. Soc., 2014, 136, 11452–11464.
65. M. Fekete, R. K. Hocking, S. L. Chang, C. Italiano, A. F. Patti, F. Arena and L. Spiccia, Energy Environ. Sci., 2013, 6, 2222–2232.
66. P. Ganesan, M. Prabu, J. Sanetuntikul and S. Shanmugam, ACS Catal., 2015, 5, 3625–3637.
67. W. Zhu, X. Yue, W. Zhang, S. Yu, Y. Zhang, J. Wang and J. Wang, Chem. Commun., 2016, 52, 1486–1489.
68. S. Dou, L. Tao, J. Huo, S. Wang and L. Dai, Energy Environ. Sci., 2016, 9, 1320–1326.
69. B. Dong, X. Zhao, G.-Q. Han, X. Li, X. Shang, Y.-R. Liu, W.-H. Hu, Y.-M. Chai, H. Zhao and C.-G. Liu, J. Mater. Chem. A, 2016, 4, 13499–13508.
70. C. Xia, Q. Jiang, C. Zhao, M. N. Hedhili and H. N. Alshareef, Adv. Mater., 2016, 28, 77–85.
71. Y. Liu, H. Cheng, M. Lyu, S. Fan, Q. Liu, W. Zhang, Y. Zhi, C. Wang, C. Xiao, S. Wei, B. Ye and Y. Xie, J. Am. Chem. Soc., 2014, 136, 15670–15675.
72. X. Xu, F. Song and X. Hu, Nat. Commun., 2016, 7, 12324.
73. A. T. Swesi, J. Masud and M. Nath, Energy Environ. Sci., 2016, 9, 1771–1782.
74. H. Jiang, Y. Yao, Y. Zhu, Y. Liu, Y. Su, X. Yang and C. Li, ACS Appl. Mater. Interfaces, 2015, 7, 21511–21520.
75. Z. Kou, L. Zhang, Y. Ma, X. Liu, W. Zang, J. Zhang, S. Huang, Y. Du, A. K. Cheetham and J. Wang, Appl. Catal., B, 2019, 243, 678–685.
76. K. Xu, H. Ding, H. Lv, P. Chen, X. Lu, H. Cheng, T. Zhou, S. Liu, X. Wu, C. Wu and Y. Xie, Adv. Mater., 2016, 28, 3326–3332.
77. Y.-J. Tang, C.-H. Liu, W. Huang, X.-L. Wang, L.-Z. Dong, S.-L. Li and Y.-Q. Lan, ACS Appl. Mater. Interfaces, 2017, 9, 16977–16985.
78. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
79. H. Jónsson, G. Mills and K. W. Jacobsen, Classical and Quantum Dynamics in Condensed Phase Simulations, in Proceedings of the International School of Physics, LERICI, Villa Marigola, 1998, pp. 385–404.
80. J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics and Dynamics, Prentice Hall Upper, Saddle River, NJ, 1999.
81. N.-T. Suen, S.-F. Hung, Q. Quan, N. Zhang, Y.-J. Xu and H. M. Chen, Chem. Soc. Rev., 2017, 46, 337–365.
82. V. Artero, M. Chavarot-Kerlidou and M. Fontecave, Angew. Chem., Int. Ed., 2011, 50, 7238–7266.
83. A. Badreldin, A. E. Abusrafa and A. Abdel-Wahab, ChemSusChem, 2021, 14, 10.
84. N. K. Chaudhari, H. Jin, B. Kim and K. Lee, Nanoscale, 2017, 9, 12231–12247.
85. Y. Guo, T. Park, J. W. Yi, J. Henzie, J. Kim, Z. Wang, B. Jiang, Y. Bando, Y. Sugahara, J. Tang and Y. Yamauchi, Adv. Mater., 2019, 31, 1807134.
86. L. Li, P. Wang, Q. Shao and X. Huang, Chem. Soc. Rev., 2020, 49, 3072–3106.
87. D. Zhao, Z. Zhuang, X. Cao, C. Zhang, Q. Peng, C. Chen and Y. Li, Chem. Soc. Rev., 2020, 49, 2215–2264.
88. J. Creus, J. De Tovar, N. Romero, J. García-Antón, K. Philippot, R. Bofill and X. Sala, ChemSusChem, 2019, 12, 2493–2514.
89. D. Li, J. Shi and C. Li, Small, 2018, 14, 1704179.
90. X. Wu, C. Tang, Y. Cheng, X. Min, S. P. Jiang and S. Wang, Chem.–Eur. J., 2020, 26, 3906–3929.
91. J. Zhang, Q. Zhang and X. Feng, Adv. Mater., 2019, 31, 1808167.
92. B. You, M. T. Tang, C. Tsai, F. Abild-Pedersen, X. Zheng and H. Li, Adv. Mater., 2019, 31, 1807001.
93. D. Strmcnik, M. Uchimura, C. Wang, R. Subbaraman, N. Danilovic, D. Van Der Vliet, A. P. Paulikas, V. R. Stamenkovic and N. M. Markovic, Nat. Chem., 2013, 5, 300–306.
94. J. K. Nørskov, T. Bligaard, A. Logadottir, J. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23.
95. W. Sheng, M. Myint, J. G. Chen and Y. Yan, Energy Environ. Sci., 2013, 6, 1509–1512.
96. W. Sheng, Z. Zhuang, M. Gao, J. Zheng, J. G. Chen and Y. Yan, Nat. Commun., 2015, 6, 5848.
97. J. Durst, A. Siebel, C. Simon, F. Hasché, J. Herranz and H. Gasteiger, Energy Environ. Sci., 2014, 7, 2255–2260.
98. A. Nilsson, L. Pettersson, B. Hammer, T. Bligaard, C. Christensen and J. Nørskov, Catal. Lett., 2005, 100, 111–114.
99. J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943.
100. J. Greeley and M. Mavrikakis, Nat. Mater., 2004, 3, 810–815.
101. H. Jin, X. Liu, S. Chen, A. Vasileff, L. Li, Y. Jiao, L. Song, Y. Zheng and S.-Z. Qiao, ACS Energy Lett., 2019, 4, 805–810.
102. Q. Xu, G. Li, Y. Zhang, Q. Yang, Y. Sun and C. Felser, ACS Catal., 2020, 10, 5042–5048.
103. D. Guan, J. Zhou, Y.-C. Huang, C.-L. Dong, J.-Q. Wang, W. Zhou and Z. Shao, Nat. Commun., 2019, 10, 3755.
104. H. Vrubel and X. Hu, Angew. Chem., Int. Ed., 2012, 51, 12703–12706.
105. Y. Liu, G. Yu, G. D. Li, Y. Sun, T. Asefa, W. Chen and X. Zou, Angew. Chem., Int. Ed., 2015, 54, 10752–10757.
106. T. Ouyang, Y. Q. Ye, C. Y. Wu, K. Xiao and Z. Q. Liu, Angew. Chem., Int. Ed., 2019, 58, 4923–4928.
107. R. Michalsky, Y.-J. Zhang and A. A. Peterson, ACS Catal., 2014, 4, 1274–1278.
108. B. Hinnemann, P. G. Moses, J. Bonde, K. P. Jørgensen, J. H. Nielsen, S. Horch, I. Chorkendorff and J. K. Nørskov, J. Am. Chem. Soc., 2005, 127, 5308–5309.
109. J. Jiang, M. Gao, W. Sheng and Y. Yan, Angew. Chem., Int. Ed., 2016, 55, 15240–15245.
110. Y. R. Zheng, P. Wu, M. R. Gao, X. L. Zhang, F. Y. Gao, H. X. Ju, R. Wu, Q. Gao, R. You, W. X. Huang, S. J. Liu, S. W. Hu, J. F. Zhu, Z. Y. Li and S. H. Yu, Nat. Commun., 2018, 9, 2533.
111. D. Voiry, H. Yamaguchi, J. Li, R. Silva, D. C. Alves, T. Fujita, M. Chen, T. Asefa, V. B. Shenoy, G. Eda and M. Chhowalla, Nat. Mater., 2013, 12, 850–855.
112. S. Maiti, K. Maiti, M. T. Curnan, K. Kim, K.-J. Noh and J. W. Han, Energy Environ. Sci., 2021, 14, 3717–3756.
113. H. Huang, H. Jung, H. Jun, D. Y. Woo, J. W. Han and J. Lee, Chem. Eng. J., 2021, 405, 126977.
114. K. Tran and Z. W. Ulissi, Nat. Catal., 2018, 1, 696–703.
115. S. Back, J. Na, K. Tran and Z. W. Ulissi, Phys. Chem. Chem. Phys., 2020, 22, 19454–19458.
116. M. Sun, A. W. Dougherty, B. Huang, Y. Li and C. H. Yan, Adv. Energy Mater., 2020, 10, 1903949.
117. J. Zheng, X. Sun, C. Qiu, Y. Yan, Z. Yao, S. Deng, X. Zhong, G. Zhuang, Z. Wei and J. Wang, J. Phys. Chem. C, 2020, 124, 13695–13705.
118. R. B. Wexler, J. M. P. Martirez and A. M. Rappe, J. Am. Chem. Soc., 2018, 140, 4678–4683.
119. Y. Zheng, Y. Jiao, Y. Zhu, L. H. Li, Y. Han, Y. Chen, M. Jaroniec and S.-Z. Qiao, J. Am. Chem. Soc., 2016, 138, 16174–16181.
120. J. Kim, H. Jung, S.-M. Jung, J. Hwang, D. Y. Kim, N. Lee, K.-S. Kim, H. Kwon, Y.-T. Kim, J. W. Han and J. K. Kim, J. Am. Chem. Soc., 2021, 143, 1399–1408.
121. Y. Wu, X. Liu, D. Han, X. Song, L. Shi, Y. Song, S. Niu, Y. Xie, J. Cai, S. Wu, J. Kang, J. Zhou, Z. Chen, X. Zheng, X. Xiao and G. Wang, Nat. Commun., 2018, 9, 1425.
122. J. Lee, H. Jung, Y. S. Park, N. Kwon, S. Woo, N. C. S. Selvam, G. S. Han, H. S. Jung, P. J. Yoo, S. M. Choi, J. W. Han and B. Lim, Appl. Catal., B, 2021, 294, 120246.
123. J. L. Fajín, M. N. l. DS Cordeiro and J. R. Gomes, J. Phys. Chem. A, 2014, 118, 5832–5840.
124. I. T. McCrum and M. T. Koper, Nat. Energy, 2020, 5, 891–899.
125. H. Roh, H. Jung, H. Choi, J. W. Han, T. Park, S. Kim and K. Yong, Appl. Catal., B, 2021, 120434.
126. C.-T. Dinh, A. Jain, F. P. G. de Arquer, P. De Luna, J. Li, N. Wang, X. Zheng, J. Cai, B. Z. Gregory, O. Voznyy, B. Liu, M. Sinton, D. Crumlin and E. J. Sargent, Nat. Energy, 2019, 4, 107–114.
127. J. Huang, J. Han, T. Wu, K. Feng, T. Yao, X. Wang, S. Liu, J. Zhong, Z. Zhang, Y. Zhang and B. Song, ACS Energy Lett., 2019, 4, 3002–3010.
128. J. Zhang, T. Wang, D. Pohl, B. Rellinghaus, R. Dong, S. Liu, X. Zhuang and X. Feng, Angew. Chem., Int. Ed., 2016, 55, 6702–6707.
129. J. Staszak-Jirkovský, C. D. Malliakas, P. P. Lopes, N. Danilovic, S. S. Kota, K.-C. Chang, B. Genorio, D. Strmcnik, V. R. Stamenkovic, M. G. Kanatzidis and N. M. Markovic, Nat. Mater., 2016, 15, 197–203.
130. E. Liu, J. Li, L. Jiao, H. T. T. Doan, Z. Liu, Z. Zhao, Y. Huang, K. Abraham, S. Mukerjee and Q. Jia, J. Am. Chem. Soc., 2019, 141, 3232–3239.
131. N. Dubouis, A. Serva, R. Berthin, G. Jeanmairet, B. Porcheron, E. Salager, M. Salanne and A. Grimaud, Nat. Catal., 2020, 3, 656–663.
132. G. Cassone, F. Creazzo, P. V. Giaquinta, J. Sponer and F. Saija, Phys. Chem. Chem. Phys., 2017, 19, 20420–20429.
133. T. Cheng, L. Wang, B. V. Merinov and W. A. Goddard III, J. Am. Chem. Soc., 2018, 140, 7787–7790.
134. X. Sun, J. Dai, Y. Guo, C. Wu, F. Hu, J. Zhao, X. Zeng and Y. Xie, Nanoscale, 2014, 6, 8359–8367.
135. P. Liu, J. Zhu, J. Zhang, P. Xi, K. Tao, D. Gao and D. Xue, ACS Energy Lett., 2017, 2, 745–752.
136. Z. Zheng, L. Yu, M. Gao, X. Chen, W. Zhou, C. Ma, L. Wu, J. Zhu, X. Meng, J. Hu, Y. Tu, S. Wu, J. Mao, Z. Tian and D. Deng, Nat. Commun., 2020, 11, 3315.
137. D. C. Nguyen, T. L. L. Doan, S. Prabhakaran, D. T. Tran, D. H. Kim, J. H. Lee and N. H. Kim, Nano Energy, 2021, 82, 105750.
138. S. Bolar, S. Shit, N. C. Murmu, P. Samanta and T. Kuila, ACS Appl. Mater. Interfaces, 2021, 13, 765–780.
139. Q. Xiong, Y. Wang, P. F. Liu, L. R. Zheng, G. Wang, H. G. Yang, P. K. Wong, H. Zhang and H. Zhao, Adv. Mater., 2018, 30, 1801450.
140. Y. Shi, Y. Zhou, D.-R. Yang, W.-X. Xu, C. Wang, F.-B. Wang, J.-J. Xu, X.-H. Xia and H.-Y. Chen, J. Am. Chem. Soc., 2017, 139, 15479–15485.
141. L. Cao, Q. Luo, W. Liu, Y. Lin, X. Liu, Y. Cao, W. Zhang, Y. Wu, J. Yang, T. Yao and S. Wei, Nat. Catal., 2019, 2, 134–141.
142. A. Grimaud, O. Diaz-Morales, B. Han, W. T. Hong, Y.-L. Lee, L. Giordano, K. A. Stoerzinger, M. T. Koper and Y. Shao-Horn, Nat. Chem., 2017, 9, 457–465.
143. C. Yang, C. Laberty-Robert, D. Batuk, G. Cibin, A. V. Chadwick, V. Pimenta, W. Yin, L. Zhang, J.-M. Tarascon and A. Grimaud, J. Phys. Chem. Lett., 2017, 8, 3466–3472.
144. N. Zhang, X. Feng, D. Rao, X. Deng, L. Cai, B. Qiu, R. Long, Y. Xiong, Y. Lu and Y. Chai, Nat. Commun., 2020, 11, 4066.
145. X. Rong, J. Parolin and A. M. Kolpak, ACS Catal., 2016, 6, 1153–1158.
146. Y. Sun, H. Liao, J. Wang, B. Chen, S. Sun, S. J. H. Ong, S. Xi, C. Diao, Y. Du, J.-O. Wang, M. B. H. Breese, S. Li, H. Zhang and Z. J. Xu, Nat. Catal., 2020, 3, 554–563.
147. Z.-F. Huang, J. Song, Y. Du, S. Xi, S. Dou, J. M. V. Nsanzimana, C. Wang, Z. J. Xu and X. Wang, Nat. Energy, 2019, 4, 329–338.
148. A. Grimaud, W. T. Hong, Y. Shao-Horn and J.-M. Tarascon, Nat. Mater., 2016, 15, 121–126.
149. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
150. J. T. Mefford, X. Rong, A. M. Abakumov, W. G. Hardin, S. Dai, A. M. Kolpak, K. P. Johnston and K. J. Stevenson, Nat. Commun., 2016, 7, 11053.
151. J. S. Yoo, X. Rong, Y. Liu and A. M. Kolpak, ACS Catal., 2018, 8, 4628–4636.
152. J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184.
153. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89.
154. I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165.
155. R. Zhang, L. Wang, L. Pan, Z. Chen, W. Jia, X. Zhang and J.-J. Zou, Appl. Catal., B, 2020, 277, 119237.
156. A. D. Doyle, J. H. Montoya and A. Vojvodic, ChemCatChem, 2015, 7, 738–742.
157. D. R. Kauffman, X. Deng, D. C. Sorescu, T.-D. Nguyen-Phan, C. Wang, C. M. Marin, E. Stavitski, I. Waluyo and A. Hunt, ACS Catal., 2019, 9, 5375–5382.
158. X. Li, D. Jiao, Y. Liang and J.-X. Zhao, Sustainable Energy Fuels, 2021, 5, 3330–3339.
159. X. Xu, H. Xu and D. Cheng, Nanoscale, 2019, 11, 20228–20237.
160. D. Friebel, M. W. Louie, M. Bajdich, K. E. Sanwald, Y. Cai, A. M. Wise, M.-J. Cheng, D. Sokaras, T.-C. Weng, R. Alonso-Mori, R. C. Davis, J. R. Bargar, J. K. Nørskov, A. Nilsson and A. T. Bell, J. Am. Chem. Soc., 2015, 137, 1305–1313.
161. B. Zhang, X. Zheng, O. Vozny, R. Comin, M. Bajdich, M. Garcia-Melchor, J. Xu, M. Liu, F. P. García de Arquer, C. T. Dinh, F. Fan, M. Yuan, E. Yassitepe, A. Janmohamed, N. Chen, T. Regier, L. Han, H. L. Xin, L. Zheng, H. Yang, A. Vojvodic and E. H. Sargent, Science, 2016, 352, 333–337.
162. J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385.
163. C. Wei, Z. Feng, G. G. Scherer, J. Barber, Y. Shao-Horn and Z. J. Xu, Adv. Mater., 2017, 29, 1606800.
164. S. Zhou, X. Miao, X. Zhao, C. Ma, Y. Qiu, Z. Hu, J. Zhao, L. Shi and J. Zeng, Nat. Commun., 2016, 7, 11510.
165. B. Zhao, L. Zhang, D. Zhen, S. Yoo, Y. Ding, D. Chen, Y. Chen, Q. Zhang, B. Doyle, X. Xiong and M. Liu, Nat. Commun., 2017, 8, 14586.
166. A. Grimaud, K. J. May, C. E. Carlton, Y.-L. Lee, M. Risch, W. T. Hong, J. Zhou and Y. Shao-Horn, Nat. Commun., 2013, 4, 2439.
167. J. Lee, H. Jung, Y. S. Park, S. Woo, N. Kwon, Y. Xing, S. H. Oh, S. M. Choi, J. W. Han and B. Lim, Chem. Eng. J., 2021, 420, 127670.
168. J. Suntivich, W. T. Hong, Y.-L. Lee, J. M. Rondinelli, W. Yang, J. B. Goodenough, B. Dabrowski, J. W. Freeland and Y. Shao-Horn, J. Phys. Chem. C, 2014, 118, 1856–1863.
169. H. Lee, O. Gwon, K. Choi, L. Zhang, J. Zhou, J. Park, J.-W. Yoo, J.-Q. Wang, J. H. Lee and G. Kim, ACS Catal., 2020, 10, 4664–4670.
170. Y. Duan, S. Sun, S. Xi, X. Ren, Y. Zhou, G. Zhang, H. Yang, Y. Du and Z. J. Xu, Chem. Mater., 2017, 29, 10534–10541.
171. I. Yamada, A. Takamatsu, K. Asai, T. Shirakawa, H. Ohzuku, A. Seno, T. Uchimura, H. Fujii, S. Kawaguchi, K. Wada, H. Ikeno and S. Yagi, J. Phys. Chem. C, 2018, 122, 27885–27892.
172. W. T. Hong, R. E. Welsch and Y. Shao-Horn, J. Phys. Chem. C, 2016, 120, 78–86.
173. Y. Zhou, S. Sun, J. Song, S. Xi, B. Chen, Y. Du, A. C. Fisher, F. Cheng, X. Wang, H. Zhang and Z. J. Xu, Adv. Mater., 2018, 30, 1802912.
174. X. Huang, J. Wang, H. B. Tao, H. Tian and H. Xu, Chem. Sci., 2019, 10, 3340–3345.
175. Y. Zhu, H. A. Tahini, Z. Hu, Z. G. Chen, W. Zhou, A. C. Komarek, Q. Lin, H. J. Lin, C. T. Chen, Y. Zhong, M. T. Fernandez-Diaz, S. C. Smith, H. Wang, M. Liu and Z. Shao, Adv. Mater., 2020, 32, 1905025.
176. Y. Zhu, Q. Lin, Z. Hu, Y. Chen, Y. Yin, H. A. Tahini, H. J. Lin, C. T. Chen, X. Zhang, Z. Shao and H. Wang, Small, 2020, 16, 2001204.
177. X. Wang, Z. Pan, X. Chu, K. Huang, Y. Cong, R. Cao, R. Sarangi, L. Li, G. Li and S. Feng, Angew. Chem., Int. Ed., 2019, 58, 11720–11725.
178. D. Guan, J. Zhou, Z. Hu, W. Zhou, X. Xu, Y. Zhong, B. Liu, Y. Chen, M. Xu, H. J. Lin, C. T. Chen, J. Q. Wang and Z. Shao, Adv. Funct. Mater., 2019, 29, 1900704.
179. F. Van Buren, G. Broers, A. Bouman and C. Boesveld, J. Electroanal. Chem. Interfacial Electrochem., 1978, 87, 389–394.
180. S. Royer, D. Duprez and S. Kaliaguine, Catal. Today, 2006, 112, 99–102.
181. Y. Pan, X. Xu, Y. Zhong, L. Ge, Y. Chen, J.-P. M. Veder, D. Guan, R. O'Hayre, M. Li, G. Wang, H. Wang, W. Zhou and Z. Shao, Nat. Commun., 2020, 11, 2002.
182. P. Li, X. Duan, Y. Kuang, Y. Li, G. Zhang, W. Liu and X. Sun, Adv. Energy Mater., 2018, 8, 1703341.
183. T. Ling, D.-Y. Yan, Y. Jiao, H. Wang, Y. Zheng, X. Zheng, J. Mao, X.-W. Du, Z. Hu, M. Jaroniec and S. Z. Qiao, Nat. Commun., 2016, 7, 12876.
184. A. Parra-Puerto, K. L. Ng, K. Fahy, A. E. Goode, M. P. Ryan and A. Kucernak, ACS Catal., 2019, 9, 11515–11529.
185. R. Solmaz, A. Döner and G. Kardaş, Int. J. Hydrogen Energy, 2009, 34, 2089–2094.
186. A. Zadick, L. Dubau, N. Sergent, G. Berthome and M. Chatenet, ACS Catal., 2015, 5, 4819–4824.
187. Y. Zhang, L. Gao, E. J. M. Hensen and J. P. Hofmann, ACS Energy Lett., 2018, 3, 1360–1365.
188. T. Wu, S. Sun, J. Song, S. Xi, Y. Du, B. Chen, W. A. Sasangka, H. Liao, C. L. Gan, G. G. Scherer, L. Zeng, H. Wang, H. Li, A. Grimaud and Z. J. Xu, Nat. Catal., 2019, 2, 763–772.
189. A. C. Garcia, T. Touzalin, C. Nieuwland, N. Perini and M. T. Koper, Angew. Chem., Int. Ed., 2019, 58, 12999–13003.
190. S. H. Chang, N. Danilovic, K.-C. Chang, R. Subbaraman, A. P. Paulikas, D. D. Fong, M. J. Highland, P. M. Baldo, V. R. Stamenkovic, J. W. Freeland, J. A. Eastman and N. M. Markovic, Nat. Commun., 2014, 5, 4191.
191. E. Fabbri and T. J. Schmidt, ACS Catal., 2018, 8, 9765–9774.
192. T. Binninger, R. Mohamed, K. Waltar, E. Fabbri, P. Levecque, R. Kötz and T. J. Schmidt, Sci. Rep., 2015, 5, 12167.
193. D. A. Lutterman, Y. Surendranath and D. G. Nocera, J. Am. Chem. Soc., 2009, 131, 3838–3839.
194. M. Huynh, D. K. Bediako and D. G. Nocera, J. Am. Chem. Soc., 2014, 136, 6002–6010.
195. E. Fabbri, M. Nachtegaal, T. Binninger, X. Cheng, B.-J. Kim, J. Durst, F. Bozza, T. Graule, R. Schäublin, L. Wiles, M. Pertoso, N. Danilovic, K. E. Ayers and T. J. Schmidt, Nat. Mater., 2017, 16, 925–931.
196. Y. T. Kim, P. P. Lopes, S. A. Park, A. Y. Lee, J. Lim, H. Lee, S. Back, Y. Jung, N. Danilovic, V. Stamenkovic, J. Erlebacher, J. Snyder and N. M. Markovic, Nat. Commun., 2017, 8, 1449.
197. J. W. Bennett, D. Jones, X. Huang, R. J. Hamers and S. E. Mason, Environ. Sci. Technol., 2018, 52, 5792–5802.
198. A. Abbaspour-Tamijani, J. W. Bennett, D. T. Jones, N. Cartagena-Gonzalez, Z. R. Jones, E. D. Laudadio, R. J. Hamers, J. A. Santana and S. E. Mason, Appl. Surf. Sci., 2020, 515, 145865.
199. C. Kuai, Z. Xu, C. Xi, A. Hu, Z. Yang, Y. Zhang, C.-J. Sun, L. Li, D. Sokaras, C. Dong, S.-Z. Qiao, X.-W. Du and F. Lin, Nat. Catal., 2020, 3, 743–753.
200. A. Bergmann, T. E. Jones, E. M. Moreno, D. Teschner, P. Chernev, M. Gliech, T. Reier, H. Dau and P. Strasser, Nat. Catal., 2018, 1, 711–719.
201. H. Kwon, W. Lee and J. W. Han, RSC Adv., 2016, 6, 69782–69789.
202. M. Choi, I. A. Ibrahim, K. Kim, J. Y. Koo, S. J. Kim, J.-W. Son, J. W. Han and W. Lee, ACS Appl. Mater. Interfaces, 2020, 12, 21494–21504.
203. K. A. Persson, B. Waldwick, P. Lazic and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235438.
204. D. Y. Chung, P. P. Lopes, P. F. B. D. Martins, H. He, T. Kawaguchi, P. Zapol, H. You, D. Tripkovic, D. Strmcnik, Y. Zhu, S. Seifert, S. Lee, V. R. Stamenkovic and N. M. Markovic, Nat. Energy, 2020, 5, 222–230.
205. K. Obata and K. Takanabe, Angew. Chem., Int. Ed., 2018, 57, 1616–1620.
206. G. Zhang, X. Zheng, Q. Xu, J. Zhang, W. Liu and J. Chen, J. Mater. Chem. A, 2018, 6, 4793–4800.
207. K. Maiti, K. Kim, K.-J. Noh and J. W. Han, Chem. Eng. J., 2021, 423, 130233.
208. J. Su, Y. Yang, G. Xia, J. Chen, P. Jiang and Q. Chen, Nat. Commun., 2017, 8, 14969.
209. J. A. Gauthier, C. F. Dickens, L. D. Chen, A. D. Doyle and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 11455–11463.
210. P. Gono, F. Ambrosio and A. Pasquarello, J. Phys. Chem. C, 2019, 123, 18467–18474.
211. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106.
212. F. Calle-Vallejo, R. F. de Morais, F. Illas, D. Loffreda and P. Sautet, J. Phys. Chem. C, 2019, 123, 5578–5582.
213. V. R. Stamenkovic, D. Strmcnik, P. P. Lopes and N. M. Markovic, Nat. Mater., 2017, 16, 57–69.
214. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943.
215. L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
216. S. Lutfalla, V. Shapovalov and A. T. Bell, J. Chem. Theory Comput., 2011, 7, 2218–2223.
217. E. A. Carter, Science, 2008, 321, 800–803.
218. J. S. Yoo, Y. Liu, X. Rong and A. M. Kolpak, J. Phys. Chem. Lett., 2018, 9, 1473–1479.
219. P. Li, M. Wang, X. Duan, L. Zheng, X. Chen, Y. Zhang, Y. Kuang, Y. Li, Q. Ma, Z. Feng, W. Liu and X. Sun, Nat. Commun., 2019, 10, 1711.
220. H. N. Nong, T. Reier, H.-S. Oh, M. Gliech, P. Paciok, T. H. T. Vu, D. Teschner, M. Heggen, V. Petkov, R. Schlögl, T. Jones and P. Strasser, Nat. Catal., 2018, 1, 841–851.
221. F. Dionigi and P. Strasser, Adv. Energy Mater., 2016, 6, 1600621.
222. M. Kim, J. Park, H. Ju, J. Y. Kim, H.-S. Cho, C.-H. Kim, B.-H. Kim and S. W. Lee, Energy Environ. Sci., 2021, 14, 3053–3063.
223. R. R. Rao, M. J. Kolb, L. Giordano, A. F. Pedersen, Y. Katayama, J. Hwang, A. Mehta, H. You, J. R. Lunger, H. Zhou, N. B. Halck, T. Vegge, I. Chorkendorff, I. E. L. Stephens and Y. Shao-Horn, Nat. Catal., 2020, 3, 516–525.
224. C. Roy, B. Sebok, S. Scott, E. Fiordaliso, J. Sørensen, A. Bodin, D. Trimarco, C. Damsgaard, P. Vesborg and O. Hansen, Nat. Catal., 2018, 1, 820–829.
225. B. Wang, K. Zhao, Z. Yu, C. Sun, Z. Wang, N. Feng, L. Mai, Y. Wang and Y. Xia, Energy Environ. Sci., 2020, 13, 2200–2208.
226. X. Bo, R. K. Hocking, S. Zhou, Y. Li, X. Chen, J. Zhuang, Y. Du and C. Zhao, Energy Environ. Sci., 2020, 13, 4225–4237.
227. P. Christopher, ACS Energy Lett., 2018, 3, 3015–3016.
228. P. Quaino, F. Juarez, E. Santos and W. Schmickler, Beilstein J. Nanotechnol., 2014, 5, 846–854.
229. H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 3722–3730.
230. M. Bajdich, M. García-Mota, A. Vojvodic, J. K. Nørskov and A. T. Bell, J. Am. Chem. Soc., 2013, 135, 13521–13530.
231. Y. Jeung, H. Jung, D. Kim, H. Roh, C. Lim, J. W. Han and K. Yong, J. Mater. Chem. A, 2021, 9, 12203–12213.
232. S. Sun, X. Zhou, B. Cong, W. Hong and G. Chen, ACS Catal., 2020, 10, 9086–9097.
233. K. Qu, Y. Zheng, Y. Jiao, X. Zhang, S. Dai and S. Z. Qiao, Adv. Energy Mater., 2017, 7, 1602068.
234. J. Luo, J.-H. Im, M. T. Mayer, M. Schreier, M. K. Nazeeruddin, N.-G. Park, S. D. Tilley, H. J. Fan and M. Grätzel, Science, 2014, 345, 1593–1596.
235. J. Li, Y. Wang, T. Zhou, H. Zhang, X. Sun, J. Tang, L. Zhang, A. M. Al-Enizi, Z. Yang and G. Zheng, J. Am. Chem. Soc., 2015, 137, 14305–14312.
236. D. Kong, J. J. Cha, H. Wang, H. R. Lee and Y. Cui, Energy Environ. Sci., 2013, 6, 3553–3558.
237. Z. Peng, S. Yang, D. Jia, P. Da, P. He, A. M. Al-Enizi, G. Ding, X. Xie and G. Zheng, J. Mater. Chem. A, 2016, 4, 12878–12883.
238. S. Khatun, H. Hirani and P. Roy, J. Mater. Chem. A, 2021, 9, 74–86.
239. S. r. Dresp, F. Dionigi, M. Klingenhof and P. Strasser, ACS Energy Lett., 2019, 4, 933–942.
240. F. Dionigi, T. Reier, Z. Pawolek, M. Gliech and P. Strasser, ChemSusChem, 2016, 9, 962–972.
241. K. S. Exner, I. Sohrabnejad-Eskan and H. Over, ACS Catal., 2018, 8, 1864–1879.
242. K. S. Exner, J. Anton, T. Jacob and H. Over, Angew. Chem., Int. Ed., 2016, 55, 7501–7504.
243. K. S. Exner, J. Anton, T. Jacob and H. Over, ChemElectroChem, 2015, 2, 707–713.
244. K. S. Exner, J. Anton, T. Jacob and H. Over, Angew. Chem., Int. Ed., 2014, 53, 11032–11035.
245. K. S. Exner, J. Anton, T. Jacob and H. Over, Electrochim. Acta, 2014, 120, 460–466.
246. L. Rebollar, S. Intikhab, N. J. Oliveira, Y. Yan, B. Xu, I. T. McCrum, J. D. Snyder and M. H. Tang, ACS Catal., 2020, 10, 14747–14762.
247. J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Chem. Phys. Lett., 2008, 466, 68–71.
248. J. Rossmeisl, K. Chan, E. Skúlason, M. E. Björketun and V. Tripkovic, Catal. Today, 2016, 262, 36–40.
249. K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2015, 6, 2663–2668.
250. I. Spanos, M. F. Tesch, M. Yu, H. Tüysüz, J. Zhang, X. Feng, K. Müllen, R. Schlögl and A. K. Mechler, ACS Catal., 2019, 9, 8165–8170.
251. J. M. P. Martirez and E. A. Carter, ACS Catal., 2020, 10, 2720–2734.
252. S. Klaus, Y. Cai, M. W. Louie, L. Trotochaud and A. T. Bell, J. Phys. Chem. C, 2015, 119, 7243–7254.
253. Y. Zhou and N. López, ACS Catal., 2020, 10, 6254–6261.
254. L. Gong, X. Y. E. Chng, Y. Du, S. Xi and B. S. Yeo, ACS Catal., 2018, 8, 807–814.

---

Footnote

† These authors contributed equally.

---