Open Access Article
Open Access Article238U–206Pb dating of U-series disequilibrium zircons by secondary ion mass spectrometry†
Yong-Shu
Huang
abc,
Qiu-Li
Li
 *abc,
Yu
Liu
*abc,
Yu
Liu
 ac,
Ping-Ping
Liu
d,
Sun-Lin
Chung
e and
Xian-Hua
Li
ac,
Ping-Ping
Liu
d,
Sun-Lin
Chung
e and
Xian-Hua
Li
 abc
abc
aState Key Laboratory of Lithospheric Evolution, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China. E-mail: liqiuli@mail.iggcas.ac.cn
bCollege of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
cInnovation Academy for Earth Science, Chinese Academy of Sciences, Beijing 100029, China
dKey Laboratory of Orogenic Belts and Crustal Evolution, School of Earth and Space Sciences, Peking University, Beijing 100871, China
eInstitute of Earth Sciences, Academia Sinica, Taipei
First published on 19th March 2021
Abstract
Determining the timescales of magma accumulation and storage prior to large eruptions is fundamental to understand the pre-eruptive history of magma reservoirs. Zircon 238U–230Th dating has been widely used to recover the timescales of magma reservoirs younger than 400 ka. However, theoretically and practically, the uncertainties for zircons older than ca. 150 ka, i.e., two half-lives of 230Th, are large because (238U)/(230Th) activities start to stabilize. On the other hand, the accumulation of radiogenic 206Pb begins to increase significantly after two half-lives of 230Th. Herein we theoretically demonstrate a calibration method for SIMS (Secondary Ion Mass Spectrometry) 238U–206Pb dating within the timescales of U-series disequilibrium and apply it to zircons of the 75 ka Youngest Toba Tuff (YTT) in northern Sumatra, Indonesia. The 238U–206Pb dates vary from ca. 665 to 75 ka after common Pb and initial 230Th disequilibrium corrections. This age range agrees with that obtained by previous studies using the 238U–230Th method, but the precision of each age is improved by a factor of three or more. 238U–206Pb and 238U–230Th dating methods have advantages and disadvantages for zircons in U-series disequilibrium. The 238U–230Th method is more suited to samples younger than 150 ka, but requires a large Th/U fractionation between the zircon and magma, and a high U content. The 238U–206Pb method is more appropriate for samples older than 150 ka, but requires high U and low common Pb contents. Our approach improves the precision of in situ dating of zircon in U-series disequilibrium, which will contribute to investigations of the magmatic evolution beneath young volcanoes.
1. Introduction
Zircon is the most widely used U–Pb geochronometer because: (1) it contains abundant U and Th and does not incorporate Pb during crystallization; (2) it is very stable and resistant to disturbance by later hydrothermal activity and weathering; (3) it is widely distributed in most crustal rocks; (4) it can be used to investigate the history of the lithosphere together with a range of geochemical proxies. Given these properties, the U–Pb dating of zircon in young volcanic rocks can be used to investigate magmatic evolution in crustal magma chambers.1–4For young samples within the time-scale of U-series disequilibrium, radiogenic lead is only a part of radiogenic daughters decayed from uranium because of a number of intermediate nuclides with varying half-lives. In a U-bearing magmatic system that has remained undisturbed for ∼0.5 Ma, a state of secular equilibrium becomes established between the abundance of parent and daughter nuclides in the U-series decay chain, such that the decay rate (or “activity”) of each intermediate daughter nuclide in the chain is equal to that of the parent.5 During the crystallization of zircon in magma, nuclides in the U-series decay chain can become fractionated relative to one another, due to their different chemical properties or the lattice sites they occupy. This results in U-series disequilibrium, which can be utilized as dating tools. The 238U–230Th system is most widely used for the study of igneous systems that are in U-series disequilibrium.1,6,7 The applicable age range of 238U–230Th dating is ca. 400 ka, based on the assumption that its activity will be within the error of secular equilibrium after five half-lives of 230Th. However, the dating uncertainty will increase gradually as the (238U)/(230Th) activities begin to change less after two half-lives of 230Th (ca. 150 ka). Interestingly, the abundance of radiogenic 206Pb in zircon begins to surpass that of 230Th at that time. Though 238U–206Pb dating was never confidentially applied to date zircons within the time scale of U-series disequilibrium, it has potential to improve the precision of zircon ages older than 150 ka. However, there are many challenges involved in U–Pb dating such young zircons. The limited radiogenic Pb that has been accumulated may result in a poor precision of the isotopic measurements.8 In addition, robust correction for common Pb and initial 230Th disequilibrium in young samples under U-series disequilibrium is not straightforward. Therefore, it is necessary to establish a set of calibration and testing methods for 238U–206Pb dating on zircon within the time scale of U-series disequilibrium.
In this paper, we first theoretically derive the formulae that include the common Pb and initial 230Th disequilibrium corrections for U-series disequilibrium and develop an analytical protocol for ion microprobe U–Pb dating of young zircon. We then present 238U–206Pb dating results for zircons extracted from the 75 ka YTT collected from around the Toba Caldera in northern Sumatra, Indonesia. Our corrected results are consistent with the age range obtained by previous 238U–230Th studies,4 but have significantly improved precision, which verifies our correction protocols. In addition, we evaluate the applicability and the advantages and disadvantages of zircon 238U–206Pb and 238U–230Th dating.
2. Calibration protocols
An excess or deficit of intermediate nuclides incorporated during zircon crystallization from young magma would result in an erroneous U–Pb date, and thus a correction for the presence of initial intermediate nuclides is essential. Given that the abundance of a nuclide is directly proportional to its half-life (i.e., inversely proportional to its decay constant), intermediate nuclides with short half-lives have little effect on dating. The negligible fractionation between 238U and 234U in the magmatic system can also be ignored. In the U-series decay chain, 230Th has a relatively long half-life and its initial disequilibrium can significantly affect the final U–Pb dating result. Owing to Th–U fractionation during zircon crystallization, zircon usually has a lower Th/U ratio than the magma. The deficit of 230Th in zircon slows down the growth of radiogenic 206Pb*, which results in younger U–Pb ages.9 Therefore, an initial 230Th disequilibrium correction is essential for obtaining reliable 238U–206Pb ages. The common Pb correction is another important issue because of the limited amount of radiogenic Pb* in young zircons.2.1 230Th disequilibrium correction
A simplified schematic diagram of the U-series decay chain is shown in Fig. 1a. The radiogenic daughter (D*) of 238U contains three components: the radiogenic daughter 206PbU, the intermediate nuclide 230ThU from the decay of 238U, and negligible amounts of short half-life daughters (Fig. 1b). In addition, the initial 230Th0 incorporated during the crystallization of zircons decays to 206PbTh afterwards. Together with 206PbU, they constitute the radiogenic 206Pb* (Fig. 1a). Therefore, the measured 206Pbm contains three components: the 206PbU derived from the decay of 238U, the 206PbTh derived from the decay of initial 230Th0 and the common 206Pb (i.e., 206Pbc) (Fig. 1c). Therefore, the radiogenic daughter (D*) of 238U can be determined from the following equation:| D* = 206Pbm − 206PbTh + 230ThU − 206Pbc | (1) |
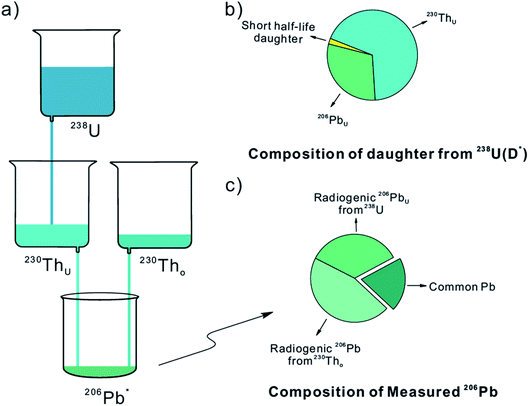 | ||
| Fig. 1 (a) Simplified diagram of the U-series decay chain; (b) composition of the daughters of 238U; (c) composition of the measured 206Pb. | ||
By assuming that the magma is in secular equilibrium, the initial 230Th0 and (230Th/238U)0 of zircon can be calculated from the following equations:
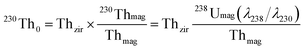 | (2) |
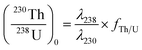 | (3) |
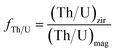 | (4) |
| 206PbTh = 230Th0(1 − e−λ230t) | (5) |
By combining eqn (1)–(5), we obtain an expression describing the (D/238U) ratio and age (t):
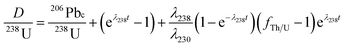 | (6) |
2.2 Common lead correction
The common Pb correction involves calculating the proportion of common Pb relative to total 206Pb, i.e., f206, where total 206Pb is the sum of common and radiogenic Pb. Radiogenic Pb is treated as being solely derived from the decay of 238U (D*) for samples in secular equilibrium, but not suitable for zircons in U-series disequilibrium. Thus, we use D to represent the total radiogenic daughters of 238U (D*) plus common Pb: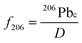 | (7) |
Having determined the proportion of common Pb, the ratio between the radiogenic daughter and 238U can be determined as
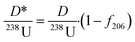 | (8) |
Typically, the proportion of common Pb (f206) can be calculated from the non-radiogenic 204Pb. However, due to the low 204Pb abundance of zircon and potential isobaric interference during measurement, the 204Pb correction can result in large uncertainties. Fortunately, 207Pb/206Pb ratios vary little (0.058–0.046) since the Phanerozoic and the signal intensity of 207Pb is about 15 times higher than that of 204Pb, which significantly improves the analytical precision.10 Therefore, the 207Pb-based common Pb correction is superior for young zircons and can be expressed as:
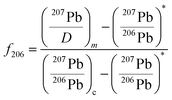 | (9) |
 | (10) |
After solving eqn (1)–(10) and using the approximation λ230 − λ238 ≈ λ230, we obtain an equation describing the relationship between the age (t) and the ratio of D*/238U:
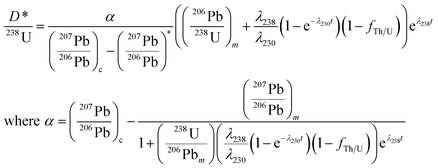 | (11) |
3. Sample analysis
3.1 Sample description
Samples were collected from the Toba Caldera, which is located in the Barisan Mountains in northern Sumatra, West Indonesia. Toba is situated on the Sunda Arc and has produced four major eruptions in its history, including the Haranggoal Dacite Tuff (HDT) at 1.2 Ma,12 the Oldest Toba Tuff (OTT) at 0.84 Ma,13 the Middle Toba Tuff (MTT) at 0.5 Ma,14 and the Youngest Toba Tuff (YTT) at 0.074 Ma.15 We collected rock samples (14SU51 and 14SU03) with a whole-rock Th/U ratio of 3.2 from the most recent YTT eruption. The rhyolitic tuff has variable SiO2 contents (68–76 wt%) and contains phenocrysts of quartz, plagioclase, K-feldspar, mica, and amphibole. Some plagioclase and amphibole are probably xenocrysts derived from rocks as old as 1.5 Ma.163.2 Analytical methods
3.3 Data processing
The linear relationship between ln(206Pb+/238U+) and ln(238U16O2+/238U+) established by the analyses of the standard zircon Plešovice was used to correct for Pb/U instrumental fractionation. The 232Th/238U ratio is calculated from the 232ThO+/(137.818 × 235UO+) ratio20 in conventional zircon U–Pb analytical procedures. The fTh/U value was calculated based on the Th/U ratios of the whole-rock and zircons. This and the measured (206Pb/238U)m and (207Pb/206Pb)m substituted into eqn (11) allow the age of the sample (t) to be determined. However, eqn (11) is a transcendental equation, and was thus solved iteratively. The uncertainties from four factors were propagated into the final age uncertainties: the uncertainties of the measured 206Pb/238U, measured 207Pb/206Pb, common Pb ratio (0.84 ± 0.05), and fractionation factor (fTh/U). The uncertainty of fTh/U is mainly due to the fact that the magma composition surrounding each zircon grain may not be completely homogeneous and that one volcanic glass or whole-rock Th/U measurement may not represent the actual Th/U ratio of the magma. Therefore, an uncertainty of 50% was assigned to the Th/U ratio of the magma (3.2 ± 1.6).3.4 Results
During the analyses, even if we used a high primary beam intensity of ∼35 nA, 207Pb generated very low signal intensity of 1 cps (average at 4 cps), indicating a very low common Pb content. However, this intensity is far above the noise level of the collector (∼0.02 cps), which highlights the reliability of measuring 207Pb in young zircons. The age obtained for the Qinghu standard (160.0 ± 1.3 Ma) is consistent with its recommended value (159.5 ± 0.2 Ma).21 We obtained 41 magmatic zircon ages from the YTT samples (ESI Table 1† and Fig. 2). The zircon U contents vary from 95 to 1630 ppm, with Th/U ∼0.5–1.56 (most are <1). The zircon 238U–206Pb ages range from 665 to 75 ka (Fig. 2).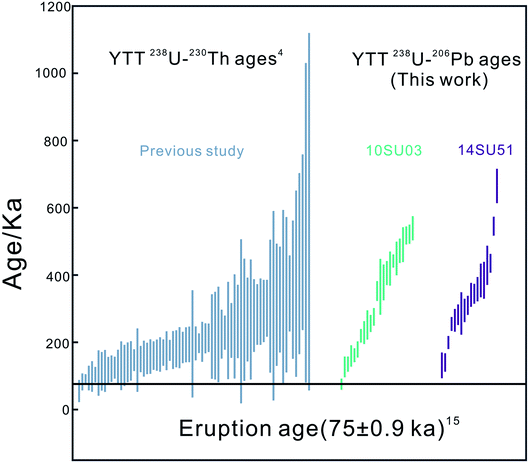 | ||
| Fig. 2 238U–206Pb dating results for magmatic zircon from YTT samples obtained in this study compared with 238U–230Th age data4 (error bars are 2σ). | ||
4. Discussion
4.1 Duration of YTT magma
The 74 ka YTT is the product of a caldera-forming “supereruption” in northern Sumatra. It records the largest volcanic eruption experienced by the modern human race.3,4 It has been recognized that there is a broad correlation between the volume of erupted magma and the repose time. Thus, the YTT supervolcano systems were continuously fed by magma, and the magma reservoir grew quiescently until something triggered the eruption. The frequent occurrence of zircon as inclusions in major phenocryst phases in rhyolites shows that zircon grows prior to eruption. Several features of zircon make it amenable to dating for the magma accumulation history.Reid and Vazquez4 investigated the chronological record of zircon crystallization across the entire compositional spectra of the YTT magma reservoir by using ion microprobe U–Th and U–Pb dates. Depth profile analyses revealed that a single zircon crystal could have grown over several hundred ka. Spot analyses provided a better assessment of the overall distributions of crystallization ages for cores and interiors. Based on the crystallization ages recorded by crystal cores, zircons nucleated at various times before but mostly after the MTT eruption (at 501 ka). As for our results, except two zircon grains with slightly older ages than the MTT eruption time, i.e., 545 ± 28 ka and 665 ± 51 ka, other 39 grains show a continuous distribution between 501 and 75 ka. Though both observations look identical, it is important to consider that the resolution of U–Th dates can be poor when U–Th approaches secular equilibrium. Our U–Pb dates improve age precision 3 times better than U–Th dating for zircon >150 ka.
4.2 Effect of the common Pb correction
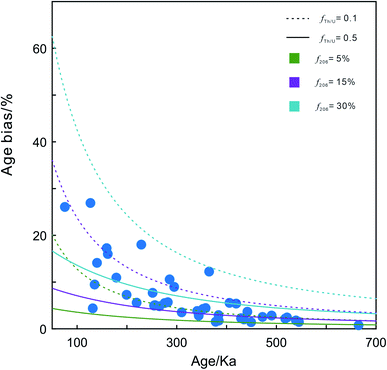
In the study of Guillong et al.,8 the interference of 204Hg made the 204Pb-based common Pb correction impossible as analyzed by LA-ICP-MS. Even the 207Pb signal was too low to be measured precisely; therefore the common Pb correction was not conducted. However, the proportion of common Pb in most zircons from the YTT analyzed by Reid and Vazquez4 was >50%. In this study, the analyzed zircons have very low common Pb contents but still high common Pb proportions (average ∼15%). Hence, the common Pb correction would significantly affect the accuracy of the dating results. The main difficulty with the 204Pb-based common Pb correction for young zircons is the high f206 with large uncertainties due to the low common Pb content. Instead, 207Pb-based common Pb correction is applied to young zircons.Apart from analytical challenges, to the best of our knowledge, the initial 230Th disequilibrium correction on 207Pb/206Pbm during the common Pb correction has not been discussed. We compared the differences in ages with and without the initial 230Th disequilibrium correction on 207Pb/206Pbm (ESI Table 1†). The results show that no initial 230Th disequilibrium correction on 207Pb/206Pbm generates younger ages. Moreover, the degree of the age difference is related to the zircon age (i.e., younger zircons have a larger age difference [Δt]; Fig. 3). In addition, we also obtained the theoretical age difference (Δt) by fixing the fractionation factor (fTh/U) between zircon and melt and the proportion of common Pb (f206; Fig. 3). Notably, the age difference is related not only to the actual zircon age, but also to the fTh/U and f206 values. A higher f206 or smaller fTh/U results in a greater effect on the age bias. We obtained one zircon age (75.4 ± 16.6 ka; ±2σ) that is consistent with the YTT eruption time.15 If the initial 230Th disequilibrium correction on 207Pb/206Pb was neglected, a much younger age of 55.8 ± 12.3 ka (±2σ) would be obtained, which is obviously wrong.
In the 235U–207Pb decay chain, 231Pa also has a long half-life (32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 year). Its deficit or excess can also affect the common Pb correction. However, our understanding of the geochemical behavior of 231Pa is limited. Heaman and LeCheminant22 suggested that the ionic radius of 231Pa is intermediate between those of Th and U; thus its partition coefficient between melt and minerals should also be intermediate between those of Th and U. This implies that initial 231Pa disequilibrium will lead to a deficit of 207Pb. However, Blundy et al.23 showed that 231Pa is very compatible in zircons, based on lattice strain partitioning models. Schmitt24 found that 231Pa is more compatible than U in zircon, based on the analysis of zircons from the Holocene Salton Buttes rhyolite, but that the initial 231Pa disequilibrium leads to only a slight excess of 207Pb. The low 231Pa content in zircon, which is theoretically ∼70 times less than 230Th,24 is difficult to measure precisely. Therefore, the effect of initial 231Pa disequilibrium was not considered in this study. Based on the consistency of the measured results, it is reasonable to infer that the extent of this effect is negligible at current analytical uncertainties.
400 year). Its deficit or excess can also affect the common Pb correction. However, our understanding of the geochemical behavior of 231Pa is limited. Heaman and LeCheminant22 suggested that the ionic radius of 231Pa is intermediate between those of Th and U; thus its partition coefficient between melt and minerals should also be intermediate between those of Th and U. This implies that initial 231Pa disequilibrium will lead to a deficit of 207Pb. However, Blundy et al.23 showed that 231Pa is very compatible in zircons, based on lattice strain partitioning models. Schmitt24 found that 231Pa is more compatible than U in zircon, based on the analysis of zircons from the Holocene Salton Buttes rhyolite, but that the initial 231Pa disequilibrium leads to only a slight excess of 207Pb. The low 231Pa content in zircon, which is theoretically ∼70 times less than 230Th,24 is difficult to measure precisely. Therefore, the effect of initial 231Pa disequilibrium was not considered in this study. Based on the consistency of the measured results, it is reasonable to infer that the extent of this effect is negligible at current analytical uncertainties.
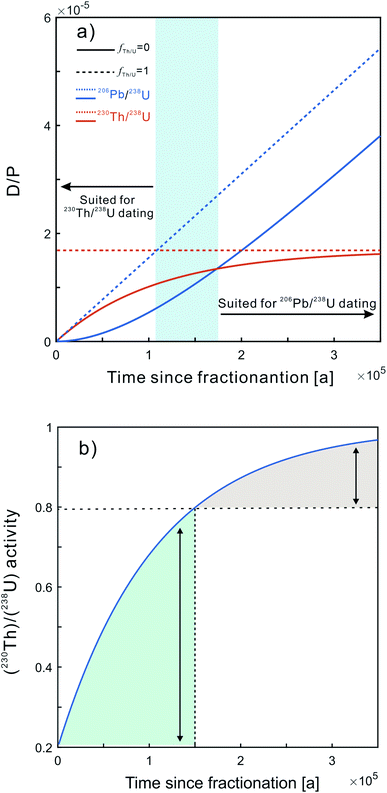
4.3 238U–206Pb versus238U–230Th dating
The U–Pb dating results obtained for the YTT zircons in this study validate that the 238U–206Pb system is applicable to zircon crystallized within the age range of U-series disequilibrium, but the applicable age range needs to be further clarified. Fig. 4a shows the relationship between the 230Th/238U and 206Pb/238U ratios as a function of age. Initially, the zircon 206Pb/238U ratio is much lower than the 230Th/238U ratio. However, the 206Pb/238U ratio will exceed the 230Th/238U ratio after ca. 150 ka (about two half-lives of 230Th) and the difference between the 206Pb/238U and 230Th/238U ratios continues to increase approaching secular equilibrium. The 238U–230Th system can accumulate more daughter isotopes due to the short half-life when the zircon is younger than ca. 150 ka. However, the error multiplication effect on 238U–230Th dating becomes more pronounced as the (238U)/(230Th) activities stabilize gradually after two 230Th half-lives (Fig. 4b). At this point, the radiogenic Pb has increased significantly and the 238U–206Pb system is a better dating method choice. It is noteworthy that the growth curves of 206Pb/238U and 230Th/238U ratios in zircon are related to the Th/U fractionation between the zircon and magma (fTh/U). The shaded field in Fig. 4a represents the range in which the 206Pb/238U and 230Th/238U growth curves intersect when 0 < fTh/U < 1.There are some differences between 238U–206Pb and 238U–230Th dating during SIMS analysis. The analytical precision is positively correlated with the secondary ion signal intensity during SIMS analysis, which mainly depends on the elemental abundance, ion yield, and primary ion beam current. For a given primary ion beam current, the signal intensity can be improved by increasing the elemental abundance and ion yields. However, there are limited variations in the elemental contents of the sample, so it is important to increase the ion yield. Based on previous studies, the Pb+ yield of zircon is about 20–30 cps ppm−1 nA−1,25 which is much higher than that of Th+ (4 cps ppm−1 nA−1),26 when oxygen flooding and a primary O2− beam are used. In order to improve the precision of Th measurements, Th oxide (ThO+) is usually analyzed.27 The yield of ThO+ is around 50 cps ppm−1 nA−1,26 which is significantly higher than that of Th+ and greatly improves the precision of Th measurements. The accumulation of radiogenic 230Th in zircons younger than ca. 150 ka is higher than that of radiogenic 206Pb, which, along with the higher yield of ThO+ than Pb+ during SIMS analysis, makes the 238U–230Th system more appropriate for dating zircon in this age range.
Potential interference during SIMS measurements is another important factor that can affect dating results. During zircon 238U–206Pb dating, heavy rare earth elements, Er, Yb, and Lu, and Hf, O, and Si can combine to form polyatomic interferents with mass numbers similar to those of Pb. These interferents can be filtered out when the mass resolution power of the instrument is >5000 (1% peak height). Interferents on 204Pb include 186W18O (e.g., cassiterite dating) and 232Th144Nd16O22+ (e.g., high-Th monazite and allanite dating) that cannot be filtered out, but for 206Pb and 207Pb, no interferents have been found at a mass resolution of >5000.28 The 230ThO+ signal is crucial for ion microprobe 238U–230Th dating, and possible interferents include 197AuO3H+ from the gold coating and the polyatomic interferent of 232Th212C16O2+ due to the partial overlap of the ion beam on the resin.7 The former can be filtered out at a mass resolution of >5000, whereas the latter is hard to resolve (i.e., it requires a mass resolution of >40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). The use of indium metal instead of epoxy resin can partly eliminate the influence of the latter interference, but the possible presence of C-containing inclusions (e.g., graphite and calcite) cannot be excluded.
000). The use of indium metal instead of epoxy resin can partly eliminate the influence of the latter interference, but the possible presence of C-containing inclusions (e.g., graphite and calcite) cannot be excluded.
In summary, the 238U–230Th and 238U–206Pb systems both have advantages and disadvantages when dating zircons in U-series disequilibrium. The largest obstacle to zircon 238U–206Pb dating in U-series disequilibrium is the very low radiogenic Pb content in young zircons. This can be overcome by selecting suitable zircon grains and improving the analytical precision. We suggest that the 238U–206Pb dating method can yield good results for zircon grains with f206 < 0.325 and requires a compromise between common lead and U contents. The use of the multiple-collector mode during SIMS analysis is required to obtain the best precision.17
5. Conclusions
We have developed theoretical and analytical methods for zircon U–Pb dating within the age range of U-series disequilibrium, including corrections for initial 230Th disequilibrium related to the 206Pb/238U and 207Pb/206Pb ratios used for common Pb correction. To verify our method, we dated young zircons from the YTT, which yielded ages similar to those obtained by the 238U–230Th method, but with a significant improvement in precision. From a theoretical and practical perspective, the 238U–230Th method is best suited for zircons younger than 150 ka and requires a high zircon U content and large Th/U fractionation between the magma and zircon. The 238U–206Pb method is advantageous for samples older than 150 ka, but requires a low common Pb content in zircon.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank H. X. Ma for zircon mounting. We are grateful to Dr Xiaoping Xia and one anonymous reviewer who helped to improve the content and presentation. This research was funded by the National Key R&D Program of China (2018YFA0702600) and National Natural Science Foundation of China (Grants 41773044 and 41773047).References
- M. R. Reid, C. D. Coath, T. M. Harrison and K. D. McKeegan, Earth Planet. Sci. Lett., 1997, 150, 27–39 CrossRef CAS.
- D. Szymanowski, J.-F. Wotzlaw, B. S. Ellis, O. Bachmann, M. Guillong and A. von Quadt, Nat. Geosci., 2017, 10, 777–782 CrossRef CAS.
- M. R. Reid, Elements, 2008, 4, 23–28 CrossRef.
- M. R. Reid and J. A. Vazquez, Geochem., Geophys., Geosyst., 2017, 18, 156–177 CrossRef CAS.
- H. Bateman, Proc. Cambridge Philos. Soc., 1908, 1908(15), 423–427 Search PubMed.
- J. A. Vazquez and M. R. Reid, Contrib. Mineral. Petrol., 2002, 144, 274–285 CrossRef CAS.
- A. K. Schmitt, D. F. Stockli and B. P. Hausback, J. Volcanol. Geotherm. Res., 2006, 158, 281–295 CrossRef CAS.
- M. Guillong, A. von Quadt, S. Sakata, I. Peytcheva and O. Bachmann, J. Anal. At. Spectrom., 2014, 29, 963–970 RSC.
- U. Schärer, Earth Planet. Sci. Lett., 1984, 67, 191–204 CrossRef.
- A. K. Schmitt, M. Grove, T. M. Harrison, O. Lovera, J. Hulen and M. Walters, Geochim. Cosmochim. Acta, 2003, 67, 3423–3442 CrossRef CAS.
- J. t. Stacey and J. Kramers, Earth Planet. Sci. Lett., 1975, 26, 207–221 CrossRef CAS.
- S. Nishimura, E. Abe, T. Yokoyama, S. Wirasantosa and A. Dharma, Paleolimnol. Lake Biwa Jpn. Pleistocene, 1977, 5, 313–332 Search PubMed.
- J. Diehl, T. C. Onstott, C. Chesner and M. Knight, Geophys. Res. Lett., 1987, 14, 753–756 CrossRef CAS.
- C. A. Chesner, W. I. Rose, A. Deino, R. Drake and J. Westgate, Geology, 1991, 19, 200–203 CrossRef.
- D. F. Mark, M. Petraglia, V. C. Smith, L. E. Morgan, D. N. Barfod, B. S. Ellis, N. J. Pearce, J. Pal and R. Korisettar, Quat. Geochronol., 2014, 21, 90–103 CrossRef.
- C. A. Chesner, Quat. Int., 2012, 258, 5–18 CrossRef.
- X.-H. Li, Y. Liu, Q.-L. Li, C.-H. Guo and K. R. Chamberlain, Geochem., Geophys., Geosyst., 2009, 10, Q04010 Search PubMed.
- M. Whitehouse, S. Claesson, T. Sunde and J. Vestin, Geochim. Cosmochim. Acta, 1997, 61, 4429–4438 CrossRef CAS.
- Y. Liu, Q.-L. Li, G.-Q. Tang, X.-H. Li and Q.-Z. Yin, J. Anal. At. Spectrom., 2015, 30, 979–985 RSC.
- J. Hiess, D. J. Condon, N. McLean and S. R. Noble, Science, 2012, 335, 1610–1614 CrossRef CAS PubMed.
- X. Li, G. Tang, B. Gong, Y. Yang, K. Hou, Z. Hu, Q. Li, Y. Liu and W. Li, Chin. Sci. Bull., 2013, 58, 4647–4654 CrossRef CAS.
- L. Heaman and A. LeCheminant, Chem. Geol., 2001, 172, 77–93 CrossRef CAS.
- J. Blundy and B. Wood, Earth Planet. Sci. Lett., 2003, 210, 383–397 CrossRef CAS.
- A. K. Schmitt, Am. Mineral., 2007, 92, 691–694 CrossRef CAS.
- Y. Liu, X.-H. Li, Q.-L. Li, G.-Q. Tang and Q.-Z. Yin, J. Anal. At. Spectrom., 2011, 26, 845–851 RSC.
- Q. Li, Y. Liu, G. Tang, K. Wang, X. Ling and J. Li, J. Anal. At. Spectrom., 2018, 33, 1536–1544 RSC.
- I. N. Bindeman, A. K. Schmitt and J. W. Valley, Contrib. Mineral. Petrol., 2006, 152, 649–665 CrossRef CAS.
- T. Tsunogae and H. Yurimoto, Geochem. J., 1995, 29, 197–205 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ja00510j |
| This journal is © The Royal Society of Chemistry 2021 |