Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Charge-transfer engineering strategies for tailored ionic conductivity at oxide interfaces
F.
Gunkel
 *,
D. V.
Christensen
*,
D. V.
Christensen
 and
N.
Pryds
and
N.
Pryds
 *
*
Department of Energy Conversion and Storage, Technical University of Denmark, DK-2800 Kgs., Lyngby, Denmark. E-mail: felgu@dtu.dk
First published on 13th August 2020
Abstract
Exploiting the electronic charge-transfer across oxide interfaces has emerged as a versatile tool to tailor the electronic and magnetic properties of oxides. Such charge-transfer concepts have been applied to drive insulating oxides into metallic states, to trigger magnetism in non-magnetic oxides, and to render gate-tunable low-dimensional superconductors. While the richness in the electronic and magnetic properties of these systems is the main focus of research, the implications for the ionic transport at oxide interfaces have not received much attention so far. In this communication, we propose that charge-transfer strategies can also be applied to boost ionic charge carrier concentrations at interfaces by orders of magnitude. Based on numerical space-charge modeling, we will illustrate how the ‘p-type’ charge-transfer predicted between SrO-terminated SrTiO3 and LaAlO3 may foster 2-dimensional oxygen ion conduction at the interface. The ion conduction is effectively separated from impurity dopants, which may allow large concentrations of oxygen vacancies to be achieved in the absence of trapping phenomena. The interface promises high ionic conductivity with nanoscale confinement, potentially allowing the design of field-tunable ionic devices.
The rich physical and chemical properties of complex oxides have sparked new fields of research based on electronic and ionic charge transport.1–4 Various sustainable electronics and energy concepts employ novel oxide devices that exhibit tailored electronic properties (electronics), tailored ionic properties (ionics), or both (ionotronics) by combining appropriate oxides with nanoscale precision.3,5–7
Controlling ions in these systems in a similar way to how we control electrons reflects an overarching goal within the field: controlled ionic conduction and atomically defined ionic defect structures enable the realization of electrochemical devices such as batteries, fuel cells, electrolyzers, gas separation membranes, memristive memory devices, sensors, or tailored field-effect and spintronic devices.4,8–15 A major challenge in the field is the precise control of the sluggish motion of ‘large’ and ‘slow’ ions, which typically limits charging times in batteries, operation temperatures of fuel cells, and switching performance of memristive memory devices. Novel concepts aiming to enhance, accelerate, and control ionic motion in solids are therefore highly desired.
To date, typical control strategies for oxygen ion conductivity are based on the chemical doping of ion-conducting oxides, i.e. the admixture of lower-valence cations, which proportionally increases the concentration of oxygen vacancies in most oxides.6,16,17 At high concentration, however, the interaction between dopants and associated vacancy defects, or in between the vacancy defects themselves suppresses ion conduction.18–20 Therefore, it is highly desirable to spatially separate dopants and vacancy defects by a heterogeneous doping approach21 or by exploiting space charge layers at grain boundaries.22 Epitaxy of oxides has moreover been used to stabilize ion conducting crystallographic phases17,23 and to harvest strain effects to modulate and lower the energy barriers for ion migration.24–26
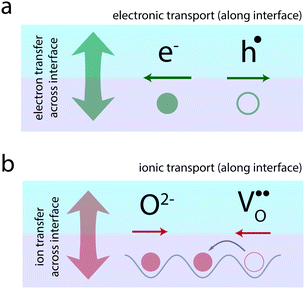
Atomically-defined oxide interfaces have evolved as a huge playground for generating novel electronic phenomena based on the interaction between the charge, spin, orbital, and lattice degrees of freedom of the materials at their atomic interfaces.1,2 A major concept applied in the field is the concept of electronic charge-transfer which employs the transfer of electrons (or holes) between neighboring materials, in order to tailor the electronic transport along their interface (Fig. 1a). Charge-transfer here refers to the static exchange of charge across the interface driven by the alignment of the Fermi level of the two neighboring materials. This charge-transfer process then allows tailoring of the electronic transport along the interface through a confined modulation of the charge carrier concentrations.
Ionic materials, such as oxides and their interfaces, oftentimes need to be considered as mixed ionic–electronic systems,27–33i.e. electronic charges as well as ions participate in the charge-transfer process across the interface (Fig. 1b). The resulting ionic structure often dictates the observed electronic or magnetic behavior.34–37
Beyond electronic phenomena, ionic charge-transfer also yields new opportunities to tailor and functionalize the ionic properties of oxide interfaces: by forcing charge-transfer to take place primarily via exchange of ions from one side of the interface to the other, one may tailor the ionic conductivity along the interface (Fig. 1b). Here, ion-transfer refers to ions (or ionic defects) crossing the interface in order to align their electrochemical potential, resulting in a static ionic space charge layer evolving at the interface. Ion conduction, respectively, refers to the migration of the ions along the interface under an applied electric field. In analogy to electrons and holes, such ionic transport can often be understood in terms of the migration of vacancies of the respective ion. This is particularly the case in oxides, where oxygen ion conduction typically takes place via oxygen vacancy migration in the opposite direction (Fig. 1b). Therefore, if one could use charge-transfer processes to accumulate oxygen vacancies at an interface, one may dramatically enhance the oxygen ion conductivity along the interface.
Similar to the electronic conductivity, ionic conductivity allows two inherent tuning parameters: the total concentration of ionic species that contribute to ion transport and the mobility of individual ions. Charge-transfer phenomena particularly allow tuning of the concentration of ions (and ionic defects) at oxide interfaces. Lattice relaxation and interface-induced strain can lower the energy barriers for ion migration.24–26
In this communication, we discuss the potential of using p-type charge-transfer at atomically tailored oxide interfaces for enhanced oxygen ion conductivity. As we argue, an accumulation layer of oxygen vacancy defects forms at such interfaces as a result of the alignment of the chemical potential for oxygen vacancies across the interface. Here, we particularly address the atomically defined interface of the two complex oxides LaAlO3 and SrTiO3, serving as a model system for charge-transfer oxide interfaces.38–40
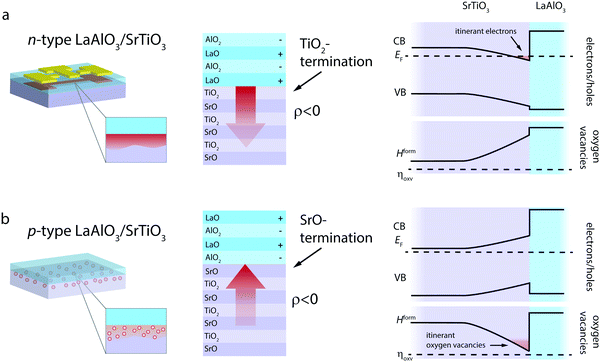
LaAlO3/SrTiO3 interfaces can be achieved in two distinct terminations, denoted as n-type and p-type interfaces (Fig. 2), whereas the charge-transfer process is driven by the polar nature of LaAlO3.39,40 The n-type LaAlO3/SrTiO3 interface, characterized by a TiO2-termination of SrTiO3 and thus an atomic stacking of (TiO2)/(LaO)+ at the interface, reflects a major success story of electronic charge-transfer engineering in complex oxides. Since its discovery in 2004,39 it has been the prime example to demonstrate controlled metal-to-insulator transitions,14,41 gate-tunable superconductivty,42 coexisting ferromagnetism and superconductivity,43 and enhanced electron mobility14,44,45 arising at an oxide interface. These phenomena are based on the net transfer of negative charge (i.e. electrons and/or negatively charged ionic defects) from LaAlO3 into SrTiO3 (Fig. 2a).39,40
In contrast, the p-type interface, characterized by a SrO-termination of SrTiO3 and thus an atomic stacking of (SrO2)/(AlO2)− at the interface, promises to cause the transfer of positive net charge across the interface, i.e. the transfer of holes and/or positively charged ionic defects from LaAlO3 into SrTiO3 (Fig. 2b). In this case, the electric field established at the interface in response to the charge-transfer has the opposite sign as compared to the n-type case (red arrows in Fig. 2).
Experimentally, the p-type LaAlO3/SrTiO3 interface was found to be electronically insulating39,40,46 and only a few studies report on significant hole formation at the interface.47 The observed insulating behavior of p-type interfaces is typically explained by the formation of oxygen vacancies on the SrTiO3 side of the interface, i.e. an ionic compensation of charge-transfer at the interface. This process is detrimental to the potential use of the p-type LaAlO3/SrTiO3 interface in electronic applications. For ionic applications, however, this process is desired and bears the opportunity for oxygen ion conductivity along the interface. As we suggest below, this ionic charge-transfer boosts the ionic charge carrier concentration at the interface by three to four orders of magnitude as compared to the bulk. Moreover, effective spatial separation of ionic charge carriers and potential trapping defects can be achieved, yielding a promising starting point also for enhanced mobility of the vacancies. To demonstrate this, we conducted thermodynamic space-charge calculations that allow evaluation of both electronic and ionic contributions to the charge-transfer at the interface.38
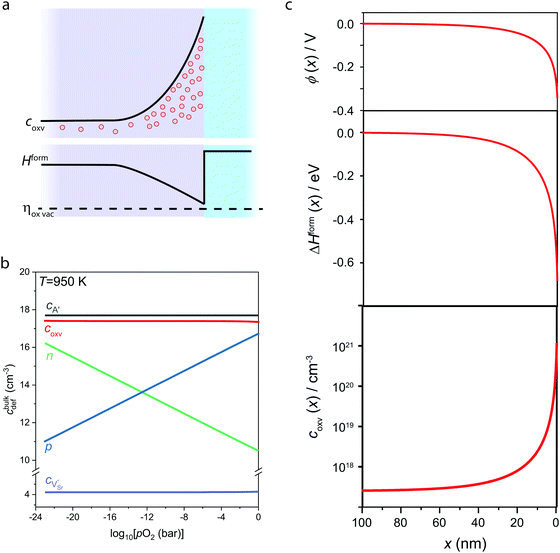
In Fig. 3, we consider the p-type LaAlO3/SrTiO3 interface exposed to elevated temperature (T = 950 K). At this temperature, oxygen ions have sufficient mobility to participate in the charge-transfer process.48 In order to model the ionic properties of the interface, we assume that the atomically defined termination at the interface forces a charge-transfer of order of σq ≈ +1 × 1014 e cm−2,38–40 which defines the electric field at the interface via the Gauss law. We then self-consistently calculate the space-potential ϕ(x) at the interface (Fig. 3c) by solving Poisson's equation
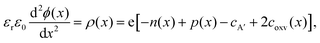 | (1) |
The bulk concentrations of electronic and ionic defects serve as boundary conditions, and are obtained from standard defect chemical treatment of SrTiO3 with a typical background impurity concentration of cA′ = 5 × 1017 cm−2, which yields bulk concentrations of electrons, holes, and oxygen vacancies in different oxygen environments (Fig. 3b).29,48–50 Notably, the oxygen vacancy concentration in the bulk SrTiO3 is almost constant and within the ppm level over a wide range of oxygen pressures, as under these conditions oxygen vacancies primarily compensate impurity dopants which are unavoidably incorporated during thin film or single crystal synthesis. As ionics applications typically need to operate in oxygen or oxygen-rich atmospheres the high oxygen pressure regime (10−8 ⪅ pO2/bar ⪅ 1) is most relevant for our discussion.
Similar to electronic band bending, the non-zero space charge potential (Fig. 3c, top) resulting from the charge-transfer affects also the local concentration of mobile ionic defect species and in particular oxygen vacancies. In analogy to adapting a common Fermi energy across the interface, also the electrochemical potential for oxygen vacancies, ηoxv, (and all other ionic species) strives for equilibration
ηoxv = Hform0 + 2eϕ(x) + kBTln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) coxv(x) = const., coxv(x) = const., | (2) |
| Hform(x) = Hform0 + 2eϕ(x) | (3) |
At negative potential, such as resulting in the case of the p-type LaAlO3/SrTiO3 interface (Fig. 3c, top), this particularly results in a reduced effective enthalpy of formation close to the interface (center) and hence accumulation of oxygen vacancies toward the interface (bottom). It is evident that the concentration of oxygen vacancies reaches up to 1021 cm−3, which is about four orders of magnitude higher than the bulk concentration (2.5 × 1017 cm−3). The accumulation layer of oxygen vacancies at the interface corresponds to a local enhancement of ionic charge carriers which at elevated temperature facilitates ionic charge transport along the interface. Note that elevated temperatures are required as ionic charge carrier transport along the interface will take place via drift-diffusion. Therefore, the ionic conduction along the interface is expected to be a thermally activated process, which is fundamentally different from the behavior of electron gas reported for the n-type LAO/STO interface. Enhanced oxygen ion conduction is nevertheless inferred from the accumulation of oxygen vacancies toward the interface, as the diffusion coefficient (related to ion mobility via Einstein-relation) scales directly with the vacancy concentration.48
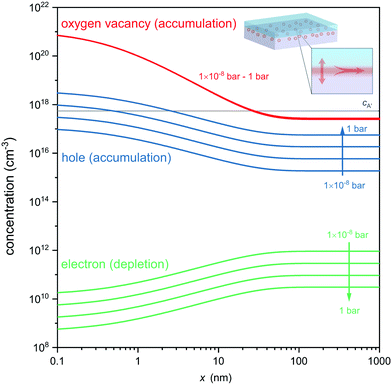
Fig. 4 displays the concentration profiles expected for oxygen vacancies, electrons and holes at different oxygen atmospheres. Note that logarithmic scales were used in Fig. 4 to allow comparison of the concentration profiles of oxygen vacancies, electrons and electron holes, which differ by orders of magnitude in different pO2 environments. Under each of these conditions an accumulation layer of oxygen vacancies is established, indicating the robustness of the formed ionic space charge layer against a variation in an ambient oxygen atmosphere. This also highlights that the expected oxygen vacancies cannot be removed by oxidation of the entire heterostructure, as their origin is not a classical reduction, but the charge-transfer process and band alignment at the atomically engineered interface. Unlike classical reduction, these oxygen vacancies are highly confined to about 10 nm from the interface and exist in the absence of compensating electrons (which are even depleted from the interface in response to the electric field, cf.Fig. 4). Moreover, the ionic charge-transfer is favored as compared to hole-transfer under these conditions (coxv/p ≈ 103), yielding a high transfer number for ionic conductivity along the interface. Based on the assessment of the carrier concentrations, the interface conductivity should hence be governed to a wide extent by oxygen ion conduction, while electron and electron hole contributions are orders of magnitude smaller. Finally, the high ionic charge carrier concentration is achieved in the absence of significant extrinsic doping of the interface (gray line in Fig. 4) so that trapping of oxygen vacancies is avoided (coxv/cA′ ≈ 103).
In summary, some of the main future promises of the p-type LaAlO3/SrTiO3 heterointerface are
(1) High thermal stability.
(2) High ionic transfer number.
(3) Absence of trapping effects at large carrier concentration.
(4) Strong confinement of enhanced oxygen ion conductivity.
Conclusions
Our model calculations show how charge-transfer phenomena in oxide heterostructures may be used to tailor ionic conductivity at oxide interfaces. Yet, experimental verification of enhanced interface ion conduction at this particular interface is challenging, as potential interface contributions need to be separated from substrate contributions,24,27,32 posing additional challenges to thin film synthesis, sample design, and the characterization of such nanoscaled ionic systems. Electrical characterization of the ionic contributions of transport along the interface may moreover require the use of electron-blocking electrodes to isolate ionic conductivity from electronic conductivity. In fact, the electron hole contribution stemming from the bulk of STO may otherwise mask the ion conduction contribution of the interface.24,51,52 Characteristic pO2-dependencies of transport properties can help to identify residual electronic contributions (∝pO2±1/4) and to separate unambiguously ionic contributions (which are expected to be independent of an oxygen atmosphere, see Fig. 4). In any case, careful reference measurements on the involved bulk materials are required as (ion and electronic) bulk contribution stemming from STO single crystals has oftentimes be suspected to be misinterpreted as thin film or interface contributions.24,51,52 Moreover, a careful evaluation of temperature dependence can provide further insights in this case, as electronic contributions such as the p-type carrier concentrations in the bulk of STO have well-known and characteristic activation energies,50 which typically differ from the activation of ion migration which typically results in a significantly steeper temperature dependence. Furthermore, the charge-transfer relies on the atomic configuration at the interfaces, making atomically defined oxide epitaxy indispensable for achieving an enhancement of ionic conductivity. One should also note that SrTiO3 reflects a well-established model system for mixed ionic–electronic conduction in oxides, but it is not the most promising ion conductor by itself. Therefore, for use in classical ionics applications such as ion conducting electrolytes, one may envision achievement of a similar charge-transfer process at an interface to zirconia or ceria, which should be accessible if the interface termination can be controlled in the desired way.The nanoscale control of ions in the solid may ultimately result in realizing highly tailored and controllable ion-conducting channels in nanoscaled all oxide devices. The inherent confinement of this ion channel may pave a way for novel field-tunable ionic devices, as electric field-effects superimposed to the inherent space charge layer may allow tuning of the ionic carrier concentration as well as their spatial distribution. In this way, one may compose an ionic device that acts like an ion valve operating at elevated temperature and selectively allowing for ion migration along the interface.
There is no fundamental restriction to use similar design principles to enhance also ionic conduction in Li-ion conductors or proton conductors, when atomically defined interfaces to a polar material (such as LaAlO3) can be achieved. Our concept hence emphasizes the chances and opportunities of designing interfaces with tailored ionic charge-transfer properties for ionic devices in oxides and beyond. Therefore, adopting band engineering strategies applied in electronics for tunable ionic interface properties is a promising future perspective for achieving novel devices and scientific insights. While our thermodynamic modelling results illustrate the potential of charge-transfer phenomena to engineer ionic properties, a joint experimental effort across the research community will be required to realize tailored ion conducting interfaces based on charge-transfer in ionic devices.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
F. G. is thankful for funding from the European Union's Horizon 2020 Research and Innovation Program under the Marie Sklodowska-Curie grant agreement no. 713683 (COFUNDfellowsDTU). N. P. would like to thank the Independent Research Fund Denmark, Grant No. 6111-00145B and the BioWings project funded by the European Union's Horizon 2020, Future and Emerging Technologies (FET) programme (Grant No. 801267) for support.References
- H. Y. Hwang, Y. Iwasa, M. Kawasaki, B. Keimer, N. Nagaosa and Y. Tokura, Nat. Mater., 2012, 11, 103 CrossRef CAS PubMed
.
- D. G. Schlom and J. Mannhart, Nat. Mater., 2011, 10, 168 CrossRef CAS PubMed
.
- S. Lee, A. Sangle, P. Lu, A. Chen, W. Zhang, J. S. Lee, H. Wang, Q. Jia and J. L. MacManus-Driscoll, Adv. Mater., 2014, 26, 6284, DOI:10.1002/adma.201401917
.
- D. V. Christensen, Y. Chen, V. Esposito and N. Pryds, APL Mater., 2019, 7, 013101 CrossRef
.
- F. Gunkel, D. V. Christensen, Y. Z. Chen and N. Pryds, Appl. Phys. Lett., 2020, 116, 120505 CrossRef CAS
.
- A. Tarancon, M. Burriel, J. Santiso, S. J. Skinner and J. A. Kilner, J. Mater. Chem., 2010, 20, 3799 RSC
.
- N. H. Pryds and V. Esposito, J. Electroceram., 2016, 38, 1 CrossRef
.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243 RSC
.
- A. R. Akbashev, L. Zhang, J. T. Mefford, J. Park, B. Butz, H. Luftman, W. C. Chueh and A. Vojvodic, Energy Environ. Sci., 2018, 11, 1762 RSC
.
- M. L. Weber and F. Gunkel, J. Phys.: Energy, 2019, 1, 031001 Search PubMed
.
- M. L. Weber, C. Baeumer, D. N. Mueller, L. Jin, C.-L. Jia, D. S. Bick, R. Waser, R. Dittmann, I. Valov and F. Gunkel, Chem. Mater., 2019, 31, 2337 CrossRef CAS
.
- R. Waser, R. Dittmann, G. Staikov and K. Szot, Adv. Mater., 2009, 21, 2632 CrossRef CAS
.
- R. Dittmann and J. P. Strachan, APL Mater., 2019, 7, 110903 CrossRef
.
- D. Christensen, F. Trier, W. Niu, Y. Gan, Y. Zhang, T. Jespersen, Y. Chen and N. Pryds, Adv. Mater. Interfaces, 2019, 6, 1900772 CrossRef CAS
.
- M. Bibes, J. E. Villegas and A. Barthelemy, Adv. Phys., 2011, 60, 5 CrossRef CAS
.
- A. B. Stambouli and E. Traversa, Renewable Sustainable Energy Rev., 2002, 6, 433 CrossRef CAS
.
- S. Sanna, V. Esposito, A. Tebano, S. Licoccia, E. Traversa and G. Balestrino, Small, 2010, 6, 1863 CrossRef CAS PubMed
.
- J. Koettgen, S. Grieshammer, P. Hein, B. O. Grope, M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2018, 20, 14291 RSC
.
- F. Pietrucci, M. Bernasconi, A. Laio and M. Parrinello, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 094301 CrossRef
.
- D. Parfitt, A. Chroneos, A. Tarancón and J. A. Kilner, J. Mater. Chem., 2011, 21, 2183 RSC
.
- S. J. Litzelman, R. A. De Souza, B. Butz, H. L. Tuller, M. Martin and D. Gerthsen, J. Electroceram., 2009, 22, 405 CrossRef CAS
.
- S. Kim and J. Maier, J. Electrochem. Soc., 2002, 149, J73 CrossRef CAS
.
- S. Sanna, V. Esposito, J. W. Andreasen, J. Hjelm, W. Zhang, T. Kasama, S. B. Simonsen, M. Christensen, S. Linderoth and N. Pryds, Nat. Mater., 2015, 14, 500 CrossRef CAS PubMed
.
- J. Garcia-Barriocanal, A. Rivera-Calzada, M. Varela, Z. Sefrioui, E. Iborra, C. Leon, S. J. Pennycook and J. Santamaria, Science, 2008, 321, 676 CrossRef CAS PubMed
.
- N. Schichtel, C. Korte, D. Hesse and J. Janek, Phys. Chem. Chem. Phys., 2009, 11, 3043 RSC
.
- K. M. Kant, V. Esposito and N. Pryds, Appl. Phys. Lett., 2010, 97, 143110 CrossRef
.
- F. Gunkel, P. Brinks, S. Hoffmann-Eifert, R. Dittmann, M. Huijben, J. E. Kleibeuker, G. Koster, G. Rijnders and R. Waser, Appl. Phys. Lett., 2012, 100, 52103/1 CrossRef CAS
.
- R. Merkle and J. Maier, Angew. Chem., Int. Ed., 2008, 47, 3874 CrossRef CAS PubMed
.
- R. Meyer, A. F. Zurhelle, R. A. De Souza, R. Waser and F. Gunkel, Phys. Rev. B, 2016, 94, 115408 CrossRef
.
-
D. M. Smyth, The defect chemistry of metal oxides, Oxford University Press, 2000 Search PubMed
.
- F. Baiutti, G. Logvenov, G. Gregori, G. Cristiani, Y. Wang, W. Sigle, P. A. van Aken and J. Maier, Nat. Commun., 2015, 6, 8586 CrossRef CAS PubMed
.
- R. A. D. Souza, F. Gunkel, S. Hoffmann-Eifert and R. Dittmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 241401(R) CrossRef
.
- R. A. D. Souza, Phys. Chem. Chem. Phys., 2009, 11, 9939–9969 RSC
.
- F. Gunkel, C. Bell, H. Inoue, B. Kim, A. G. Swartz, T. A. Merz, Y. Hikita, S. Harashima, H. K. Sato, M. Minohara, S. Hoffmann-Eifert, R. Dittmann and H. Y. Hwang, Phys. Rev. X, 2016, 6, 031035 Search PubMed
.
- M. Salluzzo, S. Gariglio, D. Stornaiuolo, V. Sessi, S. Rusponi, C. Piamonteze, G. M. De Luca, M. Minola, D. Marré, A. Gadaleta, H. Brune, F. Nolting, N. B. Brookes and G. Ghiringhelli, Phys. Rev. Lett., 2013, 111, 087204 CrossRef CAS PubMed
.
- F. Gunkel, S. Wicklein, P. Brinks, S. Hoffmann-Eifert, M. Huijben, G. Rijnders, R. Waser and R. Dittmann, Nanoscale, 2015, 7, 1013 RSC
.
- G. Herranz, M. Basletic, M. Bibes, C. Carretero, E. Tafra, E. Jacquet, K. Bouzehouane, C. Deranlot, A. Hamzic, J. M. Broto, A. Barthelemy and A. Fert, Phys. Rev. Lett., 2007, 98, 216803/1 CrossRef CAS PubMed
.
- F. Gunkel, R. Waser, A. H. H. Ramadan, R. A. De Souza, S. Hoffmann-Eifert and R. Dittmann, Phys. Rev. B, 2016, 93, 245431 CrossRef
.
- A. Ohtomo and H. Y. Hwang, Nature, 2004, 427, 423 CrossRef CAS PubMed
.
- N. Nakagawa, H. Y. Hwang and D. A. Muller, Nat. Mater., 2006, 5, 204 CrossRef CAS
.
- A. D. Caviglia, S. Gariglio, N. Reyren, D. Jaccard, T. Schneider, M. Gabay, S. Thiel, G. Hammerl, J. Mannhart and J. M. Triscone, Nature, 2008, 456, 624 CrossRef CAS PubMed
.
- N. Reyren, S. Thiel, A. D. Caviglia, L. F. Kourkoutis, G. Hammerl, C. Richter, C. W. Schneider, T. Kopp, A.-S. Ruetschi, D. Jaccard, M. Gabay, D. A. Muller, J. M. Triscone and J. Mannhart, Science, 2007, 317, 1196 CrossRef CAS PubMed
.
- L. Li, C. Richter and J. Mannhart, Nat. Phys., 2011, 7, 762 Search PubMed
.
- F. Trier, D. V. Christensen and N. Pryds, J. Phys. D: Appl. Phys., 2018, 51, 293002 CrossRef
.
- F. Gunkel, R. A. Heinen, S. Hoffmann-Eifert, L. Jin, C.-L. Jia and R. Dittmann, ACS Appl. Mater. Interfaces, 2017, 9, 10888 CrossRef CAS PubMed
.
- F. V. E. Hensling, C. Baeumer, M.-A. Rose, F. Gunkel and R. Dittmann, Mater. Res. Lett., 2020, 8, 31 CrossRef CAS
.
- H. Lee, N. Campbell, J. Lee, T. J. Asel, T. R. Paudel, H. Zhou, J. W. Lee, B. Noesges, J. Seo, B. Park, L. J. Brillson, S. H. Oh, E. Y. Tsymbal, M. S. Rzchowski and C. B. Eom, Nat. Mater., 2018, 17, 231–236 CrossRef CAS
.
- R. A. De Souza, Adv. Funct. Mater., 2015, 25, 6326 CrossRef CAS
.
- R. Moos and K. H. Hardtl, J. Am. Ceram. Soc., 1997, 80, 2549 CrossRef CAS
.
- F. Gunkel, S. Hoffmann-Eifert, R. Dittmann, S. Mi, C. Jia, P. Meuffels and R. Waser, Appl. Phys. Lett., 2010, 97, 12103 CrossRef
.
- X. Guo, Science, 2009, 324, 465 CrossRef CAS
.
- A. Cavallaro, M. Burriel, J. Roqueta, A. Apostolidis, A. Bernardi, A. Tarancón, R. Srinivasan, S. N. Cook, H. L. Fraser, J. A. Kilner, D. W. McComb and J. Santiso, Solid State Ionics, 2010, 181, 592 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2020 |