Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigating the effect of a fluoroethylene carbonate additive on lithium deposition and the solid electrolyte interphase in lithium metal batteries using in situ NMR spectroscopy†
Anna B.
Gunnarsdóttir
 a,
Sundeep
Vema
a,
Sundeep
Vema
 ab,
Svetlana
Menkin
ab,
Svetlana
Menkin
 a,
Lauren E.
Marbella‡
a,
Lauren E.
Marbella‡
 a and
Clare P.
Grey
a and
Clare P.
Grey
 *a
*a
aDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK. E-mail: cpg27@cam.ac.uk
bThe Faraday Institution, Quad One, Harwell Science and Innovation Campus, Didcot OX11 0RA, UK
First published on 2nd July 2020
Abstract
Using lithium metal as the negative electrode in a rechargeable lithium battery can increase the energy density, but to date, its use is limited due to uncontrolled and inhomogeneous electrodeposition upon cycling, leading to both low coulombic efficiencies and safety issues. The solid electrolyte interphase (SEI) has been identified as a key component in controlling microstructural growth but its role is still not well-understood. Here we explore the effect that fluoroethylene carbonate (FEC), a common electrolyte additive, along with pulse plating, has on the SEI on lithium metal and the electrodeposition of lithium. In situ NMR techniques, which are both non-invasive and quantitative, are used to monitor the microstructural growth during lithium deposition. We show how lithium whisker growth in a commercial carbonate electrolyte leads to increased SEI formation and low current efficiency, whereas using an FEC additive leads to denser lithium metal electrodeposits. We use 6,7Li isotopic labelling to monitor the exchange between lithium metal and the electrolyte and develop a numerical model to describe the process, which is discussed in the context of the standard model of electrochemical kinetics. The model allows us both to extract an exchange current density at the open circuit voltage, which takes into account the growth of the SEI and allows the extent of Li metal corrosion to be quantified. The results demonstrate that the isotope exchange rate depends significantly on the electrolyte and the corresponding SEI. The numerical simulations show that with an FEC additive the exchange is twice as fast as without, which is attributed to faster lithium ion transport in the SEI. Furthermore, the simulations indicate that FEC results in an accelerated SEI formation rate, more than four times faster than without the additive. These beneficial SEI properties, namely the fast lithium transport and faster SEI formation, help to explain why the fluorinated FEC additive results in a more uniform lithium deposition. The fast lithium ion transport will lead to a more homogeneous current distribution at the electrode surface. In the event that the SEI layer is ruptured, passivation of the freshly exposed lithium will occur more rapidly further leading to more homogeneous deposition.
Introduction
The search for higher energy density rechargeable lithium batteries has created a renewed interest in lithium (Li) metal anodes. Li metal has the highest volumetric and gravimetric energy density of all negative electrodes, however, it suffers from both capacity fading and safety issues.1,2 The uneven electrodeposition of Li on the metal anode results in high surface area microstructures that can ultimately lead to potentially hazardous situations such as cell short-circuiting and thermal runaway. The microstructures formed under Li deposition can exhibit a wide range of morphologies including needle, whisker, bush-like, mossy and fractal dendrites.3,4 A detailed understanding of the parameters that dictate the different growth modes of microstructural Li is necessary to develop effective strategies to mitigate microstructural growth and to enable the use of Li metal anodes in batteries.Generally, the morphology of metal electrodeposits is influenced by the current distribution over the electrode surface, which is affected by factors such as the geometry of the cell, the nature of the electrode's surface, the specific resistivity of the electrolyte solution, the activation overpotential and the concentration overpotential.5 Of these parameters, the surface of the Li metal electrode is particularly complex because of the solid-electrolyte interphase (SEI) that forms instantaneously when Li metal is immersed in an electrolyte due to the decomposition of the electrolyte and precipitation of the reduction products on the electrode surface. Also, ‘pristine’ Li metal is covered by a native SEI layer, composed mostly of lithium oxides, hydroxides and carbonates, which forms even under inert atmospheres (e.g. in a glovebox), from trace amounts of oxygen, nitrogen, water and a variety of organic solvents. The morphology of Li deposits and the cycling performance is highly dependent on the choice of electrolyte system where improved cycling efficiencies are generally attributed to a uniform and highly ionic conductive SEI layer.6–11 Thus, the main approach to tackle inhomogeneous Li deposition has been the development of a suitable liquid electrolyte system, by controlling the type of solvents, salts, and additives, and by varying the salt concentrations, with the goal of manipulating the corresponding chemical composition of the SEI. A fundamental question to address, in order to systematically tackle microstructural growth, is how the nature of the SEI on Li metal affects the plating and stripping on Li metal. Here we study the effect of the common additive, fluoroethylene carbonate (FEC), which has been shown to improve the coulombic efficiency of Li deposition compared to the standard LP30 electrolyte.11–15 Many studies have highlighted chemical differences in the nature of this SEI: X-ray photoelectron spectroscopy (XPS) studies have reported increased fluorine content in the SEI formed with FEC,16 and a LiF-rich SEI.15 Others have reported that a more ordered SEI is formed with FEC, which results in homogeneous lithium stripping.17,18 The challenge now is to identify why these differences alter the deposition and stripping performance, motivating further fundamental studies.
Electrochemical models based on the concentration gradients developed in the electrolyte have been established to describe fractal dendritic growth during Li electrodeposition.19–22 Two different current regimes are predicted where the limiting current density, jlim, is defined as: 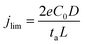 where e is the elementary charge, C0 is the initial electrolyte concentration, D is the ambipolar diffusion coefficient, ta is the transport number for the anion in the electrolyte and L is the distance between the two electrodes.22 In the high-current regime, for a current density j > jlim, diffusion limitation leads to fractal dendritic growth at a characteristic time known as the Sand's time (the time at which the concentration of the anions drops to zero at the electrode surface under the influence of an applied potential).20–22 The onset of dendrite growth for Li metal has been shown experimentally to correlate well with this theory.23,24 Below jlim, according to this theory, the concentration gradient in the electrolyte will reach a steady-state with a non-zero concentration of the ions at the electrode and dendrite growth via this mechanism is not expected.15,16 However, irregular microstructural growth occurs in most cases, which has been associated with local inhomogeneities on the Li metal surface or in the SEI where preferential deposition sites result in so-called “hot spots” with high local current density.3,6,23,25,26 These preferential deposition sites can originate from inhomogeneous transport properties in the SEI or cracks in the SEI, where Li grows through the protrusions caused by internal stresses beneath the SEI, giving rise to mossy and/or whisker-like structures.27–30
where e is the elementary charge, C0 is the initial electrolyte concentration, D is the ambipolar diffusion coefficient, ta is the transport number for the anion in the electrolyte and L is the distance between the two electrodes.22 In the high-current regime, for a current density j > jlim, diffusion limitation leads to fractal dendritic growth at a characteristic time known as the Sand's time (the time at which the concentration of the anions drops to zero at the electrode surface under the influence of an applied potential).20–22 The onset of dendrite growth for Li metal has been shown experimentally to correlate well with this theory.23,24 Below jlim, according to this theory, the concentration gradient in the electrolyte will reach a steady-state with a non-zero concentration of the ions at the electrode and dendrite growth via this mechanism is not expected.15,16 However, irregular microstructural growth occurs in most cases, which has been associated with local inhomogeneities on the Li metal surface or in the SEI where preferential deposition sites result in so-called “hot spots” with high local current density.3,6,23,25,26 These preferential deposition sites can originate from inhomogeneous transport properties in the SEI or cracks in the SEI, where Li grows through the protrusions caused by internal stresses beneath the SEI, giving rise to mossy and/or whisker-like structures.27–30
The morphology and plating behaviour of Li metal is commonly studied with techniques such as scanning electron microscopy (SEM),31operando optical microscopy,22,32,33 transmission electron microscopy (TEM)28 and cryo-TEM.17,34 Recently, a new analytic method, titration gas chromatography (TGG), was used to quantify ex situ the amount of inactive Li formed when plating and stripping Li on a copper current collector.35 Electron paramagnetic resonance (EPR) has been demonstrated as a semi-quantitative and non-invasive technique to observe operando Li microstructural growth in a flooded cell.36 Of these techniques, in situ nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI) are unique as non-invasive techniques that can also provide quantitative and temporal information on Li metal deposition. Operando NMR has been used to study Li and Na plating and stripping by continuously acquiring NMR spectra during an electrochemical measurement.23,37–43 Bhattacharyya et al. developed a method to quantify and distinguish between different types of microstructures that form during Li deposition based on the skin depth effect of conductors and the bulk magnetic susceptibility (BMS) of Li metal in a magnetic field.37 As electromagnetic waves penetrate metals to a certain depth called the skin depth, NMR is sensitive to the total surface area of the Li electrode.37,44 The increase in signal intensity upon cycling can thus be attributed to the formation of high surface area structures. Furthermore, the resonance of microstructural Li can be distinguished from the bulk Li metal due to shifts caused by BMS effects.44 Note that operando and in situ are often used interchangeably, the former referring to measurements made while the device is operating while the latter is more general and refers to measurements made of the intact device.
In this paper, we use in situ NMR to study the differences in plating behaviour and transport properties of the SEI in two electrolyte systems; the standard carbonate electrolyte 1 M LiPF6 in ethylene carbonate and dimethyl carbonate (EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC 1
DMC 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v, referred to as LP30) and the same electrolyte with the FEC additive (LP30 + FEC). Symmetrical Li–Li cells were operated below jlim where fractal dendritic growth is not expected, in order to study the mossy and microstructural growth of Li. We show that under constant current, a compact layer of microstructures form on the electrode surface in LP30 + FEC with high current efficiency compared to a more open whisker-like growth for LP30. In addition, experiments were performed using pulse electrolysis, an electrochemical method that has been used to deposit a range of metals where the advantages cited in the literature include improved control over the size of the metal deposits and less porous morphology.45–49 Previous studies on Li pulse plating have both demonstrated a smoother morphology and a less porous microstructural layer on the Li electrode.31,50–53 However, in order to study the effectiveness of Li pulse plating it is crucial to use a quantitative technique such as in situ NMR spectroscopy.
1 v/v, referred to as LP30) and the same electrolyte with the FEC additive (LP30 + FEC). Symmetrical Li–Li cells were operated below jlim where fractal dendritic growth is not expected, in order to study the mossy and microstructural growth of Li. We show that under constant current, a compact layer of microstructures form on the electrode surface in LP30 + FEC with high current efficiency compared to a more open whisker-like growth for LP30. In addition, experiments were performed using pulse electrolysis, an electrochemical method that has been used to deposit a range of metals where the advantages cited in the literature include improved control over the size of the metal deposits and less porous morphology.45–49 Previous studies on Li pulse plating have both demonstrated a smoother morphology and a less porous microstructural layer on the Li electrode.31,50–53 However, in order to study the effectiveness of Li pulse plating it is crucial to use a quantitative technique such as in situ NMR spectroscopy.
Finally, we use 6,7Li isotopic labelling to monitor the exchange between the bulk Li metal and the electrolyte with NMR. Previously, isotopic labelling has been used to study the solid/liquid interface in heterogeneous systems including solids such as ion exchanger beads and ionic crystals.54–57 Ilott and Jerschow used isotope exchange NMR measurements between an enriched 6Li metal and a natural abundance 7Li electrolyte to study the kinetics at the Li metal-electrolyte interface.58 Here we use this method to study how the nature of the SEI in the two electrolytes under study affects the rate of isotope exchange. A numerical model of the isotope exchange between the lithium metal and electrolyte was developed based on the work of Huang and Tsai on isotope exchange in heterogeneous systems.57 The exchange current, as described by Butler–Volmer theory, was used to capture the exchange flux at equilibrium.59 The model describes a 6Li-enriched Li metal electrode, soaked in a natural abundance lithium electrolyte and is thus comparable to a lithium metal anode at an open circuit voltage (OCV). From the numerical simulations we estimate the rates of exchange and SEI formation, and from that identify the key beneficial effects of the FEC additive: faster Li+ transport through the SEI and faster SEI formation.
Experiment and theory
Experimental
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v ethylene carbonate/dimethyl carbonate (EC/DMC; Sigma Aldrich, LP30). For experiments using an additive, fluoroethylene carbonate (FEC; Sigma Aldrich, 99%) was added to the electrolyte in 1
1 v/v ethylene carbonate/dimethyl carbonate (EC/DMC; Sigma Aldrich, LP30). For experiments using an additive, fluoroethylene carbonate (FEC; Sigma Aldrich, 99%) was added to the electrolyte in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 ratio by volume (LP30 + FEC). The water content of the LP30 electrolyte was measured with Karl Fischer titration and was <40 ppm. For in situ NMR experiments, Li electrodes were prepared by cutting fresh Li from a Li rod (Sigma, 99.9% trace metal basis, 12.7 mm diameter) and rolled with an Al roller inside a plastic bag (polyester pouch, VWR) to an approximate thickness of 0.15 mm. This ensures that the native SEI layer is minimal when the Li metal is immersed in the electrolyte. Similarly, the 6Li metal (Cambridge Isotope Laboratories, 95% 6Li) supplied in mineral oil was rinsed with hexane (Sigma Aldrich) and rolled with an Al roller inside a plastic bag. In all coin cells, pre-cut lithium metal disks (LTS research, 99.95%) were used. The materials were stored and handled in an Ar atmosphere glovebox (O2, H2O < 1 ppm, MBraun).
10 ratio by volume (LP30 + FEC). The water content of the LP30 electrolyte was measured with Karl Fischer titration and was <40 ppm. For in situ NMR experiments, Li electrodes were prepared by cutting fresh Li from a Li rod (Sigma, 99.9% trace metal basis, 12.7 mm diameter) and rolled with an Al roller inside a plastic bag (polyester pouch, VWR) to an approximate thickness of 0.15 mm. This ensures that the native SEI layer is minimal when the Li metal is immersed in the electrolyte. Similarly, the 6Li metal (Cambridge Isotope Laboratories, 95% 6Li) supplied in mineral oil was rinsed with hexane (Sigma Aldrich) and rolled with an Al roller inside a plastic bag. In all coin cells, pre-cut lithium metal disks (LTS research, 99.95%) were used. The materials were stored and handled in an Ar atmosphere glovebox (O2, H2O < 1 ppm, MBraun).
The 6/7Li NMR isotope exchange measurements were performed on a Bruker Avance III 300 spectrometer, operating at a Larmor frequency of 300.1 MHz for 1H and 116.6 MHz for 7Li. The measurements were recorded with a MicWB40 probe inside a Micro2.5 triple axis gradient system at 298 K, using a water-cooling unit, and using a 10 mm 1H–19F/7Li coil. 7Li shifts were referenced to a 1 M aqueous solution of LiCl at 0 ppm. The electrode was centred in the NMR coil, with the Li metal placed perpendicular to the B0 field and parallel to the B1 radio-frequency (rf) field to get maximum excitation.63 Single pulse experiments were recorded on a series of 7Li spectra. The recycle delay of 15 s and 48 transients in the 7Li NMR resulted in an experimental time of ∼12 min per spectrum. The recycle delay was chosen to ensure full relaxation of the electrolyte components, with the delay >5 × T1.
Pulsed-field gradient (PFG) NMR was performed using the same MicWB40 probe at 298 K. A stimulated echo (STE) pulse sequence was used with a gradient pulse length of 2.5 ms, diffusion time of 200 ms, recycle delay of 3 s, number of transients 32, and by varying the gradient in 16 steps (3.2–146 G cm−1). The data was fit to the Stejskal–Tanner equation using Bruker Topspin Software.64 The gradient strength was calibrated by measuring the Li+ diffusion coefficient of 0.25 M LiCl in water at 298 K, with the diffusion coefficient set to 0.96 × 10−9 m2 s−1.65
Theory
| Li+ + e− ⇄ Li0 | (1) |
| j0 = Fk0[Li+]α[Li0]1−α | (2) |
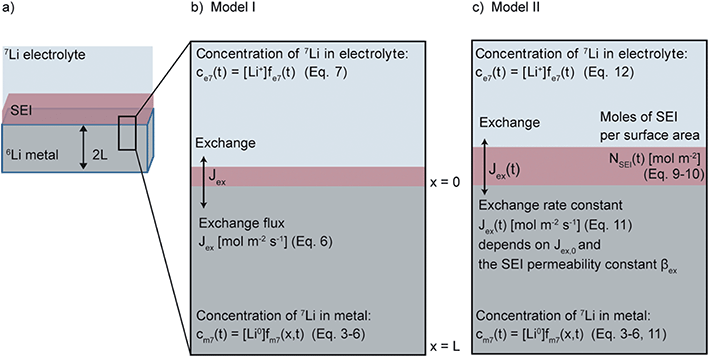
Eqn (2) can be rewritten in terms of the exchange flux at the interface J0 [mol m−2 s−1], where j0 = FJ0. This equilibrium process (strictly the OCV process) can be followed via the isotope exchange current when an enriched Li metal electrode is soaked in a non-enriched electrolyte (for example), because the 6,7Li concentrations are not in equilibrium (i.e. the concentrations of 6,7Li are different in the Li metal and electrolyte). In contrast to the traditional model of current density j0 described in eqn (2), the rate of exchange determined in the current measurement will depend not only on the electron transfer kinetics of Li+/Li0 but as well on the rate of the subsequent transport of the Li+ through the SEI. To make a distinction between our model and the traditional one, and to generalise our model, we will hereafter refer to the isotope exchange flux occurring at OCV measured here as Jex [mol m−2 s−1]; furthermore, since the SEI growth is continuous, Jex, is expected to be time dependent (as explored below via two different models). The implications of these models within the standard Butler–Volmer formulation are discussed later.
To model the isotope exchange intensity curves measured we need to consider the concentration of 7Li in the metal, cm7, at distance x from the SEI-metal interface and at time t, described in the following equation:
| cm7(x,t) = [Li0]fm7(x,t) | (3) |
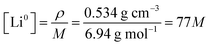 where ρ is the density of lithium metal and M the molar mass. The initial condition for the fraction of 7Li in the metal is fm7(x,0) = 0.05, since we use a 95% enriched 6Li metal. Note that at time t = 0 in the simulations, approximately 10 minutes have passed since immersing the enriched Li metal in the electrolyte and the start of the NMR experiment. This will only result in a minimal error in the initial starting condition as the experiment is performed over multiple hours and the second data point in the experimental measurements (at t ∼25 min) shows minimal change from the first data point (t = 0 min) in mole fraction of 7Li in both electrolyte and metal. To test for this, the initial conditions of the first few points of fm7(x,0) were increased to 0.055, which qualitatively did not result in any significant changes between the fitted parameters between the two electrolytes.
where ρ is the density of lithium metal and M the molar mass. The initial condition for the fraction of 7Li in the metal is fm7(x,0) = 0.05, since we use a 95% enriched 6Li metal. Note that at time t = 0 in the simulations, approximately 10 minutes have passed since immersing the enriched Li metal in the electrolyte and the start of the NMR experiment. This will only result in a minimal error in the initial starting condition as the experiment is performed over multiple hours and the second data point in the experimental measurements (at t ∼25 min) shows minimal change from the first data point (t = 0 min) in mole fraction of 7Li in both electrolyte and metal. To test for this, the initial conditions of the first few points of fm7(x,0) were increased to 0.055, which qualitatively did not result in any significant changes between the fitted parameters between the two electrolytes.
The concentration of 7Li electrolyte as a function of time is, ce7(t) = [Li+]fe7(t) with the initial condition for the fraction of 7Li in the electrolyte, fe7(0) = 0.92 (the natural abundance of 7Li). Since the diffusion coefficient in lithium metal, Dm, is more than four orders of magnitude smaller than the diffusion Li+ coefficient in the electrolyte (Table 1), the diffusion of Li+ throughout the electrolyte is considered instantaneous.
| Symbol | Description | Value/unit | Determination |
|---|---|---|---|
| S a | Surface area of Li metal | 8.2 × 10−5 m2 | Measured |
| L | Half thickness of the Li metal | 0.12 × 10−3 m | Estimated from Sa and weight of Li metal |
| V e | Volume of the electrolyte | 400 μL | Measured |
| D m | Self-diffusion coefficient in Li metal | 7.11 × 10−15 m2 s−1 | Measured by NMR relaxometry at 298 K (in ref. 68) |
| D LP30 | Diffusion coefficient in LP30 | 1.70 × 10−10 m2 s−1 | Measured by PFG-NMR |
| D LP30+FEC | Diffusion coefficient in LP30 + FEC | 1.74 × 10−10 m2 s−1 | Measured by PFG-NMR |
| [Li+]LP30 | Concentration of LP30 electrolyte | 1000 mol m−3 | From supplier |
| [Li+]LP30+FEC | Concentration of LP30 + FEC electrolyte | 909 mol m−3 | Diluted with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 ratio of FEC 10 ratio of FEC |
The self-diffusion of Li atoms within the metal is described by Fick's law:
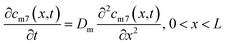 | (4) |
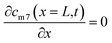 | (5) |
Due to the difference in isotope ratio between the electrolyte and metal, the flux at equilibrium Jex, will lead to change in the isotope ratio of the metal and the electrolyte:
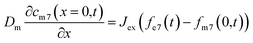 | (6) |
The partial differential equations of the concentration of 7Li in the metal are coupled to the ordinary differential equation that describes the concentration of 7Li in the electrolyte, described as follows:
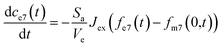 | (7) |
Model I assumes that the SEI of Li metal is of fixed thickness and fits the experimental curves with one fitting parameter Jex and eqn (3)–(7), as shown schematically in Fig. 1b.
Model II It was necessary to extend the model to take into account the temporal evolution of the SEI. In the system under study, where the SEI forms without any applied current, simultaneous oxidation of the Li metal to Li+ is required in order to maintain charge balance. This is illustrated here by one typical SEI reduction reaction, involving the ring-opening of the EC solvent molecule,69 as follows:
| (i) Limetal0 → Li+ + e− |
| (ii) 2Li+ + 2e− + EC → (CH2OCO2Li)2 + C2H4 |
When taken together, the overall reaction corresponds to:
| 2Limetal0 + EC → (CH2OCO2Li)2 + C2H4 | (8) |
Other SEI reduction reactions similarly consume Limetal0 rather than Li+. SEI formation has previously been modelled as being proportional to the exchange current density at the metal/electrolyte interface.70 A similar approach is used here where the SEI formation, dNSEI/dt, is taken to be proportional to Jex:
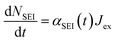 | (9) |
aSEI(t) = αSEI,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βSEINSEI(t)) exp(−βSEINSEI(t)) | (10) |
Jex(t) = Jex,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βexNSEI(t)) exp(−βexNSEI(t)) | (11) |
In addition, the SEI formation will affect the isotope ratio in the electrolyte. According to eqn (8), the overall Li+ ion concentration in the electrolyte should remain constant, however, differences in isotope ratio between the electrolyte and metal will result in changes to the isotope concentration in the electrolyte, ce7. Since the consumption of 7Li+ in the electrolyte to form the SEI is 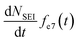 and the rate of 7Li0 metal oxidised to Li+ is
and the rate of 7Li0 metal oxidised to Li+ is 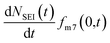 , the change in moles of the 7Li isotope in the electrolyte as a result of the SEI formation is
, the change in moles of the 7Li isotope in the electrolyte as a result of the SEI formation is 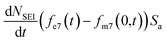 , and eqn (7) becomes:
, and eqn (7) becomes:
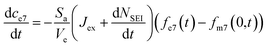 | (12) |
The final model, termed Model II and shown schematically in Fig. 1c, solves eqn (3)–(6) and (9)–(12) with the four fitting parameters, Jex,0, αSEI,0, βex and βSEI.
To use the models to fit the experimental data, the equations for Model I and II were discretised using the method of lines and solved using an ode-solver in MATLAB (ode45 function).72 A nonlinear least-square solver (lsqcurvefit function) was used to fit the experimental data, the 7Li intensity of the metal and the 7Li diamagnetic intensity (including electrolyte and SEI), to the numerical model. The nlparci function was used to generate a 90% confidence interval of the fitting parameters. The skin depth of the Li metal is taken into account when fitting the model to the NMR intensity of the metal peak, the NMR being only sensitive to the surface of the Li metal (see eqn S(2) in the ESI†).
Note, the exact chemical composition of the SEI is unknown and thus the thickness of the SEI in both electrolytes, s(t), can only be compared by assuming a chemical composition with a molar mass, M, and a density ρ:58
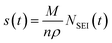 | (13) |
Results
Constant current deposition in LP30 and LP30 + FEC
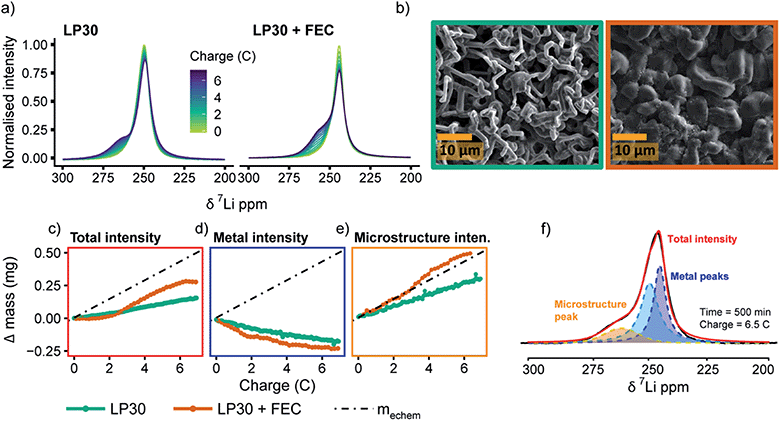
Fig. 2a shows the 7Li in situ NMR spectra continuously acquired during a 0.5 mA cm−2 constant current experiment. The resonance from Li metal depends on the orientation of the Li metal anode strip with respect to the static magnetic field, B0, due to Li metal's temperature independent paramagnetism (TIP).37,44 Aligning the cell perpendicular to the B0 field results in a 7Li resonance at around 245 ppm for the pristine Li metal37 (Fig. 2a) and all in situ cells presented in this work were aligned in this fashion. When depositing Li in both LP30 and LP30 + FEC, a new peak around 260 ppm emerges that continues to grow as a current of 0.5 mA cm−2 is passed (Fig. 2a). This new resonance is indicative of mossy structures growing near to the Li metal surface.37,39 Whisker-like morphologies are observed in the SEM micrographs as the major morphology after plating for 3.5 mA h cm−2 in LP30 electrolyte, whereas dense, thick buds (diameter of surface features ∼5–10 μm) are observed for LP30 + FEC (Fig. 2b).The overall increase in the 7Li NMR signal intensity for Li metal can be attributed to the formation of high surface area deposits where the signal intensity is directly proportional to the volume of Li metal excited by the radio-frequency (rf) field.37,39 The change in the total integrated intensity between 220–280 ppm, termed “total intensity” for the rest of the paper, was converted into the mass change (i.e., the change in the Li mass detected by NMR spectroscopy.), Δ mass (Fig. 2c). The quantification of the NMR signal followed the theory developed by Bhattacharyya et al. and is described in more detail in the ESI.†37,39Δ mass is then plotted against charge passed (in C, coulombs) in order to compare it to the total amount of mass of Li deposited based on the electrochemistry, mechem = 0.072 mg C−1 (Fig. 2c). The charge passed in Fig. 2 corresponds roughly to 3.5 mA h cm−2 (the slight differences between cells arising from small variations in electrode area). mechem was calculated by Faraday's law of electrolysis for the ideal case without considering the coulombic losses associated with the formation of the SEI, the competing reaction to Li metal deposition.
For both electrolyte systems, the mass increase calculated from the total intensity is lower than that expected from the applied electrochemistry (Fig. 2c), i.e., mNMR < mechem. There are three possible scenarios that can account for this. In the first scenario, part of the Li is plated as a smooth deposit and does not result in an increased intensity of the Li signal, since it does not change the overall Li metal surface area. This is due to the skin depth effect of metals, where the rf field penetrates only the surface of the metal, ∼12 μm for Li, (note that the diamagnetic SEI does not impede rf penetration).37 In the second scenario, the growth of dense Li metal microstructures may also lead to an attenuation of the rf signal and poor excitation of the underlying bulk film.38,43 Third, the competing reduction reaction, SEI formation, results in lower Li metal deposition than expected based on the current passed, i.e., lower current efficiency.
To gain more insight into the morphological changes on the electrodes, as well as the causes of mNMR < mechem, we performed spectral fittings to determine how the relative fractions of the peaks assigned to Li microstructures vs. “bulk metal” change upon plating. The spectra were deconvoluted by using two peaks around 245–252.5 ppm (“bulk metal”) and one peak at around 257.5–262.5 ppm corresponding to the microstructural peak (see an example in Fig. 2f and more detailed explanation in the ESI†).38 We note that previous work has shown both experimentally and with simulations that dendrites and structures growing away from the Li metal surface give rise to larger shift around 270 ppm compared to microstructures close to the surface.38,39 In the current study, the in situ PEEK capsule cell applies constant pressure within the cell and more compact structures form, leading to a narrower range of shifts.38,60 The observed shifts of the microstructure peaks (Fig. S1†) are thus similar for both electrolytes although the microstructures have very distinct morphologies as seen in the SEM figures (Fig. 2b).42
For the LP30 + FEC electrolyte, the initial increase in microstructure intensity is compensated by a concurrent decrease in the metal intensity (Fig. 2d and e, orange, respectively), both corresponding roughly to mechem (i.e., the decrease of metal signal is −0.07 mg C−1 and increase in microstructural intensity 0.08 mg C−1 ∼ mechem) and thus the total signal intensity (total volume of Li detected by NMR) (Fig. 2c, orange) stays almost constant. This is ascribed to an attenuation of the rf field by the thick microstructures formed in LP30 + FEC (Fig. 2b), so that the rf field penetration into the bulk metal is less than that for the initial Li film. The intensity of the bulk metal peak in the LP30 electrolyte similarly decreases with charge (Fig. 2d, green), but now the steady intensity increase in intensity of the microstructure peak is lower than that observed for LP30 + FEC, corresponding to only 0.053 mg C−1, i.e., approximately 74% of what is expected by the electrochemistry. We attribute this to poorer current efficiency as a result of the higher surface area Li whiskers formed in the LP30 electrolyte, as compared to the dense buds formed in LP30 + FEC, coupled with the larger extent of SEI formation on freshly exposed surface.
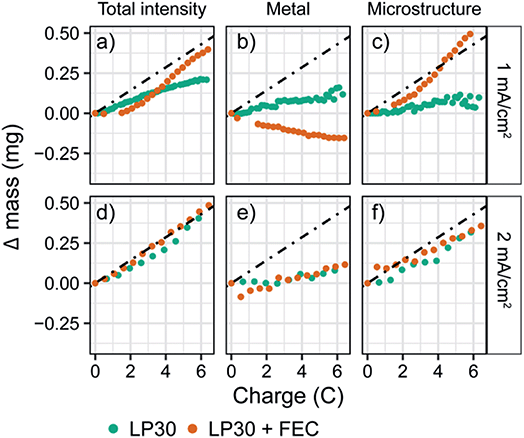
To explore the effect of current density on both the plating efficiency and the resulting morphology we performed in situ NMR at higher constant current densities of 1 and 2 mA cm−2 (Fig. S24 and S25†). The quantified intensities of the deconvoluted peaks are shown in Fig. 3. For a constant current of 1 mA cm−2, the bulk metal peak for LP30 + FEC electrolyte again decreases due to an attenuation of the signal (Fig. 3b, orange), while the increase in the microstructural peak corresponds roughly to mechem (Fig. 3c, orange). For the LP30 electrolyte, the bulk metal peak now stays close to constant indicating that more porous structures, growing away from the electrode's surface, are formed; these microstructures no longer shield the bulk metal leaving the intensity detected by the NMR unchanged. Again, the total increase in intensity for LP30 electrolyte is less than mechem, indicating that some of the charge is used to form the SEI.
In contrast, for the higher constant current of 2 mA cm−2, a close to constant intensity of the metal peak is observed for both electrolyte systems, with a slight increase occurring after passing 5 coulombs (3.25 mA h cm−2, Fig. 3e). Now mNMR is only slightly lower than mechem for both electrolytes, indicating a higher current efficiency for the LP30 electrolyte at 2 mA cm−2. This is tentatively ascribed to the competing reactions of SEI formation and Li deposition where at higher overpotentials, electrodeposition of Li metal occurs more rapidly than the kinetically-limited degradation reaction involving the electrolyte species.73 The morphology of the lithium deposits for the two electrodes is now very similar (Fig. S7†).
Voltage traces in coin cells as an indirect way to study surface kinetics
To study the distinctive SEI formed in the two electrolytes and the corresponding plating behaviour, symmetrical Li–Li coin cells were assembled and cycled using continuous plating and stripping cycles for current densities of 0.5, 1 and 2 mA cm−2 applied for a total capacity of 2 mA h cm−2 per cycle (Fig. 4). The full cycling data can be found in the ESI (Fig. S2–S4†). A different protocol was used in the first cycle for the three current densities in order to compare the ‘peaking behaviour’ seen on stripping: while either 0.5, 1 or 2 mA cm−2 was applied during plating, a current density of 1 mA cm−2 was used on stripping for the second half of the first cycle (Fig. 4b–d).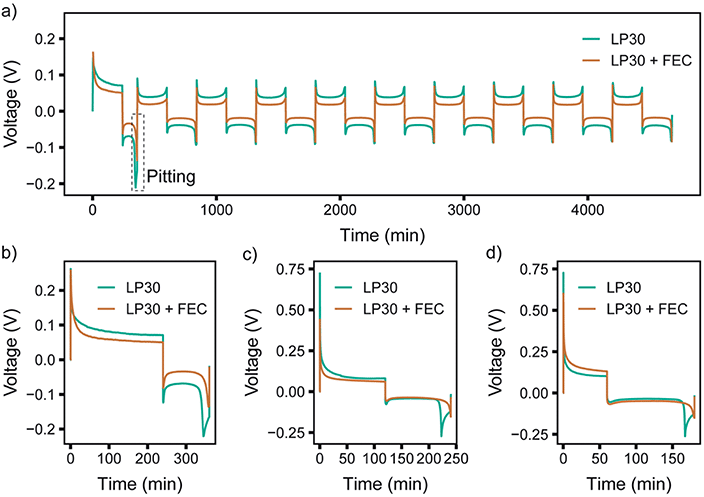 | ||
| Fig. 4 Galvanostatic cycling of symmetric Li-coin cells during (a) the first 10 cycles at 0.5 mA cm−2 for both stripping and plating. In the first cycle, shown in the enlargement in (b), 0.5 mA cm−2 was used for plating and 1.0 mA cm−2 for stripping. First cycle using (c) 1.0 and (d) 2.0 mA cm−2 plating and 1.0 mA cm−2 for stripping. LP30 (green) and LP30 + FEC (orange). The full cycling data for 1 and 2 mA cm−2 can be found in Fig. S3–S4.† | ||
The study of the voltage traces follows the methodology introduced in previous studies,33,74 to observe the characteristic peaking behaviour that originates from pitting of the stripping electrode. Previous reports have assigned the typical voltage profile to specific deposition and pitting processes: when plating Li, there is initially a large overpotential associated with the nucleation of Li deposits, which then decreases rapidly towards a local minimum due to an increased surface area for deposition. When switching polarity after the first deposition, the microstructures formed previously in the first half cycle are oxidised and removed from the stripping electrode. When all of the microstructures have been dissolved completely (or been detached from the electrode surface forming ‘dead Li’) the overpotential increases rapidly. A peak is seen as the overpotential drops again, labelled “pitting” in Fig. 4a, as this behaviour has been assigned to the onset of bulk metal dissolution or pitting of the Li metal surface and an increase in surface area.33,74 When comparing different electrolytes, a more pronounced peaking behaviour has been associated with substantial impedance differences and spatial variations in the SEI layers that lead to non-uniform stripping and the formation of dead Li.33
For the first cycle in LP30 a more apparent “pitting” peak is observed that occurs at an earlier time compared to LP30 + FEC (occurring at ∼78% and ∼92% capacity, respectively for 0.5 mA cm−2). Other studies have suggested that this is due to inhomogeneous dissolution of the lithium whiskers that result in dead Li formation and early peaking behaviour. However, the lower plating efficiency quantified with in situ NMR can also lead to the early peaking behaviour observed when lower amounts of microstructures are present. With 1 and 2 mA cm−2, the peaking in the first cycle (where the stripping current is kept at 1 mA cm−2) occurs at 85% and 89% capacity respectively. This correlates well with the in situ NMR, which indicated higher plating efficiencies for the higher current densities in LP30. The voltage traces are flatter for the LP30 + FEC electrolyte, as compared to those for LP30, consistent with both the higher plating efficiency seen in the in situ NMR and of studies showing minuscule dead lithium formation in LP30 + FEC.18,35 The lower overpotential observed for LP30 + FEC is somewhat consistent between cells (Fig. S2–S4†), but the overpotential is affected both by the resistances in the cell (in particular of the SEI) and the surface area (which increases during electrodeposition) accounting for variations between cells.
Pulse plating Li metal
To test the differences in Li deposition between the two electrolytes further, in situ NMR measurements using pulsed currents were carried out. When applying a pulsed current, short pulses for a period TON are applied, which is followed by a rest period TOFF where no current is passed (schematic, Fig. S5†). During the rest period, TOFF, two main processes occur:(i) Diffusion of Li ions leading to relaxation of concentration gradients in the electrolyte and around protruding points on the electrode, and within the liquid components of the SEI layer; this should result in a more uniform lithium ion distribution near the electrode's surface.49
(ii) The chemical formation and growth of the SEI on fresh Li sites (the initial SEI formation has been suggested to be completed in less than 1 s75,76 but as demonstrated below the full passivation of Li metal can take longer time, up to hours to days). Cracked and newly formed SEI typically has a lower impedance than more mature SEI, which has been suggested to result in preferential deposition sites.28,33 The formation and maturation of the SEI during rest periods is likely to increase its impedance and result in levelling effects. As a consequence, Li deposition is anticipated to be more homogeneous using pulse plating. The formation of the SEI during the rest period TOFF has also been suggested to increase the current efficiency.51
To compare different time scales, both relatively long and short pulse lengths were initially chosen, with TON = TOFF of either 1 s or 5 ms. The electrochemistry for pulse plating at 1 mA cm−2 and TON, TOFF = 1 s in LP30 electrolyte is shown in Fig. 5 (see Fig. S26 and S27† for additional pulse plating data for other electrolyte formulations); this corresponds to a duty cycle of θduty = TON/(TON + TOFF) = 0.5 and an average current density of 0.5 mA cm−2. Thus, the data can be readily compared to the constant current experiments at 0.5 mA cm−2.
 | ||
| Fig. 5 Representative pulsed current plot for a symmetric Li in situ cell at 1 mA cm−2 with TON,TOFF = 1 s in the LP30 + FEC electrolyte, also shown in Fig. S26.† | ||
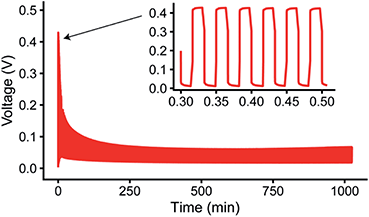
Fig. 6a shows a comparison of the microstructure masses determined by NMR for both constant plating and pulse plating experiments in LP30. During pulse plating with TON, TOFF = 1 s and TON, TOFF = 5 ms (Fig. 6a), the NMR-derived Li mass changes (Δ mass) give a slope that corresponds closely to the microstructural mass predicted from the electrochemistry (mechem), indicating high current efficiency of Li metal plating. For both cases, the bulk metal intensity stays close to constant, indicating that the microstructure morphology is more porous as compared to that seen for constant plating at 0.5 mA cm−2, and thus does not attenuate the rf field. The resulting morphology (Fig. 6b) for TON, TOFF = 1 s, comprises a mixture of both whisker- and dense-like buds, whereas short pulse lengths, TON, TOFF = 5 ms, result in the formation of narrow whiskers (Fig. 6c). This demonstrates that applying short pulses in the LP30 electrolyte does not seem to result in more uniform and dense morphologies. To study the effect of the pulse length, we systematically varied the pulse waveforms with TON, TOFF = 500 ms, 100 ms or 50 ms (Fig. S6†) measured with in situ NMR spectroscopy. Overall, the slope of the microstructural intensity for all the pulse waveforms is close to mechem (Table S2†) indicating higher current efficiency compared to that observed for constant currents. Surprisingly, the most dense microstructures are observed for TON, TOFF = 500 ms and increasingly more open and whisker-like morphologies are seen as the time intervals decrease (Fig. S8†).
 | ||
Fig. 6 Pulse plating in LP30 (a) The deconvoluted intensities of the in situ spectra for LP30 during constant plating (CP) at 0.5 mA cm−2 (green, also plotted in Fig. 2) and pulse plating (PP) at 1 mA cm−2 with TON, TOFF = 1 s (purple) and TON, TOFF = 5 ms (yellow). The dashed line indicates mechem, the mass deposited according to the current passed by the electrochemistry. SEM images of the Li metal morphology using 1 mA cm−2 and (b) TON, TOFF = 1 s (c) TON, TOFF = 5 ms. (d) The deconvoluted intensities of the in situ spectra during pulse plating with TON![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TOFF = 5 ms TOFF = 5 ms![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 ms using current densities of 1 mA cm−2 (pink) and 2 mA cm−2 (blue). SEM images of the Li metal morphology using TON 15 ms using current densities of 1 mA cm−2 (pink) and 2 mA cm−2 (blue). SEM images of the Li metal morphology using TON![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TOFF = 5 ms TOFF = 5 ms![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 ms and (e) 1 mA cm−2 (f) 2 mA cm−2. 15 ms and (e) 1 mA cm−2 (f) 2 mA cm−2. | ||
To further investigate the effect of the rest period on mitigating microstructural growth, longer rest periods of TOFF were explored. Previous studies50,51,77 have suggested that in order for pulse plating to be beneficial, setting the timings such that TON < TOFF is crucial, the studies even proposing an optimal TON![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TOFF ratio of close to 1
TOFF ratio of close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.50 Thus, we explored TON = 5 ms with a longer rest period TOFF = 15 ms and jinst = 1 and 2 mA cm−2. This gives average current densities of 0.25 and 0.5 mA cm−2. The deconvoluted intensities (Fig. 6d) from the in situ NMR measurements show microstructural growth corresponding roughly to mechem. Furthermore, the morphology for the lower jinst = 1 mA cm−2 remains relatively smooth which can be seen both in the SEM image (Fig. 6e) and with the decreasing metal intensity (Fig. 6d, pink). The attenuation of the bulk metal signal indicates (for reasons discussed in the previous section) that pulsed currents with TON < TOFF do indeed lead to more dense deposition near the electrode surface. The SEM images of the plated electrode in Fig. 6e seem to show a significant amount of SEI is present on the Li deposits. To investigate this further and make sure that this was not dried electrolyte, the electrode was transferred back into the glovebox and rinsed with anhydrous DMC. The rinsed electrode (Fig. S10†) was comparable to that in Fig. 6e, indicating that there is significant SEI formed on the Li deposits that is not readily removed by washing.
3.50 Thus, we explored TON = 5 ms with a longer rest period TOFF = 15 ms and jinst = 1 and 2 mA cm−2. This gives average current densities of 0.25 and 0.5 mA cm−2. The deconvoluted intensities (Fig. 6d) from the in situ NMR measurements show microstructural growth corresponding roughly to mechem. Furthermore, the morphology for the lower jinst = 1 mA cm−2 remains relatively smooth which can be seen both in the SEM image (Fig. 6e) and with the decreasing metal intensity (Fig. 6d, pink). The attenuation of the bulk metal signal indicates (for reasons discussed in the previous section) that pulsed currents with TON < TOFF do indeed lead to more dense deposition near the electrode surface. The SEM images of the plated electrode in Fig. 6e seem to show a significant amount of SEI is present on the Li deposits. To investigate this further and make sure that this was not dried electrolyte, the electrode was transferred back into the glovebox and rinsed with anhydrous DMC. The rinsed electrode (Fig. S10†) was comparable to that in Fig. 6e, indicating that there is significant SEI formed on the Li deposits that is not readily removed by washing.
For the higher current density, jinst = 2 mA cm−2, the morphology again becomes uneven (Fig. 6f), which can also be seen in the intensity of the metal peak (Fig. 6d, blue) that even grows slightly, suggesting roughening on the stripping electrode. Interestingly, we consistently see that the “bulk metal” peak in the in situ NMR tends to increase when a relatively high current density is applied, 2 mA cm−2, both using constant and pulsed current (Fig. 3e, 6d and 7d). An increase in the bulk metal peak can derive from roughening of the stripping electrode as a result of pitting.43,78 The effect of pitting on the NMR spectra for LP30, 2 mA cm−2 and TON = 5 ms, TOFF = 15 ms, was explored by disassembling the in situ cell after plating and NMR spectra were taken of the separate electrodes (Fig. S11†). The stripping electrode gives a broader signal, shifted upfield about 2.5 ppm to a value of 247.5 ppm, indicating roughening of the electrode that is consistent with the pits shown in the SEM (Fig. S12†).78 The experiment is not necessarily quantitative as NMR signal intensities depend strongly on the amount of metal inside the NMR coil and considerable errors are introduced when taking the cells in and out of the coil, making it difficult to estimate the extent of pitting on the Li electrode in the current study. Further studies are required to understand the pitting effect where the two Li electrodes can be separated in the coil either in a flooded cell used for MRI studies or with a so-called ‘long-design’ often used for in situ supercapacitor studies to separate the electrodes in the NMR coil.23,78,79
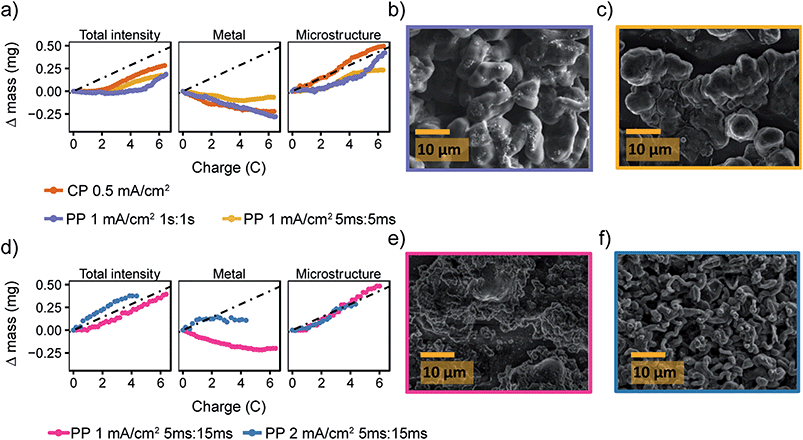 | ||
Fig. 7 Pulse plating in LP30 + FEC (a) the deconvoluted intensities of the in situ spectra for LP30 + FEC during constant plating (CP) at 0.5 mA cm−2 (orange, also plotted in Fig. 2) and pulse plating (PP) at 1 mA cm−2 with TON, TOFF = 1 s (purple) and TON, TOFF = 5 ms (yellow). The dashed line indicates mechem, the mass deposited according to the current passed by the electrochemistry. SEM images of the Li metal morphology using 1 mA cm−2 and (b) TON, TOFF = 1 s (c) TON, TOFF = 5 ms. (d) The deconvoluted intensities of the in situ spectra during pulse plating with TON![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TOFF = 5 ms TOFF = 5 ms![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 ms using current densities of 1 mA cm−2 (pink) and 2 mA cm−2 (blue). SEM images of the Li metal morphology using TON 15 ms using current densities of 1 mA cm−2 (pink) and 2 mA cm−2 (blue). SEM images of the Li metal morphology using TON![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TOFF = 5 ms TOFF = 5 ms![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 ms and (e) 1 mA cm−2 (f) 2 mA cm−2. 15 ms and (e) 1 mA cm−2 (f) 2 mA cm−2. | ||
The pulse plating experiments were repeated in LP30 + FEC (Fig. 7a) where both long (1 s, purple) and short (5 ms, yellow) pulse lengths seem to delay the onset of the microstructural growth. For both experiments, the microstructural intensity stays constant for the first two coulombs of charge before increasing with a slope close to mechem. Thus, we conclude that the mNMR < mechem is a result of smooth deposition that is not detected by the NMR as a result of skin depth effects. The SEM images (Fig. 7b and c) show the resulting relatively smooth and dense morphology of the Li deposits. For TON![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TOFF = 5 ms
TOFF = 5 ms![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 ms and jinst = 1 mA cm−2, the morphology is even more uniform (Fig. 7e) and for jinst = 2 mA cm−2, as seen for LP30 (Fig. 6f), the morphology becomes rougher again (Fig. 7d and f).
15 ms and jinst = 1 mA cm−2, the morphology is even more uniform (Fig. 7e) and for jinst = 2 mA cm−2, as seen for LP30 (Fig. 6f), the morphology becomes rougher again (Fig. 7d and f).
Overall, pulse plating appears to be more beneficial for Li deposition in the LP30 + FEC electrolyte, which suggests that local concentration gradients at the metal surface are levelled out more effectively. This is not expected to arise from the better transport in the electrolyte as similar Li+ diffusion coefficients were measured by PFG-NMR for LP30 with an without an additive (DLP30 = 1.70 × 10−10 m2 s−1 and DLP30+FEC = 1.74 × 10−10 m2 s−1). That little to no effect is seen on the transport properties on adding FEC is consistent with the molecular dynamics (MD) simulations of Hou et al.80
Examining the Li+ transport properties of the SEI: 7Li in situ NMR measurements of isotope exchange
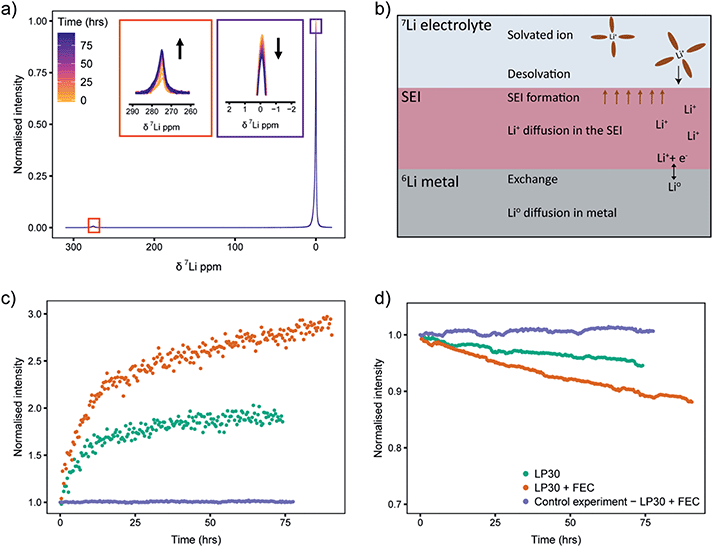
To understand the effect that the FEC additive has on the SEI formed on Li metal and the corresponding plating behaviour, we performed isotope exchange measurements in both LP30 and LP30 + FEC electrolytes. Using NMR, we observe in situ the isotope exchange of 6Li/7Li ions between 6Li-enriched Li metal (95% 6Li and 5% 7Li) and natural abundance electrolyte (i.e. 92.4% 7Li and 7.6%, 6Li).38,58 When 6Li metal is soaked in the 7Li electrolyte, the exchange between the two isotopes can be described as:| 7Lielectrolyte + 6Limetal ↔ 7Limetal + 6Lielectrolyte | (14) |
Static 7Li NMR (Fig. 8a for LP30 electrolyte, Fig. S13b† for LP30 + FEC) was used to follow the changes in signal intensities as a function of time. When the 6Li-metal is soaked in the 7Li-electrolyte, the 7Li NMR signal centred around 0 ppm decreases and the 7Li metal signal, centred at approximately 275 ppm (the metal is positioned parallel to B0 field), grows in (Fig. 8a).44 This is due to the continuous oxidation and reduction between the metal and the electrolyte during equilibrium as described in eqn (1). Because of the skin depth effect, the NMR is only sensitive to the surface layers of the metal whereas the signal intensity for the diamagnetic peak corresponds to the whole volume of the electrolyte and the SEI.
Integration of 7Li NMR signal intensities as a function of time (Fig. 8c and d) shows significant differences between the two electrolytes; in LP30 + FEC (Fig. 8c, orange) the 7Li metal intensity increases faster and the 7Li electrolyte peak intensity drops more quickly compared to LP30 (Fig. 8c and d, green), indicating more rapid exchange of lithium between the metal and electrolyte in the presence of FEC. These trends are shown to be reproducible in Fig. S14.† The processes that can affect the isotope exchange rate are shown in the schematic Fig. 8b. For the metal, the relevant processes are the exchange rate at the surface of the metal and self-diffusion of Li atoms within the metal. In the electrolyte and the SEI, the relevant processes are the desolvation of the Li+ ion in the electrolyte, diffusion of Li+ in the SEI layer, and the chemical formation of the SEI.
A control experiment, using a natural abundance Li metal electrode (“7Li rich”, 92.4% 7Li and 7.6% 6Li) in LP30 + FEC electrolyte was performed to observe the trends when the effect of isotope exchange is eliminated. The changes in intensities are minimal (Fig. 8c and d, purple) indicating that the formation of the SEI should not change the overall Li+ concentration in the electrolyte substantially. The NMR intensity of the electrolyte even increases very slightly (Fig. 8d), which is ascribed to the SEI and partial dissolution of the SEI into the electrolyte.53
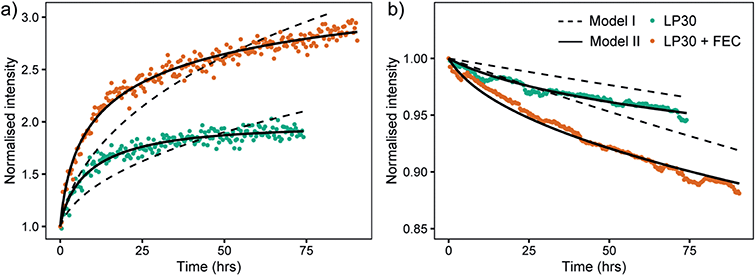
A mathematical model to describe the 6Li/7Li isotopic exchange was developed to extract the associated kinetic data from the NMR experiments, see detailed description in the theory section. Initially, a simplified model was formulated that only takes into account the isotope exchange between the metal and the electrolyte and neglects the formation of the SEI (Model I). The fitting of the experimental curves with Model I and eqn (3)–(7) involves only one fitting parameter, Jex and implicitly assumes that the SEI remains constant with time (Fig. 9, dashed lines). Jex describes the equilibrium exchange flux of Li between the electrolyte and the metal and includes desolvation of Li+ ions, diffusion through the SEI. Values for Jex obtained from the least-square fit are 0.77 × 10−6 mol m−2 s−1 for LP30 and 1.5 × 10−6 mol m−2 s−1 for LP30 + FEC (approximately twice as fast for LP30 + FEC). However, as can be seen in Fig. 9 the experimental curves are not well described by Model I (dashed lines).
The model was then further extended to take into account the long-term formation of the SEI (Model II).58 To describe the rate of SEI formation the model assumes the formation of the SEI to be proportional to the isotope exchange flux, Jex and includes the dimensionless SEI formation constant, αSEI(t) (eqn (9)). The rate of SEI formation slows down with time, as can be seen from the impedance analysis in Fig. S20–S22† where the resistance of the SEI formed in LP30 + FEC reaches an equilibrium after approximately 20 hours. This is described with a decreasing exponential (eqn (10)), which includes the fitting parameter βSEI, the SEI growth constant. In addition, the model includes how the maturation of the SEI leads to reduced permeability and the exchange flux becomes time-dependent, Jex(t), described in eqn (11). The fit to the experimental curves is shown in Fig. 9 (Model II, black lines) and the corresponding parameters are presented in Table 2.
| Symbol | Description/unit | LP30 | LP30 + FEC | Ratio (LP30 + FEC)/LP30 |
|---|---|---|---|---|
| J ex,0 | Isotope exchange flux at the time of the first NMR measurement [10−6 mol m−2 s−1] | 1.6 | 3.1 | 1.9 |
| J ex,74 | Isotope exchange flux at 74 h [10−6 mol m−2 s−1] | 0.49 | 1.2 | 2.5 |
| β ex | SEI permeability constant [m2 mol−1] | 19 | 7.8 | 0.41 |
| α SEI,0 | SEI formation proportionality constant dimensionless | 0.38 | 0.85 | 2.2 |
| β SEI | SEI growth constant [m2 mol−1] | 8.7 | 17 | 2.0 |
| k ex,0 | Exchange rate constant at time of first NMR measurement [10−10 m s−1] | 1.8 | 3.7 | 2.1 |
| k SEI,0 | The SEI formation rate constant [10−10 m s−1] | 0.68 | 3.1 | 4.6 |
| k SEI,74 | The SEI formation rate constant at 74 h [10−10 m s−1] | 0.13 | 0.17 | 1.3 |
| N SEI | Number of moles of SEI formed per surface area at time 74 h [mmol m−2] | 61 | 120 | 2.0 |
At the beginning of the experiment, the exchange flux for LP30 + FEC, Jex,0 (Table 2), is again roughly two times that for LP30. The ratio between Jex,0 for LP30 + FEC and LP30 is roughly the same for both Model I and Model II (factor of two), although the resulting values of the fitted parameter are different. To examine the sensitivity of the fit to the Jex,0 values and verify the fit for Model II, the values of Jex,0 were also fixed to the Jex values from Model I, reported above. The result, Fig. S19,† shows that we cannot fit the data with the Jex,0 values from Model I. The exchange flux Jex(t) is plotted as a function of time in Fig. S17b.† The decrease in the permeability of the SEI due to the growing SEI, captured with βex, is greater in LP30, which leads to an increased difference in the effective exchange rate at 74 h, shown in Fig. S17.† The ratio of Jex,74 between the two electrolytes is 2.5 and indicates increasingly reduced transport properties in the LP30-derived SEI.
Multiplying the exchange flux determined at the beginning of the experiment by the Faraday constant gives the isotope exchange current, which results in 15 μA cm−2 for LP30 and 30 μA cm−2 for LP30 + FEC. The SEI current at OCV is calculated similarly and is around 6 μA cm−2 in LP30 and 26 μA cm−2 in LP30 + FEC (eqn (9)). Using the Butler–Volmer formulism to describe the exchange current (eqn (2)), we similarly define the isotope exchange current jex and obtain an estimate of kex [m s−1], the isotope exchange rate constant:
| jex(t) = F × Jex(t) = Fkex(t)[Li+]α[Li0]1−α | (15) |
The value of the transfer coefficient α, is assumed to be 0.5, which has been found to fit a range of experimental data adequately67,81 and the calculated values of kex are listed in Table 2. The SEI formation rate constant can now be defined as kSEI = αSEIkex (see eqn (9)). At the start of the experiment, kSEI for LP30 + FEC is approximately five times that in LP30 (Table 2). The SEI then reaches equilibrium faster, as seen with higher value of βSEI (Table 2) and the sharp decrease in αSEI(t) shown in Fig. S18.† This is consistent with the impedance acquired in symmetrical Li–Li coin cells at OCV (Fig. S22†) where the impedance in the LP30 + FEC stabilises and plateaus compared to it consistently rising in LP30.
According to the simulation, the number of moles per surface area formed in the two electrolytes, NSEI (Fig. S17a†) is also greater for the LP30 + FEC electrolyte, indicating a thicker SEI is being formed. We have estimated the thickness of the SEI by using eqn (13) and assuming it to be pure Li2CO3 so as to provide a qualitative understanding of the extent of SEI formation. Averaging over the whole experiment (74 hours) the SEI formation rate is 6.1 nm h−1 in LP30 and 12 nm h−1 for LP30 + FEC. The values are relatively large and seem to overestimate the thickness of the SEI but are on a similar scale to what was estimated in an earlier isotope exchange study (14 nm h−1 in LP30).58 One possible reason for this overestimation of thickness is the assumption that all of the reduced electrolyte species are deposited to form the SEI. However, it has been shown experimentally that a wide range of the reduced electrolyte species are soluble and go into the electrolyte.75,82,83 We also note that the comparison of SEI thicknesses needs to be interpreted with caution as the chemical composition and density is expected to differ between the two electrolytes.
The confidence interval of the fitted parameters is reported in Table S3.† The most important observation from the error analysis is the large interval for βSEI in LP30, which gives the range 0–18 m2 mol−1, whereas the confidence interval for LP30 + FEC is 11–23 m2 mol−1. This may indicate that the exponential decay of the SEI growth rate with time (eqn (10)) does not fully capture the SEI formation process in LP30. Alternatively, and more plausibly, this could also demonstrate the instability of the SEI formed in LP30 which has been shown to form more soluble SEI products in studies on silicon compared to LP30 + FEC.84 This explanation is consistent with the impedance data (Fig. S20†), where the resistance of the SEI for LP30, RSEI, keeps growing with time.
Discussion
Localised deposition has previously been associated with slow Li+ transport properties in the SEI, which leads to induced stresses beneath the SEI and can cause fracture, resulting in Li whisker growth.28,30,85 The numerical simulations of the isotope exchange curves show that the Li+–Li0 exchange rate, quantified here via the isotope exchange flux Jex, through the LP30 + FEC chemically-derived SEI is twice as fast as transport through the LP30-derived SEI (Table 2) and the more whisker-like morphology that forms in LP30 can, at least in part, be explained by the slower Li+ transport in the SEI. Furthermore, rapid passivation on fresh Li metal surfaces has been argued to be a key parameter of a good SEI layer.86 If the SEI breaks, fast SEI repair will reduce the impedance differences on different sites on the electrode's surface resulting in more homogeneous deposition.33 The simulations of the isotope exchange indicate that the SEI growth rate is more than four times faster in LP30 + FEC, clearly demonstrating the faster kinetics associated with FEC degradation. This is consistent with the higher reduction potential of FEC80 that has been shown to occur at ∼1.3 V compared to ∼0.8 V (vs. Li/Li+) for the EC solvent molecule.87 NMR studies (albeit on silicon anodes88,89) have also shown that the organic polymers within the SEI formed with FEC additives contain more cross-linking groups, consistent with a more elastic and flexible SEI, that can accommodate to a greater extent the growth of Li deposits without cracking or rupturing.Our results from the isotope exchange simulations should be contrasted with those of Boyle et al. who measured the exchange current density for Li metal deposition (using an ultramicroelectrode and fast scan rates of >1000 mV s−1 to minimise SEI effects) and found that j0 was approximately 1.5 times larger for a carbonate electrolyte with vs. without FEC.67 They attributed the faster electron transfer kinetics to the slightly lower Li+ concentration when the FEC is added to the electrolyte and thus weaker interactions between ions.67 In our study, the exchange is measured at OCV and depends on both the electron kinetics and the mass transport through the SEI. This latter point is evident in the simulations where Jex was found to be time-dependent because of the growing SEI, the exchange flux decreasing over the whole time period (Fig. S17†). We further note that the exchange current estimated by isotope exchange is three orders of magnitude lower than that obtained by Boyle et al. by Li plating on a tungsten-ultramicroelectrode (with little to no SEI) and an order of magnitude lower than that estimated by impedance spectroscopy (with SEI).67 This is partly because the NMR measurements are not started until approximately 10 minutes after the Li metal is immersed in the electrolyte. The numbers extracted from our measurements are particularly relevant to the corrosion seen for Li metal anodes90,91 (particularly when high surface area mossy and dendritic structures are formed) and also for Li formed on graphitic anodes under high currents/low temperatures.
Our results suggest that the lower coulombic efficiencies frequently reported for the commercial carbonate electrolyte15 are due to both low current efficiency with continuous SEI formation as a result of the formation of higher surface area Li whiskers and the formation of dead lithium (in cycling experiments). The former is demonstrated by using in situ NMR, where the mass of the Li deposits can be quantified and readily compared to the mass expected to be deposited from the electrochemistry, mechem (Table S1†). This is also consistent with the earlier “peaking” behaviour seen for the LP30 electrolyte during the 1st stripping (Fig. 4). For the faster plating current density of 2 mA cm−2, the current efficiency (Fig. 3) and the morphology of the Li deposits become similar for the two electrolytes (see SEM, Fig. S7,† consistent with other studies18). This demonstrates that although the SEI in LP30 + FEC has better transport properties, at high current densities it is still not fast enough to allow for a sufficiently uniform transport through the SEI. We note that there may be differences between the chemically formed SEI studied with the isotope exchange and that formed on cycling in terms of composition and morphology. Further experiments are in progress to explore this in more detail using dynamic nuclear polarization (DNP) NMR.92
The SEI formed during the rest period in pulse plating is directly related to the isotope exchange measurements, as it forms under OCV. For the pulse plating experiments, the morphology of the Li deposits in LP30 were seen to be highly dependent on both plating and rest time. Previous Monte Carlo simulations have suggested shorter pulses are beneficial in mitigating Li dendrite growth.77 In our experiments in LP30, the longer pulses of both TON, TOFF = 1 s and 500 ms resulted in a denser morphology than achieved on constant plating whereas TON, TOFF = 5 ms resulted in the formation of narrow whiskers. Therefore, recommending short pulses for Li deposition, nominally to ensure minimal concentration gradients at the electrode's surface, may not always be appropriate. The results illustrate the important effect of the rest period in pulse plating Li metal, where both diffusion and the healing of the SEI layer takes place. Applying a longer rest time for the short pulses, using TON = 5 ms and TOFF = 15 ms, improved the plating with smoother deposits forming (Fig. 5e). Of note, as shown both with the impedance measurements (Fig. S22†) and the isotope exchange simulations, full passivation of the Li metal surface is not achieved on the timescale of the rest periods used in the pulse plating experiments. Despite this, all in situ pulse plating experiments demonstrated that less charge was wasted to form the SEI during plating and indicates that even time intervals of 15 ms can be sufficient to at least partially heal hotspots formed during plating. Note that this process still consumes lithium (and electrolyte) (via reactions such as those described in eqn (8)) and hence is another mechanism responsible for degradation in a metal cell: in experiments performed with a fixed and finite lithium concentration (e.g., when plating using a lithium-ion cathode as the lithium source), this will lead to more rapid cell death.
Pulse plating in LP30 + FEC led consistently to more dense morphologies and was seen to delay the onset of microstructural formation (Fig. 6a). There are three possible explanations for pulse plating being more effective in LP30 + FEC. As we have shown in the first section, the microstructures formed under constant plating in LP30 + FEC are generally more uniform compared to LP30. Hence, local concentration gradients that develop at the electrode during plating, which are amplified at rough sites and protrusions, are less pronounced for the smoother metal surface in LP30 + FEC. Thus, (i) relaxation of local concentration gradients will not be as important as in the case for LP30. (ii) Based on our simulations, SEI passivation will occur more rapidly, reducing impedance differences over the electrode's surface. (iii) The SEI in LP30 + FEC allows for more rapid Li+ transport than in LP30, demonstrated by the Li+ exchange rate, and thus more homogeneous plating is expected.
Conclusion
Overall, this work has presented a careful comparison of the SEI formed in the standard carbonate electrolyte, LP30, and in LP30 + FEC with quantitative and non-invasive NMR measurements. Our in situ NMR measurements have shown that both the plating efficiency and growth mode of lithium deposition are governed by the nature of the SEI as well as the applied current density. Pulse plating was shown to be more effective in LP30 + FEC, delaying the onset of microstructural growth.Using 6Li/7Li isotope exchange NMR measurements, Li+ exchange between Li metal and the electrolyte was studied (at OCV), the exchange occurring simultaneously with SEI growth. The measured exchange flux was related to the traditional Butler–Volmer model of electrochemical kinetics. Measuring the 6Li/7Li isotope exchange is shown to be an easy and effective method to monitor the exchange current (affected by transport through the SEI) and the growth of SEI on lithium metal anodes. The exchange current is shown to decrease with time, corresponding to a decreased permeability of the SEI. By performing numerical simulations, we demonstrate that the method can be used to compare the exchange rates at equilibrium (OCV) and the kinetics of SEI formation on Li metal, for a range of different electrolytes and electrolyte additives. The values obtained are highly relevant for understanding why pulse plating can lead to smoother deposition, and allow Li corrosion to be directly quantified.
The two electrolytes studied in this work show clear differences: the 6Li/7Li exchange is twice as fast in LP30 + FEC (due to faster Li+ transport in the SEI), and the SEI formation rate is more than four times faster, as compared to LP30. For LP30, the slower Li+ transport can lead to non-uniform current distribution during plating, localised deposition resulting in stress-build up in the SEI and whisker-growth. The high surface area of the whiskers leads to low current efficiency due to constant SEI formation, the slow SEI formation rate also impeding the full repair of the SEI.
Via this NMR study we identify and quantify some of the key SEI parameters – namely the lithium ion transport and the rate of healing – that are important in controlling the nature of lithium metal deposition. Future studies with a much wider range of additives and electrolytes are in progress to use this methodology to help design an optimal SEI layer on lithium metal that achieves uniform plating and stripping at commercially relevant current densities (>0.5 mA cm−2) with high coulombic efficiencies.
Data availability
The raw intensity data from the isotope exchange measurements, the raw EIS data and the Matlab codes to run the simulations according to the mathematical model presented in the current study are available in the Apollo University of Cambridge repository at https://doi.org/10.17863/CAM.54707Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. B. G and S. V acknowledge the support from the Royal Society (RP/R1/180147). A. B. G also acknowledges EPSRC-EP/M009521/1 for funding and S. V. acknowledges the Faraday Institution (SOLBAT, FIRG007) and Cambridge Trust for funding. S. M thanks the Blavatnik Cambridge Fellowships. L. E. M. gratefully acknowledges financial support through a H2020 Marie Skłodowska- Curie Individual Fellowship and a Charles and Katharine Darwin Research Fellowship (Darwin College). C. P. G thanks the EU/ERC for an Advanced Fellowship (Grant Agreement No. 835073). A. B. G thanks the NanoDTC Cambridge for travel funding. We would like to thank Dr Adam Best (CSIRO) and Dr Amangeldi Torayev (University of Oxford) for useful discussions. Finally, we would like to thank Sharon Connor for careful reading of the manuscript and one of the reviewers for their helpful comments concerning the exchange model.References
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 172 CrossRef CAS.
- W. Xu, J. Wang, F. Ding, X. Chen, E. Nasybulin, Y. Zhang and J.-G. G. Zhang, Energy Environ. Sci., 2014, 7, 513–537 RSC.
- K. N. Wood, M. Noked and N. P. Dasgupta, ACS Energy Lett., 2017, 2, 664–672 CrossRef CAS.
- B. Liu, J.-G. G. Zhang and W. Xu, Joule, 2018, 2, 833–845 CrossRef CAS.
- M. Paunovic and M. Schlesinger, Fundamentals of Electrochemical Deposition, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2006 Search PubMed.
- Y. S. Cohen, Y. Cohen and D. Aurbach, J. Phys. Chem. B, 2000, 104, 12282–12291 CrossRef CAS.
- S. Jurng, Z. L. Brown, J. Kim and B. L. Lucht, Energy Environ. Sci., 2018, 11, 2600–2608 RSC.
- X. Q. Zhang, X. Chen, X. B. Cheng, B. Q. Li, X. Shen, C. Yan, J. Q. Huang and Q. Zhang, Angew. Chem., Int. Ed., 2018, 100081, 5301–5305 CrossRef PubMed.
- J. Qian, W. Xu, P. Bhattacharya, M. Engelhard, W. A. Henderson, Y. Zhang and J. G. Zhang, Nano Energy, 2015, 15, 135–144 CrossRef CAS.
- J. Zheng, M. H. Engelhard, D. Mei, S. Jiao, B. J. Polzin, J. G. Zhang and W. Xu, Nat. Energy, 2017, 2, 1–15 Search PubMed.
- E. Markevich, G. Salitra, F. Chesneau, M. Schmidt and D. Aurbach, ACS Energy Lett., 2017, 2, 1321–1326 CrossRef CAS.
- R. Mogi, M. Inaba, Y. Iriyama, T. Abe and Z. Ogumi, J. Electrochem. Soc., 2002, 149, A385 CrossRef CAS.
- J. Heine, P. Hilbig, X. Qi, P. Niehoff, M. Winter and P. Bieker, J. Electrochem. Soc., 2015, 162, A1094–A1101 CrossRef CAS.
- F. Ding, W. Xu, X. Chen, J. Zhang, M. H. Engelhard, Y. Zhang, B. R. Johnson, J. V. Crum, T. A. Blake, X. Liu and J.-G. Zhang, J. Electrochem. Soc., 2013, 160, A1894–A1901 CrossRef CAS.
- X. Q. Zhang, X. B. Cheng, X. Chen, C. Yan and Q. Zhang, Adv. Funct. Mater., 2017, 27, 1–8 Search PubMed.
- Z. L. Brown, S. Jurng, C. C. Nguyen and B. L. Lucht, ACS Appl. Energy Mater., 2018, 1, 3057–3062 CrossRef CAS.
- Y. Li, Y. Li, A. Pei, K. Yan, Y. Sun, C. L. Wu, L. M. Joubert, R. Chin, A. L. Koh, Y. Yu, J. Perrino, B. Butz, S. Chu and Y. Cui, Science, 2017, 358, 506–510 CrossRef CAS PubMed.
- Y. Li, W. Huang, Y. Li, A. Pei, D. T. Boyle and Y. Cui, Joule, 2018, 2, 2167–2177 CrossRef CAS.
- J. L. Barton and J. O. Bockris, Proc. R. Soc. A, 1962, 268, 485–505 CAS.
- J. N. Chazalviel, Phys. Rev. A, 1990, 42, 7355–7367 CrossRef CAS PubMed.
- H. J. S. Sand, London, Edinburgh, Philos. Mag., 1901, 1, 45–79 CrossRef CAS.
- C. Brissot, M. Rosso, J. N. Chazalviel and S. Lascaud, J. Power Sources, 1999, 81, 925–929 CrossRef.
- H. J. Chang, A. J. Ilott, N. M. Trease, M. Mohammadi, A. Jerschow and C. P. Grey, J. Am. Chem. Soc., 2015, 137, 15209–15216 CrossRef CAS PubMed.
- P. Bai, J. Li, F. R. Brushett and M. Z. Bazant, Energy Environ. Sci., 2016, 9, 3221–3229 RSC.
- K. Nishikawa, T. Mori, T. Nishida, Y. Fukunaka and M. Rosso, J. Electroanal. Chem., 2011, 661, 84–89 CrossRef CAS.
- G. Yoon, S. Moon, G. Ceder and K. Kang, Chem. Mater., 2018, 30, 6769–6776 CrossRef CAS.
- K. Nishikawa, T. Mori, T. Nishida, Y. Fukunaka, M. Rosso and T. Homma, J. Electrochem. Soc., 2010, 157, A1212 CrossRef CAS.
- A. Kushima, K. P. So, C. Su, P. Bai, N. Kuriyama, T. Maebashi, Y. Fujiwara, M. Z. Bazant and J. Li, Nano Energy, 2017, 32, 271–279 CrossRef CAS.
- O. Crowther and A. C. West, J. Electrochem. Soc., 2008, 155, A806 CrossRef CAS.
- J. Yamaki, S. Tobishima, K. Hayashi, K. Saito, Y. Nemoto and M. Arakawa, J. Power Sources, 1998, 74, 219–227 CrossRef CAS.
- H. Yang, E. O. Fey, B. D. Trimm, N. Dimitrov and M. S. Whittingham, J. Power Sources, 2014, 272, 900–908 CrossRef CAS.
- J. Steiger, D. Kramer and R. Mönig, Electrochim. Acta, 2014, 136, 529–536 CrossRef CAS.
- K. N. Wood, E. Kazyak, A. F. Chadwick, K. H. Chen, J. G. Zhang, K. Thornton and N. P. Dasgupta, ACS Cent. Sci., 2016, 2, 790–801 CrossRef CAS PubMed.
- X. Wang, M. Zhang, J. Alvarado, S. Wang, M. Sina, B. Lu, J. Bouwer, W. Xu, J. Xiao, J. G. Zhang, J. Liu and Y. S. Meng, Nano Lett., 2017, 17, 7606–7612 CrossRef CAS PubMed.
- C. Fang, J. Li, M. Zhang, Y. Zhang, F. Yang, J. Z. Lee, M.-H. Lee, J. Alvarado, M. A. Schroeder, Y. Yang, B. Lu, N. Williams, M. Ceja, L. Yang, M. Cai, J. Gu, K. Xu, X. Wang and Y. S. Meng, Nature, 2019, 572, 511–515 CrossRef CAS PubMed.
- J. Wandt, C. Marino, H. A. Gasteiger, P. Jakes, R. A. Eichel and J. Granwehr, Energy Environ. Sci., 2015, 8, 1358–1367 RSC.
- R. Bhattacharyya, B. Key, H. Chen, A. S. Best, A. F. Hollenkamp and C. P. Grey, Nat. Mater., 2010, 9, 504–510 CrossRef CAS PubMed.
- H. J. Chang, N. M. Trease, A. J. Ilott, D. Zeng, L. S. Du, A. Jerschow and C. P. Grey, J. Phys. Chem. C, 2015, 119, 16443–16451 CrossRef CAS.
- S. Chandrashekar, N. M. Trease, H. J. Chang, L.-S. S. Du, C. P. Grey and A. Jerschow, Nat. Mater., 2012, 11, 311–315 CrossRef CAS PubMed.
- A. J. Ilott, M. Mohammadi, H. J. Chang, C. P. Grey and A. Jerschow, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10779–10784 CrossRef CAS PubMed.
- P. M. Bayley, N. M. Trease and C. P. Grey, J. Am. Chem. Soc., 2016, 138, 1955–1961 CrossRef CAS PubMed.
- V. Küpers, M. Kolek, P. Bieker, M. Winter and G. Brunklaus, Phys. Chem. Chem. Phys., 2019, 21, 26084–26094 RSC.
- H. Wang, N. Sa, M. He, X. Liang, L. F. Nazar, M. Balasubramanian, K. G. Gallagher and B. Key, J. Phys. Chem. C, 2017, 121, 6011–6017 CrossRef CAS.
- N. M. Trease, L. Zhou, H. J. Chang, B. Y. Zhu and C. P. Grey, Solid State Nucl. Magn. Reson., 2012, 42, 62–70 CrossRef CAS PubMed.
- H. Y. Cheh, J. Electrochem. Soc., 1971, 118, 551–557 CrossRef CAS.
- Y. Fukunaka, J. Electrochem. Soc., 1989, 136, 3278 CrossRef CAS.
- A. Ul-Hamid, H. Dafalla, A. Quddus, H. Saricimen and L. M. Al-Hadhrami, Appl. Surf. Sci., 2011, 257, 9251–9259 CrossRef CAS.
- K. I. Popov, M. D. Maksimović, B. M. Ocokoljić and B. J. Lazarević, Surf. Technol., 1980, 11, 99–109 CrossRef CAS.
- N. Ibl, Surf. Technol., 1980, 10, 81–104 CrossRef CAS.
- Q. Li, S. Tan, L. Li, Y. Lu and Y. He, Sci. Adv., 2017, 3, 1–10 CAS.
- A. Maraschky and R. Akolkar, J. Electrochem. Soc., 2018, 165, D696–D703 CrossRef CAS.
- G. García, S. Dieckhöfer, W. Schuhmann and E. Ventosa, J. Mater. Chem. A, 2018, 6, 4746–4751 RSC.
- D. Rehnlund, C. Ihrfors, J. Maibach and L. Nyholm, Mater. Today, 2018, 21, 1010–1018 CrossRef CAS.
- G. E. Boyd, A. W. Adamson and L. S. Myers, J. Am. Chem. Soc., 1947, 69, 2836–2848 CrossRef CAS PubMed.
- F. G. Helfferich, in Mass Transfer and Kinetics of Ion Exchange, 1983 Search PubMed.
- M. Kosmulski, M. Jaroniec and J. Szczypa, Adsorpt. Sci. Technol., 1985, 2, 97–119 CrossRef CAS.
- T.-C. Huang and F.-N. Tsai, J. Chem. Eng. Jpn., 1977, 10, 131–136 CrossRef CAS.
- A. J. Ilott and A. Jerschow, J. Phys. Chem. C, 2018, 122, 12598–12604 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods Fundamentals of Electrochemistry, 2001 Search PubMed.
- O. Pecher, J. Carretero-Gonzalez, K. J. J. Griffith and C. P. P. Grey, Chem. Mater., 2017, 29, 213–242 CrossRef CAS.
- J. M. Stratford, P. K. Allan, O. Pecher, P. A. Chater and C. P. Grey, Chem. Commun., 2016, 52, 12430–12433 RSC.
- H. Wickham, R. Francois, L. Henry and K. Müller, Cran, 2017.
- A. J. Ilott, S. Chandrashekar, A. Klöckner, H. J. Chang, N. M. Trease, C. P. Grey, L. Greengard and A. Jerschow, J. Magn. Reson., 2014, 245, 143–149 CrossRef CAS PubMed.
- E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288–292 CrossRef CAS.
- K. Zick, Diffusion NMR User Manual, Bruker Corporation, 2016.
- P. Atkins, J. de Paula and J. Keeler, Atkins' Physical Chemistry, Oxford University Press, Oxford, United Kingdom, 2018 Search PubMed.
- W. Huang, D. T. Boyle, Y. Li, Y. Li, A. Pei, H. Chen and Y. Cui, ACS Nano, 2019, 13, 737–744 CrossRef CAS PubMed.
- R. Messer and F. Noack, Appl. Phys., 1975, 6, 79–88 CAS.
- D. Aurbach, J. Power Sources, 2000, 89, 206–218 CrossRef CAS.
- J. Christensen and J. Newman, J. Electrochem. Soc., 2004, 151, A1977 CrossRef CAS.
- M. Tang and J. Newman, J. Electrochem. Soc., 2012, 159, A1922–A1927 CrossRef CAS.
- L. F. Shampine and M. W. Reichelt, J. Sci. Comput., 1995, 18, 1–22 Search PubMed.
- D. Aurbach and M. Moshkovich, J. Electrochem. Soc., 1998, 145, 2629 CrossRef CAS.
- G. Bieker, M. Winter and P. Bieker, Phys. Chem. Chem. Phys., 2015, 17, 8670–8679 RSC.
- D. Aurbach and A. Zaban, J. Electroanal. Chem., 1994, 367, 15–25 CrossRef CAS.
- M. Odziemkowski, J. Electrochem. Soc., 1993, 140, 1546 CrossRef CAS.
- A. Aryanfar, D. Brooks, B. V. Merinov, W. A. Goddard, A. J. Colussi and M. R. Hoffmann, J. Phys. Chem. Lett., 2014, 5, 1721–1726 CrossRef CAS PubMed.
- L. E. Marbella, S. Zekoll, J. Kasemchainan, S. P. Emge, P. G. Bruce and C. P. Grey, Chem. Mater., 2019, 31, 2762–2769 CrossRef CAS PubMed.
- H. Wang, T. K. J. Köster, N. M. Trease, J. Ségalini, P. L. Taberna, P. Simon, Y. Gogotsi and C. P. Grey, J. Am. Chem. Soc., 2011, 133, 19270–19273 CrossRef CAS PubMed.
- T. Hou, G. Yang, N. N. Rajput, J. Self, S.-W. Park, J. Nanda and K. Persson, Nano Energy, 2019, 64, 103881 CrossRef CAS.
- M. W. Verbrugge and B. J. Koch, J. Electrochem. Soc., 1994, 141, 3053 CrossRef CAS.
- K. Tasaki, A. Goldberg, J.-J. Lian, M. Walker, A. Timmons and S. J. Harris, J. Electrochem. Soc., 2009, 156, A1019 CrossRef CAS.
- M. Tang, S. Lu and J. Newman, J. Electrochem. Soc., 2012, 159, A1775–A1785 CrossRef CAS.
- Y. Jin, N. J. H. Kneusels, P. C. M. M. Magusin, G. Kim, E. Castillo-Martínez, L. E. Marbella, R. N. Kerber, D. J. Howe, S. Paul, T. Liu and C. P. Grey, J. Am. Chem. Soc., 2017, 139, 14992–15004 CrossRef CAS PubMed.
- Y. He, X. Ren, Y. Xu, M. H. Engelhard, X. Li, J. Xiao, J. Liu, J. G. Zhang, W. Xu and C. Wang, Nat. Nanotechnol., 2019, 14, 1042–1047 CrossRef CAS PubMed.
- M. He, R. Guo, G. M. Hobold, H. Gao and B. M. Gallant, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 73–79 CrossRef CAS PubMed.
- C. Xu, F. Lindgren, B. Philippe, M. Gorgoi, F. Björefors, K. Edström and T. Gustafsson, Chem. Mater., 2015, 27, 2591–2599 CrossRef CAS.
- Y. Jin, N. J. H. Kneusels, L. E. Marbella, E. Castillo-Martínez, P. C. M. M. Magusin, R. S. Weatherup, E. Jónsson, T. Liu, S. Paul and C. P. Grey, J. Am. Chem. Soc., 2018, 140, 9854–9867 CrossRef CAS PubMed.
- A. L. Michan, M. Leskes and C. P. Grey, Chem. Mater., 2016, 28, 385–398 CrossRef CAS.
- D. Lin, Y. Liu, Y. Y. Li, Y. Y. Li, A. Pei, J. Xie, W. Huang and Y. Cui, Nat. Chem., 2019, 11, 382–389 CrossRef CAS PubMed.
- A. Kolesnikov, M. Kolek, J. F. Dohmann, F. Horsthemke, M. Börner, P. Bieker, M. Winter and M. C. Stan, Adv. Energy Mater., 2020, 2000017, 1–9 Search PubMed.
- M. A. Hope, B. L. D. Rinkel, A. B. Gunnarsdóttir, K. Märker, S. Menkin, S. Paul, I. V Sergeyev and C. P. Grey, Nat. Commun., 2020, 11, 2224 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta05652a |
| ‡ Present address: Department of Chemical Engineering, Columbia University, 500 W 120th St, New York, NY 10027, USA. |
| This journal is © The Royal Society of Chemistry 2020 |