Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Assessing negative thermal expansion in mesoporous metal–organic frameworks by molecular simulation†
Jack D.
Evans
 *a,
Johannes P.
Dürholt
*a,
Johannes P.
Dürholt
 b,
Stefan
Kaskel
b,
Stefan
Kaskel
 a and
Rochus
Schmid
a and
Rochus
Schmid
 b
b
aDepartment of Inorganic Chemistry, Technische Universität Dresden, Bergstraβe 66, 01062 Dresden, Germany. E-mail: jack.evans@tu-dresden.de
bComputational Materials Chemistry Group, Fakultät für Chemie und Biochemie, Ruhr-Universität Bochum, Bochum 44801, Germany
First published on 30th August 2019
Abstract
Most conventional materials display expansion in response to heating, so there is considerable interest in identifying materials that display the opposite behavior, negative thermal expansion (NTE). The current study investigated the temperature-induced contraction of seven mesoporous metal–organic frameworks (MOFs) of varying topology and composition, which exhibit outstanding porosity, using molecular simulation. We found exceptional NTE for the most porous MOFs, as well as a correlation between the coefficient of NTE and porosity. The large molecular subunits of the MOFs were further studied to find they intrinsically display NTE, corresponding to terahertz vibrational modes. As a result, NTE has a considerable effect on the mechanical properties of these MOFs and is an important consideration for understanding the mechanical stability of new extremely porous materials.
1 Introduction
Conventional dense materials are expected to expand in response to heating, however, a number of materials display the opposite behavior, shrinking with increasing temperature.1 This phenomenon, known as negative thermal expansion (NTE), is considered counterintuitive and is observed in only few inorganic solids and certain classes of framework materials.2 The technological importance of NTE relies on the application of this thermal volume contraction to negate the positive thermal expansion of conventional materials.3 For example, this control of thermal expansion is crucial in materials used for dental fillings.4A number of physical features can cause NTE. These include phase transitions, transverse vibrational modes and rigid unit modes.5 For example, ZrW2O8 shows a remarkable contraction between 0.3–1050 K owing to coupled rotations of rigid unit vibrational modes.1 NTE appears to occur more frequently in framework materials. In particular, several families of zeolites exhibit NTE.6,7
Metal–organic frameworks (MOFs) are porous materials, subject to increasing attention, that can produce a wide variety of porous framework structures through the combination of organic ligand units and metal nodes.8 Many MOFs exhibit NTE, including the prototypical MOF-5 and UiO-66.9–11 MOFs have advantages over traditional dense solids due to their high porosity, with large voids encapsulated by the structure. Mesoporous MOFs, with pore diameters larger than 20 Å, have structures that appear to be well suited for NTE. Firstly, owing to their large free volume, enabling massive contractions. Secondly, the large molecular subunits are expected to produce transverse phonon modes with increasing temperature, resulting in contraction.
Herein, we use molecular simulation to investigate NTE for a representative collection of mesoporous MOFs, illustrated in Fig. 1. These MOFs demonstrate record values of porosity, approaching 90% free volume, and encapsulate mesopores ranging between 23–43 Å, Table 1. Classical molecular simulation was employed to predict structural changes from 40–400 K and identify the origins for NTE in these materials. We also considered the intrinsic temperature-induced structural changes of the large molecular subunits that make up the frameworks and thus contribute to their NTE. Finally, the changes in mechanical properties originating from these pronounced structural deformations were computed to provide essential insight into the stability of these materials. This work highlights that the immense porosity achieved by MOF materials can be leveraged for large volumetric contraction for use in applications outside of gas storage.
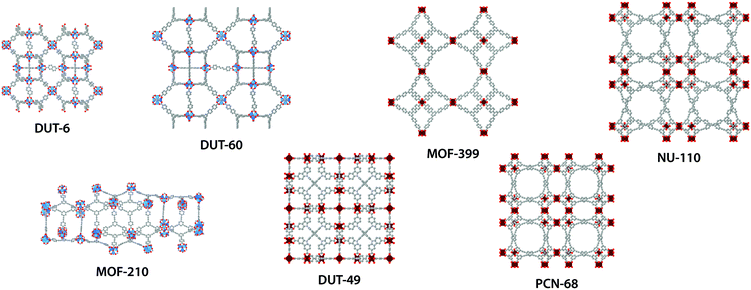 | ||
| Fig. 1 Atomistic structures of DUT-6,12,13 DUT-60,14 MOF-210,13 DUT-49,15 MOF-399,16 PCN-68 (ref. 17) and NU-110.18 ZnO4-tetrahedra blue; Cu2O8-paddlewheel dark red; C gray; O red; N light blue (hydrogen atoms are omitted for clarity). | ||
2 Computational methods
Initial framework properties, such as pore volume and largest pore diameter, were calculated from the deposited crystal structures using the Zeo++ code.19,20All molecular dynamics simulations were performed using the MOF-FF force field,21,22 employing the LAMMPS program package.23 Parameters were assigned using the hierarchical automated parameter assignment (HAPA) procedure,24 retrieving the matched parameters from the MOF+ database.25 Additional parameters for the organic linkers were adapted from the MM3 force field, which also represents the basis for the functional form of MOF-FF.
Coulomb interactions were truncated at 12 Å by employing the damped shifted force method from Fennell and Gezelter.26 The MOF-FF parameterization methodology was carefully validated by reproducing the NTE behavior of MOF-5 and HKUST-1, featuring the same inorganic structural building units as the investigated mesoporous MOFs.27,28 Moreover, the mean cell parameters of the simulated structures, over the investigated temperature range, differ from the experimental crystal structures by less than 3% (Table S1†).
The framework response to temperature was simulated by N, P, T molecular dynamics employing a Nosé–Hoover chain thermostat29 and Martyna–Tuckerman–Tobias–Klein (MTTK) barostat.30,31 These temperature and pressure controls have been previously assessed for use in describing flexible MOF systems.32 Systems were heated from 40 to 400 K in 20 K intervals. The timestep for the simulations was 1 fs and the thermostat and barostat dampening parameters were 100 fs and 2000 fs, respectively. Each temperature included an equilibration period of 0.5 ns followed by a production period of 1.0 ns, where the average volume and dynamics were investigated. The complete mechanical properties were calculated from the trajectories by analysis of the fluctuations of unit cell vectors.33
The Hessians H of the optimized structures as 2 × 2 × 2 super-cells were calculated with a double-sided finite difference scheme based on the analytical forces using a distortion of 0.001 Å. Based on these Hessians, phonon calculations were conducted using the phonopy software package.34
The largest ligand was extracted from each MOF and the same force field parameters were assigned to the molecule as for the entire MOF structure. Molecular dynamics were conducted in the N, V, T ensemble, and the dynamics of the oxygen atoms of the ligand were constrained in one plane. Trajectory periods and the thermostat were identical to that of the framework simulations. The average radius of gyration of the oxygen atoms was calculated to provide a representative value of the planar size of the ligands.
Representative input files for molecular simulations are available online in our data repository at https://github.com/jackevansadl/supp-data.
3 Results and discussion
3.1 Negative thermal expansion
Dynamics of the investigated MOFs were simulated between 40–400 K, with 20 K increases in temperature, and average cell parameters were computed. As displayed in the ESI,† each of the MOFs exhibit considerable contraction in response to heating, and no significant changes to the unit cell shapes were observed.This contraction produces pronounced NTE, Fig. 2a, with frameworks displaying a change in volume between 1–3%. In general, NTE materials show total volume contractions <1.5%, making the magnitude of contraction observed by these materials exceptional.35
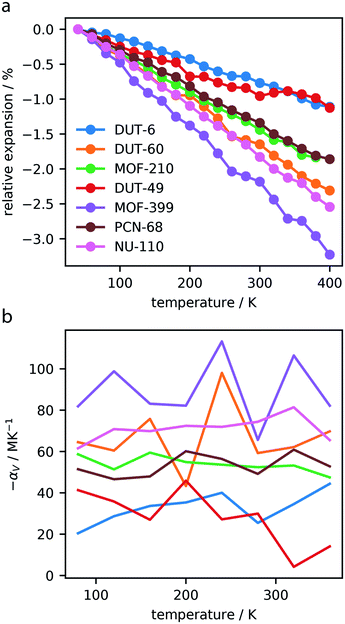 | ||
| Fig. 2 Relative expansion of the investigated MOFs (a). Volumetric thermal expansion coefficient, αV, calculated over the temperature range, computed for intervals of 40 K (b). | ||
The volumetric thermal expansion coefficient (αV), defined in eqn (1), provides a measure of the expansion rate.
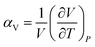 | (1) |
The volumetric thermal expansion coefficient was calculated at different temperatures within the range investigated, and we found a relatively constant rate of contraction, Fig. 2b. However, there was a noticeable change in contraction rate observed at approximately 300 K for DUT-49, which is discussed in Section 3.3. Given that NTE in MOF materials is considered a phonon-mediated phenomenon35 it is unsurprising that NTE persists over this entire temperature range. Notably, this has also been experimentally observed for MOF-5, which shows NTE from 80–500 K.36
The associated volumetric thermal expansion coefficients were also calculated over the entire temperature range, presented in Table 2, which provides a comparable metric for these materials. We find that a majority of the investigated MOFs show NTE coefficients >50 MK−1, and MOF-399 has an amazingly high coefficient of 87.6 MK−1. There are very few materials with “colossal” thermal expansion, such as Ag3[Co(CN)6], which is defined by |αV| > 100.37
| −αV/MK−1 | −αa/MK−1 | −αb/MK−1 | −αc/MK−1 | |
|---|---|---|---|---|
| DUT-6 | 32.6 | 10.5 | 10.8 | 10.7 |
| DUT-60 | 65.0 | 21.8 | 21.0 | 20.7 |
| MOF-210 | 54.7 | 15.9 | 20.0 | 19.7 |
| DUT-49 | 29.8 | 10.8 | 9.8 | 9.0 |
| MOF-399 | 87.6 | 31.5 | 27.5 | 28.6 |
| PCN-68 | 53.7 | 18.1 | 18.1 | 17.7 |
| NU-110 | 71.6 | 25.4 | 23.9 | 22.8 |
Similarly, the linear thermal expansion coefficient (αL), defined in eqn (2), can be computed to provide a measure of the expansion rate with respect to each cell length.
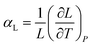 | (2) |
Careful analysis of the linear contraction of each cell parameter, αa,b,c in Table 2, shows that most of the investigated frameworks exhibit an isotropic contraction with little variation in cell shape even though no symmetry constrains were applied. However, the only framework considered in this study that has a trigonal unit cell, MOF-210, shows a distinct difference in linear contraction in the a-direction producing an anisotropic response.
Currently only DUT-49, from the MOFs studied in this work, has been investigated for NTE.38 Previous reported temperature-dependent powder X-ray diffraction (PXRD) experiments, between 100–600 K, of DUT-49 showed a constant shift of reflections to higher 2θ values, revealing NTE. Pawley refinements give volumetric and linear thermal expansion coefficients of −55.4 MK−1 and −19.4 MK−1, respectively. The magnitude of NTE observed experimentally is greater than expected from the computational work presented here. From previous studies, it is known that guests and defects will significantly affect NTE in an experimental system and we are currently investigating the underlying reasons for this discrepancy in DUT-49.11,39 Nevertheless, DUT-49 does experimentally demonstrate NTE with considerable magnitude.
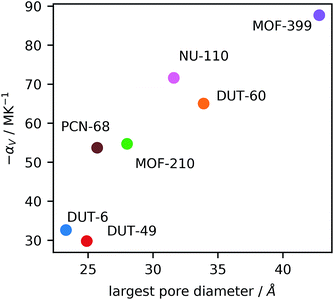
Interestingly, there appears to be a correlation between the porosity features of the MOFs and the magnitude of NTE, Fig. 3, suggesting the use of large pores and high levels of porosity as one way to design new and exceptional NTE materials. This was previously observed for studies of NTE in a series of isoreticular MOFs (pcu topology),9 however, here we find it occurs across different topologies, although the network certainly influences NTE, as observed for the comparison of DUT-49 and PCN-68 and reported by Bouëssel du Bourg et al. for other MOF structures.40
This relationship mirrors previous studies in Cd(CN)2 frameworks, which showed that guest molecules within the framework can reduce NTE and even produce positive expansion.39 Recently, Schneider et al. reported on a similar phenomenon in the MOF HKUST-1, whereby infiltration with TCNQ reduces NTE.41 Large empty cavities provide the open space for transverse vibrational modes often responsible for NTE behavior. We suggest that large empty cavities can accommodate larger amplitude vibrations, thereby producing a greater degree of NTE.
The magnitude of NTE is also linked to the mechanical properties of the material through eqn (3), which can be derived from eqn (1),42 where S is the entropy and B is the bulk modulus.
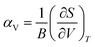 | (3) |
There is also a relationship between the porosity of a material and the bulk moduli, as reported previously in ceramics and zeolite materials.43,44 Often these highly porous materials have extremely small bulk modulus, 4.97 and 2.07 GPa for DUT-60 and MOF-399,14 respectively, which are very low for crystalline solids. Thus, the unique softness of mesoporous MOFs may also be responsible for the remarkable contraction observed.
We have shown that guest and defect-free mesoporous MOFs can show significant temperature-induced contraction. Few materials show total volume contractions >1.5%, resulting from temperature changes, making the NTE exhibited by these MOFs unique and suggests ultra-porous materials may have technological applications aside from gas storage.
3.2 Origins of expansion
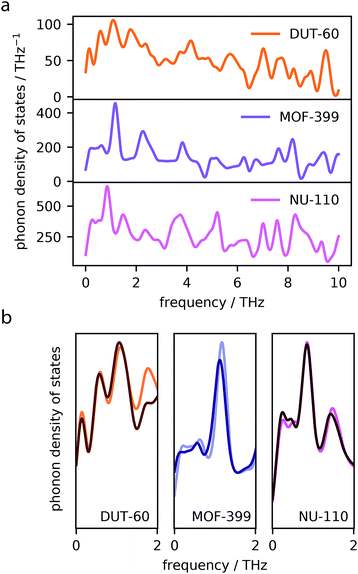
The phenomenon of NTE in MOFs and related network materials is generally a result of phonon vibrations.45 Specifically, NTE results from the often complex combination of transverse vibrational modes throughout the periodic lattice and rigid unit modes.46,47To confirm the presence of transverse phonon modes in the investigated MOFs, we computed the normal modes of vibration and subsequently generated total phonon density of states for MOF-399, DUT-60 and NU-110, the three best performing frameworks, using finite-displacements and the harmonic approximation.34 The total phonon density of states are displayed in Fig. 4a.
The MOF structures show several phonon modes with low frequency, <2 THz, which often give rise to NTE.48 Phonon modes of this frequency are attributed to collective vibrational modes, which can be visualized using the Molden49,50 software package with the normal mode data files available online from our data repository at https://github.com/jackevansadl/supp-data. For DUT-60 we can confirm these low-energy vibrational modes correspond to “trampoline”-like vibrations of the ligands that are also NTE-contributing modes in MOF-5.51
Phonons that soften in response to contraction of the lattice have negative Grüneisen parameters, which directly contribute to the NTE observed in the material.52 Please note, the softening described here relates to phonons shifting to lower frequencies. A comparison of the phonon density of states at different volumes, corresponding to the average MOF unit cell volume at 40 and 300 K highlight which of these low-energy modes give rise to NTE (Fig. 4b). For each MOF, we find one or several peaks that display softening upon contraction, which contribute to the NTE observed in these systems.
3.3 Intrinsic ligand response
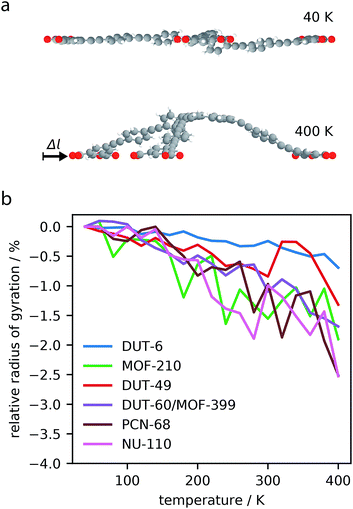
The analysis of phonon modes has highlighted the contribution of “trampoline”-like dynamics of the large ligands to NTE in mesoporous MOFs. To decouple the effect of these transverse vibrational modes from other contributions to NTE, such as rigid unit modes, constrained dynamics of the largest molecular subunits of the MOFs (for MOFs constructed from two ligands the largest ligand was chosen) were investigated, Fig. 5a.The ligands show considerable contraction following the increase in temperature. DUT-6, the smallest ligand tested, showed less than 1% contraction, while the largest ligand, NU-110, showed greater than 2% contraction in length. This investigation clearly demonstrates the intrinsic contraction from constrained molecular units.
Interestingly, we find the magnitude of correlation is not entirely correlated with the size of the ligand. The largest molecular subunit of DUT-60, which has an average radius of 12 Å at 40 K, shows a similar amount of contraction as NU-110, with an average radius 20 Å at 40 K. This suggests that the chemical constituents of the subunit strongly influences the amount of contraction. The ligand of DUT-60 and MOF-399 is comprised entirely of phenyl groups, whereas NU-110 contains additional alkyne groups to produce a larger ligand. It appears the alkyne functionality produces less contraction for a larger molecular unit, which has also been observed in expanded UiO-66 framework.53
Furthermore, simulations of the DUT-49 molecular unit demonstrates a change in contraction rate at approximately 300 K, which was also observed for the entire framework as discussed in Section 3.1. This demonstrates how the individual dynamics of the ligands in the DUT-49 system can be transferred directly to the properties of the total framework. This direct transfer of dynamics may be related to the unique flexibility exhibited by DUT-49.38,54
To clearly highlight this relationship between the contraction of the constrained ligands we can compare the molecular thermal expansion coefficient, as defined in eqn (4) where Rg is the radius of gyration, and the volumetric thermal expansion coefficient as displayed in Fig. S8.†
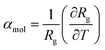 | (4) |
We find the majority of the MOFs studied display a linear relationship between the molecular and volumetric response, inferring that constrained molecular contraction can be directly related to that of the framework. However, we do observe a large variation for MOF-399 suggesting the large NTE response includes framework-dependent properties, such as large pore volume and specific rigid unit modes.5
The intrinsic dynamics of constrained ligands, discussed here, implies a chemical pathway for directly tuning the expansion properties of MOF materials. In particular, this highlights the design potential of MOFs for NTE applications.
3.4 Mechanical consequences of negative thermal expansion
Although NTE is a sought after property, this may also significantly affect the desired application of many of these materials. The maximum contraction of 3% observed in these systems has a minor effect on their porosity. However, as reported by previous studies, this contraction has an important affect on the mechanical stability. For example, some MOF materials have shown pressure-induced softening before the point of instability.40,55 To investigate the effect that temperature-induced contraction has on the mechanical stability of these materials, cell fluctuations from the molecular dynamics simulations were analyzed to compute the elasticity tensor, Cij. This elastic tensor contains key quantities that characterize the mechanical behavior of the structures in the elastic regime. For example, the directional Young's modulus is derived from the elasticity tensor. We found that all materials show temperature-induced softening, as illustrated in Fig. 6a for MOF-399, which demonstrates considerable softening of the Young's modulus.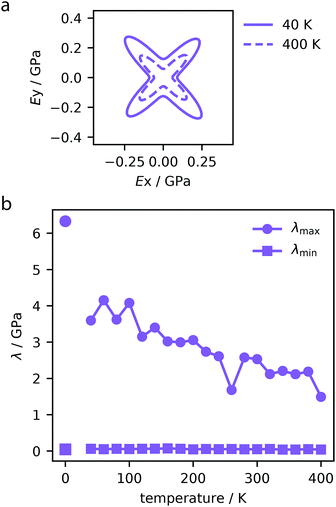 | ||
| Fig. 6 Directional Young's modulus of MOF-399 computed for trajectories at 40 and 400 K (a). Maximum and minimum (λmax and λmin) eigenvalues of the stiffness matrix for MOF-399 over the studied temperature range (b). The values at 0 K correspond to density functional theory simulations reported previously.14 | ||
In particular, the eigenvalues of the Cij matrix are required to be positive for the structure to be elastically stable.56 The maximum and minimum values of these eigenvalues indicate the most rigid and softest deformation mode. As we do not impose symmetry constraints, these are useful metrics in non-cubic crystals.57 Notably, increasing temperature was found to soften the stiffest deformation mode, however, it does not change the softest mode, displayed for each MOF in the ESI.† For example, MOF-399 shows a 50% decrease in the stiffest deformation mode (Fig. 6b).
Therefore, NTE is of great consequence to the mechanical stability of these often fragile systems. Although MOF-399 has the potential to demonstrate record-breaking porosity, this has yet to be reported experimentally, suggesting mechanical or chemical fragility. Previously, we employed density functional theory calculations to determine the maximum eigenvalue of the stiffness matrix of this material, which was found to be 6.33 GPa.14 However, the finite temperature calculations shown here demonstrate that at room temperature this material will be significantly less mechanically robust than first thought. We note that certain MOFs can be more resilient to temperature, such as PCN-68 which shows little variation in mechanical properties over the temperature range.
Recently, the decrease in stiffness with increasing temperature was experimentally reported for the MOF HKUST-1, which shows a decrease in Young's modulus in the temperature range 25–100 °C.58 This provides further design rules to push the limits of ultrahigh porosity in these materials. Namely, this temperature-induced softening should be considered to design the most mechanically robust porous materials over the relevant experimental temperature range.
4 Conclusions
We used molecular simulation to investigate NTE for a number of mesoporous MOFs. Given that MOFs have framework structures with large internal voids, perhaps unsurprisingly, they all showed contraction following a temperature increase, or NTE. The MOFs demonstrate impressive values of NTE > 50 MK−1, but more importantly, the magnitude of contraction for the temperature range 40–400 K is extremely large, with MOF-399 exhibiting more than 3% volume contraction.The origin of NTE in DUT-60, MOF-399 and NU-110 was investigated by calculation of phonon modes. We identified a number of low-energy phonon modes that contribute to the NTE observed in these systems. In DUT-60 these are observed to correspond to transverse “trampoline”-like vibrations of the ligands within the lattice. Subsequently, we considered temperature-induced structure changes intrinsic to the large molecular subunits, which construct the studied MOFs, and found that they alone produce considerable NTE.
Finally, the effect of NTE on the mechanical properties was tested. There was significant softening of the most rigid modes by NTE, and this softening represents an important consideration for the mechanical stability and working temperature range of these highly porous materials.
This work demonstrates the potential for large NTE exhibited by structures with high porosity. Futhermore, the extent of NTE in these materials highlights another important characteristic to consider when designing ultra-porous materials. For example, to design new materials with record-breaking surface area, NTE must be limited to ensure that a robust and experimentally realizable material is produced.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank V. Bon for fruitful discussions. This project received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme (grant agreement no. 742743) in addition to the Deutsche Forschungsgemeinschaft (grant agreement no. FOR2433). J. D. E. acknowledges the support the Alexander von Humboldt foundation and HPC platforms provided by a GENCI grant (A0010807069) and the Center for Information Services and High Performance Computing (ZIH) at TU Dresden. J. P. D. is grateful for the financial support of the Fonds der Chemischen Industrie (FCI).Notes and references
- T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92 CrossRef CAS.
- J. S. O. Evans, J. Chem. Soc., Dalton Trans., 1999, 3317–3326 RSC.
- K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001 CrossRef.
- A. Versluis, W. H. Douglas and R. L. Sakaguchi, Dent. Mater., 1996, 12, 290–294 CrossRef CAS.
- W. Miller, C. W. Smith, D. S. Mackenzie and K. E. Evans, J. Mater. Sci., 2009, 44, 5441–5451 CrossRef CAS.
- M. P. Attfield, Chem. Commun., 1998, 601–602 RSC.
- M. P. Attfield and A. W. Sleight, Chem. Mater., 1998, 10, 2013–2019 CrossRef CAS.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef.
- D. Dubbeldam, K. Walton, D. Ellis and R. Snurr, Angew. Chem., Int. Ed., 2007, 46, 4496–4499 CrossRef CAS.
- S. S. Han and W. A. Goddard, J. Phys. Chem. C, 2007, 111, 15185–15191 CrossRef CAS.
- M. J. Cliffe, J. A. Hill, C. A. Murray, F.-X. Coudert and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 11586–11592 RSC.
- N. Klein, I. Senkovska, K. Gedrich, U. Stoeck, A. Henschel, U. Mueller and S. Kaskel, Angew. Chem., Int. Ed., 2009, 48, 9954–9957 CrossRef CAS.
- H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. O. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428 CrossRef CAS.
- I. M. Hönicke, I. Senkovska, V. Bon, I. A. Baburin, N. Bönisch, S. Raschke, J. D. Evans and S. Kaskel, Angew. Chem., Int. Ed., 2018, 57, 13780–13783 CrossRef.
- U. Stoeck, S. Krause, V. Bon, I. Senkovska and S. Kaskel, Chem. Commun., 2012, 48, 10841 RSC.
- H. Furukawa, Y. B. Go, N. Ko, Y. K. Park, F. J. Uribe-Romo, J. Kim, M. O'Keeffe and O. M. Yaghi, Inorg. Chem., 2011, 50, 9147–9152 CrossRef CAS.
- D. Yuan, D. Zhao, D. Sun and H.-C. Zhou, Angew. Chem., Int. Ed., 2010, 49, 5357–5361 CrossRef CAS.
- O. K. Farha, I. Eryazici, N. C. Jeong, B. G. Hauser, C. E. Wilmer, A. A. Sarjeant, R. Q. Snurr, S. T. Nguyen, A. Özgür Yazaydın and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 15016–15021 CrossRef CAS.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- R. L. Martin, B. Smit and M. Haranczyk, J. Chem. Inf. Model., 2011, 52, 308–318 CrossRef.
- S. Bureekaew, S. Amirjalayer, M. Tafipolsky, C. Spickermann, T. K. Roy and R. Schmid, Phys. Status Solidi B, 2013, 250, 1128–1141 CrossRef CAS.
- J. P. Dürholt, G. Fraux, F.-X. Coudert and R. Schmid, J. Chem. Theory Comput., 2019, 15, 2420–2432 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- J. P. Dürholt and R. Schmid, in preparation.
- https://www.mofplus.org/, accessed June 2019.
- C. J. Fennell and J. D. Gezelter, J. Chem. Phys., 2006, 124, 234104 CrossRef PubMed.
- M. Tafipolsky and R. Schmid, J. Phys. Chem. B, 2009, 113, 1341 CrossRef CAS.
- M. Tafipolsky, S. Amirjalayer and R. Schmid, J. Phys. Chem. C, 2010, 114, 14402–14409 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Mol. Phys., 1996, 87, 1117–1157 CrossRef CAS.
- S. Rogge, L. Vanduyfhuys, A. Ghysels, M. Waroquier, T. Verstraelen, G. Maurin and V. Van Speybroeck, J. Chem. Theory Comput., 2015, 11, 5583–5597 CrossRef CAS.
- J. R. Ray, J. Appl. Phys., 1982, 53, 6441–6443 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- C. S. Coates and A. L. Goodwin, Mater. Horiz., 2019, 6, 211–218 RSC.
- N. Lock, Y. Wu, M. Christensen, L. J. Cameron, V. K. Peterson, A. J. Bridgeman, C. J. Kepert and B. B. Iversen, J. Phys. Chem. C, 2010, 114, 16181–16186 CrossRef CAS.
- A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. O. Evans, D. A. Keen, L. Peters and M. G. Tucker, Science, 2008, 319, 794–797 CrossRef CAS PubMed.
- S. Krause, V. Bon, I. Senkovska, U. Stoeck, D. Wallacher, D. M. Többens, S. Zander, R. S. Pillai, G. Maurin, F.-X. Coudert and S. Kaskel, Nature, 2016, 532, 348–352 CrossRef CAS.
- A. Phillips, A. Goodwin, G. Halder, P. Southon and C. Kepert, Angew. Chem., Int. Ed., 2008, 47, 1396–1399 CrossRef CAS.
- L. B. du Bourg, A. U. Ortiz, A. Boutin and F.-X. Coudert, APL Mater., 2014, 2, 124110 CrossRef.
- C. Schneider, D. Bodesheim, M. G. Ehrenreich, V. Crocellà, J. Mink, R. A. Fischer, K. T. Butler and G. Kieslich, J. Am. Chem. Soc., 2019, 141, 10504–10509 CrossRef CAS.
- M. T. Dove and H. Fang, Rep. Prog. Phys., 2016, 79, 066503 CrossRef.
- N. Ramakrishnan and V. S. Arunachalam, J. Am. Ceram. Soc., 1993, 76, 2745–2752 CrossRef CAS.
- J. D. Evans and F.-X. Coudert, Chem. Mater., 2017, 29, 7833–7839 CrossRef CAS.
- R. Mittal, M. Gupta and S. Chaplot, Prog. Mater. Sci., 2018, 92, 360–445 CrossRef CAS.
- M. T. Dove, V. Heine and K. D. Hammonds, Mineral. Mag., 1995, 59, 629–639 CrossRef CAS.
- M. T. Dove, Am. Mineral., 1997, 82, 213–244 CAS.
- M. Ryder, B. V. de Voorde, B. Civalleri, T. D. Bennett, S. Mukhopadhyay, G. Cinque, F. Fernandez-Alonso, D. D. Vos, S. Rudić and J.-C. Tan, Phys. Rev. Lett., 2017, 118, 255502 CrossRef.
- G. Schaftenaar, E. Vlieg and G. Vriend, J. Comput.-Aided Mol. Des., 2017, 31, 789–800 CrossRef CAS.
- G. Schaftenaar and J. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134 CrossRef CAS.
- L. H. N. Rimmer, M. T. Dove, A. L. Goodwin and D. C. Palmer, Phys. Chem. Chem. Phys., 2014, 16, 21144–21152 RSC.
- K. W. Chapman, M. Hagen, C. J. Kepert and P. Manuel, Phys. B, 2006, 385–386, 60–62 CrossRef CAS.
- H.-L. Zhou, J. Bai, J.-W. Ye, Z.-W. Mo, W.-X. Zhang, J.-P. Zhang and X.-M. Chen, ChemPlusChem, 2016, 81, 817–821 CrossRef CAS.
- J. D. Evans, L. Bocquet and F.-X. Coudert, Chem, 2016, 1, 873–886 CAS.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, J. Phys. Chem. Lett., 2013, 4, 1861–1865 CrossRef CAS.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, J. Chem. Phys., 2013, 138, 174703 CrossRef.
- J. Heinen, A. D. Ready, T. D. Bennett, D. Dubbeldam, R. W. Friddle and N. C. Burtch, ACS Appl. Mater. Interfaces, 2018, 10, 21079–21083 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta06644f |
| This journal is © The Royal Society of Chemistry 2019 |