Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ab initio investigation of the stability of electrolyte/electrode interfaces in all-solid-state Na batteries†
Valentina
Lacivita
 *a,
Yan
Wang
*a,
Yan
Wang
 b,
Shou-Hang
Bo
c and
Gerbrand
Ceder
*ad
b,
Shou-Hang
Bo
c and
Gerbrand
Ceder
*ad
aMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: vlacivita@lbl.gov; gceder@berkeley.edu
bAdvanced Materials Lab, Samsung Research America, 3 Van de Graaff Drive, Burlington, MA 01803, USA
cUniversity of Michigan—Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, 800 Dong Chuan Road, Minhang District, Shanghai 200240, China
dDepartment of Materials Science & Engineering, University of California Berkeley, Berkeley, CA 94720, USA
First published on 11th February 2019
Abstract
All-solid-state batteries show great potential for achieving high energy density with less safety problems; however, (electro)chemical issues at the solid electrolyte/electrode interface may severely limit their performance. In this work, the electrochemical stability and chemical reactivity of a wide range of potential Na solid-state electrolyte chemistries were investigated using density functional theory calculations. In general, lower voltage limits are predicted for both the reduction and oxidation of Na compounds compared with those of their Li counterparts. The lower reduction limits for the Na compounds indicate their enhanced cathodic stability as well as the possibility of stable sodium metal cycling against a number of oxides and borohydrides. With increasing Na content (or chemical potential), improved cathodic stability but also reduced anodic stability are observed. An increase in the oxidation voltage is shown for Na polyanion systems, including borohydrides, NaSICON-type oxides, and aluminates, due to the covalent stabilization of the anions. In addition, the oxides exhibit remarkable chemical stability when in contact with various cathode materials (layered transition metal oxides and fluorophosphates), whereas the chalcogenides predictably display narrow electrochemical windows and high chemical reactivity. Our findings indicate some promising candidates for solid-state conductors and/or protective coating materials to enable the operation of high-energy-density all-solid-state Na batteries.
1 Introduction
The increasing demand for rechargeable batteries that deliver high energy density without safety hazards is driving the development of all-solid-state batteries (SSBs), in which liquid electrolytes are replaced by solid alkali conductors. Research in this field has led to the discovery of numerous solid electrolytes with room-temperature (RT) ionic conductivities of up to 10–20 mS cm−1, which are comparable or even superior to those of common liquid electrolytes. These promising solid electrolytes include NaSICON-type oxides,1,2 garnets,3,4 and thiophosphates, such as Li10GeP2S12 (ref. 5) and Li7P3S11 (ref. 6) for lithium batteries, and Na3PS4 (ref. 7) and Na3PSe4 (ref. 8) for sodium batteries.However, the high resistivity at the electrolyte/electrode interface severely limits the power and rate capabilities of SSBs. This high internal resistivity is attributed to chemical and/or electrochemical compatibility issues at the interface as well as mechanical issues (e.g., poor interfacial contact and volume changes). Examples of electrode/solid electrolyte combinations undergoing interfacial reactions include LiCoO2/Li2S–P2S5 (ref. 9) and LiCoO2/Li7La3Zr2O12,10 and their interfaces have been characterized using transmission electron microscopy. First-principles density functional theory (DFT) calculations have proven to be a valuable tool for the systematic investigation of the (electro)chemical compatibility at electrode/electrolyte interfaces.11–13 DFT-computed 0 K phase diagrams can be used to derive the phase equilibria at the interface and to estimate the driving force for interface reactions and electrolyte decomposition when an external potential is applied.
Richards et al.12 and Zhu et al.11,13 have applied this computational approach to a number of electrolyte/electrode (and coating/cathode) interfaces relevant for all-solid-state lithium batteries. Contrary to the common belief that solid-state electrolytes have high intrinsic stability, they demonstrated that many electrolyte/electrode combinations display quite limited chemical and electrochemical compatibility. In most cases, an interface layer with multiple decomposition phases was predicted to form at the electrode/electrolyte contact. This interlayer, however, can be beneficial for the system stability if it is both ion-conducting and passivating. In this case, the interlayer acts as an electronic insulator, bridging the difference in the chemical potentials μ of all the atomic species between the electrolyte and electrodes.
Beyond a purely thermodynamic model, kinetic barriers for decomposition and chemical reactions may intervene to widen the effective voltage stability window of the electrolyte and possibly change the constitution of the interphase layer at the electrolyte/cathode interface. An estimate of the upper kinetic voltage limit for the electrolyte decomposition can be obtained by calculating the voltage corresponding to the topotactic extraction of an atom of the mobile species, as proposed by Tian et al.14 These authors used a combination of DFT calculations and experiments to investigate the electrochemical stability of Na3PX4 (X = S, Se) solid electrolytes and their compatibility with various layered transition metal (TM) oxide cathodes for sodium-ion batteries. They verified that the anodic voltage limit measured for the electrolytes always lies between the computed thermodynamic upper bound and the potential for topotactic desodiation. Moreover, they reported evidence for electrolyte/cathode reactions for which the formation of intermediate products is kinetically favored over stable thermodynamic phases. One example is the Na3PS4–NaCrO2 interface, for which they observed the formation of Na3PS3O at temperatures below 500 °C instead of the predicted products Na3PO4 and NaCrS2. More recently, Tang et al.15 applied finite-temperature ab initio molecular dynamics simulations to assess kinetic effects on the interface reactivity. They observed that contrary to thermodynamic models predicting the formation of stable [PO4]3− groups via anion-exchange reactions, the formation of [SO4]2−-containing compounds and Na3P is kinetically favored. In the same study, the authors also calculated the electrochemical stability and chemical reactivity of some well-known Na solid-state electrolytes with different cathode, anode, and buffer materials.
In this work, we aim to extend previous computational surveys on solid-state Na conductors14,15 to provide a systematic and comprehensive overview of promising electrolyte/electrode and coating/electrode combinations for Na SSBs. We apply the computational approaches described in ref. 11–14 to estimate the electrochemical stability window of numerous solid-state electrolyte candidates, the kinetic voltage limits for Na extraction, and the chemical reactivity with different cathode materials. We investigate an extensive selection of materials, including known Na-ion conductors and possible decomposition or reaction products as well as possible coating layers. In addition, a comparison with relevant Li compounds is performed. In line with previous assessments,14,15 we confirm general trends such as the greater electrochemical stability of oxides than that of sulfides/selenides and the existence of a large thermodynamic driving force for anion-exchange reactions between thiophosphates and layered TM oxide cathodes. Moreover, we show that sodium electrolytes generally exhibit improved cathodic (low-voltage) stability compared with their lithium analogues, thus giving prospects for the stable cycling of Na metal anodes. We find that the differences between sodium and lithium compounds in anodic (high-voltage) limits are not simply deducible from the electrochemical scale, but also relate to structural factors, such as the cation–anion radius ratio. Both the thermodynamic and kinetic upper voltage limits of compounds are favorably extended by covalent stabilization in polyanions such as phosphates and boranes, which emerge as materials that can tolerate charging potentials as high as 4–5 V.
2 Methods
In the current work, we adopt the methodology described in ref. 12,16, and 17. We consider three different indicators of the stability of the solid-state electrolyte: (1) the pure thermodynamic voltage stability versus the metal anode (M), (2) the upper kinetic voltage limit for the extraction of one alkaline atom from the solid-state electrolyte, and (3) the chemical reactivity at the electrolyte/cathode interface.2.1 Voltage window and interface chemical stability
Phase diagrams were constructed using the Python Materials Genomics (pymatgen) library18 and a dataset of energies from DFT relaxation of compounds initialized using structural information obtained from the Inorganic Crystal Structure Database (ICSD)19 or structures generated by a data-mined chemical substitution algorithm20 (see Table S1 of the ESI† for more details). DFT calculations were performed using the generalized gradient approximation (GGA) to the exchange–correlation functional in the Perdew–Burke–Ernzerhof formulation,21 as implemented in the Vienna Ab initio Simulation Package (VASP),22 within the projector-augmented wave formalism.23 The energy cutoff was set to 520 eV, and a k-point grid with a density of at least 500/(number of atoms) was used for all the computations. For compounds containing TM elements with localized d electrons, the GGA + U variation24 of the density functional was adopted. Consistency across GGA and GGA + U calculations is maintained by the application of the mixing scheme as described in ref. 25. Moreover, GGA errors of reaction energies involving gas/liquid phase molecules were corrected using Wang et al.'s method.26 Following Richards et al.,12 the formation energies were calculated from the nearest phases (i.e., the phases that define the low energy facet containing the target composition in the phase diagram) for which the experimental energies are available in the Kubaschewski27 or NIST-JANAF28 thermochemical tables. For example, the formation energy of NaZr2(PO4)3, a compound not listed in the thermochemical tables, is calculated as the DFT energy of the reaction 2ZrO2 + P2O5 + NaPO3 → NaZr2(PO4)3, to which are added the experimental formation energies of ZrO2, P2O5 and NaPO3. Such an approach allows benefitting from the higher accuracy of DFT reaction energies that are calculated between compounds whose elements are in the same oxidation states.29 If no experimental data are available for some nearest phases, the corresponding elemental precursors are used for reference.| Φ(c,μM) = E(c) − nM(c)μM | (1) |
| ΔV = −(Edef − E0 − μM), | (2) |
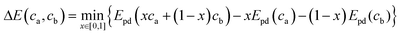 | (3) |
In the above equation x is the mixing fraction of the electrode and electrolyte compositions, ca and cb, respectively; Epd(ca) and Epd(cb) are the respective convex hull minimum energies; and Epd(xca + (1 − x)cb) is the convex hull function returning the lowest energy equilibrium of the phases at the given composition.
2.2 Materials selection
Solid-state electrolyte (or coating) candidates were selected based on their Na content and electrochemical performance, as reported in the literature. We focused particularly on known solid-state Na-ion conductors with high ionic conductivity or with the potential for high ionic conductivity.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) mH) β′′ form (Na1.67Al11O17), has also been characterized.36 The latter exhibits a higher conductivity (σ ≈ 2 mS cm−1 at RT) and has been proven to be stable against Na.37
mH) β′′ form (Na1.67Al11O17), has also been characterized.36 The latter exhibits a higher conductivity (σ ≈ 2 mS cm−1 at RT) and has been proven to be stable against Na.37
For comparison, we also considered the stability of NaAlO2 and of the Na-rich aluminates Na5AlO4, Na7Al3O8, Na14Al4O13, and Na17Al5O16.38 NaAlO2 is a side product in β-alumina mixtures and has been used as a cathode coating material on LiCoO2.39 To our knowledge, no data on the ionic conductivity and stability window of the Na-rich aluminates have been reported yet.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and tetragonal (I4/mmm) antiperovskite structures, respectively. Recently, Zhu et al.46 analyzed their Na-ion transport mechanisms and reported low ionic conductivities (σ ≈ 10−8 S cm−1 at RT, activation energy Ea = 0.6–0.7 eV). Nonetheless, chemical modifications leave substantial room for improvement, e.g., by aliovalent substitution the conductivity of Na2.9Sr0.05OBr0.6I0.4 reaches 0.19 mS cm−1 at 200 °C.47
m) and tetragonal (I4/mmm) antiperovskite structures, respectively. Recently, Zhu et al.46 analyzed their Na-ion transport mechanisms and reported low ionic conductivities (σ ≈ 10−8 S cm−1 at RT, activation energy Ea = 0.6–0.7 eV). Nonetheless, chemical modifications leave substantial room for improvement, e.g., by aliovalent substitution the conductivity of Na2.9Sr0.05OBr0.6I0.4 reaches 0.19 mS cm−1 at 200 °C.47
Other oxides such as Na2SO4, Na3PO4, and Na4SiO4, are generally characterized by low ionic conductivity. However, they can be used as coating materials or end-members of better performing electrolyte solid-solutions such as Na2SO4/Na4SiO4,48 Na3PO4/Na2SO4,49,50 Na3AlF6/Na2SO4,50 and Na3PO4/Na4SiO4.51
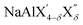 (with 0 < δ < 4 and X′/X′′ = Cl, Br, I), have been used as electrolytes in the cathode composite to enable operation of molten Na metal halide batteries at substantially lower temperatures compared with the traditional ZEBRA system.63 The aluminum fluorides Na3AlF6 (cryolite) and Na5Al3F14 (chaolite) exhibit fast Na-ion diffusion at high temperatures as revealed by nuclear magnetic resonance measurements.64,65
(with 0 < δ < 4 and X′/X′′ = Cl, Br, I), have been used as electrolytes in the cathode composite to enable operation of molten Na metal halide batteries at substantially lower temperatures compared with the traditional ZEBRA system.63 The aluminum fluorides Na3AlF6 (cryolite) and Na5Al3F14 (chaolite) exhibit fast Na-ion diffusion at high temperatures as revealed by nuclear magnetic resonance measurements.64,65
3 Results
3.1 Comparison of the electrochemical stability window of Na and Li binaries
Fig. 1 compares the stability windows of simple Na binary compounds with those of their Li analogues. Although these compounds may not be considered solid-electrolyte candidates by themselves due to their generally poor ionic conductivity (except for Li3P66), it is instructive to compare their electrochemical stability as a basis to understand the behavior of more complex compounds. These binaries are generally used as synthesis precursors, e.g., M2S or M2Se in chalcogenide-based glassy electrolytes, or as additives (especially the halides) to improve the electrochemical performance of more complex electrolyte materials.67–70 In all of these binary materials, the anion is fully reduced; therefore, further reaction with the metal anode cannot occur and they are all stable down to 0 V against M/M+.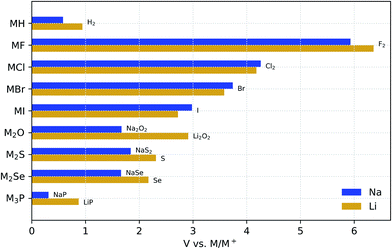 | ||
| Fig. 1 Electrochemical stability window of Na and Li binary compounds. The oxidation products are shown at the anodic limits. | ||
The RT crystal structures of the Na and Li binaries are isomorphic (see Table 1), which ensures that the differences in the thermodynamic voltage stability windows are exclusively due to differences in the chemistry. Indeed, all the hydrides, halides, and chalcogenides have a face-centered cubic structure (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with M+ cations located in octahedral or tetrahedral sites depending on whether they are 1
m) with M+ cations located in octahedral or tetrahedral sites depending on whether they are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (rock-salt) or 2
1 (rock-salt) or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (anti-fluorite) binaries, respectively. The phosphides, instead, have both a hexagonal structure.
1 (anti-fluorite) binaries, respectively. The phosphides, instead, have both a hexagonal structure.
| M = Na | M = Li | |||||
|---|---|---|---|---|---|---|
| SG | V 0calc | ΔHfexp | SG | V 0calc | ΔHfexp | |
| MH |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0.58 | −0.58 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0.94 | −0.94 |
| MF |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
5.93 | −5.94 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
6.36 | −6.39 |
| MCl |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
4.26 | −4.26 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
4.18 | −4.23 |
| MBr |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
3.74 | −3.74 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
3.58 | −3.64 |
| MI |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
2.98 | −2.98 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
2.80 | −2.80 |
| M2O |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1.67 | −4.30 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
2.91 | −6.20 |
| M2S |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1.84 | −3.80 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
2.31 | −4.64 |
| M2Se |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1.66 | −3.44 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
2.17 | −4.36 |
| M3P | P63/mmc | 0.31 | — | P63/mmc | 0.87 | — |
For simple binaries, such as MF, MCl, MBr, and MI, the anodic decomposition is into the elements and this creates a direct relationship between the formation enthalpy of the compound, ΔH, and the anodic voltage limit: ΔH ≈ −V. As Table 1 shows, the anodic stability of Na binaries is generally lower than that of Li binaries. This trend might be expected from the fact that the standard reduction potential for the reaction Na+(aq) + e− → Na(s) is 0.33 V above that of Li, although reference to half-cell reduction potentials, which are dependent on the solvent and solute concentration, is not rigorously applicable.72 The exceptions to this trend are pairings with large anions such as Cl−, Br−, and I−, where the reduced size mismatch with Na+ plays a stabilizing role compared to the equivalent Li binaries. Such stabilization of the Na compounds with large anions, as compared to their Li equivalents, is confirmed by the experimental formation enthalpies in Table 1. We attribute this stabilization to the better match of the Na+ radius with those of the large halogen anions. In simple high-symmetry crystal structures, such as the rock-salt structure of these compounds, the lattice constant is the only geometric parameter that can be adjusted. When very small ions such as Li+ are paired with large anions, such as Br− and I−, the difference in ionic radii creates a mismatch between anion–anion and cation–anion distances, which is, Fig. S1† shows the differences between the anodic voltages of Li and Na halides (ΔV) as a function of the anion radius.
Fig. 1 also shows that the nature of the oxidation products depends on the valence electron configuration of the anions. The oxidation of hydrides and halides yields their elementary references directly, whereas anions with higher valence (e.g., O2−, S2−, and P3−) usually transform into phases where the anion has an intermediate oxidation state. For example, both alkali oxides M2O transform into peroxides M2O2 upon oxidation. However, although Li2O2 is known to be a fairly reactive species,73,74 Na2O2 is a stable bulk phase in an oxygen atmosphere,75 which may contribute to the reduction of the anodic limit of Na2O with respect to that of Li2O. Similarly to Na2O, the Na chalcogenides oxidize to intermediate phases with partially oxidized anions that are stable at RT, i.e., Na2S4 (ref. 76) and Na2Se2.77 The Li chalcogenides lack these intermediate stable phases, which explains the direct oxidation of both Li2S and Li2Se to their elementary references at higher anodic voltages.
3.2 Electrochemical stability windows of Na solid-state electrolytes
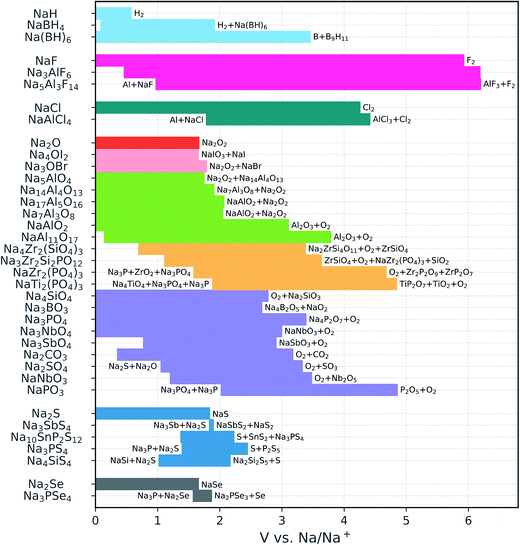 | ||
| Fig. 2 Calculated electrochemical stability windows of Na solid-state electrolyte candidates. Some oxidation reactions and reduction reactions against Na metal are reported (see Table S1† for a complete list). The compounds are grouped by anion (the binaries are included for reference); the different oxide subgroups are distinguished by different colors. | ||
The sulfides and particularly the selenides display very narrow windows, which is in line with the relatively low electronegativity of the chalcogen anions and the versatility of their valence electron shell with oxidation states from −2 to +6. None of the chalcogenides is stable against Na metal, in agreement with previous reports.14,15,37 Moreover, a reduction product of the phosphorus selenides and sulfides is Na3P, which is a mixed ionic and electronic conductor78 and prohibits the passivation of the electrolyte. This is in contrast with Li3P that is an electronic insulator and can therefore passivate P-containing chalcogenide conductors.
The voltage stability ranges of the oxides are much wider than those of the chalcogenides. In particular, oxides with relatively high Na content such as Na4SiO4, Na3BO3, Na3PO4, and Na3SbO4 are all stable down to 0 V versus Na/Na+. The cathodic stability becomes more limited in the presence of easily reducible species, e.g., C4+, Sb5+, or condensed polyanions such as [PO3]− and [NbO3]−. The latter, however, boost the oxidation limits to somewhat higher voltages (3–5 V).
Among the NaSICONs, the P-containing compounds exhibit excellent anodic stability, resisting oxidation up to approximately 5 V. At low voltage, all the explored NaSICON compositions are predicted to decompose. However, we compute a much lower driving force for reduction for the pure silicate Na4Zr2(SiO4)3 (decomposition energy |ΔE| = 0.15 eV/atom) than for the phosphates (|ΔE| = 0.54 eV/atom for NaZr2(PO4)3 and 0.86 eV/atom for NaTi2(PO4)3). This finding is consistent with previous experimental assessments suggesting that silicates are kinetically stabilized.45 Fig. S2† shows the relative decomposition energies as a function of the voltage versus Na metal. We also note that the cathodic stability of the NaSICON-type phosphates is considerably worse than that of Na3PO4, which is predicted to be stable. By looking at the reduction products of NaZr2(PO4)3 and NaTi2(PO4)3, which always involve a metal oxide and a reduced phosphide, one may deduce that the presence of a high content of Na+ stabilizes the PO4 group more than the transition metals do.
In contrast to the NaSICONs, the Na aluminates are thermodynamically stable against Na metal. The only exception is the β-alumina phase NaAl11O17: the 0 K enthalpy calculations indicate that this phase is unstable with respect to the decomposition into NaAlO2 + Al below 0.14 V. However, the reaction energy for the β-alumina decomposition is less than 25 meV/atom. Moreover, commonly found excess sodium induces structural disorder which makes it possible that β-alumina is stabilized by the Na-ion configurational entropy at higher temperatures. The β-alumina phase is oxidized at approximately 4 V. This is the maximum anodic stability attained by the Na aluminates, whose oxidation voltage progressively shifts to lower potentials with increasing Na content, approaching the limit of the sodium oxide binary. The antiperovskites Na4OI2 and Na3OBr also have oxidation limits close to that of the Na2O binary, consistent with the presence of fully reduced anions in all of these structures. In contrast, the borohydrides are characterized by remarkable covalent stabilization with respect to the NaH binary: the oxidation voltage increases from 0.58 V for NaH to 3.46 V for Na2B12H12. The latter is also stable in contact with Na metal.
| Thermodynamic window (V) | Kinetic limit (V) | |
|---|---|---|
| a Data from ref. 14. | ||
| Na3PSe4 | 1.57–1.87 | 2.75a |
| Na3PS4 | 1.39–2.45 | 3.05a |
| Na3SbS4 | 1.83–1.90 | 3.22 |
| Na10SnP2S12 | 1.37–2.23 | 2.68 |
| NaZr2(PO4)3 | 1.58–4.68 | 4.78 |
| Na4Zr2(SiO4)3 | 0.69–3.38 | 4.13 |
| NaAl11O17 | 0.14–3.79 | 4.79 |
| NaAlCl4 | 1.78–4.42 | 4.84 |
| Na3AlF6 | 0.46–6.19 | 6.35 |
| NaBH4 | 0.02–2.07 | 4.91 |
| Na2B12H12 | 0.00–3.46 | 4.31 |
3.3 Chemical reactivity at the cathode/electrolyte interface
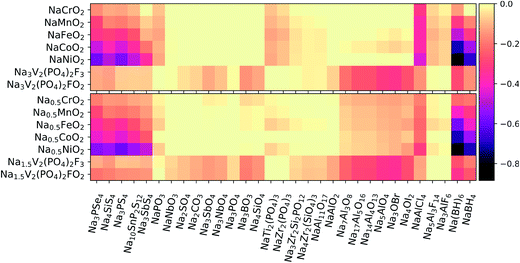
Using eqn (3), we calculated the maximum driving force for the reaction between the solid-state electrolytes and different cathodes. Positive electrodes such as common layered TM oxides (TM = Cr, Mn, Fe, Co)79 and fluorine-doped vanadium phosphates80,81 were considered in both fully discharged and half-charged (i.e., more oxidizing) states. Fig. 3 presents heat maps of the corresponding predicted reaction energies. The energy values and reaction products are listed in Tables S2–S5 of the ESI.†We first consider the chemical reactivity against layered TM oxides. All the P-containing chalcogenide electrolytes are predicted to undergo O for Se/S anion exchange, in agreement with previous reports.12,13,15 However, the predicted reaction products may slightly vary because of differences in datasets used to construct the high-dimensional phase diagrams. For instance, Tang et al.15 predicted that the reaction at the Na3PS4/NaCrO2 interface would produce Na3PO4 + NaCrS2, whereas we predict Na3PSO3 to be an additional intermediate phase, similar to the findings of Tian et al.14
In line with ref. 14 and 15, the substitution of P with other cations (e.g., Si and Sb) in the conductor generally improves the chemical stability of the interface with the TM oxide cathodes: by switching from Na3PS4 to Na3SbS4, the reaction energies decrease by approximately 40–90% against the fully discharged TM oxide cathodes and by ∼20–50% against the half-charged cathodes. In moving from the early to the late TMs in the cathode (Cr → Ni), an increasing tendency toward TM reduction by the chalcogen anions is observed. In contrast to the chalcogenides, the oxide electrolytes display negligible (i.e., |ΔE| < 25 meV/atom) or rather low reaction energies. Among the oxides, the most reactive interfaces are those of the Na-rich aluminates and antiperovskites against the half-charged cathodes; however, the breakdown energies |ΔE| are still lower than 150 meV/atom and thus much lower than the |ΔE| values of up to 580 meV/atom calculated for the chalcogenides. The chloride NaAlCl4 behaves quite differently from the fluorides Na3AlF6 and Na5Al3F14. In fact, whereas Cl− is easily oxidized to Cl4+ and/or displaced into TM-based compounds, the fluorides are much less reactive: |ΔE| is on the order of 10–80 meV/atom, to be compared with ∼200–300 meV/atom for the chloride. Finally, the borohydrides are confirmed to be strong reducing agents, especially when coupled with Co- and Ni-containing cathodes. Overall, NaCrO2 appears to be the TM oxide that is most widely compatible with the different types of electrolytes. Experimental findings by Tian et al.14 support this conclusion for pairings with Na3PX4 (X = S, Se) electrolytes.
Polyanionic cathodes such as fluorophosphates appear to be somewhat compatible with various solid-state electrolytes, including sulfides and selenides. Among the oxides, NaSICON electrolytes are particularly stable against vanadium fluorophosphate cathodes. Some reactivity (|ΔE| ≈ 50–80 meV/atom) is predicted only for the Si-containing NaSICONs in contact with the partially desodiated electrodes, whose average potential (∼3.5 V vs. Na/Na+) is close to the intrinsic oxidation limits of such electrolytes (see Fig. 2). We also predict fairly low reactivity for NaAl11O17 (|ΔE| ≈ 50 and 70 meV/atom against discharged and half-charged cathodes, respectively), whereas aluminates with higher Na content show an increasing driving force for chemical reactions, which is consistent with their lowered anodic stability limit (Fig. 2). The halo-aluminates are relatively stable against the fluorophosphate cathodes, particularly the fluorides Na3AlF6 and Na5Al3F14 which are substantially inert (|ΔE| < 10 meV/atom). The borohydrides instead react by reducing P5+ to P3− and releasing protons or H2.
4 Discussion
With the discovery of numerous solid-state ion conductors that have conductivities capable of competing with those of liquid electrolytes, the critical issue for the development of SSB devices has shifted to achieving optimal (electro)chemical compatibility at the interfaces. The thermodynamic stability of these interfaces can be evaluated by construction of (grand potential) phase diagrams based on DFT calculations. The predictive capability and scalability of this approach has been demonstrated in previous work examining a wide range of chemical systems relevant for Li SSBs.11–13 In the field of Na SSBs, computational and experimental investigations have mainly focused on chalcogenide electrolytes and their interactions with the electrodes, also providing insight into important kinetic effects.14,15In this work, we have extended the previous analysis to consider a wide selection of Na solid-state electrolytes and coating candidates. In line with the literature, we find that the chalcogenide conductors exhibit poor chemical and electrochemical stabilities. The oxides display much larger voltage stability windows and generally lower reactivity against the cathode. Comparison of the calculated thermodynamic stability windows for polyanionic Na and Li compounds (see Fig. S3†) reveals two substantial differences. The first difference is that the cathodic (reduction) limits against Na/Na+ are lower than those for similar lithiated materials, with several Na polyanion compounds being stable against Na metal. For instance, Na3PO4, Na4SiO4, and NaAlO2 are all stable down to 0 V versus Na/Na+, whereas the corresponding lithiated compounds are reduced at 0.74, 0.26, and 0.15 V against Li/Li+, respectively. The other difference is that the anodic (oxidation) voltage limits of the Li compounds are generally higher than those of the Na compounds. While these observations are consistent with the standard redox potential of Na being higher than that of Li, significant structural effects can modify this expectation. For example, the higher compatibility of Na+ with very large anions such as I−, Br− or [B12H12]2− stabilizes the corresponding electrolyte structures and raises their oxidation potentials with respect to the equivalent Li compounds. In addition, by considering pairs such as MPO3/M3PO4 or MNbO3/M3NbO4 (M = Li, Na), we observe that with increasing alkali chemical potential μM (and content), both Na and Li compounds exhibit improved cathodic stability but reduced anodic stability. The latter is problematic as high alkaline content seems to correlate with high ionic conductivity.
The lower reducing capability of Na (vs. Li) broadens the selection of stable electrolyte/anode interfaces that are predicted to have either no decomposition or a very small driving force for reduction by Na. These interfaces are type A interfaces according to the classification scheme proposed by Wenzel et al.82 and later adopted by Zhu et al.,13 and in our analysis they are primarily formed by some oxides and borohydrides. Among the oxides, Tang et al.15 identified binaries such as Sc2O3, ZrO2, and HfO2 as promising coating materials for the anode. To these materials, we add Na-based ternaries such as Na3PO4, Na3NbO4, and Na4SiO4, antiperovskites, and aluminum oxides. The Na aluminum oxides, in particular, are remarkably stable against reduction by Na metal, whereas Li aluminates in contact with Li metal have Al reduced and form Li–Al alloys (see Fig. S3†).
Somewhat surprisingly, the stability of the [SiO4]4− and [PO4]3− groups in contact with Na metal as observed in the ternary salts Na4SiO4 and Na3PO4 does not hold for the NaSICONs: our results indicate that no composition is thermodynamically stable against Na metal, which reduces the polyanions when they are in a structure with Zr or Ti metal. The presence of these TM ions providing charge compensation for the polyanions instead of Na+ diminishes the sodium content of the NaSICONs and the lower Na content appears to correlate with a diminished cathodic stability. Likewise, pure phosphate NaSICONs are less stable against Na metal than Si-containing NaSICONs whose chemistry allows for a higher Na content. The interphase products Na3P and NaSi (see Table S1†) provide mixed electronic and ionic conduction, matching the NaSICON/Na pair with interfaces of type B according to the classification scheme of Wenzel et al.82 The simultaneous ion and electron transport provided by these reaction products can lead to the progressive consumption of the solid-state electrolyte.
The interfaces generated by decomposition of most of the chalcogenides against Na metal are also type B interfaces (Table S1†). In contrast, the electronically insulating and therefore passivating interphases Li3P and Li2S produced by reduction of lithium thiophosphates against Li constitute interfaces of type C. This difference points towards the use of oxides that are stable in contact with Na metal as protective layers to enable Na metal cycling. An example of an eligible anode coating candidate is orthophosphate Na3PO4. Indeed, the higher ionic character of the covalent bonds between phosphorus and oxygen, as compared to P–S or P–Se, widens the calculated energy gap of Na3PO4 (Eg = 4.01 eV) and prevents its reduction by Na metal, in contrast to the analogous chalcogenides Na3PS4 (Eg = 2.68 eV) and Na3PSe4 (Eg = 1.56 eV). Moreover, Na3PO4 displays a very low driving force for the reaction with superionic conductors such as Na3PS4 (|ΔE| ≤ 20 meV/atom), Na3PSe4 (|ΔE| ≤ 17 meV/atom) or Na3SbS4 (no reaction predicted). Hence, the combination of Na/Na3PO4/Na3PS4 may allow stable cycling of Na metal, with the thiophosphate undergoing only minimal anion-exchange reactions at the interface with the buffer layer (the calculated reaction energy is <25 meV/atom). In addition, the use of Na-containing protective oxides instead of the Na-free binaries suggested by Tang et al.15 should, in principle, provide better diffusion of Na+ through the buffer.
Because the cations in the electrolytes are fully oxidized, the anodic limits are typically controlled by oxidation of the anion. In general, higher anion electronegativity correlates with a larger oxidation voltage. This trend explains the excellent stability of fluorides (>6 V) and poor performance of sulfides and selenides, whose oxidative breakdown is predicted to occur well before 3 V vs. Na/Na+. The oxides show remarkable variability in terms of anodic stability. Structures governed mainly by ionic interactions, such as the antiperovskites, display somewhat low oxidation limits, comparable to that of the simple binary oxide Na2O. The oxidation limit increases in polyanionic compounds by virtue of the covalent interaction of the highly electronegative O with main group elements such as P, Si or B. As suggested by the parallel with the molecular orbital theory, this covalent bonding lowers the energy of the valence states and protects them from oxidation. Exemplary cases include the phosphates NaPO3/Na3PO4 and the NaSICONs. The latter also benefit from the positive Madelung potential exerted by Ti4+ and Zr4+ on the polyanion, which further opposes the anion oxidation. The covalent stabilization of the valence states is most dramatically observed when comparing the binary NaH with the borohydrides, particularly the borane Na2B12H12, where the B–B skeletal bonding that builds up the [B12H12]2− cluster framework results in extended electron delocalization.83–85 For the borohydrides, the anodic stability can also be greatly enhanced by kinetic factors, as indicated by the calculated potential for desodiation. If superionic conduction could be achieved at RT, e.g., by doping NaBH4 into Na2B12H12, the borane would become an eligible electrolyte candidate for SSBs.
Among the positive electrodes, the fluorophosphates show good chemical compatibility with a wide range of solid electrolytes. In fact, the fluorophosphates display limited reactivity even with the chalcogenides. Sulfides and selenides are highly reactive in contact with Co and Ni layered oxides and would be progressively consumed by the formation of interphases with a metallic character, e.g., Co3Se4 (ref. 86) or Ni3S2 (ref. 87) (type B interfaces), thereby requiring the application of a buffer layer. Again, similar to the electrolyte/Na anode interface, a viable solution could be the use of Na3PO4 (or NaPO3) as a cathode coating.
NaSICON ceramics and Na-β-alumina are the Na superionic conductors with the highest resilience to variations in cathode chemistry, forming essentially stable interfaces with all the positive electrodes considered here. Na-β(β′′)-alumina is also stable against sodium metal and can now be processed into flexible ceramic membranes (≤50 μm),88 which makes it usable as a solid-state electrolyte separator for stable Na metal cycling in a full solid-state cell. Using NaSICON ceramics instead of Na-β-alumina would enable the working potential of the SSB to be increased if a compositional gradient from silicate (stable at low voltage) to phosphate (at high voltage) could be implemented or if the two electrolytes could be combined in a single cell. However, the high co-sintering temperatures currently needed to deliver highly conductive NaSICONs impose serious processing challenges. Finally, concerning the cathode composite, our results suggest the possibility of combining a high-energy-density cathode such as Na3V2(PO4)2FO2 (ref. 81) with a fast ionic conductor such as Na3PS4, provided that a protective buffer layer (e.g., Na3PO4 or NaPO3) is applied. Given that chalcogenides are notably characterized by a higher degree of plasticity than oxides, this solution would ensure interparticle contact in addition to efficient ionic and electronic transport at the positive electrode, thus completing an optimized full solid-state cell design.
5 Conclusion
We have addressed the question of interfacial stability in solid-state sodium batteries by assessing the electrochemical stability and thermodynamic phase equilibria of numerous potential solid-state electrolyte/electrode combinations using DFT calculations. In addition, a direct comparison between Na- and Li-containing materials revealed differences in electrochemical behavior which are critical for tailoring the design of SSBs. More specifically, we observed that Na compounds generally display lower reduction and oxidation potentials than their Li counterparts. The enhanced cathodic stability of Na-based oxides provides multiple options to enable stable Na metal cycling, including their use as buffer layers to protect chalcogenide conductors from reduction or their direct use as solid-state electrolytes (e.g., Na-β-alumina). On the other hand, the anodic stability of sodium compounds can be improved over their lithium equivalents by structure stabilization factors such as the higher compatibility of Na+ with large anions, e.g., I− or [B12H12]2−. High voltage stability (>4–5 V) was predicted for sodium halides and oxides (especially phosphate NaSICONs), and the borohydride superionic conductor Na2B12H12 where covalent stabilization plays a major role. Finally, we identified several promising electrolyte/cathode combinations, demonstrating, among other things, the limited chemical reactivity of the layered TM oxide NaCrO2 and polyanionic fluorophosphate cathodes with many potential solid electrolytes. Our findings will provide valuable guidance for the effective design of future solid-state sodium batteries as well as other technologically relevant electrochemical systems.Conflicts of interest
There are no conflicts to declare.Disclaimers
This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or the Regents of the University of California.Copyright notice
This manuscript has been authored by an author at Lawrence Berkeley National Laboratory under Contract No. DE-AC02-05CH11231 with the U.S. Department of Energy. The U.S. Government retains, and the publisher, by accepting the article for publication, acknowledges, that the U.S. Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for U.S. Government purposes.Acknowledgements
The Authors thank the Samsung Advanced Institute of Technology for their funding of this research. This work used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231. We used also computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562.References
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G. Adachi, Ionic Conductivity of Solid Electrolytes Based on Lithium Titanium Phosphate, J. Electrochem. Soc., 1990, 137(4), 1023–1027 CrossRef CAS.
- J. W. Fergus, Ion transport in sodium ion conducting solid electrolytes, Solid State Ionics, 2012, 227, 102–112 CrossRef CAS.
- S. Ohta, T. Kobayashi and A. Takahiko, “High lithium ionic conductivity in the garnet-type oxide Li7−X La3(Zr2−X, NbX)O12 (X = 0–2), J. Power Sources, 2011, 196(6), 3342–3345 CrossRef CAS.
- V. Thangadurai, D. Pinzaru, S. Narayanan and A. K. Baral, Fast Solid-State Li Ion Conducting Garnet-Type Structure Metal Oxides for Energy Storage, J. Phys. Chem. Lett., 2015, 6(2), 292–299 CrossRef CAS PubMed.
- N. Kamaya, et al., A lithium superionic conductor, Nat. Mater., 2011, 10(9), 682–686 CrossRef CAS PubMed.
- Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, A sulphide lithium super ion conductor is superior to liquid ion conductors for use in rechargeable batteries, Energy Environ. Sci., 2014, 7(2), 627–631 RSC.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Superionic glass-ceramic electrolytes for room-temperature rechargeable sodium batteries, Nat. Commun., 2012, 3, 856 CrossRef PubMed.
- S.-H. Bo, Y. Wang, J. C. Kim, W. D. Richards and G. Ceder, Computational and Experimental Investigations of Na-Ion Conduction in Cubic Na3PSe4, Chem. Mater., 2016, 28(1), 252–258 CrossRef CAS.
- A. Sakuda, A. Hayashi and M. Tatsumisago, “Interfacial Observation between LiCoO2 Electrode and Li2S−P2S5 Solid Electrolytes of All-Solid-State Lithium Secondary Batteries Using Transmission Electron Microscopy, Chem. Mater., 2010, 22(3), 949–956 CrossRef CAS.
- K. H. Kim, et al., Characterization of the interface between LiCoO2 and Li7La3Zr2O12 in an all-solid-state rechargeable lithium battery, J. Power Sources, 2011, 196(2), 764–767 CrossRef CAS.
- Y. Zhu, X. He and Y. Mo, Origin of Outstanding Stability in the Lithium Solid Electrolyte Materials: Insights from Thermodynamic Analyses Based on First-Principles Calculations, ACS Appl. Mater. Interfaces, 2015, 7(42), 23685–23693 CrossRef CAS PubMed.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Interface Stability in Solid-State Batteries, Chem. Mater., 2016, 28(1), 266–273 CrossRef CAS.
- Y. Zhu, X. He and Y. Mo, “First principles study on electrochemical and chemical stability of solid electrolyte–electrode interfaces in all-solid-state Li-ion batteries, J. Mater. Chem. A, 2016, 4(9), 3253–3266 RSC.
- Y. Tian, et al., Compatibility issues between electrodes and electrolytes in solid-state batteries, Energy Environ. Sci., 2017, 10(5), 1150–1166 RSC.
- H. Tang, et al., Probing Solid–Solid Interfacial Reactions in All-Solid-State Sodium-Ion Batteries with First-Principles Calculations, Chem. Mater., 2018, 30(1), 163–173 CrossRef CAS.
- Y. Mo, S. P. Ong and G. Ceder, First Principles Study of the Li10GeP2 S12 Lithium Super Ionic Conductor Material,, Chem. Mater. , 2012, 24(1), 15–17 CrossRef CAS.
- S. P. Ong, L. Wang, B. Kang and G. Ceder, “Li−Fe−P−O2 Phase Diagram from First Principles Calculations, Chem. Mater., 2008, 20(5), 1798–1807 CrossRef CAS.
- S. P. Ong, et al., Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- F. Karlsruhe, Inorganic Crystal Structure Database, available: https://icsd.fiz-karlsruhe.de.
- G. Hautier, C. Fischer, V. Ehrlacher, A. Jain and G. Ceder, Data Mined Ionic Substitutions for the Discovery of New Compounds, Inorg. Chem., 2011, 50(2), 656–663 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943–954 CrossRef CAS.
- A. Jain, et al., Formation enthalpies by mixing GGA and GGA+U calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(4), 045115 CrossRef.
- L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA+U framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(19), 195107 CrossRef.
- O. Kubaschewski, C. B. Alcock and P. J. Spencer, Materials Thermochemistry, Pergamon Press, Oxford, 6th edn, 1993 Search PubMed.
- M. W. J. Chase, NIST-JANAF Thermochemical Tables, American Chemical Society, Washington, DC, 4th edn, 1998, American Institute of Physics for the National Institute of Standards and Technology, New York, 1998 Search PubMed.
- G. Hautier, S. P. Ong, A. Jain, C. J. Moore and G. Ceder, Accuracy of density functional theory in predicting formation energies of ternary oxides from binary oxides and its implication on phase stability, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(15), 155208 CrossRef.
- Y.-F. Y. Yao and J. T. Kummer, Ion exchange properties of and rates of ionic diffusion in beta-alumina, J. Inorg. Nucl. Chem., 1967, 29(9), 2453–2475 CrossRef CAS.
- D. Kundu, E. Talaie, V. Duffort and L. F. Nazar, The Emerging Chemistry of Sodium Ion Batteries for Electrochemical Energy Storage, Angew. Chem., Int. Ed., 2015, 54(11), 3431–3448 CrossRef CAS PubMed.
- Z. Wen, Y. Hu, X. Wu, J. Han and Z. Gu, Main Challenges for High Performance NAS Battery: Materials and Interfaces, Adv. Funct. Mater., 2013, 23(8), 1005–1018 CrossRef CAS.
- H. Sakaebe, ZEBRA Batteries, in Encyclopedia Of Applied Electrochemistry, Springer, New York, NY, 2014, pp. 2165–2169 Search PubMed.
- T. Oshima, M. Kajita and A. Okuno, Development of Sodium-Sulfur Batteries, Int. J. Appl. Ceram. Technol., 2004, 1(3), 269–276 CrossRef CAS.
- C. Beevers and M. Ross, The Crystal Structure of “Beta Alumina” Na2O·11Al2O3, Z. für Kristallogr. - Cryst. Mater., 1937, 97(1–6), 59–66 CAS.
- J. Thery and D. Briançon, Chimie minérale-sur les propriétés d'un nouvel aluminate de sodium NaAl5O8, C. R. Acad. Sci., 1962, 254, 2782 CAS.
- S. Wenzel, T. Leichtweiss, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, Interfacial Reactivity Benchmarking of the Sodium Ion Conductors Na 3 PS 4 and Sodium β-Alumina for Protected Sodium Metal Anodes and Sodium All-Solid-State Batteries, ACS Appl. Mater. Interfaces, 2016, 8(41), 28216–28224 CrossRef CAS PubMed.
- M. G. Barker, P. G. Gadd and S. C. Wallwork, A new sodium aluminate Na17Al5O16, J. Chem. Soc., Chem. Commun., 1982,(9), 516–517 RSC.
- B. Shen, et al., Improved electrochemical performance of NaAlO2-coated LiCoO2 for lithium-ion batteries, J. Solid State Electrochem., 2017, 21(4), 1195–1201 CrossRef CAS.
- H. Y.-P. Hong, “Crystal structures and crystal chemistry in the system Na1+xZr2SixP3−xO12, Mater. Res. Bull., 1976, 11(2), 173–182 CrossRef CAS.
- J. B. Goodenough, H. Y.-P. Hong and J. A. Kafalas, Fast Na+-ion transport in skeleton structures, Mater. Res. Bull., 1976, 11(2), 203–220 CrossRef CAS.
- S. Chen, et al., Challenges and Perspectives for NASICON-Type Electrode Materials for Advanced Sodium-Ion Batteries, Adv. Mater., 2017, 29(48), 1700431 CrossRef PubMed.
- U. Von Alpen, M. F. Bell and H. H. Höfer, Compositional dependence of the electrochemical and structural parameters in the Nasicon system (Na1+xSixZr2P3−xO12), Solid State Ionics, 1981, 3, 215–218 CrossRef.
- W. Zhou, Y. Li, S. Xin and J. B. Goodenough, Rechargeable Sodium All-Solid-State Battery, ACS Cent. Sci., 2017, 3(1), 52–57 CrossRef CAS PubMed.
- K. D. Kreuer and U. Warhus, NASICON solid electrolytes, Mater. Res. Bull., 1986, 21(3), 357–363 CrossRef CAS.
- J. Zhu, et al., Sodium Ion Transport Mechanisms in Antiperovskite Electrolytes Na3OBr and Na4OI2: An in Situ Neutron Diffraction Study, Inorg. Chem., 2016, 55(12), 5993–5998 CrossRef CAS PubMed.
- Y. Wang, et al., Structural manipulation approaches towards enhanced sodium ionic conductivity in Na-rich antiperovskites, J. Power Sources, 2015, 293, 735–740 CrossRef CAS.
- M. D. Leblanc, U. M. Gundusharma and E. A. Secco, Electrical conductivity of superionic solid solutions of Na2SO4 with Mx (XO4)y -[M=Na, K, Rb, Cd, Gd and X=W, Mo, S, Si;x=1, 2, 4 andy=1, 3], Solid State Ionics, 1986, 20(1), 61–68 CrossRef CAS.
- J. T. S. Irvine and A. R. West, Sodium ion-conducting solid electrolytes in the system Na3PO4-Na2SO4, J. Solid State Chem., 1987, 69(1), 126–134 CrossRef CAS.
- H. Hruschka, E. Lissel and M. Jansen, Na-Ion conduction in the solid solutions of Na3PO4/Na2SO4 and Na3AlF6/Na2SO4, Solid State Ionics, 1988, 28, 159–162 CrossRef.
- M. Pompetzki, R. E. Dinnebier and M. Jansen, Sodium dithiophosphate(V): Crystal structure, sodium ionic conductivity and dismutation, Solid State Sci., 2003, 5(11–12), 1439–1444 CrossRef CAS.
- M. Jansen and U. Henseler, Synthesis, structure determination, and ionic conductivity of sodium tetrathiophosphate, J. Solid State Chem., 1992, 99(1), 110–119 CrossRef CAS.
- N. Tanibata, K. Noi, A. Hayashi and M. Tatsumisago, Preparation and characterization of highly sodium ion conducting Na3PS4-Na4SiS4 solid electrolytes, RSC Adv., 2014, 4(33), 17120–17123 RSC.
- A. Banerjee, et al., Na3SbS4: A Solution Processable Sodium Superionic Conductor for All-Solid-State Sodium-Ion Batteries, Angew. Chem., 2016, 128(33), 9786–9790 CrossRef.
- W. D. Richards, et al., Design and synthesis of the superionic conductor Na10SnP2S12, Nat. Commun., 2016, 7, 11009 CrossRef CAS PubMed.
- T. J. Udovic, et al., Sodium superionic conduction in Na2B12H12, Chem. Commun., 2014, 50(28), 3750–3752 RSC.
- M. Matsuo, Y. Nakamori, S. Orimo, H. Maekawa and H. Takamura, Lithium superionic conduction in lithium borohydride accompanied by structural transition, Appl. Phys. Lett., 2007, 91(22), 224103 CrossRef.
- K. Takahashi, et al., All-solid-state lithium battery with LiBH4 solid electrolyte, J. Power Sources, 2013, 226, 61–64 CrossRef CAS.
- D. M. F. Santos and C. A. C. Sequeira, Sodium borohydride as a fuel for the future, Renewable Sustainable Energy Rev., 2011, 15(8), 3980–4001 CrossRef CAS.
- Z. Lu and F. Ciucci, Metal Borohydrides as Electrolytes for Solid-State Li, Na, Mg, and Ca Batteries: A First-Principles Study, Chem. Mater., 2017, 29(21), 9308–9319 CrossRef CAS.
- B. L. Ellis and L. F. Nazar, Sodium and sodium-ion energy storage batteries, Curr. Opin. Solid State Mater. Sci., 2012, 16(4), 168–177 CrossRef CAS.
- S. Ha, J.-K. Kim, A. Choi, Y. Kim and K. T. Lee, “Sodium–Metal Halide and Sodium–Air Batteries, ChemPhysChem, 2014, 15(10), 1971–1982 CrossRef CAS PubMed.
- S. Bhavaraju, A. V. Joshi, M. Robins and A. Eccleston, Intermediate temperature sodium-metal halide battery, US9537179B2, 25-Sep-2014.
- D. R. Spearing, J. F. Stebbins, and I. Farnan, Diffusion and the Dynamics of Displacive Phase Transitions in Cryolite (Na3AIF6) and Chiolite (NasAl3F14): Multi-Nuclear NMR Studies, p. 14 Search PubMed.
- L. Foy and P. A. Madden, Ionic Motion in Crystalline Cryolite, J. Phys. Chem. B, 2006, 110(31), 15302–15311 CrossRef CAS PubMed.
- G. Nazri, Preparation, structure and ionic conductivity of lithium phosphide, Solid State Ionics, 1989, 34(1), 97–102 CrossRef CAS.
- H. Maekawa, et al., Halide-Stabilized LiBH 4 , a Room-Temperature Lithium Fast-Ion Conductor, J. Am. Chem. Soc., 2009, 131(3), 894–895 CrossRef CAS PubMed.
- I.-H. Chu, et al., Room-Temperature All-solid-state Rechargeable Sodium-ion Batteries with a Cl-doped Na3PS4 Superionic Conductor, Sci. Rep., 2016, 6, 33733 CrossRef CAS PubMed.
- S. Ujiie, T. Inagaki, A. Hayashi and M. Tatsumisago, “Conductivity of 70Li2S·30P2S5 glasses and glass–ceramics added with lithium halides, Solid State Ionics, 2014, 263, 57–61 CrossRef CAS.
- S. Zhai, L. Li, F. Chen, Q. Jiao, C. Rüssel and C. Lin, “Glass Formation and Ionic Conduction Behavior in GeSe2–Ga2Se3–NaI Chalcogenide System, J. Am. Ceram. Soc., 2015, 98(12), 3770–3774 CrossRef CAS.
- Å. Olin, Chemical Thermodynamics of Selenium. Elsevier, 2005 Search PubMed.
- S. P. Ong, et al., Voltage, stability and diffusion barrier differences between sodium-ion and lithium-ion intercalation materials, Energy Environ. Sci., 2011, 4(9), 3680–3688 RSC.
- B. M. Gallant, et al., Chemical and Morphological Changes of Li–O2 Battery Electrodes upon Cycling, J. Phys. Chem. C, 2012, 116(39), 20800–20805 CrossRef CAS.
- V. Viswanathan, et al., Electrical conductivity in Li2O2 and its role in determining capacity limitations in non-aqueous Li-O2 batteries, J. Chem. Phys., 2011, 135(21), 214704 CrossRef CAS PubMed.
- S. Kang, Y. Mo, S. P. Ong and G. Ceder, “Nanoscale Stabilization of Sodium Oxides: Implications for Na–O2 Batteries, Nano Lett., 2014, 14(2), 1016–1020 CrossRef CAS PubMed.
- R. Tegman, The crystal structure of sodium tetrasulphide, Na2 S4, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29(7), 1463–1469 CrossRef CAS.
- H. Föppl, E. Busmann and F.-K. Frorath, Die Kristallstrukturen von α-Na2S2 und K2S2, β-Na2S2 und Na2Se2, Z. Anorg. Allg. Chem., 1962, 314(1–2), 12–20 CrossRef.
- X. Yu, G. Giorgi, H. Ushiyama and K. Yamashita, First-principles study of fast Na diffusion in Na3P, Chem. Phys. Lett., 2014, 612, 129–133 CrossRef CAS.
- P.-F. Wang, Y. You, Y.-X. Yin and Y.-G. Guo, Layered Oxide Cathodes for Sodium-Ion Batteries: Phase Transition, Air Stability, and Performance, Adv. Energy Mater., 2018, 8(8), 1701912 CrossRef.
- R. K. B. Gover, A. Bryan, P. Burns and J. Barker, The electrochemical insertion properties of sodium vanadium fluorophosphate, Na3V2(PO4)2F3, Solid State Ionics, 2006, 177(17), 1495–1500 CrossRef CAS.
- M. Bianchini, P. Xiao, Y. Wang and G. Ceder, Additional Sodium Insertion into Polyanionic Cathodes for Higher-Energy Na-Ion Batteries, Adv. Energy Mater., 2017, 7(18), 1700514 CrossRef.
- S. Wenzel, T. Leichtweiss, D. Krüger, J. Sann and J. Janek, “Interphase formation on lithium solid electrolytes—An in situ approach to study interfacial reactions by photoelectron spectroscopy, Solid State Ionics, 2015, 278, 98–105 CrossRef CAS.
- R. Hoffmann and W. N. Lipscomb, Theory of Polyhedral Molecules. I. Physical Factorizations of the Secular Equation, J. Chem. Phys., 1962, 36(8), 2179–2189 CrossRef CAS.
- K. Wade, The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds, J. Chem. Soc., Chem. Commun., 1971,(15), 792–793 RSC.
- R. B. King and D. H. Rouvray, Chemical applications of group theory and topology. 7. A graph-theoretical interpretation of the bonding topology in polyhedral boranes, carboranes, and metal clusters, J. Am. Chem. Soc., 1977, 99(24), 7834–7840 CrossRef CAS.
- W. Li, et al., Hydrothermal Synthesis of Monolithic Co3Se4 Nanowire Electrodes for Oxygen Evolution and Overall Water Splitting with High Efficiency and Extraordinary Catalytic Stability, Adv. Energy Mater., 2017, 7(17), 1602579 CrossRef.
- Z. W. Lu, B. M. Klein and D. J. Singh, Electronic structure of heazlewoodite Ni3S2, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(19), 13542–13545 CrossRef CAS.
- E. Yi, E. Temeche and R. M. Laine, “Superionically Conducting β’’-Al2O3 Thin Films Processed Using Flame Synthesized Nanopowders, J. Mater. Chem. A, 2018, 6, 12411–12419 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta10498k |
| This journal is © The Royal Society of Chemistry 2019 |