Open Access Article
Open Access ArticleThe effect of water on the validity of Löwenstein's rule†
Christopher J.
Heard
 *,
Lukáš
Grajciar
*,
Lukáš
Grajciar
 and
Petr
Nachtigall
and
Petr
Nachtigall

Department of Physical and Macromolecular Chemistry, Charles University, Hlavova 8, 12496 Prague 2, Czech Republic. E-mail: heardc@natur.cuni.cz
First published on 6th May 2019
Abstract
The common understanding of zeolite acidity is based on Löwenstein's rule, which states that Al–O–Al aluminium pairs are forbidden in zeolites. This rule is generally accepted to be inviolate in zeolites. However, recent computational research using a 0 K DFT model has suggested that the rule is violated for the acid form of several zeolites under anhydrous conditions [Fletcher et al., Chem. Sci., 8, (2017), 7483]. The effect of water loading on the preferred aluminium distribution in zeolites, however, has so far not been taken into account. In this article, we show by way of ab initio molecular dynamics simulations that Löwenstein's rule is obeyed under high water solvation for acid chabazite (H-CHA) but disobeyed under anhydrous conditions. We find that varying the water loading in the pores leads to dramatic effects on the structure of the active sites and the dynamics of solvation. The solvation of Brønsted protons in the surrounding water was found to be the energetic driving force for the preferred Löwenstein Al distribution and this driving force is absent in non-Löwenstein (Al–O(H)–Al) moieties. The preference for solvated protons further implies that the catalytically active species in zeolites is a protonated water cluster, rather than a framework Brønsted site. Hence, an accurate treatment of the solvation conditions is crucial to capture the behaviour of zeolites and to properly connect simulations to experiments. This work should lead to a change in modelling paradigm for zeolites, from single molecules towards high solvation models where appropriate.
Introduction
Zeolites are three-dimensional aluminosilicate materials characterized by high stability, porosity and Brønsted acidity, which are among the reasons they are the most widely used class of industrial catalysts worldwide.1 Zeolites are made up of corner-sharing tetrahedral units of SiO4 and AlO4−. For each AlO4− there is a charge-compensating ion, which is often a proton. According to Löwenstein's rule,2 which is an established axiom of zeolite science, tetrahedral units containing aluminium may not be located adjacent to each other.Experimentally, Löwenstein's rule is found to be generally obeyed. However, a small number of Löwenstein-disobeying (NLöw) examples have been proposed for aluminosilicates: in the aluminate sodalites,3 zeolite stilbite,4 in bicchulite5–7 and gehlenite-type8 materials, where Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratios below 1 can be achieved, aluminosilicate glasses9,10 and metastable, disordered phases, such as cordierite11 and anorthite.12 Among related materials that have been shown to disobey Löwenstein's rule are layered Na-4-micas13 and gallobicchulite.14 Most of the analyses reporting on violations of Löwenstein's rule have been either indirect, or applied to materials generated under exotic conditions.11,12,15,16 Often, the synthesis procedures that lead to NLöw Al distributions include very high temperatures,11,12 for which the availability of water is low. It has also been shown experimentally that zeolite building units may be found which disobey Löwenstein's rule,17 but these species are not transferred to the final zeolite upon condensation.
Al ratios below 1 can be achieved, aluminosilicate glasses9,10 and metastable, disordered phases, such as cordierite11 and anorthite.12 Among related materials that have been shown to disobey Löwenstein's rule are layered Na-4-micas13 and gallobicchulite.14 Most of the analyses reporting on violations of Löwenstein's rule have been either indirect, or applied to materials generated under exotic conditions.11,12,15,16 Often, the synthesis procedures that lead to NLöw Al distributions include very high temperatures,11,12 for which the availability of water is low. It has also been shown experimentally that zeolite building units may be found which disobey Löwenstein's rule,17 but these species are not transferred to the final zeolite upon condensation.
Computationally, the preference of Löwenstein-obeying (Löw) over NLöw isomers has been demonstrated in zeolites, both in zeolite-A18 and in hydrated secondary building unit fragments.19 However, recent theoretical work has suggested that the global minimum configuration for the acid form of several zeolites, including chabazite (CHA) may violate the rule under anhydrous conditions.20 The authors conclude that the lack of NLöw geometries observed in experiment may be due to kinetic trapping in the Löw configurations that are favoured by the Na+ precursor form, rather than an overall thermodynamic preference for Löw configurations.
The unclear literature picture of preferred aluminium distributions in zeolites is complicated by the general lack of consideration of solvation effects when applying theoretical methods. The presence of water affects the stability, acidity and reactivity of the zeolite.21 Zeolites are synthesized in the presence of excess water, which resides in the zeolite pores.22 Also, zeolites are frequently found under conditions of high water loading during operation, either as molecular sieves or as microporous catalysts.23,24 In the case of hydrolysis reactions, water is involved directly in structural transformations25,26 and may be exploited in novel synthetic routes, such as the ADOR process.27,28 Most theoretical treatments that include water inside the zeolite pore have been limited to low water loading effects,29–32 and only a few computational studies have considered the effects of high water solvation in zeolites.33–40
To date, there have been no studies which investigate the effect of water loading on the preferred aluminium distribution. However, given the widespread acceptance of Löwenstein's rule, it is important to consider the conditions under which it may be violated, and to propose an explanation for the conditions under which it is valid. Here, we show that the level of water solvation has a profound effect on the preferred aluminium distribution and the catalytically active site. While we confirm the violation of the Löwenstein's rule under anhydrous conditions, we observe its recovery under high water loading. This reversal originates in the ability of water to solvate the acidic Brønsted acidic proton. This ability is hindered in the Al–O(H)–Al moieties of NLöw configurations, leading to NLöw becoming unfavourable under high water loading conditions. This work shows that the active site of acid zeolites under solvation is a homogeneous Brønsted acidic water cluster, rather than a heterogeneous framework acid site. These results have significant implications on how to view and model acid zeolites under realistic conditions.41
Computational details
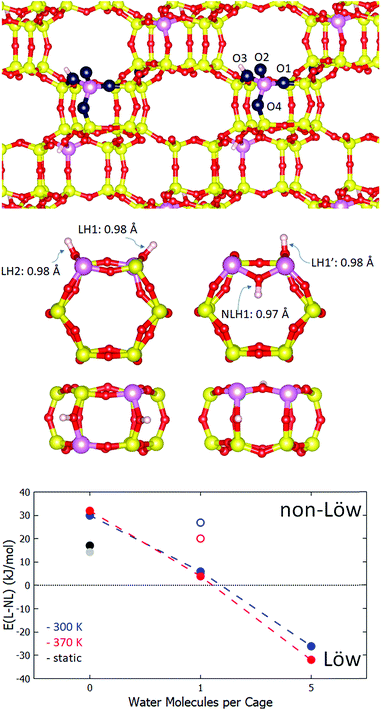
For the investigation of Löwenstein's rule in H-CHA, the 36 T site supercell model of chabazite was adopted, with an Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio of 17, for which both Al atoms are in one of the cages (Fig. 1). A second model was employed to investigate general proton solvation effects, with an Si
Al ratio of 17, for which both Al atoms are in one of the cages (Fig. 1). A second model was employed to investigate general proton solvation effects, with an Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio of 11, corresponding to one Al atom per cage. The effect of the water loading in the zeolite channel system was investigated for three regimes: a completely anhydrous model, a single water molecule in the low-solvation model, and fifteen water molecules in the unit cell, corresponding to 1g cm−3 water density and five molecules per cage, in the high solvation model. The CHA accessible volume fraction of 17.4% was taken from the IZA database.42 Molecules were initially placed in the zeolite pore structure by overlapping the unit cell with a cubic water box containing a random packing of spc water molecules with the gromacs solvate code.43
Al ratio of 11, corresponding to one Al atom per cage. The effect of the water loading in the zeolite channel system was investigated for three regimes: a completely anhydrous model, a single water molecule in the low-solvation model, and fifteen water molecules in the unit cell, corresponding to 1g cm−3 water density and five molecules per cage, in the high solvation model. The CHA accessible volume fraction of 17.4% was taken from the IZA database.42 Molecules were initially placed in the zeolite pore structure by overlapping the unit cell with a cubic water box containing a random packing of spc water molecules with the gromacs solvate code.43
All calculations were performed using density functional theory as implemented in the VASP 5.4 code,44–47 with the generalised gradient exchange correlation functions of Perdew, Burke and Ernzerhof,48 and an additional dispersion correction, of the D3 form of Grimme et al.49 with Becke–Johnson damping.50 While the PBE functional is known to over-structure bulk water, it is of comparable quality to other GGA functionals for small water clusters.51 The BJ damping correction is also found to improve the description of water structure and is included in this work.50 Gaussian smearing of the Fermi–Dirac distribution was implemented, with a smearing width of 0.1 eV. Electronic states were sampled at the Gamma point only, which is sufficient for the supercell model used herein. Wavefunctions are described by a plane-wave basis expanded to a kinetic energy cutoff of 400 eV. For geometry optimisation, a force convergence criterion of 0.01 eV Å−1 was set. For the calculation of vibrational modes, the finite differences method was employed, with 4 points per degree of freedom, with 0.01 Å displacement. Energetics and dynamic properties were determined by ab initio molecular dynamics simulations of 10–15 ps with a timestep of 0.5 fs, employing the Nosé–Hoover thermostat in the NVT ensemble, with a target temperature of 300 or 370 K, following an equilibration of between 2–3 ps. Hydrogen atoms were assigned the mass of deuterium, in order to enhance sampling efficiency.
Results and discussion
Following a recent work of Fletcher et al.,20 we have selected chabazite as the zeolite to investigate, as it is a well-studied system both computationally and experimentally and represents a good model for an aluminosilicate zeolite with a three-dimensional pore structure and small pores. Furthermore, CHA has found important roles in industry, as a selective catalytic reduction (SCR) catalyst in vehicle exhaust after-treatment52 and in methane partial oxidation.53,54 It is not necessarily true that the behaviour of H-CHA is generalizable to other frameworks, such as dense zeolites with one-dimensional channel systems. However, preliminary calculations on the 1D channel-containing zeolite H-ABW (see ESI†) suggest that our findings have reasonable generality. Specifically, the CHA framework consists of a hexagonal arrangement of double six rings (D6R), connected together by 4-rings.42 The pore structure consists of 8 ring windows, through which protons and water may transfer. The silicon/aluminium atoms make up a symmetry class of one T site, which is surrounded by four inequivalent oxygen sites (O1–O4), as displayed schematically in Fig. 1. Each oxygen is a constituent part of three rings. O1 makes up two 4-rings and a 6-ring, O2 makes up a 4-ring and two 8-rings, O3 makes up a 4-ring a 6-ring and an 8-ring, and O4 makes up two 4-rings and an 8-ring. The D6R of the two Al configurations, Löw and NLöw, chosen in order to test Löwenstein's rule, are displayed in Fig. 1 (centre panel). The hydrogen atoms are labelled LH1 and LH2 (Löw configuration) and LH1′ and NLH1 (NLöw configuration). These two aluminium configurations are the most stable Löw and NLöw isomers under anhydrous conditions according to the recent work of Fletcher et al.20 In this work, we aim to find the underlying role of water in Löwenstein's rule, and it is beyond the scope of this study to exhaustively search all configurations under hydrated conditions. Therefore, we use the most stable Löw/NLöw pair to represent realistic models of H-CHA. Local geometry optimisation under anhydrous conditions was performed, showing a preference for the NLöw isomer of 17 kJ mol−1, in good agreement with Fletcher et al. (14.2 kJ mol−1). The bond lengths found for LH1, LH2 and LH1′ were 0.975, 0.975 and 0.978 Å, respectively, with vibrational frequencies of 3729, 3726 and 3683 cm−1, respectively. The O–H bond of NLH1 is slightly shorter, at 0.973 Å, with a higher vibrational frequency of 3739 cm−1.To determine what are the effects of the degree of water solvation in the pore, and of the temperature, we move from the athermal, ultra-high vacuum model, to an explicit solvation model at 300 K. Ab initio NVT molecular dynamics simulations were performed for NLöw and Löw isomers under various water loadings. The lower panel of Fig. 1 shows the relative average internal energies, taken directly from the MD simulation, of both isomers in which anhydrous (0 H2O), low water (1 H2O) and high water (5 H2O/cage) conditions are applied. Under anhydrous conditions, there is a preference of 30 kJ mol−1 for the NLöw isomer, which represents a qualitative shift from the athermal situation, stabilising the NLöw isomer by a further 13 kJ mol−1. In the low water case, the water molecule adsorbs through the oxygen atom (Ow) to the proton at the Brønsted site (Hb). Throughout the three separate simulations, corresponding to water adsorption to LH1, LH1′ and NLH1, the proton and the water to which it is adsorbed remain fixed to the site they begin at. When water is absorbed to the LH1′ site, the NLöw isomer is preferred by 27 kJ mol−1, which is slightly less than in the anhydrous case (30 kJ mol−1). For the case in which water adsorbs to the Al–O(H)–Al proton (NLH1), the NLöw isomer is further destabilised, and is only 6 kJ mol−1 more stable than the Löw isomer. This is because the hydrogen in this Al–O(H)–Al site is unable to form such strong bonds to water as in other sites. Under high water solvation, there are enough water molecules to adsorb simultaneously to both protons, so the LH1/LH2 and LH1′/NLH1 pairs no longer need to be treated separately. We performed two molecular dynamics simulations, one for high water loading with the NLöw configuration, and one for the Löw configuration. A dramatic change in relative stability occurs. Under high water loading at 300 K, there is a preference for Löw isomers of 26 kJ mol−1. This means that moving from the anhydrous to the high water loading regime incurs a switch of 56 kJ mol−1 and the recovery of Löwenstein's rule. The recovery of the Löwenstein's rule under high water loading conditions is consistent with the fact that experimentally, non-Löwenstein isomers are uncommon in zeolites. Synthesis conditions more closely resemble the high water loading regime than the anhydrous one.
Temperature effects are considered by performing simulations under the same three water loadings at 370 K. The relative energies are also plotted in Fig. 1 (red points), and show minor quantitative changes in relative stabilities, but the same qualitative behaviour as at 300 K.
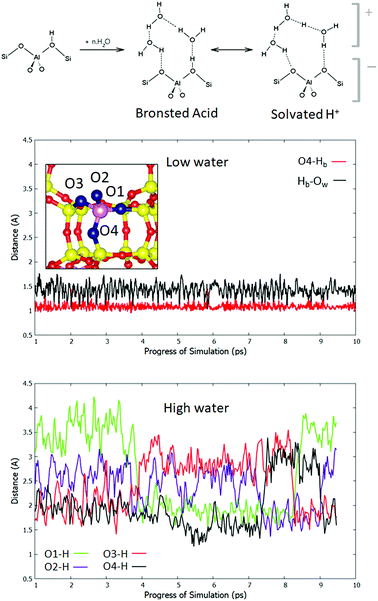
To understand the observed effect of solvating water, we consider the role of water loading on the location of the Brønsted acidic proton. It has been suggested in previous computational studies that four water molecules per cage are sufficient to cause proton solvation.35 The two limiting cases are depicted in the scheme in Fig. 2. In one case, the proton remains bound to the framework through a Hb–Of bond, and the water in the pore interacts with it through fluctuating hydrogen bonds. In the second case, Hb leaves the framework and is solvated by the water, which forms a cationic complex of (H2O)n·H3O+ that interacts with the anionic AlO4− moiety. The real behaviour may be intermediate between the two, or a dynamic alternation between them. In order to analyse the dynamics of the acidic hydrogen, the definition of Brønsted proton solvation must first be chosen. In this work we adopt a definition such that a proton is considered to be attached to the framework if it is closer to any framework oxygen Of, than to any of the water oxygen atoms Ow. If this is not true, the proton is said to be solvated. To test the extent to which protons are solvated in the pore, we move to a system in which there is one aluminium atom per cage (Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al = 11), with a minimum of four T sites between each pair of Al atoms. This is therefore a standard, Löwenstein-obeying model of H-CHA without the effects of closely coupled Al pairs. Fig. 2 shows an Of–H distance trace for both low and high water loading cases. In the low loading regime, the most stable adsorption site, O4, is displayed, showing an Of–Hb distance of average length 1.09 Å. This is longer than that of the anhydrous O4–Hb bond (1.00 Å), owing to the adsorption of the single water molecule. As observed in the 1 H2O scenario for the NLöw and Löw isomers, free H3O+ is never observed. A small minority (4%) of configurations exist, which correspond with our definition of proton solvation, but these states are transient and rare. The Hb–Ow bond is also plotted and has an average of 1.43 Å. For the high water loading case the situation is more complex, because the Brønsted proton may hop between any of the four sites, or become solvated. The exchange of protons means no particular atom should be considered separately. Therefore, we plot the minimum Of–H distance for each of the four Of atoms around an aluminium site, taking into account all hydrogens in the system. This allows for the exchange of protons between all Brønsted sites and solvation by water to be monitored. We observe that the minimum Of–Hb distance is never below 1.14 Å for any of the four framework oxygen atoms, suggesting that even for non-solvated configurations, the bond between Hb and the framework is significantly weakened (Fig. 2, bottom panel). Indeed, only 10% of configurations have a minimum Of–H distance below 1.5 Å, while 19% of configurations have a minimum Of–H distance greater than 1.9 Å. For each Of in turn, the range over which the Of–Hb distance varies is far greater than in the low water conditions, implying that there is a significant proportion of configurations in which there lies no proton near a given Of site. The structure of the trace shows that there are coupled hops between pairs of Of sites. For example, the traces of O1 and O3 are in anti-phase with each other, which is consistent with a Grotthus-type proton shuttle mechanism between the pair. A similar relationship is observed between oxygen atoms O2 and O4. According to the adopted definition of solvation, the Brønsted proton is solvated >99% of the time. Hence, we can conclude that the equilibrium lies firmly on the side of solvated Brønsted protons, and a charge separation to cationic protonated water and the anionic framework is preferred.
Al = 11), with a minimum of four T sites between each pair of Al atoms. This is therefore a standard, Löwenstein-obeying model of H-CHA without the effects of closely coupled Al pairs. Fig. 2 shows an Of–H distance trace for both low and high water loading cases. In the low loading regime, the most stable adsorption site, O4, is displayed, showing an Of–Hb distance of average length 1.09 Å. This is longer than that of the anhydrous O4–Hb bond (1.00 Å), owing to the adsorption of the single water molecule. As observed in the 1 H2O scenario for the NLöw and Löw isomers, free H3O+ is never observed. A small minority (4%) of configurations exist, which correspond with our definition of proton solvation, but these states are transient and rare. The Hb–Ow bond is also plotted and has an average of 1.43 Å. For the high water loading case the situation is more complex, because the Brønsted proton may hop between any of the four sites, or become solvated. The exchange of protons means no particular atom should be considered separately. Therefore, we plot the minimum Of–H distance for each of the four Of atoms around an aluminium site, taking into account all hydrogens in the system. This allows for the exchange of protons between all Brønsted sites and solvation by water to be monitored. We observe that the minimum Of–Hb distance is never below 1.14 Å for any of the four framework oxygen atoms, suggesting that even for non-solvated configurations, the bond between Hb and the framework is significantly weakened (Fig. 2, bottom panel). Indeed, only 10% of configurations have a minimum Of–H distance below 1.5 Å, while 19% of configurations have a minimum Of–H distance greater than 1.9 Å. For each Of in turn, the range over which the Of–Hb distance varies is far greater than in the low water conditions, implying that there is a significant proportion of configurations in which there lies no proton near a given Of site. The structure of the trace shows that there are coupled hops between pairs of Of sites. For example, the traces of O1 and O3 are in anti-phase with each other, which is consistent with a Grotthus-type proton shuttle mechanism between the pair. A similar relationship is observed between oxygen atoms O2 and O4. According to the adopted definition of solvation, the Brønsted proton is solvated >99% of the time. Hence, we can conclude that the equilibrium lies firmly on the side of solvated Brønsted protons, and a charge separation to cationic protonated water and the anionic framework is preferred.
To investigate the stability of Al–O(H)–Al sites under high water loading, we return to the Löw and NLöw isomers of H-CHA with Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al = 17. We performed dynamical simulations at 300 K with high water loading. The pair distribution functions (PDFs) were calculated between the relevant framework oxygens and all hydrogen atoms in the system. The results for LH1 and LH1′ are qualitatively similar and are compared in the ESI.† In order to directly compare the effect of water on Löw and NLöw configurations, we show the PDFs for LH1 and NLH1 (Fig. 3). In LH1 this function has no peak around 1.0 Å, which confirms the loss of the framework Brønsted acid group, and thus the solvation of the proton. The first peak of any significant size is at 1.8 Å, which is due to the hydrogen bond between the framework oxygen and the nearest proton of the water molecule. This peak spans a broad region from 1.3 to 2.2 Å, owing to fluctuations in the H-bonding. There is a further peak at 3.2 Å, which corresponds to the distance between the framework oxygen and a further Hw hydrogen on the nearest protonated water molecule. Beyond 4 Å, there are contributions from water molecules in further solvation shells. The behaviour of the NLöw configuration is remarkably different. A prominent peak is observed at 1.04 Å, corresponding to the survival of the Of–NLH1 bond for a significant proportion of the simulation. In fact, this bond is not lost at all for the duration of the dynamical simulation. The next peak, which is centred at 3.0 Å corresponds to the distance from Of to the nearest Hw. This has a significant frequency, because there is a water molecule attached to the NLH1 proton that moves less throughout the simulation. Owing to the retention of the Of–Hb bond, the distance to the Hw is slightly shorter in the NLH1 case than for LH1. Further from Of, there is a broad region starting at 3.4 Å, which, as in the LH1 case, corresponds to more distant Hw atoms in the pore volume.
Al = 17. We performed dynamical simulations at 300 K with high water loading. The pair distribution functions (PDFs) were calculated between the relevant framework oxygens and all hydrogen atoms in the system. The results for LH1 and LH1′ are qualitatively similar and are compared in the ESI.† In order to directly compare the effect of water on Löw and NLöw configurations, we show the PDFs for LH1 and NLH1 (Fig. 3). In LH1 this function has no peak around 1.0 Å, which confirms the loss of the framework Brønsted acid group, and thus the solvation of the proton. The first peak of any significant size is at 1.8 Å, which is due to the hydrogen bond between the framework oxygen and the nearest proton of the water molecule. This peak spans a broad region from 1.3 to 2.2 Å, owing to fluctuations in the H-bonding. There is a further peak at 3.2 Å, which corresponds to the distance between the framework oxygen and a further Hw hydrogen on the nearest protonated water molecule. Beyond 4 Å, there are contributions from water molecules in further solvation shells. The behaviour of the NLöw configuration is remarkably different. A prominent peak is observed at 1.04 Å, corresponding to the survival of the Of–NLH1 bond for a significant proportion of the simulation. In fact, this bond is not lost at all for the duration of the dynamical simulation. The next peak, which is centred at 3.0 Å corresponds to the distance from Of to the nearest Hw. This has a significant frequency, because there is a water molecule attached to the NLH1 proton that moves less throughout the simulation. Owing to the retention of the Of–Hb bond, the distance to the Hw is slightly shorter in the NLH1 case than for LH1. Further from Of, there is a broad region starting at 3.4 Å, which, as in the LH1 case, corresponds to more distant Hw atoms in the pore volume.
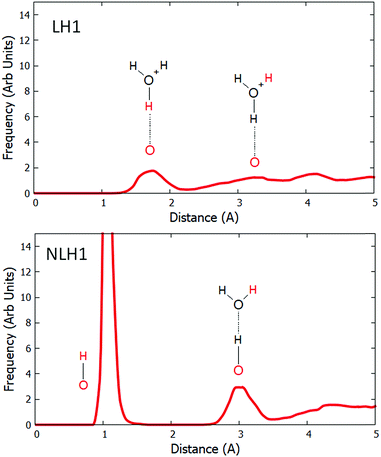 | ||
| Fig. 3 The pair distribution function between Of and all hydrogens for the LH1 and NLH1 configurations. Each schematic inset shows the O–H pair which contributes to the peak in red colour. | ||
The proton which is attached to the Al–O–Al moiety in H-CHA with a non-Löwenstein aluminium distribution is pinned to the site, and thus does not benefit from the solvation which is found to be spontaneous in Löwenstein-obeying configurations at both Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratios considered in the current work. This pinning to the framework, it should be noted, is nothing more than a re-expression of the reduced acidity of the Al–O(H)–Al proton to such an extent that it remains unsolvated even under high water loading. To further support the notion that the deprotonation of Al–O(H)–Al sites is energetically unfavourable, we have considered the reverse scenario, in which the initial state is the deprotonated moiety, with H+ solvated in the micropore. A proton is irreversibly transferred back to the Al–O–Al site via a Grotthus mechanism within 1 ps. Hence, it appears there is no stable position on the free energy landscape for the solvated proton and the lack of deprotonation of the Al–O(H)–Al site is a thermodynamic effect. To confirm the reduced acidity of the NLH1 proton, we calculated the relative deprotonation energies of the NLöw and Löw isomers in the anhydrous regime with a simple model. The structures were geometry optimised before (H-CHA) and after (CHA−) the removal of the proton. The energy of the deprotonation (Edep) was calculated by the formula: Edep = EH-CHA − ECHA−. Absolute deprotonation energies calculated using a homogeneous background charge to compensate for a charged unit cell may be inaccurate. However, relative deprotonation energies between isomers provide a semi-quantitative description of the differences between isomers with reasonable accuracy.55 Therefore, we consider only the relative value here. LH1′ is found to be the most acidic proton, and NLH1 as the least, by a large margin of 71 kJ mol−1. The LH1 and LH2 protons are intermediate in acidity, and equivalent within the error of the method, at 26 and 29 kJ mol−1, respectively. These results are perfectly consistent with the vibrational frequencies of the O–H bonds in the anhydrous regime. Thus, the picture emerges of a strongly bonded, less-acidic proton in the Al–O(H)–Al group, which in the absence of solvating water, stabilises the framework, but in the presence of water, becomes an energetic hindrance. The proton is bound to the framework and therefore is unable to achieve the energetic stabilisation afforded by solvation by the water in the pore that is achieved by Löwenstein-obeying configurations.
Al ratios considered in the current work. This pinning to the framework, it should be noted, is nothing more than a re-expression of the reduced acidity of the Al–O(H)–Al proton to such an extent that it remains unsolvated even under high water loading. To further support the notion that the deprotonation of Al–O(H)–Al sites is energetically unfavourable, we have considered the reverse scenario, in which the initial state is the deprotonated moiety, with H+ solvated in the micropore. A proton is irreversibly transferred back to the Al–O–Al site via a Grotthus mechanism within 1 ps. Hence, it appears there is no stable position on the free energy landscape for the solvated proton and the lack of deprotonation of the Al–O(H)–Al site is a thermodynamic effect. To confirm the reduced acidity of the NLH1 proton, we calculated the relative deprotonation energies of the NLöw and Löw isomers in the anhydrous regime with a simple model. The structures were geometry optimised before (H-CHA) and after (CHA−) the removal of the proton. The energy of the deprotonation (Edep) was calculated by the formula: Edep = EH-CHA − ECHA−. Absolute deprotonation energies calculated using a homogeneous background charge to compensate for a charged unit cell may be inaccurate. However, relative deprotonation energies between isomers provide a semi-quantitative description of the differences between isomers with reasonable accuracy.55 Therefore, we consider only the relative value here. LH1′ is found to be the most acidic proton, and NLH1 as the least, by a large margin of 71 kJ mol−1. The LH1 and LH2 protons are intermediate in acidity, and equivalent within the error of the method, at 26 and 29 kJ mol−1, respectively. These results are perfectly consistent with the vibrational frequencies of the O–H bonds in the anhydrous regime. Thus, the picture emerges of a strongly bonded, less-acidic proton in the Al–O(H)–Al group, which in the absence of solvating water, stabilises the framework, but in the presence of water, becomes an energetic hindrance. The proton is bound to the framework and therefore is unable to achieve the energetic stabilisation afforded by solvation by the water in the pore that is achieved by Löwenstein-obeying configurations.
Zeolites span a wide range of topological types, with pores of various sizes, and channels in one-, two- or three-directions. The presence of sufficient water to solvate protons is not necessarily guaranteed in extreme cases for which H-CHA (Si/Al = 11, 17) is not a representative model. In these cases, the results presented here cannot rule out the possibility of NLöw configurations remaining stable upon hydration. One such possibility is for zeolites with narrow one-dimensional channels at low Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratios. The zeolite H-ABW has such a structure and was shown by Fletcher et al. to have an even stronger preference for NLöw configurations than H-CHA in the athermal, anhydrous regime. Our calculations (see ESI†) indicate that at sufficient water loading (3 H2O molecules/Brønsted site), the energetic preference switches from NLöw to Löw configurations. The solvation of protons from Al–O(H)–Si groups is fast and irreversible, while the solvation of protons from Al–O(H)–Al groups is not found to occur. The similarity in behaviour between H-ABW and H-CHA suggests that topology is not directly important in affecting solvation-driven stabilisation. However, it remains possible that the amount of water incorporated into such a narrow channel is the limiting factor. It is beyond the scope of the current work to determine the limiting water loadings in different zeolite topologies, but we predict that this may play a role in the change in preference between NLöw and Löw configurations in practice.
Al ratios. The zeolite H-ABW has such a structure and was shown by Fletcher et al. to have an even stronger preference for NLöw configurations than H-CHA in the athermal, anhydrous regime. Our calculations (see ESI†) indicate that at sufficient water loading (3 H2O molecules/Brønsted site), the energetic preference switches from NLöw to Löw configurations. The solvation of protons from Al–O(H)–Si groups is fast and irreversible, while the solvation of protons from Al–O(H)–Al groups is not found to occur. The similarity in behaviour between H-ABW and H-CHA suggests that topology is not directly important in affecting solvation-driven stabilisation. However, it remains possible that the amount of water incorporated into such a narrow channel is the limiting factor. It is beyond the scope of the current work to determine the limiting water loadings in different zeolite topologies, but we predict that this may play a role in the change in preference between NLöw and Löw configurations in practice.
Conclusions
Ab Initio molecular dynamics simulations of the acid form of zeolite CHA confirm that Löwenstein's rule is disobeyed under anhydrous conditions, in accordance with the recent findings of Fletcher et al. We show that this inherent energetic preference towards non-Löwenstein configurations is weakened under partial solvation. Further, Löwenstein's rule is found to be recovered under high water loading conditions.The relative instability of the non-Löwenstein aluminium distribution under high water loading is attributed to the reduced Brønsted acidity of protons in Al–O(H)–Al configurations. This is confirmed statistically through O–H pair distributions and calculations of relative deprotonation energies. Temperature is found to have a moderate quantitative effect on the energetics in the range considered.
We may now offer an alternative interpretation for the conflicting literature regarding Löwenstein versus non-Löwenstein preference in zeolites. We show that non-Löwenstein configurations are inherently preferred in the absence of water. The presence of water changes the energetic preference towards Löwenstein-obeying aluminium configurations, which may explain the lack of NLöw configurations observed experimentally in zeolites. This dramatic change in Al distribution preference is concurrent with a change in the structure of the active site. Under water solvation, the Brønsted acid site takes the form of a protonated water cluster, rather than a static framework cation, suggesting that the catalytic activity under aqueous conditions is due to highly acidic protonated water clusters. These findings have significant ramifications in how we view acid zeolites as catalysts and shows the importance of considering an accurate description of water solvation.
We have considered H-CHA in this work as a model to provide a proof of principle. However, these results should be general for acid zeolites, except possibly in extreme cases of ultrasmall pore volume and high Al content, where the small number of water molecules per Brønsted acid site may not solvate all protons. It has already been shown by others that violations of Löwenstein's rule are possible in the anhydrous regime for several zeolites, and it is reasonable to expect that the recovery of the rule under high solvation will also be general. We may extend this proposal even to other porous aluminosilicates, as this behaviour only requires the possibility for water to interact with the framework and solvate a Brønsted proton. A further extension of this principle would be to investigate additional types of proton-solvating species, of which water is only one example.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Charles University Centre of Advanced Materials (CUCAM) (OP VVV Excellent Research Teams, project number CZ.02.1.01/0.0/0.0/15_003/0000417) is acknowledged. PN acknowledges the Czech Science Foundation (19-21534S). This work was supported by The Ministry of Education, Youth and Sports from the Large Infrastructures for Research, Experimental Development and Innovations project “IT4Innovations National Supercomputing Center – LM2015070“.Notes and references
- Y. Li, L. Li and J. Yu, Chem, 2017, 3, 928–949 CrossRef CAS.
- R. Loewenstein, Am. Mineral., 1954, 39, 92–96 Search PubMed.
- W. Depmeier, Phys. Chem. Miner., 1988, 15, 419–426 CAS.
- J. F. Stebbins, P. D. Zhao, S. K. Lee and X. Cheng, Am. Mineral., 1999, 84, 1680–1684 CAS.
- S. E. Dann, P. J. Mead and M. T. Weller, Inorg. Chem., 1996, 35, 1427–1428 CAS.
- A. K. Gupta and N. D. Chatterjee, Am. Mineral., 1978, 63, 58–65 CAS.
- K. Sahl, Fiz. Krist., 1980, 152, 13–21 CrossRef CAS.
- P. Florian, E. Veron, T. F. G. Green, J. R. Yates and D. Massiot, Chem. Mater., 2012, 24, 4068–4079 CrossRef CAS.
- A. R. Allu, A. Gaddam, S. Ganisetti, S. Balaji, R. Siegel, G. C. Mather, M. Fabian, M. J. Pascual, N. Ditaranto, W. Milius, J. Senker, D. A. Agarkov, V. V. Kharton and J. M. F. Ferreira, J. Phys. Chem. B, 2018, 122, 4737–4747 CrossRef CAS PubMed.
- E. V. Dubinsky and J. F. Stebbins, Am. Mineral., 2006, 91, 753–761 CrossRef CAS.
- A. Putnis, C. A. Fyfe and G. C. Gobbi, Phys. Chem. Miner., 1985, 12, 211–216 CrossRef CAS.
- B. L. Phillips, R. J. Kirkpatrick and M. A. Carpenter, Am. Mineral., 1992, 77, 484–494 CAS.
- E. Pavón, F. J. Osuna, M. D. Alba and L. Delevoye, Chem. Commun., 2014, 50, 6984–6986 RSC.
- S. E. Dann, P. J. Mead and M. T. Weller, Angew. Chem., Int. Ed. Engl., 1995, 34, 2414–2416 CrossRef CAS.
- J. Klinowski, J. M. Thomas, C. A. Fyfe and J. S. Hartman, J. Phys. Chem., 1981, 85, 2590–2594 CrossRef CAS.
- S. E. Tarling, P. Barnes and J. Klinowski, Acta Crystallogr., Sect. B: Struct. Sci., 1988, 44, 128–135 CrossRef.
- B. B. Schaack, Ph.D. thesis, Ruhr Universitaet Bochum, 2009.
- R. G. Bell, R. A. Jackson and C. R. A. Catlow, Zeolites, 1992, 12, 870–871 CrossRef CAS.
- C. R. A. Catlow, A. R. George and C. M. Freeman, Chem. Commun., 1996, 1311–1312, 10.1039/cc9960001311.
- R. E. Fletcher, S. Ling and B. Slater, Chem. Sci., 2017, 8, 7483–7491 RSC.
- L. Zhang, K. Chen, B. Chen, J. L. White and D. E. Resasco, J. Am. Chem. Soc., 2015, 137, 11810–11819 CrossRef CAS PubMed.
- C. S. Cundy and P. A. Cox, Microporous Mesoporous Mater., 2005, 82, 1–78 CrossRef CAS.
- R. M. Ravenelle, F. Schüβler, A. D'Amico, N. Danilina, J. A. van Bokhoven, J. A. Lercher, C. W. Jones and C. Sievers, J. Phys. Chem. C, 2010, 114, 19582–19595 CrossRef CAS.
- A. Vjunov, M. A. Derewinski, J. L. Fulton, D. M. Camaioni and J. A. Lercher, J. Am. Chem. Soc., 2015, 137, 10374–10382 CrossRef CAS PubMed.
- M.-C. Silaghi, C. Chizallet, E. Petracovschi, T. Kerber, J. Sauer and P. Raybaud, ACS Catal., 2014, 5, 11–15 CrossRef.
- M. Nielsen, R. Y. Brogaard, H. Falsig, P. Beato, O. Swang and S. Svelle, ACS Catal., 2015, 5, 7131–7139 CrossRef CAS.
- P. Eliášová, M. Opanasenko, P. S. Wheatley, M. Shamzhy, M. Mazur, P. Nachtigall, W. J. Roth, R. E. Morris and J. Čejka, Chem. Soc. Rev., 2015, 44, 7177–7206 RSC.
- W. J. Roth, P. Nachtigall, R. E. Morris, P. S. Wheatley, V. R. Seymour, S. E. M. Ashbrook, P. Chlubna, L. Grajciar, M. Polozij, A. Zukal, O. Shvets and J. Cejka, Nat. Chem., 2013, 5, 628–633 CrossRef CAS PubMed.
- X. Solans-Monfort, M. Sodupe, V. Branchadell, J. Sauer, R. Orlando and P. Ugliengo, J. Phys. Chem. B, 2005, 109, 3539–3545 CrossRef CAS PubMed.
- M. Krossner and J. Sauer, J. Phys. Chem., 1996, 100, 6199–6211 CrossRef CAS.
- H. Koller, G. Engelhardt and R. A. van Santen, Top. Catal., 1999, 9, 163–180 CrossRef CAS.
- Y. Jeanvoine, J. G. Ángyán, G. Kresse and J. Hafner, J. Phys. Chem. B, 1998, 102, 5573–5580 CrossRef CAS.
- V. Termath, F. Haase, J. Sauer, J. Hutter and M. Parrinello, J. Am. Chem. Soc., 1998, 120, 8512–8516 CrossRef CAS.
- K. Schwarz, E. Nusterer and P. E. Blöchl, Catal. Today, 1999, 50, 501–509 CrossRef CAS.
- M. V. Vener, X. Rozanska and J. Sauer, Phys. Chem. Chem. Phys., 2009, 11, 1702–1712 CAS.
- K. L. Joshi, G. Psofogiannakis, A. C. T. van Duin and S. Raman, Phys. Chem. Chem. Phys., 2014, 16, 18433–18441 RSC.
- K. De Wispelaere, B. Ensing, A. Ghysels, E. J. Meijer and V. Van Speybroeck, Chem.–Eur. J., 2015, 21, 9385–9396 CAS.
- M. Fischer, Phys. Chem. Chem. Phys., 2016, 18, 15738–15750 RSC.
- K. De Wispelaere, C. S. Wondergem, B. Ensing, K. Hemelsoet, E. J. Meijer, B. M. Weckhuysen, V. Van Speybroeck and J. Ruiz-Martínez, ACS Catal., 2016, 6, 1991–2002 CrossRef CAS.
- A. Vjunov, M. Wang, N. Govind, T. Huthwelker, H. Shi, D. Mei, J. L. Fulton and J. A. Lercher, Chem. Mater., 2017, 29, 9030–9042 CrossRef CAS.
- L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Chem. Soc. Rev., 2018, 47, 8307–8348 RSC.
- http://www.iza-structure.org/databases/, 2017.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. J. Gillan, D. Alfè and A. Michaelides, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- E. Borfecchia, P. Beato, S. Svelle, U. Olsbye, C. Lamberti and S. Bordiga, Chem. Soc. Rev., 2018, 47, 8097–8133 RSC.
- D. K. Pappas, E. Borfecchia, M. Dyballa, I. A. Pankin, K. A. Lomachenko, A. Martini, M. Signorile, S. Teketel, B. Arstad, G. Berlier, C. Lamberti, S. Bordiga, U. Olsbye, K. P. Lillerud, S. Svelle and P. Beato, J. Am. Chem. Soc., 2017, 139, 14961–14975 CrossRef CAS PubMed.
- M. H. Groothaert, P. J. Smeets, B. F. Sels, P. A. Jacobs and R. A. Schoonheydt, J. Am. Chem. Soc., 2005, 127, 1394–1395 CrossRef CAS PubMed.
- L. Grajciar, C. O. Areán, A. Pulido and P. Nachtigall, Phys. Chem. Chem. Phys., 2010, 12, 1497–1506 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc00725c |
| This journal is © The Royal Society of Chemistry 2019 |