Wearable solid-state capacitors based on two-dimensional material all-textile heterostructures

Abstract

Two-dimensional (2D) materials are a rapidly growing area of interest for wearable electronics, due to their flexible and unique electrical properties. All-textile-based wearable electronic components are key to enable future wearable electronics. Single component electrical elements have been demonstrated; however heterostructure-based assemblies, combining electrically conductive and dielectric textiles such as all-textile capacitors are currently missing. Here we demonstrate a superhydrophobic conducting fabric with a sheet resistance R_s ∼ 2.16 kΩ □⁻¹, and a pinhole-free dielectric fabric with a relative permittivity ε_r ∼ 2.35 enabled by graphene and hexagonal boron nitride inks, respectively. The different fabrics are then integrated to engineer the first example of an all-textile-based capacitive heterostructure with an effective capacitance C ∼ 26 pF cm⁻² and a flexibility of ∼1 cm bending radius. The capacitor sustains 20 cycles of repeated washing and more than 100 cycles of repeated bending. Finally, an AC low-pass filter with a cut-off frequency of ∼15 kHz is integrated by combining the conductive polyester and the capacitor. These results pave the way toward all-textile vertically integrated electronic devices.

---

1. Introduction

Wearable electronics require flexibility, durability, resistance to washing, comfortable sensation and lightweight components.^1–3 In recent years, electronic textiles, or fiber-based clothing systems have emerged as ideal platforms for future wearable electronics^4,5 because of their softness, breathability and biocompatibility, compared to other substrates, such as plastic, paper or elastomers.⁶ Electronic fabrics composed of these devices encompass conductors,⁷ resistors,⁸ capacitors,⁹ and transistors,¹⁰ and have been demonstrated using metals,¹¹ polymers¹² or carbon-based materials¹³ through various methods of textile integration, such as coating,¹⁴ deposition,¹⁵ spinning,¹⁶ printing,¹⁷ and chemical functionalization.¹⁸ However, the stability of conductive polymers to washing strongly affects the fabric performance. For instance, the work in ref. 19 showed that the resistances of conductive interconnections on textiles prepared with poly(3,4-ethylenedioxythiophene)–poly(styrenesulfonate) (PEDOT : PSS) increased by one order of magnitude after 15 washing cycles. On the other hand, the low biocompatibility of metallic fibre composites makes them hardly compatible with biological cells. In fact, metal nanoparticles used to fabricate textile electronics such as nickel,²⁰ silver²¹ and copper²² all have shown cytotoxicity. The work in ref. 22 proved that the survival of hepatocytes (i.e. liver cells) after exposure to Cu nanoparticles was no more than 60% as assessed by MTT (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) assay (which is a method to assess cell metabolic activity).²³ In addition, the hydrophobicitiy of fabrics are highly common in technical textiles and would play a significant role in protecting wearable electronics²⁴ and improve their washability, thus making them a requirement.

Graphene and other two-dimensional (2D) materials show outstanding thermal, electrical, optical and mechanical properties,²⁵ and they can be easily processed in solution²⁶ in large quantities^27,28 to produce printable inks^29,30 and thin films.³¹ The environmental-stability and biocompatibility of graphene inks^32,33 have recently sparked huge interest in the textile industry enabling environmentally friendly, bendable, and washable conductive fabrics³⁴ and polymers.³⁵ Examples of graphene-based conductive textiles^36,37 currently employ graphene oxide (GO) because of its oxygen functional groups such as epoxide (C–O–C), hydroxyl (–OH), and carboxyl (–COOH) groups,³⁶ providing strong affinity to cotton, wool and silk textiles, via hydrogen bonding. The GO fabric usually requires a chemical or thermal reduction step, to improve the conductivity, during the manufacturing process of the graphene fabric;^38,39 however high temperature and strong chemical reactions might damage the textile fibers.^40,41 Recently, a graphene-cotton strain sensor with a sheet resistance (R_s) as low as 500 Ω □⁻¹ has been demonstrated using a low-temperature (180 °C) reduced graphene oxide (RGO) coating via hot-press.³⁴ However, RGO still retained a more defective structure than the pristine graphene counterpart. In this regard, fabrics incorporating pristine graphene could offer a cheap and environment-friendly option for highly conducting and flexible textiles, while avoiding the reduction step.

The future development of wearable electronic textiles requires also indispensable components such as charge storage devices in the form of textiles, able to store electrical,^42,43 thermal,⁴⁴ and solar energy.⁴⁵ CNT/graphene hybrid textile electrodes and a filter paper separator are reported to operate as flexible and wearable electrochemical capacitors in an Na₂SO₄ electrolyte.⁴⁶ However, capacitors using aqueous electrolytes suffer from handling difficulties and the potential risk of leakage,⁴⁷ making them incompatible with wearable devices. Pristine graphene and hexagonal boron nitride (h-BN) inks produced by liquid-phase exfoliation (LPE) have enabled printed graphene/h-BN/graphene solid state capacitors on PET,⁴⁸ graphene/h-BN heterostructure FETs and integrated circuits on textiles.³⁰ Despite these advances, the combination of electrical textile components into an electronic textile heterostructure is still missing and it will be essential in advancing the functionality of wearable electronics.

Here we demonstrate conducting graphene/polyester and dielectric h-BN/polyester textiles by uniformly coated polyester fabrics with graphene and h-BN inks. The two functional textiles are then vertically stacked into an all-textile graphene/h-BN capacitor heterostructure achieving a capacitance of ∼26 pF cm⁻².

2. Results and discussion

2.1. Graphene and h-BN Inks

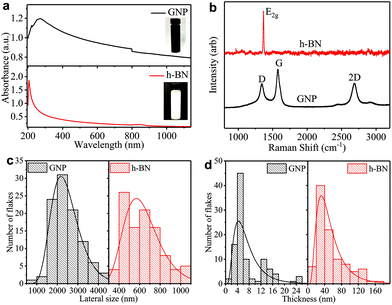
We prepare the graphene and h-BN inks by ultrasonication of graphene nanoplatelets (GNP) in ethanol and bulk h-BN flakes in deionized water, respectively (see ‘Methods’). We disperse the flakes in solvents with a low boiling point (<101 °C) to easily enable solvent removal at room temperature, hastening the throughput of the ‘dip and dry’ process. The concentrations of GNP (c_GNP) and h-BN (c_h-BN) flakes in the inks are estimated from the optical absorption spectra of GNP (black curve) and h-BN (red curve) inks in Fig. 1(a)via the Beer–Lambert law. Considering the absorption coefficients (at 660 nm) of GNP (2460 L g⁻¹ m⁻¹)²⁶ and h-BN (2350 L g⁻¹ m⁻¹)⁴⁹ with the respective dilution ratio, we obtain c_GNP ∼ 3.77 mg ml⁻¹ and c_h-BN ∼ 0.20 mg ml⁻¹.

Fig. 1 (a) The optical absorption spectra of the ethanol-based GNP ink (black curve) and water-based h-BN ink (red curve). (b) The Raman spectra of GNP (black curve) and h-BN (red curve) flakes acquired on a Si/SiO₂ substrate. The (c) lateral size and (d) thickness log-normal distribution of GNP and h-BN flakes from atomic force microscopy statistics.

We monitor the quality of GNP and h-BN flakes by Raman spectroscopy. Fig. 1(b) shows characteristic peaks of GNP at ∼1337, ∼1574 and ∼2687 cm⁻¹ (black curve), which correspond to the D, G, and 2D bands, respectively. While the G peak is always present in GNPs, originating from the E_2g phonon vibration mode, the D peak is activated by a defect.^50,51 However, we mainly attribute the origin of most of these defects to the edges of GNPs, rather than to defects in the basal plane.⁵² The 2D peak is the second order resonance of the G peak and no defects are required for its activation. For h-BN (red curve), a single peak appears at ∼1367 cm⁻¹ corresponding to E_2g phonon vibration mode.^53,54

The atomic force microscopy (AFM) statistics reveal the lateral size (S) and thicknesses (t) of GNP and h-BN flakes. Fig. 1c shows the distribution of the lateral size of GNP (black) and h-BN flakes (red), respectively. The log-normal fits (black and red curves) are peaked at ∼2189 nm and ∼567 nm, respectively. Fig. 1d shows plots of the thickness distribution of GNP (black) and h-BN (red) flakes, respectively. The log-normal fit shows peaks at ∼5 nm for GNP (black curve) and ∼31 nm for h-BN flakes (red curve), indicating the presence of single and multi-layer flakes with an average number of layers per flake of ∼12 for GNP, and ∼89 for h-BN, assuming an approximate 1 nm water layer⁵⁵ and an interlayer distance of 0.34 nm.

2.2. GNP/polyester and h-BN/polyester fabrics

The ‘dip and dry’ process is a one-step common approach to deposit functional materials on textiles by immersion in a solution followed by solvent removal. We prepare GNP/polyester and h-BN/polyester fabrics as follows. We use repeated ‘dip and dry’ processes (see ‘Methods’) of pristine polyester fabrics in GNP and h-BN inks, respectively, obtaining GNP textile (GNP/polyester) from the GNP ink and polyester, and h-BN textile (h-BN/polyester) from the h-BN ink and polyester. An additional hot-press (200 °C) step on the GNP/polyester is performed to enhance the adhesion between GNP and polyester, following the strategy proposed in ref. 56.

The preparation of both functional textiles is monitored and characterized by optical microscopy, SEM, electrical and contact angle measurements as follows. Fig. 2(a) shows the optical image of the white pristine polyester fabric, which is then coated with the GNP ink as shown in Fig. 2(b). Fig. 2(c) shows the SEM micrograph of the pristine polyester fabric organized in a compact woven textile with the fiber size ranging from 15 to 20 μm, while Fig. 2(d) shows the SEM micrograph of the GNP/polyester fabric coated with 10 repeated cycles of GNP by the ‘dip and dry’ process. The fabric surface is uniformly covered with the GNP deposited layer that both the weave structure and the gaps between the fibers can hardly be seen after the coating. Similar results have been reported in the work in ref. 14 for graphene flakes coated onto the polyester fabric by a similar ‘dip and dry’ method, and are attributed to the strong adhesion between graphene flakes and polyester via Van der Waals interactions between them, as well as between neighbouring graphene flakes.⁵⁷

Fig. 2 Optical microscopy of (a) the pristine polyester fabric and (b) the polyester fabric coated with the GNP ink. The SEM micrographs revealing the micromorphology of (c) the pristine polyester and (d) the GNP/polyester (after 10 cycles of ‘dip and dry’ GNP coating).

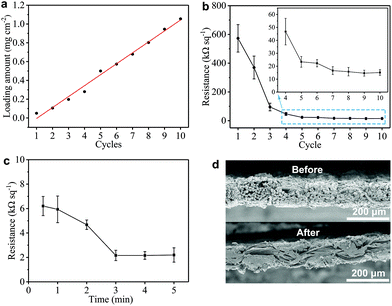
We also monitor the mass loading (m_GNP) of GNPs onto the GNP/polyester fabric as a function of ‘dip and dry’ process cycles shown in Fig. 3(a). Importantly, we notice that the m_GNP as a function of coating cycles increases almost linearly (where the red line shows the linear fit in Fig. 3(a)) over 10 cycles and eventually reaches ∼1 mg cm⁻².

Fig. 3 (a) The GNP loading as a function of ‘dip and dry’ cycles, where the red line shows the linear fit. Plots of the R_s of the GNP/polyester as a function of (b) ‘dip and dry’ cycles from 1 to 10 (the inset shows a zoom in the range of 4 to 10 cycles), and (c) a hot-press time across 5 min. (d) The comparison of cross-sectional SEM micrographs of the GNP/polyester before and after the hot-press step (200 °C, 4 min).

The electrical properties of the GNP/polyester fabric are then investigated by measuring R_s as a function of the ‘dip and dry’ cycles as shown in Fig. 3(b). The R_s decreases asymptotically reaching a stable value after 7 cycles, going from R_s ∼ 573 MΩ □⁻¹ after the 1st cycle (m_GNP ∼ 0.11 mg cm⁻²), to R_s ∼ 15.78 kΩ □⁻¹ after the 8th cycle (m_GNP ∼ 0.80 mg cm⁻²) and R_s ∼ 15.13 kΩ □⁻¹ after the 10th cycle (m_GNP ∼ 1.06 mg cm⁻²). We limit the coating cycle repetitions to 10 due to the negligible reduction in R_s beyond the 7th cycle (<3.9% from the 8th cycle to the 10th cycle).

Temperature annealing via a hot-press step has been shown to improve the adhesion of a graphene-based ink coating onto a fabric substrate.⁵⁶ We treat our GNP/polyester with a hot-press step (4 min at 200 °C) to promote the adhesion between graphene flakes and the polyester fabric. Considering the pristine polyester melting point between 205 to 260 °C, we select 200 °C as a suitable hot-press temperature that approaches the melting temperature to improve adhesion, but it stays below the melting temperature to avoid weakening the mechanical properties of the polyester fabric. Then we investigate the R_s of the GNP/polyester (m_GNP ∼ 1.06 mg cm⁻²) as a function of the hot-press time. Fig. 3(c) shows R_s decreasing from ∼6.21 kΩ □⁻¹ (after 30 s annealing), to ∼4.68 kΩ □⁻¹ (after 2 min annealing) before plateauing to ∼2.16 kΩ □⁻¹ (beyond 3 min annealing). The little increase in R_s from 3 min to 5 min of hot-press is irrelevant as the values fall within the error bars. Fig. 3(d) exhibits a comparison of the SEM cross-sectional micrographs of the GNP/polyester before and after the hot-press step (200 °C, 4 min), with an evident difference in the micromorphology of the fabric.

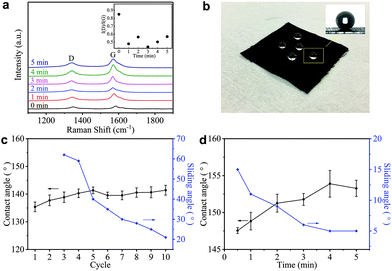
Such a difference in the micromorphology caused by the hot-press step has already been reported for pristine graphene/cotton⁵⁶ and GO/cotton fabrics.³⁴ This could certainly contribute towards improving the conductivity of our GNP/polyester as already demonstrated for graphene inks.⁵⁶ However, given the almost irrelevant R_s reduction in the first minute of heat-treatment, we tend to exclude a main role of the mechanical pressure as we rather attribute the R_s reduction to an improvement of the crystallinity of the GNP flakes. This is further supported by the Raman spectra (in the 1000–2000 cm⁻¹ region, Fig. 4(a)) of the GNP/polyester, as a function of the hot-press time. The inset shows the reduction in the ratio of the intensity of the D peak, I(D), over the intensity of the G peak, I(G), as a function of the hot-press time. I(D)/I(G) decreases from ∼0.85 before hot-press treatment to ∼0.5 between 1 and 5 min of hot-press time, suggesting a slight increase in the average size of the sp² domains and deoxygenation in the functional groups,²⁹ as shown for a GO/cotton fabric in our previous work.³⁴

Fig. 4 (a) The Raman spectra (in the 1000–2000 cm⁻¹ region) of the GNP/polyester as a function of the hot-press time. (b) The GNP/polyester (m_GNP ∼ 1.06 mg cm⁻²) hydrophobic property after the hot-press step (200 °C, 4 min). The CA (black curves) and SA (blue curves) as a function of (c) ‘dip and dry’ cycles from 1 to 10, and (d) the hot-press time.

Hydrophobicity is key to protect wearable electronics. Fig. 4(b) shows water droplets spherically assembled on the GNP/polyester after the hot-press step confirming water-resistant performance. To further investigate the hydrophobic properties of our fabric, we measure the contact angle (CA) and sliding angle (SA) of the GNP/polyester, before and after the hot-press step. Fig. 4(c) and (d) show the CA (black curve) and SA (blue curve) as a function of ‘dip and dry’ cycles and hot-press time, respectively. Before the hot-press step, the GNP/polyester (m_GNP ∼ 1.06 mg cm⁻²) shows a CA ∼ 141.41° and SA ∼ 21°, while the pristine polyester only shows a CA ∼ 80°. The hot-press step (4 min) causes it to reach a CA ∼ 153.28° and SA ∼ 5°, consistent with a superhydrophobic behavior (which is defined as a surface displaying a CA of water greater than 150° and an SA less than 10°),⁵⁸ which is generally formed by hydrophobic materials with rough micro/nanostructures.⁵⁹ It is worth noting that functional fabrics prepared by coating GO or RGO on textiles achieved a maximum CA of ∼143°⁶⁰ and ∼140°,⁶¹ respectively. Hence, the super-hydrophobic behaviour in our GNP/polyester fabric results from the lower amount of hydrophobic polar groups on hot-pressed GNPs with respect to RGO.

The h-BN/polyester was also prepared by repeated ‘dip and dry’ coating processes of the polyester fabric in the h-BN ink. The h-BN mass loading (m_h-BN) reaches 0.76 mg cm⁻² after 12 cycles, but can hardly be increased by further coating cycles. The thickness (t) of the h-BN/polyester is t ∼ 0.04 mm.

2.3. Flexible textile-based capacitor

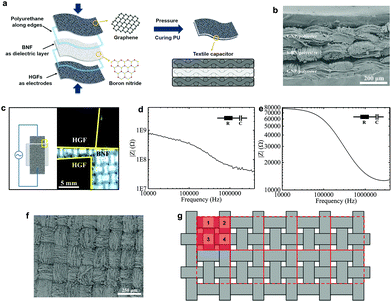
The flexible textile-based capacitor (FTC) is composed of the GNP/polyester (R_s ∼ 2.16 kΩ □⁻¹, CA ∼ 153.28°, SA ∼ 5°) and the h-BN/polyester (m_h-BN ∼ 0.76 mg cm⁻², t ∼ 0.04 mm) as electrodes and dielectric layer, respectively. We design the FTC by stacking these functional textiles to form a conductive/dielectric/conductive (CDC) sandwich-like heterostructure, resembling that of a typical parallel plate capacitor, following the schematic in Fig. 5(a). The CDC heterostructure is sealed at the edges with 0.1 mg of polyurethane (Puruikai Co. Ltd, China), to avoid disturbing the contact between fabrics. Then it is pressed mechanically using a manual hydraulic press (Specac, UK) at 5 kPa for 1 min at ambient temperature, to improve adhesion between the layers. Subsequently, we heat the CDC heterostructure at 70 °C for 1 h to anneal the polyurethane and create the FTC. Fig. 5(b) shows the cross-section images of the FTC heterostructure. The specific design of the FTC is described in Fig. 5(c), where the h-BN/polyester dielectric has a larger width (w ∼ 1.5 cm) than the GNP/polyester (w ∼ 1.0 cm), resulting in an area of the capacitor (A) of ∼1 cm² (1 cm × 1 cm).

Fig. 5 (a) The schematic of the textile-based capacitor integrating GNP/polyesters as electrodes and h-BN/polyesters as dielectrics. (b) The cross-sectional SEM micrograph of the FTC showing the functional textile heterostructure. (c) The layout of the FTC (left) showing h-BN/polyester and CMC/polyester optical images (right). Typical Bode plots obtained for the (d) FCC and (e) FTC, which follow an R–C series equivalent circuit model. (f) The top-view SEM micrograph of the GNP/polyester (m_GNP ∼ 0.69 mg cm⁻²) and (g) the diagram of the weave in the fabric with the repeating units in red.

We also consider the case where the pristine polyester and CMC present in the dielectric fabric may affect the capacitance. Hence, to quantify the effect of h-BN on the dielectric layer of the textile capacitor, we create a control capacitor (FCC) using the same GNP/polyester electrodes and a polyester dielectric fabric coated with CMC only in the same proportion used for the FTC, but excluding the h-BN flakes. Impedance spectroscopy (IS) is used to characterise the capacitance of FTC and FCC as it is most accurate at measuring capacitances in the pF range, typically not achievable by cyclic voltammetry (CV).³⁰ Bode plots of FTC and FCC are shown in Fig. 5(d) and (e), where the impedance amplitude (|Z|) as a function of frequency is measured with an impedance analyzer. Using an equivalent circuit model of a resistor and capacitor (R–C) in series, the impedance amplitude can be expressed as |Z| = (R² + (2π f C)⁻²)^0.5, where Z is the impedance, R is the series resistance, f is the frequency and C is the capacitance.⁴⁸ The capacitance per unit area of the FTC (C_FTC) is ∼26 pF cm⁻² while the FCC only shows a maximum capacitance (C_FCC) of ∼5 fF cm⁻², demonstrating that the charge storage contribution due to the CMC polymer is negligible, and C_FTC mainly originates from the presence of h-BN flakes.

We can estimate the approximate relative permittivity (ε_r) of the h-BN/polyester from the relationship formula: ε_r = C d (ε₀A_eff)⁻¹,⁴⁸ where d is the distance between two electrodes, ε₀ is the permittivity of the vacuum and A_eff is the effective area of the capacitor. However, the texture and roughness of the GNP/polyester and h-BN/polyester can make partial, full or no contact with each other in the FTC, thus affecting the A_eff. This is confirmed by the roughness of the weave observed on the surface of the GNP/polyester (m_GNP ∼ 0.69 mg cm⁻²) in Fig. 5(f) and the clear morphology of ‘hills’ and ‘valleys’ in the GNP/polyester and h-BN/polyester (see Fig. 5(b)) caused by the weave. To quantify this contribution on the final A_eff, we describe the woven structure of the textile as shown in Fig. 5(g). The whole fabric can be subdivided into many repeated units as red squares (the area of a single red square is marked as A₀), where four ‘hills’ (light red squares) exist in single repeated units and their areas are marked as A₁, A₂, A₃, and A₄, separately. We then define the contact ratio (CR) as (A₁ + A₂ + A₃ + A₄)/A₀, which results in a CR = 0 when A₁ + A₂ + A₃ + A₄ = 0 (i.e. no contact between the GNP/polyester and h-BN/polyester, giving A_eff = 0) and CR = 1 when A₁ + A₂ + A₃ + A₄ = A₀ (i.e. full contact between the GNP/polyester and h-BN/polyester is made, giving A_eff = A). We estimated a CR ∼ 0.5 by contrast analysis (see ‘Methods’) on SEM micrographs, acquired on the GNP/polyester and h-BN/polyester (Fig. 1S†) indicating an A_eff = 0.5 A. Using C ∼ 26 pF cm⁻², A ∼ 0.5 cm², ε₀ ∼ 8.854 × 10⁻¹² F m⁻¹ and d ∼ 0.04 mm as the values for our FTC, we obtain an approximate relative permittivity of ε_r ∼ 2.35 for the h-BN/polyester, which is in line with values reported previously for h-BN inks (i.e. ε_r ∼ 2–8)^30,48 and greater than the dielectric permittivity of polyester (ε_r ∼ 1.44).⁶²

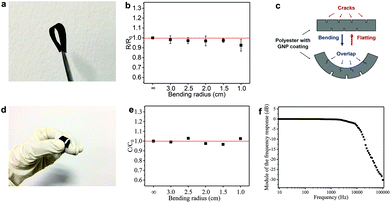
The flexibility (measured in terms of response to uniaxial bending) is an important performance metric for wearable electronics. The flexibility of the GNP/polyester electrodes and the FCT is tested by measuring R_s and C, respectively, as a function of different bending radii (using rods from 3.0 to 1.0 cm diameters). Fig. 6(a) shows a photograph of the GNP/polyester (m_GNP ∼ 1.06 mg cm⁻², after 4 min of hot-press) under 180° bending. Fig. 6(b) shows the R_s change (R/R₀), defined as the value of R_s (R) upon bending over the original value of R_s (R₀) as a function of the bending radius, where the ∞ corresponds to the GNP/polyester in its original flat state. We obtained R/R₀ ∼ 0.93 at a bending radius of 1.0 cm, demonstrating a negligible change in the R_s with bending, compared to recently reported R_s response to bending of an RGO-coated cotton fabric showing more than one order of magnitude at a bending radius of 2.5 cm.³⁴ This large change was attributed to the cracking and subsequent sliding and rearranging of the fractured islands of the RGO film under tension.³⁴ Here we attribute the small R_s change to the transition between cracks and overlaps³⁴ on the conductive coating of textile. As described in Fig. 6(c), there is a counterbalancing effect between the two sides of the fabric upon bending. The cracks on the compressed side of the GNP/polyester tend to be narrower and eventually overlap, resulting in a reduced R_s. On the other hand, the cracks on the side under tension would widen, thus resulting in an increase of R_s, which compensates the overall resistance keeping R_s unchanged.

Fig. 6 (a) The GNP/polyester upon 180° bending. (b) The R/R₀ of the GNP/polyester as a function of the bending radius. (c) The proposed mechanism resulting in a negligible R_s change in the GNP/polyester during bending. (d) The FTC upon bending. (e) The C/C₀ of the FTC as a function of the bending radius. (f) Bode plots of an all-textile AC low-pass R–C filter.

We also tested the flexibility of the FTC (C ∼ 17.83 pF cm⁻²), under the same bending conditions as above. Fig. 6(d) shows an image of the FTC while bending. The C change (C/C₀, defined as the value of C upon bending over the original value of C) of FTC is presented in Fig. 6(e) as a function of the bending radius. The estimated C/C₀ is less than 4% across different bending radii: ∼0.99 (radius ∼3.0 cm), ∼1.02 (radius ∼2.5 cm), ∼0.98 (radius ∼2.0 cm), ∼0.97 (radius ∼1.5 cm), and ∼1.03 (radius ∼1.0 cm). It is important to note that the C in our devices is acquired while bending, unlike previous reports where C acquisition is performed after bending.^63–65,66 The FTC in our work shows a consistent response under flexion, which is essential in textile electronics. We further investigate the stability of the FTC after repeated bending and washing cycles. The FTC (see ESI†) can sustain 20 cycles of repeated washing and more than 100 cycles of repeated bending.

In order to demonstrate the potential applications of the FTC, we designed an all-textile AC low-pass filter device. The R–C series filter is composed of an FTC (C ∼ 11.82 pF) and a GNP/polyester fabric engineered to match a resistance of 1.5 MΩ. The response versus frequency in decibels (Bode plot) of the filter (Fig. 6f) shows a typical curve of a low-pass filter with a cutoff frequency at ∼15 kHz, from the formula of f = (2πRC)⁻¹.⁶⁷

3. Methods

3.1. Formulation of GNP and h-BN inks

The graphene flakes (Cambridge Nanosystems, GR1) produced by cracking methane and carbon dioxide in a plasma torch is dispersed in ethanol via an ultrasonic bath (Fisherbrand FB15069, 800 W) for 3 h to create a GNP ink. The h-BN flakes are dispersed in deionized water via an ultrasonic bath for 24 h with carboxymethylcellulose sodium salt (CMC, average molecular weight MW = 700 000) (4 mg ml⁻¹) as a polymer stabilization agent.³⁰ Then the h-BN dispersion is centrifuged (Beckman Coulter Proteomelab XL-A, with a SW 32 Ti swinging bucket rotor) at 3000 rpm for 20 min, and the top 80% of the centrifuged dispersion is collected for further characterization.

3.2. Preparation of conductive and dielectric textiles

Commercial polyester fabrics (unit mass of 6.73 mg cm⁻²) are cleaned with deionized water to remove dust and contaminants, and are then dried. Subsequently, the cleaned polyester fabrics (size 1 cm × 2 cm) are immersed in the GNP ink with continuous stirring for 3 min, then transferred on glass slides and dried in an oven at 60 °C for 5 min to evaporate the ethanol solvent. The above process is defined as ‘dip and dry’ coating and can be repeated for several cycles to prepare the GNP/polyester with a higher concentration of GNP flakes. The fabrication of the h-BN/polyester is similar to that of the GNP/polyester, using 12 cycles of repeated ‘dip and dry’ processes with the h-BN ink (with 4 mg ml⁻¹ CMC). The hot-press step of the GNP/polyester is set at 200 °C on a Pixmax G3 SWING 38.

3.3. Characterization

The R_s of the GNP/polyester is tested using source measure unit (SMU) instruments (KEITHLEY 2400 SourceMeter, US) and a multimeter (Resistance Model ∼10 kΩ, 100 kΩ, Extech Instruments, US). The capacitances of the FTC and the FCC are estimated with Bode plots by using an impedance analyzer (Agilent 4294A Precision Impedance Analyzer). The CA and SA tests on GNP/polyesters are performed with a Drop Shape Analyzer 100 (KRÜSS GmbH, Germany), using deionized water droplets at ambient temperature in volumes of 5 μL and 10 μL, respectively. The weight of the textile is measured by using an automatic weighing machine (Sartorius Weighing Technology GmbH, Germany). The thickness of the h-BN/polyester is determined using a YG141 Fabric-Thickness Gauge (Ningfang Company, China). The bending tests on GNP/polyesters and FTCs are carried out by attaching them onto rods with bending radii of 1.0, 1.5, 2.0, 2.5, and 3.0 cm, while the repeated bending test is carried out on the FTC with a bending radius of 1.0 cm. The UV–vis absorption spectra of GNP and h-BN inks are measured on an Agilent Technologies Cary 7000 with a wavelength range from 200 nm to 1400 nm.⁶⁸ The flake concentration of the GNP ink and h-BN ink can be estimated via the Beer–Lambert law (A = αcl, where A is the absorbance, l is the light path length, c is the concentration of dispersed flakes, and α is the absorption coefficient). The GNP and h-BN inks are diluted 1 : 100 and 1 : 20 with ethanol and water/CMC, respectively. The Raman spectra used to monitor the quality of GNP and h-BN flakes are acquired using a Renishaw inVia Raman spectrometer (Renishaw PLC, UK) with a 514 nm laser. A Bruker Dimension Icon Atomic Force Microscope (AFM) in Peak Force Tapping mode is used to estimate the lateral size and thickness distribution of GNP and h-BN flakes, where the statistics are based on 100 individual flakes. The lateral size S of a flake is defined as S = (xy)^0.5, where x and y are the length and width of the flake. The average number of flake layers on the ink are calculated by assuming an approximately 1 nm water layer⁵⁵ and interlayer distances of 0.33 nm for GNP and 0.55 nm for h-BN flake. The scanning electron microscopy (SEM) images of the pristine polyester fabric and the GNP/polyester are characterized on a Sigma HD FE-SEM unit (FEI Magellan 400L XHR, US). The cross-section SEM images of the GNP/polyester before and after the hot-press step, and the FTC are characterized on a SU1510 SEM unit (Hitachi, Ltd, Japan). The optical images of the GNP/polyester and FTC are obtained using an Optiphot 300 (Nikon, Japan). The SEM images of the GNP/polyester (m_GNP ∼ 0.69 mg cm⁻²) are used to estimate the A₀, A₁, A₂, A₃, and A₄ of each repeated unit, where the CR of the capacitor is determined from the average value of (A₁ + A₂ + A₃ + A₄)/A₀ from 15 individual repeated units. In the washing test, a waterproof polyurethane-protective layer (WBM Seam Tapes) was hot pressed (PixMax Swing heat press) around the top and bottom of the FTC at 120 °C for 5 s in-line with the current industry standards to protect textile electronics. The sample was then placed inside a rotawash washing fastness tester (Skyline, SL-F09) to wash the sample for 20 cycles according to the international standard ISO105-C06:2010. ECE detergent with phosphate was used in test method A1S and was undertaken without steel balls.

4. Conclusions

In this work, we have reported a highly flexible, conductive, superhydrophobic polyester fabric (sheet resistance of ∼2.16 kΩ □⁻¹, contact angle of ∼153.28°, and sliding angle of ∼5°) and a flexible dielectric polyester fabric (approximate relative permittivity ∼2.35) by simple ‘dip and dry’ coating of graphene ink and h-BN ink, respectively. We use these functional fabrics to assemble the first all-textile flexible, washable capacitive heterostructure, demonstrating an effective capacitance of ∼26 pF cm⁻² and robust mechanical flexibility (down to a bending radius of 1 cm). An application of an AC low-pass filter is demonstrated by combining the graphene fabric and the capacitor heterostructure. Our results demonstrate the key role of 2D materials in the development of wearable electronics, and set the ground for new strategies for the integration of two-dimensional materials with fabrics to create unique e-textile devices.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors acknowledge the financial support of the EPSRC (grant EP/P02534X/1), National Natural Science Foundation of China (21174055), the Graduate Students Innovation Project of Jiangsu Province in China (SJLX16_0483), the National First-Class Discipline Program of Light Industry Technology and Engineering (LITE2018-21), the Trinity College, Cambridge, the Isaac Newton Trust, and the International Joint Research Laboratory for Advanced Functional Textile Materials.

Notes and references

1. M. Amjadi, K. U. Kyung, I. Park and M. Sitti, Adv. Funct. Mater., 2016, 26, 1678–1698.
2. F. Axisa, P. M. Schmitt, C. Gehin, G. Delhomme, E. McAdams and A. Dittmar, IEEE Trans. Inf. Technol. Biomed., 2005, 9, 325–336.
3. G. Zhou, F. Li and H.-M. Cheng, Energy Environ. Sci., 2014, 7, 1307–1338.
4. Y. Yang, Q. Huang, L. Niu, D. Wang, C. Yan, Y. She and Z. Zheng, Adv. Mater., 2017, 29.
5. W. Zeng, L. Shu, Q. Li, S. Chen, F. Wang and X. M. Tao, Adv. Mater., 2014, 26, 5310–5336.
6. M. Gao, L. Li and Y. Song, J. Mater. Chem. C, 2017, 5, 2971–2993.
7. H. Cheng, C. Hu, Y. Zhao and L. Qu, NPG Asia Mater., 2014, 6, e113.
8. J. Lilja and P. Salonen, Electron. Lett., 2011, 47, 602–604.
9. M. Stoppa and A. Chiolerio, Sensors, 2014, 14, 11957–11992.
10. M. Maccioni, E. Orgiu, P. Cosseddu, S. Locci and A. Bonfiglio, Appl. Phys. Lett., 2006, 89, 143515.
11. C.-H. Xue, J. Chen, W. Yin, S.-T. Jia and J.-Z. Ma, Appl. Surf. Sci., 2012, 258, 2468–2472.
12. C. Cochrane, V. Koncar, M. Lewandowski and C. Dufour, Sensors, 2007, 7, 473–492.
13. H. Lee, H. Kim, M. S. Cho, J. Choi and Y. Lee, Electrochim. Acta, 2011, 56, 7460–7466.
14. G. Yu, L. Hu, M. Vosgueritchian, H. Wang, X. Xie, J. R. McDonough, X. Cui, Y. Cui and Z. Bao, Nano Lett., 2011, 11, 2905–2911.
15. Y. Li, X. Cheng, M. Leung, J. Tsang, X. Tao and M. Yuen, Synth. Met., 2005, 155, 89–94.
16. Z. Dong, C. Jiang, H. Cheng, Y. Zhao, G. Shi, L. Jiang and L. Qu, Adv. Mater., 2012, 24, 1856–1861.
17. Y. Mao, M. Zhu, W. Wang and D. Yu, Soft Matter, 2018, 14, 1260–1269.
18. J. Cao and C. Wang, Appl. Surf. Sci., 2017, 405, 380–388.
19. M. Åkerfeldt, A. Lund and P. Walkenström, Text. Res. J., 2015, 85, 1789–1799.
20. R. Shukla, V. Bansal, M. Chaudhary, A. Basu, R. R. Bhonde and M. Sastry, Langmuir, 2005, 21, 10644–10654.
21. K. Soto, K. Garza and L. Murr, Acta Biomater., 2007, 3, 351–358.
22. T. Wang, X. Chen, X. Long, Z. Liu and S. Yan, PLoS One, 2016, 11, e0149484.
23. M. Ahamed, M. A. Siddiqui, M. J. Akhtar, I. Ahmad, A. B. Pant and H. A. Alhadlaq, Biochem. Biophys. Res. Commun., 2010, 396, 578–583.
24. S. Gorgutsa, K. Bachus, S. LaRochelle, R. D. Oleschuk and Y. Messaddeq, Smart Mater. Struct., 2016, 25, 115027.
25. K. Novoselov, Rev. Mod. Phys., 2011, 83, 837.
26. Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. McGovern, B. Holland, M. Byrne and Y. K. Gun'Ko, Nat. Nanotechnol., 2008, 3, 563.
27. K. R. Paton, E. Varrla, C. Backes, R. J. Smith, U. Khan, A. O'Neill, C. Boland, M. Lotya, O. M. Istrate and P. King, Nat. Mater., 2014, 13, 624.
28. P. G. Karagiannidis, S. A. Hodge, L. Lombardi, F. Tomarchio, N. Decorde, S. Milana, I. Goykhman, Y. Su, S. V. Mesite and D. N. Johnstone, ACS Nano, 2017, 11, 2742–2755.
29. F. Torrisi, T. Hasan, W. Wu, Z. Sun, A. Lombardo, T. S. Kulmala, G.-W. Hsieh, S. Jung, F. Bonaccorso and P. J. Paul, ACS Nano, 2012, 6, 2992–3006.
30. T. Carey, S. Cacovich, G. Divitini, J. Ren, A. Mansouri, J. M. Kim, C. Wang, C. Ducati, R. Sordan and F. Torrisi, Nat. Commun., 2017, 8, 1202.
31. D. Purdie, D. Popa, V. Wittwer, Z. Jiang, G. Bonacchini, F. Torrisi, S. Milana, E. Lidorikis and A. Ferrari, Appl. Phys. Lett., 2015, 106, 253101.
32. E. B. Secor, T. Z. Gao, A. E. Islam, R. Rao, S. G. Wallace, J. Zhu, K. W. Putz, B. Maruyama and M. C. Hersam, Chem. Mater., 2017, 29, 2332–2340.
33. D. McManus, S. Vranic, F. Withers, V. Sanchez-Romaguera, M. Macucci, H. Yang, R. Sorrentino, K. Parvez, S.-K. Son and G. Iannaccone, Nat. Nanotechnol., 2017, 12, 343.
34. J. Ren, C. Wang, X. Zhang, T. Carey, K. Chen, Y. Yin and F. Torrisi, Carbon, 2017, 111, 622–630.
35. F. Torrisi, D. Popa, S. Milana, Z. Jiang, T. Hasan, E. Lidorikis and A. C. Ferrari, Adv. Opt. Mater., 2016, 4, 1088–1097.
36. J. W. Jeon, S. Y. Cho, Y. J. Jeong, D. S. Shin, N. R. Kim, Y. S. Yun, H. T. Kim, S. B. Choi, W. G. Hong and H. J. Kim, Adv. Mater., 2017, 29.
37. R. Jalili, S. H. Aboutalebi, D. Esrafilzadeh, R. L. Shepherd, J. Chen, S. Aminorroaya-Yamini, K. Konstantinov, A. I. Minett, J. M. Razal and G. G. Wallace, Adv. Funct. Mater., 2013, 23, 5345–5354.
38. D. R. Dreyer, S. Park, C. W. Bielawski and R. S. Ruoff, Chem. Soc. Rev., 2010, 39, 228–240.
39. S. Pei and H.-M. Cheng, Carbon, 2012, 50, 3210–3228.
40. L. Cabrales and N. Abidi, J. Therm. Anal. Calorim., 2010, 102, 485–491.
41. H. Zhao, J. H. Kwak, Z. C. Zhang, H. M. Brown, B. W. Arey and J. E. Holladay, Carbohydr. Polym., 2007, 68, 235–241.
42. Y. Yang, Q. Huang, L. Niu, D. Wang, C. Yan, Y. She and Z. Zheng, Adv. Mater., 2017, 29, 1606679.
43. L. Bao and X. Li, Adv. Mater., 2012, 24, 3246.
44. A. Jamekhorshid, S. Sadrameli and M. Farid, Renewable Sustainable Energy Rev., 2014, 31, 531–542.
45. Y.-H. Lee, J.-S. Kim, J. Noh, I. Lee, H. J. Kim, S. Choi, J. Seo, S. Jeon, T.-S. Kim and J.-Y. Lee, Nano Lett., 2013, 13, 5753–5761.
46. H. Cheng, Z. Dong, C. Hu, Y. Zhao, Y. Hu, L. Qu, N. Chen and L. Dai, Nanoscale, 2013, 5, 3428–3434.
47. S. Yamazaki, A. Takegawa, Y. Kaneko, J.-I. Kadokawa, M. Yamagata and M. Ishikawa, Electrochem. Commun., 2009, 11, 68–70.
48. A. G. Kelly, D. Finn, A. Harvey, T. Hallam and J. N. Coleman, Appl. Phys. Lett., 2016, 109, 1400–3493.
49. J. Shen, Y. He, J. Wu, C. Gao, K. Keyshar, X. Zhang, Y. Yang, M. Ye, R. Vajtai and J. Lou, Nano Lett., 2015, 15, 5449–5454.
50. A. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 075414.
51. A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14095.
52. V. Bianchi, T. Carey, L. Viti, L. Li, E. H. Linfield, A. G. Davies, A. Tredicucci, D. Yoon, P. G. Karagiannidis and L. Lombardi, Nat. Commun., 2017, 8, 15763.
53. R. V. Gorbachev, I. Riaz, R. R. Nair, R. Jalil, L. Britnell, B. D. Belle, E. W. Hill, K. S. Novoselov, K. Watanabe and T. Taniguchi, Small, 2011, 7, 465–468.
54. S. Reich, A. Ferrari, R. Arenal, A. Loiseau, I. Bello and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205201.
55. A. G. Kelly, T. Hallam, C. Backes, A. Harvey, A. S. Esmaeily, I. Godwin, J. Coelho, V. Nicolosi, J. Lauth and A. Kulkarni, Science, 2017, 356, 69–73.
56. P. Cataldi, L. Ceseracciu, A. Athanassiou and I. S. Bayer, ACS Appl. Mater. Interfaces, 2017, 9, 13825–13830.
57. J. Zhao, W. Ren and H.-M. Cheng, J. Mater. Chem. A, 2012, 22, 20197–20202.
58. S. Qiang, K. Chen, Y. Yin and C. Wang, Mater. Des., 2017, 116, 395–402.
59. H. Wang, Y. Xue, J. Ding, L. Feng, X. Wang and T. Lin, Angew. Chem., Int. Ed., 2011, 50, 11433–11436.
60. N. D. Tissera, R. N. Wijesena, J. R. Perera, K. N. de Silva and G. A. Amaratunge, Appl. Surf. Sci., 2015, 324, 455–463.
61. K. Krishnamoorthy, U. Navaneethaiyer, R. Mohan, J. Lee and S.-J. Kim, Appl. Nanosci., 2012, 2, 119–126.
62. S. Sankaralingam and B. Gupta, IEEE Trans. Instrum. Meas., 2010, 59, 3122–3130.
63. G. Wang, H. Wang, X. Lu, Y. Ling, M. Yu, T. Zhai, Y. Tong and Y. Li, Adv. Mater., 2014, 26, 2676–2682.
64. X. Lu, Y. Zeng, M. Yu, T. Zhai, C. Liang, S. Xie, M. S. Balogun and Y. Tong, Adv. Mater., 2014, 26, 3148–3155.
65. A. Ramadoss, B. Saravanakumar and S. J. Kim, Nano Energy, 2015, 15, 587–597.
66. Q. Huang, L. Liu, D. Wang, J. Liu, Z. Huang and Z. Zheng, J. Mater. Chem. A, 2016, 4, 6802–6808.
67. R. Worsley, L. Pimpolari, D. McManus, N. Ge, R. Ionescu, J. A. Wittkopf, A. Alieva, G. Basso, M. Macucci and G. Iannaccone, ACS Nano, 2019, 13, 51–60.
68. D. G. Purdie, D. Popa, V. J. Wittwer, Z. Jiang, G. Bonacchini, F. Torrisi, S. Milana, E. Lidorikis and A. C. Ferrari, Appl. Phys. Lett., 2015, 25, 253101.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr00463g

---