Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mono- and dinuclear Ni(I) products formed upon bromide abstraction from the Ni(I) ring-expanded NHC complex [Ni(6-Mes)(PPh3)Br]†
William J. M.
Blackaby
a,
Sara
Sabater
 a,
Rebecca C.
Poulten
a,
Michael J.
Page
a,
Andrea
Folli
a,
Rebecca C.
Poulten
a,
Michael J.
Page
a,
Andrea
Folli
 *b,
Vera
Krewald
*b,
Vera
Krewald
 *a,
Mary F.
Mahon
*a,
Damien M.
Murphy
*a,
Mary F.
Mahon
*a,
Damien M.
Murphy
 b,
Emma
Richards
b,
Emma
Richards
 *b and
Michael K.
Whittlesey
*b and
Michael K.
Whittlesey
 *a
*a
aDepartment of Chemistry, University of Bath, Claverton Down, Bath BA2 7AY, UK. E-mail: m.f.mahon@bath.ac.uk; v.krewald@bath.ac.uk; m.k.whittlesey@bath.ac.uk
bSchool of Chemistry, Cardiff University, Park Place, Cardiff CF10 3AT, UK. E-mail: FolliA@cardiff.ac.uk; RichardsE10@cardiff.ac.uk
First published on 5th December 2017
Abstract
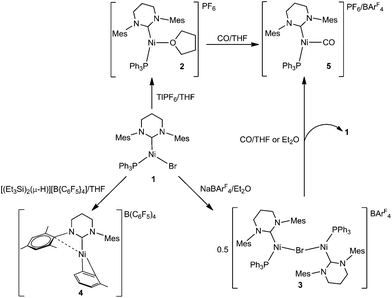
Bromide abstraction from the three-coordinate Ni(I) ring-expanded N-heterocyclic carbene complex [Ni(6-Mes)(PPh3)Br] (1; 6-Mes = 1,3-bis(2,4,6-trimethylphenyl)-3,4,5,6-tetrahydropyrimidin-2-ylidene) with TlPF6 in THF yields the T-shaped cationic solvent complex, [Ni(6-Mes)(PPh3)(THF)][PF6] (2), whereas treatment with NaBArF4 in Et2O affords the dimeric Ni(I) product, [{Ni(6-Mes)(PPh3)}2(μ-Br)][BArF4] (3). Both 2 and 3 act as latent sources of the cation [Ni(6-Mes)(PPh3)]+, which can be trapped by CO to give [Ni(6-Mes)(PPh3)(CO)]+ (5). Addition of [(Et3Si)2(μ-H)][B(C6F5)4] to 1 followed by work up in toluene results in the elimination of phosphine as well as halide to afford a co-crystallised mixture of [Ni(6-Mes)(η2-C6H5Me)][B(C6F5)4] (4), and [6MesH⋯C6H5Me][B(C6F5)4]. Treatment of 1 with sodium salts of more strongly coordinating anions leads to substitution products. Thus, NaBH4 yields the neutral, diamagnetic dimer [{Ni(6-Mes)}2(BH4)2] (6), whereas NaBH3(CN) gives the paramagnetic monomeric cyanotrihydroborate complex [Ni(6-Mes)(PPh3)(NCBH3)] (7). Treatment of 1 with NaOtBu/NHPh2 affords the three-coordinate Ni(I) amido species, [Ni(6-Mes)(PPh3)(NPh2)] (8). The electronic structures of 2, 5, 7 and 8 have been analysed in comparison to that of previously reported 1 using a combination of EPR spectroscopy and density functional theory.
Introduction
In a very recent review, Lin and Power referred to Ni(I) as a ‘… “rare” oxidation state of growing importance’.1,2 In terms of monodentate ligands, the early dependence on tertiary phosphines to stabilise Ni(I)3,4 has largely been superseded by the use of N-heterocyclic carbenes (NHCs) and these have facilitated the isolation of a wide range of fully characterised four-, three- and even two-coordinate Ni(I) species.5,6Over the last few years, we have used so-called ring-expanded NHCs (RE-NHCs; carbenes with ring sizes >5) for the preparation of three- and two-coordinate Ni(I) complexes with interesting stoichiometric7 and catalytic chemistry,8 as well as novel magnetic properties.9 In all cases, the starting point for our chemistry has been the three-coordinate species [Ni(RE-NHC)(PPh3)Br].10 The first of these to be prepared, [Ni(6-Mes)(PPh3)Br] (1, Scheme 1),8 has continued to be the focus of much of our attention as it tends to yield readily isolable products.
Herein, we describe the stoichiometric reactivity of 1 with a range of bromide abstracting agents to afford seven new Ni(I) complexes. Five of these are monomeric (cationic as well as neutral) and their adoption of T- or Y-shaped structures has been probed using DFT calculations.
Results and discussion
Bromide abstraction from 1 by [Tl]+, NaBArF4 and [(Et3Si)2(μ-H)][B(C6F5)4]
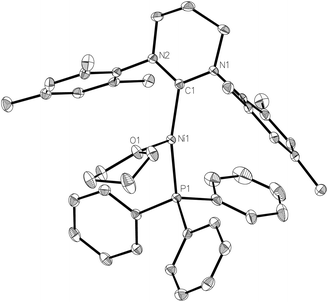
We have previously shown that the addition of free 6-Mes to 1 results in transfer of the bromide ligand to the outer-sphere to give the two-coordinate, cationic product [Ni(6-Mes)2]Br.9 Initial efforts to abstract bromide from 1 with more typical halide abstractors such as AgX reagents (X = BF4, NO3, OTf) yielded only mixtures of products containing the pyrimidinium salt [6-MesH]X and the plating out of what appeared to be metallic nickel. However, when 1 was treated with TlPF6 in THF, the three-coordinate cationic THF complex [Ni(6-Mes)(PPh3)(THF)][PF6] (2) was isolated as a pale yellow solid in 85% yield (Scheme 1).The X-ray crystal structure of 2 (Fig. 1) revealed a distorted T-shaped geometry at the Ni(I) centre, with C–Ni–P and C–Ni–O angles of 156.58(4)° and 103.74(4)° respectively. In contrast to the precursor complex 1, the Ni–C6-Mes bond length was slightly elongated (1.9601(12) Å cf. 1.942(2) Å), although the Ni–P bond was unchanged. The Ni–O distance of 2.0603(9) Å was intermediate between those reported for the neutral β-diketiminato species [LRNi(THF)] (LR = [HC(C(tBu)NC6H3(iPr)2)2]−, 2.000(1) Å)11–13 and the cationic, bis-THF complex [(THF)2Ni(CNArMes2)3][OTf] (ArMes2 = 2,6-(2,4,6-Me3C6H2)2C6H3; 2.174(2) Å, 2.1935(19) Å).14
The 1H NMR spectrum of 2 displayed a series of broad resonances between ca. δ 17–0 which could not be integrated. As the signals for the bound THF could not be assigned, we were unable to establish spectroscopically the lability of the THF ligand. However, X-ray crystallography repeatedly revealed the presence of THF following recrystallization of 2 from a number of solvents (CH2Cl2, C6H5F, C6H6) suggesting that the THF cannot be easily dissociated from the nickel.
The formation of TlBr as a side-product in the synthesis of 2 proved problematic, as even following multiple recrystallisations, complete removal was not always achievable. This manifested itself in EPR spectra of 2 (ESI†), but more obviously in reactions with CO (vide infra). Fig. 2 shows the EPR spectrum of a ‘clean’ sample of complex 2 (Fig. 2d). The spin Hamiltonian parameters of the EPR spectra of all of the species shown in Fig. 2 are listed in Table 1, and are discussed further below.
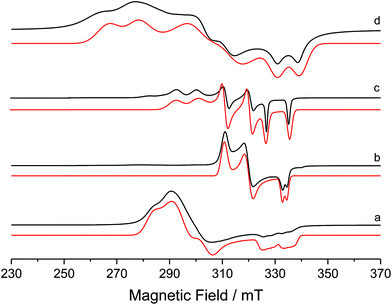 | ||
| Fig. 2 Experimental (black) and simulated (red) X-band CW EPR spectra of (a) 1, (b) 5, (c) 8 and (d) 2 in frozen THF solution at 140 K. | ||
| g values | Euler angles/rad | A values/MHz | Euler angles/rad | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| g 1 | g 2 | g 3 | g iso | α | β | γ | A 1 | A 2 | A 3 | a iso | α | β | γ | |
| [Ni(6-Mes)(PPh3)Br] 1 | ||||||||||||||
| Expt | 2.050 | 2.265 | 2.365 | 2.227 | −2.270 | 2.619 | 1.643 | 184 | 194 | 250 | 209 | 0.035 | 1.580 | 1.936 |
| −6# | −27# | 70# | 12# | 1.580# | 1.566# | −1.328# | ||||||||
| DFT | 2.055 | 2.252 | 2.285 | 2.197 | −2.276 | 2.246 | 1.628 | 173 | 173 | 204 | 183 | 0.176 | 1.590 | 1.968 |
| −19# | −21# | 51# | 4# | 0.093# | 1.578# | 1.859# | ||||||||
| [Ni(6-Mes)(PPh3)(THF)][PF6] 2 | ||||||||||||||
| Expt | 2.025 | 2.210 | 2.490 | 2.242 | 1.497 | 2.540 | 1.458 | 292 | 210 | 419 | 307 | 0.646 | 2.969 | −0.474 |
| DFT | 2.013 | 2.315 | 2.389 | 2.239 | −1.580 | 1.203 | 1.622 | −7 | −15 | −19 | −14 | 1.700 | 1.635 | −0.436 |
| [Ni(6-Mes)(PPh3)(CO)][PF6] 5 | ||||||||||||||
| Expt | 2.035 | 2.121 | 2.185 | 2.114 | −3.114 | 3.064 | −1.605 | 21 | 29 | 48 | 33 | 1.738 | 1.560 | 1.287 |
| DFT | 2.044 | 2.117 | 2.155 | 2.105 | 3.100 | 3.051 | −1.654 | 14 | 24 | 42 | 26 | 1.728 | 1.558 | 1.235 |
| [Ni(6-Mes)(PPh3)(NCBH3)] 7 | ||||||||||||||
| Expt | 2.028 | 2.225 | 2.373 | 2.209 | 1.176 | 2.554 | −1.575 | 260 | 300 | 260 | 273 | −0.815 | 1.427 | 1.780 |
| DFT | 2.020 | 2.286 | 2.303 | 2.203 | −1.950 | 1.051 | 1.568 | 185 | 187 | 220 | 197 | −0.865 | 1.423 | 1.778 |
| [Ni(6-Mes)(PPh3)(NPh2)] 8 | ||||||||||||||
| Expt | 2.050 | 2.150 | 2.290 | 2.163 | −1.459 | 0.209 | 0.877 | 230 | 265 | 300 | 265 | 1.621 | 1.602 | −1.216 |
| DFT | 2.059 | 2.162 | 2.238 | 2.152 | −1.513 | 0.227 | 0.930 | 248 | 249 | 280 | 259 | 1.554 | 1.610 | −1.190 |
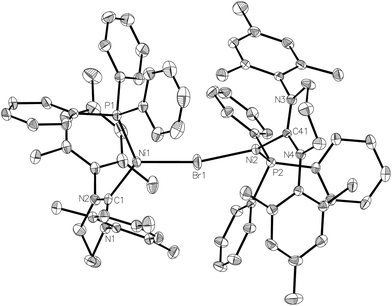
In an attempt to circumvent the problem of TlBr contamination, 1 was reacted instead with NaBArF4 in THF. No bromide abstraction resulted. However, a reaction between 1 and NaBArF4 took place upon changing the solvent to Et2O, affording large orange crystals. These proved to be of the unusual cationic, mono-bromide bridged dimer, [{Ni(6-Mes)(PPh3)}2(μ-Br)][BArF4] (3, Scheme 1) rather than 2. The structure of 3 (Fig. 3) comprised of two {Ni(6-Mes)(PPh3)} fragments and a close to symmetrically Ni bound μ-bromide ligand (Ni1–Br1 2.3803(6) Å, Ni2–Br1 2.3688(6) Å) in an arrangement distorted from linearity (∠Ni1–Br1–Ni2 167.64(3)°). This is adopted presumably to minimise the steric demands of the ligand substituents in the solid-state. Unsurprisingly, these steric demands also preclude the ligands from eclipsing each other relative to the Ni⋯Ni axis. Thus, there is 46.8(1)° angle between the mean planes containing atoms Br1, Ni1, P1, C1 and Br1, Ni2, P2, C41, respectively. The Ni⋯Ni separation exceeds 4.7 Å.
3 exhibited a paramagnetic NMR spectrum in Et2O solution, as well as a room temperature magnetic moment (μeff, Evans method) of 2.51 μB, consistent with the presence two Ni(I) centres.15 Density functional theory (DFT) calculations based on the crystal structure coordinates with optimised hydrogen atom positions afforded Mulliken spin populations of 0.78 at each Ni centre, thus correctly representing the formal Ni(I) oxidation states. Broken-symmetry DFT predicted antiferromagnetic coupling between the two nickel centres, with a medium strength negative exchange coupling constant (density functional dependent: TPSSh: −97.6 cm−1, B3LYP: −76.1 cm−1, PBE0: −64.3 cm−1, M06: −69.3 cm−1). This coupling appears weak enough to allow significant population of the high-spin state at room temperature: indeed, a Boltzmann population distribution analysis showed that ca. 40% of the triplet state would be populated at 300 K (ESI†).
EPR spectroscopy revealed that, at least in diethyl ether solution,16 the two Ni(I) centres were [Ni(6-Mes)(PPh3)Br] (1) and (solvated) [Ni(6-Mes)(PPh3)]+. Thus, the CW EPR spectrum (140 K, frozen Et2O glass; ESI†) clearly contained signal intensity from 1, as well as a second Ni(I) centre. The similar profile of this second species to that of 2 suggests it is the diethyl ether complex, [Ni(6-Mes)(PPh3)(OEt2)]+. Dissociation of 3 was also supported by the appearance of [Ni(6-Mes)(PPh3)(CO)][BArF4] (5-BArF4, vide infra) by IR spectroscopy following treatment of the dimer with CO in Et2O solution.
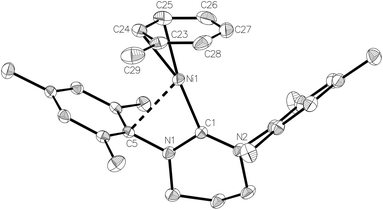
Treatment of 1 with an equimolar amount of [(Et3Si)2(μ-H)][B(C6F5)4]17 in fluorobenzene resulted in an instantaneous colour change from yellow to red. Upon layering with toluene, light green crystals formed, which consisted of a co-crystallised mixture of the Ni(I) toluene salt, [Ni(6-Mes)(η2-C6H5Me)][B(C6F5)4] (4), and [(6-MesH)⋯C6H5Me][B(C6F5)4].
The X-ray structure of the metal-containing cation is shown in Fig. 4. The metrics of the coordinated toluene ligand revealed short Ni–C24/C25 distances (2.054(3) Å and 2.092(3) Å), intermediate Ni–C23/C26 distances (2.152(3) Å, 2.202(3) Å) and two substantially longer interactions (Ni–C27 2.271(3) Å, Ni–C28 2.241(3) Å), consistent with an η2 rather than η6 bound arene ligand.5m,18 To overcome electron deficiency, this then formally 13-electron nickel centre exhibits a close interaction with the ipso-C of one of the mesityl rings (Ni–C5 2.525(2) Å; cf. Ni–C14 3.367(2) Å). Comparable stabilising close contacts have been seen in other coordinatively unsaturated metal complexes bearing bulky NHCs.19
Further analysis revealed that the toluene ligand lies almost parallel to one of the fluoroaryl ligands of the [B(C6F5)4]− anion. A value of 9.9° for the angle between the relevant least-squares aromatic ring planes, 3.78 Å for the centroid–centroid distance between these rings and 3.27 Å for the shortest distance from the centroid of one ring to the mean plane of the other support the presence of offset π–π stacking and additional π-stabilisation of the complex.
The ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) toluene stabilised pyrimidinium cation varied from one synthesis to another. The ‘best’ ratio, determined crystallographically, in terms of optimising the percentage of nickel complex yielded, was 65
toluene stabilised pyrimidinium cation varied from one synthesis to another. The ‘best’ ratio, determined crystallographically, in terms of optimising the percentage of nickel complex yielded, was 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35. This was achieved by (i) performing the complete reaction in a glovebox and (ii) washing the [(Et3Si)2(μ-H)][B(C6F5)4] five times with hexane and drying overnight. Although the irreproducibility in yield of 4 frustrated efforts to further characterise the complex, the synthetic approach was validated by isolation of the corresponding mesitylene analogue [Ni(6-Mes)(η2-C6H3Me3)][B(C6F5)4] (ESI†) through reaction of 1 with [(Et3Si)2(μ-H)][B(C6F5)4] in C6H5F, followed by crystallisation from C6H5F/mesitylene. Again co-crystallisation with pyrimidinium salt ([(6-MesH)⋯C6H3Me3][B(C6F5)4]) was found.
35. This was achieved by (i) performing the complete reaction in a glovebox and (ii) washing the [(Et3Si)2(μ-H)][B(C6F5)4] five times with hexane and drying overnight. Although the irreproducibility in yield of 4 frustrated efforts to further characterise the complex, the synthetic approach was validated by isolation of the corresponding mesitylene analogue [Ni(6-Mes)(η2-C6H3Me3)][B(C6F5)4] (ESI†) through reaction of 1 with [(Et3Si)2(μ-H)][B(C6F5)4] in C6H5F, followed by crystallisation from C6H5F/mesitylene. Again co-crystallisation with pyrimidinium salt ([(6-MesH)⋯C6H3Me3][B(C6F5)4]) was found.
Synthesis and characterisation of [Ni(6-Mes)(PPh3)(CO)]+
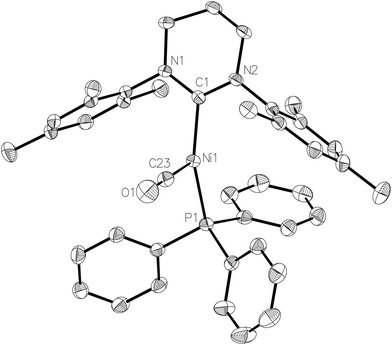
Exposure of a THF solution of 2 to 1 atm CO led to an almost instantaneous colour change from yellow to pale green. Removal of the CO atmosphere after ca. 1 min, followed by recrystallization of the residue from THF/hexane gave light green/yellow crystals of the Ni(I) carbonyl complex, [Ni(6-Mes)(PPh3)(CO)][PF6] (5-[PF6]). The EPR spectrum of 5-[PF6] (Fig. 2b) and the corresponding DFT calculations of the spin Hamiltonian parameters is discussed in further detail below.The X-ray crystal structure (Fig. 5) revealed a similarly distorted T-shaped geometry to that of 2 (∠C–Ni–P = 151.93(9)°). Both the Ni–CO bond length (Ni1–C23 = 1.787(3) Å) as well as the ν(CO) in the IR spectrum (2032 cm−1) showed good agreement with the few other (predominantly neutral) reported Ni(I)–CO complexes.20–23 As expected, 5-[PF6] displayed broad, paramagnetic 1H and 13C NMR spectra, although upon subjecting a THF solution to 1 atm 13CO, we observed the rapid appearance of an isotopically enhanced carbonyl resonance in the 13C NMR spectrum at δ 198.1, consistent with reversible coordination of the carbonyl ligand.22 Since the SOMO is an orbital with antibonding character between the Ni centre and the CO ligand, one would expect a weakened Ni–CO bond, and it may be this that facilitates the facile exchange with 13CO.22,23
As aforementioned, the presence of residual TlBr in samples of 2 was apparent from reactions with CO, particularly after prolonged periods. At times >1 min, the initial pale green solution of 5-[PF6] became orange, and then over ca. 48 h, yellow. A small number of crystals were isolated from this yellow solution and structurally characterised as the Ni(II) salt, [Ni(6-Mes)(PPh3)(CO)Br][PF6] (ESI†).
Reactions of 1 with NaBH3X (X = H, CN) and NaNPh2
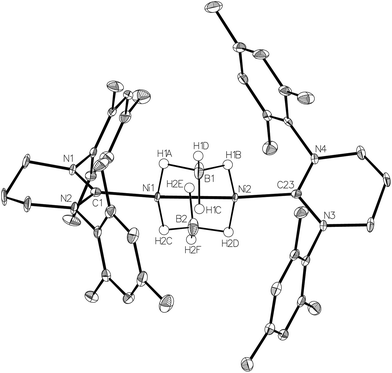
Efforts to abstract the bromide ligand from 1 using sodium salts of more coordinating anions generated the Ni(I) products 6–8 shown in Scheme 2.NaBH4 addition to a yellow THF suspension of 1 in the presence of EtOH rapidly generated a green solution, from which dark green crystals of the dimeric borohydride complex, [{Ni(6-Mes)}2(μ-BH4)2] (6) were isolated in 90% yield. The X-ray crystal structure of 6 is shown in Fig. 6 and revealed asymmetry across the {Ni2B2} moiety. Thus, B1 is closer to Ni2 than to Ni1, and the reverse situation prevails for B2 (Ni1⋯B1 2.180(2), Ni1⋯B2 2.143(3), Ni2⋯B1 2.144(2), Ni2⋯B2 2.181(3) Å). Overall, the data suggest a rare μ2,η1:η1 coordination mode24,25 for the borohydride based on B1, with H1C being equidistant from both metal centres (Ni1–H1C 2.16(4) Å; Ni2–H1C 2.11(4) Å). The B2 based borohydride has a similar coordination mode once experimental errors are taken into consideration. However, H2E may be closer to Ni1 (1.92(4) Å) than to Ni2 (2.12(4) Å), which would indicate a tendency towards an even more unusual μ2,η2:η1 coordination mode.25 In an effort to further probe the bonding of the borohydrides, a neutron dataset was collected, but a phase transition hampered acquisition of any additional insights (see Experimental). IR spectroscopy provided little in the way of diagnostic characterisation of any particular coordination mode, as only a single, broad ν(B–H) absorption band was measured at 2378 cm−1 in KBr.
6 adds to the surprisingly few examples of structurally characterised nickel borohydride complexes,26–28 in amongst which there is just a single example of a bridging borohydride species29 and a Ni(I)–BH4 complex.27,30
The 2.4218(4) Å separation of the two Ni centres is suggestive of a Ni–Ni bond,1 which explains the diamagnetism of the complex in solution.31 The borohydride groups appear fluxional, with just a single broad resonance apparent in both the 1H (ca. δ −5.1) and 11B{1H} (ca. δ −30) NMR spectra. The proton signal sharpened slightly with 11B decoupling, but remained broad even down to 198 K.
NaBH4 was replaced by NaBH3(CN) in an effort to prepare a Ni–Ni dimer analogous to 6 but with an asymmetric and potentially simpler coordination mode. Instead, the paramagnetic, monomeric Ni(I) complex, [Ni(6-Mes)(PPh3)(NCBH3)] (7, Fig. 7) was formed. Cyanotrihydroborate complexes remain (like their [BH4]− counterparts) extremely rare for nickel,32 and unknown for Ni(I). Trigonal planar 7 exhibited a Ni–N bond length of 1.924(2) Å which, although shorter than that reported in [(tren)Ni(μ-NCBH3)]22+ (tren = 2,2′,2′′-triaminoethylamine),32a is consistent with values reported for a number of monomeric cobalt derivatives.33 The EPR spectrum of 7 (see ESI†) confirms the paramagnetism of this complex, but is again poorly resolved due to overlapping intensity originating from the precursor complex 1.
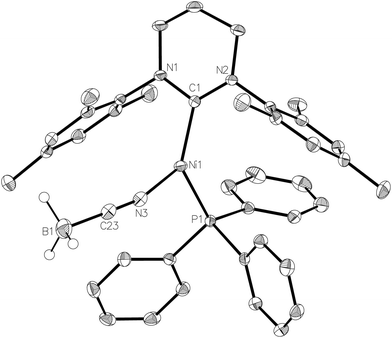
We have previously reported that 1 reacts with NaOtBu to provide a low yielding route to the Ni(0) product, [Ni(6-Mes)(PPh3)2].34 A repeat of this reaction in the presence of diphenylamine35 afforded the three-coordinate Ni(I) amido complex, [Ni(6-Mes)(PPh3)(NPh2)] (8), as a deep-red solid that could be isolated in high (72%) yield.
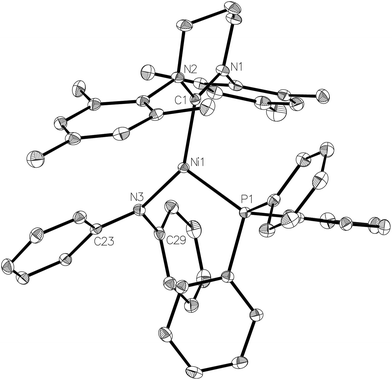
The X-ray crystal structure of the complex (Fig. 8) revealed a more acute C–Ni–P angle (109.25(4)°) than that found in the starting bromide complex (117.01(6)°), which most likely results from the need to alleviate steric clashes between the P- and N-bound phenyl groups. Indeed, replacing the phenyl groups with methyl groups in silico and fully relaxing the geometry showed that steric effects play a role in shaping the geometry of 8: in the case of the (hypothetical) [Ni(6-Mes)(PPh3)(NMe2)] complex 8-Me with a less bulky NMe2 ligand, the C–Ni–N angle decreased by 6.7° while the P–Ni–C angle increased by 6.5°. Concomitantly, the Ni–N bond decreased from 1.94 Å in the crystal structure to 1.84 Å in 8-Me (fully relaxing the crystal structure of 8 results in a bond length of 1.90 Å). Sterics may also account for the non-planarity of the amido group (dihedral angle between Ni1, N3, C23 and C29 of ca. 160°), as well as the elongation of the Ni–N distance (1.9350(12) Å) compared to those in either [Ni(dtbpe){N(2,6-iPr2C6H3)H}] (1.881(2) Å; dtbpe = tBu2P(CH2)2PtBu2)36 or [Ni(PPh3)2{N(SiMe3)2}] (1.88(1) Å).4,37
Electronic structure analysis of complexes 1, 2, 5, 7 and 8
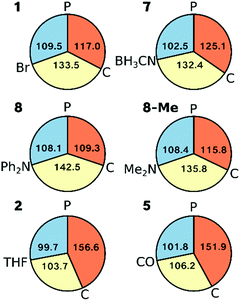
Inspection of the angles around Ni in complexes 1, 2, 5, 7 and 8 (as well as 8-Me) shows that the L–Ni–P angle varies least across all complexes (<10°, Fig. 9). Complexes 1 and 7 can be classed as Y-shaped (∠C–Ni–L, ∠P–Ni–C > ∠L–Ni–P, Fig. 9), whereas complexes 2 and 5 are T-shaped (∠P–Ni–C > ∠C–Ni–L, ∠L–Ni–P angles, see Fig. 9). Complex 8 represents a more symmetric Y-shaped case with a larger C–Ni–L angle than in 1 and 7 (142.5° vs. 133.5°, 132.4°) and a smaller P–Ni–C angle (109.2° vs. 117.0°, 125.1°). Although one may also view complex 8 as a T-shaped complex with ∠C–Ni–L as the largest angle, this appears to be purely due to steric and not electronic effects, as is seen by 8-Me adopting a more Y-shaped geometry.The overall geometric changes in fully relaxing the crystal structures are small (see ESI†). Most importantly, the striking consistency of the Ni–P and Ni–C bond lengths in the crystal structures across the series (variation <0.03 Å and <0.02 Å, respectively) is preserved upon geometry optimisation (variation <0.03 Å and <0.04 Å, respectively: ESI†).
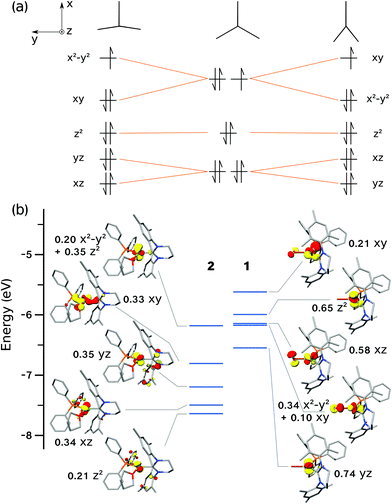
The tendency of three-coordinate transition metal d9 complexes to form either T- or Y-shaped geometries is due to the Jahn–Teller effect, thus lifting orbital degeneracy (dxy, dx2−y2) at the ideal D3h symmetry (Fig. 10a). MO theory predicts that the SOMO in a T-shaped d9 complex will be of dx2−y2 character, whereas in a Y-shaped d9 complex, it will be of dxy character (Fig. 10a), in agreement with the dominant character of the DFT-calculated orbitals (Fig. 10b). For Ni(I) complexes, this was most recently discussed by the groups of Holland and Lee,13,21 and prior to that, by Pietrzyk.38 Holland and co-workers21 rationalised the formation of T- vs. Y-shaped complexes with a charge donation analysis (natural bond orbital analysis).39 Their findings indicated that a T-shape is inherently favoured by d9 complexes, but a Y-shape can result when there is increased donation of charge from the ligands to the metal centre, thus effectively partially reducing the metal centre. In the present case, the analysis of Mulliken40 and Chelpg41 charges did not reveal a clear connection between charges and geometry. Likewise, the Mulliken spin populations on the Ni ion do not show a significant variation across the series (ESI†).
The CW X-band EPR spectra of complexes 1, 2, 5 and 8 were shown in Fig. 2. The resulting spin Hamiltonian parameters, notably the g-tensor and A(31P)-tensor components were extracted by simulation, and are listed in Table 1. All spectra display a rhombic g profile, with one component (g1) close to the free spin value of ge (2.0023), indicating that there is considerable 3dz2 character in the SOMO. The large Δg shifts observed for the g2,3 parameters result from the large spin–orbit coupling constant for Ni (ζNi+ = 565 cm−1).
The considerably broadened linewidths mainly arise from g-strain effects and not fully resolved superhyperfine coupling to the 31P nucleus of the PPh3 ligand. In the case of complex 1, an additional hyperfine broadening of ca. 60 MHz is present. This is in the order of the largest A3 value for the Br nucleus (50.69% 79Br, 49.31% 81Br; both possessing nuclear spin 3/2), hence impeding resolution of the quartets arising from the coupling of the unpaired electron to this nuclear spin. The DFT-derived parameters are also listed in Table 1 and are in reasonable agreement with the experimentally determined values. All complexes, with the exception of 5, display large, predominantly isotropic superhyperfine coupling to the 31P nucleus, in good agreement with the calculated values.
The relative orientations of the g- and A-tensors for the cationic complex 5 are shown in Fig. 11, alongside the spin density. As a comparison, g- and A-tensor orientations and spin densities derived from the DFT calculations of EPR parameters for starting complex 1 are given in Fig. 11b (corresponding figures for complexes 2, 7 and 8 are given in the ESI†).
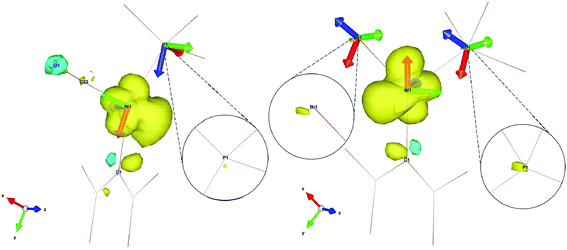 | ||
| Fig. 11 Spin density contour plot with g- and A-frames for [Ni(6-Mes)(PPh3)(CO)][PF6] (5, left) and [Ni(6-Mes)(PPh3)Br] (1, right). Ligands are truncated for clarity. | ||
As already mentioned, the 31P superhyperfine interaction is almost entirely isotropic, therefore an explanation for the much smaller HFC in the case of complex 5 compared to starting complex 1 (see aiso(31P) in Table 1) can be found by simply looking at the overall spin density on the 31P nuclei, neglecting the relative orientations of the A(31P) frames in each of the complexes (isotropic interaction is orientation independent). As the insets in Fig. 11 clearly show, there is a significantly less spin density on the 31P nucleus of 5 when compared to 1, which readily explains the much lower hyperfine interaction found experimentally and computationally. In fact, the spin density on the 31P nucleus of 5 is so small that two of the principal values of the A(31P) tensor for this complex are smaller than the overall broadening caused by g-strain effects and are completely unresolved at X-band. Only the A3(31P) component of the tensor is visible at X-band. In the spectrum in Fig. 2, the A3(31P) component is found on g1 because of almost exact and complete alignment between the Az axis and the gx axis, as deducible by Fig. 11. The extent of anisotropy and rhombicity for 5 is much lower than for the other complexes, and is similar to that reported previously for [LMeNi(CO)] (LMe = [HC(C(Me)NC6H3(iPr)2)2]−),21 with g values of 2.01, 2.17 and 2.19 and T-shape geometry.
Notably, the calculated 31P superhyperfine coupling for the two cationic complexes (2 and 5) are an order of magnitude smaller than for the series of neutral complexes reported. Whilst the experimental and calculated values for 5 are in reasonable agreement, the experimentally observed hyperfine for 2 does not match the DFT-derived values and bears closer resemblance to the neutral complexes; currently, we do not have an explanation for this observation.
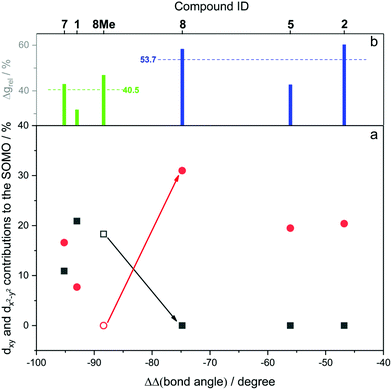
Fig. 12 shows the computed SOMO d-character of the different complexes as a function of the difference between the largest and the two smaller angles (e.g. (∠C–Ni–Br) − (∠P–Ni–C) − (∠Br–Ni–P) for 1, denoted as ΔΔ(bond angle)), taken as an index for the deviation from ideal D3h symmetry. Noticeable in Fig. 12a is the smaller difference in dxy and dx2−y2 contributions to the SOMO for complexes 1 and 7 (closest examples to D3h symmetry where dxy and dx2−y2 are degenerate), and the increasingly higher dx2−y2 character (simultaneously to dxy contributions approaching zero) when moving away from ideal D3h symmetry towards T-shape symmetry. Both these observations seem to be in good agreement with what was described previously and represented in Fig. 9. Very interesting is the case of complex 8, which as we noted above may be regarded as a T-shape complex with ∠C–Ni–L as the largest angle. However, a fully geometry optimised version of the same complex where the amido phenyl substituents were replaced by methyl substituents (8-Me, vide supra) showed angles that are similar to the Y-shape complexes 1 and 7. Our interpretation is that this compound is electronically inclined to be a Y-shape (similar to the other neutral compounds of the present series), however large steric strain pushes the amido group towards the carbene ligand, thus geometrically distorting it towards a T-shape. Orbital distribution and coordination geometry should reflect the shape and magnitude of the g tensor associated with the paramagnetic centre. In Fig. 12b, experimental Δgrel, a parameter used to evaluate the shape of the diagonalised g tensor and calculated according to eqn (1), is also reported as a function of the ΔΔ(bond angle).
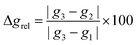 | (1) |
It can be seen that an increase in the dx2−y2 contribution to the SOMO corresponds to a shift of the g2 value away from g3 towards g1, and indeed for T-shape complexes g2 is closer to g1 than to g3, highlighting a geometry induced shape shifting of the g tensor.
Conclusions
Treatment of the three-coordinate Ni(I) complex [Ni(6-Mes)(PPh3)Br] (1) with a variety of bromide abstracting reagents has yielded a series of new mono- and dinuclear nickel products. Of most interest are the three-coordinate d9 complexes, 2, 5, 7 and 8, of general formula [Ni(6-Mes)(PPh3)X]0/+ that distort from ideal D3h symmetry by forming either T-shaped or Y-shaped geometries. These structural differences manifest in different electronic structure characteristics, namely that the SOMO for a T-shape complex is expected to be of dx2−y2 character, whereas for a Y-shape complex, it will be of dxy character. Electron paramagnetic resonance spectroscopy was used to derive spin Hamiltonian parameters for this series of three-coordinate Ni(I) complexes, which showed that all complexes have a rhombic g-tensor profile and that the 31P superhyperfine couplings are predominantly isotropic. The much lower magnitude of 31P superhyperfine coupling constants observed for the CO-containing complex 5 was explained with a smaller spin density found at the phosphorus ligand as predicted by density functional theory calculations. The overall computed spin densities in this series are polarised differently for the Y- and T-shaped complexes, namely with a larger lobe trans to the phosphine ligand in the former case as opposed to a larger lobe trans to the ligand in the latter case. This directly affects the shape and magnitude of the g-tensor: while all complexes have a rhombic g-tensor with g1 ≪ g2 < g3, a larger dx2−y2 contribution to the SOMO shifts g2 closer to g1.Experimental
General considerations
All manipulations were carried out using standard Schlenk, high vacuum and glovebox techniques. Solvents were purified using an MBraun SPS solvent system (hexane, Et2O) or under a nitrogen atmosphere from sodium benzophenone ketyl (benzene, THF). C6D6 and THF-d8 were vacuum transferred from potassium. NMR spectra were recorded on Bruker Avance 400/500 NMR and Agilent 500 MHz spectrometers and referenced to solvent signals as follows: benzene (1H, δ 7.16; 13C{1H}, δ 128.0), THF (1H, δ 3.58; 13C{1H}, δ 67.6); 31P{1H}, externally to 85% H3PO4 (δ 0.0); 19F, externally to CFCl3 (δ 0.0). Elemental analyses were performed by Elemental Microanalysis Ltd, Okehampton, Devon, UK. 1 and [(Et3Si)2(μ-H)][B(C6F5)4] were prepared according to literature methods.8,17[Ni(6-Mes)(PPh3)(THF)][PF6] (2)
A THF (10 mL) solution of TlPF6 (95 mg, 0.27 mmol) was added to a J. Young's resealable ampoule containing 1 (163 mg, 0.23 mmol) and the beige suspension was stirred for 2 h. This was cannula filtered, the filtrate concentrated to half volume and hexane (10 mL) added slowly to form a pale yellow precipitate. This was isolated by cannula filtration, recrystallised from THF/hexane and dried in vacuo. Yield: 138 mg (85%). 1H NMR (500 MHz, THF-d8, 298 K): δ 16.9 (br s), 9.9 (br s), 6.0 (br s), 5.3 (br s), 3.1 (br s); anal. calcd for C44H51N2OF6P2Ni (858.48): C 61.56%, H 5.99%, N 3.26%; found: C 61.39%, H 5.85%, N 3.18%; μeff (Evans method, THF, 298 K): 2.2μB.[{Ni(6-Mes)(PPh3)}2(μ-Br)][BArF4] (3)
1 (100 mg, 0.14 mmol) and NaBArF4 (130 mg, 0.15 mmol) were dissolved in Et2O (10 mL) and the solution stirred for 16 h in a J. Young's resealable ampoule. The solution was concentrated, filtered and layered with pentane (10 mL) to form orange crystals. Yield: 125 mg (81%). Anal. calcd for C112H98BN4F24P2BrNi2 (2225.96): C 60.43%, H 4.44%, N 2.52%; found: C 60.07%, H 4.68%, N 2.36%; μeff (Evans method, Et2O, 298 K): 2.5μB.[Ni(6-Mes)(PPh3)(CO)][PF6] (5)
To a degassed THF solution (0.5 mL) of 2 (20 mg, 0.02 mmol), 1 atm of CO was added to the stirring solution. An immediate colour change to dark yellow/green occurred, and after 1 minute the solution was reduced to dryness. The residue was extracted into THF (0.5 mL), filtered and layered with hexane (2 mL) to produce green crystals. Yield: 15 mg (79%). 1H NMR (500 MHz, THF-d8, 298 K): δ 16.9 (br s), 10.7 (br s), 9.9 (br s), 8.4 (s), 7.7 (br s), 7.3 (s), 7.0 (s), 6.4 (br s), 5.3 (br s), 4.9 (br s), 3.9 (br s), 3.4 (br s), 2.5 (br s), 2.3 (br s), 2.3 (br s); IR (ν, cm−1: THF): 2035 (CO); IR (ν, cm−1: KBr): 2030 (CO); anal. calcd for C41H43N2OF6PNi2 (814.39): C 60.47%, H 5.32%, N 3.44%; found: C 60.45%, H 5.58%, N 2.96%; μeff (Evans method, THF, 298 K): 1.8μB.[{Ni(6-Mes)}2(μ-BH4)2] (6)
1 (100 mg, 0.138 mmol) and NaBH4 (16 mg, 0.423 mmol) were placed in a J. Young's resealable ampoule in THF (10 mL). EtOH (1 mL) was added and the suspension was stirred for 5 min at room temperature to give a dark green solution. The volatiles were removed in vacuo, the residue extracted into benzene (2 × 10 mL) and evaporated to dryness. The green crude was washed with hexane (2 × 10 mL) at 195 K to give 6 as a green solid. Yield: 47 mg (90%). Crystals suitable for X-ray diffraction were obtained by slow diffusion of hexane into a concentrated THF solution of 6. 1H NMR (THF-d8, 400 MHz, 298 K): δ 6.71 (s, 8H, CH), 3.10 (t, 8H, 3JHH = 5.7 Hz, NCH2), 2.37 (s, 12H, CH3), 2.02 (br s, 28H, CH3 and NCH2CH2), −5.72 (br s, 8H, BH4); 13C{1H} NMR (THF-d8, 100 MHz, 298 K): δ 213.0 (s, NCN), 144.6 (s, N-ipso-C), 136.2 (s, o-C), 136.1 (p-C), 129.7 (CH), 45.2 (NCH2), 22.7 (CH2), 21.7 (CH3), 18.6 (CH3); 11B NMR (THF-d8, 128 MHz, 298 K): δ −32.0 (br s); IR (ν, cm−1: KBr): 2378 (BH4); anal. calcd for C44H64B2N4Ni2 (787.98): C 67.06%, H 8.19%, N 7.11%; found: C 66.97%, H 8.28%, N 6.98%.[Ni(6-Mes)(PPh3)(NCBH3)] (7)
1 (100 mg, 0.138 mmol) and NaBH3(CN) (14 mg, 0.222 mmol) were placed in a J. Young's resealable ampoule in THF (10 mL). EtOH (1 mL) was added and the suspension was stirred for 5 min at room temperature to give a pale orange solution. The solution was reduced to dryness and the residue extracted into benzene (2 × 10 mL). Upon removal of the benzene, the orange residue was washed with EtOH (2 × 10 mL) to give 7 as a pale yellow solid. Yield: 50 mg (53%). Crystals suitable for X-ray diffraction were obtained by slow diffusion of hexane into a concentrated solution of 7 in THF at 238 K. 1H NMR (500 MHz, C6D6, 298 K): δ 24.8 (br s), 12.4 (br s), 10.1 (s), 8.8 (br s), 5.5 (br s), 4.4 (br s), 3.9 (s), 1.6 (s); 11B NMR (500 MHz, C6D6, 298 K): δ −20.2; μeff (Evans method, THF, 298 K): 1.9μB. Repeated attempts to determine elemental microanalysis on crystalline samples of the complex consistently gave low %C values (e.g. elemental analysis calcd (%) for C41H46N3PBNi: C, 72.28; H, 6.81; N, 6.16; found C, 69.98; H, 6.75; N, 5.77).[Ni(6-Mes)(PPh3)(NPh)2] (8)
1 (100 mg, 0.138 mmol), NaOtBu (17 mg, 0.171 mmol), PPh3 (36 mg, 0.138 mmol) and NHPh2 (26 mg, 0.152 mmol) were placed in a J. Young's resealable ampoule in THF (10 mL). The suspension was stirred for 10 min at room temperature to give a dark red solution. The volatiles were removed in vacuo, the residue extracted into Et2O (2 × 10 mL) and evaporated to dryness. The orange residue was washed with cold pentane (2 × 10 mL) to give 8 as a bright red solid. Yield: 80 mg (72%). Crystals suitable for X-ray diffraction were obtained by slow diffusion of pentane into a concentrated solution of 8 in diethyl ether at 238 K. 1H NMR (500 MHz, C6D6, 298 K): δ 19.2 (br s), 8.2 (br s), 7.5 (br s), 7.1 (s), 6.9 (s), 6.8 (br s), 6.0 (br s), 5.1 (br s), 3.0 (br s), −15.6 (br s), −20.0 (s); μeff (Evans method, THF, 298 K): 2.0μB. The sensitivity of the complex precluded all attempts to determine elemental microanalysis.X-ray crystallography
Using Mo(Kα) radiation, single crystals of compounds 2, 3 and 7 were analysed using an Agilent Xcalibur diffractometer, while datasets for 4 and 5, as well as 2a (vide infra; ESI† only) were collected on a Nonius kappaCCD machine. An Agilent Supernova diffractometer was used to study 6, 8 and [Ni(6-Mes)(η2-C6H3Me3)][B(C6F5)4] (ESI† only) using Cu(Kα) radiation. All experiments were conducted at 150 K, with the exception of that for 6, which was achieved at 100 K. Details of the data collections and refinements are given in Table 2. The structures were uniformly solved using SHELXS,42 and refined using full-matrix least squares in SHELXL43via the Olex-244 software suite. Only noteworthy refinement details follow.| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|
| Empirical formula | C44H51F6N2NiOP2 | C116H108BBrF24N4Ni2OP2 | C53H36.5BF20N2Ni0.5 | C45H51F6N2NiO2P2 | C44H64B2N4Ni2 | C45H54BN3NiOP | C56H63N3NiOP |
| Formula weight | 858.52 | 2300.14 | 1121.50 | 886.53 | 788.03 | 753.40 | 883.77 |
| Crystal system | Monoclinic | Triclinic | Monoclinic | Monoclinic | Monoclinic | Monoclinic | Monoclinic |
| Space group | P21/c |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
C2/c | P21/c | P21/c | P21/n | P21/n |
| a/Å | 16.0749(1) | 12.9050(4) | 31.5490(3) | 14.3080(3) | 14.17049(12) | 14.2120(4) | 18.99247(14) |
| b/Å | 14.8045(1) | 17.3278(5) | 10.32800(10) | 16.4910(3) | 20.24524(15) | 16.5650(4) | 11.96944(9) |
| c/Å | 19.0391(1) | 25.2732(6) | 28.8100(3) | 18.8500(4) | 14.83697(15) | 18.0386(6) | 20.99341(16) |
| α/° | 90 | 75.082(2) | 90 | 90 | 90 | 90 | 90 |
| β/° | 111.435(1) | 84.432(2) | 92.977(1) | 95.145(1) | 91.0848(8) | 108.838(3) | 91.1551(7) |
| γ/° | 90 | 87.444(2) | 90 | 90 | 90 | 90 | 90 |
| U/Å3 | 4217.55(5) | 5434.1(3) | 9374.73(16) | 4429.80(15) | 4255.74(6) | 4019.2(2) | 4771.45(6) |
| Z | 4 | 2 | 8 | 4 | 4 | 4 | 4 |
| ρ calc/g cm−3 | 1.352 | 1.406 | 1.589 | 1.329 | 1.230 | 1.245 | 1.230 |
| μ/mm−1 | 0.598 | 0.836 | 0.341 | 0.574 | 1.343 | 0.560 | 1.219 |
| F(000) | 1796.0 | 2364.0 | 4540.0 | 1852.0 | 1688.0 | 1604.0 | 1884.0 |
| Crystal size/mm3 | 0.36 × 0.31 × 0.19 | 0.845 × 0.77 × 0.563 | 0.2 × 0.1 × 0.1 | 0.2 × 0.1 × 0.1 | 0.25 × 0.25 × 0.25 | 0.621 × 0.378 × 0.062 | 0.236 × 0.157 × 0.048 |
| 2θ range for data collection/° | 5.7 to 54.97 | 6.908 to 54.968 | 7.078 to 54.872 | 7.294 to 49.404 | 15.77 to 144.026 | 6.814 to 54.968 | 6.214 to 146.89 |
| Index ranges | −20 ≤ h ≤ 20 | −16 ≤ h ≤ 16 | −40 ≤ h ≤ 40 | −16 ≤ h ≤ 16 | −17 ≤ h ≤ 15 | −13 ≤ h ≤ 18 | −23 ≤ h ≤ 22 |
| −19 ≤ k ≤ 19 | −22 ≤ k ≤ 17 | −13 ≤ k ≤ 13 | −19 ≤ k ≤ 19 | −24 ≤ k ≤ 19 | −21 ≤ k ≤ 20 | −14 ≤ k ≤ 14 | |
| −24 ≤ l ≤ 24 | −32 ≤ l ≤ 32 | −37 ≤ l ≤ 37 | −22 ≤ l ≤ 22 | −18 ≤ l ≤ 18 | −23 ≤ l ≤ 22 | −24 ≤ l ≤ 26 | |
| Reflections collected | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 090 090 |
46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 948 948 |
75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915 915 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528 528 |
59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 289 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 736 |
67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012 012 |
| Independent reflections, Rint | 9656, 0.0282 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 033, 0.0376 033, 0.0376 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 665, 0.0610 665, 0.0610 |
7457, 0.0463 | 8330, 0.0847 | 9218, 0.0347 | 9580, 0.0510 |
| Data/restraints/parameters | 9656/0/511 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 033/121/1365 033/121/1365 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 665/0/701 665/0/701 |
7457/128/565 | 8330/0/511 | 9218/25/502 | 9580/0/567 |
| Goodness-of-fit on F2 | 1.089 | 1.023 | 1.122 | 1.053 | 1.017 | 1.028 | 1.027 |
| Final R1, wR2 [I > = 2σ(I)] | 0.0284, 0.0809 | 0.0635, 0.1396 | 0.0503, 0.1086 | 0.0435, 0.1070 | 0.0528, 0.1401 | 0.0472, 0.1128 | 0.0343, 0.0828 |
| Final R1, wR2 [all data] | 0.0370, 0.0830 | 0.1297, 0.1745 | 0.0852, 0.1192 | 0.0555, 0.1154 | 0.0580, 0.1457 | 0.0703, 0.1267 | 0.0400, 0.0860 |
| Largest diff. peak/hole/e Å−3 | 0.60/−0.36 | 1.19/−0.93 | 0.51/−0.30 | 0.52/−0.48 | 0.68/−0.64 | 0.88/−0.94 | 0.39/−0.29 |
A small amount of racemic twinning was accounted for in the refinement of 2a (ESI† only). This structure represents a P21 polymorph of compound 2, the latter solving in space group P21/c. In 3, the asymmetric was seen to contain one anion, one cation and one molecule of diethyl ether. While the cation and solvent were both ordered, disorder prevailed for four of the [BAr4F]− trifluoromethyl substituents. In particular, the fluorine atoms attached to C88, C111 and C103 were each modelled over two sites in 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35, 55
35, 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 and 65
45 and 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 ratios, respectively, while the entire CF3 group containing C87 exhibited 65
35 ratios, respectively, while the entire CF3 group containing C87 exhibited 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 disorder. In 3 (and all subsequent structures containing disordered [BAr4F]− trifluoromethyl groups) C–F and F⋯F distances within each disordered region were restrained to being similar in the final least squares. In addition, the ADPs for fractional occupancy atoms were also restrained, to assist convergence.
35 disorder. In 3 (and all subsequent structures containing disordered [BAr4F]− trifluoromethyl groups) C–F and F⋯F distances within each disordered region were restrained to being similar in the final least squares. In addition, the ADPs for fractional occupancy atoms were also restrained, to assist convergence.
The cation in the asymmetric unit of 4 also fell prey to disorder. In particular, there is a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio of the tolyl-Ni-carbene moiety present versus the tolyl⋯pyrimidinium pair, the latter being stabilised by a C–H⋯π interaction. In 5, the asymmetric unit was seen to comprise one cationic nickel containing species, one [PF6]− anion and one THF molecule. The crystal was small, which contributed to weak diffraction at higher Bragg angles. Hence, data were truncated to a θ value of 24.7°.
50 ratio of the tolyl-Ni-carbene moiety present versus the tolyl⋯pyrimidinium pair, the latter being stabilised by a C–H⋯π interaction. In 5, the asymmetric unit was seen to comprise one cationic nickel containing species, one [PF6]− anion and one THF molecule. The crystal was small, which contributed to weak diffraction at higher Bragg angles. Hence, data were truncated to a θ value of 24.7°.
The borohydride hydrogen atoms in the structure of compound 6 were readily located and refined with a common Uiso in each [BH4]− moiety. No distance restraints employed. C25 was modelled for 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 disorder, and the minor component of this atom was refined isotropically. A data collection was also performed on this compound, at room temperature (designated 6a, ESI†), in which the asymmetric unit was seen to consist of one half of a dimer molecule, wherein the metal centres and carbene carbon atoms were noted to coincide with a crystallographic 2-fold rotation axis. This necessarily means that the apical NHC carbons (C3 and C15) are each disordered in a 50
13 disorder, and the minor component of this atom was refined isotropically. A data collection was also performed on this compound, at room temperature (designated 6a, ESI†), in which the asymmetric unit was seen to consist of one half of a dimer molecule, wherein the metal centres and carbene carbon atoms were noted to coincide with a crystallographic 2-fold rotation axis. This necessarily means that the apical NHC carbons (C3 and C15) are each disordered in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio. This disorder precluded addition of the hydrogen atoms bound to C2 and C14 using the riding model; hence, they were omitted from the refinement. The borohydride hydrogens were located, and refined without restraints, but their credibility is somewhat questionable given their associated Uiso values and the overall atomic displacement parameters. The reason for implementing a room temperature data collection for 6a was to resolve a phase transition that arose in the course of a neutron experiment conducted on 6, using VIVALDI, at the ILL. The rationale for doing a neutron experiment arose because, at 100 K, the borohydride moieties appeared to coordinate unsymmetrically to the nickel centres. Unfortunately, during cooling at the neutron source, the large crystals cracked. This ultimately resulted in collection of a neutron data set at room temperature, which suggested a different space group (C2/c) to that for the structure determined at 100 K using X-rays (P21/c).
50 ratio. This disorder precluded addition of the hydrogen atoms bound to C2 and C14 using the riding model; hence, they were omitted from the refinement. The borohydride hydrogens were located, and refined without restraints, but their credibility is somewhat questionable given their associated Uiso values and the overall atomic displacement parameters. The reason for implementing a room temperature data collection for 6a was to resolve a phase transition that arose in the course of a neutron experiment conducted on 6, using VIVALDI, at the ILL. The rationale for doing a neutron experiment arose because, at 100 K, the borohydride moieties appeared to coordinate unsymmetrically to the nickel centres. Unfortunately, during cooling at the neutron source, the large crystals cracked. This ultimately resulted in collection of a neutron data set at room temperature, which suggested a different space group (C2/c) to that for the structure determined at 100 K using X-rays (P21/c).
This phase transition, from a diffraction perspective, results in averaging the electron density that arises from the borohydrides across the sample and, overall, the ambient temperature neutron data did not afford any additional insight into the bonding subtleties which the experiment aimed to probe.
The asymmetric unit in 7 was seen host to one molecule of THF in addition to one molecule of the nickel complex. C3 in the latter was equally disordered over two sites, and the four chemically equivalent C–C distances involving C3/C3A were restrained to being similar in the final least squares. Three of the five atoms in the solvent were also refined to take account of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 disorder. Once again, the chemically equivalent distances involving fractional occupancy atoms in this moiety were restrained to being similar, and ADP restraints were also incorporated to assist convergence.
25 disorder. Once again, the chemically equivalent distances involving fractional occupancy atoms in this moiety were restrained to being similar, and ADP restraints were also incorporated to assist convergence.
In addition to one molecule of the complex, the asymmetric unit in 8 was noted to contain one molecule of guest diethyl ether.
Analysing the crystal structure of [Ni(6-Mes)(η2-C6H3Me3)][B(C6F5)4] (ESI† only) was nothing short of excruciating, and it involved three data collections, some 350 refinements and approximately 10 data integrations. The issue appears to be that the compound is undergoing a phase transition. A more detailed treatment is presented in the ESI.†
Crystallographic data for all compounds have been deposited with the Cambridge Crystallographic Data Centre as supplementary publications CCDC 1578636–1578644, 1582301 and 1584193 for 2, 3, 4, 5, 6, 7, 8, 2a (ESI†), [Ni(6-Mes)(η2-C6H3Me3)][B(C6F5)4] (ESI†), 6a (ESI†) and [Ni(6-Mes)(PPh3)(CO)Br][PF6] (ESI†) respectively.
EPR spectroscopy
Samples for EPR measurements were prepared under an N2 atmosphere in a glovebox. A solution of each complex was prepared by dissolving ca. 4 mg of 1–3, 5, 7 and 8 in 200 μL of dry THF (in all cases, a small quantity of dry toluene was also added to improve the quality of the polycrystalline glass formed in frozen solution, and thereby enhance the quality of the EPR spectra). The solutions were transferred to an EPR tube, sealed in the glove box and then cooled to 77 K before rapid transfer to the pre-cooled EPR cavity. The X-band CW EPR measurements were performed on a Bruker EMX spectrometer utilizing an ER4119HS resonator, 100 kHz field modulation at 140 K.Computational details
All density functional theory (DFT) calculations were carried out with ORCA (version 4.0.0.2).45 The geometries were taken from crystallographic refinements, either optimising only the positions of the hydrogen atoms or fully relaxing the geometry. The geometry optimisations used the BP86 density functional,46 making use of the zeroth order relativistic correction ZORA retaining onecenter terms.47 The scalar-relativistically recontracted versions of Ahlrich's triple-zeta quality basis sets (ZORA-def2-TZVP) were used on all atoms except carbon and hydrogen for which ZORA-def2-SVP basis sets were used.48 The resolution of the identity (RI) approximation and the auxiliary basis SARC/J were used.49 The integration accuracy was increased to 7.0, the grid was set to 7 in ORCA nomenclature, and ‘tight’ SCF criteria were used. The optimisations considered solvent effects through the conductor-like polarisable continuum model, with the solvents as indicated in the experimental part.50 Dispersion effects were taken into account with Grimme's D3BJ model including Becke–Johnson damping.51 Mulliken spin populations were inspected to confirm convergence to the targeted electronic structure.Broken-symmetry DFT calculations used the functionals TPSSh,52 B3LYP,53 PBE0,54 M06L,55 additionally making use of the chain-of-spheres approximation (RIJCOSX) and using the ‘flipspin’ feature in ORCA to generate the initial guess for the broken-symmetry solution, with otherwise unchanged calculation setups.56 The exchange coupling constants were taken directly from the ORCA output, using the definition by Yamaguchi.57 For the calculation of EPR parameters, it was found that calculations with a different family of basis sets gave superior results. Generally, the IGLO-II basis set was used on all atoms, with CP for Ni and aug-pc-3 for Br,58 in conjunction with the PBE0 density functional and the RIJCOSX approximation as for the BS-DFT calculations, making use of the AutoAux feature in ORCA. The grid sizes were set to Grid6 and GridX9 in ORCA nomenclature, with increased grids (7) on the Ni ion and all directly bound atoms as well as the nitrogen atoms in the carbene ligand. The spin–orbit mean field operator (SOMF(1X)) was used, and the origin for the g-tensor was taken at the centre of the electronic charge.59 All tensor orientations, spin densities and molecular orbitals depicted and discussed in the main text and the ESI† are derived from calculations at this level of theory.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank the Universities of Bath (studentships for WJMB and RCP; Prize Fellowship to VK) and Cardiff (Cardiff University Research Fellowship to ER), EPSRC (MJP, AF) for financial support and the Royal Society for a Newton International Fellowship for SS. We acknowledge the Institute Laue-Langevin Scientific Coordination Office for the allocation of neutron beam time on VIVALDI (proposal 5-12-276) and Dr Marie-Hélène Lemée-Cailleau for the data collection on 6. We dedicate this paper to Professor Phil Power on the occasion of his 65th birthday.References
- C. Y. Lin and P. P. Power, Chem. Soc. Rev., 2017, 46, 5347–5399 RSC.
- For an additional very recent review of Ni(I), see: P. Zimmermann and C. Limberg, J. Am. Chem. Soc., 2017, 139, 4233–4242 CrossRef CAS PubMed.
- (a) P. Heimbach, Angew. Chem., Int. Ed. Engl., 1964, 3, 648–649 CrossRef; (b) L. Porri, M. C. Gallazzi and G. Vitulli, Chem. Commun., 1967, 228–228 RSC; (c) P. Dapporto, G. Fallani, S. Midollini and L. Sacconi, J. Chem. Soc., Chem. Commun., 1972, 1161–1161 RSC; (d) P. Dapporto, G. Fallani and L. Sacconi, Inorg. Chem., 1974, 13, 2847–2850 CrossRef CAS; (e) A. Gleizes, M. Dartiguenave, Y. Dartiguenave, J. Galy and H. F. Klein, J. Am. Chem. Soc., 1977, 99, 5187–5189 CrossRef CAS; (f) F. Scott, C. Krüger and P. Betz, J. Organomet. Chem., 1990, 387, 113–121 CrossRef CAS. For more recent examples, see: (g) L. M. Guard, M. M. Beromi, G. W. Brudvig, N. Hazari and D. J. Vinyard, Angew. Chem., Int. Ed., 2015, 54, 13352–13356 CrossRef CAS PubMed; (h) M. M. Schwab, D. Himmel, S. Kacprzak, V. Radtke, D. Kratzert, P. Weis, M. Wernet, A. Peter, Z. Yassine, D. Schmitz, E.-W. Scheidt, W. Scherer, S. Weber, W. Feuerstein, F. Breher, A. Higelin and I. Krossing, Chem. – Eur. J., 2017 DOI:10.1002/chem.201704436.
- D. C. Bradley, M. B. Hursthouse, R. J. Smallwood and A. J. Welch, J. Chem. Soc., Chem. Commun., 1972, 872–873 RSC.
- (a) X. L. Hu, I. Castro-Rodriguez and K. Meyer, Chem. Commun., 2004, 2164–2165 RSC; (b) B. R. Dible, M. S. Sigman and A. M. Arif, Inorg. Chem., 2005, 44, 3774–3776 CrossRef CAS PubMed; (c) S. Miyazaki, Y. Koga, T. Matsumoto and K. Matsubara, Chem. Commun., 2010, 46, 1932–1934 RSC; (d) M. S. Varonka and T. H. Warren, Organometallics, 2010, 29, 717–720 CrossRef CAS; (e) C. A. Laskowski, A. J. M. Miller, G. L. Hillhouse and T. R. Cundari, J. Am. Chem. Soc., 2011, 133, 771–773 CrossRef CAS PubMed; (f) S. Nagao, T. Matsumoto, Y. Koga and K. Matsubara, Chem. Lett., 2011, 40, 1036–1038 CrossRef CAS; (g) K. Zhang, M. Conda-Sheridan, S. R. Cooke and J. Louie, Organometallics, 2011, 30, 2546–2552 CrossRef CAS PubMed; (h) C. A. Laskowski, G. R. Morello, C. T. Saouma, T. R. Cundari and G. L. Hillhouse, Chem. Sci., 2013, 4, 170–174 RSC; (i) J. G. Wu, A. Nova, D. Balcells, G. W. Brudvig, W. Dai, L. M. Guard, N. Hazari, P. H. Lin, R. Pokhrel and M. K. Takase, Chem. – Eur. J., 2014, 20, 5327–5337 CrossRef CAS PubMed; (j) S. Pelties, E. Carter, A. Folli, M. F. Mahon, D. M. Murphy, M. K. Whittlesey and R. Wolf, Inorg. Chem., 2016, 55, 11006–11017 CrossRef CAS PubMed; (k) D. D. Beattie, E. G. Bowes, M. W. Drover, J. A. Love and L. L. Schafer, Angew. Chem., Int. Ed., 2016, 55, 13290–13295 CrossRef CAS PubMed; (l) K. Matsubara, Y. Fukahori, T. Inatomi, S. Tazaki, Y. Yamada, Y. Koga, S. Kanegawa and T. Nakamura, Organometallics, 2016, 35, 3281–3287 CrossRef CAS; (m) K. Matsubara, H. Yamamoto, S. Miyazaki, T. Inatomi, K. Nonaka, Y. Koga, Y. Yamada, L. F. Veiros and K. Kirchner, Organometallics, 2017, 36, 255–265 CrossRef CAS; (n) A. B. Dürr, H. C. Fisher, I. Kalvet, K.-N. Truong and F. Schoenebeck, Angew. Chem., Int. Ed., 2017, 56, 13431–13435 CrossRef PubMed.
- C. A. Laskowski and G. L. Hillhouse, J. Am. Chem. Soc., 2008, 130, 13846–13847 CrossRef CAS PubMed.
- R. C. Poulten, I. Lopez, A. Llobet, M. F. Mahon and M. K. Whittlesey, Inorg. Chem., 2014, 53, 7160–7169 CrossRef CAS PubMed.
- C. J. E. Davies, M. J. Page, C. E. Ellul, M. F. Mahon and M. K. Whittlesey, Chem. Commun., 2010, 46, 5151–5153 RSC.
- R. C. Poulten, M. J. Page, A. G. Algarra, J. J. Le Roy, I. Lopez, E. Carter, A. Llobet, S. A. Macgregor, M. F. Mahon, D. M. Murphy, M. Murugesu and M. K. Whittlesey, J. Am. Chem. Soc., 2013, 135, 13640–13643 CrossRef CAS PubMed.
- M. J. Page, W. Y. Lu, R. C. Poulten, E. Carter, A. G. Algarra, B. M. Kariuki, S. A. Macgregor, M. F. Mahon, K. J. Cavell, D. M. Murphy and M. K. Whittlesey, Chem. – Eur. J., 2013, 19, 2158–2167 CrossRef CAS PubMed.
- P. L. Holland, T. R. Cundari, L. L. Perez, N. A. Eckert and R. J. Lachicotte, J. Am. Chem. Soc., 2002, 124, 14416–14424 CrossRef CAS PubMed.
- An Et2O analogue [LRNi(OEt2)] (LR = [HC(C(Me)NC6H3(iPr)2)2]− exhibits a Ni–O distance of 2.0415(14) Å. S. Pfirrmann, C. Limberg, C. Herwig, R. Stösser and B. Ziemer, Angew. Chem., Int. Ed., 2009, 48, 3357–3361 CrossRef CAS PubMed.
- Interestingly, Yoo and Lee have reported recently that the neutral T-shaped Ni(I) complex [(acriPNP)Ni] (acriPNP = 4,5-bis(diisopropylphosphino)-2,7,9,9-tetramethyl-9H-acridin-10-ide) does not form a stable adduct with THF. C. Yoo and Y. Lee, Angew. Chem., Int. Ed., 2017, 56, 9502–9506 CrossRef CAS PubMed.
- B. J. Fox, M. D. Millard, A. G. DiPasquale, A. L. Rheingold and J. S. Figueroa, Angew. Chem., Int. Ed., 2009, 48, 3473–3477 CrossRef CAS PubMed.
- The magnetic moment of solid 3 measured on a Gouy balance at room temperature was 2.39μB.
- The EPR spectrum of 3 in THF (140 K) showed essentially 1.
- (a) J. B. Lambert, S. H. Zhang, C. L. Stern and J. C. Huffman, Science, 1993, 260, 1917–1918 CAS; (b) M. Nava and C. A. Reed, Organometallics, 2011, 30, 4798–4800 CrossRef CAS PubMed; (c) S. J. Connelly, W. Kaminsky and D. M. Heinekey, Organometallics, 2013, 32, 7478–7481 CrossRef CAS.
- (a) S. Pfirrmann, S. Yao, B. Ziemer, R. Stösser, M. Driess and C. Limberg, Organometallics, 2009, 28, 6855–6860 CrossRef CAS; (b) A. Velian, S. Lin, A. J. M. Miller, M. W. Day and T. Agapie, J. Am. Chem. Soc., 2010, 132, 6296–6297 CrossRef CAS PubMed; (c) Y. Hoshimoto, Y. Hayashi, H. Suzuki, M. Ohashi and S. Ogoshi, Organometallics, 2014, 33, 1276–1282 CrossRef CAS.
- (a) N. Imlinger, K. Wurst and M. R. Buchmeiser, J. Organomet. Chem., 2005, 690, 4433–4440 CrossRef CAS; (b) V. César, N. Lugan and G. Lavigne, J. Am. Chem. Soc., 2008, 130, 11286–11287 CrossRef PubMed; (c) E. L. Kolychev, S. Kronig, K. Brandhorst, M. Freytag, P. G. Jones and M. Tamm, J. Am. Chem. Soc., 2013, 135, 12448–12459 CrossRef CAS PubMed; (d) G. Sipos, A. Ou, B. W. Skelton, L. Falivene, L. Cavallo and R. Dorta, Chem. – Eur. J., 2016, 22, 6939–6946 CrossRef CAS PubMed.
- (a) P. Stavropoulos, M. Carrie, M. C. Muetterties and R. H. Holm, J. Am. Chem. Soc., 1990, 112, 5385–5387 CrossRef CAS; (b) P. J. Schebler, B. S. Mandimutsira, C. G. Riordan, L. M. Liable-Sands, C. D. Incarvito and A. L. Rheingold, J. Am. Chem. Soc., 2001, 123, 331–332 CrossRef CAS PubMed; (c) B. Horn, S. Pfirrmann, C. Limberg, C. Herwig, B. Braun, S. Mebs and R. Metzinger, Z. Anorg. Allg. Chem., 2011, 637, 1169–1174 CrossRef CAS.
- N. A. Eckert, A. Dinescu, T. R. Cundari and P. R. Holland, Inorg. Chem., 2005, 44, 7702–7704 CrossRef CAS PubMed.
- M. J. Ingleson, B. C. Fullmer, D. T. Buschhorn, H. Fan, M. Pink, J. C. Huffman and K. G. Caulton, Inorg. Chem., 2008, 47, 407–409 CrossRef CAS PubMed.
- Recently reported four-coordinate pincer phosphine complexes [(PNP)Ni(CO)] exhibit much shorter Ni–CO distance and significantly lower frequency Ni–CO stretches. (a) Ref. 13; ; (b) C. Yoo, S. Oh, J. Kim and Y. Lee, Chem. Sci., 2014, 5, 3853–3858 RSC.
- T. M. Gilbert, F. J. Hollander and R. G. Bergman, J. Am. Chem. Soc., 1985, 107, 3508–3516 CrossRef CAS.
- R. Carreño, V. Riera, M. A. Ruiz, C. Bois and Y. Jeannin, Organometallics, 1993, 12, 1946–1953 CrossRef.
- (a) T. Saito, M. Nakajima, A. Kobayashi and Y. Sasaki, J. Chem. Soc., Dalton Trans., 1978, 482–485 RSC; (b) P. J. Desrochers, S. LeLievre, R. J. Johnson, B. T. Lamb, A. L. Phelps, A. W. Cordes, W. W. Gu and S. P. Cramer, Inorg. Chem., 2003, 42, 7945–7950 CrossRef CAS PubMed; (c) A. J. Churchard, M. K. Cyranski, L. Dobrzycki, A. Budzianowski and W. Grochala, Energy Environ. Sci., 2010, 3, 1973–1978 RSC; (d) P. J. Desrochers, C. A. Sutton, M. L. Abrams, S. F. Ye, F. Neese, J. Telser, A. Ozarowski and J. Krzystek, Inorg. Chem., 2012, 51, 2793–2805 CrossRef CAS PubMed; (e) S. Chakraborty, J. Zhang, Y. J. Patel, J. A. Krause and H. R. Guan, Inorg. Chem., 2013, 52, 37–47 CrossRef CAS PubMed; (f) H. W. Suh, L. M. Guard and N. Hazari, Polyhedron, 2014, 84, 37–43 CrossRef CAS; (g) S. Murugesan, B. Stöger, M. Weil, L. F. Veiros and K. Kirchner, Organometallics, 2015, 34, 1364–1372 CrossRef CAS PubMed; (h) C. P. Kruse, T. Deb, A. M. Aboelenen, C. M. Anderson, J. L. Petersen and M. P. Jensen, Eur. J. Inorg. Chem., 2016, 2474–2485 CrossRef CAS.
- M. Kandiah, G. S. McGrady, A. Decken and P. Sirsch, Inorg. Chem., 2005, 44, 8650–8652 CrossRef CAS PubMed.
- H. Tak, H. Lee, J. Kang and J. Cho, Inorg. Chem. Front., 2016, 3, 157–163 RSC.
- Y. Journaux, V. Lozan, J. Klingele and B. Kersting, Chem. Commun., 2006, 83–84 RSC.
- A triphenylphosphine analogue of the triphos complex reported in ref. 27 was identified very tentatively many years before. D. G. Holah, A. N. Hughes, B. C. Hui and K. Wright, Can. J. Chem., 1974, 52, 2990–2999 CrossRef CAS.
- (a) R. A. Jones and B. R. Whittlesey, Inorg. Chem., 1986, 25, 852–856 CrossRef CAS; (b) M. Ito, T. Matsumoto and K. Tatsumi, Inorg. Chem., 2009, 48, 2215–2223 CrossRef CAS PubMed; (c) F. Olechnowicz, G. L. Hillhouse and R. F. Jordan, Inorg. Chem., 2015, 54, 2705–2712 CrossRef CAS PubMed; (d) F. Olechnowicz, G. L. Hillhouse, T. R. Cundari and R. F. Jordan, Inorg. Chem., 2017, 56, 9922–9930 CrossRef CAS PubMed.
- (a) B. G. Segal and S. J. Lippard, Inorg. Chem., 1977, 16, 1623–1629 CrossRef CAS; (b) D. G. Holah, A. N. Hughes and N. I. Khan, Can. J. Chem., 1984, 62, 1016–1021 CrossRef CAS.
- (a) R. J. Barton, D. G. Holah, S. Z. Hu, A. N. Hughes, S. I. Khan and B. E. Robertson, Inorg. Chem., 1984, 23, 2391–2395 CrossRef CAS; (b) D. J. Elliot, S. Haukilahti, D. G. Holah, A. N. Hughes, S. Maciaszek, R. J. Barton, Y. Luo and B. E. Robertson, Can. J. Chem., 1988, 66, 1770–1775 CrossRef CAS.
- S. Sabater, M. J. Page, M. F. Mahon and M. K. Whittlesey, Organometallics, 2017, 36, 1776–1783 CrossRef CAS.
- Additional PPh3 was also added to prevent phosphine dissociation and formation of the two-coordinate Ni(I) amido complex, [Ni(6-Mes)(NPh2)], which will be the subject of a future publication.
- D. J. Mindiola and G. L. Hillhouse, J. Am. Chem. Soc., 2001, 123, 4623–4624 CrossRef CAS PubMed.
- Two-coordinate Ni(I) amido complexes show significantly shorter Ni–N distances. (a) Ref. 6; ; (b) M. I. Lipschutz, X. Z. Yang, R. Chatterjee and T. D. Tilley, J. Am. Chem. Soc., 2013, 135, 15298–15301 CrossRef CAS PubMed; (c) C. Y. Lin, J. C. Fettinger, F. Grandjean, G. J. Long and P. P. Power, Inorg. Chem., 2014, 53, 9400–9406 CrossRef CAS PubMed.
- (a) P. Pietrzyk, K. Podolska and Z. Sojka, J. Phys. Chem., 2008, 112, 12208–12219 CrossRef CAS PubMed; (b) P. Pietrzyk, K. Podolska and Z. Sojka, Chem. – Eur. J., 2009, 15, 11802–11807 CrossRef CAS PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, USA, 2013 Search PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- (a) G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, A46, 467–473 CrossRef CAS; (b) G. M. Sheldrick, SHELXL-97, a computer program for crystal structure refinement, University of Göttingen, 1997 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- (a) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef; (b) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- (a) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS; (b) E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC; (b) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC; (c) D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed; (d) D. A. Pantazis and F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 363–374 CrossRef CAS.
- (a) F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS; (b) B. I. Dunlap, J. W. D. Connolly and J. R. Sabin, J. Chem. Phys., 1979, 71, 3396–3402 CrossRef CAS; (c) M. Feyereisen, G. Fitzgerald and A. Komornicki, Chem. Phys. Lett., 1993, 208, 359–363 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- (a) K. Yamaguchi, Y. Takahara and T. Fueno, in Applied Quantum Chemistry, ed. V. H. Smith Jr., H. F. Scheafer and K. Morokuma, D. Reidel, Boston, 1986, p 155 Search PubMed; (b) T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, K. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223–230 CrossRef CAS.
- (a) M. Schindler and W. Kutzelnigg, J. Chem. Phys., 1982, 76, 1919 CrossRef CAS; (b) W. Kutzelnigg, U. Fleischer and M. Schindler, The IGLO- Method: Ab Initio Calculation Interpretation of NMR Chemical Shifts Magnetic Susceptibilities, Springer-Verlag, Heidelberg, Germany, 1990, p. 23 Search PubMed; (c) F. Jensen, J. Chem. Phys., 2001, 115, 9113 CrossRef CAS; (d) F. Jensen, J. Chem. Phys., 2002, 116, 7372 CrossRef CAS; (e) F. Jensen, J. Chem. Phys., 2002, 117, 9234 CrossRef CAS.
- B. A. Hess, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1578636–1578644, 1582301 and 1584193. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt04187j |
| This journal is © The Royal Society of Chemistry 2018 |