Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular-level insight into the binding of arginine to a zwitterionic Langmuir monolayer†
Joaquín Klug*ab,
Diego Masonea and
Mario G. Del Pópolo ab
ab
aCONICET & Facultad de Ciencias Exactas y Naturales, Universidad Nacional de Cuyo, Mendoza, CP5500, Argentina. E-mail: mdelpopolo@fcen.uncu.edu.ar
bAtomistic Simulation Centre, School of Mathematics and Physics, Queen's University Belfast, University Road, Belfast BT7 1NN, Northern Ireland, UK. E-mail: m.del-popolo@qub.ac.uk
First published on 14th June 2017
Abstract
Solutions of the cationic amino-acid arginine (Arg+) in contact with a phospholipid monolayer are investigated by molecular dynamics simulations. The results show that Arg+ binds strongly to the lipid/water interface, with adsorption free-energies ranging from −43.8 to −22.2 kJ mol−1, depending on the amino-acids concentration. The large binding energies are attributed to hydrogen bonding between the charged moieties Arg+ and the phosphate and carbonyl groups of the phospholipids, that compensate for changes in the levels of hydration upon adsorption. We show that a concentrated layer of Arg+, tightly bound to the interface, has little effect on the compression isotherm and the lateral mechanical properties of the monolayer, while having a substantial impact on the interfacial electrostatic potential and the lateral mobility of the lipids. These effects are readily explained in terms of the arrangement that the amino-acids adopt when bound to the monolayer.
1 Introduction
The physical binding of metabolites and pharmacological agents to the cell membrane is a key step in the process of cellular intake. Several experimental models have been developed to investigate the interaction of bioactive molecules with self-assembled lipid structures that mimic cell membranes. Langmuir monolayers, giant unilamellar vesicles, and solid-supported membranes are among the preferred experimental set-ups, as the composition of the lipid phase and of the surrounding solutions can be easily controlled.1,2 Although not membranes themselves, Langmuir monolayers (LM) offer a distinctive advantage for sensing adsorbate–lipid interactions. LM are water-supported monomolecular layers of amphiphilic species,3,4 whose packing fraction can be adjusted using the barriers of a Langmuir trough.2,5 As the monolayer is compressed or expanded, lipids explore different phases and undergo a series of phase transitions that manifest themselves on the shape of the lateral-pressure/area isotherm, along with changes in the interfacial electrostatic potential and the reflectivity of the liquid surface.Since the physical properties of Langmuir monolayers can be sensitive to the composition of the sub-phase, they have been used extensively to investigate the interaction between lipids and different biomolecules, such as peptides,6,7 proteins,8,9 polysaccharides,10,11 DNA,12,13 anesthetics,14,15 antimicrobial compounds,16,17 and anti-cancer drugs.18,19 Unfortunately, the standard measurements performed on typical monolayer experiments do not deliver molecular-level insight into the structure and dynamics of these systems. Nor do they allow the decomposition of the binding energy of adsorbates into different contributions, or the identification of specific adsorbate–lipid interactions. The lattes information is, in fact, valuable and could be used to optimise the response of a lipid aggregate to a particular adsorbate, for example.20
Molecular simulations provide a microscopic view of the system's behaviour that can help to interpret experimental trends and data. Molecular Dynamics (MD), in particular, has been extensively used to analyse Langmuir monolayers with atomistic21–32 and coarse-grained32–40 levels of detail. A wide variety of amphiphilic molecules have been examined by simulations, ranging from fatty acids to detergents and lipo-peptides, but undoubtedly the most popular amphiphiles have been phospholipids and their mixtures with other lipids and sterols, as the resulting monolayers have a closer resemblance to natural bio-membranes.
As discussed in more detail below, simulations have been able to reproduce experimental compression isotherms22,25,32,35–37,40 and the interfacial electrostatic potential27,41–43 of phospholipids' monolayers with varying degrees of accuracy. Also, some studies have focused on the interaction of ions,44,45 drugs,24 dyes,46 and proteins23,47 with LM, but only a few of them have examined the effect of adsorbates on the compression isotherm45 and interfacial potential,24,45 or have discussed the adsorption mechanism in terms of a binding free-energy profile.46,48
In the present work we look into the binding of a cationic amino-acid (arginine, Arg+) to a zwitterionic dipalmitoylphosphatidylcholine (DPPC) monolayer. The interest in Arg+ stems from the fact that it is the main component of cell-penetrating-peptides (CPP). These are highly hydrophilic polycationic peptides, that readily cross natural and artificial lipid bilayers by a mechanism which is still unknown.20 For the current purposes, it is enough to say that the strength of the binding of Arg+ to the lipid surface, and possibly the associated effects on the local mechanical properties of the membrane, modulate the translocation rate.49,50 The aim of this paper is to describe how the adsorption of Arg+ affects the compression isotherm of the DPPC monolayer, its interfacial electrostatic potential, and the lateral mobility of the lipids, all properties that can be accessed experimentally. We also correlate these properties with the amino-acids' adsorption free energy, which is in turn interpreted in terms of changes of hydration and specific interactions between the amino-acids' and lipids' functional groups.
2 Computational details
The simulated systems were made of 64 DPPC molecules forming a mono-molecular layer adsorbed on a water slab. Periodic boundary conditions were used along the X, Y and Z directions, the latter being perpendicular to the plane of the monolayer. The simulation box was orthorhombic, with constant Z-dimension Lz, while the other two dimensions (Lx = Ly) were allowed to adjust in response to an imposed surface tension. Three different systems were considered: in the first case the aqueous sub-phase was made of pure water; in the other two it was a concentrated solution of Arg+ and its corresponding counter-ion Cl−. The number of phospholipids, water molecules, amino-acids and chloride ions making up each system is reported in Table 1. Fig. 1 shows a representative configuration of our Langmuir monolayer configuration, together with the molecular structure of DPPC, Arg+ and Cl−. The ellipses highlight the most relevant functional groups. Note that the form of arginine used in this work has three charged moieties, the guanidinium, the carboxylate and the amino groups; while only the choline and the phosphate groups of DPPC bear a whole electrical charge.| System | NDPPC | NArg+ | Nw | [ArgCl] | Lz [nm] |
|---|---|---|---|---|---|
| Pure DPPC | 64 | 0 | ∼4100 | 0 | 12.2 |
DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg (64 Arg (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) 10) |
64 | 10 | ∼6600 | 0.084 | 16.5 |
DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg (64 Arg (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) 20) |
64 | 20 | ∼6600 | 0.168 | 16.5 |
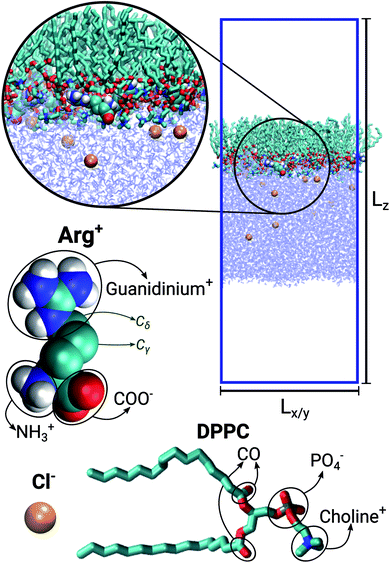 | ||
Fig. 1 Representative snapshot of the DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ARG (64 ARG (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) system. Lz and Lx = Ly indicate the dimensions of the simulation box. Molecular models for chloride, arginine and DPPC. 10) system. Lz and Lx = Ly indicate the dimensions of the simulation box. Molecular models for chloride, arginine and DPPC. | ||
Molecular interactions were modelled combining the force-field of Berger et al.51 for DPPC, with the TIP4P/2005 (ref. 52) water model, as proposed and thoroughly tested by Mohammad-Aghaie et al.25 Arg+ and Cl− were described by the GROMOS-53a6 force-field.53 Long-range coulombic forces were accounted for using the particle mesh Ewald method,54 with a real space cut-off of 1.7 nm, that was also applied to the Lennard-Jones potentials, and a Fourier spacing of 0.16 nm. A dipole correction55 term was used in order to mitigate the effects of the permanent dipole moment of our asymmetric monolayer-water set-up. Simulations were carried out on the NγPzT ensemble, where N is the number of particles, T = 310 K is the temperature, Pz = 1 bar is the normal component of the pressure tensor, and γ is the surface tension. The Berendsen algorithm was used for the thermostat and barostat,56 with time constants of 0.1 and 1.0 ps respectively. Water bond angles and lengths were constrained with the SETTLE57 algorithm, while all the other chemical bonds were constrained with LINCS.58 All calculations were run with the GROMACS 4.5.5 code,59 using an integration time step of 2 fs and a neighbours-list update frequency of 10 MD steps. For the calculation of compression isotherms (Section 3.1), ten different surface tensions were imposed. In the absence of dissolved Arg+, each system was equilibrated for 120 ns and production runs were henceforth extended for another 50 ns. To the final configuration of these simulations, amino-acids, counter-ions and more water, were added to the sub-phase. Systems were then equilibrated for 150 ns and productions runs extended up to at least 250 ns, but in a few cases reached 350 ns. Long simulation times were required to ensure proper equilibration of the interfacial area, as properly discussed in ref. 25.
The free energy profiles reported in Section 3.2 were computed by Umbrella Sampling (US). The reaction coordinate was the Z-distance, d, between the centre of mass of the monolayer and the centre of mass of one Arg+ molecule. 27 US windows, defined by harmonic restraining potentials, uniformly sampled the reaction coordinate between 0 and 3.5 nm. Force-constants ranged from 500 to 3000 kJ (mol−1 Å−2), with the largest values used to sample the penetration of the amino-acid into the monolayer's hydrophobic region. Each US simulation was initiated from the final state of one of the unbiased trajectories used for the calculation of the compression isotherm. After applying the restraining potential to one of the amino-acids, the system was equilibrated for 5 ns, and the simulation was subsequently extended up to 55 ns. Free energy profiles were recovered with the Weighted Histogram Analysis Method (WHAM).60
3 Results and discussion
3.1 Pressure/area isotherm and surface potential
In a typical Langmuir trough experiment the surface pressure, Π, is defined as the reduction in the surface tension of the aqueous sub-phase, γsp, due to the presence of the monolayer:| Π = γsp − γm/sp, | (1) |
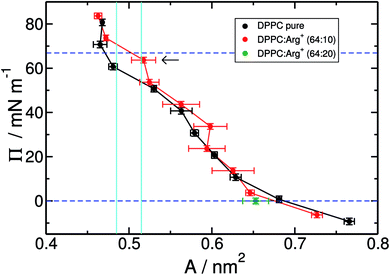
Fig. 2 shows the compression isotherms for DPPC, with and without arginine dissolved in the water slab. Overall, the two isotherms display the signatures of the 2D phases observed in experiments and simulations of DPPC on pure water.25,32,61,62 At 310 K and molecular areas larger than 0.52 nm2, lipids are in the liquid expanded-phase (LE). Below 0.48 nm2 the monolayer is in the liquid-condensed phase (LC). The region in between, delimited by the cyan vertical lines in Fig. 2, corresponds to the LC–LE coexistence region. As a point of comparison, it is worth noticing that in the absence of Arg+ our results closely match the isotherms reported by Mohammad-Aghaie et al.,25 that were computed with the same combination of force-fields but from somewhat shorter MD trajectories.
It is clear from Fig. 2 that the addition of arginine to the sub-phase has little effect on the overall shape of the isotherm, except for a noticeable upward shift on the surface-pressure at coexistence (horizontal arrow in Fig. 2), and much larger area fluctuations within the LE region. As we will see later, these increasing fluctuations, which translate into larger uncertainties on the estimated mean areas per lipid, are the result of the much more sluggish dynamics of the DPPC molecules in the presence of amino-acids. Notice, in particular, that within the LE phase one of the red points (A ∼ 0.6 nm2–Π ∼ 30 mN m−1) seems to lie outside the general trend of the curve. This is most likely due to noise, as the shift from the neighbouring black curve is almost within the error bar of the red point.
The overall similarity between the isotherms could imply that the charged solutes interact very little with the lipid surface, or that they adsorb on the monolayer without greatly altering the lateral packing of DPPC. Visualisation of the simulation trajectories, and a careful analysis of the in-plane (X–Y) radial distribution functions confirms that: (i) Arg+ molecules adsorb and interact specifically with the hydrophilic head of DPPC, without ever leaving the lipid/water interface during the course of 350 ns-long simulations; (ii) Arg+'s remain entirely on the aqueous side of the interface, as illustrated in Fig. 3, but diffuse on the X–Y plane; (iii) chlorides disperse in water forming a cloud of counter-ions; (iv) arginines do not modify in a significant way the X–Y radial distribution function between the alkyl chains, nor the ordering of the lipids' head groups (see Fig. S1 and S2 of ESI†). In addition, one extra simulation performed within the LE phase with twice the amount of dissolved Arg+ (0.168 M), still showed 100% of amino-acid adsorption (right panels in Fig. 3) without a significant impact on the resulting area per lipid (green dot in Fig. 2). Incidentally, atomistic simulations have shown that a large concentration of adsorbed Arg+ has almost no effect on the area per lipid of a zwitterionic DMPC bilayer.63
 | ||
Fig. 3 Lateral and bottom views of instantaneous configurations of the 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (left) and 64 10 (left) and 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 (right) DPPC 20 (right) DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg+ systems. Only DPPC and Arg+ molecules are shown. Arg+ systems. Only DPPC and Arg+ molecules are shown. | ||
The surface potential of a Langmuir layer is a measurable property that can be exploited to probe the binding of molecules to the lipid film.2 It is defined as the change in electrostatic potential, Δϕ, that occurs at a point immediately above the sub-phase, when the monolayer is inserted at the vacuum/liquid interface:
| Δϕ = ϕair/m/sp − ϕair/sp | (2) |
In this equation, ϕair/m/sp and ϕair/sp represent the electrostatic potential above the surface in the presence and absence of the monolayer. These quantities can be readily computed from simulations by double integration of the total charge density perpendicular to the monolayer plane, q(z), according to the following equation:27
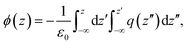 | (3) |
Our results for the DPPC monolayer on pure water, and the 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and 64
10 and 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 DPPC
20 DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
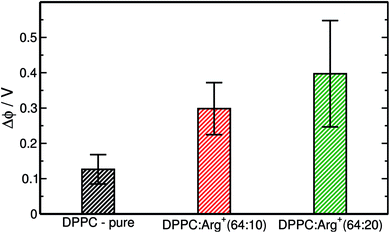
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg+ systems, are presented in Fig. 4. These particular data were computed within the LE phase, at Π ∼ 1 mN m−1, but similar trends are observed at other compression points. The surface potential for DPPC on pure water predicted by our simulations (ΔϕDPPC = 0.13 V) is slightly lower than the experimental values, that range from 0.20 V to 0.45 V.61,64–66 The reason for such discrepancy may well be attributed to the lack of electronic polarisability in our water model,27 an effect that if included in the force-field, would render almost unfeasible the execution of the long simulations required to equilibrate the area per lipid in the presence Arg+. More importantly, Fig. 4 shows that Δϕ increases significantly with the amount of arginine added to the sub-phase, due to the accumulation of positive charge at the interface. This observation suggests that surface potential measurements should be more suitable than compression isotherms to determine the degree of binding of positively charged amino-acids to zwitterionic monolayers.
Arg+ systems, are presented in Fig. 4. These particular data were computed within the LE phase, at Π ∼ 1 mN m−1, but similar trends are observed at other compression points. The surface potential for DPPC on pure water predicted by our simulations (ΔϕDPPC = 0.13 V) is slightly lower than the experimental values, that range from 0.20 V to 0.45 V.61,64–66 The reason for such discrepancy may well be attributed to the lack of electronic polarisability in our water model,27 an effect that if included in the force-field, would render almost unfeasible the execution of the long simulations required to equilibrate the area per lipid in the presence Arg+. More importantly, Fig. 4 shows that Δϕ increases significantly with the amount of arginine added to the sub-phase, due to the accumulation of positive charge at the interface. This observation suggests that surface potential measurements should be more suitable than compression isotherms to determine the degree of binding of positively charged amino-acids to zwitterionic monolayers.
3.2 Energetics of arginine adsorption on DPPC
Insight into the bonding of Arg+ to the lipid phase was gained by computing the adsorption free energy profile for a single amino-acid molecule approaching the monolayer. Two simulation conditions were considered: the monolayer supported on pure water, and the 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 DPPC
20 DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg+ system of Fig. 2, where 20 amino-acids were pre-adsorbed on the interface. The latter system allowed for the assessment of adsorbate concentration on the binding free energy. Both systems were prepared and maintained in the LE phase during the umbrella sampling simulations, by applying a lateral pressure of 10 mN m−1.
Arg+ system of Fig. 2, where 20 amino-acids were pre-adsorbed on the interface. The latter system allowed for the assessment of adsorbate concentration on the binding free energy. Both systems were prepared and maintained in the LE phase during the umbrella sampling simulations, by applying a lateral pressure of 10 mN m−1.
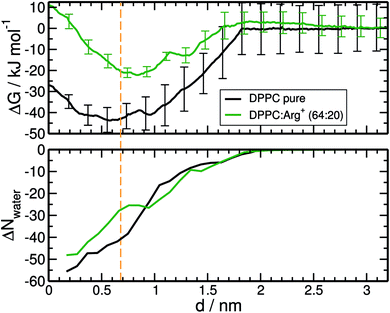
The resulting free energy profiles are presented in the upper panel of Fig. 5. They both show a deep minimum near the plane defined by the PO4− groups of DPPC (marked with the orange vertical line), indicating that adsorption is highly favourable, and explaining why the amino-acids never detach from the interface during the course of the unbiased MD trajectories reported in the previous section. The computed adsorption energies are −43.8 kJ mol−1 for DPPC on pure water, and −22.2 kJ mol−1 for the highly concentrated 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 system, with minima located at 0.58 and 0.84 nm respectively. The concentration dependence of the binding energy can be ascribed to a combination of electrostatic repulsion between the approaching Arg+ and those already present at the interface, and the reduced availability of binding sites when the monolayer is partially covered with amino-acids. As discussed below, Arg+ interacts specifically with the PO4− and CO groups of DPPC. It is also noticeable that electrostatic repulsion with the pre-adsorbed molecules introduces a small activation barrier of around 3.3 kJ mol−1.
20 system, with minima located at 0.58 and 0.84 nm respectively. The concentration dependence of the binding energy can be ascribed to a combination of electrostatic repulsion between the approaching Arg+ and those already present at the interface, and the reduced availability of binding sites when the monolayer is partially covered with amino-acids. As discussed below, Arg+ interacts specifically with the PO4− and CO groups of DPPC. It is also noticeable that electrostatic repulsion with the pre-adsorbed molecules introduces a small activation barrier of around 3.3 kJ mol−1.
As with any ion-transfer reaction,67 the number of water molecules in the first solvation shell of Arg+ changes during the adsorption process. This was quantified by counting the number of water molecules within a cut-off distance of 0.9 nm, computed from the mid point between atoms Cγ and Cδ of the amino-acid (see Fig. 1). Such combination of cut-off and reference point guarantees the inclusion of the water molecules associated to all the functional groups of Arg+. In the bulk of the sub-phase, the so defined arginine solvation shell contains 64 molecules, no matter the number of pre-adsorbed arginines or counter-ions. As the amino-acid approaches the monolayer it loses water of solvation, but to a certain extent that depends on the composition of the system. This can be seen from the bottom panel of Fig. 5, that shows the change in the number of solvating water molecules as a function of the distance to the monolayer. As the approaching Arg+ reaches the plane of the PO4− groups, i.e. near the minimum of the free-energy curve, it retains much more water when other amino-acids are already present at the interface (ΔN ∼ −27 vs. ΔN ∼ −41). This happens because, at high interfacial concentrations, arginines tend to align vertically with respect to the monolayer plane, retaining thus a larger fraction of solvation shell upon adsorption (right panels Fig. 3). At low concentrations they tend to flatten on the interface (left panels Fig. 3) and keep a smaller solvation shell.
Specific intermolecular contacts between the most relevant functional groups of Arg+ and DPPC (Fig. 1), were identified by analysing mutual coordination numbers (computed up to the first minimum of the corresponding radial distribution functions) and the average number of hydrogen bonds. The results are summarised in Table 2. Each horizontal entry has been split into two rows. The upper ones correspond to the 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 DPPC
10 DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg+ system, and the bottom ones to the 64
Arg+ system, and the bottom ones to the 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 concentration.
20 concentration.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 DPPC
10 DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg+ system, and the bottom rows to the 64
Arg+ system, and the bottom rows to the 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 concentration
20 concentration
| Arg+/DPPC | H-Bonds | Coord. number | |||
|---|---|---|---|---|---|
| PO4− | CO | PO4− | CO | Choline+ | |
| NH3+ | 1.2 ± 0.2 | 1.6 ± 0.2 | 1.31 | 1.79 | — |
| 1.5 ± 0.1 | 1.1 ± 0.1 | 1.66 | 0.36 | ||
| Guanidinium+ | 1.5 ± 0.3 | 1.2 ± 0.2 | 1.78 | 1.87 | — |
| 1.3 ± 0.2 | 0.8 ± 0.2 | 1.46 | 1.38 | ||
| COO− | — | — | — | — | 2.10 |
| 1.84 | |||||
| Total | 5.6 ± 0.4 | 8.85 | |||
| 4.8 ± 0.3 | 6.70 | ||||
NH3+ and guanidinium+ form close and directional contacts with the PO4− and CO moieties of DPPC, with populations determined by the surface concentration of amino-acids. As stated before, at high concentration, Arg+ molecules align vertically with respect to the interface. This is reflected by the decrease in NH3+–CO coordination and H-bond numbers, and the concomitant increase in PO4−–NH3+ contacts. At the same time, the guanidinium+ groups lose coordination and binding to both PO4− and CO, as the carboxylate moiety (COO−) gets farther away from the choline moiety of DPPC. In support of our findings, a number of spectroscopic measurements performed on vesicles and Langmuir monolayers,68–71 have shown clear changes on the stretching mode of the CO and PO4− groups of several phospholipids upon adsorption of positively charged molecules, including amino-acids. These observations have been interpreted in terms of changes of hydration and hydrogen-bonding patterns. Also, previous simulations of Arg+ in contact with a DMPC bilayer have demonstrated that the guanidinium+ groups interact with the PO4−, displacing at most two water molecules per amino-acid.63
3.3 Arginine modulates the lateral mobility of DPPC
As discussed in the previous sections, arginine binds tightly to the lipids' head groups while retaining lateral mobility. This may affect the diffusivity of the lipids in varying extends, depending on the contact dynamics between the amino-acids and the DPPC molecules. Assessing the impact of adsorbates on the diffusion coefficient of the lipids is important, not only to understand how the sub-phase composition affects the molecular dynamics of the monolayer, but also because transport coefficients can be measured experimentally.72 Diffusion coefficients may then provide an alternative, or complementary, way of sensing amino-acid–lipid interactions in LM set-ups.The lateral mean-square displacement of DPPC was computed at different lateral pressures for each of the systems described in Table 1. As expected, within the LC phase the lipids' dynamics are very sluggish, making the evaluation of diffusion coefficients from simulations too uncertain. Within the LE phase, the DPPC molecules move more readily and diffusion coefficients, D, could be reliably computed using the Einstein relation.73 Fig. 6 collects the results obtained at a lateral pressure of ∼1 mN m−1. It is clear that the presence of Arg+ in the sub-phase has a drastic effect on the lateral mobility of DPPC. For the monolayer supported on pure water D = 1.3 × 10−7 cm2 s−1, while the experimental values for DPPC in the LE phase range from 1.0 × 10−7 to 5 × 10−7 cm2 s−1.72,74–76 Arg+ lowers the diffusivity of the lipids by one order of magnitude, leading to D ∼ 1.0 × 10−8 cm2 s−1, independently of the amino-acid concentration.
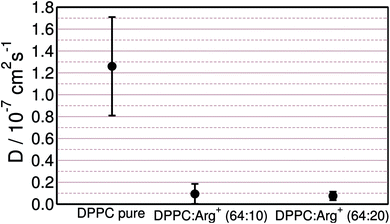 | ||
Fig. 6 DPPC self-diffusion coefficients computed for the monolayer on pure water, and the 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and 64 10 and 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 DPPC 20 DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg+ systems, at Π ∼ 1 mN m−1. Arg+ systems, at Π ∼ 1 mN m−1. | ||
The reason for the decrease in self-diffusion coefficients is the formation of small DPPC clusters held together by a single Arg+ molecule. As discussed in Section 3.2, the molecular contacts that confer stability to the binding of arginine to DPPC occur between the cationic groups of the amino-acid and the PO4− and CO groups. However, the mere existence of such contacts does not necessarily explain the slowdown of the lipids mobility, as contacts could break and form quickly.
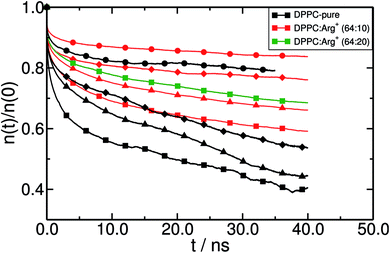
In order to gain insight into the dynamical behaviour of the small DPPC clusters, we computed a “cage correlation function” n(t), as described in ref. 77. n(t) monitors the rate at which DPPC molecules interchange their closest partners. This is done by identifying all the neighbours of each lipid within a cut-off distance Rc at time to = 0, and computing the average number of molecules still belonging to the same coordination shell at any later time t. In our simulations, Rc = 0.75 nm, which corresponds to the first minimum of the radial distribution function between the PO4− groups. The results are presented in Fig. 7. Clearly, Arg+ reduces the rate of first-neighbours exchange, which translates into longer lifetimes of the DPPC aggregates that the amino-acids help keeping together. The effect can be detected at all surface pressures, but is systematically more evident within the LE phase. Also, note that increasing the concentration of Arg+ increases the lifetime of the lipid's first coordination shell (compare the green and red lines with squares, in Fig. 7).
4 Conclusions
We have investigated by means of molecular dynamics simulations how and to what extent arginine affects the compression isotherm, the interfacial potential, and the lateral mobility of the lipids in a Langmuir monolayer. Free energy calculations show that Arg+ binds strongly to the DPPC hydrophilic surface, with adsorption energies of −43.8 kJ mol−1 for the bare interface, and −22.2 kJ mol−1 in the case of the monolayer pre-covered with Arg+ (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 DPPC
20 DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg+ ratio). The large binding energy to the bare surface can be attributed to hydrogen bonding between the charged moieties of Arg+ and the PO4− and CO groups of DPPC, which compensates for changes in the levels of hydration of the lipids and the amino-acid upon adsorption. As the concentration of pre-adsorbed amino-acids increases, arginine molecules align more vertically with respect to the plane of the monolayer, and electrostatic repulsion lowers the binding energy and even introduces a small activation barrier (∼3.3 kJ mol−1) on the adsorption free-energy profile.
Arg+ ratio). The large binding energy to the bare surface can be attributed to hydrogen bonding between the charged moieties of Arg+ and the PO4− and CO groups of DPPC, which compensates for changes in the levels of hydration of the lipids and the amino-acid upon adsorption. As the concentration of pre-adsorbed amino-acids increases, arginine molecules align more vertically with respect to the plane of the monolayer, and electrostatic repulsion lowers the binding energy and even introduces a small activation barrier (∼3.3 kJ mol−1) on the adsorption free-energy profile.
Apart from a small upward shift on the surface-pressure at coexistence, Arg+ does not greatly affect the compression isotherm of DPPC at 310 K. This happens because, both in the LC and LE phase, the amino-acids remain on the aqueous side of the interface without showing significant insertion between the lipids. In fact, at the highest surface concentration explored, a population of arginine molecules hang vertically from the monolayer plane and into the aqueous phase. However, the accumulation of interfacial charge has a significant effect on the interfacial potential, that goes from 0.13 V for the bare lipid/water interface, to 0.40 V when the DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg+ ratio is 64
Arg+ ratio is 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20.
20.
The dynamical properties of the lipids are strongly affected by the presence of Arg+ in the sub-phase. At an even moderate concentration of amino-acid (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 DPPC
10 DPPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Arg+), the self-diffusion coefficient of DPPC decreases in one order of magnitude with respect to that of the monolayer supported on pure water. This is due to the formation of transient, but long-lived, DPPC–Arg+ complexes that increase the average caging time of the lipids. In these complexes, each arginine molecule connects to one, or bridges together two or three lipid molecules.
Arg+), the self-diffusion coefficient of DPPC decreases in one order of magnitude with respect to that of the monolayer supported on pure water. This is due to the formation of transient, but long-lived, DPPC–Arg+ complexes that increase the average caging time of the lipids. In these complexes, each arginine molecule connects to one, or bridges together two or three lipid molecules.
Ultimately, we have shown that the strong adsorption of Arg+ on DPPC has little impact on the lateral mechanical properties of the monolayer, but has a significant and measurable effect on its electrical and dynamical properties. We believe that our results provide new molecular-level insight into the interfacial behaviour of self-assembled lipid structures doped with highly hydrophilic amino-acids.
Acknowledgements
The authors thank CONICET, SECTyP-UNCUYO, and FONCyT (PICT-2012-2759) for research funding. We are also grateful to the EU Commission Marie Curie RISE “ENACT” Programme (643998), and SNCAD-MinCyT for computer time allocation in the clusters Mendieta (CCAD-UNC) and Toko (UNCUYO).References
- Y.-H. M. Chan and S. G. Boxer, Curr. Opin. Chem. Biol., 2007, 11, 581–587 CrossRef CAS PubMed.
- H. Brockman, Curr. Opin. Chem. Biol., 1999, 9, 438–443 CAS.
- V. M. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779–819 CrossRef CAS.
- G. Brezesinski and H. Möhwald, Adv. Colloid Interface Sci., 2003, 100, 563–584 CrossRef PubMed.
- R. Maget-Dana, Biochim. Biophys. Acta, Biomembr., 1999, 1462, 109–140 CrossRef CAS.
- E. Maltseva and G. Brezesinski, ChemPhysChem, 2004, 5, 1185–1190 CrossRef CAS PubMed.
- A. Won and A. Ianoul, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2277–2283 CrossRef CAS PubMed.
- L. Caseli, D. C. Masui, R. P. Furriel, F. A. Leone, M. E. Zaniquelli, J. Orbulescu and R. M. Leblanc, J. Colloid Interface Sci., 2008, 320, 476–482 CrossRef CAS PubMed.
- M. M. Domon, M. N. Nasir, S. Pikula and F. Besson, J. Colloid Interface Sci., 2013, 403, 99–104 CrossRef CAS PubMed.
- Z. Kozarac, B. Ćosović, D. Möbius and M. Dobrić, J. Colloid Interface Sci., 2000, 226, 210–217 CrossRef CAS.
- F. J. Pavinatto, A. Pavinatto, L. Caseli, D. S. dos Santos, T. M. Nobre, M. E. Zaniquelli and O. N. Oliveira, Biomacromolecules, 2007, 8, 1633–1640 CrossRef CAS PubMed.
- M. N. Antipina, I. Schulze, M. Heinze, B. Dobner, A. Langner and G. Brezesinski, ChemPhysChem, 2009, 10, 2471–2479 CrossRef CAS PubMed.
- M. Dittrich, M. Bottcher, J. S. L. Oliveira, B. Dobner, H. Mohwald and G. Brezesinski, Soft Matter, 2011, 7, 10162–10173 RSC.
- S. A. Kane and S. D. Floyd, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 8400–8408 CrossRef CAS.
- S.-Y. Choi, S.-G. Oh and J.-S. Lee, Colloids Surf., B, 2001, 20, 239–244 CrossRef CAS PubMed.
- M. Gagoś, J. Gabrielska, M. D. Serra and W. I. Gruszecki, Mol. Membr. Biol., 2005, 22, 433–442 CrossRef PubMed.
- K. Hąc-Wydro, J. Kapusta, A. Jagoda, P. Wydro and P. Dynarowicz-Łątka, Chem. Phys. Lipids, 2007, 150, 125–135 CrossRef PubMed.
- A. Karewicz, D. Bielska, B. Gzyl-Malcher, M. Kepczynski, R. Lach and M. Nowakowska, Colloids Surf., B, 2011, 88, 231–239 CrossRef CAS PubMed.
- S.-S. Feng, K. Gong and J. Chew, Langmuir, 2002, 18, 4061–4070 CrossRef CAS.
- A. T. Jones and E. J. Sayers, J. Controlled Release, 2012, 161, 582–591 CrossRef CAS PubMed.
- P. Ahlstrom and H. J. C. Berendsen, J. Phys. Chem., 1993, 97, 13691–13702 CrossRef CAS.
- Y. N. Kaznessis, S. Kim and R. G. Larson, Biophys. J., 2002, 82, 1731–1742 CrossRef CAS PubMed.
- S. K. Kandasamy and R. G. Larson, Biophys. J., 2005, 88, 1577–1592 CrossRef CAS PubMed.
- M. Pickholz, O. N. Oliveira and M. S. Skaf, Biophys. Chem., 2007, 125, 425–434 CrossRef CAS PubMed.
- D. Mohammad-Aghaie, E. Macé, C. A. Sennoga, J. M. Seddon and F. Bresme, J. Phys. Chem. B, 2010, 114, 1325–1335 CrossRef CAS PubMed.
- H.-Z. Gang, J.-F. Liu and B.-Z. Mu, J. Phys. Chem. B, 2011, 115, 12770–12777 CrossRef CAS PubMed.
- T. R. Lucas, B. A. Bauer, J. E. Davis and S. Patel, J. Comput. Chem., 2012, 33, 141–152 CrossRef CAS PubMed.
- M. Chen, X. Lu, X. Liu, Q. Hou, Y. Zhu and H. Zhou, Langmuir, 2014, 30, 10600–10607 CrossRef CAS PubMed.
- C.-P. Kong, E. Peters, Q.-C. Zheng and H.-X. Zhang, et al., Phys. Chem. Chem. Phys., 2014, 16, 9634–9642 RSC.
- M. Gorczyca, B. Korchowiec, J. Korchowiec, S. Trojan, J. Rubio-Magnieto, S. V. Luis and E. Rogalska, J. Phys. Chem. B, 2015, 119, 6668–6679 CrossRef CAS PubMed.
- W. Lin, A. J. Clark and F. Paesani, Langmuir, 2015, 31, 2147–2156 CrossRef CAS PubMed.
- S. L. Duncan and R. G. Larson, Biophys. J., 2008, 94, 2965–2986 CrossRef CAS PubMed.
- A. J. Kox, J. P. J. Michels and F. W. Wiegel, Nature, 1980, 287, 317–319 CrossRef CAS.
- J. Harris and S. A. Rice, J. Chem. Phys., 1988, 89, 5898–5908 CrossRef CAS.
- S. Karaborni and S. Toxvaerd, J. Chem. Phys., 1992, 96, 5505–5515 CrossRef CAS.
- S. O. Nielsen, C. F. Lopez, P. B. Moore, J. C. Shelley and M. L. Klein, J. Phys. Chem. B, 2003, 107, 13911–13917 CrossRef CAS.
- S. Baoukina, L. Monticelli, S. J. Marrink and D. P. Tieleman, Langmuir, 2007, 23, 12617–12623 CrossRef CAS PubMed.
- J. Giner-Casares, L. Camacho, M. Martin-Romero and J. Lopez Cascales, Langmuir, 2008, 24, 1823–1828 CrossRef CAS PubMed.
- W. Shinoda, R. DeVane and M. L. Klein, J. Phys. Chem. B, 2010, 114, 6836–6849 CrossRef CAS PubMed.
- V. Miguel, M. A. Perillo and M. A. Villarreal, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2903–2910 CrossRef CAS PubMed.
- E. Harder and B. Roux, J. Chem. Phys., 2008, 129, 234706 CrossRef PubMed.
- J. Chowdhary, E. Harder, P. E. M. Lopes, L. Huang, A. D. MacKerell and B. Roux, J. Phys. Chem. B, 2013, 117, 9142–9160 CrossRef CAS PubMed.
- E. Harder, A. D. MacKerell Jr and B. Roux, J. Am. Chem. Soc., 2009, 131, 2760–2761 CrossRef CAS PubMed.
- G. Casares, J. José, L. Camacho, M. T. Martín-Romero and J. J. López Cascales, ChemPhysChem, 2008, 9, 2538–2543 CrossRef PubMed.
- B. Liu, M. I. Hoopes and M. Karttunen, J. Phys. Chem. B, 2014, 118, 11723–11737 CrossRef CAS PubMed.
- G. Casares, J. José, L. Camacho, M. T. Martín-Romero and J. J. López Cascales, ChemPhysChem, 2010, 11, 2241–2247 CrossRef PubMed.
- J. A. Freites, Y. Choi and D. J. Tobias, Biophys. J., 2003, 84, 2169–2180 CrossRef CAS PubMed.
- C. Laing, S. Baoukina and D. P. Tieleman, Phys. Chem. Chem. Phys., 2009, 11, 1916–1922 RSC.
- L. Li, I. Vorobyov and T. W. Allen, J. Phys. Chem. B, 2013, 117, 11906–11920 CrossRef CAS PubMed.
- C. Schwieger and A. Blume, Biomacromolecules, 2009, 10, 2152–2161 CrossRef CAS PubMed.
- O. Berger, O. Edholm and F. Jähnig, Biophys. J., 1997, 72, 2002 CrossRef CAS PubMed.
- J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- C. Oostenbrink, T. A. Soares, N. F. A. van der Vegt and W. F. van Gunsteren, Eur. Biophys. J., 2005, 34, 273–284 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- I.-C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, et al., J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- V. L. Shapovalov, E. A. Kotova, T. I. Rokitskaya and Y. N. Antonenko, Biophys. J., 1999, 77, 299–305 CrossRef CAS PubMed.
- A. Rosengarth, A. Wintergalen, H.-J. Galla, H.-J. Hinz and V. Gerke, FEBS Lett., 1998, 438, 279–284 CrossRef CAS PubMed.
- F. E. Herrera, A. Bouchet, F. Lairion, E. A. Disalvo and S. Pantano, J. Phys. Chem. B, 2012, 116, 4476–4483 CrossRef CAS PubMed.
- H. Nakahara, S. Nakamura, H. Kawasaki and O. Shibata, Colloids Surf., B, 2005, 41, 285–298 CrossRef CAS PubMed.
- A. M. Farnoud and J. Fiegel, J. Phys. Chem. B, 2013, 117, 12124–12134 CrossRef CAS PubMed.
- D. S. Alvares, M. L. Fanani, J. R. Neto and N. Wilke, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 393–402 CrossRef CAS PubMed.
- W. Schmickler, Electrochim. Acta, 1996, 41, 2329–2338 CrossRef CAS.
- W. Hübner and A. Blume, Chem. Phys. Lipids, 1998, 96, 99–123 CrossRef.
- A. Hädicke and A. Blume, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 1196–1206 CrossRef PubMed.
- V. P. Geraldo, F. J. Pavinatto, T. M. Nobre, L. Caseli and O. N. Oliveira, Chem. Phys. Lett., 2013, 559, 99–106 CrossRef CAS.
- M. Dyck, A. Kerth, A. Blume and M. Lösche, J. Phys. Chem. B, 2006, 110, 22152–22159 CrossRef CAS PubMed.
- F. Caruso, F. Grieser, P. J. Thistlethwaite and M. Almgren, Biophys. J., 1993, 65, 2493–2503 CrossRef CAS PubMed.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford university press, 1989 Search PubMed.
- R. Peters and K. Beck, Proc. Natl. Acad. Sci. U. S. A., 1983, 80, 7183–7187 CrossRef CAS.
- M. Gudmand, M. Fidorra, T. Bjørnholm and T. Heimburg, Biophys. J., 2009, 96, 4598–4609 CrossRef CAS PubMed.
- D.-W. Jeong, K. Kim, S. Lee, M. C. Choi and S. Q. Choi, Langmuir, 2014, 30, 14369–14374 CrossRef CAS PubMed.
- M. G. Del Pópolo, C. L. Mullan, J. D. Holbrey, C. Hardacre and P. Ballone, J. Am. Chem. Soc., 2008, 130, 7032–7041 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra05359b |
| This journal is © The Royal Society of Chemistry 2017 |