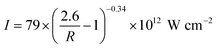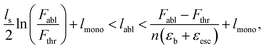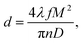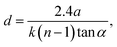Femtosecond laser-induced breakdown spectroscopy
Timur A.
Labutin
*a,
Vasily N.
Lednev
b,
Alexey A.
Ilyin
cd and
Andrey M.
Popov
a
aDepartment of Chemistry, Lomonosov Moscow State University, Leninskie Gory, 1-3, 119991, Moscow, Russia. E-mail: timurla@laser.chem.msu.ru
bNational University of Science and Technology “MISiS”, Leninskiy Prospect, 2, 119049, Moscow, Russia. E-mail: vasilylednev@gmail.com
cFar Eastern Federal University, Sukhanova Street, 8, 690950, Vladivostok, Russia. E-mail: kunashir@gmail.com
dInstitute of Automation and Control Processes of FEB RAS, Radio Street, 5, 690041, Vladivostok, Russia
First published on 30th October 2015
Abstract
The presented review summarizes nearly two decades of studies on femtosecond laser-induced breakdown spectrometry (fs-LIBS). When an ultra-short (<1 ps) laser pulse is used for ablation, the physics of laser-induced plasma changes dramatically in comparison with ablation by pico or nanosecond pulses. A femtosecond laser pulse interacts only with the electron subsystem, while nanosecond pulses continuously interact with different thermodynamic states of material, starting from solid through liquid into plasma. The properties of ultra-short laser radiation, the timescale of fs-laser ablation and the radiative properties of fs plasma are briefly described. We consider the advantages of fs-LIBS, namely, low ablation thresholds, high-spatial resolution, and rapid analysis of samples, which require minimal invasion and allow high-efficiency transportation of laser radiation in filamentation mode for remote analysis. Moreover, we discussed possible limitations of the technique and different approaches to overcome such constraints while retaining the unique possibilities of fs-LIBS.
1 Introduction
A pulsed solid-state Nd:YAG laser with nanosecond pulse duration is a typical “workhorse” for a laser-induced breakdown spectrometry setup. A perspective tool became available for novel LIBS applications with the development of a new generation of ultra-short laser systems with femtosecond pulse duration in the late 1980s. Femtosecond laser-induced breakdown spectrometry (fs-LIBS) can improve figures of merit for LIBS quantitative analysis (e.g. better reproducibility, absence of fractional evaporation and reduction in damage) due to changes in laser–matter interaction.Fs-LIBS has made a long “journey” of more than 25 years from the generation of the first ultrashort pulses to elemental analysis. The first generation of femtosecond laser pulses was demonstrated in 1970s;1 the invention of Ti:Sapphire laser in the 1980s attracted growing attention to femtosecond systems.2 The invention of the chirped-pulse amplification technique in 1985 was a revolutionary breakthrough in femtosecond laser systems, resulting in the appearance of powerful femtosecond laser pulses.3 The first plasma spectroscopy studies induced by femtosecond pulses (700 fs) were carried out four years later and were mainly focused on plasma physics problems.4 The rapid growth of publications on femtosecond laser plasma started when powerful commercial laser systems became available. The first emission spectrum for femtosecond laser plasma was ascribed to controlled laser machining in 1998.5 The first application of femtosecond pulses to analytical chemistry problems was demonstrated only in 2000 by Margetic et al.6 Seven years later, Gurevich and Hergenröder7 presented the first review on the achievements and future perspectives of fs-LIBS. After this review, numerous studies on fs-LIBS have been published. In the current review, we summarized the state-of-the-art findings in studies of femtosecond ablation and plasma physics, instrumentation and applications.
Ultrashort pulse duration gave numerous benefits with respect to fs-LIBS: low ablation threshold, absence of fractionation vaporization, improved spatial resolution for 3D mapping applications, small ablated mass, and reduced sample damage. All these benefits originate from the physics of femtosecond ablation and plasma, which are described in Section 2. In Section 3, we summarize the analytical performance of fs-LIBS and discuss its perspectives. The possibility of high-efficiency transportation of laser radiation in filamentation mode for remote analysis and applications of filaments in LIBS, which is also called filament-induced breakdown spectroscopy (FIBS), are discussed in Section 4. Special attention is given to the comparison of analytical figures of merit (sensitivity, accuracy, and precision) as well as unique applications (filament-induced breakdown spectroscopy).
2 Fundamentals of femtosecond laser-induced plasmas
2.1 Properties of ultra-short laser radiation and typical equipment
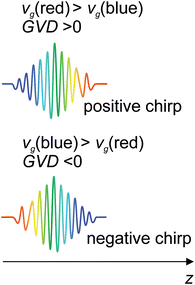
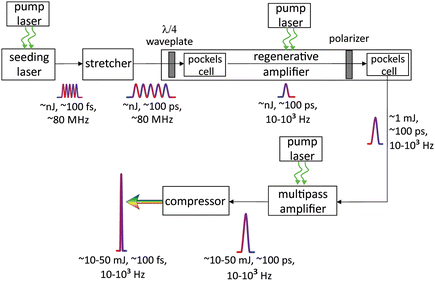
Femtosecond pulse generation is based on Kerr lensing in the gain medium8,9 and a Ti:Sapphire crystal is commonly used for this purpose. In contrast to a nanosecond laser (Q-switched), the output energy of femtosecond oscillators (∼1 nJ) is clearly insufficient to exceed a threshold for plasma generation. Therefore, a femtosecond laser for LIBS is supposed to use one or more additional amplifiers to a seeding laser, as shown in Fig. 1. Normally, the seeding laser produces a train of femtosecond pulses with a central wavelength near 800 nm and a repetition rate of ∼80 MHz. A femtosecond pulse can be broadened due to a self-phase modulation in the media with a nonlinear refractive index and group velocity dispersion (GVD) by optical elements of the laser. The pulse duration of the seeding laser can be tuned by modifying the GVD of the cavity, which is determined as follows:where k(ω) is the wave vector and vg is the group velocity. One can easily see that the group velocity is different for various wavelengths. The influence of the dispersion properties of a material on the instantaneous frequency of a femtosecond pulse is characterized by a chirp. The pulse is said to be positively “chirped” when the instantaneous frequency is red-shifted in a pulse front and blue-shifted in a trail, as shown in Fig. 2.
 | ||
| Fig. 1 Typical scheme of femtosecond laser system. Pulse repetition rate is reduced to 1–10 Hz for systems with pulse energy exceeding 10 mJ. | ||
The positive chirp of intracavity elements can be compensated by the media with a negative GVD-like grating or prism pairs to obtain short output pulses.
To avoid damage to the Ti:Sapphire crystal, it is essential to keep the power density in the amplifier below the Ti:Sapphire damage threshold. This can be achieved using a chirped pulse amplification technique, which incorporates a stretcher that reduces power and broadening pulses before they enter a regenerative amplifier with consequent narrowing of pulses by a compressor after amplification. Usually, the stretcher and compressor represent a pair of gratings or prisms. The pulse repetition rate is reduced to 10 to 103 Hz by Pockels cells to provide maximal amplification without overheating the gain medium in a regenerative amplifier. Thus, the pulse energy increases from several nJ to roughly mJ level. The amplification in a multipass amplifier is limited by the number of passes (usually 2–8) due to difficulties in focusing into a single Ti:Sapphire rod. Finally, a pulse is usually compressed down to a duration of 30–500 fs, although sub-4 fs pulses can be obtained in specially designed laser systems.10,11 Femtosecond pulses are also broadened by optical components of the LIBS system. The output pulse duration for a Gaussian transform-limited pulse is determined as follows:9
The temporal profile of the femtosecond laser pulse and the intensities of the pulse components are of key importance in laser–target interaction. During generation, amplification, and spectral and temporal shaping, a number of physical processes affect the temporal shape of the pulse. The final pulse may consist of pre-pulses, post-pulses and a main pulse on top of a very broad pedestal (see Fig. 3).12,13 This nanosecond pedestal or amplified spontaneous emission (ASE), corresponds to noise photons amplifying in the same way as the main pulse. The ASE duration does not exceed 10 ns and may contain up to 25% of the total pulse energy,14 with the ratio of the peak intensity of the main pulse to the peak intensity of the ASE ∼ 105 to 108 (contrast ratio).12,13 Pre- and post-pulses are caused by Fresnel reflections in optical elements12,13 and radiation leakage out of the regenerative amplifier on each pass of a beam in a cavity.7 Their durations are greater than or equal to the main pulse, and the contrast ratio varies over a wide range from 102 to 108, depending on the laser system. Pre-pulses can create plasma before the arrival of a main pulse, leading to a reduction in the main pulse energy deposition in an analyzed sample.13 Saturable absorbers, frequency doubling and additional Pockels cells can be used to correct temporal shape and improve contrast ratio. Usually, pulse duration and temporal shape are controlled by fast photodiodes, streak cameras and auto- and cross-correlation methods.9
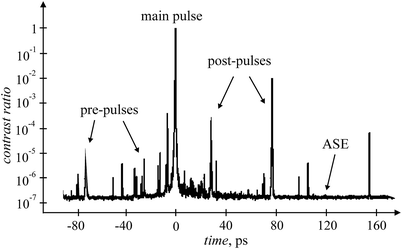 | ||
| Fig. 3 Temporal profile of fs laser pulse with ASE, pre- and post-pulses obtained by a 3rd order cross-correlator. | ||
2.2 Filamentation
Visually, a laser-induced filament in air represents a long, luminous thread due to emission of the first negative system of N2+ B2Σu+ → X2Σg+ and the second positive system of N2 C3Πu → B3Πg. A filament can appear at a high peak laser intensity. A theoretical estimation was carried out by Chiao et al.15 in 1964. Although the first filament was induced in liquids by powerful nanosecond pulses in 1965,16 it was observed in air only in 1995 when powerful femtosecond laser systems with a peak power of several GW became available.17 Therefore, filamentation in the atmosphere has been a subject of intensive investigation over the past two decades. Generally, these investigations are related to the self-focusing of laser beams, conical emission, and supercontinuum generation.18–20 A detailed description of filament physics and applications can be found in several reviews.21–24Filamentation arises due to strong spatiotemporal self-modulation of femtosecond pulses, i.e. self-focusing initiates a plasma that defocuses the propagating laser beam. A series of self-focusing events from the front part of the pulse gives rise to the luminous plasma channel or so-called filament. The back part of the pulse experiences self-phase modulation and self-stepping, resulting in strong spectral broadening (supercontinuum). On average, the filamentation area is 50–200 μm in diameter and its length varies depending on pulse power, medium and laser wavelength.23,25 A continuous filament was observed with a length of ∼100 m (ref. 26) and, more recently, up to 1 km.27 It should be noted that tuning of pulse chirping allows precise control of filament initiation at desired distances up to 20 km.28
For a laser radiation, the power of which exceeds a self-focusing threshold in the air (1.7–10 GW for λ = 800 nm),29–31 many filaments emerge due to non-homogeneity of intensity distribution in the cross-section of the laser beam21,22 and (pre-)post-pulse filamentation.32 For weakly focused laser beams, intensity clamping is observed as a consequence of balance between Kerr-type self-focusing and plasma induced defocusing. In an air filament, the intensity does not exceed the threshold value of ∼5 × 1013 W cm−2 even with an increase in the femtosecond pulse energy.23,33 This situation corresponds to a low NA (numerical aperture < 3–5 × 10−3) or a nonlinear focusing regime in filamentation.34 In the case of a high-NA or a linear focusing regime, geometrical focusing and plasma defocusing are the primary contributors to the filamentation process, while Kerr-type self-focusing plays a secondary role. In this case, the intensity exceeds the threshold value of 5 × 1013 W cm−2.33,35 Xu et al.33 suggested a simple formula for the estimation of the intensity of the laser radiation in the filament:
Electron density in plasma filaments varies from 1014 to 1018 cm−3, depending on the experimental conditions.29,36–38 Basically, electrons appear due to multiphoton ionization (MPI); the ionization rate is proportional to IK, where K is the number of absorbed photons necessary to ionize molecules. Ionization potentials of air molecules are 15.6 eV (N2) and 12.1 eV (O2). Therefore, K(O2) = 8 and K(N2) = 11 for λ = 800 nm (photon energy is 1.55 eV). Kasparian et al.39 have shown that K(O2) ≈ 6.5 and K(N2) ≈ 7.5 for intensity I < 1014 W cm−2, indicating the occurrence of tunnel ionization (TI). In other words, at such intensities, electrons in a molecule pass through the potential barrier and escape from the molecule. Electron avalanche ionization is characteristic of plasma induced by ns pulses. Seed electrons starting an avalanche arise due to MPI of impurities with low ionization potential.40 The energy of the electrons is then increased by an inverse Bremsstrahlung effect, i.e. electrons absorb photons in the field of ions or atoms (molecules). This process requires approximately 350 fs in air.41 Thus, electron avalanche ionization can also take place in filaments induced by laser pulses with durations exceeding this value. For I < 2 × 1014 W cm−2, photoelectrons ejected from molecules have an initial kinetic energy of a few eV, which corresponds to an initial free-electron temperature of ∼104 to 105 K.42,43 These values are much smaller than initial temperature (60 eV) of plasma induced by ns pulse with I = 2 × 1011 W cm−2.44 This is why electron density in filaments is less than that of nanosecond plasma, which can reach critical values of 1.7 × 1021 cm−3 (at λ = 800 nm). It is interesting to note that the velocity of filament expansion is 2 × 108 m s−1,32 which is close to the speed of light. In the case of a ns pulse, plasma expanding due to single photon UV and avalanche ionization has velocity = ∼105 m s−1.45
In contrast to extensive studies on self-focusing, harmonics and supercontinuum generation, molecular and atomic emission of plasma generated by laser filamentation is less investigated. Temporal characteristics of atomic and molecular emission of laser plasma filaments can be found in ref. 21 and 46–48. The application of laser filamentation to spectrochemical analysis will be considered in Section 4.
2.3 Interaction of femtosecond pulses with condensed matter
Negligible heat transfer from the irradiated area and an absence of plasma–laser interactions are the main features of femtosecond laser ablation in comparison with its nanosecond equivalent. Therefore, absorbed laser energy is localized in a relatively small (even less than a μm for near-field focusing49) region with simply-controlled dimensions.50,51 Moreover, the absorption wave moving towards the laser beam is absent in femtosecond plasma.Interaction of a femtosecond pulse with matter involves many physical phenomena, such as light absorption, non-linear ionization, plasma formation, thermal conduction, and ablation. Comprehensive reviews of these phenomena can be found in recently published studies.52,53 In regards to LIBS, plasma and ablation dynamics are very important. First, let us consider the early stage of plasma evolution. Free electrons in a metal absorb laser photons via the inverse Bremsstrahlung process at the very beginning of the irradiation and do not obey the Fermi–Dirac distribution in the absorption region of laser radiation (∼10 nm depth). The non-thermalized ballistic electrons transfer absorbed laser energy to deeper sample layers (∼100 nm).54 A few femtoseconds is required to establish a thermal equilibrium through electron–electron collisions in the electron subsystem.53 Hot electrons overcome the potential barrier52 and are emitted from the surface. Moreover, photo-induced electrons overcome the barrier due to multiphoton absorption, because barrier energy exceeds photon energy at λ = 800 nm for most materials. At this time period, the ions of the lattice are cold because electron–lattice thermalization occurs on a picosecond time scale. Electrons emitted from the surface create an electrostatic field, which pulls ions out of the surface. This fast ion ejection is known as the double layer effect55 or electrostatic ion removal.52 It was shown that approximately several tens of femtoseconds are necessary to remove ions.52 After free electrons and ions are generated, electrons can increase their energy due to a “parachute effect”56 and impact ionization is also started.57
Another mechanism of plasma formation is realized for dielectrics and semiconductors because additional energy is needed to create free carriers in a conduction band. Absorption of one or two photons is enough for electron transition from valence band to conduction band due to a relatively narrow bandgap. When the electron density reaches ∼1018 to 1019 cm−3, an electron avalanche is launched. At this stage, electrons absorb energy via inverse Bremsstrahlung effect, and avalanche ionization prevails over other ionization mechanisms.53 Seed electrons in the conduction band are generated by MPI in dielectrics. As soon as a definite density of these electrons is achieved, avalanche ionization is initiated. In the case of high laser intensities, TI also takes place in the superficial layer of a sample.53,58 Another mechanism of plasma formation typically observed for dielectrics is Coulomb explosion (CE). Emission of electrons from a surface leads to accumulation of an excessive positive charge in the superficial layer of the sample. For a strong field, electrostatic repulsive forces between ions disintegrate this layer (to several nanometers depth), resulting in CE during the first hundreds of femtoseconds.53 Coulomb explosion was observed at extreme intensities of ∼1019 W cm−2 for metals,58 whereas it is still debated for semiconductors at high intensities (I ≥ 1014 W cm−2).53
In ambient conditions, the gas layer in the vicinity of a sample can be ionized by laser radiation and/or high-energy free electrons ejected from the sample. It should be noted that the front part of the laser beam reflected from the sample can interfere with the trail of the beam, resulting in an increase in the laser intensity by a factor of 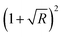 above a surface with reflectivity R.59 Free electrons from gas and electrons removed from the sample can become seed electrons for avalanche ionization,60 which can be supported by post-pulses.
above a surface with reflectivity R.59 Free electrons from gas and electrons removed from the sample can become seed electrons for avalanche ionization,60 which can be supported by post-pulses.
The early stage of plasma evolution was investigated both experimentally and theoretically in ref. 60–62. In the case of a vacuum (4 × 1013 W cm−2, 50 fs, 800 nm), the electron cloud above the surface of Cu is split into fast-moving (∼107 m s−1) and slow-moving (∼104 m s−1) parts, and this can be explained by the generation of a repulsive electric field within the electron cloud. Electron density in the fast-moving cloud decreases from ∼1020 to ∼1017 to 1016 cm−3 during the first 4–12 ps. In the case of ambient gas, target plasma with air breakdown is observed (100 fs, ∼4 × 1014 W cm−2, 800 nm). For target plasma formation, a simulation reveals the existence of double layers (electrons and ions) with a maximum electron density of 1020 cm−3. The electron front in the air breakdown area moves faster than electrons near the target surface due to attraction of a lesser quantity of ions. Air molecules are ionized primarily due to MPI with consequent electron avalanche, while impact ionization by target electrons plays a secondary role. Electron density is about 1020 cm−3 near the target and 1019 cm−3 at the electron front. Zhao and Shin62 claim that emission of Si+ and Si2+ ions is observed from several tens to 150 fs due to CE, whereas electrostatic ion removal and thermal ejection are characteristic for Cu+ and Cu2+ ions. It should be noted that the air breakdown threshold by femtosecond pulses is ∼2 to 4 × 1014 W cm−2 at λ = 800 nm.63–65 The above mentioned mechanisms of plasma formation can be treated as non-thermal mechanisms, which launch ablation on a femtosecond time scale. A brief description of laser–matter interactions related to thermal and mechanical effects will be given below. These processes occur on a picosecond time scale and result in a larger amount of ejected material.
Laser–matter interaction at the femtosecond scale is usually described by a two-temperature model,66 where electrons and lattice are characterized by different temperatures. Electrons transfer absorbed laser energy to an initially cold lattice through electron–phonon interactions, which lead to electron–lattice thermalization over a few picoseconds.67–69 The temperature of the lattice also increases after the laser pulse, resulting in melting of the irradiated layer. Heating to melting temperature requires tens of picoseconds.70,71 The melting depth reaches hundreds of nanometers and depends on laser fluence and material. It should be stressed that ultrafast melting is observed for semiconductors on a time scale of ∼100 fs at intensities of ∼1012 W cm−2.68 Transfer of ∼10% to 15% valence electrons to conduction band leads to lattice instability and disordering.72 Because ultrafast disordering occurs at temperatures below the melting point, it is also called non-thermal or cold melting. A high temperature in superficial layers (tens of nanometers in depth) up to 3 × 104 K can lead to direct evaporation to gas phase with a phase trajectory lying above the critical point (supercritical regime or atomization).67,73 Critical point phase separation is observed at temperatures close to the critical point. In this case, the phase trajectory of the sample layer crosses the liquid branch of the binodal and enters into the region of metastable liquid.67,74 The lifetime of this state is only several picoseconds and the substance instantaneously disintegrates into a gas–liquid mixture.67,74,75
Tensile stress caused by thermoelastic and shock waves leads to formation of voids at a certain depth. Some of the voids coalesce, resulting in mechanical layer decomposition and spallation over tens of picoseconds.70,76 This mechanism arises if the lifetime of a metastable liquid state exceeds the time of mechanical fracture at temperatures below the critical point. Otherwise, phase explosion occurs with disintegration of matter into gas and droplets.74,75 This mechanism is similar to critical point phase separation but unlike this, phase explosion is observed at lower temperatures. Although ∼80% of the ablated mass of metals at irradiance of ∼1013 to 1014 W cm−2 is ejected by mechanical decomposition,67,74 this mechanism can be suppressed by recoil pressure of the vapour/cluster plume at high laser fluences.53 Finally, plasma expansion and intensive ejection of vapor and droplets lead to shock wave formation in the surrounding gas.69,77 Summarizing our considerations, the main processes of plasma formation and ablation at laser intensities of ∼1013 to 1015 W cm−2 are shown in Fig. 4.
 | ||
| Fig. 4 Sketch of the main physical phenomena, leading to plasma formation and ablation. CPPS is critical point phase separation and SCR means supercritical regime. | ||
The competing processes lead to the formation of several fractions in a plasma plume. Three different velocity populations can be distinguished during plasma expansion. Coulomb explosion first produces ions with high kinetic energy, which are followed by neutrals formed by adiabatic expansion with velocities in the nanosecond regime and finally those from nanoscale clusters.78 These nanoparticles produce broadband continuum radiation in the plasma similar to black body emission from a macroscopic object.79 Moreover, different ablation mechanisms for various types of solids lead to considerable variation in the fractional composition of ejected matter and nanoparticles. Noël et al.80 and Axente et al.81 considered plasma composition during femtosecond ablation of copper and fused silica. A ‘‘slow’’ component of high intensity is located close to the target, whereas a ‘‘fast’’ component of lower emission intensity is observed at a larger distance. It was shown that with the use of fast imaging and optical emission spectroscopy, two clouds of nanoparticles were generated during femtosecond laser ablation in vacuum (10−4 Pa): a fast frontal plume component mainly consisted of small clusters (“fast” component) and larger particles were located mostly at the back (“slow” component). Spectra registered during metal ablation revealed that the emission from the “fast” component consisted of mainly spectral lines of neutral atoms and ions, whereas a blackbody-like continuum dominates the emission of the “slow” component (Fig. 5a). Unlike metal ablation, the plasma generated by a femtosecond laser on a fused silica target had only a “fast” component (Fig. 5b). The characteristic expansion velocity of this unique component was about one order of magnitude higher than that of the “fast” component in the case of metals.
 | ||
| Fig. 5 Plume emission intensity vs. distance and wavelength: (a) recorded 20 ns after the laser pulse for ablation of copper with fluence of 4 J cm−2 (reproduced from Noël et al.80 with the permission of Elsevier Science); (b) fused silica for different delay times between the laser pulse and the observation gate (reproduced from Axente et al.81 with the permission of IOP Publishing). | ||
Because a sufficient part of the pulse energy presents ASE, this can influence the ablation process.14,69,82 It was shown that ASE can create a relatively thick melt layer on a surface before the main pulse with an increasing ejected volume of material. A schematic view of femtosecond ablation with ASE is shown in Fig. 6 (time τ = 0 corresponds to a main pulse with duration tp).69 A sample surface is heated (Fig. 6a) and can be melted by the pre-pulse or ASE before the main pulse. Main pulse interaction leads to hot plasma formation with emission of electrons and breakdown in the ambient gas (Fig. 6b). After electron and lattice temperatures become similar at τ ≈ τeq, different layers of material can be evaporated, melted or maintained in a plasma or metastable state. Homogeneous nucleation then occurs in the superheated melt (Fig. 6d). Some delay in phase explosion or mechanical decomposition can be explained by boiling crisis (Fig. 6e),69 observed earlier for ablation by nanosecond pulses because of the formation of a continuous vapor layer or film over the liquid melt.83,84 Phase explosion starts at τ = 700 ps to 1 ns, when pressure decreases due to vapor expansion. A shock wave can be detected up to τ ≈ 100 ns (Fig. 6f). Vapor and sub-micrometer particles are ejected up to 500–700 ns (Fig. 6g). Sometimes continuous liquid jets or melt droplets with a size of several micrometers are observed up to τ ≈ 1 μs.
 | ||
| Fig. 6 Schematic view of plasma formation and ablation. tp is the duration of the main fs pulse and τeq is the characteristic time of the equilibrium established between electrons and lattice. | ||
Thus, the features of femtosecond pulses are durations less than thermalization in any medium, chirping and controlled filamentation, which permit laser energy transfer over a long distance in the atmosphere. At the same time, the mechanism of ablation and plasma formation strongly depend on material, laser fluence, wavelength, pulse duration, and layer depth. In contrast to nanosecond pulses, there is no shielding effect or absorption wave of laser radiation in ambient gas, resulting in a smaller initial temperature and electron density and, as a result, in reduced continuum radiation. In combination with smaller ablation thresholds, this leads to considerable ejection of material on a picosecond time scale. A minimally heat-affected zone, sputtering and mechanical deformation can provide high depth/spatial resolution and precise machining due to negligible heat transfer from the energy absorption area.
3 Analytical performance of femtosecond LIBS
3.1 Depth profiling
A unique feature of femtosecond laser ablation is a small amount of melting in comparison with ablation produced by nanosecond pulses. As a result, the craters produced by an fs laser have more even walls without the clear rims than those produced by ns lasers,85 and the structure, diameter and depth of craters are accurately reproduced. Lopez-Claros et al.86 recently studied the thresholds for single-shot femtosecond ablation of different metals (Pb, Ag, Zn, Sn, Cr, Cu, W, Ni and Fe). The craters exhibited a similar size (∼40 μm at 4–9 J cm−2) and shape, regardless of the sample type, energy range (for energies per pulse <400 μJ) and accumulated energy dosage (<500 laser shots on the same sample position). Such a peculiarity allows the use of fs-LIBS to accurately construct in-depth profiles of metallic alloys. Because the goal of a quantitative in-depth analysis is to obtain the local concentration of an analyte as a function of the layer depth with respect to a distance perpendicular to the solid surface,87 analysts have to solve two tasks. It is essentially important to find a conversion function from the dependence of LIBS intensity on pulse number, i.e. “measured profile”, into a relation between content and depth, i.e. “true” depth profile. Another obstacle for in-depth measurements by LIBS is accuracy validation by means of independent methods, ideally non-destructive techniques that do not involve removing material from a surface. To quantitatively describe the ability of a technique to distinguish the local content between two depth profiles, the term depth resolution is used. According to IUPAC terminology, this is “the distance between the 84 and 16 percent level of the depth profile of an element in a perfect sandwich sample with an infinitesimally small overlap of the compounds.”88The general practice for estimating depth resolution for techniques with laser ablation is to calculate the average value of the ablation rate from pulse-to-pulse measurements of crater deepening by several profilometry techniques in terms of μm per pulse or nm per pulse.89 Ideally, this should be permanent and the crater is linearly deepened under the fixed fluence. An ablation depth per pulse, labl, for ultrafast laser processing of metallic alloys can be estimated by the following inequality:52
Another way of deeply penetrating a sample is provided by non-diffracting Bessel beams. These have an intensity distribution across a beam, which can be described by a Bessel function of the nth-order Jn:93 the beam shape has a central core with a series of concentric rings. A unique feature of such a beam is that the intensity profile of its central core propagates without experiencing appreciable spreading. A circular slit94 or a conical axicon95 are the usual tools for generating Bessel beams. The most spectacular demonstration of the ability of Bessel beams is drilling λ/4 = 200 nm channels with an aspect ratio of ∼100 by a single shot of a 650 nJ to 230 fs pulse in glass.96 The robustness of Bessel beams to the presence of obstacles and their self-healing ability makes them very attractive for laser processing of dielectrics with powerful femtosecond pulses. Because there have been, to the best of our knowledge, no studies on the use of LIBS techniques for spectral monitoring of ablation processes with Bessel beams of zeroth or first order, we suggest that this field of LIBS application should prove promising, especially in micromachining and material processing.
Generally, LIBS is applied to the measurement of the thickness of coatings97 and layers as an auxiliary tool to detect a transition between two different layers. In this case, to decide whether the crater bottom crossed the interface between two layers, analysts should observe a sharp change in the pulse-to-pulse variations of a LIBS signal. If it increases (or decreases), the layer containing an analyte has begun (or ended). However, mixing of layers of different materials due to melting and resolidification during a multiple shot depth profiling can lead to worsening of the resolution with respect to the ablation rate. This means that the changes between two consecutive single shot LIBS spectra cannot reflect the changes in the average depth composition, and the ablation rate will be an inaccurate estimation of the depth resolution. Recently, Banerjee and Fedosejevs98 introduced the concept of “depth sensitivity” to describe an approach for estimating the accuracy of distinguishing the boundary between a two-layer system by the use of single-shot LIBS signals from each component. As an example, they calculated depth sensitivity as “the Cu layer depth where the Si emission falls to 1/e from its pure Si value” for a thin Cu–Si interface layer. This was 2.5–4 nm for crater depths of 25–100 nm. This term can be interpreted as the minimum change in depth that can be reliably detected by changes in the LIBS signal of the sample constituents. Evidently, the depth sensitivity is preferable as a measure of the ability to perform depth profiling by LIBS techniques because of the simplicity of its measurement, compared with the ablation rate.
The very first study on the application of femtosecond LIBS to measure the thickness of multilayered coatings of Cu–Ag sandwiches was performed by Margetic et al.89 Two types of Cu–Ag samples were prepared by thermal deposition of Cu and Ag layers on a Si wafer: double and triple sandwiches of alternating Cu and Ag layers. The thickness of each copper and silver layer was ∼600 nm. With a fluence of about 1 J cm−2, they detected five boundaries between layers after ∼25–30 laser shots. Because the depth profiles of Cu and Ag were constructed by the accumulation of 10 pulses, an accurate estimation of depth resolution in terms of “depth sensitivity” has to give a larger value of at least 200 nm, instead of an ablation rate of 15–30 nm per pulse. By comparing ns-LIBS with fs-LIBS, Pouli et al.99 measured the thickness of different types of thin organic films used as protective coatings on historical and archaeological metal objects. They established that ns pulses were inadequate to assess the polymer coating on an Al–Mg substrate because of their weak absorption, while fs pulses yielded well-resolved profiles with a depth resolution of 1 μm. More recently, de Bonis et al.100 compared 40 ns pulses vs. 40 fs pulses to measure the depth of a patina to clean corroded bronzes. Because the ablation rate of a 40 ns laser was four times larger than that for a 40 fs laser, the resolution of femtosecond LIBS depth profiling was better and accuracy with respect to the Cu/Sn ratio was also better due to minimal fractionation.
Unlike the depth profile with a sharp leap due to the interface between two layers, this accuracy problem of LIBS should be overcome to construct “continuous” depth profiles. In principal, LIBS is a microdestructive technique101 because analyzed material in the plasma is removed from a surface. In spite of attempts to analyze the ablated particles,102 it is not possible to accurately establish the local composition of the material after it has been removed from the sample. Therefore, it is necessary to compare the results of in-depth measurements by LIBS with other analytical techniques. Accuracy can be proved by in-depth measurements of the same area by non-destructive techniques before ablation. Electron spectroscopy for chemical analysis or Auger electron spectroscopy can be applied for non-destructive profiling of ultrathin layers (0.5–5 nm). For larger sampling depths (up to several μm), there is Rutherford backscattering spectroscopy (RBS) of low mass and high energy ions in the MeV range with a depth resolution of about 1–5 nm.103 RBS depth profiles are infrequently matched to fs-LIBS data because of the cost of the technique (requiring a He+ source), although it is suitable for determining the thickness of a specific coating or deposition. At the same time, in-depth results of LIBS are sometimes compared with other microdestructive techniques such as glow-discharge OES, electron probe microanalysis (EPMA), SIMS, and laser ablation ICP-MS due to their low cost and simplicity in comparison with RBS. To assure accuracy in quantitative analysis, such a comparison demands an assumption of either sample homogeneity or that the depth profiles are the same at different points of a sample surface. Recently, Galmed et al.104 examined the ability of fs-LIBS to achieve depth profiling for a Ti thin film deposited onto a Si substrate during thermal annealing. They estimated the thickness of a Ti coating after annealing to be 213 nm. Because such a depth corresponded to the intersection between Si and Ti signals, they established that LIBS can be considered as a rapid analytical technique for accurately estimating the thickness of coatings.
However, there was only one study on the comparison of a “continuous” profile obtained by fs-LIBS with the in-depth measurements by other techniques. Das et al.105 also tried to quantitatively locate the interfaces of an interdiffusion zone (depth = ∼20–25 μm) in a thermal barrier-coated sample using 150 fs laser pulses with a fluence of 18 J cm−2. The average ablation rate was less than 200 nm per pulse. It is interesting to note that each layer was prepared by different techniques: a β-(Ni,Pt)Al bond coat was prepared through a combination of electroplating, high temperature diffusion and chemical vapor deposition processes, while a ceramic outer layer was deposited on the bond coat by an electron beam physical vapor deposition technique. This provided an interdiffusion zone below the bond coat. By comparing an fs-LIBS depth profile for an Al line with the one obtained by EPMA, they found that LIBS could indicate the ceramic layer/bond coat interface, while the absence of sharp changes in the Al intensity across the β layer/interdiffusion zone and interdiffusion zone/substrate interfaces meant that it was not possible to identify these interfaces from the spectral intensity profile of Al.
Although it is possible to achieve a very shallow ablation depth per pulse, such as ≤2 nm per pulse, with the use of ns-LIBS, for example, due to angle-resolved laser ablation,106 the main advantage of femtosecond pulses is still the production of more reproducible craters with an even bottom. By measuring in-depth profiles of Ti ultrathin layers on a steel sheet with the use of doubled 12 ns pulses, Kratochvíl et al.107 recently showed that the roughness of a crater bottom was about 50 nm at a depth of 150 nm after a single laser shot. The technique was capable of measuring the surface density of Ti on a sheet at a level of several hundreds of pg mm−2 only for a single shot because of the etching of the Ti layer by the first pulse. This means that the “depth sensitivity” of fs-LIBS is better, at least by two orders of magnitude, than that provided by ns-LIBS due to the even bottom as a result of low melting.
3.2 Lateral resolution
Chemical mapping, i.e. the distribution of a component across a sample surface, requires high spatial resolution, ideally, at near-atomic level or, at least, at the nanoscale level. Because of low melting, focusing ultrafast laser pulses onto a sample surface can produce a crater without high rims and other irregularities (e.g. droplets), which are usually observed for nanosecond laser ablation. Therefore, their applications to construct a map are limited by the crater size, which is slightly wider than a spot. The diffraction-limited beam diameter d at the focus of a lens with focal length f and aperture D is given by the following relation:52where M2 is a propagation constant characterizing the deviation from the ideal Gaussian beam and n is the refractive index of the lens. Gaussian beams give a spot with a minimal diameter (because M2 ≈ 1), while the beams with flat-top profiles, which are widely used for in-depth measurements, give a wider spot because they have an M2 value much higher than 10. As a result, the crater diameters from the two beams differ significantly and spatial resolution for ablation with a flat-top beam is worsened. As an example, Banerjee et al.92 demonstrated that a Gaussian beam produced craters with a diameter of ∼7–9 μm, while craters made by a flat-top beam had a size of ∼90 μm. Because the vast majority of available femtosecond lasers provide a Gaussian distribution across a beam, several studies reporting such a beam profile for mapping can be mentioned; these studies include mapping of sunflower cells,108 leaves,109,110 films on silicon111,112 and aluminium alloys.113 There are several studies on attempts to achieve micromachining on alloys. Tong et al.114 examined the use of an fs-LIBS system as a diagnostics instrument for real-time control of femtosecond micromachining in the fabrication of microheater structures on thermally sprayed materials. Recently, the spectacular demonstration performed by Wessel et al.115 involved searching microcracks or defects in Ti–Al alloys. The spatial resolution of 2 μm allowed the detection of long and narrow cracks and microindentation zones. By comparing SEM and Ti line-LIBS images of an area under investigation, one can see in Fig. 7 that fs-LIBS allows the detection of a crack of such a length. Due to the high repetition rate of an fs laser (1 kHz), the operation of mapping is not very time-consuming. Another interesting idea related to chemical mapping by fs-LIBS is the production of precise 3D maps. More recently, Hou et al.116 combined 2D cross-sectional contour maps with layer-by-layer measurements. They obtained the enrichment of two surface layers by Li and Al for stuffed lithium garnets Li7La3Zr2O12. High depth resolution (∼700 nm) allowed this demonstration in the first instance, while the lateral resolution achieved was moderate (crater size of ∼40 μm), although a Gaussian beam was used. It may be noted that the analyte in these cases of fs-LIBS mapping was the major or, at least, a minor component.
 | ||
| Fig. 7 (a) SEM micrograph of Ti–Al sample surface before ablation and (b) fs-LIBS map constructed on the intensity of the Ti I line. Reproduced from Wessel et al.115 with the permission of Elsevier Science. | ||
Unlike diffraction-limited beams, non-diffracting Bessel beams have a central core with diameter d expressed as follows:117
 | ||
| Fig. 8 (a) and (b) Simulated intensity distributions in vacuum of TM and TE polarized beams, respectively. SEM images of irradiation of borosilicate Corning 0211 glass samples with (c) the longitudinal component of a 30 nJ single TM pulse; (d) the transverse component of a 120 nJ single TE pulse; (e) multiple 80 nJ TM pulses; and (f) multiple 40 nJ TE pulses. The scale bar is the same for (c)–(f). Reproduced from Hnatovsky et al.119 with permission of the American Physical Society. | ||
To overcome a diffraction limit in far-field optical spectroscopy, near-field microscopy is developed to observe objects on the nanometer scale.120 The main concept of near-field scanning optical microscopy (NSOM) is to place a detector very close to the sample surface at a distance much smaller than the irradiation wavelength. To realize such a configuration, an incident beam passes through a narrow fiber probe (∼100 nm) and radiation reflected from a surface is collected by the same probe. The first demonstration of the NSOM technique with respect to LIBS measurements was carried out by Russo's group.49 By ablating a silicon wafer with 100 fs to 0.18 nJ single laser pulse, they obtained a crater on a silicon wafer with a diameter of only 30 nm but a weak LIBS spectrum of silicon was detected with 5.9 nJ pulses, which produced a crater size of ∼1 μm. They then observed emission lines from sodium and potassium in a mica sample using a NSOM tool for a 40 nJ single pulse and the crater size was ∼450 nm.121,122 The sensitivity of such a low energy effect was poor; for example, the average single-shot limit of detection for Na was 2700 ppm. To improve sensitivity, they incorporated a double-pulse fs to ns scheme for micrometer resolution.123 By comparing NSOM technology and far-field propagation of a cylindrical beam for LIBS purposes, one can see that the latter produces a crater with a diameter of ∼80 nm, while the former can achieve craters with a size of ∼30 nm. However, the energy delivered to a surface by the two techniques is significantly different: 30 nJ in the cylindrical beam vs. 0.18 nJ for NSOM. Because LIBS spectra were detected for 40 nJ in the NSOM configuration, the capability of a cylindrical beam for higher spatial resolution in LIBS appears to be reasonable.
3.3 Signal enhancement in femtosecond LIBS
In the pioneering study6 on the use of a characteristic emission of femtosecond laser plasma for analytical studies, the pulse energy did not exceed 400 μJ. Based on the calibration plots, it is possible to conclude that the useful signal is roughly comparable with the experimental error in the case of the samples containing a few percent of Zn. When comparing the emission properties of laser-induced plasma, generated by pulses of various duration, it was demonstrated that, after a period of time of 10 ns, the emission intensity is basically determined by the pulse energy.124 Sabsabi et al.125 used a laser with an energy of 50 mJ. As a consequence, the detection limit of Ag in aluminium alloys was reported to be ∼2 ppm at pulse durations of 80 fs, 2 ps and 270 ps. However, the cost of femtosecond laser systems with an energy of dozens of mJ is very high. Moreover, an advantage of femtosecond evaporation is that a small-sized crater with minimal thermal effects can be implemented when the fluence is slightly above the ablation threshold. Under these conditions, the spectral lines of the major and some minor constituents are usually observed in the spectra of laser plasma. Although it was shown that the emission signal is proportional to the pulse energy due to the absence of plasma shielding,126,127 an improvement in the sensitivity of fs-LIBS is more urgent compared to a conventional LIBS technique operating with nanosecond lasers. We first consider various options for optimization and improvement of the single pulse scheme.Scaffidi et al.131 proposed that in the case of a collinear double-pulse for fs to ns LIBS, the highest intensity of a spectrum of pure Fe is observed at a focus position of 2.5 mm both above and below the sample surface. This was in good agreement with results, according to which the maximal signal was detected at a focus of 0.5 mm above/below the surface. Sometimes, the laser beam is focused directly on the surface of samples,132–134 assuming that this leads to the maximal fluence and, as a consequence, to the highest intensity of spectra.
Finally, Zuhlke et al.135 performed a fundamental investigation on the influence of focusing conditions on the fs-LIBS signal of silicon in a vacuum and in atmosphere. They found out that under vacuum conditions (2 Pa), there were two peaks of similar magnitude of Si I, intensity = 288.16 nm, corresponding to pre- and post-focus and a local minimum at the focus. At 1 atm, the LIBS signal had a single prefocus peak and a continual drop-off in signal through and beyond the focus. This phenomenon was attributed to continuum generation in air plasma, diminishing the energy per pulse and effectively lowering the fluence due to an increase of the total divergence angle in near and post-focus regions. The available data led to the conclusion that at the optimal fluence for the materials and semiconductors, the maximal signal can be achieved at a focus above the surface. It is also recommended to determine lens-to-sample distance (LTSD) before the analytical measurements. Despite numerous studies, it is still of great importance to continue investigations into the influence of fluence and focusing on the analytical signal as well as on the form and size of craters of dielectric samples.
A somewhat different situation was described by Harilal et al.138 although the optimal value of SNR was observed at 2.5–6.5 kPa, the signal intensities were maximal at a pressure level of about 0.5 atm. Apparently, this is because the plasma core did not fit into the area of the plasma used for observation (1 mm above surface) within selected temporal parameters of registration (delay 100 ns, gate 1 μs). Moreover, time resolved images of the laser plume clearly demonstrated that the plasma core had been expanded and had moved rapidly away from the surface under reduced pressure and the maximal intensity of plasma emission was observed at a height significantly higher than 1 mm above the surface. To sum up, the ambient atmosphere influences the fs-plasma in the same way as it influences the ns-plasma, thus the maximal signal enhancement can be obtained at a reduced pressure in noble gases. One should keep in mind that the pulse energy obviously influences the plasma dynamics and, as a consequence, the optimal pressure value can vary. Most likely, the intensity increase of a certain line depends on electron density and temperature, for instance, the emission intensity of a plasma on a Zn target was maximal at 530–1300 Pa, depending on whether the line was atomic or ionic.139
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K), producing a majority of multiple ionized aluminium atoms and a larger Al II area with the density state more than one order of magnitude higher (∼1023 m−3) than for a single pulse. The same results were obtained for an fs-LIBS study of a brass alloy with pulse shape optimization.142 The regions of neutral and ionized species were formed due to an increasing temperature profile together with the corresponding ionization degrees. Neutral Cu and Zn atoms were mainly located in the vicinity of the surface, while ions were located closer to the plasma front. Hartig et al.143 compared the effect of pulse width (45 fs to 1.5 ps) and shape resulting from application of both positive and negative chirp on SNR and peak-to-peak signal variations in fs-LIBS of copper and uranium. Although the intensities of specific lines depended on both the sign of the chirp and the pulse duration, an increase of only 27% and 18% in the SNR for uranium and copper, respectively, was observed compared to the SNR measured at the shortest pulse duration. The SNR and peak intensity were decreased for pulse durations longer than 1 ps, regardless of the chirp sign. Thus, on the basis of these relevant papers, we may conclude that pulse shaping can give some enhancement of figures of merit of LIBS measurements, especially if the technique is adapted to a specific analyte. It should also be noted that simple pulse width variation does not provide a significant increase in signal or SNR.
000 K), producing a majority of multiple ionized aluminium atoms and a larger Al II area with the density state more than one order of magnitude higher (∼1023 m−3) than for a single pulse. The same results were obtained for an fs-LIBS study of a brass alloy with pulse shape optimization.142 The regions of neutral and ionized species were formed due to an increasing temperature profile together with the corresponding ionization degrees. Neutral Cu and Zn atoms were mainly located in the vicinity of the surface, while ions were located closer to the plasma front. Hartig et al.143 compared the effect of pulse width (45 fs to 1.5 ps) and shape resulting from application of both positive and negative chirp on SNR and peak-to-peak signal variations in fs-LIBS of copper and uranium. Although the intensities of specific lines depended on both the sign of the chirp and the pulse duration, an increase of only 27% and 18% in the SNR for uranium and copper, respectively, was observed compared to the SNR measured at the shortest pulse duration. The SNR and peak intensity were decreased for pulse durations longer than 1 ps, regardless of the chirp sign. Thus, on the basis of these relevant papers, we may conclude that pulse shaping can give some enhancement of figures of merit of LIBS measurements, especially if the technique is adapted to a specific analyte. It should also be noted that simple pulse width variation does not provide a significant increase in signal or SNR.
This observation is also in agreement with a study of fs and ns LIBS of brasses by Freeman et al.146 The intensity of background radiation was high for at least 100 ns after an ns pulse, while it became negligible after 25 ns for an fs pulse. Moreover, there were attempts to reduce continuum radiation by a specific process in fs laser plasma. In particular, Liu et al.147 reported that continuum emission of the plasma produced in femtosecond ablation of Si could be polarized. Later, the same authors tried to apply this effect to LIBS measurements of aluminium,148 copper and graphite149 to cut off continuum emission and enhance signal-to-background ratio (SBR) with the use of a polarizer. Unfortunately, mainly scattered laser light (s- or p-polarized) was removed by the polarizer, while only approximately 15% of the continuum was polarized due to its reflection by the target surface and polarization of the outgoing radiation in accordance with the Fresnel equations.150
| Sample | Analytical line, nm | Lasers in DP combination | Optical scheme, interpulse delay, other conditionsa | Enhancement factor |
|---|---|---|---|---|
| a O – orthogonal scheme, C – collinear scheme. b This value was obtained in terms of a decrease in a signal detection threshold. c This value was obtained near the ablation threshold. d In terms of electron density and excitation temperature. | ||||
| Pure copper | Cu I 515.32 | 100 fs, 800 nm, 6 mJ + 7 ns, 1064 nm, 30 mJ | O (ns spark 1 mm height), 5 μs | 30 |
| Cu I 324.75 | 80 fs, 800 nm, 1 mJ + 1 mJ | C, 106 ps | 11 | |
| Cu I 324.75 | 120 fs, 800 nm, 50 J cm−2 + 50 J cm−2 | C, 106 ps | 9 | |
| Cu I 510.55, 515.32, 521.82 | 250 fs, 527 nm, 0.6 J cm−2 + 0.6 J cm−2 | C, 2 ns, 200 ps, 10−9 bar | 4.5–6.5 | |
| Cu I | 100 fs, 800 mm, 25 μJ + 25 μJ | C, 300 ps, 10−4 Pa | 4 | |
| Cu II 490 (unresolved), Cu II 505.18 | 250 fs, 527 nm, 0.6 J cm−2 + 0.6 J cm−2 | C, 2 ns, 200 ps, 10−9 bar | 6.5–11 | |
| Bronze, brass | Cu I 282.44, 465.11 | 250 fs, 527 nm, 3 mJ + 7 ns, 532 nm, 45 mJ | O (ns spark 0.5 mm height), 8 μs | 70–280 |
| Cu I 465.11, 510.55, 515.32, 521.82 | 100 fs, 800 nm, 0.5 mJ + 0.5 mJ | C, 27 ps | 3.5–5 | |
| Cu I 521.82 | 100 fs, 800 nm, 10 mJ + 5 ns, 1064 nm, 150 mJ | O (fs spark 0.6 mm height), 3.5 μs | 2.5–4 | |
| Cu I 450.94 | 450 fs, 248 nm, 0.5 mJ + 0.5 mJ | C, 200–400 ps | 9.5 (2b) | |
| Zn I 481.05 | 450 fs, 248 nm, 0.5 mJ + 0.5 mJ | C, 200–400 ps | 7.2 (2b) | |
| Zn I 481.01, 472.21, 481.05 | 100 fs, 800 nm, 0.5 mJ + 0.5 mJ | C, 27 ps | 3.5–5 | |
| Zn I 472.21 | 250 fs, 527 nm, 3 mJ + 7 ns, 532 nm, 45 mJ | O (ns spark 0.5 mm height), 8 μs | 14 | |
| Sn I 284.00 | 250 fs, 527 nm, 3 mJ + 7 ns, 532 nm, 45 mJ | O (ns spark 0.5 mm height), 8 μs | 30 | |
| Pb I 280.20 | 250 fs, 527 nm, 3 mJ + 7 ns, 532 nm, 45 mJ | O (ns spark 0.5 mm height), 8 μs | 10–15 | |
| Pure gold | Au I | 100 fs, 800 mm, 25 μJ + 25 μJ | C, 200 ps, 10−4 Pa | 5.3 |
| Pure aluminum | Al I 394.40, Al I 396.15 | 100 fs, 800 nm, 6 mJ + 7 ns, 1064 nm, 30 mJ | O (ns spark 1 mm height), 5 μs | 80 |
| Al I 396.15 | 100 fs, 800 nm, 10 mJ + 5 ns, 1064 nm, 150 mJ | O (fs spark 0.6 mm height), 55 μs | 3–3.5 | |
| Al I 394 + 396 (unresolved) | 30 fs, 785 nm, 125 nJ + 125 nJ | C, 800 ps | 6 | |
| Al I 394.4, 396.15 | 150 fs, 800 nm, 0.5 mJ + 0.5 mJ | C, 9 ps, 10−5 Pa | 0.5 | |
| Al II 358.7, 466.3, 559.32 | 150 fs, 800 nm, 0.5 mJ + 0.5 mJ | C, 9 ps, 10−5 Pa | 1.7–3.5 | |
| Al II 281.62 | 450 fs, 248 nm, 0.5 mJ + 0.5 mJ | C, 400 ps | 5.6 | |
| Aluminum alloy | Al I 396.152 | 50 fs, 800 nm, 40 μJ + 40 μJ | C, 150 ps | 4.3 |
| Al I 396.152 | 50 fs, 800 nm, 40 μJ + 40 μJ | C, 150 ps, Ar jet | 3 | |
| Mg I 518.36 | 50 fs, 800 nm, 40 μJ + 40 μJ | C, 150 ps | 7.5 | |
| Mg I 518.36 | 50 fs, 800 nm, 40 μJ + 40 μJ | C, 150 ps, Ar jet | 2 | |
| Pure titanium | Integral Ti I (430.6, 445.7, 453.6) | 100 fs, 620 nm, 2 mJ + 2 mJ | C, 0.9 ns, 10−6 Torr | 2–7 |
| Ti I 451.80 | 250 fs, 527 nm, 0.8 mJ + 7 ns, 532 nm, 25 mJ | O (ns spark 1 mm height), 500 μs | 35 | |
| Ti I 453.3 + 453.5 (unresolved) | 30 fs, 785 nm, 125 nJ + 125 nJ | C, 800 ps | 2.5 | |
| Integral Ti II (334.9, 368.5, 375.9, 376.1) | 100 fs, 620 nm, 2 mJ + 2 mJ | C, 0.9 ns, 10−6 Torr | 2–7 | |
| Ti II 346.15 | 250 fs, 527 nm, 0.8 mJ + 7 ns, 532 nm, 25 mJ | O (ns spark 1 mm height), 500 μs | 500 | |
| Ti III 251.60 | 250 fs, 527 nm, 0.8 mJ + 7 ns, 532 nm, 25 mJ | O (ns spark 1 mm height), 500 μs | 900 | |
| Pure iron | Fe II 274.65 | 450 fs, 248 nm, 0.5 mJ + 0.5 mJ | C, 400 ps | 9.1 |
| Steel | Fe I 438.41, Fe II 419.95 | 350 fs, 257.5 nm, 10 μJ + 1030 nm, 10 μJ | C, 40 ps | 3–5 |
| Cr I 425.48, Cr II 449.71 | 350 fs, 257.5 nm, 10 μJ + 1030 nm, 10 μJ | C, 40 ps | 3–5 | |
| CMSX-4 superalloy | Ni I 352.45 | 150 fs, 775 nm, 160 μJ + 640 μJ | O (2nd fs spark 30 μm height), 10.36 ns | ∼500c (9b) |
| Cr I 425.44 | 150 fs, 775 nm, 160 μJ + 640 μJ | O (2nd fs spark 30 μm height), 10.36 ns | ∼500c (9b) | |
| Al I 394.40 | 150 fs, 775 nm, 160 μJ + 640 μJ | O (2nd fs spark 30 μm height), 10.36 ns | ∼500c (9b) | |
| Pure nickel | Ni I 447.047, 464.865, 478.653, 547.691 | 33 fs, 810 nm, 0.2 mJ + 0.2 mJ | C, 50 ps | 5–13 |
| Bilayer Ag/Al plate | Al I 394.40, 396.15 | 60 fs, 800 nm, 0.3–30 μJ + 0.3–30 μJ | C, 104 ps | 7–3.5 |
| Ag I 405.85, 421.62, 431.32, 520.91, 546.54 | 60 fs, 800 nm, 0.3–30 μJ + 0.3–30 μJ | C, 104 ps | 13–3 | |
| Pure silicon | Si I 288.16 | 450 fs, 248 nm, 0.5 mJ + 0.5 mJ | C, 400 ps | 4.3 |
| Si I 288.16 | 800 μJ pulses with 50 fs, 800 nm, 125 μJ + 125 μJ | C, 0–80 ps | 1.1–2 | |
| Si I 288.16 | 100 fs, 800 nm, 28 μJ + 28 μJ | C, 60 ps | 2 | |
| Si I 212.41, 221.67, 243.52, 251.61, 288.16 | 100 fs, 800 nm, 1 mJ + 1 mJ | C, 70 ps | 1.2d | |
| Si II 505.6 | 80 fs, 800 nm, 1 mJ + 1 mJ | C, 106 ps | 6 | |
| Si II 505.6 | 100 fs, 800 nm, 28 μJ + 28 μJ | C, 60 ps | 2 | |
| Single-crystalline silicon | Si I 252 (unresolved), 288.16 | 500 fs, 343 nm, 400 nJ + 6 ns, 355 nm, 1.5–3 mJ | O (ns spark 45 μm height), 500 ns | 360 |
| Pure boron | B II 412, 477, 497, 700 | 150 fs, 800 nm, 0.5 mJ + 0.5 mJ | C, 15 ps, 10−5 Pa | 1–1.4 |
| BaSO4 | Ba II 455.40 | 450 fs, 248 nm, 0.5 mJ + 0.5 mJ | C, 400 ps | 8.1 |
| CaF2 | Ca II 317.93 | 80 fs, 800 nm, 1 mJ + 1 mJ | C, 106 ps | 2 |
| Gd2O3 | Gd I 419.08, Gd II 409.86 | 100 fs, 800 nm, 2 mJ + 532 nm, 10 ns, 30 mJ | O (ns spark 0.9 mm height), 2–4 μs | 10–25 |
| Polymethyl methacrylate-PMMA | Ca II 393.4, 396.8 | 45 fs, 800, 300 μJ + 300 μJ | C, 80 ps | 6.5 |
| Ca I 422.6, Na I 589.0, 589.6 | 45 fs, 800, 300 μJ + 300 μJ | C, 80 ps | 4 | |
| CN 388.3, C2 516.5 | 45 fs, 800, 300 μJ + 300 μJ | C, 80 ps | 2 | |
| CH 431.4 | 45 fs, 800, 300 μJ + 300 μJ | C, 80 ps | 1.5 | |
| Air | Intensity at 400, 450, 500 | 120 fs, 800 nm, 86 μJ + 26 μJ | C, 40 ps | 5 |
| N II 500.5 | 33 fs, 810 nm, 0.8 mJ + 1.0 mJ | O, 0 fs | 32 | |
| H I 656.2 | 33 fs, 810 nm, 0.8 mJ + 1.0 mJ | O, 0 fs | 8 | |
| N I 746.8 | 33 fs, 810 nm, 0.8 mJ + 1.0 mJ | O, 0 fs | 7.5 | |
| O I 777.2 | 33 fs, 810 nm, 0.8 mJ + 1.0 mJ | O, 0 fs | 6 | |
Besides traditional applications of a DP regime for signal enhancement, there are a number of studies165–168 that describe the use of a second pulse as a probe to study the evolution of plasma, including the evaluation of nanoparticle compositions.
3.4 Self-absorption
Self-absorption effect is stronger for the fs-LIBS technique than its ns equivalent. By comparing ablation of copper alloys by 80 fs and 270 ps pulses, le Drogoff et al.125 observed the strong deviation of a calibration curve for an Ag resonance line from linearity in the range of 100–450 ppm. They tried to achieve the best sensitivity with high energy pulses of ∼50 mJ per pulse and a fluence of ∼20 J cm−2 due to the absence of plasma shielding with the use of femtosecond pulses. However, self-reversal of a resonance Mg line as well as self-absorption of a resonance Ag line were considerably more pronounced as the laser pulse duration was reduced. To explain this behavior, the authors assumed that two factors acted in combination: the higher ablation efficiency of femtosecond laser ablation169 resulted in a higher number density of atoms, while a lower plasma temperature170 increased the population density of the ground-state species. Elhassan et al.171 demonstrated similar behavior with Zn/Cu, Sn/Cu, and Pb/Cu ratios in the ablation of bronze alloys by 500 fs pulses of 11.2 mJ. At the same time, there were no significant differences in the plasma temperature and the electron density between nanosecond and femtosecond ablation under their experimental conditions. Fornarini et al.172 observed that calibration graphs for lead and tin had a tendency to show lower than linear dependences regardless of pulse duration. They used two fs-systems with fluences of 6.5 J cm−2 (8.2 mJ per pulse) and 15 J cm−2 (3.0 mJ per pulse). In this case, the authors have attributed their observations to the so-called phenomenon of “fractionation” because calibration curves for Zn/Cu ratios were close to linear for nanosecond and femtosecond ablation of bronze alloys. Similarly, Margetic et al.6 demonstrated the absence of a non-linear trend in a calibration curve for Zn/Cu ratios for brass alloy ablation at different pressures and laser fluences. In any case, possible strong self-absorption should be taken into account when choosing between fs-LIBS and ns-LIBS as an analytical method.4 Filament-induced breakdown spectrometry (FIBS)
4.1 Filament-induced breakdown spectrometry basics
The unique LIBS capability to perform express elemental analysis of a remote sample makes this method very suitable for military and safety applications as well as space exploration missions (ChemCam instrument in the Curiosity mission by NASA). However, conventional ns-LIBS is limited to a distance of a hundred meters due to the difficulty in delivering high laser intensities that are sufficient to induce ablation and ionization of the remote target. There are two main limiting factors: diffraction from focusing optics and fluctuation of atmospheric optical properties. Ideally, the focal plane of a lens should be equal to the distance between the laser and sample but even high quality optics suffer from spherical aberrations at a distance of several tens of meters. To overcome this, a large and heavy optical system should be constructed that limits the mobility of a remote LIBS system. A second problem that cannot be solved, even with an ideal optical system, is the fluctuation of atmospheric optical properties for an optical path length of several tens of meters. Fluctuation in the refractive index of air (turbulence vortexes) is generally combined with aerosol particle movements, which together completely distort a laser beam at a distance of several tens of meters.201 Increasing the efficiency and measurement range and improving the signal-to-noise ratio are important issues for LIBS applications.To the best of our knowledge, conventional remote sensing of a solid target with fs laser pulses was only studied by Rohwetter et al.202 They used positive chirping to prevent filamentation. Such a variant of remote LIBS appears to be unproductive because it offers no benefits compared to nanosecond remote LIBS, bearing in mind the increase in complexity and the cost of the fs system. A new era of laser-assisted remote elemental analysis was started when filaments were used to produce plasma on a solid sample surface. The capability of filamentation to overcome diffraction limits and deliver high laser intensities at long distances without focusing was demonstrated in the early 2000s.39,203,204 However, the first application205 of filaments to the remote induction of laser plasma was made by Teramobile's team in 2004 for samples located at a distance of 90 m. Teramobile's system consists of a terra-watt laser and a detection system installed in a 20-foot standard freight container, allowing field measurement campaigns. A detailed description of the system and the main results of the project can be found in numerous studies206–211 as well as at Teramobile's official site.212
Thereafter, such a variant of LIBS was more frequently named filament-induced breakdown spectrometry (FIBS), and we will also use this term in this review. In the above mentioned pioneer study, the femtosecond non-focused laser beam (800 nm, 80 fs, 250 mJ) initiated multiple filaments (up to 30) at 7 m from the pure metal samples (Cu and Al), which were located 90 m from the system.205 Filament-induced plasma emission was collected by a 20 cm telescope and guided to a spectrograph equipped with a gated detector. The spectra revealed the absence of broad–band emission within the first 100 ns, indicating a low temperature and electron density in the plasma. Atomic lines of Cu I and Fe I were clearly observed with a better contrast compared to a nanosecond LIBS system. In the next Teramobile study on FIBS,213 the length and initiation point of a filament from a target was optimized by varying the beam diameter and chirp. Line emission from a metallic target was registered at distances up to 180 m from the laser. Moreover, the authors assumed that this distance could be extended up to 1 km and is restricted only by the collecting optics and the detector efficiency. This is the principal advantage of FIBS over remote ns LIBS systems with laser beam focusing, which is of great interest with respect to the remote sensing of dangerous or unreachable sites like explosives or chemical pollutants.
4.2 Filament-induced ablation
Filament-induced ablation can be defined as the ablation of a solid/liquid surface by a femtosecond pulse with a power density above the filamentation threshold in surrounding media. In other words, ablation is induced by both the filaments and the femtosecond laser pulse. It should be noted that filaments contain only a small fraction of energy compared to a laser pulse (less than 1%)21,36,205 but plasma channels (filaments) change laser–matter interaction. The majority of studies on FIBS were focused on the feasibility proof of remote analysis for different types of samples, i.e. the detection of atomic/molecular spectra from a large distance for major sample components. The physics of filament-induced ablation and the resulting plasma have been studied superficially in a few studies.Crater studies were carried out for a 5 cm diameter femtosecond laser beam that ablated a remote copper target.213 Multiple craters (up to 30) with 100–200 μm diameters were formed by individual filaments. The authors studied the influence of optical path length on crater properties. They compared craters produced on metallic plates located at 25 and 90 m from the laser by a beam producing multiple filaments (each ∼100 μm in diameter). The diameter of the first crater was about 5 mm (compare with 50 mm laser beam at laser output), while the second crater diameter was significantly larger (about 30 mm). The authors explained this as being due to a random walk of the filament around its mean position due to fluctuations in the air and the stochastic nature of multifilamentation. For smaller distances (up to 50 m) in air, the crater diameter did not change, as was shown for filament-induced (800 nm, 180 fs, 25 mJ) ablation of GaAs.214 A direct comparison of femtosecond and filament-induced ablation has been carried out by Valenzuela et al.215 Under the same experimental conditions Ti:Sapphire laser pulses (800 nm, 100 fs, 25 mJ) were sharply focused (no filamentation), slightly focused (assisted filamentation) and self-focused (filamentation) on steel and titanium targets. A crater study revealed a substantial decrease in evaporated mass for filament-induced ablation compared to femtosecond (sharply focused) ablation.
Plasma emission duration did not exceed several hundred nanoseconds, compared to a time scale of a few microseconds for non-filament ablation by femtosecond or nanosecond pulses. For example, filament-induced plasma on a copper target could be detectable for the first 130 ns (conditions: 800 nm, 80 fs, 250 mJ per pulse, 10 Hz); this did not depend significantly on the distance between laser and target.213 A twelve times longer plasma emission duration (1 μs) was detected for molecular species in the case of organic film sampling.216
Broadband emission for femtosecond induced plasma is significantly lower compared to pico/nano-second cases.202 However, FIBS provided the smallest continuum background emission compared to fs/pico/nano second pulses.205,217 First, fs-LIBS provides a colder plasma with faster decay compared to ns-LIBS.146 Second, the electron density in filaments is two-three orders lower compared to fs-LIBS, thus reducing broadband emission from plasma. The continuum emission for filament-induced plasma can originate from supercontinuum generation during filament propagation in air. Nevertheless, supercontinuum emission spreads within a narrow cone and its intensity is linearly proportional to the propagation distance. Consequently, this process can be effectively controlled by a chirping technique (see further in the text). In addition, the background emission level can be substantially decreased when strong and short filaments are formed to induce plasma, thus even non-gated detectors can be used.217
Filament-induced plasma temperature and electron density was measured by Xu et al.218 The electron density was measured by Stark broadening of Pb I lines to decrease within 200 ns from 8 × 1017 to 1 × 1017 cm−3. The plasma temperature was measured by the Boltzmann plot method and was shown to decrease from 7000 to 4500 K during the first 100 ns. Judge et al.219 studied the plasma temperature induced by a filament on composite graphite samples at a distance of 6 m. A significant difference in plasma temperature (9000 vs. 5500 K) calculated from atomic lines (Al I, K I) and molecular bands of C2 (Swan system) was obtained. The authors explained this fact to be due to non-equilibrium plasmas formed on different micro domains in the samples that were superimposed by multiple filaments.
Ambient air properties (air turbulence and aerosols) influenced filament properties and consequently filament-induced plasma. The total area of sampling by multiple filaments strongly depends on air turbulence.213,214 The influence of temperature, pressure, humidity and precipitation (snow) on FIBS signals has been investigated by Xu et al.220 A compact laser system was used to perform an FIBS study under polar conditions. Femtosecond laser pulses (800 nm, 45 fs, 225 mJ) induced filaments in air at temperatures below −10 °C under clear sky and snowy conditions. Strong turbulence in the air was observed due to a 40 degree temperature gradient between the measuring system and the target. Moreover, dense snow fall and weak fog lowered the air visibility to 3.2 km, and therefore significantly suppressed measured signals. Despite the adverse conditions, resonance Al I lines were detected with a high signal-to-noise ratio at a distance of 60 m. The maximum distance was estimated to be 730 m for clear-sky conditions.
4.3 Optimizing filament-induced breakdown spectrometry
Laser beam energy is not effectively used for the excitation of filament-induced plasma due to defocusing and lowering peak intensity of the laser beam at filament clamps, resulting in slight conversion of pulse energy into plasma. Zeng et al.223 suggested spatio-temporal chirping to increase peak intensity in a filament core. Two cylindrical lenses (concave and convex) confined the beam to an elliptical profile. The filament length was significantly shorter than for the initial laser beam. This was explained by the spatial separation of different components at the focus and a chirp-free pulse in the focal spot. Nitrogen molecule ionization increased by one order of magnitude in the filament core. The suggested technique can be of great interest for improving the spatial resolution for LIDAR applications while retaining the capability of filament initiation at any position for long distances. The same authors observed224 a significant (3–5 times) intensity increase in atomic lines of Al and Fe with the use of a spatio-temporal chirped pulse (800 nm, 50 fs, 8 mJ) for FIBS of aluminum and steel samples. Consequently, the spatio-temporal chirping technique allows initiation of the filament at longer distances and more effective conversion of laser energy.
4.4 Applications
Most applications of FIBS are associated with the unique capability of filamentation to conserve laser beam divergence without any optical systems at distances up to 20 km.28 Moreover, it was demonstrated that remote analysis of a distant object can be performed by FIBS even under snowy conditions.220| Analyte | Matrix | Distance (estimated)a, m | Laser parameters | Conditions | Reference |
|---|---|---|---|---|---|
| a Experimental distance between laser system and sample is presented first, while the estimated maximum distance is shown in brackets. | |||||
| Cu I, Fe I | Copper, steel | 180 (up to 1000) | 800 nm, 80 fs, 250 mJ | Open air; field conditions | 205 and 213 |
| Al I | Aluminum | 60 (730) | 800 nm, 45 fs, 225 mJ | Open air, −20 °C, snowing | 220 |
| Al I, Mg II | Aluminum | 50 (1900) | 800 nm, 90 fs, 108 mJ | Lab air | 217 |
| Ca I, PH2, NH2, CN | White egg, yeast | 50 (1500) | 800 nm, 45 fs, 7 mJ | Lab air | 225 |
| K I, Al I, C2 | Composite graphite | 6 | 800 nm, 60 fs, 3 mJ | Lab air | 219 |
| Mg I | White marble, red clay | 6 (not estimated) | 248 nm, 450 fs, 20 mJ | Air | 221 |
| Pb I | Lead | 5 (325) | 800 nm, 45 fs, 12 mJ | Lab air | 218 |
| Cr I | Leaves, soil | 0.95–1.03 | 800 nm, 50 fs, 4 mJ | Lab air | |
| Si I, Mg I, Ca I, Al I, C2, CN | Corn, barley wheat | 4 (not estimated) | 800 nm, 45 fs, 12 mJ | Air; laboratory conditions | 226 |
| CN, NH2 | Dinitrotoluene, ammonium perchlorate | 1.5 (not estimated) | 266 and 800 nm, 100 fs, 15 mJ | Lab air | 222 |
Tzortzakis et al.221 made the first step towards FIBS analysis of cultural heritage, studying elemental compositions of typical materials in sculptures and large monuments (white marble, red clay, and limestone) at a distance of 4.5 m. The authors were able to distinguish these materials by small differences in their spectral features (for example, Mg I lines for red clay).
The feasibility of FIBS classification of biological objects was described in ref. 225. Egg white and yeast were sampled by filaments at a distance of 6 m. The spectra had low levels of broadband emission (continuum) and contained atomic lines (Ca, Na) and molecular bands (NH2, PH2, CN) of major components. The more complex goal of agricultural sample differentiation (wheat, barley and corn) by FIBS was undertaken in ref. 226. Samples were pressed into pellets and then sampled by FIBS at a distance of 4 m. The spectra were quite similar (C2 and CN molecular bands and Si, C, Mg, Al, Na, Ca, Mn, Fe, Sr and K lines) due to the samples having almost the same elemental composition. Despite this, the authors were able to distinguish three types of samples from intensity ratios in the plasma spectra. Recently, it was demonstrated that FIBS can be used for monitoring of toxic metals such as Cr in leaves227 and soils228 but this was only tested at a short distance (∼1 m).
Detection of explosive material (dinitrotoluene and ammonium perchlorate) on metal plates by UV FIBS was demonstrated in ref. 222. Molecular bands of CN and NH2 were detected at a distance of 50 m. However, the authors have not described any attempts to identify explosive/non-explosive materials by FIBS. Another team has tried to identify organic films as test samples for detection of explosive materials.216 Two polymers, namely, poly methyl methacrylate (PMMA) and Futurex were ablated by a filament in air. Surprisingly, the authors detected strong CN molecular bands without any molecular nitrogen emission in PMMA plasma spectra. These results indicate that, despite a unique capability to induce plasma at long distances by filaments, a lot of investigations have to be carried out towards meaningful explosive discrimination by FIBS.
Isotopic analysis of zirconium by FIBS was recently performed at distances up to 7 m by Russo's group.159 Besides semi-quantitative isotopic analysis without the use of calibration standards, they investigated the properties of plasmas generated at different filament propagation distances.
5 Conclusion
In conclusion, femtosecond laser pulses are believed to provide a brighter future for numerous LIBS applications due to the absence of fractionation; improved spatial resolution; and lower ablation threshold. This can be useful for applications, where minimal invasion is required, such as analysis of artefacts171,236–238 and biological samples,239 or even bacterial classification.240,241 Besides this, the fs-LIBS technique can be successfully used as an assistant monitoring tool in such applications as micromachining or surgery,242,243 where fs lasers are used. However, to date, femtosecond laser systems with single pulse energy in the range of a few mJ are still very expensive and very complex for conventional LIBS measurements. Because femtosecond lasers provide low ablation thresholds, the plasma near the threshold has a low level of background emission; unlike nanosecond ablation, one could expect an improvement in LIBS sensitivity in terms of better limits of detection (LOD). The typical repetition rate of femtosecond lasers is in the kHz range, thus a long exposure time for a non-gated detector can be applied to sum thousands of spectra in a CCD matrix over several seconds, which significantly increases the signal-to-noise ratio, thus improving the sensitivity of fs-LIBS. However, a lower plasma temperature and a shorter plasma life for fs-LIBS should limit the total intensity. In Table 3, we have collected the best LODs available in the literature to weigh the pros and cons of detection capabilities of fs- and ns-LIBS. To avoid matrix effects, we gathered LOD values for matrices matched as closely as possible. For example, LODs given for “Thin films or coatings” were retrieved for films of oil or other coatings on the substrate. Moreover, such a division allows the elimination of spectral interferences of main components. Indeed, comparison of LODs for Mn between Cu alloys for fs-LIBS and Fe-alloys for ns-LIBS appears to be unreasonable. We have also tried to gather values obtained for the same analytical line of an element. However, several elements (such as Fe) are presented by different lines. Because there is a large amount of data on enhancing LIBS sensitivity, in Table 3, data for single-pulse LIBS are given only to avoid inappropriate comparison between techniques. This means that no values for double-pulse techniques, laser-induced fluorescence, resonance ablation or sorption on a specific matter are listed. Because values for laser fluence are not given by some authors, we compared laser energy per pulse only. Fs-LIBS at approximately the same pulse energy has, in general, higher values of LODs than ns-LIBS in spite of the higher ablation efficiency, i.e. the sensitivity of fs-LIBS is, at least, the same as of ns-LIBS. Therefore, such an expensive tool as fs-LIBS cannot be considered as the best practical way to improve sensitivity.| Element | Femtosecond LIBS | Nanosecond LIBS | ||||
|---|---|---|---|---|---|---|
| Alloys | ||||||
| Ag | 1.4 | 50 mJ (400) | Ref. 125 | 0.2 | 60 mJ (100) | Ref. 244 |
| Cu | 3.2 | 1 | ||||
| Si | 30 | 8 | ||||
| Ni | 10 | 7 | 60 mJ (1000) | Ref. 245 | ||
| Fe | 22 | 50 mJ (100) | Ref. 170 | 3.7 | 60 mJ (100) | Ref. 244 |
| Mg | 2.1 | 0.13 | 60 mJ (1000) | Ref. 245 | ||
| Mn | 6.7 | 2 | 60 mJ (50) | Ref. 246 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Water | ||||||
| Al | 0.19 | 1.1 mJ (4000) | Ref. 247 | 0.7 | ≤100 mJ | Ref. 248 |
| Ca | 0.01 | 0.003 | 16 mJ (12) | Ref. 249 | ||
| Mg | 1 | 0.1 | 150 mJ () | Ref. 250 | ||
| Na | 0.0009 | 0.0004 | 16 mJ (12) | Ref. 249 | ||
| Zn | 2.5 | 0.05 | 14 mJ (30) | Ref. 251 | ||
| Ba | 0.08 | 1 mJ (4000) | Ref. 252 | 0.007 | 16 mJ (12) | Ref. 249 |
| Cu | 0.78 | 0.39 | 90 mJ (500) | Ref. 253 | ||
| Fe | 2.6 | 7 mJ (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
Ref. 254 | 37 | 40 mJ (100) | Ref. 255 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Tissue | ||||||
| Al | 29 | 840 μJ (500) | Ref. 256 | 0.82 | 80 mJ (1200) | Ref. 257 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Thin films or coatings | ||||||
| Mg | 3010 | 221 μJ (1) | Ref. 258 | 0.24 | 90 mJ (200) | Ref. 259 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Leaves | ||||||
| Ca | 0.007 | 1.5 mJ (15) | Ref. 260 | 0.007 | 70 mJ (15) | Ref. 260 |
| Cu | 7 | 1 | ||||
| Fe | 12 | 3 | ||||
| Mg | 0.02 | 0.01 | ||||
| Mn | 2 | 1 | ||||
| P | 0.4 | 0.1 | ||||
| Zn | 80 | 4 | ||||
Improved resolution in 2D and 3D mapping applications was demonstrated by fs-LIBS. Under the best conditions, conventional ns-LIBS systems can provide spatial resolution of ∼50 μm.261 Other problems associated with “long” laser pulses are thermal ablation effects and higher ablation thresholds, which are responsible for “matrix effects”. As a result, spatial resolution for ns-LIBS is limited by materials, their surface morphology and their compositions.262 Craters with sizes less than diffraction-limited laser beam diameters can be produced due to the absence of a heat-affected zone for femtosecond laser ablation. NSOM technology combined with femtosecond laser ablation can achieve crater diameters as small as 450 nm,121 which are visible on an fs-LIBS spectrum. Interesting achievements in operating with ultrafast laser beams, especially cylindrical vector beams,119 give expectations of a new breakthrough for fs-LIBS with a spatial resolution below 80 nm. Another unique capability of fs-LIBS is high-resolution depth profiling of layers or coatings. For example, a depth sensitivity of about 3 nm (ref. 98) has been recently reported in thickness measurements of buried layers. However, either high depth sensitivity or high spatial resolution can be achieved in fs-LIBS. Thus, a Gaussian beam provides small and deep craters, while a flat-top beam produces wider and shallower ablation craters. It should be noted that the higher the spatial resolution, the lower the sensitivity will be because an increasingly smaller mass (and number of atoms) is ablated with an increasing concentration of beam energy in a space.
In spite of the poor detectability of single pulse fs-LIBS, the spatial resolution allows microanalytical measurements that result in minimal sample damage. For example, fs-LIBS was recently tested with respect to the detection of cancer antigen 125 in blood plasma.263 The combination of efficient energy coupling and a lower ablation threshold for femtosecond laser sampling is very suitable for the analysis of biological materials such as bacteria, cells, and leaves and cultural heritage objects such as ceramics, bronze statues, glasses and coatings, where minimal damage is a primary concern. Fs-LIBS can also be an auxiliary tool to monitor material processing by femtosecond lasers for cleaning of corroded alloys and preparing sub-micron grooves on a layered surface. In this case, LIBS provides spectral information for stopping or continuing material processing.
The low emissivity of plasma due to relatively low fs laser pulse energy can be overcome by the use of an additional ns laser in an orthogonal configuration, which can deliver enough energy to reheat plasma while preserving the advantages of fs ablation.
A new era of laser remote sensing has been started by filament-induced breakdown spectrometry (FIBS), which utilizes the unique capability of powerful femtosecond laser pulses to initiate filamentation in air. Filamentation makes it possible to overcome laser beam diffraction and to conserve the laser beam diameter at long distances (up to 20 km) without any focusing optics. This allows laser pulses to be delivered with the high power density needed to induce ablation of remote samples. Conventional focusing systems for remote LIBS utilize focusing optics to achieve the power density needed for analytically meaningful plasma. Ideally, the focal length of a lens should be proportional to the distance between laser and sample, resulting in an optical system with a large dimension and mass. Nevertheless, even ideally focusing optics cannot deliver a sufficiently powerful laser beam at a distance beyond several tens of meters due to fluctuation of atmospheric properties (refraction index fluctuation and interaction with aerosol particles). Filamentation allows a laser beam to be delivered with enough power density to induce plasma breakdown, even under heavy meteorological conditions (e.g. snow). Currently, the maximum distance for FIBS measurements is determined by collecting optics efficiency and detector system sensitivity. It was demonstrated that state-of-the-art FIBS systems can perform measurements at a distance of ∼200 m, while the maximum estimated distance can reach up to 2 km with the use of more sensitive gated detectors.
The feasibility of elemental remote sensing by filaments was demonstrated for metallic, inorganic and organic samples. FIBS measurements published in the literature were motivated by remote sensing of dangerous materials (e.g. explosives and drugs), cultural heritage objects, and isotopic analysis. To date, FIBS studies were mainly focused on feasibility demonstration rather than on quantitative analysis. The analytical figures of merit for FIBS were roughly estimated at the tenth ppm level in one study presented in the literature.217 The estimated limits of detection were at a level of a tenth to hundreds of ppm for additives in aluminum samples located at a distance of 50 m. The high cost and complexity of powerful femtosecond laser systems are the main limiting factors for the deployment of filament-induced breakdown spectrometry in everyday practice.
Acknowledgements
Labutin T. A. and Popov A. M. thank the Russian Science Foundation for the financial support (agreement No. 14-13-01386) in the preparation of Section 3. Lednev V. N. gratefully acknowledges the financial support of the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST «MISiS» (agreement No. K4-2015-052) for the preparation of Section 4. Ilyin A. A. thanks the Russian Science Foundation for financial support (agreement No. 14-50-00034) for the preparation of Section 2. Some results presented in this section were obtained using scientific equipment from TsKP LaMI of IACP FEB RAS.References
- C. V. Shank and E. P. Ippen, Sub-picosecond kilowatt pulses from a mode locked cw dye laser, Appl. Phys. Lett., 1974, 24, 373 CrossRef CAS
.
- P. F. Moulton, Ti-doped Sapphire Tunable Solid State Laser, Optics News, 1982, 8, 9 CrossRef
.
- D. Strickland and G. Mourou, Compression of amplified chirped optical pulses, Opt. Commun., 1985, 56, 219 CrossRef
.
- J. A. Cobble, G. A. Kyrala, A. A. Hauer, A. J. Taylor, C. C. Gomez, N. D. Delamater and G. T. Schappert, Kilovolt X-ray spectroscopy of a subpicosecond-laser-excited source, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 454 CrossRef CAS
.
- B.-M. Kim, M. D. Feit, A. M. Rubenchik, B. M. Mammini and L. B. Da Silva, Optical feedback signal for ultrashort laser pulse ablation of tissue, Appl. Surf. Sci., 1998, 127–129, 857 CrossRef CAS
.
- V. Margetic, A. Pakulev, A. Stockhaus, M. Bolshov, K. Niemax and R. Hergenroder, A comparison of nanosecond and femtosecond laser-induced plasma spectroscopy of brass samples, Spectrochim. Acta, Part B, 2000, 55, 1771 CrossRef
.
- E. L. Gurevich and R. Hergenröder, Femtosecond laser-induced breakdown spectroscopy: physics, applications, and perspectives, Appl. Spectrosc., 2007, 61, 233A CrossRef CAS PubMed
.
- J. Herrmann, Theory of Kerr-lens mode-locking – role of self-focusing and radially varying gain, J. Opt. Soc. Am. B, 1994, 11, 498 CrossRef
.
-
Femtosecond Laser Pulses. Principles and Experiments, ed. C. Rulliere, Springer-Verlag, 2005 Search PubMed
.
- K. Yamane, Z. Zhang, K. Oka, R. Morita, M. Yamashita and A. Suguro, Optical pulse compression to 3.4 fs in the monocycle region by feedback phase compensation, Opt. Lett., 2003, 28, 2258 CrossRef PubMed
.
- G. Steinmeyer and G. Stibenz, Generation of sub-4-fs pulses via compression of a white-light continuum using only chirped mirrors, Appl. Phys. B, 2006, 82, 175 CrossRef CAS
.
- O. A. Konoplev, Temporal high-contrast structure of ultrashort pulses: a plea for standardization of nomenclature and conventions, Proc. SPIE, 2000, 3934, 102 CrossRef
.
- S. Fourmaux, S. Payeur, S. Buffechoux, P. Lassonde, C. St-Pierre, F. Martin and J. C. Kieffer, Pedestal cleaning for high laser pulse contrast ratio with a 100 TW class laser system, Opt. Express, 2011, 19, 8486 CrossRef CAS PubMed
.
- V. V. Semak, J. G. Thomas and B. R. Campbell, Drilling of steel and HgCdTe with the femtosecond pulses produced by a commercial laser system, J. Phys. D: Appl. Phys., 2004, 37, 2925 CrossRef CAS
.
- R. Y. Chiao, E. Garmire and C. H. Townes, Self-trapping of optical beams, Phys. Rev. Lett., 1964, 13, 479 CrossRef
.
- N. F. Pilipetskii and A. R. Rustamov, Observation of self-focusing of light in liquids, JETP Lett., 1965, 2, 55 Search PubMed
.
- A. Braun, G. Korn, X. Liu, D. Du, J. Squier and G. Mourou, Self-channeling of high-peak-power femtosecond laser pulses in air, Opt. Lett., 1995, 20, 73 CrossRef CAS PubMed
.
- P. Béjot and J. Kasparian, Conical emission from laser filaments and higher-order Kerr effect in air, Opt. Lett., 2011, 36, 4812 CrossRef PubMed
.
- V. P. Kandidov, O. G. Kosareva and A. A. Koltun, Nonlinear-optical transformation of a high-power femtosecond laser pulse in air, Quantum Electron., 2003, 33, 69 CrossRef CAS
.
- Y. E. Geints and A. A. Zemlyanov, Self-focusing of a focused femtosecond laser pulse in air, Appl. Phys. B: Lasers Opt., 2010, 101, 735 CrossRef CAS
.
- S. L. Chin, T. J. Wang, C. Marceau, J. Wu, J. S. Liu, O. Kosareva, N. Panov, Y. P. Chen, J. F. Daigle, S. Yuan, A. Azarm, W. W. Liu, T. Seideman, H. P. Zeng, M. Richardson, R. Li and Z. Z. Xu, Advances in intense femtosecond laser filamentation in air, Laser Phys., 2012, 22, 1 CrossRef
.
- A. Couairon and A. Mysyrowicz, Femtosecond filamentation in transparent media, Phys. Rep., 2007, 441, 47 CrossRef CAS
.
- V. P. Kandidov, S. A. Shlenov and O. G. Kosareva, Filamentation of high-power femtosecond laser radiation, Quantum Electron., 2009, 39, 205 CrossRef CAS
.
- S. L. Chin, S. A. Hosseini, W. Liu, Q. Luo, F. Théberge, N. Aközbek, A. Becker, V. P. Kandidov, O. G. Kosareva and H. Schröder, The propagation of powerful femtosecond laser pulses in optical media: physics, applications, and new challenges, Can. J. Phys., 2005, 83, 863 CrossRef CAS
.
- D. V. Apeksimov, O. A. Bukin, E. E. Bykova, Yu. E. Geints, S. S. Golik, A. A. Zemlyanov, A. A. Il’in, A. M. Kabanov, G. G. Matvienko, V. K. Oshlakov, A. V. Petrov and E. B. Sokolova, Filamentation of the focused Ti:Sapphire laser pulse in air at two harmonics, Plasma Phys. Rep., 2013, 39, 1074 CrossRef CAS
.
- G. Mechain, C. D. Amico, Y.-B. Andre, S. Tzortzakis, M. Franco, B. Prade, A. Mysyrowicz, A. Couairon, E. Salmon and R. Sauerbrey, Range of plasma filaments created in air by a multi-terawatt femtosecond laser, Opt. Commun., 2005, 247, 171 CrossRef CAS
.
- M. Durand, A. Houard, B. Prade, A. Mysyrowicz, A. Durécu, B. Moreau, D. Fleury, O. Vasseur, H. Borchert and K. Diener, Kilometer range filamentation, Opt. Express, 2013, 21, 26836 CrossRef PubMed
.
- M. Rodriguez, R. Bourayou, G. Méjean, J. Kasparian, J. Yu, E. Salmon, A. Scholz, B. Stecklum, J. Eislöffel and U. Laux, Kilometer-range nonlinear propagation of femtosecond laser pulses, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 036607 CrossRef PubMed
.
- A. A. Ionin, S. I. Kudryashov, S. V. Makarov, L. V. Seleznev and D. V. Sinitsyn, Multiple filamentation of intense femtosecond laser pulses in air, JETP Lett., 2009, 90, 423 CrossRef CAS
.
- A. A. Ilyin and S. S. Golik, Absorption of laser-radiation energy by femtosecond laser spark in air, Tech. Phys. Lett., 2014, 40, 1 CrossRef CAS
.
- W. Liu and S. L. Chin, Direct measurement of the critical power of femtosecond Ti:Sapphire laser pulse in air, Opt. Express, 2005, 13, 5750 CrossRef CAS PubMed
.
- N. Zhang, W.-X. Bao, J.-H. Yang and X.-N. Zhu, Determination of the temporal structure of femtosecond laser pulses by means of laser-induced air plasma, Chin. Phys. B, 2013, 22, 054209 CrossRef
.
- S. Xu, X. Sun, B. Zeng, W. Chu, J. Zhao, W. Liu, Y. Cheng, Z. Xu and S. L. Chin, Simple method of measuring laser peak intensity inside femtosecond laser filament in air, Opt. Express, 2012, 20, 299 CrossRef PubMed
.
- K. Lim, M. Durand, M. Baudelet and M. Richardson, Transition from linear-to nonlinear-focusing regime in filamentation, Sci. Rep., 2014, 4, 7217 CrossRef PubMed
.
- P. P. Kiran, S. Bagchi, S. R. Krishnan, C. L. Arnold, G. R. Kumar and A. Couairon, Focal dynamics of multiple filaments: microscopic imaging and reconstruction, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 013805 CrossRef
.
- Y. E. Geints, A. A. Ionin, A. A. Zemlyanov, S. I. Kudryashov, L. V. Seleznev, D. V. Sinitsyn and E. S. Sunchugasheva, Features of focused propagation of intense femtosecond laser pulses in air under low pressure, Atmos. Oceanic Opt., 2012, 25, 185 CrossRef CAS
.
-
A. Couairon and A. Mysyrowicz, in Progress in Ultrafast Intense Laser Science, ed. K. Yamanouchi, S. L. Chin, P. Agostini and G. Ferrante, Springer, 2006, vol. I, pp. 235–258 Search PubMed
.
- F. Théberge, W. Liu, P. T. Simard, A. Becker and S. L. Chin, Plasma density inside a femtosecond laser filament in air: strong dependence on external focusing, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 036406 CrossRef PubMed
.
- J. Kasparian, R. Sauerbrey and S. L. Chin, The critical laser intensity of self-guided light filaments in air, Appl. Phys. B: Lasers Opt., 2000, 71, 877 CrossRef CAS
.
-
N. B. Delone, Basics of interaction of laser radiation with matter, Editions Frontieres, 1993 Search PubMed
.
- H. L. Xu, A. Azarm, J. Bernhardt, Y. Kamali and S. L. Chin, The mechanism of nitrogen fluorescence inside a femtosecond laser filament in air, Chem. Phys., 2009, 360, 171 CrossRef CAS
.
- J. Yu, D. Mondelain, J. Kasparian, E. Salmon, S. Geffroy, C. Favre, V. Boutou and J.-P. Wolf, Sonographic probing of laser filaments in air, Appl. Opt., 2003, 42, 7117 CrossRef PubMed
.
- G. N. Gibson, R. R. Freeman and T. J. McIlrath, Dynamics of the high-intensity multiphoton ionization of N2, Phys. Rev. Lett., 1991, 67, 1230 CrossRef CAS PubMed
.
-
Y. P. Raizer, Laser-Induced Discharge Phenomena, Consultants Bureau, 1977 Search PubMed
.
- A. A. Ilyin, I. G. Nagorny and O. A. Bukin, Supersonic regimes of plasma expansion during optical breakdown in air, Appl. Phys. Lett., 2010, 96, 171501 CrossRef
.
- A. A. Ilyin, S. S. Golik and K. A. Shmirko, Absorption and emission characteristics of femtosecond laser plasma filaments in the air, Spectrochim. Acta, Part B, 2015, 112, 16 CrossRef CAS
.
- F. Martin, R. Mawassi, F. Vidal, I. Gallimberti, D. Comtois, H. Pépin, J. C. Kieffer and H. P. Mercure, Spectroscopic study of ultrashort pulse laser-breakdown plasmas in air, Appl. Spectrosc., 2002, 56, 1444 CrossRef CAS
.
- B. R. Arnold, S. D. Roberson and P. M. Pellegrino, Excited state dynamics of nitrogen reactive intermediates at the threshold of laser induced filamentation, Chem. Phys., 2012, 405, 9 CrossRef CAS
.
- V. Zorba, X. Mao and R. E. Russo, Optical far- and near-field femtosecond laser ablation of Si for nanoscale chemical analysis, Anal. Bioanal. Chem., 2010, 396, 173 CrossRef CAS PubMed
.
- S.-S. Wellershoff, J. Hohlfeld, J. Güdde and E. Matthias, The role of electron–phonon coupling in femtosecond laser damage of metals, Appl. Phys. A: Mater. Sci. Process., 1999, 69, S99 CAS
.
- F. Korte, S. Nolte, B. N. Chichkov, T. Bauer, G. Kamlage, T. Wagner, C. Fallnich and H. Welling, Far-field and near-field material processing with femtosecond laser pulses, Appl. Phys. A: Mater. Sci. Process., 1999, 69, S7 CrossRef CAS
.
- E. G. Gamaly and A. V. Rode, Physics of ultra-short laser interaction with matter: from phonon excitation to ultimate transformations, Prog. Quantum Electron., 2013, 37, 215 CrossRef
.
-
Ultrafast Laser Processing: From Micro- to Nanoscale, ed. K. Sugioka and Y. Cheng, Pan Stanford Publishing, 2013 Search PubMed
.
- M. Lisowski, P. A. Loukakos, U. Bovensiepen, J. Stahler, C. Gahl and M. Wolf, Ultra-fast dynamics of electron thermalization, cooling and transport effects in Ru(001), Appl. Phys. A: Mater. Sci. Process., 2004, 78, 165 CrossRef CAS
.
- N. M. Bulgakova, A. V. Bulgakov and O. F. Bobrenok, Double layer effects in laser-ablation plasma plumes, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5624 CrossRef CAS
.
- A. Brantov, W. Rozmus, R. Sydora, C. E. Capjack, V. Y. Bychenkov and V. T. Tikhonchuk, Enhanced inverse Bremsstrahlung heating rates in a strong laser field, Phys. Plasmas, 2003, 10, 3385 CrossRef CAS
.
- W. Hu, Y. C. Shin and G. King, Energy transport analysis in ultrashort pulse laser ablation through combined molecular dynamics and Monte Carlo simulation, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094111 CrossRef
.
- N. M. Bulgakova, R. Stoian and A. Rosenfeld, Laser-induced modification of transparent crystals and glasses, Quantum Electron., 2010, 40, 966 CrossRef CAS
.
- N. M. Bulgakova, V. P. Zhukov, A. Y. Vorobyev and C. Guo, Modeling of residual thermal effect in femtosecond laser ablation of metals: role of a gas environment, Appl. Phys. A: Mater. Sci. Process., 2008, 92, 883 CrossRef CAS
.
- W. Hu, Y. C. Shin and G. King, Early-stage plasma dynamics with air ionization during ultrashort laser ablation of metal, Phys. Plasmas, 2011, 18, 093302 CrossRef
.
- J. Li, X. Wang, Z. Chen, R. Clinite, S. S. Mao, P. Zhu, Z. Sheng, J. Zhang and J. Cao, Ultrafast electron beam imaging of femtosecond laser-induced plasma dynamics, J. Appl. Phys., 2010, 107, 083305 CrossRef
.
- X. Zhao and Y. C. Shin, Coulomb explosion and early plasma generation during femtosecond laser ablation of silicon at high laser fluence, J. Phys. D: Appl. Phys., 2013, 46, 335501 CrossRef
.
- X.-L. Liu, X. Lu, X. Liu, T.-T. Xi, F. Liu, J.-L. Ma and J. Zhang, Tightly focused femtosecond laser pulse in air: from filamentation to breakdown, Opt. Express, 2010, 18, 26007 CrossRef CAS PubMed
.
- A. E. Martirosyan, C. Altucci, A. Bruno, C. de Lisio, A. Porzio and S. Solimeno, Time evolution of plasma afterglow produced by femtosecond laser pulses, J. Appl. Phys., 2004, 96, 5450 CrossRef CAS
.
- V. V. Bukin, N. S. Vorob'ev, S. V. Garnov, V. I. Konov, V. I. Lozovoi, A. A. Malyutin, M. Y. Shchelev and I. S. Yatskovskii, Formation and development dynamics of femtosecond laser microplasma in gases, Quantum Electron., 2006, 36, 638 CrossRef CAS
.
- S. I. Anisimov, B. L. Kapeliovich and T. L. Perel’man, Electron-emission from surface of metals induced by ultrashort laser pulses, Soviet Physics – JETP, 1975, 39, 375 Search PubMed
.
- M. E. Povarnitsyn, T. E. Itina, M. Sentis, K. V. Khishchenko and P. R. Levashov, Material decomposition mechanisms in femtosecond laser interactions with metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 23, 235414 CrossRef
.
- B. Rethfeld, K. Sokolowski-Tinten, D. von der Linde and S. I. Anisimov, Timescales in the response of materials to femtosecond laser excitation, Appl. Phys. A: Mater. Sci. Process., 2004, 79, 767 CrossRef CAS
.
-
I. Mingareev, Ultrafast dynamics of melting and ablation at large laser intensities, PhD thesis, RWTH- Aachen, 2009
.
- D. S. Ivanov and L. V. Zhigilei, Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 064114 CrossRef
.
- B. Rethfeld, K. Sokolowski-Tinten, D. von der Linde and S. I. Anisimov, Ultrafast thermal melting of laser-excited solids by homogeneous nucleation, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 092103 CrossRef
.
- A. Rousse, C. Rischel, S. Fourmaux, I. Uschmann, S. Sebban, G. Grillon, P. Balcou, E. Förster, J. P. Geindre, P. Audebert, J. C. Gauthier and D. Hulin, Non-thermal melting in semiconductors measured at femtosecond resolution, Nature, 2001, 410, 65 CrossRef CAS PubMed
.
- J. P. Colombier, P. Combis, R. Stoian and E. Audouard, High shock release
in ultrafast laser irradiated metals: scenario for material ejection, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104105 CrossRef
.
- M. E. Povarnitsyn, K. V. Khishchenko and P. R. Levashov, Phase transitions in femtosecond laser ablation, Appl. Surf. Sci., 2009, 255, 5120 CrossRef CAS
.
- A. A. Ionin, S. I. Kudryashov, L. V. Seleznev, D. V. Sinitsyn, A. F. Bunkin, V. N. Lednev and S. M. Pershin, Thermal melting and ablation of silicon by femtosecond laser radiation, J. Exp. Theor. Phys., 2013, 116, 347 CrossRef CAS
.
- M. E. Povarnitsyn, T. E. Itina, P. R. Levashov and K. V. Khishchenko, Simulation of ultrashort double-pulse laser ablation, Appl. Surf. Sci., 2011, 257, 5168 CrossRef CAS
.
- I. Mingareev and A. Horn, Time-resolved investigations of plasma and melt ejections in metals by pump-probe shadowgrpahy, Appl. Phys. A: Mater. Sci. Process., 2008, 92, 917 CrossRef CAS
.
- O. Albert, S. Roger, Y. Glinec, J. C. Loulergue, J. Etchepare, C. Boulmer-Leborgne, J. Perriere and E. Millon, Time-resolved spectroscopy measurements of a titanium plasma induced by nanosecond and femtosecond lasers, Appl. Phys. A: Mater. Sci. Process., 2003, 76, 319 CrossRef CAS
.
- D. Scuderi, R. Benzerga, O. Albert, B. Reynier and J. Etchepare, Spectral and temporal characteristics of metallic nanoparticles produced by femtosecond laser pulses, Appl. Surf. Sci., 2006, 252, 4360–4363 CrossRef CAS
.
- S. Noël, J. Hermann and T. Itina, Investigation of nanoparticle generation during femtosecond laser ablation of metals, Appl. Surf. Sci., 2007, 253, 6310 CrossRef
.
- E. Axente, S. Noël, J. Hermann, M. Sentis and I. N. Mihailescu, Correlation between plasma expansion and damage threshold by femtosecond laser ablation of fused silica, J. Phys. D: Appl. Phys., 2008, 41, 105216 CrossRef
.
- I. Mingareev and A. Horn, Melt dynamics of aluminum irradiated with ultrafast laser radiation at large intensities, J. Appl. Phys., 2009, 106, 013513 CrossRef
.
- N. M. Bulgakova and A. V. Bulgakov, Pulsed laser ablation of solids: transition from normal vaporization to phase explosion, Appl. Phys. A: Mater. Sci. Process., 2001, 73, 199 CrossRef CAS
.
- A. A. Ilyin, I. G. Nagorny, O. A. Bukin, A. V. Bulanov and K. A. Shmirko, Features of development of optical breakdown on an inclined aluminum surface, Tech. Phys. Lett., 2012, 38, 975 CrossRef CAS
.
- B. N. Chichkov, C. Momma, S. Nolte, F. Yon Alvensleben and A. Tünnermann, Femtosecond, picosecond and nanosecond laser ablation of solids, Appl. Phys. A: Mater. Sci. Process., 1996, 63, 109 CrossRef
.
- M. Lopez-Claros, J. M. Vadillo and J. J. Laserna, Determination of plasma ignition threshold fluence during femtosecond single-shot laser ablation on metallic samples detected by optical emission spectroscopy, J. Anal. At. Spectrom., 2015, 30, 1730 RSC
.
- S. Hofmann, Quantitative Depth Profiling in Surface Analysis: A Review, Surf. Interface Anal., 1980, 2, 148 CrossRef CAS
.
- Compendium of Analytical Nomenclature: Orange Book of IUPAC. Definitive Rules; 1997. Part 17.4 Terms related to surface analysis.
- V. Margetic, M. Bolshov, A. Stockhaus, K. Niemax and R. Hergenröder, Depth profiling of multi-layer samples using femtosecond laser ablation, J. Anal. At. Spectrom., 2001, 16, 616 RSC
.
- A. Baskevicius, A. Alesenkov, G. Chozevskis, J. Litvaityte, O. Balachninaite, D. Paipulas, A. Melninkaitis and V. Sirutkaitis, Optimization of Laser-Ablation Micromachining by Choice of Scanning Algorithms and Use of Laser-Induced-Breakdown Spectroscopy, J. Laser Micro/Nanoeng., 2013, 8, 24 CrossRef CAS
.
- O. Samek, V. Hommes, R. Hergenröder and S. V. Kukhlevsky, Femtosecond pulse shaping using a liquid-crystal display: applications to depth profiling analysis, Rev. Sci. Instrum., 2005, 76, 086104 CrossRef
.
- S. P. Banerjee, Z. Chen, I. Utkin and R. Fedosejevs, Detection of buried layers in silicon devices using LIBS during hole drilling with femtosecond laser pulses, Appl. Phys. A: Mater. Sci. Process., 2013, 111, 791 CrossRef CAS
.
- D. McGloin and K. Dholakia, Bessel beams: diffraction in a new light, Contemp. Phys., 2005, 46, 15 CrossRef
.
- J. Durnin, J. J. Miceli Jr and J. H. Eberly, Diffraction-free beams, Phys. Rev. Lett., 1987, 58, 1499 CrossRef PubMed
.
- J. Arlt and K. Dholakia, Generation of high-order Bessel beams by use of an axicon, Opt. Commun., 2000, 177, 297 CrossRef CAS
.
- F. Courvoisier, J. Zhang, M. K. Bhuyan, M. Jacquot and J. M. Dudley, Applications of femtosecond Bessel beams to laser ablation, Appl. Phys. A: Mater. Sci. Process., 2013, 112, 29 CrossRef CAS
.
- D. E. Roberts, A. du Plessis, J. Steyn, L. R. Botha, C. A. Strydom and I. J. van Rooyen, Femtosecond laser induced breakdown spectroscopy of silver within surrogate high temperature gas reactor fuel coated particles, Spectrochim. Acta, Part B, 2010, 65, 918 CrossRef
.
- S. P. Banerjee and R. Fedosejevs, Single shot depth sensitivity using femtosecond Laser Induced Breakdown Spectroscopy, Spectrochim. Acta, Part B, 2014, 92, 34 CrossRef CAS
.
- P. Pouli, K. Melessanaki, A. Giakoumaki, V. Argyropoulos and D. Anglos, Measuring the thickness of protective coatings on historic metal objects using nanosecond and femtosecond laser induced breakdown spectroscopy depth profiling, Spectrochim. Acta, Part B, 2005, 60, 1163 CrossRef
.
- A. de Bonis, B. de Filippo, A. Galasso, A. Santagata, A. Smaldone and R. Teghil, Comparison of the performances of nanosecond and femtosecond Laser Induced Breakdown Spectroscopy for depth profiling of an artificially corroded bronze, Appl. Surf. Sci., 2014, 302, 275 CrossRef CAS
.
- D. W. Hahn and N. Omenetto, Laser-Induced Breakdown Spectroscopy (LIBS), Part II: Review of Instrumental and Methodological Approaches to Material Analysis and Applications to Different Fields, Appl. Spectrosc., 2012, 66, 347 CrossRef CAS PubMed
.
- C. Liu, X. L. Mao, S. S. Mao, X. Zeng, R. Greif and R. E. Russo, Nanosecond and Femtosecond Laser Ablation of Brass:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Particulate and ICPMS Measurements, Anal. Chem., 2004, 76, 379 CrossRef CAS PubMed
Particulate and ICPMS Measurements, Anal. Chem., 2004, 76, 379 CrossRef CAS PubMed .
- C. Jeynes, N. P. Barradas and E. Szilagyi, Accurate Determination of Quantity of Material in Thin Films by Rutherford Backscattering Spectrometry, Anal. Chem., 2012, 84, 6061 CrossRef CAS PubMed
.
- A. H. Galmed, A. K. Kassem, H. von Bergmann and M. A. Harith, A study of using femtosecond LIBS in analyzing metallic thin film–semiconductor interface, Appl. Phys. B: Lasers Opt., 2011, 102, 197 CrossRef CAS
.
- D. K. Das, J. P. McDonald, S. M. Yalisove and T. M. Pollock, Depth-profiling study of a thermal barrier coated superalloy using femtosecond laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2008, 63, 27 CrossRef
.
- C. C. García, M. Corral, J. M. Vadillo and J. J. Laserna, Angle-resolved laser-induced breakdown spectrometry for depth profiling of coated materials, Appl. Spectrosc., 2000, 54, 1027 CrossRef
.
- T. Kratochvíl, T. Černohorský, P. Knotek, L. Kalina, J. Návesník, M. Pouzar and M. Zvolská, Fast determination of the surface density of titanium in ultrathin layers using LIBS spectrometry, J. Anal. At. Spectrom., 2014, 29, 1806 RSC
.
- A. Assion, M. Wollenhaupt, L. Hag, F. Mayorov, C. Sarpe-Tudoran, M. Winter, U. Kutschera and T. Baumert, Femtosecond laser-induced-breakdown spectrometry for Ca2+ analysis of biological samples with high spatial resolution, Appl. Phys. B: Lasers Opt., 2003, 77, 391 CrossRef CAS
.
- O. Samek, J. Lambert, R. Hergenröder, M. Liška, J. Kaiser, K. Novotný and S. Kukhlevsky, Femtosecond laser spectrochemical analysis of plant samples, Laser Phys. Lett., 2006, 3, 21 CrossRef CAS
.
- J. Kaiser, O. Samek, L. Reale, M. Liška, R. Malina, A. Ritucci, A. Poma, A. Tucci, F. Flora, A. Lai, L. Mancini, G. Tromba, F. Zanini, A. Faenov, T. Pikuz and G. Cinque, Monitoring of the Heavy-Metal Hyperaccumulation in Vegetal Tissues by X-ray Radiography and by Femto-Second Laser Induced Breakdown Spectroscopy, Microsc. Res. Tech., 2007, 70, 147 CrossRef CAS PubMed
.
- M. T. Taschuk, Y. Y. Tsui and R. Fedosejevs, Detection and Mapping of Latent Fingerprints by Laser-Induced Breakdown Spectroscopy, Appl. Spectrosc., 2006, 60, 1322 CrossRef CAS PubMed
.
- S. P. Banerjee, Z. Chen and R. Fedosejevs, High resolution scanning microanalysis on material surfaces using UV femtosecond laser induced breakdown spectroscopy, Optic Laser Eng., 2015, 68, 1 CrossRef
.
- I. V. Cravetchi, M. T. Taschuk, Y. Y. Tsui and R. Fedosejevs, Evaluation of femtosecond LIBS for spectrochemical microanalysis of aluminium alloys, Anal. Bioanal. Chem., 2006, 385, 287 CrossRef CAS PubMed
.
- T. Tong, J. Li and J. P. Longtin, Real-time control of ultrafast laser micromachining by laser-induced breakdown spectroscopy, Appl. Opt., 2004, 43, 1971 CrossRef PubMed
.
- W. Wessel, A. Brueckner-Foit, J. Mildner, L. Englert, L. Haag, A. Horn, M. Wollenhaupt and T. Baumert, Use of femtosecond laser-induced breakdown spectroscopy (fs-LIBS) for micro-crack analysis on the surface, Eng. Fract. Mech., 2010, 77, 1874 CrossRef
.
- H. Hou, L. Cheng, T. Richardson, G. Chen, M. Doeff, R. Zheng, R. E. Russo and V. Zorba, Three-Dimensional Elemental Imaging of Li-ion Solid-State Electrolytes Using fs-Laser Induced Breakdown Spectroscopy (LIBS), J. Anal. At. Spectrom., 2015, 30, 2295 RSC
.
- M. Duocastella and C. B. Arnold, Bessel and annular beams for materials processing, Laser Photonics Rev., 2012, 6, 607 CrossRef
.
- Q. Zhan, Cylindrical vector beams: from mathematical concepts to applications, Adv. Opt. Photonics, 2009, 1, 1 CrossRef CAS
.
- C. Hnatovsky, V. Shvedov, W. Krolikowski and A. Rode, Revealing Local Field Structure of Focused Ultrashort Pulses, Phys. Rev. Lett., 2011, 106, 123901 CrossRef PubMed
.
- E. Betzig and J. K. Trautman, Near-Field Optics: Microscopy, Spectroscopy, and Surface Modification Beyond the Diffraction Limit, Science, 1992, 257, 189 CAS
.
- V. Zorba, X. Mao and R. E. Russo, Ultrafast laser induced breakdown spectroscopy for high spatial resolution chemical analysis, Spectrochim. Acta, Part B, 2011, 66, 189 CrossRef
.
- R. E. Russo, T. W. Suen, A. A. Bol'shakov, J. Yoo, O. Sorkhabi, X. Mao, J. Gonzalez, D. Oropeza and V. Zorba, Laser plasma spectrochemistry, J. Anal. At. Spectrom., 2011, 26, 1596 RSC
.
- Y. Lu, V. Zorba, X. Mao, R. Zheng and R. E. Russo, UV fs to ns double-pulse laser induced breakdown spectroscopy for high spatial resolution chemical analysis, J. Anal. At. Spectrom., 2013, 28, 743 RSC
.
- G. W. Rieger, M. Taschuk, Y. Y. Tsui and R. Fedosejevs, Comparative study of laser-induced plasma emission from microjoule picosecond and nanosecond KrF-laser pulses, Spectrochim. Acta, Part B, 2003, 58, 497 CrossRef
.
- B. le Drogoff, M. Chaker, J. Margot, M. Sabsabi, O. Barthélemy, T. W. Johnston, S. Laville and F. Vidal, Influence of the Laser Pulse Duration on Spectrochemical Analysis of Solids by Laser-Induced Plasma Spectroscopy, Appl. Spectrosc., 2004, 58, 122 CrossRef CAS PubMed
.
- T. Gunaratne, M. Kangas, S. Singh, A. Gross and M. Dantus, Influence of bandwidth and phase shaping on laser
induced breakdown spectroscopy with ultrashort laser pulses, Chem. Phys. Lett., 2006, 423, 197 CrossRef CAS
.
- V. Piñon and D. Anglos, Optical emission studies of plasma induced by single and double femtosecond laser pulses, Spectrochim. Acta, Part B, 2009, 64, 950 CrossRef
.
- E. Tognoni, V. Palleschi, M. Corsi and G. Cristoforetti, Quantitative micro-analysis by laser-induced breakdown spectroscopy: a review of the experimental approaches, Spectrochim. Acta, Part B, 2002, 57, 1115 CrossRef
.
- J. T. Schiffern, D. W. Doerr and D. R. Alexander, Optimization of collinear double-pulse femtosecond laser-induced breakdown spectroscopy of silicon, Spectrochim. Acta, Part B, 2007, 62, 1412 CrossRef
.
- D. Santos, R. E. Samad, L. C. Trevizan, A. Z. de Freitas, N. D. Vieira and F. J. Krug, Evaluation of Femtosecond Laser-Induced Breakdown Spectroscopy for Analysis of Animal Tissues, Appl. Spectrosc., 2008, 62, 1137 CrossRef CAS PubMed
.
- J. Scaffidi, W. Pearman, J. C. Carter and S. M. Angel, Observations in collinear femtosecond–nanosecond dual-pulse laser-induced breakdown spectroscopy, Appl. Spectrosc., 2006, 60, 65 CrossRef CAS PubMed
.
- Ş. Yalçın, Y. Y. Tsui and R. Fedosejevs, Pressure dependence of emission intensity in femtosecond laser-induced breakdown spectroscopy, J. Anal. At. Spectrom., 2004, 19, 1295 RSC
.
- L. A. Emmert, R. C. Chinni, D. A. Cremers, C. R. Jones and W. Rudolph, Comparative study of femtosecond and nanosecond laser-induced breakdown spectroscopy of depleted uranium, Appl. Opt., 2011, 50, 313 CrossRef CAS PubMed
.
- A. W. Schill, D. A. Heaps, D. N. Stratis-Cullum, B. R. Arnold and P. M. Pellegrino, Characterization of near-infrared low energy ultra-short laser pulses for portable applications of laser induced breakdown spectroscopy, Opt. Express, 2007, 15, 14044 CrossRef PubMed
.
- C. A. Zuhlke, J. Bruce III, T. P. Anderson, D. R. Alexander and C. G. Parigger, A Fundamental Understanding of the Dependence of the Laser-Induced Breakdown Spectroscopy (LIBS) Signal Strength on the Complex Focusing Dynamics of Femtosecond Laser Pulses on Either Side of the Focus, Appl. Spectrosc., 2014, 68, 1021 CrossRef CAS PubMed
.
- M. P. Mateo, V. Piñon, D. Anglos and G. Nicolas, Effect of ambient conditions on ultraviolet femtosecond pulse laser induced breakdown spectra, Spectrochim. Acta, Part B, 2012, 74–75, 18 CrossRef CAS
.
- A. Nakimana, H. Tao, X. Gao, Z. Hao and J. Lin, Effects of ambient conditions on femtosecond laser-induced breakdown spectroscopy of Al, J. Phys. D: Appl. Phys., 2013, 46, 285204 CrossRef
.
- S. S. Harilal, N. Farid, J. R. Freeman, P. K. Diwakar, N. L. LaHaye and A. Hassanein, Background gas collisional effects on expanding fs and ns laser ablation plumes, Appl. Phys. A: Mater. Sci. Process., 2014, 117, 319 CrossRef CAS
.
- N. Smijesh and R. Philip, Emission dynamics of an expanding ultrafast-laser produced Zn plasma under different ambient pressures, J. Appl. Phys., 2013, 114, 093301 CrossRef
.
- M. Guillermin, C. Liebig, F. Garrelie, R. Stoian, A.-S. Loir and E. Audouard, Adaptive control of femtosecond laser ablation plasma emission, Appl. Surf. Sci., 2009, 255, 5163 CrossRef CAS
.
- M. Guillermin, J. P. Colombier, S. Valette, E. Audouard, F. Garrelie and R. Stoian, Optical emission and nanoparticle generation in Al plasmas using ultrashort laser pulses temporally optimized by real-time spectroscopic feedback, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035430 CrossRef
.
- M. Guillermin, A. Klini, J. P. Colombier, F. Garrelie, D. Gray, C. Liebig, E. Audouard, C. Fotakis and R. Stoian, Tuning spectral properties of ultrafast laser ablation plasmas from brass using adaptive temporal pulse shaping, Opt. Express, 2010, 18, 11159 CrossRef CAS PubMed
.
- K. C. Hartig, J. P. McNutt, P. Ko, T. W. Jacomb-Hood and I. Jovanovic, Pulse chirp effects in ultrafast laser-induced breakdown spectroscopy, J. Radioanal. Nucl. Chem., 2013, 296, 135 CrossRef CAS
.
- S. M. Angel, D. N. Stratis, K. L. Eland, T. Lai, M. A. Berg and D. M. Gold, LIBS using dual- and ultra-short laser pulses, Fresenius' J. Anal. Chem., 2001, 369, 320 CrossRef CAS PubMed
.
- B. le Drogoff, J. Margot, F. Vidal, S. Laville, M. Chaker, M. Sabsabi, T. W. Johnston and O. Barthélemy, Influence of the laser pulse duration on laser-produced plasma properties, Plasma Sources Sci. Technol., 2004, 13, 223 CrossRef CAS
.
- J. R. Freeman, S. S. Harilal, P. K. Diwakar, B. Verhoff and A. Hassanein, Comparison of optical emission from nanosecond and femtosecond laser produced plasma in atmosphere and vacuum conditions, Spectrochim. Acta, Part B, 2013, 87, 43 CrossRef CAS
.
- Y. Liu, S. Singha, T. E. Witt, Y. Cheng and R. J. Gordon, Observation of near total polarization in the ultrafast laser ablation of Si, Appl. Phys. Lett., 2008, 93, 161502 CrossRef
.
- J. S. Penczak, Y. Liu and R. J. Gordon, Polarization Resolved Laser-Induced Breakdown Spectroscopy of Al, J. Phys. Chem. A, 2009, 113, 13310 CrossRef CAS PubMed
.
- Y. Zhao, S. Singha, Y. Liu and R. J. Gordon, Polarization-resolved laser-induced breakdown spectroscopy, Opt. Lett., 2009, 34, 494 CrossRef PubMed
.
- J. S. Penczak, Y. Liu, R. D. Schaller, D. H. Rich and R. J. Gordon, The mechanism for continuum polarization in laser induced breakdown spectroscopy of Si(111), Spectrochim. Acta, Part B, 2012, 74–75, 3 CrossRef CAS
.
- J. Serrano, J. Moros and J. J. Laserna, Exploring the Formation Routes of Diatomic Hydrogenated Radicals Using Femtosecond Laser-Induced Breakdown Spectroscopy of Deuterated Molecular Solids, J. Anal. At. Spectrom., 2015, 30, 2343 RSC
.
- Y. Dikmelik and J. B. Spicer, Femtosecond laser-induced breakdown spectroscopy of explosives and explosive-related compounds, Proc. SPIE, 2005, 5794, 757 CrossRef CAS
.
- Y. Dikmelik, C. McEnnis and J. B. Spicer, Femtosecond and nanosecond laser-induced breakdown spectroscopy of trinitrotoluene, Opt. Express, 2008, 16, 5332 CrossRef CAS PubMed
.
- F. C. de Lucia Jr, J. L. Gottfried and A. W. Miziolek, Evaluation of femtosecond laser-induced breakdown spectroscopy for explosive residue detection, Opt. Express, 2009, 17, 419 CrossRef
.
- S. Sunku, M. K. Gundawar, A. K. Myakalwar, P. P. Kiran, S. P. Tewari and S. V. Rao, Femtosecond and nanosecond laser induced breakdown spectroscopic studies of NTO, HMX, and RDX, Spectrochim. Acta, Part B, 2013, 79–80, 31 CrossRef CAS
.
- S. Sunku, E. N. Rao, G. M. Kumar, S. P. Tewari and S. V. Rao, Molecular formation dynamics of 5-nitro-2,4-dihydro-3H-1,2,4-triazol-3-one,1,3,5-trinitroperhydro-1,3,5-triazine, and 2,4,6-trinitrotoluene in air, nitrogen, and argon atmospheres studied using femtosecond laser induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2013, 87, 121 CrossRef
.
- B. Yee, K. C. Hartig, P. Ko, J. McNutt and I. Jovanovic, Measurement of boron isotopic ratio with non-gated molecular spectroscopy of femtosecond laser-produced plasma, Spectrochim. Acta, Part B, 2013, 79–80, 72 CrossRef CAS
.
- H. Hou, G. C.-Y. Chan, X. Mao, V. Zorba, R. Zheng and R. E. Russo, Femtosecond Laser Ablation Molecular Isotopic Spectrometry for Zirconium Isotope Analysis, Anal. Chem., 2015, 87, 4788 CrossRef CAS PubMed
.
- H. Hou, G. C.-Y. Chan, X. Mao, R. Zheng, V. Zorba and R. E. Russo, Femtosecond filament-laser ablation molecular isotopic spectrometry, Spectrochim. Acta, Part B, 2015, 113, 113 CrossRef CAS
.
- V. I. Babushok, F. C. de Lucia Jr, J. L. Gottfried, C. A. Munson and A. W. Miziolek, Double pulse laser ablation and plasma: laser induced breakdown spectroscopy
signal enhancement, Spectrochim. Acta, Part B, 2006, 61, 999 CrossRef
.
- E. Tognoni and G. Cristoforetti, Basic mechanisms of signal enhancement in ns double-pulse laser-induced breakdown spectroscopy in a gas environment, J. Anal. At. Spectrom., 2014, 29, 1318 RSC
.
- A. Santagata, R. Teghil, G. Albano, D. Spera, P. Villani, A. de Bonis, G. P. Parisi and A. Galasso, fs/ns dual-pulse LIBS analytic survey for copper-based alloys, Appl. Surf. Sci., 2007, 254, 863 CrossRef CAS
.
- M. E. Povarnitsyn, T. E. Itina, K. V. Khishchenko and P. R. Levashov, Suppression of Ablation in Femtosecond Double-Pulse Experiments, Phys. Rev. Lett., 2009, 103, 195002 CrossRef CAS PubMed
.
- S. Noël, E. Axente and J. Hermann, Investigation of plumes produced by material ablation with two time-delayed femtosecond laser pulses, Appl. Surf. Sci., 2009, 255, 9738 CrossRef
.
- R. Teghil, A. Santagata, A. de Bonis, G. Albano, P. Villani, D. Spera, G. P. Parisi and A. Galasso, Applications of ultra-short pulsed laser ablation: thin films deposition and fs/ns dual-pulse laser-induced breakdown spectroscopy, Phys. Scr., 2008, 78, 058113 CrossRef
.
- A. Santagata, G. Albano, D. Spera, R. Teghil, P. Villani, G. P. Parisi, A. de Bonis and D. J. Sordelet, Emission spectra investigation of fs induced NPs probed by the ns laser pulse of a fs/ns DP-LIBS orthogonal configuration, Appl. Surf. Sci., 2009, 255, 5159 CrossRef CAS
.
- J. Hermann, L. Mercadier, E. Axente and S. Noël, Properties of plasmas produced by short double pulse laser ablation of metals, J. Phys.: Conf. Ser., 2012, 399, 012006 CrossRef
.
- A. Guarnaccio, G. P. Parisi, D. Mollica, A. de Bonis, R. Teghil and A. Santagata, Fs to ns double-pulse Laser Induced Breakdown Spectroscopy of copper-based-alloys: generation and elemental analysis of nanoparticles, Spectrochim. Acta, Part B, 2014, 101, 261 CrossRef CAS
.
- A. Semerok, C. Chaléard, V. Detalle, J.-L. Lacour, P. Mauchien, P. Meynadieκ, C. Nouvellon, B. Sallé, P. Palianov, M. Perdrix and G. Petite, Experimental investigations of laser ablation efficiency of pure metals with femto, pico and nanosecond pulses, Appl. Surf. Sci., 1999, 138–139, 311 CrossRef CAS
.
- B. le Drogoff, J. Margot, M. Chaker, M. Sabsabi, O. Barthélemy, T. W. Johnston, S. Laville, F. Vidal and Y. von Kaenel, Temporal characterization of femtosecond laser pulses induced plasma for spectrochemical analysis of aluminum alloys, Spectrochim. Acta, Part B, 2001, 56, 987 CrossRef
.
- A. Elhassan, A. Giakoumaki, D. Anglos, G. M. Ingo, L. Robbiola and M. A. Harith, Nanosecond and femtosecond Laser Induced Breakdown Spectroscopic analysis of bronze alloys, Spectrochim. Acta, Part B, 2008, 63, 504 CrossRef
.
- L. Fornarini, R. Fantoni, F. Colao, A. Santagata, R. Teghil, A. Elhassan and M. A. Harith, Theoretical Modeling of Laser Ablation of Quaternary Bronze Alloys: Case Studies Comparing Femtosecond and Nanosecond LIBS Experimental Data, J. Phys. Chem. A, 2009, 113, 14364 CrossRef PubMed
.
- J. Scaffidi, J. Pender, W. Pearman, S. R. Goode, B. W. Colston Jr, J. C. Carter and S. M. Angel, Dual-pulse laser-induced breakdown spectroscopy with combinations of femtosecond and nanosecond laser pulses, Appl. Opt., 2003, 42, 6099 CrossRef PubMed
.
- J. Scaffidi, W. Pearman, M. Lawrence, J. C. Carter, B. W. Colston Jr and S. M. Angel, Spatial and temporal dependence of interspark interactions in femtosecond–nanosecond dual-pulse laser-induced breakdown spectroscopy, Appl. Opt., 2004, 43, 5243 CrossRef CAS PubMed
.
- J. Scaffidi, W. Pearman, J. C. Carter, B. W. Colston Jr and S. M. Angel, Temporal dependence of the enhancement of material removal in femtosecond–nanosecond dual-pulse laser-induced breakdown spectroscopy, Appl. Opt., 2004, 43, 6492 CrossRef PubMed
.
- D. Scuderi, O. Albert, D. Moreau, P. P. Pronko and J. Etchepare, Interaction of a laser-produced plume with a second time delayed femtosecond pulse, Appl. Phys. Lett., 2005, 86, 071502 CrossRef
.
- A. Santagata, A. de Bonis, P. Villani, R. Teghil and G. P. Parisi, Fs/ns-dual-pulse orthogonal geometry plasma plume reheating for copper-based-alloys analysis, Appl. Surf. Sci., 2006, 252, 4685 CrossRef CAS
.
- A. Santagata, R. Teghil, A. de Giacomo, M. Dell’Aglio, G. P. Parisi, A. de Bonis and A. Galasso, Optical emission spectroscopy investigation of an ultra-short laser induced titanium plasma reheated by a ns laser pulse, Appl. Surf. Sci., 2007, 253, 7792 CrossRef CAS
.
- J. P. McDonald, D. K. Das, J. A. Nees, T. M. Pollock and S. M. Yalisove, Approaching non-destructive surface chemical analysis of CMSX-4 superalloy with double-pulsed laser induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2008, 63, 561 CrossRef
.
- V. Piñon, C. Fotakis, G. Nicolas and D. Anglos, Double pulse laser-induced breakdown spectroscopy with femtosecond laser pulses, Spectrochim. Acta, Part B, 2008, 63, 1006 CrossRef
.
- V. Piñón, D. Anglos and G. Nicolás, Improvement of laser induced breakdown spectroscopy technique using double pulse schemes, Opt. Pura Apl., 2010, 43, 113 Search PubMed
.
- S. Singha, Z. Hu and R. J. Gordon, Ablation and plasma emission produced by dual femtosecond laser pulses, J. Appl. Phys., 2008, 104, 113520 CrossRef
.
- S. Amoruso, R. Bruzzese and X. Wang, Plume composition control in double pulse ultrafast laser ablation of metals, Appl. Phys. Lett., 2009, 95, 251501 CrossRef
.
- S. Amoruso, R. Bruzzese, X. Wang, G. O'Connell and J. G. Lunney, Multidiagnostic analysis of ultrafast laser ablation of metals with pulse pair irradiation, J. Appl. Phys., 2010, 108, 113302 CrossRef
.
- S. Noël and J. Hermann, Reducing nanoparticles in metal ablation plumes produced by two delayed short laser pulses, Appl. Phys. Lett., 2009, 94, 053120 CrossRef
.
- O. Balachninaitė, A. Baškevičius, K. Stankevičiūtė, K. Kuršelis and V. Sirutkaitis, Double-pulse laser-induced breakdown spectroscopy with 1030 and 257.5 nm wavelength femtosecond laser pulses, Lith. J. Phys., 2010, 50, 105 CrossRef
.
- M. Oba, Y. Maruyama, K. Akaoka, M. Miyabe and I. Wakaida, Double-pulse LIBS of gadolinium oxide ablated by femto- and nano-second laser pulses, Appl. Phys. A: Mater. Sci. Process., 2010, 101, 545 CrossRef CAS
.
- F. Bourquard, J.-P. Colombier, M. Guillermin, A.-S. Loir, C. Donnet, R. Stoian and F. Garrelie, Temporal pulse shaping effects on aluminium and boron ablation plumes generated by ultrashort pulsed laser ablation and analyzed by time- and space-resolved optical spectroscopy, Appl. Surf. Sci., 2012, 258, 9374 CrossRef CAS
.
- J. Guo, T. Wang, J. Shao, T. Sun, R. Wang, A. Chen, Z. Hu, M. Jin and D. Ding, Emission enhancement ratio of the metal irradiated by femtosecond double-pulse laser, Opt. Commun., 2012, 285, 1895 CrossRef CAS
.
- A. Chen, S. Li, S. Li, Y. Jiang, J. Shao, T. Wang, X. Huang, M. Jin and D. Ding, Optimally enhanced optical emission in laser-induced air plasma by femtosecond double-pulse, Phys. Plasmas, 2013, 20, 103110 CrossRef
.
- S. S. Harilal, P. K. Diwakar and A. Hassanein, Electron-ion relaxation time dependent signal enhancement in ultrafast double-pulse laser-induced breakdown spectroscopy, Appl. Phys. Lett., 2013, 103, 041102 CrossRef
.
- J. Penczak, R. Kupfer, I. Bar and R. J. Gordon, The role of plasma shielding in collinear double-pulse femtosecond laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2014, 97, 34 CrossRef CAS
.
- J. Mildner, C. Sarpe, N. Götte, M. Wollenhaupt and T. Baumert, Emission signal enhancement of laser ablation of metals (aluminium and titanium) by time delayed femtosecond double pulses from femtoseconds to nanoseconds, Appl. Surf. Sci., 2014, 302, 291 CrossRef CAS
.
- A. Semerok and C. Dutouquet, Analytical performances of laser-induced micro-plasma of Al samples with single and double ultrashort pulses in air and with Ar-jet: a comparative study, Spectrochim. Acta, Part B, 2014, 99, 163 CrossRef CAS
.
- X. Liu, S. Sun, X. Wang, Z. Liu, Q. Liu, P. Ding, Z. Guo and B. Hu, Effect of laser pulse energy on orthogonal double femtosecond pulse laser-induced breakdown spectroscopy, Opt. Express, 2013, 21, A704 CrossRef CAS PubMed
.
- H. Qi, S. Li, Y. Qi, A. Chen, Z. Hu, X. Huang, M. Jin and D. Ding, Effect of sample position on collinear femtosecond double-pulse laser-induced breakdown spectroscopy of silicon in air, J. Anal. At. Spectrom., 2014, 29, 1105 RSC
.
- Y. Qi, H. Qi, Q. Wang, Z. Chen and Z. Hun, The influence of double pulse delay and ambient pressure on femtosecond laser ablation of silicon, Opt. Laser Technol., 2015, 66, 68 CrossRef CAS
.
- X. Zhao and Y. C. Shin, Laser–plasma interaction and plasma enhancement by ultrashort doublepulseablation, Appl. Phys. B: Lasers Opt., 2015, 120, 81 CrossRef CAS
.
- J. Shen, Z. Yang, X. Liu, Y. Shi, P. Zhao, S. Sun and B. Hu, Analysis of Enhanced Laser-Induced Breakdown Spectroscopy with Double Femtosecond Laser Pulses, Plasma Sci. Technol., 2015, 17, 147 CrossRef CAS
.
- M. Wang, S. Wang, Z. Cao, P. Wang and C. Wang, Investigation of double-pulse femtosecond laser induced breakdown spectroscopy of polymethyl methacrylate (PMMA), Proc. SPIE, 2015, 9351, 93511Q CrossRef
.
- J. J. Laserna, R. Fernández Reyes, R. González, L. Tobaria and P. Lucena, Study on the effect of beam propagation through atmospheric turbulence on standoff nanosecond laser induced breakdown spectroscopy measurements, Opt. Express, 2009, 17, 10265 CrossRef CAS PubMed
.
- P. Rohwetter, J. Yu, G. Mejean, K. Stelmaszczyk, E. Salmon, J. Kasparian, J.-P. Wolf and L. Woste, Remote LIBS with ultrashort pulses: characteristics in picosecond and femtosecond, J. Anal. At. Spectrom., 2004, 19, 437 RSC
.
- K. Y. Andrianov, V. P. Kandidov, O. G. Kosareva, S. L. Chin, A. Talebpur, S. Petit, W. Liu, A. Ivasaki and M. C. Nadeau, Influence of beam quality on filamentation of high-power femtosecond laser pulses in air, Izv. Akad. Nauk SSSR, Ser. Fiz., 2002, 66, 1091 CAS
.
- V. P. Kandidov, O. G. Kosareva, S. A. Shlenov, N. A. Panov, V. Y. Fedorov and A. E. Dormidonov, Dynamic small-scale self-focusing of a femtosecond laser pulse, Quantum Electron., 2005, 35, 59 CrossRef CAS
.
- K. Stelmaszczyk, P. Rohwetter, G. Mejean, J. Yu, E. Salmon, J. Kasparian, R. Ackermann, J. P. Wolf and L. Woste, Long-distance remote laser-induced breakdown spectroscopy using filamentation in air, Appl. Phys. Lett., 2004, 85, 3977 CrossRef CAS
.
- H. Wille, M. Rodriguez, J. Kasparian, D. Mondelain, J. Yu, A. Mysyrowicz, R. Sauerbrey, J. P. Wolf and L. Woste, Teramobile: a mobile femtosecond-terawatt laser and detection system, Eur. Phys. J., 2002, 20, 183 Search PubMed
.
- R. S. Hatzes, Kilometer-range non-linear propagation of fs laser pulses, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 036607 CrossRef PubMed
.
- C. D'Amico, A. Houard, M. Franco, B. Prade and A. Mysyrowicz, Coherent and incoherent radial THz radiation emission from femtosecond filaments in air, Opt. Express, 2007, 15, 15274 CrossRef
.
- G. Méchain, T. Olivier, M. Franco, A. Couairon, B. Prade and A. Mysyrowicz, Femtosecond filamentation in air at low pressures. Part II: laboratory experiments, Opt. Commun., 2006, 261, 322 CrossRef
.
- J. Kasparian, R. Ackermann, Y.-B. Andre, G. Mechain, G. Mejean, B. Prade, P. Rohwetter, E. Salmon, K. Stelmaszczyk, J. Yu, A. Mysyrowicz, R. Sauerbrey, L. Woste and J.-P. Wolf, Progress towards lightning control using lasers, Journal of the European Optical Society: Rapid Publications, 2008, 3, 08035 CrossRef
.
- Y. Petit, S. Henin, J. Kasparian, J.-P. Wolf, P. Rohwetter, K. Stelmaszczyk, Z. Q. Hao, W. M. Nakaema, L. Wöste and A. Vogel, Influence of pulse duration, energy, and focusing on laser-assisted water condensation, Appl. Phys. Lett., 2011, 98, 041105 CrossRef
.
- http://www.teramobile.org .
- P. Rohwetter, K. Stelmaszczyk, L. Wöste, R. Ackermann, G. Méjean, E. Salmon, J. Kasparian, J. Yu and J.-P. Wolf, Filament-induced remote surface ablation for long range laser-induced breakdown spectroscopy operation, Spectrochim. Acta, Part B, 2005, 60, 1025 CrossRef
.
- M. Weidman, K. Lim, M. Ramme, M. Durand, M. Baudelet and M. Richardson, Stand-off filament-induced ablation of gallium arsenide, Appl. Phys. Lett., 2012, 101, 034101 CrossRef
.
- A. Valenzuela, C. Munson, A. Porwitzky, M. Weidman and M. Richardson, Comparison between geometrically focused pulses versus filaments in femtosecond laser ablation of steel and titanium alloys, Appl. Phys. B: Lasers Opt., 2014, 116, 485 CrossRef CAS
.
- M. Weidman, M. Baudelet, M. Fisher, C. Bridge, C. Brown, M. Sigman, P. J. Dagdigian and M. Richardson, Molecular signal as a signature for detection of energetic materials in filament-induced breakdown spectroscopy, Proc. SPIE, 2009, 7304, 73041G CrossRef
.
- W. Liu, H. L. Xu, G. Méjean, Y. Kamali, J.-F. Daigle, A. Azarm, P. T. Simard, P. Mathieu, G. Roy and S. L. Chin, Efficient non-gated remote filament-induced breakdown spectroscopy of metallic sample, Spectrochim. Acta, Part B, 2007, 62, 76 CrossRef
.
- H. L. Xu, J. Bernhardt, P. Mathieu, G. Roy and S. L. Chin, Understanding the advantage of remote femtosecond laser-induced breakdown spectroscopy of metallic targets, J. Appl. Phys., 2007, 101, 033124 CrossRef
.
- E. J. Judge, G. Heck, E. B. Cerkez and R. J. Levis, Discrimination of Composite Graphite Samples Using Remote Filament-Induced Breakdown Spectroscopy, Anal. Chem., 2009, 81, 2658 CrossRef CAS PubMed
.
- H. L. Xu, P. T. Simard, Y. Kamali, J.-F. Daigle, C. Marceau, J. Bernhardt, J. Dubois, M. Châteauneuf, F. Théberge and G. Roy, Filament-induced breakdown remote spectroscopy in a polar environment, Laser Phys., 2012, 22, 1767 CrossRef CAS
.
- S. Tzortzakis, D. Anglos and D. Gray, Ultraviolet laser filaments for remote laser-induced breakdown spectroscopy (LIBS) analysis:
applications in cultural heritage monitoring, Opt. Lett., 2006, 31, 1139 CrossRef PubMed
.
- D. Mirell, O. Chalus, K. Peterson and J.-C. Diels, Remote sensing of explosives using infrared and ultraviolet filaments, J. Opt. Soc. Am. B, 2008, 25, B108 CrossRef CAS
.
- B. Zeng, W. Chu, H. Gao, W. Liu, G. Li, H. Zhang, J. Yao, J. Ni, S. L. Chin and Y. Cheng, Enhancement of peak intensity in a filament core with spatiotemporally focused femtosecond laser pulses, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 063819 CrossRef
.
- B. Zeng, T.-J. Wang, S. Hosseini, Y. Cheng, Z. Xu, W. Liu and S. L. Chin, Enhanced remote filament-induced breakdown spectroscopy with spatio-temporally chirped pulses, J. Opt. Soc. Am. B, 2012, 29, 3226 CrossRef CAS
.
- H. L. Xu, W. Liu and S. L. Chin, Remote time-resolved filament-induced breakdown spectroscopy of biological materials, Opt. Lett., 2006, 31, 1540 CrossRef CAS PubMed
.
- H. L. Xu, G. Méjean, W. Liu, Y. Kamali, J.-F. Daigle, A. Azarm, P. T. Simard, P. Mathieu, G. Roy and J.-R. Simard, Remote detection of similar biological materials using femtosecond filament-induced breakdown spectroscopy, Appl. Phys. B: Lasers Opt., 2007, 87, 151 CrossRef CAS
.
- Y.-W. Zhang, X. Gao, Y. Zhang, C. Song and J.-Q. Lin, Analysis of heavy metals in poplar leaves by femtosecond filament-induced breakdown spectroscopy, Acta Phys. Sin., 2015, 64, 175203 Search PubMed
.
- X. Gao, C. Du, C. Li, L. Liu, C. Song, Z.-Q. Hao and J.-Q. Lin, Detection of heavy metal Cr in soil by the femtosecond filament induced breakdown spectroscopy, Acta Phys. Sin., 2014, 63, 095203 Search PubMed
.
- H. L. Xu, Y. Kamali, C. Marceau, P. T. Simard, W. Liu, J. Bernhardt, G. Méjean, P. Mathieu, G. Roy and J.-R. Simard, Simultaneous detection and identification of multigas pollutants using filament-induced nonlinear spectroscopy, Appl. Phys. Lett., 2007, 90, 101106 CrossRef
.
- Y. Kamali, J.-F. Daigle, F. Théberge, M. Châteauneuf, A. Azarm, Y. Chen, C. Marceau, S. C. Lessard, F. Lessard and G. Roy, Remote sensing of trace methane using mobile femtosecond laser system of T&T Lab, Opt. Commun., 2009, 282, 2062 CrossRef CAS
.
- Q. Luo, H. L. Xu, S. A. Hosseini, J.-F. Daigle, F. Théberge, M. Sharifi and S. L. Chin, Remote sensing of pollutants using femtosecond laser pulse fluorescence spectroscopy, Appl. Phys. B: Lasers Opt., 2005, 82, 105 CrossRef
.
- J.-F. Daigle, G. Méjean, W. Liu, F. Théberge, H. L. Xu, Y. Kamali, J. Bernhardt, A. Azarm, Q. Sun and P. Mathieu, Long range trace detection in aqueous aerosol using remote filament-induced breakdown spectroscopy, Appl. Phys. B: Lasers Opt., 2007, 87, 749 CrossRef CAS
.
- J.-F. Daigle, Y. Kamali, G. Roy and S. L. Chin, Remote filament-induced fluorescence spectroscopy from thin clouds of smoke, Appl. Phys. B: Lasers Opt., 2008, 93, 759 CrossRef CAS
.
- S. L. Chin, H. L. Xu, Q. Luo, F. Théberge, W. Liu, J. F. Daigle, Y. Kamali, P. T. Simard, J. Bernhardt and S. A. Hosseini, Filamentation ‘remote’ sensing of chemical and biological agents/pollutants using only one femtosecond laser source, Appl. Phys. B: Lasers Opt., 2009, 95, 1 CrossRef CAS
.
- J. Odhner and R. Levis, Optical Spectroscopy Using
Gas-Phase Femtosecond Laser Filamentation, Annu. Rev. Phys. Chem., 2014, 65, 605 CrossRef CAS PubMed
.
- A. de Giacomo, M. Dell'Aglio, O. de Pascale, R. Gaudiuso, A. Santagata and R. Teghil, Laser Induced Breakdown Spectroscopy methodology for the analysis of copper-based-alloys used in ancient artworks, Spectrochim. Acta, Part B, 2008, 63, 192 Search PubMed
.
- S. Almaviva, R. Fantoni, L. Caneve, F. Colao, L. Fornarini, A. Santagata and R. Teghil, Use of ns and fs pulse excitation in laser-induced breakdown spectroscopy to improve its analytical performances: a case study on quaternary bronze alloys, Spectrochim. Acta, Part B, 2014, 99, 185 CrossRef CAS
.
- M. Oujja, M. Sanz, F. Agua, J. F. Conde, M. García-Heras, A. Dávila, P. Oñate, J. Sanguino, J. R. Vázquez de Aldana, P. Moreno, M. A. Villegas and M. Castillejo, Multianalytical characterization of Late Roman glasses including nanosecond and femtosecond laser induced breakdown spectroscopy, J. Anal. At. Spectrom., 2015, 30, 1590 RSC
.
- R. K. Gill, F. Knorr, Z. J. Smith, M. Kahraman, D. Madsen, D. S. Larsen and S. Wachsmann-Hogiu, Characterization of Femtosecond Laser-Induced Breakdown Spectroscopy (fsLIBS) and Applications for Biological Samples, Appl. Spectrosc., 2014, 68, 949 CrossRef CAS PubMed
.
-
L. Guyon, M. Baudelet, J. Yu, J. Wolf, T. Amodeo, E. Frejafon and P. Laloi, Laser-Induced Breakdown Spectroscopy Analysis of Bacteria: What Femtosecond Lasers Make Possible, in 15th International Conference on Ultrafast Phenomena, OSA Technical Digest Series, 2006 Search PubMed
.
- M. Baudelet, J. Yu, M. Bossu, J. Jovelet, J.-P. Wolf, T. Amodeo, E. Fréjafon and P. Laloi, Discrimination of microbiological samples using femtosecond laser-induced breakdown spectroscopy, Appl. Phys. Lett., 2006, 89, 163903 CrossRef
.
- D. C. Jeong, P. S. Tsai and D. Kleinfeld, Prospect for feedback guided surgery with ultra-short pulsed laser light, Curr. Opin. Neurobiol., 2012, 22, 24–33 CrossRef CAS PubMed
.
- H. Huang, L.-M. Yang, S. Bai and J. Liu, Smart surgical tool, J. Biomed. Opt., 2015, 20, 028001 CrossRef PubMed
.
- M. Sabsabi, R. Héon and L. St-Onge, Critical evaluation of gated CCD detectors for laser-induced breakdown spectroscopy analysis, Spectrochim. Acta, Part B, 2005, 60, 1211 CrossRef
.
- P. Fichet, D. Menut, R. Brennentot, E. Vors and A. Rivoallan, Analysis by laser-induced breakdown spectroscopy of complex solids, liquids, and powders with an echelle spectrometer, Appl. Opt., 2003, 42, 6029 CrossRef CAS PubMed
.
- M. Sabsabi and P. Cielo, Quantitative Analysis of Aluminum Alloys by Laser-Induced Breakdown Spectroscopy and Plasma Characterization, Appl. Spectrosc., 1995, 49, 499 CrossRef CAS
.
- A. A. Ilyin and S. S. Golik, Femtosecond laser-induced breakdown spectroscopy of sea water, Spectrochim. Acta, Part B, 2013, 87, 192 CrossRef CAS
.
- P. Fichet, M. Tabarant, B. Salle and C. Gautier, Comparisons between LIBS and ICP/OES, Anal. Bioanal. Chem., 2006, 385, 338 CrossRef CAS PubMed
.
- K. M. Lo and N. H. Cheung, ArF Laser-Induced Plasma Spectroscopy for Part-per-Billion Analysis of Metal Ions in Aqueous Solutions, Appl. Spectrosc., 2002, 56, 682 CrossRef CAS
.
- F.-Y. Yueh, R. C. Sharma, J. P. Singh, H. Zhang and W. A. Spencer, Evaluation of the Potential of Laser-Induced Breakdown Spectroscopy for Detection of Trace Element in Liquid, J. Air Waste Manage. Assoc., 2002, 52, 1307 CAS
.
- S. T. Järvinen, S. Saari, J. Keskinen and J. Toivonen, Detection of Ni, Pb and Zn in water using electrodynamic single-particle levitation and laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2014, 99, 9 CrossRef
.
- S. S. Golik, O. A. Bukin, A. A. Il’in, E. B. Sokolova, A. V. Kolesnikov, M. Y. Babiy, Y. N. Kul'chin and A. A. Gal'chenko, Determination of detection limits for elements in water by femtosecond laser-induced breakdown spectroscopy, J. Appl. Spectrosc., 2012, 79, 471 CrossRef CAS
.
- J. Xiu, S. Zhong, H. Hou, Y. Lu and R. Zheng, Quantitative Determination of Manganese in Aqueous Solutions and Seawater by Laser-Induced Breakdown Spectroscopy (LIBS) Using Paper Substrates, Appl. Spectrosc., 2014, 68, 1039 CrossRef CAS PubMed
.
- S. S. Golik, A. A. Ilyin, M. Y. Babiy, Y. S. Biryukova, V. V. Lisitsa and O. A. Bukin, Determination of Iron in Water Solution by Time-Resolved Femtosecond Laser-Induced Breakdown Spectroscopy, Plasma Sci. Technol., 2015, 17, 975 CrossRef
.
- H. Loudyi, K. Rifaï, S. Laville, F. Vidal, M. Chaker and M. Sabsabi, Improving laser-induced breakdown spectroscopy (LIBS) performance for iron and lead determination in aqueous solutions with laser-induced fluorescence (LIF), J. Anal. At. Spectrom., 2009, 24, 1421 RSC
.
- D. Santos Jr, R. E. Samad, L. C. Trevizan, A. Z. de Freitas, N. D. Vieira Jr and F. J. Krug, Evaluation of Femtosecond Laser-Induced Breakdown Spectroscopy for Analysis of Animal Tissues, Appl. Spectrosc., 2008, 62, 1137 CrossRef PubMed
.
- M. D. Adamson and S. J. Rehse, Detection of trace Al in model biological tissue with laser-induced breakdown spectroscopy, Appl. Opt., 2007, 46, 5844 CrossRef CAS PubMed
.
- T. Owens, S. S. Mao, E. K. Canfield, C. P. Grigoropoulos, X. Mao and R. E. Russo, Ultrafast thin-film laser-induced breakdown spectroscopy of doped oxides, Appl. Opt., 2010, 49, C67 CrossRef CAS
.
- J. Xiu, V. Motto-Ros, G. Panczer, R. Zheng and J. Yu, Feasibility of wear metal analysis in oils with parts per million and sub-parts per million sensitivities using laser-induced breakdown spectroscopy of thin oil layer on metallic target, Spectrochim. Acta, Part B, 2014, 91, 24 CrossRef CAS
.
- G. G. Arantes de Carvalho, J. Moros, D. Santos Jr, F. J. Krug and J. J. Laserna, Direct determination of the nutrient profile in plant materials by femtosecond laser-induced breakdown spectroscopy, Anal. Chim. Acta, 2015, 876, 26 CrossRef CAS PubMed
.
- Ş. Yalçın, S. Örer and R. Turan, 2-D analysis of Ge implanted SiO2 surfaces by laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2008, 63, 1130 CrossRef
.
- I. Lopez-Quintas, V. Pinon, M. P. Mateo and G. Nicolas, Effect of surface topography in the generation of chemical maps by laser-induced plasma spectroscopy, Appl. Surf. Sci., 2012, 258, 9432 CrossRef CAS
.
- Y. Markushin, P. Sivakumar, D. Connolly and N. Melikechi, Tag-femtosecond laser-induced breakdown spectroscopy for the sensitive detection of cancer antigen 125 in blood plasma, Anal. Bioanal. Chem., 2015, 407, 1849 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2016 |