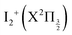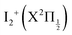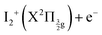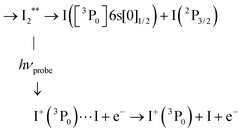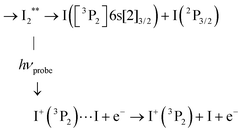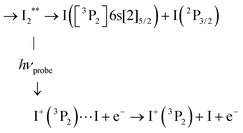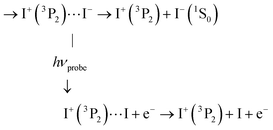Open Access Article
Open Access ArticleReal-time dynamics of vibronic wavepackets within Rydberg and ion-pair states of molecular iodine†
Jean-Michel
Mestdagh
 a,
Lou
Barreau
a,
Lou
Barreau
 b and
Lionel
Poisson
b and
Lionel
Poisson
 *b
*b
aUniversité Paris-Saclay, CEA, CNRS, Laboratoire Interactions Dynamiques et Lasers, 91191 Gif-sur-Yvette, France
bUniversité Paris-Saclay, CNRS, Institut des Sciences Moléculaires d’Orsay, 91405 Orsay, France. E-mail: lionel.poisson@universite-paris-saclay.fr
First published on 14th March 2024
Abstract
Real-time dynamics of vibrationally and electronically excited I2 molecules has been investigated experimentally using the pump–probe technique. A 2-photon excitation was performed either at 269 nm or 266 nm. An electronic and vibrational wavepacket was built as coherent superposition of a few (269 nm excitation) or many (266 nm excitation) Rydberg states of the 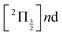 and
and 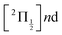 series partly coupled with ion-pair states. The probe operated by ionisation or photodetachement. The energy and angular distribution of the resulting photoelectrons, I+ photocations and I− photoanions were monitored. During the dynamics that is turned on by the pump excitation, the wavepacket splits and explores a variety of electronic states of Rydberg and ion-pair character. The experimental results were complemented by molecular dynamics calculations. This provided invaluable information to identify wavepacket motion along ion-pair potential energy curves.
series partly coupled with ion-pair states. The probe operated by ionisation or photodetachement. The energy and angular distribution of the resulting photoelectrons, I+ photocations and I− photoanions were monitored. During the dynamics that is turned on by the pump excitation, the wavepacket splits and explores a variety of electronic states of Rydberg and ion-pair character. The experimental results were complemented by molecular dynamics calculations. This provided invaluable information to identify wavepacket motion along ion-pair potential energy curves.
1 Introduction
Although iodine is a diatomic molecule, its excited state dynamics is rather rich, largely in line with its complex electronic structure. Both a large number of electrons in the valence shell and a strong spin–orbit coupling lead to a variety of electronic states with mixed valence, Rydberg and ion-pair characters. This has motivated many experimental and theoretical works as a benchmark for spectroscopy measurements and simulations. For example, time-resolved dynamics of I2 has been investigated since the early beginning of gas-phase femtochemistry.1,2 A large scope of open questions still exists. Here we address the dynamics of I2 near the first ionisation limit, with a time-resolved approach.Works by Bogomolov et al. in 2014, von Vangerow et al. in 2016 and Matthiasson et al. in 2022 focused on an energy region between 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 and 74
500 and 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 where Rydberg states of the iodine molecule I2** are coupled with ion-pair (IP: I+I−) states.3–5 An essential aspect of the resulting dynamics is the efficiency of bound-to-free energy transfers when the Rydberg excitation is above the dissociation limit of the IP states.3,4
500 cm−1 where Rydberg states of the iodine molecule I2** are coupled with ion-pair (IP: I+I−) states.3–5 An essential aspect of the resulting dynamics is the efficiency of bound-to-free energy transfers when the Rydberg excitation is above the dissociation limit of the IP states.3,4
The richness of this energy region first appeared in a seminal work by Mulliken.6 The energy landscape is the following. IP states of lowest energy form three clusters – also called first, second and third tier – whether they correlate to the I+(3P2, 3P1,0, or 1D2) + I−(1S0) asymptotes at large separation between the iodine anion and cation.7 An isolated IP state (tentatively called fourth tier) correlating to I+(1S0) + I−(1S0) is likely present at slightly larger energies and was documented theoretically only.8 I2** Rydberg states are grouped in ns, np, nd… series converging to I2+ cation states, 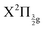 and
and 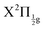 in particular.3,5,9 The I2+ cation and I2 IP states have very different geometries. Many coupling zones therefore exist between Rydberg and IP states, a driving force for the bound-to-free energy transfers mentioned above.
in particular.3,5,9 The I2+ cation and I2 IP states have very different geometries. Many coupling zones therefore exist between Rydberg and IP states, a driving force for the bound-to-free energy transfers mentioned above.
The 2022 work by Matthíasson et al. documented one-photon excited Rydberg states of ungerade symmetry.5 VUV synchrotron light was scanned over the 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600–74
600–74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 energy range (by comparison, the ionisation energy of I2 is 75
000 cm−1 energy range (by comparison, the ionisation energy of I2 is 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 069 cm−1).10 Excitation of Rydberg states I2** was detected by recording I+ and I− ion signals, taking advantage of the bound-to-free energy transfers.
069 cm−1).10 Excitation of Rydberg states I2** was detected by recording I+ and I− ion signals, taking advantage of the bound-to-free energy transfers.
In 2014, Bogomolov et al. investigated the spectroscopy and dynamics of two-photon excited Rydberg states of gerade symmetry over a similar energy range (73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500–74
500–74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1).3 Besides bound-to-free energy transfers that follow IP states, other dissociative channels were observed with formation of Rydberg states of the iodine atom. A complex dynamics with interplay between bound and dissociative molecular states of Rydberg and ion-pair character is therefore at play. This has motivated the 2016 work of the same research group in the time domain to examine this dynamics with sub-picosecond resolution.4 A femtosecond laser at 270 nm was used to pump (two pump photons at 270 nm deliver 74
500 cm−1).3 Besides bound-to-free energy transfers that follow IP states, other dissociative channels were observed with formation of Rydberg states of the iodine atom. A complex dynamics with interplay between bound and dissociative molecular states of Rydberg and ion-pair character is therefore at play. This has motivated the 2016 work of the same research group in the time domain to examine this dynamics with sub-picosecond resolution.4 A femtosecond laser at 270 nm was used to pump (two pump photons at 270 nm deliver 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 074 cm−1) and probe the I2 sample. The velocity and angular distributions of I+ ions were recorded as a function of the pump–probe time delay, using a velocity map imaging (VMI) spectrometer. Analysis of the kinetic energy release (KER) of these ions showed 6 active dissociation channels: one goes to the valence state dissociation
074 cm−1) and probe the I2 sample. The velocity and angular distributions of I+ ions were recorded as a function of the pump–probe time delay, using a velocity map imaging (VMI) spectrometer. Analysis of the kinetic energy release (KER) of these ions showed 6 active dissociation channels: one goes to the valence state dissociation 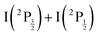 ; one reaches the IP of lowest energy and forms I+(3P2) + I−(1S0); the other four channels reach the
; one reaches the IP of lowest energy and forms I+(3P2) + I−(1S0); the other four channels reach the 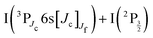 asymptotes and form the Rydberg states
asymptotes and form the Rydberg states 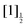 ,
, 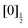 ,
, 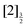 and
and 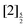 of the iodine atom. These states are built by Jl (or JK) coupling between the I+(3PJc) ion core and the 6s electron. Only the valence state dissociation channel forming
of the iodine atom. These states are built by Jl (or JK) coupling between the I+(3PJc) ion core and the 6s electron. Only the valence state dissociation channel forming 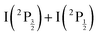 can be accessed directly by the pump excitation. In the five other channels, a predissociation process is at play with first excitation of a single 6d molecular Rydberg state,
can be accessed directly by the pump excitation. In the five other channels, a predissociation process is at play with first excitation of a single 6d molecular Rydberg state, 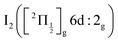 , then a predissociation towards the observed dissociation products. IP states were believed to mediate the predissociation.
, then a predissociation towards the observed dissociation products. IP states were believed to mediate the predissociation.
The present work aims at further examining the interplay between Rydberg and ion-pair states in the predissociation dynamics of I2** molecular Rydberg states: two different pump/probe configurations were used (269/807 nm and 266/334 nm); the angular distribution and KER of both I+ and I− were recorded, as well as the energy and angular distributions of photoelectrons generated by the probe laser. In the 269/807 nm experiment, the wavepacket was launched in a region where a few Rydberg states are crossed by IP states, significantly below the first adiabatic ionisation limit of I2. This situation is close to that explored in ref. 4. In the 266/334 nm experiment, the Franck–Condon region of excitation was located near the vertical ionisation limit, slightly above the first adiabatic ionisation limit. It overlapped many molecular Rydberg states that are also coupled with IP states. Such wavepackets can be called vibronic wavepackets, since they are built with states of different electronic configuration.
Section 2 of the present paper details the experimental method. Section 3 presents briefly the energy landscape where the wavepacket moves and the methodology used for running molecular dynamics simulations over this landscape, a useful complement in the discussion (Section 5). The experimental results are presented in Section 4.
2 Experimental methods
The present experimental setup is the same as that described in many of our former publications (e.g. ref. 11). It associates a molecular beam, femtosecond lasers and a VMI spectrometer as schemed in Fig. 3 of ref. 11 Specific features regarding the present work are described below.Molecular beam of I2
The I2 sample has been purchased as crystals from Merck. No further purification is achieved. Helium gas with a backing pressure of 1.1 bar is used to carry I2 molecules into the gas phase. The corresponding vapour is expanded into vacuum and carried into a beam through a 0.1 mm nozzle and a 1 mm skimmer, producing a continuous molecular beam which then enters the interaction chamber and perpendicularly crosses the quasi-collinear pump and probe laser beams.Femtosecond lasers
A Coherent Legend Elite laser providing 35 fs, 807 nm, 3 kHz pulses with a maximum energy of 4.5 mJ per pulse is used to generate both the pump and the probe laser pulses at appropriate wavelengths. Here, 2.5 mJ per pulse are shared between the pump and probe lasers. 1.0 mJ is used directly as probe in the 269/807 nm experiment. In that case, frequency doubling and mixing of the remaining 1.5 mJ delivers 190 μJ pump pulses at 268.7 nm. In the the 266/334 nm experiment, 1.5 mJ is sent to a TOPAS-Prime optical parametric amplifier (Light Conversion) that provides tunable light from 240 nm to the infra-red. It is set here to 334 nm. The remaining 1.0 mJ is frequency doubled and mixed to provide 26 μJ at 266.7 nm. In both experiments, the relative delay between the pump and the probe pulses is controlled by a motorised delay-line. The cross-correlation time between the pump and probe laser pulses is estimated at 75 fs and 150 fs in the 269/807 nm and 266/334 nm experiments, respectively. In both experiments, the lasers are linearly polarised with their polarisation direction within the plane defined by the molecular and laser beams.Charged particles detection
The ions or electrons generated by the probe laser ionisation are detected using a VMI spectrometer after perpendicular extraction with respect to the polarisation direction of the probe laser. With appropriate settings, either I+, I− or photoelectrons images are recorded as a function of the pump–probe time delay. I+, I− and photoelectrons are recorded and treated separately. When photoelectrons are considered, the VMI detection allows us to measure the energy spectrum of the photoelectrons as a function of the pump–probe time delay. Femtosecond time resolved photoelectron spectroscopy (fs-TRPES) experiments are therefore conducted.12,13 When the VMI is tuned to I+ or I− detection, the ion KER is measured. By analogy with the fs-TRPES acronym, the acronym fs-TRKERS (femtosecond-time resolved kinetic energy release spectra) is proposed here for these experiments.Data analysis
To get the full information from 2D VMI images, the 3D radial and angular distributions of the detected particle must be reconstructed. This is achieved using the pBasex algorithm based on inverse Abel transform.14 The latter includes a Legendre polynomial decomposition (even orders up to the fourth) to account for the angular anisotropy of the images. A calibration is needed to relate the radius r of particle impacts on the image (measured in pixels) to the kinetic energy E of the detected particles. The calibration function E(r) is the same whatever the mass and charge of the detected particle. It therefore applies to photoelectrons, photoanions and photocations. In practice, the calibration is achieved as in ref. 15 by operating the molecular beam with O2 and focusing the 266 nm laser alone on the O2 sample. The pBasex inversion of the resulting photoelectron image reveals a vibrational progression which, after appropriate fit, allows us deriving the calibration function E(r). The data presented here are scaled using this function.The full experimental information for the I+ cation and I− anion consists of a series of KER spectra, one for each Legendre order, as a function of the pump–probe delay τ, noted Sanion![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cation0 (KER,τ), Sanion
cation0 (KER,τ), Sanion![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cation2 (KER,τ) and Sanion
cation2 (KER,τ) and Sanion![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cation4 (KER,τ). For the photoelectrons, it is a series of kinetic energy spectra, one for each Legendre order, as a function of τ, noted Selec0(E,τ), Selec2(E,τ) and Selec4(E,τ) where E is the kinetic energy of the photoelectrons.
cation4 (KER,τ). For the photoelectrons, it is a series of kinetic energy spectra, one for each Legendre order, as a function of τ, noted Selec0(E,τ), Selec2(E,τ) and Selec4(E,τ) where E is the kinetic energy of the photoelectrons.
3 Energy landscape and molecular dynamics simulations
3.1 Energy landscape
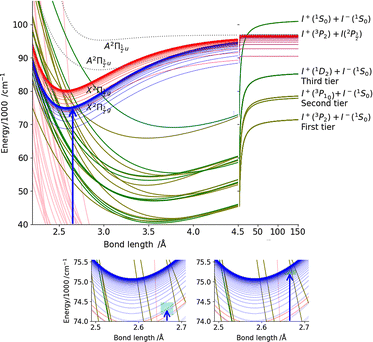
Some relevant, mostly experimental, spectroscopic constants are listed in Tables S2–S4 of the ESI† attached to the present article. They allowed us building the complex network of potential energy curves shown in Fig. 1 where the wavepacket is launched by the pump pulse. The well region of the potential curves is described by a Morse function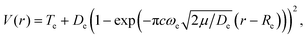 | (1) |
The Rydberg states shown in the figure are built by a simple translation of the ionic curve to which they converge. This is done using the observation of Donovan et al.16 and their reassignment in Section 7 of ref. 9. These authors identified four Rydberg series that are expected to overlap the energy region covered by the present two-photon pump excitation: 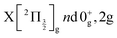 and
and 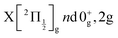 . The data of ref. 16 provide spectroscopic information for nd ranging between 5d and 9d. A sufficient fit of these data is provided assuming a constant quantum defect to each Rydberg series: 1.88, 1.96, 1.85 and 1.89, respectively. These values are used in Fig. 1 to extrapolate the data of ref. 16 and plot Rydberg potential curves up to the ionisation limits
. The data of ref. 16 provide spectroscopic information for nd ranging between 5d and 9d. A sufficient fit of these data is provided assuming a constant quantum defect to each Rydberg series: 1.88, 1.96, 1.85 and 1.89, respectively. These values are used in Fig. 1 to extrapolate the data of ref. 16 and plot Rydberg potential curves up to the ionisation limits 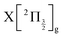 (drawn in blue) and
(drawn in blue) and 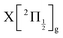 (drawn in red). This is actually very approximate at large distances when the electronic configuration switches from molecular Rydberg centred about the I2+ core to atomic Rydberg centred about I+.
(drawn in red). This is actually very approximate at large distances when the electronic configuration switches from molecular Rydberg centred about the I2+ core to atomic Rydberg centred about I+.
The bottom panel of Fig. 1 focuses attention on the Franck–Condon region of excitation, showing that far more Rydberg states are overlapped by the pump spectrum in the 266/334 nm experiment (right panel) than in the 269/807 nm experiment (left panel).
3.2 Molecular dynamics
Molecular dynamics (MD) simulations results are used to help the discussion in Section 5. The classical equations of motion are integrated using the Verlet algorithm with a time step of 1 fs.17 Energy conservation is achieved with 10−5 accuracy. The purpose of these calculations is not towards a full non-adiabatic description of the dynamics in the spirit of that described in ref. 18 where a doubly excited barium atom is embedded in an argon cluster. Such extensive treatment is beyond the scope of the present work. Instead, single state dynamics along selected energy curves taken from Fig. 1 are performed. This allows us to estimate relevant time scales in the wavepacket evolution.4 Experimental results
4.1 Pump-only experiment at 269 nm
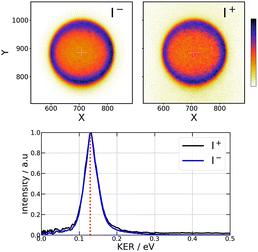
When an I2 molecule absorbs two 269 nm photons (74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 349 cm−1), enough energy is present to open the I+ + I− dissociation along first tier IP states, enabling I+ and I− ions to be detected using the VMI spectrometer. Raw VMI images of these ions are shown in the top left panels of Fig. 2. They look almost isotropic. Nevertheless, a small anisotropy is revealed by the Legendre decomposition in the pBasex inversion. Although a small β2 > 0 anisotropy cannot be precluded, its accurate measurement is limited by an artefact: the extension of the ionisation zone along the molecular beam. It can be modelled indeed by convolution of an isotropic image with a Gaussian velocity distribution along the beam direction. This bias appears for both I+ and I− measurements and, in the following, the higher orders Sanion
349 cm−1), enough energy is present to open the I+ + I− dissociation along first tier IP states, enabling I+ and I− ions to be detected using the VMI spectrometer. Raw VMI images of these ions are shown in the top left panels of Fig. 2. They look almost isotropic. Nevertheless, a small anisotropy is revealed by the Legendre decomposition in the pBasex inversion. Although a small β2 > 0 anisotropy cannot be precluded, its accurate measurement is limited by an artefact: the extension of the ionisation zone along the molecular beam. It can be modelled indeed by convolution of an isotropic image with a Gaussian velocity distribution along the beam direction. This bias appears for both I+ and I− measurements and, in the following, the higher orders Sanion![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cation2
cation2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4(KER,τ) signals will be considered only in the case of strong anisotropies that overcome this effect. Hence, here, only the isotropic part of the Legendre decomposition is considered to build the KER spectra shown in the bottom panel of Fig. 2. As seen in the figure, the central energy of the peaks well agrees with expectation from energy conservation.
4(KER,τ) signals will be considered only in the case of strong anisotropies that overcome this effect. Hence, here, only the isotropic part of the Legendre decomposition is considered to build the KER spectra shown in the bottom panel of Fig. 2. As seen in the figure, the central energy of the peaks well agrees with expectation from energy conservation.
4.2 269/807 nm pump/probe experiment
Fig. 3 is dominated by a single class of KERs between 0.09 and 0.17 eV. The time dependence of the corresponding signal, obtained by summing the anion signal over this energy range, is shown as green dots in Fig. 4. A contribution is observed at negative time. It is due to several excitation/ionisation schemes where the role of the pump (269 nm) and probe (807 nm) lasers is inverted. It is crudely described by a single exponential decay of time constant τ−. Dynamics at positive pump–probe time delay is that of interest for the present work. It appears bi-exponential and can be associated with a two-step dynamics of the type 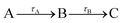 where A represents the initial wavepacket. The single exponential decay at negative time and the two-step dynamics at positive time has been used to fit the time dependency reported in Fig. 4, τ−, τA and τB being the fit parameters. The fitting equations are provided in Section S1.1 of the ESI.† Of course, convolution by the cross-correlation function of the pump and probe laser pulses is included in the fit. Best fit parameters τ−, τA and τB are listed in Table 1. Inclusion of τ− is necessary for a reliable fit of the experimental curve. However its value as best fit parameter carries no significant information because it is associated with a superposition of several processes. Only τA and τB carry relevant information for the discussion.
where A represents the initial wavepacket. The single exponential decay at negative time and the two-step dynamics at positive time has been used to fit the time dependency reported in Fig. 4, τ−, τA and τB being the fit parameters. The fitting equations are provided in Section S1.1 of the ESI.† Of course, convolution by the cross-correlation function of the pump and probe laser pulses is included in the fit. Best fit parameters τ−, τA and τB are listed in Table 1. Inclusion of τ− is necessary for a reliable fit of the experimental curve. However its value as best fit parameter carries no significant information because it is associated with a superposition of several processes. Only τA and τB carry relevant information for the discussion.
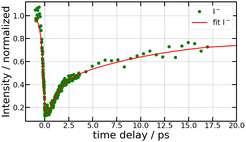 | ||
| Fig. 4 269/807 nm experiment – Sum of the Sanion0(KER,τ) fs-TRKERS for anion energies between 0.09 and 0.17 eV as a function of the pump–probe delay (green dots). The full red curve best fits the experimental signal as described in the text, using the time constants τ−, τA and τB listed in Table 1. | ||
| Ion detection | τ − (fs) | τ A (ps) | τ B (ps) |
|---|---|---|---|
| a The time dependencies of the I− signal and that of ROI C3 of I+ were fitted together after adjusting the height of their baselines at negative time and giving a higher weight to the less noisy I− signal. | |||
| I−a | 270 ± 20 | 0.85 ± 0.1 | 14.5 ± 0.5 |
| I+ ROI C3a | 270 ± 20 | 0.85 ± 0.1 | >10.0 |
| I+ ROI C2 | 165 ± 20 | 1.7 ± 0.2 | 9.0 ± 1.0 |
| I+ ROI C4,5 | 80 ± 10 | 0.39 ± 0.02 | 9.5 ± 0.5 |
| e− detection | τ − (fs) | τ A (ps) | τ B (ps) |
|---|---|---|---|
| e− Bkg1 | 110 ± 10 | 4.1 ± 0.5 | — |
| e− Bkg2 | 86 ± 10 | 1.36 ± 0.1 | — |
| e− Neg | 155 ± 20 | — | — |
| e− Dec1 | — | 2.1 ± 0.6 | |
| e− Dec2 | — | 1.0 ± 0.1 | — |
| e− Dec3 | — | 0.68 ± 0.07 | — |
| e− HE1 | — | — | 11.9 ± 1.2 |
| e− HE2 | — | — | 8.7 ± 0.9 |
| e− HE3 | — | — | 7.08 ± 0.7 |
| e− LE1 | — | 3.9 ± 0.4 | >10.0 |
| e− LE2 | — | 5.4 ± 0.5 | >10.0 |
| e− LE3 | — | 5.4 ± 0.5 | — |
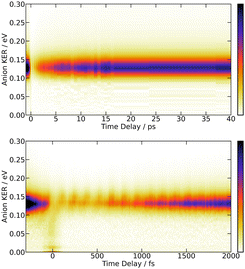
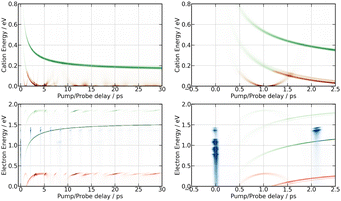
The bottom panel of Fig. 3 shows the first 2 ps of the dynamics. Two points must be mentioned. First, an oscillation regime appears. A Fourier analysis reveals that the intensity of I− anions with KER ≈ 0.15 eV oscillates with a frequency of 230 ± 15 cm−1. Second, I− anions of very small energy appear during a short time near the zero pump–probe delay. This signal is presumably associated with a dissociation along third tier ion pair curves that is energetically allowed when I2 is pumped by three photons (2 pump photons + 1 probe photon) simultaneously, during the cross correlation time of the lasers. This signal turned out to be very useful to set time zero of the experiment.
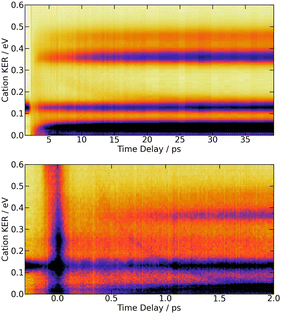 | ||
| Fig. 5 269/807 nm experiment – Top panel: 3D-plot of the fs-TRKERS signal Scation0(KER,τ) up to 40 ps time delay with the same colour map as in Fig. 3. Bottom panel: zoom on the first 2 ps with a different intensity scale to highlight the band whose central energy is changing with time delay. The top panel is reproduced on Fig. S6 of the ESI† with another colour map that enhances the weak time-dependent feature described in the text. The equivalent 3D-plot of the fs-TRKERS signal Scation2(KER,τ) are plotted on Fig. S7 of the ESI.† | ||
The bottom panel of Fig. 5 focuses attention on the first 2 ps of the dynamics. A time-dependent band is clearly visible. Its central energy decreases from 0.35 eV to 0.15 eV as the time delay goes between 0.5 and 1.0 ps. Upon close look, another time-dependent band is slightly visible on the top panel of Fig. 5. Its central energy decreases from 0.35 eV to 0.15 eV as the time delay goes between ∼5 and 20 ps.
Projection of Scation0(KER,τ) on the vertical axis is a convenient way of visualising regions of interest (ROIs) in the KER spectrum. Six ROIs are identified and labelled in the top left panel of Fig. 6. These regions match quantitatively those found by Mudrich and coworkers in ref. 3 and 4, thus Fig. 6 reproduces the labelling of these authors. Of course, this way of delimiting ROIs attenuates bands whose centre energy varies as a function of the time delay. We mentioned above that such a band exits. It is averaged within the weak broad ROI C3′.
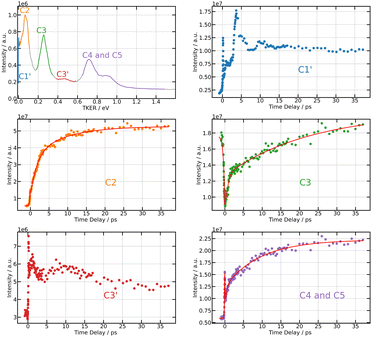 | ||
| Fig. 6 269/807 nm experiment – Top left panel: TKER spectrum obtained by integrating Scation0(KER,τ) along the KER axis (vertical axis in Fig. 5). The colours and labels C1′, C2, C3, C3′, C4 and C5 isolate 6 regions of interest (ROIs). Note that TKER is twice the I+ KER shown Fig. 5. Other panels: time dependencies of the signal associated with each ROI. Dots show the experiment. Solid lines in ROIs C2, C3, and C4,5 are fits using the time constants listed in Table 1. | ||
Unlike the time delay dependencies associated with ROIs C1′ and C3′, those associated with C2, C3 and C4,5 have a clear bi-exponential behaviour at positive delay time and a contribution existing at negative time. The fit model used above with I− signals is thus used again to derive time constants τ−, τA and τB for ROIs C2, C3 and C4,5. Note that the time delay dependence associated with ROI C3 in Fig. 6 (middle right panel) has strong similarities with that of the anion signal (Fig. 4). We will see in the discussion that both have the same origin. Hence a single set of time constants was used to fit both curves together.
Section 4.2.1 revealed an oscillation regime in the anion signal. No such behaviour appears in Fig. 6 even when considering ROI C3 (bottom left panel), presumably because of the poor signal-to-noise ratio. Absence of clean oscillation within noise is confirmed when performing a Fourier analysis of the I+ ion data (not shown here). Both probe laser ionisation and energy transfer to first tier IP states produce I+ ions, whereas only the latter process (energy transfer) generates I− ions. This could be another reason why an oscillation regime associated with energy transfer to first tier IP states is easier to observe in I− ion signals. A last observation can be done in Fig. 6. The time dependencies associated with ROIs C1′ and C3′ have fairly equally spaced over-intensities that may reflect severely damped oscillations.
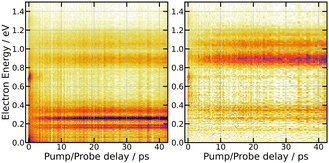 | ||
| Fig. 7 269/807 nm experiment – 3D-plot of the fs-TRPES signals Selec0(E,τ) (left panel, isotropically distributed photoelectrons) and Selec2(E,τ) (right panel, polarised electrons) with the same colour map as in Fig. 3. | ||
A series of energy bands superimposed on a continuum are observed in Fig. 7. Projection of Selec0(E,τ) on the vertical axis of the figure is a convenient way to isolate these bands and the continuum and adjust their position and width as shown in the top panel of Fig. 8. The structured part of the spectrum that appears in the figure is represented by 9 bands with Gaussian profile (three temporally decaying features Dec1, Dec2, Dec3, and six temporally increasing features at low energy LE1, LE2, LE3 and high energy HE1, HE2, HE3), the continuum by two exponential functions (Bkg1 and Bkg2). An extra band named Neg was set to model the signal at negative pump–probe delay. This set of bands and continua has been used as basis to fit the Selec0(E,τ) and Selec2(E,τ) spectra as a function of the pump–probe time delay τ, their intensities serving as fit parameters. This provides us with 12 time dependencies that are shown in the ESI.† Various shapes are observed. Nevertheless, the same kinetic model as above could be applied to fit all these curves: a bi-exponential behaviour at positive time and a contribution at negative time. This provides us with time constants τ−, τA and τB for the 12 spectral elements listed in Fig. 8. Best fit curves are shown in the ESI† and time constants τ−, τA and τB are given in Table 1.
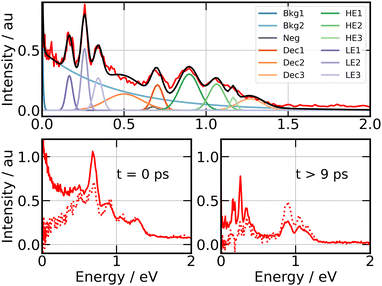 | ||
| Fig. 8 269/807 nm experiment – Top panel: photoelectron spectrum obtained by projecting Selec0(KER,τ) along the energy axis (vertical axis in Fig. 7). Colours and labels isolate 9 bands, two continua and a further band for the signal at negative time. Bottom panels: photoelectron spectra near τ = 0 ps (left panel) and above 9 ps (right panel) for isotropically distributed electrons (full line) and polarised electrons (dotted line). Both are obtained by integrating Selec0(KER,τ) and Selec2(KER,τ) over τ, respectively, between −80 fs and +80 fs for the former, above 9 ps for the latter. | ||
4.3 266/334 nm pump/probe experiment
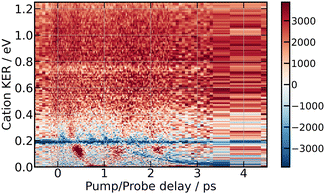
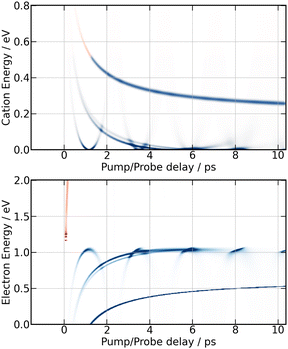
Fig. 9 summarises the experimental data when the I2 molecule is pumped at 266 nm and probed at 334 nm. From top to bottom, 3D representations of Sanion0(E,τ), Scation0(E,τ) and Selec0(E,τ) are shown up to 10 ps time delay.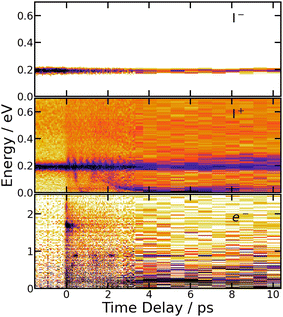 | ||
| Fig. 9 266/334 nm experiment – 3D-picture of Selec0(E,τ) (bottom panel), Scation0(E,τ) (middle panel) and Sanion0(E,τ) (top panel) using the same colour map as in Fig. 3. | ||
A band centred near 0.19 eV is observed in both figures. It presents an oscillation regime in the upper energy part, near 0.2 eV. This band has the same energy as the single one observed above with I− anions. Note that no oscillation regime is observable in the I− anion signal.
Bands whose central energy varies as a function of the pump–probe delay are also observed in these figures: one between 1.5 and 4 ps whose central energy decreases from ≈0.08 eV to ≈0 eV; another one makes recurrences near 0.7 eV at 0.5, 1.3, 2.2 ps and goes to zero in between. The second and third recurrences of the latter band are especially visible in Fig. 11. With no ambiguity, the angular distribution of the cations associated with this band shows a favoured alignment along the laser polarisation.
5 Discussion
Two pump photons input 9.22 eV electronic energy into I2 in the 269/807 nm experiment and 9.32 eV in the other. Table 2 lists useful energetics for the present discussion. Two classes of dissociation channels are opened: formation of the ion pair of lowest energy (I+(3P2) + I−(1S0)); formation of ground state iodine I(2P3/2) plus one of the four atomic Rydberg states I*((3P2)6s2[2]5/2), I*((3P2)6s2[2]3/2), I*((3P0)6s2[0]1/2) and I*((3P1)6s2[1]3/2).Note that a valence state dissociation forming 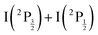 is also open by the pump laser excitation. It was observed by Mudrich and coworkers, both in their nanosecond (ref. 3) and sub-picosecond (ref. 4) experiments. It was associated with a small I+ signal at TKER ≈ 2.1 eV in the sub-picosecond experiment and was discussed as associated with successive pump and dump processes through intermediate resonances. Given the very different probe wavelength here, 807 nm versus 270 nm, no such signal is observed. Hence, after addressing the nature of initial wavepacket, we focus attention on the dissociation channels mentioned above where either atomic Rydberg states or first tier IP fragments are formed. In terms of detection, they correspond to very different situations since the latter channel produces ions that are detected directly by the VMI whereas the former channels produce neutral species which need ionisation by the probe laser to be detected.
is also open by the pump laser excitation. It was observed by Mudrich and coworkers, both in their nanosecond (ref. 3) and sub-picosecond (ref. 4) experiments. It was associated with a small I+ signal at TKER ≈ 2.1 eV in the sub-picosecond experiment and was discussed as associated with successive pump and dump processes through intermediate resonances. Given the very different probe wavelength here, 807 nm versus 270 nm, no such signal is observed. Hence, after addressing the nature of initial wavepacket, we focus attention on the dissociation channels mentioned above where either atomic Rydberg states or first tier IP fragments are formed. In terms of detection, they correspond to very different situations since the latter channel produces ions that are detected directly by the VMI whereas the former channels produce neutral species which need ionisation by the probe laser to be detected.
5.1 Initial wavepacket
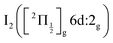 state, a 6d molecular Rydberg state. Here with slightly more energetic pump photons Rydberg states
state, a 6d molecular Rydberg state. Here with slightly more energetic pump photons Rydberg states 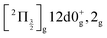 (0+g and 2g almost not distinguishable at the scale of the figure) and
(0+g and 2g almost not distinguishable at the scale of the figure) and 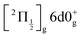 are likely populated. Direct vertical ionisation of these states by 807 nm probe photons delivers photoelectrons with 1.4 and 0.7 eV energy, respectively, as those observed experimentally (especially the 0.7 eV photoelectrons) at zero pump–probe time delay in Fig. 8 (bottom left panel). Additional peaks and a broad continuum are also present in the figure. They might be due to excitation of molecular Rydberg states belonging to other series than those shown in Fig. 1. In addition, at τ = 0 pump/probe delay, other excitation–ionisation schemes than 2-pump-excitation + 1-probe-ionisation are possible. For example vertical excitation (between 33
are likely populated. Direct vertical ionisation of these states by 807 nm probe photons delivers photoelectrons with 1.4 and 0.7 eV energy, respectively, as those observed experimentally (especially the 0.7 eV photoelectrons) at zero pump–probe time delay in Fig. 8 (bottom left panel). Additional peaks and a broad continuum are also present in the figure. They might be due to excitation of molecular Rydberg states belonging to other series than those shown in Fig. 1. In addition, at τ = 0 pump/probe delay, other excitation–ionisation schemes than 2-pump-excitation + 1-probe-ionisation are possible. For example vertical excitation (between 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 47
000 and 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) and ionisation of many low lying I2 states is accessible energetically through the following two schemes: 1-pump + 1-probe-excitation followed by 1-pump ionisation, and 1-probe-excitation + 2-pump ionisation. These schemes account quantitatively for extra features in the top panel of Fig. 8. Interestingly, they were invoked a long time ago by Donovan et al. as responsible for a continuum and many unassigned lines in the (2 + 1) REMPI investigation of the
000 cm−1) and ionisation of many low lying I2 states is accessible energetically through the following two schemes: 1-pump + 1-probe-excitation followed by 1-pump ionisation, and 1-probe-excitation + 2-pump ionisation. These schemes account quantitatively for extra features in the top panel of Fig. 8. Interestingly, they were invoked a long time ago by Donovan et al. as responsible for a continuum and many unassigned lines in the (2 + 1) REMPI investigation of the 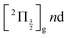 and
and 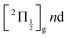 series.9,16
series.9,16
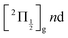 series are overlapped by the Franck–Condon region. The initial wavepacket is built as a linear combination of these states. It appears as a vibronic wavepacket where both electronic and vibrational coordinates are involved.
series are overlapped by the Franck–Condon region. The initial wavepacket is built as a linear combination of these states. It appears as a vibronic wavepacket where both electronic and vibrational coordinates are involved.
5.2 Monitoring access to atomic Rydberg states in the 269/807 nm experiment
Monitoring dissociation channels forming neutral atomic Rydberg states follows the scheme of usual femtosecond pump–probe experiments, where the probe signal starts rising at (or after) delay time zero when the probe laser interacts with reaction products or reaction intermediates and makes them detectable. ROIs C2, C4 and C5 in Fig. 6 have this behaviour. Their central energy match quantitatively ROIs found in the work by von Vangerow et al.4 This is expected since the pump wavelength is almost identical between these experiments: 269 and 270 nm. von Vangerow et al. related each ROI to a specific probe process, within a global picture of the dynamics: the initial vibrational wavepacket is launched by the pump laser in a single Rydberg state; it subsequently transfers to IP states and, either goes to dissociation and forms I+ and I− ions, or back-transfers to molecular Rydberg states, dissociates and forms atomic Rydberg states. The present section follows and complements the assignment of von Vangerow et al. concerning the three channels where atomic Rydberg are formed. The channels are labelled as the ROIs they correspond to in Fig. 6:C2 Photoionization of the atomic Rydberg state 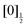
From the top left panel of Fig. 6 we know that this probe process produces I+ + I with centre TKER energy around 0.11 eV in agreement with the energetics in Table 2.
C4 Same as C2 for the 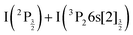 asymptote.
asymptote.
C5 Same as C2 for the 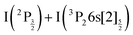 asympstote.
asympstote.
Electron energies are presented in Table 3 when Rydberg states of atomic iodine are ionised by either three probe photons at 807 nm or a single one at 334 nm. Correspondence is given in the table between photoelectron bands identified in the 269/807 nm experiment (see top panel of Fig. 8) and detection of specific atomic Rydberg states.
| Atomic Rydberg ionisation | Electron energy (eV) | |||
|---|---|---|---|---|
| 3 probe photons at 807 nm | 1 probe photon at 334 nm | |||
| I*((3P2)6s2[2]5/2) | → | I+(3P2) | 0.93 (HE1) | 0.03 |
| → | I+(3P0) | 0.13 (LE1) | <0 | |
| → | I+(3P1) | 0.05 | <0 | |
| I*((3P2)6s2[2]3/2) | → | I+(3P2) | 1.11 (HE3) | 0.21 |
| → | I+(3P0) | 0.31 (LE3) | <0 | |
| → | I+(3P1) | 0.23 (LE2) | <0 | |
| I*((3P0)6s2[0]1/2) | → | I+(3P2) | 1.71 | 0.81 |
| → | I+(3P0) | 0.91 (HE1) | 0.01 | |
| → | I+(3P1) | 0.83 (HE1) | <0 | |
| I*((3P1)6s2[1]3/2) | → | I+(3P2) | 1.82 | 0.92 |
| → | I+(3P0) | 1.02 (HE2) | 0.13 | |
| → | I+(3P1) | 0.94 (HE1) | 0.05 | |
5.3 Monitoring evolution along ion-pair (IP) states
Information provided by the photodetachment probe process (probe process 2) can be recognised in the 269/807 nm experiment when observing the delay time dependence of ion signals with KER = 0.13 eV in Fig. 6 (ROI C3 in the I+ fs-TRKERS) and Fig. 4 (main class of KER energies). Using the same notation as above with ROIs C2, C4 and C5, ROI C3 and its correspondent when observing I− is described as:
C3 Photodetachment from almost free I−, when the ion-pair moving on first tier IP state is almost dissociated:
This probe process lets the I+ signal (ROI C3) unaffected, whereas the I− signal is suppressed.
C3′ Of course, photodetachment can occur along first tier IP states when the I+(3P2) + I−(1S0) dissociation is not achieved yet. This produces an I+ signal with ROI C3′:
As with ROI C3 above, this probe process suppresses the I− signal but here, I+ is left with the KER it has at the moment of interaction with the probe laser. This likely results in a KER band whose central energy moves as a function of the pump/probe time delay.
von Vangerow et al. identified a last probe process that is also relevant to the present work:4
C1′ Photodetachment forming I+ + I at an outer turning point of the I+I− oscillation when the wavepacket oscillates within the well of second tier IP states:
5.4 Dynamics towards first tier dissociation
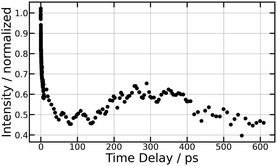
We already mentioned that first tier dissociation I+(3P2) + I−(1S0) is the only source of I− ions with KER = 0.13 eV. It is therefore best documented when observing this ion signal as a function of the pump–probe time delay for ions as shown in Fig. 4 (269/807 nm experiment) and Fig. 10 (266/334 nm experiment). In the 269/807 nm experiment, the signal is minimum near τ = 0 and makes a bi-exponential revival at increasing τ values. An oscillation regime is observed during the first one or two picoseconds of the evolution. In the 266/334 nm experiment, it makes an extremely rapid decay near τ = 0 and experiences no revival. Instead a single broad oscillation is observed between 100 and 600 ps. This contrasting observation is due to very different energies of the probe photons (1.54 and 3.71 eV, respectively), which offer two different points of view on the dynamics.These behaviours are very different from observations in ref. 15 where ion-pair dissociation of O2 is induced at 18.165 eV and probed by photodetachment. The O− signal decayed abruptly as a step function decay during the cross correlation of the lasers. No revival was observed. The very different observation here suggests a much more complex dynamics than the simple direct excitation of O+O− IP states reported in ref. 15.
Let us examine first the 269/807 nm experiment, then the 266/334 nm experiment.
When the wavepacket has transferred to IP states of the first tier, an important information from Fig. 1 is that no curve crossing can prevent dissociation and no drastic change of the electronic configuration is expected after I+⋯I− separation is larger than 2.6 Å. Accordingly, the longer time constant τB = 14.5 ps would be the time scale for reaching the large I+⋯I− separations where the less efficient two probe photon photodetachment is at play. Then, the rapid revival with τA = 0.85 ps would document the departure from regions where probe by a single photon is especially efficient. This suggests that a fraction of the wavepacket does not transfer directly to IP states in the Franck–Condon region of excitation and explores the complex network of potential curves.
An oscillation regime is clearly observed up to 1.5 ps pump/probe delay in the anion signal (Fig. 3, bottom panel). To be quantitative, a 2-D Fourier analysis of Fig. 3 has been performed and reveals σ = 230 ± 15 cm−1 oscillations for anions whose KER spectrum peaks at ≈0.15 eV. This σ value matches, within error bars, the vibrational constant of the 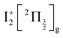 and
and 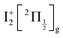 ions: ωe = 239.04 cm−1 and ωe = 229.0 cm−1, respectively (see Table S4 of the ESI†). We have seen in Section 5.1 that the initial wavepacket is built from a superposition of the Rydberg states
ions: ωe = 239.04 cm−1 and ωe = 229.0 cm−1, respectively (see Table S4 of the ESI†). We have seen in Section 5.1 that the initial wavepacket is built from a superposition of the Rydberg states 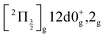 and
and 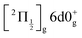 , whose cores are
, whose cores are 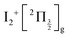 and
and 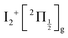 , respectively. We are left with the conclusion that the pump pulse vibrationally excites the core of the initial Rydberg wavepacket, with the consequence that the probe efficiency is, as least partially, modulated as a function of time. Although difficult to extract from the data, the lifetime of the oscillation seems consistent with the time constant τA = 0.85 ps, assigned above as associated with transfer to first tier IP states.
, respectively. We are left with the conclusion that the pump pulse vibrationally excites the core of the initial Rydberg wavepacket, with the consequence that the probe efficiency is, as least partially, modulated as a function of time. Although difficult to extract from the data, the lifetime of the oscillation seems consistent with the time constant τA = 0.85 ps, assigned above as associated with transfer to first tier IP states.
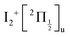 ion (120 cm−1 see Table S4 of the ESI†). This is surprising at a first glance since the molecular Rydberg and third tier IP states forming the initial wavepacket are not built about a core ungerade symmetry. Although this possibility cannot be ruled out, we can also observe that the value σ = 110 ± 15 cm−1 is close to the ωe constants of the gerade IP states 1g and 2g of the third tier (106.9 cm−1 and 108.3 cm−1 respectively, see Table S3 of the ESI†). We anticipated in Section 5.1 that with 266 nm excitation, the Franck–Condon region overlaps areas of coupling between molecular Rydberg and third tier IP curves. Actually, third tier IP curves are bound and this coupling can be considered as perturbations between molecular Rydberg states and heavy Rydberg states corresponding to vibration within third tier IP curves. The theoretical framework for describing heavy Rydberg states was developed by Reinhold and Ubachs to describe H+H− ion-pair vibrations.20 Importantly with regard to the present work, Mollet and Merkt documented the spectroscopy of a series of heavy Rydberg states of Cl2, which converges to Cl−(2S0) + Cl+(3P0).21 To achieve these measurements, advantage was taken of couplings between molecular Rydberg states of Cl2 and the two IP states just mentioned. In a sense, the work by Mollet and Merkt on Cl2 dissociation appears as a spectroscopy counterpart of the present work on I2 dissociation in the real-time domain. Of course, the energy landscape and the mixing between electronic configurations here are more complex.
ion (120 cm−1 see Table S4 of the ESI†). This is surprising at a first glance since the molecular Rydberg and third tier IP states forming the initial wavepacket are not built about a core ungerade symmetry. Although this possibility cannot be ruled out, we can also observe that the value σ = 110 ± 15 cm−1 is close to the ωe constants of the gerade IP states 1g and 2g of the third tier (106.9 cm−1 and 108.3 cm−1 respectively, see Table S3 of the ESI†). We anticipated in Section 5.1 that with 266 nm excitation, the Franck–Condon region overlaps areas of coupling between molecular Rydberg and third tier IP curves. Actually, third tier IP curves are bound and this coupling can be considered as perturbations between molecular Rydberg states and heavy Rydberg states corresponding to vibration within third tier IP curves. The theoretical framework for describing heavy Rydberg states was developed by Reinhold and Ubachs to describe H+H− ion-pair vibrations.20 Importantly with regard to the present work, Mollet and Merkt documented the spectroscopy of a series of heavy Rydberg states of Cl2, which converges to Cl−(2S0) + Cl+(3P0).21 To achieve these measurements, advantage was taken of couplings between molecular Rydberg states of Cl2 and the two IP states just mentioned. In a sense, the work by Mollet and Merkt on Cl2 dissociation appears as a spectroscopy counterpart of the present work on I2 dissociation in the real-time domain. Of course, the energy landscape and the mixing between electronic configurations here are more complex.
The energy of 334 nm probe photon is 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 cm−1 = 3.71 eV. It is larger than the electronic affinity of atomic iodine (−3.059 eV) and probe photons can photodetach the electron of I− and therefore deplete the I− signal, even at large I+⋯I− separation when I− is quasi-free. An important observation in Fig. 10 is the smooth oscillation of the I− signal where it slowly increases between 100 and 300 ps and decays between 300 and 600 ps, a time interval where the photodetachment probe is active. This behaviour is likely associated with rotation of the I+⋯I− ion-pair. The very polarisable electron cloud of I− is certainly stretched along the I+⋯I− axis, which is promoted as an alignment axis of the photodetachment transition moment. The observed behaviour therefore appears as a rotational recurrence after the rotation momentum of I2 has been aligned by the pump pulse excitation in the
940 cm−1 = 3.71 eV. It is larger than the electronic affinity of atomic iodine (−3.059 eV) and probe photons can photodetach the electron of I− and therefore deplete the I− signal, even at large I+⋯I− separation when I− is quasi-free. An important observation in Fig. 10 is the smooth oscillation of the I− signal where it slowly increases between 100 and 300 ps and decays between 300 and 600 ps, a time interval where the photodetachment probe is active. This behaviour is likely associated with rotation of the I+⋯I− ion-pair. The very polarisable electron cloud of I− is certainly stretched along the I+⋯I− axis, which is promoted as an alignment axis of the photodetachment transition moment. The observed behaviour therefore appears as a rotational recurrence after the rotation momentum of I2 has been aligned by the pump pulse excitation in the 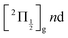 series (n > 20). The signal decay between 300 and 600 ps is 100 ps slower than its rise between 100 and 300 ps. This may be due to the slower and slower rotation of I2 as the I+⋯I− separation increases.
series (n > 20). The signal decay between 300 and 600 ps is 100 ps slower than its rise between 100 and 300 ps. This may be due to the slower and slower rotation of I2 as the I+⋯I− separation increases.
5.5 Formation dynamics of the atomic Rydberg states
Time constant τB describes a slow dissociation. Depending on which photoelectron band or which I+ ROI (C2, C4 or C5) is observed, τB has not exactly the same value. This is not surprising however. Ionisation by the probe is not active at the same I–I distance when forming these bands and ROIs. The important point is that their approximate value, >7 ps (see Table 1), matches that encountered in the section above for dissociation along first tier IP states (>10 ps). Photoelectron bands HE1, HE2, HE3 are sensitive to this probe process only. Strikingly, this time constant is consistent with the time delay observed in Fig. 6 to access the plateau in ROI C1′. The later ROI is associated with detection of the atomic Rydberg I*((3P1)6s2[1]3/2).
An additional contribution with faster dynamics (time constant τA) is present in the photoelectron bands LE1, LE2, and LE3 and in ROIs C2, C4 and C5 of I+. It likely reflects dynamics to access the molecular states where dissociation towards atomic Rydberg states occurs. This perspective is actually similar to that encountered above when discussing access to dissociation along first tier IP dissociation. The diversity of τA values in Table 1 reflects the complexity of the wavepacket motion over several molecular curves of various electronic configuration prior to final access to the molecular Rydberg curves where the dissociation proceeds.
5.6 Dynamics along energetically closed ion-pair channels
This observation must be brought together with an observation of von Vangerow et al. in a similar experiment.4 These authors showed that direct energy transfer from the initial Rydberg wavepacket to dissociation along first tier IP states is in competition with non-adiabatic transfer to energetically closed ion-pair channels of the second and third tier. An oscillation regime appears within the well of these states. It was documented by von Vangerow et al. when observing I+ ions of almost zero KER being produced by photodetachment at the outer turning point of the oscillation. This information is contained in ROI C1′ in the present 269/807 nm experiment. In Sections 5.2 and 5.3 we outlined the ROI C1′ reflects both the photodetachment probe that is under discussion here and the access to the molecular Rydberg state I*((3P1)6s2[1]3/2), which is associated with a monotonic increase of the corresponding probe signal. The important aspect of ROI C1′ in the perspective of the present discussion is therefore the structured part of its dependence with the pump/probe time delay in Fig. 6. As expected, this intensity variation is fully comparable to that reported in Fig. 5 of ref. 4: a first maximum at a 4–6 ps pump/probe delay is followed by a single, severely damped revival near 9–13 ps. The damping time of the oscillation cannot be determined accurately with a single clear revival. Nevertheless, a value of ≈8 ps was proposed in ref. 4 and assigned to the lifetime of the wavepacket within second tier IP states. This interpretation applies to the present work also, bringing the picture that a fraction of the wavepacket transfers to second tier IP states, where it makes a single round-trip. Since first and second tier IP curves do not cross, no direct transfer of the wavepacket is possible between IP states. Mediation by intermediate Rydberg states is necessary.
5.7 Direct probing of wavepacket motion along ion-pair curves
When the wavepacket is moving along IP potential energy curves, we have seen that the probe acts by photodetachment from the I− moiety. With the nomenclature of Section 5.3, this corresponds to observation of I+ ions with ROIs C1′ when the photodetachment acts as an outer turning point of oscillations within second tier IP states, and ROI C3′ when it acts along first tier IP curves. The present section does not limit the discussion to these very special situations.The photodetachment probe projects the wavepacket on potential energy curves which have a very different shape from those where the wavepacket was moving before the probe. In other words, the probe pulse deviates the wavepacket from IP potential curves to ionic curves of very different shape. When the wavepacket has reached large I–I separations, the I+–I potential onto which the wavepacket is projected is essentially flat. The I+ KER in fs-TKERS spectra is therefore equal to the intramolecular kinetic energy in the ion-pair states at the moment of photodetachment. The latter varies as a function of the pump–probe time delay. We thus expect bands in fs-TKERS whose central energy moves as the pump/probe delay varies. The same phenomenon may appear when the wavepacket is probed at smaller I–I separations when the I+–I potential is not flat. Quantitative interpretation is simply a bit more difficult and necessitates going through MD simulations as reported below. Moving bands as those just anticipated are observed in Fig. 5 (269/807 nm experiment) and Fig. 9 (266/334 nm experiment). A similar moving band has also been reported in ref. 4.
5.8 Information carried by MD calculations
To account for the moving bands just mentionned in the KER spectra of Fig. 5 and 9, MD simulations were run separately on each IP potential energy curves of the first, second and third tier. Calculation started at τ = 0 with initial conditions representing the wavepacket launched in the Franck–Condon region of excitation. The initial potential energy along an IP curve is set equal to the energy provided by the two-pump-photon excitation. In practice, the I–I distance at τ = 0 is adjusted so that the calculation is started with no initial kinetic energy along the potential energy curve. MD calculations are stopped at time delay τ. This mimics a photodetachment probe where neither the interatomic distance, nor the intramolecular kinetic energy are changed. Depending on the I–I distance where the probe process occurs, one, two or three probe photons are necessary. The excess energy of the probe photon(s) goes into the photoelectron kinetic energy, not in the I+ KER which stays therefore the same, whatever the number of probe photons. When the probe acts near the equilibrium distance of the molecular ion, the photodetachment may produce I2+ + e−. Otherwise it produces I+ + I + e−. In the latter case, the energy balance between intramolecular kinetic energy and potential energy of the newly formed I+–I pair is equal to the KER of the I+ ion after dissociation of the I+–I pair. This simulates a KER spectrum as a function of τ, which can be compared to experiment. To mimic the finite time of the probe pulse, Gaussian broadening of 60 fs width is included in the calculation. For the energy resolution, a Gaussian broadening of the pump energy is modelled by the calculation of 51 trajectories sampled within ±2σ (fwhm of 50 meV) around the mean energy. The transparency of the corresponding trajectories is weighted by the relative intensity associated.These MD calculations implicitly assume that the IP curves are neither coupled together, nor coupled to the molecular Rydberg curves they cross. Moreover, the calculations assume that the IP curves are accessed with no time delay after the pump pulse. All channels are calculated with the same population. Although these assumptions, especially the latter one, are apparently drastic, the discussion below outlines the simulations are helpful to clarify the access dynamics to second and third tier IP curves.
Simulation of the 269/807 nm experiment is shown in Fig. 12. A first striking correspondence is found between the predicted electron energies at time τ = 0 ps and the experiment reported in Fig. 7. Narrow bands near 0.7, 0.9 1.05 and 1.3 eV are observed in Fig. 7 during a short time after τ = 0 ps. They find a correspondence near τ = 0 ps in Fig. 12. The band near 0.7 eV is especially intense. It is documented with label Dec1 in Fig. 8 and Table 1. In the calculation, it corresponds to single photon photodetachment forming I2+ + e− from a second tier IP curve. Its observation in the experiment is an indication that this state was populated directly by the pump laser, presumably because the Franck–Condon region of excitation overlaped coupling zones between this second tier IP state and Rydberg states that carry the oscillator strength for ionisation.
A second striking correspondence is found between the second tier MD prediction and the experiment when observing the moving I+ band that is clearly visible in the bottom panel of Fig. 5 compared to the top right panel of Fig. 12. This correspondence concerns both the energy location and the τ-dependence. The centre energy of the band decays indeed from ≈0.4 eV to almost 0 eV when the pump–probe time delay varies between 0.5 ps and 2 ps. The agreement on the τ-dependence is particularly striking. This suggests that the wavepacket motion, which is probed on second tier IP curves, is actually accessed with no time delay after the pump pulse. This observation is qualitatively different from the comparison between the first tier MD prediction (monotonically decreasing curve in Fig. 12, top left panel) and the corresponding moving band in Fig. 5. The latter is barely visible in the top panel of Fig. 5 between 0.3 eV at 5 ps and 0.13 eV above 15 ps. The very unfavourable experimental signal/noise ratio is partly due to the diffuse character of the band, likely because first tier IP curves are not accessed directly from the pump laser excitation. We already know that an initial dynamics is at play to access these curves, resulting in a temporal broadening (see Section 5.4). Apparently, this is not the case for the access to second tier IP curves, suggesting that the initial wavepacket is partly built on second tier IP curves. We came to this conclusion already in the paragraph above. It is consistent with Fig. 1, given uncertainties on the exact location of coupling regions between molecular Rydberg and second tier IP curves in the Franck–Condon region of excitation.
Simulation of the 266/334 nm experiment is reported in Fig. 13. The energy location and τ-dependence of the curves associated with motion in the second and third tier match the moving bands, which are clearly observed experimentally in the middle panel of Fig. 9 for isotropically distributed I+ and in Fig. 11 for non-isotropically distributed ions. The moving band associated with motion within third tier states looks like a parabola with minimum near 0.9 ps. The central energy of that associated with second tier motion decays from 0.2 eV near 1.1 ps down to almost 0 eV above 3.5 ps. The interpretation done above for the 269/807 nm experiment is used again. Accordingly, the quantitative agreement that has just been mentioned between experiment and MD-predictions for motion within second and third tier IP states indicates that these states are accessed with no temporal delay after the pump pulse. Hence, the initial wavepacket of the 266/334 nm experiment likely includes states of the second and third tier. No state of the third tier appeared above in the 269/807 nm experiment. This difference between the 266/334 nm and the 269/807 nm experiment is not surprising given the Franck–Condon regions of excitation shown in Fig. 1. Only that of the 266/334 nm experiment overlaps a third tier IP curve.
 | ||
| Fig. 13 Same caption as Fig. 12 for the 266/334 nm experiment except the probe acts with one (blue) or two (red) photons. | ||
Upon close look at Fig. 9 (isotropically distributed I+) and especially at Fig. 11 (non-isotropically distributed I+), the moving band associated with motion within third tier IP states appears three times successively with maxima near 0.5, 1.3 and 2.2 ps. This reveals an oscillation regime within the well of third tier states as predicted by MD simulations in Fig. 13. The third oscillation is close to the noise, indicating efficient damping of the oscillation regime. Broadening of the wavepacket and leak of the wavepacket to other potential energy curves are likely at play. Both are consistent with the existence of energetically accessible coupling area between molecular Rydberg and IP curves, making them anharmonic.
It is interesting to observe that the moving bands associated with motion in the second and third tier in Fig. 9 and 11 originate from recurrences of over-intensity in the I+ cation signal at KER ≈ 0.2 eV. The latter are interpreted in Section 5.4 as vibrational recurrences within the well of Rydberg states excited by the pump laser. This observation is consistent with a point that appeared several times above: the initial wavepacket is split over states of different dominant electronic configurations, either Rydberg or IP. It further evolves along these state where it looses coherence.
6 Conclusion
Real-time dynamics of vibrationally and electronically excited I2 molecules has been investigated experimentally using the pump–probe technique in a setup that associates femtosecond lasers, a molecular beam and a Velocity Map Imaging (VMI) spectrometer. The pump laser excites I2 in a two photon process from ground state to a region where molecular Rydberg states are coupled with I+I− ion-pair (IP) states. The probe laser acts either by photodetachment from I− or by photoionization of molecular Rydberg states. The VMI allows detection of the energy spectrum and angular distribution of photoelectrons, I+ cations and I− anions in independent experiments (no coincidence) as a function of the pump–probe time delay. Femtosecond-time resolved photo electron spectroscopy (fs-TRPES) is performed with the VMI tuned to photoelectron detection, and femtosecond-time resolved kinetic energy release spectroscopy (fs-TRKERS) when the VMI is tuned to I+ or I− ions.Two pump/probe schemes, 269/807 nm and 266/334 nm have been used. The Franck–Condon region of excitation of the 269/807 nm experiment overlaps a limited number of Rydberg states of gerade symmetry (4 states of Rydberg series converging to the 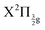 and
and 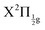 states of the I2+ molecular ion). That of the other experiment overlaps many molecular Rydberg states converging to
states of the I2+ molecular ion). That of the other experiment overlaps many molecular Rydberg states converging to 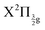 . In both experiments, the Franck–Condon region of excitation is crossed by ion-pair states of the second tier (269/807 nm experiment) and of the second and third tiers (266/334 nm experiment). The corresponding IP curves are therefore coupled to the molecular Rydberg states present in the Franck–Condon region of excitation and borrow their oscillator strength. The initial wavepacket is therefore built as coherent superposition of both on molecular Rydberg and IP states.
. In both experiments, the Franck–Condon region of excitation is crossed by ion-pair states of the second tier (269/807 nm experiment) and of the second and third tiers (266/334 nm experiment). The corresponding IP curves are therefore coupled to the molecular Rydberg states present in the Franck–Condon region of excitation and borrow their oscillator strength. The initial wavepacket is therefore built as coherent superposition of both on molecular Rydberg and IP states.
The present work reveals a complex dynamics where the initial wavepacket splits and moves within several ion-pair and molecular Rydberg states. The final step of the wavepacket evolution is dissociation as a first tier ion-pair I+ + I− (the two ions are in their ground electronic state) or as a neutral pair I + I** where I** is an atomic Rydberg state. The information stems essentially from considerations on KERs of I+ and I− (fs-TRKERS). Probing the wavepacket motion along IP curves was of special interest because it leads to the observation of KER bands whose central energy changes as a function of the pump–probe time delay. Importantly, the position of these bands and their time-delay dependence could be reproduced quantitatively by molecular dynamics calculations. This appeared as clear evidence that the initial wavepacket has a double Rydberg and ion-pair character.
The photoelectron spectra (fs-TRPES) have not been used in the present work as readily as we might have imagined. In non-coincidence experiments, processes that are well identified by specific features in KER spectra of ions are mixed together in photoelectron spectra. This was not a real difficulty here for documenting exit channels where an atomic Rydberg state is formed. These channels were readily identified by the photoelectron energy. Given a diatomic molecule was considered, a single vibrational degree of freedom was present and unravelling photoelectron spectra was easy. In complex situations where several vibrational degrees of freedom are at play, a full experimental understanding of the dynamics would largely benefit from a double coincidence approach where the energy and angular distribution of the photoelectrons is correlated with the same information on cations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors warmly thank Ch. Lefumeux for the management of the laser beamline and all the engineers and technicians taking care daily of the Lab's infrastructure. For the purpose of Open Access, a CC-BY public copyright licence has been applied by the authors to the present document and will be applied to all subsequent versions up to the Author Accepted Manuscript arising from this submission.Notes and references
- R. M. Bowman, M. Dantus and A. H. Zewail, Chem. Phys. Lett., 1989, 161, 297–302 CrossRef CAS.
- I. Fisher, M. J. J. Vrakking, D. M. Villeneuve and A. Stolow, Chem. Phys., 1996, 207, 331–354 CrossRef.
- A. S. Bogomolov, B. Gruner, S. A. Kochubei, M. Mudrich and A. V. Baklanov, J. Chem. Phys., 2014, 140, 124311 CrossRef PubMed.
- J. von Vangerow, A. S. Bogomolov, N. V. Dozmorov, D. Schomas, F. Stienkemeier, A. V. Baklanov and M. Mudrich, Phys. Chem. Chem. Phys., 2016, 18, 18896–18904 RSC.
- K. Matthasson, Á. Kvaran, G. A. Garcia, P. Weidner and B. Sztáray, Phys. Chem. Chem. Phys., 2022, 24, 17569–17576 RSC.
- R. S. Mulliken, J. Chem. Phys., 1971, 55, 288–309 CrossRef CAS.
- P. J. Jewsbury, T. Ridley, K. P. Lawley and R. J. Donovan, J. Mol. Spectrosc., 1993, 157, 33–49 CrossRef CAS.
- V. A. Alekseev, Opt. Spectrosc., 2014, 116, 329–336 CrossRef CAS.
- T. Ridley, D. A. Beattie, M. C. R. Cockett, K. P. Lawley and R. J. Donovan, Phys. Chem. Chem. Phys., 2002, 4, 1398–1411 RSC.
- L.-H. Deng, Y.-Y. Zhu, C.-L. Li and Y.-Q. Chen, J. Chem. Phys., 2012, 137, 054308 CrossRef PubMed.
- A. Lietard, G. Piani, L. Poisson, B. Soep, J.-M. Mestdagh, S. Alose, A. Perrier, D. Jacquemin and M. Takeshita, Phys. Chem. Chem. Phys., 2014, 16, 22262–22272 RSC.
- A. Stolow, Annu. Rev. Phys. Chem., 2003, 54, 89–119 CrossRef CAS PubMed.
- A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719–1757 CrossRef CAS PubMed.
- G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996 CrossRef CAS.
- A. V. Baklanov, L. M. C. Janssen, D. H. Parker, L. Poisson, B. Soep, J.-M. Mestdagh and O. Gobert, J. Chem. Phys., 2008, 129, 214306 CrossRef PubMed.
- R. J. Donovan, R. V. Flood, K. P. Lawley, A. J. Yencha and T. Ridley, Chem. Phys., 1992, 164, 439–450 CrossRef CAS.
- L. Verlet, Phys. Rev. A, 1967, 25, 978 Search PubMed.
- A. Masson, M.-C. Heitz, J.-M. Mestdagh, M.-A. Gaveau, L. Poisson and F. Spiegelman, Phys. Rev. Lett., 2014, 113, 123005 CrossRef CAS PubMed.
- R. J. Peláez, C. Blondel, C. Delsart and C. Drag, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 125001 CrossRef.
- E. Reinhold and W. Ubachs, Mol. Phys., 2005, 103, 1329–1352 CrossRef CAS.
- S. Mollet and F. Merkt, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 032510 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00118d |
| This journal is © the Owner Societies 2024 |