Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stimulated radiative association of sodium and chlorine atoms and their ions in a coupled channel treatment†
Martina
Šimsová née Zámečníková
 *ab,
Magnus
Gustafsson
*ab,
Magnus
Gustafsson
 a,
Gunnar
Nyman
a,
Gunnar
Nyman
 b and
Pavel
Soldán
b and
Pavel
Soldán
 c
c
aDepartment of Engineering Sciences and Mathematics, Division of Materials Science, Applied Physics, Luleå University of Technology, 971 87 Luleå, Sweden
bDepartment of Chemistry and Molecular Biology, University of Gothenburg, Box 462, 405 30 Gothenburg, Sweden. E-mail: martina.simsova@proton.me
cDepartment of Chemical Physics and Optics, Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague 2, Czech Republic
First published on 4th January 2024
Abstract
In an extension of previous work (Šimsová et al., Phys. Chem. Chem. Phys., 2022, 24, 25250), we study stimulated radiative association of sodium chloride (NaCl) in an environment with a black body radiation. Colliding neutral (Na and Cl) and ionic (Na+ and Cl−) fragments are considered. The coupling between the diabatic ionic and neutral channels is accounted for. The cross sections are computed and resolved on the vibrational states of the formed NaCl molecule for detailed analysis. The thermal rate coefficients for neutral colliding fragments at kinetic temperatures, T, from 1 K to 5300 K are computed for use in astrochemical modelling. The total rate coefficient is affected by more than one order of magnitude by stimulated emission from a blackbody radiator of temperature Tb = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. The effect from stimulated emission is largest for the lowest kinetic temperatures, where Tb of a few thousand kelvins has a significant effect. The rate coefficient for the colliding ionic fragments is calculated from 80 K to 3615 K. The blackbody radiation has little effect on this process.
000 K. The effect from stimulated emission is largest for the lowest kinetic temperatures, where Tb of a few thousand kelvins has a significant effect. The rate coefficient for the colliding ionic fragments is calculated from 80 K to 3615 K. The blackbody radiation has little effect on this process.
1 Introduction
Expanding circumstellar nebulae are an important part of the interstellar medium. They are formed by materials ejected from stars, and they essentially work as giant space chemical laboratories, where molecules and dust are formed and destroyed. Their environment can be very dynamic with shocks, winds and high-speed outflows, and there is the stellar and interstellar radiation always being present; even when the stellar radiation is absorbed by an optically thick circumstellar dust shell it is often re-radiated at longer wavelengths.Sodium and potassium chlorides (NaCl and KCl) have been detected several times in the interstellar medium. They were observed in the nebulae surrounding carbon-rich stars CW Leonis1,2 and V1610 Cygnus3 and also oxygen-rich stars VY Canis Majoris,4 IK Tauri,5 and QX Puppis,6 where the corresponding central objects are stars in their asymptotic giant branch7 (AGB) or post-AGB8 evolution stages. However, fairly recently, NaCl was also observed in the protostellar disk around the young accreting high-mass star Orion Src I.9
The process of radiative association belongs to the important chemical processes responsible for molecule formations in the circumstellar nebulae.10 While the experimental investigations of radiative association are very difficult,11 the theoretical studies have been plentiful in the last decades.12–25 Little is known about the formation of NaCl.26 In our previous work, making use of the detailed diabatic picture with coupling, we studied the spontaneous radiative association to form NaCl27–29 and also the non-radiative charge transfer, i.e., chemiionisation and mutual neutralisation.29 However, the ever-present radiation field provides a permanent source of radiation which by stimulating the radiative processes could significantly enhance the corresponding rates.10 For example, in the case of radiative association the rate coefficients could be increased even by factors of 100 to 1000 in the low temperature regions.30–38 That is why, in this work, we study the stimulated radiative association of NaCl, specifically the processes
| 1Σ+[Na(2S) + Cl(2P)] + ħωb → NaCl(1Σ+) +ħωb + ħω, U1 → U2, | (1) |
| A1Π[Na(2S) + Cl(2P)] + ħωb → NaCl(X1Σ+) +ħωb + ħω, A → X, | (2) |
| 1Σ+[Na+(1S) + Cl−(1S)] + ħωb → NaCl(1Σ+) +ħωb + ħω, U2 → U2. | (3) |
Process (1) and process (2) are collisional processes of the same reactants (neutral sodium and chlorine atoms in their atomic ground electronic states), however, in different molecular symmetries. While the molecular state of the reactants in process (1) is in the 1Σ+ symmetry, the molecular state of the reactants in process (2) is in the 1Π symmetry. As process (1) here is treated in the diabatic representation (in the coupled channel treatment), we will simply denote the initial and final electronic states as U1 and U2. Since process (2) is treated conventionally (uncoupled solution of the radial nuclear Schrödinger equation), we will denote the initial and final electronic states as is customary in the Born–Oppenheimer approximation: A and X. Finally, process (3) is a collisional process of a sodium cation and a chloride anion in their atomic ground electronic states. The molecular state of the reactants in process (3) is in the 1Σ+ symmetry, so in the diabatic representation the initial and final electronic state is U2. The products of processes (1)–(3) are the same, concretely sodium chloride in the lowest electronic state of the 1Σ+ symmetry. Notice that during process (2), the molecular electronic angular momentum is changed. Potential energy curves in the diabatic representation of processes (1) and (3) are illustrated in the left-hand panel of Fig. 1 together with their diabatic coupling. Potential energy curves in the adiabatic representation (in the Born–Oppenheimer approximation) of process (2) are illustrated in the right-hand panel of Fig. 1.
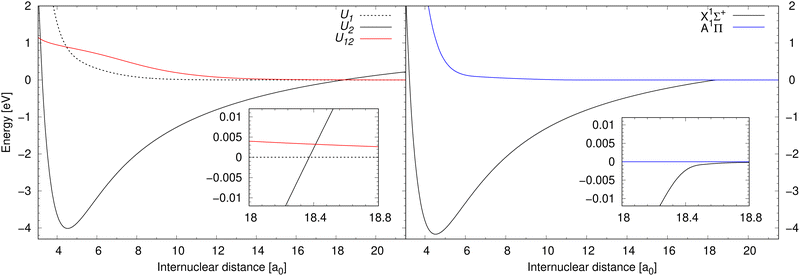 | ||
| Fig. 1 Left panel: Potential energy curves for the electronic states U1 and U2 of 1Σ+ symmetry in the diabatic representation between which processes (1) and (3) are calculated are illustrated together with their diabatic coupling U12. Right panel: Illustrates potential energy curves for the electronic states A and X of 1Π and 1Σ+ symmetry, respectively, in the adiabatic representation, between which process (2) is calculated. The data for the 1Σ+ symmetry are taken from Giese & York,39 and the data for the A1Π state are taken from Zeiri & Balint-Kurti.40 | ||
2 Methods
The same ab initio data39,40 are used as in our previous work on NaCl.27–29 The potential energy curves for the two lowest 1Σ+ electronic states of NaCl in the diabatic representation are illustrated in Fig. 2.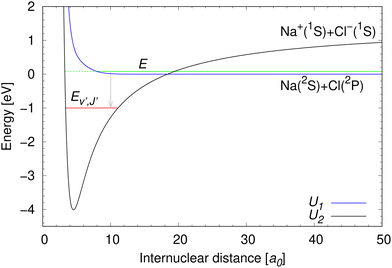 | ||
| Fig. 2 Potential energy curves of the two lowest 1Σ+ diabatic electronic states of NaCl.39 The meaning of collision energy E, energy of final bound ro-vibrational states Ev′,J′, and the dissociation limits of the diabatic U1(R) and U2(R) potential energy curves are illustrated. The initial state lives on both diabatic electronic states, which is indicated by the green full and dashed lines. | ||
2.1 Rate coefficients and cross sections
The rate coefficients for formation of a molecule with the reduced mass μ by stimulated radiative association at temperature T is determined by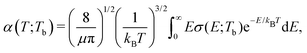 | (4) |
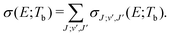 | (5) |
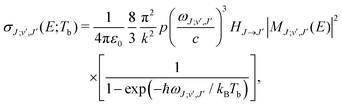 | (6) |
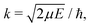 c is the speed of light and HJ→J′ are the Hönl-London factors (obviously, only final states v′, J′, for which HJ→J′ ≠ 0 are eligible for radiative association from the initial state E, J). The probabilities p of approach in the initial channel are 1/12 for process (1), 1/6 for process (2), and 1 for process (3). ωJ;v′,J′(E) is the emitted photon angular frequency, ħωJ;v′,J′(E) = E − Ev′,J′, where E > 0 and Ev′,J′ < 0 are taken with respect to the neutral dissociation limit. MJ;v′,J′(E) is the dipole-moment matrix element between the wavefunction of the initial continuum state and the wavefunction of the final bound state. The corresponding wavefunctions are obtained in the same manner as in our studies of spontaneous radiative association,27–29i.e. within the coupled diabatic picture for processes (1) and (3), and within the adiabatic approximation for process (2).
c is the speed of light and HJ→J′ are the Hönl-London factors (obviously, only final states v′, J′, for which HJ→J′ ≠ 0 are eligible for radiative association from the initial state E, J). The probabilities p of approach in the initial channel are 1/12 for process (1), 1/6 for process (2), and 1 for process (3). ωJ;v′,J′(E) is the emitted photon angular frequency, ħωJ;v′,J′(E) = E − Ev′,J′, where E > 0 and Ev′,J′ < 0 are taken with respect to the neutral dissociation limit. MJ;v′,J′(E) is the dipole-moment matrix element between the wavefunction of the initial continuum state and the wavefunction of the final bound state. The corresponding wavefunctions are obtained in the same manner as in our studies of spontaneous radiative association,27–29i.e. within the coupled diabatic picture for processes (1) and (3), and within the adiabatic approximation for process (2).
2.2 Numerical details
The cross sections for radiative association for processes (1), (2), and (3) were calculated from 10−5 eV up to 10 eV for background temperatures: 50 K, 100 K, 150 K, 200 K, 500 K, 750 K, 1000 K, 2000 K, 3000 K, 4000 K, 5000 K, 7500 K, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, 25
000 K, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, and 50
000 K, and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. The spontaneous emission case (Tb = 0 K) was calculated in previous studies.27–29 Similarly as in those studies, processes (1) and (3) were treated by non-adiabatic dynamics, while process (2) was treated by conventional perturbation theory. For process (1), the same input parameters (minimum and maximum internuclear distances for both the bound and continuum wavefunction calculations, including the radial step, and maximum rotational quantum number) as previously27–29 were used for collision energies from 0.03 eV and up, for all background temperatures. Only at low collision energies, where the effect of background temperature is profound, did we increase the included rotational quantum numbers and consequently also the maximum internuclear distance for the Numerov method. Concretely, for process (1), we set Jmax = 20 and Rmax = 45a0 up to 10−4 eV, Jmax = 23, 30, 40 up to 0.0004 eV, 0.0007 eV, and 0.001 eV, respectively, with Rmax = 23a0. Rmax = 23a0 was used up to 0.03 eV with the same Jmax as by Gustafsson.27 Lastly, the same energy grid as before27–29 suffices for rate-coefficient convergence. For process (2), the convergence was achieved by the same input parameters as previously.27–29 For process (3), much lower maximum internuclear distance, 23a0 up to 4.6 eV and 30a0 above, was used here in comparison with Šimsová née Zámečníková et al.29 as there we simultaneously calculated non-radiative continuum-continuum processes for which large internuclear distances are needed in solving the radial Schrödinger equation.
000 K. The spontaneous emission case (Tb = 0 K) was calculated in previous studies.27–29 Similarly as in those studies, processes (1) and (3) were treated by non-adiabatic dynamics, while process (2) was treated by conventional perturbation theory. For process (1), the same input parameters (minimum and maximum internuclear distances for both the bound and continuum wavefunction calculations, including the radial step, and maximum rotational quantum number) as previously27–29 were used for collision energies from 0.03 eV and up, for all background temperatures. Only at low collision energies, where the effect of background temperature is profound, did we increase the included rotational quantum numbers and consequently also the maximum internuclear distance for the Numerov method. Concretely, for process (1), we set Jmax = 20 and Rmax = 45a0 up to 10−4 eV, Jmax = 23, 30, 40 up to 0.0004 eV, 0.0007 eV, and 0.001 eV, respectively, with Rmax = 23a0. Rmax = 23a0 was used up to 0.03 eV with the same Jmax as by Gustafsson.27 Lastly, the same energy grid as before27–29 suffices for rate-coefficient convergence. For process (2), the convergence was achieved by the same input parameters as previously.27–29 For process (3), much lower maximum internuclear distance, 23a0 up to 4.6 eV and 30a0 above, was used here in comparison with Šimsová née Zámečníková et al.29 as there we simultaneously calculated non-radiative continuum-continuum processes for which large internuclear distances are needed in solving the radial Schrödinger equation.
3 Results and discussion
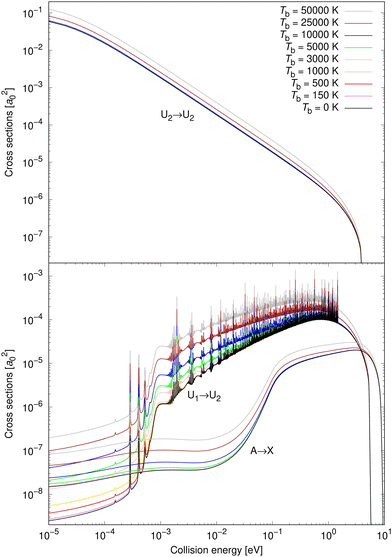
Cross sections are illustrated in Fig. 3 for eight non-zero background temperatures and compared to the spontaneous emission. The recalculated cross section for Tb = 0 K coincides with the spontaneous emission obtained by Gustafsson,27 Šimsová-Zámečníková et al.28 and Šimsová née Zámečníková et al.29 Typically, the higher the background temperature, the larger the cross sections become.30–32,35,36 Also, the effect is most noticeable at low collision energies and becomes insignificant at large collision energies.As the energy surpasses the opening of the ionic scattering channel, at 1.4845 eV, the resonances for process (1) cease. This can be understood since there are (by definition) no bound states on the ionic potential, U2, at those energies. Bound states on the U2 potential are those that give rise to Fano-Feshbach resonances when the non-adiabatic coupling is accounted for. Furthermore, no shape (orbiting) resonances are supported above the 1.4845 eV threshold either. Shape resonances would appear if the effective ionic potential had a barrier peaking above 1.4845 eV, which would permit quasibound states. There is, however, no such barrier. The reason is that the ionic potential is attractive with a 1/R dependence while the repulsive centrifugal potential has a 1/R2 dependence. Since the attractive term falls off more slowly than the repulsive, a centrifugal barrier cannot form.
In the top panel of Fig. 3, the cross sections for process (3) are illustrated for the same set of background temperatures as for process (1) and process (2). The background enhances the radiative association and is most easily seen for the higher background temperatures. The enhancement becomes less significant as the collision energy increases.
Vibrationally resolved cross sections were calculated for process (1) for chosen vibrational quantum levels of the target electronic state: v′ = 0, 1, 2, 25, 50, 75, 100, 125, 150, 175, 200, and 221, with the last one being the highest vibrational level of the U2 diabatic state below the energetic asymptotic limit of the neutral atoms. These calculations were performed for all studied background temperatures and for the spontaneous emission. In Fig. 4, some of these vibrationally resolved cross sections are compared for Tb = 0 and 3000 K. The total cross sections for these processes are also illustrated in Fig. 4.
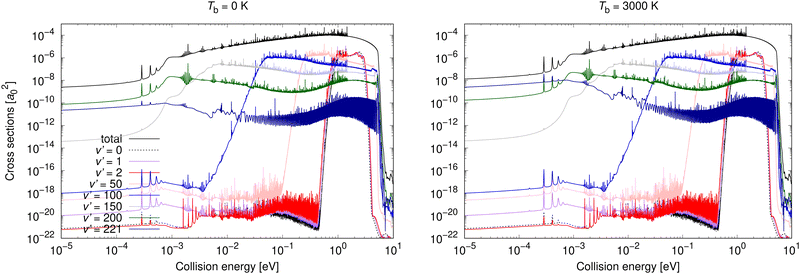 | ||
| Fig. 4 Radiative association vibrationally resolved cross sections obtained allowing for non-adiabatic dynamics for process (1) for two background temperatures: 0 K and 3000 K. | ||
From Fig. 4 it can be seen that at low collision energies the lowest vibrational levels do not contribute much to the cross sections for either of the shown background temperatures. The order of the importance of the vibrationally resolved cross sections depends on the background temperature. In particular, at low collision energies, transitions to v′ = 221 are less important at Tb = 0 K than at Tb = 3000 K, where this level contributes most of all levels to the total cross section. With increasing collision energy, the importance of lower vibrational levels increases. Typically many levels contribute significantly to the total cross section. The vibrationally resolved cross sections at all studied background temperatures are illustrated in the ESI.†
Vibrationally resolved cross sections were calculated also for process (2) for almost the same chosen vibrational levels of the target electronic state: 0, 1, 2, 25, 50, 75, 100, 125, 150, 175, 200. Some of them are illustrated for Tb = 0 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K in Fig. 5.
000 K in Fig. 5.
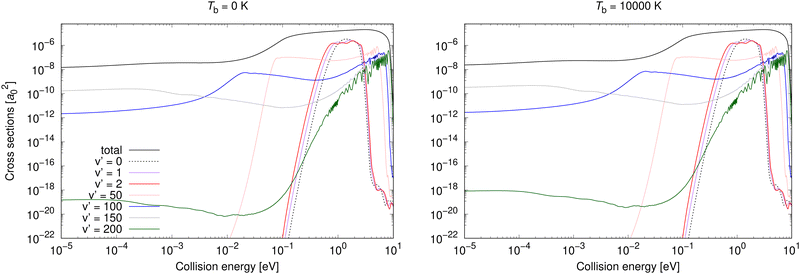 | ||
Fig. 5 Radiative association vibrationally resolved cross sections for process (2) for two background temperatures, 0 K and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. 000 K. | ||
Neither transitions to the lowest, nor to the highest, vibrational levels contribute significantly at low collision energies, which is valid for both shown background temperatures. This is different from process (1), where the highest vibrational level contributes more at both background temperatures, and the most at Tb = 3000 K. At higher collision energies, transitions to all vibrational levels contribute more similarly to the total cross section. The vibrationally resolved cross sections at all studied background temperatures are illustrated in the ESI.†
Gustafsson27 and Šimsová-Zámečníková et al.28 showed that the uncoupled solution for radiative association of Na(2S) and Cl(2P) in the Σ+-symmetry vastly underestimates the correct cross sections. Therefore, we did not study stimulated emission in that way here. However, we did calculate vibrationally resolved cross sections, which can be compared to the non-adiabatically obtained ones. These results are in the ESI,† for energies up to 0.03 eV.
Non-adiabatic vibrationally resolved cross sections for Tb = 0 K and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K for process (3) are illustrated in Fig. 6. As expected from the total cross sections from the top panel of Fig. 3, the vibrationally resolved cross sections for these background temperatures do not differ much between these background temperatures. The vibrationally resolved cross sections at other studied background temperatures are shown in the ESI,† where it can be seen that the order of importance of vibrational levels does not depend on the background temperature.
000 K for process (3) are illustrated in Fig. 6. As expected from the total cross sections from the top panel of Fig. 3, the vibrationally resolved cross sections for these background temperatures do not differ much between these background temperatures. The vibrationally resolved cross sections at other studied background temperatures are shown in the ESI,† where it can be seen that the order of importance of vibrational levels does not depend on the background temperature.
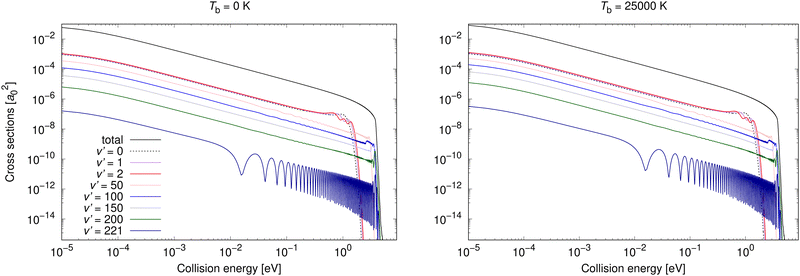 | ||
Fig. 6 Radiative association vibrationally resolved cross sections for process (3) calculated with non-adiabatic dynamics for two background temperatures, 0 K and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. 000 K. | ||
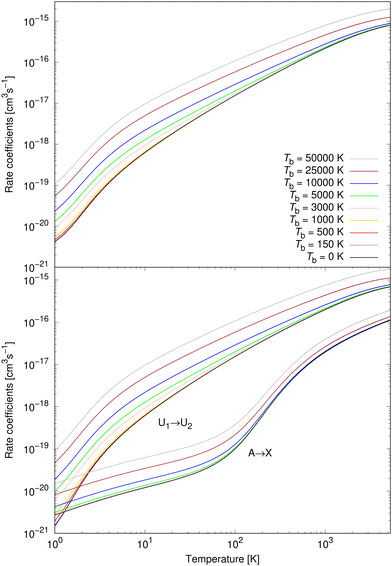
Rate coefficients for processes (1) and (2) were calculated from 1 K to 5300 K for all studied background temperatures. They are illustrated for nine background temperatures in the bottom panel of Fig. 7. Except for the very lowest temperatures, process (1) dominates over process (2), for all background temperatures. At background temperatures above about 1000 K, process (2) starts to be less efficient even at the lowest temperatures. Similarly as for cross sections, it can be seen that a non-zero background temperature enhances the rate coefficients; and the larger the background temperature is, the larger the enhancement is. The relative importance of a non-zero background temperature drops at larger temperatures.30–32,35–38
The total rate coefficient for formation of NaCl by radiative association of sodium and chlorine in their ground electronic states at several background temperatures were computed by summing the rate coefficients of processes (1) and (2). They are illustrated at chosen background temperatures in the top-panel of Fig. 7. Additionally, the total rate coefficients at several background temperatures were fitted to the Kooij function of the Arrhenius type
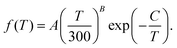 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, 25
000 K, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, and 50
000 K, and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. The fitting parameters for the total rate coefficients at background temperatures from 500 K to 7500 K are summarised in the ESI.†
000 K. The fitting parameters for the total rate coefficients at background temperatures from 500 K to 7500 K are summarised in the ESI.†
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, 25
000 K, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, and 50
000 K, and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K
000 K
| Process | T [K] | A [cm3 s−1] | B | C [K] |
|---|---|---|---|---|
T
b = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K 000 K |
||||
| x(−y) ≡ x × 10−y. | ||||
| RA Na + Cl | 1–1.675 | 1.9026(−12) | 3.48386 | −1.64608 |
| 1.675–2.3 | 1.5998(−14) | 2.34032 | 0.29014 | |
| 2.3–3.425 | 2.7916(−16) | 1.29542 | 2.68895 | |
| 3.425–11.25 | 6.8600(−17) | 0.89322 | 4.04831 | |
| 11.25–30 | 8.9452(−17) | 1.01184 | 2.63814 | |
| 30–80 | 9.0080(−17) | 1.00878 | 3.05820 | |
| 80–350 | 8.8920(−17) | 0.97253 | 5.90601 | |
| 350–750 | 9.7141(−17) | 0.90087 | 33.2892 | |
| 750–1400 | 1.2993(−16) | 0.75034 | 148.868 | |
| 1400–2400 | 2.3008(−16) | 0.52634 | 467.489 | |
| 2400–4000 | 5.3958(−16) | 0.25019 | 1137.98 | |
| 4000–5300 | 1.2069(−15) | 2.3396(−2) | 2010.80 | |
| RA Na++ Cl− | 80–500 | 1.4224(−16) | −0.50804 | 1.79631 |
| 500–1600 | 1.5036(−16) | −0.54326 | 21.1331 | |
| 1600–3615 | 1.8809(−16) | −0.62599 | 159.760 | |
T
b = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K 000 K |
||||
|---|---|---|---|---|
| RA Na + Cl | 1–1.675 | 3.4001(−12) | 3.41917 | −1.54738 |
| 1.675–2.3 | 3.1304(−14) | 2.29762 | 0.34958 | |
| 2.3–3.425 | 5.8098(−16) | 1.26849 | 2.71361 | |
| 3.425–11.25 | 1.3582(−16) | 0.85108 | 4.13555 | |
| 11.25–30 | 1.7021(−16) | 0.95308 | 2.89686 | |
| 30–80 | 1.6985(−16) | 0.94287 | 3.54081 | |
| 80–301 | 1.6724(−16) | 0.88484 | 8.54798 | |
| 301–740 | 1.8250(−16) | 0.80267 | 35.2174 | |
| 740–1400 | 2.4400(−16) | 0.64995 | 149.129 | |
| 1400–2400 | 4.1951(−16) | 0.43740 | 451.090 | |
| 2400–4000 | 9.6469(−16) | 0.16778 | 1106.95 | |
| 4000–5300 | 2.1678(−15) | −6.0313(−2) | 1985.02 | |
| RA Na++ Cl− | 80–480 | 1.8903(−16) | −0.51142 | 2.09036 |
| 480–1600 | 2.0263(−16) | −0.55634 | 26.0469 | |
| 1600–3615 | 2.6370(−16) | −0.65416 | 187.919 | |
T
b = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K 000 K |
||||
|---|---|---|---|---|
| RA Na + Cl | 1–1.675 | 6.0463(−12) | 3.39642 | −1.51413 |
| 1.675–2.3 | 5.7719(−14) | 2.28361 | 0.36746 | |
| 2.3–3.425 | 1.0930(−15) | 1.25964 | 2.72011 | |
| 3.425–11.25 | 2.5080(−16) | 0.83655 | 4.16533 | |
| 11.25–30 | 3.0949(−16) | 0.93202 | 2.99521 | |
| 30–80 | 3.0744(−16) | 0.91826 | 3.75081 | |
| 80–268 | 3.0215(−16) | 0.85341 | 9.32976 | |
| 268–676 | 3.2717(−16) | 0.76856 | 33.6494 | |
| 676–1400 | 4.3781(−16) | 0.60936 | 144.302 | |
| 1400–2400 | 7.6993(−16) | 0.38673 | 456.484 | |
| 2400–4000 | 1.7748(−15) | 0.11639 | 1114.63 | |
| 4000–5300 | 4.0480(−15) | −0.11588 | 2009.00 | |
| RA Na++ Cl− | 80–460 | 2.8797(−16) | −0.51330 | 2.23439 |
| 460–1499 | 3.0963(−16) | −0.56171 | 26.8042 | |
| 1499–2000 | 3.6014(−16) | −0.62258 | 107.663 | |
| 2000–3615 | 4.4126(−16) | −0.69081 | 255.751 | |
The rate coefficients for process (3) were calculated up to 3615 K as in Šimsová née Zámečníková et al.29 They are illustrated for several chosen temperatures in Fig. 8. As expected from the cross sections in the top panel of Fig. 3, the background radiation has little effect on the rate coefficients of process (3). The rate coefficients up to Tb = 5000 K coincide with the case where no blackbody radiation is present. Because of the lack of the effect, we summarise the fitting parameters to the Kooij function (7) for only Tb = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, 25
000 K, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, and 50
000 K, and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K.
000 K.
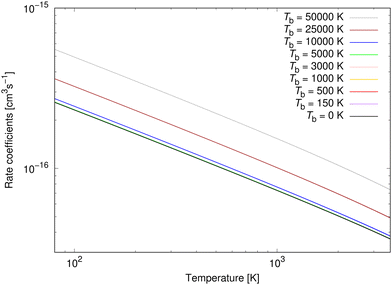 | ||
| Fig. 8 Radiative association rate coefficients for processes (3) at several background temperatures. | ||
4 Conclusions
We have computed stimulated radiative association cross sections and rate coefficients for the formation of NaCl molecules in their electronic ground state. We also present vibrationally resolved cross sections, i.e. for selected vibrational states of the formed molecule. The emission is stimulated by a blackbody radiation of temperature, Tb, which we vary from 0 to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. Overall the stimulated emission plays the biggest role at low collision energies, and at low kinetic temperatures, T.
000 K. Overall the stimulated emission plays the biggest role at low collision energies, and at low kinetic temperatures, T.
Two reactions for neutral colliding fragments, Na and Cl, are considered. One of them, process (1), involves non-adiabatic couplings and its cross section largely overshadows that of the other, process (2), except for at the lowest and the highest energies. For values of Tb of a few hundred kelvins, the cross section is only affected at energies below ∼1 meV. This is the energy above which non-adiabatic dynamics starts to play a big role,27 meaning that the emitted photons are higher in energy above 1 meV of collision energy. This can be seen in the vibrationally resolved cross section for process (1), where transitions to the highest vibrational states dominate below 1 meV. As can be seen in eqn (6), for stimulated emission to make a difference kBTb should be comparable to, or bigger than, the typical energy of the emitted photons.
The cross section for process (1) has pronounced resonances all the way up to a collision energy of 1.4845 eV, which is the threshold energy for the ionic channel. Due to the 1/R behaviour of the ionic state, there are no resonances above that energy (see Section 3). The other neutral reaction, process (2), has no resonances since the potential of the entrance state, A, is purely repulsive. Shape resonances, if present, have been observed to contribute to rate coefficients mainly at low temperatures.18 In the Born–Oppenheimer approximation there are only shape resonances. In the diabatic representation there are also Fano-Feshbach resonances. While shape resonances have only additive contributions to cross sections, the Fano-Feshbach resonances can have both additive and subtractive effects on cross sections and hence also on rate coefficients.
The third reaction, process (3), which corresponds to colliding ions, Na+ and Cl−, is also treated with non-adiabatic couplings. It is completely resonance free, since the entrance channel is open only above the ionic threshold. The same argument as for process (1) holds here. The corresponding rate coefficient falls off monotonically with increasing kinetic temperature, T, and it is significantly affected by stimulated emission only if the radiation temperature is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K or more.
000 K or more.
The total rate coefficient for colliding neutral atoms, Na and Cl, is affected by stimulated emission up to two orders of magnitude at the lowest kinetic temperatures, T, for the highest radiation temperatures, Tb. This is expected to be important in astrochemical modelling of environments with abundant radiation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The support of Kempestiftelserna (project no. SMK-2045) is greatly appreciated by MŠ and MG. The support of Knut and Alice Wallenberg Foundation (project no. KAW 2020.0081) is greatly appreciated by MŠ and GN. GN is grateful to the support of the Swedish Research Council grant 2020-05293. This research was conducted using the resources of High Performance Computing Center North (HPC2N). The computations and data handling were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) at HPC2N partially funded by the Swedish Research Council through grant agreement no. HPC2N 2023-028. Computational resources were provided by the e-INFRA CZ project (ID:90254), supported by the Ministry of Education, Youth and Sports of the Czech Republic.Notes and references
- J. Cernicharo and M. Guélin, Astron. Astrophys., 1987, 183, L10–L12 CAS.
- M. Agúndez, J. P. Fonfría, J. Cernicharo, C. Kahane, F. Daniel and M. Guélin, Astron. Astrophys., 2012, 543, A48 CrossRef.
- J. L. Highberger, K. J. Thomson, P. A. Young, D. Arnett and L. M. Ziurys, Astrophys. J., 2003, 593, 393–401 CrossRef CAS.
- L. M. Ziurys, S. N. Milam, A. J. Apponi and N. J. Woolf, Nature, 2007, 447, 1094–1097 CrossRef CAS PubMed.
- S. N. Milam, A. J. Apponi, N. J. Woolf and L. M. Ziurys, Astrophys. J., 2007, 668, L131–L134 CrossRef CAS.
- C. Sánchez Contreras, J. Alcolea, V. Bujarrabal and A. Castro-Carrizo, Astron. Astrophys., 2018, 618, A164 CrossRef PubMed.
- F. Herwig, Ann. Revue Astron. Astrophys., 2005, 43, 435–479 CrossRef CAS.
- H. Van Winckel, Ann. Revue Astron. Astrophys., 2003, 41, 391–427 CrossRef.
- A. Ginsburg, B. McGuire, R. Plambeck, J. Bally, C. Goddi and M. Wright, Astrophys. J., 2019, 872, 54 CrossRef CAS.
- A. E. Glassgold, Ann. Revue Astron. Astrophys., 1996, 34, 241–277 CrossRef CAS.
- D. Gerlich and S. Horning, Chem. Rev., 1992, 92, 1509–1539 CrossRef CAS.
- D. R. Bates, Mon. Not. R. Astron. Soc., 1951, 111, 303–314 CrossRef CAS.
- J. A. Babb and A. Dalgarno, Phys. Rev. A, 1995, 51, 3021–3026 CrossRef CAS PubMed.
- F. A. Gianturco and P. G. Giorgi, Astrophys. J., 1997, 479, 560–567 CrossRef CAS.
- A. S. Dickinson and F. X. Gadéa, Mon. Not. R. Astron. Soc., 2000, 318, 1227–1231 CrossRef CAS.
- F. Mrugaŀa, V. Špirko and W. P. Kraemer, J. Chem. Phys., 2003, 118, 10547–10560 CrossRef.
- X. J. Liu, Y. Z. Qu, B. J. Xiao, C. H. Liu, Y. Zhou, J. G. Wang and R. J. Buenker, Phys. Rev. A, 2010, 81, 022717 CrossRef.
- L. Augustovičová, V. Špirko, W. P. Kraemer and P. Soldán, Chem. Phys. Lett., 2012, 531, 59–63 CrossRef.
- T. Stoecklin, F. Lique and M. Hochlaf, Phys. Chem. Chem. Phys., 2013, 15, 13818–13825 RSC.
- G. Nyman, M. Gustafsson and S. V. Antipov, Int. Rev. Phys. Chem., 2015, 34, 385–428 Search PubMed.
- M. Zámečníková, P. Soldán, M. Gustafsson and G. Nyman, Mon. Not. R. Astron. Soc., 2019, 489, 2954–2960 CrossRef.
- M. Zámečníková, M. Gustafsson, G. Nyman and P. Soldán, Mon. Not. R. Astron. Soc., 2020, 492, 3794–3802 CrossRef.
- D. Jones (née Burdakova), M. Gustafsson and G. Nyman, Mon. Not. R. Astron. Soc., 2022, 517, 4892–4901 CrossRef.
- T. Bai, Z. Qin and L. Liu, Mon. Not. R. Astron. Soc., 2022, 510, 1649–1656 CrossRef CAS.
- P. Szabó and M. Gustafsson, J. Chem. Phys., 2023, 159, 144112 CrossRef PubMed.
- T. J. Millar, C. Walsh, M. Van de Sande and A. J. Markwick, Astron. Astrophys., 2023 DOI:10.1051/0004-6361/202346908.
- M. Gustafsson, J. Chem. Phys., 2020, 153, 114305 CrossRef CAS PubMed.
- M. Šimsová-Zámečníková, P. Soldán and M. Gustafsson, Astron. Astrophys., 2022, 664, A5 CrossRef.
- M. Šimsová née Zámečníková, M. Gustafsson and P. Soldán, Phys. Chem. Chem. Phys., 2022, 24, 25250–25257 RSC.
- P. C. Stancil and A. Dalgarno, Astrophys. J., 1997, 479, 543–546 CrossRef CAS.
- P. C. Stancil and A. Dalgarno, Astrophys. J., 1997, 490, 76–78 CrossRef CAS.
- B. Zygelman, P. C. Stancil and A. Dalgarno, Astrophys. J., 1998, 508, 151–156 CrossRef CAS.
- A. S. Dickinson, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 4329–4334 CrossRef CAS; A. S. Dickinson, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 049801 CrossRef.
- S. Bovino, M. Tacconi and F. A. Gianturco, Astrophys. J., 2011, 740, 101 CrossRef; S. Bovino, M. Tacconi and F. A. Gianturco, Astrophys. J., 2012, 748, 150 CrossRef.
- L. Augustovičová, V. Špirko, W. P. Kraemer and P. Soldán, Mon. Not. R. Astron. Soc., 2013, 435, 1541–1546 CrossRef.
- L. Augustovičová, W. P. Kraemer and P. Soldán, Astrophys. J., 2014, 782, 46 CrossRef.
- L. Augustovičová, M. Zámečníková, W. P. Kraemer and P. Soldán, Chem. Phys., 2015, 462, 65–70 CrossRef.
- M. Zámečníková, W. P. Kraemer and P. Soldán, J. Quant. Spectrosc. Radiat. Transfer, 2017, 191, 88–95 CrossRef.
- T. J. Giese and D. M. York, J. Chem. Phys., 2004, 120, 7939–7948 CrossRef CAS PubMed.
- Y. Zeiri and G. G. Balint-Kurti, J. Chem. Phys., 1983, 99, 1–24 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05602c |
| This journal is © the Owner Societies 2024 |