Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Soft X-ray absorption and fragmentation of tin-oxo cage photoresists†
Jarich
Haitjema
 a,
Sonia
Castellanos
a,
Sonia
Castellanos
 a,
Olivier
Lugier‡
a,
Ivan
Bespalov
a,
Olivier
Lugier‡
a,
Ivan
Bespalov
 a,
Rebecka
Lindblad
de,
Martin
Timm
e,
Christine
Bülow
ef,
Vicente
Zamudio-Bayer
a,
Rebecka
Lindblad
de,
Martin
Timm
e,
Christine
Bülow
ef,
Vicente
Zamudio-Bayer
 e,
J. Tobias
Lau
e,
J. Tobias
Lau
 ef,
Bernd
von Issendorff
f,
Ronnie
Hoekstra
ab,
Katharina
Witte§
g,
Benjamin
Watts
ef,
Bernd
von Issendorff
f,
Ronnie
Hoekstra
ab,
Katharina
Witte§
g,
Benjamin
Watts
 g,
Thomas
Schlathölter
g,
Thomas
Schlathölter
 *bc and
Albert M.
Brouwer
*bc and
Albert M.
Brouwer
 *ah
*ah
aAdvanced Research Center for Nanolithography, P.O. Box 93019, 1090 BA Amsterdam, The Netherlands. E-mail: a.m.brouwer@uva.nl
bZernike Institute for Advanced Materials, Rijksuniversiteit Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: t.a.schlatholter@rug.nl
cUniversity College Groningen, University of Groningen, Hoendiepskade 23/24, 9718 BG Groningen, The Netherlands
dDepartment of Physics, Lund University, 22100 Lund, Sweden
eAbteilung für Hochempfindliche Röntgenspektroskopie, Helmholtz Zentrum Berlin für Materialien und Energie, Albert-Einstein-Straße 15, 12489 Berlin, Germany
fPhysikalisches Institut, Albert-Ludwigs-Universität Freiburg, Hermann-Herder-Straße 3, 79104 Freiburg, Germany
gPaul Scherrer Institut, Villigen 5232, Switzerland
hUniversity of Amsterdam, van’t Hoff Institute for Molecular Sciences, P.O. Box 94157, 1090 GD Amsterdam, The Netherlands
First published on 24th January 2024
Abstract
“Tin-oxo cage” organometallic compounds are considered as photoresists for extreme ultraviolet (EUV) photolithography. To gain insight into their electronic structure and reactivity to ionizing radiation, we trapped bare gas-phase n-butyltin-oxo cage dications [(BuSn)12O14(OH)6]2+ in an ion trap and investigated their fragmentation upon soft X-ray photoabsorption by means of mass spectrometry. In complementary experiments, the tin-oxo cages with hydroxide and trifluoroacetate counter-anions were cast in thin films and studied using X-ray transmission spectroscopy. Quantum-chemical calculations were used to interpret the observed spectra. At the carbon K-edge, a distinct pre-edge absorption band can be attributed to transitions in which electrons are promoted from C1s orbitals to the lowest unoccupied molecular orbitals, which are delocalized orbitals with strong antibonding (Sn–C σ*) character. At higher energies, the most prominent resonant transitions involve C–C and C–H σ* valence states and Rydberg (3s and 3p) states. In the solid state, the onset of continuum ionization is shifted by ∼5 eV to lower energy with respect to the gas phase, due to the electrostatic effect of the counterions. The O K-edge also shows a pre-edge absorption, but it is devoid of any specific features, because there are many transitions from the different O1s orbitals to a large number of vacant orbitals. In the gas phase, formation of the parent [(BuSn)12O14(OH)6]3+ radical ion is not observed at the C K-edge nor at the O K-edge, because the loss of a butyl group from this species is very efficient. We do observe a number of triply charged photofragment ions, some of which have lost up to 5 butyl groups. Structures of these species are proposed based on quantum-chemical calculations, and pathways of formation are discussed. Our results provide insight into the electronic structure of alkyltin-oxo cages, which is a prerequisite for understanding their response to EUV photons and their performance as EUV photoresists.
1 Introduction
Organotin compounds based on tin-oxo cage structures (see Fig. 1) are candidates for a new generation of extreme ultraviolet (EUV) photoresists: light-sensitive materials that change their solubility upon exposure to EUV light (13.5 nm, 92 eV).1–13 Tin atoms strongly absorb EUV radiation,14,15 which allows for photoresist layers to be thin (∼20 nm) and still absorb a suitable fraction of the expensive EUV photons. Patterns with small critical dimensions can then be written on the photoresist while keeping the aspect ratio (ratio between height and width of a feature) small enough to avoid pattern collapse.16 The EUV absorption coefficient of tin-oxo cage films was measured to be around 12 μm−1, ca. 2.5× higher than that of conventional photoresists based on organic polymers.17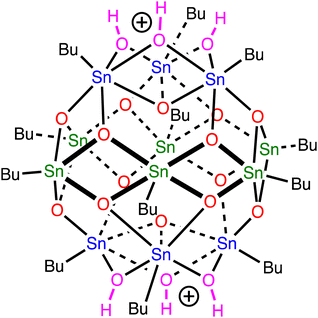 | ||
| Fig. 1 Tin-oxo cage dication structure. Sn-atoms in blue are 6-coordinated (“cap”), those in green are 5-coordinated (“belt”). | ||
The chemical reaction pathways in organometallic photoresists have been explored to some extent, but many quantitative details are still unknown. Castellanos and co-workers studied metal-oxo clusters with acrylate ligands that act as negative tone photoresist mainly through the cross-coupling of the acrylates.10,13,18–22 For the tin-oxo cages, the formation of a condensed (insoluble) metal oxide-like network, induced by removal of organic side groups, has been suggested,1,22–25 but little is known about the EUV-induced photoreactions on a molecular level. Therefore, spectroscopic and mechanistic studies are necessary to improve our understanding.
The initial absorption of EUV photons leads to photoemission of valence or semi-core electrons.26–31 The resulting semi-core vacancies typically have short lifetimes (1–10 fs range)32 and decay either by internal conversion or by Auger–Meitner processes.33,34 The emitted electrons generate a cascade of secondary electrons in surrounding photoresist molecules.35,36 These electrons are thought to induce the majority of the chemical conversions that lead to the solubility change in EUV photoresists.30
Reactions in EUV photoresists are difficult to study, because the photoresist layers for EUV lithography are typically thin and standard chemical analysis techniques such as Nuclear Magnetic Resonance and infrared spectroscopy lack the sensitivity to detect subtle changes, especially with the small quantities of material in thin films. Therefore, we explore X-ray absorption spectroscopy at the carbon and oxygen K-edges for the analysis of thin films of tin-oxo cages, and we probe the same transitions for the free dications in the gas phase, where we monitor the photofragmentation pathways via mass spectrometry.
Soft X-ray induced photofragmentation of complex molecular systems has been previously studied for biomolecules such as proteins,37–39 peptides,40 and oligonucleotides41 but also for size-selected metallic clusters.42,43 However, a study on an organometallic system that is relevant for EUV lithography, such as the tin-oxo cage, has to our knowledge not been reported. We aim to provide new insights into its electronic structure and emphasize the importance of the Sn–C σ and σ* bond orbitals, which are the main constituents of the highest occupied and lowest unoccupied molecular orbitals, respectively. These orbitals play a key role in the photochemistry of tin-oxo cages both in the ultraviolet and in the extreme ultraviolet regimes.
2 Experimental and computational details
Compounds used were prepared as described in the literature. The tin-oxo cage was synthesized with tosylate counterions,44 after which the material was converted to hydroxide form (TinOH) by ion exchange using aqueous tetramethyl ammonium hydroxide.45 The tin-oxo cage in its trifluoroacetate form (TinF) was prepared by reacting TinOH with two molar equivalents of trifluoroacetic acid.31All gas phase photoabsorption experiments were performed at the BESSY II synchrotron radiation source (Helmholtz-Zentrum Berlin für Materialien und Energie, Germany). The IonTrap end station46–48 is permanently installed at the UE52-PGM beamline and it was custom-built to record partial photoion yields from ionic precursors as a function of photon energy. The photon energy was calibrated on the 1s resonance of Neon (867 eV), using the 1st, 2nd and 3rd order of the monochromator (867/433.5/289 eV). We (conservatively) estimate the accuracy as ±1 eV. Tin-oxo cage dications [(BuSn)12O14(OH)6]2+ were brought into the gas phase using electrospray ionization (ESI) of a 40 μM solution of the tin-oxo cage with hydroxide counterions in methanol.49 After phase space compression of the ion beam in a radiofrequency (RF) ion funnel and a multipole RF ion guide, the ions were mass-selected using a quadrupole RF mass filter. The precursor ions were then continuously injected into a cryogenic linear RF ion trap where they were accumulated and continuously exposed to a collinear beam of monochromatic soft X-rays. While the photon energy was scanned in steps of about 100 mV over the energy region of interest (bandwidth approx. 300 meV at the carbon K edge, 350 meV at the oxygen K edge, integration time typically 4 s per photon energy), ion bunches were extracted into a reflectron TOF system with a repetition rate of 19 Hz. From the resulting mass spectra, partial ion yields as a function of photon energy were extracted. The apparatus is optimized for determination of partial photofragment ion energies as a function of photon energy. The relative intensities of fragment ions in the photofragmentation mass spectra are only accurate over a pre-selected region of interest of several 100 Da. In the following, we will refer to this method as Near Edge X-ray Absorption Mass Spectrometry (NEXAMS).
For X-ray absorption measurements in thin films, the tin-oxo cage materials were spin coated onto 7.5 × 7.5 mm2 substrates obtained from Norcada, composed of a silicon nitride (SiNx) membrane covering a silicon substrate, with a 3 × 3 mm2 window of freestanding silicon nitride (d = 30 nm) in the middle. Spin coating was performed at 2500 rpm for 35 s, using a 20 mg mL−1 solution of TinOH/TinF in toluene using either a Suss Delta 10 or Chemat Technology Inc. Spin Master 50 spin coater. The solutions were filtered using a 0.2 μm PTFE filter prior to spin coating. A post-application bake step of 30 s at 90 °C was performed. The resulting thicknesses were approx. 30 nm (TinOH) and 60 nm (TinF) as determined by Atomic Force Microscopy.2
X-ray absorption spectra were measured using the Scanning Transmission X-Ray Microscope of the PolLux beamline at SLS (PSI).50 The X-ray beam (energy range 270–590 eV) was monochromatized using a 300 lines per mm Ni grating, with higher orders suppressed by a mirror system,51 and focused using a gold Fresnel zone plate with an outermost zone width of 35 nm (combined with a 50 μm diameter order selecting aperture). The spectral bandwidth at the carbon K edge was ∼0.3 eV. Transmitted X-ray photons were detected by means of a scintillator coupled to a photomultiplier tube. The photon energies were calibrated by comparison with reference samples: thin films of polystyrene (peak at 285.3 eV)52,53 and poly(methylmethacrylate) (288.45 eV,54,55 288.52 eV56) Our data agree with the published values to ≤0.1 eV.
X-ray absorption spectra were measured by comparing the photon flux transmitted through the sample (I), to the photon flux of the beam measured through an open sample position (I0). The spectrum of the membrane was measured separately. Twenty-five intensity values were measured while the sample was scanned along a 25 μm line, with a dwell time of 100 ms. The scan was repeated for each energy. Carbon K-edge absorption spectra were recorded over an energy range of 270–350 eV, using smaller steps in more interesting regions (0.1 eV between 282 and 293 eV, 0.25 eV between 293 and 300 eV), and larger steps in regions that do not show fine spectral features. To limit X-ray-induced damage to the sample, the beam was defocused to a spot size of ∼1 μm diameter by placing the sample 100 μm behind the focus plane.50 The absorption spectrum was calculated as A = −ln(I/I0) and the spectrum of the SiN substrate, measured separately, was subtracted (see Fig. S1, ESI†). The reported spectra are the averages of four independent scans on different areas on the same sample. By repeating the entire measurement at the same sample area, we verified that radiation damage was negligible. For processing the spectra, ATHENA software57 was used to remove the background contribution due to excitation of valence and semi-core electrons. Fitting of the band shapes, as discussed in the text, was done using Igor Pro.58
Density functional theory with the B3LYP hybrid density functional and the LANL2DZ basis set59 was employed to optimize the molecular structure of TinOH. This modest level of theory gives a good agreement with the known crystal structures of tin-oxo cages.31,60 The model of TinOH contained 4 water molecules to stabilize the OH− in a hydrogen-bonded network.60 For exploring fragmentation pathways of the bare dication, a simplified molecular structure was used, in which the butyl groups were replaced by methyl groups. For the lowest-energy isomers found, the corresponding n-butyltin analogs were constructed, and their geometries were optimized using B3LYP/Def2SVP. Single point energy calculations are reported using the Def2TZVP basis set, and zero-point vibrational energy corrections (B3LYP/Def2SVP) were included. The calculations were performed using Gaussian 16.59
For the calculations of the X-ray absorption spectra, we applied the Transition Potential method61 implemented in the Amsterdam Modeling Suite AMS2022.62 We used the LDA functional, with the TZP/large-core basis set for all C, H and O atoms. This basis set includes 1s functions on H, 2s and 2p on C and O, and 5s and 5p on Sn. For the CH2-group (or O atom) at which excitation occurs a more extended aug/TZ2P/nocore basis set was used to allow the lower Rydberg excitations to be taken into account and to include a 1s core orbital on the atom of interest. The other atoms of the butyl group were described using aug/TZ2P/large-core to provide diffuse functions. On the Sn atoms, the TZ2P basis was used. The butyl groups can exist in many low energy rotameric forms, and we have arbitrarily selected a single low symmetry conformation. Thus, all C atoms are chemically different and give rise to slightly different transitions. Because there is negligible interaction between the C 1s orbitals, we construct the complete spectrum as a superposition of the individual spectra generated for each C 1s orbital in the molecule. This allows a straightforward evaluation of the contributions of the individual C atoms to the spectra.63 To account for the systematic deviation that is commonly observed in XAS calculations64 the computed spectra are shifted by −3.6 eV to match the first peak with that in the experimental NEXAMS spectrum.
3 Results and discussion
3.1 Near edge X-ray absorption spectra
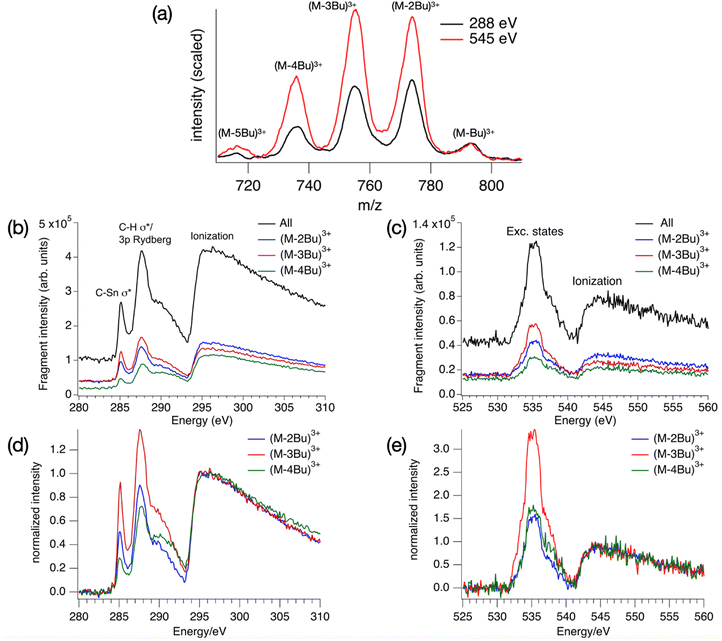
The absorption spectrum of a thin film of TinF at the carbon K-edge is shown in Fig. 2a. We also obtained a spectrum of TinOH (Fig. S1, ESI†) which is very similar, because the two small anions contribute only little to the spectrum. Fig. 2b shows the gas-phase NEXAMS spectrum of the bare tin-oxo cage dication based on the sum of the photofragment peaks (M-nBu)3+. In this shorthand notation M refers to the molecular ion, n is the number of butyl groups lost.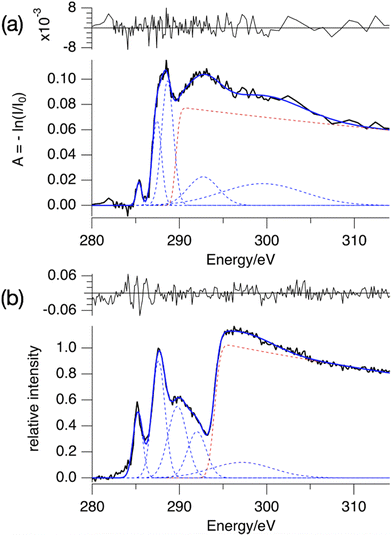 | ||
| Fig. 2 (a) X-ray absorption spectrum of TinF thin film at the C K-edge. (b) NEXAMS spectrum for tin oxo cage dications, based on the sum of photofragment peaks (M-nBu)3+, n = 1–5 (see Fig. 6). The dashed lines are the components of the fits, and their sum is represented by the blue solid lines. The red dashed line corresponds to continuum ionization. Residuals of the fit are shown. Fit parameters are given in Table S1 (ESI†). | ||
Both spectra consist of resonant features due to 1s transitions to unoccupied orbitals for photon energies below the 1s ionization threshold and a broad ionization continuum at higher photon energies. The entire spectra can be well reproduced by using a sum of Gaussians for the resonant transitions plus a step function for the ionization, which can be described as an exponential decay convolved with a Gaussian.52,65
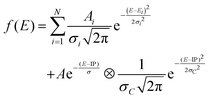 | (1) |
We fit the spectra with five Gaussians, the smallest number that gives unstructured residuals. Nearly identical fit parameters were obtained for TinOH and TinF (see ESI,† Table S1 and Fig. S1). In the spectrum of TinF in the thin film (Fig. 2a), the pre-edge region shows a distinct peak at 285.4 eV, which we attribute to electronic transitions from C 1s orbitals to the LUMO, as discussed in more detail below. A second strong band, with an asymmetric shape, is observed at ∼288 eV. The low-energy shoulder on this band is attributed to the Sn–C bonds, but the peak at 288 eV is also observed in many (saturated) hydrocarbons. We reproduce the asymmetric shape of this peak by using two Gaussians. At energies >290 eV two broad features are present, which most likely result from transitions to higher energy electronic states. The exact position of the ionization threshold is not well defined.52 The positions reported corresponds to the best fits, and are essentially the same for TinOH and TinF, obtained in independent fits. Acceptable fits can, however, be obtained when shifting the position of the threshold by ±1 eV, with properly adjusted shapes of the Gaussian functions.
The gas phase NEXAMS spectrum (Fig. 2b), obtained from the sum of the partial ion yields of all (M-nBu)3+ fragments, also shows the peak corresponding to the C 1s → LUMO transitions and the 288 eV absorption band, but an additional broad band can be detected at ∼290 eV that is hidden in the ionization continuum in the solid state. The most striking difference with the solid-state spectrum is the shift of the ionization edge by ∼5 eV to higher energy. This can be attributed mainly to the electrostatic effect of the anions. In earlier studies of the valence ionization of the same ions in the gas phase, we observed that screening by a single counterion shifted the onset of ionization from 12 eV to 10 eV.66 In the solid state, each dication is associated with two anions, which will double the electrostatic effect, and the interaction with the continuum in the film further shifts the ionization threshold to ∼8 eV.36
A further important difference is that the first peak, found here at the slightly lower energy of 285.2 eV, is relatively much more intense in the gas phase. While the absorption spectrum directly reflects the absorption cross section, the gas phase spectrum is also modulated by the branching ratios of the corresponding fragmentation processes, as discussed below.
Urquhart and co-workers have systematically studied carbon K-edge NEXAFS of alkanes in the gas phase and in the solid state.67,68 Clearly, the richness of the spectra of the small alkanes does not resemble our observations for the tin-oxo cage, which shows broader bands. The likely reason is inhomogeneous broadening: in the tin-oxo cage [(BuSn)12O14(OH)6]X2 (X = anion), the Bu groups are attached to two different types of tin atoms, and they have slightly different conformations and micro-environments. For the model alkane neopentane, a direct comparison between gas-phase and condensed phase68 reveals that in the latter, the broadening of the peaks gives rise to a spectrum dominated by two broad resonances with a high-energy shoulder, very similar to the pre-edge spectrum in Fig. 2b.
The difference in the energy of the LUMO and the ionization threshold is a measure of the electron affinity (EAa) of the tin-oxo cage material. This is an important quantity in understanding Extreme Ultraviolet photochemistry, in which low-energy electrons play a key role. By comparing the energy of the first peak and the position of the ionization step we obtain EAa = 8.8 eV in the gas phase. For the solid state we find EAa = 3.5 ± 1 eV, which is compatible with the value EAa ≈ 3 eV that was recently obtained from electron spectroscopy in the UV/VUV range.36 This implies that the n-butyltin-oxo cages in thin films are moderately strong electron acceptors, slightly weaker than e.g. C60.69
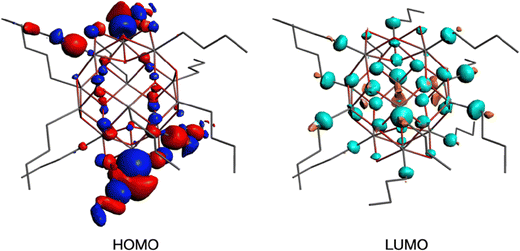
To get insight into the low energy absorption features, we calculated the X-ray absorption spectra using the transition potential (TP) method.61 This is one of the simplest methods available for this purpose70,71 and particularly suitable for large many-electron systems such as the tin-oxo cages because it is not demanding in terms of computing time. Two types of tin atoms can be identified in the tin-oxo cage structures (Fig. 1): 5-coordinated Sn, in the central “belt”, and 6-coordinated, in the two ionic “caps”. The highest occupied molecular orbitals are of σ Sn–C character, mostly located on the 6-coordinated Sn atoms. The LUMO is a delocalized orbital on the central belt and has contributions from Sn 5p AO's and Sn–C σ*. HOMO and LUMO are visualized in Fig. 3.
The calculations predict many transitions, but we focus here on the lowest-energy ones, which stand out in the experimental spectrum. The single band in the NEXAMS spectrum at 285.2 eV is a result of several transitions involving a few low energy orbitals that have substantial σ* character, like the LUMO. For brevity we will refer to this band as the C 1s – LUMO transition.
The transition probability, i.e. the oscillator strength for transitions between an initial 1s orbital and a final unoccupied molecular orbital, increases with increasing p-character of the final MO, and with the density of the MO at the C-atom where the 1s orbital is localized. The largest cross sections for transitions to the LUMOs are indeed predicted for the first C-atoms of the butyl groups on the 5-coordinated Sn atoms at the cage equator. Fig. 4 shows the contributions from the C1 atoms of the 6 butyl groups on 5-coordinated Sn atoms and those on the 6-coordinated Sn atoms at the caps. As shown in Fig. S2 (ESI†), the second, third and fourth atoms of the butyl groups hardly contribute to the low-energy transition.
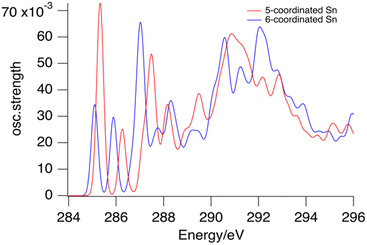 | ||
| Fig. 4 Calculated contributions of the first C-atoms of the butyl groups on 6-coordinated tin atoms (blue) and 5-coordinated tin atoms (red) to the XAS of the tin cage dication. | ||
Fig. 4 shows that the lowest-energy absorptions arise from the C-atoms in the Sn–C bonds. Together they are responsible for the band observed at 285.4 eV, but they also contribute to the broad band that is observed at 288 eV. The calculations do not accurately reproduce the absorption profile at higher energies. There are many transitions of a complex nature involving σ* and Rydberg orbitals,63,68 giving rise to a highly congested spectrum. Unravelling this complexity is outside the scope of the present work.
In the gas phase NEXAMS, the C 1s – LUMO absorption has a higher relative intensity (Fig. 2). This effect is reproduced to some extent by the calculations shown in Fig. 5. For the TinOH model we find the computed absorption cross section of the first absorption band from the carbon atoms of the butyl groups on 6-coordinated Sn to be somewhat smaller than for the isolated dication. Experimentally, however, the relative intensity of the C 1s – LUMO peak is increased more in the NEXAMS spectrum than expected based on the calculated cross section. This must be a result of more efficient fragmentation to (M-nBu)3+ fragments (Fig. 6).
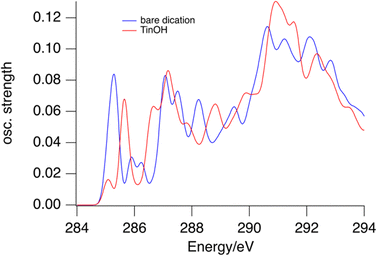 | ||
| Fig. 5 Predicted absorption spectra for bare tin-oxo cage dication (blue) and TinOH (red) for the first carbon atoms of the butyl groups. | ||
In the oxygen K-edge spectrum (Fig. 6c), a broad resonance is found at 535 eV with an ionization onset at 543 eV. These features are like those seen in studies on SnO2,72 but are otherwise difficult to assign. As shown in Fig. 3, the LUMO has contributions on the bridging oxygen atoms of the cage. TP calculations (illustrated in ESI,† Fig. S3) do not predict any characteristic low-energy transitions, in agreement with the experimental observation.
3.2 Photofragmentation processes
Photofragmentation mass spectra in the range between 700 and 820 m/z are shown in Fig. 6, along with the resulting NEXAMS spectra for the carbon and oxygen K-edge. The Sn M4,5-edge (480–500 eV) was also scanned but no clear resonances were found. Likewise, in X-ray transmission, even when using thicker tin-oxo cage films, no clear absorption resonances were found in this energy range. Also at the Sn M2,3-edge, no significant absorption was detected.73 In addition to the 3+ ions shown in Fig. 6a, (M-2Bu)4+ and (M-3Bu)4+ ions are detected at the O–K edge, and a series of (M-nBu)2+ ions are observed at both edges (see Fig. S4, ESI†). Because of experimental limitations, the quality of the data in these m/z ranges is insufficient to warrant a further discussion in the present work.Fig. 6(a) reveals a series of (M-nBu)3+ fragments at the C and O K edges, with the distribution clearly shifted towards more highly fragmented ions in the case of oxygen. In Fig. 6(d) and (e) the spectra are shown after subtraction of the pre-edge background and normalization at the onset of the ionization continuum. Clearly, the photoresponse is different for the three different fragments. At both edges, the yield of the (M-3Bu)3+ fragment stands out in the pre-edge region compared to the ionization region. This fragment is especially prominent in the 285.2 eV peak.
To understand the photofragmentation spectra, we need to consider the basic processes at play. Carbon or oxygen 1s excitation or ionization all lead to the formation of a core hole on the atom. In light atoms such as C and O, Auger–Meitner decay is the most likely initial relaxation process. The emission of the Auger–Meitner electron leaves the photoabsorbing atom either singly charged (for 1s excitation) or doubly charged (for 1s ionization) and in most cases in an excited state.74
The Auger–Meitner process itself always starts from an initial 1s core hole state |K> that decays to a state with two holes in the valence shell |LL>. Energetically high-lying final states can be repulsive and lead to prompt dissociation of bonds on fs timescales. On longer timescales, the system can return to the ground state via non-adiabatic curve crossings. In this process of internal conversion, electronic excitation is converted into vibrational excitation. In the case of lower-lying final states, internal conversion and intramolecular vibrational redistribution (IVR) can either lead to a vibrationally hot tin-oxo cage with charge state 4+ for 1s ionization (i) or 3+ for 1s excitation (ii), that is in the electronic ground state.
(i) For the ionization case, the ground state 4+ ion lacks two electrons in the highest-occupied molecular orbital (HOMO). The HOMO of the tin-oxo cages is of Sn–C σ-nature, and removal of two electrons from it effectively destroys this bond, leading to butyl group loss. Consequently, the heaviest species observed in the mass spectra is not the intact tin-oxo cage precursor M4+, but a (M-Bu)3+ trication. This ion results from butyl loss, accompanied by a charge-separation process where the butyl group carries away a positive charge, reducing electrostatic repulsion. In related experiments, the butyl cation was detected in the low mass range of the spectrum.75 As found in previous work, a single VUV photoionization of the tin-oxo cage dication gives rise to the same (M-Bu)3+ ion. In that case, the lost butyl group has to be a neutral radical.66
(ii) For the case of excitation of a 1s electron to an unoccupied molecular orbital (as observed in the pre-edge excitation spectrum), the tin-oxo core resembles the 3+ ion and will follow very similar dynamics. The cleavage of the Sn–C bond in this case does not lead to charge separation and the butyl group must be lost in neutral form. Furthermore, the intermediate (M-Bu)3+ ion will likely have a higher internal energy because here, Auger–Meitner decay starts from an excited electron configuration.66,76,77
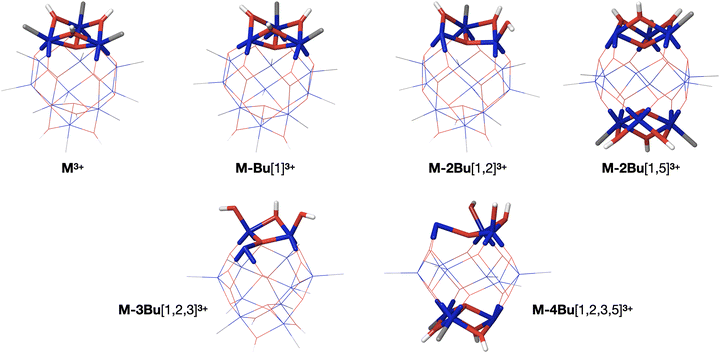
The internal energy of the (M-Bu)3+ ion will depend on the specific Auger–Meitner process involved in its formation. This energy will be reduced by the energy required to cleave the Sn–C bond and by the kinetic energy release in the fragmentation process. Subsequent relaxation processes are most likely of statistical nature, with the fragmentation pattern depending on the internal energy of the molecular ion. In the Ion Trap, the ions are continuously collisionally cooled by He buffer gas at cryogenic temperatures. This means that fragmentation processes that occur after ∼1 μs will be quenched. In related experiments, ions were trapped with much less efficient cooling after excitation (no buffer gas), and in this case (M-4Bu)3+ and (M-3Bu)3+ were barely detected, probably because they decompose further, while other fragments were observed that are not seen in the present experiments.75 We observe (M-2Bu)3+, (M-3Bu)3+, (M-4Bu)3+, and even (M-5Bu)3+, which can be the result of sequential loss of butyl groups by breaking of Sn–C bonds. The binding energies of these bonds can be expected to be different in the different steps. The (M-Bu)3+ ion is a closed-shell molecule, and the Sn–C bonds will be as strong as a typical Sn–C bond, that is ∼2.3 eV. After homolytic breaking one of these bonds, the (M-2Bu)3+ formed is a radical, with a much smaller bond strength, and (M-3Bu)3+ is again a closed shell molecule which requires more energy to lose the fourth butyl group. Fig. 7 shows the calculated dissociation energies which confirm the general expectation. Interestingly, the alternation is not reflected in fragment ion yields in the mass spectrum. This may be due to the direct fragmentation of more highly charged Mn+ precursors.
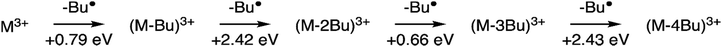 | ||
| Fig. 7 Sequential fragmentation of (M-Bu)3+. The dissociation energies were calculated at the B3LYP/Def2TZVP level at B3LYP/Def2SVP optimized geometries with zero-point energy corrections. | ||
Quantum chemical calculations allow us to estimate the dissociation energies and to predict the lowest-energy structures of the fragments (M-nBu)3+. At each stage, we first explored the energies of all different isomers using a simpler model system, with methyl groups instead of the butyl groups. Next, the energies were calculated for the corresponding lowest energy isomers of the n-butyl tin-oxo cage. The dissociation energy, i.e. the minimum internal energy loss per step, was calculated as the difference in the energies of the intact molecules and the fragments at the B3LYP/Def2TZVP level, with corrections for the zero-point vibrational energies at the B3LYP/Def2SVP level at which structures were optimized. As shown in Fig. 7, all bond breaking steps are endothermic. Nevertheless, the internal energy can be high enough to overcome the barrier. For C 1s ionization on one of the butyl groups, average excitation energies after Auger–Meitner decay are expected to be around 20 eV but maximum values can be much higher (see ref. 37 for C 1s Auger–Meitner decay in glycine). Moreover, entropy favors cleavage,78 and the dissociation is irreversible in the gas phase.
As described before, the first butyl group is lost from one of the 6-coordinated tin atoms on the caps.78–80 The second group is also lost from one of the caps, with a small preference for “opposite” caps. The most stable isomer for (M-3Bu)3+, however, is the one in which all butyl groups of one cap are lost. In the next step, it is energetically most favourable to lose a butyl from the second cap, with little difference between the two possible isomers. The sequence of structures is shown in Fig. 8.
To summarize, 1s excitation or ionization of an O 1s rather than a C 1s orbital is likely to lead to more energy deposition and/or more electron removal from the tin-oxo cage. For both K-edges, there is on average more than enough energy to facilitate a series of bond breaking events on a sub μs timescale. Due to the He buffer gas cooling in the present experiment, fragmentation does not proceed beyond (M-5Bu)3+, but as mentioned above, more extensive fragmentation is found when such cooling is absent.75
In the following we will sketch further mechanistic scenarios that can be invoked to explain the two striking experimental observations: (1) the increased yield of fragments that have lost multiple Bu groups at the O K edge compared to the C K edge (Fig. 6a), and (2) the high relatively intensity of the lowest-energy peak in the NEXAMS spectrum compared with the absorption spectrum (Fig. 2).
When comparing the |K> → |LL> Auger–Meitner decay for O 1s and C 1s, we may anticipate a larger average amount of excitation energy remaining on the O site, because the inner valence 2s orbitals of O are more strongly bound that the corresponding 2s orbitals of C. A calculation, presented in the ESI† (Fig. S5) illustrates this. Although the photogenerated ions are cooled in the trap, a higher initial internal energy still implies a higher probability for reaction. This is a first potential explanation for the larger extent of fragmentation occurring upon O 1s ionization.
Next to Auger–Meitner decay, interatomic Coulombic decay (ICD)76 and related 2-center processes81 should be considered, which allow the electrons on Sn atoms to participate in the electronic decay. In a nutshell, in ICD a valence electron decays to the 1s core hole but the second electron is ionized from the Sn atom. Oxygen atoms in the tin-oxo cage all have 3 Sn neighbours, significantly increasing the probability for ICD or related processes. Furthermore, in case of a 1s hole in O with a binding energy of ∼543 eV, also the Sn 3d orbitals at 484 eV and 493 eV are energetically available. An O 1s ICD process resulting in a Sn 3d hole could then be the trigger for a subsequent Auger–Meitner decay (or a cascade of Auger–Meitner decays) in the Sn atom. Obviously, the Sn 4s, 4p and 4d orbitals would be accessible for ICD as well. This is the second possible explanation for the higher yields of more fragmented ions in the case of O 1s excitation or ionization.
So far, we have discussed 1s core hole formation as the starting point for photofragmentation, but non-resonant ionization from more weakly bound atomic orbitals can also be important. For photons at the carbon K-edge, these are valence orbitals on C, O and Sn, but also Sn 4s, 4p and 4d. For photons at the oxygen K-edge, additionally ionization from C 1s and Sn 3d can contribute. Using tabulated cross section data and taking the chemical composition C48O20Sn12 into account (see Table S2, ESI†) we estimate that at 300 eV 69% of the photon absorption involves carbon sites, 4% oxygen sites and 27% tin sites. About half of the total cross section for Sn in this range is due to the 4d electrons, and a smaller fraction is due to 4s and 4p.77 Only the latter can give rise to multiple Auger–Meitner-like processes. Thus, at the carbon K-edge most of the tin cages will undergo ionization and a single Auger–Meitner process.
At 550 eV, above the oxygen K-edge, most of the absorption probability is from tin atoms (64%), 19% from oxygen and 18% from carbon. Valence ionization mostly leads to singly ionized M3+, which is known to decompose quantitatively to the observed (M-Bu)3+ ion even without any excess energy.66 Ionization from Sn orbitals, however, opens multiple Auger–Meitner(-like) decay channels, and more highly charged initial states can be reached. Electronically relaxed highly charged states (>4+) of the tin-oxo cage will have unoccupied Sn–C σ orbitals and lose multiple butyl groups, likely as cations to reduce the Coulombic repulsion. Weak signals that can be attributed to (M-2Bu)4+ and (M-3Bu)4+ can be detected upon excitation at 545 eV (Fig. S4, ESI†). The predominant excitation of Sn atoms is a third possible explanation for the larger contributions of (M-3Bu)3+ and (M-4Bu)3+ to the fragments at the oxygen K-edge compared to the carbon K-edge (Fig. 6a).
In a butyl group, three of the four C atoms are not very close to Sn atoms and Sn orbitals are unlikely to be involved in ICD processes of the C 1s hole. This is different for the C atoms that are bonded to an Sn atom, and which give rise to the low-energy pre-edge peak. For the C 1s orbitals in question, the binding energy is about 285 eV and Sn 4d, 4p and Sn 4s orbitals are energetically available in addition to the weakly bound valence orbitals. An ICD-induced double hole in these orbitals enables further Auger–Meitner decay of the Sn 4s, 4p or 4d vacancies, resulting in more electron emission and higher charge states. Thus, fragmentation will be enhanced, which may explain the relatively strong pre-edge peak due to excitation of the 1s of the C atoms bound to Sn. The solid-state spectrum obviously does not show this feature because it represents the absorption cross sections only.
4 Conclusion
The n-butyltin-oxo cage ion [(BuSn)12O14(OH)6]2+, which finds possible application as a photoresist in EUV lithography, shows distinct transitions related to the Sn–C bonds in absorption spectra near the carbon K-edge. The strongest features are alkane-like bands in the range 288–290 eV, but the C 1s to LUMO transitions give rise to a low-energy band at 285.4 eV in the solid film and 285.2 eV in the gas phase. The largest contribution to this band comes from the carbon atoms directly attached to the tin atoms, and especially those of the 5-coordinated tin atoms, on which the lowest unoccupied MO's have a higher density.Excitation with soft X-rays at the carbon and oxygen K-edges of tin-oxo cage ions in the gas phase leads to the loss of at least one butyl group (Bu). Tin cage fragments with 3+ charge are detected which have lost up to 5 Bu groups after absorption of a single soft X-ray photon. Ionization from the 1s core orbitals can be expected to lead to the formation of doubly ionized tin cages (charge 4+) which readily lose a butyl cation to form the detected [Sn12Bu11O14(OH)6]3+ (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (M-Bu)3+).
(M-Bu)3+).
The C 1s–Sn-C σ* transition peak in the NEXAMS spectrum is relatively strong compared to other pre-edge peaks. This could be due to interatomic Coulombic decay, in which the filling of the C 1s holes on the first carbon atoms of the butyl groups is accompanied by electron emission from Sn core orbitals (4s, 4p, 4d), allowing the formation of more highly charged states that decompose more readily.
A larger extent of fragmentation is found at the oxygen K-edge than at the carbon K-edge (Fig. 6a). Three factors can contribute to this. First, there is a strong non-resonant background excitation of Sn electrons at the oxygen K-edge. This opens pathways for multiple Auger–Meitner processes involving Sn 3s, 4s, 4p, 4d, 5s and 5p electrons, leading to more highly charged ions that can lose multiple butyl groups (as cations) before full electronic relaxation and thermalization occurs. Interatomic Coulomb decay involving the neighboring tin atoms provides another path from O 1s excitation or ionization to more highly charged species. Finally, regular Auger–Meitner decay of O 1s core holes will lead to holes in the O 2s inner valence orbitals, leaving the ions with higher internal energy than after C 1s excitation/ionization.
The distributions of photoproducts (M-2Bu)3+, (M-3Bu)3+ and (M-4Bu)3+, which constitute the majority of tin-oxo-cage fragments detected, are found to depend on the photon energy (Fig. 6). Excitation below the ionization edge relatively favors (M-3Bu)3+ over the other two fragments. In this case, one electron initially resides in a low-lying anti-bonding σ* orbital, and this can give rise to additional bond breaking, either directly in an electronically excited state, or via the additional internal energy (HOMO–LUMO gap ∼5 eV). However, it is difficult to say why a specific ion would be favored because the detected yield of each species depends on a complex interplay of its formation and decay. Moreover, the more highly fragmented ions may result from more highly charged precursors formed via Auger–Meitner-like decays involving Sn atoms instead of being produced in a linear sequence of butyl loss steps. We expect that more light can be shed on the details of the fragmentation processes using additional experiments, such as detection of emitted photoelectrons81 and time-resolved photofragmentation.82
In the solid state, the low-energy peak of the C 1s – σ* transition is considerably weaker than the alkane-type transitions and the absorption in the ionization regime. In the gas phase this peak is much more pronounced. This can in part be because of differences in electronic structure, due to the interactions between the tin cage and the counterions, but the more effective photofragmentation in the gas phase is more important. It is noteworthy that the effective cleavage of the Sn–C bonds observed in the gas phase stands in marked contrast with the relatively low quantum efficiency of the tin-oxo cage dealkylation in the solid state, and the moderate sensitivity of butyltin-oxo cage photoresists in Extreme Ultraviolet lithography.1,2 Most likely, the cage effect in the solid state precludes the separation of the butyl radicals and the tin cage, and recombination reactions reduce the overall quantum yield of photoconversion.
Author contributions
All authors contributed to the experimental investigation; J. H. synthesized the compounds; A. M. B. performed the quantum-chemical calculations; R. H. co-initiated the project and contributed to the interpretation of the results. The Ion Trap endstation at HZB was developed and maintained by J. T. L. and B. V. I. and was operated by R. L., M. T., C. B. and V. Z.-B. J. H., A. M. B., O. L., I. B., and S. C. performed the STXM measurements. K. W. and B. W. provided the instrumental facilities at PSI and helped with the measurements. J. H. analyzed the experimental data and wrote the first draft of the manuscript; all authors contributed to the review and editing. A. M. B. and T. A. S. supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Part of this work has been carried out at the Advanced Research Center for Nanolithography (ARCNL), a public–private partnership of the University of Amsterdam (UvA), the VU University Amsterdam (VU), the Netherlands Organisation for Scientific Research (NWO) and the semiconductor equipment manufacturer ASML. This work used the Dutch national e-infrastructure with the support of the SURF Cooperative using grants no. EINF-1911 and EINF-4039. The authors acknowledge Ed Zuidinga (UvA) for initial testing of the electrospray conditions and Niklas Ottosson for helpful discussions and for performing preliminary experiments that initiated this research. We thank Helmholtz-Zentrum Berlin for the allocation of synchrotron radiation beamtime (proposal number 17105145-ST). R. L. acknowledges funding from the Swedish Research Council (637-2014-6929). K. W. received funding from the European Union's Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 701647. The ion trap setup at HZB is partially funded by BMBF under project number BMBF-05K16Vf2. The PolLux end station was financed by the German Ministerium für Bildung und Forschung (BMBF) through contracts 05K16WED and 05K19WE2. We thank the Paul Scherrer Institute for access to the PolLux beam line (proposals 20180709 and 20182195).Notes and references
- B. Cardineau, R. Del Re, M. Marnell, H. Al-Mashat, M. Vockenhuber, Y. Ekinci, C. Sarma, D. A. Freedman and R. L. Brainard, Photolithographic properties of tin-oxo clusters using extreme ultraviolet light (13.5 nm), Microelectron. Eng., 2014, 127, 44–50 CrossRef CAS.
- J. Haitjema, Y. Zhang, M. Vockenhuber, D. Kazazis, Y. Ekinci and A. M. Brouwer, Extreme ultraviolet patterning of tin-oxo cages, J. Micro/Nanolithogr., MEMS, MOEMS, 2017, 16, 033510 Search PubMed.
- S. T. Meyers, J. Andersen, J. B. Edson, K. Jiang, D. A. Keszler, M. Kocsis, A. J. Telecky and B. Cardineau, Organometallic solution based high resolution patterning compositions and corresponding methods, WO2016065120A1, 2016 Search PubMed.
- S. T. Meyers, D. A. Keszler, K. Jiang, J. Anderson and A. Grenville, Organometallic solution based high resolution patterning compositions, US9310684B2, USA, 2016 Search PubMed.
- J. T. Diulus, R. T. Frederick, D. C. Hutchison, I. Lyubinetsky, R. Addou, M. Nyman and G. S. Herman, Effect of Ambient Conditions on Radiation-Induced Chemistries of a Nanocluster Organotin Photoresist for Next-Generation EUV Nanolithography, ACS Appl. Nano Mater., 2020, 3, 2266–2277 CrossRef CAS.
- R. T. Frederick, S. Saha, J. T. Diulus, F. Luo, J. M. Amador, M. Li, D.-H. Park, E. L. Garfunkel, D. A. Keszler and G. S. Herman, Thermal and radiation chemistry of butyltin oxo hydroxo: A model inorganic photoresist, Microelectron. Eng., 2019, 205, 26–31 CrossRef CAS.
- R. T. Frederick, J. T. Diulus, D. C. Hutchison, M. Nyman and G. S. Herman, Effect of Oxygen on Thermal and Radiation-Induced Chemistries in a Model Organotin Photoresist, ACS Appl. Mater. Interfaces, 2019, 11, 4514–4522 CrossRef CAS PubMed.
- N. Kenane, M. A. Grove, C. K. Perkins, T. R. Reynolds, P. H. Cheong and D. A. Keszler, Hydrolysis and Condensation of n-BuSnCl3: Enabling Deposition of Smooth Metal Oxide Photoresist Thin Films, Inorg. Chem., 2020, 59, 3934–3941 CrossRef CAS PubMed.
- M. Yogesh, M. G. Moinuddin, L. D. Khillare, S. Chinthalapalli, S. K. Sharma, S. Ghosh and K. E. Gonsalves, Organotin bearing polymeric resists for electron beam lithography, Microelectron. Eng., 2022, 260, 111795 CrossRef CAS.
- N. Thakur, M. Vockenhuber, Y. Ekinci, B. Watts, A. Giglia, N. Mahne, S. Nannarone, S. Castellanos and A. M. Brouwer, Fluorine-Rich Zinc Oxoclusters as Extreme Ultraviolet Photoresists: Chemical Reactions and Lithography Performance, ACS Mater. Au, 2022, 2, 343–355 CrossRef CAS PubMed.
- S. Kataoka and K. Sue, Enhanced Solubility of Zirconium Oxo Clusters from Diacetoxyzirconium(IV) Oxide Aqueous Solution as Inorganic Extreme-Ultraviolet Photoresists, Eur. J. Inorg. Chem., 2022, e202200050 CrossRef CAS.
- Z. Wang, X. Yao, H. An, Y. Wang, J. Chen, S. Wang, X. Guo, T. Yu, Y. Zeng, G. Yang and Y. Li, Recent Advances in Organic-inorganic Hybrid Photoresists, J. Microelectron. Manuf., 2021, 4, 21040101 CAS.
- L. Wu, I. Bespalov, K. Witte, O. Lugier, J. Haitjema, M. Vockenhuber, Y. Ekinci, B. Watts, A. M. Brouwer and S. Castellanos, Unravelling the effect of fluorinated ligands in hybrid EUV photoresists by X-ray spectroscopy, J. Mater. Chem. C, 2020, 8, 14757–14765 RSC.
- B. L. Henke, E. M. Gullikson and J. C. Davis, X-ray interactions: photoabsorption, scattering, transmission and reflection at E = 50–30
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
eV, Z = 1–92, At. Data Nucl. Data Tables, 1993, 55, 181–342 CrossRef.
000
eV, Z = 1–92, At. Data Nucl. Data Tables, 1993, 55, 181–342 CrossRef. - R. Fallica, J. K. Stowers, A. Grenville, A. Frommhold, A. P. G. Robinson and Y. Ekinci, Dynamic absorption coefficients of chemically amplified resists and nonchemically amplified resists at extreme ultraviolet, J. Micro/Nanolithogr., MEMS, MOEMS, 2016, 15, 033506 CrossRef.
- D. L. Goldfarb, R. L. Bruce, J. J. Bucchignano, D. P. Klaus, M. A. Guillorn and C. J. Wu, Pattern collapse mitigation strategies for EUV lithography, Proc. SPIE, 2012, 8322, 832205 CrossRef.
- R. Fallica, J. Haitjema, L. Wu, S. Castellanos, A. M. Brouwer and Y. Ekinci, Absorption coefficient of metal-containing photoresists in the extreme ultraviolet, J. Micro/Nanolithogr., MEMS, MOEMS, 2018, 17, 023505 Search PubMed.
- L. Wu, M. F. Hilbers, O. Lugier, N. Thakur, M. Vockenhuber, Y. Ekinci, A. M. Brouwer and S. Castellanos, Fluorescent Labeling to Investigate Nanopatterning Processes in Extreme Ultraviolet Lithography, ACS Appl. Mater. Interfaces, 2021, 13, 51790–51798 CrossRef CAS PubMed.
- N. Thakur, R. Bliem, I. Mochi, M. Vockenhuber, Y. Ekinci and S. Castellanos, Mixed-ligand zinc-oxoclusters: efficient chemistry for high resolution nanolithography, J. Mater. Chem. C, 2020, 8, 14499–14506 RSC.
- L. Wu, M. Tiekink, A. Giuliani, L. Nahon and S. Castellanos, Tuning photoionization mechanisms of molecular hybrid materials for EUV lithography applications, J. Mater. Chem. C, 2019, 7, 33–37 RSC.
- N. Thakur, L.-T. Tseng, M. Vockenhuber, Y. Ekinci and S. Castellanos, Stability studies on a sensitive EUV photoresist based on zinc metal oxoclusters, J. Micro/Nanolithogr., MEMS, MOEMS, 2019, 18, 043504 CAS.
- L. Wu, M. Baljozovic, G. Portale, D. Kazazis, M. Vockenhuber, T. Jung, Y. Ekinci and S. Castellanos, Mechanistic insights in Zr-and Hf-based molecular hybrid EUV photoresists, J. Micro/Nanolithogr., MEMS, MOEMS, 2019, 18, 013504 CAS.
- W. D. Hinsberg and S. Meyers, A numeric model for the imaging mechanism of metal oxide EUV resists, Proc. SPIE, 2017, 10146, 1014604 CrossRef.
- M. C. Sharps, D. A. Marsh, L. N. Zakharov, J. E. Hutchison and D. W. Johnson, Implications of Crystal Structure on Organotin Carboxylate Photoresists, Cryst. Res. Technol., 2017, 52, 1700081 CrossRef.
- R. P. Oleksak, R. E. Ruther, F. Luo, K. C. Fairley, S. R. Decker, W. F. Stickle, D. W. Johnson, E. L. Garfunkel, G. S. Herman and D. A. Keszler, Chemical and Structural Investigation of High-Resolution Patterning with HafSOx, ACS Appl. Mater. Interfaces, 2014, 6, 2917–2921 CrossRef CAS PubMed.
- F. M. F. de Groot and A. Kotani, Core Level Spectroscopy of Solids, CRC Press, 2008 Search PubMed.
- B. K. Agarwal, X-Ray Spectroscopy, an Introduction, Springer, Berlin, 1991 Search PubMed.
- M. Simon, L. Journel, R. Guillemin, W. C. Stolte, I. Minkov, F. Gel’mukhanov, P. Sałek, H. Ågren, S. Carniato, R. Taïeb, A. C. Hudson and D. W. Lindle, Femtosecond nuclear motion of HCl probed by resonant x-ray Raman scattering in the Cl 1s region, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 0207061 CrossRef.
- K. D. Closser, D. F. Ogletree, P. Naulleau and D. Prendergast, The importance of inner-shell electronic structure for enhancing the EUV absorption of photoresist materials, J. Chem. Phys., 2017, 146, 164106 CrossRef PubMed.
- T. Kozawa and S. Tagawa, Radiation Chemistry in Chemically Amplified Resists, Jpn. J. Appl. Phys., 2010, 49, 030001 CrossRef.
- Y. Zhang, J. Haitjema, S. Castellanos, O. Lugier, N. Sadegh, R. Ovsyannikov, E. Giangrisostomi, F. O. L. Johansson, E. Berggren, A. Lindblad and A. M. Brouwer, Extreme ultraviolet photoemission of a tin-based photoresist, Appl. Phys. Lett., 2021, 118, 171903 CrossRef CAS.
- A. Ghosh, S. Pal and N. Vaval, Lifetime of inner-shell hole states of Ar (2p) and Kr (3d) using equation-of-motion coupled cluster method, J. Chem. Phys., 2015, 143, 024305 CrossRef PubMed.
- P. Auger. Auger and P. Sur Les Rayons, β Secondaires Produits Dans Un Gaz Par Des Rayons X, C. R. Acad. Bulg. Sci., 1923, 177, 169–171 Search PubMed.
- L. Meitner, Über die Entstehung der β-Strahl-Spektren radioaktiver Substanzen, Z. Phys., 1922, 9, 131–144 CrossRef CAS.
- J. Torok, R. Del Re, H. Herbol, S. Das, I. Bocharova, A. Paolucci, L. E. Ocola, C. Ventrice Jr, E. Lifshin, G. Denbeaux and R. L. Brainard, Secondary Electrons in EUV Lithography, J. Photopolym. Sci. Technol., 2013, 26, 625–634 CrossRef CAS.
- N. Sadegh, Q. Evrard, N. Mahne, A. Giglia, S. Nannarone and A. M. Brouwer, Electron Generation in Tin-oxo Cage Extreme Ultraviolet Photoresists, J. Photopolym. Sci. Technol., 2023, 36, 373–378 Search PubMed.
- D. Egorov, L. Schwob, M. Lalande, R. Hoekstra and T. Schlathölter, Near edge X-ray absorption mass spectrometry of gas phase proteins: the influence of protein size, Phys. Chem. Chem. Phys., 2016, 18, 26213–26223 RSC.
- A. R. Milosavljević, V. Z. Cerovski, M. L. Ranković, F. Canon, L. Nahon and A. Giuliani, VUV photofragmentation of protonated leucine-enkephalin peptide dimer below ionization energy, Eur. Phys. J. D, 2014, 68, 68 CrossRef.
- A. R. Milosavljevic, F. Canon, C. Nicolas, C. Miron, L. Nahon and A. Giuliani, Gas-phase protein inner-shell spectroscopy by coupling an ion trap with a soft X-ray beamline, J. Phys. Chem. Lett., 2012, 3, 1191–1196 CrossRef CAS PubMed.
- O. González-Magaña, G. Reitsma, M. Tiemens, L. Boschman, R. Hoekstra and T. Schlathölter, Near-Edge X-ray Absorption Mass Spectrometry of a Gas-Phase Peptide, J. Phys. Chem. A, 2012, 116, 10745–10751 CrossRef PubMed.
- O. González-Magaña, M. Tiemens, G. Reitsma, L. Boschman, M. Door, S. Bari, P. O. Lahaie, J. R. Wagner, M. A. Huels, R. Hoekstra and T. Schlathölter, Fragmentation of protonated oligonucleotides by energetic photons and Cq + ions, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 032702 CrossRef.
- K. Hirsch, V. Zamudio-Bayer, J. Rittmann, A. Langenberg, M. Vogel, T. Möller, B. V. Issendorff and J. T. Lau, Initial- and final-state effects on screening and branching ratio in 2p x-ray absorption of size-selected free 3d transition metal clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 165402 CrossRef.
- M. Walter, M. Vogel, V. Zamudio-Bayer, R. Lindblad, T. Reichenbach, K. Hirsch, A. Langenberg, J. Rittmann, A. Kulesza and R. Mitrić, Experimental and Theoretical 2p Core-Level Spectra of Size-Selected Gas-Phase Aluminum and Silicon Cluster Cations: Chemical Shifts, Geometric Structure, and Coordination-Dependent Screening, Phys. Chem. Chem. Phys., 2019, 21, 6651–6661 RSC.
- C. Eychenne-Baron, F. Ribot, N. Steunou, C. Sanchez, F. Fayon, M. Biesemans, J. C. Martins and R. Willem, Reaction of Butyltin Hydroxide Oxide with p-Toluenesulfonic Acid: Synthesis, X-ray Crystal Analysis, and Multinuclear NMR Characterization of {(BuSn)12O14(OH)6}(4-CH3C6H4SO3)2, Organometallics, 2000, 19, 1940–1949 CrossRef CAS.
- C. Eychenne-Baron, F. Ribot and C. Sanchez, New synthesis of the nanobuilding block {(BuSn)12O14(OH)6}2+ and exchange properties of {(BuSn)12O14(OH)6}(O3SC6H4CH3)2, J. Organomet. Chem., 1998, 567, 137–142 CrossRef CAS.
- K. Hirsch, J. T. Lau, P. Klar, A. Langenberg, J. Probst, J. Rittmann, M. Vogel, V. Zamudio-Bayer, T. Möller and B. Von Issendorff, X-ray spectroscopy on size-selected clusters in an ion trap: from the molecular limit to bulk properties, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154029 CrossRef.
- M. Niemeyer, K. Hirsch, V. Zamudio-Bayer, A. Langenberg, M. Vogel, M. Kossick, C. Ebrecht, K. Egashira, A. Terasaki, T. Möller, B. V. Issendorff and J. T. Lau, Spin coupling and orbital angular momentum quenching in free iron clusters, Phys. Rev. Lett., 2012, 108, 057201 CrossRef CAS PubMed.
- M. Flach, K. Hirsch, M. Timm, O. S. Ablyasova, M. Da Silva Santos, M. Kubin, C. Bülow, T. Gitzinger, B. Von Issendorff, J. T. Lau and V. Zamudio-Bayer, Iron L3-edge energy shifts for the full range of possible 3d occupations within the same oxidation state of iron halides, Phys. Chem. Chem. Phys., 2022, 24, 19890–19894 RSC.
- D. Dakternieks, H. Zhu, E. R. T. Tiekink and R. Colton, Synthesis, structure and reactions of [(BuSn)12O14(OH)6]Cl2.2H2O: Solution studies using 119Sn NMR and electrospray mass spectrometry, J. Organomet. Chem., 1994, 476, 33–40 CrossRef CAS.
- J. Raabe, G. Tzvetkov, U. Flechsig, M. Böge, A. Jaggi, B. Sarafimov, M. G. Vernooij, T. Huthwelker, H. Ade, D. Kilcoyne, T. Tyliszczak, R. H. Fink and C. Quitmann, PolLux: a new facility for soft x-ray spectromicroscopy at the Swiss Light Source, Rev. Sci. Instrum., 2008, 79, 113704 CrossRef CAS PubMed.
- U. Frommherz, J. Raabe, B. Watts, R. Stefani, U. Ellenberger, R. Garrett, I. Gentle, K. Nugent and S. Wilkins, Higher Order Suppressor (HOS) for the PolLux Microspectroscope Beamline at the Swiss Light Source SLS, AIP Conf. Proc., 2010, 1234, 429–432 CrossRef.
- D. A. Outka and J. Stöhr, Curve fitting analysis of near-edge core excitation spectra of free, adsorbed, and polymeric molecules, J. Chem. Phys., 1988, 88, 3539–3554 CrossRef.
- R. J. Klein, D. A. Fischer and J. L. Lenhart, Systematic oxidation of polystyrene by ultraviolet-ozone, characterized by near-edge X-ray absorption fine structure and contact angle, Langmuir, 2008, 24, 8187–8197 CrossRef CAS PubMed.
- X. Zhang, C. Jacobsen, S. Lindaas and S. Williams, Exposure strategies for polymethyl methacrylate from in situ x-ray absorption near edge structure spectroscopy, J. Vac. Sci. Technol., B, 1995, 13, 1477–1483 CrossRef CAS.
- J. Wang, H. D. Stöver, A. P. Hitchcock and T. Tyliszczak, Chemically selective soft X-ray patterning of polymers, J. Synchrotron Radiat., 2007, 14, 181–190 CrossRef CAS PubMed.
- O. Dhez, H. Ade and S. G. Urquhart, Calibrated NEXAFS spectra of some common polymers, J. Electron Spectrosc. Relat. Phenom., 2003, 128, 85–96 CrossRef CAS.
- B. Ravel and M. Newville, ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- Igor Pro v.8; Wavemetrics: Lake Oswego, Oregon, USA.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.02, 2016 Search PubMed.
- I. Bespalov, Y. Zhang, J. Haitjema, R. M. Tromp, S. J. Van Der Molen, A. M. Brouwer, J. Jobst and S. Castellanos, Key Role of Very Low Energy Electrons in Tin-based Molecular Resists for Extreme Ultraviolet Nanolithography, ACS Appl. Mater. Interfaces, 2020, 12, 9881–9889 CrossRef CAS PubMed.
- L. Triguero, L. G. M. Pettersson and H. Ågren, Calculations of near-edge x-ray-absorption spectra of gas-phase and chemisorbed molecules by means of density-functional and transition-potential theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8097–8110 CrossRef CAS.
- G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- S. D. Perera, S. Shokatian, J. Wang and S. G. Urquhart, Temperature Dependence in the NEXAFS Spectra of n-Alkanes, J. Phys. Chem. A, 2018, 122, 9512–9517 CrossRef CAS PubMed.
- K. Lopata, B. E. Van Kuiken, M. Khalil and N. Govind, Linear-Response and Real-Time Time-Dependent Density Functional Theory Studies of Core-Level Near-Edge X-Ray Absorption, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS PubMed.
- R. Fallica, B. Watts, B. Rösner, G. Della Giustina, L. Brigo, G. Brusatin and Y. Ekinci, Changes in the near edge x-ray absorption fine structure of hybrid organic–inorganic resists upon exposure, Nanotechnology, 2018, 29, 36LT03 CrossRef PubMed.
- J. Haitjema, L. Wu, A. Giuliani, S. Castellanos, L. Nahon and A. M. Brouwer, UV and VUV-induced fragmentation of tin-oxo cage ions, Phys. Chem. Chem. Phys., 2021, 23, 20909–20918 RSC.
- S. G. Urquhart and R. Gillies, Rydberg−Valence Mixing in the Carbon 1s Near-Edge X-ray Absorption Fine Structure Spectra of Gaseous Alkanes, J. Phys. Chem. A, 2005, 109, 2151–2159 CrossRef CAS PubMed.
- S. G. Urquhart and R. Gillies, Matrix effects in the carbon 1 s near edge x-ray absorption fine structure spectra of condensed alkanes, J. Chem. Phys., 2006, 124, 234704 CrossRef PubMed.
- P. E. Schwenn, P. L. Burn and B. J. Powell, Calculation of solid state molecular ionisation energies and electron affinities for organic semiconductors, Org. Electron., 2011, 12, 394–403 CrossRef CAS.
- S. Jana and J. M. Herbert, Fractional-Electron and Transition-Potential Methods for Core-to-Valence Excitation Energies Using Density Functional Theory, J. Chem. Theory Comput., 2023, 19, 4100–4113 CrossRef CAS PubMed.
- P. Norman and A. Dreuw, Simulating X-ray Spectroscopies and Calculating Core-Excited States of Molecules, Chem. Rev., 2018, 118, 7208–7248 CrossRef CAS PubMed.
- A. Sharma, M. Varshney, H. J. Shin, K. H. Chae and S. O. Won, X-ray absorption spectroscopy investigations on electronic structure and luminescence properties of Eu:SnO2-SnO nanocomposites, Curr. Appl. Phys., 2016, 16, 1342–1348 CrossRef.
- M. Paradiz Dominguez, Q. Evrard, B. Watts and A. M. Brouwer, unpublised observations, 2022.
- C. E. Liekhus-Schmaltz, I. Tenney, T. Osipov, A. Sanchez-Gonzalez, N. Berrah, R. Boll, C. Bomme, C. Bostedt, J. D. Bozek and S. Carron, Ultrafast isomerization initiated by X-ray core ionization, Nat. Commun., 2015, 6, 8199 CrossRef PubMed.
- J. Haitjema, Y. Zhang, R. Hoekstra, T. Schlathölter and A. M. Brouwer. Extreme Ultraviolet Photofragmentation of Tin-oxo Cage Ions as Model Photoresists. manuscript in preparation, 2024.
- T. Jahnke, U. Hergenhahn, B. Winter, R. Dörner, U. Frühling, P. V. Demekhin, K. Gokhberg, L. S. Cederbaum, A. Ehresmann and A. Knie, Interatomic and intermolecular Coulombic decay, Chem. Rev., 2020, 120, 11295–11369 CrossRef CAS PubMed.
- J. J. Yeh and I. Lindau, Atomic Photoionization Cross Sections and Asymmetry parameters: 1 ≤ Z ≤ 103, At. Data Nucl. Data Tables, 1985, 32, 1–155 CrossRef CAS.
- J. H. Ma, C. Needham, H. Wang, A. Neureuther, D. Prendergast and P. Naulleau, Mechanistic Advantages of Organotin Molecular EUV Photoresists, ACS Appl. Mater. Interfaces, 2022, 14, 5514–5524 CrossRef CAS PubMed.
- J. Haitjema, Y. Zhang, N. Ottosson and A. M. Brouwer, Photoreactions of Tin Oxo Cages, Model EUV Photoresists, J. Photopolym. Sci. Technol., 2017, 30, 99–102 CrossRef CAS.
- J. H. Ma, H. Wang, D. Prendergast, A. Neureuther and P. Naulleau, Excitation selectivity in model tin-oxo resist: a computational chemistry perspective, Proc. SPIE, 2020, 11323, 113231F Search PubMed.
- G. Gopakumar, I. Unger, P. Slavíček, U. Hergenhahn, G. Öhrwall, S. Malerz, D. Céolin, F. Trinter, B. Winter and I. Wilkinson, Radiation damage by extensive local water ionization from two-step electron-transfer-mediated decay of solvated ions, Nat. Chem., 2023, 15, 1408–1414 CrossRef CAS PubMed.
- M. Hervé, A. Boyer, R. Brédy, I. Compagnon and F. Lépine, Ultrafast dynamics in molecular ions following UV and XUV excitation: a perspective, Adv. Phys.: X, 2022, 7, 2123283 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Fit parameters for the XAS spectra; C K-edge absorption spectrum of TinOH; representative C 1s XAS spectra calculated for the bare tin cage; calculated XAS of the bare tin cage dication at the O K-edge; photofragmentation MS spectra over the range 100 < m/z < 1400; absorption cross sections due to different elements at the C and O K-edges; calculated Density of States of bare tin-oxo cage dication. Energies of the relevant species from DFT calculations. See DOI: https://doi.org/10.1039/d3cp05428d |
| ‡ Present addres: University of Amsterdam, van’t Hoff Institute for Molecular Sciences, P.O. Box 94157, 1090 GD Amsterdam, The Netherlands |
| § Present addres: Berlin Partner für Wirtschaft und Technologie GmbH, Fasanenstrasse 85, 10623 Berlin, Germany. |
| This journal is © the Owner Societies 2024 |