Investigating theoretical and experimental cross sections for elastic electron scattering from isoflurane†
Jelena
Vukalović
 *ab,
Bratislav P.
Marinković
*ab,
Bratislav P.
Marinković
 a,
Jaime
Rosado
c,
Francisco
Blanco
c,
Gustavo
García
a,
Jaime
Rosado
c,
Francisco
Blanco
c,
Gustavo
García
 d and
Jelena B.
Maljković
a
d and
Jelena B.
Maljković
a
aInstitute of Physics Belgrade, University of Belgrade, Pregrevica 118, Belgrade, 11080, Serbia. E-mail: jelenam@ipb.ac.rs
bFaculty of Science, University of Banja Luka, Mladena Stojanovic’a 2, 78000 Banja Luka, Republic of Srpska, Bosnia and Herzegovina. E-mail: jelena.vukovic@pmf.unibl.org
cDepartamento de Física Atómica Molecular y Nuclear, Facultad de Ciencias Físicas, Universidad Complutense, Avda. Complutense s/n, E-28040 Madrid, Spain
dInstituto de Física Fundamental, Consejo Superior de Investigaciones Científicas, Serrano 121, 28006 Madrid, Spain
First published on 7th December 2023
Abstract
We present a comprehensive analysis of elastic electron scattering from isoflurane in the intermediate energy range of 50–300 eV. This research is motivated by the significant impact of this molecule on global warming effects. We conducted this investigation through experimental measurements using a crossed-beam apparatus and covering a wide angular range from 25 to 125 degrees. Relative differential cross sections (DCSs) were obtained and subsequently normalized on an absolute scale by using the relative flow technique, with argon as the reference gas. These DCS values were then extrapolated and integrated to determine the experimental integral cross sections (ICSs). Additionally, we employed the independent atom model and the screening corrected additivity rule with incorporated Interference effects (IAM-SCAR+I) to calculate the theoretical differential and integral cross-sections. Remarkably, the calculated cross sections align closely with the experimental measurements across the entire energy and angular range. Furthermore, this study involved a comparison of the DCSs for isoflurane with previously published DCS values for two other volatile anesthetics, sevoflurane and halothane.
1 Introduction
Since it was developed roughly 50 years ago by Ohio Medicine Products, isoflurane (2-chloro-2-(difluoromethoxy)-1,1,1-trifluoroethane, CF3CHCl–O–CHF2) has been widely used as an inhalational anesthetic.1 It is a non-flammable halogenated ether, a clear, colorless liquid with a mild odor. It has a molecular weight of 184.49 g mol−1, a boiling point of 48.5 °C, a vapor pressure of 330 mmHg,2 and an estimated dipole moment of 2.47 D.3Because of its connection to climate change, isoflurane has lately caught the scientific community's attention. It has been shown that the vast majority of anesthetics administered do not undergo metabolization4 and are consequently discharged unaltered from the patient's body into the lower atmosphere.5 Moreover, it is well-established that the release of these anesthetic compounds has been progressively increasing over time.6 The reactivity of the anesthetic compounds with OH radicals determines their fate in the atmosphere,7 and their atmospheric lifetime can be estimated by measuring the rate coefficient for this reaction. Using this approach, the atmospheric lifetime of isoflurane is calculated to be between 2 and 5.9 years,8–11 long enough to cause some damage. As a halogenated compound, isoflurane has a high global warming potential (GWP). The isoflurane GWP (for a 100 year time horizon), relative to CO2, was reported by Brown et al.,8 the WMO,12 Andersen et al.,9 Langbein et al.,11 and Ryan and Nielsen10 to be 328, 470, 510, 545, and 571, respectively. The scheme of the isoflurane structure is illustrated in Fig. 1.
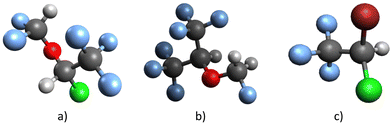 | ||
| Fig. 1 The illustration depicts the structure of (a) isoflurane, along with (b) sevoflurane and (c) halothane, providing a basis for comparison. | ||
The papers authored by Campbell and Brunger13,14 highlight the importance of electron collisions in the atmosphere. The initial one13 tackled electron collisions in atmospheres, focusing on scenarios where electron impact drives, enhances, or otherwise interacts with chemical processes. To comprehend atmospheric processes, a computational simulation incorporating theory, remotely sensed atmospheric data, atomic and molecular physics data and chemical reaction rates was employed. In the second paper,14 a time-step simulation incorporating energy-dependent electron interactions was utilized to replicate electron interactions in the Earth's nighttime mesosphere. A simplified model involving a few processes was executed under two assumptions: one considering electrons at neutral temperature and the other assuming they possess higher energy for a finite duration, gradually losing it in elastic and inelastic collisions with molecules. The results indicated minimal disparity in the predicted electron densities between the two approaches.
All of the aforementioned data suggests that isoflurane's impact on global warming should not be disregarded. Therefore, it is understandable why it is important to study how electrons interact with the referenced molecule.
Several relevant research studies on isoflurane will be presented below.
Gas electron diffraction (GED) and quantum chemical calculations were employed to investigate the geometric structure and conformational properties of the inhalation anesthetics desflurane and isoflurane.15 Both compounds exhibit a mixture of two conformers in the gas phase. The dominant conformer displays a nearly trans configuration of the C–C–O–C skeleton and a trans orientation of the CHF2 group (with the C–H bond trans to the O–C bond). In the minor conformer, the CHF2 group is gauche-oriented.
Negative ion formation through dissociative electron attachment to gas-phase isoflurane has been studied in a crossed electron-molecular beam two-sector field mass spectrometer experiment by Matias et al.16 Anion efficiency curves for the negatively charged fragments were measured across an electron energy range of approximately 0–17 eV. The product anions were predominantly detected in the energy regions of 2–3 eV and 9 eV, except for Cl−, which exhibited a dominant resonance at around 0.6 eV. Additionally, quantum chemical calculations were employed to determine the thermochemical thresholds of anion formation, aiding in the interpretation of the experimental findings.
In their study, Lange et al.17 explored the lowest-lying electronic states of isoflurane and sevoflurane within the energy range of 5.0–10.8 eV using a combination of experimental and theoretical methods. The photoabsorption spectra of isoflurane and sevoflurane were measured using synchrotron radiation across the photon range of 5.0–10.8 eV. The focus of the investigation was on low-lying excited singlet valence and Rydberg states, with the assignments supported by quantum chemical calculations, which also aided in the identification of triplet states.
The main reference for this paper is E. Lange's PhD thesis,18 which presents both theoretical and experimental investigations on elastic electron scattering from isoflurane. The thesis encompasses theoretical differential and integral cross sections (DCSs and ICSs) obtained using the Schwinger multichannel method with pseudopotentials, as well as an independent atom model incorporating screening-corrected additivity rules and interference effects (IAM-SCAR+I). Experimental DCSs were measured within an incident electron energy range of 10 to 50 eV, covering an angular range of 8° to 70°, utilizing a high-resolution electron energy loss spectrometer. The absolute scale of the experimental DCS was established by normalizing it to the IAM-SCAR+I calculation at a scattering angle of 30°. The obtained results demonstrate reasonable agreement with the theoretical predictions.
Here, experimental and theoretical cross sections for elastic electron scattering from isoflurane are presented. The experiments were conducted within a specific range of incident electron energy (E0), from 50 to 300 eV, and a limited angular range of 25° to 125°. Using the cross-beam electron spectrometer technique, absolute differential cross sections (DCSs) have been experimentally determined. Initially, relative DCSs were obtained, and then they were calibrated to the absolute scale using the relative flow method with argon (Ar) as the reference gas. In addition, we compared DCSs for isoflurane with previously published DCSs for two other volatile anesthetics, namely sevoflurane19 and halothane.20 All three anesthetics were examined using the same apparatus and under similar experimental conditions. The comparison was conducted at incident electron energies of 100, 200, and 300 eV. The accuracy of the present experimental data is supported by calculations performed within the IAM-SCAR+I model. This report also includes integral cross sections (ICSs), both theoretical and experimental, for elastic electron scattering within the specified energy range.
It is important to highlight that, according to the author's awareness, there is only a single prior publication on the topic of theoretical and experimental DCSs and ICSs for elastic electron scattering from isoflurane, i.e. the PhD thesis by E. Lange.18
2 Experiment
Our electron scattering spectrometer features an electron gun, gas needle, analysis system, and detector in a chamber shielded by two concentric μ-metal layers for reduced magnetic disturbances. The electron gun, with seven electrodes, directs electrons into the interaction volume. The incident electron beam current is 100 nA for a filament current of 2.22 A in the absence of the investigated gas. The potential difference between the filament and the grounded electrode determines electron energy (40 to 300 eV). The incident electron and gas beams collide perpendicularly, meeting the optimized beam characteristics.19,21,22 Scattered electrons interact with the target molecule before entering the energy-analyzing system, which uses a four-electrode lens to guide and concentrate them. The analyzer, consisting of two connected cylindrical analyzers, allows elastically scattered electrons to pass through based on the potential difference between the cylinders. A 3-electrode lens then focuses these electrons into a channeltron-type detector, measuring scattered electron intensity within an angular range of 25 to 125 degrees with a resolution better than ±2. Anhydrous isoflurane (>99% purity) served as the target gas, introduced via a gas needle connected to a gas line system. Under optimal vacuum conditions, the base pressure was 6 × 10−7 mbar, increasing upon introducing the gas by an order of magnitude.This study explores the absolute differential cross section for elastic electron scattering from isoflurane in two stages.
In stage 1, the study measures electron intensity for elastic scattering (relative DCSs) at various angles (25 to 125 degrees) with fixed primary electron energies (50 to 300 eV). To minimize background noise, isoflurane is introduced away from the interaction area using a side leak. The scattered electron intensity is measured for each angle at specified incident electron energy, and this background signal is subtracted from the observed signal. To maintain a constant interaction area, adjustments are made to the electrodes of the electron gun and the potentials of the analyzing system. Corrections for small-angle deviations are implemented by comparing the relative differential cross sections measured from argon, under the same experimental conditions, to previously published values.23,24
Stage 2 involves obtaining absolute data points for each energy and normalizing relative cross sections using the relative flow method (RFM) developed by Srivastava et al.25 Scattered electron intensity is measured for both isoflurane and reference gas (argon), along with gas flow rates. Pressure ratio behind the gas needle is adjusted to ensure an equal mean free path for both gases, with low pressures maintaining a mean free path approximately equal to the gas needle diameter.26 For each incident electron energy, two absolute data points are determined. Measurement cycle involves introducing target gas through the gas needle and argon through a side entrance, recording scattered electron intensity, measuring pressure increase over time, and calculating flow rates using the least-squares method. The process was similarly repeated for the reference gas, and the entire cycle was conducted 2 to 3 times. The process yields absolute differential cross sections for elastic electron scattering on the target molecule.27,28
Given the limited scope of our experimental angles, it is necessary to extrapolate measured differential cross sections to include the smallest (0 degrees) and largest (180 degrees) scattering angles. This was achieved by normalizing our theoretical data to experimental data to best match. The normalized theoretical points at small (0–30 degrees) and large angles (120–180 degrees) were considered as extrapolated experimental points. The objective is to obtain elastic integral cross sections (ICSs) that encompass the entire angular range.
Regarding measurement uncertainties, several factors were considered, including statistical variability, short-term stability uncertainty due to system instability, uncertainty related to reference absolute cross sections, and uncertainty from the correction factor for the effective interaction volume. The most significant uncertainty, around 20%, stemmed from the reference absolute cross sections for argon.23,24 To accommodate potential changes in the interaction volume, uncertainties at small scattering angles were increased by 20%. The overall uncertainty for DCSs was calculated by summing the squares of individual independent uncertainties and taking the square root. The total uncertainties of the integral cross sections (30%) arise from the absolute DCS uncertainties (25% in average) and uncertainties of the extrapolation of DCSs to 0° and to 180° (15%) and numerical integration (8%). Following the same procedure as for DCS uncertainties, the overall uncertainty was calculated by taking the square root of the sum of the squares of the individual independent uncertainties.
3 Theory
To determine the differential and integral elastic scattering cross sections, we utilized the IAM-SCAR+I approach, which combines the independent atom model (IAM) with the screening corrected additivity rule (SCAR) and incorporates interference effects (I). The details of this methodology have been extensively documented in earlier publications.29–33 Therefore, only a concise overview will be provided in this context.The molecular target is described as the combination of its constituent atoms (C, H, F, O, and Cl, in the case of isoflurane), and each atomic target is characterized by an “ab initio” interacting complex optical potential derived from:
Vopt(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = VR( ) = VR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) + iVabs( ) + iVabs(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ) | (1) |
VR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = Vs( ) = Vs(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) + Vex( ) + Vex(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) + Vpol( ) + Vpol(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), ), | (2) |
The cross sections of the molecule are determined by combining the atomic data and summing the relevant atomic amplitudes, including phase coefficients, through the application of the screening corrected additivity rule (SCAR) technique.37 This process incorporates the necessary corrections for interference (I) terms.31 By employing this methodology, we calculate the differential scattering cross section (DCS) for the molecule. Integration of the DCS over the entire range of scattered electron angles yields the integral scattering cross section (ICS).
It is worth noting that, up to this point, we have not accounted for any contributions from rotational or vibrational excitation processes. However, in the case of isofurane, rotational excitations play a significant role due to its polar nature, characterized by a permanent dipole moment of 2.47 D.3 To address this, we followed the approach outlined by Fuss et al.33 We employed the first-Born approximation to effectively incorporate the differential and integral cross sections for rotational excitation. In this approximation, we treated the molecule as a rigid rotor, assuming an initial distribution of rotationally excited states in thermal equilibrium at 300 K. Using this method, we calculated transitions for ΔJ = ±1, where J represents the rotational quantum number. Furthermore, we included corrections for large scattering angles, as described by Dickinson (see ref. 38 and references therein). These corrections were essential to account for the specific characteristics of the scattering process in these regions.
4 Results
The absolute differential cross sections (DCSs) for elastic electron-isoflurane scattering experimentally determined in this study are shown in Table 1. These measurements were conducted at incident electron energies of 50, 100, 150, 200, 250, and 300 eV, covering the angular range from 25° to 125° with 5-degree increments. Additionally, experimental integral cross sections (ICS) for these energies, derived with the procedure described above, are also shown in this table.| θ (°) | DCS (10−20 m2 sr−1) | |||||
|---|---|---|---|---|---|---|
| 50 (eV) | 100 (eV) | 150 (eV) | 200 (eV) | 250 (eV) | 300 (eV) | |
| 25 | 5.0(1.5) | 5.6(1.6) | 3.07(98) | 2.67(76) | 3.29(96) | 2.74(78) |
| 30 | 3.4(1.0) | 3.50(99) | 1.97(63) | 1.45(41) | 1.79(52) | 1.64(47) |
| 35 | 2.52(75) | 2.51(71) | 1.09(35) | 0.97(28) | 1.32(39) | 1.24(35) |
| 40 | 1.98(59) | 1.63(46) | 0.70(22) | 0.77(22) | 1.00(29) | 0.84(24) |
| 45 | 1.48(33) | 0.90(18) | 0.53(13) | 0.65(13) | 0.57(12) | 0.50(10) |
| 50 | 1.28(28) | 0.66(13) | 0.45(11) | 0.472(96) | 0.389(84) | 0.314(64) |
| 55 | 1.06(23) | 0.55(11) | 0.351(88) | 0.311(63) | 0.266(58) | 0.232(48) |
| 60 | 0.82(18) | 0.453(91) | 0.259(65) | 0.220(45) | 0.215(47) | 0.200(41) |
| 65 | 0.68(15) | 0.419(84) | 0.205(52) | 0.171(35) | 0.198(43) | 0.182(38) |
| 70 | 0.57(13) | 0.367(74) | 0.160(40) | 0.150(31) | 0.187(41) | 0.143(30) |
| 75 | 0.46(10) | 0.304(61) | 0.144(36) | 0.142(29) | 0.152(33) | 0.135(28) |
| 80 | 0.430(95) | 0.249(50) | 0.135(34) | 0.140(29) | 0.124(27) | 0.111(23) |
| 85 | 0.409(90) | 0.239(48) | 0.138(35) | 0.126(26) | 0.118(26) | 0.111(23) |
| 90 | 0.397(87) | 0.207(42) | 0.136(35) | 0.127(26) | 0.122(27) | 0.105(22) |
| 95 | 0.386(85) | 0.214(43) | 0.13e7(35) | 0.123(25) | 0.111(25) | 0.094(20) |
| 100 | 0.418(92) | 0.222(45) | 0.132(33) | 0.124(26) | 0.1058(23) | 0.083(18) |
| 105 | 0.46(10) | 0.232(47) | 0.140(35) | 0.112(23) | 0.102(23) | 0.083(18) |
| 110 | 0.53(12) | 0.244(49) | 0.143(36) | 0.112(23) | 0.096(21) | 0.085(18) |
| 115 | 0.62(14) | 0.292(59) | 0.164(41) | 0.117(24) | 0.102(23) | 0.091(19) |
| 120 | 0.70(15) | 0.332(67) | 0.170(43) | 0.124(26) | 0.099(22) | 0.097(21) |
| 125 | 0.79(17) | 0.389(78) | 0.199(50) | 0.125(26) | 0.099(22) | 0.095(20) |
| ICSs | 33.1 | 30.4 | 21.5 | 22.4 | 18.4 | 18.0 |
Fig. 2 illustrates the comparison between the theoretical (elastic, rotational and elastic + rotational) and experimental DCS values. The corresponding experimental and theoretical ICS values for elastic, inelastic, and total cross sections are shown in Fig. 3. The experimental ICSs for elastic scattering conducted by Lange18 are also included in Fig. 3. Furthermore, Fig. 4 presents a comparison of the DCSs for isoflurane, sevoflurane, and halothane at incident electron energies of 100, 200, and 300 eV.
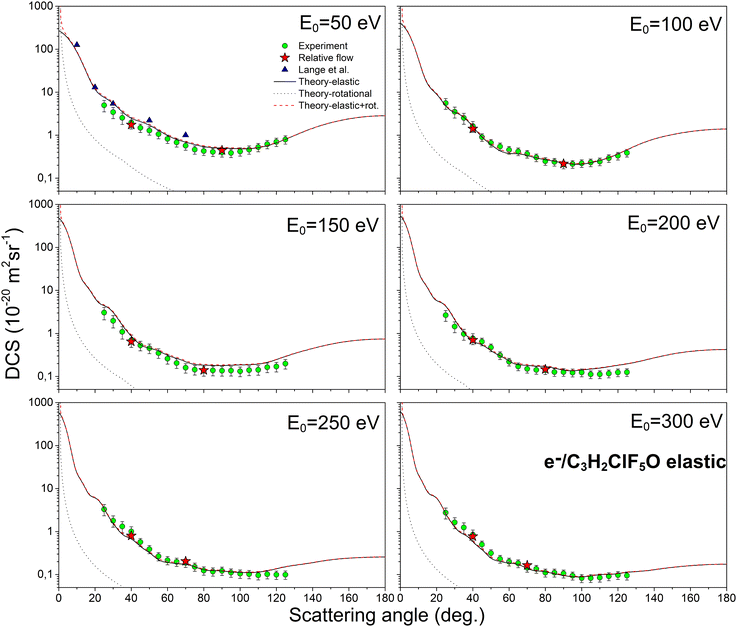 | ||
| Fig. 2 The absolute differential cross sections (in units of 10−20 m2 sr−1) for elastic electron scattering from an isoflurane molecule at energies of 50, 100, 150, 200, 250, and 300 eV. Figure includes several sets of data: the present experimental data are represented by circles (green online), the present theoretical results shown by a black solid line for elastic DCSs, black dots for rotational DCSs, and a dashed line (red online) for the combination of elastic and rotational DCSs. Additionally, experimental absolute points obtained using the relative flow method are denoted by stars (red online), and the experimental results obtained by Lange18 at 50 eV are indicated by triangles (blue online). | ||
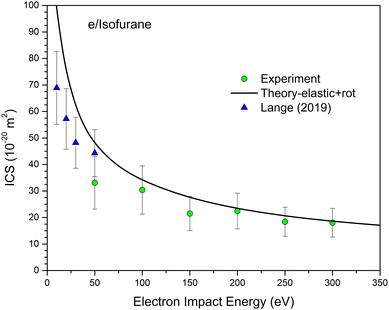 | ||
| Fig. 3 The absolute integral cross sections (in units of 10−20 m2) for elastic electron scattering from isoflurane molecule. Present experimental data are represented by circles (green online), the present theoretical results shown by a black solid line for elastic plus rotational ICSs, and the experimental results obtained by Lange19 as triangles (blue online). | ||
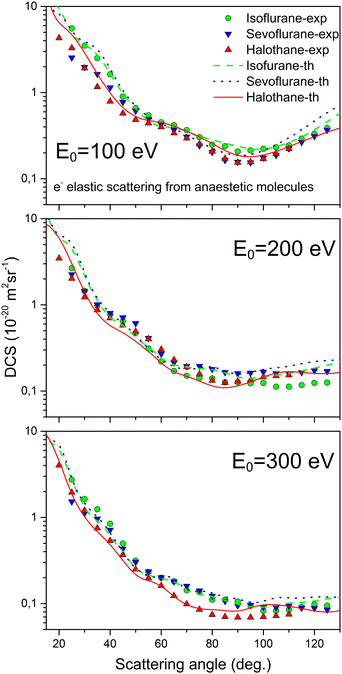 | ||
| Fig. 4 Absolute DCSs for elastic electron scattering from various anesthetic molecules at incident energies of 100, 200, and 300 eV. | ||
As depicted in Fig. 2, our experimental results are strongly supported by our theoretical differential cross sections. Notably, excellent agreement is observed at 100 eV electron energy. However, a deviation between theory and experiment is observed at 50 eV and 25 degrees scattering angle. This discrepancy likely arises from saturation of the electron multiplier detector (channeltron) during the experiment when the system is set for high-statistics measurements at minimum. Extremely high counts at small angles (for low-energy incident electrons) result from a relatively large primary electron current, low energy resolution, and the fact that cross sections in this angular range can vary by several orders of magnitude. Also, our DCS values at 150 eV are systematically smaller than calculated ones, which reflects consequently in lower ICS. It is important to emphasize that rotational excitations and elastic scattering are not distinguished in our experimental conditions. For this reason, we are comparing our experimental “quasi-elastic” cross sections with the sum of our calculated elastic and rotational cross sections. Consistent with previous observations,19,20,39 the DCSs exhibit typical behavior for molecular targets. They demonstrate a broad minimum around 100° for electron energies of 50 and 100 eV, gradually diminishing. Moreover, at scattering angles ranging from 80 to 125 degrees and electron energies of 200, 250, and 300 eV, the DCSs remain relatively constant.
In Fig. 2, by comparing the theories for pure elastic cross sections and elastic + rotational cross sections it can also be observed that the contribution of rotational excitations is very significant at very small scattering angles, especially for the incident electron energy of 50 eV. Considering that isoflurane is a polar molecule with a strong permanent dipole moment,3 such a significant role of rotational excitations in the scattering process is expected.
We compared our results obtained at 50 eV electron energy with those of Lange.18 DCSs for elastic electron-isoflurane scattering at electron energies of 10, 20, 30, and 50 eV are there reported18 within the angular range of 8°–70°. At the scattering angle of 30 degrees, a good agreement is evident, within the experimental error. However, for the remaining scattering angles, our experimental results exhibit lower values. To the best of our knowledge, there are no other available published DCS data for incident electron energies between 100 eV and 300 eV.
As mentioned earlier, we utilized relative flow measurements for normalizing our experimental data with Ar as the reference gas. Absolute differential cross-sections for Ar were acquired by Ranković et al.23 (50–200 eV and 300 eV) and Williams and Willis24 (including 250 eV), both employing electron spectrometers with different normalization methods. Opting for values from the most recent study23 ensured compatibility with our experiment's electron spectrometer and normalization procedure. For the 250 eV energy we used the values from Williams and Willis.24 We obtained two absolute points for each energy and then normalized our relative DCSs to them. As shown in Fig. 2, these points align excellently with the present experimental data.
In Fig. 3, it is evident that although the experimental and theoretical integral cross sections share similar shapes, the measured data points show lower magnitudes compared to the calculated values. Given the limited angular range of our DCS data, the reported integral cross sections heavily depend on extrapolation. To achieve optimal shape matching, we normalized our calculated DCSs to our measured absolute data, and these values were used for integration. The obtained ICSs, listed in Table 1, carry an uncertainty of approximately 30%, stemming from various reliable extrapolations (refer to Section 3 for additional details). The most significant disparities occur at electron energies of 50 and 150 eV. At 50 eV, this deviation is attributed to notable deviations at small scattering angles, caused by channeltron saturation. Similarly, at 150 eV, our measured DCSs systematically display lower values compared to the theoretical ones, resulting in lower integral cross section. For the remaining electron energies, the agreement is highly satisfactory (within the range of experimental error). At the single energy point (50 eV) where our experimental results coincide with those of Lange,18 we observed that our data point exhibits a lower magnitude.
Fig. 4 illustrates a comparison of the present DCSs for elastic electron-isoflurane scattering at 100 eV, 200 eV, and 300 eV with the absolute experimental and theoretical DCSs for elastic electron scattering from two other anesthetic gases: sevoflurane19 and halothane.20 The three anesthetics were all examined using the same apparatus and under comparable experimental conditions. Additionally, the same calculation model (IAM-SCAR+I) was employed to obtain theoretical differential cross sections for the all three gases. It is evident that their cross sections exhibit significant similarity, both in shape and on the absolute scale. Given their comparable gas kinetic diameters and molar masses, this outcome was somewhat expected.
Certain deviations between theory and experiment can be observed for all three molecules at larger scattering angles, especially at higher energies (200 and 300 eV). Two possible sources of this are envisage. First, during the experiment, we had a much lower electron count at large angles and a higher beckground contribution. On the other hand, theory also encounters challenges for medium and large scattering angles when the molecule has a large permanent dipole moment. The issue was partly resolved through the implementation of the correction proposed by Dickinson.38 Only in the case of halothane, for energies of 100 and 200 eV, there are no deviations. The reason is likely that in those cases, the electron count was the highest, and halothane is the least polar among these three molecules.
5 Conclusions
Both experimental and theoretical investigations have been focused on the elastic scattering of electrons from the isoflurane molecule. The measurements and calculations were carried out within the intermediate energy range of 50–300 eV. The experimental results encompass differential cross sections (DCSs) within the angular range of 25–125 degrees and integral cross sections (ICSs). By utilizing the relative flow technique, with Ar as reference gas, two absolute points were obtained at each electron impact energy, thus allowing the normalization of the relative DCSs onto an absolute scale. The good agreement between these two independent sets of measurements – normalized relative DCSs and relative flow absolute points – validates our experimental method. The theoretical results, obtained through the IAM-SCAR+I methodology, include elastic and rotational DCSs and elastic, inelastic, and total ICSs. Remarkably, we observed an excellent agreement between the current experimental and theoretical DCSs with the absolute values provided by the relative flow technique. The comparative DCSs for the anesthetic gases: isoflurane, sevoflurane, and halothane exhibit notable similarities, as anticipated, considering their similar sizes.This study is primarily driven by the significant global warming potential of isoflurane. In this context, electron interactions with isoflurane play a pivotal role, potentially producing reactive species and inducing molecule decomposition through processes like dissociation, dissociative ionization, or electron attachment. On the other hand, the elastic channel dominates in electron–molecule interactions across most collisional energies. As discussed in this manuscript, there is a widespread lack of collisional data in this area. As far as we know, these are the first published absolute differential cross-section data for elastic electron scattering from isoflurane at incident electron energies of 100, 150, 200, 250, and 300 eV. These data are of utmost importance for the mentioned atmospheric applications.
Author contributions
Conceptualization, all authors; methodology, J. B. M. and B. P. M.; software, F. B. and G. G.; validation, all authors; experimental investigation, J. V. and J. B. M.; resources, B. P. M.; data curation, B. P. M.; writing – original draft preparation, J. V.; writing – review and editing, B. P. M. and J. B. M.; visualization, J. V. and B. P. M.; supervision, B. P. M.; project administration, B. P. M. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Science Fund of the Republic of Serbia, Grant No. 6821, Project title – ATMOLCOL. The article is based upon work from COST Actions CA18212 – Molecular Dynamics in the GAS phase (MD-GAS) and CA20129-Multiscale Irradiation and Chemistry Driven Processes and Related Technologies (MultIChem), supported by COST (European Cooperation in Science and Technology). J. V., J. B. M. and B. P. M. acknowledge the support by the Institute of Physics Belgrade, which was made possible by grants from the Ministry of Science, Technological Development and Innovations of the Republic of Serbia. J. R., F. B. and G. G. acknowledge the partial financial support from the Spanish Ministry of Science and Innovation (Project PID2019-104727RB) and the EURAMET 21GRDO2-BIOSPHERE project.Notes and references
- D. H. Robinson and A. H. Toledo, J. Invest. Surg., 2012, 25, 141–149 CrossRef PubMed.
- PubChem Database [Online], Accessed on 20. July 2023, Available: https://pubchem.ncbi.nlm.nih.gov/.
- M. J. Arcario, C. G. Mayne and E. Tajkhorshid, J. Phys. Chem. B, 2014, 118, 12075–12086 CrossRef CAS PubMed.
- H. Gadani and A. Vyas, Anesth.: Essays Res., 2011, 5, 5–10 Search PubMed.
- Y. Shiraishi and K. Ikeda, J. Clin. Anesth., 1990, 2, 381–386 CrossRef CAS PubMed.
- T. J. Özelsel, R. V. Sondekoppam and K. Buro, Can. J. Anaesth., 2019, 66, 1291–1295 CrossRef PubMed.
- M. P. Sulbaek Andersen, S. P. Sander, O. J. Nielsen, D. S. Wagner, T. J. Sanford, Jr and T. J. Wallington, Br. J. Anaesth., 2010, 105, 760–766 CrossRef CAS PubMed.
- A. C. Brown, C. E. Canosa-Mas, A. D. Parr, J. M. T. Pierce and R. P. Wayne, Nature, 1989, 341, 635–637 CrossRef CAS PubMed.
- M. P. Sulbaek Andersen, O. J. Nielsen, B. Karpichev, T. J. Wallington and S. P. Sander, J. Phys. Chem. A, 2012, 116, 5806–5820 CrossRef CAS PubMed.
- S. M. Ryan and C. J. Nielsen, Anesth. Analg., 2010, 111, 92–98 CrossRef PubMed.
- T. Langbein, H. Sonntag, D. Trapp, A. Hoffmann, W. Malms, E. P. Röth, V. Mörs and R. Zellner, Br. J. Anaesth., 1999, 82, 66–73 CrossRef CAS PubMed.
- World Meteorological Organization, Scientific Assessment of Ozone Depletion: 2010, Geneva, Switzerland, 2011. Report No. 52 [Online], Accessed on 20. July 2023, Available: https://ozone.unep.org/sites/default/files/2019-05/00-SAP-2010-Assement-report.pdf.
- L. Campbell and M. Brunger, Int. Rev. Phys. Chem., 2016, 35, 297–351 Search PubMed.
- L. Campbell and M. J. Brunger, Atmosphere, 2023, 14, 1–17 Search PubMed.
- A. Hermann, H.-G. Mack and H. Oberhammer, J. Fluor. Chem., 2000, 101, 223–231 Search PubMed.
- C. Matias, A. Mauracher, S. Huber, S. Denifl, P. Limão-Vieira, P. Scheier, T. Märk, R. González-Méndez and C. Mayhew, Int. J. Mass Spectrom., 2015, 379, 179–186 Search PubMed.
- E. Lange, F. Ferreira da Silva, N. Jones, S. Hoffmann, D. Duflot and P. Limão-Vieira, Chem. Phys. Lett., 2019, 716, 42–48 CrossRef CAS.
- E. Lange, Doctoral dissertation, Faculty of Sciences and Technology, NOVA University Lisbon, 2019.
- J. Vukalović, J. B. Maljković, F. Blanco, G. García, B. Predojević and B. P. Marinković, Int. J. Mol. Sci., 2022, 23, 1–11 Search PubMed.
- J. B. Maljković, J. Vukalović, Z. D. Pešić, F. Blanco, G. García and B. P. Marinković, Eur. Phys. J. Plus, 2023, 138, 1–8 CrossRef.
- J. Vukalović, J. B. Maljković, K. Tökési, B. Predojević and B. P. Marinković, Int. J. Mol. Sci., 2021, 22, 1–14 Search PubMed.
- C. B. Lucas, Atomic and Molecular Beams: Production and Collimation, CRC Press, FL, USA, 2017, pp. 217–223 Search PubMed.
- M. L. Ranković, J. B. Maljković, K. Tökési and B. P. Marinković, Eur. Phys. J. D, 2018, 72, 1–9 CrossRef.
- J. F. Williams and B. A. Willis, J. Phys. B: At. Mol. Phys., 1975, 8, 1670 CrossRef CAS.
- S. K. Srivastava, A. Chutjian and S. Trajmar, J. Chem. Phys., 1975, 63, 2659 CrossRef CAS.
- D. R. Olander and V. Kruger, J. Appl. Phys., 1970, 41, 2769 CrossRef.
- J. C. Nickel, C. Mott, I. Kanik and D. C. McCollum, J. Phys. B: At. Mol. Phys., 1988, 21, 1867 CrossRef CAS.
- J. C. Nickel, P. W. Zetner, G. Shen and S. Trajmar, J. Phys. E: Sci. Instrum., 1989, 22, 730 CrossRef CAS.
- A. Lozano, F. F. da Silva, F. Blanco, P. Limão-Vieira and G. García, Chem. Phys. Lett., 2018, 706, 533–537 CrossRef CAS.
- F. Blanco, J. Rosado, A. Illana and G. García, Phys. Lett. A, 2010, 374, 4420–4424 CrossRef CAS.
- F. Blanco, L. Ellis-Gibbings and G. García, Chem. Phys. Lett., 2016, 645, 71–75 CrossRef CAS.
- A. Traoré Dubuis, A. Verkhovtsev, L. Ellis-Gibbings, K. Krupa, F. Blanco, D. B. Jones, M. J. Brunger and G. García, J. Chem. Phys., 2017, 147, 054301 CrossRef PubMed.
- M. C. Fuss, A. G. Sanz, F. Blanco, J. C. Oller, P. Limão Vieira, M. J. Brunger and G. García, Phys. Rev. A, 2013, 88, 042702 CrossRef.
- R. D. Cowan, The Theory of Atomic Structure and Spectra, University of California Press: Berkeley, CA, USA, 1981 Search PubMed.
- M. E. Riley and D. G. Truhlar, J. Chem. Phys., 1975, 63, 2182–2191 CrossRef CAS.
- X. Zhang, J. Sun and Y. Liu, J. Phys. B: At. Mol. Phys., 1992, 25, 1893 CrossRef CAS.
- F. Blanco and G. García, Phys. Lett. A, 2004, 330, 230–237 CrossRef CAS.
- A. G. Sanz, M. C. Fuss, F. Blanco, F. Sebastianelli, F. A. Gianturco and G. García, J. Chem. Phys., 2012, 137, 124103 CrossRef CAS PubMed.
- J. B. Maljković, J. Vuković, K. Tökési, B. Predojević and B. P. Marinković, Eur. Phys. J. D, 2019, 73, 27 CrossRef.
Footnote |
| † The datasets supporting this article have been uploaded at the BEAMDB (http://servo.aob.rs/emol/) database which is a node of VAMDC (https://portal.vamdc.eu/vamdc_portal/nodes.seam) portal. |
| This journal is © the Owner Societies 2024 |
