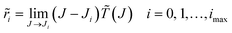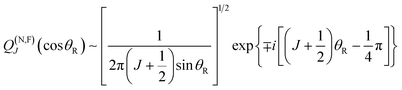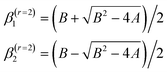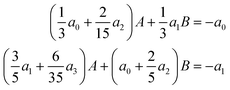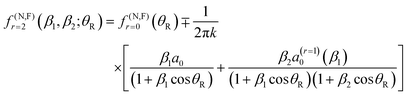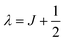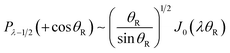Open Access Article
Open Access ArticleA single resonance Regge pole dominates the forward-angle scattering of the state-to-state F + H2 → FH + H reaction at Etrans = 62.09 meV
Chengkui
Xiahou
 a,
J. N. L.
Connor
a,
J. N. L.
Connor
 *b,
Dario
De Fazio
*b,
Dario
De Fazio
 c and
Dmitri
Sokolovski
c and
Dmitri
Sokolovski
 de
de
aSchool of Pharmacy, Qilu Medical University, Zibo Economic Zone, Zibo City 255300, Shandong, People's Republic of China
bDepartment of Chemistry, The University of Manchester, Manchester M13 9PL, UK. E-mail: j.n.l.connor@manchester.ac.uk; Tel: +44 (0)161-275-4693
cIstituto di Struttura della Materia-Consiglio Nazionale delle Ricerche, 00016 Roma, Italy
dDepartment of Physical Chemistry, University of the Basque Country, 48940 Leioa, Bizkaia, Spain
eIKERBASQUE, Basque Foundation for Science, 48011, Bilbao, Spain
First published on 14th December 2023
Abstract
The aim of the present paper is to bring clarity, through simplicity, to the important and long-standing problem: does a resonance contribute to the forward-angle scattering of the F + H2 reaction? We reduce the problem to its essentials and present a well-defined, yet rigorous and unambiguous, investigation of structure in the differential cross sections (DCSs) of the following three state-to-state reactions at a translational energy of 62.09 meV: F + H2(vi = 0, ji = 0, mi = 0) → FH(vf = 3, jf = 0, 1, 2, mf = 0) + H, where vi, ji, mi and vf, jf, mf are the initial and final vibrational, rotational and helicity quantum numbers respectively. Firstly, we carry out quantum-scattering calculations for the Fu–Xu–Zhang potential energy surface, obtaining accurate numerical scattering matrix elements for indistinguishable H2. The calculations use a time-independent method, with hyperspherical coordinates and an enhanced Numerov method. Secondly, the following theoretical techniques are employed to analyse structures in the DCSs: (a) full and Nearside–Farside (NF) partial wave series (PWS) and local angular momentum theory, including resummations of the full PWS up to second order. (b) The recently introduced “CoroGlo” test, which lets us distinguish between glory and corona scattering at forward angles for a Legendre PWS. (c) Six asymptotic (semiclassical) forward-angle glory theories and three asymptotic farside rainbow theories, valid for rainbows at sideward-scattering angles. (d) Complex angular momentum (CAM) theories of forward and backward scattering, with the Regge pole positions and residues computed by Thiele rational interpolation. Thirdly, our conclusions for the three PWS DCSs are: (a) the forward-angle peaks arise from glory scattering. (b) A broad (hidden) farside rainbow is present at sideward angles. (c) A single Regge pole contributes to the DCS across the whole angular range, being most prominent at forward angles. This proves that a resonance contributes to the DCSs for the three transitions. (d) The diffraction oscillations in the DCSs arise from NF interference, in particular, interference between the Regge pole and direct subamplitudes.
1. Introduction
An important part of physical chemistry and chemical physics is the theoretical and experimental investigation of the dynamics of chemical reactions. Of particular significance is the measurement and calculation of differential cross sections (DCSs) for the products of state-to-state reactions, because they contain detailed information on the mechanism and dynamics of the reaction. An examination of the history of this subject,1 shows that a small number of reactions have played a fundamental rôle, because their dynamics have been studied in depth, both experimentally and theoretically. These benchmark reactions are also known as canonical reactions or canonical models.1 For example, in their comprehensive analysis and discussion of about 600 papers on quantum theories of reactive scattering, Hu and Schatz2 singled out as canonical reactions the systems: H + H2 → H2 + H and F + H2 → FH + H, and isotopic variants. At the same time, Hu and Schatz2 reported that new computations have often resulted in “confusions” in their interpretation, that theorists have taken decades to understand the wealth of data produced by state-of-the-art experiments and that theory faces many challenges in the future. Unfortunately since 2006, when Hu and Schatz wrote their review2 confusions, contradictions and difficulties in the theory of chemical reactions have continued to appear in the scientific literature. These misconceptions have arisen in part from: neglect of prior work, use of inaccurate reference data, omission of physically important effects in calculations, application of inappropriate theories, misunderstandings, etc.Particularly concerning have been confusions over the reactions of muonium = Mu = μ+e−. Since the mass of Mu is approximately 1/9 that of H, the dynamics of Mu plays a fundamental rôle in understanding zero-point-energy and kinetic-isotope effects in chemical reactions.3,4 Consider, for example, the canonical reaction, Mu + H2 → MuH + H.5,6 Aldegunde et al.7 examined the rôles of zero-point energy, tunnelling and vibrational adiabaticity, concluding that “tunnelling is largely irrelevant” for understanding the dynamics of this reaction for the initial ground vibrational state, vi = 0 (in the abstract of ref. 7). However, a later re-analysis by Mielke et al.8 refuted this interpretation and concluded that tunnelling is “quite significant” (p. 166 of ref. 8), which is consistent with the earlier findings of ref. 6. Another difficulty concerns the Mu + propane (C3H8) reaction. Laude et al.9 used an approximate instanton method to calculate the thermal rate coefficient, which “disagreed dramatically” with the experimental data of Fleming et al.10,11 (see p. 4154 of ref. 12). However, a re-analysis of this system by Gao et al.,12 which included the previously-neglected vibrational anharmonicity along the reaction coordinate, obtained results that “agreed well with the experimental observations” (in the abstract of ref. 12).
Another long-standing confusion concerns the forward scattering of the canonical state-selected, F + H2 → FH(vf = 3) + H reaction, where vf is the final vibrational quantum number. Some authors, working in the energy domain (E-domain), conclude there is no contribution from resonances to the reaction mechanism,13–18 whereas other authors find that resonances do contribute.19–24 Reasons for this confusion include the following:
• The use of different potential energy surfaces (PES). One difficulty here is that it is known that small changes in a PES can sometimes significantly affect a reaction mechanism.2,25–27 In this connection, Hu and Schatz noted for the F + H2 reaction that “… some aspects … were extremely sensitive to subtle features of the PES…” (p. 9 of ref. 2).
• The dependence of the reaction dynamics on total energy, E (or translational energy, Etrans) for a given PES is used to compute a time delay and/or other attributes. This has the limitation that the reaction mechanism can change as E varies.
• Differential and integral cross sections are calculated that are degeneracy-averaged over initial states and/or summed over final states. This has the disadvantage that the averaging and summing can obscure (wash out) resonance structures in the angular scattering. Then it might be falsely concluded that there are no contributions from resonances.
• A popular technique in physical chemistry and chemical physics for calculating a collision lifetime is that of Smith,28 (see, e.g., ref. 17, 18, 22, 23 and 29–31), which is sometimes called the Wigner–Smith lifetime for single channel scattering. In particular, Castillo et al.17 used an averaged Smith lifetime for the forward scattering to “rule out the participation of a scattering resonance” (p. 6545 of ref. 17). Note that the Smith lifetime has the limitation that the derivation assumes some oscillating E dependent terms can be neglected (see the Abstract and text following eqn (42) in ref. 28; see also additional corrections in the Appendix of ref. 32). Although the Smith lifetime is expressed in terms of exact quantities, namely the scattering matrix and its energy derivative, Baz’ et al. pointed out that the derivation also makes approximations such as the Wentzel–Kramers–Brillouin approximation (p. 169 of ref. 33). Büttiker makes the same point on p. 298 of ref. 34. Note that an extension of the Smith lifetime is the “lifetime Q matrix”, see e.g., ref. 22 and 23.
• The Smith lifetime is not unique. There are actually many ways to define a quantum time delay using real E data as input, e.g., ref. 34–45. It is not obvious which definition, if any, should be used. It is also worth noticing that time delays designed for unperturbed, or only weakly perturbed, systems, cannot be interpreted as physical time intervals, as explained in ref. 44 and 45, which reduces their overall appeal.
The aim of the present paper is to bring clarity through simplicity to this problem of whether resonances contribute to the vf = 3 DCSs of the F + H2 reaction or not. We reduce the problem to its essentials and present a well-defined, yet unambiguous, investigation of the DCSs for the following three state-to-state reactions
| F + H2(vi = 0, ji = 0, mi = 0) → FH(vf = 3, jf = 0, 1, 2, mf = 0) + H | (R1) |
• A realistic PES is used.46
• A set of accurate, yet realistic, helicity-resolved quantum scattering matrix elements are employed for the three reactions. This avoids the problem of using approximate scattering matrix elements, which may confuse the interpretation. Conversely, our quantum results can be used to test the validity of approximations.
• We avoid problems such as the obscuration of resonance information by not averaging over initial states nor summing over final states.
• A single fixed value of Etrans (or E) is used. In our calculations this value is, Etrans = 62.09 meV. This avoids the problem of the reaction mechanism possibly changing as the energy varies.
• We use a rigorous complex angular momentum (CAM) approach,47–51 which is also known as Regge theory.52–55 A very important point is that, for the Etrans we use, there is a just a single simple Regge pole in the first quadrant of the CAM plane for all three transitions. This is the simplest situation in CAM theory and is the easiest to understand and interpret. We denote the position of this single pole by J0; it has the values, 12.488 + 0.9404i, 12.471 + 0.9397i, 12.4446 + 0.9014i, for the 300, 310, 320 cases respectively.
• Near a simple resonance pole, the (modified) scattering matrix takes the form ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0/(J − J0). We use the standard definition of a resonance in CAM theory, which has the following physical interpretation:47–54
0/(J − J0). We use the standard definition of a resonance in CAM theory, which has the following physical interpretation:47–54
(a) The real part of J0 satisfies Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J0 ≈ kR, where k is the incident wavenumber and R is the mean interaction radius for the reaction zone.
J0 ≈ kR, where k is the incident wavenumber and R is the mean interaction radius for the reaction zone.
(b) The imaginary part of J0 is related to the life-angle, written Δ0θR (also called the angular-life) by Δ0θR = 1/(2Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J0). The value of Δ0θR can vary from very large (long-lived or complex collision) to very small (short-lived or direct collision) as well as any value in between. It controls the decay of surface (or creeping) waves which propagate around the interaction zone.
J0). The value of Δ0θR can vary from very large (long-lived or complex collision) to very small (short-lived or direct collision) as well as any value in between. It controls the decay of surface (or creeping) waves which propagate around the interaction zone.
(c) The residue, ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, measures the numerical contribution of the n = 0 pole in the CAM representation for the scattering amplitude and hence the influence of the pole on observables. Note that the physical interpretation of the n = 0 pole in the first quadrant of the CAM plane is unambiguous.
0, measures the numerical contribution of the n = 0 pole in the CAM representation for the scattering amplitude and hence the influence of the pole on observables. Note that the physical interpretation of the n = 0 pole in the first quadrant of the CAM plane is unambiguous.
• We employ both forward and backward representations of the scattering amplitude in CAM theory. This lets us develop the theory for θR = 0°–180°, i.e., valid across the whole angular range (although our emphasis will be on the small angle scattering). Here θR is the reactive-scattering angle, i.e., the angle between the incoming F atom and the outgoing FH molecule in the centre-of-mass collision system.
• We do not make any “Breit–Wigner” or “narrow resonance” assumptions about the resonance pole. Also, it is known that resonances can be both classically-forbidden and classically-allowed and our formalism includes both cases.
• We ask the important and interesting question: for what angular range in the DCSs does the Regge pole make a major contribution to the scattering? We find θR ≲ 50° for all three transitions.
• We apply the recently introduced “CoroGlo ≡ Coro(na)/Glo(ry)” test,56 which lets us distinguish at small angles whether the peak at θR = 0° arises from a corona or from a glory. Our CoroGlo test results suggest that the scattering at forward angles is a glory for all three transitions.
• We use six theories for glory scattering to prove that the forward-angle scattering is indeed an example of a glory for all three transitions.
• At larger angles, we use rigorous uniform and transitional asymptotic (semiclassical) approximations to prove there is a broad rainbow in the farside (F) scattering. This is an example of a well-known connection between Regge poles and rainbow scattering.48–51 Note: a broad rainbow is sometimes called a hidden rainbow.
• We also carry out local angular momentum (LAM) analyses of the angular scattering. This lets us exploit another well-known connection between LAMs and Regge poles.
• Interference between the nearside (N) and farside (F, Regge) scattering gives rise to broadly spaced NF diffraction oscillations across the whole angular range; this is sometimes called Fraunhofer scattering.
In summary, our investigation using CAM theory provides an unambiguous example of a well-characterised resonance for the F + H2 reaction in scheme (R1). We also emphasise that CAM theory is a natural and powerful mathematical technique to use when the scattering amplitude is expressed as a partial wave series (PWS) containing many terms. This is because we can apply the Watson transform (or related transforms) to exactly transform the PWS into a second series with a small number of terms, to which asymptotic (semiclassical) techniques can be applied.
More generally, we note that CAM theory has been an active area of research over the past 40 years. Reviews, with guides to the literature, can be found in ref. 57–63. Specific applications to chemical reactions are in ref. 56 and 64–92.
This paper is structured as follows. Section 2 discusses the calculation and properties of the input scattering matrix elements. The extraction of the Regge pole positions and their residues from the input data is described in Section 3, with particular emphasis on the stability of the poles. Section 4 describes the partial wave theory we require, in particular the Legendre PWS, together with its NF decomposition and resummation. Our results for the full and NF DCSs, including resummations, are presented in Section 5. The corresponding full and NF LAMs are described in Section 6. The newly introduced “CoroGlo test”56 for reactive DCSs is applied in Section 7; it lets us distinguish between glory and corona forward-angle scattering. The properties of the quantum deflection function (QDF) are described in Section 8. The QDF is essential for the glory and rainbow analyses in Sections 9 and 10 respectively. Section 11, which is the longest and contains five sub-sections, presents our CAM analysis of the three DCSs. Our conclusions are in Section 12. Readers interested in just the CAM aspects of the calculations can proceed to Sections 3 and 11. From a mathematical point of view, in Sections 2–7 we have J ∈ ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) 0 = {0, 1, 2,…}, in Sections 8–10, J ∈
0 = {0, 1, 2,…}, in Sections 8–10, J ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) , and in Section 11, J ∈
, and in Section 11, J ∈ ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) . Many of our results are presented graphically.
. Many of our results are presented graphically.
2. Properties of the input scattering matrix elements
The quantum scattering calculations were performed for the Fu–Xu–Zhang (FXZ) PES.46 The numerical S matrix elements for indistinguishable H2 were computed by a time-independent method, which uses hyperspherical coordinates and an enhanced Numerov method.93 Additional details of the numerical calculations can be found in ref. 89 and 93–98. Converged S matrix elements and DCSs were obtained at a translational energy of Etrans = 62.09 meV (more precisely, 62.085787 meV). We used masses of mH = 1.0078 u and mF = 18.9984 u; these values correspond to an initial translational wavenumber of k = 3.89338 a0−1. The values of Jmax were 19 for each transition. The numerical values for the modified scattering matrix elements that we use are reported in the Appendix. The accuracy is estimated to be 0.1% for the moduli with somewhat less accuracy for the phases.From now on, we will often not add the subscript “000 → 3jf0” to keep the notation simple, and also write ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J in place of
J in place of 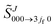 . When the set {
. When the set {![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J} is continued to J ∈
J} is continued to J ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) or J ∈
or J ∈ ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) , we will write
, we will write ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (J).
(J).
Fig. 1 shows graphs of |![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J| versus J for the three transitions, with the corresponding graphs for arg
J| versus J for the three transitions, with the corresponding graphs for arg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J/rad versus J displayed in Fig. 2. On inspection of Fig. 1 and 2, we note the following:
J/rad versus J displayed in Fig. 2. On inspection of Fig. 1 and 2, we note the following:
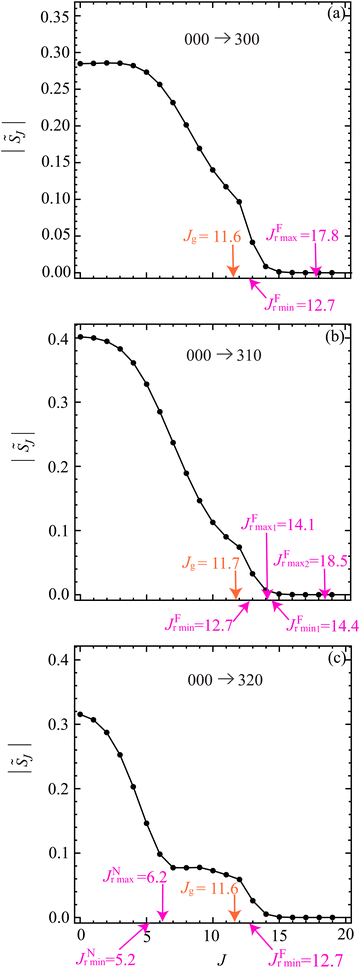 | ||
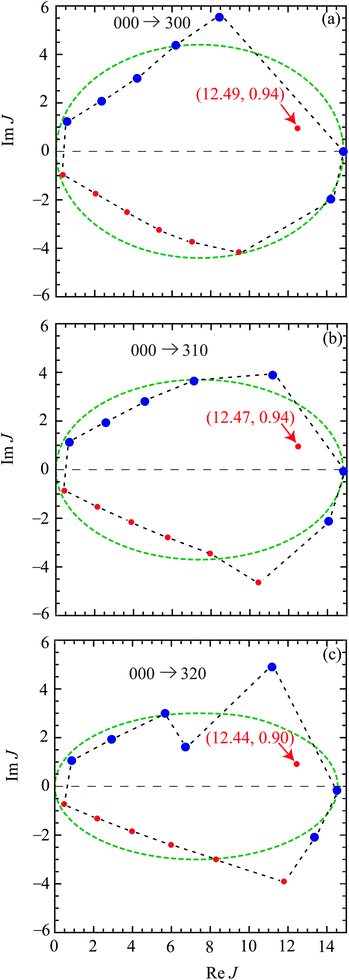
Fig. 1 Plots of |![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J| versus J at Etrans = 62.09 meV. The black solid circles are the numerical S matrix data, {| J| versus J at Etrans = 62.09 meV. The black solid circles are the numerical S matrix data, {|![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J|}, at integer values of J, which have been joined by straight lines. The orange arrow indicates the value of the glory angular momentum variable, Jg. The pink arrows indicate the values of the nearside (N) and farside (F) rainbow angular momentum variable. The notation and values of Jg, and the rainbow angular momenta, are taken from Fig. 6. The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. J|}, at integer values of J, which have been joined by straight lines. The orange arrow indicates the value of the glory angular momentum variable, Jg. The pink arrows indicate the values of the nearside (N) and farside (F) rainbow angular momentum variable. The notation and values of Jg, and the rainbow angular momenta, are taken from Fig. 6. The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. | ||
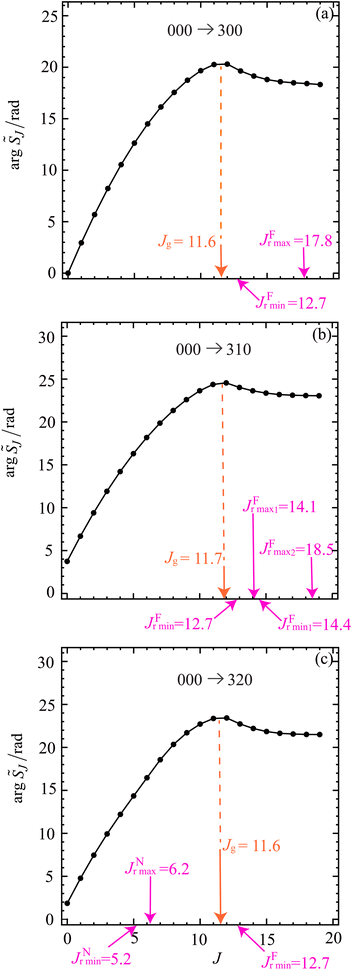 | ||
Fig. 2 Plots of arg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J/rad versus J at Etrans = 62.09 meV. The black solid circles are the numerical S matrix data, {arg J/rad versus J at Etrans = 62.09 meV. The black solid circles are the numerical S matrix data, {arg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J/rad}, at integer values of J, which have been joined by straight lines. The dashed orange lines and orange arrow indicates the value of the glory angular momentum variable, Jg. The pink arrows indicate the values of the nearside (N) and farside (F) rainbow angular momentum variable. The notation and values of Jg, and the rainbow angular momenta, are taken from Fig. 6. The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. J/rad}, at integer values of J, which have been joined by straight lines. The dashed orange lines and orange arrow indicates the value of the glory angular momentum variable, Jg. The pink arrows indicate the values of the nearside (N) and farside (F) rainbow angular momentum variable. The notation and values of Jg, and the rainbow angular momenta, are taken from Fig. 6. The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. | ||
• The |![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J| plots for all three transitions are largest at small values of J. The |
J| plots for all three transitions are largest at small values of J. The |![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J| curves for 300 and 310 are similar in shape, with both having small shoulders at J = 12. In contrast, for the 320 plot, there is a plateau from J = 7 to J = 12, with a small maximum at J = 9. Overall, the shapes of the |
J| curves for 300 and 310 are similar in shape, with both having small shoulders at J = 12. In contrast, for the 320 plot, there is a plateau from J = 7 to J = 12, with a small maximum at J = 9. Overall, the shapes of the |![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J| curves are relatively simple; this is in contrast to some other reactions, for example, the H + HD → H2 + D reaction.56
J| curves are relatively simple; this is in contrast to some other reactions, for example, the H + HD → H2 + D reaction.56
• The plots of arg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J/rad versus J are seen to be roughly quadratic in shape for all three transitions. The broad maxima define the glory angular momentum variable, Jg, which has the values 11.6, 11.7, 11.6 for the 300, 310, 320 cases respectively, and are marked in orange on Fig. 1 and 2. These observations imply that Jg will be an important variable in the asymptotic (or semiclassical ≡ SC) analysis of forward glory scattering in Section 9.
J/rad versus J are seen to be roughly quadratic in shape for all three transitions. The broad maxima define the glory angular momentum variable, Jg, which has the values 11.6, 11.7, 11.6 for the 300, 310, 320 cases respectively, and are marked in orange on Fig. 1 and 2. These observations imply that Jg will be an important variable in the asymptotic (or semiclassical ≡ SC) analysis of forward glory scattering in Section 9.
• Marked in pink on Fig. 1 and 2 are the N and F rainbow angular momentum variables, denoted Jr and defined later, which will be used to prove the existence of broad, also called hidden, F rainbows for the three DCSs in Section 10.
3. Regge poles obtained using Thiele rational interpolation
Our next task is to extract a stable Regge pole(s) lying in the first quadrant of the CAM plane from the set, {![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J}, for each of the three transitions. We do this using Thiele rational interpolation (denoted, TRI). Briefly, the Thiele algorithm firstly constructs a finite continued fraction in J, denoted,
J}, for each of the three transitions. We do this using Thiele rational interpolation (denoted, TRI). Briefly, the Thiele algorithm firstly constructs a finite continued fraction in J, denoted, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (J), with J ∈
(J), with J ∈ ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) . Secondly, this continued fraction is simplified to a Padé form, which consists of the ratio of two factored polynomials in J. The zeros in the numerator correspond to the zeros of
. Secondly, this continued fraction is simplified to a Padé form, which consists of the ratio of two factored polynomials in J. The zeros in the numerator correspond to the zeros of ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (J), whilst the zeros in the denominator define the positions of the poles in the whole CAM plane, which are labelled, i = 0, 1,…, imax. The residues at the poles are then defined in the usual way as
(J), whilst the zeros in the denominator define the positions of the poles in the whole CAM plane, which are labelled, i = 0, 1,…, imax. The residues at the poles are then defined in the usual way asMore details about TRI can be found in ref. 83 and 84.
Our results for the locations of the zeros and poles in the whole CAM plane are shown in Fig. 3 for the three transitions. In every case, the input data consists of the set, {![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J|J = 0(1)14}. Note: before examining Fig. 3, we first eyeball plots of, Re
J|J = 0(1)14}. Note: before examining Fig. 3, we first eyeball plots of, Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (J), Im
(J), Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (J), |
(J), |![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (J)|, all versus J, to see if TRI has provided a physically-acceptable interpolation for real values of J. We find that TRI passes this eyeballing test. We then observe the following on inspection of Fig. 3:
(J)|, all versus J, to see if TRI has provided a physically-acceptable interpolation for real values of J. We find that TRI passes this eyeballing test. We then observe the following on inspection of Fig. 3:
• There are 7 zeros (shown blue) and 7 poles (shown red).
• There is one marked pole in the first quadrant of the CAM plane for each transition. The positions of these three poles and the corresponding residues are reported in Table 1, as well as their quantum life-angles. These are the poles used in the CAM calculations in Section 11. Note that the positions of the poles for the three transitions are very close to each other.
| Transition | Regge pole number | Regge pole position | Regge pole residue | Quantum life-angle/deg |
|---|---|---|---|---|
| 000 → 300 | 0 | 12.488 + 0.9404i | 0.02665 − 0.04793i | 30.46 |
| 000 → 310 | 0 | 12.471 + 0.9397i | −0.03628 − 0.00654i | 30.49 |
| 000 → 320 | 0 | 12.4446 + 0.9014i | −0.01869 + 0.02722i | 31.78 |
• There are no Froissart doublets, i.e., a pair of almost overlapping zeros and poles.
• The remaining poles and zeros [except possibly the zero at (6.7, 1.6) for the 320 case] are boundary poles, which approximately separate the stable and unstable regions of the CAM plane.
• It is known, from many TRI pole computations,60,67–70,83,84,91,92,99–102 that an elliptical curve approximately separates the stable and unstable regions. The green-dashed ellipses in Fig. 3 approximately show the boundary between these two regions. Alternatively, the boundary poles and zeros can be joined by straight lines, creating a polygon (black-dashed lines in Fig. 3).
• It can be seen that the first-quadrant pole for each transition lies inside the ellipse and polygon, which suggests all three poles are stable. This important point is considered further in the next subsection.
3.1 Stability of the poles in the first quadrant of the CAM plane
We have checked the stability of the poles lying in the first quadrant of the CAM plane as follows:• The pole positions and residues were calculated by two independent computer programs: one coded in Mathematica 12.1.1,83 the other (called Padé II) using Fortran 77.84 Both programs produce the same results that are reported in Table 1.
• The input data for the TRI were varied slightly, e.g., using {![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J|J = 1(1)14}, {
J|J = 1(1)14}, {![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J|J = 0(1)15}, etc. The results in Table 1 only changed by a small amount.
J|J = 0(1)15}, etc. The results in Table 1 only changed by a small amount.
• Random noise of the order 10−3 was added to the input data. Again the results in Table 1 only changed slightly.
• We carried out TRI reconstructions for two energies close to the reference energy of Etrans = 62.086 meV, namely at, Etrans = 62.036 and 62.126 meV and again found a single stable pole in the first quadrant at these energies for the three transitions.
The above results strongly suggest that the poles in Table 1 are indeed stable. We will refer to them as “Regge poles”, because we expect poles obtained by a direct solution of the Schrödinger equation with an “outgoing wave” boundary condition, i.e., true Regge poles, will agree with the TRI poles in the first quadrant.
4. Partial wave theory
Here we outline the partial wave theory that we require and establish our notations.4.1 Partial wave series
Since mi = mf = 0, the partial wave series (PWS) for the scattering amplitude can be expanded in a basis set of Legendre polynomials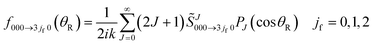 | (1) |
The differential cross section (DCS) is then given by
| σ000→3jf0(θR) = |f000→3jf0(θR)|2 jf = 0, 1, 2 | (2) |
Our angular distributions for the F + H2 reaction in Section 5 show that the full DCSs calculated from eqn (1) and (2) exhibit oscillatory structures. To help understand these oscillations, we make a nearside-farside (NF) decomposition of the scattering amplitude. This is outlined next.
4.2 Nearside-farside decomposition
We exactly decompose the full scattering amplitude into the sum of two contributing terms, the N and F subamplitudes.66,103,104| f(θR) = f(N)(θR) + f(F)(θR) | (3) |
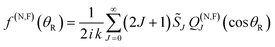 | (4) |
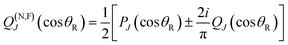 | (5) |
| σ(N,F)(θR) = |f(N,F)(θR)|2 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR ≫ 1, we obtain, e.g., ref. 66
θR ≫ 1, we obtain, e.g., ref. 66which has a standard travelling angular wave interpretation.
A local angular momentum (LAM) analysis can also be used to provide information on the total angular momentum variable that contributes to the scattering at an angle θR, under semiclassical conditions.105–108 It is defined by
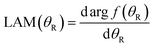 | (7) |
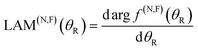 | (8) |
In eqn (4)–(6) and (8), we have used the Fuller NF decomposition.109 Note that NF DCS and NF LAM theories have been reviewed by Child (ref. 63, Section 11.2).
4.3 Resummation of the partial wave series
It is known that a resummation105–108,110,111 of the PWS (1) can significantly improve the physical effectiveness of the NF decomposition, (3)–(6) and (8) by removing un-physical structures in the N, F DCSs. A detailed account and discussion of resummation theory has been presented by Totenhofer et al. for a Legendre PWS,82 so we do not repeat this material here.We have investigated resummation orders of r = 0 [no resummation, i.e., eqn (1)] and r = 1, 2, and 3. We find there is a diminishing effect for cleaning the N, F DCSs and N, F LAMs of unphysical oscillations, which occurs on going from r = 0, 1, 2, 3. In the following, we have used the r = 2 equations, which we summarize next. Notice: we sometimes label eqn (1) and related un-resummed equations with a subscript, r = 0.
Firstly, we define
aJ = (2J + 1)![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J J = 0, 1, 2,… J J = 0, 1, 2,… | (9) |
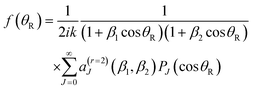 | (10) |
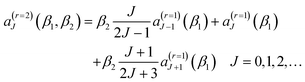 | (11) |
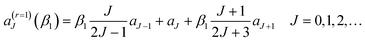 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR)(1 + β2
θR)(1 + β2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR) ≠ 0. We determine the real-, or complex-, valued, resummation parameters, β1 ≡ β(r=2)1 and β2 ≡ β(r=2)2 in eqn (10) and (11) by solving the two simultaneous non-linear equations
θR) ≠ 0. We determine the real-, or complex-, valued, resummation parameters, β1 ≡ β(r=2)1 and β2 ≡ β(r=2)2 in eqn (10) and (11) by solving the two simultaneous non-linear equations| a(r=2)J=0(β1,β2) = 0 and a(r=2)J=1(β1,β2) = 0 |
where A and B are the solutions of the simultaneous linear equations
This choice for β1 and β2 is the suggestion of Anni et al.105 A NF decomposition of eqn (10) can also be made. We write
| f(θR) = f(N)r=2(β1,β2; θR) + f(F)r=2(β1,β2; θR) |
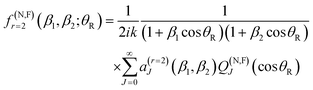 | (13) |
with a0 =
![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J=0 and a(r=1)0(β1) =
J=0 and a(r=1)0(β1) = ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J=0 + β1
J=0 + β1![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J=1.
J=1.
The corresponding N, F r = 2 resummed DCSs are then
| σ(N)r=2(β1, β2; θR) = |f(N)r=2(β1, β2; θR)|2 | (14) |
| σ(F)r=2(β1, β2; θR) = |f(F)r=2(β1, β2; θR)|2 | (15) |
In addition, N, F LAMs for r = 2 can be defined by analogy with eqn (8), namely
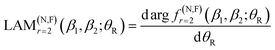 | (16) |
5. Full and nearside-farside DCSs including resummations
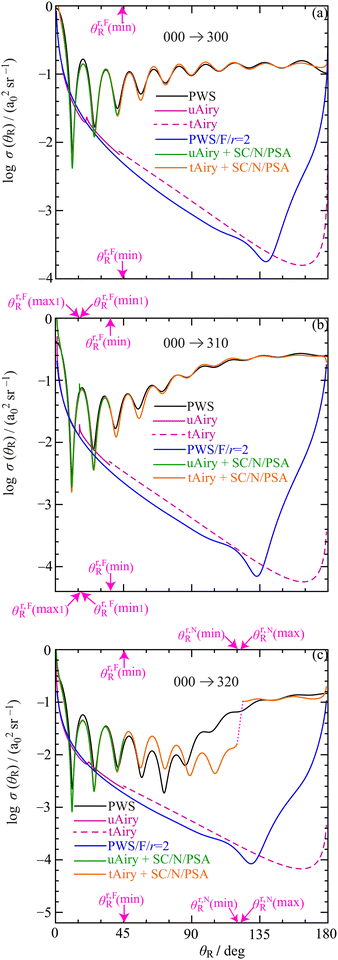
Fig. 4 shows logarithmic plots of the full and N, F r = 2 DCSs versus θR for the three transitions. The following colour conventions are used for the DCSs, as well as in some other figures: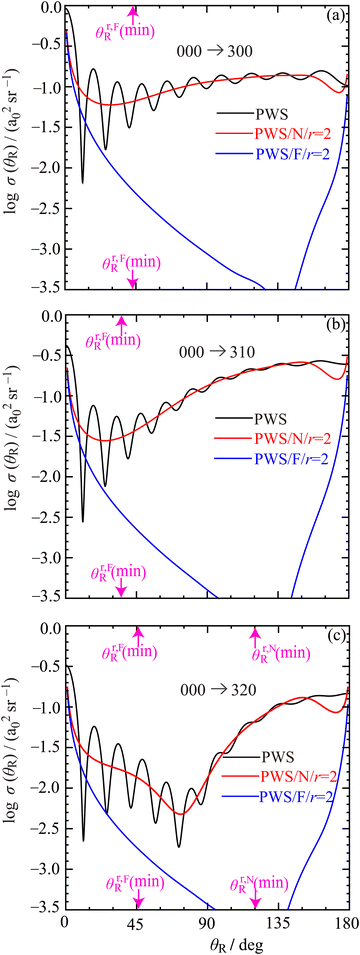 | ||
Fig. 4 Plots of full and N, F log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ(θR) versus θR at Etrans = 62.09 meV. Black curve: PWS. Red curve: PWS/N/r = 2. Blue curve: PWS/F/r = 2. The locations of the nearside (N) and farside (F) rainbow angles, θr,NR(min) and θr,FR(min) respectively, are shown as pink arrows pointing toward the abscissa. For clarity, not all rainbow angles in Fig. 6 are shown. The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. σ(θR) versus θR at Etrans = 62.09 meV. Black curve: PWS. Red curve: PWS/N/r = 2. Blue curve: PWS/F/r = 2. The locations of the nearside (N) and farside (F) rainbow angles, θr,NR(min) and θr,FR(min) respectively, are shown as pink arrows pointing toward the abscissa. For clarity, not all rainbow angles in Fig. 6 are shown. The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. | ||
• Full PWS DCS, black solid. Labelled, PWS.
• N r = 2 PWS DCS, red solid. Labelled, PWS/N/r = 2.
• F r = 2 PWS DCS, blue solid. Labelled, PWS/F/r = 2.
The full DCSs for the three transitions are seen to be similar, with the following properties as θR increases from 0° to 180°:
• A forward peak at θR = 0°, followed by diffraction (high frequency) – also called Fraunhofer – oscillations, which are damped as θR increases.
• The periods of the oscillations are approximately constant, with ΔθR/deg ≈ 15; the periods slowly increase as θR gets larger.
• The full DCS decreases in magnitude as θR moves away from 0° before increasing again.
• More generally, we note that the full DCSs plotted in Fig. 4 are typical of many reactions where there is a contribution from a Regge pole(s) at small and intermediate values of θR. This was pointed out by Dobbyn et al.66 more than 20 years ago.
Next we examine the N and F r = 2 DCSs in Fig. 4 and observe the following:
• The variation of the N and F DCSs with θR is slower than that for the corresponding full DCSs. Then, by the fundamental identity for full and N, F r = 2 DCSs,76 the diffraction oscillations arise from the NF interference term in the fundamental identity.76 This is analogous to the interference pattern in the double-slit experiment as explained in Appendix A of ref. 65 in a molecular scattering context.
• The three reactions are N dominant, increasingly so as we move towards larger angles. The behaviour of the N and F DCSs at small angles, which give rise to a forward peak in the full DCS, suggests the possibility of glory scattering.
6. Full and nearside-farside LAMs including resummations
In Fig. 5, we show linear plots of the full and N, F r = 2 LAMs versus θR for the three transitions. The following colour conventions are used for the LAMs: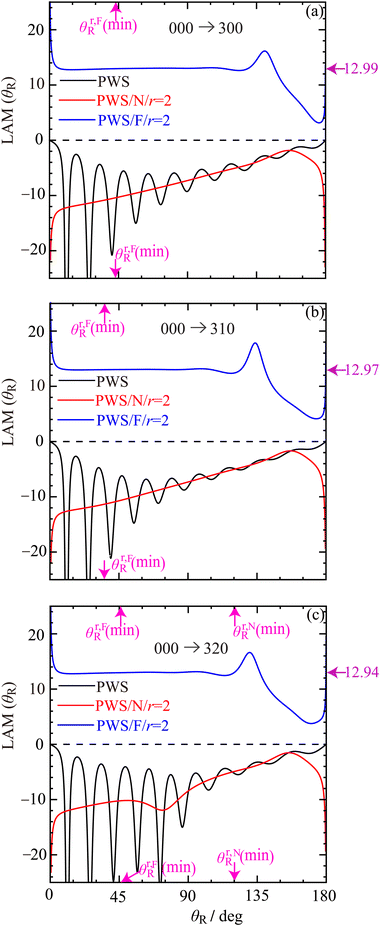 | ||
Fig. 5 Plots of full and N, F LAM(θR) versus θR at Etrans = 62.09 meV. Black curve: PWS. Red curve: PWS/N/r = 2. Blue curve: PWS/F/r = 2. The purple arrow pointing towards the right ordinate shows, Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J0 + 1/2. The locations of the nearside (N) and farside (F) rainbow angles,θr,NR(min) and θr,FR(min) respectively, are shown as pink arrows pointing toward the abscissa. For clarity, not all rainbow angles in Fig. 6 are shown. The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. J0 + 1/2. The locations of the nearside (N) and farside (F) rainbow angles,θr,NR(min) and θr,FR(min) respectively, are shown as pink arrows pointing toward the abscissa. For clarity, not all rainbow angles in Fig. 6 are shown. The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. | ||
• Full PWS LAM, black solid. Labelled, PWS.
• N r = 2 PWS LAM, red solid. Labelled, PWS/N/r = 2.
• F r = 2 PWS LAM, blue solid. Labelled, PWS/F/r = 2.
We observe the following in the LAM plots in Fig. 5:
• The full LAMs possess oscillations at small θR which are damped as θR increases.
• The periods of these oscillations are similar to those for the full DCSs.
• The full LAM and full DCS plots are consistent with each other.
More interesting is the information contained in the N and F r = 2 LAM graphs:
• The N LAMs for the 300 and 310 cases increase monotonically away from small θR values, except for angles close to the backward direction. This is also the situation for the 320 case, except for a small angular range around, θR ≈ 60°. This behaviour of the N LAM for the three transitions is similar to that for the repulsive collision of two hard-spheres.83,108 It tells us that the N scattering is dominated by direct hard-sphere-type dynamics.
• The F r = 2 LAM curves are approximately constant for the angular range, θR ≈ 10° to θR ≈ 100°. Physically, this behaviour corresponds to a rotating complex that decays as it rotates.108 It is known that the following result relates a F LAM to a dominant Regge pole83,108
LAM(F)r=2(β1, β2; θR) ≈ Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J0 + 1/2 J0 + 1/2 | (17) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J0 + 1/2 for the three transitions are marked by purple arrows on the right-hand ordinates in Fig. 5 using the values for J0 in Table 1. It can be seen there is good agreement between the left- and right-hand sides of eqn (17). Notice also that the right-hand side of eqn (17) is independent of θR.
J0 + 1/2 for the three transitions are marked by purple arrows on the right-hand ordinates in Fig. 5 using the values for J0 in Table 1. It can be seen there is good agreement between the left- and right-hand sides of eqn (17). Notice also that the right-hand side of eqn (17) is independent of θR.
• The F r = 2 LAMs are unphysical for θR ≳ 100° and close to the forward direction. Similar behaviour has been noted in earlier LAM calculations.83,108
• The full and N, F LAMs are related by the fundamental identity for full and N, F r = 2 LAMs.76
• The full and N, F LAMs are examples of a “weak value112”.
The DCS and LAM results discussed in Section 5 and above respectively and in previous work83,108 suggest that the forward angle oscillations in the DCSs in Fig. 4 for the three transitions are examples of a glory. However, qualitatively similar oscillations can occur in DCSs from other mechanisms, e.g., corona scattering.56,113 We next apply the recently introduced “CoroGlo” test56 to help distinguish between these two possibilities.
7. Application of the CoroGlo test
Both a corona and a glory give rise to a peak in the DCS(θR) at θR = 0°, accompanied by subsidiary maxima. A corona in molecular collisions is usually modelled by Fraunhofer scattering from a hard-sphere,56 whereas a glory arises from constructive N, F interference, as illustrated in Fig. 4 and 5 for the DCSs and LAMs respectively; the theory for a forward glory has been developed and applied in ref. 74, 83, 88 and 114–119. The CoroGlo test56 lets us distinguish between the two cases in the asymptotic limit from the ratio of the DCS(θR) at θR = 0° to the value of the DCS(θR) at its adjacent maximum. We have:56| Corona diffraction ratio (CDR) ≈ 57.1, |
| Glory diffraction ratio (GDR) ≈ 6.2. |
Next we measure the ratio of the forward diffraction peak to its adjacent maximum for the accurate quantum PWS DCSs in Fig. 4, and compare with the above values. Denoting the ratio from the quantum calculations as RQ, we find:
| 000 → 300, RQ = 5.6 |
| 000 → 310, RQ = 5.5 |
| 000 → 320, RQ = 5.7 |
8. Properties of the quantum deflection functions
The Quantum Deflection Function (QDF), denoted![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (J), plays a fundamental rôle in the SC theory of glories and rainbows.114 It is defined by
(J), plays a fundamental rôle in the SC theory of glories and rainbows.114 It is defined by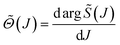 | (18) |
![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (J)/deg versus J for the three transitions. We usually use degree five B-spline interpolation for the continuation of the set {
(J)/deg versus J for the three transitions. We usually use degree five B-spline interpolation for the continuation of the set {![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J} for J = 0, 1, 2,…, Jmax to
J} for J = 0, 1, 2,…, Jmax to ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (J). Examination of Fig. 6 reveals the following:
(J). Examination of Fig. 6 reveals the following:
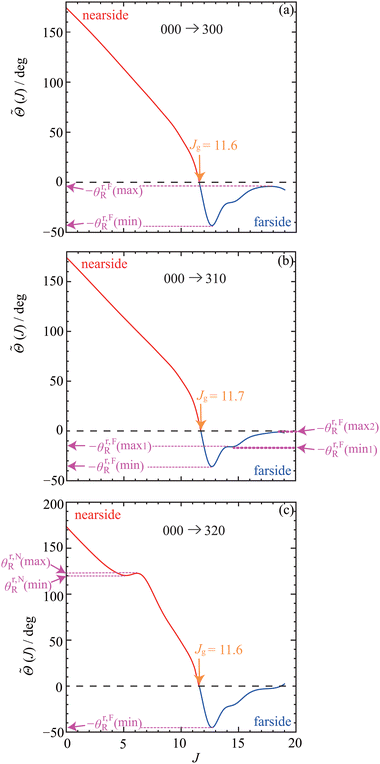
• For the 300 and 310 cases, the N ![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (J) are monotonic; whereas for the 320 case there is a small shoulder near
(J) are monotonic; whereas for the 320 case there is a small shoulder near ![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (J) ≈ 122°, which gives rise to a nearby local rainbow minimum and a rainbow maximum, denoted, θr,NR(min) and θr,NR(max), respectively.
(J) ≈ 122°, which gives rise to a nearby local rainbow minimum and a rainbow maximum, denoted, θr,NR(min) and θr,NR(max), respectively.
• The glory angular momentum variable at Jg ≈ 11.6 where ![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (Jg) = 0 is clearly visible and well defined for the three transitions. For the 320 case, there is a second glory (not indicated) near Jg = 18.7. However, here, |
(Jg) = 0 is clearly visible and well defined for the three transitions. For the 320 case, there is a second glory (not indicated) near Jg = 18.7. However, here, |![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (Jg)| ≈ 10−7; so it makes a negligible contribution to a forward glory.
(Jg)| ≈ 10−7; so it makes a negligible contribution to a forward glory.
• There is a pronounced F Airy-type rainbow visible for all three transitions located at J = JFr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min, where
min, where ![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (J) = −θr,FR(min). For J > JFr
(J) = −θr,FR(min). For J > JFr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min, the QDF curves for the three transitions are seen to have a shoulder, which in the 310 case results in a nearby local rainbow minimum and a rainbow maximum, located at −θr,FR(min1) and −θr,FR(max1) respectively. Note also there is a local rainbow at large J for the 310 case, located at, −θr,FR(max2), but again because |
min, the QDF curves for the three transitions are seen to have a shoulder, which in the 310 case results in a nearby local rainbow minimum and a rainbow maximum, located at −θr,FR(min1) and −θr,FR(max1) respectively. Note also there is a local rainbow at large J for the 310 case, located at, −θr,FR(max2), but again because |![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (JFr
(JFr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) max2)| is very small, it makes a negligible contribution to the DCS.
max2)| is very small, it makes a negligible contribution to the DCS.
• For clarity, the values of the glory and rainbow angular momenta in J space have also been marked on Fig. 1 and 2, with the corresponding QDF values shown in Fig. 6.
Having established the properties of the QDFs, we next prove for the three transitions that glory scattering occurs at forward and small angles (Section 9). And at larger sideward angles there is a broad (or hidden) rainbow (Section 10).
9. Glory analysis for the forward-angle region
A systematic SC (asymptotic) theory of glory scattering in the forward-angle region has been developed56,114–116 for QDFs of the type shown in Fig. 6, and various applications have been made.56,83,114,116–119 We have presented the working equations recently in ref. 56, 83 and 118; so here we just briefly report the six approximations we have applied to the three transitions:• Integral Transitional Approximation (ITA). This is valid for angles on, and close to, the caustic direction, θR = 0°. It is a global approximation because it uses ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (J) for all values of J.
(J) for all values of J.
• Semiclassical Transitional Approximation (STA). This is obtained when the integral in the ITA is evaluated by the stationary phase approximation. It is a local approximation.
• Uniform semiclassical Bessel approximation (uBessel). This is the most accurate SC result currently available. It is valid both on, and away, from, θR = 0°. It is a local approximation because it assumes the glory scattering receives most of its contribution from the two real stationary phase points close to J ≈ Jg, provided the corresponding values of |![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (J)| are not too small. Note: previously called the uniform semiclassical approximation (USA).83,88,114–118
(J)| are not too small. Note: previously called the uniform semiclassical approximation (USA).83,88,114–118
• Primitive Semiclassical Approximation (PSA). This results when the Bessel functions in the uBessel approximation are replaced by their asymptotic forms. It has the advantage that the N and F SC subamplitudes can be readily identified. However, it diverges as, θR → 0°.
• Classical Semiclassical Approximation (CSA). When the NF interference term in the PSA is omitted, the CSA is obtained. It also diverges as, θR → 0°, but is useful for understanding general trends in the DCS.
• 4Hankel Semiclassical Approximation (4Hankel). This is a special case of the 6Hankel SC approximation,88 which is uniformly valid for both glory scattering and the rainbow scattering around the minimum in the ![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (J) versus J plots in Fig. 6, i.e., for
(J) versus J plots in Fig. 6, i.e., for ![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (J) ≈ −θr,FR(min). If we neglect the stationary phase contribution for J > JFr
(J) ≈ −θr,FR(min). If we neglect the stationary phase contribution for J > JFr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min, then the 6Hankel approximation reduces to the 4Hankel approximation.
min, then the 6Hankel approximation reduces to the 4Hankel approximation.
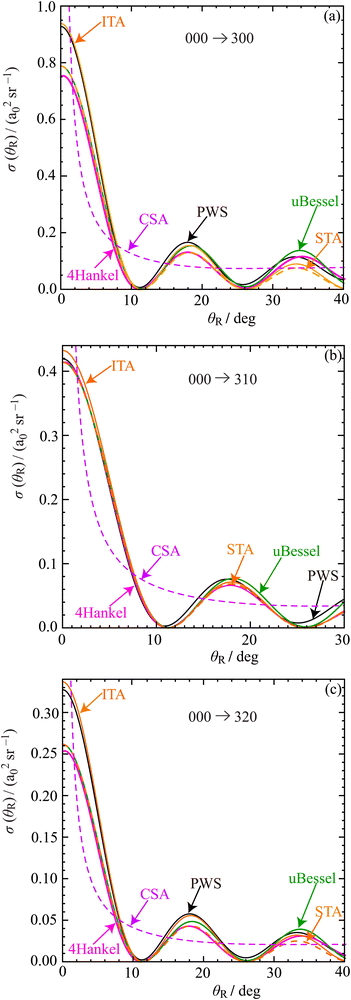
Fig. 7 shows a linear plot of the PWS DCS for each transition, which is compared with the ITA, STA, uBessel, 4Hankel and CSA DCSs. At θR = 0°, the ITA DCS agrees closely with the PWS DCS (as expected), with the STA, uBessel and 4Hankel DCSs sometimes being slightly smaller. At larger angles in the oscillatory regime, all five DCSs agree for both the amplitude and period of the oscillations. Also, the CSA DCS passes through the oscillations and its divergence as θR → 0° can be clearly seen.
Note that the DCSs in Fig. 7 are plotted for angles that are less than the rainbow angle, θr,FR(min), which forms the natural boundary for the applicability of the uBessel, 4Hankel, and CSA approximations.
In conclusion, we have proved using asymptotic techniques that the forward peak in the DCSs for all three transitions is an example of a glory. This also confirms the suggestion from the CoroGlo test in Section 7.
10. Rainbow analysis for sideward angles
A systematic SC theory of F rainbow scattering in the sideward-angle region has been developed56,83,120,121 for QDFs of the type shown in Fig. 6, and different applications have been made.56,83,88,121–124 We have presented the working equations recently in ref. 56, 83, 88 and 122; so here we just briefly report the three approximations that we have applied to the DCSs for the three transitions:• Uniform Airy semiclassical approximation (uAiry), or in a more systematic notation, SC/F/uAiry. This is the most accurate SC result currently available. The uAiry approximation is valid for angles in Fig. 6 around the F rainbow, i.e., around the angle, θR = θr,FR(min). The region, θR < θr,FR(min), is the bright side of the rainbow, where there are two real roots in the SC theory, which coalesce at, θR = θr,FR(min). The uAiry approximation becomes numerically indeterminate at, θR = θr,FR(min), where the tAiry approximation below should be used. The uAiry approximation is also valid on the dark side of the rainbow, where, θR > θr,FR(min). However, this requires the use of complex-valued roots, which is awkward for numerical input data. Thus the uAiry approximation is usually used only on the rainbow's bright side; we do this here.
• Transitional Airy semiclassical approximation (tAiry), or in a more systematic notation, SC/F/tAiry. The tAiry makes a quadratic approximation for ![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (J) about J = Jr; it only depends on the properties of
(J) about J = Jr; it only depends on the properties of ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (J) at J = Jr. It has the numerical advantage that it can be readily used for, θR < θr,FR(min) (bright side), θR = θr,FR(min), and θR > θr,FR(min) (dark side). Typically, the tAiry approximation becomes less accurate as θR moves away from the rainbow angle.
(J) at J = Jr. It has the numerical advantage that it can be readily used for, θR < θr,FR(min) (bright side), θR = θr,FR(min), and θR > θr,FR(min) (dark side). Typically, the tAiry approximation becomes less accurate as θR moves away from the rainbow angle.
• 6Hankel semiclassical approximation (6Hankel). This approximation is uniform for both glory and rainbow scattering. It has already been mentioned in Section 9, together with its special case, the 4Hankel approximation. Similar to the uAiry approximation, it is usually applied only on the bright side of the rainbow. We find that the 6Hankel DCSs for rainbow scattering are very similar to the uAiry results discussed below. So we do not show the 6Hankel DCSs in Fig. 8 and 9.
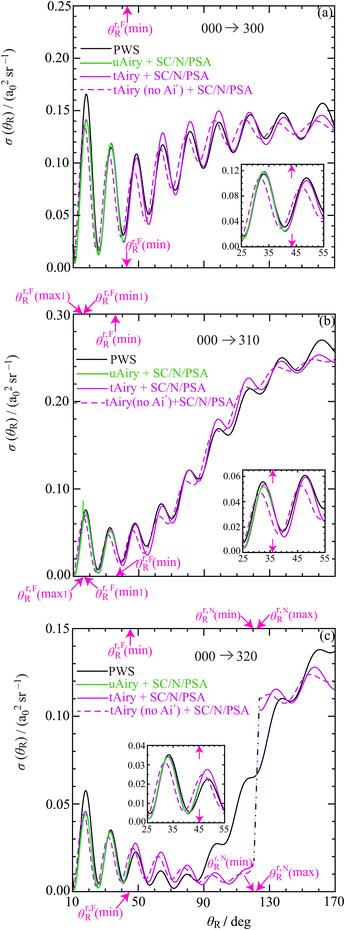 | ||
| Fig. 8 Plots of σ(θR) versus θR for the rainbow-angular region at Etrans = 62.09 meV. The DCSs plotted are: PWS (black solid curve), uAiry + SC/N/PSA (green solid curve), tAiry + SC/N/PSA (lilac solid curve), tAiry(omitting the Ai′ term) + SC/N/PSA (lilac dashed curve). The pink arrows mark the locations of the rainbow angles, θr,FR(max/min) and θr,NR(max/min), which are also shown in Fig. 6. The insets show the DCSs in more detail close to the rainbow angle, θr,FR(min). The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. The orange dotted and blue dashed/dotted lines in (c) bridge the angular region where SC/N/PSA fails for tAiry and tAiry(no Ai′) respectively. | ||
 | ||
| Fig. 9 Logarithmic plots of σ(θR) versus θR for the rainbow-angular region at Etrans = 62.09 meV. The DCSs plotted are: PWS (black solid curve), uAiry + SC/N/PSA (green solid curve), tAiry + SC/N/PSA (orange solid curve), PWS/F/r = 2 (blue solid curve), uAiry (purple solid curve), tAiry (purple dashed curve). The pink arrows mark the locations of the rainbow angles, θr,FR(max/min) and θr,NR(max/min), which are also shown in Fig. 6. The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. The pink dotted line in (c) bridges the angular region where SC/N/PSA fails for tAiry. | ||
We also make the following comments on the uAiry and tAiry cases, before discussing the DCSs in Fig. 8 and 9:
• The scattering subamplitude for both Airy approximations takes the form
| p(⋯)Ai(⋯) + q(⋯)Ai′(⋯) |
• To calculate a DCS, we have to add the N SC subamplitude to the F xAiry (x = u, t) subamplitude to get the full scattering amplitude. We use a primitive semiclassical approximation (PSA) for the N subamplitude, as given e.g., by eqn (53) of ref. 124.
It is denoted SC/N/PSA in a systematic notation. Note: this SC/N/PSA is different from the PSA obtained as a limiting case of the uBessel approximation in Section 9.
• The natural boundaries for the applicability of the xAiry (x = u, t) and SC/N/PSA approximations are the presence of other rainbows in the ![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (J) versus J graphs. These additional rainbow maxima and minima are marked in Fig. 6.
(J) versus J graphs. These additional rainbow maxima and minima are marked in Fig. 6.
10.1 Discussion of rainbow DCSs
On inspection of Fig. 8, we note the following:• The DCSs for the 000 → 300 transition are shown in Fig. 8(a), which has a F rainbow angle of, θr,FR(min) = 45.3°. Plotted are: PWS (black solid curve), uAiry + SC/N/PSA (green solid curve) and tAiry + SC/N/PSA (lilac solid curve). Notice that the uAiry case is for the bright side of the rainbow only and the resulting DCS extends from small angles up to, θR = θr,FR(min), whereas the tAiry + SC/N/PSA DCS is plotted over a much wider angular range. The inset shows the DCSs for a small angular range around the rainbow angle. It is clear that the good agreement between the two Airy curves with the PWS DCS proves the existence of a broad (or hidden) rainbow. Its presence in the DCS is revealed by the diffraction oscillations (also called Fraunhofer oscillations), which arise from NF interference.
Also plotted in the DCS is the tAiry(no Ai′) + SC/N/PSA approximation, as a lilac dashed curve. It can be seen that neglecting the Ai′ term generally results in poorer agreement with the PWS DCS compared with the full tAiry + SC/N/PSA, which includes the Ai′ term.
• Fig. 8(b) displays the DCSs for the 000 → 310 transition. The results are seen to be similar to the 300 case, so the above discussion will not be repeated. For this transition, we have, θr,FR(min) = 35.8°. The small spike at θR ≈ 15.9° occurs because there is rainbow maximum at θr,FR(max1) = 15.85° and a rainbow minimum at θr,FR(min1) = 15.91°, where the uAiry approximation fails. These rainbow angles are marked in Fig. 6(b).
• DCSs for the 000 → 320 transition are plotted in Fig. 8(c), which has, θr,FR(min) = 45.1°. Again the results are similar to the 300 and 310 cases, so we do not repeat the above discussion. A minor complication concerns the N rainbows at θr,NR(min) = 120.3° and θr,NR(max) = 122.7° [see Fig. 6(c)]. The SC/N/PSA fails at, and close to, these values. So in the DCS plot we have bridged this gap by adding straight lines passing through, θR = 121°, 122°, 123°.
In order to examine the scattering for the F rainbow in more detail, we show in Fig. 9 logarithmic plots of the DCSs versus θR for the three transitions. In addition, we have also included DCSs for the PWS/F/r = 2, SC/F/uAiry [up to θR = θr,FR(min)] and SC/F/tAiry subamplitudes. We see that there are no pronounced rainbows (or supernumerary rainbows) in the F scattering around, θR = θr,FR(min). Rather the rainbows are of the broad (hidden) type. Also there is good agreement between the PWS/F/r = 2 and the SC/F/xAiry (x = u, t) DCSs for θR ≲ 135°. This is an important test of the splitting in eqn (3)–(6), since there is no guarantee that the Fuller decomposition will produce physically meaningful N and F DCSs, even though it is mathematically exact.
In conclusion, we have proved that the sideward scattering in the DCSs for all three transitions contains an example of a broad (hidden), rainbow.
11. CAM theory and results for DCSs
There is a well-known connection between F rainbows and Regge poles.48–51,125 We next use the CAM approach to analyse structure in the DCSs for the three transitions.11.1 Preliminaries
We first note the following properties of CAM theory that are relevant to our DCS analysis:• There are two possibilities to consider (1) CAM theory valid at backward angles, (2) CAM theory valid at forward angles. These two cases arise because CAM theory often uses a Legendre function (of the first kind of complex degree, J0 = Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J0 + iIm
J0 + iIm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J0) with two different, although related, arguments. For the backward representation, we use, PJ0(−cos
J0) with two different, although related, arguments. For the backward representation, we use, PJ0(−cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR), which is equal to unity at θR = π, but is logarithmically divergent as θR → 0.127 Whereas, for the forward representation, we use, PJ0(+cos
θR), which is equal to unity at θR = π, but is logarithmically divergent as θR → 0.127 Whereas, for the forward representation, we use, PJ0(+cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR), which is equal to unity at θR = 0, but is logarithmically divergent as θR → π.126
θR), which is equal to unity at θR = 0, but is logarithmically divergent as θR → π.126
Our starting point below is the usual backward (Regge) representation, which is valid for, 0 < θR ≤ π.
• It is often convenient in CAM theory to use the variable
![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (λ) ≡
(λ) ≡ ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) λ−1/2 ≡
λ−1/2 ≡ ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J and λn = Jn + 1/2, for n = 0, 1, 2,…, nmax.
J and λn = Jn + 1/2, for n = 0, 1, 2,…, nmax.
• The following two identities, valid for 0 < θR ≤ π, are needed below:
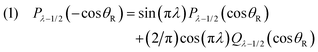 | (19) |
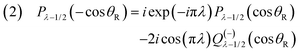 | (20) |
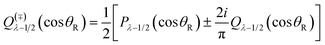 | (21) |
Again, singularities on the rhs of eqn (20) cancel at θR = π. Also notice that eqn (21) for the CAM plane is a generalization of the N, F result in eqn (5).
11.2 Backward CAM (Regge) representation
We start with a CAM theory valid at backward angles, namely the usual Regge representation.48–51,57 It is also called the SP(1, 0) representation, when derived as a special case from a more general and flexible CAM theory;127,128 here S and P stand for Subamplitude and Pole respectively. We can write exactly| f(θR) = fback(θR) + fpole(θR) | (22) |
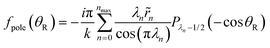 | (23) |
![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (λ) lying in the first quadrant of the CAM plane, labelled by n = 0, 1, 2,…, nmax. The corresponding residues for the poles at {λn} are denoted {
(λ) lying in the first quadrant of the CAM plane, labelled by n = 0, 1, 2,…, nmax. The corresponding residues for the poles at {λn} are denoted {![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) n}.
n}.
The term, fback(θR), in eqn (22) is the background subamplitude (or integral), which can be written as a contour integral in the CAM plane126,129 (its explicit form is not needed). There are two ways to calculate, fback(θR), namely
(1) Exactly. Using eqn (22), written in the form
| fback(θR) = fPWS(θR) − fpole(θR) |
![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J matrix elements in the Appendix, are to be used to compute the full scattering amplitude; eqn (23) is used for fpole(θR).
J matrix elements in the Appendix, are to be used to compute the full scattering amplitude; eqn (23) is used for fpole(θR).
(2) Approximately, in the asymptotic (SC) limit. This is accomplished as follows. When the PES contains a repulsive component at small J values, which is often the case for elastic, inelastic and reactive collisions, then the S matrix has a local symmetry.64,65,128–130 This allows the contour in the background integral to be moved so that it lies along a line of steepest descent. Then, evaluating the integral asymptotically along this line, we obtain a primitive semiclassical approximation (PSA) for the N background subamplitude. This is the same as the N SC result already encountered for rainbow scattering in Section 10, where it was denoted SC/N/PSA – see e.g., eqn (53) of ref. 124, or below.
Another name, more commonly used in CAM theory, is the “direct” subamplitude, which we will use below. To summarize, we can now write
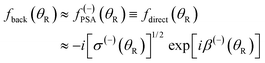 | (24) |
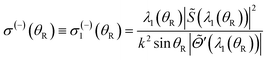 | (25) |
β(−)(θR) ≡ β(−)1(θR) = arg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (λ1(θR)) − λ1(θR)θR (λ1(θR)) − λ1(θR)θR | (26) |
![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (λ1(θR)) = +θR, see eqn (18).
(λ1(θR)) = +θR, see eqn (18).
In the next section, we apply the Regge theory outlined above to the three transitions.
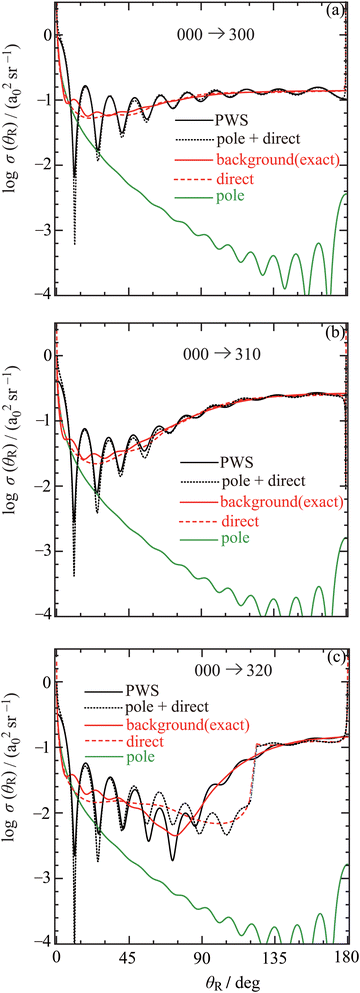
11.3 DCS results for the backward (Regge) CAM representation
In Fig. 10, we show logarithmic plots of the DCSs versus θR for the three transitions using the Regge representation, with nmax = 0. The following colour conventions are employed for the DCSs:• Full PWS DCS, black solid. Labelled, “PWS”.
• Pole DCS, green solid. Labelled, “pole”.
• Background(exact) DCS, red solid. Labelled, “background(exact)”.
• Direct DCS, red dashed. Labelled, “direct”.
• Pole + direct DCS, black dotted. Labelled, “pole + direct”.
We begin by observing the following in Fig. 10, which applies to all three transitions:
• The oscillations in the PWS DCSs extend over the whole angular range; although they become damped as θR increases. The oscillations arise from interference between the pole and background(exact) subamplitudes, or to a good approximation, the pole and direct subamplitudes. This tells us that a Regge pole contributes to the DCSs for all three transitions, making a larger contribution at smaller angles, where the oscillations are more pronounced.
• It is helpful for Section 11.4, where we deduce two approximate forward CAM formulae, to note singularities in the above subamplitudes and hence the corresponding DCSs. At, θR = π, the direct (and hence pole + direct) subamplitudes in Fig. 10 are singular. At, θR = 0, all the subamplitudes are singular, except for the PWS one.
We next make more detailed observations on the DCSs in the three panels:
• For the 000 → 300 transition in Fig. 10(a), the pole DCS has a familiar shape.130 In particular, for θR ≳ 90°, there are oscillations which arise from the interference of two decaying surface (or creeping) waves propagating around the core of the interaction potential; these combine to form a glory in backward-angle region. In contrast, for θR ≲ 90°, the pole DCS is almost monotonic and the pole subamplitude (23) makes an increasingly larger contribution to the full DCS as θR gets smaller.
The background(exact) DCS is seen to vary slowly with θR, except for angles very close to the forward direction. The direct DCS agrees closely with the background(exact) DCS, except for some oscillations around θR = 30°. This is the first time the approximations in fdirect(θR) have been tested.
The pole + direct DCS agrees closely with the full PWS DCS.
• Similar results can be seen in Fig. 10(b) for the 000 → 310 transition, so we do not repeat the discussion just given for the 300 case.
• For the 000 → 320 transition in Fig. 10(c), the agreement between the direct and background(exact) DCSs, and pole + direct and PWS DCSs is less good, especially for 60° ≲ θR ≲ 135°. This can be understood by inspection of the QDF for the 320 case in Fig. 6(c), which is seen to have a more complicated structure in the N region compared to Fig. 6(a) and (b). In particular, there are rainbows at θr,NR(min) = 120.3° and θr,NR(max) = 122.7°. The steepest descent approximation used to derive the direct subamplitude will fail at (and for angles around) these rainbow values. So in the DCS plot, we have bridged this gap by adding straight lines passing through, θR = 121°, 122°, 123° for the direct and pole + direct DCSs [this was also done in Fig. 8(c)].
In conclusion, we have proved that a single Regge pole (i.e., a resonance) contributes to the whole angular range for the DCSs for all three transitions.
11.4 CAM results for DCSs in the forward-angle region
It was found in Section 11.3 that the Regge pole subamplitude made the largest contribution to the DCSs in the forward-angle region. It is therefore useful to examine the angular scattering in this region in greater detail.The identity (19) lets us convert Pλ−1/2(−cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR) exactly into a sum of terms involving Pλ−1/2(+cos
θR) exactly into a sum of terms involving Pλ−1/2(+cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR) and Qλ−1/2(+cos
θR) and Qλ−1/2(+cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR). Now in the sum, fback(θR) + fpole(θR), the main rôle of the Qλn−1/2(+cos
θR). Now in the sum, fback(θR) + fpole(θR), the main rôle of the Qλn−1/2(+cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR) term as θR → 0, is to cancel the singularity in the background subamplitude. This suggests that omitting the Qλn−1/2(+cos
θR) term as θR → 0, is to cancel the singularity in the background subamplitude. This suggests that omitting the Qλn−1/2(+cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR) term from fpole(θR) in eqn (19) and (23) may give a useful result in the forward-angle region. We then obtain the following approximate pole contribution:
θR) term from fpole(θR) in eqn (19) and (23) may give a useful result in the forward-angle region. We then obtain the following approximate pole contribution:
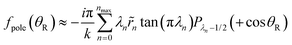 | (27) |
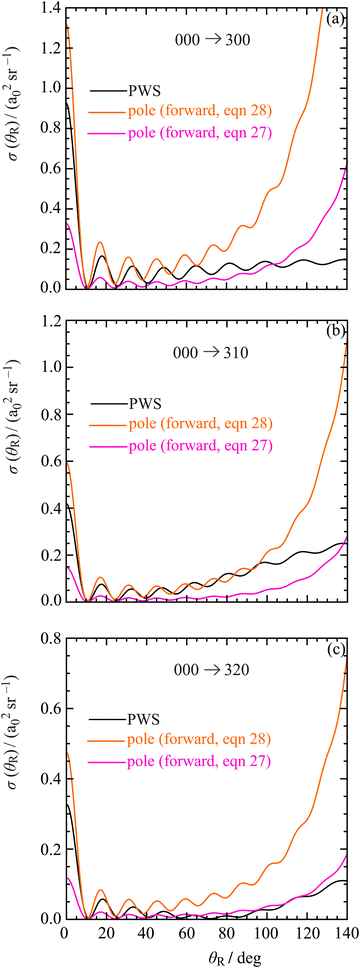 | ||
| Fig. 11 Plots of σ(θR) versus θR for forward angles, θR ≤ 140°, at Etrans = 62.09 meV. The DCSs plotted are: PWS (black solid curve), pole, [forward, using eqn (28)] (orange solid curve), pole, [forward, using eqn (27)] (pink solid curve). The transitions are: (a) 000 → 300, (b) 000 → 310, (c) 000 → 320. | ||
We can repeat the above procedure using the identity (20), but this time neglecting the term Q(−)λ−1/2(+cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR). We obtain after simplification
θR). We obtain after simplification
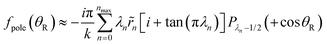 | (28) |
In conclusion, the two approximate CAM representations derived above provide useful additional information on the forward-angle DCS scattering using Regge poles.
11.5 Comparison with earlier CAM results for DCSs in the forward-angle region
The problem of obtaining a useful CAM expression for the forward-angle region has been considered earlier by two of us (DS and DDeF) together with Cavalli and Aquilanti,79 although application was made to a different transition, namely 000 → 200. We now show how a formula given in ref. 79 can be deduced from eqn (28). We insert the following results into eqn (28):(1) The identity, i + tan(πλ) = i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp(−iπλ)/cos(πλ).
exp(−iπλ)/cos(πλ).
(2) Define the unmodified S matrix, where S(λ) = exp(−iπ(λ − 1/2))![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (λ), for which the unmodified residues at the poles are, rn = exp(−iπ(λn − 1/2))
(λ), for which the unmodified residues at the poles are, rn = exp(−iπ(λn − 1/2))![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) n.
n.
(3) Insert the Hilb approximation for the Legendre function, namely
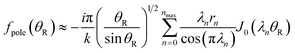 | (29) |
12. Conclusions
We have investigated the long-standing problem of whether a resonance contributes to the forward-angle scattering of three state-to-state F + H2 reactions in scheme (R1). We proved that the answer is, “Yes”.We reduced the problem to its essentials and presented a well-defined, yet rigorous and unambiguous, investigation of the DCSs using CAM theory. We began by carrying out quantum scattering calculations for the FXZ PES, obtaining accurate numerical {![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J} for indistinguishable H2 at Etrans = 62.09 meV. We then used a variety of theoretical techniques to analyse structures in the DCSs:
J} for indistinguishable H2 at Etrans = 62.09 meV. We then used a variety of theoretical techniques to analyse structures in the DCSs:
• Full and NF PWS DCS and PWS LAM theory, including resummations of the full PWS up to second order.
• The recently introduced “CoroGlo” test, which suggested that the scattering at forward angles is a glory, not a corona.
• The CoroGlo result was confirmed by the DCSs calculated from six asymptotic (SC) forward-glory theories.
• We reported results for three asymptotic (SC) rainbow theories, which demonstrated the existence of a broad (hidden) farside Airy-type rainbow at sideward angles for the three transitions.
• We employed CAM theories of forward and backward scattering, with the Regge pole positions and residues being found by Thiele rational interpolation. At Etrans = 62.09 meV, there is just one Regge pole in the first quadrant of the CAM plane, which is the simplest situation for applications of CAM theory.
• The single Regge pole contributes to a DCS across the whole angular range, being most prominent at forward angles. We have therefore proved that a Regge resonance contributes to a DCS for the three transitions.
• The diffraction oscillations in the DCSs arise from NF interference, in particular, interference between the Regge pole subamplitude and the direct (or background) subamplitude.
Conflicts of interest
There are no conflicts to declare.Appendix
This appendix lists the values of the set {![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J} in Cartesian format for J = 0, 1, 2,…, 19, which are used in the main text. The
J} in Cartesian format for J = 0, 1, 2,…, 19, which are used in the main text. The ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) J matrix values are for the reaction F + H2(vi = 0, ji = 0, mi = 0) → FH(vf = 3, jf = 0, 1, 2, mf = 0) + H at Etrans = 62.09 meV.
J matrix values are for the reaction F + H2(vi = 0, ji = 0, mi = 0) → FH(vf = 3, jf = 0, 1, 2, mf = 0) + H at Etrans = 62.09 meV.
| J | 000 → 300 | 000 → 310 | 000 → 320 |
|---|---|---|---|
| 0 | 0.2848 + 0.001004i | −0.3322 − 0.2259i | −0.09018 + 0.3023i |
| 1 | −0.2798 + 0.0551i | 0.370 + 0.1521i | 0.01865 − 0.3064i |
| 2 | 0.2368 − 0.160i | −0.3946 + 0.01044i | 0.1104 + 0.2652i |
| 3 | −0.1027 + 0.2663i | 0.3036 − 0.2334i | −0.2211 − 0.1221i |
| 4 | −0.1247 − 0.2531i | −0.02648 + 0.3602i | 0.1901 − 0.07116i |
| 5 | 0.2727 + 0.01744i | −0.2723 − 0.1828i | −0.03114 + 0.1429i |
| 6 | −0.09042 + 0.240i | 0.2238 − 0.1766i | −0.07155 − 0.06742i |
| 7 | −0.2105 − 0.0969i | 0.1259 + 0.2007i | 0.07422 − 0.02173i |
| 8 | 0.05494 − 0.1937i | −0.1499 + 0.1154i | 0.005603 + 0.07699i |
| 9 | 0.1683 − 0.01901i | −0.1202 − 0.08387i | −0.07454 + 0.02201i |
| 10 | 0.09628 + 0.1017i | 0.008351 − 0.1124i | −0.05466 − 0.04799i |
| 11 | 0.01848 + 0.1157i | 0.06542 − 0.06211i | −0.01291 − 0.06514i |
| 12 | 0.01139 + 0.09599i | 0.06207 − 0.04045i | −0.008203 − 0.05846i |
| 13 | 0.02934 + 0.02932i | 0.01444 − 0.0293i | −0.01929 − 0.01752i |
| 14 | 0.008132 + 0.002446i | 0.0005049 − 0.007069i | −0.005085 − 0.001086i |
| 15 | 0.001326 − 0.0000626i | −0.0002334 − 0.001159i | −0.0007524 + 0.0001116i |
| 16 | 0.0001612 − 0.00004257i | −0.00005643 − 0.0001466i | −0.00008272 + 0.00003041i |
| 17 | 0.00001753 − 6.678 × 10−6i | −7.94 × 10−6 − 0.00001664i | −8.371 × 10−6 + 3.88 × 10−6i |
| 18 | 1.813 × 10−6 − 8.496 × 10−7i | −9.399 × 10−7 − 1.783 × 10−6i | −8.338 × 10−7 + 4.38 × 10−7i |
| 19 | 1.93 × 10−7 − 1.134 × 10−7i | −1.08 × 10−7 − 1.939 × 10−7i | −8.934 × 10−8 + 4.822 × 10−8i |
Acknowledgements
We thank Professors V. Aquilanti and S. Cavalli (Università degli Studi di Perugia, Italy) for scientific discussions. Support of this research is gratefully acknowledged by the P. R. China Zibo City Integration Project (grant number: 2021SNPT0069); by the Spanish PID2021-126273NB-I00 grant fundered by MICINN/AEI/10.13039/501100011033 and by the European Regional Development Fund, “A way of making Europe”, as well as by the Basque Government (grant number: IT1470-22); by the Italian High Performance Computing Center at CINECA for computer time awarded via the Italian Supercomputer Resource Allocation (ISCRA-B project, code HP10BREFY9).References
- J. N. L. Connor, Annu. Rep. Prog. Chem., Sect. A: Phys. Inorg. Chem., 1973, 70, 5 CAS.
- W. Hu and G. C. Schatz, J. Chem. Phys., 2006, 125, 132301 CrossRef PubMed.
- D. C. Walker, Muon and Muonium Chemistry, Cambridge University Press, Cambridge, UK, 1983, ch. 7 Search PubMed.
- D. C. Walker, Acc. Chem. Res., 1985, 18, 167 CrossRef CAS.
- J. N. L. Connor, Hyperfine Interact., 1981, 8, 423 CrossRef CAS.
- D. K. Bondi, D. C. Clary, J. N. L. Connor, B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1982, 76, 4986 CrossRef CAS.
- J. Aldegunde, P. G. Jambrina, E. García, V. J. Herrero, V. Sáez-Rábanos and F. J. Aoiz, Mol. Phys., 2013, 111, 3169 CrossRef CAS.
- S. L. Mielke, B. C. Garrett, D. G. Fleming and D. G. Truhlar, Mol. Phys., 2015, 113, 160 CrossRef CAS.
- G. Laude, D. Calderini, R. Welsch and J. O. Richardson, Phys. Chem. Chem. Phys., 2020, 22, 16843 RSC.
- D. G. Fleming, S. P. Cottrell, I. McKenzie and K. Ghandi, Phys. Chem. Chem. Phys., 2015, 17, 19901 RSC.
- D. G. Fleming, D. G. Arseneau, S. P. Cottrell and J. N. T. Peck, Phys. Chem. Chem. Phys., 2020, 22, 6326 RSC.
- L. G. Gao, D. G. Fleming, D. G. Truhlar and X. Xu, J. Phys. Chem. Lett., 2021, 12, 4154 CrossRef CAS PubMed.
- L. Yu Rusin, M. B. Sevryuk and J. P. Toennies, arXiv, 2010, preprint, arXiv:1009.1578v1 DOI:10.48550/arXiv.1009.1578.
- V. M. Azriel’, V. M. Akimov, L. I. Kolesnikova, L. Yu Rusin, M. B. Sevryuk and J. P. Toennies, Khim. Fiz., 2009, 28(11), 3 Search PubMed . English translation: Russ. J. Phys. Chem. B, 2009, 3, 857.
- L. Y. Rusin, M. B. Sevryuk and J. P. Toennies, Khim. Fiz., 2007, 26(8), 11 CAS . English translation: Russ. J. Phys. Chem. B, 2007, 1, 452.
- L. Yu Rusin, M. B. Sevryuk and J. P. Toennies, Khim. Fiz., 2003, 22(9), 10 CAS.
- J. F. Castillo, D. E. Manolopoulos, K. Stark and H.-J. Werner, J. Chem. Phys., 1996, 104, 6531 CrossRef CAS.
- D. E. Manolopoulos, J. Chem. Soc., Faraday Trans., 1997, 93, 673 RSC.
- S. D. Chao and R. T. Skodje, J. Chem. Phys., 2000, 113, 3487 CrossRef CAS.
- S. D. Chao and R. T. Skodje, J. Chem. Phys., 2003, 119, 1462 CrossRef CAS.
- V. Aquilanti, S. Cavalli, D. De Fazio, A. Volpi, A. Aguilar, X. Giménez and J. M. Lucas, Phys. Chem. Chem. Phys., 2002, 2, 401 RSC.
- V. Aquilanti, S. Cavalli, A. Simoni, A. Aguilar, J. M. Lucas and D. De Fazio, J. Chem. Phys., 2004, 121, 11675 CrossRef CAS PubMed.
- V. Aquilanti, S. Cavalli, D. De Fazio, A. Simoni and T. V. Tscherbul, J. Chem. Phys., 2005, 123, 054314 CrossRef PubMed.
- D. De Fazio, S. Cavalli, A. Simoni and T. V. Tscherbul, in Semiclassical and Other Methods for Understanding Molecular Collisions and Chemical Reactions, ed. S. Sen, D. Sokolovski, and J. N. L. Connor, Collaborative Computational Project on Molecular Quantum Dynamics (CCP6), Daresbury Laboratory, Warrington, UK, 2005, pp. 119–126. ISBN: 0-9545289-3-X Search PubMed.
- A. Kuppermann, Faraday Discuss., 1998, 110, 212 Search PubMed.
- A. Kuppermann and Y.-S. M. Wu, Chem. Phys. Lett., 2001, 349, 537 CrossRef CAS.
- M. Hankel, S. C. Smith, R. J. Allan, S. K. Gray and G. G. Balint-Kurti, J. Chem. Phys., 2006, 125, 164303 CrossRef PubMed.
- F. T. Smith, Phys. Rev., 1960, 118, 349 CrossRef . Erratum, Phys. Rev., 1960, 119, 2098.
- E. Privat, G. Guillon and P. Honvault, J. Chem. Phys., 2021, 154, 104303 CrossRef CAS PubMed.
- G. Guillon and T. Stoecklin, J. Chem. Phys., 2009, 130, 144306 CrossRef CAS PubMed.
- S. Cavalli and D. De Fazio, Phys. Scr., 2007, 76, C21 CrossRef CAS.
- F. T. Smith, J. Chem. Phys., 1962, 36, 248 CrossRef CAS.
- A. I. Baz’, Y. B. Zeldovich and A. M. Perelomov, Scattering, Reactions and Decay in Nonrelativistic Quantum Mechanics, translated from Russian by Z. Lerman, Israel Program for Scientific Translations, Jerusalem, Israel, 1969.
- Time in Quantum Mechanics, ed. J. G. Muga, R. Sala Mayato, and Í. L. Egusquiza, Lect. Notes in Physics, No. 734, Springer, Berlin, Germany, 2nd edn, 2007, vol. 1 Search PubMed.
- M. Razavy, Quantum Theory of Tunneling, World Scientific, Singapore, 2nd edn, 2014 Search PubMed.
- D. Sokolovski and J. N. L. Connor, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 6512 CrossRef CAS PubMed.
- D. Sokolovski and J. N. L. Connor, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1500 CrossRef PubMed.
- D. Sokolovski and J. N. L. Connor, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 4677 CrossRef PubMed.
- D. Sokolovski, in Time in Quantum Mechanics, ed. J. G. Muga, R. Sala Mayato, and Í. L. Egusquiza, Lect. Notes in Physics, No. 734 (2007), Springer, Berlin, Germany, 2nd edn, 2007, ch. 7, vol. 1 Search PubMed.
- D. Sokolovski and R. Sala Mayato, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 022105 CrossRef.
- D. Sokolovski, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 042115 CrossRef.
- D. Sokolovski and E. Akhmatskaya, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 022104 CrossRef.
- D. Sokolovski and E. Akhmatskaya, Ann. Phys., 2013, 339, 307 CAS.
- D. Sokolovski and E. Akhmatskaya, Commun. Phys., 2018, 1, 47 CrossRef.
- D. Sokolovski and E. Akhmatskaya, Sci. Rep., 2021, 11, 10040 CrossRef CAS PubMed.
- B. Fu, X. Xu and D. H. Zhang, J. Chem. Phys., 2008, 129, 011103 CrossRef PubMed.
- R. G. Newton, The complex j-Plane. Complex Angular Momentum in Nonrelativistic Quantum Scattering Theory, Benjamin, New York, USA, 1964 Search PubMed.
- H. M. Nussenzveig, Diffraction Effects in Semiclassical Scattering, Cambridge University Press, Cambridge, UK, 1992 Search PubMed.
- W. T. Grandy Jr., Scattering of Waves from Large Spheres, Cambridge University Press, Cambridge, UK, 2000 Search PubMed.
- J. A. Adam, Phys. Rep., 2002, 356, 229 CrossRef CAS.
- J. A. Adam, Rays, Waves and Scattering: Topics in Classical Mathematical Physics, Princeton University Press, Princeton, New Jersey, USA, 2017 Search PubMed.
- T. Regge, Il Nuovo Cimento, 1959, 14, 951 CrossRef CAS; Reprinted in: T. Regge, An Eclectic Genius: From Quantum Gravity to Computer Play, ed. L. Castellani, A. Ceresole, R. D’Auria and P. Frè, World Scientific, Singapore, 2020, pp. 46–71 Search PubMed.
- T. Regge, Il Nuovo Cimento, 1960, 18, 947 CrossRef CAS; Reprinted in: T. Regge, An Eclectic Genius: From Quantum Gravity to Computer Play, ed. L. Castellani, A. Ceresole, R. D’Auria and P. Frè, World Scientific, Singapore, 2020, pp. 72–81 Search PubMed.
- V. de Alfaro and T. Regge, Potential Scattering, North-Holland, Amsterdam, Netherlands, 1965 Search PubMed.
- T. Regge and S. Sandrelli, L’Infinito Cercare: Autobiografia di un Curioso, Einaudi, Torino, Italy, 2012 Search PubMed.
- C. Xiahou and J. N. L. Connor, Phys. Chem. Chem. Phys., 2021, 23, 13349 RSC.
- J. N. L. Connor, in Semiclassical Methods in Molecular Scattering and Spectroscopy, Proceedings of the NATO Advanced Study Institute held in Cambridge, England in September 1979, ed. M. S. Child, Reidel, Dordrecht, Netherlands, 1980, pp. 45–107 Search PubMed.
- K.-E. Thylwe, in Resonances, The Unifying Route Towards the Formulation of Dynamical Processes. Foundations and Applications in Nuclear, Atomic and Molecular Physics, Proceedings of a Symposium held at Lertorpet, Värmland, Sweden, 1987, ed. E. Brändas and N. Elander, Lect. Notes in Physics, Springer, Berlin, 1989, vol. 325, pp. 281–311 Search PubMed.
- J. N. L. Connor, J. Chem. Soc. Faraday Trans., 1990, 86, 1627 RSC.
- J. N. L. Connor, J. Chem. Phys., 2013, 138, 124310 CrossRef CAS PubMed.
- A. Z. Msezane, in Semiclassical and Other Methods for Understanding Molecular Collisions and Chemical Reactions, ed. S. Sen, D. Sokolovski and J. N. L. Connor, Collaborative Computational Project on Molecular Quantum Dynamics (CCP6), Daresbury Laboratory, Warrington, UK, 2005, pp. 95–103, ISBN: 0-9545289-3-X Search PubMed.
- D. Sokolovski, A. Z. Msezane, Z. Felfli, S. Yu. Ovchinnikov and J. H. Macek, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 261, 133 CrossRef CAS.
- M. S. Child, Semiclassical Mechanics with Molecular Applications, Oxford University Press, Oxford, UK, 2nd edn, 2014, p. 226 Search PubMed.
- D. Sokolovski, J. N. L. Connor and G. C. Schatz, Chem. Phys. Lett., 1995, 238, 127 CrossRef CAS.
- D. Sokolovski, J. N. L. Connor and G. C. Schatz, J. Chem. Phys., 1995, 103, 5979 CrossRef CAS.
- A. J. Dobbyn, P. McCabe, J. N. L. Connor and J. F. Castillo, Phys. Chem. Chem. Phys., 1999, 1, 1115 RSC.
- D. Sokolovski, J. F. Castillo and C. Tully, Chem. Phys. Lett., 1999, 313, 225 CrossRef CAS.
- D. Sokolovski and J. F. Castillo, Phys. Chem. Chem. Phys., 2000, 2, 507 RSC.
- D. Sokolovski, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 024702 CrossRef.
- D. Vrinceanu, A. Z. Msezane, D. Bessis, J. N. L. Connor and D. Sokolovski, Chem. Phys. Lett., 2000, 324, 311 CrossRef CAS.
- F. J. Aoiz, L. Bañares, J. F. Castillo and D. Sokolovski, J. Chem. Phys., 2002, 117, 2546 CrossRef CAS.
- D. Sokolovski, Russ. J. Phys. Chem., 2002, 76(Suppl. 1), S21 Search PubMed.
- F. J. Aoiz, L. Bañares, J. F. Castillo, D. Sokolovski, F. Fernández-Alonso, B. D. Bean, J. D. Ayers, A. E. Pomerantz and R. N. Zare, in Femtochemistry and Femtobiology: Ultrafast Dynamics in Molecular Science, University of Castilla-La Mancha, Toledo, Spain, 2001, ed. A. Douhal and J. Santamaria, World Scientific, Singapore, 2002, pp. 61–72 Search PubMed.
- D. Sokolovski, Chem. Phys. Lett., 2003, 370, 805 CrossRef CAS.
- D. Sokolovski and A. Z. Msezane, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 032710 CrossRef.
- P. D. D. Monks, C. Xiahou and J. N. L. Connor, J. Chem. Phys., 2006, 125, 133504 CrossRef CAS PubMed.
- D. Sokolovski, S. K. Sen, V. Aquilanti, S. Cavalli and D. De Fazio, J. Chem. Phys., 2007, 126, 084305 CrossRef CAS PubMed.
- D. Sokolovski, D. De Fazio, S. Cavalli and V. Aquilanti, J. Chem. Phys., 2007, 126, 121101 CrossRef CAS PubMed.
- D. Sokolovski, D. De Fazio, S. Cavalli and V. Aquilanti, Phys. Chem. Chem. Phys., 2007, 9, 5664 RSC . In eqn (15) for “πλ”, read “π(λ − 1/2)”. On p. 5667, for “plan”, read, ”plane”. On p. 5667, “for semiclassical approximation (13)”, read, “for semiclassical approximation (3)”. In the caption to Fig. 6, “for Section II”, read “Section 2”, and for “Section III”, read “Section 3”.
- D. Sokolovski, Phys. Scr., 2008, 78, 058118 CrossRef.
- J. N. L. Connor, X. Shan, A. J. Totenhofer and C. Xiahou, in Multidimensional Quantum Mechanics with Trajectories, ed. D. V. Shalashilin and M. P. de Miranda, Collaborative Computational Project on Molecular Quantum Dynamics (CCP6), Daresbury Laboratory, Warrington, UK, 2009, pp. 38–47, ISBN: 978-0-9545289-8-0 Search PubMed.
- A. J. Totenhofer, C. Noli and J. N. L. Connor, Phys. Chem. Chem. Phys., 2010, 12, 8772 RSC.
- C. Xiahou, J. N. L. Connor and D. H. Zhang, Phys. Chem. Chem. Phys., 2011, 13, 12981 RSC.
- D. Sokolovski, E. Akhmatskaya and S. K. Sen, Comput. Phys. Commun., 2011, 182, 448 CrossRef CAS.
- E. Akhmatskaya, D. Sokolovski and C. Echeverría-Arrondo, Comput. Phys. Commun., 2014, 185, 2127 CrossRef CAS.
- X. Shan and J. N. L. Connor, J. Phys. Chem. A, 2014, 118, 6560 CrossRef CAS PubMed.
- D. Sokolovski and E. Akhmatskaya, Lect. Notes Comput. Sci., 2014, 8579, 522 Search PubMed.
- C. Xiahou and J. N. L. Connor, Phys. Chem. Chem. Phys., 2014, 16, 10095 RSC.
- D. Sokolovski, E. Akhmatskaya, C. Echeverría-Arrondo and D. De Fazio, Phys. Chem. Chem. Phys., 2015, 17, 18577 RSC.
- M. Hankel and J. N. L. Connor, AIP Adv., 2015, 5, 077160 CrossRef.
- C. Xiahou, X. Shan and J. N. L. Connor, J. Phys. Chem. A, 2019, 123, 10500 CrossRef CAS PubMed.
- E. Akhmatskaya and D. Sokolovski, Comput. Phys. Commun., 2022, 277, 108370 CrossRef CAS.
- D. De Fazio, Phys. Chem. Chem. Phys., 2014, 16, 11662 RSC.
- S. Cavalli, V. Aquilanti, K. C. Mundim and D. De Fazio, J. Phys. Chem. A, 2014, 118, 6632 CrossRef CAS PubMed.
- F. Esposito, C. M. Coppola and D. De Fazio, J. Phys. Chem. A, 2015, 119, 12615 CrossRef CAS PubMed.
- D. De Fazio, S. Cavalli and V. Aquilanti, J. Phys. Chem. A, 2016, 120, 5288 CrossRef CAS PubMed.
- D. De Fazio, V. Aquilanti and S. Cavalli, Front. Chem., 2019, 7, 328 CrossRef CAS PubMed.
- D. De Fazio, V. Aquilanti and S. Cavalli, J. Phys. Chem. A, 2020, 124, 12 CrossRef CAS PubMed.
- D. Sokolovski and S. Sen, in Semiclassical and Other Methods for Understanding Molecular Collisions and Chemical Reactions, ed. S. Sen, D. Sokolovski, and J. N. L. Connor, Collaborative Computational Project on Molecular Quantum Dynamics (CCP6), Daresbury Laboratory, Warrington, UK, 2005, pp. 104–111, ISBN: 0-9545289-3-X Search PubMed.
- J. Gilewicz and M. Pindor, J. Comput. Appl. Math., 1997, 87, 199 CrossRef.
- J. Gilewicz and M. Pindor, J. Comput. Appl. Math., 1999, 105, 285 CrossRef.
- J. Gilewicz and Y. Kryakin, J. Comput. Appl. Math., 2003, 153, 235 CrossRef.
- J. N. L. Connor, P. McCabe, D. Sokolovski and G. C. Schatz, Chem. Phys. Lett., 1993, 206, 119 CrossRef CAS.
- P. McCabe and J. N. L. Connor, J. Chem. Phys., 1996, 104, 2297 CrossRef CAS.
- R. Anni, J. N. L. Connor and C. Noli, Phys. Rev. C: Nucl. Phys., 2002, 66, 044610 CrossRef.
- C. Noli and J. N. L. Connor, Russ. J. Phys. Chem., 2002, 76(Suppl. 1), S77 Search PubMed . Also available at https://arXiv.org/abs/physics/0301054.
- R. Anni, J. N. L. Connor and C. Noli, Khim. Fiz., 2004, 23(2), 6 CAS . Also available at: https://arXiv.org/abs/physics/0410266.
- J. N. L. Connor and R. Anni, Phys. Chem. Chem. Phys., 2004, 6, 3364 RSC.
- R. C. Fuller, Phys. Rev. C: Nucl. Phys., 1975, 12, 1561 CrossRef CAS.
- J. J. Hollifield and J. N. L. Connor, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 1694 CrossRef CAS.
- J. J. Hollifield and J. N. L. Connor, Mol. Phys., 1999, 97, 293 CrossRef CAS.
- D. Sokolovski, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 042125 CrossRef.
- D. Yuan, S. Yu, W. Chen, J. Sang, C. Luo, T. Wang, X. Xu, P. Casavecchia, X. Wang, Z. Sun, D. H. Zhang and X. Yang, Nat. Chem., 2018, 10, 653 CrossRef CAS PubMed.
- J. N. L. Connor, Phys. Chem. Chem. Phys., 2004, 6, 377 RSC.
- J. N. L. Connor, Mol. Phys., 2005, 103, 1715 CrossRef CAS.
- C. Xiahou and J. N. L. Connor, Mol. Phys., 2006, 104, 159 CrossRef CAS.
- X. Shan and J. N. L. Connor, J. Chem. Phys., 2012, 136, 044315 CrossRef PubMed.
- X. Shan and J. N. L. Connor, Phys. Chem. Chem. Phys., 2011, 13, 8392 RSC.
- X. Shan and J. N. L. Connor, J. Phys. Chem. A, 2012, 116, 11414 CrossRef CAS PubMed.
- J. N. L. Connor and R. A. Marcus, J. Chem. Phys., 1971, 55, 5636 CrossRef CAS; For a commentary, see: J. N. L. Connor, Current Contents: Physical, Chemical and Earth Sciences, 1991, vol. 31(50), p. 10 Search PubMed; J. N. L. Connor, Current Contents: Engineering, Technology and Applied Sciences, 1991, vol. 22(50), p. 10. Also available at https://garfield.library.upenn.edu/classics1991/A1991GR14400001.pdf Search PubMed.
- C. Xiahou and J. N. L. Connor, J. Phys. Chem. A, 2009, 113, 15298 CrossRef CAS PubMed.
- X. Shan, C. Xiahou and J. N. L. Connor, Phys. Chem. Chem. Phys., 2018, 20, 819 RSC.
- C. Xiahou, X. Shan and J. N. L. Connor, Phys. Scr., 2019, 94, 065401 CrossRef CAS.
- X. Shan, C. Xiahou and J. N. L. Connor, Mol. Phys., 2023, 121, e2198616 CrossRef.
- J. N. L. Connor and W. Jakubetz, Mol. Phys., 1978, 35, 949 CrossRef CAS.
- J. N. L. Connor and D. C. Mackay, Mol. Phys., 1979, 37, 1703 CrossRef CAS.
- K.-E. Thylwe, J. Phys A: Math. Gen., 1983, 16, 1141 CrossRef CAS.
- K.-E. Thylwe and J. N. L. Connor, J. Phys. A: Math. Gen., 1985, 18, 2957 CrossRef CAS.
- J. N. L. Connor and D. C. Mackay, Chem. Phys. Lett., 1978, 59, 163 CrossRef . In eqn (15), for “−i(i/k)”, read, “ −(i/k)”.
- J. N. L. Connor, Mol. Phys., 1975, 29, 745 CrossRef CAS.
| This journal is © the Owner Societies 2024 |