Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interatomic Coulombic decay in small helium clusters
Sévan
Kazandjian
a,
Max
Kircher
 b,
Gregor
Kastirke
b,
Joshua B.
Williams
b,
Markus
Schöffler
b,
Gregor
Kastirke
b,
Joshua B.
Williams
b,
Markus
Schöffler
 b,
Maksim
Kunitski
b,
Reinhard
Dörner
b,
Tsveta
Miteva
b,
Maksim
Kunitski
b,
Reinhard
Dörner
b,
Tsveta
Miteva
 a,
Selma
Engin
a,
Florian
Trinter
a,
Selma
Engin
a,
Florian
Trinter
 *bc,
Till
Jahnke
*de and
Nicolas
Sisourat
*a
*bc,
Till
Jahnke
*de and
Nicolas
Sisourat
*a
aSorbonne Universite, CNRS, Laboratoire de Chimie Physique Matiere et Rayonnement, UMR 7614, F-75005 Paris, France. E-mail: nicolas.sisourat@sorbonne-universite.fr
bInstitut für Kernphysik, Goethe-Universität Frankfurt, Max-von-Laue-Straße 1, 60438 Frankfurt am Main, Germany
cMolecular Physics, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: trinter@fhi-berlin.mpg.de
dMax-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
eEuropean XFEL GmbH, Holzkoppel 4, 22869 Schenefeld, Germany. E-mail: till.jahnke@xfel.eu
First published on 8th September 2023
Abstract
Interatomic Coulombic decay (ICD) is an ultrafast non-radiative electronic decay process wherein an excited atom transfers its excess energy to a neighboring species leading to the ionization of the latter. In helium clusters, ICD can take place, for example, after simultaneous ionization and excitation of one helium atom within the cluster. After ICD, two helium ions are created and the system undergoes a Coulomb explosion. In this work, we investigate theoretically ICD in small helium clusters containing between two and seven atoms and compare our findings to two sets of coincidence measurements on clusters of different mean sizes. We provide a prediction on the lifetime of the excited dimer and show that ICD is faster for larger clusters. This is due to (i) the increased number of neighboring atoms (and therefore the number of decay channels) and (ii) the substantial decrease of the interatomic distances. In order to provide more details on the decay dynamics, we report on the kinetic-energy distributions of the helium ions. These distributions clearly show that the ions may undergo charge exchange with the neutral atoms within the cluster, such process is known as frustrated Coulomb explosion. The probability for these charge-exchange processes increases with the size of the clusters and is reflected in our calculated and measured kinetic-energy distributions. These distributions are therefore characteristics of the size distribution of small helium clusters.
I. Introduction
Interatomic Coulombic decay (ICD) is an ultrafast non-radiative electronic decay process wherein an excited atom transfers its excess energy to a neighboring entity, ionizing it.1–3 This general phenomenon has been investigated in a variety of systems, see ref. 4–6 for recent reviews and ref. 7 for a complete list of publications reporting ICD studies.In this work, we present experimental and theoretical results of a detailed study on ICD in small helium clusters. In these systems, ICD can take place after simultaneous ionization and excitation of one helium atom within the cluster (e.g., via photon-induced shake-up ionization). The excited ion transfers its excess energy to another helium atom, which is ionized as a result. After the energy transfer, the two ions repel each other due to Coulomb repulsion, which triggers—depending on the cluster size—more or less complex breakup processes of the cluster. A general equation for ICD in clusters containing m helium atoms is:
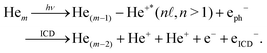 | (1) |
Extensive studies on ICD in the helium dimer8–11 showed that the two helium atoms within the dimer can exchange energy over large distances, up to 14 Å. Furthermore, it was demonstrated that the distributions of the kinetic energy released by the two ions (so-called KER spectrum) reflect the nodal structures of the involved excited dimer cation vibrational wave functions, implying that ICD is slower than the vibrational motion in the decaying states. Time-resolved studies of the KER spectra confirmed the nuclear motion preceding ICD.10,11 ICD in a helium trimer was recently used to investigate the so-called frustrated Coulomb explosion of loosely bound matter.12 It was shown that the helium ions, formed after ICD, can undergo charge exchange with the neutral atoms of the clusters, leading to the ejection of a fast neutral atom and a slow ion. Moreover, recent works on ICD in helium nanodroplets13,14 also reported that helium ions can lose a significant amount of kinetic energy compared to the dimer case. This energy loss was explained in ref. 13 with a billiard-like collision scenario between one helium ion and another helium atom within the droplet. Other mechanisms are discussed in ref. 14, depending on whether ICD takes place at the surface or in the bulk of the nanodroplets.
By combining a semi-classical method15 with a diatomics-in-molecules approach (DIM),16–20 we give the first complete theoretical description of the ICD process and the subsequent fragmentation of helium clusters containing up to seven atoms. We report here on the ICD lifetime and the asymptotic kinetic-energy distributions of the two helium ions for these clusters. We discuss in detail the charge-exchange mechanism between the helium ions and the neighboring neutral atoms in the course of the Coulomb explosion (i.e., after ICD). In the systems investigated here, this mechanism is the dominant one to create slow ions. Furthermore, we demonstrate that signatures of these processes can be clearly obtained in several experimental observables, as our theoretical findings are supported by corresponding measurements. These have been performed at beamline UE112_PGM-1 of the BESSY II synchrotron (Berlin, Germany).21
The outline of the article is the following: the theoretical approach and computational details are described in Section II and details on the experimental setup and the measurements are given in Section III. We then discuss in Section IV the results obtained for the ICD lifetime and the kinetic energy of the ions for helium clusters containing up to seven atoms. We discuss the latter observables with respect to the size of the clusters. The conclusion in Section V summarizes the main ideas and opens up a road map towards the study of larger clusters.
II. Computational methods
We used a semi-classical approach combining a classical description of the nuclear motion with quantum electronic-structure calculations.15 The nuclear quantum wave packet is replaced by a swarm of classical trajectories. The initial conditions are chosen to reproduce the spatial quantum probability distributions, the initial momenta are neglected. We assume that the decaying states are uniformly populated. The trajectories are thus started on the potential energy surface (PES) of one of the ionized-excited electronic states, chosen randomly. The probability to decay to the final state f is given by the decay rate times the time step:| pdecay = ΓfΔt. | (2) |
The PES and decay rates are calculated within the DIM approach. The DIM approach has been widely used to compute the electronic energies of rare-gas clusters18,23,24 and has recently been adapted to the calculation of ICD rates.16 The DIM approach is a configuration interaction (CI) technique, which uses potential energy curves of each pair of atoms within the cluster to build the CI matrix. Similarly, the decay rates of the whole cluster are obtained from the decay rates of each pair of atoms in the system. In this work, we focus on the electronic states corresponding to simultaneous ionization and excitation to He+*(2p). Within the DIM approach and if the off-diagonal terms are neglected, the ICD rates for a given electronic state are given by the sum of the rates for each pair of atoms (forming the corresponding molecular states) within the cluster. The rates of He–He+*(2s) states are small.9,12 The states corresponding to He(m−1)–He+*(2s) were therefore neglected as they are expected to contribute less to ICD. The necessary input data were taken from the literature: the He2+*(2p) potential energy curves and ICD rates were interpolated from ref. 25, the He2+(1s−1) curves were taken from ref. 26, and the He2 potential has been described with Tang's potential.27 We used a Coulomb potential to represent the He+–He+ interaction, as this approximation is valid for all ICD-relevant distances.25
The initial nuclear geometries were chosen in order to reproduce the spatial quantum nuclear probability-density distribution. We used the quantum Monte Carlo wave function reported in ref. 28, where the wave functions for helium clusters up to 7 atoms are provided. We, therefore, limit our investigation to such size. For all cluster sizes, we generated 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 geometries by using a Monte Carlo Metropolis sampling. For each of those geometries, the nuclei are propagated using a Verlet's algorithm with a time step of 5 a.u. As mentioned above, the excited state populated after the ionization–excitation step is chosen randomly. During the dynamics, the populated electronic state at time t + Δt is chosen such that the corresponding electronic wave function has the maximum overlap with the wave function of the populated electronic state at t. This naturally enables charge–transfer processes during the dynamics while conserving the total energy. In the DIM approach, the charge may be delocalized between two atoms that are far apart if they are symmetrically equivalent. This raises a problem with the maximum-overlap algorithm described above as it can enable unphysical, long-distance charge–transfer processes. In order to avoid them, we added an arbitrary condition stating that the wave function at t + Δt is chosen such that the overlap with the wave function at t or at t − Δt is at least 0.7. If this condition is not met, the trajectory remains in the same adiabatic electronic state. The trajectories in the final states are propagated for 2 ps. During the propagation, we perform a Mulliken population analysis on the DIM eigenvectors to obtain the charge of each atom. In the following, we focus on the ICD processes that lead to two atomic ions. In order to remove larger ionic fragments from the analysis, only trajectories where two ions have a charge of 0.7 e or more are taken into account. This rejects 7% of the trajectories in the case of He7 and less for the smaller cluster sizes.
000 geometries by using a Monte Carlo Metropolis sampling. For each of those geometries, the nuclei are propagated using a Verlet's algorithm with a time step of 5 a.u. As mentioned above, the excited state populated after the ionization–excitation step is chosen randomly. During the dynamics, the populated electronic state at time t + Δt is chosen such that the corresponding electronic wave function has the maximum overlap with the wave function of the populated electronic state at t. This naturally enables charge–transfer processes during the dynamics while conserving the total energy. In the DIM approach, the charge may be delocalized between two atoms that are far apart if they are symmetrically equivalent. This raises a problem with the maximum-overlap algorithm described above as it can enable unphysical, long-distance charge–transfer processes. In order to avoid them, we added an arbitrary condition stating that the wave function at t + Δt is chosen such that the overlap with the wave function at t or at t − Δt is at least 0.7. If this condition is not met, the trajectory remains in the same adiabatic electronic state. The trajectories in the final states are propagated for 2 ps. During the propagation, we perform a Mulliken population analysis on the DIM eigenvectors to obtain the charge of each atom. In the following, we focus on the ICD processes that lead to two atomic ions. In order to remove larger ionic fragments from the analysis, only trajectories where two ions have a charge of 0.7 e or more are taken into account. This rejects 7% of the trajectories in the case of He7 and less for the smaller cluster sizes.
Our method neglects nuclear quantum effects (e.g., zero-point energy29 or exchange effects). However, it aims at describing the energy distributions of fragments due to Coulomb explosion. These fragments have in general high kinetic energy, the nuclear quantum effects are therefore expected to have a small contribution. More details on the semiclassical method can be found in ref. 12 and 15. The DIM approach for computing the decay rates is reported in ref. 16.
III. Experiment
The experiments were carried out at the XUV beamline UE112_PGM-1 of the synchrotron BESSY II at Helmholtz-Zentrum Berlin in Germany21 in the single-bunch timing mode with a bunch spacing of 800 ns. We used linear horizontally polarized photons of 65.505 eV photon energy generated by the beamline's elliptical undulator. We employed cold target recoil ion momentum spectroscopy, i.e., a COLTRIMS reaction microscope30–32 for our studies. The helium clusters were produced in a supersonic gas jet, which passed two skimmers of 300 μm diameter each before being crossed with the photon beam at right angle. By changing the He stagnation pressure, the condensation properties of the supersonic expansion can be adjusted such that apart from monomers the condensed part of the gas jet contains mainly a certain cluster size. We used a gas nozzle of 5 μm diameter cooled down to 8 K and driving pressures of 1.7 bar to produce He3–5 clusters and 2.2 bar to produce He6–9 clusters, respectively, and achieved a fraction of about 1% clusters in the otherwise uncondensed atomic supersonic gas jet. These cluster-source settings were predetermined in preparatory measurements making use of matter wave diffraction. In these measurements, we employed a 100 nm transmission grating installed in the path of the gas jet in order to select the clusters from the condensed gas beam.33–37 As all clusters have the same velocity, they can be sorted by mass because their diffraction angle behind the transmission grating depends on their de Broglie wavelength. This allowed for a characterization of the cluster beam and for determining appropriate source settings for the measurements presented in this article.The ion arm of the COLTRIMS spectrometer consisted of a 4 cm long acceleration region, the electron arm of 6 cm acceleration and 12 cm field-free drift region, i.e., Wiley-McLaren time-of-flight focusing geometry.38 Both arms were equipped with a microchannel-plate detector of active areas of 120 mm diameter for the ion detector and 80 mm diameter for the electron detector and with hexagonal delay-line position readout.39,40 Electrons and ions were guided by a homogeneous electric field of 3.05 V cm−1 onto the two time- and position-sensitive detectors. The electric-field strength was selected such that 4π sr collection solid angle for electrons and ions has been achieved for electrons up to 0.5 eV kinetic energy and molecular fragmentation in He+/He+ pairs with a KER up to 9.5 eV. From the times-of-flight and the positions-of-impact, the three-dimensional momentum vectors of all charged fragments of the photoreaction were retrieved as well as derived quantities, e.g., kinetic energies and emission angles. By measuring the momenta of the ionic fragments and the low-energy electrons in coincidence, reactions of clusters in which ICD occurred were discriminated from He monomer reactions.
IV. Results and discussion
A. Lifetime
Fig. 1 shows the calculated population in the ionized-excited states as functions of time for different cluster sizes. For all clusters from He3 to He7, the decay is complete in a few ps. For the dimer, the decay is much slower: a complete depopulation is achieved after about 100 ps. On such a long time scale, the IC-decay is in competition with radiative decay of Hen+*(n = 2).22 The reason for this is the large mean nuclear distance in He2 of around 52 Å.34,36 The interaction potential at such distances is so weak that the nuclear motion is virtually frozen, and the radiative decay is dominant. Only trajectories starting at interatomic distances smaller than about 12 Å undergo ICD. Over all trajectories for the dimer, 70% decay radiatively. It should be noted that the decay of the helium dimer via ICD, as shown in Fig. 1, is in good agreement with what has been measured experimentally by Trinter et al.11 (not shown).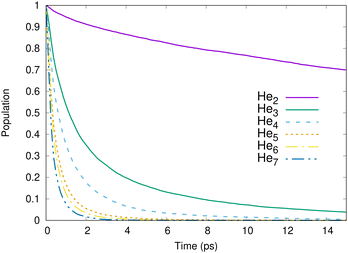 | ||
| Fig. 1 Calculated population of the ionized-excited states for He2 to He7 as a function of time after the ionization-excitation of one helium atom within the cluster. | ||
We define the half-life (t1/2) as the time required for the population in the decaying states to decrease by 50%. The half-life is given in Table 1 for the different cluster sizes. As can be seen, ICD is faster when the number of atoms within the cluster increases because more decay channels are open. However, the number of neighboring atoms alone cannot explain the fast increase of the decay rate. For example, in the pentamer an excited helium ion has twice more neighboring atoms than in the trimer while the half-life is reduced by a factor of about 3.5. Additionally, the longevity of the dimer is orders of magnitude larger than that of the other cluster sizes. This discrepancy is explained by the significant changes in the quantum nuclear wave functions as the size of the clusters grows. The mean internuclear distance dramatically shrinks when more atoms are introduced, from more than 50 Å for He2 to 7.0 Å for He7 (approaching the established value of about 2.0–2.5 Å for liquid helium41), as seen in Table 1. We note that clusters containing between five and seven atoms do have a similar mean distance. In this case, the half-life is roughly proportional to the number of neighbors, 1/(N − 1).
| N | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| t 1/2 (ps) | 38 | 1.1 | 0.60 | 0.32 | 0.28 | 0.23 |
| 〈r〉 (Å) | 56.9 | 9.2 | 8.2 | 7.2 | 7.2 | 7.0 |
B. Ion–ion coincidence spectra
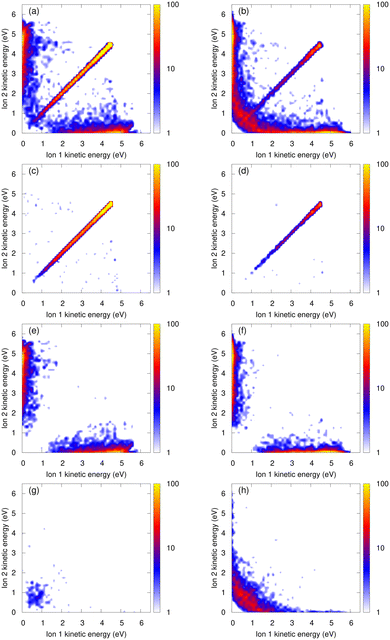
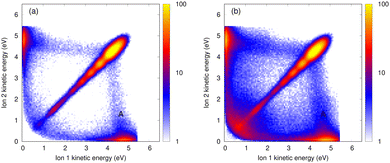
The kinetic energy of the ions contains information on the nuclear dynamics of both the excited state and the Coulomb explosion process. Particularly, detailed information can be extracted from the coincidence spectrum of the kinetic energies for the two ions in the final state. For example, with this spectrum an asymmetric Coulomb explosion, i.e., processes with very different energy of the two ions can be directly identified. In Fig. 2, we show the ion–ion coincidence spectra for He4 (left panels) and He7 (right panels) obtained from our calculations. In Fig. 3, we report the measured spectra for a mean cluster size of 3–5 atoms [panel (a)] and 6–9 atoms [panel (b)]. A good agreement between experiments and theory is seen. The total coincidence spectra exhibit an intense diagonal feature. This corresponds to a symmetric, dimer-like Coulomb explosion where the two ions acquire the same amount of kinetic energy. Moreover, a non-diagonal feature is also observed, especially along the x and y axes, where one ion is fast while the other one is slow. The intensity of this part increases with the number of atoms. Its presence can only be explained by some kind of collision with the neutral atoms within the cluster.The presence of slow ions after ICD-triggered Coulomb explosion of small helium clusters and in nanodroplets has been experimentally reported in ref. 12–14, respectively. In ref. 13, a simple model where one of the ions undergoes an elastic collision with a surrounding neutral atom is employed to explain this observation. However, we found that this model fails at reproducing quantitatively the intensity of the non-diagonal part reported in Fig. 2 (i.e., for the small helium clusters considered here). There is a slightly tilted feature [most prominently visible in the measured energy maps, noted by A in Fig. 3(a) and (b)], which is located at an energy of approximately 4–5 eV of one of the ions and a broad range of energies of the other one. As demonstrated earlier,12 this feature can be attributed to a single, binary collision between one of the ionic fragments with a neutral atom during the Coulomb explosion.
An analysis of our classical trajectories shows that a second, alternative mechanism takes place, involving a charge transfer between a (fast) helium ion and a (slow) neutral helium atom (see also ref. 12). In order to highlight the importance of these charge-transfer processes, we show in the second row of Fig. 2 the calculated coincidence spectra filtered only on trajectories where no charge transfer takes place. The spectra exhibit merely a single diagonal feature, except for some sparse points in the non-diagonal part corresponding to a few elastic collisions. For He4, 8% of the trajectories without charge transfer exhibit an elastic collision. This corresponds to 4% of all trajectories. For He7, these values are 17% and 2%, respectively: even though the probability of an elastic collision is higher when there are more neighbors, the percentage of charge transfer is so high (about 90%) that only 2% of the trajectories exhibit an elastic collision and no charge transfer. In the third row, we show trajectories where one ion transfers its charge during the Coulomb explosion. Before the charge transfer, the ion is accelerated due to Coulomb repulsion, while the neutral atom is almost immobile. The charge is transferred with only little kinetic-energy exchange, resulting in one slow ion and one fast neutral atom. The system thus ends up with a fast-slow ion pair, hence the non-diagonal part along the axes of the coincidence spectra. After the charge transfer, the fast and slow ions start repelling each other. Momentum conservation implies that during this repulsion the faster ion receives more of the available energy. This is why in the charge-transfer scenarios, some ions have around 6 eV, while this value is capped at 5 eV for trajectories without charge transfer. Naturally, what can happen to one ion may happen to both of them. The lowest row of Fig. 2 shows events where both ions transfer their charge at some point during the Coulomb explosion. This results in trajectories with two slow ions, the majority of them having a kinetic energy of 2 eV or less.
The total coincidence spectra may thus be divided in four parts, which are almost non-overlapping: a diagonal part corresponding to trajectories with no charge transfer; a non-diagonal part with one fast and one slow ion, corresponding to trajectories with one charge transfer; a wide low-energy part corresponding to trajectories where both ions transferred their charges; and a further non-diagonal part belonging to binary collisions (without charge transfer, more prominently visible in the experimental data) located at approximately 4–5 eV kinetic energy of one of the two ions.
As the number of atoms in the clusters increases, the number of charge-transfer processes increases. Results from our simulations for clusters with sizes from two to seven atoms are shown in Table 2. Charge-transfer processes are obviously impossible in the dimer case. In some rare occurrences, the two ions of the helium trimer may undergo charge transfer. For clusters containing four atoms or more, the majority of trajectories undergo at least one charge exchange.
| N | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| No charge transfer | 1.00 | 0.69 | 0.45 | 0.25 | 0.17 | 0.11 |
| One charge transfer | 0.00 | 0.31 | 0.51 | 0.63 | 0.64 | 0.62 |
| Two charge transfers | 0.00 | 0.01 | 0.04 | 0.12 | 0.19 | 0.27 |
The counts along the diagonal line in the experimental coincidence spectra can be compared to the total counts. The ratio of the two gives about 0.6 for the mean cluster size of 3–5 atoms and 0.4 for 6–9 atoms. Our calculations predict slightly smaller ratios: our simulations show that charge transfer can take place at distances of up to 5 Å between the two helium atoms. Our DIM approach might overestimate the range of distances for which charge-transfer processes occur. The theoretical branching ratio of the charge-transfer processes would then be overestimated as well, which would explain the slight disagreement between our experiments and theory. We, nevertheless, expect the charge-transfer processes to be very efficient and the trend predicted by the DIM approach with respect to the cluster size to be correct.
C. KER and single-ion kinetic-energy spectra
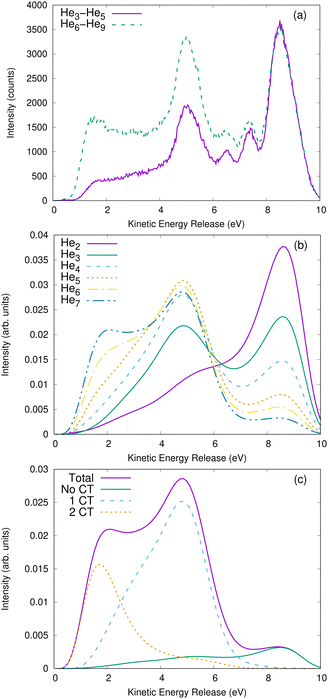
Even though the coincidence spectra contain all the information regarding the kinetic-energy distribution of the ions after the Coulomb explosion, a one-dimensional graph enables an easier quantitative comparison of the observed features. In Fig. 4 [panels (a) and (b)], we show the total KER spectra. The KER is the sum of the kinetic energy of the two ions. Panel (a) depicts the measured distributions, panel (b) the results from our simulations.Inspecting the theoretical results, the KER spectrum of the dimer has a main peak at 9 eV, which corresponds to the energy of two ions placed at the shortest distance accessible to a He2+* pair. The intensity of the KER spectra is lower at smaller KERs. The He3 to He7 KER spectra also exhibit a peak at 9 eV and a second one around 5 eV, which is not seen in the dimer case. Furthermore, for He5 to He7, a shoulder widens this second peak to energies as low as 1 eV. The intensity of the peak at 5 eV and its shoulder increase with the number of atoms, whereas the relative intensity of the peak at 9 eV decreases. As our theoretical approach enables an unequivocal separation of the simulated trajectories by the number of charge-transfer processes, we show the different contributions to the KER spectra in panel (c) of Fig. 4 (as an example, for He7). As shown above, the peak around 9 eV corresponds to trajectories with no charge transfer, the peak around 5 eV to trajectories with one charge transfer, and the wide feature around 2 eV to trajectories with two charge-transfer processes.
The comparison of the spectra, shown in Fig. 4(b), for the different clusters shows that the shape of the distributions switches over between He3 and He4. This change reflects the complex geometry of these extremely floppy clusters.42 However, it is difficult to attribute the change to specific geometrical properties. One could speculate that He2 and He3 are quantum (halo) systems,36,42,43 while clusters of He4 and larger tend towards more classical systems.
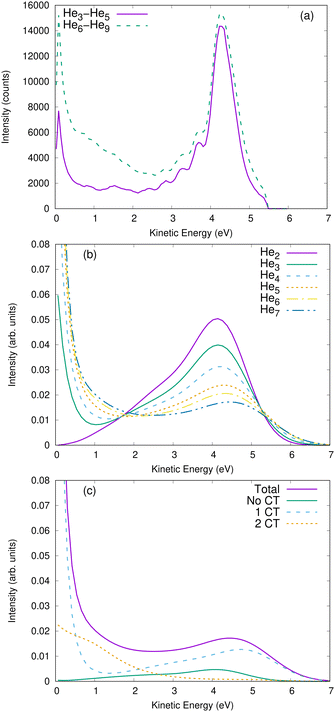
In some cases, a coincident detection of ions is experimentally not feasible. A simpler measurement would consist of measuring the kinetic energy of the ions individually. Accordingly, we show for comparison in Fig. 5 such single-ion energy spectra. Panel (a) depicts the measured spectra for clusters of a size of 3–5 atoms and clusters of a size of 6–9 atoms. In panel (b), the ion-energy spectra for He2 to He7 clusters are shown, as obtained from our theoretical modeling. For He2, the spectrum is constituted of one peak around 4.5 eV, which is half the energy of the main peak in the KER spectrum. For larger clusters, the spectra extend to higher kinetic energies (i.e., the ions may have kinetic energy up to 6 eV). This is in line with the observation in the coincidence spectra that charge-transfer processes induce an asymmetrical repartition of the energy, enabling one ion to get more than half of the available Coulomb energy in order to meet momentum conservation. The slow ions can be detected as an intense peak around 0 eV. This peak gets slightly wider for the larger clusters. The decomposition of these spectra according to the number of charge transfers shows that the ions faster than 5 eV indeed come from trajectories with one single charge transfer. These fast ions are accompanied by a very slow ion, which has almost no kinetic energy. However, when the two charges get transferred, there is no fast ion that can take most of the energy available by the Coulomb repulsion. Therefore, the two ions receive 1–2 eV kinetic energy. Ions with similar energies have already been detected experimentally in nanodroplets by Shcherbinin et al.13 Our results hint that they might come from Coulomb explosion starting inside the droplet, where both ions can transfer their charges. This should be compared with ICD triggered at the surface of the droplet, where only one ion may go through the cluster and transfer its charge, resulting in one fast ion and one slow ion. The slow ion might not be easily distinguished from the background noise created by the ionization of isolated atoms, but the signature of the fast ion is a shoulder at around 6 eV in the spectra. Such a shoulder can be seen in the spectra of the helium nanodroplets reported in ref. 13.
Our findings suggest that it should be possible to experimentally “count” the number of charge transfers even without a coincidence apparatus. For example, ions with a kinetic energy of more than 5 eV mainly result from trajectories with one charge transfer, while ions with a kinetic energy around 1 eV mainly come from trajectories with two charge transfers. Furthermore, as shown in Table 2, the number of charge-transfer processes depends strongly on the size of the clusters. As an example, we have integrated the ion kinetic-energy spectra (shown in Fig. 5) between 3 eV and 5 eV and from 5 eV onward. We report in Table 3 the ratio I between the two areas as a function of the cluster size. As seen in the table, this ratio depends strongly on N, providing a simple way to measure the cluster size.
| N | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| I | 0.21 | 0.28 | 0.37 | 0.49 | 0.53 | 0.60 |
V. Conclusion
We have described theoretically the dynamics of the ICD process and the subsequent Coulomb explosion in small helium clusters and compared the results of this modeling to two measurements on He clusters of different mean sizes. Our detailed study confirms that the ICD lifetime and thus the radiative decay branching ratio strongly depend on the cluster size. Furthermore, the dynamics of the cluster after the excitation step and during the Coulomb explosion, which follows the IC-decay, is surprisingly rich. For example, charge-transfer processes in He3 to He7 play a vital role in the Coulomb explosion and considerably change the kinetic-energy distribution of the resulting ions (as compared to the dimer case). The probability of charge transfer is directly linked to the number of atoms in the cluster, and with increasing cluster size even the probability of more than one charge-transfer process becomes non-negligible. Fingerprints of the different charge-transfer processes are present in the calculated and measured kinetic-energy spectra. For (much) larger clusters, the probability for charge transfer may still depend on the cluster size, since charge-transfer processes are expected to take place mainly in the bulk of the clusters and only weakly at the surface.Author contributions
SK: investigation, software, writing – original draft, writing – review & editing. MKi: formal analysis, investigation, writing – review & editing. GK: investigation. JBW: investigation. MS: investigation. MKu: investigation. RD: funding acquisition, project administration, supervision, writing – review & editing. TM: Investigation, writing – review & editing. SE: investigation, writing – review & editing. FT: investigation, writing – review & editing. TJ: formal analysis, funding acquisition, investigation, project administration, supervision, writing – review & editing. NS: funding acquisition, investigation, project administration, software, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from Agence Nationale de la Recherche through the program ANR-16-CE29-0016-01 and from the Research Executive Agency (REA) under the European Union's Horizon 2020 research and innovation program Grant Agreement No. 705515. We acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG) as part of the DFG research unit FOR1789/II and Bundesministerium für Bildung und Forschung (BMBF). We thank Helmholtz-Zentrum Berlin (HZB) for the allocation of synchrotron radiation beamtime. We thankfully acknowledge the financial support by HZB. Open Access funding provided by the Max Planck Society.References
- L. S. Cederbaum, J. Zobeley and F. Tarantelli, Giant Intermolecular Decay and Fragmentation of Clusters, Phys. Rev. Lett., 1997, 79, 4778 CrossRef CAS.
- S. Marburger, O. Kugeler, U. Hergenhahn and T. Möller, Experimental Evidence for Interatomic Coulombic Decay in Ne Clusters, Phys. Rev. Lett., 2003, 90, 203401 CrossRef CAS PubMed.
- T. Jahnke, A. Czasch, M. S. Schöffler, S. Schössler, A. Knapp and M. Käsz, et al., Experimental Observation of Interatomic Coulombic Decay in Neon Dimers, Phys. Rev. Lett., 2004, 93, 163401 CrossRef CAS PubMed.
- U. Hergenhahn, Interatomic and intermolecular coulombic decay: The early years, J. Electron Spectrosc. Relat. Phenom., 2011, 184, 78–90 CrossRef CAS.
- T. Jahnke, Interatomic and intermolecular Coulombic decay: the coming of age story, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 082001 CrossRef.
- T. Jahnke, U. Hergenhahn, B. Winter, R. Dörner, U. Frühling and P. V. Demekhin, et al., Interatomic and Intermolecular Coulombic Decay, Chem. Rev., 2020, 120, 11295–11369 CrossRef CAS PubMed.
- See https://www.pci.uni-heidelberg.de/tc/usr/icd/ICD.refbase.html for a complete list of ICD publications; 2023.
- T. Havermeier, T. Jahnke, K. Kreidi, R. Wallauer, S. Voss and M. Schöffler, et al., Interatomic Coulombic Decay following Photoionization of the Helium Dimer: Observation of Vibrational Structure, Phys. Rev. Lett., 2010, 104, 133401 CrossRef CAS PubMed.
- N. Sisourat, N. V. Kryzhevoi, P. Kolorenč, S. Scheit, T. Jahnke and L. S. Cederbaum, Ultralong-range energy transfer by interatomic Coulombic decay in an extreme quantum system, Nat. Phys., 2010, 6, 508–511 Search PubMed.
- N. Sisourat, N. V. Kryzhevoi, P. Kolorenč, S. Scheit and L. S. Cederbaum, Impact of nuclear dynamics on interatomic Coulombic decay in a He dimer, Phys. Rev. A, 2010, 82, 053401 CrossRef.
- F. Trinter, J. B. Williams, M. Weller, M. Waitz, M. Pitzer and J. Voigtsberger, et al., Evolution of Interatomic Coulombic Decay in the Time Domain, Phys. Rev. Lett., 2013, 111, 093401 CrossRef CAS PubMed.
- S. Kazandjian, J. Rist, M. Weller, F. Wiegandt, D. Aslitürk and S. Grundmann, et al., Frustrated Coulomb explosion of small helium clusters, Phys. Rev. A, 2018, 98, 050701(R) CrossRef.
- M. Shcherbinin, A. C. LaForge, V. Sharma, M. Devetta, R. Richter and R. Moshammer, et al., Interatomic Coulombic decay in helium nanodroplets, Phys. Rev. A, 2017, 96, 013407 CrossRef.
- F. Wiegandt, F. Trinter, K. Henrichs, D. Metz, M. Pitzer and M. Waitz, et al., Direct observation of interatomic Coulombic decay and subsequent ion-atom scattering in helium nanodroplets, Phys. Rev. A, 2019, 100, 022707 CrossRef CAS.
- N. Sisourat, Nuclear dynamics of decaying states: A semiclassical approach, J. Chem. Phys., 2013, 139, 074111 CrossRef CAS PubMed.
- N. Sisourat, S. Kazandjian, A. Randimbiarisolo and P. Kolorenč, Interatomic Coulombic decay widths of helium trimer: A diatomics-in-molecules approach, J. Chem. Phys., 2016, 144, 084111 CrossRef PubMed.
- A. K. Belyaev, A. S. Tiukanov and W. Domcke, Generalized diatomics-in-molecule method for polyatomics, Phys. Scr., 2009, 80, 048124 CrossRef.
- P. J. Kuntz and J. Valldorf, A DIM model for homogeneous noble gas ionic clusters, Z. Phys. D, 1988, 8, 195–208 CrossRef CAS.
- F. O. Ellison, A Method of Diatomics in Molecules. I. General Theory and Application to H2O, J. Am. Chem. Soc., 1963, 85, 3540–3544 CrossRef CAS.
- F. O. Ellison, N. T. Huff and J. C. Patel, A Method of Diatomics in Molecules. II. H and H3+1, J. Am. Chem. Soc., 1963, 85, 3544–3547 CrossRef CAS.
- G. Schiwietz, M. Beye and T. Kachel, UE112_PGM-1: An open-port low-energy beamline at the BESSY II undulator UE112, J. Large-Scale Res. Facilities, 2015, 1, A33 CrossRef.
- G. W. F. Drake, J. Kwela and A. van Wijngaarden, He+ 2p state lifetime by a quenching-asymmetry measurement, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 113 CrossRef CAS PubMed.
- M. Ovchinnikov, B. L. Grigorenko, K. C. Janda and V. A. Apkarian, Charge localization and fragmentation dynamics of ionized helium clusters, J. Chem. Phys., 1998, 108, 9351–9361 CrossRef CAS.
- D. Bonhommeau, M. Lewerenz and N. Halberstadt, Fragmentation of ionized doped helium nanodroplets: theoretical evidence for a dopant ejection mechanism, J. Chem. Phys., 2008, 128, 054302 CrossRef CAS PubMed.
- P. Kolorenč, N. V. Kryzhevoi, N. Sisourat and L. S. Cederbaum, Interatomic Coulombic decay in a He Dimer: Ab initio potential-energy curves and decay widths, Phys. Rev. A, 2010, 82, 013422 CrossRef.
- J. Xie, B. Poirier and G. I. Gellene, Accurate, two-state ab initio study of the ground and first-excited states of He2+, including exact treatment of all Born–Oppenheimer correction terms, J. Chem. Phys., 2005, 122, 184310 CrossRef PubMed.
- K. T. Tang, J. P. Toennies and C. L. Yiu, Accurate Analytical He-He van der Waals Potential Based on Perturbation Theory, Phys. Rev. Lett., 1995, 74, 1546 CrossRef CAS PubMed.
- S. W. Rick, D. L. Lynch and J. D. Doll, A variational Monte Carlo study of argon, neon, and helium clusters, J. Chem. Phys., 1991, 95, 3506–3520 CrossRef CAS.
- S. Mukherjee and M. Barbatti, A Hessian-Free Method to Prevent Zero-Point Energy Leakage in Classical Trajectories, J. Chem. Theory Comput., 2022, 18, 4109–4116 CrossRef CAS PubMed.
- R. Dörner, V. Mergel, O. Jagutzki, L. Spielberger, J. Ullrich and R. Moshammer, et al., Cold Target Recoil Ion Momentum Spectroscopy: a ‘momentum microscope’ to view atomic collision dynamics, Phys. Rep., 2000, 330, 95–192 CrossRef.
- J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L. P. H. Schmidt and H. Schmidt-Böcking, Recoil-ion and electron momentum spectroscopy: reaction-microscopes, Rep. Prog. Phys., 2003, 66, 1463 CrossRef CAS.
- T. Jahnke, T. Weber, T. Osipov, A. L. Landers, O. Jagutzki and L. P. H. Schmidt, et al., Multicoincidence studies of photo and Auger electrons from fixed-in-space molecules using the COLTRIMS technique, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 229–238 CrossRef CAS.
- W. Schöllkopf and J. P. Toennies, Nondestructive Mass Selection of Small van der Waals Clusters, Science, 1994, 266, 1345–1348 CrossRef PubMed.
- R. E. Grisenti, W. Schöllkopf, J. P. Toennies, G. C. Hegerfeldt, T. Köhler and M. Stoll, Determination of the Bond Length and Binding Energy of the Helium Dimer by Diffraction from a Transmission Grating, Phys. Rev. Lett., 2000, 85, 2284 CrossRef CAS PubMed.
- M. Kunitski, S. Zeller, J. Voigtsberger, A. Kalinin, L. P. H. Schmidt and M. Schöffler, et al., Observation of the Efimov state of the helium trimer, Science, 2015, 348, 551–555 CrossRef CAS PubMed.
- S. Zeller, M. Kunitski, J. Voigtsberger, A. Kalinin, A. Schottelius and C. Schober, et al., Imaging the He2 quantum halo state using a free electron laser, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14651–14655 CrossRef CAS PubMed.
- S. Zeller, M. Kunitski, J. Voigtsberger, M. Waitz, F. Trinter and S. Eckart, et al., Determination of Interatomic Potentials of He2, Ne2, Ar2, and H2 by Wave Function Imaging, Phys. Rev. Lett., 2018, 121, 083002 CrossRef CAS PubMed.
- W. C. Wiley and I. H. McLaren, Time-of-Flight Mass Spectrometer with Improved Resolution, Rev. Sci. Instrum., 1955, 26, 1150–1157 CrossRef CAS.
- O. Jagutzi, V. Mergel, K. Ullmann-Pfleger, L. Spielberger, U. Spillmann and R. Dörner, et al., A broad-application microchannel-plate detector system for advanced particle or photon detection tasks: large area imaging, precise multi-hit timing information and high detection rate, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 477, 244–249 CrossRef.
- O. Jagutzki, J. S. Lapington, L. B. C. Worth, U. Spillman, V. Mergel and H. Schmidt-Böcking, Position sensitive anodes for MCP read-out using induced charge measurement, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 477, 256–261 CrossRef CAS.
- D. M. Brink and S. Stringari, Density of states and evaporation rate of helium clusters, Z. Phys. D, 1990, 15, 257–263 CrossRef CAS.
- J. Voigtsberger, S. Zeller, J. Becht, N. Neumann, F. Sturm and H. K. Kim, et al., Imaging the structure of the trimer systems 4He3 and 3He4He2, Nat. Commun., 2014, 5, 5765 CrossRef CAS PubMed.
- M. Kunitski, Q. Guan, H. Maschkiwitz, J. Hahnenbruch, S. Eckart and S. Zeller, et al., Ultrafast manipulation of the weakly bound helium dimer, Nat. Phys., 2021, 17, 174–178 Search PubMed.
| This journal is © the Owner Societies 2023 |