Open Access Article
Open Access ArticleGas-phase formation of glycolonitrile in the interstellar medium†
Luis
Guerrero-Méndez
a,
Anxo
Lema-Saavedra
b,
Elena
Jiménez
 cd,
Antonio
Fernández-Ramos
cd,
Antonio
Fernández-Ramos
 *ab and
Emilio
Martínez-Núñez
*ab and
Emilio
Martínez-Núñez
 *a
*a
aDepartamento de Química Física, Facultade de Química, Universidade de Santiago de Compostela, Avda. das Ciencias s/n 15782, Santiago de Compostela, Spain. E-mail: qf.ramos@usc.es; emilio.nunez@usc.es
bCentro Singular de Investigación en Química Biológica y Materiales Moleculares (CIQUS), Universidade de Santiago de Compostela, C/Jenaro de la Fuente s/n, 15782, Santiago de Compostela, Spain
cDepartamento de Química Física, Facultad de Ciencias y Tecnologías Químicas, Universidad de Castilla-La Mancha, Avda. Camilo José Cela 1b, 13071, Ciudad Real, Spain
dInstituto de Investigación en Combustión y Contaminación Atmosférica (ICCA), Universidad de Castilla-La Mancha, Camino de Moledores s/n, 13071, Ciudad Real, Spain
First published on 24th July 2023
Abstract
Our automated reaction discovery program, AutoMeKin, has been utilized to investigate the formation of glycolonitrile (HOCH2CN) in the gas phase under the low temperatures of the interstellar medium (ISM). The feasibility of a proposed pathway depends on the absence of barriers above the energy of reactants and the availability of the suggested precursors in the ISM. Based on these criteria, several radical–radical reactions and a radical–molecule reaction have been identified as viable formation routes in the ISM. Among the radical–radical reactions, OH + CH2CN appears to be the most relevant, considering the energy of the radicals and its ability to produce glycolonitrile in a single step. However, our analysis reveals that this reaction produces hydrogen isocyanide (HNC) and formaldehyde (CH2O), with rate coefficients ranging from (7.3–11.5) × 10−10 cm3 molecule−1 s−1 across the temperature range of 10–150 K. Furthermore, the identification of this remarkably efficient pathway for HNC elimination from glycolonitrile significantly broadens the possibilities for any radical–radical mechanism proposed in our research to be considered as a feasible pathway for the formation of HNC in the ISM. This finding is particularly interesing given the persistently unexplained overabundance of hydrogen isocyanide in the ISM. Among the radical–molecule reactions investigated, the most promising one is OH + CH2CHNH, which forms glycolonitrile and atomic hydrogen with rate coefficients in the range (0.3–6.6) × 10−10 cm3 molecule−1 s−1 within the 10–150 K temperature range. Our calculations indicate that the formation of both hydrogen isocyanide and glycolonitrile is efficient under the harsh conditions of the ISM.
1. Introduction
Glycolonitrile (GLN) is a simple organic molecule that has been proposed as a key precursor to the formation of adenine.1,2 In 2019, the first detection of glycolonitrile in the interstellar medium (ISM) was reported.3 The detection of GLN highlights the importance of understanding the formation of this molecule, as it can provide insight into the origins of prebiotic molecules in the universe.The formation mechanism of organic molecules in the ISM can be explained by several types of reactions. Due to the extremely low temperatures of the interstellar clouds (10–150 K), gas-phase reactions are expected to have barrier heights that approach zero with respect to reactants.4 Reactions can take place on grain surfaces or through gas-phase chemistry. Although the former can account for the formation of molecules in hot cores that surround protostars and young stars, explaining how molecules in cold, dense sources are formed is still a significant challenge.4
Gas-phase reactions in the ISM are expected to occur with submerged barriers,5,6 which typically requires that at least one of the reactants must be a radical or an ion. Furthermore, the stabilization of the formed products is not favoured at the extremely low densities of the ISM, unless radiative stabilization is competitive.4
Several studies have investigated various formation pathways of GLN on ices and/or grains.7–11 In addition, a few gas-phase reactions have been proposed for the formation of GLN; however, all of these mechanisms exhibit significant reaction barriers.10 To date, no gas-phase reactions with submerged barriers have been proposed for the formation of GLN. In the year 2001, Woon conducted ab initio calculations to show that GLN can be formed from the reaction of CH2O + HNC on ice, despite the fact that it exhibits a barrier height of 46 kcal mol−1.11 Recent calculations by the same author reveal that the reactions between C+ and HCN embedded in the surface of icy grain mantles can explain the formation of GLN.7 Early computational studies have also explored isomers of C2H3NO.12,13
Danger et al. have shown that GLN can be formed (in competition with methanolamine) from ices containing CH2O, NH3 and CN at 40 K.8 It was also demonstrated, using infrared spectroscopy and mass spectrometry, that the reaction between HCN and CH2O is only feasible in the presence of water.9
When using a limited chemical reaction network (CRN) in which GLN can only form on dust grains, the resulting GLN abundances are significantly underestimated.3 This outcome led the authors of the study to recognize that “key gas phase routes for the formation of this molecule might be missing in our chemical network”.3 Recently, Zhao et al. employed the astrochemical code NAUTILUS and an updated gas-grain CRN to demonstrate that adjusting the cosmic-ray ionization rate is necessary to most accurately replicate the observed abundances of GLN.10
This work aims to unravel the barrierless GLN formation pathways through theoretical calculations by examining two distinct types of formation reactions:
| R1 + R2 → GLN + hν | (1) |
| R3 + M → GLN + H | (2) |
To unravel all possible elementary steps involved in the above reactions, we utilize AutoMeKin, an automated program developed in our laboratory for discovering reaction mechanisms in an automated manner.14 As the decomposition and formation pathways of GLN are interconnected, to study reaction (1) the decomposition pathways of GLN are analyzed. Conversely, investigating the fragmentation mechanisms of HOCH2CHN radical, hereinafter GLN-H, is used to study reaction (2). The decomposition products of GLN (R1 and R2) and GLN-H (R3 and M) are compared with a database of molecules that have already been detected in the ISM to assess the feasibility of each pathway.
Finally, the most promising mechanisms are evaluated for feasibility by conducting kinetic simulations that replicate the conditions of the ISM.
2. Computational details
2.1 Automated reaction mechanism mapping
The program AutoMeKin,14–16 developed in our laboratory, was used to locate the minima and transition states (TSs) on the potential energy surface (PES) of GLN and GLN-H. Our open-source code facilitates an automated and efficient exploration of the decomposition pathways of a molecule by leveraging a combination of reactive molecular dynamics (MD) simulations, graph-theoretic tools, and interactive dashboards. To enhance efficiency, the PES is initially explored using semi-empirical calculations (hereinafter Level1). The stationary points on the PES are then refined using a level of DFT/ab initio electronic structure theory (hereinafter Level2) in a subsequent step. Similar to previous studies, Level1 in this work refers to PM717 while Level2 is ωB97XD/Def2-TZVPP. The latter is known to perform exceptionally well in predicting barrier heights,18 and Gaussian0919 was employed for these calculations. Additionally, thanks to a new algorithm, it is now possible to sample barrierless pathways with our program.6Although AutoMeKin has made extensive use of MD simulations and graph-theoretic tools, the code now includes a new Python library, called amk_tools, which enables the parsing, processing, and transformation of the obtained CRNs.6 Furthermore, new Python scripts are utilized to customize the energy profiles generated by amk_tools,6 and to compare the resulting fragmentation products (R1, R2, R3, and M) with a database of molecules identified in the ISM.
For each system (GLN and GLN-H), AutoMeKin's workflow was iterated 30 times. Each iteration comprised several steps, such as MD simulations, optimization of minima and TSs, and generation of CRNs. For each set of MD simulations, 500 trajectories were performed, with a maximum simulation time of 0.5 ps. The screening settings used in our recent indole decomposition study have been adopted here.6 These settings are used to filter TSs with very low imaginary frequencies, and to remove redundant structures. Further details on the applied methodology can be found in ref. 6.
To determine whether the CRNs obtained in our iterative procedure have converged, kinetic Monte Carlo (KMC) simulations were used to solve the chemical master equation.20 Specifically, the abundances of the products, obtained after exciting 103 molecules of GLN and GLN-H at 250 kcal mol−1, were calculated. RRKM theory was utilized to evaluate the rate coefficients for each state-to-state process:21
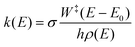 | (3) |
Although our research is limited to the investigation of the barrierless formation channels of GLN, the full CRNs can be found in Zenodo.24 In the CRNs, the designations for the minima, transition states, and fragments are MIN, TS, and PROD (or PR), respectively. These designations are accompanied by numerical labels to differentiate between various structures. Additionally, the labels for GLN and GLN-H structures are independent.
2.2 Kinetic simulations
The two predominant pathways chosen for the kinetic analysis exhibit two distinct and consecutive dynamical bottlenecks:i. A free energy bottleneck (TS1) to the barrierless formation of a vibrationally excited species (S*),
| A + B → S* | (4) |
| S* → C + D | (5) |
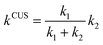 | (6) |
The association rate coefficient k1 was calculated using the formula proposed by Georgievskii and Klippenstein for dipole–dipole interactions,29 which is expressed as:
| k1 = Cμ−1/2(dAdB)2/3T−1/6 | (7) |
The vibrationally excited species S* can also undergo a radiative stabilization process which can potentially compete with reaction (5):
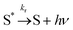 | (8) |
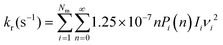 | (9) |
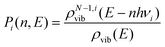 | (10) |
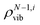 refers to the density of states for the molecule with the ith mode absent.
refers to the density of states for the molecule with the ith mode absent.
3. Results
This section outlines the plausible pathways of GLN formation in the ISM, classified into radical–radical and radical–molecule reactions. It is worth noting that one of the pathways discussed below does not fit into either of the two categories mentioned earlier, as it involves reactions between a molecule and a biradical. Despite this, it has been included in the category of reactions between radicals because it was obtained through the study of singlet GLN decomposition, similar to other radical–radical reactions.The figures displaying the reaction pathways incorporate zero-point energy corrections and the relative energies are referenced with respect to the energy of the starting materials. Primary pathways are shown in the main text, while additional, longer pathways are included in the ESI.† The pathways are denoted by the structural formula of the smallest precursor, followed by Roman numerals in the event that multiple pathways of the same type are present.
3.1 Radical–radical reactions
Fig. 1 shows the only identified pathway for the formation of GLN from CN and CH3O. Additionally, Fig. S2 (ESI†) displays five additional formation pathways (CN-II to CN-VI) from the reactants CN + CH2OH.
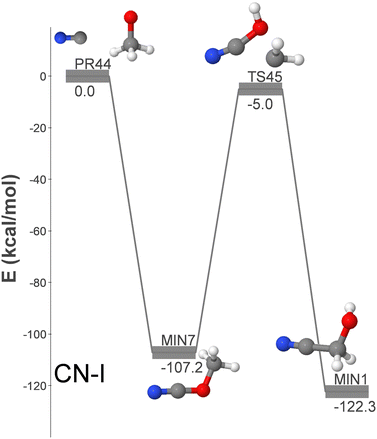 | ||
| Fig. 1 DFT-computed energy profile (energy in kcal mol−1) for the barrierless formation of GLN from CN + CH3O. | ||
The pathways are arranged in decreasing order of relevance for the formation of GLN in the ISM. The CN-I pathway is the sole CN + CH3O (PR44) route discovered in our study for the submerged-barrier formation of GLN. As only the methoxy radical isomer has been identified in the ISM thus far, it is the most pertinent route among those outlined in this section. It involves the association of both radicals to produce methyl cyanate (MIN7), which then transforms into GLN (MIN1) via isomerization. As elaborated below, this isomerization process paves the way for proposing a novel formation mechanism.
The CN-II pathway involves the one-step formation of GLN through the CN + CH2OH (PR24) reaction, which leads to the creation of a CC bond between the cyano and hydroxymethyl radicals. Moreover, the CN-III, CN-IV, CN-V and CN-VI pathways all start with the same reactants (PR24) and involve the primary formation of isocyanomethanol (MIN8). This intermediate compound is then connected to GLN via one (CN-III), two (CN-IV) or three steps (CN-V and CN-VI).
The minimum energy path (MEP) for the isomerization process is shown in Fig. 2. The mechanism bears similarities to roaming,38 where the methylene and cyanic acid fragments initially separate as if they were undergoing dissociation. However, the two radicals ultimately recombine (frustrating the dissociation) to yield methyl cyanate and GLN. The MEP is quite extensive: on the methyl cyanate side, the methylene fragment initially abstracts a hydrogen atom from the oxygen before subsequently recombining. On the GLN side, the CH2 fragment is inserted into the carbon–oxygen bond. The PES around the saddle point region is rather flat, and the energy of TS45 is just 2 kcal mol−1 higher than the asymptotic limit of CH2 + HOCN. Consequently, depending on their orientation, the arrangement of the fragments can result in the formation of either methyl cyanate or GLN, making both outcomes feasible. Earlier studies reported similar dynamic effects where a single transition state participates in two mechanisms.6,36,37 If such non-statistical behavior also exists for TS45, it would support the feasibility of forming GLN from the CH2 and HOCN fragments. Quasi-classical trajectory simulations could help confirm this possibility.
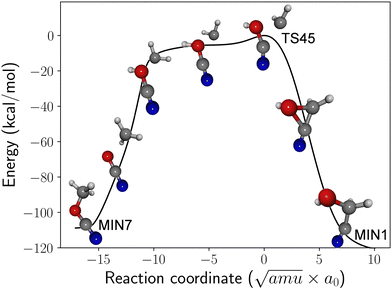 | ||
| Fig. 2 DFT-computed minimum energy path (energy in kcal mol−1) for roaming-like isomerization between methyl cyanate (MIN7) and glycolonitrile (MIN1) through TS45. | ||
If the proposed formation pathway from CH2 and HOCN fragments is validated in future research, it is worth noting that the initial excitation energy of GLN would be approximately 120 kcal mol−1. This substantial amount of energy increases the likelihood of GLN undergoing further unimolecular reactions, potentially competing with radiative stabilization.
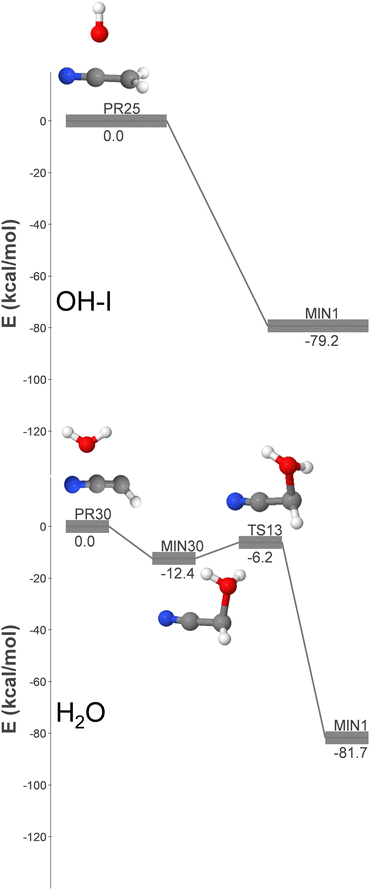 | ||
| Fig. 3 DFT-computed energy profiles (energy in kcal mol−1) for the barrierless formation of GLN from OH + CH2CN (OH-I pathway) and H2O + HCCN (H2O pathway). | ||
Based on the reasons outlined in this section, it can be concluded that the OH + CH2NC reaction is the primary radical–radical pathway for the formation of GLN identified in this study. As a result, the kinetic simulations described in Section 3.3 will be focussed on this particular radical–radical mechanism.
The lower panel of Fig. 3 (pathway H2O) shows that the association of H2O and HCCN (PR30) results in the formation of a highly unstable intermediate (MIN30), which can undergo subsequent isomerization via hydrogen migration to yield GLN. The high energy of MIN30 significantly reduces the radiative stabilization rate compared to pathway OH-I. Moreover, the formation of GLN requires an additional step, which diminishes the kinetic significance of this pathway relative to that of OH-I. Put simply, the formation rate coefficient for this pathway would be reduced.
Fig. 4 shows the HCO-I pathway, the only three-step route that incorporates two reactants detected in the ISM: namely formyl and aminocarbyne radicals (PR29). An alternative (longer) pathway, HCO-VII, shown in Fig. S5 (ESI†), connects MIN10 with GLN via an additional step. Fig. S5 (ESI†) shows additional GLN formation pathways that begin with isomers of the reactants that have not yet been detected in the ISM. These pathways could become relevant in the event of new detections.
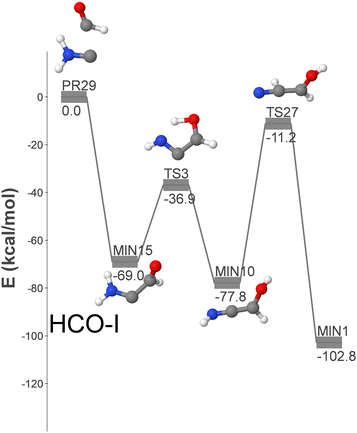 | ||
| Fig. 4 DFT-computed energy profile (energy in kcal mol−1) for the barrierless formation of GLN from HCO and H2NC (HCO-I pathway). | ||
Pathway HCO-I is initiated with the formation of MIN15, followed by two isomerization steps that involve hydrogen migrations over submerged barriers and lead to the formation of GLN. Due to the relatively high energy of the reactants and the involvement of three elementary steps, this pathway is considered less significant than OH-I.
3.2 Radical–molecule reactions
This study has identified only two radical–molecule pathways that can lead to the formation of GLN in a single step. One of these pathways is the reaction between the hydroxyl radical and methyl cyanide:| OH + CH3CN → GLN + H | (11) |
| CH2OH + HCN → GLN + H | (12) |
We have discovered another potentially interesting reaction in the ISM:
| OH + CH3CN → H2O + CH2CN | (13) |
However, the addition reaction between OH and CH3CN leading to CH3C(OH)N, competes with reaction (13) under low-pressure conditions at 10 K, with a computed rate coefficient of approximately 5 × 10−14 cm3 molecule−1 s−1. As the temperature exceeds 200 K, the addition reaction becomes pressure-independent, and our calculated values align well with experimental data within the temperature range of 256 to 388 K.51
We have also investigated pathways that involve multiple elementary steps and have identified the following reaction, whose energy profile is depicted in Fig. 5:
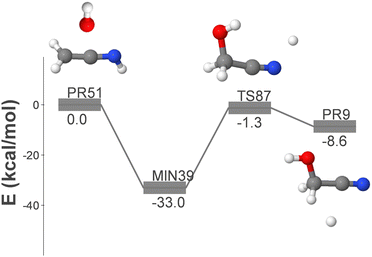
| OH + CH2CNH → GLN + H | (14) |
The reactants of reaction (14) are the hydroxyl radical and ketenimine (CH2CNH), which was first detected in the ISM in 2006.52 This reaction proceeds through only two elementary steps, making it an ideal candidate for a gas phase process for the formation of GLN. The initial association results in the formation of MIN39, which ultimately loses a hydrogen atom, leading to the formation of GLN and atomic hydrogen.
Fig. S6 (ESI†) shows an alternative, longer route, which involves the aminocarbyne radical and formaldehyde as reactants. The presence of the latter was first detected in the ISM in 1969.53 This reaction mechanism proceeds via the highly unstable intermediate MIN82, which rearranges via H-migration to form MIN39. This pathway shares the final dissociation step with the one shown in Fig. 5.
3.3 Kinetic simulations
Among the radical–radical reactions, pathway OH-I, which involves the combination of OH and CH2CN to form GLN in a single step, is the most promising and efficient route for the formation of GLN. However, as shown in Fig. 6, GLN can potentially dissociate into hydrogen isocyanide (HNC) and formaldehyde (CH2O) by surmounting a barrier of 67.6 kcal mol−1, making the formation of these two products possible.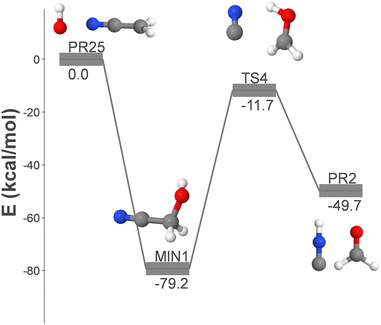 | ||
| Fig. 6 DFT-computed energy profile (energy in kcal mol−1) for the formation of HNC + CH2O from OH + CH2CN. | ||
The initially formed glycolonitrile molecules exhibit a unimolecular rate of HNC + CH2O formation (∼106 s−1), which is four orders of magnitude higher than their rate of radiative stabilization (∼102 s−1). This suggests that the formation of GLN through this pathway is not efficient. Nevertheless, due to the submerged nature of TS4, the following process becomes an efficient pathway for the formation of hydrogen isocyanide and formaldehyde:
| OH + CH2CN → HNC + CH2O | (15) |
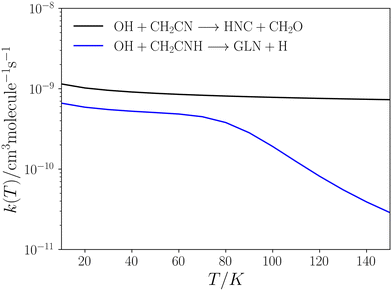 | ||
| Fig. 7 Low-pressure rate coefficients for reactions 14 (blue) and 15 (black) calculated using the CUS model. | ||
The fact that, in eqn (15), the resulting product is HNC instead of HCN is significant and could potentially help to explain the observed overabundance of HNC in the ISM, as compared to its expected equilibrium value.54,55 Various previous studies have attempted to account for this discrepancy by proposing possible photolytic sources of HCN and HNC in the ISM. These studies have reported measured or calculated HNC/HCN branching ratios in the range of 0.1–0.3.56–59
The discovery of the efficient formation of HNC from GLN enables us to propose all barrierless radical–radical reactions of the present study as viable sources of HNC in the interstellar medium (ISM), albeit with slightly lower efficiency compared to reaction (15).
In this section we have also examined the rate coefficients for the radical–molecule process displayed in Fig. 5 (reaction (14)).
This pathway exhibits two elementary steps that mimic reaction (15). Fig. 7 presents the rate coefficients for this reaction in the low-pressure regime, covering the temperature range of 10–150 K. In reaction (15), the formation of GLN is identified as the rate-determining step throughout the entire temperature range. However, in reaction (14), the rate-determining step is the formation of GLN-H, but only until approximately 90 K. At this point the contribution of k2 to the overall formation rate coefficient becomes significant (see Table S2, ESI†). This observation explains the noticeable decline in the rate coefficient of reaction (14) (see Fig. 7).
4. Conclusions
In this study, we have employed automated reaction discovery methods along with CUS and CVT kinetic calculations to investigate the possible formation pathways of glycolonitrile. Our findings can be summarized as follows:1. Our results indicate that the gas-phase reactions involving hydroxyl radical with cyanomethyl and ketenimine are the most promising pathways for the formation of glycolonitrile.
2. In the reaction between hydroxyl and cyanomethyl radicals, glycolonitrile undergoes further decomposition, resulting in the formation of hydrogen isocyanide and formaldehyde. While this finding rules out this pathway as a viable alternative for glycolonitrile formation, it reveals an intriguing gas-phase reaction that significantly contributes to the efficient production of interstellar HNC.
3. The discovery of a highly efficient HNC elimination pathway from GLN expands the potential for any radical–radical mechanism proposed in our study to serve as a viable formation route for HNC in the interstellar medium (ISM).
4. The only viable gas-phase pathway for glycolonitrile formation identified in this study is the reaction between hydroxyl with ketenimine, which also generates atomic hydrogen.
5. The kinetic calculations performed in this study reveal the efficiency of both hydrogen isocyanide and glycolonitrile formation under the harsh conditions of the interstellar medium.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Spanish Ministry of Science and Innovation (MICINN) through the CHEMLIFE project (Ref. PID2020-113936GB-I00). It was also partially supported by the Consellería de Cultura, Educación e Ordenación Universitaria (Centro singular de investigación de Galicia acreditación 2019–2022, ED431G 2019/03 and Grupo de referencia competitiva ED431C 2021/40) and the European Regional Development Fund (ERDF), and MICINN through Grant #PID2019-107307RB-I00. ALS thanks Xunta de Galicia for financial support through a predoctoral grant.References
- C. Menor-Salván and M. R. Marín-Yaseli, Chem. Soc. Rev., 2012, 41, 5404–5415 RSC.
- A. W. Schwartz, H. Joosten and A. B. Voet, BioSystems, 1982, 15, 191–193 CrossRef CAS PubMed.
- S. Zeng, D. Quénard, I. Jiménez-Serra, J. Martín-Pintado, V. M. Rivilla, L. Testi and R. Martín-Doménech, Mon. Not. R. Astron. Soc.: Lett., 2019, 484, L43–L48 CrossRef CAS.
- C. Puzzarini, Front. Astron. Space Sci., 2022, 8, 811342 CrossRef.
- C. Robertson, R. Hyland, A. J. D. Lacey, S. Havens and S. Habershon, J. Chem. Theory Comput., 2021, 17, 2307–2322 CrossRef CAS PubMed.
- D. Garay-Ruiz, M. Álvarez-Moreno, C. Bo and E. Martínez-Núñez, ACS Phys. Chem. Au, 2022, 2, 225–236 CrossRef CAS PubMed.
- D. E. Woon, ApJ, 2021, 906, 20 CrossRef CAS.
- G. Danger, F. Duvernay, P. Theulé, F. Borget and T. Chiavassa, ApJ, 2012, 756, 11 CrossRef.
- G. Danger, A. Rimola, N. Abou Mrad, F. Duvernay, G. Roussin, P. Theule and T. Chiavassa, Phys. Chem. Chem. Phys., 2014, 16, 3360–3370 RSC.
- G. Zhao, D. Quan, X. Zhang, G. Feng, J. Zhou, D. Li, Q. Meng, Q. Chang, X. Yang, M. He and M.-S. Ma, ApJS, 2021, 257, 26 CrossRef CAS.
- D. E. Woon, Icarus, 2001, 149, 277–284 CrossRef CAS.
- I. Fourré, O. Matz, Y. Ellinger and J.-C. Guillemin, Astron. Astrophys., 2020, 639, A16 CrossRef.
- S. Arulmozhiraja and P. Kolandaivel, J. Mol. Struct. THEOCHEM, 1998, 429, 165–173 CrossRef.
- E. Martínez-Núñez, G. L. Barnes, D. R. Glowacki, S. Kopec, D. Peláez, A. Rodríguez, R. Rodríguez-Fernández, R. J. Shannon, J. J. P. Stewart, P. G. Tahoces and S. A. Vazquez, J. Comput. Chem., 2021, 42, 2036–2048 CrossRef PubMed.
- E. Martínez-Núñez, J. Comput. Chem., 2015, 36, 222–234 CrossRef PubMed.
- E. Martínez-Núñez, Phys. Chem. Chem. Phys., 2015, 17, 14912–14921 RSC.
- J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- V. K. Prasad, Z. Pei, S. Edelmann, A. Otero-de-la-Roza and G. A. DiLabio, J. Chem. Theory Comput., 2022, 18, 151–166 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT2010 Search PubMed.
- D. T. Gillespie, J. Comput. Phys., 1976, 22, 403–434 CrossRef CAS.
- R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell Science Publishing, Oxford, 1990 Search PubMed.
- T. Beyer and D. Swinehart, Commun. ACM, 1973, 16, 379 CrossRef.
- G. Danger, F. Duvernay, P. Theulé, F. Borget, J.-C. Guillemin and T. Chiavassa, Astron. Astrophys., 2013, 549, A93 CrossRef.
- L. Guerrero-Mendez, A. Lema-Saavedra, E. Jimenez, A. Fernández-Ramos and E. Martinez-Nunez, Zenodo, ch. May 16, 2023 DOI:10.5281/zenodo.7941351.
- L. G. Gao, J. Zheng, A. Fernández-Ramos, D. G. Truhlar and X. Xu, J. Am. Chem. Soc., 2018, 140, 2906–2918 CrossRef CAS PubMed.
- D. González, A. Lema-Saavedra, S. Espinosa, E. Martínez-Núñez, A. Fernández-Ramos, A. Canosa, B. Ballesteros and E. Jiménez, Phys. Chem. Chem. Phys., 2022, 24, 23593–23601 RSC.
- A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett and D. G. Truhlar, Reviews in Computational Chemistry, 2007, pp. 125–232 Search PubMed.
- D. Ferro-Costas, D. G. Truhlar and A. Fernández-Ramos, Comput. Phys. Commun., 2020, 256, 107457 CrossRef CAS.
- Y. Georgievskii and S. J. Klippenstein, J. Chem. Phys., 2005, 122, 194103 CrossRef PubMed.
- S. J. Klippenstein, Y. C. Yang, V. Ryzhov and R. C. Dunbar, J. Chem. Phys., 1996, 104, 4502–4516 CrossRef CAS.
- W. S. Adams, ApJ, 1941, 93, 11 CrossRef CAS.
- J. Cernicharo, N. Marcelino, E. Roueff, M. Gerin, A. Jiménez-Escobar and G. M. Muñoz Caro, ApJL, 2012, 759, L43 CrossRef.
- C. Bermudez, S. Bailleux and J. Cernicharo, Astron. Astrophys., 2017, 598, A9 CrossRef.
- E. T. Polehampton, K. M. Menten, S. Brünken, G. Winnewisser and J.-P. Baluteau, Astron. Astrophys., 2005, 431, 203–213 CrossRef CAS.
- S. Brünken, C. A. Gottlieb, M. C. McCarthy and P. Thaddeus, ApJ, 2009, 697, 880 CrossRef.
- R. Rodríguez-Fernández, S. A. Vázquez and E. Martínez-Núñez, Phys. Chem. Chem. Phys., 2013, 15, 7628–7637 RSC.
- V. Bakken, D. Danovich, S. Shaik and H. B. Schlegel, J. Am. Chem. Soc., 2001, 123, 130–134 CrossRef CAS PubMed.
- D. Townsend, S. A. Lahankar, S. K. Lee, S. D. Chambreau, A. G. Suits, X. Zhang, J. Rheinecker, L. B. Harding and J. M. Bowman, Science, 2004, 306, 1158–1161 CrossRef CAS PubMed.
- C. E. Heiles, ApJ, 1968, 151, 919 CrossRef CAS.
- W. M. Irvine, P. Friberg, A. Hjalmarson, S. Ishikawa, N. Kaifu, K. Kawaguchi, S. C. Madden, H. E. Matthews, M. Ohishi, S. Saito, H. Suzuki, P. Thaddeus, B. E. Turner, S. Yamamoto and L. M. Ziurys, ApJ, 1988, 334, L107–111 CrossRef CAS PubMed.
- A. C. Cheung, D. M. Rank, C. H. Townes, D. D. Thornton and W. J. Welch, Nature, 1969, 221, 626–628 CrossRef.
- M. Guelin and J. Cernicharo, Astron. Astrophys., 1991, 244, L21 CAS.
- L. E. Snyder, J. M. Hollis and B. L. Ulich, ApJ, 1976, 208, L91–L94 CrossRef CAS.
- A. Usero, S. García-Burillo, A. Fuente, J. Martín-Pintado and N. J. Rodríguez-Fernández, Astron. Astrophys., 2004, 419, 897–912 CrossRef CAS.
- A. Fuente, S. García-Burillo, M. Gerin, D. Teyssier, A. Usero, J. R. Rizzo and P. de Vicente, ApJ, 2005, 619, L155 CrossRef CAS.
- M. Ohishi, D. McGonagle, W. M. Irvine, S. Yamamoto and S. Saito, ApJ, 1994, 427, L51 CrossRef CAS PubMed.
- C. Cabezas, M. Agúndez, N. Marcelino, B. Tercero, S. Cuadrado and J. Cernicharo, Astron. Astrophys., 2021, 654, A45 CrossRef CAS.
- L. E. Snyder and D. Buhl, ApJ, 1971, 163, L47 CrossRef CAS.
- P. M. Solomon, K. B. Jefferts, A. A. Penzias and R. W. Wilson, ApJ, 1971, 168, L107 CrossRef CAS.
- A. J. Hynes and P. H. Wine, J. Phys. Chem., 1991, 95, 1232–1240 CrossRef CAS.
- D. González, A. Canosa, E. Martínez-Núñez, A. Fernández-Ramos, B. Ballesteros and E. Jiménez, Phys. Chem. Chem. Phys., 2023 Search PubMed , submitted.
- F. J. Lovas, J. M. Hollis, A. J. Remijan and P. R. Jewell, ApJ, 2006, 645, L137 CrossRef CAS.
- L. E. Snyder, D. Buhl, B. Zuckerman and P. Palmer, Phys. Rev. Lett., 1969, 22, 679–681 CrossRef CAS.
- R. D. Brown, Nature, 1977, 270, 39–41 CrossRef CAS.
- W. M. Irvine, D. Bockelee-Morvan, D. C. Lis, H. E. Matthews, N. Biver, J. Crovisier, J. K. Davies, W. R. F. Dent, D. Gautier, P. D. Godfrey, J. Keene, A. J. Lovell, T. C. Owen, T. G. Phillips, H. Rauer, F. P. Schloerb, M. Senay and K. Young, Nature, 1996, 383, 418–420 CrossRef CAS PubMed.
- M. J. Wilhelm, E. Martínez-Núñez, J. González-Vázquez, S. A. Vázquez, J. M. Smith and H.-L. Dai, ApJ, 2017, 849, 15 CrossRef.
- M. J. Wilhelm, M. Nikow, L. Letendre and H.-L. Dai, J. Chem. Phys., 2009, 130, 044307 CrossRef PubMed.
- Z. Homayoon, S. A. Vázquez, R. Rodríguez-Fernández and E. Martínez-Núñez, J. Phys. Chem. A, 2011, 115, 979–985 CrossRef CAS PubMed.
- S. A. Vazquez and E. Martinez-Nunez, Phys. Chem. Chem. Phys., 2015, 17, 6948–6955 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Convergence of the product abundances vs. iteration number, additional barrierless formation pathways and computed rate coefficients. See DOI: https://doi.org/10.1039/d3cp02379f |
| This journal is © the Owner Societies 2023 |