Two- and three-body fragmentation of multiply charged tribromomethane by ultrafast laser pulses†
Surjendu
Bhattacharyya
 a,
Kurtis
Borne
a,
Farzaneh
Ziaee
a,
Shashank
Pathak
a,
Kurtis
Borne
a,
Farzaneh
Ziaee
a,
Shashank
Pathak
 a,
Enliang
Wang
ab,
Anbu Selvam
Venkatachalam
a,
Enliang
Wang
ab,
Anbu Selvam
Venkatachalam
 a,
Nathan
Marshall
a,
Kevin D.
Carnes
a,
Charles W.
Fehrenbach
a,
Travis
Severt
a,
Itzik
Ben-Itzhak
a,
Nathan
Marshall
a,
Kevin D.
Carnes
a,
Charles W.
Fehrenbach
a,
Travis
Severt
a,
Itzik
Ben-Itzhak
 a,
Artem
Rudenko
a and
Daniel
Rolles
a,
Artem
Rudenko
a and
Daniel
Rolles
 *a
*a
aJ. R. Macdonald Laboratory, Department of Physics, Kansas State University, Manhattan, KS 66506, USA. E-mail: rolles@phys.ksu.edu
bHefei National Laboratory for Physical Sciences at the Microscale and Department of Modern Physics, University of Science and Technology of China, Hefei 230026, China
First published on 27th October 2022
Abstract
We investigate the two- and three-body fragmentation of tribromomethane (bromoform, CHBr3) resulting from multiple ionization by 28-femtosecond near-infrared laser pulses with a peak intensity of 6 × 1014 W cm−2. The analysis focuses on channels consisting exclusively of ionic fragments, which are measured by coincidence momentum imaging. The dominant two-body fragmentation channel is found to be Br+ + CHBr2+. Weaker HBr+ + CBr2+, CHBr+ + Br2+, CHBr2+ + Br2+, and Br+ + CHBr22+ channels, some of which require bond rearrangement prior to or during the fragmentation, are also observed. The dominant three-body fragmentation channel is found to be Br+ + Br+ + CHBr+. This channel includes both concerted and sequential fragmentation pathways, which we identify using the native frames analysis method. We compare the measured kinetic energy release and momentum correlations with the results of classical Coulomb explosion simulations and discuss the possible isomerization of CHBr3 to BrCHBr–Br (iso-CHBr3) prior to the fragmentation.
1 Introduction
The fragmentation dynamics of molecules induced by intense near-infrared laser pulses are the subject of a large body of literature,1–16 both because of their fundamental role in understanding the interaction of intense fields with matter and because of practical implications, e.g., ultrafast plasma dynamics5 and coherent control of chemical reactions.12,13 Often, these fragmentation dynamics involve not only bond-breaking but also the formation of new chemical bonds that lead to transient (transition state, roaming intermediate, etc.) structures or stable isomers of the parent molecules on an ultrafast time scale.17–37 These transient species can further undergo unimolecular dissociation to form products with new chemical bonds. A considerable amount of attention has been paid to such photodissociation and isomerization dynamics,38,39 in particular for halocarbons like chlorofluorocarbons (CFCs), which play a prominent role in the ozone-depletion process.40–42 Even simple halons such as tribromomethane (CHBr3), also known as bromoform, have a detrimental effect on the ozone layer. Owing to the photochemical activity of bromoform, especially at lower altitudes, it is considered a significant source of bromine (Br) and methylidyne (CH) radicals in the atmosphere.42–46In addition to radical formation, the production of molecular fragments such as molecular halogens and hydrogen halides after photoionization of halons has been of recent interest.47–50 It has been suggested that the formation of the molecular channel, CF2 + Cl2, from the infrared multiphoton dissociation of CF2Cl2, takes place via a symmetric three-center transition state with a constraint on one C–Cl bond length at a critical distance.39 The involvement of isomerization for the formation of molecular channels has been reported based on evidence obtained from dispersed fluorescence and ab initio calculations.51,52 Furthermore, based on ab initio computations and modeling, it has been claimed that isomerization is a key pathway to molecular products for several halons like CF2Cl2, CF2Br2, and CHBr3 in the gas phase.38
The effect of the wave-packet motion on the concerted elimination of I2+ from CH2I2 has been investigated by Geißler et al. through a set of IR pump–IR probe measurements.47 Strong-field-induced sequential ionization of aligned CH3I and bond rearrangement in CH3Cl have been reported by Luo et al.53,54 Sandor et al. have reported the angle-dependent strong-field ionization of singly-halogenated methane molecules, CH3Cl and CH3Br.55 Very recently, Mogyorosi et al. reported CH(A2Δ) radical formation in bromoform vapor with near-infrared femtosecond laser pulses at ∼1.1 × 1016 W cm−2 (calculated) in argon plasma.56
In this work, we report the two- and three-body fragmentation of CHBr3 using strong-field-induced ionization at a peak intensity of 6 × 1014 W cm−2 with the intent to provide experimental data that can guide modeling of strong-field ionization and fragmentation. Moreover, this work may help with the interpretation of future time-resolved studies on CHBr3 using strong-field-induced fragmentation as a probe. The possible two-body breakup pathways are discussed based on the measured kinetic energy release (KER) and Coulomb explosion simulations (CES). We identified sequential and concerted mechanisms in three-body breakup channels and used momentum and energy correlations combined with distributions of KER and KE of the fragments to provide insight about the fragmentation dynamics. Our study was inspired by reports of ultrafast roaming-mediated isomerization of CHBr3 upon ultraviolet photoexcitation in both gas and liquid phases.36
2 Methods
2.1 Experimental
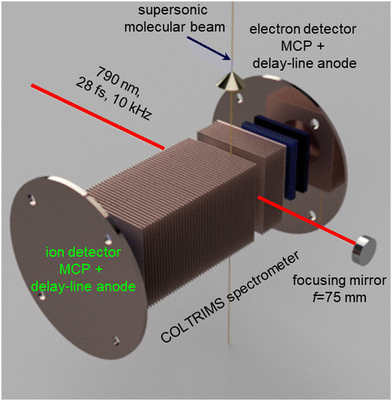
Fig. 1 shows a schematic diagram of the experimental setup used for the present investigation. A detailed description of the setup is provided in previous reports.57–59 We used the linearly polarized beam of an amplified Ti:Sapphire laser, (PULSAR),60 with a repetition rate of 10 kHz, a central wavelength of 790 nm (60 nm FWHM), and a pulse duration of 28 fs (FWHM in intensity), focused into a supersonic molecular beam by a concave spherical mirror with a focal length of 75 mm. The polarization of the laser beam was parallel to the spectrometer axis and perpendicular to the molecular beam. The data presented here were recorded with a pulse energy of 13 μJ, corresponding to a peak intensity of 6 × 1014 W cm−2 in the interaction region.The peak intensity was determined by an independent calibration measurement of the Ne+ momentum distribution along the laser polarization direction. This distribution displays a characteristic kink at the recoil momentum value that corresponds to the emission of photoelectrons with a kinetic energy equal to twice the ponderomotive energy (i.e., the average quiver energy of a free electron in the laser field), Up, and which represents the transition from direct to rescattered electrons.61
The intense laser pulses interact with the molecular beam at the center of a cold target recoil ion momentum spectrometer (COLTRIMS).62,63 A uniform extraction field of 96.6 V cm−1 along a 240 mm long spectrometer was used to accelerate the resulting ions toward the ion detector. This time- and position-sensitive detector consists of 80 mm diameter, efficiency enhanced “funnel”64 microchannel plates (MCPs) in a Z-stack configuration, equipped with a delay-line anode.65
The analog MCP and delay-line signals were first amplified and then fed into constant-fraction discriminators (CFDs). The CFD outputs were recorded by a multihit time-to-digital converter (TDC), which registered the accurate timing information on an event-by-event basis.62,63 The momenta of the recoil ions were calculated from the recorded time and position information by solving the classical equations of motion of charged particles in the spectrometer field in the lab-fixed frame.66
The CHBr3 (99%), purchased from Sigma Aldrich, was used without further purification. A stainless-steel gas bubbler was filled with approximately 10 ml of the sample and subjected to several freeze–pump–thaw cycles in order to minimize atmospheric contaminations, like O2, N2, and H2O. The bubbler was connected to a flat nozzle with a 30 μm diameter. Since the vapor pressure of CHBr3 is only 5 Torr at 293 K, it was expanded into the ultra-high vacuum setup using helium carrier gas at 250 Torr. Careful inspection of the time-of-flight mass spectra and the parent ion kinetic-energy distribution confirmed that there was no CHBr3-cluster formation under these conditions (see Fig. S1 in the ESI†).
2.2 Coulomb explosion simulation
The total Coulomb potential energy Etot (in units of eV) of a multiply charged molecule due to a distribution of N point charges can be expressed as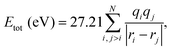 | (1) |
3 Results and discussion
3.1 Two-body fragmentation channels
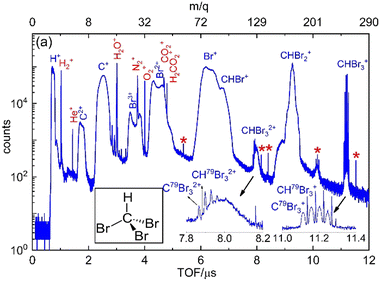
Fig. 2 displays the ion time-of-flight (TOF) spectrum of CHBr3 ionized by the 790 nm near-infrared laser pulses. The singly-charged bromoform, CHBr3+, exhibits four sharp peaks, with their peak strengths in good agreement with the ratio expected for the natural isotopic abundance of 79Br (50.69%) and 81Br (49.31%). Isotopologues of the bromoform dications, CHBr32+, are also noticeable as the four sharp peaks of CBr32+ on top of a broader structure (see inset in Fig. 2), which we attribute to residual gas in the vacuum chamber that includes some traces (most likely iodine) of other samples used in earlier experiments. In addition to the singly- and doubly-charged bromoform ions, a host of other ionic fragments are observed, most of them having broad peaks, which is a common signature of fragments with large kinetic energy.In a photoion–photoion coincidence (PIPICO) spectrum, the yield of two ions detected in coincidence is plotted as a function of the time-of-fight of the first hit (TOF1) and the second hit (TOF2). These ion pairs form sharp diagonal lines with negative slopes if they satisfy momentum conservation, indicating that they originate from the same molecule. These sharp features, shown in Fig. 3 as a PIPICO spectrum, have been the key for separating ion pairs measured in coincidence using coincidence time of flight plots.69,70 The dominant two-body breakup channels observed in the PIPICO spectrum are Br+ + CHBr2+, HBr+ + CBr2+, CHBr+ + Br2+, Br+ + CHBr22+ and CHBr2+ + Br2+. The yield of the H+ + CBr3+ channel is too low to be separated from the random coincidence events having similar times of flight.
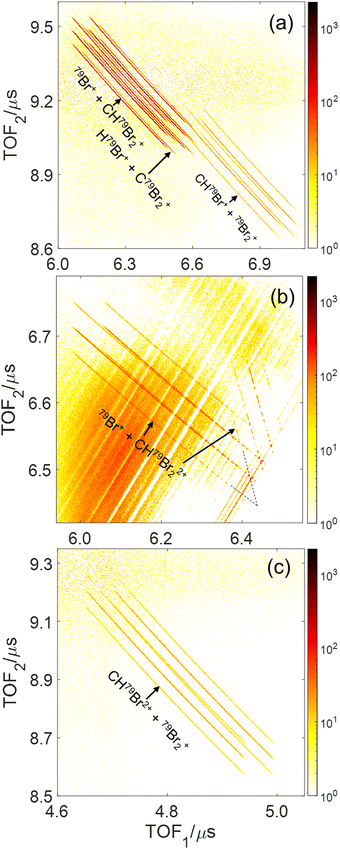 | ||
| Fig. 3 Photoion–Photoion Coincidence (PIPICO) plots of dissociative double and triple ionization of CHBr3 for the same conditions as in Fig. 2 after subtraction of random coincidences (see text). The three panels show the regions of interest (see Fig. S2 in the ESI† for the complete PIPICO plot), where the main two-body breakup channels (a) Br+ + CHBr2+, HBr+ + CBr2+, and CHBr+ + Br2+, (b) Br+ + CHBr22+ and (c) CHBr2+ + Br2+, appear. Note that each ion-pair channel produces multiple diagonal lines due to the two naturally occurring Br isotopes, as labeled for example in Fig. S2(d) (ESI†). The coincidence TOF stripes, shown in panel (b), are split into two branches with different slopes because the two fragments, Br+ and CHBr22+, flip roles in hitting the detector first. | ||
Although the parent molecule, CHBr3, has only C–H and C–Br bonds, some of the fragment ions undergoing two-body breakup contain H–Br and Br–Br bonds, providing clear evidence of bond rearrangement before or during the fragmentation process. Note that due to the fairly high-count rate in our experiment (20 kHz ion counts at a 10 kHz laser repetition rate), the PIPICO spectrum in Fig. S2(a)–(c) (ESI†) also contains a significant amount of random (also known as false) coincidences from events where the two detected ions did not originate from the same molecule. These random coincidences produce broad “islands” in the PIPICO plot. The PIPICO spectra in Fig. 3 are shown after subtraction of these random coincidence events. For this purpose, the spectrum of random coincidence events is produced by pairing two measured fragments from different laser shots (or a fragment-pair from one laser shot with the third fragment from another laser shot in the case of 3-body breakup). This artificially generated spectrum containing purely random-coincidence events is scaled to match a random coincidence feature in the measured spectrum and then subtracted.18,33,71,72 Additionally, the random coincidence yields are strongly suppressed during analysis by selecting only those ion pairs that fulfill momentum conservation.
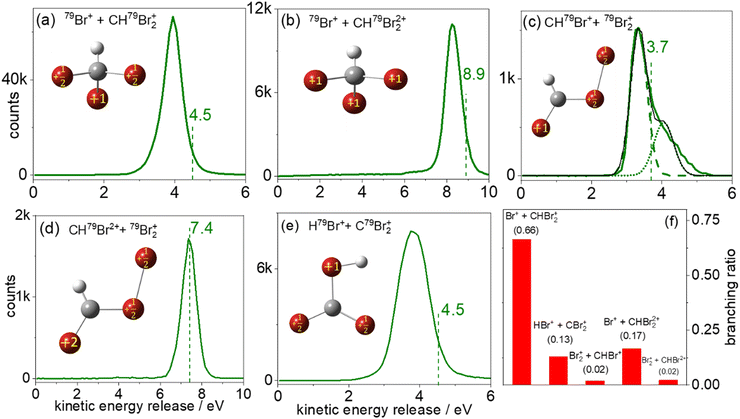
Fig. 4(a) shows the measured KER distribution for the 79Br+ + CH79Br2+ breakup channel. This measured KER distribution peaks at 4.0 eV. Using eqn (1), the Coulomb energy is calculated for three different arrangements of the two positive charges in the CHBr32+ molecule: (i) one positive charge is placed on one of the Br atoms, and the other charge is placed at the center of mass of the CH79Br2 fragment. In this arrangement, the charges are separated by 5.16 a.u. and the calculated KER is 5.27 eV, that is about 1.3 eV higher than the measured value. (ii) The two positive charges are placed on two of the Br atoms which are 6.05 a.u. apart from each other. Due to the larger charge separation the Coulomb repulsion is reduced, yielding a KER of 4.50 eV, which still overestimates the measured KER by 0.5 eV. (iii) Finally, one of the positive charges is placed on one of the Br atoms, and the other positive charge is equally distributed between the remaining two Br atoms in the CH79Br2 fragment. The calculated KER in this case also overestimates the measured KER by ∼0.5 eV as shown by the vertical dashed line in Fig. 4(a). Conceptually, the splitting of the unit charge into equal fractions between two identical Br atoms of the CHBr2+ can be understood as a redistribution of the valence electrons.
The fact that the Coulomb explosion model [i.e., eqn (1)] typically overestimates the measured KER is well known,66,73–75 as it oversimplifies the problem. The main issues leading to this limitation are non-Coulombic potential energy surfaces (PES), internal energy carried by the fragments, and the fact that the charge distribution is not really a point charge. In addition, another factor that often contributes to the overestimation of the experimental KER values by the CES is the motion of the fragments during the ionization process. However, in our estimate, the latter limitation does not play an important role in this specific case since the motion of the heavy Br-containing fragments is negligible on the time scale of the 28 fs laser pulse used here. As we recently pointed out,66 despite the shortcomings of the Coulomb explosion model, it still does a reasonable job in predicting energy and momentum correlations, and therefore it is a useful simple tool in interpreting fragmentation experiments.
Fig. 4(b) displays the 79Br+ + CH79Br22+ two-body breakup of the bromoform trication. This is the second most prominent channel and has a branching ratio of about 17% of all two-body breakup channels containing only 79Br isotopes. The measured KER distribution of the Br+ + CHBr22+ channel peaks at 8.3 eV. The KERs calculated using CES assuming the similar charge distribution as described above in model (iii) are shown by a vertical dashed line and again overestimate the measured value, though the relative deviation is clearly smaller, as one would expect for higher charge states of a fragmenting molecule.
The KER distribution of the CHBr2+ + Br2+ channel, shown in Fig. 4(d), is peaked at 7.4 eV. Contrary to the CHBr+ + Br2+ channel, no high-energy component is observed in the CHBr2+ + Br2+ channel. However, KER values of both channels involving the formation of the molecular bromine cation are significantly lower than the KER of the di- and tricationic two-body channels involving single C–Br bond cleavage.
One possible route that may lead to Br2+ formation is the isomerization of CHBr3 into the Br migrated BrCHBr–Br dication, followed by cleavage of the C–Br bond finally leading to CHBr+ + Br2+. The photoabsorption increases the internal energy of the molecule, which may initiate the isomerization process. Although both the equilibrium geometry and the isomers correspond to the local minima of the potential energy surface, the isomers have one or more bond lengths which are larger than in the equilibrium geometry. In this case, the charges could be further separated after ionization, resulting in lower KER. For simplicity, we assume the optimized ground-state geometry of the Br migrated isomer, BrCHBr–Br (iso-CHBr3) in the dicationic state [sketched in Fig. 4(c) and (d)], as the starting geometry for the CES with one (two) unit(s) of charge residing on the Br of CHBr+ (CHBr2+) and one unit of charge is equally distributed between the two Br atoms in the Br2+ fragment.
Interestingly, the KER value of 3.7 eV evaluated using CES splits the difference between the two peaks at 3.3 eV and 4.0 eV in the CHBr2+ + Br2+ channel, as observed in Fig. 4(c). The CES model does an excellent job of predicting the KER value of the CHBr2+ + Br2+ channel, as can be seen in Fig. 4(d).
The two KER peaks centered at 3.3 and 4.0 eV in Fig. 4(c) suggest that two fragmentation pathways may be contributing to this fragmentation channel. Although we cannot infer further information about the nature of the two contributions from the KER distributions alone, we speculate that the higher-energy feature may be concerted Br2+ elimination assisted by the scissor-mode vibration in the dication as observed for X2 (where X = Cl, Br, I) elimination from RCHX2,49 while the lower-energy feature may correspond to Br2+ elimination from the BrCHBr–Br isomer formed in the dicationic state before Coulomb explosion. The normal mode frequencies associated with the motion of the Br nuclei in the neutral ground-state CHBr3 molecule span timescales (energies) from 50 fs (669 cm−1) to 215 fs (155 cm−1). Furthermore, Mereshchenko et al. suggested that gas-phase isomerization of S1 CHBr3 into S0 BrHCBr–Br (iso-CHBr3) induced by a 250 nm photon occurs on a 100 fs timescale.36 Therefore, we conclude that the timescale of the dynamics related to the motion of the Br nuclei is significantly longer than the laser pulse duration used in the present investigation, and that it is thus reasonable to assume that isomerization happens on the CHBr32+ PES and proceeds on a timescale longer than the laser pulse. Ab initio calculations at the ωB97x-d/aug-cc-VDZ level of theory (see Fig. S4 in ESI†) show a stable equilibrium geometry of the BrCHBr–Br isomer on the singlet ground state of the dication, thus providing a supportive argument for this speculation. Further corroboration for the transient formation of this isomer may be provided by future pump–probe experiments, as suggested in our most recent report.66
The HBr+ + CBr2+ channel, displayed in Fig. 4(e), which also requires the formation of a new bond – in this case between hydrogen and a bromine atom – has a branching ratio of 13% of all two-body breakup channels. The measured KER peaks at 3.9 eV. The CES for the charge distribution shown in the inset of Fig. 4(e) yields a KER of 4.5 eV (dashed green line). We also performed CES on the optimized ground-state geometry of the doubly-charged H-migrated isomer, H–Br⋯CBr2. In this case the charge distribution used was one unit of charge residing on the Br of HBr+ and one unit of charge equally distributed between the two Br atoms in the CBr2+ fragment. This simulation yielded the same KER value of 4.5 eV. It thus appears that the KER measurement, alone, cannot distinguish between the formation of HBr+ + CBr2+via concerted detachment or via H-migrated isomer formation, i.e., the [H–Br⋯CBr2]2+ ground state.
3.2 Three-body fragmentation channels
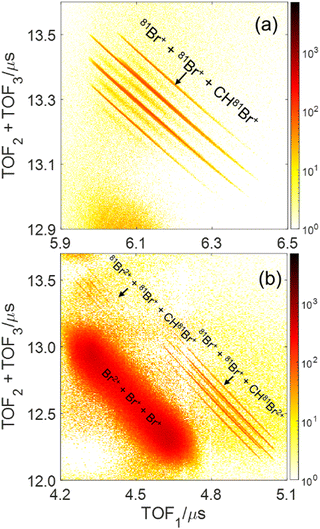
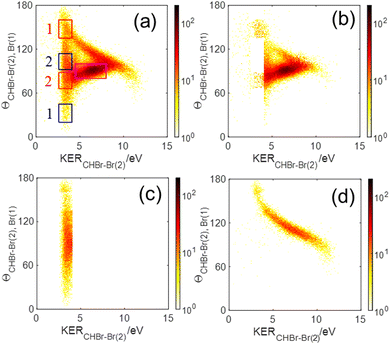
The main three-body channels observed in our experiment, Br+ + Br+ + CHBr+, Br+ + Br+ + CHBr2+ and Br2+ + Br+ + CHBr+, appear as sharp diagonal lines in the zoomed-in regions of interest of the triple photoion coincidence (TRIPICO) spectrum of CHBr3 shown in Fig. 5 (the full TRIPICO spectrum is displayed in Fig. S3, ESI†). The multiplicity of these diagonal lines stems from the natural abundance of 79Br and 81Br isotopes as explained in Section 3.1 in relation to the two-body fragmentation channels, and for similar reasons we discuss only the 3-body fragmentation of the CH81Br3 isotopologue. Specifically, the 81Br+ + 81Br+ + CH81Br+, 81Br+ + 81Br+ + CH81Br2+ and 81Br2+ + 81Br+ + CH81Br+ channels, because they are better separated from the stripes of the other isotopologues and from the background. To avoid possible artifacts, caused by the time order in which the indistinguishable 81Br+ fragments (of the 81Br+ + 81Br+ + CH81Br+ channel) are detected, we randomly swap their order for half of the events. Finally, to simplify notation we drop the isotopic labeling of the Br in the following subsections, except the reminder in the subtitles.One of the questions of interest when multiple bonds are breaking is the time order of the fragmentation process. Are all bonds breaking simultaneously – in a concerted way – or are they breaking sequentially, i.e., with sufficient delay to observe that sequence.76,77 More specifically, if the delay (Δτ) between two bond-breaking processes is less than the mean rotational period τrot of the intermediate fragment, i.e. Δτ/τrot < 1, then it is called a concerted pathway. In one of the limiting cases when both bonds break simultaneously, i.e. Δτ/τrot = 0, then it is called synchronous concerted. Asynchronous concerted is defined as 0 < Δτ/τrot < 1, while Δτ/τrot > 1 is the condition to be called sequential bond breaking.77 It is important to note, also, that the signature of synchronous-concerted breakup is equal energy sharing if the fragments’ masses are similar, while the a-synchronous concerted fragmentation yields different energy sharing.76 To determine if the fragmentation is sequential or concerted, we employ the native frames method,78,79 which is based on the use of the conjugate momenta of the Jacobi coordinates that describe the relative position of the fragments. These conjugate momenta can be associated with the first and second steps of sequential fragmentation of an ABC molecule, as follows
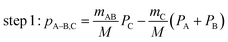 | (2) |
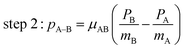 | (3) |
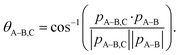 | (4) |
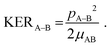 | (5) |
To identify sequential or concerted fragmentation, one needs a clear signature. The rotation of the intermediate molecule, AB, in the fragmentation plane has been used successfully as such a signature.80–84 In the native frames method, such rotation yields a uniform θA–B,C angular distribution if the rotation lasts long enough to erase any angular preference due to the first fragmentation step.78,79
The sequential breakup via the CHBr–Br2+(2) intermediate dication appears in Fig. 6(a) as a narrow KERCHBr–Br(2) stripe, centered about 3.45 eV, with a broad θCHBr–Br(2),Br(1) angular distribution, as expected. However, this angular distribution is not uniform, but rather peaks at 90°. There are two main reasons for this non-uniform angular distribution. The first is rotation of the intermediate CHBr22+ dication out of the fragmentation plane, which drives the angular distribution away from the edges causing dips at 0° and 180°. The second is the finite momentum resolution of the experiment, which has a similar effect on the angular distribution. Together, they lead to a distribution with reflection symmetry about the peak at 90°.
We note that the sequential breakup distribution via the CHBr–Br2+(2) intermediate, shown in Fig. 6(a), overlaps with the concerted fragmentation contribution at the region marked by the red rectangle (“gate”) labeled ‘2’, and with the sequential breakup via CHBr–Br2+(1) at the region marked by the ‘1’ red rectangle. To separate the sequential breakup via the CHBr–Br2+(2) intermediate dication from the competing fragmentation processes overlapping with it, we eliminate the events within the ‘1’ and ‘2’ red “gates” and replace them by equivalent events from the respective blue gates. Specifically, for each event in a blue gate, we generate an equivalent event which is rotated into the respective red gate by 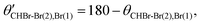 while maintaining all the rest of the event information the same. The results of this reconstruction are shown in Fig. 6(c). Similarly, sequential breakup with the other order of Br+ ejection, namely Br+(2) + CHBr–Br2+(1), is analyzed and reconstructed using the same algorithm, and then plotted in Fig. 6(d) to show how this channel appears when using the conjugate momenta appropriate for the breakup via the CHBr–Br2+(2) intermediate dication.
while maintaining all the rest of the event information the same. The results of this reconstruction are shown in Fig. 6(c). Similarly, sequential breakup with the other order of Br+ ejection, namely Br+(2) + CHBr–Br2+(1), is analyzed and reconstructed using the same algorithm, and then plotted in Fig. 6(d) to show how this channel appears when using the conjugate momenta appropriate for the breakup via the CHBr–Br2+(2) intermediate dication.
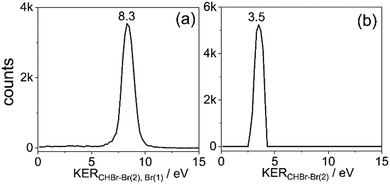
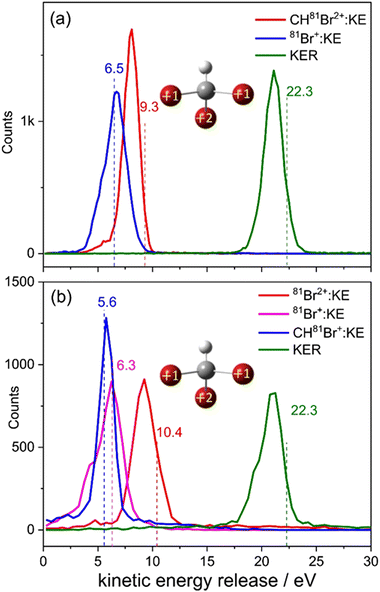
Now that sequential fragmentation proceeding via Br+ + CHBr22+ breakup followed by the dissociation of the dication into Br+ + CHBr+ was separated from the other competing fragmentation processes, we can investigate it in further detail. First, the kinetic energy released in each fragmentation step is plotted in Fig. 7.
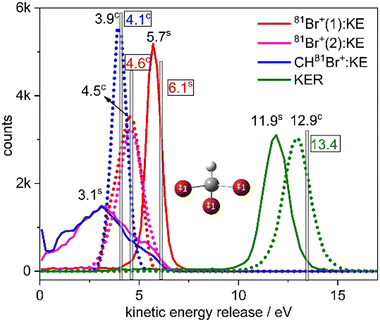
The KER in the second step is approximately half of the KER in the first step mainly due to the larger Coulomb repulsion between the Br ion and the dication. The total KER distribution of this sequential fragmentation process is centered about 11.9 eV, while the first and second Br+ fragments have a kinetic energy (KE) of about 5.7 and 3.1 eV, respectively, in the lab-fixed frame. Due to the rotation of the CHBr22+ intermediate, the latter has a much broader KE distribution, as shown in Fig. 8.
Next, we compare in Fig. 8 the distributions of KER and kinetic energy (KE) of the individual fragments for concerted and sequential fragmentation into Br+ + Br+ + CHBr+. The KER upon concerted fragmentation is about 1 eV higher than for sequential breakup, suggesting that either the fragments, especially the CHBr+, have more internal energy at the end of the sequential breakup, or that the concerted breakup pathway starts about 1 eV higher on the potential energy surface (or a another potential surface that is higher by 1 eV). Further work is needed to establish which of these is playing the dominant role.
Fig. 8 clearly shows that the kinetic energies of the two Br+ fragments resulting from sequential breakup are significantly different from each other. The Br+ ejected first is more energetic (peaking about 5.7 eV), while the Br+ ejected second (peaking about 3.1 eV) has a much wider KE distribution in the lab-fixed frame due to rotation of the intermediate CHBr22+ from which it is ejected. In contrast, the KE of the two Br+ fragments resulting from concerted fragmentation, shown in Fig. 9, are practically equal, as expected for synchronous-concerted breakup. Consistently, the KE of the CHBr+ fragment associated with the same process is just slightly lower due to its higher mass.
On the practical side, these differences in KE of the Br+ fragments allow one to suppress contributions from either concerted or sequential fragmentation by setting simple conditions (“gates”) on the kinetic energies of the two Br+ fragments, instead of the complete native frames analysis including reconstruction discussed above. For example, sequential breakup can be significantly suppressed by eliminating events with a Br+ with KE above about 5.1 eV, though at the cost of losing some concerted fragmentation events, as demonstrated in Fig. 10(f).
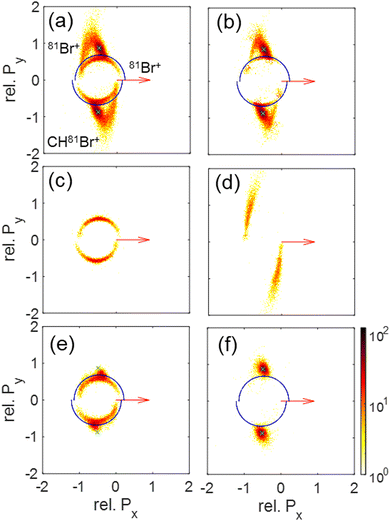 | ||
| Fig. 10 Newton plots of the Br+ + Br+ + CHBr+ fragmentation channel showing the momentum correlations between the fragments. The first Br+ fragment is used as a reference and its momentum is rotated to coincide with the x-axis (red arrow), while the other Br+ and the CHBr+ momenta, scaled to the reference Br+ momentum, are plotted on the top and bottom part, respectively. Panels (a)–(d) include the same events as the corresponding panels of Fig. 6, sorted using the native frames analysis. Specifically, they show (a) all Br+ + Br+ + CHBr+ events, (b) those events after subtraction of sequential breakup, (c) sequential breakup events in which the reference Br+ is ejected in the first step, and (d) sequential breakup events in which the reference Br+ is ejected in the second step. (e) All Br+ + Br+ + CHBr+ events, but with the KE of one of the Br+ fragments larger than 5.1 eV to select the contribution from sequential breakup (see text). (f) Similar to panel (e) but with the KE of each Br+ fragment smaller than 5.1 eV to select the contribution from concerted breakup (see text). | ||
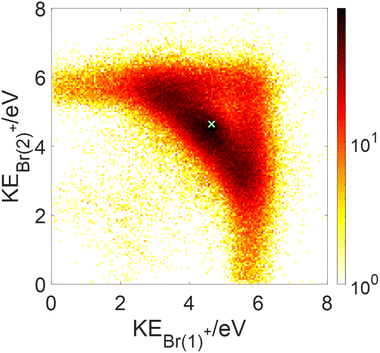
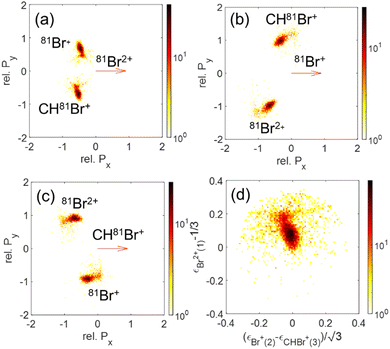
Since our data analysis provides the three-dimensional momenta of all three fragments in the moving molecular frame, the correlation among these momenta can be visualized in a Newton plot, as commonly done.80–84 In this plot, the relative magnitude and direction of the momentum of each fragment are displayed with respect to the momentum of one of them which serves as a reference fragment. Fig. 10 displays Newton plots with respect to Br+, whose momentum is normalized to one and fixed along the Px direction (red arrow). The momenta of the other two fragments are normalized to the reference fragment's momentum and are plotted in the upper and lower halves of the plot. The choice of the Br+ fragment as a reference is motivated by the identification of sequential breakup, where a Br+ is ejected in the first step, according to our native frames analysis above. This sequential breakup is expected to appear as a circular feature in such a Newton plot.80–84
The fragmentation processes identified above using the native frames method are clearly visible in Fig. 10(a). First, a circular structure consisting of two slightly offset semicircles (marked by the thin blue semicircles) is the result of sequential breakup, as shown in panel (c) (panel (d) shows the sequential fragmentation events for which the Br+ reference fragments are emitted in the second step). As discussed above, this sequential fragmentation proceeds by dissociation of the transient CHBr33+ into Br+ + CHBr22+ followed by the dissociation of the dication into Br+ + CHBr+ after this dication rotates for a time longer than its rotational period. Second, two localized maxima (marked by the green cross “×” symbol) around (−0.5, ±0.9), are the result of synchronous-concerted breakup. These events can be selected by requiring that both Br+ KEs are smaller than 5.1 eV, as shown in Fig. 10(f). Third, a curved “tail” starts at the position of the maxima and curves back toward the circular structure. This feature is also identified as concerted breakup, however, in contrast to the localized maxima, this fragmentation is asynchronous as indicated by the increasingly unequal energy sharing of the Br+ fragments as one moves along the “tail” away from the maxima (see also Fig. 9).
Next, we model the synchronous-concerted fragmentation by placing one unit charge at the position of each of the Br atoms in the CHBr3 equilibrium geometry, and the CES yields the momentum correlation, shown by the green cross “×” symbols in Fig. 10(a), (b), (e) and (f), which are in excellent agreement with the location of the maxima around (−0.5, ±0.9) and (−0.5, ±0.9).
In addition to the Newton plot, which highlights the momentum correlation, a Dalitz plot85,86 can be used to show the energy correlation between two variables of choice in a three-body fragmentation. In the Dalitz plot representation, the x and y axes are defined as (ε1 − ε2)/√3 and ε3 − 1/3, respectively, where εi is the scaled kinetic energy, 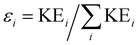 , and KEi is the kinetic energy of the ith fragment.
, and KEi is the kinetic energy of the ith fragment.
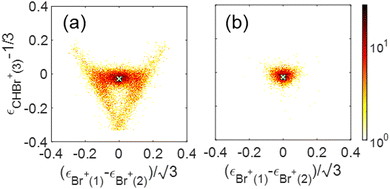
We show a Dalitz plot for the Br+ + Br+ + CHBr+ channel in Fig. 11. In Fig. 11(a), which includes all of the events from this channel, a clear peak is observed close to the origin of the plot, which is consistent with a synchronous-concerted breakup leading to almost equal energy sharing among the three fragment ions, as well as with our CES prediction shown by the green cross “×” symbol. Similar to the Newton diagram of Fig. 10(f), the events from this specific pathway can be efficiently sorted out by selecting the events with both Br+ KEs below 5.1 eV, as shown in Fig. 11(b). A horizontal band on both sides of this maximum visible in Fig. 11(a) reflects the events with unequal energy sharing between the two Br+ ions and can be tentatively assigned to the asynchronous-concerted fragmentation pathway, corresponding to the curved “tail” observed in the Newton diagrams of Fig. 10(a) and (b). Finally, two diagonal structures in Fig. 11(a) reflect the events resulting from the sequential fragmentation discussed above, with each diagonal associated with either of the Br+ ions being emitted in the first step.
Returning to our CES modeling of concerted three-body breakup using unit point charges placed on each of the three Br atoms, we focus on the KER and KEs estimates, which are shown as vertical lines in Fig. 8. The KER obtained from the CES for the concerted breakup is 13.4 eV which is approximately 0.5 eV (only 4%) higher than the peak of the measured concerted fragmentation distribution. The CES yields a KE of 4.6 eV for the Br+ fragments, coinciding quite well with the measured KE peaks (at 4.5 eV) of the Br+ fragments associated solely with concerted fragmentation. Furthermore, the CES prediction of 4.1 eV for the CHBr+ fragment's kinetic energy only slightly overestimates the measured KE peak at 3.9 eV (explicitly by only ∼5%).
Finally, we would like to discuss the CES of the Br+ + Br+ + CHBr+ channel which could also have contributions from the concerted breakup of the triply charged Br-migrated isomer, (BrHCBr-Br)3+. The CES for concerted breakup placing a unit charge on each of the three Br atoms of this isomer yields KEs in the ranges of 4.8–4.9 and 3.9–4.4 eV for the two Br+ fragments, with an angle of 120–126° between their momenta, while the KE of the third fragment, CHBr+, would be 3.3–3.8 eV. These values are very close to the values obtained from the CES of the triply ionized parent molecule, CHBr33+, suggesting that it is not possible to distinguish between the parent CHBr3 and the BrCHBr–Br isomer using the concerted breakup of the trication. However, this distinction may be possible via the four- and five-body breakup channels, as we have shown in prior work.66
Fig. 12(a) and (b) show the KER and KE distributions of the Br+ + Br+ + CHBr2+ and Br2+ + Br+ + CHBr+ channels, respectively. The KER and KEs computed by CES for concerted three-body breakup with unit point charges placed on each of the three Br atoms are shown as vertical dashed lines in Fig. 12. The simulated KER values for both the channels are within 1.2 eV compared to the respective measured peak values. Unlike the three-body dissociation from the tricationic bromoform, there is only one peak in the KER and KE distributions of the fragments produced from the tetracationic bromoform.
The momentum and energy correlation are shown as Newton and Dalitz plots for the Br+ + Br+ + CHBr2+ and Br2+ + Br+ + CHBr+ channels in Fig. 13 and 14, respectively. These figures are dominated by concerted fragmentation, which appears as peaks in these correlation maps. This dominance of concerted fragmentation is consistent with the fact that we see no sign of sequential breakup in our native frames analysis of these two channels.
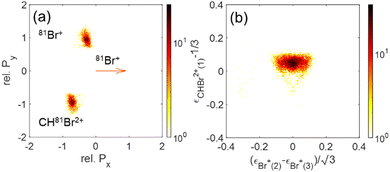 | ||
| Fig. 13 (a) Newton plots of the Br+ + Br+ + CHBr2+ channel with Br+ as reference fragment. (b) Dalitz plot for the same fragmentation channel. | ||
4 Concluding remarks
The two- and three-body fragmentation of CHBr3 after double, triple, and quadruple ionization induced by a strong 790 nm near-infrared laser field is investigated by measuring the momenta of two and three fragment ions in coincidence. We concentrate on ionic two- and three-body breakup channels, i.e., excluding production of any neutral fragments. Among these channels, the dominant two-body breakup channel is found to be Br+ + CHBr2+, while other exotic channels such as HBr+ + CBr2+, CHBr+ + Br2+ and CHBr2+ + Br2+, which require formation of new bonds not present in the parent molecule, were also observed. The KER distribution of the CHBr+ + Br2+ channel exhibits a two-component structure, suggesting the existence of two fragmentation pathways, which may be transient isomerization prior to fragmentation and concerted breakup. The two three-body fragmentation channels of the tetracationic bromoform, i.e., the transient CHBr34+, are observed to undergo solely concerted fragmentation. In contrast, the fragmentation of the main three-body channel, Br+ + Br+ + CHBr+, occurs both sequentially and in a concerted manner. This was determined by employing the native frames method, which also allowed us to separate the two fragmentation mechanisms from each other and study them in detail. In the concerted fragmentation case, the similarity of the measured kinetic energies of the fragments suggests that the process is predominantly synchronous, although a non-negligible fraction of events manifests an unequal energy sharing between the two Br+ ions, which is the signature of asynchronous-concerted fragmentation.76 The sequential fragmentation proceeds by Br+ + CHBr22+ breakup as a first step, followed by the dissociation of the intermediate CHBr22+ dication into Br+ + CHBr+. The kinetic energies of the first and second ejected Br+ fragments are significantly different, a fact that can be used to separate concerted and sequential fragmentation events from each other.The overall agreement between experimental results and CES demonstrates that a classical CES can be a suitable approximation for modeling the kinematics of the strong-field-induced two- and three-body fragmentation. Furthermore, our experimental results can pave the way for future time-resolved studies on CHBr3 using strong-field-induced fragmentation as a probe. Combining the Coulomb explosion imaging method presented here (and in our prior publication that focused primarily on the fragmentation of CHBr3 into four and five ionic fragments66) with a pump–probe scheme should be well suited to study the predicted roaming dynamics on the femtosecond time scale and pave the way for making molecular movies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the technical staff of JRML for support during the preparation of the experiment. We also acknowledge Max Sayler and other former members of Itzik Ben-Itzhak's group for the development of the computer code to reconstruct lost delay-line signals, which was implemented in the data analysis for this paper. This work was supported primarily by the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, US Department of Energy, Grant no. DEFG02-86ER13491. The PULSAR laser was provided by Grant no. DE-FG02-09ER16115 from the same funding agency. S. B. was supported by Grant no. DE-SC0020276; K. B. and E. W. by Grant no. DE-SC0019451; N. M. was supported by the National Science Foundation (NSF) Grant no. PHYS-1753324 to D. R. The ab initio calculation was performed on the supercomputing system in the Supercomputing Center of the University of Science and Technology of China.References
- G. A. Mourou, T. Tajima and S. V. Bulanov, Rev. Mod. Phys., 2006, 78, 309–371, DOI:10.1103/RevModPhys.78.309.
- P. Gibbon, Short Pulse Laser Interactions with Matter: An Introduction, Imperial College Press, London, 2005 Search PubMed.
- W. L. Kruer, The Physics of Laser Plasma Interactions, CRC Press, Taylor & Francis Group, Florida, 2018 Search PubMed.
- V. Malka, J. Faure, Y. A. Gauduel, E. Lefebvre, A. Rousse and K. T. Phuoc, Nat. Phys., 2008, 4, 447–453, DOI:10.1038/nphys966.
- J. A. Dharmadhikari, A. K. Dharmadhikari, K. C. Kasuba, H. Bharambe, J. S. D’Souza, K. D. Rathod and D. Mathur, Sci. Rep., 2016, 6, 27515, DOI:10.1038/srep27515.
- A. Adak, P. K. Singh, D. R. Blackman, A. D. Lad, G. Chatterjee, J. Pasley, A. P. L. Robinson and G. R. Kumar, Phys. Plasmas, 2017, 24, 072702, DOI:10.1063/1.4990059.
- P. W. Brumer and M. Shapiro, Principles of the Quantum Control of Molecular Processes, John Wiley & Sons, Inc., Hoboken, New Jersey, 2003 Search PubMed.
- S. A. Z. Rice and M. Zhao, Optical Control of Molecular Dynamics, Wiley-Interscience, 2000 Search PubMed.
- M. J. J. Vrakking and S. Stolte, Chem. Phys. Lett., 1997, 271, 209–215, DOI:10.1016/S0009-2614(97)00436-3.
- J. G. Underwood, M. Spanner, M. Y. Ivanov, J. Mottershead, B. J. Sussman and A. Stolow, Phys. Rev. Lett., 2003, 90, 223001, DOI:10.1103/PhysRevLett.90.223001.
- T. Brixner, N. H. Damrauer and G. Gerber, Adv. At., Mol., Opt. Phys., 2001, 46, 1–54, DOI:10.1016/S1049-250X(01)80062-8.
- M. E. Corrales, J. Gonzalez-Vazquez, G. Balerdi, I. R. Sola, R. de Nalda and L. Banares, Nat. Chem., 2014, 6, 785–790, DOI:10.1038/nchem.2006.
- M. E. Corrales, R. de Nalda and L. Banares, Nat. Commun., 2017, 8, 1345, DOI:10.1038/s41467-017-01139-6.
- A. Owens, A. Yachmenev and J. Kupper, J. Phys. Chem. Lett., 2018, 9, 4206–4209, DOI:10.1021/acs.jpclett.8b01689.
- S. Pathak, L. M. Ibele, R. Boll, C. Callegari, A. Demidovich, B. Erk, R. Feifel, R. Forbes, M. Di Fraia, L. Giannessi, C. S. Hansen, D. M. P. Holland, R. A. Ingle, R. Mason, O. Plekan, K. C. Prince, A. Rouzee, R. J. Squibb, J. Tross, M. N. R. Ashfold, B. F. E. Curchod and D. Rolles, Nat. Chem., 2020, 12, 795–802, DOI:10.1038/s41557-020-0507-3.
- N. Ekanayake, M. Nairat, B. Kaderiya, P. Feizollah, B. Jochim, T. Severt, B. Berry, K. R. Pandiri, K. D. Carnes, S. Pathak, D. Rolles, A. Rudenko, I. Ben-Itzhak, C. A. Mancuso, B. S. Fales, J. E. Jackson, B. G. Levine and M. Dantus, Sci. Rep., 2017, 7, 4703, DOI:10.1038/s41598-017-04666-w.
- D. Townsend, S. A. Lahankar, S. K. Lee, S. D. Chambreau, A. G. Suits, X. Zhang, J. Rheinecker, L. B. Harding and J. M. Bowman, Science, 2004, 306, 1158–1161, DOI:10.1126/science.1104386.
- S. Zhao, B. Jochim, P. Feizollah, J. Rajput, F. Ziaee, P. Kanaka Raju, B. Kaderiya, K. Borne, Y. Malakar, B. Berry, J. Harrington, D. Rolles, A. Rudenko, K. D. Carnes, E. Wells, I. Ben-Itzhak and T. Severt, Phys. Rev. A, 2019, 99, 053412, DOI:10.1103/PhysRevA.99.053412.
- Z. Lu, Y. C. Chang, Q. Z. Yin, C. Y. Ng and W. M. Jackson, Science, 2014, 346, 61–64, DOI:10.1126/science.1257156.
- N. Ekanayake, M. Nairat, N. P. Weingartz, M. J. Michie, B. G. Levine and M. Dantus, J. Chem. Phys., 2018, 149, 244310, DOI:10.1063/1.5065387.
- N. Ekanayake, T. Severt, M. Nairat, N. P. Weingartz, B. M. Farris, B. Kaderiya, P. Feizollah, B. Jochim, F. Ziaee, K. Borne, P. Kanaka Raju, K. D. Carnes, D. Rolles, A. Rudenko, B. G. Levine, J. E. Jackson, I. Ben-Itzhak and M. Dantus, Nat. Commun., 2018, 9, 5186, DOI:10.1038/s41467-018-07577-0.
- S. Larimian, S. Erattupuzha, S. Mai, P. Marquetand, L. Gonzalez, A. Baltuska, M. Kitzler and X. H. Xie, Phys. Rev. A, 2017, 95, 011404(R), DOI:10.1103/PhysRevA.95.011404.
- D. Mathur, A. K. Dharmadhikari, J. A. Dharmadhikari and P. Vasa, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 154004, DOI:10.1088/1361-6455/aa7c85.
- M. Kubel, R. Siemering, C. Burger, N. G. Kling, H. Li, A. S. Alnaser, B. Bergues, S. Zherebtsov, A. M. Azzeer, I. Ben-Itzhak, R. Moshammer, R. de Vivie-Riedle and M. F. Kling, Phys. Rev. Lett., 2016, 116, 193001, DOI:10.1103/PhysRevLett.116.193001.
- H. Wu, S. A. Zhang, J. Zhang, Y. Yang, L. Deng, T. Q. Jia, Z. G. Wang and Z. R. Sun, J. Phys. Chem. A, 2015, 119, 2052–2057, DOI:10.1021/jp510667z.
- C. E. Liekhus-Schmaltz, I. Tenney, T. Osipov, A. Sanchez-Gonzalez, N. Berrah, R. Boll, C. Bomme, C. Bostedt, J. D. Bozek, S. Carron, R. Coffee, J. Devin, B. Erk, K. R. Ferguson, R. W. Field, L. Foucar, L. J. Frasinski, J. M. Glownia, M. Guhr, A. Kamalov, J. Krzywinski, H. Li, J. P. Marangos, T. J. Martinez, B. K. McFarland, S. Miyabe, B. Murphy, A. Natan, D. Rolles, A. Rudenko, M. Siano, E. R. Simpson, L. Spector, M. Swiggers, D. Walke, S. Wang, T. Weber, P. H. Bucksbaum and V. S. Petrovic, Nat. Commun., 2015, 6, 8199, DOI:10.1038/ncomms9199.
- H. Ibrahim, B. Wales, S. Beaulieu, B. E. Schmidt, N. Thire, E. P. Fowe, E. Bisson, C. T. Hebeisen, V. Wanie, M. Giguere, J. C. Kieffer, M. Spanner, A. D. Bandrauk, J. Sanderson, M. S. Schuurman and F. Legare, Nat. Commun., 2014, 5, 4422, DOI:10.1038/ncomms5422.
- K. Nakai, T. Kato, H. Kono and K. Yamanouchi, J. Chem. Phys., 2013, 139, 181103, DOI:10.1063/1.4830397.
- J. Laksman, E. P. Mansson, A. Sankari, D. Ceolin, M. Gisselbrecht and S. L. Sorensen, Phys. Chem. Chem. Phys., 2013, 15, 19322–19329, 10.1039/c3cp52625a.
- P. M. Kraus, M. C. Schwarzer, N. Schirmel, G. Urbasch, G. Frenking and K. M. Weitzel, J. Chem. Phys., 2011, 134, 114302, DOI:10.1063/1.3561311.
- K. Hoshina, H. Kawamura, M. Tsuge, M. Tamiya and M. Ishiguro, J. Chem. Phys., 2011, 134, 064324, DOI:10.1063/1.3549137.
- J. Laksman, D. Ceolin, M. Gisselbrecht and S. L. Sorensen, J. Chem. Phys., 2010, 133, 144314, DOI:10.1063/1.3502116.
- I. Ben-Itzhak, A. M. Sayler, M. Leonard, J. W. Maseberg, D. Hathiramani, E. Wells, M. A. Smith, J. F. Xia, P. Q. Wang, K. D. Carnes and B. D. Esry, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 233, 284–292, DOI:10.1016/j.nimb.2005.03.123.
- T. Endo, S. P. Neville, V. Wanie, S. Beaulieu, C. Qu, J. Deschamps, P. Lassonde, B. E. Schmidt, H. Fujise, M. Fushitani, A. Hishikawa, P. L. Houston, J. M. Bowman, M. S. Schuurman, F. Légaré and H. Ibrahim, Science, 2020, 370, 1072–1077, DOI:10.1126/science.abc2960.
- T. Severt, D. R. Daugaard, T. Townsend, F. Ziaee, K. Borne, S. Bhattacharyya, K. D. Carnes, D. Rolles, A. Rudenko, E. Wells and I. Ben-Itzhak, Phys. Rev. A, 2022, 105, 053112, DOI:10.1103/PhysRevA.105.053112.
- A. S. Mereshchenko, E. V. Butaeva, V. A. Borin, A. Eyzips and A. N. Tarnovsky, Nat. Chem., 2015, 7, 562–568, DOI:10.1038/Nchem.2278.
- D. Mishra, J. Reino-González, R. Obaid, A. C. LaForge, S. Díaz-Tendero, F. Martín and N. Berrah, Phys. Chem. Chem. Phys., 2022, 24, 433–443, 10.1039/D1CP04011A.
- A. Kalume, L. George and S. A. Reid, J. Phys. Chem. Lett., 2010, 1, 3090–3095, DOI:10.1021/jz101250s.
- M. R. Cameron and G. B. Bacskay, J. Phys. Chem. A, 2000, l, 11212–11219, DOI:10.1021/jp002429i.
- M. J. Molina and F. S. Rowland, Nature, 1974, 249, 810–812, DOI:10.1038/249810a0.
- S. Solomon, R. W. Portmann and D. W. J. Thompson, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 445–449, DOI:10.1073/pnas.0604895104.
- L. A. Barrie, J. W. Bottenheim, R. C. Schnell, P. J. Crutzen and R. A. Rasmussen, Nature, 1988, 334, 138–141, DOI:10.1038/334138a0.
- B. W. Toulson, M. Borgwardt, H. Wang, F. Lackner, A. S. Chatterley, C. D. Pemmaraju, D. M. Neumark, S. R. Leone, D. Prendergast and O. Gessner, Struct. Dyn., 2019, 6, 054304, DOI:10.1063/1.5113798.
- J. Lindner, K. Ermisch and R. Wilhelm, Chem. Phys., 1998, 238, 329–341, DOI:10.1016/S0301-0104(98)00303-6.
- P. Zou, J. N. Shu, T. J. Sears, G. E. Hall and S. W. North, J. Phys. Chem. A, 2004, 108, 1482–1488, DOI:10.1021/jp0310394.
- W. L. Liu and B. C. Chang, J. Chin. Chem. Soc., 2001, 48, 613–617, DOI:10.1002/jccs.200100092.
- D. Geissler, B. J. Pearson and T. Weinacht, J. Chem. Phys., 2007, 127, 204305, DOI:10.1063/1.2805186.
- S. L. Horton, Y. S. Liu, R. Forbes, V. Makhija, R. Lausten, A. Stolow, P. Hockett, P. Marquetand, T. Rozgonyi and T. Weinacht, J. Chem. Phys., 2019, 150, 174201, DOI:10.1063/1.5086665.
- U. Marvet, Q. G. Zhang, E. J. Brown and M. Dantus, J. Chem. Phys., 1998, 109, 4415–4427, DOI:10.1063/1.477045.
- Q. Zhang, U. Marvet and M. Dantus, J. Chem. Phys., 1998, 109, 4428–4442, DOI:10.1063/1.477046.
- E. D. Tweeten, B. J. Petro and R. W. Quandt, J. Phys. Chem. A, 2003, 107, 19–24, DOI:10.1021/jp021610j.
- B. J. Petro, E. D. Tweeten and R. W. Quandt, J. Phys. Chem. A, 2004, 108, 384–391, DOI:10.1021/jp035981r.
- S. Luo, W. Hu, J. Yu, X. Li, L. He, C. Wang, F. Liu and D. Ding, J. Phys. Chem. A, 2017, 121, 6547–6553, DOI:10.1021/acs.jpca.7b05588.
- S. Luo, S. Zhou, W. Hu, J. Yu, X. Li, P. Ma, L. He, C. Wang, F. Guo, Y. Yang and D. Ding, J. Phys. Chem. A, 2018, 122, 8427–8432, DOI:10.1021/acs.jpca.8b06415.
- P. Sandor, A. Sissay, F. Mauger, M. W. Gordon, T. T. Gorman, T. D. Scarborough, M. B. Gaarde, K. Lopata, K. J. Schafer and R. R. Jones, J. Chem. Phys., 2019, 151, 194308, DOI:10.1063/1.5121711.
- K. Mogyorosi, K. Sarosi and V. Chikan, J. Phys. Chem. A, 2020, 124, 8112–8119, DOI:10.1021/acs.jpca.0c05206.
- C. M. Maharjan, Momentum Imaging Studies of Electron and Ion dynamics in a Strong Laser Field, PhD thesis, Kansas State University, 2007 Search PubMed.
- Y. Malakar, W. L. Pearson, M. Zohrabi, B. Kaderiya, P. Kanaka Raju, F. Ziaee, S. Xue, A. T. Le, I. Ben-Itzhak, D. Rolles and A. Rudenko, Phys. Chem. Chem. Phys., 2019, 21, 14090–14102, 10.1039/c8cp07032f.
- Y. Xiong, K. Borne, A. M. Carrascosa, S. K. Saha, K. J. Wilkin, M. Yang, S. Bhattacharyya, K. Chen, W. Du, L. Ma, N. Marshall, J. P. F. Nunes, S. Pathak, Z. Phelps, X. Xu, H. Yong, K. Lopata, P. M. Weber, A. Rudenko, D. Rolles and M. Centurion, Faraday Discuss., 2021, 228, 39–59, 10.1039/D0FD00125B.
- X. M. Ren, A. M. Summers, P. Kanaka Raju, A. Vajdi, V. Makhija, C. W. Fehrenbach, N. G. Kling, K. J. Betsch, Z. Wang, M. F. Kling, K. D. Carnes, I. Ben-Itzhak, C. Trallero-Herrero and V. Kumarappan, J. Opt., 2017, 19, 124017, DOI:10.1088/2040-8986/aa9865.
- A. Rudenko, K. Zrost, C. D. Schroter, V. L. B. de Jesus, B. Feuerstein, R. Moshammer and J. Ullrich, J. Phys. B: At., Mol. Opt. Phys., 2004, 37, L407–L413, DOI:10.1088/0953-4075/37/24/L03.
- R. Dorner, V. Mergel, O. Jagutzki, L. Spielberger, J. Ullrich, R. Moshammer and H. Schmidt-Bocking, Phys. Rep., 2000, 330, 95–192, DOI:10.1016/S0370-1573(99)00109-X.
- J. Ullrich, R. Moshammer, A. Dorn, R. Dorner, L. P. H. Schmidt and H. Schmidt-Bocking, Rep. Prog. Phys., 2003, 66, 1463–1545, DOI:10.1088/0034-4885/66/9/203.
- K. Fehre, D. Trojanowskaja, J. Gatzke, M. Kunitski, F. Trinter, S. Zeller, L. P. H. Schmidt, J. Stohner, R. Berger, A. Czasch, O. Jagutzki, T. Jahnke, R. Dorner and M. S. Schoffler, Rev. Sci. Instrum., 2018, 89, 045112, DOI:10.1063/1.5022564.
- O. Jagutzki, V. Mergel, K. Ullmann-Pfleger, L. Spielberger, U. Spillmann, R. Dörner and H. Schmidt-Böcking, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 477, 244–249, DOI:10.1016/S0168-9002(01)01839-3.
- S. Bhattacharyya, K. Borne, F. Ziaee, S. Pathak, E. Wang, A. S. Venkatachalam, X. Li, N. Marshall, K. D. Carnes, C. W. Fehrenbach, T. Severt, I. Ben-Itzhak, A. Rudenko and D. Rolles, J. Phys. Chem. Lett., 2022, 5845–5853, DOI:10.1021/acs.jpclett.2c01007.
- U. Ablikim, C. Bomme, E. Savelyev, H. Xiong, R. Kushawaha, R. Boll, K. Amini, T. Osipov, D. Kilcoyne, A. Rudenko, N. Berrah and D. Rolles, Phys. Chem. Chem. Phys., 2017, 19, 13419–13431, 10.1039/c7cp01379e.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Peterssonet al., Gaussian 09 Rev B.01, Gaussian, Inc., 2009 Search PubMed.
- J. H. D. Eland, Mol. Phys., 1987, 61, 725–745, DOI:10.1080/00268978700101421.
- I. Ben-Itzhak, S. G. Ginther and K. D. Carnes, Nucl. Instrum. Methods Phys. Res., Sect. B, 1992, 66, 401–414, DOI:10.1016/0168-583X(92)95411-J.
- I. Ben-Itzhak, P. Q. Wang, A. M. Sayler, K. D. Carnes, M. Leonard, B. D. Esry, A. S. Alnaser, B. Ulrich, X. M. Tong, I. V. Litvinyuk, C. M. Maharjan, P. Ranitovic, T. Osipov, S. Ghimire, Z. Chang and C. L. Cocke, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 063419, DOI:10.1103/PhysRevA.78.063419.
- X. Gong, Q. Song, Q. Ji, K. Lin, H. Pan, J. Ding, H. Zeng and J. Wu, Phys. Rev. Lett., 2015, 114, 163001, DOI:10.1103/PhysRevLett.114.163001.
- Z. L. Streeter, F. L. Yip, R. R. Lucchese, B. Gervais, T. N. Rescigno and C. W. McCurdy, Phys. Rev. A, 2018, 98, 053429, DOI:10.1103/PhysRevA.98.053429.
- C. Cheng, Z. L. Streeter, A. J. Howard, M. Spanner, R. R. Lucchese, C. W. McCurdy, T. Weinacht, P. H. Bucksbaum and R. Forbes, Phys. Rev. A, 2021, 104, 023108, DOI:10.1103/PhysRevA.104.023108.
- M. E. Corrales, G. Gitzinger, J. González-Vázquez, V. Loriot, R. de Nalda and L. Bañares, J. Phys. Chem. A, 2012, 116, 2669–2677, DOI:10.1021/jp207367a.
- C. E. M. Strauss and P. L. Houston, J. Phys. Chem., 1990, 94, 8751–8762, DOI:10.1021/j100388a003.
- C. Maul and K. H. Gericke, Int. Rev. Phys. Chem., 1997, 16, 1–79, DOI:10.1080/014423597230307.
- J. Rajput, T. Severt, B. Berry, B. Jochim, P. Feizollah, B. Kaderiya, M. Zohrabi, U. Ablikim, F. Ziaee, P. Kanaka Raju, D. Rolles, A. Rudenko, K. D. Carnes, B. D. Esry and I. Ben-Itzhak, Phys. Rev. Lett., 2018, 120, 103001, DOI:10.1103/PhysRevLett.120.103001.
- T. Severt, Imaging Light-induced Molecular Fragmentation Dynamics, PhD thesis, Kansas State University, 2021 Search PubMed.
- S. Hsieh and J. H. D. Eland, J. Phys. B: At., Mol. Opt. Phys., 1997, 30, 4515–4534, DOI:10.1088/0953-4075/30/20/015.
- N. Neumann, D. Hant, L. P. H. Schmidt, J. Titze, T. Jahnke, A. Czasch, M. S. Schöffler, K. Kreidi, O. Jagutzki, H. Schmidt-Böcking and R. Dörner, Phys. Rev. Lett., 2010, 104, 103201, DOI:10.1103/PhysRevLett.104.103201.
- R. Guillemin, P. Decleva, M. Stener, C. Bomme, T. Marin, L. Journel, T. Marchenko, R. K. Kushawaha, K. Jänkälä, N. Trcera, K. P. Bowen, D. W. Lindle, M. N. Piancastelli and M. Simon, Nat. Commun., 2015, 6, 6166, DOI:10.1038/ncomms7166.
- A. Khan, L. C. Tribedi and D. Misra, Phys. Rev. A, 2017, 96, 012703, DOI:10.1103/PhysRevA.96.012703.
- A. Khan, L. C. Tribedi and D. Misra, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 030701, DOI:10.1103/PhysRevA.92.030701.
- R. H. Dalitz, Phil. Mag. Ser., 1953, 44, 1068–1080, DOI:10.1080/14786441008520365.
- U. Galster, P. Kaminski, M. Beckert, H. Helm and U. Müller, Eur. Phys. J. D, 2001, 17, 307–318, DOI:10.1007/s100530170005.
Footnote |
| † Electronic supplementary information (ESI) available: Ion time-of-flight spectra, kinetic energy release distributions, complete PIPICO plots, energy correlation maps, optimized structures of iso-CHBr32+ and the associated transition states, additional KER and KEs for the Br+ + Br+ + CHBr+ channel and Coulomb explosion simulation of the Wigner distribution. See DOI: https://doi.org/10.1039/d2cp03089f |
| This journal is © the Owner Societies 2022 |