Photodissociation dynamics of N,N-dimethylformamide at 225 nm and 245 nm

Abstract

N,N-Dimethylformamide, (CH₃)₂NCH=O, is the simplest tertiary amide and a model compound for investigating the photofragmentation of peptide bonds. We report the results of a velocity-map imaging study into the photodissociation dynamics of DMF following excitation at 225 nm and 245 nm. Excitation at either wavelength generates a variety of products, with the primary dissociation pathways involving cleavage of either the N–CO amide bond or an N–CH₃ bond. Excitation at 225 nm is predominantly to the S₂ 2¹A′′ state via a parallel transition, with dissociation of the amide bond occurring either on this state or on a lower singlet surface following internal conversion. The topographies of all of the potential energy surfaces involved result in dissociation from a range of planar (apart from the methyl-group hydrogen atoms) and non-planar molecular geometries. Dissociation from planar geometries leads to little product internal excitation, correspondingly high photofragment velocities, and near-limiting values of the recoil-anisotropy parameter β. Dissociation from non-planar geometries leads to significant product internal excitation, with correspondingly lower photofragment velocities and breakdown of the axial recoil approximation to give reduced values of β. Excitation at 245 nm involves the same excited-state surfaces, but at the longer wavelength the S₂ state can only be reached from non-equilibrium geometries of the ground state, leading to a reduction in the recoil anisotropy parameter relative to excitation at 225 nm. The potential energy curves associated with cleavage of the N–CH₃ bond are less well characterised. However, the pathway is characterised by an isotropic angular distribution and a TKER distribution peaking at low energies, both of which can be rationalised in terms of the molecular geometry and the orientation of the transition dipole involved in the excitation step.

---

1 Introduction

Peptide bonds form the backbone of proteins and are of key interest for biochemical processes. Understanding the photostability and photofragmentation of such bonds provides insight into UV-radiation damage to biological systems. Monopeptides have been considered previously as useful model compounds for investigating the peptide bond fragmentation dynamics in a variety of experimental^1–7 and theoretical^8–11 studies. N,N-Dimethylformamide (DMF) is the simplest tertiary amide, a planar molecule^12–15 (apart from the hydrogen atoms on the two methyl groups), and its amide bond offers an ideal candidate to model the photodissociation dynamics of peptide bonds. Additionally, DMF has been postulated to play an important role in the formation of adenine in astrochemical environments.¹⁶

Experimental and theoretical studies of DMF have focused primarily on dynamics following excitation at wavelengths below 200 nm. Summarising first the theoretical studies, a number of authors have reported potential energy surfaces (PESs) for the ground and electronically excited states. Based on experimental gas-phase spectra of DMF,^17,18 Serrano-Andrés and Fülscher¹⁹ used the complete active space with second order perturbation theory (CASPT2) to determine vertical excitation energies from the ground state. Liu et al.⁸ discussed the photolysis mechanism of DMF following excitation at 193 nm based on complete active space self consistent field (CASSCF) calculations of the relevant PESs. Eckert-Maksić and Antol⁹ also performed CASSCF calculations in the context of understanding DMF photolysis, and were able to characterize several significant points such as energy minima, saddle points, and conical intersections and to determine how the geometry of DMF changes to reach those points. Lipciuc et al.⁷ determined transition dipole moments for excitations to the first three valence singlet states via CASSCF calculations, and generated cuts through the PESs along N–CO and N–CH₃ bonds based on CASPT2 calculations. The arguably most comprehensive theoretical study on DMF has been conducted by Shastri et al.¹¹ These authors correlated the electronic absorption spectrum over the wavelength range 125–221 nm with results from density functional calculations, providing an in-depth discussion of relevant molecular orbitals, vibrational frequencies, and electronically excited singlet and triplet states. They reported potential energy curves for the first five excited states of DMF, including valence and Rydberg states, as a function of bond length. These potential energy curves guide the interpretation of the results reported in this paper, and are summarised in Fig. 1. Note that we include in this figure the 2¹A′′ Rydberg state, which was not found in the valence-state calculations carried out by Lipciuc et al.⁷ This now becomes the S₂ state in place of the higher-lying 2¹A′ state that was identified as such by Lipciuc et al. Note that the first two excited singlet states exhibit energy barriers along the N–CO bond, impeding prompt dissociation along that coordinate.

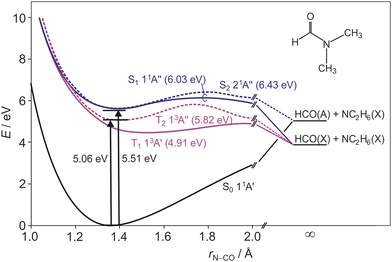Fig. 1 Schematic cuts through the ground state and first two excited singlet and triplet state potential energy surfaces of DMF along the N–CO stretch coordinate, adapted from ref. 11. Barrier heights for each surface are given in parentheses after the state labels, and the dissociation limit for each surface is indicated.

There are comparatively fewer experimental studies on DMF. Forde et al.^1,2 performed photodissociation studies at 193 nm and recorded recoil translational energy distributions and angular distributions for the dissociation products. The studies indicated two main dissociation channels: cleavage of the N–CO amide bond to form HCO and N(CH₃)₂; and fission of one of the two N–CH₃ bonds, forming HCONCH₃ and CH₃. Cleavage of the N–CO bond was found to lead to formation of ground-state HCO(X̃) with either ground state N(CH₃)₂(X̃) or electronically excited N(CH₃)₂(Ã). The products were measured to have a recoil anisotropy of β = 1.2 ± 0.2, implying a rapid bond dissociation to a state for which the transition dipole from the ground state lies predominantly parallel to the breaking bond.

Lipciuc et al.⁷ investigated the 193 nm photolysis of DMF using velocity-map imaging. They observed the same N–CO and N–CH₃ bond breaking channels as Forde et al., and measured complete scattering distributions for each observed photoproduct. For products associated with the N–CO bond breaking channels the β-parameter was found to show a strong dependence on the fragment velocity, with faster products exhibiting larger values of β. This was attributed to excitation of out-of-plane vibrations on the same timescale as dissociation. Excitation is primarily to the 3¹A′ state, via a transition with a transition dipole almost parallel to the N–CO bond. Dissociation occurs either on this state or following population transfer to the 1¹A′′ or 2¹A′ states. All three excited states have non-planar minima. For molecules dissociating rapidly from near-planar geometries with little out-of-plane nuclear motion, most of the available energy is released into product translation, leading to near-limiting values of β in good agreement with the axial recoil approximation. Conversely, molecules in which out-of-plane motions are excited will experience forces during dissociation that lead to rotational and vibrational excitation of the products, reducing their translational energy, and also to deviations from axial recoil, reducing β.

Previous experimental studies on the photoexcitation of DMF have neglected possible excitation to Rydberg states. However, DMF and related molecules exhibit sharp excitation bands corresponding to transitions to these states.^20–23 The relevance of Rydberg and Rydberg/valence surfaces for amides has been discussed in detail elsewhere.^24–26 The experimental studies described above have focused either on multi-photon absorption⁵ or on photolysis at wavelengths below 200 nm,^1,2,7 perhaps because experiments at wavelengths longer than 200 nm are more challenging due to the lower UV absorption cross-section of the molecule.^17,18 In the present study, we report data from a multimass velocity-map imaging study into the photofragmentation dynamics of DMF at excitation wavelengths of 225 nm and 245 nm. This work is complementary to our previous study of the dynamics at 193 nm.⁷

2 Methods

The experimental set-up is similar to that described by Hopkins et al.²⁷ Briefly, helium (BOC, 99.9%) at a pressure of ∼1 bar was bubbled through liquid N,N-dimethylformamide (Sigma-Aldrich, 99.8%) to generate a ∼0.5% mixture of DMF in He. The gas mixture underwent a supersonic expansion through a pulsed solenoid valve (Parker Hannifin, Series 9, 10 Hz), which was collimated by a 1 mm skimmer before passing through the repeller plate of the ion optics assembly into the interaction region of a velocity-map imaging (VMI) time-of-flight (ToF) mass spectrometer. Here the molecular beam was intersected at right angles by the UV photolysis laser beam and VUV probe beam.

The 225 nm or 245 nm photolysis beam used to initiate photolysis was generated using a tuneable, pulsed, frequency-doubled dye laser (Sirah Cobra Stretch), pumped by the third harmonic of a Nd:YAG laser (Continuum Surelite II). The beam was linearly polarised in the imaging plane (perpendicular to the time-of-flight axis). Following a short time delay of 15–18 ns, the neutral photofragments were ionised by the 118.2 nm VUV probe laser beam. The 118 nm radiation was produced by frequency tripling the third harmonic of a Nd:YAG laser (Continuum Surelite I) in a phase-matched mixture²⁸ of 27 mbar Xenon (BOC, 99.9%) and 298 mbar Argon (BOC, 99.9%).^29–31 The probe beam was linearly polarized along the time-of-flight axis (perpendicular to the imaging plane) to ensure that any anisotropy observed in the velocity-map images is caused by the photolysis laser polarization.

The velocity-map imaging ion lens used to map the ionised photofragments onto the detector consists of repeller, extractor, and ground electrodes. The repeller plate has a 4 mm diameter hole in the centre through which the molecular beam is admitted to the interaction region. The extractor and ground electrodes have 24 mm holes in the centre to transmit the expanding product scattering distributions. The ratio of potentials applied to the extractor and repeller plates is tuned to achieve velocity-mapping conditions,^32,33 mapping the three-dimensional scattering distribution of the nascent photofragments via a 56 cm flight tube onto a two-dimensional position sensitive ion detector. The ion detector comprises a pair of chevron-mounted microchannel plates (MCPs) coupled to a P47 phosphor screen. Each incoming ion generates an optical signal on the phosphor, which is captured by a second-generation Pixel Imaging Mass Spectrometry (PImMS2) camera.^34–36 The photofragment scattering distributions are read out from the camera in the form of an (x, y, t) data point for each detected ion. The data sets can be integrated over the (x, y) coordinates to obtain product time-of-flight spectra, or over the relevant arrival time ranges to generate velocity-map images for each photofragment.

Data sets were acquired under pump–probe conditions, and also, for the purposes of background subtraction, under pump-only and probe-only conditions. This allowed any one-laser signals to be subtracted from the overall signal in order to obtain the true pump–probe signal. Each ion signal generally excites multiple pixels and time bins within the PImMS sensor, which is corrected by running the data set through a centroiding algorithm. The velocity-map images are two-dimensional projections of the full three-dimensional scattering distribution for each photoproduct. The scattering distributions are cylindrically symmetrical about the polarisation vector of the photolysis laser, such that an inverse Abel transform can be used to obtain the central slice through each distribution, which contains all of the information required in order to extract product speed and angular distributions. The Abel inversion was performed using the Basex software package.³⁷ From the inverted images we extracted radial and angular distributions, converting the radial distributions into kinetic energy distributions using a calibration determined in previous measurements on the 355 nm photolysis of Cl₂.

3 Results and discussion

3.1 Ultraviolet absorption spectrum of N,N-dimethylformamide

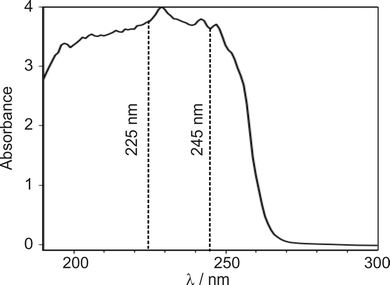
Several authors have reported UV/VIS spectra of DMF.^11,17,18 However, these studies mainly reported results at shorter wavelengths, where the excitation cross-section is larger. A liquid-phase UV absorption spectrum of the DMF used in the present study, recorded over the wavelength range 190–350 nm on a Thermo Fisher Scientific Evolution 220 spectrometer, is shown in Fig. 2.

Fig. 2 UV absorption spectrum of liquid DMF, recorded on a Thermo Fisher Scientific Evolution 220 spectrometer. Dashed vertical lines indicate the photolysis wavelengths of 225 and 245 nm chosen for the velocity-map imaging experiments.

The absorption spectrum exhibits a peak between 220–230 nm with a wide shoulder on the red-edge extending to wavelengths of about 255 nm. We decided to investigate pump wavelengths of 225 nm, which is in the centre of the absorption peak, and 245 nm, marking the end of the shoulder, at which significant absorption is observed, while minimising potential contribution from the 225 nm feature.

3.2 Photolysis of DMF at 225 nm

3.2.1 Fragmentation pathways. The time-of-flight mass spectrum for the products of 225 nm photolysis of DMF is shown in the upper panel of Fig. 3, and reveals the important fragmentation pathways for DMF at 225 nm. The one-laser contributions have been subtracted from the pump–probe signal. While the time-of-flight resolution of our instrument is not sufficient to completely separate all mass-adjacent fragments, we see clear peaks at mass-to-charge (m/z) ratios of 15, 18, 28, 29, 30, 42, and 44, which can be assigned to the ionised photoproducts CH₃⁺, NH₄⁺, CO⁺, HCO⁺, C₂H₆⁺ or HCOH⁺ or HNCH₃⁺, NC₂H₄⁺, and NC₂H₆⁺, respectively. The same products were observed in our previous study of DMF photolysis at 193 nm.⁷ The small negative peaks at m/z 58 and 73 correspond to HCONCH₃⁺ and the parent ion, respectively. These ions are formed efficiently through one-laser dissociative ionisation of neutral DMF by the 118 nm probe laser, and are reduced in intensity in the pump–probe signal due to depletion of neutral DMF via photolysis. The result is a negative signal intensity for these peaks when the probe-only signal is subtracted from the pump–probe signal.

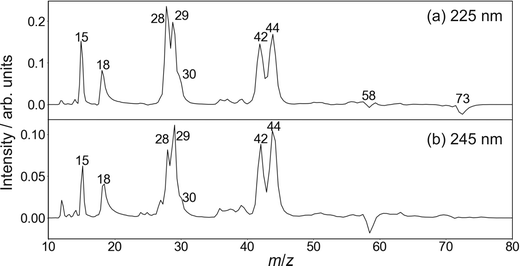Fig. 3 Time-of-flight mass spectra of the photofragments formed following photoexcitation of DMF at 225 nm (upper panel) and 245 nm (lower panel).

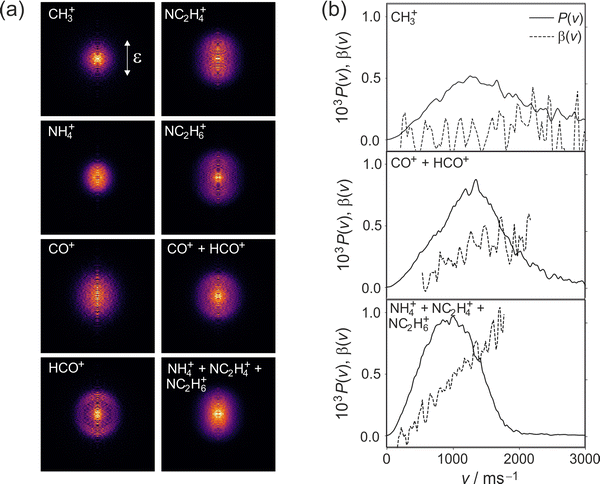
Cleavage of the N–CO amide bond generates HCO and NC₂H₆ products, and we therefore expect to see signal arising from this pathway at m/z = 44 and 29. We do indeed see signal at these two m/z values. However, dissociative ionisation of the nascent fragments in the probe step, as well as neutral predissociation of some of the nascent HCO products,^7,38 has the result that we see signal associated with the NC₂H₆ products at m/z = 44 (NC₂H₆⁺), 43 (NC₂H₅⁺), 42 (NC₂H₄⁺) and 18 (NH₄⁺), and signal associated with the HCO fragment at m/z = 29 (HCO⁺) and 28 (CO⁺). We note that formation of NH₄⁺ has been confirmed in isotope labelling experiments, and involves significant structural rearrangement of nascent internally excited N(CH₃)₂⁺ ions.⁷ Since there is little kinetic energy release during this secondary reaction, the NH₄⁺ products essentially inherit the speed and angular distribution of the N(CH₃)₂⁺ ions from which they are formed, and the images resemble the central region of the images of these parent primary ions. The arrival time distribution for the NH₄⁺ fragment has a significant tail extending to longer flight times, implying that the rearrangement and dissociation occur on a relatively long timescale, with the final products forming both within the interaction region of the experiment and along the flight tube between the interaction region and the detector.

Fission of either N–CH₃ bond in the parent DMF molecule generates the fragments CH₃ and HCONCH₃. Only the former is ionizable using one 118 nm photon,⁷ appearing at m/z = 15 in the mass spectrum. Low intensity signals, presumably associated with H-atom loss either from neutral or ionised CH₃, can be observed at m/z = 12, 13, and 14.

Based on its mass-to-charge ratio, the small signal at m/z = 30, observed as a shoulder on the much larger signals at m/z = 28 and 29, may correspond either to C₂H₆⁺, HCOH⁺, or HNCH₃⁺. While formation of C₂H₆⁺ would require significant molecular rearrangement, the latter two ions can be formed via quite plausible mechanisms. Whatever its identity, this minor fragment is not considered further in the following.

3.2.2 Product speed and angular distributions. Fig. 4(a) shows the symmetrised and Abel-inverted velocity-map images recorded for the ionised DMF photolysis products CH₃⁺, NH₄⁺, CO⁺, HCO⁺, NC₂H₄⁺, and NC₂H₆⁺. As noted above, several of these fragments arise from dissociative ionisation and/or predissociation of the nascent HCO and NC₂H₆ products (the velocity-map images imply, for example, that the more highly internally excited/lower-velocity HCO⁺ ions experience H loss to form CO⁺). As a result of momentum conservation, loss of one or two H atoms from the neutral or ionised products has only a very small effect on the velocity distributions. We have also shown previously⁷ that formation of NH₄⁺ from NC₂H₆⁺ is associated with only very small kinetic energy release. As a result, we can sum the velocity and angular distributions for the m/z = 18, 42, 43, and 44 products and for the m/z = 28 and 29 products in order to obtain very good approximations to the distributions for the nascent products. The resulting speed and angular distributions – expressed in terms of the recoil anisotropy parameter β – for the CH₃, HCO, and NC₂H₆ photofragments are shown in Fig. 4(b). The values of β for each fragment, averaged over the velocity distribution, are shown in Table 1.

Fig. 4 (a) Symmetrized and Abel-inverted velocity-map images for fragments observed following 225 nm photolysis of DMF; (b) speed and angular distributions for each product channel as explained in the text.

Table 1 Recoil anisotropy parameters β averaged over the speed distributions for the photolysis products formed from DMF following irradiation at 225 and 245 nm, respectively. The quoted uncertainties are one standard deviation of the noise on the β(v) distributions, determined from the residual of β(v) and a polynomial fit through the distribution

Species	m/z	β 225nm	β 245nm
CH3^+	15	0.07 ± 0.17	−0.05 ± 0.33
NH4^+ + NC2Hx	18/42/43/44	0.52 ± 0.07	0.30 ± 0.09
CO^+ + HCO^+	28/29	0.20 ± 0.09	0.17 ± 0.13

---

We note that the velocity distributions are all fairly broad, implying population of a wide range of rotational and vibrational states in the recoiling fragments. The β parameter for the CH₃ fragments is close to zero, while the HCO and NC₂H₆ fragments exhibit non-zero β parameters that increase markedly with fragment velocity. These features of the speed and angular distributions will be discussed in more detail below.

Table 2 shows calculated vertical excitation energies to the three lowest lying electronic singlet states and two lowest lying triplet states of DMF, together with oscillator strengths for the associated transitions. Frequency calculations show the zero-point energies for the various states to be very similar, so we have not included these explicitly when considering the excitation energies. Two sets of values are given: the results of density functional theory calculations by Shastri et al.;¹¹ and the results of CASPT2 calculations by Serrano-Andres et al.¹⁹ The recent DFT calculations by Shastri et al. indicate that the 1¹A′′ and 2¹A′′ states are likely to be energetically accessible at 225 nm, with the CASPT2 calculations of Serrano-Andres et al. predicting that the states lie slightly higher in energy. The (n → π*) transition to the first excited 1¹A′′ singlet state has a near-zero oscillator strength, making it unlikely to be populated directly by absorption of a 225 nm photon. In contrast, the (4a′′ → 3s) transition to the second excited 2¹A′′ singlet state has a much higher oscillator strength, implying that this state is most likely to be populated in the absorption step.

Table 2 Theoretical and experimental vertical excitation energies from the electronic ground state to the first three excited singlet states and the first two excited triplet states

Symmetry		Excitation energies/eV		Oscillator strength
		DFT^a	CASPT2^b	DFT^a	CASPT2^b
a Shastri et al.^11 b Serrano-Andres et al.^19
1^1A′	(Ground state)
1^1A′′	(n → π*)	5.59 (222 nm)	5.64 (220 nm)	<0.001	0.001
2^1A′′	(4a′′ → 3s)	5.62 (221 nm)	5.92 (209 nm)	0.021	0.005
2^1A′	(16a′ → π*)	5.99 (207 nm)	6.48 (191 nm)	0.009	0.002
1^3A′	(n(σ) → π*)	4.73 (262 nm)	5.41 (229 nm)	—	—
1^3A′′	(n(π) → π*)	5.08 (244 nm)	5.06 (245 nm)	—	—

---

The measured β parameters provide further insight into the excited states involved in the photodissociation. The transition dipole for the π ← n(σ) excitation to the first excited 1¹A′′ singlet state lies perpendicular to the breaking N–CO bond. This would give rise to a negative value for β, which approaches a value of −1 for a pure perpendicular transition. In contrast, excitation to the second excited 2¹A′′ singlet state involves movement of electron density from the n(π)-orbital located at the nitrogen atom to the Rydberg 3s-orbitals on the CH₃-groups,¹¹ resulting in a parallel transition and a correspondingly positive value of β between 0 and 2. As noted above, the measured values of β for both the HCO and NC₂H₆ products are positive. This is consistent with excitation to the second excited 2¹A′′ singlet state, in agreement with the predictions made above on the basis of the calculated oscillator strengths for the two transitions.

Having established that excitation at 225 nm is most probably to the 2¹A′′ singlet state, we now explore the subsequent processes leading to cleavage of the N–CO and N–CH₃ bonds and production of the observed photofragments.

3.2.2.1 N–CO bond cleavage. To understand the partitioning of the available energy amongst the various accessible translational and internal degrees of freedom, it is helpful to replot the HCO and NC₂H₆ velocity distributions in terms of the total kinetic energy release (TKER). The total available energy is calculated from the 5.510 eV energy of a 225 nm photon and the N–CO bond dissociation energy of 3.89 eV.² For products formed in their electronic ground states, the available energy is 1.62 eV. When the HCO fragment is formed in its first electronically excited state the available energy becomes 0.47 eV.³⁹ The TKER distribution for the HCO + NC₂H₆ products is shown in Fig. 5(a), with the energetic limits corresponding to formation of HCO in its ground and first-excited electronic states marked as dashed lines.

Fig. 5 Total kinetic energy release (TKER) distribution for the (a) N–CO and (b) N–CH₃ bond fission channels following 225 nm photolysis of DMF. The total available energies for the possible product channels are indicated by dashed vertical lines.

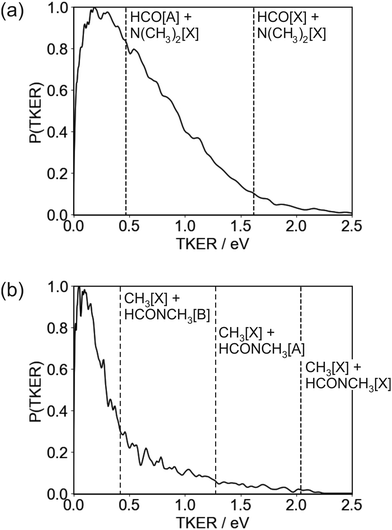
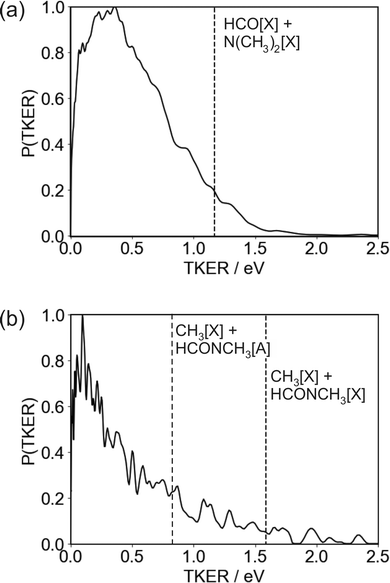
The TKER distribution peaks at low energies, implying that the majority of photofragments are formed with significant amounts of internal energy. The lower energy part of the distribution, below 0.47 eV, is consistent with formation of HCO in either its electronic ground or first excited state, with the excited state not accessible for products with TKER above this value. While product internal excitation is clearly a key feature of the fragmentation dynamics, the long tail extending out to the maximum available energy indicates that for a significant proportion of products the majority of the available energy is released into relative translation of the recoiling fragments. A small proportion of fragments are formed with energies higher than the supposed maximum. A small amount of ‘extra’ energy can often be explained by the presence of a small fraction of vibrationally excited DMF in the molecular beam. However, in this case we believe the high energy tail extends too far above the nominal maximum available energy for this to be the explanation. Trajectory studies by Eckert-Makzic and coworkers⁹ indicate that following excitation to low-lying excited singlet states, a significant fraction of trajectories become trapped in minima on these states. We therefore postulate that in our experiment a small number of these ‘trapped’ excited-state molecules survive long enough to undergo dissociative ionisation by the probe laser, and that this is the source of the high energy tail on the TKER distribution for the N–CO bond cleavage channel. While ‘probe-only’ dissociative ionisation is removed from our signal during the background-subtraction process, this second dissociative ionisation signal requires both pump and probe lasers, so is not removed when the one-laser signals are subtracted.

The high amount of internal excitation in the majority of products is explained by the topography of the excited state potential energy surface(s) over which the system evolves during dissociation. The 2¹A′′ surface to which DMF is initially excited correlates to NC₂H₆(X̃) + HCO(Ã) products, and exhibits a significant energy barrier of around 0.81 eV (see Fig. 1) along the N–CO bond stretching coordinate,¹¹ with the energy maximum corresponding to a bond length of ∼1.8 Å. In contrast to the planar structure of ground-state DMF, the energy minimum of the 2¹A′′ surface is non-planar. The dissociating molecules are therefore likely to follow a variety of trajectories across the potential energy surface. Some of these trajectories will surmount the barrier with little out-of-plane motion, in which case there will be few torsional forces acting and correspondingly little internal excitation of the products, with the majority of the energy being released into product translation. For these products the lack of out-of-plane motion also maintains the spatial relationship between the polarisation vector of the excitation light and the axis of the dissociating bond (i.e. the axial recoil approximation holds), yielding relatively large positive values for the recoil anisotropy parameter β. Other trajectories will explore out-of-plane geometries that ‘skirt around’ the barrier. The torsional forces acting during dissociation in these cases lead to rotational and/or vibrational excitation of the photofragments, and therefore a correspondingly smaller amount of energy released into translation. The out-of-plane motion also leads to breakdown of the axial recoil approximation and a corresponding reduction in β. The correlation between product internal excitation and breakdown of the axial recoil approximation explains the observed increase in β with increasing photofragment velocity. Similar behaviour has been seen previously in the dissociation of DMF on the higher-lying 3¹A′ singlet surface following photoexcitation at 193 nm.⁷

As noted above, the TKER distribution for the HCO + NC₂H₆ products is not consistent with dissociation only on the 2¹A′′ surface, since many of the HCO products must be formed in their electronic ground state in order to account for the products formed with TKER greater than 0.47 eV. Coupling between the 2¹A′′ and 1¹A′′ surfaces can lead to transfer of population to the lower excited singlet surface, which correlates to ground state products. The topographies of the two singlet surfaces are qualitatively similar, with a barrier along the N–CO stretching coordinate and a non-planar minimum-energy geometry, so we see a similar increase in β with increasing product velocity and decreasing product internal excitation. Population transfer from the 1¹A′′ first excited singlet state to the 1¹A′ ground state is also possible via a conical intersection at highly non-planar geometries, as is intersystem crossing to the 1³A′ first excited triplet state.⁸ In common with the second excited singlet state, the former of these pathways correlates to formation of ground state NC₂H₆ and electronically excited HCO, while the T₁ state correlates to ground state products.

3.2.2.2 N–CH₃ bond cleavage. Cleavage of one of the N–CH₃ bonds leads to the formation of CH₃ and HCONCH₃ products, of which only the former can be ionised by our 118 nm probe laser. We therefore see a significant signal in the time-of-flight spectrum (see Fig. 3) at m/z = 15, corresponding to the CH₃ fragment, but no signal at m/z = 58 corresponding to the HCONCH₃ co-fragment. In contrast to the velocity-map images observed for the N–CO bond cleavage channel, the velocity-map image for the CH₃ fragment reveals a relatively isotropic angular distribution. As explained previously by Lipciuc et al.,⁷ the isotropic scattering distribution is simply a result of the molecular geometry. Excitation via a transition to the 2¹A′′ state, which has a transition dipole moment parallel to the N–CO bond, yields an ensemble of excited-state molecules with a cos² θ distribution of the N–CO axis about the polarisation vector of the photolysis laser. In the case of the 193 nm photolysis studied by Lipciuc et al., the excitation was via a parallel transition to the 3¹A′ state rather than the 2¹A′′ state, but the same arguments apply. Ejection of CH₃ at an angle of approximately 60 degrees to the N–CO axis, as determined by the molecular geometry, combined with this cos² θ distribution of molecular orientations, yields an almost isotropic distribution of CH₃ velocity vectors relative to the photolysis polarisation axis, as observed.

The TKER distribution for the N–CH₃ bond cleavage products is sharply peaked at low kinetic energy, indicating that the majority of the available energy is released into internal excitation. Following excitation to the 2¹A′′ state there are various possible pathways by which the molecule can evolve to the separated CH₃ + NCOCH₃ products. At 193 nm, the dissociation is thought to proceed via excitation to the 3¹A′ state and subsequent coupling to and dissociation on the 2¹A′ state. Couplings involving the 2¹A′′ state which is initially excited at 225 nm have not been comprehensively studied, but it is clear that several potential dissociation pathways are possible, involving either direct dissociation over a small barrier on the 2¹A′′ state to form electronically excited products, or coupling to a lower-lying state. Three product channels are energetically accessible at an excitation wavelength of 225 nm, corresponding to ground-state CH₃ partnered by HCONCH₃ in its electronic ground, first, or second excited state, respectively. None of these are ruled out by the form of the TKER distribution, though the sharp peak at low kinetic energies below the energy cutoff for production of CH₃[X̃] + HCONCH₃[B̃] does perhaps suggest a significant contribution from this product channel. If this is the case then it is certainly not the only product channel, as the TKER distribution extends out to the energy thresholds of both of the lower energy channels. Given the geometry of the DMF molecule (see inset to Fig. 1, it is also very likely that a considerable amount of the internal excitation is in rotational and vibrational modes of the products). Assuming the N_CH₃ bond cleavage is reasonably rapid, which it must be to compete with the N–CO bond dissociation pathway, the force exerted away from the centre of mass of the HCONCH₃ fragment is likely to result in considerable rotational excitation of this fragment. Significant excitation of the umbrella vibrational mode in CH₃ as well as other vibrational modes in both fragments is also highly likely.

3.3 Photolysis of DMF at 245 nm

3.3.1 Fragmentation pathways. The lower panel of Fig. 3 shows the background-subtracted ToF spectrum for the ionised products of DMF photolysis at 245 nm. As for the 225 nm data, the one-laser signals have been subtracted from the pump–probe signal. Qualitatively, we observe the same products arising from N–CO and N–CH₃ bond cleavage as we saw following 225 nm photolysis, including the various products of dissociative ionisation of the nascent neutral products. One notable observation is that on moving from 225 nm to 245 nm photolysis, the relative intensities of the m/z = 28 (CO⁺) and 29 (HCO⁺) peaks are reversed. This perhaps implies that HCO is formed with lower internal energy at the longer photolysis wavelength, leading to a smaller degree of predissociation and/or dissociation following ionisation by the 118 nm probe laser.

3.3.2 Product speed and angular distributions. Fig. 6(a) shows the symmetrised and Abel-inverted velocity-map images recorded for the ionised DMF photolysis products CH₃⁺, NH₄⁺, CO⁺, HCO⁺, NC₂H₄⁺, and NC₂H₆⁺. As before, we have summed the velocity and angular distributions for the m/z = 18, 42, 43, and 44 products and for the m/z = 28 and 29 products in order to obtain good approximations to the distributions for the nascent products, shown in Fig. 6(b). The values of β averaged over the velocity distribution for each fragment are shown in Table 1.

Fig. 6 (a) Symmetrized and Abel-inverted velocity-map images for fragments observed following 245 nm photolysis of DMF; (b) speed and angular distributions for each product channel as explained in the text.

3.3.2.1 N–CO bond cleavage channel. Qualitatively, the velocity-map images recorded at 245 nm for the N–CO bond cleavage products are similar to those observed at 225 nm, though the scattering distributions are somewhat less anisotropic at the longer wavelength, as reflected in the lower values of β. We see the same increase in β with photofragment velocity as previously, but the limiting values at high photofragment velocities are significantly reduced.

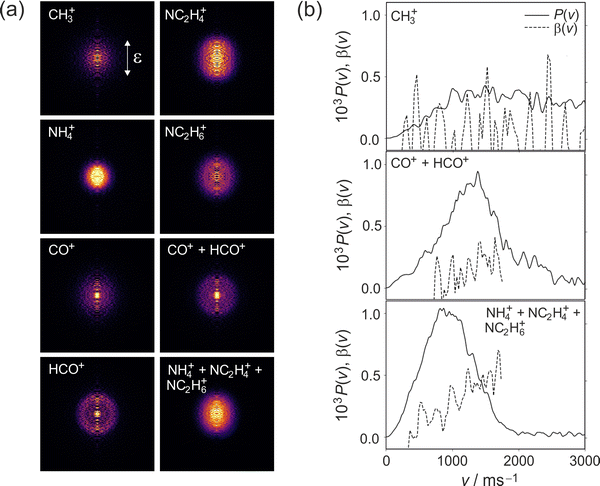
Referring to the excitation energies in Table 2 we see that for ground-state molecules at their equilibrium geometry all of the singlet states lie significantly higher in energy than the 5.06 eV energy of a 245 nm photon. However, the strong similarities between the scattering distributions observed at 225 and 245 nm, coupled with the very similar absorption intensities at the two wavelengths, lead us to believe that excitation is to the S₂ state in both cases. The apparent energy shortfall is explained by the fact that the 2.749 eV zero-point energy of ground-state DMF (calculated at UB3LYP/6-311++g(d,p) level) means that the vibrational ground state of the molecule spans a significant range of molecular geometries. Distortion of the molecular geometry towards the equilibrium geometry of the S₂ state, which involves significant out of plane motion of the molecular backbone, reduces the excitation energy to the S₂ state considerably.⁹ Based on the smaller β parameters observed at the longer wavelength, the geometrical distortion results in a rotation of the S₀ → S₂ transition dipole away from the C–N bond axis. As noted above, though the maximum β parameters are roughly halved at 245 nm compared with photolysis at 225 nm, we see a similar increase in β with photofragment velocity. As before, we believe this arises as a result of dissociation from a range of molecular geometries. Dissociation from more planar geometries yields higher photofragment velocities and larger values of β, and dissociation from significantly non-planar geometries results in a higher degree of internal excitation and therefore lower photofragment velocities and β parameters.

It is also possible that excitation to the S₁ state plays a small role at molecular geometries away from the equilibrium structure. This state also becomes energetically accessible at such geometries, and the S₀ → S₁ transition dipole lies perpendicular to the amide bond even at the equilibrium molecular geometry, which would result in a reduction in the observed value of β. However, the oscillator strength for the transition to S₁ is at least an order of magnitude lower than that for excitation to the S₂ state, so any involvement of this state is unlikely to account for the observed two-fold reduction in β. Shastri et al.¹¹ suggested based on the calculated vertical excitation energies that the two low-lying triplet states may also make a contribution to the absorption band under study. The excitations to the T₁ and T₂ states are respectively perpendicular and parallel in character relative to the amide bond, but on the basis of oscillator strength arguments any such contributions are likely to be minor. As noted previously for dissociation at 245 nm, involvement of the S₁, T₁, and S₀ states in the exit channel, accessed via internal conversion or intersystem crossing, is certainly likely and has been proposed previously.⁸

The TKER distribution for the HCO + NC₂H₆ products is shown in Fig. 7(a). The calculated maximum kinetic energy is shown as a vertical dashed line on the plot. The TKER distribution measured at 245 nm is very similar to that observed following photolysis at 225 nm, peaking at low kinetic energies but with a long tail extending out beyond the nominal maximum available energy. As for the 225 nm data, we believe the high-energy tail to be caused by dissociative ionisation of a small number of molecules that become trapped within minima on the low-lying singlet surfaces. As already noted, dissociation occurs from a range of molecular geometries, with dissociation from planar geometries yielding little internal excitation and relatively fast products, and dissociation from non-planar geometries leading to a higher degree of photofragment internal excitation and correspondingly lower photofragment velocities.

Fig. 7 Total kinetic energy release (TKER) distribution for the (a) N–CO and (b) N–CH₃ bond fission channels following 245 nm photolysis of DMF. The total available energies for the possible product channels are indicated by dashed vertical lines.

3.3.2.2 N–CH₃ bond cleavage channel. As was the case at 225 nm, the CH₃ velocity-map image recorded at a photolysis wavelength of 245 nm (see Fig. 6(a)) reveals an isotropic angular distribution and relatively slow products. The TKER distribution for this channel is shown in Fig. 7(b). At the longer wavelength only two product channels are energetically accessible, corresponding to ground-state CH₃ partnered by HCONCH₃ in either its ground or first-excited electronic state. Based on the TKER distribution we are unable to rule out either of these pathways. The signal-to-noise ratio for the CH₃ products is fairly low following 245 nm photolysis, and this somewhat limits what we can say about this pathway. However, while different states are almost certainly involved in the dissociation, we believe the general picture and the explanations for the isotropic angular distribution and low-peaking kinetic energy distribution are similar to those outlined previously for dissociation at 225 nm.

4 Conclusions

We have reported the results of a comprehensive experimental study on the photofragmentation dynamics of N,N-dimethylformamide following excitation at 225 nm and 245 nm, respectively. To our knowledge, this is the first study into the dissociation dynamics of DMF in this wavelength region. At both excitation wavelengths, we observe products corresponding to cleavage of both the N–CO amide bond and one of the N–CH₃ bonds, as well as products arising from secondary fragmentation or dissociative ionisation of the primary products.

The velocity-map images allow us to determine speed and angular distributions for each fragment, as well as total kinetic energy releases associated with each fragmentation channel. We have interpreted these data in light of complementary theoretical studies by Shastri et al.¹¹ and Serrano-Andres et al.,¹⁹ and by comparison with results from a previous study performed in our own group into the photolysis of DMF at 193 nm,⁷ in order to determine the electronic states involved in the photofragmentation at each wavelength. We conclude that excitation at both 225 nm and 245 nm is predominantly to the S₂ 2¹A′′ state via a parallel transition, with dissociation along the N–CO bond occurring either on this state or on a lower singlet surface following internal conversion. At the shorter wavelength, the S₂ state is energetically accessible via a vertical transition from the equilibrium geometry of the molecule, while geometrical distortion of the molecular structure is required in order to access this state at the longer wavelength. Dissociation occurs either on the S₂ surface or following population transfer to S₁. Both singlet surfaces, as well as the low lying T₁ and T₂ triplet surfaces, share similar topographical features, exhibiting a barrier along the N–CO stretching coordinate, and possessing non-planar minimum-energy geometries. As a result, dissociation occurs from a variety of molecular geometries. Dissociation from planar geometries leads to little product internal excitation and correspondingly high photofragment velocities, with near-limiting values of the recoil-anisotropy parameter β. In contrast, dissociation from non-planar geometries leads to significant product internal excitation, with correspondingly lower photofragment velocities and breakdown of the axial recoil approximation to give reduced values of β.

Less detailed information is available on the potential energy curves along the N–CH₃ bond coordinate than for the N–CO coordinate. However, at both wavelengths we see an isotropic angular distribution for the CH₃ product, and a TKER distribution peaking at low kinetic energies, indicating significant internal excitation in the fragments. This is similar to the behaviour observed previously at 193 nm,⁷ and can be rationalised in terms of the geometry of the molecule and the orientation of the breaking bond relative to the transition dipole for the initial excitation.

Having now established the photochemical pathways involved in the cleavage of the model peptide bond in DMF at a number of different photolysis wavelengths, future work is likely to focus on investigating the effects of the various different amino acid side chains in the photofragmentation of a series of simple di- and tri-peptides.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank the EPSRC for funding through Programme Grants EP/L005913/1, EP/T021675/1, and EP/V026690/1.

References

1. N. R. Forde, T. L. Myers and L. J. Butler, Faraday Discuss., 1997, 108, 221–242.
2. N. R. Forde and L. J. Butler, J. Chem. Phys., 1999, 110, 8954–8968.
3. S. Shin, A. Kurawaki, Y. Hamada, K. Shinya, K. Ohno, A. Tohara and M. Sato, J. Mol. Struct., 2006, 791, 30–40.
4. M. Ruzi and D. T. Anderson, J. Chem. Phys., 2012, 137, 194313.
5. X. Qiu, Z. Ding, Y. Xu, Y. Wang and B. Zhang, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 033405.
6. P. Salén, V. Yatsyna, L. Schio, R. Feifel, R. Richter, M. Alagia, S. Stranges and V. Zhaunerchyk, J. Chem. Phys., 2016, 144, 244310.
7. M. L. Lipciuc, S. H. Gardiner, T. N. Karsili, J. W. Lee, D. Heathcote, M. N. Ashfold and C. Vallance, J. Chem. Phys., 2017, 147, 013941.
8. D. Liu, W. Fang, Z. Lin and X. Fu, J. Chem. Phys., 2002, 117, 9241–9247.
9. M. Eckert-Maksić and I. Antol, J. Phys. Chem. A, 2009, 113, 12582–12590.
10. M. Eckert-Maksić, M. Vazdar, M. Ruckenbauer, M. Barbatti, T. Müller and H. Lischka, Phys. Chem. Chem. Phys., 2010, 12, 12719–12726.
11. A. Shastri, A. K. Das, S. Krishnakumar, P. J. Singh and B. N. Raja Sekhar, J. Chem. Phys., 2017, 147, 224305.
12. M. B. Shundalau, P. S. Chybirai, A. I. Komyak, A. P. Zazhogin, M. A. Ksenofontov and D. S. Umreiko, J. Appl. Spectrosc., 2011, 78, 326–336.
13. X. Zhou, J. A. Krauser, D. R. Tate, A. S. VanBuren, J. A. Clark, P. R. Moody and R. Liu, J. Chem. Phys., 1996, 100, 16822–16827.
14. T. C. Jao, I. Scott and D. Steele, J. Mol. Spectrosc., 1982, 92, 1–17.
15. V. Renugopalakrishnan, G. Madrid, G. Cuevas and A. T. Hagler, Proc. - Indian Acad. Sci., Chem. Sci., 2000, 112, 35–42.
16. R. Saladino, C. Crestini, G. Costanzo, R. Negri and E. Di Mauro, Bioorg. Med. Chem., 2001, 9, 1249–1253.
17. H. D. Hunt and W. T. Simpson, J. Am. Chem. Soc., 1953, 75, 4540–4543.
18. K. Kaya and S. Nagakura, Theor. Chim. Acta, 1967, 7, 117–123.
19. L. Serrano-Andrés and M. P. Fülscher, J. Am. Chem. Soc., 1996, 118, 12190–12199.
20. H. Basch, M. B. Robin and N. A. Kuebler, J. Chem. Phys., 1968, 49, 5007–5018.
21. J. M. Gingell, N. J. Mason, H. Zhao, I. C. Walker and M. R. Siggel, Chem. Phys., 1997, 220, 191–205.
22. D. H. Ter Steege, C. Lagrost, W. J. Buma, D. A. Leigh and F. Zerbetto, J. Chem. Phys., 2002, 117, 8270–8280.
23. M. A. Larsen, T. I. Sølling, R. Forbes, A. E. Boguslavskiy, V. Makhija, K. Veyrinas, R. Lausten, A. Stolow, M. M. Zawadzki, L. Saalbach, N. Kotsina, M. J. Paterson and D. Townsend, J. Chem. Phys., 2019, 150, 054301.
24. M. N. Ashfold, G. A. King, D. Murdock, M. G. Nix, T. A. Oliver and A. G. Sage, Phys. Chem. Chem. Phys., 2010, 12, 1218–1238.
25. G. M. Roberts and V. G. Stavros, Chem. Sci., 2014, 5, 1698–1722.
26. M. J. Paterson and D. Townsend, Int. Rev. Phys. Chem., 2020, 39, 517–567.
27. W. S. Hopkins, M. L. Lipciuc, S. H. Gardiner and C. Vallance, J. Chem. Phys., 2011, 135, 034308.
28. J. M. Gray, J. Bossert, Y. Shyur, B. Saarel, T. C. Briles and H. J. Lewandowski, J. Chem. Phys., 2021, 154, 024201.
29. A. H. Kung, J. F. Young and S. E. Harris, Appl. Phys. Lett., 1973, 22, 301–302.
30. A. H. Kung, J. F. Young and S. E. Harris, Appl. Phys. Lett., 1976, 28, 294.
31. N. P. Lockyer and J. C. Vickerman, Laser Chem., 1997, 17, 139–159.
32. D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447.
33. A. T. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484.
34. A. Nomerotski, M. Brouard, E. Campbell, A. Clark, J. Crooks, J. Fopma, J. J. John, A. J. Johnsen, C. Slater, R. Turchetta, C. Vallance, E. Wilman and W. H. Yuen, J. Instrum., 2010, 5, C07007.
35. E. S. Wilman, S. H. Gardiner, A. Nomerotski, R. Turchetta, M. Brouard and C. Vallance, Rev. Sci. Instrum., 2012, 83, 013304.
36. A. T. Clark, J. P. Crooks, I. Sedgwick, R. Turchetta, J. W. Lee, J. J. John, E. S. Wilman, L. Hill, E. Halford, C. S. Slater, B. Winter, W. H. Yuen, S. H. Gardiner, M. L. Lipciuc, M. Brouard, A. Nomerotski and C. Vallance, J. Phys. Chem. A, 2012, 116, 10897–10903.
37. V. Dribinski, A. Ossadtchi, V. A. Mandelshtam and H. Reisler, Rev. Sci. Instrum., 2002, 73, 2634–2642.
38. N. R. Forde, L. J. Butler, B. Ruscic, O. Sorkhabi, F. Qi and A. Suits, J. Chem. Phys., 2000, 113, 3088–3097.
39. M. E. Jacox, NIST Chemistry Webbook, NIST Standard Reference Database No. 69, National Institute of Standards and Technology, Gaithersburg, MD, 2022.

---