Vibrationally resolved absorption spectra and ultrafast exciton dynamics in α-phase and β-phase zinc phthalocyanine aggregates†
Shishi
Feng
,
Yu-Chen
Wang
,
WanZhen
Liang
 and
Yi
Zhao
and
Yi
Zhao
 *
*
State Key Laboratory of Physical Chemistry of Solid Surfaces, iChEM, Fujian Provincial Key Laboratory of Theoretical and Computational Chemistry, and College of Chemistry and Chemical Engineering, Xiamen University, Xiamen, 361005, People's Republic of China. E-mail: yizhao@xmu.edu.cn
First published on 3rd January 2022
Abstract
The vibrationally resolved absorption spectra and ultrafast exciton dynamics in α-phase and β-phase zinc phthalocyanine (ZnPc) aggregates are theoretically investigated using a non-Markovian stochastic Schrödinger equation combined with first-principles calculations. It is found that although similar double-peak structures arise in the Q-band region of the absorption spectra in both phases, these peaks are different in nature and exhibit distinct types of behavior with respect to the aggregation length. The analysis on the basis of an effective two-state model indicates that the two absorption peaks in the α phase are from mixing between the charge-transfer (CT) state and the bright Frenkel exciton (FE) state. By contrast, in the β-phase, the low-energy peak is solely contributed by a low-lying bright FE state, whereas the high-energy peak originates from the interplay between the CT state and another high-lying bright FE state. For the relaxation processes right after photoexcitation from the Q-band region, it is found that within the first dozens of femtoseconds the ZnPc aggregates of both phases tend to temporarily fall into some intermediate states where the population distribution and average electronic energy do not obviously evolve. In addition, it is found that the optical transition of the low-lying bright FE state in the β phase is not favorable for the formation of bound CT states due to the absence of enough driving forces.
1 Introduction
Owing to its characteristics of good thermal stability, easily adjustable electronic properties, long exciton lifetime, and high absorbance in the visible and near-infrared regions, zinc phthalocyanine (ZnPc) has been widely applied in organic photovoltaics as a donor material.1–11 The ultimate performance of the devices is closely associated with the microscopic structure features of the materials such as molecular orientation and stacking arrangements.In ZnPc thin films, the microscopic structures are sensitive to the preparation conditions, e.g., the deposition or annealing temperatures,12–15 pressures,16 substrates,15,17 and film thickness.15,18,19 So far, several polymorphs of ZnPc have been found in the thin films,15,18,19 among which the two most common phases are the α and β phases, which are generally distinguished via their X-ray diffraction patterns.20 It is known that the kinetically favorable α-phase ZnPc is metastable and can transform to the β phase via vapor21 or thermal treatments.7,13,22,23
Both α-phase and β-phase ZnPc have significant differences in their optical properties.8,12,14,24–27 For instance, it has been shown that during the α-to-β phase-transition process, the absorbance of the thin film from the ultraviolet to the near-infrared regions can be enlarged by 1.5 to 2 times, which has been attributed to the increment in the angle between the molecular plane and the incident direction of the light.27 In addition, both phases exhibit two absorption peaks in the Q-band region, but along with the phase transition, it is remarkable that the relative intensities of the two peaks are reversed. For α-phase ZnPc, the intensity of the high-energy peak is larger than the low-energy peak, whereas the opposite situation occurs for the β phase.7,17,25,28–31 Furthermore, evidence from time-resolved photoluminescence spectra has indicated that the ultrafast exciton dynamics that occur right after photo-excitation in the two phases can also exhibit significant differences.27 Since the optical properties are crucial for the performance of the optoelectronic devices, it is necessary to establish unambiguous structure–spectra and structure–dynamics relationships for α-phase and β-phase ZnPc, so as to provide possible guidelines for fabrication conditions or material design routes.
Nevertheless, the intricate microstructures in the thin films have severely hindered our understanding of the above two relationships. For the origin of the two absorption peaks in the Q-band region, various conjectures, such as a mixture of monomers and multimers,29,32,33 or a mixture of J- and H-aggregates,7,28,30 have been proposed in the literature for a long time, although none of them has been supported by convincing evidence. Besides, the difference between the relative peak intensities of α-phase and β-phase ZnPc is yet to be explained. Recently, by adopting a comprehensive model Hamiltonian for the α-phase ZnPc aggregates and performing explicit quantum dynamics calculations,34,35 we have clearly demonstrated that the two peaks in the Q-band region originate from mixing between the bright Frenkel exciton (FE) state and the charge-transfer (CT) state, and the relative peak intensities are closely associated with the intermolecular distances, aggregation lengths and remote excitation energy transfer. However, it is unclear whether or not the same methodology also applies to the β phase and can explain the reversed relative intensity phenomenon during the α-to-β phase transition. As for the exciton dynamics, elaborate and systematic experimental studies on the photoinduced ultrafast dynamical processes that occur in ZnPc thin films have rarely been reported.27 Previously, we theoretically investigated the exciton decoherence process34 and examined the possibility of the direct photogeneration of free carriers in α-phase ZnPc aggregates.35 It is of interest to study further the differences between the exciton dynamics in the α and β phases.
In this work, we combine the non-Markovian stochastic Schrödinger equation (NMSSE)36–39 and first-principles calculations to theoretically investigate the vibrationally resolved absorption spectra and ultrafast exciton dynamics after photo-excitation in the α-phase and β-phase ZnPc aggregates. By adopting a comprehensive model Hamiltonian that involves various kinds of electronic states, electronic couplings and electron–phonon interactions, we investigate in detail the origin of the differences between the spectral characteristics of α-phase and β-phase ZnPc, and thoroughly compare the ultrafast photoinduced exciton dynamics in the two phases. This paper is arranged as follows: Section 2 describes the theoretical methods and the details of the calculations, Section 3 presents the results and discussion, and Section 4 provides the conclusions.
2 Method
2.1 Model Hamiltonian
Following our previous work,34,35 for the (α- or β-phase) ZnPc aggregate that consists of N monomers, the total Hamiltonian Ĥagg is given by| Ĥagg = Ĥel + Ĥph + Ĥel–ph, | (1) |
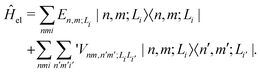 | (2) |
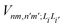 is the electronic coupling between |n, m; Li〉 and |n′,m′; Li′〉, and it satisfies
is the electronic coupling between |n, m; Li〉 and |n′,m′; Li′〉, and it satisfies 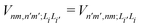 . The superscript prime beside the summation notation in the second row in eqn (2), Σ′, indicates that at least one of the conditions i′ ≠ i, n′ ≠ n, and m′ ≠ m should be met. With the above notation convention, a locally excited (LE) state with the nth monomer being excited is represented by |n, n; Li〉, whereas a bound CT state with the nth monomer being in the cationic state is denoted as |n, n ± 1; Li〉. In this paper, the states with |n − m| ≥ 2 are regarded being as charge-separated (CS) states. It is worth mentioning that the LE part of the electronic Hamiltonian is usually recognized as the Frenkel exciton Hamiltonian in the literatures,40 and the corresponding eigenstates are referred to as the (delocalized) FE states.
. The superscript prime beside the summation notation in the second row in eqn (2), Σ′, indicates that at least one of the conditions i′ ≠ i, n′ ≠ n, and m′ ≠ m should be met. With the above notation convention, a locally excited (LE) state with the nth monomer being excited is represented by |n, n; Li〉, whereas a bound CT state with the nth monomer being in the cationic state is denoted as |n, n ± 1; Li〉. In this paper, the states with |n − m| ≥ 2 are regarded being as charge-separated (CS) states. It is worth mentioning that the LE part of the electronic Hamiltonian is usually recognized as the Frenkel exciton Hamiltonian in the literatures,40 and the corresponding eigenstates are referred to as the (delocalized) FE states.
The vibrational Hamiltonian can be written as
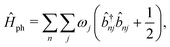 | (3) |
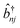 and
and ![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) nj are the creation and annihilation operator of the jth normal mode in the nth monomer, respectively, with the corresponding frequency ωj. The electron–phonon interaction is given by
nj are the creation and annihilation operator of the jth normal mode in the nth monomer, respectively, with the corresponding frequency ωj. The electron–phonon interaction is given by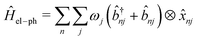 | (4) |
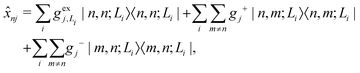 | (5) |
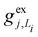 gj+, and gj− are the electron–phonon interaction parameters with respect to the excited state, cationic state and anionic state of the monomer, respectively. Here, we have assumed that the CT or CS states with the same charge distribution share the same set of electron–phonon interaction constants, i.e., gj+ and gj− are irrelevant to the index Li.
gj+, and gj− are the electron–phonon interaction parameters with respect to the excited state, cationic state and anionic state of the monomer, respectively. Here, we have assumed that the CT or CS states with the same charge distribution share the same set of electron–phonon interaction constants, i.e., gj+ and gj− are irrelevant to the index Li.
Finally, the transition dipole moment operator of the aggregate is written as
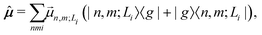 | (6) |
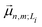 is the transition dipole moment vector between |g〉 and |n, m; Li〉. All the undetermined parameters in eqn (2)–(6) are obtained from first-principles calculations, as detailed in Section 2.3.
is the transition dipole moment vector between |g〉 and |n, m; Li〉. All the undetermined parameters in eqn (2)–(6) are obtained from first-principles calculations, as detailed in Section 2.3.
2.2 Exciton dynamics and vibrationally resolved absorption spectra
The exciton dynamics and the vibrationally resolved absorption spectra in the α-phase and β-phase ZnPc aggregates are simulated via the NMSSE developed by our group,36,37 which can explicitly deal with various kinds of electronic couplings and electron–phonon interactions with relatively low numerical costs and satisfactory accuracy. The central equation of motion of the NMSSE is written as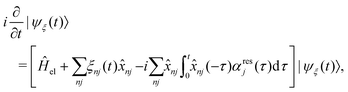 | (7) |
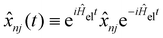 , and the residual correlation function is given by
, and the residual correlation function is given by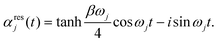 | (8) |
The exciton dynamics with preassigned initial conditions can be simulated directly using eqn (7). As for the vibrationally resolved absorption spectra, we start from the line shape function defined as
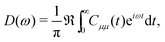 | (9) |
 represents taking the real part, and the correlation function in eqn (9) is expressed as
represents taking the real part, and the correlation function in eqn (9) is expressed as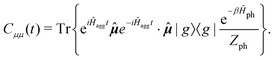 | (10) |
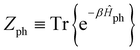 is the phonon partition function, where Tr represents taking the trace over all phonon degrees of freedom. Within the NMSSE framework, the correlation function is given by
is the phonon partition function, where Tr represents taking the trace over all phonon degrees of freedom. Within the NMSSE framework, the correlation function is given byCμμ(t) = M[〈g|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |ψξ(t)〉]ξ, |ψξ(t)〉]ξ, | (11) |
|ψξ(0)〉 = ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |g〉. |g〉. | (12) |
All vibrational modes of the aggregates are included in the simulations of the exciton dynamics and vibrationally resolved absorption spectra so as to give a comprehensive description of the vibrational effects. For a more detailed implementation of the NMSSE, the readers can refer to ref. 34 and 35.
2.3 Computational details
The experimental crystal structure of β-phase ZnPc17,41 is adopted for investigation. As for the α phase, since the crystal structure is currently unavailable in the literature, we use the structure of α-phase CuPc42 as the initial geometry and then replace the Cu atom with a Zn atom while fixing the positions of the other atoms. To guarantee the self-consistency of the results, all the electronic structure calculations for the two phases are kept at the same level with the same set of computational parameters. The crystal structures of the two phases are further optimized at constant lattice parameters using density functional theory (DFT) and the Perdew–Burke–Ernzerhof (PBE) functional43 in the Vienna ab initio simulation package.44 The projected augmented wave (PAW) pseudopotential is used, the kinetic energy cutoff is set as 600 eV, and a Γ-centered 2 × 6 × 2 k-point mesh is used. The width of the smearing is set as 0.01 eV. The energy and force convergent criteria are 10−5 eV and 0.001 eV Å−1, respectively.As can be seen in eqn (1)–(6), the parameters required in the spectral and dynamic simulations of the ZnPc aggregates include the excitation energies and transition dipole moments of the quasi-diabatic states, the electronic couplings between these states, the vibrational frequencies of the ZnPc monomer, and the electron–phonon interaction parameters. Here, the parameterization of the electronic Hamiltonian is based on the ZnPc tetramer model. Concretely speaking, at the first step, the ZnPc tetramers are extracted from the optimized crystal structures, and their adiabatic excited-state calculations are performed using the quantum chemistry package Q-Chem 5.145 with the configuration interaction singles (CIS) method with the mixed basis set, where the metal zinc is treated with pseudopotentials LANL2DZ and the other elements are treated with 6-31G(d). The solvent model of density with the dielectric constant of 5.0 is used to simulate the surrounding crystal environment for both ground- and excited-state calculations. In our previous studies,34,35 we have justified that the CIS method can correctly describe both the excited-state energies and transition densities of the ZnPc dimer, and thereby is also suitable for the tetramers. Then, we apply the recently developed fragment particle–hole densities (FPHD) diabatization scheme46 to the adiabatic results to obtain all of the quasi-diabatic states (LE, CT, and CS states) as well as the corresponding state energies, electronic couplings, and transition dipole moments. In the diabatization procedure, the first 98 adiabatic excited states are included for the diabatization. This produces 98 quasi-diabatic states characterized by different charge and excitation distributions, but only the lowest- and second lowest-lying states are retained for each distribution. After the diabatization procedure, the electronic Hamiltonian parameters of the tetramer are extended to obtain the parameters of an aggregate, the details of which are given in the ESI.†
The vibrational frequencies and electron–phonon interaction parameters are obtained based on the ground-state and excited-state calculations of the ZnPc monomer either in the solvent or embedded in the crystal environment. For the solvent case, the solvent model of density with a dielectric constant of 4.7 is used. As for the crystal environment, the stereo effect is taken into account by using the quantum mechanics/molecular mechanics (QM/MM) method implemented with GAUSSIAN16.47 It is known that the excitation energies of the ZnPc monomer have a strong functional dependence.48 Here, the long-range corrected hybrid functional ωB97XD is used for the QM part since this functional has been proved to give accurate descriptions for the vibrational frequencies and excited-state energy gradient of the ZnPc monomer in the gas phase.34,49 A mixed basis set treating the zinc with pseudopotentials LANL2DZ and the other elements with 6-31G(d) is adopted. The MM part is treated using the universal force field (UFF). The QM/MM boxes of the α and β phases contain 36 and 25 molecules, respectively. The anharmonicity effect is considered by scaling the frequencies using the factor of 0.989. Under the approximation that all electronic states being considered share the same set of normal modes with the only difference being in equilibrium geometries, the electron–phonon interaction parameters associated with different electronic states can be calculated according to
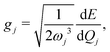 | (13) |
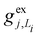 , gj+, and gj− in eqn (5) are obtained by calculating the energy gradients of the Li-th neutral singlet excited state, the cationic state, and the anionic state, respectively, along the direction of Qj. The concrete values of the calculated
, gj+, and gj− in eqn (5) are obtained by calculating the energy gradients of the Li-th neutral singlet excited state, the cationic state, and the anionic state, respectively, along the direction of Qj. The concrete values of the calculated 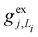 , gj+ and gj− are provided in the ESI.† All of the spectral and dynamical simulations in this paper are performed at 300 K based on the calculated Hamiltonian parameters.
, gj+ and gj− are provided in the ESI.† All of the spectral and dynamical simulations in this paper are performed at 300 K based on the calculated Hamiltonian parameters.
3 Results and discussion
3.1 Electronic properties in the diabatic representation
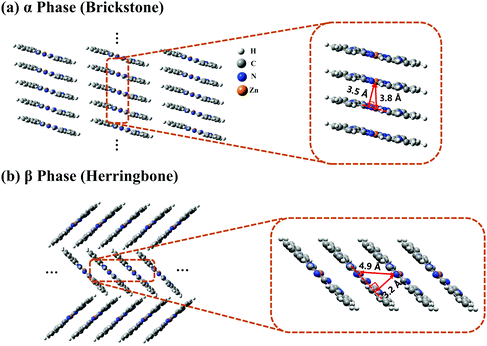
The crystal stacking arrangements of the α-phase and β-phase ZnPc studied in this paper are the brickstone and herringbone structures, respectively, as presented in Fig. 1, where the geometry structures of the corresponding tetramers are also shown. The atomic coordinates of the tetramers are listed in Tables S1 and S2 in the ESI† for the α and β phases, respectively. We only consider the one-dimensional stacking arrangements of the aggregates in our simulations because the distance between two neighbouring columns is large and the inter-column electronic couplings are negligible. From Fig. 1, it can be seen that when transforming from the α phase to the β phase, the shortest intermolecular distance decreases from 3.5 to 3.2 Å, and the nearest Zn–Zn interatomic distance increases from 3.8 to 4.9 Å. Correspondingly, along the stacking direction, the molecular plane in the β phase is much more tilted than that in the α phase. In addition, the monomer structure in the α phase is slightly more symmetrical than that in the β phase. These structural discrepancies lead to some differences in the vertical excitation energies and oscillator strengths of the adiabatic states, as listed in Tables S3 and S4 (ESI†).To clearly reveal the relationship between the structure and the electronic properties, we apply the FPHD diabatization scheme46 to construct quasi-diabatic states as the linear combinations of the adiabatic ones. The first 98 adiabatic excited states of the ZnPc tetramer are used in the diabatization procedure for both phases. The resulting 98 quasi-diabatic states are categorized as LE, CT, or CS states, according to their concrete charge and excitation distributions. Since the states of very high energies are irrelevant to the current research, we only consider the lowest-lying and second lowest-lying quasi-diabatic states (labeled as L1 and L2, respectively) for each charge and excitation distribution. As such, in the tetramer case, the total number of quasi-diabatic states we considered is 32, and for an aggregate consisting of N monomers, the total number is 2N2.
For the sake of convenience, in the following we directly use the indexes L1 and L2 as prefixes to distinguish the category of the quasi-diabatic states. For example, L1-LE states denote the LE states in the L1 category.
The energy level diagrams of the quasi-diabatic states are shown in Fig. 2. As can be seen, there are many similarities between the energy diagrams of the α and β phases. For example, for both phases, the diagrams reveal a mirror symmetry, and the energies of the quasi-diabatic states are strongly location-dependent. The energies of the CS states are much higher than those of the CT states in both phases, demonstrating that the Coulombic interaction is rather sensitive to the electron–hole distance. The above results are in accordance with our previous work.35 Nevertheless, remarkable differences between the two phases can also be found. Owing to the high symmetry of the ZnPc molecule in the α-phase aggregate, the L1 and L2 states of the same charge and excitation distributions are quasi-degenerate with a small energy splitting of around 0.07 eV. However, in the β phase, this quasi-degeneracy is removed due to the asymmetric structural deformation of the monomer, and the energy splitting increases to around 0.12 eV for the LE states and 0.24 eV for the CT and CS states.
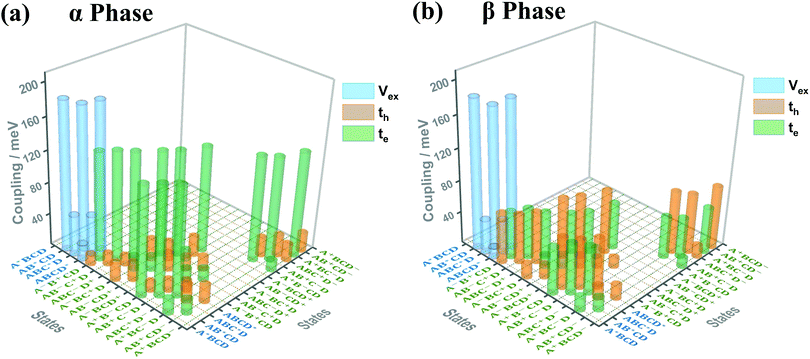
Fig. 3(a) and (b) present the electronic coupling values between the quasi-diabatic states of the α-phase and β-phase tetramers, respectively. The concrete numerical values can be found in Tables S7 and S8 (ESI†). Similar to the state energies, the electronic couplings in different phases also exhibit significant discrepancies. For example, in the α phase the couplings for electron transfer are much larger than those for hole transfer, whereas in the β phase the magnitude of the two kinds of couplings are all around 50 meV. Moreover, from the data presented in Tables S7 and S8 (ESI†), it can be found that in the α phase the excitonic couplings between the L1-LE states are very close to those between the L2-LE states, both of which are around 180 meV. By contrast, in the β phase, although the couplings between the L1-LE states are similar to those in the α phase, the couplings between the L2-LE states are only about 60 meV. As can be seen in the following, the remarkable differences between the electronic properties of the L1 and L2 states in the β phase profoundly influence the absorption spectra and the exciton dynamics.
3.2 Vibrationally resolved absorption spectra
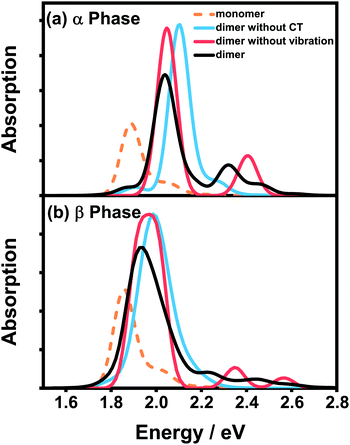
Fig. 4 presents the vibrationally resolved absorption spectra of the ZnPc dimer in a mixed solvent of N-methylpyrrolidone and chloroform. The monomer spectra are also shown for comparison. To be in line with the absorption spectra of the aggregates presented soon afterwards, here we consider two types of the dimer configuration, the α-phase and β-phase types. From Fig. 4, it can be seen that the dimer spectra for both configurations exhibit fruitful fine structures in the Q-band region. Concretely speaking, in the α-phase configuration four obvious absorption peaks appear at 1.87, 2.03, 2.32 and 2.45 eV, whereas in the β-phase configuration three visible peaks at 1.94, 2.23 and 2.44 eV are shown. These fine structures can not be explained by the traditional aggregate concept, and should be accounted for by the complicated participation of the CT state and electron–phonon interaction.
To distinguish the contributions from the two factors, we further calculate the spectra without one of them and compare the results with the original spectra. For the α-phase configuration, when the CT state is ignored (blue line in Fig. 4(a)), the spectrum is dominated by a single absorption peak with several vibronic side-peaks. On the other hand, when the electron–phonon interaction is neglected (red line in Fig. 4(a)), the spectrum shows two distinct peaks with an energy gap of 0.36 eV, which is in accordance with our previous results that the strong mixing between the CT state and the bright FE state can cause energy splitting of the original single peak. Comparing the three dimer spectra in Fig. 4(a), one can conclude that the two dominant peaks at 2.03 and 2.32 eV originate from the mixing between the FE and CT states, whereas the other two weak peaks are of a vibronic nature.
The situation becomes completely different for the β-phase configuration. As can be seen in Fig. 4(b), when the CT state is neglected (blue line), the spectrum only exhibits a single wide peak without any recognizable vibronic structure. Whereas when the electron–phonon interaction is omitted (red line), the spectrum is unexpectedly characterized by three peaks, approximately corresponding to the three peaks of the full result (black line) one by one. Therefore, the fine structure in the spectra of the β-configuration dimer is completely electronic in nature, and the nuclear vibrations only have trivial effects on reducing the effective excitonic couplings. To further elucidate the nature of the three absorption peaks, we analyze the components of the corresponding electronic eigenstates in the absence of the electron–phonon interaction. It is found that the lowest-energy peak is mainly from the L2-LE states, whereas the two high-energy peaks correspond to the mixtures of the L1-CT and L1-LE states. This indicates that the L1 and L2 states play completely different roles in the absorption spectra of the β-configuration dimer, as can be inferred from the obvious differences in their electronic properties.
Fig. 5(a) and (b) display the absorption spectra of the α-phase and β-phase aggregates, respectively, for several different aggregation lengths. Compared with the dimer spectra, it can be found that the fine vibronic structures are smeared out in the spectra of the aggregates, and the characteristic peaks become wider as well. As can be seen in Fig. 5, along with the formation of the α-phase aggregate, the high-energy peak surpasses the low-energy peak. By contrast, in the β phase, the low-energy peak is always the more prominent one in the Q-band region regardless of the length of the aggregate. Fig. 5 also presents the experimental spectra of the ZnPc thin films from two different fabrication conditions. The results displayed by the black dashed and grey dotted lines correspond to the annealed ZnPc Langmuir–Blodgett thin film and the thin film deposited on the glass/ITO substrates, respectively. As such, the two experimental spectra show small discrepancies in the peak positions, but their peak shapes and relative peak intensities are very similar to each other. It can be seen that the calculated spectra of both phases are highly consistent with the experimental results.
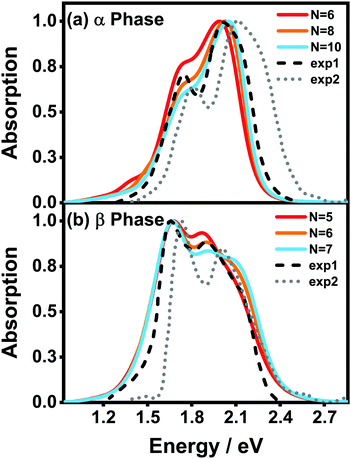 | ||
| Fig. 5 Normalized vibrationally resolved absorption spectra of (a) α-phase and (b) β-phase ZnPc aggregates with different aggregation lengths. The gray-doted and black-dashed lines are the experimental results extracted from ref. 17 and 31, respectively. The calculated spectra are red-shifted by 0.461 eV and 0.303 eV for the α and β phases, respectively, for better comparison. The spectra are broadened using the Gaussian line shape function with a full width of 0.05 eV. | ||
It can also be seen that, as the aggregation length increases, the intensity ratio between the high- and low-energy peaks in the α phase gradually increases, whereas the opposite trend appears in the β phase. The same trend in the α phase has already been observed in an experiment29 in which the absorbances of ZnPc thin films of different thicknesses were compared. Furthermore, in the β phase, a third peak at around 2.1 eV gradually emerges as the aggregation length increases. Similar extra peaks can be vaguely identified in the two experimental spectra shown in Fig. 5(b). All of the above results indicate that our model and simulations successfully capture most of the factors that influence the absorption spectra of a realistic ZnPc thin film.
Before starting quantitative analyses, we first provide a preliminary physical picture toward understanding the peculiar behavior of the spectra. Similar to the dimer case, the fruitful features in the absorption spectra of the aggregates are a consequence of the interplay between the bright FE state and the CT state. Along with the formation of the aggregate, due to the interference between LE states, the absorption spectra will be dominated by a single peak corresponding to the (delocalized) bright FE state. As the dark CT state takes part, the two states may mix together to constitute two new eigenstates, which causes the splitting of the original absorption peak.52 The energies and oscillator strengths of the new states, which correspond to the positions and intensities of the absorption peaks, respectively, depend strongly on the couplings and the energy alignment between the FE and CT states. It is known that for an H-aggregate (such as the ZnPc studied here) with positive excitonic couplings, the energy of the FE state gradually increases as the aggregation length increases, and eventually arrives at a stationary value of twice the excitonic coupling. As a result, the spectral characteristics can exhibit fruitful behavior as the aggregation length varies. Moreover, since the CT state is usually transition-forbidden, the peak intensities are determined by the FE proportions of the corresponding eigenstates, that is, the higher the FE proportion, the stronger the peak intensity.
In the following, we use analytical formulas derived from an effective two-state model to quantitatively analyze the spectral characteristics of the α-phase and β-phase aggregates.
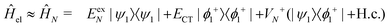 | (14) |
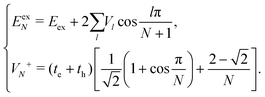 | (15) |
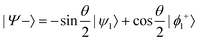 and
and 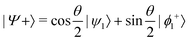 , where
, where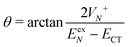 | (16) |
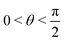 or
or 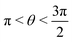 , whereas for VN+ < 0 we require that
, whereas for VN+ < 0 we require that 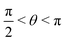 or
or 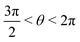 . Under this convention, |Ψ−〉 and |Ψ+〉 correspond to the low-energy and high-energy eigenstates, respectively.
. Under this convention, |Ψ−〉 and |Ψ+〉 correspond to the low-energy and high-energy eigenstates, respectively.
Based on the above two-state model, we have derived analytical formulas for the positions and intensities of the CT-mediated absorption peaks. The concrete expressions35 are
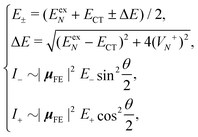 | (17) |
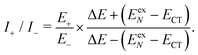 | (18) |
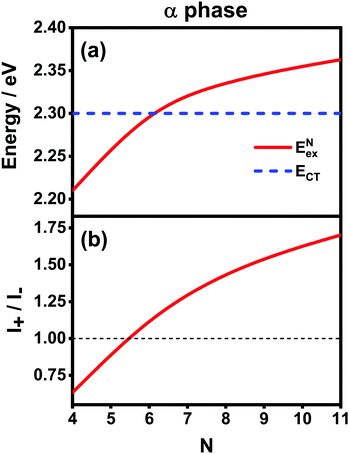
Now we use the above analytical formulas to analyze the spectral characteristics of the α-phase aggregates. Since the energy gap between E+ and E− is much smaller than their absolute values, the ratio E+/E− is approximately equal to unity. Thus, according to eqn (18), the intensity ratio I+/I− is mainly determined by EexN − ECT and ΔE. It can be easily proved that ΔE + (EexN − ECT) and ΔE − (EexN − ECT) are monotonically increasing and monotonically decreasing functions of EexN − ECT, respectively. Furthermore, from the first row of eqn (15), it is obvious that as the aggregation length increases, the energy of the FE state EexN is gradually lifted by the positive excitonic couplings and slowly approaches the stationary value 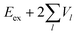 . By contrast, the energy of the CT state is independent of the aggregation length. Thereby, as N increases, the numerator in eqn (18) gradually increases with a simultaneous decrease in the denominator, and consequently the intensity ratio I+/I− gradually increases. This is qualitatively consistent with the numerical results presented in Fig. 5(a).
. By contrast, the energy of the CT state is independent of the aggregation length. Thereby, as N increases, the numerator in eqn (18) gradually increases with a simultaneous decrease in the denominator, and consequently the intensity ratio I+/I− gradually increases. This is qualitatively consistent with the numerical results presented in Fig. 5(a).
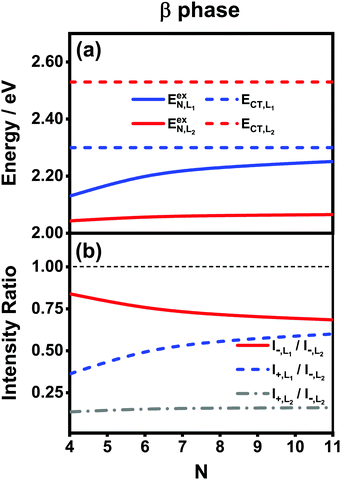
Fig. 6 presents the energy of the FE state and the intensity ratio calculated using eqn (15) and (18), respectively, where we have assumed the following parameter values, Eex = 1.90 eV, ECT = 2.30 eV, V1 = 0.18 eV, V2 = 0.05 eV, V3 = 0.02 eV, te = −0.13 eV, and th = 0.02 eV, to imitate the α-phase ZnPc aggregate. Indeed, from Fig. 6(a), it can be seen that as the aggregation length increases, the energy of the FE state quickly exceeds that of the CT state. At almost the same time, the intensity of the high-energy peak surpasses that of the low-energy one, as is displayed in Fig. 6(b). The analytical results are quantitatively consistent with the numerical results presented in Fig. 5(a), justifying the applicability of the effective two-state model to the α-phase aggregates and verifying that the two absorption peaks of the α-phase aggregate indeed originate from the mixing between the FE and CT states.
To solve this problem, here we extend the original model to a four-state version. Inspired by the fact that the electronic couplings between the L1 and L2 states are very small, it is reasonable to assume that the two categories of states are independent of each other. Therefore, we apply the methodology of the two-state model to the L1 and L2 states separately and then combine the analytical results. Concretely speaking, we calculate two sets of analytical results, each of which contains EexN,Li, ECT,Li, ΔELi, E±,Li, VN,Li+, θLi, and I±,Li, where the subscript Li with i = 1, 2 is used to denote the corresponding category. For example, the four different peak intensities can be calculated using
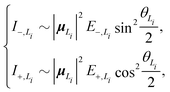 | (19) |
Fig. 7(a) presents the energies of the bright FE states in the β phase calculated using the analytical formulas, where the energies of the CT states are also shown for comparison. Here, the following parameter values Eex = 1.82 eV, ECT = 2.30 eV, V1 = 0.18 eV, V2 = 0.04 eV, V3 = 0.01 eV and te = th = −0.06 eV are adopted for the L1 category, whereas those for the L2 category are Eex = 1.93 eV, ECT = 2.53 eV, V1 = 0.07 eV, te = −0.05 eV and th = −0.08 eV. The ratio |μL1|/|μL2| is 1.01. From Fig. 7(a), it is found that the FE and CT states of the two categories indeed exhibit obvious differences in the energies. For the L1 category (solid and dashed blue lines), the energy of the FE state varies significantly with respect to the aggregation length, and the energy gap between the FE and CT states quickly decreases as N increases. This is similar to the situation in the α phase except that the energies of the two states do not cross. As such, the degree of mixing between the FE and CT states is expected to gradually rise as the aggregation length increases, which brings about two absorption peaks with varying relative intensities in the high-energy region. For the L2 category (solid and dashed red lines), owing to the small magnitude of the excitonic coupling, the energy of the FE state is only weakly related to the aggregation length. Moreover, the energy gap between the FE and CT states is always as large as around 0.5 eV, much greater than the coupling between the two states. Therefore, the L2-FE and L2-CT states do not have the trend to mix with each other, and the L2-FE state solely contributes to the absorption spectra in the low-energy region. Consequently, we expect that the absorption spectra of the β-phase aggregate can at most exhibit three peaks, among which the lowest-lying peak is attributed to the L2-FE state and the other two high-lying peaks originate from mixing between the L1-FE and L1-CT states.
We now turn to the analysis of the peak intensity. According to our notation convention, I−,L2, I±,L1 and I+,L2 denote the intensities of the L2-FE peak, the two L1-CT-mediated peaks and the very weak L2-CT peak, respectively, in order of increasing energy. Fig. 7(b) displays the analytical results of three different intensity ratios, I−,L1/I−,L2, I+,L1/I−,L2 and I+,L2/I−,L2, where the intensity of the lowest-lying peak, I−,L2, is adopted as a reference. As can be seen, all of the three intensity ratios are smaller than 1.00 regardless of the length of the aggregate, indicating that the lowest-lying peak always dominates in the absorption spectrum, which is in line with the experimental and numerical results shown in Fig. 5(b). Among the three high-energy peaks, the L2-CT peak (grey dash-dotted line) has a very low relative intensity as expected and therefore can hardly be identified in the absorption spectra. As for the two L1-CT-mediated peaks, in a short aggregate, the lower-energy peak (I−,L1, red solid line) has a strong intensity close to that of the L2-FE peak, whereas the higher-energy peak (I+,L1, blue dashed line) is relatively weak in intensity and is expected to be submerged by the broad structureless background in the spectrum. As the aggregation length increases, the relative intensity of the former gradually declines accompanied by an increase in the relative intensity of the latter. Accordingly, in the high-energy region of the absorption spectrum, the relative intensity of the characteristic peak (I−,L1) should gradually decrease accompanied by the slow emergence of an extra peak (I+,L1). This is in full accord with the results shown in Fig. 5(b) and explains the existence of the extra peak. Thereby, we conclude that for the β-phase aggregate, the lowest-lying absorption peak corresponds to the bright L2-FE state, whereas the fine structure in the high-energy region comes from the interplay between the L1-CT state and the bright L1-FE state.
3.3 Exciton dynamics in the α and β phases
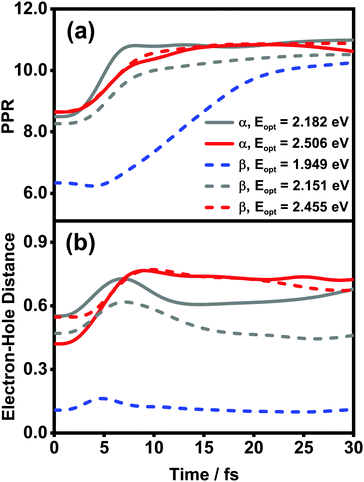
As mentioned before, the photoinduced quantum dynamics processes in α-phase and β-phase ZnPc can also differ significantly with each other. In this part, we use the NMSSE to investigate the ultrafast exciton dynamics within dozens of femtoseconds directly after photoexcitation. The aggregates consisting of 11 monomers are chosen for both phases in the study.Fig. 8 shows the energy level diagrams and oscillator strengths of the adiabatic electronic states of the two phases. Among all of the adiabatic states, we choose those states with the largest oscillator strengths as the initial states of the dynamics to imitate the photoexcitation process. For the α phase, the two selected excitation energies (denoted as Eopt in the following) are 2.182 eV and 2.506 eV, corresponding to the low-energy and high-energy absorption peaks in the Q-band region, respectively. As for the β phase, the three adiabatic states with the energies of 1.949 eV, 2.151 eV and 2.455 eV are selected. The first one represents the lowest-lying L2-FE peak, whereas the other two correspond to the two L1-CT-mediated peaks.
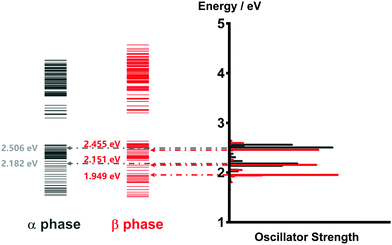 | ||
| Fig. 8 Energy level diagrams and oscillator strengths of the adiabatic electronic states of the α-phase and β-phase aggregates formed from 11 monomers. | ||
It is noted that there exist large energy gaps in the energy level diagrams of both phases. The adiabatic states above the gap are mainly constituted by the CS states, whereas those below the gap are mostly formed by the LE and CT states. Thereby, free carriers can hardly be generated by photoexcitation from the Q-band region, as has been confirmed in our previous work.35
The population evolution of different states in the α and β phases is presented in Fig. 9 and 10, respectively. In the α phase, as has been discussed previously,35 the optical excitation from the Q-band region can give rise to strong mixing between the LE and CT states. At the initial time, the proportion of the LE state is smaller than that of the CT state for the lower excitation energy (2.182 eV), whereas the opposite situation occurs for the higher one (2.506 eV). Nonetheless, after a rapid population exchange process between the LE and CT states within the first 10 femtoseconds, the aggregates seem to fall into some static states where the population distributions do not obviously evolve. For the β phase, similar interplay between the LE and CT states arises for the photoexcitation of the two L1-CT-mediated peaks as can be seen in Fig. 10(b) and (c). However, for the optical transition of the L2-FE peak shown in Fig. 10(a), the LE and CT states only weakly mix with each other, and the population curves are rather flat. The above dynamic results are in line with previous analyses of the absorption spectra.
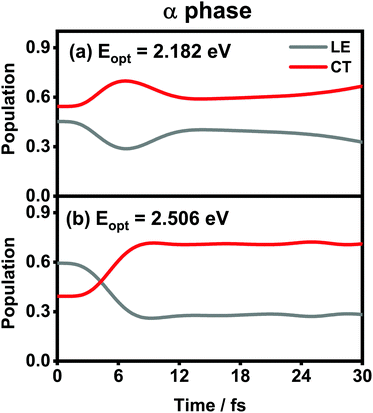 | ||
| Fig. 9 Population evolution of the LE and CT states after optical excitation in the α-phase aggregate with excitation energies of (a) 2.182 eV and (b) 2.506 eV. Adapted with permission from ref. 35 © 2015 American Chemical Society. | ||
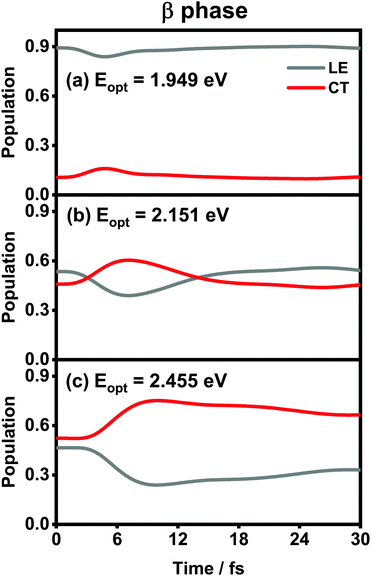 | ||
| Fig. 10 Population evolution of the LE and CT states after optical excitation in the β-phase aggregate with excitation energies of (a) 1.949 eV, (b) 2.151 eV and (c) 2.455 eV. | ||
To further elucidate the details about the ultrafast processes, we calculate the average electronic energy value Ē(t) according to
Ē(t) = Tr{Ĥel![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) el(t)}, el(t)}, | (20) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) el(t) is the reduced density matrix of the electronic degree of freedom obtained using the NMSSE. The results are shown in Fig. 11. It is found that for both low and high excitation energies in the α phase (grey and red solid lines, respectively), the average electronic energies gradually decrease at first and then seem to approach some static values, although for the low-energy case there exists a transient rise within the first 5 femtoseconds. Similar behavior can also be seen for the three optical transitions (red, grey and blue dashed lines) in the β phase. Nevertheless, it should be noted that the static values of the average electronic energies appearing in this ultrafast time scale are far from the thermal equilibrium state. From Fig. 8, it can be seen that there are a large number of low-energy dark states situated within the energy range between 1.5 eV and 1.8 eV. The above results indicate that for the relaxation processes within the first dozens of femtoseconds right after the Q-band photoexcitation, the ZnPc aggregates in both phases tend to fall temporarily into some intermediate states where the population distributions and the average electronic energies do not obviously evolve.
el(t) is the reduced density matrix of the electronic degree of freedom obtained using the NMSSE. The results are shown in Fig. 11. It is found that for both low and high excitation energies in the α phase (grey and red solid lines, respectively), the average electronic energies gradually decrease at first and then seem to approach some static values, although for the low-energy case there exists a transient rise within the first 5 femtoseconds. Similar behavior can also be seen for the three optical transitions (red, grey and blue dashed lines) in the β phase. Nevertheless, it should be noted that the static values of the average electronic energies appearing in this ultrafast time scale are far from the thermal equilibrium state. From Fig. 8, it can be seen that there are a large number of low-energy dark states situated within the energy range between 1.5 eV and 1.8 eV. The above results indicate that for the relaxation processes within the first dozens of femtoseconds right after the Q-band photoexcitation, the ZnPc aggregates in both phases tend to fall temporarily into some intermediate states where the population distributions and the average electronic energies do not obviously evolve.
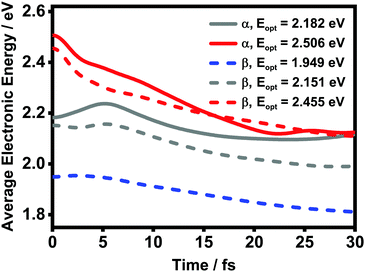 | ||
| Fig. 11 Time evolution of the average electronic energy value Ē after optical excitation in the ZnPc aggregates. The solid and dashed lines are results of the α and β phases, respectively. | ||
The diffusion and dissociation degrees of the exciton can be reflected by the population participation ratio (PPR) and the average electron–hole distance, respectively. The PPR in the LE subspace is calculated using
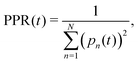 | (21) |
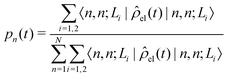 | (22) |
4 Conclusions
In summary, with the use of the NMSSE and first-principles calculations, we have theoretically investigated the vibrationally resolved absorption spectra and the ultrafast exciton dynamics in α-phase and β-phase ZnPc aggregates. By utilizing analytical formulas based on an effective two-state model and the four-state extension, we have identified the nature of the two absorption peaks in the Q-band region and have established quantitative structure–spectra relationships for both phases.We have found that both of the two absorption peaks in the α phase stem from the mixing between the CT and bright FE states. By contrast, in the β phase, the low-energy absorption peak is contributed solely by a low-lying FE state, whereas the high-energy peak originates from the intricate interplay between the CT state and another bright FE state. As a result, the relative peak intensities in the two phases exhibit opposite behavior with respect to the aggregation length. In the dynamics simulations, we have investigated the relaxation processes right after photoexcitation from the Q-band region. The results indicate that within the first dozen or so femtoseconds, the ZnPc aggregates in both phases tend to temporarily fall into some intermediate states where the average electronic energies and the population distributions of the LE and CT states do not obviously evolve. In addition, we have found that the optical transition of the low-lying bright FE state in the β phase is not favorable for the formation of bound CT states due to the absence of sufficient driving forces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Science Foundation of China (Grant no. 22033006, 21833006 and 21773191).Notes and references
- J. Drechsel, B. Männig, F. Kozlowski, M. Pfeiffer, K. Leo and H. Hoppe, Appl. Phys. Lett., 2005, 86, 244102 CrossRef.
- M. Riede, T. Mueller, W. Tress, R. Schueppel and K. Leo, Nanotechnology, 2008, 19, 424001 CrossRef CAS PubMed.
- S. Pfuetzner, J. Meiss, A. Petrich, M. Riede and K. Leo, Appl. Phys. Lett., 2009, 94, 253303 CrossRef.
- M. V. Martínez-Díaz, G. D. L. Torre and T. Torres, Chem. Commun., 2010, 46, 7090–7108 RSC.
- M.-E. Ragoussi, M. Ince and T. Torres, Eur. J. Org. Chem., 2013, 6475–6489 CrossRef CAS.
- L. Martín-Gomis, F. Fernández-Lázaro and Á. Sastre-Santos, J. Mater. Chem. A, 2014, 2, 15672–15682 RSC.
- D. Roy, N. M. Das, N. Shakti and P. S. Gupta, RSC Adv., 2014, 4, 42514–42522 RSC.
- R. R. Cranston and B. H. Lessard, RSC Adv., 2021, 11, 21716–21737 RSC.
- G. J. Dutton and S. W. Robey, J. Phys. Chem. C, 2013, 117, 25414–25423 CrossRef CAS.
- T. Chikamatsu, M. Shahiduzzaman, K. Yamamoto, M. Karakawa, T. Kuwabara, K. Takahashi and T. Taima, ACS Omega, 2018, 3, 5678–5684 CrossRef CAS PubMed.
- L. M. Blinov, V. V. Lazarev, S. G. Yudin and S. P. Palto, Crystallogr. Rep., 2019, 64, 315–321 CrossRef CAS.
- S. Senthilarasu, S.-J. Baek, S. D. Chavhan, J. Lee and S.-H. Lee, J. Nanosci. Nanotechnol., 2008, 8, 5414–5417 CrossRef CAS PubMed.
- L. Gaffo, M. R. Cordeiro, A. R. Freitas, W. C. Moreira, E. M. Girotto and V. Zucolotto, J. Mater. Sci., 2010, 45, 1366–1370 CrossRef CAS.
- M. Kozlik, S. Paulke, M. Gruenewald, R. Forker and T. Fritz, Org. Electron., 2012, 13, 3291–3295 CrossRef CAS.
- C. Schünemann, C. Elschner, A. Levin, M. Levichkova, K. Leo and M. Riede, Thin Solid Films, 2011, 519, 3939–3945 CrossRef.
- J. S. Louis, D. Lehmann, M. Friedrich and D. R. T. Zahn, J. Appl. Phys., 2007, 101, 013503 CrossRef.
- M. Shahiduzzaman, T. Horikawa, T. Hirayama, M. Nakano, M. Karakawa, K. Takahashi, J.-M. Nunzi and T. Taima, J. Phys. Chem. C, 2020, 124, 21338–21345 CrossRef CAS.
- S. Heutz, S. M. Bayliss, R. L. Middleton, G. Rumbles and T. S. Jones, J. Phys. Chem. B, 2000, 104, 7124–7129 CrossRef CAS.
- S. Senthilarasu, Y. B. Hahn and S.-H. Lee, J. Appl. Phys., 2007, 102, 043512 CrossRef.
- R. R. Cranston and B. H. Lessard, RSC Adv., 2021, 11, 21716–21737 RSC.
- F. Iwatsu, T. Kobayashi and N. Uyeda, J. Phys. Chem., 1980, 84, 3223–3230 CrossRef CAS.
- S. Senthilarasu, R. Sathyamoorthy and S. K. Kulkarni, Mater. Sci. Eng., B, 2005, 122, 100–105 CrossRef.
- D. L. Gonzalez Arellano, E. K. Burnett, S. Demirci Uzun, J. A. Zakashansky, V. K. Champagne III, M. George, S. C. B. Mannsfeld and A. L. Briseno, J. Am. Chem. Soc., 2018, 140, 8185–8191 CrossRef CAS PubMed.
- J. Kim and S. Yim, J. Nanoelectron. Optoelectron., 2011, 6, 249–252 CrossRef CAS.
- H. Ahn and T.-C. Chu, Opt. Mater. Express, 2016, 6, 3586–3593 CrossRef CAS.
- S. Hammer, T. Ferschke, G. V. Eyb and J. Pflaum, Appl. Phys. Lett., 2019, 115, 263303 CrossRef.
- M. Kato, M. Nakaya, Y. Matoba, S. Watanabe, K. Okamoto, J.-P. Bucher and J. Onoe, J. Chem. Phys., 2020, 153, 144704 CrossRef CAS PubMed.
- Y. Qiu, P. Chen and M. Liu, Langmuir, 2008, 24, 7200–7207 CrossRef CAS PubMed.
- A. A. Zanfolim, D. Volpati, C. A. Olivati, A. E. Job and C. J. L. Constantino, J. Phys. Chem. C, 2010, 114, 12290–12299 CrossRef CAS.
- D. Roy, N. M. Das, M. Gupta, V. Ganesan and P. S. Gupta, AIP Conf. Proc., 2014, 1591, 968 CrossRef CAS.
- D. Roy, N. M. Das, M. Gupta and P. S. Gupta, AIP Conf. Proc., 2016, 1731, 030007 CrossRef.
- G. Maggioni, M. G. Manera, J. Spadavecchia, M. Tonezzer, S. Carturan, A. Quaranta, C. de Julián Fernández, R. Rella, P. Siciliano, G. Della Mea, L. Vasanelli and P. Mazzoldi, Sens. Actuators, B, 2007, 127, 150–156 CrossRef CAS.
- G. S. S. Saini, S. Singh, S. Kaur, R. Kumar, V. Sathe and S. K. Tripathi, J. Phys.: Condens. Matter, 2009, 21, 225006 CrossRef CAS PubMed.
- S. Feng, Y.-C. Wang, Y. Ke, W. Liang and Y. Zhao, J. Chem. Phys., 2020, 153, 034116 CrossRef CAS PubMed.
- S. Feng, Y.-C. Wang, W. Liang and Y. Zhao, J. Phys. Chem. A, 2021, 125, 2932–2943 CrossRef CAS PubMed.
- X. Zhong and Y. Zhao, J. Chem. Phys., 2013, 138, 014111 CrossRef PubMed.
- Y. Ke and Y. Zhao, J. Chem. Phys., 2017, 147, 184103 CrossRef PubMed.
- Y.-C. Wang, Y. Ke and Y. Zhao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1375 Search PubMed.
- Y.-C. Wang and Y. Zhao, Chin. J. Chem. Phys., 2020, 33, 653–667 CrossRef CAS.
- M. Schröter, S. D. Ivanov, J. Schulze, S. P. Polyutov, Y. Yan, T. Pullerits and O. Kühn, Phys. Rep., 2015, 567, 1–78 CrossRef.
- M. K. Debe and D. R. Field, J. Vac. Sci. Technol., A, 1991, 9, 1265–1271 CrossRef CAS.
- A. Hoshino, Y. Takenaka and H. Miyaji, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 393–403 CrossRef PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr., H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Z. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. V. Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- Y.-C. Wang, S. Feng, W. Liang and Y. Zhao, J. Phys. Chem. Lett., 2021, 12, 1032–1039 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- V. N. Nemykin, R. G. Hadt, R. V. Belosludov, H. Mizuseki and Y. Kawazoe, J. Phys. Chem. A, 2007, 111, 12901–12913 CrossRef CAS PubMed.
- R. F. Theisen, L. Huang, T. Fleetham, J. B. Adams and J. Li, J. Chem. Phys., 2015, 142, 094310 CrossRef PubMed.
- F. Gao, W. Liang and Y. Zhao, Sci. China: Chem., 2010, 53, 297–309 CrossRef CAS.
- F. Gao, Y. Zhao and W. Liang, J. Phys. Chem. B, 2011, 115, 2699–2708 CrossRef CAS PubMed.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- N. J. Hestand, R. Tempelaar, J. Knoester, T. L. C. Jansen and F. C. Spano, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195315 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Including the atomic coordinates and adiabatic excited state properties of the α-phase and β-phase ZnPc tetramers; energies and transition dipole moments of quasi-diabatic states of the α-phase and β-phase ZnPc tetramers; electronic couplings between the quasi-diabatic states of the α-phase and β-phase ZnPc tetramers; electron–phonon coupling constants of all vibrational modes associated with the localized excited, cationic and anionic states of the ZnPc monomer for α- and β-phase aggregates in the crystal environment. See DOI: 10.1039/d1cp03600a |
| This journal is © the Owner Societies 2022 |