Toward Å–fs–meV resolution in electron microscopy: systematic simulation of the temporal spread of single-electron packets
Wyatt A.
Curtis
and
David J.
Flannigan
 *
*
Department of Chemical Engineering and Materials Science, University of Minnesota, 421 Washington Avenue SE, Minneapolis, MN 55455, USA. E-mail: flan0076@umn.edu; Tel: +1-612-625-3867
First published on 11th October 2021
Abstract
Though efforts to improve the temporal resolution of transmission electron microscopes (TEMs) have waxed and waned for decades, with relatively recent advances routinely reaching sub-picosecond scales, fundamental and practical challenges have hindered the advance of combined Å–fs–meV resolutions, particularly for core-loss spectroscopy and real-space imaging. This is due in no small part to the complexity of the approach required to access timescales upon which electrons, atoms, molecules, and materials first begin to respond and transform – attoseconds to picoseconds. Here we present part of a larger effort devoted to systematically mapping the instrument parameter space of a TEM modified to reach ultrafast timescales. With General Particle Tracer, we studied the statistical temporal distributions of single-electron packets as a function of various fs pulsed-laser parameters and electron-gun configurations and fields for the exact architecture and dimensions of a Thermo Fisher Tecnai Femto ultrafast electron microscope. We focused on easily-adjustable parameters, such as laser pulse duration, laser spot size, photon energy, Wehnelt aperture diameter, and photocathode size. In addition to establishing trends and dispersion behaviors, we identify regimes within which packet duration can be 100s of fs and approach the 300 fs laser limit employed here. Overall, the results provide a detailed picture of the temporal behavior of single-electron packets in the Tecnai Femto gun region, forming the initial contribution of a larger effort.
Introduction
Four-dimensional ultrafast electron microscopy (UEM) with femtosecond/picosecond (fs/ps) temporal resolution1–4 has been used to inform a diverse and growing set of chemical, materials, and biological problems, such as phonon behaviors at atomic-to-nanoscale dimensions,5–17 the spatiotemporal evolution of photoinduced phase transitions,18–23 and the interaction of free electrons with photons at nanomaterial and biointerfaces.24–35 High temporal resolution (i.e., 100 fs to 1 ns) in UEM is typically achieved by interfacing a modified transmission electron microscope (TEM) with a fs pulsed laser such that stroboscopic photon-pump/electron-probe experiments can be conducted, though incorporation of an electromagnetic cavity or beam blanker into the column provides a laser-free (or hybrid) option with comparable temporal resolution.36–47 With laser-driven UEM, however, spatial and temporal coherence of the probe electron packets quickly degrade with increasing density due to deleterious electron–electron interactions,48–50 in addition to broadening effects imposed by electric and magnetic fields specific to the base TEM platform. This poses practical challenges to achieving high combined spatial, energy, and temporal resolutions for this form of ultrafast TEM, as a balance must be struck between signal acquisition time, electrons per packet and packets per unit time (i.e., beam current), and specimen relaxation time (τrelaxation).Methods for overcoming the resolution-limiting effects of electron–electron interactions in UEM focus on either undoing the broadening, as in proposed approaches employing pulse compression schemes,51,52 or avoiding it altogether, as with conventional beams that are chopped or blanked (mentioned above), or by reducing the photoelectron packet density by simply using a lower pulsed-laser fluence.1 Indeed, instrument-limited ∼2 Å real-space resolution and sub-eV energy resolution have been demonstrated with both laser-free and laser-driven pulsed electron beams.41,53,54 However, photoexcitation (or any type of triggering event) for stroboscopic study of dynamics requires extremely precise and highly robust spatial and temporal specimen reversibility. Accordingly, Å-resolved fs/ps real-space imaging of structural dynamics has yet to be demonstrated, despite the pulsed beams having sufficient coherence under certain operating conditions. As importantly, the high repetition rates (f) used to offset low packet densities and to reduce data acquisition times (true for both laser-driven and laser-free approaches) relegates such high-f approaches to studies employing weak excitations (i.e., small perturbations) or to events having approximately nanosecond or shorter lifetimes; more generally, to events where τrelaxation < f−1.4 Ideally, and especially for chemical and nanomaterials systems, one would identify an experimental parameter space where combined Å–fs–meV resolutions can be reached and preserved while being applied to the largest-possible set of phenomena and compositions (i.e., the widest range of τrelaxation for triggered events).
For fs laser-driven UEM, settings that lead to the (statistical) generation of a single photoelectron at the source (which is ideally collected into the illumination system55) should produce the most coherent beam at the highest beam current for a given f owing to the absence of electron–electron interactions.1,56–58 Under such conditions, resolutions are then dictated by the fs laser-pulse properties and by space-charge-independent broadening effects inherent to the base TEM (i.e., by fields specific to the instrument architecture, dimensions, materials, and geometries).57–61 Accordingly, it would be useful to systematically study and quantify the impact of laser-pulse properties, electric and magnetic fields, and – importantly – specific instrument specifications on single-electron-packet resolutions, coherence, and collection efficiency in order to: (i) define theoretical limits, (ii) identify simple, low-cost approaches to tunable optimization, and (iii) begin to build-up a knowledgebase to better establish cause-effect relationships and to address unfounded dogma that has emerged where key data is missing.
Here, our contribution to a necessarily larger, multifaceted effort is a systematic set of simulations of single-electron-packet temporal distributions (τelectron) as a function of fs laser-pulse properties for the specific gun/accelerator architecture and dimensions of an FEI Tecnai Femto UEM (Thermo Fisher). Using the General Particle Tracer software package in tandem with field maps calculated using Poisson Superfish,62,63 we studied the effects of easily-tunable laser-pulse properties and electron-gun dimensions on the temporal duration of single-electron packets. Adjustable parameters included the Wehnelt aperture diameter (DW), the photoelectron emission spot size (i.e., the fs UV probe-laser spot size on a truncated LaB6 cathode), the laser photon energy (hν), the laser pulse duration (τlaser), and the diameter of the cathode emitting surface (Dtip). In addition to identifying trends and uncovering unexpected behaviors, the goal here was to establish a foundation for additional systematic studies of increasing complexity for an entire laser-driven UEM system so as to ultimately generate an operational phase diagram for better targeting specific applications. While the simulations and results are specific to the Tecnai Femto system, the insights uncovered here are expected to be at least qualitatively applicable to other base TEM models and UEM systems.
Experimental
Elements of the simulations
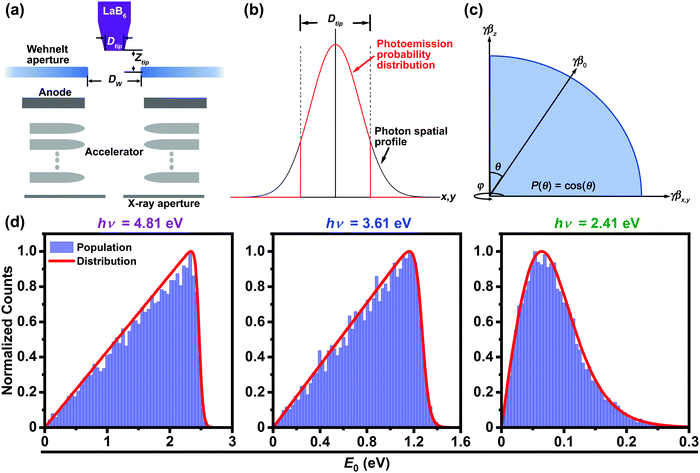
General Particle Tracer (GPT, Pulsar Physics) was used to map particle trajectories through the electron gun and the electrostatic accelerator of a Thermo Fisher/FEI Tecnai Femto UEM (Fig. 1a).63 To reduce computation time, simulations of n = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 non-interacting electrons simultaneously generated from the cathode were performed. In the gun region, a series of dynodes comprise the accelerator and raise the electron energy to 200 keV. Once fully accelerated, the beam impinges upon an X-ray aperture, which here is the final element of the simulated electron gun. Two-dimensional, cylindrically-symmetric electrostatic field maps were calculated for the specific architecture and dimensions of the Tecnai Femto UEM (base instrument is Tecnai T20 G2)† using Poisson Superfish.62
000 non-interacting electrons simultaneously generated from the cathode were performed. In the gun region, a series of dynodes comprise the accelerator and raise the electron energy to 200 keV. Once fully accelerated, the beam impinges upon an X-ray aperture, which here is the final element of the simulated electron gun. Two-dimensional, cylindrically-symmetric electrostatic field maps were calculated for the specific architecture and dimensions of the Tecnai Femto UEM (base instrument is Tecnai T20 G2)† using Poisson Superfish.62
In UEM mode, the electron gun consists of an unbiased Wehnelt triode with an aperture of diameter DW and a truncated LaB6 cathode with an emitting surface of diameter Dtip and a work function of Φ = 2.4 eV. The aperture can be variably positioned relative to the emitting surface at a distance Ztip in the Wehnelt assembly. Here, a fixed Ztip of 0.35 mm was used, as previous simulations of the Tecnai Femto indicated that this is the optimal position for maximizing electron collection efficiency in single-electron mode for DW = 0.7 mm.55 Further, a fixed Ztip was used in order to specifically study the effects of photoemission spot size (i.e., assumed to be the fwhm size of the laser spot on the LaB6 surface) and DW on τelectron. As with previous simulations on minimally-modified TEMs for ultrafast operation,55 the effects of emission spot size and DW are of interest because they are readily adjustable and tunable.
Single-electron packets were approximated by generating a set of non-interacting particles having momentum distributions and spatial coordinates specific to the photoemission characteristics under consideration. This approximates a series of single-electron photoemission events. Note the distinction between photoemission spot size and Dtip, which manifests in the emission probability (P) for a Gaussian laser-spot spatial profile (Fig. 1b). Further, LaB6 shank emission was not considered, as the laser spot can be trained entirely on the flat cathode surface.54,58 This is experimentally achieved by encircling the LaB6 with a high Φ material such that hν < Φ and by simply focusing the laser-spot size such that it is smaller than Dtip.1,8,58
The probability of photoemission (P) was varied as the cosine of the initial emission angle, θ [i.e., P(θ) = cos(θ)] (Fig. 1c).55,64 Note that different approaches to treating the angular photoemission distribution in UEM and ultrafast electron diffraction (UED) simulations have been adopted. One common approach is to assume a uniform distribution of photoemission probabilities within the hemisphere subtended by the photocathode emitting surface.57,59,65 Compared to the cos(θ) approach, uniformly-distributed trajectories will produce photoelectron packets with increased temporal distortions due to the larger fraction of off-axis emission events. Only the cos(θ) distribution was employed here. Following this, the product of the Lorentz factor (γ) and the normalized relativistic velocity (β) was used as the momentum factor (γβ) to initialize the GPT simulations.
Initial photoelectron kinetic-energy distributions were modeled as calculated transmission coefficients for free electrons encountering a step potential (Fig. 1d). Photoemission was approximated by shifting the Fermi–Dirac distribution by the amount of the incident photon energy hν; the three photon energies studied here (2.41, 3.61, and 4.81 eV) are harmonics (2nd–4th, respectively) of the UEM laser system at Minnesota (Yb:KGW, hvfundamental = 1.2 eV). Note that this approach is an approximation for near-threshold photoemission from the surface of LaB6.66 All reported single-electron-packet properties are those that are present 2.5 ns after photoemission. This ensured that all packets were fully increased to 200 keV and had reached the X-ray aperture, regardless of initial trajectory. Finally, τelectron (single-electron temporal distribution for n individual, integrated non-interacting particles) was calculated by dividing the root-mean-square longitudinal packet length by the average longitudinal velocity.
Results and discussion
Dependence of τelectron on photoemission spot size and E0 for key values of DW
To establish a baseline behavior for τelectron, three discrete values of E0 were first simulated (0.10, 1.76, and 2.40 eV) for two Wehnelt aperture diameters (0.7 and 1.0 mm, Fig. 2). These E0 values were selected because 0.10 and 2.4 eV are near the extremes of the full range of E0 for the oft-used hν = 4.8 eV and Φ = 2.4 eV for generating photoelectrons in UEM experiments, while 1.76 eV is the average value of the calculated distribution for hν = 4.81 eV (Fig. 1d, left panel). The two values of DW were chosen because they are standard (0.7 mm) and optimum (1.0 mm) diameters used in thermionic and single-electron UEM modes (per simulation), respectively.55 Because the particles in each bunch are non-interacting, one can separate the space-charge-independent broadening effects for different values of E0. Further, the use of single, discrete values of E0 at this stage, rather than the distributions shown in Fig. 1d, provides direct insight into the degree of influence of those effects.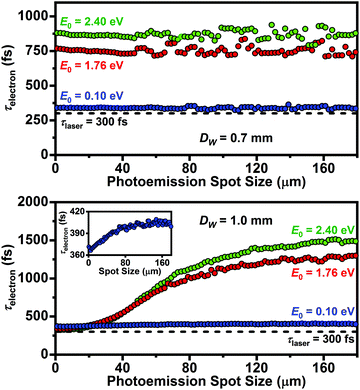 | ||
| Fig. 2 Single-electron-packet duration (τelectron; fwhm) as a function of LaB6 photoemission spot size for DW = 0.7 mm (top) and DW = 1.0 mm (bottom). Note that three discrete initial photoelectron kinetic energies (E0 = 0.10, 1.76, and 2.40 eV) were compared (i.e., here, the full distributions shown in Fig. 1d were not yet used in order to first focus on the effect of photoemission spot size and DW). The horizontal black dashed line in each panel (τlaser) represents the selected probe laser-pulse duration of 300 fs (fwhm) typical of the current system at Minnesota. The inset (bottom panel) is the 0.10 eV plot for DW = 1.0 mm with the y-axis rescaled to visualize the subtle response of τelectron. | ||
The simulations indicate that a strong dependence of τelectron on photoemission spot size exists for DW = 1.0 mm as compared to the standard 0.7 mm aperture, which instead shows very little variation across the entire range of spot sizes investigated (0–180 μm). In particular, the two larger E0 values (i.e., larger initial kinetic energies due to larger hν values) for DW = 1.0 mm show a large drop in τelectron to near the laser-pulse duration (τlaser = 300 fs) with decreasing spot size. This is intriguing because it suggests that experimental parameter space exists wherein one can overcome degraded temporal resolution for cases where hν > Φ when using a tightly-focused laser. Further, the simulated value of τelectron is approximately the same for all values of E0 at spot sizes smaller than ∼20 μm (Fig. 2, bottom panel). This suggests that one might be able to both preserve optimum temporal resolution while also increasing photoemission probability when operating in the single-electron regime. However, it is important to note that the behaviors and thus optimum settings will change when each laser pulse produces multiple photoelectrons and electron–electron interactions are present. Again, throughout this study we focused solely on the idealized single-electron regime, but work is needed to better understand the behaviors of packets with increasing density generated with fs laser pulses. It should be noted that the general increase in τelectron with E0 (i.e., hν), which is especially apparent for DW = 0.7 mm, is a well-known effect in UED experiments. The simulations here indicate this effect is also present in UEM, despite the more complex instrument architecture. However, this increased complexity may also offer additional flexibility for offsetting negative effects with simple adjustments to key components once the parameter space is mapped, as suggested by the results in Fig. 2.
The effect of photoemission spot size on τelectron shown in Fig. 2 is due in part to the precise trajectories of the photoelectrons in the gun region. Integrated over n electrons, larger emission spot sizes will have a larger fraction of off-optical-axis particles, which then leads to broadening of the temporal distribution. Photoelectrons emitted from surface regions that are far from the optical axis, as well as those that are not parallel to the axis when emitted, will contribute to the broadening due to prolonged dwell times and delays in acceleration. Importantly, the Wehnelt aperture is the main electrostatic component affecting tip-region dwell time, with the diameter (DW) strongly impacting overall behavior and thus serving as a source of tunability and optimization. This is intuitively straightforward to understand. Decreasing DW effectively moves the associated electrostatic field closer to the optical axis, thus impacting a larger fraction of the total (integrated) emitted population and increasing the sensitivity of τelectron to off-axis and non-parallel photoelectrons. The DW = 1.0 mm data in Fig. 2 further illustrate this effect; photoemission spots below a certain diameter dictated by the specific DW will have minimally-impacted populations. Thus, the onset of an increase in τelectron will move to larger spot sizes as DW is also increased.
Unlike the 1.0 mm aperture, the standard 0.7 mm aperture appears to impact all photoelectrons regardless of emission spot size. Practically, this may be beneficial, as one need not worry about carefully controlling spot size in order to have a consistent τelectron. However, it does not provide for simple tunability or for reaching resolutions close to τlaser beyond using lower hν (at the expense of beam current for a given f). Relatedly, temporal distortions of electron packets have been indirectly observed for UEM systems having independent control over Wehnelt bias and for photoelectrons emitted from shank regions of conical cathodes for reasons similar to those here, though differences in magnitude are potentially due to differing geometries and to the absence of electron–electron interactions in the simulations.54,60 Such distortions are also not unlike those introduced by magnetic lenses.65,67,68
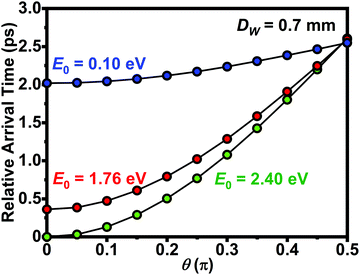
The increase in τelectron with hν (Fig. 2) can be explained as follows. One contribution comes from the distribution of initial trajectories, which will create an effective dispersion in the longitudinal velocities. This will result in a general statistical broadening of the temporal distribution due to electron acceleration.57,59 However, the effect will diminish with decreasing E0 due to the lower initial velocities. Another related contribution comes from the resulting variation in electron-gun dwell times (i.e., the time needed for each electron to reach a fixed position after the final electron-gun element). Importantly, the difference in dwell time between the extremes in initial trajectory (θ = 0 and 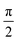 , Fig. 1c) increases with increasing E0. For example, for E0 = 0.10 eV the spread in dwell time increases 500 fs for θ increasing from 0 to
, Fig. 1c) increases with increasing E0. For example, for E0 = 0.10 eV the spread in dwell time increases 500 fs for θ increasing from 0 to 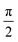 , but over the same trajectory range, it increases by 2.6 ps for E0 = 2.40 eV (Fig. 3). More generally, electron packets with larger E0 will, on average, have a shorter dwell time (i.e., shorter arrival time) relative to smaller E0 at any given trajectory within the relevant range despite the non-linear behavior. It is important to note that the dwell-time delay is not due to electrostatic accelerator-induced broadening, because all electrons are emitted with identical longitudinal velocities. Instead, it is a result of the increased interactions of large-angle trajectories with the Wehnelt aperture for larger E0.
, but over the same trajectory range, it increases by 2.6 ps for E0 = 2.40 eV (Fig. 3). More generally, electron packets with larger E0 will, on average, have a shorter dwell time (i.e., shorter arrival time) relative to smaller E0 at any given trajectory within the relevant range despite the non-linear behavior. It is important to note that the dwell-time delay is not due to electrostatic accelerator-induced broadening, because all electrons are emitted with identical longitudinal velocities. Instead, it is a result of the increased interactions of large-angle trajectories with the Wehnelt aperture for larger E0.
Systematic study of the effect of DW on τelectron for an hν-driven distribution of E0
The results discussed above, which provide a foundation upon which to increase the complexity of the simulations, have significant implications for n photoelectrons comprising a temporally-integrated packet consisting of a range of E0 (Fig. 1d) rather than a single discrete value. Accordingly, Fig. 4 summarizes the results of such simulations, where the E0 distribution for the hν = 4.81 eV case shown in Fig. 1d was used instead of the discrete value E0 = 2.40 eV (Fig. 2 and 3). Further, the simulations were performed for six different DW ranging 0.7–1.2 mm, all as a function of the photoemission spot size.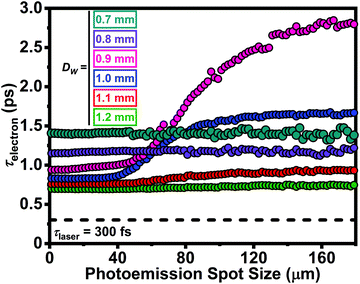 | ||
| Fig. 4 Single-electron packet duration (τelectron, fwhm) as a function of photoemission spot size for DW ranging 0.7–1.2 mm. The LaB6Dtip was 180 μm. The horizontal black dashed line (τlaser) represents the selected probe laser-pulse duration of 300 fs (fwhm). The hν = 4.81 eV distribution in Fig. 1d was used as the E0. | ||
Several notable behaviors emerge from the simulations summarized in Fig. 4. Perhaps the most notable is that, for spot sizes smaller than ∼50 μm, τelectron decreases with increasing DW, reaching a value of ∼700 fs (fwhm) for the largest aperture (again, for the broadest E0 distribution generated from hν = 4.81 eV with τlaser = 300 fs). This again indicates that DW is an adjustable parameter for optimizing temporal resolution of minimally-modified thermionic UEM systems that lack independent control over Wehnelt bias. As is the case for discrete values of E0 (Fig. 2), this effect is due to a reduction in the influence of Wehnelt electrostatic fields on off-axis photoelectrons [emphasizing again the P(θ) = cos(θ) distribution used here]. Interestingly, there is a rather abrupt onset of aperture influence on τelectron dispersion with photoemission spot size when increasing from DW = 0.8 to 0.9 mm, with a nearly similarly-abrupt relaxation when increasing from 1.0 to 1.1 mm (though a relatively modest dispersion of ∼100 fs is still seen for DW = 1.1 mm). At least with respect to τelectron, the simulations indicate that a DW larger than ∼1 mm provides the highest temporal resolution (for a given DW) combined with the least sensitivity to photoemission spot size. Further, the sensitivity of τelectron to spot size for DW = 0.9 and 1.0 mm is connected to the cosine functional form of emission probability (Fig. 1c) and, therefore, the precise (integrated) distribution of photoelectron kinetic energies (Fig. 1d).
Compared to data shown in Fig. 2 (i.e., compared to E0 = 2.40 eV for each DW), the single-electron packets generated from a distribution of E0 shown in Fig. 4 are generally further temporally broadened. This is due to a further increase in longitudinal-velocity spread and broadening of the associated distribution in electron-gun dwell times (see Fig. 3 for the case of discrete values of E0). Such broadening typically manifests in energy and longitudinal-velocity distributions of single electrons propagating in accelerating fields.59,61 Here, however, the effect appears to also emerge in non-accelerating fields due to the electrostatic forces imposed by an unbiased Wehnelt aperture and the portion of the E0 distribution that dominates the overall behavior for specific combinations of non-zero photoemission spot sizes and DW. Indeed, the effect becomes quite deleterious in terms of τelectron for standard DW aperture sizes (e.g., 0.7 mm), regardless of spot size; here, τelectron is broadened to 1.4 ps from the laser limit, despite the general shortened dwell time for higher-energy photoelectrons (Fig. 3).
Simulations of E0 (hν) distributions for select DW
As Fig. 4 summarizes the behavior of τelectron as a function of photoemission spot size for various DW and for the hν = 4.81 eV distribution of E0 (Fig. 1d), a systematic approach dictates that simulations for the other two select E0 distributions (again, as specified by the available laser harmonics) also be performed and compared. Accordingly, Fig. 5 summarizes the results for DW = 0.9 and 1.2 mm for all three E0 distributions. These aperture values were chosen because they show (for the E0 = 2.41 eV distribution; Fig. 4) the strongest dispersion, in the case of the 0.9 mm aperture, and the weakest and mostly-insensitive temporal broadening (i.e., the best temporal resolution that is robust across all spot sizes), in the case of the 1.2 mm aperture.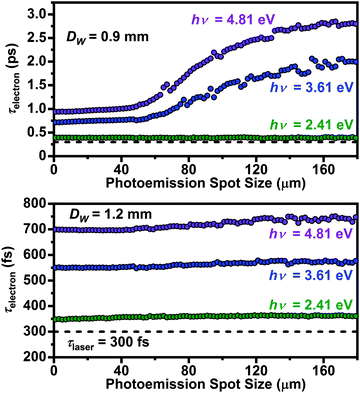 | ||
| Fig. 5 Single-electron packet duration (τelectron, fwhm) as a function of photoemission spot size for discrete laser photon energies (hν = 2.41, 3.61, and 4.81 eV) for DW = 0.9 mm (top) and 1.2 mm (bottom). The LaB6Dtip was 180 μm. The horizontal black dashed line (τlaser) in each panel represents the selected probe laser-pulse duration of 300 fs (fwhm). The E0 distributions shown in Fig. 1d were used for each corresponding photon energy. | ||
As can be seen, the trend for E0 = 2.41 eV (i.e., hν = 4.81 eV) generally continues for the other distributions with some notable and important variations. Photoexcitation with hν closer to the LaB6Φ value (here, fixed at 2.4 eV) produces an overall improvement in τelectron for both values of DW, regardless of photoemission spot size. Further, the strong dispersion seen for DW = 0.9 mm and hν = 4.81 eV is also observed for hν = 3.61 eV (scales approximately linearly) but is relaxed across all spot sizes for hν = 2.41 eV (i.e., hν approximately equivalent to Φ). Indeed, τelectron for hν = 2.41 eV is broadened by ∼50 fs (17%) relative to τlaser across all spot sizes for both values of DW (again, however, such a condition would introduce practical challenges with beam current and thus f).
Generally, a decrease in τelectron as hν approaches Φ is expected, as both the total integrated energy and the overall energy spread of the photoelectron distribution are reduced (see Fig. 1d).61,67 Despite the differing architectures, dimensions, and field strengths, such an effect also exists in dedicated UED instruments and arises from the dependence on the longitudinal velocity spread and the average field strength of the accelerating cavity (which here is 1.7 kV mm−1).59 Further, the longitudinal velocity spread depends upon E0 and the angular distributions of the photoelectrons. Here the specific accelerator-induced temporal broadening was calculated to be 650 fs for hν = 4.81 eV, 474 fs for hν = 3.61 eV, and 171 fs for hν = 2.41 eV. Convoluting this with τlaser (root sum square), the minimum τelectron for DW = 1.2 mm was found to be 716, 561, and 345 fs (fwhm) for hν = 4.81, 3.61, and 2.41 eV, respectively (spot size = 0, Fig. 5 bottom panel). For DW = 0.9 mm, the minimum τelectron increases by ∼200 fs for 4.81 and 3.61 eV and by ∼50 fs for 2.41 eV due to increased interactions with the Wehnelt aperture for a larger fraction of the overall integrated photoelectron distribution.
Though not the subject of this particular study, it is worth briefly emphasizing that one must also consider the impact of the laser-pulse properties and instrument architecture on beam coherence and beam current (i.e., photoelectron collection efficiency) for studying ultrafast dynamics with Å–fs–meV TEM (in addition to τrelaxation and reversibility). For example, using hν = Φ may generally provide the highest coherence and shortest τelectron (i.e., best temporal resolution), but it will also result in the lowest photoelectron yield and the lowest beam current.69 This poses a challenge, as long acquisition times and/or high repetition rates must be used in order to minimize signal acquisition times and the deleterious impacts of lab and instrument instabilities. To offset the low beam current, one can use a higher laser fluence when hν is close to Φ, but this introduces other challenges due to electron–electron interactions and associated reductions in coherence and τelectron and will negate any gains achieved by matching hν to Φ. The view here is that τelectron is one of three important parameters that need to be quantitatively understood, the other two being coherence and current, and they are all interwoven with one another. Thus, generation of operational phase diagrams for these parameters for specific instruments should be coupled with specific lab conditions in order to define ultimate resolution limits. This is likely to require multiple systematic studies of increasing complexity, which are then tested with careful experimentation under optimal conditions.
Effect of τlaser on τelectron
In addition to hν, the laser-pulse duration (τlaser) for photoelectron-generation was a specific parameter studied here. As optimization and trends of τelectron were the focus, values of τlaser < 300 fs were studied, as it was hypothesized that shorter τlaser will generally lead to shorter τelectron. Indeed, as noted above, in the single-electron regime, temporal resolution is expected to be directly impacted by laser parameters, including τlaser. Accordingly, Fig. 6 summarizes the results for τlaser ranging 50 to 300 fs at 50 fs steps. Otherwise identical conditions to those for Fig. 4 were used, where the E0 distribution for hν = 4.81 eV was simulated (Fig. 1d). | ||
Fig. 6 Single-electron packet duration (τelectron, fwhm) as a function of photoemission spot size for laser-pulse durations (τlaser, fwhm) spanning 50 to 300 fs (panel a legend for τlaser applies to all panels) for DW of 1.0 mm (a and b) and 1.2 mm (c and d). Dtip = 180 μm and the E0 distribution for hν = 4.81 eV (Fig. 1d) were used for all simulations. Panels (b and d) show linear fits to the difference between τelectron (i.e., τel) for τlaser = 50 fs (τel − τel,50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fs) and all other laser-pulse durations for DW = 1.0 and 1.2 mm, respectively. The shaded bands around each line represent the 95% confidence level. fs) and all other laser-pulse durations for DW = 1.0 and 1.2 mm, respectively. The shaded bands around each line represent the 95% confidence level. | ||
The immediate and most important result shown in Fig. 6 is that, even for the shortest τlaser = 50 fs, the minimum τelectron observed is broadened by several hundred fs (e.g., τelectron = 625 fs at ∼20 μm spot size for DW = 1.2 mm, Fig. 6c). This suggests that simply using a shorter fs laser pulse is insufficient for significantly improving UEM temporal resolution in the single-electron regime. This stems from the influence the Wehnelt aperture and electrostatic interactions have on τelectron, as observed when comparing the results for DW = 1.0 and 1.2 mm (e.g., much larger dispersion for the smaller aperture). This dispersion seems to be a general limitation to τelectron, despite the complete absence of electron–electron interactions in the single-electron regime.67Fig. 6 also shows that, while improvement in τelectron occurs when reducing τlaser from 300 to 50 fs (regardless of DW), shorter laser-pulse durations result in diminishing returns in temporal resolution. For example, for DW = 1.2 mm, the minimum τelectron is ∼690 fs for τlaser = 300 fs, compared to 625 fs for τlaser = 50 fs. One must also contend with larger spectral bandwidths at shorter τlaser and the associated impacts on τelectron, in addition to challenges imposed by electrostatic effects. The effect of diminishing returns when going to shorter τlaser is summarized in Fig. 6b and d, where the difference between τlaser = 50 fs and all other durations is plotted as a function of the photoemission spot size.
Effect of LaB6 tip size (Dtip) on τelectron
Finally, the diameter of the emitting surface of the truncated LaB6 cathode (Dtip) was another adjustable parameter explored here owing to the hypothesized influence different tip sizes will have on the electrostatic fields in the gun region. The effects of four commonly-used Dtip on τelectron as a function of photoemission spot size were investigated (Fig. 7). For each simulation, DW was fixed at 1.0 mm, the E0 distribution for hν = 4.81 eV was used (Fig. 1d), and τlaser was fixed at 300 fs (fwhm). It was found that Dtip generally has a significant effect on τelectron, though the magnitude and sensitivity strongly depend on the photoemission spot size. Indeed, at a spot size of ∼10 μm, τelectron is roughly identical for all Dtip (∼850 fs), but increasing to 16 μm (the limit of the smallest tip) causes τelectron for Dtip = 50 μm to increase to nearly 1.25 ps. Further, τelectron varies by nearly a factor of two for the three largest tip sizes at a fixed spot size of 35 μm. This behavior supports the hypothesis that the tip size itself impacts the electrostatic fields in the gun region, which in turn influences τelectron. This is practically important, as it indicates τelectron may significantly change if the tip size is changed (e.g., by changing cathodes) but the laser spot size is not (e.g., by changing the focal spot size). Moving to larger spot sizes, the dispersion behavior is such that τelectron plateaus to a single value, as observed for many cases above, suggesting a relatively poor but consistent temporal resolution can be expected for Dtip > ∼150 μm. In general, the results indicate the dispersion behavior is such that variations in τelectron are initially small for tight laser focus which then passes through a strongly-dispersive regime before again plateauing an elevated but consistent and robust value for large spot sizes. The trend in Fig. 7 also suggests that the strongly-dispersive regime will shift to larger spot sizes for larger Dtip (compare the 100 and 180 μm simulations). This suggests that a practical approach to preserving high temporal resolution while having a somewhat forgiving spot-size requirement would be to use a large cathode and a laser spot size that is smaller than that at which the dispersion sets in (i.e., smaller than the tip-dependent threshold dispersion value).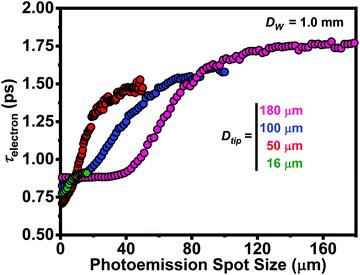 | ||
| Fig. 7 Dependence of τelectron (fwhm) on photoemission spot size for four LaB6 emitting surface diameters (Dtip = 16, 50, 100, and 180 μm). Wehnelt diameter was fixed at DW = 1.0 mm, the incident laser-pulse duration was fixed at τlaser = 300 fs (fwhm), and the E0 distribution for hν = 4.81 eV shown in Fig. 1d was used each Dtip. Photoemission spot sizes were limited to the available emitting surface (i.e., shank emission for spot sizes larger than Dtip were ignored, as justified by the reasons given above). | ||
In summary, we have systematically explored the impact of various laser-pulse and electron-gun conditions and parameters on the duration of single-electron packets using GPT simulations and properties specific to the FEI Tecnai Femto UEM. We have identified a number of simple, adjustable parameters for optimizing the temporal resolution, and we have also identified operating phase spaces of both low and high sensitivity to those parameters. This work constitutes one part of a larger effort aimed at quantifying the ultimate spatial, temporal, and energy resolutions of ultrafast TEMs such that combined Å–fs–meV operating conditions might be achieved and experimentally demonstrated. This foundational effort, wherein temporal resolution under space-charge-free conditions was explored, will complement studies focused on understanding beam coherence and beam current in order to conduct multi-dimensional parameter-space mapping. An additional hope is that this work will continue to spur significant efforts into expanding TEM temporal resolution at levels comparable to spatial and energy resolutions.
Author contributions
W. A. C. contributions were data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review and editing. D. J. F. contributions were conceptualization, data curation, funding acquisition, methodology, project administration, resources, supervision, visualization, writing – original draft, writing – review and editing. See the NISO CRediT taxonomy for definitions of contributing roles (http://credit.niso.org).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based on work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award No. DE-SC0018204. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-1839286. This work was supported partially by the National Science Foundation through the University of Minnesota MRSEC under Award Number DMR-2011401. Acknowledgement is made to the Donors of the American Chemical Society Petroleum Research Fund for partial support of this research under Award No. 60584-ND10. We thank Dr Erik Kieft of Thermo Fisher Scientific for assistance with modeling the FEI Tecnai Femto architecture and for ensuring accurate electrostatic field maps were generated.References
- V. A. Lobastov, R. Srinivasan and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 7069–7073 CrossRef CAS PubMed.
- A. H. Zewail, Science, 2010, 328, 187–193 CrossRef CAS PubMed.
- D. J. Flannigan and A. H. Zewail, Acc. Chem. Res., 2012, 45, 1828–1839 CrossRef CAS PubMed.
- D. A. Plemmons, P. K. Suri and D. J. Flannigan, Chem. Mater., 2015, 27, 3178–3192 CrossRef CAS.
- A. Yurtsever and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3152–3156 CrossRef CAS PubMed.
- A. Yurtsever, S. Schaefer and A. H. Zewail, Nano Lett., 2012, 12, 3772–3777 CrossRef CAS PubMed.
- D. R. Cremons, D. A. Plemmons and D. J. Flannigan, Nat. Commun., 2016, 7, 11230 CrossRef CAS PubMed.
- D. T. Valley, V. E. Ferry and D. J. Flannigan, Nano Lett., 2016, 16, 7302–7308 CrossRef CAS PubMed.
- D. R. Cremons, D. X. Du and D. J. Flannigan, Phy. Rev. Mater., 2017, 1, 073801 CrossRef.
- D. R. Cremons, D. A. Plemmons and D. J. Flannigan, Struct. Dyn., 2017, 4, 044019 CrossRef PubMed.
- A. J. McKenna, J. K. Eliason and D. J. Flannigan, Nano Lett., 2017, 17, 3952–3958 CrossRef CAS PubMed.
- A. Feist, N. Rubiano da Silva, W. Liang, C. Ropers and S. Schäfer, Struct. Dyn., 2018, 5, 014302 CrossRef PubMed.
- Y. C. Zhang and D. J. Flannigan, Nano Lett., 2019, 19, 8216–8224 CrossRef CAS PubMed.
- S. A. Reisbick, Y. C. Zhang and D. J. Flannigan, J. Phys. Chem. A, 2020, 124, 1877–1884 CrossRef CAS PubMed.
- A. Nakamura, T. Shimojima, Y. Chiashi, M. Kamitani, H. Sakai, S. Ishiwata, H. Li and K. Ishizaka, Nano Lett., 2020, 20, 4932–4938 CrossRef CAS PubMed.
- E. J. VandenBussche and D. J. Flannigan, Philos. Trans. R. Soc., A, 2020, 378, 20190598 CrossRef PubMed.
- Y. Kurman, R. Dahan, H. H. Sheinfux, K. Wang, M. Yannai, Y. Adiv, O. Reinhardt, L. H. G. Tizei, S. Y. Woo, J. Li, J. H. Edgar, M. Kociak, F. H. L. Koppens and I. Kaminer, Science, 2021, 372, 1181–1186 CrossRef CAS PubMed.
- M. S. Grinolds, V. A. Lobastov, J. Weissenrieder and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18427–18431 CrossRef CAS PubMed.
- V. A. Lobastov, J. Weissenrieder, J. Tang and A. H. Zewail, Nano Lett., 2007, 7, 2552–2558 CrossRef CAS PubMed.
- S. Z. Ji, O. Granas, K. Rossnagel and J. Weissenrieder, Phys. Rev. B, 2020, 101, 094303 CrossRef CAS.
- X. Fu, F. Barantani, S. Gargiulo, I. Madan, G. Berruto, T. LaGrange, L. Jin, J. Wu, G. M. Vanacore, F. Carbone and Y. Zhu, Nat. Commun., 2020, 11, 5770 CrossRef CAS PubMed.
- T. Danz, T. Domrose and C. Ropers, Science, 2021, 371, 371–374 CrossRef CAS PubMed.
- S. A. Reisbick, Y. Zhang, J. Chen, P. E. Engen and D. J. Flannigan, J. Phys. Chem. Lett., 2021, 12, 6439–6447 CrossRef CAS PubMed.
- B. Barwick, D. J. Flannigan and A. H. Zewail, Nature, 2009, 462, 902–906 CrossRef CAS PubMed.
- D. J. Flannigan, B. Barwick and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9933–9937 CrossRef CAS PubMed.
- A. Yurtsever, J. S. Baskin and A. H. Zewail, Nano Lett., 2012, 12, 5027–5032 CrossRef CAS PubMed.
- A. Yurtsever, R. M. van der Veen and A. H. Zewail, Science, 2012, 335, 59–64 CrossRef CAS PubMed.
- A. Yurtsever and A. H. Zewail, Nano Lett., 2012, 12, 3334–3338 CrossRef CAS PubMed.
- S. T. Park, A. Yurtsever, J. S. Baskin and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9277–9282 CrossRef CAS PubMed.
- B. Barwick and A. H. Zewail, ACS Photonics, 2015, 2, 1391–1402 CrossRef CAS.
- T. T. A. Lummen, R. J. Lamb, G. Berruto, T. LaGrange, L. Dal Negro, F. J. G. de Abajo, D. McGrouther, B. Barwick and F. Carbone, Nat. Commun., 2016, 7, 13156 CrossRef CAS PubMed.
- M. Kaplan, B. K. Yoo, J. Tang, T. E. Karam, B. L. Liao, D. Majumdar, D. Baltimore, G. J. Jensen and A. H. Zewail, Angew. Chem., Int. Ed., 2017, 56, 11498–11501 CrossRef CAS PubMed.
- Y. Lu, B. K. Yoo, A. H. C. Ng, J. Kim, S. Yeom, J. Tang, M. M. Lin, A. H. Zewail and J. R. Heath, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 22014–22019 CrossRef CAS PubMed.
- A. Konecna, V. Di Giulio, V. Mkhitaryan, C. Ropers and F. J. G. de Abajo, ACS Photonics, 2020, 7, 1290–1296 CrossRef CAS.
- M. Liebtrau, M. Sivis, A. Feist, H. Lourenco-Martins, N. Pazos-Perez, R. A. Alvarez-Puebla, F. J. G. de Abajo, A. Polman and C. Ropers, Light: Sci. Appl., 2021, 10, 82 CrossRef CAS PubMed.
- A. Lassise, P. H. A. Mutsaers and O. J. Luiten, Rev. Sci. Instrum., 2012, 83, 043705 CrossRef CAS PubMed.
- J. Q. Qiu, G. H. Ha, C. G. Jing, S. V. Baryshev, B. W. Reed, J. W. Lau and Y. M. Zhu, Ultramicroscopy, 2016, 161, 130–136 CrossRef CAS PubMed.
- W. Verhoeven, J. F. M. van Rens, E. R. Kieft, P. H. A. Mutsaers and O. J. Luiten, Ultramicroscopy, 2018, 188, 85–89 CrossRef CAS PubMed.
- J. F. M. van Rens, W. Verhoeven, J. G. H. Franssen, A. C. Lassise, X. F. D. Stragier, E. R. Kieft, P. H. A. Mutsaers and O. J. Luiten, Ultramicroscopy, 2018, 184, 77–89 CrossRef CAS PubMed.
- J. F. M. van Rens, W. Verhoeven, E. R. Kieft, P. H. A. Mutsaers and O. J. Luiten, Appl. Phys. Lett., 2018, 113, 163104 CrossRef.
- C. Kisielowski, P. Specht, B. Freitag, E. R. Kieft, W. Verhoeven, J. F. M. van Rens, P. Mutsaers, J. Luiten, S. Rozeveld, J. Kang, A. J. McKenna, P. Nickias and D. F. Yancey, Adv. Funct. Mater., 2019, 29, 1807818 CrossRef.
- C. G. Jing, Y. M. Zhu, A. Liu, K. Schliep, X. W. Fu, Y. B. Zhao, E. Montgomery, W. Rush, A. Kanareykin, M. Katz and J. Lau, Ultramicroscopy, 2019, 207, 112829 CrossRef CAS PubMed.
- I. G. C. Weppelman, R. J. Moerland, L. Zhang, E. Kieft, P. Kruit and J. P. Hoogenboom, Struct. Dyn., 2019, 6, 024102 CrossRef CAS PubMed.
- W. Verhoeven, J. F. M. van Rens, A. H. Kemper, E. H. Rietman, H. A. van Doorn, I. Koole, E. R. Kieft, P. H. A. Mutsaers and O. J. Luiten, Rev. Sci. Instrum., 2019, 90, 083703 CrossRef CAS PubMed.
- J. W. Lau, K. B. Schliep, M. B. Katz, V. J. Gokhale, J. J. Gorman, C. Jing, A. Liu, Y. Zhao, E. Montgomery, H. Choe, W. Rush, A. Kanareykin, X. Fu and Y. Zhu, Rev. Sci. Instrum., 2020, 91, 021301 CrossRef CAS PubMed.
- X. W. Fu, E. D. Wang, Y. B. Zhao, A. Liu, E. Montgomery, V. J. Gokhale, J. J. Gorman, C. G. Jing, J. W. Lau and Y. M. Zhu, Sci. Adv., 2020, 6, eabc3456 CrossRef PubMed.
- C. J. R. Duncan, D. A. Muller and J. M. Maxson, Phys. Rev. Appl., 2020, 14, 014060 CrossRef CAS.
- M. R. Armstrong, K. Boyden, N. D. Browning, G. H. Campbell, J. D. Colvin, W. J. DeHope, A. M. Frank, D. J. Gibson, F. Hartemann, J. S. Kim, W. E. King, T. B. LaGrange, B. J. Pyke, B. W. Reed, R. M. Shuttlesworth, B. C. Stuart and B. R. Torralva, Ultramicroscopy, 2007, 107, 356–367 CrossRef CAS PubMed.
- A. Gahlmann, S. Tae Park and A. H. Zewail, Phys. Chem. Chem. Phys., 2008, 10, 2894–2909 RSC.
- Z. Tao, H. Zhang, P. M. Duxbury, M. Berz and C.-Y. Ruan, J. Appl. Phys., 2012, 111, 044316 CrossRef.
- A. Gliserin, A. Apolonski, F. Krausz and P. Baum, New J. Phys., 2012, 14, 073055 CrossRef.
- P. Baum and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18409–18414 CrossRef CAS PubMed.
- B. Barwick, H. S. Park, O. H. Kwon, J. S. Baskin and A. H. Zewail, Science, 2008, 322, 1227–1231 CrossRef CAS PubMed.
- K. Bikker, M. Picher, O. Cregut, T. LaGrange, B. W. Reed, S. T. Park, D. J. Masiel and F. Banhart, Ultramicroscopy, 2016, 171, 8–18 CrossRef PubMed.
- E. Kieft, K. B. Schliep, P. K. Suri and D. J. Flannigan, Struct. Dyn., 2015, 2, 051101 CrossRef PubMed.
- H. S. Park, J. S. Baskin, O. H. Kwon and A. H. Zewail, Nano Lett., 2007, 7, 2545–2551 CrossRef CAS PubMed.
- P. Baum, Chem. Phys., 2013, 423, 55–61 CrossRef CAS.
- D. A. Plemmons and D. J. Flannigan, Chem. Phys. Lett., 2017, 683, 186–192 CrossRef CAS.
- M. Aidelsburger, F. O. Kirchner, F. Krausz and P. Baum, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19714–19719 CrossRef CAS PubMed.
- L. Piazza, D. J. Masiel, T. LaGrange, B. W. Reed, B. Barwick and F. Carbone, Chem. Phys., 2013, 423, 79–84 CrossRef CAS.
- S. A. Aseyev, A. S. Sadkov, B. N. Mironov, A. A. Ischenko, S. V. Chekalin and E. A. Ryabov, J. Exp. Theor. Phys., 2019, 128, 379–383 CrossRef CAS.
- K. Halbach and R. F. Holsinger, Part. Accel., 1976, 7, 213–222 Search PubMed.
- M. J. de Loos and S. B. van der Geer, Proc. 5th Eur. Part. Acc. Conf., Sitges, 1996, 1241.
- Z. T. Pei and C. N. Berglund, Jpn. J. Appl. Phys., Part 2, 2002, 41, L52–L54 CrossRef CAS.
- C. Weninger and P. Baum, Ultramicroscopy, 2012, 113, 145–151 CrossRef CAS.
- S. Mogren and R. Reifenberger, Surf. Sci., 1987, 186, 232–246 CrossRef CAS.
- P. Baum, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124005 CrossRef.
- D. Kreier, D. Sabonis and P. Baum, J. Opt., 2014, 16, 075201 CrossRef.
- K. Torgasin, K. Morita, H. Zen, K. Masuda, T. Katsurayama, T. Murata, S. Suphakul, H. Yamashita, T. Nogi, T. Kii, K. Nagasaki and H. Ohgaki, Phys. Rev. Accel. Beams, 2017, 20, 073401 CrossRef.
Footnote |
| † Provided by Dr Erik Kieft of Thermo Fisher Scientific. |
| This journal is © the Owner Societies 2021 |