A framework for constructing linear free energy relationships to design molecular transition metal catalysts†
Zhenzhuo
Lan
 a and
Shaama
Mallikarjun Sharada
a and
Shaama
Mallikarjun Sharada
 *ab
*ab
aMork Family Department of Chemical Engineering and Materials Science, University of Southern California, Los Angeles, CA, USA. E-mail: ssharada@usc.edu
bDepartment of Chemistry, University of Southern California, Los Angeles, CA, USA
First published on 6th July 2021
Abstract
A computational framework for ligand-driven design of transition metal complexes is presented in this work. We propose a general procedure for the construction of active site-specific linear free energy relationships (LFERs), which are inspired from Hammett and Taft correlations in organic chemistry and grounded in the activation strain model (ASM). Ligand effects are isolated and quantified in terms of their contribution to interaction and strain energy components of ASM. Scalar descriptors that are easily obtainable are then employed to construct the complete LFER. We successfully demonstrate proof-of-concept by constructing and applying an LFER to CH activation with enzyme-inspired [Cu2O2]2+ complexes. The key benefit of using ASM is a built-in compensation or error cancellation between LFER prediction of interaction and strain terms, resulting in accurate barrier predictions for 37 of the 47 catalysts examined in this study. The LFER is also transferable with respect to level of theory and flexible towards the choice of reference system. The absence of interaction-strain compensation or poor model performance for the remaining systems is a consequence of the approximate nature of the chosen interaction energy descriptor and LFER construction of the strain term, which focuses largely on trends in substrate and not catalyst strain.
1 Introduction
In the field of homogeneous catalysis with molecular transition metal complexes, there is a growing need for systematic approaches to probe the influence of active site-bound ligands on catalytic activity, as this is a necessary step towards rational catalyst screening and design. Significant progress has been made in screening and design of heterogeneous catalysts in recent decades.1,2 Experiment-3,4 and theory-based5–8 screening methods for molecular catalysts are still emerging. This is largely a consequence of complex interplay between metal oxidation and spin states, ligands, substrates, solvent, counter-ions, and other factors, whose individual and combined contributions to catalytic activity can be challenging to capture.Quantitative molecular catalyst design strategies can be categorized broadly into scaling relationships or volcano plots relying on energetic descriptors and valence bond approaches,9–13 those based on artificial intelligence and machine learning methods,14 and linear free energy relationships (LFERs) that rely on capturing ligand electronic and steric effects using a set of scalar, structural descriptors.8,15 LFERs describe reaction rate or equilibrium dependence on structural and electronic attributes of the system.16 This dependence is linear when the reaction mechanism is not altered upon variation of substituents. LFERs were originally developed as Hammett relationships in organic aromatic chemistry to describe the influence of (meta- or para-) substituents on the dissociation rate of benzoic acid. In Hammett relationships, the electrophilicity descriptor is a Hammett parameter (σm or σp) and the slope of the Hammett plot describes the sensitivity of the mechanism to substituent electrophilicity.17 Taft extended this framework to ortho-substituted groups via the inclusion of an additive term that captures the impact of substituent steric bulk.18 The resulting free energy relationship has two additive terms, one describing the electronic effect and another describing the steric effect of substituents on reaction rates or equilibria.
Such frameworks can offer systematic means to probe and predict the impact of ligands bound to a transition metal active site on catalyst performance metrics such as activity, selectivity, and stability.4 The construction of an LFER framework requires quantitative information regarding various ligand effects as well as the identification of appropriate scalar descriptors for these effects. It may seem intuitive to categorize ligand effects into their ability to tune the electronic character of the active site and their spatial extent, or steric bulk, that can impact substrate approach to the active site. These effects however, are often interrelated and difficult to isolate.19,20 As a result, the Taft equation describing reaction rate dependence on substituent electronic and steric effects cannot be generally applied across reaction chemistries with transition metal complexes. Our goal is to instead avoid explicit classification of ligand effects into electronic and steric terms, and develop an approach that relies on describing ligand effects in terms of directly measurable impacts on the activated catalyst–substrate system.
This study aims to establish a framework for constructing LFERs for CH activation with metal–oxygen active sites by quantifying trends in barriers obtained via systematic catalyst perturbations. Instead of breaking down ligand contributions into electronic and steric terms, we examine their impact on interaction and strain energy differences between transition and initial states of the catalyst–substrate system described by the activation strain model (ASM), also known as the distortion-interaction model.21,22 We utilize mechanistic findings from our prior study of CH activation with dioxo–dicopper complexes to calculate activation barriers using density functional theory (DFT).23 Our previous studies also identify descriptors for capturing trends in interaction23 and strain energies24 based on systematic ligand variations. An active site-specific LFER that combines both these effects is constructed in this work, as developing a single set of design rules that is valid across several active sites is a formidable task on account of the diversity in oxidation and spin states achievable with transition metal centers.25 We examine LFER accuracies in predicting activation barriers by examining several model [Cu2O2]2+ complexes constructed using imidazole N-donor ligands. The LFER is highly reliable, and predicts most barriers to within 10 kJ mol−1 of their DFT values. This is the consequence of a natural compensation or cancellation of errors observed between LFER predictions of constituent interaction and strain energies. Our functional and basis set tests show that the LFER is also transferable and can be used alongside multiple levels of theory. Analyses of outliers and sensitivity reveal that the Hammett parameter, used as a descriptor for ligand interaction effects, is the most likely cause for model deviations. In addition, as the model largely captures strain arising from substrate deformation (C-H stretch) in the transition state, LFER predictions are poorer for systems where catalyst strain deviates significantly from the reference system. Therefore, while we successfully demonstrate proof-of-concept for ASM-driven construction of LFERs, there is a need for descriptors that are more appropriate for transition metal complexes. Future work, in addition to expansion to other active sites, will include the search for interaction descriptors that are more suitable for metal–ligand bonds (such as metal ligand electronic parameters, MLEPs)26 which will enable construction of LFERs that are generalizable across several classes of ligands.
2 Methods
In this section, we outline the procedure for constructing a generalizable LFER model and illustrate its application to CH activation with model [Cu2O2]2+ complexes. We choose the dioxo–dicopper active site as it is found to selectively oxidize various types of CH bonds in several enzymes and their synthetic mimics.27,282.1 Activation strain model & LFER
The guiding hypothesis for this work is that ligand effects on reaction kinetics can be completely characterized by their impact on changes in interaction between catalyst and substrate and strain induced in the process of bond breakage/formation. The LFER model can be constructed by identifying suitable descriptors for capturing these interaction and strain energies. To this end, we employ the activation strain model or the distortion-interaction model. ASM proposes that the activation energy for a reaction step (ΔE‡) comprises destabilizing strain (ΔESTR) induced by geometric deformation from the initial to transition structure and stabilizing interaction between catalyst and substrate (ΔEINT).22,29| ΔE‡ = ΔEINT + ΔESTR | (1) |
To develop an LFER expression using ASM, we invoke the original equation put forth by Taft for ortho-substituted aromatics to quantify electronic and steric substituent effects:18
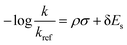 | (2) |
By employing simplifying approximations, we can rewrite the Taft LFER using ASM. First, we assume that zero-point energies, enthalpy, entropy, and pre-exponential terms in the rate coefficient expression are less sensitive to the choice of ligand compared to electronic energies. Therefore, the LHS of eqn (2) can be rewritten as:
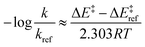 | (3) |
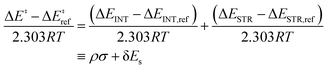 | (4) |
2.2 LFER construction: CH activation with dioxo–dicopper complexes
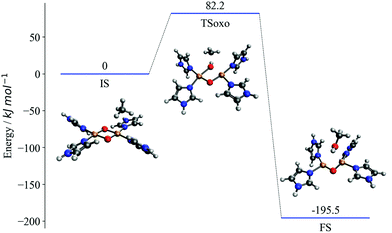
The proposed mechanism of CH activation has been debated extensively in the literature.46–52 By contrasting with experimental substrate variation-based curves,23 we demonstrate in our previous work that (in the absence of spin-crossing) the one-step oxo-insertion mechanism is preferred to the two-step radical recombination mechanism on the singlet potential energy surface. Fig. 1 represents the potential energy surface for the singlet oxo-insertion mechanism along with the geometries of initial, transition, and final states, labeled IS, TSoxo, and FS, respectively. The mechanism is concerted, and proceeds via simultaneous C–H and Cu–O bond breaking and C–O and O–H bond formation.
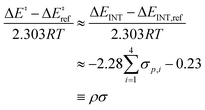 | (5) |
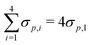 ) and the non-zero intercept is a consequence of choosing the amine reference (Xam = H for ΔEref and ΔEINT). Using the Hammett parameter associated with para-substituted ligands, σp, as the electronic descriptor, we find that the slope ρ = −2.28 is in excellent agreement with experiment (−2.2) at 148 K (−125 °C).53 Therefore, the mechanism is sensitive to choice of ligand electrophilicity and TSoxo is more stabilized when the active site is coordinated to electron-withdrawing ligands compared to electron-donating ligands. These variations in stabilization are captured in the ΔEINT component of ASM.
) and the non-zero intercept is a consequence of choosing the amine reference (Xam = H for ΔEref and ΔEINT). Using the Hammett parameter associated with para-substituted ligands, σp, as the electronic descriptor, we find that the slope ρ = −2.28 is in excellent agreement with experiment (−2.2) at 148 K (−125 °C).53 Therefore, the mechanism is sensitive to choice of ligand electrophilicity and TSoxo is more stabilized when the active site is coordinated to electron-withdrawing ligands compared to electron-donating ligands. These variations in stabilization are captured in the ΔEINT component of ASM.
While this analysis indicates that the Hammett parameter may be a reliable descriptor for interaction energies, we find poor fit to linear models for amine N-donors, which is expected as these amines are not aromatic.23 Furthermore, we are limited to using the Hammett parameter for the substituent only (e.g. CH3) rather than the entire N-donor (NH2CH3) as values (experimental or otherwise) for the latter are not readily available. Alternative scalar descriptors such as the charge of the active site oxygen atom or catalyst HOMO levels do not easily lend themselves to LFER construction. As a consequence of these limitations, we proceed with the Hammett parameter, σp, for LFER development but demonstrate proof-of-concept for complexes constructed using only imidazole N-donors. Going forward, our goal is to identify interaction descriptors that are more suitable for metal–ligand bonds than organic aromatic systems to develop LFERs that are transferable across various ligand backbones, which in this case consist of amines, diamines, imidazoles, and pyridines.
The resulting strain-only LFER, where ΔEINT is invariant, is determined to be:24
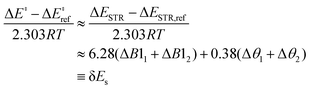 | (6) |
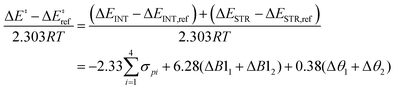 | (7) |
To apply these types of LFER models, one needs a DFT barrier calculations for a single reference system (ΔEref) and descriptors for the reference and system of interest. The model (eqn (7)) can then predict the barrier (ΔE‡) for the system of interest without the need for several tedious transition structure and barrier calculations.
2.3 LFER model performance tests
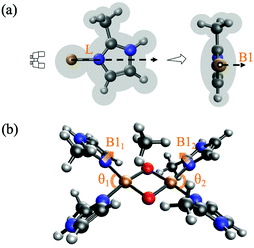
We examine the viability of the proposed framework for LFER construction by analyzing the accuracy of eqn (7). This work probes ΔE predictions for fully relaxed systems where active sites are bound to monodentate imidazole N-donors (C3N2H3Xim). Xim is substituted at the C atom between the two N atoms as shown in Fig. 3(a). Fig. 3(b) represents the geometry of [Cu2O2]2+ complexes with four imidazole groups. Eleven symmetric complexes are constructed using four identical Xim groups, denoted S1–S11. In addition, a diverse set of 38 [Cu2O2]2+ complexes are obtained by mixed, asymmetric substitution of Xim groups as shown in Table 1, named A1–A38, where both the types of N-donors as well as their positions (illustrated in Fig. 3(b)) are varied.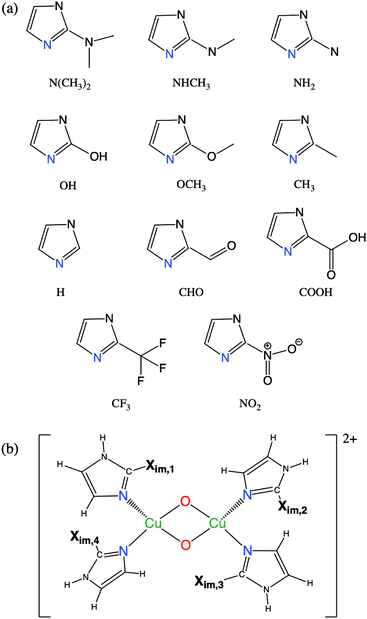 | ||
| Fig. 3 (a) Geometry of eleven imidazole groups substituted with Xim groups (S1–S11) and (b) geometry of monodentate [Cu2O2]2+ complexes with four imidazole groups. | ||
| Index | Xim,1 | Xim,2 | Xim,3 | Xim,4 |
|---|---|---|---|---|
| A1 | OCH3 | H | OCH3 | H |
| A2 | CH3 | H | CH3 | H |
| A3 | CF3 | H | CF3 | H |
| A4 | NO2 | H | NO2 | H |
| A5 | CH3 | OCH3 | CH3 | OCH3 |
| A6 | OCH3 | CF3 | OCH3 | CF3 |
| A7 | OCH3 | NO2 | OCH3 | NO2 |
| A8 | CH3 | CF3 | CH3 | CF3 |
| A9 | CH3 | NO2 | CH3 | NO2 |
| A10 | CF3 | NO2 | CF3 | NO2 |
| A11 | H | H | CF3 | H |
| A12 | H | H | CH3 | H |
| A13 | H | H | NO2 | H |
| A14 | H | H | OCH3 | H |
| A15 | H | H | CF3 | CF3 |
| A16 | H | H | CH3 | CH3 |
| A17 | H | H | NO2 | NO2 |
| A18 | H | H | OCH3 | OCH3 |
| A19 | H | CF3 | CF3 | H |
| A20 | CH3 | H | H | CH3 |
| A21 | H | NO2 | NO2 | H |
| A22 | OCH3 | H | H | OCH3 |
| A23 | CF3 | H | CF3 | CF3 |
| A24 | CH3 | H | CH3 | CH3 |
| A25 | H | NO2 | NO2 | NO2 |
| A26 | OCH3 | H | OCH3 | OCH3 |
| A27 | NO2 | CF3 | CF3 | NO2 |
| A28 | CH3 | CF3 | CF3 | CH3 |
| A29 | CH3 | NO2 | NO2 | CH3 |
| A30 | OCH3 | CF3 | CF3 | OCH3 |
| A31 | OCH3 | CH3 | CH3 | OCH3 |
| A32 | OCH3 | NO2 | NO2 | OCH3 |
| A33 | H | CH3 | H | OCH3 |
| A34 | H | CF3 | H | OCH3 |
| A35 | H | NO2 | H | OCH3 |
| A36 | H | CF3 | H | CH3 |
| A37 | H | NO2 | H | CH3 |
| A38 | NO2 | H | CF3 | H |
We use the ab initio quantum chemistry software, Q-Chem (Version 5.1 and above)60 to carry out all DFT calculations. Barriers are calculated for CH4 activation using the range-separated hybrid functional, ωB97X-D,61,62 and the Stuttgart Relativistic Small Core (srsc) effective core potential for Cu63 and triple-ζ 6-311+G* basis set with diffuse and polarization functions for the remaining atoms. The level of theory is identical to that employed for constructing the strain LFER. For the interaction LFER, the same functional was employed alongside a smaller basis set (6-31G*). Wavefunction stability analysis is used to determine stable, broken-symmetry (BS) wavefunctions.64,65 The extent of spin contamination is found to be similar across all systems in both initial (〈S2〉average = 0.098) and transition structures (〈S2〉average = 1.284). Consistent with our LFER construction studies, the second-generation absolutely-localized molecular orbital-EDA, or ALMO-EDA, is employed to calculate the ΔEINT term in ASM.66–71 The LFER model prediction is deemed accurate if the predicted barrier is within 10 kJ mol−1 of the ‘true’ DFT value, in line with the rule of thumb typically applied to energy differences that are meaningfully resolvable by DFT.
2.4 Model sensitivity & transferability
Sensitivity analysis refers to the examination of uncertainty in model output. The analysis determines the source of uncertainty, or the degree to which the model output varies with variation of each input parameter. This analysis is aimed at identifying model sensitivity to the three sets of LFER descriptors – σp, Sterimol B1, and bite angle θ. We select a global variance-based sensitivity analysis, known as the Sobol method72 implemented in the SALib Python package.73 A first-order Sobol sensitivity analysis calculates the percentage influence of the variance of each descriptor on the barrier variance and thus determines the relative significance of descriptors.An LFER model, once constructed, must be usable alongside any level of theory. In other words, a truly generalizable LFER requires DFT calculations at the desired level of theory for only a single reference system. The reference calculation and descriptors can then be plugged into eqn (7) to predict barriers for arbitrary ligands coordinated to the [Cu2O2]2+ center. To determine whether this is the case with our ASM-based LFER model, we identify density functional approximations that benchmarking studies demonstrate to be reliable predictors of activation barriers.74,75 We also examine sensitivity to size and choice of basis set. The chosen levels of theory are described in Table 2, where the ‘baseline’ refers to ωB97X-D/6-311+G* (srsc for Cu) utilized to assess LFER model performance. Strain descriptors and IS and TSoxo structures are calculated at these levels of theory to contrast LFER predictions with DFT results. Owing to difficulties converging optimization cycles for SCAN0, single point IS and TSoxo calculations are performed with SCAN0 on structures optimized at the baseline level of theory.
| Purpose | Class | Functional | Basis set (effective core potential) |
|---|---|---|---|
| Baseline | Range-separated hybrid functional | ωB97X-D76 | 6-311+G* (Cu: srsc) |
| Functional test | Global hybrid functional | PBE077 | 6-311+G* (Cu: srsc) |
| Functional test | Hybrid meta-generalized gradient approximation | SCAN078 | 6-311+G* (Cu: srsc) |
| Functional test | Range-separated hybrid functional | ωB97X-V79 | 6-311+G* (Cu: srsc) |
| Basis set test | Range-separated hybrid functional | ωB97X-D | 6-31G* |
| Basis set test | Range-separated hybrid functional | ωB97X-D | def-SVP |
| Basis set test | Range-separated hybrid functional | ωB97X-D | def-SVPD |
3 Results
Table 3 shows the interaction and strain descriptors and CH activation barriers for the symmetrically substituted (S1–S11) complexes. Note that even though the N-donor variation is based on electrophilicity of the substituent and S1–S11 are ordered with respect to increasing electron-withdrawing character of the substituent, DFT barriers do not necessarily follow the same trend. The corresponding data for asymmetrically substituted A1–A38 systems is reported in the ESI† (Table S1).| Index | Xim | ∑σp | θ 1 | θ 2 | B11 | B12 | ΔE‡DFT | ΔE‡LFER |
|---|---|---|---|---|---|---|---|---|
| S1 | N(CH3)2 | −3.32 | 94.585 | 98.370 | 1.95 | 1.92 | 94.0 | 116.4 |
| S2 | NHCH3 | −2.80 | 96.874 | 96.742 | 1.59 | 1.57 | 97.3 | 101.0 |
| S3 | NH2 | −2.64 | 97.006 | 97.099 | 1.57 | 1.59 | 88.4 | 100.5 |
| S4 | OH | −1.48 | 98.724 | 98.938 | 1.66 | 1.68 | 87.5 | 99.8 |
| S5 | OCH3 | −1.08 | 98.754 | 98.896 | 1.67 | 1.70 | 102.5 | 97.7 |
| S6 | CH3 | −0.68 | 92.672 | 92.937 | 1.72 | 1.71 | 85.0 | 83.2 |
| S7 | H | 0.00 | 95.678 | 95.803 | 1.65 | 1.62 | 82.2 | 82.2 |
| S8 | CHO | 1.68 | 95.278 | 95.264 | 1.62 | 1.63 | 81.4 | 69.7 |
| S9 | COOH | 1.80 | 97.469 | 97.316 | 1.62 | 1.61 | 79.2 | 73.1 |
| S10 | CF3 | 2.20 | 95.536 | 97.808 | 1.79 | 1.88 | 75.2 | 76.8 |
| S11 | NO2 | 3.12 | 97.179 | 96.610 | 1.65 | 1.59 | 63.1 | 63.5 |
The parity plot in Fig. 4 depicts LFER predictions (ΔELFER) relative to DFT barriers (ΔEDFT) for both symmetric (S1–S11) and asymmetric (A1–A38) systems. We find that LFER predictions are reliable for nearly 80% of all the systems examined in this study. Out of 47 systems (excluding reference S7), 37 LFER predictions are within 10 kJ mol−1 of the DFT value, shown by the shaded region about the x = y parity line in Fig. 4. Of these, 23 predictions are within 5 kJ mol−1 of the DFT value.
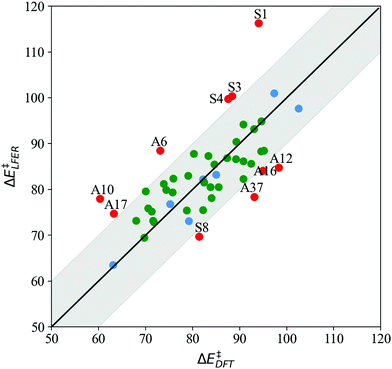 | ||
| Fig. 4 LFER predictions (ΔE‡LFER) vs. BS DFT barriers (ΔE‡DFT) at the ωB97X-D/srsc,6-311+G* level of theory (kJ mol−1) for 11 symmetrically substituted (S1–S11, blue) and 38 asymmetrically substituted catalysts (A1–A38, green). Points lying in the shaded region indicate LFER prediction is within 10 kJ mol−1 of the DFT value. All model outliers are marked in red and labeled “A”/“S” to indicate asymmetric/symmetrically substituted catalysts (structures listed in Tables 1 and 3, respectively). | ||
For S1–S11, model predictions are within 10 kJ mol−1 of DFT results for 6 systems (excluding the S7 reference), with a mean absolute error (MAE) of 3.1 kJ mol−1. The overall MAE is higher (7.7 kJ mol−1) on account of 4 outliers, with substituents (Xim) N(CH3)2, NH2, OH and CHO. For the asymmetrically substituted A1–A38, LFER predictions are within 10 kJ mol−1 of DFT results for 32 complexes, with MAE = 4.1 kJ mol−1. The overall MAE is slightly higher at 5.7 kJ mol−1. It is worth noting that with only a few exceptions (A6, A10, A37), LFER accurately predicts barriers for mixed ligand systems that contain both electron-donating and withdrawing N-donors relative to reference Xim = H, namely A7, A8, A9, A28, A29, A30, A32, A34, A35, and A36, for which MAE = 4.8 kJ mol−1.
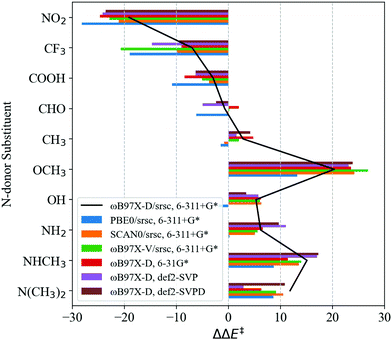
Transferability tests using levels of theory described in Table 2 are carried out for S1–S11. Before contrasting LFER performance, we determine whether trends in DFT barriers across N-donor substitutions are consistent across various levels of theory. In Fig. 5, we report BS barrier difference (ΔΔE‡) between a substituted imidazole and the reference (Xim = H, S7). The black curve in Fig. 5 corresponds to our baseline level of theory. In general, ΔΔE‡ across various functional and basis set combinations are within 10 kJ mol−1 of the baseline. The sole exception is S10 (Xim = CF3), for which PBE0 and ωB97X-V barriers are 12.0 kJ mol−1 and 13.7 kJ mol−1 lower than the baseline, respectively.
Based on the general agreement in trends across various levels of theory, we contrast LFER predictions calculated using eqn (7) with these levels of theory. Descriptors for LFERs are obtained at the same level of theory as the reference calculation. These descriptors as well as the resulting DFT and LFER barriers are listed in Table S2 of ESI.†Fig. 6 depicts LFER performance for each level of theory. In all cases, LFER performance resembles the baseline scenario, with similar MAEs and outliers. Functional tests result in MAEs of 9.9, 8.8, and 10.0 kJ mol−1 for PBE0, SCAN0, and ωB97X-V, respectively. Basis set tests yield MAEs of 9.0, 8.4, and 7.6 kJ mol−1 for 6-31G*, def2-SVP, and def2-SVPD, respectively. The LFER is therefore transferable across basis sets and density functional approximations. We also identify between 3 and 5 outliers at every level of theory. While S1 is an outlier in all cases, small variations are observed in the remaining outliers compared to the baseline scenario.
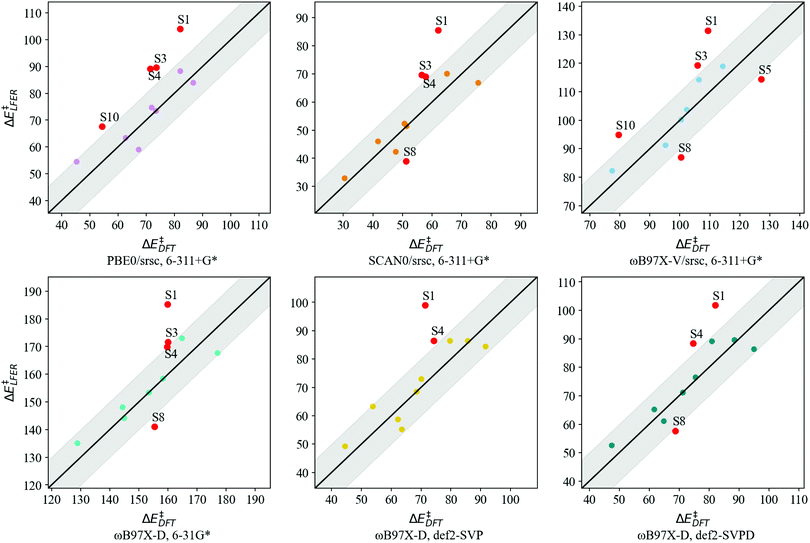 | ||
| Fig. 6 LFER predicted BS barriers vs. DFT barriers (kJ mol−1) for S1–S11 at levels of theory listed in Table 2. Points lying in the shaded region indicate LFER prediction is within 10 kJ mol−1 of the DFT value. All model outliers are marked in red and labeled “S” to indicate symmetrically substituted catalysts. | ||
We also calculate the first-order sensitivity of the LFER model to the chosen descriptors for interaction (σp) and strain (B1,θ). Fig. S1 of ESI,† depicts the first order sensitivities with respect to each of the 4 σp's, and each of 2B1 and θ values. The 4 σp's combined constitute the greatest determinant of LFER performance, with a total sensitivity of 70.3%. Model sensitivities to the 2B1 and 2θ descriptors are 12.8% and 16.9%, respectively. Therefore, LFER performance is least sensitive to one of the strain descriptors, B1, and most sensitive to the interaction descriptor, σp.
4 Discussion
The cornerstone of our catalyst design philosophy is that the influence of active site-bound ligands on kinetics can be isolated and captured using the activation strain model. The LFERs constructed using descriptor-based estimation of ASM components are then employed to predict the activity of catalysts bound to arbitrary ligands. Accordingly, for CH activation with catalysts consisting of the [Cu2O2]2+ active site, we isolate and quantify (1) ΔEINT with σp as the descriptor, and (2) ΔESTR with B1 and θ as descriptors, based on careful, systematic N-donor variations in each case. The resulting complete LFER is given by eqn (7). In this section, we lay out the reasoning behind accurate barrier predictions for the vast majority of catalysts examined. By assessing model sensitivities, descriptors, and by further decomposing strain energies into substrate and catalyst components, we also outline the possible reasons behind model failures, shown in red in Fig. 4. In short, our analysis shows that LFER accuracies rely on error cancellation between individual interaction and strain terms. However, the extent of absence of these cancellations arising from the choice of descriptors or model inadequacies in capturing ASM terms is difficult to deconvolute. Therefore, we emphasize that the analysis presented in this section is only semi-quantitative, aimed at identifying the most probable causes for model failure.4.1 LFER performance: activation-strain compensation
First, we analyze the rationale behind accurate LFER barrier predictions for nearly 80% of the systems examined in this study. We do so by breaking down the LFER prediction into its component ΔEINT and ΔESTR values. Table 4 shows this decomposition for the symmetrically substituted S1–S11 catalysts. The differences between model predictions and DFT results for A1–A38 are reported in Table 3 of the ESI.† In general, LFER is a poor predictor of individual interaction and strain components. However, the sum of these deviations in interaction and strain energies cancel out in most cases. To determine whether these deviations and their mutual cancellation are grounded in underlying model properties, we revisit the procedure for LFER construction.| Index | ΔEINT,LFER − ΔEINT,DFT | ΔESTR,LFER − ΔESTR,DFT | ΔE‡LFER − ΔE‡DFT |
|---|---|---|---|
| S1 | 8.4 | 14.0 | 22.3 |
| S2 | 13.0 | −9.3 | 3.7 |
| S3 | 15.9 | −3.8 | 12.1 |
| S4 | 5.8 | 6.6 | 12.4 |
| S5 | 5.4 | −10.1 | −4.8 |
| S6 | 5.0 | −6.8 | −1.8 |
| S7 | 0.0 | 0.0 | 0.0 |
| S8 | −1.3 | −10.4 | −11.7 |
| S9 | −21.9 | 15.8 | −6.1 |
| S10 | −9.9 | 11.4 | 1.6 |
| S11 | −26.6 | 27.0 | 0.4 |
To construct the interaction component of the LFER (eqn (1)), we vary N-donor electrophilicity and capture the effect on ΔEINT by forcing ΔESTR to be constant. Constant strain is achieved by freezing the active site and substrate. The active site distances as well as the C–H stretch in TSoxo are therefore identical to the reference in all systems. Consider the cases wherein electron-withdrawing substituents are bound to imidazole (S8–S11). While the decrease in barrier relative to the reference S7 manifests purely in ΔEINT during model construction, the barrier is also lowered due to reduced CH stretch in the fully relaxed system examined in this study. In the case of S11, the CH stretch is 1.415 Å in TSoxo, reduced from 1.447 Å in the reference S7 system. Therefore, this leads to a corresponding decrease in ΔESTR. In other words, in a completely relaxed system the barrier is redistributed between the ΔEINT and ΔESTR components of ASM compared to LFER construction wherein ΔESTR is invariant. For an electron-withdrawing substituent therefore, the LFER model is expected to predict more negative ΔEINT than what is observed with DFT, or ΔEINT,LFER − ΔEINT,DFT ≤ 0. Correspondingly, the observed DFT strain energy is lower than LFER, or ΔESTR,LFER − ΔESTR,DFT≥0. The converse is true for electron-donating groups, for which LFER is expected to predict higher interaction and lower strain energies. This compensation enables cancellation of LFER errors in ASM components, leading to reliable barrier predictions for both the symmetric and asymmetrically substituted complexes. LFER transferability tests in Fig. 6 show that this compensation occurs irrespective of the choice of underlying level of theory.
We also believe that this compensation between interaction and strain energies are built into the activation strain model. We observe this phenomena in the course of constructing the strain-only component of the LFER with bidentate diamine N-donors, wherein ΔEINT is invariant and all structures are fully relaxed.24 The strain model described by eqn (6) captures variations both in substrate strain (C–H stretch) induced by the spatial extent (or steric bulk) of the catalyst and strain arising from deformation of the catalyst. Substrate strain is typically the dominant contributor to ΔESTR and also exhibits higher sensitivity to N-donors. The outliers for the strain model consist of systems in which the catalyst ceases to be planar and exhibits bending in the TSoxo structure. We find that ΔEINT is no longer invariant for these outliers. While the likelihood of catalyst deformation in the transition structure may be challenging to determine a priori to aid model construction, we note an interesting trend, shown in Table S6 of ESI.† Model deviations in ΔESTR are directly correlated with the deviation of ΔEINT with a slope of unity (R2 = 0.93). In other words, concurrent with the decrease in overall observed strain, driven by larger decrease in substrate strain and small increase in catalyst strain, is an increase in interaction energy towards more repulsive catalyst–substrate interactions. While our limiting choice of an aromatic interaction descriptor precludes extending the compensation analysis to these diamine N-donors, this analysis highlights an important consequence of employing the ASM. The built-in compensation between interaction and strain components is leveraged effectively in the complete LFER despite the fact that individual activation and strain components are poorly predicted by our model.
4.2 Analysis of model descriptors & outliers
The LFER effectively leverages compensation between interaction and strain energies defined by ASM to accurately predict barriers. The model described in eqn (7), however, still has limitations that lead to incorrect barrier predictions for 10 systems examined in this study. The LFER outliers for symmetric substitutions identified in Fig. 4 – S1, S3, S4, and S8 – either do not exhibit the interaction-strain compensation described above (S1, S4, S8) or the compensation does not lead to adequate error cancellation (S3), as shown in Table 4. Each of these outliers is also observed in at least 4 out of the 6 transferability tests shown in Fig. 6.The choice of scalar descriptors and model construction to enable capture of all ligand interaction and strain effects using these descriptors are both critical to LFER performance. The analysis of model sensitivity shows that LFER model performance is determined to the greatest extent (70.3%) by the interaction descriptor, σp, with each of the four σp values contributing equally (17.6%). Our choice of para-substituted Hammett parameters is based on excellent agreement of Hammett slopes with experiment.23 Their use as descriptors is justified as long as we limit the scope of LFER applicability to aromatic N-donors (e.g. imidazoles). However, we make a critical assumption that the descriptor refers only to the property of the substituent (say, OCH3) and not the entire N-donor ligand (C3N2H3OCH3). The interaction of the complete N-donor with the active site is therefore only partially captured by our choice of σp, leading to possible LFER deviations from true barriers. The second consequence of choosing substituent and not N-donor σp is the fact that the impact of physical separation of the electron-donating or withdrawing group from the active site is incorporated into the slope of the interaction term, not unlike traditional Hammett analysis.17 This further limits the scope of ligands for which the LFER model is valid.
To overcome these issues associated with Hammett parameters, our objective going forward is to identify alternative descriptors that can directly capture the impact of the complete N-donor ligand on the active site. The metal–ligand electronic parameter (MLEP) and the associated bond-strength order (BSO), both measures of metal–ligand bond strength in transition metal complexes, show promise as descriptors because they yield the most direct description of metal–ligand coordination and are easily calculated from vibrational analysis.26,80,81 Unlike Hammett parameters however, there is little prior evidence to the best of our knowledge of the use of MLEP's, BSO's, or related quantities in linear models similar to Hammett or Taft relationships. Examination of these parameters and construction of structure–function relationships therefore constitute future work towards constructing a generalizable LFER.
Although sensitivity analysis shows that the LFER model is less sensitive to strain descriptors (12.8% and 16.9% to the 2B1 and 2θ parameters, respectively), we find that these parameters overestimate strain contributions in some cases, leading to barrier deviations. For instance, S1 is the most extreme outlier among all the systems examined and for all levels of theory, seen in Fig. 6. While we cannot eliminate the possibility that σp may be an inadequate descriptor of ΔEINT, Table 4 shows that, contrary to the expected compensation effect, the strain difference (ΔESTR,LFER − ΔESTR,DFT) is large and positive. The large LFER strain estimate can be traced back to the strain descriptor, Sterimol B1, for S1 in Table 3, which is much larger than the values obtained for the remaining symmetrically substituted systems. Although our prior study24 develops the strain LFER based on catalysts that possess a wide range of B1 (1.55–2.82 Å) and θ (71.848–100.811°), it is likely that the absence of compensation in S1 stems in part from B1 overestimating the importance of steric bulk.
The sources of error are more challenging to deconvolute for the remaining outliers in symmetrically substituted catalysts – S3, S4, and S8. With S3, for instance, the absence of compensation could arise from a combination of σp overestimating N-donor electrophilicity and the fact that ΔESTR,LFER is very close to instead of being significantly lower than ΔESTR,DFT. Although the strain descriptors for S8 are very close to reference S7, the LFER strain is lower than the true value. To probe the origins of such deviations, we turn to EDA results for further decomposing strain energy into substrate and catalyst components.
Catalyst and substrate strain terms are obtained from isolated fragment energy differences between TSoxo and IS calculated using EDA. These components are listed in Table S4 of the ESI.† The catalyst component of strain is the consequence of two phenomena – (1) deformation of the catalyst in TSoxo, reflected in N-donor rotations relative to IS, and (2) change in intrafragment interactions between N-donors between TSoxo and IS. Although the two are difficult to isolate, the latter can be approximately quantified by carrying out EDA between two N-donors bound to each Cu at their respective geometries in TSoxo and IS. For the S1–S11 systems, these intramolecular interactions (Table S5 of ESI†) have non-negligible impact on lowering catalyst strain energy. The average catalyst strain energy is 63.1 kJ mol−1 for S1–S11, of which these intramolecular interactions can range between −5.3 kJ mol−1 and −20.9 kJ mol−1 with an average of −12.4 kJ mol−1. While these quantities are significantly smaller than substrate strain (125.9 kJ mol−1 on average for S1–S11), we find that trends are non-negligible.
Applying this analysis to S8, we find that the catalyst strain energy is 12.0 kJ mol−1 in excess of the reference S7. It is therefore possible that failure to capture this component leads to lower LFER strain even though the compensation effect predicts positive ΔESTR,LFER − ΔESTR,DFT. We emphasize however that this deviation is not unique to S8 and that even S5 shows catalyst strain that is 12.2 kJ mol−1 higher than S7. The absence of adequate compensation or error cancellation between the two terms constituting the ASM framework is ultimately what leads to large errors in LFER barrier predictions.
A6 and A10 exhibit the largest deviations among asymmetrically substituted systems, with barriers overestimated by 15.4 and 17.7 kJ mol−1, respectively (Table S3 of ESI†). In both cases, the magnitude of the strain deviations are higher than the compensation offered by interaction deviations. LFER overestimates strain energy because true catalyst strain is lower than the reference by 13.9 kJ mol−1 and 9.4 kJ mol−1 for A6 and A10, respectively. On the other hand, LFER underestimates barriers by 13.4 kJ mol−1 and 14.7 kJ mol−1 for A12 and A37, respectively. In A12, LFER underestimates strain by 14.5 kJ mol−1 but overestimates interaction by only 1.1 kJ mol−1, with the former originating in part, from higher catalyst strain relative to reference S7. In A37, LFER underestimates both strain and interaction terms by 7.1 kJ mol−1 and 7.7 kJ mol−1, respectively. It is therefore possible that a combination of factors described previously are contributing to these deviations. Although the deviations have opposite signs as is expected for A16 and A17, inadequate compensation between interaction and strain terms lead to poor barrier predictions, with errors of −10.8 kJ mol−1 and 11.5 kJ mol−1, respectively.
In summary, we find that the LFER model errors can exceed 10 kJ mol−1 in scenarios where individual interaction and strain deviations do not cancel each other. The absence of cancellation of errors can arise from the underlying choice of interaction and strain descriptors and/or because the strain component of the LFER is designed to primarily capture substrate strain.
4.3 Ligand weighting & position effects
An implicit assumption of our LFER framework is that all N-donors contribute equally to the interaction term, as a result of which the weight of each of the four σp's in eqn (7) is unity. We also assume that the 2 N-donors closest to the substrate contribute equally to the strain term. This is reasonable because most TSoxo structures exhibit some degree of symmetry, where the activated substrate is positioned close to the middle of the active site, seen in Fig. 1.We test the assumption of equal weighting of the interaction term by analyzing the dependence of barriers on the location of the N-donor relative to the Cu–O bond being broken in the course of CH activation. We select two monodentate amine N-donors (Xam = CH3, CF3) and substitute one of them in one of the four positions as shown in Fig. 3(b), with NH3 (Xam = H) groups as the remaining three N-donors. The procedure for calculating barriers is similar to the LFER construction method for the interaction term to minimize strain effects. The active site and substrate are constrained to the reference [Cu2(NH3)4O2]2+ relaxed geometry. Barriers are calculated at the ωB97X-D/srsc, 6-311+G* level of theory.
Table 5 shows that these barriers lie in a narrow range (within 10 kJ mol−1), spanning 4.7 kJ mol−1 for CH3 and 9.7 kJ mol−1 for CF3. Therefore, the assumption of equal N-donor contributions to the interaction term is reasonable and equal weights can be assigned to the interaction descriptors for N-donors coordinated to the active site. We note that this is valid exclusively in situations where the active site and the connecting N-atoms are planar. The relative contributions of various N-donors in non-planar complexes, which can occur when more than 2 N-donors are bound to each Cu, is yet to be examined.
| N-Donor | Position | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| CH3 | 76.0 | 73.6 | 71.3 | 72.1 |
| CF3 | 56.0 | 63.4 | 53.7 | 61.8 |
While the ranges of barriers in the analysis present in Table 5 are within 10 kJ mol−1, the sensitivity of barriers to the position of the Xam = CF3 group may not be negligible. A subset of asymmetric catalysts described in Table 1 are employed to further examine these position effects on LFER predictions for fully relaxed systems. For example, consider A3, A15, and A19, each consisting of two Xim = CF3 and Xim = H N-donors in distinct positions. In A3 and A15, each CF3-bound imidazole group is coordinated to a different Cu in trans- and cis-like configuration, respectively. In A19, both CF3-bound imidazole groups are coordinated to the same Cu. The DFT barriers lie in a range similar to the CF3 systems in Table 5 – 73.8 kJ mol−1 for A3, 84.0 kJ mol−1 for A15, and 82.4 kJ mol−1 for A19. The LFER interaction term is identical for all three systems. LFER predicts higher barriers for A3 (81.2 kJ mol−1) and A19 (81.5 kJ mol−1) compared to A15 (78.1 kJ mol−1), on account of proximity of the CF3 group to the substrate, reflected in one of the two B1 descriptors. The predicted barrier is very close to the DFT value for A19 and higher for A3 although still within the allowable margin of error. In the case of A15, the LFER prediction is lower than DFT by 5.9 kJ mol−1 on account of modest increase in catalyst and substrate strain in the latter that is either not captured or adequately compensated for by the model. A3 does not exhibit the added strain predicted by the model despite N-donor proximity to the substrate being similar to A19. This is because, unlike in the case of A19, the Xim,4 does not undergo twisting relative to the active site plane in A3. The remaining three N-donors show similar deformation in the two systems. Similar conclusions can be drawn from examining other asymmetric systems which only vary in positions, such as A4, A17, and A21, with two Xim = NO2 and two Xim = H N-donors.
Taken together with the results in Table 5, we conclude that N-donor positions do impact interaction and strain components of the ASM, although the resulting range in barriers is relatively narrow. This range may not be resolvable with high fidelity by the LFER model or even be usable in model construction to assign position-dependent weights to N-donor descriptors.
4.4 Choice of reference for LFER construction & application
A comment on the choice of reference system to compute ΔEref and descriptor reference values in the LFER model is necessary. In principle, the choice of reference system must not affect model performance for a truly generalizable LFER. In this work, each additive term is constructed separately using a different reference system – imidazole (Xim,ref = H) for the interaction term and bidentate diamine H2NCH2NH2 for the strain term.23,24 The resulting complete LFER model, with the imidazole (Xim,ref = H) as a reference, can accurately predict most barriers for the systems examined in this study. Therefore, the model is reasonably flexible to the underlying choice of reference. The choice of linear fit with or without an intercept during model construction does not affect model performance, with the former only requiring the use of additional terms in the LFER. In our framework, we set the intercept to zero to match the Taft formalism. The construction of interaction and strain terms themselves, on the other hand, requires careful selection of reference and N-donor variations. For instance, our previous study calculates Hammett (interaction) slopes for both amine (Xam,ref = H) and imidazole N-donors. As the amine N-donors are not aromatic, σp is not a suitable descriptor for interaction terms, and the resulting model fit is poor (R2 = 0.63). Using the amine N-donor-based interaction model with either the ammonia or imidazole reference, instead of the imidazole-based model employed in this work, leads to poor model performance. The quantitative outcomes of all these scenarios are summarized in Table S7 of the ESI.†4.5 Transferability
The LFER constructed using the baseline level of theory shows similar performance – MAEs and outliers – when the reference is calculated using a different basis set and/or functional approximation. This is a promising indicator that the LFER framework may be transferable and therefore serves as an easily generalizable platform for ligand design. It is worth noting that our choice of functionals for transferability tests are based on conventional wisdom that a fraction of Hartree–Fock (HF) exchange improves barrier estimates. Recent studies show exceptions to this rule both in the gas phase and in surface chemistry.82,83 In the gas phase, rehybridization of the atom undergoing transformation in the TS leads to anomalous behavior of hybrid functionals.82 Therefore, while the carbon atom in our study is not rehybridized in the course of hydroxylation, a broader test of functional transferability is necessary for LFER construction if the reactions involve transition state rehybridization. An additional challenge with transferability can arise when attempting to construct LFERs for key steps of a catalytic cycle instead of the single stoichiometric step examined in this study. For an iron-oxo complex for CH activation, Gani and Kulik show that the ΔEINT and ΔESTR terms exhibit distinct functional sensitivity towards the hydrogen atom transfer and oxo-formation steps in the catalytic cycle, leading to different trends in barriers for the two steps with varying extent of HF exchange.84 Future work into the expansion of the framework to study catalytic cycles must therefore include additional functional transferability tests of ASM (and therefore LFER) components.The LFER framework, constructed using the activation strain model by isolating and assigning descriptors for each contribution, constitutes a reliable predictor of activation energies for the N-donor class examined in this study. We find that the model relies on compensation or error cancellation between the interaction and strain components. The analysis presented in this work highlights key strengths of the model, including transferability with respect to level of theory and robustness with respect to choice of reference. We also identify critical model limitations that affect performance and transferability across N-donor classes, including that imposed by the choice of interaction descriptor and incomplete description of catalyst strain effects.
5 Conclusions
Inspired from the Hammett and Taft equations in organic aromatic chemistry that quantify substituent effects on reaction kinetics, this work is aimed at developing a simple yet comprehensive design framework for transition metal complex catalysts. Using the activation strain model, we present a procedure for constructing active site-specific linear free energy relationships that is easily generalizable across a wide range of catalytic reactions. The procedure allows us to understand ligand effects in terms of measurable quantities – their impact on catalyst–substrate interaction and strain induced upon deformation to the transition state – rather than by assigning ‘electronic’ and ‘steric’ effects, which can difficult to isolate and quantify in a systematic manner. We propose a piecewise construction method for the LFER, in which the impact of ligands on the interaction and strain components of the activation barrier are captured separately via careful selection of ligands and simulation constraints. This involves activation barrier and EDA calculations along with the identification of a suitable set of descriptors for each term in the ASM. To subsequently predict the catalytic activity for the desired set of ligands, the LFER needs DFT barrier calculations for only a single reference system and inexpensively obtained descriptors for the reference and the desired system.The LFER construction procedure and resulting performance are illustrated for CH4 hydroxylation with enzyme-inspired [Cu2O2]2+ complexes. We combine the outcomes of our previous two studies that isolate interaction and strain effects via systematic N-donor ligand variations and determine that the former effect can be described by the Hammett parameter (σp) and the latter with a combination of bite angle (θ) and Sterimol parameter (B1). The resulting LFER can accurately predict barriers for most catalysts where the [Cu2O2]2+ is bound to arbitrary imidazole N-donors and is transferable with respect to level of theory. This is the consequence of a natural compensation observed between LFER predictions of interaction and strain energies.
Analysis of model sensitivity and outliers reveals that the choice of interaction descriptor is the most probable cause of model deviations in systems where this compensation is not observed. Use of the Hammett parameter as descriptor severely limits the ligand space that can be explored with the current LFER and may not adequately describe the interaction effect of the entire ligand. To expand LFER catalyst scope and enable a more complete description of metal–ligand effects, our future work involves exploration of alternative descriptors, specifically MLEPs. Another limitation of the LFER model is that it captures primarily trends in substrate strain and not catalyst strain, which can also lead to barrier deviations when the catalyst strain is far from the reference value. Going forward, we aim to construct a more complete LFER model by identifying a suitable set of N-donor variations to isolate and quantify trends in catalyst strain.
This work constitutes the first step towards developing a systematic, generalizable framework for active site-specific design of transition metal complex catalysts. We successfully demonstrate proof-of-concept that an LFER grounded in the activation strain model has the ability to predict activation barriers for catalyst constructed with imidazole N-donor ligands. The choice of descriptors and quantification of more complex, intramolecular effects are essential next steps towards developing a truly generalizable LFER that can accurately predict barriers for a broader spectrum of ligands.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge startup resources and graduate fellowship from University of Southern California, the TLARGI fellowship, and USC's Center for Advanced Research Computing for supporting this work.Notes and references
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef PubMed.
- J. Greeley, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 605–635 CrossRef PubMed.
- E. N. Bess, D. M. Guptill, H. M. Davies and M. S. Sigman, Chem. Sci., 2015, 6, 3057–3062 RSC.
- M. S. Sigman, K. C. Harper, E. N. Bess and A. Milo, Acc. Chem. Res., 2016, 49, 1292–1301 CrossRef CAS PubMed.
- T. Z. Gani and H. J. Kulik, ACS Catal., 2018, 8, 975–986 CrossRef CAS.
- P. C. Andrikopoulos, C. Michel, S. Chouzier and P. Sautet, ACS Catal., 2015, 5, 2490–2499 CrossRef CAS.
- D. H. Ess, W. A. Goddard III and R. A. Periana, Organometallics, 2010, 29, 6459–6472 CrossRef CAS.
- D. J. Durand and N. Fey, Chem. Rev., 2019, 119, 6561–6594 CrossRef CAS PubMed.
- S. Shaik, D. Kumar and S. P. De Visser, J. Am. Chem. Soc., 2008, 130, 10128–10140 CrossRef CAS PubMed.
- S. Shaik, W. Lai, H. Chen and Y. Wang, Acc. Chem. Res., 2010, 43, 1154–1165 CrossRef CAS PubMed.
- M. D. Wodrich, B. Sawatlon, M. Busch and C. Corminboeuf, Acc. Chem. Res., 2021, 54, 1107–1117 CrossRef CAS PubMed.
- M. Anand, B. Rohr, M. J. Statt and J. K. Nørskov, J. Phys. Chem. Lett., 2020, 11, 8518–8526 CrossRef CAS PubMed.
- D. J. Martin, C. F. Wise, M. L. Pegis and J. M. Mayer, Acc. Chem. Res., 2020, 53, 1056–1065 CrossRef CAS PubMed.
- J. P. Janet, C. Duan, A. Nandy, F. Liu and H. J. Kulik, Acc. Chem. Res., 2021, 54, 532–545 CrossRef CAS PubMed.
- E. Burello and G. Rothenberg, Int. J. Mol. Sci., 2006, 7, 375–404 CrossRef CAS.
- J. Shorter and N. Chapman, Adv. Linear Free Energy Relat., 1972, pp. 321, 368 Search PubMed.
- L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS.
- R. W. Taft Jr, J. Am. Chem. Soc., 1952, 74, 2729–2732 CrossRef.
- Z. Freixa and P. W. Van Leeuwen, Dalton Trans., 2003, 1890–1901 RSC.
- T. L. Brown and K. J. Lee, Coord. Chem. Rev., 1993, 128, 89–116 CrossRef CAS.
- F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- Z. Lan and S. M. Sharada, Phys. Chem. Chem. Phys., 2018, 20, 25602–25614 RSC.
- Z. Lan and S. M. Sharada, Phys. Chem. Chem. Phys., 2020, 22, 7155–7159 RSC.
- A. Nandy and H. J. Kulik, ACS Catal., 2020, 10, 15033–15047 CrossRef CAS.
- D. Setiawan, R. Kalescky, E. Kraka and D. Cremer, Inorg. Chem., 2016, 55, 2332–2344 CrossRef CAS PubMed.
- C. E. Elwell, N. L. Gagnon, B. D. Neisen, D. Dhar, A. D. Spaeth, G. M. Yee and W. B. Tolman, Chem. Rev., 2017, 117, 2059–2107 CrossRef CAS PubMed.
- E. I. Solomon, D. E. Heppner, E. M. Johnston, J. W. Ginsbach, J. Cirera, M. Qayyum, M. T. Kieber-Emmons, C. H. Kjaergaard, R. G. Hadt and L. Tian, Chem. Rev., 2014, 114, 3659–3853 CrossRef CAS PubMed.
- F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS.
- A. Behn, P. M. Zimmerman, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2011, 135, 224108 CrossRef PubMed.
- S. Mallikarjun Sharada, P. M. Zimmerman, A. T. Bell and M. Head-Gordon, J. Chem. Theory Comput., 2012, 8, 5166–5174 CrossRef CAS PubMed.
- M. v. Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62 Search PubMed.
- G. T. de Jong and F. M. Bickelhaupt, ChemPhysChem, 2007, 8, 1170–1181 CrossRef CAS PubMed.
- L. M. Mirica, X. Ottenwaelder and T. D. P. Stack, Chem. Rev., 2004, 104, 1013–1045 CrossRef CAS PubMed.
- S. Mahapatra, J. A. Halfen, E. C. Wilkinson, G. Pan, C. J. Cramer, L. J. Que and W. B. Tolman, J. Am. Chem. Soc., 1995, 117, 8865–8866 CrossRef CAS.
- J. A. Halfen, S. Mahapatra, E. C. Wilkinson, S. Kaderli, V. G. Young, L. Que, A. D. Zuberbühler and W. B. Tolman, Science, 1996, 271, 1397–1400 CrossRef CAS PubMed.
- X. Ottenwaelder, D. J. Rudd, M. C. Corbett, K. O. Hodgson, B. Hedman and T. D. P. Stack, J. Am. Chem. Soc., 2006, 128, 9268–9269 CrossRef CAS PubMed.
- D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2011, 7, 1511–1523 CrossRef CAS PubMed.
- M. Flock and K. Pierloot, J. Phys. Chem. A, 1999, 103, 95–102 CrossRef CAS.
- T. Yanai, Y. Kurashige, E. Neuscamman and G. K. L. Chan, J. Chem. Phys., 2010, 132, 024105 CrossRef PubMed.
- C. J. Cramer, B. A. Smith and W. B. Tolman, J. Am. Chem. Soc., 1996, 118, 11283–11287 CrossRef CAS.
- P. Å. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109 CrossRef PubMed.
- C. J. Cramer, A. Kinal, M. Włoch, P. Piecuch and L. Gagliardi, J. Phys. Chem. A, 2006, 110, 11557–11568 CrossRef CAS PubMed.
- C. J. Cramer, M. Włoch, P. Piecuch, C. Puzzarini and L. Gagliardi, J. Phys. Chem. A, 2006, 110, 1991–2004 CrossRef CAS PubMed.
- B. F. Gherman and C. J. Cramer, Coord. Chem. Rev., 2009, 253, 723–753 CrossRef CAS.
- M. F. Qayyum, R. Sarangi, K. Fujisawa, T. D. P. Stack, K. D. Karlin, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2013, 135, 17417–17431 CrossRef CAS PubMed.
- P. P.-Y. Chen and S. I. Chan, J. Inorg. Biochem., 2006, 100, 801–809 CrossRef CAS PubMed.
- K. Yoshizawa and Y. Shiota, J. Am. Chem. Soc., 2006, 128, 9873–9881 CrossRef CAS PubMed.
- Y. Shiota and K. Yoshizawa, Inorg. Chem., 2009, 48, 838–845 CrossRef CAS PubMed.
- Y. Shiota, G. Juhász and K. Yoshizawa, Inorg. Chem., 2013, 52, 7907–7917 CrossRef CAS PubMed.
- J. C. S. Da Silva, R. C. R. Pennifold, J. N. Harvey and W. R. Rocha, Dalton Trans., 2016, 45, 2492–2504 RSC.
- C. J. Cramer and Y. Pak, Theor. Chem. Acc., 2001, 105, 477–480 Search PubMed.
- C. Citek, C. T. Lyons, E. C. Wasinger and T. D. P. Stack, Nat. Chem., 2012, 4, 317–322 CrossRef CAS PubMed.
- A. Verloop, W. Hoogenstraaten and J. Tipker, Drug Design, Elsevier, 1976, pp. 165–207 Search PubMed.
- A. Verloop, Pesticide Chemistry: Human Welfare and Environment, Elsevier, 1983, pp. 339–344 Search PubMed.
- K. C. Harper, E. N. Bess and M. S. Sigman, Nat. Chem., 2012, 4, 366 CrossRef CAS PubMed.
- C. B. Santiago, A. Milo and M. S. Sigman, J. Am. Chem. Soc., 2016, 138, 13424–13430 CrossRef CAS PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- A. V. Brethomé, S. P. Fletcher and R. S. Paton, ACS Catal., 2019, 9, 2313–2323 CrossRef.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. Distasio Jr, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O-Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. V. Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, J. Chem. Phys., 1996, 104, 9047–9052 CrossRef CAS.
- S. Mallikarjun Sharada, D. Stuck, E. J. Sundstrom, A. T. Bell and M. Head-Gordon, Mol. Phys., 2015, 113, 1802–1808 CrossRef.
- R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 8753–8765 CrossRef CAS PubMed.
- P. R. Horn, E. J. Sundstrom, T. A. Baker and M. Head-Gordon, J. Chem. Phys., 2013, 138, 134119 CrossRef PubMed.
- P. R. Horn and M. Head-Gordon, J. Chem. Phys., 2015, 143, 114111 CrossRef PubMed.
- P. R. Horn and M. Head-Gordon, J. Chem. Phys., 2016, 144, 084118 CrossRef PubMed.
- P. R. Horn, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2016, 144, 114107 CrossRef PubMed.
- P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079 RSC.
- I. M. Sobol, Math. Comput. Simul., 2001, 55, 271–280 CrossRef.
- J. Herman and W. Usher, J. Open Source Software, 2017, 2, 97 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2001, 105, 2936–2941 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- K. Hui and J.-D. Chai, J. Chem. Phys., 2016, 144, 044114 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- D. Cremer and E. Kraka, Dalton Trans., 2017, 46, 8323–8338 RSC.
- E. Kraka and M. Freindorf, in Characterizing the Metal–Ligand Bond Strength via Vibrational Spectroscopy: The Metal–Ligand Electronic Parameter (MLEP), ed. A. Lledós and G. Ujaque, Springer International Publishing, Cham, 2020, pp. 227–269 Search PubMed.
- A. Mahler, B. G. Janesko, S. Moncho and E. N. Brothers, J. Chem. Phys., 2018, 148, 244106 CrossRef PubMed.
- S. Mallikarjun Sharada, T. Bligaard, A. C. Luntz, G.-J. Kroes and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 19807–19815 CrossRef CAS.
- T. Z. Gani and H. J. Kulik, J. Chem. Theory Comput., 2017, 13, 5443–5457 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02278d |
| This journal is © the Owner Societies 2021 |