Multiple particle tracking study of thermally-gelling nanoemulsions

Abstract

We perform multiple particle tracking (MPT) on a thermally-gelling oil-in-water nanoemulsion system. Carboxylated and plain polystyrene probes are used to investigate the role of colloidal probe size and surface chemistry on MPT in the nanoemulsion system. As temperature increases, hydrophobic groups of PEG-based gelators (PEGDA) partition into the oil/water interface and bridge droplets. This intercolloidal attraction generates a wide variety of microstructures consisting of droplet-rich and droplet-poor phases. By tailoring the MPT colloidal probe surface chemistry, we can control the residence of probes in each domain, thus allowing us to independently probe each phase. Our results show stark differences in probe dynamics in each domain. For certain conditions, the mean squared displacement (MSD) can differ by over four orders of magnitude for the same probe size but different surface chemistry. Carboxylated probe surface chemistries result in “slippery” probes while plain polystyrene probes appear to tether to the nanoemulsion gel network. We also observe probe hopping between pores in the gel for carboxylated probes. Our approach demonstrates that probes with different surface chemistries are useful in probing the local regions of a colloidal gel and allows the measurement of local properties within structurally heterogeneous hydrogels.

---

1. Introduction

Colloidal gels are formed when sufficient colloid-colloid attractive interactions are introduced into colloidal suspensions.¹ At low to moderate particle loadings, colloids aggregate and give rise to fractal clusters and chains, ultimately resulting in a space-filling interconnected network.² Such types of attraction are commonly provided by depletion,^3–5 colloid surface charge^6,7 or polymer bridging⁸ that can be controlled by external stimuli such as temperature, depleting agents, ionic strength, and pH values. By changing the colloid volume fraction and attractive potential, colloidal gels show diverse microstructures and mechanical properties.¹ Due to their viscoelastic properties, colloidal gels are used in various fields such as the food industry,⁹ drug delivery,⁸ tissue engineering,⁶ membranes¹⁰ and drilling fluids.⁷

Recently, our group has developed a thermally-gelling nanoemulsion system in which nano-sized polydimethylsiloxane droplets are dispersed in a continuous phase composed of water, sodium dodecyl sulfate and poly(ethylene glycol) diacrylate.¹¹ At high temperatures, the hydrophobic groups of the PEG-based gelators partition into the oil/water interfaces and form interdroplet bridging, giving rise to a thermally-responsive gel. It has been shown that the temperature-dependent properties such as gel point, shear modulus and yield stress can be tuned via droplet size, oil volume fraction (ϕ), gelator concentration (P) and gelator chemistry.^11,12 This system provides a wide parameter space and allows one to engineer the nanoemulsions’ properties for specific practical applications.¹³ For instance, our group has recently shown the application of these nanoemulsions in 3D printing to obtain hierarchical mesostructured hydrogels with potential utility in drug delivery, tissue engineering and membranes.¹⁰ In addition, the interdroplet attractive potential can be finely modulated by adjusting temperature. This ability to tune the attractive potential without adding another component to the solution (e.g. depleting agent, salt, acid, etc.) allows ones to precisely control assembly conditions and the resulting microstructures.

In this article, we use multiple particle tracking to study the changes in microenvironment of the thermally-gelling nanoemulsion during gelation. Previously, we studied the mechanism of gelation by using rheological characterization, neutron scattering and cryo-transmission electron microscopy.¹² For nanoemulsions with ϕ < ϕ_c, where ϕ_c is a critical oil volume fraction, gelation is induced by homogenous percolation with a broad gel transition in which the droplet-droplet cluster formed and subsequently percolated. On the other hand, when ϕ > ϕ_c, gelation occurs through phase separation with a sharp sol–gel transition. In this regime, the strong interdroplet attraction can dynamically arrest the phase separation, and the nanoemulsions show bi-continuous microstructures consisting of droplet-rich and droplet-poor domains.

Microstructures of the nanoemulsions spanning a wide range of ϕ (0.1 to 0.33) and T (22 to 65 °C) were further studied using confocal microscopy.¹⁴ We developed a technique where we labeled oil droplets by a lipophilic dye and locked the microstructures in place by photo-crosslinking the telechelic polymers at target temperatures, thus enabling direct visualization of the internal structures at room temperature. Using confocal microscopy and bulk rheological characterization, it was determined that the nanoemulsions undergo a two-stage gelation at rising temperatures: homogenous percolation followed by phase separation. This is contrary to what had been found previously, where the gelation is induced by single mechanism depending on ϕ.¹² However, we also showed that the thermal response of the nanoemulsion was sensitive to oil droplet size and temperature history, which could explain the difference in observations.

Although there are some differences in the results due to slight differences in composition, both works^12,14 showed that at sufficiently high ϕ and relatively high T, the nanoemulsions undergo phase separation and become dynamically arrested. Using inverted optical microscope with the texture analysis microscopy,¹⁵ Gao et al. captured the microscopic dynamic process of coarsening through spinodal decomposition to the arrested state. As expected, the nanoemulsion forms heterogeneous, bi-continuous networks consisting of droplet-rich and droplet-poor domains, consistent with the results by using confocal microscopy.¹⁴ The microstructures were further studied by analyzing the large amplitude oscillatory shear (LAOS) rheology with simultaneous neutron scattering.¹⁶ Interestingly, Kim et al. found out that the nanoemulsion gel shows two-step yielding. This nonlinear mechanical response is due to the initial compression and rupture of dense fractal domains, followed by clusters breakage into a homogeneous dispersion.

Although the work of the LAOS study focused more on the evolution of the heterogeneous nanoemulsion gel microstructures under yielding, it also suggests that the internal structures are of a hierarchical nature, and that it may be possible to obtain more information by locally probing the networks. However, there are few direct microscopic studies on thermogelling nanoemulsions. Moreover, the characterization of the nanoemulsion is primarily performed with bulk rheology. Although it has been shown that such studies can be aided by microscopy, direct probing without compromising the microstructures would be beneficial.

Here, we performed video microscopy multiple particle tracking (MPT) to study the thermally-gelling nanoemulsion at various temperatures. For this study, we chose a nanoemulsion with ϕ = 0.15. At this oil loading, the nanoemulsion microstructure shows a correlation length that spans 0.1 to 10 μm at different temperatures.¹⁴ For such a highly heterogeneous system, MPT is a useful tool for quantitative analysis because the probes embedded in the sample can reveal the local rheological properties of the material on a microscopic scale.^7,17–32 We show that by tailoring the colloidal probe surface chemistry we can control the residence of the probes to be either in the droplet-rich or droplet-poor phase, thus allowing us to investigate each domain independently. Our results show stark differences in probe dynamics in each domain, and the dynamics also show significant probe-size dependency. Unmodified polystyrene beads appear to tether strongly to the nanoemulsion gel at elevated temperatures, whereas carboxylate-modified polystyrene beads appear to be “slippery” and explore the large pores in the nanoemulsion gel. This work introduces a method to target specific regions in a nanoemulsion gel for characterization via MPT, and has implications for the design of new nanoemulsion-based composite materials.

2. Experimental

2.1 Materials

Nanoemulsion and confocal imaging. Poly(ethylene glycol) diacrylate (PEGDA, M_n = 700 g mol⁻¹), sodium dodecyl sulfate (SDS), silicone oil (PDMS, viscosity = 5 cSt at 25 °C), lipophilic dye PKH26 (excitation and emission wavelengths λ_ex/λ_em = 551/567 nm) and photoinitiator 2-hydroxy-2-methylpropiophenone (Darocur 1173) were purchased from Sigma-Aldrich and used without further purification.

Particle tracking. Fluorescent polystyrene beads were purchased from Polysciences (Fluoresbrite® YG, λ_ex/λ_em = 441/486 nm). Two types of probes with selected sizes were used in this work: polystyrene beads with no surface modification (diameter 2a = 1 and 2 μm) and polystyrene beads surface modified with carboxylate groups (2a = 1, 1.5 and 2 μm).

2.2 Synthesis of nanoemulsion

The oil-in-water (O/W) nanoemulsion in this work consisted of PDMS droplets (D = 36 nm with polydispersity = 20%) dispersed in a continuous phase of PEGDA with volume fraction = 0.33, SDS at a concentration of 0.175 M and de-ionized water. The oil volume fraction (ϕ) of the nanoemulsion was 0.15. To generate the nanoemulsion, a pre-emulsion was first prepared by adding the silicone oil into the aqueous mixture of PEGDA and SDS under magnetic stirring with a speed of 700 rpm. Stirring was maintained for at least 15 min to ensure there was no macroscopic phase separation. This pre-emulsion was processed into the nanoemulsion by using a high-pressure homogenizer (EmulsiFlex-C3, Avestin). The homogenization was conducted at a pressure of 18 000 psi for 15 passes, and the emulsion was cooled to 4 °C between each pass. The diameter of the droplets was measured using dynamic light scattering (90Plus PALS, Brookhaven Instruments) after diluting the oil phase from ϕ = 0.15 to ϕ = 0.002 by using an aqueous diluting agent consisting of PEGDA in de-ionized water (P = 0.33). Dilution using this solution was shown to have negligible influence on the oil droplet size and polydispersity.¹¹ The final nanoemulsion was stored at 4 °C until further use.

2.3 Multiple particle tracking

Before adding the fluorescent probes into the nanoemulsion, the beads were washed in a solution with the same composition as the continuous phase of the nanoemulsion by centrifugation and redispersed by vortexing. This process was repeated three times for all beads to remove potential chemical residuals in the stock bead solutions. After the washing step, the beads were added into the nanoemulsion with a volume fraction ≈0.02%. Depending on the probe size, 50–100 randomly dispersed beads were tracked within the microscope field of view.

The nanoemulsion containing the colloidal probes was then sealed in a custom-built chamber that was designed to maintain thermal homogeneity when mounted on a microscope heating stage (ΔT ≤ 0.2 °C across the chamber). A schematic of the device is shown in ESI,† Fig. S1. The slides were fixed in place using UV-curing glue. After the sample was loaded into the chamber, both ends were sealed by epoxy glue.

Particle tracking was performed using an inverted fluorescence microscope (Axiovert 40 CFL, Zeiss) equipped with a 40× objective (N.A. = 0.75). A filter set (XF404, Omega Optical) was used which allowed only fluorescent beads to be excited and imaged. The temperature of the sample was controlled by a heating stage (TSA02i, Instec) mounted on the microscope stage. An objective warmer (OW-1, Warner Instruments) was used to minimize the potential thermal fluctuation due to the air between the objective and the sample.¹⁵ The temperature was calibrated by an additional digital thermometer (#51 II, Fluke).

The sample was placed on the stage when the heating stage reached the target temperature. Images were taken after 10 minutes by using a charged couple device (CCD) camera (Manta G-145, Allied Vision) at a speed of 30 frames per second with a shutter speed of 8 ms. A total of 900 frames were collected for each movie. The time for the largest beads to settle due to gravity in the chamber is ≈120 min in our system,³³ which is much larger than the experimental time scale ≈10 min. Moreover, although the Peclet number ≈0.5 indicates the gravitational settling is not negligible compared to Brownian motion for largest beads,¹³ we will show that the settling effect does not perturb the native microstructure of the gelling nanoemulsions in Section 3.3. For each type of bead at the target temperature, 5–8 movies were recorded to ensure a large ensemble of bead trajectories. The experiments were performed separately for beads with different surface chemistry and sizes suspended in freshly prepared nanoemulsions.

2.4 Microrheology

Probe dynamics from the movies were then analyzed by publicly available Matlab codes,³⁴ which are based on IDL codes originally developed by Crocker and Grier.³⁵ The mean squared displacement (MSD) is calculated by analyzing the bead trajectories:

MSD = 〈Δr²(τ)〉 = 〈[r(t + τ) − r(t)]²〉, (1)

where r is the position of the bead, t is time, τ is lag time and the bracket represents the time and/or ensemble average. However, eqn (1) needs to be corrected for a static error caused by the inherent noise in particle tracking.^36,37 An additional experiment was performed to determine the static error – the probes were immobilized in a 3 wt% agarose gel and the apparent MSD (so-called static error) was calculated (see ESI,† Table S1 for the static errors of all beads). The static error was then subtracted from eqn (1).

The measured MSD was used to calculate the sample viscoelasticity via the generalized Stokes–Einstein relation (GSER).^18,38 The complex shear modulus, G* is described as,

where ω = 1/τ is the frequency, k_B is the Boltzmann constant, T is the absolute temperature, a is the bead radius, i is the imaginary unit and F_u is the Fourier transform function. In order to use GSER to calculate the shear moduli, eqn (2) needs to be modified.³⁸ By assuming the local power law applies at the frequency of interest, eqn (2) can be transformed to:Here Γ is the gamma function and .

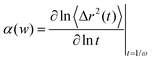Finally, the elastic modulus, G′(ω) and the viscous modulus, G′′(ω) are calculated as,

G′(ω) = |G*(ω)|cos(πα(ω)/2), (4)

G′′(ω) = |G*(ω)|sin(πα(ω)/2). (5)

2.5 Bulk rheology

Bulk rheology was measured using a stress-controlled rheometer (ARG2, TA Instruments) equipped with a Peltier plate to control temperature. A stainless steel 2° cone with a diameter of 60 mm was used to perform small amplitude oscillatory shear (SAOS) measurements at a strain of γ = 0.05%.¹¹ A solvent trap was used to reduce potential evaporation of the sample during the measurement and a few drops of de-ionized water were added on top of the cone. For both temperature ramp and frequency ramp characterizations, a preshear was applied by constant rotation at a rate of 20 rad s⁻¹ for 30 seconds, followed by a one minute period where the sample remained quiescent at T = 20 °C. For frequency sweep measurements, after the preshear was finished, the nanoemulsion was raised to the target temperature and then remained quiescent for 10 minutes. Freshly loaded nanoemulsion was used for each target temperature. For temperature ramp measurements, the temperature was raised at a speed of 2 °C min⁻¹ with a fixed angular frequency ω = 20 rad s⁻¹. The moduli were measured at a lag time of 5 seconds.

2.6 Confocal microscopy

The microstructures of the nanoemulsions with and without beads were captured by a laser scanning confocal microscope (LSM 700, Zeiss) equipped with a 63× oil-immersion objective (N.A. = 1.4). To prepare samples for imaging, the nanoemulsion was first mixed with 1 vol% of fluorescent dye PKH26 and 1 vol% of the photoinitiator Darocur. The addition of these chemicals has been shown to have negligible effect on the nanoemulsion microstructure.¹⁴ For the samples containing probe beads, the beads were also added at this stage at the same volume fraction as used for particle tracking (beads were also washed as stated previously). Then, 150 μL of the mixture was loaded in a glass chamber (Lab-Tek™ #155411, Thermo Fisher Scientific). The sample was placed in a preheated oven at the target temperature for 10 minutes. Subsequently, the sample was exposed to UV light (λ = 365 nm) for one minute in the oven. The crosslinking of PEGDA locks the nanoemulsion microstructure in place to allow for direct visualization of the structure at room temperature on the confocal microscope.

3. Results and discussion

3.1 Thermally-gelling nanoemulsion system

The thermally-gelling oil-in-water (O/W) nanoemulsion is composed of silicone oil (poly(dimethyl siloxane), PDMS, 5 cSt) droplets (diameter 〈D〉 = 36 nm) dispersed in a continuous phase consisting of a telechelic polymer, poly(ethylene glycol) diacrylate (PEGDA, M_n = 700 g mol⁻¹), at a volume fraction P = 0.33, and a surfactant, sodium dodecyl sulfate (SDS), at a concentration of 0.175 M. The oil volume fraction ϕ was chosen to be 0.15. At ϕ = 0.15, the nanoemulsion microstructure shows a wide span of characteristic lengths (≈1 to 20 μm) at different temperatures.¹⁴ For such a highly heterogeneous system, multiple particle tracking (MPT) is a useful tool for quantitative analysis because the probes embedded in the sample can reveal the local rheological properties of the material.^7,17–29 In addition, at ϕ = 0.15, the viscoelastic moduli of the nanoemulsion above the gel temperature ranges from about 10 to 400 Pa.^11,14 With our experimental setup, the static error³⁶ is ≈2 × 10⁻⁵ μm² which sets the limit of the largest measurable elastic modulus to ≈150 Pa, as calculated by the generalized Stokes–Einstein relation (GSER).³⁹ We acknowledge the inherent limit of the video microscopy particle tracking in our setup where materials with large elasticity cannot be well characterized. However, within the limit of 150 Pa, MPT is capable of capturing the local microenvironment in the gelling nanoemulsion. The focus of our work is to demonstrate one of the first studies in utilizing tracers of different surface chemistry to probe the local dynamics of spatially heterogeneous gelled nanoemulsions.

The thermal gelation of the nanoemulsions occurs due to interdroplet bridging via telechelic polymer gelators containing hydrophobic end groups.¹¹ When the temperature increases, the hydrophobic end groups of PEGDA partition into the oil/water interface which results in interdroplet bridging (Fig. 1A). This attractive interaction eventually results in an interconnected gel networks that span the system, transforming the nanoemulsion from a liquid-like material to a viscoelastic solid, as shown in Fig. 1B. At room temperature, the nano-sized droplets are well dispersed because of a large Laplace pressure and electrostatic repulsion provided by the surfactant.^13,40,41 Above the gel temperature, the droplets self-assemble and form a space-filling network, turning the nanoemulsion dispersion into a gel state. This increase in the apparent size of the droplet-rich phase also results in increased turbidity, consistent with what has been reported previously.⁴²

Fig. 1 Thermally-gelling nanoemulsion (P = 0.33, ϕ = 0.15) and its viscoelasticity. (A) Schematic of the thermally-gelling mechanism. (B) Photographs of the nanoemulsion at T = 25 °C (transparent liquid) and T = 50 °C (turbid gel). (C) Frequency sweep of viscoelastic moduli from T = 30.0 to 50.0 °C (γ = 0.05%) from bulk rheology. Filled symbol = G′; open symbol = G′′.

Bulk small-amplitude oscillatory shear experiments were performed to measure the viscoelastic moduli (G′ and G′′) over a range of temperatures spanning the gel point (Fig. 1C). At T = 30.0 °C, the storage module scales as G′ ∼ ω² and the loss modulus scales as G′′ ∼ ω¹, representing a liquid-like behavior.^11,14 At T = 32.5 °C, G′ ≈ G′′ ∼ ωⁿ over a wide span of frequencies, where n is the relaxation exponent.⁴³ Winter and Chambon suggested that the critical gel point is found when G′(ω) and G′′(ω) show the same power law exponents on a log–log plot.⁴⁴ We find that n ≈ 0.5 (Fig. 1C), which indicates stoichiometrically balanced end-linking networks.⁴⁵ At the critical gel point, the colloidal system forms a sample-spanning gel network.⁴⁵ Above the gel point, the elastic modulus G′ is larger than the viscous modulus G′′ for all frequencies and both moduli become nearly independent of frequency.

3.2 Direct visualization of microstructures

The macroscopic viscoelasticity of a material is determined by its microstructure.^46,47 We used confocal microscopy to directly visualize the microstructure of the nanoemulsions at various temperatures. By taking advantage of the abundance of telechelic polymers (PEGDA) in the continuous phase, we locked the microstructure in place at target temperatures by photo-crosslinking the PEGDA with UV light for 1 minute. This approach enabled us to study the various microstructures at room temperature using fluorescence confocal microscopy. Fig. 2 shows representative 2D images of the nanoemulsion at T = 30.0 to 50.0 °C. We added a small amount of a lipophilic fluorescent dye (PKH26) for visualization. It has been shown that the addition of fluorescent dye and photoinitiator has negligible effect on the nanoemulsion structure.¹⁴

Fig. 2 Representative 2D images of nanoemulsion microstructures by confocal microscopy at T = 30.0 to 50.0 °C. The red fluorescent regions are the droplet-rich phase and the dark regions are the droplet-poor phase. Scale bars = 5 μm.

At T = 30.0 °C, the nanoemulsion exists predominantly as small clusters (≈0.7 μm) that are dispersed in the continuous phase. These clusters display liquid-like rheology (Fig. 1C) and the moduli do not change over a wide period of time at a fixed frequency and strain (ESI,† Fig. S2). In addition, at T = 30.0 °C where the thermally bridging is not prominent (below the gel temperature) and the PEG-SDS association in low temperature regime has not taken place,⁴² the clusters formed are likely due to the combination of short-range attraction by weakly bridging and perhaps PEGDA depletion, and electrostatic repulsion by ionic groups of SDS on the droplets. These observations suggest the likelihood of forming a clustered fluid, which is consistent with weak droplet interactions at this moderate temperature.^40,48–50 Future studies are needed to fully characterize the nature of these clusters below the gel temperature.

At T = 32.5 °C, the droplets begin to form droplet-rich and droplet-poor regions which become more distinctive at T = 35.0 °C. In this temperature regime, thick droplet strands co-exist with small clusters.¹⁴ Although it is difficult to discern a spanning network from the 2D images, results from bulk rheology suggest the gel point is within this temperature range. From Fig. 1C, the moduli at the gel point are small (G′ ≈ G′′ ∼ 0.1 to 10 Pa). The small values of G′ and G′′ indicate a very weak gel, suggesting that the nanoemulsions form a sparsely connected structure.

When further increasing the temperature to T > 35.0 °C, the attraction between droplets increases.^11,15 Stronger attraction can induce dynamically arrested phase separation in a colloidal system.¹ The strand-like droplet-rich regions of the nanoemulsions become smaller when the temperature increases beyond the gel point,⁵¹ as shown in Fig. 2. At these high temperatures, the spanning networks give the nanoemulsion a solid-like behavior. This solid-like behavior is evident in Fig. 1C, which shows that G′ reaches a plateau that is nearly independent of frequency and has a value that is an order of magnitude larger than G′′.

Quantitative analysis of microstructures can be obtained by calculating correlation lengths of droplet-rich domains, L_C.^14,52,53 Using the image processing software ImageJ, we first applied a fast Fourier transform to the image and obtained the scattered light intensity. Then, we calculated the radially averaged light intensity I(q) of the processed image, where q is the wave vector. Finally, we computed the correlation length as L_C = 2π/q_max, where q_max is the wave vector of the maximum averaged light intensity (ESI,† Fig. S3 for an example). Table 1 lists L_C from T = 30.0 to 50.0 °C. The results are consistent to what has been reported in prior work.¹⁴ Before the onset of phase separation (T = 35.0 °C), L_C gradually increases as temperature rises, and shows a sharp increase at T = 35.0 °C. After the phase transition, L_C decreases as temperature continues to rise. The results are consistent with the images in Fig. 2. Readers interested in a systematic study relating L_C to rheological properties of this nanoemulsion are referred to previous work by our group.¹⁴

Table 1 Correlation lengths of droplet-rich domains (L_C), sizes of droplet-rich domains (L_rich) and sizes of droplet-poor domains (L_poor) from T = 30.0 to 50.0 °C. Error bars = 1 standard deviation from 5–8 images

T (°C)	L C (μm)	L rich (μm)	L poor (μm)
30.0	1.66 ± 0.08	0.67 ± 0.34	0.40 ± 0.16
32.5	17.3 ± 14.2	5.01 ± 2.68 0.55 ± 0.21	0.62 ± 0.55
35.0	32.9 ± 12.4	5.98 ± 4.01 0.49 ± 0.26	0.95 ± 0.54
37.5	3.46 ± 0.26	2.12 ± 2.28	2.90 ± 3.82
40.0	3.38 ± 0.29	1.95 ± 1.51	2.46 ± 3.54
42.5	2.54 ± 0.21	1.74 ± 1.42	2.10 ± 3.75
45.0	2.35 ± 0.23	1.69 ± 1.40	1.87 ± 1.88
47.5	2.08 ± 0.14	1.32 ± 1.40	1.52 ± 1.24
50.0	1.82 ± 0.31	1.24 ± 0.97	1.45 ± 1.94

---

In addition to L_C, we also computed the size of droplet-rich and droplet-poor domains, denoted as L_rich and L_poor respectively. By using ImageJ, we applied a built-in function “Analyze Particles” to the images after performing the “Threshold” function. For L_poor, the white/black values of images were first inverted before “Threshold”. We set the average minimum Feret diameter to be L_rich or L_poor, where the Feret diameter is defined as the distance between two parallel lines that are tangential to the outline of a 2D object (ESI,† Fig. S4 for detailed description). For example, L_rich would be the diameter of sphere-like clusters at low temperatures and the width of the strand-like aggregates at high temperatures. An additional step is performed for computing L_rich at T = 32.5 and 35.0 °C. At these two temperatures, the histogram of sizes of droplet-rich domains shows a bimodal distribution with a local minimum in the probability distribution at 2 μm, distinguishing the two populations. This bimodal distribution is qualitatively seen in Fig. 2. Therefore, for these two temperatures we calculate and report two averaged minimum Feret diameters. Moreover, At T = 30.0 to 35.0 °C, due to the lack of isolated droplet-poor domains, L_poor was computed by measuring the separation distance between two near droplet-rich domains (ESI,† Fig. S5 for an example). At least 50 measurements were obtained at each temperature. Table 1 lists L_rich and L_poor from T = 30.0 to 50.0 °C.

Here we acknowledge the large standard deviation listed in Table 1. The major reason for the large variation is because the droplet-rich and droplet-poor domains are spatially heterogeneous. Additionally, the concave surfaces of the objects might contribute to the deviation.^54,55 For example, the minimum Feret diameter of a concave droplet-rich strand would be larger than the width of the strand.

The results from Fig. 2 show that the nanoemulsion forms different interconnecting droplet-rich and droplet-poor phases at various temperatures. Next, we probe each domain by controlling the surface chemistry of MPT beads, and study how these two domains exhibit probe-size dependent dynamics.

3.3 Microstructures with particle tracking probes embedded

Fig. 3 shows representative images of the nanoemulsions mixed with green fluorescent polystyrene colloidal probes containing two different surface chemistries at selected temperatures. The top row is the samples mixed with carboxylate-modified polystyrene beads (hereafter denoted as carboxylate beads), and the bottom row is mixed with bare polystyrene beads (no surface modification, hereafter denoted as plain beads). The continuous phase of the nanoemulsions consists of excess SDS surfactant that adsorbs to the bare polystyrene beads and stabilizes them. The bead volume fraction is 0.02%, which is the same concentration used for the MPT experiments. Interestingly, all the carboxylate beads reside in the droplet-poor phase and nearly all the plain beads reside in the droplet-rich phase across all temperatures. This is confirmed by the fluorescent color of the beads – the carboxylate beads remain green in each image (their native emission color), but the plain beads appear yellow, due to the addition of red fluorescence (from the PKH26 dye in the droplets) and green fluorescence from the beads. To further validate the light spectrum addition argument, we mixed 1 μm plain beads in a nanoemulsion suspension of P = 0.33 and ϕ = 0.05 at T = 40 °C. At this low volume fraction, the nanoemulsion forms a microstructure that allows only part of the plain beads to reside in the droplet-rich domains. Representative images are shown in Fig. 4. As expected, only the region of a bead in the droplet-rich phase becomes yellow, while the other part remains green. Fig. 4 also indicates that the yellow color is not a result of the adsorption of lipophilic dye to the entire bead surface. Fig. 3 and 4 illustrate that, by properly tailoring the surface chemistries of the beads, we can independently probe droplet-rich and droplet-poor domains via MPT. Further images from experiments with higher bead loadings are shown in ESI,† Fig. S6.

Fig. 3 Representative confocal images of the nanoemulsion mixed with particle tracking probes at T = 35.0, 40.0 and 45.0 °C. Upper row: Nanoemulsion mixed with carboxylate-modified polystyrene beads (carboxylate beads); bottom row: nanoemulsion mixed with bare polystyrene beads (plain beads). Carboxylate beads reside in the droplet-poor phase (dark region) and plain beads reside in the droplet-rich phase (red fluorescent region). Scale bars = 5 μm.

Fig. 4 Confocal images of 1 μm plain beads embedded in the nanoemulsion with P = 0.33 and ϕ = 0.05 at T = 40.0 °C. Only the part of bead partitioning into the droplet-rich phase is yellow, while other parts remain green. This images support the hypothesis that the change in color observed for colloidal probes is correlated with their residence in the droplet-rich phase. Scale bar = 1 μm.

Qualitatively, the addition of the beads does not affect the microstructures formed by the nanoemulsions, as seen in Fig. 3. Quantitatively, we compare L_C of the pure nanoemulsion and the nanoemulsion mixed with carboxylate beads and plain beads at T = 35.0, 40.0 and 45.0 °C (Table S2, ESI†). The microstructures are not influenced by the addition of the beads as L_C of all systems are nearly the same at each temperature. We also performed a temperature-ramp rheology measurement to show that the addition of beads have negligible effect on the bulk linear viscoelasticity of the nanoemulsion (ESI,† Fig. S7). In addition, although plain beads reside in the droplet-rich phase, we show that plain beads do not induce droplet aggregation (ESI,† Fig. S8).

3.4 Bead-nanoemulsion droplet interaction

We hypothesize that the telechelic PEGDA polymer can thermally bridge the plain beads to the nanoemulsions, leading to the strong association of plain beads with droplet-rich regions. This hypothesis assumes that the hydrophobic end group of PEGDA associates with the plain bead surface. If such a polymer-bead association takes place, then plain beads should thermally cluster in the presence of PEGDA without nanoemulsions.

To test our hypothesis, we designed a bead-aggregation experiment. We mixed carboxylate and plain beads of diameter = 1 μm in a solution having the same composition as the continuous phase of the nanoemulsion and added 1 vol% of photoinitiator. The bead volume fraction was ≈0.2%, and we performed the experiment at two different temperatures. For samples at T = 25 °C, the mixtures were directly exposed to UV light after sitting at room temperature for 10 minutes. For T = 40 °C, the samples were placed in the oven for 10 minutes and then immediately exposed to UV light. We also repeated the same experiment with a lower PEGDA volume fraction P = 0.05 (this was the lowest PEGDA concentration that could be used for photopolymerization). A total of eight samples (2 types of beads, 2 PEGDA concentrations, 2 temperatures) were investigated. The microstructures of the samples were observed by confocal microscopy.

Results are shown in Fig. 5. Under all conditions, carboxylate beads do not aggregate. On the other hand, plain beads aggregate at T = 40 °C, and the beads form larger clusters when more PEGDA is introduced. For a quantitative characterization, we define two quantities N_c and N_a. N_c is the average coordination number, which is defined as the average number of beads surrounding a central bead (center-to-center distance less than 1 μm in 2D images). N_a is the average aggregation size, which is defined as the average number of beads within a single aggregate. For all samples at T = 25 °C, N_c and N_a are zero, which means that the particles are well dispersed. For the plain bead groups at T = 40 °C, when P increases from 0.05 to 0.33, N_c increases from 0.84 ± 0.94 to 1.1 ± 0.91 and N_a increase from 2.3 ± 0.79 to 2.9 ± 2.0. Two other quantities, N_x and N_y, are also defined to signify the changes in the aggregation, where N_x is the fraction of beads in the aggregates (dimer, trimers, etc.) and N_y is the fraction of beads in the aggregates excluding dimers. At T = 40 °C, N_x and N_y increase from 0.50 to 0.78 and 0.13 to 0.44 respectively, as P increases from 0.05 to 0.33. This experiment shows that the plain bead-PEGDA mixture forms particle aggregates at high temperatures. In addition, stronger aggregation is induced when the PEGDA concentration is increased. In fact, telechelic polymer bridging via hydrophobic end-functionalized groups has been already found between solid particle surfaces,^56–59 as well as in microemulsions^60–62 and micelles.^63,64 In Fig. 6, we propose a schematic of how nanoemulsion droplets associate with plain beads. On the other hand, we believe the absence of bridging in the carboxylate beads is because of the charged carboxylated group present on the polystyrene surface. Although the surfaces of carboxylate beads and nanoemulsion droplets can provide strong electrostatic repulsion (having zeta potentials of −45 and −42 mV respectively), the telechelic polymer bridging is stronger for the droplets presumably due to the more favorable chemical environment for the hydrophobic end group of PEGDA as it resides at the droplet surface.

Fig. 5 Representative confocal images to validate that plain beads share the same thermally-gelling mechanism as the nanoemulsion via PEGDA bridging. N_c is the averaged coordination number and N_a is the averaged size of an aggregate (number of beads). For all carboxylate bead groups and plain bead groups at T = 25 °C, N_c = N_a = 0, indicating beads are well dispersed in the solution. For the plain bead group at T = 40 °C, N_c and N_a increase from 0.84 ± 0.94 to 1.1 ± 0.91 and from 2.3 ± 0.79 to 2.9 ± 2.0, respectively, as P is increased from 0.05 to 0.33, indicating that clusters are induced by PEGDA, and that more PEGDA induces stronger aggregation. Scale bars = 5 μm. Error bars = 1 standard deviation.

Fig. 6 Schematic of the postulated correlation between plain polystyrene beads and nanoemulsion droplets.

3.5 Multiple particle tracking microrheology of nanoemulsion suspensions

Having shown that we can control whether the probe beads are in the droplet-rich (plain probe beads) or droplet-poor phase (carboxylate probe beads), we now use MPT to probe the material properties in each domain and compare the results. If the material has homogenous rheological properties across the probe length scale, then the scaled MSD, a〈Δr²(τ)〉, will be independent of probe size. If the material is heterogeneous on length scales comparable to or larger than the probe size, the scaled MSD for different bead sizes will not collapse onto a master curve.^7,20,22,65

Fig. 7 and 9 show the scaled MSD plotted versus lag time, τ, for all beads at various temperatures. All of the scaled MSDs shown here have been corrected for static errors. A slope of one on the log–log MSD plot represents diffusive probe dynamics in a Newtonian fluid. For a MSD slope between zero and one, the fluid is non-Newtonian and shows viscoelastic behavior. For a MSD slope that is equal to zero, the material is solid-like and the beads are locally trapped.

Fig. 7 Scaled MSD of carboxylate beads of different sizes at rising temperatures. The bead diameters are (A) 1 μm, (B) 1.5 μm and (C) 2 μm. The logarithmic slope = 1 represents diffusive probe motion. All carboxylate beads show a similar trend: as the gelation proceeds, the scaled MSD decreases, and this decrease is progressively larger for larger beads. Inset: MSD at τ = 5 s plotted versus temperature.

3.5.1 MPT using carboxylate bead probes. Fig. 7 shows the results for carboxylate beads with diameter 2a = 1, 1.5 and 2 μm in the nanoemulsions at various temperatures. All of the carboxylate beads show a similar trend: as the gelation proceeds, the scaled MSD decreases, and this decrease is progressively larger for larger beads. This trend is consistent with the shrinking droplet-poor domains as nanoemulsions cluster via polymer bridging. At low temperatures (T = 30.0 to 35.0 °C), for all beads the scaled MSDs are diffusive and in good agreement, which suggests the nanoemulsion is homogeneous at these length scales being probed. This agreement breaks down when the temperature is increased to 37.5 °C, where a〈Δr²(τ)〉 of 2 μm beads is lower than the other two bead sizes, and a〈Δr²(τ)〉 for 1.5 μm probes begins to show a clear temperature dependence at T = 42.5 °C. Differences among the MSDs for the three probe sizes increase with increasing temperature. At T = 50.0 °C and τ = 10 s, a〈Δr²(τ)〉 of the 1.5 and 2 μm beads are smaller than that of 1 μm beads by half and one order of magnitude respectively. In addition, a〈Δr²(τ)〉 of 2 μm beads has a slope which decreases with increasing lag time. While not reaching a plateau per se, the MSD suggests restricted probe dynamics consistent with beads being partially trapped in droplet-poor domain cages in the nanoemulsion gel. At smaller τ, probes are undergoing Brownian motion and show diffusive dynamics; at larger τ, probes become restricted in cages. The restriction is prominent when the size of the droplet-poor domains is closer to the size of the beads, which also explains why the scaled MSDs do not collapse onto a master curve for different sizes of beads at high temperatures. Therefore, it is not surprising the 2 μm carboxylate beads are more sensitive to the gelation since the gel pore size, represented by L_poor, is ≈1 to 2 μm at elevated temperatures (Table 1).

In Fig. 7A, 1 μm carboxylate beads show an interesting behavior. First, despite the fact that the nanoemulsion forms a strong gel, the MSD remains diffusive and does not decrease significantly at rising temperatures. In fact, for the probes which do not associate with the network, they show viscoelastic MSD only when they are trapped by the materials.²⁵ Even at T = 50.0 °C, the size of the droplet-poor domain is still larger than the 1 μm beads (Table 1), which indicates the 1 μm beads can still diffuse through this domain without much restriction compared to larger beads. Second, the MSDs of 1 μm beads are different than those of other two sizes of beads at rising temperatures. For 1 μm beads, the MSD first increases from T = 30.0 to 37.5 °C (Fig. 7A, T = 30.0 °C, magenta, which overlaps with T = 32.5 °C, blue, and T = 35.0 °C, cyan) and decreases after T = 40.0 °C (yellow), which can also be seen in the inset that plots the MSD at a lag time τ = 5 s. This initial increase in MSD with temperature is less obvious for 1.5 μm beads and is almost absent for 2 μm beads. We believe that the higher mobility in this temperature range is due to the decrease in viscosity in the continuous phase (see ESI,† Fig. S9 for continuous phase viscosity as a function of temperature). At temperatures above T = 37.5 °C, the droplet-poor domain cages are well established (Fig. 2), and the decrease in MSD results from the steric restriction of the cages and the hydrodynamic interaction from the surrounding droplet-rich phases.⁶⁶ Fig. S10 (ESI†) shows the plot of MSD versus dimensionless lag time for carboxylate beads and includes an extended discussion in the increase and subsequent decrease of MSD at rising temperatures.

As the size of beads approaches to the size the droplet-poor domains, bead hopping can occur.^66–68 Hopping is a phenomenon when beads jump from one confinement cage to another, and the residence time trapped in a cage is longer than the jump time. In prior MPT studies, cages were formed by polymer networks, whereas in our system the cages arise from the macroporous gelled nanoemulsion. The size of the droplet-poor domains are ≈1.5 μm at T = 50.0 °C (Table 1), which is comparable to the size of the 2 μm beads. Indeed, we found some of the 2 μm carboxylate beads exhibit hopping. (Note that since we calculated the ensemble-average MSD across all particle trajectories, cage-hopping events have already been accounted for in the raw data and are not subtracted from MSD shown in Fig. 7). Fig. 8 shows the representative spatial and temporal probe trajectories for hopping beads. After constrained motions for a relatively long time, hopping happens at a very short time scale wherein the probe jumps from one droplet-poor phase cage to another. In addition, the trajectories shown in Fig. 8 are consistent with the size of the droplet-poor phase in Fig. 2 and Table 1. From Fig. 8, the movement is ∼0.1 μm, along with size of the 2 μm beads, the size of the droplet-poor domain is about 2.1 μm, which is consistent to the results in Table 1 and Fig. 2 (note that L_poor is defined as the minimum Feret diameter, which is the size of the domain in the smallest dimension).

Fig. 8 Representative spatial and temporal probe trajectories when hopping happens at T = 50.0 °C using 2 μm carboxylate beads. Arrows indicate hopping events.

3.5.2 MPT using plain bead probes. Fig. 9 shows the behavior of plain beads with 2a = 1 and 2 μm in the nanoemulsions at various temperatures. Overall, the plain beads are sensitive to the nanoemulsion gelation and have dynamics which range from simple diffusion in a Newtonian fluid at low temperatures to nearly flat MSDs at high temperatures, indicative of a solid-like material.

Fig. 9 Scaled MSD of plain beads for different sizes at rising temperatures. The diameters are (A) 1 μm and (B) 2 μm. As temperature increases, the scaled MSD decreases and becomes flat. Both sizes of plain beads are sensitive to the temperature change, suggesting that measurements of material stiffness are dependent on the correlation between the probes and the network.

The MSDs of plain beads are probe-size dependent. At low temperatures, although the scaled MSDs ∼ τ¹ for both sizes, 2 μm beads have smaller a〈Δr²(τ)〉. We believe this is due to the larger beads having a larger surface area to interact with the droplets or clusters in the nanoemulsion (see ESI,† Table S3 for the discussion on viscosity of the nanoemulsion obtained by bulk rheology and MPT at T = 30.0 °C). This association also affects the probe dynamics as the temperature increases. At T = 35.0 °C, a〈Δr²(τ)〉 of 2 μm beads shows a clear decrease from T = 30.0 and 32.5 °C; while for 1 μm beads, this decrease happens at T = 37.5 °C. At T = 35.0 °C, the size of the droplet-rich domain (≈6 μm from Table 1) is larger than both sizes of plain beads, which means that beads of both sizes can be entirely engulfed in the droplet-rich domain. Larger beads interact with more droplets. Such interaction can effectively limit bead motion and cause the observed decrease in the scaled MSD, which is more obvious at higher temperatures where beads show a flat MSD.

However, the smaller a〈Δr²(τ)〉 for 2 μm beads at the same T does not hold when further increasing the temperature. When T is above 40.0 °C, the scaled MSD of 1 μm beads decreases faster than 2 μm beads and eventually has smaller a〈Δr²(τ)〉, indicating that the smaller beads are more tightly trapped within the networks at high temperature. The more restricted probe dynamics of the smaller beads are explained by the size of the droplet-rich domains in Table 1. At temperatures above 40.0 °C, L_rich decreases from 1.95 to 1.24 μm, which means that 2 μm beads cannot be entirely enveloped in the droplet-rich phase. Instead, the beads partially enter the droplet-poor phase, which leads to less bridging to the nanoemulsion-rich gelled region and more mobile beads, as shown in Fig. 9.

The beads at T = 35.0 °C (cyan) show counter-intuitive scaled MSDs: although T = 35.0 °C is beyond the gel point from rheometer measurement (Fig. 1C), the probes exhibit diffusive behavior in which a〈Δr²(τ)〉 ∼ τ¹. It has been estimated the interdroplet attractive potential energy via PEGDA bridging is ≈0.89k_BT at 35.0 °C.^11,15 Compared to the attraction at higher temperatures, this weaker attraction might result in voids within the droplet-rich domains, which allows probes to easily move even in the denser phases, and the probe-size dependent scaled MSD implies spatial heterogeneity within the droplet-rich phase across the different length scales being probed. In addition, the rheometer measures rheological response from the cumulating interdroplet interaction across a bulk scale while MPT probes the local microenvironment, suggesting that a weaker gel is probed at the smaller length scales, this will be further discussed in Section 3.5.4.

3.5.3 Comparison of MPT with different probe surface chemistries. By comparing Fig. 7 (carboxylate beads, reside in droplet-poor domains) and Fig. 9 (plain beads, reside in droplet-rich domains), it can be observed that the probe surface chemistry strongly affects the MPT results. This difference between the probe surface chemistry is also seen in Fig. 10, which shows MSD at τ = 10 s in the droplet-poor and droplet-rich domains having dramatically different probe dynamics. The results suggest that plain beads that tether to the network are more sensitive to the nanoemulsion gelation. As an example, at T = 50.0 °C (black dots) the MSD of the plain beads is smaller than that of the carboxylate beads by over 4 orders of magnitude. Similar differences are also observed for beads with diameter of 2 μm. Therefore, along with the data shown in Fig. 7 and 9, the MPT of the nanoemulsion is strongly dependent on the probe surface chemistry, and each of them shows probe-size dependency, which correlates the results from Fig. 3.

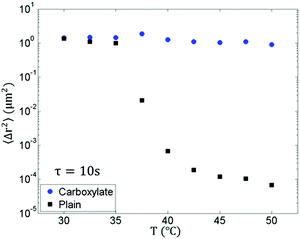Fig. 10 MSD at a lag time of 10 s versus T for 1 μm carboxylate and plain beads at rising temperatures.

Our results are consistent with other works studying the effect of probe surface chemistry in microrheology, even though different systems were investigated.^{20,24,25,27,68–70} One of the most well-studied systems is solutions of the semiflexible polymer F-actin (filamentous actin).^{20,24,25,68,69} Prior work showed that probe surface chemistry can be modified such that probes adhered to the F-actin networks. For example, the binding of the beads to the networks is enhanced by using carboxylate polystyrene beads and is reduced by grafting bovine serum album (BSA) or polyethylene glycol (PEG) to the surface of the polystyrene beads.⁶⁸ Beads bound to the polymer networks are more sensitive to the material's changes in viscoelasticity as compared to those that do not adhere to the polymers. In addition, for beads that are strongly correlated with the network, also known as ‘sticky beads’,⁶⁸ the viscoelasticity of the material obtained by microrheology is closer to the bulk rheology characterization. On the other hand, the dynamics of probes having weak or no interaction with the networks depend on the ratio of the probe to mesh size a/ξ, as discussed above.

3.5.4 Viscoelasticity on the macroscopic and microscopic scales. We calculate the viscoelastic moduli of the nanoemulsion suspensions from the MPT results using eqn (3)–(5). The results from MPT are compared with bulk rheology measurements (Fig. 1C) at a frequency ω ≈ 20 rad s⁻¹, shown in Fig. 11 (ESI,† Fig. S11 and S12 contain the frequency dependent viscoelastic moduli from MPT). Because the plain beads are more sensitive to the gelation, we do not include the results from the carboxylate beads in the comparison here (see ESI,† Fig. S13). Fig. 11 shows the trends seen in both micro- and macro-characterizations are similar. At low temperatures, G′′ dominates, and both moduli grow as temperature increases. Here, we define a temperature T_S at which G′ ≈ G′′ on Fig. 11. Note that T_S is not necessarily the gel point T_gel that is defined by the Winter and Chambon criterion (power-law exponents of G′ and G′′ being equal in a frequency-sweep measurement, Fig. 1C). From Fig. 11, T_S obtained from bulk rheology and microrheology using 1 and 2 μm beads is approximately 32.5 °C, 40.0 °C and 37.5 °C (from the frequency sweep data, T_gel ≈ 32.5 °C, 37.5 °C and 35 °C respectively). It is seen that the larger plain beads are more sensitive to the gelation; however, in the G′-dominant regime, smaller plain beads detect a higher gel strength. Moreover, for both sizes of the plain beads, the viscoelastic moduli are smaller than that measured by bulk rheology. While the MSDs at elevated temperatures are small, they are still larger than the static error which sets the maximum measureable G′ by MPT to approximately 150 Pa.

Fig. 11 Comparison of the viscoelastic moduli from bulk rheology and microrheology using plain beads at frequency ω ≈ 20 rad s⁻¹. Filled symbol = G′; open symbol = G′′.

We believe the discrepancy in modulus between the macro- and microrheology is a result of measuring bead dynamics across different length scales in the gels. The rheometer measures the bulk rheological response from the entire gel. On the other hand, in MPT the plain beads probe the droplet-rich phase with a length scale on the order of 1 μm. As seen in our data (Fig. 9 and Table 2), at T = 32.5 °C, both sizes of plain beads cannot detect the gelling nanoemulsion. However, at this temperature, the G′ measured by bulk rheometry is also very weak, so it is not unreasonable that the plain beads show little elastic response. Interestingly, at T = 35.0 °C, the 2 μm plain beads start to measure an increasing G′ while the 1 μm plain beads remain diffusive in the sample.

Table 2 Comparison between normalized L_rich (L_rich/D, normalized by 1 μm or 2 μm beads) and the G′ (ω ≈ 20 rad s⁻¹) measured by bulk rheometry and MPT at rising temperatures

T (°C)	L rich/D1μm	L rich/D2μm	G bulk′ (Pa)	G 1μm′ (Pa)	G 2μm′ (Pa)
30.0	0.65	0.31	(Nanoemulsion is liquid-like)
32.5	4.84	2.32	1.43	—	—
35.0	5.77	2.77	27.35	—	0.10
37.5	2.05	0.98	140.70	1.15	8.34
40.0	1.88	0.90	246.00	26.74	9.09
42.5	1.68	0.81	342.30	26.04	10.40
45.0	1.64	0.78	399.80	31.70	14.98
47.5	1.27	0.61	413.20	33.56	16.40
50.0	1.20	0.58	421.90	51.34	21.17

---

Our data at T = 35.0 °C suggests two points: first, because the droplet attraction is not strong, it is likely that small voids exist in the droplet-rich phase, although they cannot be clearly visualized with confocal microscopy due to the resolution limits. Second, the droplet distribution in the droplet-rich phase is not homogeneous. According to Table 1, L_rich (≈30 μm) is large enough that both sizes of beads can be entirely enveloped in the droplet-rich domain. Therefore, the 2 μm beads have more association with the droplets due to their larger surface area and thus show an increased value of G′.

To provide a clearer physical picture of the difference between plain beads of varying size and the local microenvironment that they probe in the sample, we compare the normalized L_rich (normalized by the diameter of 1 μm and 2 μm beads, noted as L_rich/D) with the G′ measured by bulk rheometry and MPT at rising temperatures in Table 2. At T ≤ 37.5 °C, droplet-rich domains are larger than both sizes of plain beads (L_rich/D > 1). The 2 μm plain beads measure a stronger gel since they can associate with more droplets. However, when T > 37.5 °C where only 1 μm plain beads can be completely enveloped in the droplet-rich domain, the 1 μm plain beads measure a stronger gel than the 2 μm plain beads. We believe it is because the 2 μm plain beads cannot be entirely trapped in the droplet-rich phase that generates the elastic properties of the nanoemulsion system (L_rich/D < 1). Future work is needed to expand the sizes of beads, especially using beads smaller than 1 μm.

MPT hence detects a weaker gel than bulk rheometry. This trend is consistent with prior work studying the effect of probe-size on microrheology in a LAPONITE® solution⁷ and associative poly(ethylene oxide) solutions,²² as well as the microrheology studies in a microgel particle suspension.²⁶

4. Conclusion

We carried out a systematic multiple particle tracking (MPT) study on thermally-gelling O/W nanoemulsions. In this work, we investigated the role of the colloidal probe size and surface chemistry on MPT in the nanoemulsion system. As temperature increases, hydrophobic groups of PEG-based gelators (PEGDA) partition into oil/water interfaces and bridge droplets. This inter-colloidal attraction generates a wide variety of microstructures consisting of droplet-rich and droplet-poor phases. By tailoring the MPT colloidal probe surface chemistry, we control the residence of probes and independently measure the probe dynamics within each phase. Our results show stark differences in the probe dynamics within each domain. At T = 50.0 °C, the mean squared displacement (MSD) can differ by over four orders of magnitude for the 1 μm beads but with different surface chemistry. Carboxylate-modified polystyrene beads predominantly reside in the droplet-poor phase. The lack of association of carboxylate beads with the network results in “slippery” motion. The scaled MSD of carboxylate beads is consistent with a decreased size of the droplet-poor domain at elevated temperatures. In addition, we also observed probe hopping between pores in the gel for “slippery” probes when the beads become comparable in size to pores in the gel.

On the other hand, polystyrene beads without surface modification (plain beads) predominantly reside in the droplet-rich phase. We showed that the telechelic PEGDA polymer can bridge plain beads to each other at elevated temperatures, which suggests that PEGDA can also thermally bridge the plain beads to the nanoemulsion droplets. This bridging interaction with the network makes plain beads more sensitive to the viscoelastic changes of the nanoemulsion as temperature rises. The microrheological properties are also dependent on the size of the plain beads: larger beads are more sensitive to the gelation transitions while smaller beads detect larger moduli at higher temperatures.

Our approach allows for the unique ability to probe different regions of a colloidal gel and is useful for measuring local properties in these mesostructured hydrogels. Our quantitative results obtained from systematic studies shed light on the microstructures of thermally-gelling nanoemulsions. From our study, the probe-hopping phenomenon provides direct evidence that the droplet-poor phase is interconnected, and the results from plain beads suggest the presence of inhomogeneity within the droplet-rich phase. Furthermore, the selectivity of bead residence in different phases serves as a potential synthesis method for nanoemulsion-based composite materials. A novel aspect to these materials is that the added solid colloids with manipulated surface chemistry allows one to precisely control the residence of colloids in different phases within nanoemulsion gels. Based on the results presented here, we would expect different composite structures depending on the surface chemistry of the added colloids. Future work will look at structures formed at higher particle loadings. For instance, Janus particles with heterogeneous surface modification could provide the fine control of the particle position at the interface between droplet-rich and droplet-poor domains.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was primarily supported by NSF through the Massachusetts Institute of Technology Materials Research Science and Engineering Center DMR – 1419807. L.-C. C. was supported in part by a scholarship from Think Global Education Trust (Taiwan). The authors thank Lynna Chen, P. Douglas Godfrin and Paul W. Bisso for insightful discussions.

References

1. E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101.
2. V. Trappe and P. Sandkühler, Curr. Opin. Colloid Interface Sci., 2004, 8, 494–500.
3. P. N. Segrè, V. Prasad, A. B. Schofield and D. A. Weitz, Phys. Rev. Lett., 2001, 86, 6042–6045.
4. C. J. Dibble, M. Kogan and M. J. Solomon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 1–11.
5. L. C. Hsiao, H. Kang, K. H. Ahn and M. J. Solomon, Soft Matter, 2014, 10, 9254–9259.
6. Q. Wang, L. Wang, M. S. Detamore and C. Berkland, Adv. Mater., 2008, 20, 236–239.
7. J. P. Rich, G. H. McKinley and P. S. Doyle, J. Rheol., 2011, 55, 273–299.
8. Y. Guan and Y. Zhang, Soft Matter, 2011, 7, 6375–6384.
9. E. Dickinson, J. Sci. Food Agric., 2013, 93, 710–721.
10. L. C. Hsiao, A. Z. M. Badruddoza, L.-C. Cheng and P. S. Doyle, Soft Matter, 2017, 13, 921–929.
11. M. E. Helgeson, S. E. Moran, H. Z. An and P. S. Doyle, Nat. Mater., 2012, 11, 344–352.
12. M. E. Helgeson, Y. Gao, S. E. Moran, J. Lee, M. Godfrin, A. Tripathi, A. Bose and P. S. Doyle, Soft Matter, 2014, 10, 3122–3133.
13. A. Gupta, H. B. Eral, T. A. Hatton and P. S. Doyle, Soft Matter, 2016, 12, 2826–2841.
14. L. C. Hsiao and P. S. Doyle, Soft Matter, 2015, 11, 8426–8431.
15. Y. Gao, J. Kim and M. E. Helgeson, Soft Matter, 2015, 11, 6360–6370.
16. J. Kim, D. Merger, M. Wilhelm and M. E. Helgeson, J. Rheol., 2014, 58, 1359–1390.
17. T. G. Mason, K. Ganesan, J. H. van Zanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282–3285.
18. T. M. Squires and T. G. Mason, Annu. Rev. Fluid Mech., 2010, 42, 413–438.
19. T. A. Waigh, Rep. Prog. Phys., 2005, 68, 685–742.
20. B. S. Chae and E. M. Furst, Langmuir, 2005, 21, 3084–3089.
21. B. R. Dasgupta and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 1–9.
22. Q. Lu and M. J. Solomon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 1–11.
23. A. Maestro, L. J. Bonales, H. Ritacco, T. M. Fischer, R. G. Rubio and F. Ortega, Soft Matter, 2011, 7, 7761–7771.
24. J. L. McGrath, J. H. Hartwig and S. C. Kuo, Biophys. J., 2000, 79, 3258–3266.
25. M. T. Valentine, Z. E. Perlman, M. L. Gardel, J. H. Shin, P. Matsudaira, T. J. Mitchison and D. A. Weitz, Biophys. J., 2004, 86, 4004–4014.
26. D. van den Ende, E. H. Purnomo, M. H. G. Duits, W. Richtering and F. Mugele, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 1–9.
27. L. H. Wong, N. A. Kurniawan, H.-P. Too and R. Rajagopalan, Biomech. Model. Mechanobiol., 2014, 13, 839–849.
28. A. Kowalczyk, C. Oelschlaeger and N. Willenbacher, Polymer, 2015, 58, 170–179.
29. C. Oelschlaeger, F. Bossler and N. Willenbacher, Biomacromolecules, 2016, 17, 580–589.
30. T. Moschakis, Curr. Opin. Colloid Interface Sci., 2013, 18, 311–323.
31. T. Moschakis, B. S. Murray and E. Dickinson, J. Colloid Interface Sci., 2010, 345, 278–285.
32. T. Moschakis, B. S. Murray and E. Dickinson, Langmuir, 2006, 22, 4710–4719.
33. W. M. Deen, Introduction to Chemical Engineering Fluid Mechanics, Cambridge University Press, 2016.
34. Kilfoil Lab, http://people.umass.edu/kilfoil/downloads.html.
35. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
36. T. Savin and P. S. Doyle, Biophys. J., 2005, 88, 623–638.
37. A. Kowalczyk, C. Oelschlaeger and N. Willenbacher, Meas. Sci. Technol., 2015, 26, 1–15.
38. T. G. Mason, Rheol. Acta, 2000, 39, 371–378.
39. K. M. Schultz and E. M. Furst, Soft Matter, 2012, 8, 6198–6205.
40. M. E. Helgeson, Curr. Opin. Colloid Interface Sci., 2016, 25, 39–50.
41. T. G. Mason, J. N. Wilking, K. Meleson, C. B. Chang and S. M. Graves, J. Phys.: Condens. Matter, 2006, 18, 635–666.
42. J. Kim, Y. Gao, C. Hebebrand, E. Peirtsegaele and M. E. Helgeson, Soft Matter, 2013, 9, 6897–6910.
43. F. Chambon and H. H. Winter, J. Rheol., 1987, 31, 683–697.
44. H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382.
45. H. H. Winter, Encycl. Polym. Sci. Technol., 2016, 1–15.
46. J. Mewis and N. J. Wagner, Colloidal Suspension Rheology, Cambridge University Press, 2012.
47. C. J. Rueb and C. F. Zukoski, J. Rheol., 1997, 41, 197–218.
48. P. D. Godfrin, N. E. Valadez-Pérez, R. Castañeda-Priego, N. J. Wagner and Y. Liu, Soft Matter, 2014, 10, 5061–5071.
49. P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503.
50. S. Mossa, F. Sciortino, P. Tartaglia and E. Zaccarelli, Langmuir, 2004, 20, 10756–10763.
51. J. C. Conrad, H. M. Wyss, V. Trappe, S. Manley, K. Miyazaki, L. J. Kaufman, A. B. Schofield, D. R. Reichman and D. A. Weitz, J. Rheol., 2010, 54, 421–438.
52. S. Wassén, N. Lorén, K. van Bemmel, E. Schuster, E. Rondeau and A.-M. Hermansson, Soft Matter, 2013, 9, 2738–2749.
53. Y. Gao and M. E. Helgeson, Opt. Express, 2014, 22, 10046–10063.
54. N. W. Song, K. M. Park, I.-H. Lee and H. Huh, Metrologia, 2009, 46, 480–488.
55. H. G. Merkus, Particle Size Measurements: Fundamentals, Practice, Quality, Springer, 2009.
56. R. A. Lauten, A.-L. Kjøniksen and B. Nyström, Langmuir, 2000, 16, 4478–4484.
57. R. A. Lauten, A.-L. Kjøniksen and B. Nyström, Langmuir, 2001, 17, 924–930.
58. M. A. Cohen-Stuart, Adv. Colloid Interface Sci., 1986, 24, 143–239.
59. A. Courvoisier, F. Isel, J. François and M. Maaloum, Langmuir, 1998, 14, 3727–3729.
60. H. Bagger-Jörgensen, L. Coppola, K. Thuresson, U. Olsson and K. Mortensen, Langmuir, 1997, 13, 4204–4218.
61. E. Michel, M. Filali, R. Aznar, G. Porte and J. Appell, Langmuir, 2000, 16, 8702–8711.
62. G. Porte, C. Ligoure, J. Appell and R. Aznar, J. Stat. Mech.: Theory Exp., 2006, 2006, 1–14.
63. V. Testard, O. Julian and C. Ligoure, Macromolecules, 2008, 41, 7219–7226.
64. S. Panmai, R. K. Prud’homme and D. G. Peiffer, Colloids Surf., A, 1999, 147, 3–15.
65. T. Savin and P. S. Doyle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 1–15.
66. I. Y. Wong, M. L. Gardel, D. R. Reichman, E. R. Weeks, M. T. Valentine, A. R. Bausch and D. A. Weitz, Phys. Rev. Lett., 2004, 92, 1–4.
67. R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164.
68. J. He and J. X. Tang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 1–13.
69. M. Ehrenberg and J. L. McGrath, Acta Biomater., 2005, 1, 305–315.
70. L. L. Josephson, E. M. Furst and W. J. Galush, J. Rheol., 2016, 60, 531–540.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm01191a

---