Avoiding the pull-in instability of a dielectric elastomer film and the potential for increased actuation and energy harvesting
Shengyou
Yang
a,
Xuanhe
Zhao
bc and
Pradeep
Sharma
 *ad
*ad
aDepartment of Mechanical Engineering, University of Houston, Houston, TX 77204, USA
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
cDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
dDepartment of Physics, University of Houston, Houston, TX 77204, USA. E-mail: psharma@uh.edu; Fax: +1-713-743-4503; Tel: +1-713-743-4502
First published on 1st June 2017
Abstract
Pull-in instability often occurs when a film of a dielectric elastomer is subjected to an electric field. In this work, we concoct a set of simple, experimentally implementable, conditions that render the dielectric elastomer film impervious to pull-in instability for all practical loading conditions. We show that a uniaxially pre-stretched film has a significantly large actuation stretch in the direction perpendicular to the pre-stretch and find that the maximal specific energy of a dielectric elastomer generator can be increased from 6.3 J g−1 to 8.3 J g−1 by avoiding the pull-in instability.
Soft dielectrics are capable of achieving significantly large deformations and find application in humanlike robots,1,2 stretchable electronics,3 actuators,4–6 and energy harvesters7–11 among others.12,13 However, soft dielectrics under applied electric fields are also vulnerable to various types of electromechanical instabilities.14–19 Instabilities are often thought to be detrimental to material and device functionality and often avoided by design. Recent works have, however, focused on harnessing instabilities for various applications such as artificial muscles,20,21 dynamic surface patterning,22,23 giant voltage-triggered deformation,24,25 and energy harvesting.26,27
A commonly used actuator is a dielectric thin film coated with two compliant electrodes. Upon application of a potential difference between the two electrodes, the dielectric film thins down in the thickness direction and expands laterally. When the thickness decreases to a certain threshold, the film is unable to sustain the electric field and the so-called pull-in instability occurs.14–16,26,28 To avoid failure and to enhance the actuation strain and the harvested electrical energy density, pull-in instability is often suppressed by using a pre-stress,28 materials that exhibit load-dependent stiffening29,30 and charge-controlled operation.6,31 Moreover, pull-in instability can also be delayed or eliminated by pre-stretch.32–34 In this work we analyze how properly chosen (and experimentally realizable) boundary conditions can be exploited to avoid or delay pull-in instability. We show that the pull-in instability can be summarily avoided by a judicious combination of dead-loads and controlled-displacement boundary conditions which renders the pertinent Hessian matrix of the equilibrium state positive-definite under all practical conditions. By prevention of pull-in instability and through exploitation of the competition between various pertinent factors such as electromechanical loading conditions, consideration of buckling, and pre-stretch, among others, we theoretically highlight a significantly increased ability for energy harvesting and actuation. However, realizing the theoretical maximum energy conversion experimentally has still remained elusive and the reduction of the disparity between experiments and theoretical predictions appears to be a challenging task.7–10
Consider an elastic dielectric film with dimensions (L1, L2, L3) in its undeformed state. Subjected to the voltage Φ and the dead load P2 at a prescribed stretch λ1, the incompressible film deforms to a homogeneous state with stretches λ1, λ2, and λ3 = λ1−1λ2−1. Moreover, the film gains a magnitude of total charge Q that distributes uniformly on either side of the compliant electrodes. The homogeneously deformed film is shown in Fig. 1. We remark that the loading device actually controls the normal displacement (or the stretch λ1) only on the two sides of the film in the X1 direction. Since the deformation is homogeneous under these circumstances, the entire film exhibits prescribed stretch λ1.
The nominal electric field and the nominal electric displacement are defined as Ẽ = Φ/L3 and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = Q/L1L2, respectively. The true electric field and the electric displacement are defined as E = Φ/(λ3L3) and D = λ3Q/(L1L2). Furthermore, the nominal and true stresses from the dead load P2 are denoted, respectively, as s2 = P2/(L1L3) and σ2 = λ2P2/(L1L3).
= Q/L1L2, respectively. The true electric field and the electric displacement are defined as E = Φ/(λ3L3) and D = λ3Q/(L1L2). Furthermore, the nominal and true stresses from the dead load P2 are denoted, respectively, as s2 = P2/(L1L3) and σ2 = λ2P2/(L1L3).
The free energy of the system is28,35
G = L1L2L3W(λ1,λ2,![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ) − P2λ2L2 − ΦQ. ) − P2λ2L2 − ΦQ. | (1) |
We remark that the stretch λ1, the dead load P2, and the voltage Φ in eqn (1) are prescribed parameters. In contrast to Yang et al.36 and Dorfmann and Ogden37 the dielectric film in this work admits only a class of homogeneous deformations. Thus, the general coordinate λ1 has a zero variation δλ1 = 0 for any homogeneous perturbation. When other two generalized coordinates λ2 and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) vary by small amounts δλ2 and δ
vary by small amounts δλ2 and δ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , the free energy of the system varies by
, the free energy of the system varies by
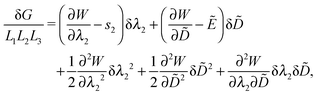 | (2) |
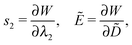 | (3) |
 | (4) |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) as well as λ1. Indeed, the partial derivative in eqn (4) is to be understood as the partial derivative of W with respect to λ1 at the pre-stretch λ1. It is exactly the coefficient of the zero δλ1 in the first variation of the energy. Thus, it has been omitted in the variation form for simplicity. In equilibrium, from Cauchy’s stress theorem, s1 in eqn (4) is equal to the stress generated by the force applied on the left and right surfaces, and the magnitude of the force is s1L2L3.
as well as λ1. Indeed, the partial derivative in eqn (4) is to be understood as the partial derivative of W with respect to λ1 at the pre-stretch λ1. It is exactly the coefficient of the zero δλ1 in the first variation of the energy. Thus, it has been omitted in the variation form for simplicity. In equilibrium, from Cauchy’s stress theorem, s1 in eqn (4) is equal to the stress generated by the force applied on the left and right surfaces, and the magnitude of the force is s1L2L3.
From the principle of minimum energy, the stability of the equilibrium solution requires a positive-definite second variation in eqn (2) for arbitrary δλ2 and δ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , that is, the Hessian matrix
, that is, the Hessian matrix
 | (5) |
Consider an ideal dielectric elastomer with the free energy function,28,35
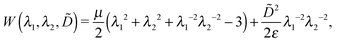 | (6) |
 | (7a) |
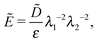 | (7b) |
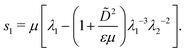 | (8) |
Eqn (7) contains two algebraic equations with two variables λ2 and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) and three prescribed parameters λ1, s2, and Ẽ. A quartic equation in terms of λ2 can be obtained by eliminating
and three prescribed parameters λ1, s2, and Ẽ. A quartic equation in terms of λ2 can be obtained by eliminating ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , such that
, such that
| (μ − λ12εẼ2)λ24 − s2λ23 − μλ1−2 = 0, | (9) |
 | (10) |
 | (11) |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) . Otherwise, eqn (7) has no solution for realistic physical situations that admit positive λ2 and nonnegative
. Otherwise, eqn (7) has no solution for realistic physical situations that admit positive λ2 and nonnegative ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) .
.
The electromechanical stability of the electrostatic system directly relates to the property of the Hessian matrix [eqn (5)] that, at equilibrium [eqn (7)], is given by
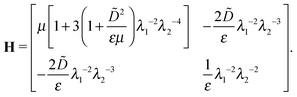 | (12) |
The 1 × 1 principal minors of the Hessian matrix [eqn (12)] are the diagonal entries H11 > 0 and H22 > 0, and the only 2 × 2 principal minor is the determinant of the Hessian matrix [eqn (12)], which is always positive, namely
 | (13) |
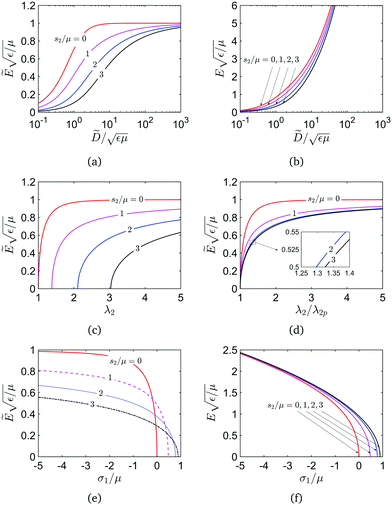
To further understand the behavior of the dielectric film in equilibrium, two special cases are discussed. Case I is a dielectric film at a prescribed stretch λ1 = 1 under an electric field and several dead loads s2, while case II is a dielectric film at a zero dead load s2 = 0 under an electric field and several prescribed stretches λ1.
In Fig. 2, we plot the behavior of the dielectric film for case I, i.e. λ1 = 1. Fig. 2(a) shows that the nominal electric field increases monotonically with the increase of the nominal electric displacement. The nominal electric field is bounded by eqn (11) and the critical nominal electric field for the nonexistence of equilibrium solutions at λ1 = 1 is  . With a constant nominal electric field but an increase of the dead load s2, the nominal electric displacement increases in Fig. 2(a), since a dead load leads to a reduced thickness but a larger area, thus resulting in a larger capacity (and charge). Fig. 2(b) shows the relation of the nominal electric displacement and the true electric field under several dead loads s2.
. With a constant nominal electric field but an increase of the dead load s2, the nominal electric displacement increases in Fig. 2(a), since a dead load leads to a reduced thickness but a larger area, thus resulting in a larger capacity (and charge). Fig. 2(b) shows the relation of the nominal electric displacement and the true electric field under several dead loads s2.
In Fig. 2(c), the variation of the stretch λ2 is plotted. Both the nominal electric field and the dead load s2 can increase the stretch λ2. At the critical value  , the stretch λ2 increases to infinity and the thickness (λ3 = λ2−1) decreases to zero, which, of course, is impossible in reality since prior to such a blowup, electric breakdown will ensue due to the large true electric field or, alternatively, mechanical rupture will take place. The actuation stretch is defined as λ2/λ2p, where λ2p is the pre-stretch that exists due to the prescribed stretch λ1 and the dead load s2. At a prescribed stretch λ1 = 1, the actuation stretch λ2/λ2p under several dead loads s2 is shown in Fig. 2(d).
, the stretch λ2 increases to infinity and the thickness (λ3 = λ2−1) decreases to zero, which, of course, is impossible in reality since prior to such a blowup, electric breakdown will ensue due to the large true electric field or, alternatively, mechanical rupture will take place. The actuation stretch is defined as λ2/λ2p, where λ2p is the pre-stretch that exists due to the prescribed stretch λ1 and the dead load s2. At a prescribed stretch λ1 = 1, the actuation stretch λ2/λ2p under several dead loads s2 is shown in Fig. 2(d).
The true stress σ1 = λ1s1 shown in Fig. 2(e) is directly related to electrical buckling and will be analyzed in the following. At a zero dead load in Fig. 2(e), the true stress is σ1/μ = 1 − (1 − εẼ2/μ)−1/2, and the nominal electric field induces a compressive state in the film, i.e. σ1 < 0, and the magnitude |σ1| increases monotonically with the increase of the nominal electric field. On the other hand, at a zero electric field, a dead load s2 expands the film (λ2 > 1) and induces a tensile state i.e. σ1/μ = 1 − λ2−2 > 0 in Fig. 2(e). Interestingly, there exists a competition between the electric field and the dead load due to their opposite effects on the stress σ1. At a low electric field, the dead load makes the dielectric film extend within the plane. When the electric field increases, the stress σ1 gradually decreases from a tensile stress (σ1 > 0) to a compressive one (σ1 < 0). Without considering electric breakdown (under a high true electric field) and rupture by stretch (at a high stretch λ2), the continually increasing |σ1| of the compressive stress will finally make the dielectric film buckle.
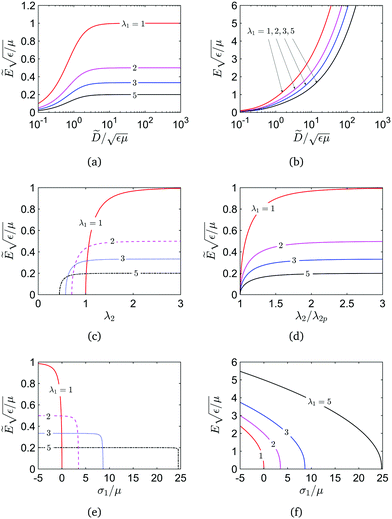
Fig. 3 plots the behavior of the dielectric film for case II, i.e. s2 = 0. We note that eqn (11) gives the limit of the nominal electric field, for example,  for a prescribed stretch λ1 = 1, while it is 0.2 for λ1 = 5 in Fig. 3(a), (c) and (e). The increase of the stretch λ1 in Fig. 3(a) increases the film surface area, leading to higher capacity and gain of additional charge. In other words, at a prescribed nominal electric field below
for a prescribed stretch λ1 = 1, while it is 0.2 for λ1 = 5 in Fig. 3(a), (c) and (e). The increase of the stretch λ1 in Fig. 3(a) increases the film surface area, leading to higher capacity and gain of additional charge. In other words, at a prescribed nominal electric field below 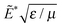 , a larger stretch λ1 corresponds to a higher nominal electric displacement. Fig. 3(b) shows the corresponding relation between the true electric field and the nominal electric displacement.
, a larger stretch λ1 corresponds to a higher nominal electric displacement. Fig. 3(b) shows the corresponding relation between the true electric field and the nominal electric displacement.
In Fig. 3(c), the increase of the stretch λ1 in the length direction will make the film decrease its width (or the pre-stretch λ2p at a zero electric field), pre-stretch but an electric field, on the other hand, will tend to make the film expand in-plane and exhibit a larger stretch (λ2). At s2 = 0, the actuation stretch λ2/λ2p under several prescribed stretches λ1 is shown in Fig. 3(d).
The true stress from eqn (7) and (8) at s2 = 0 is obtained as σ1/μ = λ1s1/μ = λ12 − λ1−1(1 − λ12εẼ2/μ)−1/2. Without the electric field, the true stress σ1/μ is λ12 − λ1−1. When the electric field increases from zero, for example, at a prescribed stretch λ1 > 1 in Fig. 3(e) and (f), the true stress σ1 will decrease from a tensile stress (σ1 > 0) to a compressive one (σ1 < 0).
It is well-known that a thin film subjected to a lateral compression is easy to buckle. In our model, the deformation in the X1 direction is controlled by two well-lubricated plates, and a compressive stress (σ1 < 0) in the film can occur under some conditions (see Fig. 2(e), f, 3e and f for example). In the following, we will discuss electric buckling of a dielectric film subjected to electromechanical loads.
The special case, loss of tension, is of interest because it is a turning point for the compression–tension behavior of the dielectric film. The compressive stress can make the film buckle and should be avoided.5,7,36,37 When the nominal stress s1 in eqn (8) becomes zero, it is in the so-called state of loss of tension. From the equilibrium equations [eqn (7)], the nominal electric field at loss of tension is
 | (14) |
 due to s2 = P2/(L1L3) ≥ 0.
due to s2 = P2/(L1L3) ≥ 0.
At the state of loss of tension, if we, for example, continue to prescribe the stretch λ1 and the dead load s2 but increase the nominal electric field, the stress s1 in eqn (8) will decrease from zero to negative and the film will be in a state of compression. Inspired by Euler’s buckling of a long, slender, ideal column, we analyze here the electrical buckling of a dielectric film. Euler’s formula for the buckling of a column with two fixed end supports is
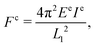 | (15) |
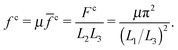 | (16) |
It is assumed that the dielectric film begins to buckle when the magnitude of the compressive stress σ1 = λ1s1 < 0 in eqn (8) reaches fc in eqn (16). Together with the equilibrium equations [eqn (7)], the critical nominal electric field for the electrical buckling can be expressed as
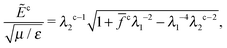 | (17) |
 and
and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) c = π2/(L1/L3)2. Compared with the length (L1) and the width (L2) of the film, the thickness (L3) is often much smaller. Then the buckling stress
c = π2/(L1/L3)2. Compared with the length (L1) and the width (L2) of the film, the thickness (L3) is often much smaller. Then the buckling stress ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) c in eqn (16) is very small, for example,
c in eqn (16) is very small, for example, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) c < 0.1 for a film with an aspect ratio L1/L3 > 10. Therefore, the critical nominal electric field in eqn (17) for buckling is very close to that in eqn (14) for the loss of tension.
c < 0.1 for a film with an aspect ratio L1/L3 > 10. Therefore, the critical nominal electric field in eqn (17) for buckling is very close to that in eqn (14) for the loss of tension.
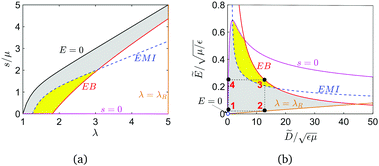
Fig. 4 shows the critical electric fields for the loss of tension [eqn (14)] and electrical buckling [eqn (17)] in which the aspect ratio is chosen to be L1/L3 = 10. The difference between the two critical nominal electric fields is negligible at a stretch λ1 > 1, while it is minor at a stretch λ1 < 1. Moreover, the critical electric field for the loss of tension is always below that of electrical buckling. Therefore, there is no electrical buckling when a loss of tension occurs in the film, but the film will buckle if the electric field increases.
For each curve in Fig. 4(a), there exists a peak that corresponds to the maximum of the critical nominal electric field. At that peak, any infinitesimal variation of the stretch λ1 will make the film buckle; however, the decrease of the nominal electric field will avoid the electrical buckling. On the other hand, if a point on the buckling curve is on the left-hand side of the peak, the increase of the stretch λ1 will avoid the electrical buckling, while a point is on the right-hand side of the peak, the electrical buckling can be avoided by a decrease of the stretch λ1. The corresponding relation between the critical true electric field and the stretch λ1 is shown in Fig. 4(b).
A high actuation strain for an actuator driven by an electric field is desirable. Without an electric field, the pre-stretch λ2p due to the prescribed stretch λ1 and the dead load s2 can be determined by eqn (7) with Ẽ = 0. The effects of s2 and λ1 on the pre-stretch λ2p are shown in Fig. 5(a). The pre-stretch is λ2p = λ1−1/2 at s2 = 0, while it is approximately equal to s2/μ at a high dead load.
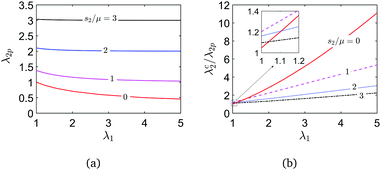 | ||
| Fig. 5 Effects of the prescribed stretch λ1 and the dead load s2 on (a) the pre-stretch λ2p and (b) the critical actuation stretch λc2/λ2p. | ||
Subjected to the electric field, the dielectric film thins down and expands in the plane. When the electric field increases to the critical value in eqn (17), the electrical buckling occurs in the dielectric film with a critical stretch λ2c. The critical actuation stretch is defined as λc2/λ2p. Fig. 5(b) plots the effects of the stretch λ1 and the dead load s2 on the actuation stretch λc2/λ2p. It shows that when the dielectric film is subjected to a prescribed stretch λ1, the actuation stretch in the direction normal to the prescribed stretch is significantly larger, especially in the case of a larger prescribed stretch (λ1) and at a zero dead load (s2 = 0). Hence the actuation stretch can be dramatically increased by a prescribed stretch. A similar observation has also reported before in the analysis of the electromechanical instability of a uniaxial pre-stressed dielectric film.28
Inspired by the aforementioned discussion related to the avoidance of pull-in instability, we now show the possibility of increasing the capacity of the energy conversion of a dielectric elastomer generator. It is known that the usual modes of failure in a dielectric film include electrical breakdown (EB), electromechanical instability (EMI or pull-in instability), loss of tension, and rupture by stretch. The area of the cycle enclosed by these four modes of failure is exactly the maximal energy that can be converted in a dielectric film subjected to equal biaxial in-plane forces.7 With the same dielectric film but mechanical boundary conditions suggested in this work, the pull-in instability can be avoided and then the four modes of failure reduce to three. This reduction admits the possibility of enhanced energy conversion. In the following, we will show that not only the maximal energy of a dielectric elastomer generator but also the specific energy enclosed by a rectangular in the voltage–charge plane and the amplification of voltage (ratio of the input voltage to the output voltage) can be increased significantly.
In a previous work,7 the dielectric film is subjected to equal biaxial in-plane forces and voltage in the thickness direction, such that the equal nominal stresses s1 = s2 and the equal stretches λ1 = λ2 at equilibrium. It should be noted that there is no difference between the forms of the equilibrium equations in the work7 and in this paper, but the difference is the control parameters. Unlike the equal biaxial in-plane forces,7 this paper takes a prescribed stretch λ1 and a dead load s2 as control parameters. Since the equilibrium equations have the same forms, the equilibrium solutions of a film subjected to equal biaxial in-plane forces – as discussed by Koh et al.7 – can be achieved by choosing properly controlled parameters (λ1, s2) in this work; however, the pull-in instability will be avoided. This similarity makes feasible the direct use of their model in this work for the illustration of enhanced energy conversion by the proposed avoidance of the pull-in instability.
To make this communication self-contained, we briefly review the four modes of failure when subjected to equal nominal stresses s = s1 = s2 and equal stretches λ = λ1 = λ2 in equilibrium [eqn (7)]. First, the curve under a zero electric field (E = 0) in Fig. 6(a) is determined by eqn (7a) with ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = 0, while it is the origin in Fig. 6(b). Next, the electrical breakdown (EB) curve is governed by eqn (7) with Ẽ = EEBλ−2, where EEB = 3 × 108 V m−1 is the critical true electric field when EB occurs.7,38 Other material parameters used in the numerical calculations are μ = 106 N m−2 and ε = 3.54 × 10−11 F m−1 as well as the mass density ρ = 1000 kg m−3. Then, the curve of the loss of tension is the horizontal axis in Fig. 6(a), while it is represented by eqn (7) with s = 0 in Fig. 6(b). The curve of rupture by stretch in Fig. 6(a) is the vertical line λ = λR while in Fig. 6(b) it is determined by eqn (7b) with λ = λR, where λR ≤ 6 when the film ruptures when subjected to equal biaxial stretch.15 Here we use λR = 5. Last, the curve of electromechanical instability (EMI) is based on eqn (6) and (7) in the work by Koh et al.7
= 0, while it is the origin in Fig. 6(b). Next, the electrical breakdown (EB) curve is governed by eqn (7) with Ẽ = EEBλ−2, where EEB = 3 × 108 V m−1 is the critical true electric field when EB occurs.7,38 Other material parameters used in the numerical calculations are μ = 106 N m−2 and ε = 3.54 × 10−11 F m−1 as well as the mass density ρ = 1000 kg m−3. Then, the curve of the loss of tension is the horizontal axis in Fig. 6(a), while it is represented by eqn (7) with s = 0 in Fig. 6(b). The curve of rupture by stretch in Fig. 6(a) is the vertical line λ = λR while in Fig. 6(b) it is determined by eqn (7b) with λ = λR, where λR ≤ 6 when the film ruptures when subjected to equal biaxial stretch.15 Here we use λR = 5. Last, the curve of electromechanical instability (EMI) is based on eqn (6) and (7) in the work by Koh et al.7
In Fig. 6, the shaded areas enclosed by various modes of failure (also the E = 0 curve) define the maximal energy of conversion, that is, the maximal specific energy. In the work by Koh et al.7 four modes of failure leads to a maximal specific energy of 6.3 J g−1. In contrast, the EMI (pull-in instability) is avoided in our proposed scheme and the remaining three modes of failure admit a maximal specific energy of 8.3 J g−1, increasing the capacity of the dielectric elastomer generator by nearly 33%.
The aforementioned maximal-energy cycle is idealized and may be difficult to realize in practice. The rectangular7 and triangular39 cycles are often used for energy conversion. We refer the reader to the Koh et al.7,39 for the detailed circuit design that pumps electric charge from a low-voltage battery to a high-voltage battery. A rectangle with vertices 1–2–3–4 is plotted in Fig. 6(b), where the energy enclosed by the rectangle is called the specific energy. The electric voltage corresponding to vertices (1,2) is the input voltage Φin, while the electric voltage corresponding to vertices (3,4) is the output voltage Φout. The specific energy and the amplification of voltage for various Φin are plotted in Fig. 7(a) and (b). Evidently, the avoidance of pull-in instability can enhance the ability of energy conversion of a dielectric elastomer generator by increasing the specific energy and the voltage amplification.
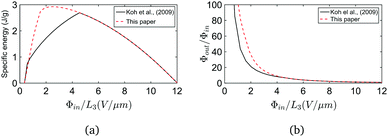 | ||
| Fig. 7 Specific energy (a) and amplification of voltage (b) for cycles represented by various rectangles in Fig. 6(b). | ||
In summary, in this work, we propose the avoidance of the pull-in instability of a dielectric film by introducing controlled-displacement boundary conditions, which ensure that the Hessian matrix is always positive definite in equilibrium regardless of the values assigned to the prescribed stretch, the dead load, and the electric field. The limit of the nominal electric field for the existence of equilibrium solutions is presented. We also show that the critical electric field for the loss of tension is slightly below that of electrical buckling and a uniaxial pre-stretched dielectric film can exhibit a significantly larger actuation strain in the direction perpendicular to the pre-stretch. Here we should emphasize that the film needs to be highly pre-stretched, uniaxially, to avoid loss of tension (or electrical buckling) when the electric field is high and the dead load is low. Finally, we find that the maximal specific energy that can be harvested may be increased from 6.3 J g−1 to 8.3 J g−1 by avoiding pull-in instability.
Acknowledgements
The authors gratefully acknowledge support from NSF CMMI Grant No. 1463205 and the M. D. Anderson Professorship.References
- N. Lu and D.-H. Kim, Soft Robotics, 2014, 1, 53–62 CrossRef.
- S. Shian, K. Bertoldi and D. R. Clarke, Adv. Mater., 2015, 27, 6814–6819 CrossRef CAS PubMed.
- J. A. Rogers, T. Someya and Y. Huang, Science, 2010, 327, 1603–1607 CrossRef CAS PubMed.
- R. Shankar, T. K. Ghosh and R. J. Spontak, Soft Matter, 2007, 3, 1116–1129 RSC.
- M. Moscardo, X. Zhao, Z. Suo and Y. Lapusta, J. Appl. Phys., 2008, 104, 093503 CrossRef.
- C. Keplinger, M. Kaltenbrunner, N. Arnold and S. Bauer, Proc. Natl. Acad. Sci., 2010, 107, 4505–4510 CrossRef CAS PubMed.
- S. J. A. Koh, X. Zhao and Z. Suo, Appl. Phys. Lett., 2009, 94, 262902 CrossRef.
- S. J. A. Koh, C. Keplinger, T. Li, S. Bauer and Z. Suo, IEEE/ASME Transactions on Mechatronics, 2011, 16, 33–41 CrossRef.
- J. Huang, S. Shian, Z. Suo and D. R. Clarke, Adv. Funct. Mater., 2013, 23, 5056–5061 CrossRef CAS.
- R. Kaltseis, C. Keplinger, S. J. A. Koh, R. Baumgartner, Y. F. Goh, W. H. Ng, A. Kogler, A. Tröls, C. C. Foo and Z. Suo, et al. , RSC Adv., 2014, 4, 27905–27913 RSC.
- S. Bauer, S. Bauer-Gogonea, I. Graz, M. Kaltenbrunner, C. Keplinger and R. Schwödiauer, Adv. Mater., 2014, 26, 149–162 CrossRef CAS PubMed.
- Q. Deng, L. Liu and P. Sharma, Journal of the Mechanics and Physics of Solids, 2014, 62, 209–227 CrossRef CAS.
- Q. Deng, L. Liu and P. Sharma, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012603 CrossRef PubMed.
- K. Stark and C. Garton, Nature, 1955, 176, 1225–1226 CrossRef.
- J.-S. Plante and S. Dubowsky, Int. J. Solids Struct., 2006, 43, 7727–7751 CrossRef CAS.
- X. Zhao and Z. Suo, Appl. Phys. Lett., 2009, 95, 031904 CrossRef.
- X. Zhao and Z. Suo, Phys. Rev. Lett., 2010, 104, 178302 CrossRef PubMed.
- Q. Wang, L. Zhang and X. Zhao, Phys. Rev. Lett., 2011, 106, 118301 CrossRef PubMed.
- Q. Wang and X. Zhao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 042403 CrossRef PubMed.
- S. Ashley, Sci. Am., 2003, 289, 52–59 CrossRef CAS PubMed.
- P. Brochu and Q. Pei, Macromol. Rapid Commun., 2010, 31, 10–36 CrossRef CAS PubMed.
- S. Yang, K. Khare and P.-C. Lin, Adv. Funct. Mater., 2010, 20, 2550–2564 CrossRef CAS.
- Q. Wang, D. Robinson and X. Zhao, Appl. Phys. Lett., 2014, 104, 231605 CrossRef PubMed.
- C. Keplinger, T. Li, R. Baumgartner, Z. Suo and S. Bauer, Soft Matter, 2012, 8, 285–288 RSC.
- T. Li, C. Keplinger, R. Baumgartner, S. Bauer, W. Yang and Z. Suo, Journal of the Mechanics and Physics of Solids, 2013, 61, 611–628 CrossRef.
- X. Zhao and Q. Wang, Applied Physics Reviews, 2014, 1, 021304 CrossRef.
- N. Hu and R. Burgueño, Smart Mater. Struct., 2015, 24, 063001 CrossRef.
- X. Zhao and Z. Suo, Appl. Phys. Lett., 2007, 91, 061921 CrossRef.
- S. M. Ha, W. Yuan, Q. Pei, R. Pelrine and S. Stanford, Adv. Mater., 2006, 18, 887–891 CrossRef CAS.
- X. Niu, H. Stoyanov, W. Hu, R. Leo, P. Brochu and Q. Pei, Journal of Polymer Science Part B: Polymer Physics, 2013, 51, 197–206 CrossRef CAS.
- B. Li, J. Zhou and H. Chen, Appl. Phys. Lett., 2011, 99, 244101 CrossRef.
- G. Kofod, J. Phys. D: Appl. Phys., 2008, 41, 215405 CrossRef.
- S. Akbari, S. Rosset and H. R. Shea, Appl. Phys. Lett., 2013, 102, 071906 CrossRef.
- L. Jiang, A. Betts, D. Kennedy and S. Jerrams, J. Phys. D: Appl. Phys., 2016, 49, 265401 CrossRef.
- Z. Suo, X. Zhao and W. H. Greene, Journal of the Mechanics and Physics of Solids, 2008, 56, 467–486 CrossRef CAS.
- S. Yang, X. Zhao and P. Sharma, J. Appl. Mech., 2017, 84, 031008 CrossRef.
- L. Dorfmann and R. W. Ogden, International Journal of Engineering Science, 2014, 77, 79–101 CrossRef.
- R. Pelrine, R. Kornbluh, Q. Pei and J. Joseph, Science, 2000, 287, 836–839 CrossRef CAS PubMed.
- S. Shian, J. Huang, S. Zhu and D. R. Clarke, Adv. Mater., 2014, 26, 6617–6621 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |