Open Access Article
Open Access ArticleInfluence of the glycocalyx on the size and mechanical properties of plasma membrane-derived vesicles†
Purvil
Jani
 a,
Marshall J.
Colville
ab,
Sangwoo
Park
a,
Marshall J.
Colville
ab,
Sangwoo
Park
 ab,
Youlim
Ha
ab,
Youlim
Ha
 a,
Matthew J.
Paszek
a,
Matthew J.
Paszek
 *abc and
Nicholas L.
Abbott
*abc and
Nicholas L.
Abbott
 *a
*a
aRobert Frederick Smith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA. E-mail: mjp31@cornell.edu; nabbott@cornell.edu
bField of Biophysics, Cornell University, Ithaca, NY 14853, USA
cNancy E. and Peter C. Meining School of Biomedical Engineering, Cornell University, Ithaca, NY 14853, USA
First published on 9th December 2024
Abstract
Recent studies have reported that the overexpression of MUC1 glycoproteins on cell surfaces changes the morphology of cell plasma membranes and increases the blebbing of vesicles from them, supporting the hypothesis that entropic forces exerted by MUC1 change the spontaneous curvature of cell membranes. However, how MUC1 is incorporated into and influences the size and biophysical properties of plasma-membrane-blebbed vesicles is not understood. Here we report single-vesicle-level characterization of giant plasma membrane vesicles (GPMVs) derived from cells overexpressing MUC1, revealing a 40× variation in MUC1 density between GPMVs from a single preparation and a strong correlation between GPMV size and MUC1 density. By dispersing GPMVs in aqueous liquid crystals (LCs), we show that the elasticity of the LC can be used to strain individual GPMVs into spindle-like shapes, consistent with the straining of fluid-like membranes. To quantify the influence of MUC1 on membrane mechanical properties, we analyze the shapes of strained GPMVs within a theoretical framework that integrates the effects of MUC1 density and GPMV size on strain. We measure the spontaneous curvature of GPMV membranes to be 2–10 μm−1 and weakly influenced by the 40× variation in MUC1 density, a conclusion we validate by performing independent experiments in which MUC1 is enzymatically removed from GPMVs. Overall, our study advances the understanding of heterogeneity in size and MUC1 density in GPMVs, and establishes single-vesicle-level methods for characterization of mechanical properties within a heterogeneous population of GPMVs. Furthermore, our measurements highlight differences between membrane properties of GPMVs and their parent cells.
Introduction
The glycocalyx at the surface of eukaryotic cells is a complex assembly of proteins and carbohydrates.1 Glycoprotein components of the glycocalyx play an important role in various cellular functions, including signal transduction,2 modulation of microenvironment at the cell surface3,4 and regulation of adhesion to extracellular matrix.5,6 Notably, overexpression of glycoproteins such as the mucin MUC1 has been linked to the progression of aggressive cancer.7,8 Although studies of the role of mucins in cancer have focused on their biochemical aspects, it is increasingly understood that they may also influence cancer through biophysical processes.9,10Past studies have shown that mammalian epithelial cells can be genetically engineered to express varying levels of MUC1 on their plasma membranes in an inducible manner.5 The overexpression ofMUC11 on these cells was found to change the shapes of cells and to give rise to circulatory tumor cell-like behaviors (i.e., detachment from extracellular matrix, survival in suspension, reattachment, and division). Later reports revealed that the overexpression of MUC1 favors the formation of bleb and tubular projections from the plasma membranes of cells (Fig. 1(A)), leading to the proposal that MUC1 over-expression can change the spontaneous curvatures of plasma membranes by more than 3 orders of magnitude (Fig. 1(B)).11 While studies of whole cells suggest a role for MUC1 in changing the morphology and mechanical properties of cell membranes, a complete account requires consideration of the influence of the cell cytoskeleton on cell shape and mechanical properties.11,12 To study the influence of MUC1 on membrane mechanical properties in absence of confounding effects of the cytoskeleton, here we explore the properties of cell-derived giant plasma membrane vesicles (GPMVs).
 | ||
| Fig. 1 (A) (Upper) Schematic illustration of the plasma membrane of a mammalian cell. (Middle) Electron micrographs showing three plasma membrane morphologies of genetically modified human breast epithelial cells that accompany an increase in mucin density in the glycocalyx. (Lower) Schematic illustration of bending of membranes driven by entropic forces generated by mucins. (B) Predicted values of spontaneous curvature as a function of mucin density on cells. Reprinted from ref. 11, Copyright (2019), with permission from Elsevier. | ||
GPMVs are micrometer-sized (∼1–10 μm) vesicles blebbed from the plasma membranes of cells, and they lack the cytoskeleton and organelles that are present in whole cells.13 They have been widely used as model systems for studying the properties of their parent cell plasma membranes14 (e.g., phase separation,15 bending rigidity,16 protein localization17), to create simplified cell mimics,18 and as carriers for drug delivery.19 Select prior studies have reported proteomic analyses of GPMVs, revealing that over 93% of proteins found in cell membranes can be detected in GPMVs.20 However, the extent to which the parent cell membrane composition and organization is generally reflected in GPMVs is not yet fully understood. Additionally, the possibility that GPMV size and membrane composition are correlated across a population of GPMVs derived from a single preparation of cells has not been investigated.
A key goal of the study reported in this paper was to characterize the variation of GPMV size and MUC1 density across a population of GPMVs obtained from a single preparation of cells. By performing single-vesicle-level characterization, we aimed to simultaneously measure the MUC1 density and size of individual GPMVs, and thus explore the possible correlation between these two key GPMV properties. To achieve this goal, we prepared GPMVs from genetically engineered mammalian epithelial cells that express high levels of MUC1 with a domain of green fluorescent protein (GFP). We measured the fluorescence intensity of the GFP to quantify the relative density of MUC1 on individual GPMVs. These measurements revealed a large variation in MUC1 density across GPMVs from a single preparation. Significantly, our measurements also unmasked a strong positive correlation between GPMV size and MUC1 density. Overall, these observations provide new insights into the interplay between the local membrane composition and the size of membrane blebs that form GPMVs. The understanding that GPMV size and MUC1 density are strongly correlated provided important guidance to the design of the second key part of our study, which aimed to quantify the influence of MUC1 density on membrane mechanical properties.
Specifically, in the second part of this paper, we study the influence of MUC1 on membrane spontaneous curvature of individual GPMVs within a population shed by cells. Previously reported methods for measuring the spontaneous curvatures of bilayer membranes include analyzing vesicle shapes using the theory of membrane curvature elasticity,21–23 and using optical tweezers to pull membrane tubes from giant unilamellar vesicles (GUVs).24–26 However, these methods are either semi-quantitative and/or too low in throughput to allow efficient characterization of heterogeneity within a population of GPMVs shed from cells. Here, we explore how the elasticity of synthetic water-based liquid crystals (LCs) can be used to strain individual GPMVs within a population. In particular, we show that GPMVs can be readily dispersed into and strained by aqueous LCs, a capability that arises from key characteristics of LC phases, namely the presence of liquid-like mobility and some degree of crystalline solid-like long-range order27 (the latter gives rise to elasticity that is used to strain GPMVs). We reveal that LCs enable characterization of the mechanical properties of single GPMVs in a high-throughput manner by simultaneously imaging ∼10–100 GPMVs in a single field of view. The study reported in this paper uses LCs prepared from aqueous solutions of disodium cromoglycate (DSCG) (Fig. 2(A)), a molecule that assembles into anisometric aggregates (Fig. 2(B)), forming mesophases depending on temperature and the concentration of DSCG molecules.28 In the nematic LC phase, the DSCG aggregates exhibit long-range orientational order (Fig. 2(C)). We reveal that, when GPMVs derived from highMUC1 expressing cells are dispersed into osmotically balanced nematic DSCG, the LC elastic stresses strain the GPMVs into spindle-like shapes. These shapes are consistent with the straining of fluid-like membranes of synthetic GUVs (Fig. 2(D) and (E)),29 and contrast to the folded shapes of solid-like membranes of human red blood cells strained in DSCG reported previously (Fig. 2(F) and (G)).30 We analyze the shape-responses of GPMVs to LC elastic forces within a thermodynamic framework that describes a competition between the LC elastic energy (ELC), an interfacial energy of the LC–GPMV interface (ES), and the membrane bending energy of the GPMV membranes (EB). Importantly, because our study involves single-vesicle-level characterization of both GPMV size and MUC1 density, our conclusions regarding the effects of MUC1 density on spontaneous curvatures of individual GPMVs are robust to the strong correlation observed between GPMV size and MUC1 density.
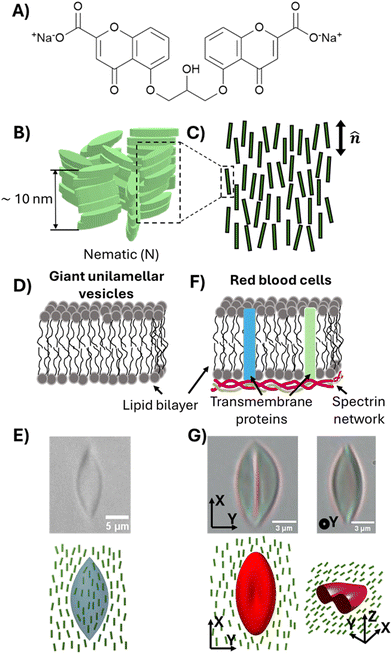 | ||
| Fig. 2 (A) The chemical structure of disodium cromoglycate (DSCG). (B) Schematic illustration of aggregates of DSCG molecules in an aqueous solution. (C) Illustration of orientational ordering of DSCG aggregates in a nematic phase. (D) Schematic illustration of the membranes of giant unilamellar vesicles consisting of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC). (E) Bright-field micrograph and schematic illustration of a DOPC GUV strained in 15 wt% DSCG solution (nematic).29 (F) Schematic illustration of the plasma membranes of red blood cells. (G) Bright-field micrographs and schematic illustration of an RBC strained in 17.3 wt% DSCG solution (nematic).30 | ||
The results presented in this paper highlight the fact that single-vesicle-level analysis of GPMVs is needed for reliable characterization of the mechanical properties of GPMVs. Specifically, we show that if the correlation between GPMV size and MUC1 density is not correctly incorporated into an analysis of the shape-response of GPMVs to LC elastic forces, erroneous conclusions regarding the influence of MUC1 on GPMV mechanical properties are reached. Our single-vesicle-level analysis, which accounts for this correlation, reveals the spontaneous curvature of GPMVs to be less than approximately 10 μm−1, which is 2 orders of magnitude smaller than previously predicted spontaneous curvatures of the corresponding parent cells (see discussion above).11 To provide additional support for our conclusions regarding the effects of MUC1 density on the spontaneous curvature of GPMVs, we report a second and independent set of experiments. In these experiments, we prepared two GPMV samples with identical size distributions and enzymatically removed MUC1 from GPMVs in one of the samples using the StcE mucinase, a procedure that allowed us to isolate the influence of MUC1 density on straining of GPMVs.
Overall, the results described in this study provide new and important insights into heterogeneity in membrane compositions, sizes, and mechanical properties of GPMVs derived from mammalian cells. In particular, our observations provide support for the hypothesis that the structure and composition of GPMVs differ from the plasma membranes of the cells from which the GPMVs are blebbed. More broadly, our observations emphasize the importance of characterizing GPMVs at the single-vesicle level and provide novel approaches for measuring the mechanical properties (i.e., spontaneous curvature) of soft biological assemblies at the single-assembly level in a high-throughput manner.
Materials
Disodium cromoglycate was purchased from VWR International. Distilled and deionized water (resistivity of more than 18.2 MΩ) (Milli-Q system, Millipore, Bedford, MA) was used to prepare aqueous solutions in all experiments described in this paper. Dulbecco's Modified Eagle's Medium (DMEM)/F12, donor horse serum, epidermal growth factor and penicillin/streptomycin were purchased from Thermo Fisher Scientific (Waltham, MA). Bovine pancreas insulin, hydrocortisone, cholera toxin, and N-ethyl maleimide were purchased from Sigma Aldrich (St. Louis, MO). Polyimide solutions were purchased from HD Microsystems (Parlin, NJ) and were used to prepare slides for optical cells by spin-coating them on glass slides as per the manufacturer's instructions.Methods
Cell lines and cell culture
MCF10A human breast epithelial cells were obtained from ATCC and were cultured in Dulbecco's modified Eagle's medium (DMEM)/F12 media supplemented with 5% horse serum, 20 ng mL−1 epidermal growth factor, 10 μg mL−1 insulin, 500 ng mL−1 hydrocortisone, 100 ng mL−1 cholera toxin, and 1× penicillin/streptomycin at 37 °C, 5% CO2. MCF10A cells were modified to exhibit titratable cell-surface expression of MUC1-green fluorescent protein (GFP) construct using tetracycline-inducible system and were clonally selected (1E7 clone) as reported previously.31,32 Moreover, the cytoplasmic signaling domains of the MUC1 were removed to minimize the biochemical activity of the mucins (MUC1-GFP-ΔCT). To induce expression of MUC1-GFP, 1E7 cells were seeded at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per cm2 in standard 25 cm2 polycarbonate culture flasks, and cultured for 48 hours at 37 °C, 5% CO2. The media was replaced with complete growth media supplemented with 1000 ng mL−1 of doxycycline and the cultures were returned to the incubator (37 °C, 5% CO2) for 24 hours to achieve the desired expression level.
000 cells per cm2 in standard 25 cm2 polycarbonate culture flasks, and cultured for 48 hours at 37 °C, 5% CO2. The media was replaced with complete growth media supplemented with 1000 ng mL−1 of doxycycline and the cultures were returned to the incubator (37 °C, 5% CO2) for 24 hours to achieve the desired expression level.
Formation of GPMVs
GPMVs were generated and isolated as described previously.13 Briefly, cultures were rinsed 2 times with GPMV buffer (10 mM HEPES, 150 mM NaCl, 2 mM CaCl2, pH 7.4) to remove residual culture media. The rinse was aspirated and replaced with 1 mL of fresh GPMV buffer supplemented with 2 mM N-ethyl maleimide (NEM), and cultures were incubated at 37 °C for 1 hour to induce blebbing. After incubation, the flask was gently shaken to release the GPMVs. GPMVs were collected from the culture flask by pipetting the buffer into a microcentrifuge tube. Detached cells and debris were separated from GPMVs by centrifugation at 100g for 5 minutes, after which the GPMV-containing supernatant was transferred to a clean microcentrifuge tube. GPMVs were stored at 4 °C and used within 24 hours to minimize the loss of lipid asymmetry.33Preparation of lyotropic chromonic liquid crystals
Lyotropic LC was prepared by mixing 17.3 wt% of disodium cromoglycate (DSCG) with 82.7 wt% of distilled and deionized water. The mixture was repeatedly vortexed (for at least 12 hours) and heated (up to 70 °C) until a homogenous solution was obtained. The pH of the solution was then adjusted to 7.4. DSCG solution prepared at 17.3 wt% concentration formed a nematic phase at room temperature (25 °C) and was in an osmotic balance with the interior of cells and GPMVs (∼280 mosm per kg).30Imaging of cells and GPMVs
Optical sample chambers were prepared by using two polyimide-coated glass cover slips which were rubbed in one direction with a nylon cloth and separated by double-sided tapes with thickness of 100 μm. The polyimide coating promoted planar anchoring of nematic DSCG with unidirectional alignment along the direction of rubbing. Cells or GPMVs (suspended in PBS and GPMV buffer, respectively) were added to 17.3 wt% DSCG solution (pre-warmed to 40 °C, isotropic phase) at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 volume ratio (cell/GPMV suspension: DSCG solution), such that the final concentration of DSCG in the mixture was 13.8 wt%. The dispersion was then cooled quickly into the nematic phase by plunging into ice to avoid the aggregation of GPMVs by the moving nematic–isotropic phase boundaries.34,35 The sample was then allowed to stand at room temperature (20 °C) for 20 minutes before being introduced into optical chambers in the nematic phase via capillarity. The optical chambers were sealed with vacuum grease to minimize the evaporation of water. Samples were imaged on an inverted epifluorescence microscope (IX81, Olympus Life Science) using a 60× water immersion objective. Polarized light microscopy was performed on an upright microscope (BX41, Olympus Life Science) using a 60× objective. The GPMVs reported in our observations had a uniform coverage of MUC1 across their membranes. However, we observed a small fraction of GPMVs (<5%) to have non-uniform coverage of MUC1 with MUC1-rich and MUC1-poor regions on their membranes (Fig. S1, ESI†). This fraction of GPMVs was excluded from our analysis.
4 volume ratio (cell/GPMV suspension: DSCG solution), such that the final concentration of DSCG in the mixture was 13.8 wt%. The dispersion was then cooled quickly into the nematic phase by plunging into ice to avoid the aggregation of GPMVs by the moving nematic–isotropic phase boundaries.34,35 The sample was then allowed to stand at room temperature (20 °C) for 20 minutes before being introduced into optical chambers in the nematic phase via capillarity. The optical chambers were sealed with vacuum grease to minimize the evaporation of water. Samples were imaged on an inverted epifluorescence microscope (IX81, Olympus Life Science) using a 60× water immersion objective. Polarized light microscopy was performed on an upright microscope (BX41, Olympus Life Science) using a 60× objective. The GPMVs reported in our observations had a uniform coverage of MUC1 across their membranes. However, we observed a small fraction of GPMVs (<5%) to have non-uniform coverage of MUC1 with MUC1-rich and MUC1-poor regions on their membranes (Fig. S1, ESI†). This fraction of GPMVs was excluded from our analysis.
Treatment with StcE mucinase
StcE mucinase was prepared as reported previously.31,36–38 Briefly, the cDNA for StcE-Δ35 was inserted into pET28b expression vector and synthesized by custom gene synthesis (Twist Bioscience, San Francisco, CA). The cDNA was then transfected into chemically competent NiCo21 (DE3) E. coli (NEB) cells. The cells were cultured in LB medium at 37 °C until reaching an optical density of 0.6–0.8 when measured at a wavelength of 600 nm. At this point, the enzymes were expressed by incubating with 0.5 mM isopropyl β-D-1-thiogalactopyranoside (IPTG) and grown overnight at 24 °C. Cells were then centrifuged at 3000g for 20 min and resuspended in cold (4 °C) lysis buffer (20 mM HEPES, 500 mM NaCl, and 10 mM imidazole, pH 7.5) containing complete protease inhibitor cocktail (Roche, Basel, Switzerland). The cells were lysed by sonication (Q125, Qsonica, Newtown, CT). By using immobilized metal affinity chromatography (IMAC) on a GE ÄKTA Avant fast protein liquid chromatography (FPLC) system, recombinant enzymes were purified from the cells. After applying the lysate to a HisTrap HP column (Cytiva, Marlborough, MA), 20 column volumes of wash buffer (20 mM HEPES, 500 mM NaCl, and 20 mM imidazole, pH 7.5) were used in the wash stage. A linear gradient of 20 to 250 mM imidazole in buffer (20 mM HEPES and 500 mM NaCl, pH 7.5) was used for elution. Target protein-containing eluted fractions were gathered and subjected to additional refinement using a HiPrep 26/60 Sephacryl S-200 HR (Cytiva, Marlborough, MA) column that had been equilibrated with a storage buffer (20 mM HEPES and 150 mM NaCl, pH 7.5). Amicon Ultra 30 kDa MWCO filters (Millipore Sigma, Bedford, MA) were used to concentrate the final protein. GPMVs were prepared from cells as described above in GPMV buffer. GPMVs were then incubated with 100 nM of StcE in GPMV buffer at 37 °C for 1 hour. The cleavage of MUC1 was confirmed by comparing the GFP fluorescence intensity of StcE-treated GPMVs with GPMVs without the StcE treatment, using BD Accuri C6 Plus flow cytometer (BD Biosciences, Franklin Lakes, NJ).Calculation of spontaneous curvature
We analyzed the strained shapes assumed by GPMVs in LCs within the framework of a theoretical model that yields the membrane spontaneous curvature. The model includes an account of the size-dependent scaling of the relative importance of the LC elastic energy (ELC), an interfacial depletion energy (ES) and membrane bending energy (EB). As reported previously, the LC elastic energy can be expressed as,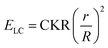 | (1) |
| ES = τSA | (2) |
 | (3) |
 | (4) |
We evaluated the bending energy of the GPMV membranes by using the Helfrich free energy40 shown below.
 | (5) |
The Helfrich free energy can be evaluated for a spheroid shape as,
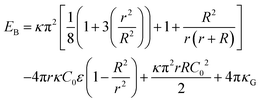 | (6) |
Statistical analysis
GPMV aspect ratios, GFP fluorescence intensities per area, and spontaneous curvatures were quantified by analysis of 86 individual GPMVs for the data shown in Fig. 3 and 4. GFP fluorescence intensities reported in Fig. 5(B) were obtained by performing flow cytometry on more than 34000 1E7 GPMVs and more than 46000 1E7 GPMVs + StcE. Data in Fig. 5(C)–(E) were obtained by analysis of more than 600 individual GPMVs (each for 1E7 GPMVs, and 1E7 GPMVs + StcE) from 3 independent experiments. Two-sample t-tests were performed to assess the statistical significance of data reported in Fig. 4 and 5 using OriginPro 2024 (OriginLab). For Fig. 5(D) and (E), center lines of boxes show the medians of the data; bottom and top of the boxes indicate the 25th and 75th percentile of the data, respectively; bottom and top whiskers indicate the 5th and 95th percentile of the data, respectively.Results
As detailed in Methods, we performed experiments using a mammary epithelial cell line, MCF10A, that is genetically modified to express the glycoprotein, MUC1, on the cell surface in an inducible manner (referred to as the ‘1E7’ cell line, see Methods). We quantified the relative levels of MUC1 density by measuring the fluorescence intensity of the green fluorescent protein (GFP) domain that was inserted between the O-glycan-rich tandem repeats and the membrane-proximal domains of MUC1, as described previously.31In our initial studies, we explored if LC elastic stresses were sufficiently large to strain 1E7 epithelial cells. When dispersed in the osmotically-balanced chromonic LC phase prepared from DSCG (13.8 wt%), we found that the 1E7 cells were not measurably strained (see below for a discussion regarding osmotic equilibrium between the LC and cells). This result is consistent with either the influence of various intracellular structures (i.e., cytoskeleton, nucleus, and other organelles) on the shape-responses of cells to mechanical stresses,42 and/or the size-dependent scaling of interfacial (ES) and LC elastic energies (ELC) reported previously.29 The latter predicts that large objects such as 1E7 cells (characteristic size of 15–20 μm) will be weakly strained by LC elasticity (Fig. S2, ESI†). To take advantage of the size-dependent straining of soft inclusions by LCs, and to probe the influence of MUC1 on membrane mechanical properties in absence of effects from the cellular cytoskeleton, we studied the straining of giant plasma membrane vesicles (GPMVs) derived from the 1E7 cells. Overall, the approach described below based on GMPVs has the advantage that it decouples changes in membrane mechanical properties from other variables that influence the shape responses of cells to stimuli.43,44
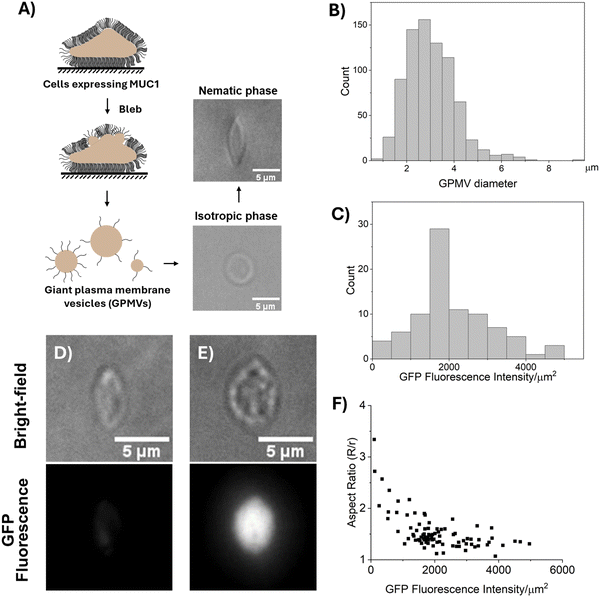
We prepared GPMVs by N-ethyl maleimide (NEM) treatment of 1E7 cells (Fig. 3(A)).13 A recent study has shown that GPMVs prepared by NEM treatment retain the lipid asymmetry of the cell plasma membrane.45 The GPMVs were measured to have average and maximum diameters of 3.03 μm and 10 μm, respectively (Fig. 3(B)). Below, we first describe our observations of the shapes of GPMVs when dispersed into isotropic and nematic phases of DSCG.
I. Shape response of GPMVs to LCs
As shown in Fig. 3(A), we dispersed GPMVs into 13.8 wt% DSCG solution (pre-warmed to 40 °C, isotropic phase; see Methods) that was previously shown to possess a physiological osmotic pressure (∼280 mosm per kg). This solution was prepared by adding 1 part of GPMV dispersion (in GPMV buffer) to 4 parts of 17.3 wt% DSCG solution, resulting in a final DSCG concentration of 13.8 wt% and ensuring an osmotic equilibrium across the GPMV membrane.30 Within the isotropic phase, the GPMVs were observed to be spherical with no visible protrusions (Fig. 3(A)), an observation that contrasts to the tubular morphology of the plasma membranes of their parent cells. This observation hints at potential differences between the membranes of GPMVs and those of their parent cells (we describe these differences in more detail in the Discussion section). Next, we rapidly cooled the dispersion to 20 °C (nematic phase) by plunging it into ice. The rapid thermal quench was used to avoid the aggregation of GPMVs caused by slow-moving nematic–isotropic phase boundaries.34,35,46 After 20 minutes of equilibration at room temperature (20 °C), we observed the GPMVs to be measurably strained in the nematic phase of the DSCG solution (Fig. 3(A)). The strained GPMVs adopted spindle-like shapes and generated an LC director profile that was consistent with a weak tangential anchoring of DSCG on GPMV membranes (Fig. S3, ESI†). The spindle-like shapes of the GPMVs in LCs are similar to the shapes of fluid membranes of synthetic 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) GUVs but contrast to the folded morphologies of solid-like membranes of RBCs strained in nematic DSCG (Fig. 2(E) and (G)).29,30 This observation suggests that MUC1 decorated membranes of GPMVs behave as fluid membranes in nematic DSCG.Next, we sought to understand if the extent to which the LC-induced strain of GPMVs varied with the density of MUC1. By measuring the fluorescence intensity of GFP, we quantified the density ofMUC1 on GPMVs to vary by more than a factor of 40 across a population of GPMVs prepared from a single batch of 1E7 cells (Fig. 3(C)). Several possible explanations likely underlie this observation. For example, it is possible that the cell plasma membrane is not uniformly decorated by MUC1, hence, GPMVs blebbed from different parts of the cell membrane may acquire different levels of MUC1. Another possibility is that the GPMVs that bleb early have high MUC1 on their surfaces, thus depleting the concentration of MUC1 in the cell membrane. This, in turn, causes late blebs to contain low levels of MUC1. In a broader context, our observation that the level of incorporation of MUC1 into GPMVs is highly heterogeneous motivated our single-vesicle-level analysis described below for characterizing the mechanical properties of GPMV membranes. Moreover, it emphasizes the need to account for vesicle-to-vesicle variation in membrane composition when using GPMVs as models to study membrane properties.
As shown in Fig. 3(D)–(F), we observed that the aspect ratios of GPMVs decreased as the GFP fluorescence intensity per area increased. In particular, we observed that an increase in the GFP fluorescence intensity per area from ∼100 a.u. μm−2 to ∼5000 a.u. μm−2 coincided with a decrease in GPMV aspect ratio from ∼3 to ∼1. This observation hints that the presence of MUC1 on the membranes of GPMVs changes membrane mechanical properties, making the membranes more rigid with increasing MUC1 density.
However, as discussed above, we have also reported previously that synthetic GUVs are strained in nematic DSCG in a size-dependent manner that is described by29
 | (7) |
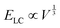 ; and (2) the interfacial energy arising from the depletion of DSCG aggregates near the GUV membrane (ES ∼ 10−17–10−15 J) that increases with the GUV size as,
; and (2) the interfacial energy arising from the depletion of DSCG aggregates near the GUV membrane (ES ∼ 10−17–10−15 J) that increases with the GUV size as,  . Consistent with depletion of DSCG from near the GUV membrane, we have previously reported observations of association of pairs of GUVs with flat facets between them in DSCG (i.e., association via a depletion interaction).29 Here we note that the influence of the membrane bending energy on GUV shape in the DSCG is negligible, as is evident from the rate of change of the membrane bending energy (EB ∼ 10−20–10−19 J) with respect to the GUV aspect ratio, namely
. Consistent with depletion of DSCG from near the GUV membrane, we have previously reported observations of association of pairs of GUVs with flat facets between them in DSCG (i.e., association via a depletion interaction).29 Here we note that the influence of the membrane bending energy on GUV shape in the DSCG is negligible, as is evident from the rate of change of the membrane bending energy (EB ∼ 10−20–10−19 J) with respect to the GUV aspect ratio, namely  . This term is negligible in magnitude when compared to
. This term is negligible in magnitude when compared to  and
and  (for a GUV with R/r = 1.3 and a constant volume of 500 μm3) (see Section 4 of the ESI† for further details). Moreover, this conclusion holds for R/r ranging from 1.05 to 4 and V ranging from 5 μm3 to 5000 μm3, indicating that the spindle-like shapes assumed by the GUVs in the LC are not influenced by EB. Below we investigate how both the size of GPMVs and their MUC1 densities influence the shape-response of the GPMVs (as shown in Fig. 3(F)) to the elastic environment provided by nematic DSCG, including whether or not EB plays a significant role in the GPMV shape-response.
(for a GUV with R/r = 1.3 and a constant volume of 500 μm3) (see Section 4 of the ESI† for further details). Moreover, this conclusion holds for R/r ranging from 1.05 to 4 and V ranging from 5 μm3 to 5000 μm3, indicating that the spindle-like shapes assumed by the GUVs in the LC are not influenced by EB. Below we investigate how both the size of GPMVs and their MUC1 densities influence the shape-response of the GPMVs (as shown in Fig. 3(F)) to the elastic environment provided by nematic DSCG, including whether or not EB plays a significant role in the GPMV shape-response.
II. Correlation between MUC1 density and GPMV sizes, and influence on GPMV strain in LCs
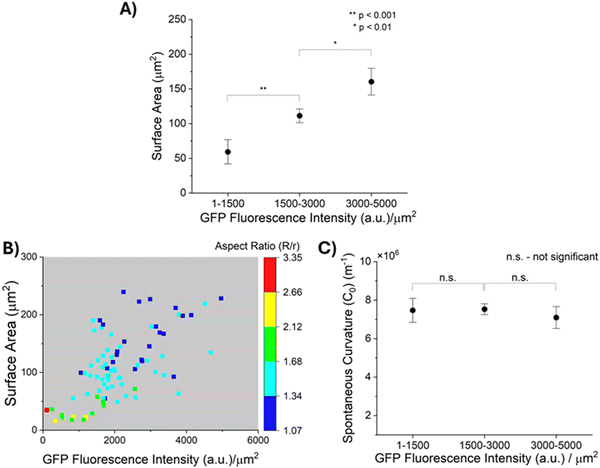
As described above, prior reports suggest that entropic forces exerted by MUC1 favor the bending of cell plasma membranes into curvatures that depend on the density of MUC1.11 This led us to speculate that the density of MUC1 and the size of plasma membrane blebs that form GPMVs may not be independent. Because GPMVs generated from 1E7 cells by chemically-induced vesiculation are heterogeneous in both size and density of MUC1 on their membranes (Fig. 3(B) and (C)), we explored whether or not the two properties of GPMVs were correlated within a population of GPMVs. As shown in Fig. 4(A), we observed that the surface areas of GPMVs are strongly correlated with the density of MUC1 on them. Specifically, we observed that small GPMVs tend to have low GFP fluorescence intensities per μm2 whereas large GPMVs have high GFP fluorescence intensities per μm2 (see Fig. S4, ESI† for further details on quantification of fluorescence intensity). This observation suggests that MUC1 density influences the size of GPMVs blebbed from the 1E7 cells. Theories and simulations of membranes decorated with polymer brushes have reported that an increase in polymer density leads to an increase in spontaneous curvature of the membranes (hence, a decrease in their radius of curvature).11,47 Interestingly, however, the correlation evident in our experiments (Fig. 4(A)) is the opposite of this prediction.Additionally, as reported in the color-map in Fig. 4(B), after transfer of the GPMVs to nematic DSCG, we observed that the extent of straining of GPMVs not only decreases with increase in MUC1 density but also with an increase in the GPMV size. For example, for GPMVs with surface areas ranging from 25 μm2 to 75 μm2, we measured aspect ratios to decrease from 3.34 to 1.34 with increase in the GFP fluorescence intensity per area on their membrane. In addition, however, for GPMVs with GFP fluorescence intensities per area of 1000–2000 a.u. μm−2, we observed that their aspect ratios decrease from 1.79 to 1.18 with increase in surface area. Although the factors that cause MUC1 density to be correlated with GPMV size are not yet fully understood, the data shown in Fig. 4(A) and (B) clearly demonstrate that an interpretation of the shape-response of the GPMVs to the LC elasticity requires that the correlation between GPMV size and MUC1 density be integrated into the analysis (this point is discussed further below).
III. Decoupling the influence of GPMV size and MUC1 density on GPMV shape-response to LC elastic stresses
Next, we describe our analysis of the shapes of individual GPMVs in LCs using the model described in Methods (eqn (1)–(6)). Specifically, our analysis allows us to decouple the influence of GPMV size and MUC1 density on LC-induced straining of GPMVs, thus providing an accurate determination of membrane mechanical properties (i.e., spontaneous curvature) based on the LC-induced GPMV shape-response. In this formulation, the values of bending modulus (κ) and spontaneous curvature (C0) determines the magnitude of the membrane bending energy (EB) relative to the LC elastic energy (ELC) and the interfacial energy (ES). Past studies have reported that brushes of polyethylene glycol (PEG) anchored on phospholipid membranes can generate bending moduli of up to 2 × 10−19 J.48,49 Moreover, Dimova and co-workers have reported the bending modulus of GPMVs to be less than 2 × 10−19 J.16 We found that a membrane bending modulus of this magnitude generates a GPMV bending energy that is negligible compared to LC elasticity and thus does not influence the straining of GPMVs in LC (Fig. S5, ESI†). Guided by this observation, in the analysis below, we set the bending modulus (κ) of GPMV membranes to be constant and equal to 10−19 J. We measured the lengths of the semi-major axes (R) and semi-minor axes (r) of individual strained GPMVs from their bright-field micrographs and calculated their surface area and volume using eqn (3) and (4), respectively. We then minimized the total energy (E) to calculate the spontaneous curvature of individual GPMVs observed in our experiments. By using the data shown in Fig. 4(B), in which there is a 40× change in MUC1 density, we found that the spontaneous curvatures of the GPMVs ranged from 4 μm−1 to 10.7 μm−1 (Fig. S6, ESI†). To determine if the magnitude of the spontaneous curvature was dependent on MUC1 density, we binned the spontaneous curvature values into three GPMV populations based on the magnitude of the GFP fluorescence intensity per area measured for each GPMV, as shown in Fig. 4(C). Inspection of Fig. 4(C) reveals that we observed no significant change in the spontaneous curvatures of GPMVs as the GFP fluorescence intensity per area changed by more than an order of magnitude (104 a.u. μm−2 to 4964 a.u. μm−2). This observation reveals that the apparent variation in GPMV aspect ratio with MUC1 density evident in Fig. 3(F) is a consequence of the strong correlation between MUC1 density and GPMV size (and the influence of GPMV size on its aspect ratio, described by eqn (7)). This result also emphasizes the importance of using single-vesicle measurements in heterogeneous GPMV systems, to enable a correct accounting for correlations between properties of GPMVs within a population.IV. Independent validation of the influence of MUC1 on spontaneous curvature of GPMV membranes by using StcE mucinase
To validate our conclusion (see above) that the variation in MUC1 density does not measurably influence GPMV strain in LCs, we designed a second experiment that aimed to minimize the influence of GPMV size (as reported above) on conclusions related to the influence of MUC1 density on GPMV strain. To this end, we split samples of GPMVs derived from 1E7 cells into two aliquots and treated one half of the GPMV preparation with a mucin-selective protease StcE (secreted protease of C1 esterase inhibitor).37 The other aliquot was used as a control. Accordingly, the two aliquots contained GPMVs with the same distribution of sizes. Treatment of the preparation with the StcE mucinase cleaved mucin and GFP domains from the membranes of the GPMVs (Fig. 5(A)) but not MUC1 anchor proteins.37 Notably, the results reported in ref. 11 suggest that the entropic forces generated by the MUC1 chains (and not the MUC1 anchors) are likely the major factor contributing to the spontaneous curvature of cell plasma membranes.Because treatment by StcE mucinase leads to the removal of the GFP domain, quantification of removal of MUC1 from GPMVs was performed by measurements of GFP fluorescence intensity. By measuring the GFP fluorescence intensity of both 1E7 GPMVs and 1E7 GPMVs + StcE via flow cytometry, we determined that the mean GFP fluorescence intensity decreased by more than an order of magnitude after treatment with StcE mucinase (Fig. 5(B)). This result is consistent with the removal of more than 90% of MUC1 from GPMV membranes. Moreover, brightfield microscopy revealed that GPMVs from both populations have a similar size distribution as shown in Fig. 5(C).
Next we strained both the StcE-treated GPMVs and untreated GPMVs in 13.8 wt% DSCG solution (as described above) and observed that both populations of GPMVs were strained to similar extents, although a very small statistically significant difference was measured between the two sample types: R/r = 1.62 ± 0.01 for 1E7 GPMVs and R/r = 1.58 ± 0.01 for 1E7 GPMVs + StcE (mean ± standard error) (p < 0.01, two sample t-test) (Fig. 5(D)). This result supports our conclusion that the density of MUC1 does not have a substantial influence on the shapes of GPMVs that are strained in 13.8 wt% DSCG solution. Finally, we calculated the spontaneous curvatures of GPMVs from the measured GPMV strain values (as described above) and noted a small but statistically significant increase in the spontaneous curvature of the GPMVs caused by treatment with StcE mucinase (1E7 GPMVs: C0 = 6.02 ± 0.08 μm−1; 1E7 GPMVs + StcE: C0 = 10.4 ± 0.24 μm−1; p < 0.0001, two sample t-test) (Fig. 5(E)). We noted that the change in spontaneous curvature caused by StcE treatment was similar to the low level of variation in spontaneous curvature associated with the 40× change in MUC1 density found within the population of GPMVs (Fig. 4(C) and associated text).
Discussion
The observations reported above lead us to conclude that the shapes of GPMVs in LCs are not measurably influenced by the MUC1 densities present on the GPMVs in our experiments. While prior studies have reported that MUC1 expression levels influence cellular shapes in a manner consistent with an effect of MUC1 on membrane spontaneous curvature, it is possible that MUC1 densities on cells are higher than those on GPMVs derived from the cells. As reported previously, cells expressing high levels of MUC1 are observed to form tubular and bleb-like projections on their plasma membranes.11 In contrast to cells, as shown in Fig. 3(A) and Fig. S7 (ESI†), we observed that the GPMVs derived from high MUC1 expressing cells are spherical in shape with no visible membrane projections. The blebbing of GPMVs likely occurs by a weakening of the binding between the cytoskeleton and plasma membrane, followed by expansion of the bleb-forming plasma membrane by intracellular pressure.14,50–52 A recent study has reported that MUC1 accumulates at regions of membranes with negative curvatures (protrusions) and avoids regions of positive curvatures (invaginations).53 It is possible that MUC1 preferentially partitions away from regions of the cell plasma membranes that form blebs. This hypothesis is consistent with recent studies that have reported that large glycocalyx constituents do not partition into apoptotic blebs as the blebs peel away from the cell cytoskeleton.54,55Previously, we have reported that DOPC GUVs strained to R/r > 1.54 in DSCG undergo a change in their surface area to volume ratio (via an efflux of internal volume through transient pores formed in their membranes upon straining), allowing them to adopt the highly strained shapes.29,35 Guided by this prior conclusion, we next analyzed if the straining of GPMVs in LCs may also involve an efflux of internal volume and increase in surface area-to-volume ratio (an efflux of internal volume, if it were to occur, would lead to an incorrect prediction of spontaneous curvature by our model). To address this possibility, we re-analyzed the experimental data shown in Fig. 5 by excluding GPMVs with R/r > 1.54. For this sub-population of GPMVs, we found the influence of MUC1 on spontaneous curvature to remain small (1E7 GPMVs: C0 = 7.02 ± 0.09 μm−1; 1E7 GPMVs + StcE: C0 = 10.48 ± 0.35 μm−1, p < 0.0001) (Fig. S8, ESI†). This leads us to conclude that any efflux of internal volume, if it does occur for the most highly strained GPMVs, does not impact our conclusions regarding the effects of MUC1 on mechanical properties of GPMVs.
To provide insight into the absence of a substantial influence of MUC1 density on the shapes of the GPMVs in LCs, we used the thermodynamic model described by eqn (1)–(6) to predict the range of spontaneous curvature values that change the aspect ratios of GPMVs in 13.8 wt% nematic DSCG. As shown in Fig. 5(F), we calculate that GPMV shapes in LC (i.e., the GPMV aspect ratios) are influenced by a relatively narrow range of spontaneous curvature values (2–10 μm−1). For spontaneous curvatures below 2 μm−1, the membrane bending energy (EB) is negligible compared to LC elastic energy (ELC) and the shapes of the strained GPMVs are determined by a balance between LC elasticity (ELC) and interfacial energy (ES). On the other hand, for spontaneous curvatures above 10 μm−1, ELC and ES are negligible compared to EB, and GPMVs are not strained by the LC (aspect ratio = 1). This analysis, when combined with our observation that GPMVs are strained to aspect ratios greater than 1, leads us to conclude that the spontaneous curvatures of the membranes of the GPMVs are less than 10 μm−1 (Fig. 5(F)). Although this value is within the range of spontaneous curvatures predicted previously from the study of cells,11 it is 2 orders of magnitude smaller than that predicted for the membranes of the corresponding parent cells of GPMVs used in this study (i.e., expressing high levels of MUC1 density, 103–104 mucins per μm2) (Fig. 1(B)).
The magnitudes of spontaneous curvature values that can be measured by the approach described in this paper are in the range reported previously for phospholipid membranes with asymmetric distributions of gangliosides,24,56 polymers,22 and ions,25,26,57 suggesting that the methodology reported in this paper has broad potential applicability. In addition, the range of spontaneous curvature values that influence GPMV aspect ratios can, in principle, be tuned further by changing the elastic constants of the LC (Fig. 5(F), where K is the average LC elastic constant) via either changing the concentration of DSCG or the temperature. For example, a change in DSCG concentration from 18 wt% to 12.5 wt% can lead to a decrease in the average LC elastic constant by approximately a factor of 5.39 Although changing the LC elastic constants can enable probing of a wider range of changes in membrane mechanical properties (Fig. 5(F)), changes in DSCG concentration are accompanied by changes in osmotic pressure which will potentially lead to shrinking or swelling of GPMVs (i.e., changes in their surface area-to-volume ratio). Hence, similar to the experimental design used in this study, future designs of experiments that vary the DSCG concentration will also need to consider the complex interdependence of LC elasticity, osmotic pressure and temperature on the GPMV strain-response.
Finally, we note that the analysis of GPMV shapes reported in this paper assumes that the MUC1 density does not change the interfacial depletion energy (τ) between the GPMV membrane and the LC phase formed from DSCG. This assumption is consistent with our observation that the treatment of 1E7 GPMVs with the StcE mucinase causes little change in the straining of GPMVs in LCs (Fig. 5(D)) and does not lead to a measurable change in the ordering of LC around GPMVs (Fig. S3, ESI†). Because we observe that GPMVs are strained to R/r > 1, and because out model predicts that GPMVs will not be strained (R/r = 1) if they possess spontaneous curvatures greater than ∼ 10 μm−1 (EB ≫ ELC ∼ ES), we conclude that, regardless of the value of τ assumed, our model predicts that the spontaneous curvatures of the GPMVs used in our experiments are less than 10 μm−1. We also consider it possible that unfavorable interactions between MUC1 and DSCG might cause a reduction in the radius of gyration of MUC1 and collapse of the polypeptide chains (relative to that in a “good” solvent).58,59 A previous study (using Monte Carlo simulations) has reported the spontaneous curvature of membranes with grafted polymers to decrease with the solvent quality, and that “poor” solvents can even reverse the direction of curvature of the membrane such that the membrane bends towards the polymer chains.60 Because we do not observe GPMVs with membranes bent towards the external leaf containing MUC1, and because treatment of 1E7 GPMVs with the StcE mucinase causes little change in the straining of GPMVs in LCs, it is unlikely that the quality of the aqueous DSCG solution as a solvent for MUC1 influences the values of spontaneous curvature of GPMVs reported in our study.
Conclusions
In conclusion, this study reveals that the sizes and MUC1 density of GPMVs are strongly correlated, and explores the spontaneous curvature of GPMVs that differ in both size and MUC1 density by analyzing the shape-response of single GPMVs to the mechanical environment created by LCs. Specifically, our quantitation of the relative density of MUC1 on GPMVs, achieved by measuring the fluorescence intensity of a GFP domain inserted in the MUC1, reveals a 40× vesicle-to-vesicle variation in the MUC1 density within a single population of GPMVs. This finding is consistent with past reports of large vesicle-to-vesicle variations in phase transition temperatures of GPMV membranes, indicative of compositional differences between vesicles.15,61 Moreover, this finding emphasizes the importance of characterizing GPMVs at the single-vesicle level in order to reach reliable conclusions regarding the effects of MUC1 on membrane mechanical properties, as reported in this paper.Our single-vesicle-level characterization of GPMVs enabled us to identify a statistically significant correlation between the MUC1 densities and sizes of GPMVs, with larger GPMVs displaying higher density of MUC1. This observation suggests that MUC1 may play a role in controlling the size of cell-membrane blebs that form GPMVs, and potentially other plasma membrane blebs such as those that form microvesicles (MVs). While previous reports suggest that overexpression of MUC1 leads to an increase in MV production,11 our observations hint at novel pathways by which expression of MUC1 may control the size of vesicular blebs from the plasma membrane, thereby potentially influencing intercellular communication. In particular, the positive correlation observed between MUC1 density and GPMV size is the inverse of the correlation predicted if MUC1 was to exercise influence over GPMV size via previously proposed effects of spontaneous curvature. It is possible that the correlation between MUC1 density and GPMV size results from the influence of MUC1 on membrane rigidity via promotion of cholesterol and fatty acid metabolism62,63 and/or enrichment of MUC1 in membrane microdomains.64,65
We also report that GPMVs obtained from cells overexpressing MUC1 are strained by LC elastic forces into spindle-like shapes, consistent with a fluid-like behavior of GPMV membranes in LCs. This observation underlies our analysis that decouples the effects of GPMV size and MUC1 density on the straining of individual GPMVs in LCs. By quantifying GPMV size, relative MUC1 density and GPMV strain in LC at the single-GPMV level, our analysis reveals that the 40× change in the density of MUC1 has no significant influence on the spontaneous curvature of GPMVs. Further validation of this conclusion was obtained by performing independent experiments, in which we enzymatically removed MUC1 from GPMVs using the StcE mucinase (based on analysis of more than 600 data points each for 1E7 GPMVs, and 1E7 GPMVs + StcE). This result provides support for the hypothesis that, for the range of MUC1 densities on GPMVs used in our experiments, the influence of MUC1 on the membrane bending energy is negligible in comparison to the LC elastic energy. Moreover, our analysis of the shape responses of GPMVs derived from high MUC1 expressing cells to LC elasticity reveals that the spontaneous curvature of GPMVs is less than ∼10 μm−1, which is 2 orders of magnitude smaller than that previously predicted on their parent cell membranes.11 These observations provide support for the proposal that the density of MUC1 on GPMVs is less than that on their parent cell plasma membranes.
Overall, the results reported in this paper highlight the compositional heterogeneity of GPMVs and the influence of membrane composition on the blebbing process that leads to GPMVs. This coupling is reflected in a strong correlation between MUC1 density and GPMV size in our experiments. In addition, because we measured the spontaneous curvature of the GPMVs to be at the low end of the range inferred previously from studies of cells,11 our results hint at differences between plasma membranes of GPMVs and their parent cells, such as differences in their compositions as well as other membrane properties (e.g., membrane tension). More broadly, we envision that the experimental advances described in this study can be utilized for studying plasma membrane biophysics in other biological systems. For example, the methodology may be useful for studying the mechanisms of curvature sensing proteins in plasma membranes of cells.53,66
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the National Science Foundation (CBET-2245376 and DMR-2003807) (N. L. A.) and National Institutes of Health (NCI CA276398 and NIGMS GM138692) (M. J. P.).References
- L. Mockl, Front. Cell Dev. Biol., 2020, 8, 253 CrossRef PubMed.
- P. K. Singh and M. A. Hollingsworth, Trends Cell Biol., 2006, 16, 467–476 CrossRef CAS.
- M. S. Patankar, J. A. Gubbels, M. Felder and J. P. Connor, Front. Biosci., 2012, 4, 631–650 CrossRef.
- A. Peixoto, M. Relvas-Santos, R. Azevedo, L. L. Santos and J. A. Ferreira, Front. Oncol., 2019, 9, 380 CrossRef.
- C. R. Shurer, M. J. Colville, V. K. Gupta, S. E. Head, F. Kai, J. N. Lakins and M. J. Paszek, ACS Biomater. Sci. Eng., 2018, 4, 388–399 CrossRef CAS PubMed.
- J. Wesseling, S. W. van der Valk, H. L. Vos, A. Sonnenberg and J. Hilkens, J. Cell Biol., 1995, 129, 255–265 CrossRef CAS.
- M. A. Hollingsworth and B. J. Swanson, Nat. Rev. Cancer, 2004, 4, 45–60 CrossRef CAS PubMed.
- D. H. Wi, J. H. Cha and Y. S. Jung, BMB Rep., 2021, 54, 344–355 CrossRef CAS PubMed.
- A. Buffone and V. M. Weaver, J. Cell Biol., 2020, 219, e201910070 CrossRef PubMed.
- J. Chin-Hun Kuo, J. G. Gandhi, R. N. Zia and M. J. Paszek, Nat. Phys., 2018, 14, 658–669 Search PubMed.
- C. R. Shurer, J. C. Kuo, L. M. Roberts, J. G. Gandhi, M. J. Colville, T. A. Enoki, H. Pan, J. Su, J. M. Noble, M. J. Hollander, J. P. O’Donnell, R. Yin, K. Pedram, L. Mockl, L. F. Kourkoutis, W. E. Moerner, C. R. Bertozzi, G. W. Feigenson, H. L. Reesink and M. J. Paszek, Cell, 2019, 177, 1757–1770 CrossRef CAS PubMed.
- L. Blanchoin, R. Boujemaa-Paterski, C. Sykes and J. Plastino, Physiol. Rev., 2014, 94, 235–263 CrossRef CAS PubMed.
- E. Sezgin, H. J. Kaiser, T. Baumgart, P. Schwille, K. Simons and I. Levental, Nat. Protoc., 2012, 7, 1042–1051 CrossRef CAS.
- Y. Li, S. Y. Liu, W. Y. Xu, K. M. Wang, F. J. He and J. B. Liu, Sens. Diagn., 2023, 2, 806–814 RSC.
- T. Baumgart, A. T. Hammond, P. Sengupta, S. T. Hess, D. A. Holowka, B. A. Baird and W. W. Webb, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3165–3170 CrossRef CAS.
- J. Steinkuhler, E. Sezgin, I. Urbancic, C. Eggeling and R. Dimova, Commun. Biol., 2019, 2, 337 CrossRef.
- K. R. Levental and I. Levental, Methods Mol. Biol., 2015, 1232, 65–77 CrossRef CAS PubMed.
- T. Einfalt, M. Garni, D. Witzigmann, S. Sieber, N. Baltisberger, J. Huwyler, W. Meier and C. G. Palivan, Adv. Sci., 2020, 7, 1901923 CrossRef CAS.
- C. Luo, X. X. Hu, R. Z. Peng, H. D. Huang, Q. L. Liu and W. H. Tan, ACS Appl. Mater. Interfaces, 2019, 11, 43811–43819 CrossRef CAS.
- B. Bauer, M. Davidson and O. Orwar, Angew. Chem., Int. Ed., 2009, 48, 1656–1659 CrossRef CAS PubMed.
- W. Harbich, H. J. Deuling and W. Helfrich, J. Phys., 1977, 38, 727–729 CrossRef CAS.
- Y. G. Liu, J. Agudo-Canalejo, A. Grafmüller, R. Dimova and R. Lipowsky, ACS Nano, 2016, 10, 463–474 CrossRef CAS.
- H. G. Döbereiner, O. Selchow and R. Lipowsky, Eur. Biophys. J. Biophys., 1999, 28, 174–178 CrossRef.
- R. Dasgupta, M. S. Miettinen, N. Fricke, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5756–5761 CrossRef CAS.
- M. Karimi, J. Steinkuhler, D. Roy, R. Dasgupta, R. Lipowsky and R. Dimova, Nano Lett., 2018, 18, 7816–7821 CrossRef CAS PubMed.
- M. Simunovic, K. Y. C. Lee and P. Bassereau, Soft Matter, 2015, 11, 5030–5036 RSC.
- P. J. Collings and J. W. G. Goodby, Introduction to liquid crystals: chemistry and physics, 2nd edn, 2019 Search PubMed.
- J. Lydon, J. Mater. Chem., 2010, 20, 10071–10099 RSC.
- P. C. Mushenheim, J. S. Pendery, D. B. Weibel, S. E. Spagnolie and N. L. Abbott, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5564–5569 CrossRef CAS.
- K. Nayani, A. A. Evans, S. E. Spagnolie and N. L. Abbott, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 26083–26090 CrossRef CAS PubMed.
- S. Park, M. J. Colville, J. H. Paek, C. R. Shurer, A. Singh, E. J. Secor, C. J. Sailer, L. T. Huang, J. C. H. Kuo, M. C. Goudge, J. Su, M. Kim, M. P. DeLisa, S. Neelamegham, J. Lammerding, W. R. Zipfel, C. Fischbach, H. L. Reesink and M. J. Paszek, Nat. Mater., 2024, 23, 429–438 CrossRef CAS PubMed.
- M. J. Paszek, C. C. DuFort, M. G. Rubashkin, M. W. Davidson, K. S. Thorn, J. T. Liphardt and V. M. Weaver, Nat. Methods, 2012, 9, 825–827 CrossRef CAS.
- D. Marquardt, F. A. Heberle, T. Miti, B. Eicher, E. London, J. Katsaras and G. Pabst, Langmuir, 2017, 33, 3731–3741 CrossRef CAS PubMed.
- N. Zimmermann, G. Jünnemann-Held, P. J. Collings and H. S. Kitzerow, Soft Matter, 2015, 11, 1547–1553 RSC.
- P. Jani, K. Nayani and N. L. Abbott, Soft Matter, 2021, 17, 9078–9086 RSC.
- S. Park, S. Choi, A. A. Shimpi, L. A. Estroff, C. Fischbach and M. J. Paszek, Adv. Mater., 2024, 36(43), 2311505 CrossRef CAS.
- S. A. Malaker, K. Pedram, M. J. Ferracane, B. A. Bensing, V. Krishnan, C. Pett, J. Yu, E. C. Woods, J. R. Kramer, U. Westerlind, O. Dorigo and C. R. Bertozzi, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 7278–7287 CrossRef CAS PubMed.
- A. C. Yu, L. J. Worrall and N. C. Strynadka, Structure, 2012, 20, 707–717 CrossRef CAS PubMed.
- S. Zhou, K. Neupane, Y. A. Nastishin, A. R. Baldwin, S. V. Shiyanovskii, O. D. Lavrentovich and S. Sprunt, Soft Matter, 2014, 10, 6571–6581 RSC.
- W. Helfrich, Z. Naturforsch. C, 1973, 28, 693–703 CrossRef CAS.
- E. T. Whittaker and G. N. Watson, A Course in Modern Analysis, Cambridge University Press, Cambridge, England, 4th edn, 1996 Search PubMed.
- D. A. Fletcher and R. D. Mullins, Nature, 2010, 463, 485–492 CrossRef CAS PubMed.
- E. Sezgin, Biochim. Biophys. Acta, Biomembr., 2022, 1864, 183857 CrossRef CAS PubMed.
- R. E. Scott, Science, 1976, 194, 743–745 CrossRef CAS.
- S. Kakuda, P. Suresh, G. Li and E. London, J. Lipid Res., 2022, 63, 100155 CrossRef CAS.
- X. G. Wang, D. S. Miller, J. J. de Pablo and N. L. Abbott, Soft Matter, 2014, 10, 8821–8828 RSC.
- S. Kutti Kandy and R. Radhakrishnan, Biophys. J., 2022, 121, 3674–3683 CrossRef CAS.
- A. Mahendra, H. P. James and S. Jadhav, Chem. Phys. Lipids, 2019, 218, 47–56 CrossRef CAS PubMed.
- E. Evans and W. Rawicz, Phys. Rev. Lett., 1997, 79, 2379–2382 CrossRef CAS.
- J. Hagmann, M. M. Burger and D. Dagan, J. Cell. Biochem., 1999, 73, 488–499 CrossRef CAS.
- C. C. Cunningham, J. Cell Biol., 1995, 129, 1589–1599 CrossRef CAS PubMed.
- A. Boulbitch, R. Simson, D. A. Simson, R. Merkel, W. Häckl, M. Bärmann and E. Sackmann, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 3974–3985 CrossRef CAS.
- C. H. Lu, K. Pedram, C. T. Tsai, T. T. Jones, X. Li, M. L. Nakamoto, C. R. Bertozzi and B. Cui, Nat. Commun., 2022, 13, 3093 CrossRef CAS.
- S. A. Freeman, A. Vega, M. Riedl, R. F. Collins, P. P. Ostrowski, E. C. Woods, C. R. Bertozzi, M. I. Tammi, D. S. Lidke, P. Johnson, S. Mayor, K. Jaqaman and S. Grinstein, Cell, 2018, 172, 305–317 CrossRef CAS PubMed.
- T. Le, I. Ferling, L. Qiu, C. Nabaile, L. Assuncao, C. D. Roskelley, S. Grinstein and S. A. Freeman, Dev. Cell, 2024, 59, 853–868 CrossRef CAS.
- T. Bhatia, J. Agudo-Canalejo, R. Dimova and R. Lipowsky, ACS Nano, 2018, 12, 4478–4485 CrossRef CAS PubMed.
- Z. T. Graber, Z. Shi and T. Baumgart, Phys. Chem. Chem. Phys., 2017, 19, 15285–15295 RSC.
- A. M. Tom, S. Vemparala, R. Rajesh and N. V. Brilliantov, Phys. Rev. Lett., 2016, 117, 147801 CrossRef.
- A. M. Tom, S. Vemparala, R. Rajesh and N. V. Brilliantov, Soft Matter, 2017, 13, 1862–1872 RSC.
- M. Werner and J. U. Sommer, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 383–392 CrossRef CAS.
- S. A. Johnson, B. M. Stinson, M. S. Go, L. M. Carmona, J. I. Reminick, X. Fang and T. Baumgart, Biochim. Biophys. Acta, 2010, 1798, 1427–1435 CrossRef CAS PubMed.
- S. P. Pitroda, N. N. Khodarev, M. A. Beckett, D. W. Kufe and R. R. Weichselbaum, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5837–5841 CrossRef CAS PubMed.
- M. Poirot, S. Silvente-Poirot and R. R. Weichselbaum, Curr. Opin. Pharmacol., 2012, 12, 683–689 CrossRef CAS PubMed.
- K. Handa, F. Jacobs, B. M. Longenecker and S. Hakomori, Biochem. Biophys. Res. Commun., 2001, 285, 788–794 CrossRef CAS.
- S. Staubach, H. Razawi and F. G. Hanisch, Proteomics, 2009, 9, 2820–2835 CrossRef CAS.
- R. Dharan, S. Goren, S. K. Cheppali, P. Shendrik, G. Brand, A. Vaknin, L. Yu, M. M. Kozlov and R. Sorkin, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2208993119 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01317d |
| This journal is © The Royal Society of Chemistry 2025 |