The manipulation of natural mineral chalcopyrite CuFeS₂via mechanochemistry: properties and thermoelectric potential

Abstract

In this study, the properties of the natural mineral chalcopyrite CuFeS₂ after mechanical activation in a planetary mill were studied. The intensity of mechanical activation was controlled by changing the revolutions of the mill in the range 100–600 min⁻¹. A series of characterization techniques, such as XRD, SEM, TEM, TA (DTA, TG, and DTG), particle size analysis, and UV-vis spectroscopy was applied and reactivity studies were also performed. Several new features were revealed for the mechanically activated chalcopyrite, e.g. the poly-modal distribution of produced nanoparticles on the micrometer scale, agglomeration effects by prolonged milling, possibility to modify the shape of the particles, X-ray amorphization and a shift from a non-cubic (tetragonal) structure to pseudo-cubic structure. The thermoelectric response was evaluated on the “softly” compacted powder via the spark plasma sintering method (very short holding time, low sintering temperature, and moderate pressure) by measuring the Seebeck coefficient and electrical and thermal conductivity above room temperature. The milling process produced samples with lower resistivity compared to the original non-activated sample. The Seebeck data close to zero confirmed the “compensated” character of natural chalcopyrite, reflecting its close-to stoichiometric composition with low concentration of both n- and p-type charge carriers. Alternatively, an evident correlation between thermal conductivity and energy supply by milling was observed with the possibility of band gap manipulation, which is associated with the energy delivered by the milling procedure.

---

1 Introduction

There are numerous potential, cost-effective natural minerals for application as advanced materials, e.g. energy materials. The tetrahedrite–tennantite series of natural minerals can serve as a good example.¹ Among these minerals, chalcopyrite CuFeS₂ is a good candidate owing to its unique optical, electrical, magnetic, and thermal properties.^2,3 Chalcopyrite obtained from a deep-sea hydrothermal vent was reported to be a suitable thermoelectric energy material.⁴

Chalcopyrite has a tetrahedral coordination with respect to sulphur and different long-range ordering. This mineral is an n-type semiconductor, which crystallizes in a tetragonal system, where CuS₄ and FeS₄ tetrahedrals form a double-sphalerite structure.⁵ The structural information for natural tetrahedral chalcopyrite (α-CuFeS₂) was first described in 1917.⁶ Subsequently, other forms of chalcopyrite were revealed, namely the stable cubic form (β-CuFeS_2−x) and unstable tetragonal form (γ-CuFeS₂).⁷ Between them, the β-form has less sulphur with the exact formula of CuFeS_1.82, which is sometimes replaced with talnakhite Cu_17.6Fe_17.6S₃₂.⁸ β-CuFeS_2−x shows good chemical reactivity (see Fig. S1 in the ESI†) and can be synthesized at high temperatures² and/or by high-energy milling.⁹ To date, the relationship between both the synthetic forms in terms of their chemical reactivity¹⁰ and thermoelectric performance^8,11–13 has been widely studied.

Herein, our aim was to conduct a systematic study of natural chalcopyrite samples prepared via mechanical activation in a planetary mill. Mechanical activation^7,14 was applied as an effective tool for the manipulation of synthetic chalcopyrite several times.^15–17 Synthetic chalcopyrite was previously obtained by mechanochemical synthesis;^15,18 however, in this case, parasitic sulphidic phases, such as pyrite FeS₂ and bornite Cu₅FeS₄, were also obtained.

Herein, several advanced characterization techniques were applied to obtain information on the changes in physical and chemical properties, reactivity in (s)–(l) and (s)–(s) reactions as well as thermoelectric characteristics of this potential natural energy material.

Moreover, several new facts are elucidated, including the prospective application of the natural mineral together with its synthetic counterpart, the possibility of band gap manipulation by milling, and the quantitative correlation between thermal conductivity and energy supply by milling as representative examples. Furthermore, changes in the milling process from the classical dependence on milling time to dependence on revolution of milling can contribute to the production of energy from the friction to impact mode.

2 Materials and methods

2.1 Materials

Natural chalcopyrite CuFeS₂ (deposit Zhezkazgan, Kazakhstan) containing an admixture of 0.95% SiO₂ and 2.82% insoluble residue was used.¹⁹ The chalcopyrite sample was sieved to a specific particle size (200 μm), and then treated by mechanical activation. The sample with a particle size of less than 35 μm served as a reference (non-activated) substance.

2.2 Methods

2.2.1 Mechanical activation. Mechanical activation was performed using a Pulverisette 6 (Fritsch, Germany) laboratory planetary ball mill working under the following conditions: 250 mL tungsten carbide milling chamber, tungsten carbide balls with a diameter of 10 mm and total mass of 360 g, mill revolutions in the range of 100–600 min⁻¹, milling time of 60 min, argon atmosphere, and ball-to-powder ratio of 72 : 1.

2.2.2 Spark plasma sintering. Sintering of the mechanically activated sample by spark plasma sintering (SPS) was applied to obtain homogeneous densified solid samples (not powdered) suitable for the thermoelectric study. To perform the electric and thermal transport characterization, the powder was placed in a graphite die (inner diameter of 10 mm) and sintered into pellets about ∼5 mm thick at 450 °C and 50 MPa at a heating rate of 323 °C min⁻¹ with the holding time of 3 min in an HP D10-SD (FCT Systeme GmbH, Germany) spark plasma sintering furnace (SPS) model under vacuum.

2.3 Characterization techniques

2.3.1 X-ray diffractometry (XRD). The XRD patterns of the mechanically activated samples were collected using a D8 Advance diffractometer (Bruker, Germany) with CuK_α radiation in the Bragg–Brentano configuration. The generator was set up at 40 kV and 40 mA. The divergence and receiving slits were 0.3° and 0.1 mm, respectively. The XRD patterns were recorded in the range of 2θ = 20–65° at a step size of 0.03° and step time of 10 s. The JCPDS PDF-2 database was utilized for phase identification.

For the determination of the crystalline phase content of CuFeS₂, the relative method proposed by Ohlberg and Strickler was used.²⁰ The effect of mechanical activation can be evaluated based on the mass fraction of the crystalline phase (crystallinity) in the activated sample, X, compared with the reference (non-activated) phase, assuming that it corresponds to 100% crystallinity. Thus it holds that

where U₀ and U_x denote the background of the reference (non-activated phase) and mechanically activated phases, while I₀ and I_x are the integral intensities of the diffraction lines of the reference (non-activated phase) and mechanically activated phases, respectively.

In this work, the complementary value to crystallinity, X, was called amorphization, A (sometimes this value is called X-ray amorphization). The values of A were calculated using the following equation:

A = 100 − X (%) (2)

where X is defined by eqn (1).

2.3.2 Scanning electron microscopy (SEM). The morphology and size of the powder particles were investigated using a Tescan Vega 3 LMU (Tescan, Czech Republic) scanning electron microscope (SEM) at an accelerating voltage of 20 kV. For the samples to be conductive, the powder was covered by a layer of gold on a JFC 1100 fine coat ion sputter. To obtain information about the chemical composition of the particles, a Tescan Bruker XFlash Detector 410 M (Bruker, Germany) energy-dispersive X-ray spectrometer (EDX) was used.

2.3.3 Transmission electron microscopy (TEM). Transmission electron microscopy (HR-TEM) together with selected area electron diffraction (SAED) and energy-dispersive X-ray spectroscopy (EDS) were used for the characterization of the chalcopyrite samples. TEM measurements were performed using a JEM 2100 (JEOL, Japan) 200 kV microscope with an LaB₆ electron source and equipped with energy dispersive X-ray spectrometer (EDS) for chemical analysis. A small amount of sample was ultrasonically homogenized in absolute alcohol for 5 min. Then, a droplet of the suspension was applied on a lacey carbon-coated Ni grid and dried. Prior to the TEM analysis, the samples were coated with carbon to prevent charging under the electron beam.

2.3.4 Adsorption specific surface area analysis (S_a). A NOVA 1200e Surface Area & Pore Size Analyzer (Quantachrome Instruments, Great Britain) nitrogen-adsorption apparatus was employed to get information about the adsorption specific surface area. The values of the adsorption specific surface area, S_a, were calculated using the Brunauer–Emmett–Teller (BET) equation in the relative pressure range of 0.05–0.35.

2.3.5 Particle size analysis and granulometric specific surface area (S_g). A Scirocco 2000M (MALVERN Instruments, Great Britain) Mastersizer apparatus working in laser diffraction mode was employed to measure the particle size distribution in the range of 0.1–600 μm. Based on the measured data, the granulometric specific area, S_g, was calculated.²¹ All measurements were performed in triplicate. For the calculation of S_g, the following formula was usedwhere ρ is density and D [3,2] is the surface area moment mean diameter.

2.3.6 UV-Vis spectroscopy. Absorption spectra were measured using a Helios Gamma (Thermo Electron Corporation, UK) UV-Vis spectrophotometer in the range of 200–800 nm in a quartz cell by dispersing the samples in absolute ethanol under ultrasonic stirring. All experiments were repeated at least three times.

The band gap energy (E_g) can be determined by utilizing the Tauc eqn (4), as follows:

(αhν)^1/n = A(hν − E_g) (4)

where α is the absorption coefficient, A is a constant, h is Planck's constant, ν is frequency and n is a constant associated with different types of electronic transitions (0.5 for a direct allowed, 2 for an indirect allowed, 1.5 for a direct forbidden and 3 for an indirect forbidden transition). The optical band gap, E_g, was estimated by plotting (αhν)² as a function of the photon energy hν. Extrapolating the straight line portion of the Tauc plot for zero absorption coefficient (α = 0) gives the optical band gap energy.

2.4 Reactivity

2.4.1 Leaching. To evaluate the chemical reactivity of mechanically activated CuFeS₂, leaching tests were performed. For the solubilization of Cu and Fe, hydrochloric acid was used.²² Both metals from chalcopyrite are released in form of soluble chlorides¹⁷ according to the equation

CuFeS₂ + 4HCl → CuCl₂ + FeCl₂ + 2H₂S (5)

The leaching was investigated in a 500 mL glass reactor containing 250 mL of HCl solution (10%). The stirrer was revolved at a rate of 400 min⁻¹. After heating the reactor to a temperature of 343 K, 500 mg of CuFeS₂ was added to start the leaching process. Aliquots (1 mL) of the solution were withdrawn at appropriate intervals of 2, 5, 10, 15, 20, 30, 45 and 60 min for the determination of the concentration of the dissolved metals by atomic absorption spectroscopy.

2.4.2 Thermal analysis. TG-DTA measurements were performed using a Netzsch STA 449 F3 Jupiter instrument (Netzsch, Germany). Homogenized samples of approximately 200 mg were placed in an Al₂O₃ crucible and the reference crucible was empty. The experiments were conducted by heating the samples to 700 °C at the constant heating rate of 10 °C min⁻¹ in a pure (>99.99 vol%) argon with a constant flow (70 mL min⁻¹).

2.5 Thermoelectricity

The SPS sintered material in the form of pellets exhibited a low density (84% for the milled samples and 63% for the non-milled sample) due to the very “soft” sintering conditions. A diamond wire saw was used to shape the samples for characterization. The electrical resistivity and Seebeck coefficient were measured on about 2 × 2 × 8 mm³ bars under a nitrogen flow in the temperature range of 300 to 620 K via the four-probe method using a custom-made instrument.²³ Thermal conductivity was calculated as a product of thermal diffusivity, heat capacity and density. The first two properties were measured on graphite-coated discs (about 1.5 mm high and 10 mm in diameter) under nitrogen flow between 163 and 673 K using a Netzsch LFA 467 instrument and Pyroceram 9606 as the standard for heat capacity. The density was determined at room temperature from the dimensions and mass of the sample and considered temperature independent.

3 Results and discussion

3.1 Properties of mechanically activated chalcopyrite CuFeS₂

3.1.1 Particle size analysis. The particle size distribution for the initial (non-milled) and mechanically activated samples of chalcopyrite is shown in Fig. 1. There is a large difference in the particle size of the samples in this study. The mono-modal distribution with a small shoulder indicates the presence of particles with a size of around 10–100 μm for the non-milled sample (Fig. 1, plot 1). In the case when milling at revolutions of n = 400–500 min⁻¹ was applied (Fig. 1, plots 2 and 3), this distribution shifted towards a lower particle size. Overall, for the mechanically activated samples, a decrease in particle size was observed, namely, a change from mono-modal to poly-modal distribution with the presence of several modes. These modes are not equivalent. In the case of finer particles (e.g., smaller than 5 μm), the most intense modes were around 0.5 μm and in the region of 3–4 μm. In the case of coarser particles (e.g., larger than 20 μm), the intensity of the corresponding modes decreased, in accordance with the supplied milling energy, as shown in plots 2–4 in Fig. 1. This is a result of the agglomeration phenomenon, which commonly occurs during the dry milling of sulphides.^7,24–26 However, two effects competed upon the supply of a higher milling energy, namely, agglomeration and particles breakage.²⁶ An overall picture of the particle size analysis of all the samples in this study is given in the ESI† (Fig. S2).

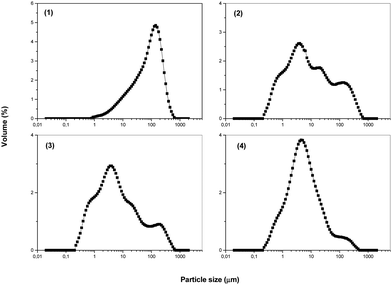Fig. 1 Particle size analysis for mechanically activated chalcopyrite CuFeS₂: (1) non-milled sample and samples milled at revolutions of 400 min⁻¹ (2), 500 min⁻¹ (3) and 600 min⁻¹ (4).

From a phenomenological point of view, the following conclusions can be formulated:

– Milling in a planetary mill can be applied to prepare nanosize particles. The application of particles with the desired size and nanoscale dimensions was tested from 90-ties, and later elaborated based on the concept of nano-structuring.^27–29 In this case, the positive influence on thermoelectric performance was verified and can also be expected in our case (see the results on thermoelectric performance in Section 3.2 of this work).

– Milling can be also applied to manipulate the nanoparticle distribution. The separate contribution of the three particle sizes (smaller than 5 nm, 5–100 nm and 100–1000 nm) on the lattice thermal conductivity was studied in the literature for PbTe.³⁰

It was demonstrated in our study that a broad distribution of CuFeS₂ particles sizes (0.1–600 μm) can be achieved by mechanical activation and it is possible to manipulate this distribution by changing the milling conditions (Fig. 1).

This is a new effect of milling, where a polymodal distribution is obtained. The particle size distribution was measured in triplicate. The dependence was obtained by granulometric analysis and the values of the granulometric specific surface area, S_g, were calculated statistically from the obtained data.

3.1.2 Surface area analysis. To study the changes in the surface area of solids, gas adsorption and particle size distribution measurements were applied. Both methods are mutually independent and together with the surface area size, they can supply information on the agglomeration effects and the size of the internal pores and cracks as a result of mechanical activation.²⁴ The values of the adsorption surface area, S_a, and granulometric surface area, S_g, can be determined from the corresponding measurements.

For the chalcopyrite CuFeS₂ mechanically activated at various mill revolutions (100–600 min⁻¹), their corresponding surface area values are presented in Fig. 2. The trend for the dependence of the S_a and S_g values on the milling energy represented by the increased revolutions of the mill, n, is the same. After a sharp increase at the beginning of milling (0–200 min⁻¹), a slow decrease was observed. The increase is a result of the formation of fine particles. Subsequently, a plethora of crystallites is formed with developed grain boundaries and a new internal surface area among them, which is characterized by the presence of inner pores. However, the effect of agglomeration also started to be evident at a higher n.

Fig. 2 The adsorption specific surface area S_a (1) and granulometric specific surface area S_g (2) for chalcopyrite CuFeS₂ milled at various revolutions n.

The peculiarity of planetary milling is the possibility of changing the milling conditions depending on the supply of milling energy. At the beginning, the impact mode of the balls is dominant, while at higher energies, it is combined with the shear mode (attrition).

In our case, at up to 200 min⁻¹, the dominant comminution of the chalcopyrite particles by the impact mode occurred with the production of a fresh surface. Subsequently, at a higher milling energy (200–600 min⁻¹), the impact mode is combined with the shear mode.^24,31–34 In this case, the formation of the new surface area slowed down because of the intervention of chalcopyrite particle agglomeration. The parallel decrease in the S_a and S_g values illustrates this phenomenon, where the chalcopyrite particles are so tightly compressed due to their agglomeration that the nitrogen applied in the adsorption measurements cannot penetrate the inner surfaces and/or pores between crystallites.²⁴ The particles are larger in this case.²⁶

The effects of porosity on the thermoelectric performance are obvious. The numerous boundaries and interfaces produced by mechanical activation have an impact on the behavior of phonons, which are highly scattered, thus reducing the thermal conductivity more than the electrical conductivity.^14,29 When nanoscale particles are formed (evidence shown later), quantum-confined effects occur, which enhance the power factor, S²σ.²⁹ A comprehensive study of the thermoelectric properties as a result of the surface morphology and structural changes³⁵ induced by mechanical activation is needed (see results in Section 3.2).

3.1.3 SEM and TEM characterization. The morphology of the chalcopyrite particles upon increasing mechanical activation is illustrated by the SEM micrographs in Fig. 3. The combination of larger and smaller grains with an irregular shape and unequal size was observed for the non-activated sample (Fig. 3(1)). The observed poly-dispersity of the grains in the non-activated sample is attributed to the sample preparation by sieving below 200 μm. As shown in Fig. 3(2), the comminuted grains of the sample treated at 200 min⁻¹ are more homogeneous in shape, which is a result of the mechanical activation applied at lower mechanical energy. The abundant smaller particles are dominant, which had an impact on the specific surface area (Fig. 2). By prolonged milling (Fig. 3(3) and (4)), the tendency to form agglomerates was clearly visible. The size of the particles gradually increased with an increase in the milling frequency, which supports the results illustrated in Fig. 1 and 2. The flattered particles observed in Fig. 3(3) and (4) are a result of the plastic deformation of chalcopyrite, which due to the higher energy supply, is the subsequent step in milling after agglomeration.^26,36

Fig. 3 Scanning electron micrographs (SEM) of chalcopyrite CuFeS₂ mechanically activated at various mill revolutions of (1) 0 min⁻¹, (2) 200 min⁻¹, (3) 400 min⁻¹, and (4) 600 min⁻¹.

The high-resolution TEM image for the sample mechanically activated at 400 min⁻¹ is shown in Fig. 4. The low-magnification image (Fig. 4(a)) and selected area electron diffraction SAED (Fig. 4(b)) confirm that the sample is composed of agglomerated fine crystallites. Furthermore, the d-values of the most intense diffraction rings match the values of chalcopyrite.

Fig. 4 (a) The low-resolution TEM micrograph of chalcopyrite CuFeS₂ mechanically activated at 400 min⁻¹. (b) The SAED pattern with d-value of the diffraction rings given in Å. (c) High-resolution TEM micrograph (HR-TEM). A nanosized crystallite is marked by the dashed line. (101) Lattice planes with d-spacing of 4.7 Å are indicated in two other crystallites.

The high-resolution TEM image (Fig. 4(c)) shows that the sample on the TEM grid contained small crystallites with a diameter of 10–20 nm, which matches the average crystallite size determined by XRD (see Fig. 1). The (101) lattice planes (0.47134 nm) are resolved in crystallites with a suitable orientation. The randomly oriented nanoparticles were tightly agglomerated, and therefore nanoparticles with different orientations overlapped in the viewing direction. Consequently, the exact differentiation of individual nanoparticles was impeded. In a few cases, mainly in the thinnest parts of the agglomerates at the very edges, some nanoparticles were better resolved and one of these nanocrystallites is circled in Fig. 4(c).

3.1.4 Bulk changes. The X-ray diffraction patterns of the mechanically activated chalcopyrite CuFeS₂ depending on the revolutions of the planetary mill are depicted in Fig. 5. The three most intense diffraction lines, i.e., (112), (220/204) and (312/116), match well with the JCPDS card of chalcopyrite (JCPDS 037-0471). The patterns for natural chalcopyrite in this study are consistent with the patterns of synthetic chalcopyrite prepared by milling of Cu, Fe and S elements.^11,15,18 They correspond to a tetragonal body-centered symmetry belonging to the I42d space group. As shown in Fig. 5, the diffraction patterns showed the tendency to become broader in shape with a decrease in intensity upon increasing the supply of mechanical energy. This indicates a reduction in the size of the chalcopyrite particles and/or formation of defects by the creation of microstrain.³⁷

Fig. 5 Powder X-ray diffraction patterns of mechanically activated chalcopyrite CuFeS₂ (revolutions of mill are depicted on the patterns).

Fig. 6 shows the dependence of amorphization A on the revolutions of the mill n together with the value of the experimentally determined energy gap E_g. Amorphization represents an integral value incorporating both size reduction and defect formation. The amorphization value for the mechanically activated chalcopyrite reached more than 70% for the most intensively treated sample. The patterns also show that the increase in A is sharp at the beginning of milling, and then decreased, showing the same trend in surface area in Fig. 2. This indicates that in both cases, bulk and surface defects are formed during milling. Quantitatively, an increase in specific surface area, S_a, from 0.51 m² g⁻¹ to 4.5 m² g⁻¹ for the non-activated sample and sample milled at 600 min⁻¹, respectively, was determined. In parallel, for the same samples, an increase in amorphization, A, from 0 (100% crystallinity) to 71% (29% crystallinity) was calculated.

Fig. 6 Amorphization A (1) and band gap E_g (2) vs. revolutions of mill n for mechanically activated chalcopyrite CuFeS₂.

Thus, according to the results from these experiments, high-energy milling can be applied to prepare strongly defect particles. The concept of defect engineering plays an important role in the thermoelectric performance.^38–40 In principle, it can influence the thermoelectric properties via two basic strategies, i.e., band engineering by tuning the electronic band structure, and thus enhancing the power factor, if relevant with respect to doping and bandgap value, and/or phonon engineering by stimulating phonon scattering, and thus reducing the lattice thermal conductivity.³⁸ During mechanical activation, various microstructural defects can be formed including zero-, one- and two-dimensional defects, which can selectively influence the scattering of low-, mid- and high-frequency phonons.⁴¹ Thus, band engineering and phonon engineering can effectively contribute to the thermoelectric efficiency of materials.^42–44 In our case, the samples were not optimized with respect to doping, and thus their electronic properties were essentially impacted by the mechanical activation by the defect and particle size control, which play key roles in thermal transport (see Thermoelectric performance section).

3.1.5 Chemical reactivity (leaching). In hydrometallurgy, the method of solid–liquid chemical reactivity (leaching) is applied for the dissolution of metals from minerals.² The metals start to be leached from the surface in the direction of the bulk of solids. Therefore, the study of chemical reactivity can be a useful method to evaluate solids disordered by mechanical activation, where different compositions can be expected in their surface and sub-surface layers. Changes in the composition of solids are mirrored in the shape of their leaching curves. If the phase composition of the reacting solid is homogeneous, the leaching curves are usually flat.²⁶ However, if irregularities appear in the leaching curves, heterogeneity in the solid composition can be expected.

To evaluate the chemical reactivity of the mechanically activated chalcopyrite, copper and iron leaching in HCl lixiviant was proposed (see eqn (2)). The results are depicted in Fig. 7.

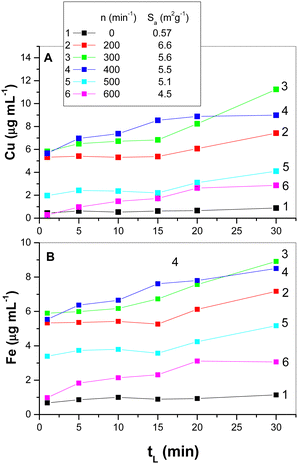Fig. 7 Cu (A) and Fe (B) leached from mechanically activated chalcopyrite CuFeS₂; t_L is the leaching time and n is the number of mill revolutions. (The inset in A shows the values of adsorption specific area S_A from Fig. 2.)

In this case, both metals dissolve from chalcopyrite as chlorides in a liquid form and hydrogen sulphide is formed as a gas product. For comparison, the results for the non-activated chalcopyrite are also shown.

Leaching of mechanically activated chalcopyrite belongs to the surface-sensitive reactions.⁴⁵ Consistent with this statement, the values of the specific surface area, S_a, for the mechanically activated samples are presented in the inset of Fig. 7(A). For all the mechanically activated samples, a more significant increase in leached metals started at t_L = 15 min (with the exception of the sample activated at 400 min⁻¹, where this phenomenon was already observed at t_L = 10 min). Mechanical activation by milling at revolutions of n = 300–400 min⁻¹ gave the best results for metals recovery. The application of higher revolutions at n = 500–600 min⁻¹ was not as effective, and thus the metal recoveries were lower. The beginning of the agglomeration phenomena discussed in the previous paragraph (Section 3.1) corresponds to a decrease in the specific surface area, S_a (see inset in Fig. 7(A)). In this case, the effect of agglomeration (see also Fig. 3 in part 3) prevailed over the positive effect of the increasing milling energy and played a decisive role in the chemical reactivity of the mechanically activated CuFeS₂. Moreover, the regime of ball movement in the mill changed with an increase in the revolutions of the mill from the most effective cascading regime to the cataracting and centrifugal ones. It is known that two last regimes are less effective at transferring the milling energy to solids.^34,46

The improved leaching observed after 15 min is related to the chemical changes of the partly leached species, namely, it is a result of the shortening and weakening of the Cu–S and Fe–S bonds in the sub-surface layers of the activated chalcopyrite. Here, the rupture of the chemical bonds and rearrangement of the surface are expected. The explanation for what happened to the partly leached chalcopyrite before and after the breaking point on the leaching curves is a rather speculative. The literature describes the chemical reactivity of the α- and β-forms of chalcopyrite¹⁰ (see Fig. S1 in the ESI†). The shape of the leaching curves for the β-form of chalcopyrite in this case is identical with our results obtained for the mechanically activated samples. Moreover, the flat shape of the leaching curves for the non-activated chalcopyrite (α-form) is also identical.

However, we do not have experimental support to explain what is responsible for this effect. The applied method of X-ray diffractometry in our study could not discriminate between the α- and β-forms of chalcopyrite. The reason for this is that the peaks in the XRD patterns (Fig. 5) of the mechanically activated chalcopyrite are broad, and thus give information related to the induced strain and size of the nanocrystals (see also Section 3.2 in the next paragraph). However, it is not possible to clearly distinguish individual phases (see also Fig. S3 in the ESI†).

Recently, the concept of forming pseudocubic (or cubic-like) species from non-cubic (tetragonal) α-chalcopyrite CuFeS₂ was elaborated.¹² The properties of the corresponding (cubic) β- chalcopyrite CuFeS_1.82 (also known as talnakhite Cu_17.6Fe_17.6S₃₂) were described in detail.¹³ From the perspective of thermoelectric performance, cubic or cubic-like chalcopyrite shows ultralow thermal conductivity in comparison with its tetragonal form.⁸

3.1.6 Thermal decomposition. To elucidate the existence of the α- and β-forms in chalcopyrite, their thermal reactivity was studied. It is known that sulphur-deficient β-chalcopyrite (cubic) is formed by heating the α-form (tetragonal), which is stable at room temperature.^47–49 The temperature for the α → β transformation can be influenced by the intervention of mechanical activation.^9,50 The methodology of thermal analysis can be utilized to study the behavior of these forms, where DTA is performed to determine the peak temperature, T_m, and DTG for the mass changes during heating, Δm.

The DTA curves illustrating the α → β transformation are shown in Fig. 8. In addition to this information, the DTG curves were also recorded (not shown here) to illustrate the weight loss Δm in the mechanically activated chalcopyrite. The DTA curves show a shift in the temperature, T_m, for the formation of β-chalcopyrite to lower values. Namely, the temperature decreased from 503.4 °C to 490.5 °C for the non-activated and mechanically activated (n = 500 min⁻¹) samples, respectively.

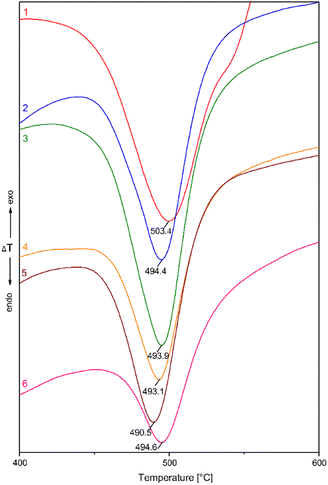Fig. 8 DTA curves of the mechanically activated chalcopyrite at mill revolutions (n) of (1) 0 min⁻¹, (2) 200 min⁻¹, (3) 300 min⁻¹, (4) 400 min⁻¹, (5) 500 min⁻¹ and (6) 600 min⁻¹.

The change in both thermoanalytical parameters (T_m and Δm) was dependent on the revolutions of the mill, n, by which mechanical energy was supplied to the samples. Fig. 9 shows a summary of both quantitative measures, where the decrease in the peak temperature, T_m, for the formation of β-chalcopyrite from the α-form (non-activated sample) is evident. However, an irregularity was detected in the region of n = 400–600 min⁻¹, where the highest energy input was applied. The weight loss, Δm, values also changed with an increase in energy. In this case, Δm of ∼25% was detected for the non-activated sample in comparison with that of ∼6–12% for the mechanically activated samples. According to these results, the loss in sulphur corresponding to the formation of CuFeS_2−x (β-chalcopyrite) from the non-activated CuFeS₂ was 25%, in comparison with all the mechanically activated samples, where this value was only 6–12%. This provides proof that partial decomposition occurred during milling.

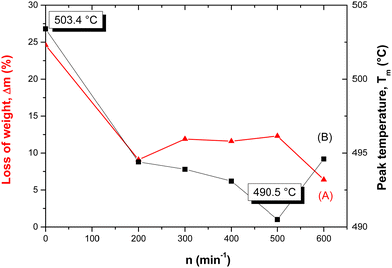Fig. 9 The loss of weight Δm (A) and peak temperature T_m (B) of mechanically activated chalcopyrite CuFeS₂vs. mill revolutions n.

Usually the reactivity in solid-state reactions influenced by mechanical intervention corresponds to the delivered mechanical energy. In some cases, when the supply of energy is not optimized, the reactivity can be hampered by relaxation processes⁵¹ such as agglomeration.⁵⁰ In our case, agglomeration was detected at higher energies (see Fig. 2, 3 and 6). However, in the thermal analysis of the mechanically activated samples, the weight loss weight, Δm, the big jump in the region of n = 0–200 min⁻¹ was substantially reduced at n > 200 min⁻¹. This is because in the region of n > 200 min⁻¹, the transformation of α-chalcopyrite is hampered by the presence of non-identified species. The presence of pseudo-cubic chalcopyrite (see also Section 3.2) can serve as a speculative explanation. In the sample with n = 0 min⁻¹ (non-activated tetragonal chalcopyrite), the β-form is absent. However, its previously formed species in the mechanically activated chalcopyrite can explain the low values of Δm for n > 200 min⁻¹.

3.1.7 Band gap manipulation. The band gap, E_g, between the valence and conduction band represents a crucial parameter, which determines the properties of semiconductors. Broadening or narrowing of the E_g is a consequence of microstructure changes in solids. Consequently, external tuning of E_g can influence the performance of solids in photocatalysis, optoelectronics and thermoelectrics. Several external interventions can be applied for band gap tuning. The influence of pressure,^52–55 temperature^56–58 and doping^59,60 was observed in the past.

The first paper showing a possibility of band gap manipulation for several semiconductors was published in 1967.⁵⁷ In this case, the impact of temperature variation was studied. The following equation satisfactorily representing the experimental data for various species such as C (diamond), Si, Ge, 6H-SiC, GaAs, InP and InAs was derived

E_g = E₀ − αT²/(T + β) (6)

where E_g is the energy gap, E₀ is its value at 0 K, and α and β are empirical parameters, which have no real physical significance. The relative position of the conduction and valence bands herein was interpreted as the temperature-dependent expansion of the lattice.

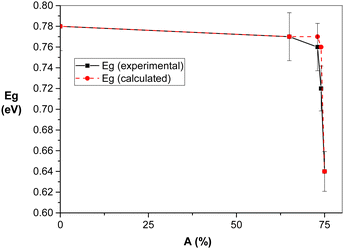
According to the dependence of optical band gap, E_g, on the mill revolutions, n, in Fig. 6, the decrease in E_g value with an increase in the milling energy (manifested by an increase in mill revolutions) is evident. However, the decrease in the band gap was not monotonous, where the most intense change was observed for n = 400–600 min⁻¹, which is simultaneously a critical region for other properties, such as thermal and chemical reactivity. Fig. 10 presents the dependence of bandgap, E_g, on the amorphization, A, of chalcopyrite. Strong sensitivity was documented for the highly disordered species, where A > 73% corresponds to the mill revolutions of n > 400 min⁻¹.

Fig. 10 Band gap E_gvs. amorphization degree A for mechanically activated chalcopyrite CuFeS₂.

In our previous work, the possibility of band gap tuning in high-energy milled chalcopyrite was evidenced for the first time,⁶¹ where the same trend as that observed in the present study was documented. In the cited paper, the mechanical activation was performed by the traditional procedure, i.e., by changing the milling time. The mechanism of supplying mechanical energy to CuFeS₂via ball milling was the same during the whole milling event. Thus, the impact-to-shear ratio was constant.

In the present study, changes in the revolutions of the mill in the range of 200–600 min⁻¹ (by constant milling time of 60 min) instead of changes caused by just changing the milling time to 60–240 min in the previous study (by constant mill revolutions of 550 min⁻¹) were applied.⁶¹ According to,³⁴ the impact-to-shear ratio of the milling balls is not constant in this case because the regime of ball movement changes.

The dependence of band gap, E_g, on the amorphization, A, of chalcopyrite in Fig. 10 is similar to the dependence of the band gap on temperature in Varshni's work (see Fig. S4 in the ESI†). The linear-quadratic relation was derived for the experimental data in Fig. 10, as follows:

E_g = E₀ − [γA²/(100 − δ)²] (7)

where E₀ is band gap for non-activated CuFeS₂, A is amorphization, γ = (π/100)² is a coefficient, δ is the milling efficiency defined as E_g min/E_g (experimental) × 100 (%) and E_g min = 0.64 eV is the minimum band gap for non-activated CuFeS₂.

Besides the solid-state synthesis studied herein, the wet synthesis of CuFeS₂ and its band gap tunability was also studied.⁶²E_g spanned in the range of 0.5–2.0 eV, which also includes the range 0.64–0.78 eV observed in our study.

This tunability offers the possibility to tune the properties of thermoelectric materials, namely, their efficiency. The properties such as lattice modification, bond length and influence of strain (among others) play an important role.⁶³ Usually the lattice displacement induced by phonon vibration causes a change in the band energy.⁶⁴

In summary, high-energy milling, as a non-equilibrium process, can be also used in addition to temperature, pressure and doping as an effective tool for band gap engineering.

3.2 Properties of mechanically activated chalcopyrite CuFeS₂ after spark plasma sintering

The production of CuFeS₂ powder and modification of its properties by mechanical activation is documented as a gold clue herein. However, any thermoelectric application requires a densified form of samples (pellets), which can be prepared from powder by several non-equilibrium methods such as hot pressing (HP) and/or spark plasma sintering (SPS).¹⁴ This compaction process eliminates porosity (usually more than 90% of the theoretical density is required for compact pellets). In our case, the very soft and fast process using SPS technology was applied, as shown in Section 2.2.2.

3.2.1 Bulk changes. The changes in the lattice parameters a and c and volume of the elemental cell, V, for the mechanically activated tetragonal chalcopyrite CuFeS₂ after sintering are shown in Fig. 11. Using the Rietveld refinement, the trend of the related Rietveld parameters is presented, where their decrease with an increase in milling energy is well-documented. However, for higher milling energies (n = 300–500 min⁻¹), an irregular “jump” was also evidenced. The tendency to generate changes in physico-chemical properties in this energy range was also observed for the mechanically activated (non-sintered) samples in the previous paragraphs, as shown in Fig. 2, 6, 7 and 9. The phenomenon of “memory effect” probably plays a role, where the structural changes in the powdered chalcopyrite evoked by mechanical activation were preserved despite the drastic intervention of pressure and temperature during the treatment of pellets by SPS. In principle, the concept for the formation of the tetragonal “pseudo-cubic” structure of chalcopyrite CuFeS₂¹² in this energy interval is acceptable. In this case, the tetragonal chalcopyrite represents an ideal “pseudo-cubic” structure. The authors of this concept highlight the possibility of the coexistence of a long-range cubic framework with localized short-range non-cubic (tetragonal) lattice distortions.

Fig. 11 Dependence of lattice parameters a (1) and c (2) and volume of the elemental cell V (3) vs. mill revolutions n for mechanically activated and sintered chalcopyrite CuFeS₂.

The dependence of the lattice parameters of chalcopyrite on the mechanical energy supply (modified by varying the mill revolutions) is presented in Fig. 11, where their tendency to decrease for n = 0–400 min⁻¹ is clearly manifested. In this region, the pure tetragonal structure was preserved, and its lattice parameter was in the range of a = 5.2887–5.2832 Å. In this range, the value of a = 5.2851 Å for pure tetragonal chalcopyrite was documented.¹³ However, for n ≥ 400 min⁻¹, the opposite trend expected for a cubic structure was observed, but the values for the lattice parameter still indicated a tetrahedral structure. In this range, the concept of tetragonal “pseudo-cubic” structure of chalcopyrite CuFeS₂ is acceptable.

The irregular behavior of the chalcopyrite nanoparticles was also manifested by the evolution of their crystallite size, as shown in Fig. 12. The general trend of particle comminution from 56 nm for n = 200 min⁻¹ to 28 nm, and finally 18–20 nm by higher energy supply is documented. As described previously (Fig. 1–3), the agglomeration phenomena started to be effective, and it seems that despite the intense SPS, the powder “remembered” its history.

Fig. 12 The dependence of particle size d on mill revolutions n for mechanically activated and sintered chalcopyrite CuFeS₂.

3.2.2 Thermoelectric performance. Based on the fact that we performed the mechanical activation of pure chalcopyrite, which was not optimized with respect to doping, the strongest and evident impact of the milling process was observed on the thermal conductivity (see Fig. 13). The electronic properties (see Fig. 14) remained poor because of the undoped character of the original chalcopyrite, where the doping was modified naturally, but unintentionally by the milling process and thermal cycling above 600 K during thermoelectric characterization in inert gas. However, the modification of the properties associated with SPS is unlikely given that the process was very short and the sample only remained at temperatures above 600 K for minutes.

Fig. 13 The thermal conductivity of chalcopyrite CuFeS₂ as a function of temperature T (1) and mill revolutions n (2).

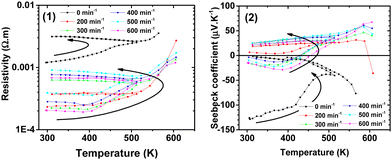Fig. 14 The electrical resistivity ρ (1) and Seebeck coefficient S (2) of chalcopyrite CuFeS₂ as a function of temperature T.

Nonetheless, compiling our results and comparing the discussed literature data, we can unambiguously confirm the decrease in thermal conductivity with an increase in mill revolutions (Fig. 13), where we depict the temperature dependence of the thermal conductivity of the prepared samples above 160 K. The positive role of milling in the decrease in the thermal conductivity is evidenced in the second panel in Fig. 13, where the absolute value of the thermal conductivity at ambient temperature and 573 K is shown to be dependent on the mill revolutions. The significant loss of sulphur due to milling, and as a result lower thermal conductivity can be excluded given that the electric transport data for all the samples confirm their p- and n-type conductivity behaviour, which is unrealistic for significant sulphur non-stoichiometry.¹¹

In the case of the reference sample (non-milled), its low relative density of ∼60% due to the soft sintering conditions is responsible for its low thermal conductivity maximum of only ∼5 W m⁻¹ K⁻¹ (see Fig. 13). It should be noted that the thermal conductivity cycling (not shown) between 163 ≥ 673 ≥ 300 K was not a reproducible process for any of the studied samples, where the thermal conductivity further decreased during the cooling run from 673 K to 300 K. As a tentative explanation for this process, we propose a minor grain-surface loss of sulphur emerging at ∼500 K, and simultaneously a small, but systematic modification of the chemical composition of the grains. Due to the contamination of the material by the determined parasitic iron-based phases of Fe₂(SO₄)₃·2(OH)₆·H₂O, FeSO₄·H₂O and FeSO₄·(H₂O)₄ (see also ref. 18), the chalcopyrite matrix is iron depleted, which favors the chalcopyrite copper-rich phase exhibiting p-type conductivity.⁶⁵ Moreover, at close to 500 K, we observed anomalies in the electrical resistivity, which may not reflect the “bulk” change in sulphur concentration inside the agglomerate-grains but more realistically, the chemical modification of the interfacial properties between grains. Consequently, we present the thermal and electric transport data for temperatures only up to 600 K, where if cycled between 300 ≥ 600 ≥ 300 K, thermoelectric transport data only showed a minor change in the charge carrier character of the cycled sample. Specifically, the thermoelectric power slightly tended to small positive values and the increase in electrical resistivity was moderate. Temperature cycling above 600 K simultaneously led to a substantial increase in resistivity at 300 K when cooled and the compensated low-doped character of all the samples (understand p- and n-type charge carriers simultaneously led to S ≈ 0 μV K⁻¹) was modified to clearly p-type semiconductor (S > +100 μV K⁻¹) with two orders higher resistivity with respect to their pristine value.

Further, we comment on the disagreement between the previously published¹⁹ and current data, which are both based on mechanically activated identical chalcopyrite samples. This difference is due to the fact that in the previous paper, sintering was performed using the hot press technique, which simultaneously led to: (i) an increase in the crystalline size, (ii) essentially more dense samples and (iii) due to the higher sintering temperature and much longer sintering time, a modified stoichiometry, where partial sulphur deficiency with robust n-type conductivity was straightforward, as reported by Li et al.¹¹ Alternatively, extremely soft sintering via SPS preserved the ideal CuFeS₂ stoichiometry without necessary doping. The electrical properties did not vary much with respect to the milling procedure, where the electrical resistivity is high because of the low doping, low compactness of the samples and contamination of the material by oxy-, hydroxy- and iron-based phases, which could complicate the charge carrier percolation.

4 Conclusions

The properties of the natural mineral chalcopyrite CuFeS₂ after mechanical activation in a planetary mill were studied. The intensity of mechanical activation was modified by changing revolutions of the mill in the range of 100–600 min⁻¹. Several new effects were revealed and described for the mechanically activated chalcopyrite, as follows:

– Poly-modal distribution of produced nanoparticles in the micrometer range. This effect was complicated by the agglomeration upon the supply of higher milling energy.

– The agglomeration effects were confirmed by the change in the specific surface area values and SEM analysis.

– The possibility to modify the shape of particles, X-ray amorphization and tendency of XRD to peak broadening as a result of microstructural defects and nanosizing was also identified.

– The shift from a non-cubic (tetragonal) structure to pseudo-cubic (or cubic-like) structure seemed to be an explanation for the described effects in the mechanically activated species. The thermoanalytical studies documented the formation of cubic chalcopyrite by heating the tetragonal form in an inert atmosphere.

– The possibility of band gap manipulation and correlation between thermal conductivity and energy supply by milling were also revealed.

– The decrease in thermal conductivity due to nano-structuring, while preserving the electric transport characteristics.

Author contributions

Conceptualization: Peter Baláž. Funding acquisition: Peter Baláž, Matej Baláž. Investigation: Erika Dutková, Matej Baláž, Nina Daneu. Methodology: Peter Baláž, Erika Dutková, Mária Bali Hudáková. Project administration: Peter Baláž, Erika Dutková. Resources: Peter Baláž, Matej Baláž. Supervision: Peter Baláž. Validation: Peter Baláž. Visualization: Erika Dutková, Nina Daneu, Nina Daneu, Lenka Findoráková, Jiří Hejtmánek, Petr Levinský, Mária Bali Hudáková, Róbert Džunda. Writing – original draft: Peter Baláž. Writing – review & editing: Peter Baláž, Erika Dutková, Matej Baláž, Nina Daneu, Lenka Findoráková, Jiří Hejtmánek, Petr Levinský, Karel Knížek, Mária Bali Hudáková, Róbert Džunda, Radovan Bureš, Viktor Puchý.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by the Slovak Research and Development Agency APVV (project APVV-18-0357). The support through the Slovak Grant Agency VEGA (project 2/0112/22) is also acknowledged. P. L. and J. H. acknowledge the financial support of the Operational Program Research, Development and Education financed by European Structural and Investment Funds and the Czech Ministry of Education, Youth and Sports (project no. SOLID21 CZ.02.1.01/0.0/0.0/16_019/0000760).

References

1. X. Lu, D. T. Morelli, Y. Xia, F. Zhou, V. Ozolins, H. Chi, X. Y. Zhou and C. Uher, Adv. Energy Mater., 2013, 3, 342–348.
2. F. Habashi, Chalcopyrite, Its Chemistry and Metallurgy, McGraw-Hill, New York, 1978.
3. B. S. Shah, J. B. Raval, D. Kumar, S. H. Chaki and M. P. Deshpande, J. Alloys Compd., 2023, 938, 168566.
4. R. Ang, A. U. Khan, N. Tsujii, K. Takai, R. Nakamura and T. Mori, Angew. Chem., Int. Ed., 2015, 54, 12909–12913.
5. A. V. Powell, J. Appl. Phys., 2019, 126, 100901.
6. C. L. Burdick and J. H. Ellis, J. Am. Chem. Soc., 1917, 39, 2518–2525.
7. P. Baláž, Extractive Metallurgy of Activated Minerals, Elsevier, Amsterdam, 2000.
8. H. Y. Xie, X. L. Su, X. M. Zhang, S. Q. Hao, T. P. Bailey, C. C. Stoumpos, A. P. Douvalis, X. B. Hu, C. Wolverton, V. P. Dravid, C. Uher, X. F. Tang and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 10905–10914.
9. E. Gock, Erzmetall, 1978, 31, 282–288 (in German).
10. R. C. H. Ferreira and A. R. Burkin, Inst. Min. Metall., 1975, 54–66.
11. J. H. Li, Q. Tan and J. F. Li, J. Alloys Compd., 2013, 551, 143–149.
12. J. W. Zhang, R. H. Liu, N. A. Cheng, Y. B. Zhang, J. H. Yang, C. Uher, X. Shi, L. D. Chen and W. Q. Zhang, Adv. Mater., 2014, 26, 3848–3853.
13. D. Zhang, B. Zhang, Z. Z. Zhou, K. L. Peng, H. Wu, H. Y. Wang, G. W. Wang, G. Han, G. Y. Wang, X. Y. Zhou and X. Lu, Chem. Mater., 2021, 33, 9795–9802.
14. Y. C. Lan, A. J. Minnich, G. Chen and Z. F. Ren, Adv. Funct. Mater., 2010, 20, 357–376.
15. E. Dutkova, Z. Bujnakova, J. Kovac, I. Skorvanek, M. J. Sayagues, A. Zorkovska, J. Kovac and P. Balaz, Adv. Powder Technol., 2018, 29, 1820–1826.
16. P. Balaz, M. Balaz, E. Dutkova, M. Hegedus, M. Rajnak, K. Knizek, J. Hejtmanek, J. Navratil, M. Achimovicova and J. Briancin, Acta Phys. Pol., A, 2020, 137, 647–649.
17. Y. Li, N. Kawashima, J. Li, A. P. Chandra and A. R. Gerson, Adv. Colloid Interface Sci., 2013, 197, 1–32.
18. S. K. Pradhan, B. Ghosh and L. K. Samanta, Phys. E, 2006, 33, 144–146.
19. P. Balaz, E. Dutkova, P. Levinsky, N. Daneu, L. Kubickova, K. Knizek, M. Balaz, J. Navratil, J. Kasparova, V. Ksenofontov, A. Moller and J. Hejtmanek, Mater. Lett., 2020, 275, 128107.
20. S. M. Ohlberg and D. W. Strickler, J. Am. Ceram. Soc., 1962, 45, 170–171.
21. T. Allen, Particle Size Measurement, Chapman and Hall, London, 1981.
22. S. Palaniandy, Int. J. Miner. Process., 2015, 136, 56–65.
23. K. Knizek, J. Hejtmanek, Z. Jirak, C. Martin, M. Hervieu, B. Raveau, G. Andre and F. Bouree, Chem. Mater., 2004, 16, 1104–1110.
24. K. Tkáčová, Mechanical Activation of Minerals, Elsevier, Amsterdam, 1989.
25. M. S. Bafghi, A. H. Emami, A. Zakeri and J. V. Khaki, Powder Technol., 2010, 197, 87–90.
26. S. X. Zhao, G. R. Wang, H. Y. Yang, G. B. Chen and X. M. Qiu, Trans. Nonferrous Met. Soc. China, 2021, 31, 1465–1474.
27. L. D. Hicks and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 12727–12731.
28. L. D. Hicks and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 16631–16634.
29. M. S. Dresselhaus, G. Chen, M. Y. Tang, R. G. Yang, H. Lee, D. Z. Wang, Z. F. Ren, J. P. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043–1053.
30. Z. T. Tian, K. Esfarjani, J. Shiomi, A. S. Henry and G. Chen, Appl. Phys. Lett., 2011, 99, 053122.
31. G. Heinicke, Tribochemistry, Akademie Verlag, Berlin, 1984.
32. Q.-Q. Zhao, S. Yamada and G. Jimbo, KONA, 1989, 29–36.
33. P. Baláž, Mechanochemistry in Nanoscience and Minerals Engineering, Springer, Berlin Heidelberg, 2008.
34. C. F. Burmeister and A. Kwade, Chem. Soc. Rev., 2013, 42, 7660–7667.
35. D. Kojda, R. Mitdank, S. Weidemann, A. Mogilatenko, Z. Wang, J. Ruhhammer, M. Kroener, W. Tollner, P. Woias, K. Nielsch and S. F. Fischer, Phys. Status Solidi A, 2016, 213, 557–570.
36. Q. W. Zhang and F. Saito, Adv. Powder Technol., 2012, 23, 523–531.
37. T. Ungar, Scr. Mater., 2014, 57, 777–781.
38. Z. Li, C. Xiao, H. Zhu and Y. Xie, J. Am. Chem. Soc., 2016, 138, 14810–14819.
39. J. He and T. M. Tritt, Science, 2017, 357, eaak9997.
40. Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. B. Luo, Z. Z. Luo, J. W. Xu, Q. Y. Yan and M. G. Kanatzidis, Chem. Soc. Rev., 2021, 50, 9022–9054.
41. N. Jia, X. Y. Tan, J. W. Xu, Q. Y. Yan and M. G. Kanatzidis, Acc. Mater. Res., 2022, 3, 237–246.
42. Y. X. Wu, Z. W. Chen, P. F. Nan, F. Xiong, S. Q. Lin, X. Y. Zhang, Y. Chen, L. D. Chen, B. H. Ge and Y. Z. Pei, Joule, 2019, 3, 1276–1288.
43. S. Tippireddy, F. Azough, Vikram, F. T. Tompkins, A. Bhui, R. Freer, R. Grau-Crespo, K. Biswas, P. Vaqueiro and A. V. Powell, Chem. Mater., 2022, 34, 5860–5873.
44. T. Ghosh, M. Dutta, D. Sarkar and K. Biswas, J. Am. Chem. Soc., 2022, 144, 10099–10118.
45. Z. Bujnakova, M. Balaz, M. Zduriencikova, J. Sedlak, M. Caplovicova, L. Caplovic, E. Dutkova, A. Zorkovska, E. Turianicova, P. Balaz, O. Shpotyuk and S. Andrejko, Mater. Sci. Eng., C, 2017, 71, 541–551.
46. S. Bernotat and K. Schonert, Size Reduction, Ullmann`s Encyclopedia of Industrial Chemistry, VCH Verlagsgeselschaft, Wienheim, 1998, vol. B2, pp. 5.1.395–395.5.39.
47. J. E. Hiller and K. Probsthain, Z. Kristallogr., 1956, 108, 108–129.
48. A. Lenchev, Z. Chem., 1978, 18, 417–418.
49. H. Shima, J. Jpn. Assoc. Mineral., Petrol. Econ. Geol., 1962, 47, 123.
50. P. Balaz, K. Tkacova and E. G. Avvakumov, J. Therm. Anal. Calorim., 1989, 35, 1325–1330.
51. A. Z. Juhasz and B. Kollath, Acta Chim. Hung., 1993, 130, 725.
52. L. F. Yang, L. D. Dai, H. P. Li, H. Y. Hu, M. L. Hong, X. Y. Zhang and P. F. Liu, Geosci. Front., 2021, 12, 1031–1037.
53. R. A. Susilo, Y. Liu, H. W. Sheng, H. L. Dong, R. Sereika, B. Kim, Z. X. Hu, S. J. Li, M. Z. Yuan, C. Petrovic and B. Chen, J. Mater. Chem. C, 2022, 10, 1825–1832.
54. J. J. Feng, C. Li, W. Deng, B. C. Lin, W. H. Liu, R. A. Susilo, H. L. Dong, Z. Q. Chen, N. Zhou, X. L. Yi, X. Z. Xing, F. Ke, Z. X. Liu, H. W. Sheng, Z. X. Shi and B. Chen, J. Phys. Chem. Lett., 2022, 13, 1123–1130.
55. M. Maczka, S. Sobczak, P. Ratajczyk, F. F. Leite, W. Paraguassu, F. Dybala, A. P. Herman, R. Kudrawiec and A. Katrusiak, Chem. Mater., 2022, 34, 7867–7877.
56. Z. M. Gibbs, H. Kim, H. Wang, R. L. White, F. Drymiotis, M. Kaviany and G. J. Snyder, Appl. Phys. Lett., 2013, 103, 262109.
57. Y. O. Varshni, Physica, 1967, 34, 149–154.
58. I. A. Vainshtein, A. F. Zatsepin and V. S. Kortov, Phys. Solid State, 1999, 41, 905–908.
59. W. He, Z. X. Wang, T. Zheng, L. Y. Wang and S. W. Zheng, J. Electron. Mater., 2021, 50, 3856–3861.
60. P. Shyni and P. P. Pradyumnan, RSC Adv., 2021, 11, 4539–4546.
61. P. Balaz, E. Dutkova, M. Balaz, R. Dzunda, J. Navratil, K. Knizek, P. Levinsky and J. Hejtmanek, ChemistryOpen, 2021, 10, 806–814.
62. B. Bhattacharyya and A. Pandey, J. Am. Chem. Soc., 2016, 138, 10207–10213.
63. W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem., Int. Ed., 2016, 55, 6826–6841.
64. N. Jia, J. Cao, X. Y. Tan, J. F. Dong, H. F. Liu, C. K. I. Tan, J. W. Xu, Q. Y. Yan, X. J. Loh and A. Suwardi, Mater. Today Phys., 2021, 21, 100519.
65. H. Y. Xie, X. L. Su, Y. G. Yan, W. Liu, L. J. Chen, J. F. Fu, J. H. Yang, C. Uher and X. F. Tang, NPG Asia Mater., 2017, 9, e390.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01788e

---