 Open Access Article
Open Access ArticleFirst-principles design of nanostructured electrode materials for Na-ion batteries: challenges and perspectives
Arianna
Massaro
 *ab,
Francesca
Fasulo
*ab,
Francesca
Fasulo
 bc,
Adriana
Pecoraro
bc,
Adriana
Pecoraro
 bc,
Aniello
Langella
bc,
Aniello
Langella
 a,
Ana B.
Muñoz-García
a,
Ana B.
Muñoz-García
 bc and
Michele
Pavone
bc and
Michele
Pavone
 *ab
*ab
aDepartment of Chemical Sciences, Università di Napoli “Federico II”, Compl. Univ. Monte Sant’Angelo, via Cintia 21, 80126, Napoli, Italy. E-mail: arianna.massaro@unina.it; michele.pavone@unina.it
bNational Reference Centre for Electrochemical Energy Storage (GISEL) - INSTM, 50121 Florence, Italy
cDepartment of Physics “E. Pancini”, Università di Napoli “Federico II”, Compl. Univ. Monte Sant’Angelo, via Cintia 21, 80126, Napoli, Italy
First published on 21st June 2023
Abstract
Post-lithium batteries are emerging as viable solutions for sustainable energy transition. Effective deployment in the market calls for great research efforts in the identification of novel component materials and the assessment of related working principles. Computational modelling can be a key player in boosting innovation and development by enabling rational strategies for the design of appropriately tuned materials with optimized activity towards battery operating processes. By gaining access to the structural and electronic features of functional electrodes, state-of-the-art DFT methods can unveil the subtle structure–property relationship that affects the uptake, transport, and storage efficiency. Hereby, we aim at reviewing the research status of theoretical advances in the field of Na-ion batteries (NIBs) and illustrating to what extent atomistic insights into sodiation/desodiation mechanisms of nanostructured materials can assist the development of effective anodes and cathodes for stable and highly performing devices. Thanks to increasing computer power and fruitful cooperation between theory and experiments, the route for effective design methodologies is being paved and will feed the upcoming developments in NIB technology.
1. Introduction
The chance to enable reversible electrical-to-chemical energy conversion is powering the technological progress in a multitude of applications. Rechargeable batteries are among the most sought after electrical energy storage (EES) systems, with the pioneering Li-ion battery (LIB) technology reaching a huge technological and social impact, as evidenced by the recognition through the 2019 Nobel Prize in Chemistry.1,2 Lately, the urgent need for a green economy is pushing the production of sustainable EES systems on a very large scale, and other applications than microelectronics have put battery research in the spotlight.3 The scarce availability and the restricted geographical distribution of lithium and other typical LIB components (e.g., cobalt) are expected to limit the large-scale integration of Li batteries in electric vehicles or stationary electrical grids.4 Energy storage research is currently heading toward creating new options based on cheaper and widespread resources with the general goal of obtaining similar or better performances than state-of-the-art LIBs.5 Thanks to easily available sodium raw materials, Na-ion batteries (NIBs) are among the most valid sustainable alternatives, and the similarities with LIBs have facilitated a rapid development of component materials starting from those already known.6,7 However, most LIB components are not as effective as in Na-analogues: while the size of Na+ helps the diffusion through liquid electrolytes, it hampers a convenient and reversible intercalation into the electrode structure.7–10 The Li-to-Na replacement in many cathodes leads to extremely intertwined electrochemistry, involving unexpected phase transformations upon cycling, while Na+ insertion into state-of-the-art graphitic materials results in largely unstable intercalated compounds.7–10 Thus, the scientific community of chemists, physicists and materials scientists plays an active role in developing novel functional materials for highly performing NIB electrodes. Significant breakthrough has already been achieved by pursuing nano-engineering strategies to improve charge transfer kinetics at the electrode/electrolyte interface.11,12 Lithium-to-sodium transition has been fed with dynamic research advances and fast progress in materials development. To commercialize NIBs as cost-efficient batteries based on abundant elements, specific advantages over LIBs should be attained in the near future in order to face the increasing demand in resource and chains supply. From a scientific and chemical point of view, investigating the efficiency of host electrode materials toward Na uptake and storage and the electrochemical stability of Na conductive electrolyte systems will represent the main contribution. Many challenges that were not conceived for LIBs are actually present for NIBs and should be addressed with the aim of creating new options for future energy storage devices, and this also includes the use of Na in solid-state, metal/air- and metal/sulphur-batteries.The identification of novel materials and an in-depth comprehension of their electrochemical behaviour are crucial steps in the whole production process prior to the ultimate application in real devices. Electrochemical reactions within batteries are complex phenomena, often including undesired and even detrimental processes that determine the overall system performance. In this context, computer-aided design can be extremely beneficial for spanning the atomic-to-macro length scales in order to understand the intertwined physico-chemical processes at play and to gain the desired improvement in stability and performance. With this purpose, computational approaches are widely applied to other energy storage technologies relying on different materials or working processes. The promising Na–S and Na–O2 batteries rely on conversion reactions at the sulphur–carbon composite or oxygen-exposed porous electrode, respectively (i.e., positive electrodes) led by Na ions deriving from Na metal oxidation (i.e., negative electrode). By addressing the stability of common discharge products (short- or long-chain sodium polysulfides, Na2Sx, or sodium oxide, superoxide, and peroxide, Na2O, NaO2 and Na2O2, respectively), and the related feasible reactivity with electrolyte components, first-principles calculations have elucidated the main structure–properties relationship undermining the overall cell capacity and delivered new insights into how to improve shuttle effects, slow kinetics and poor electron conductivity.13–17
At the foundation of any computational approach there are quantum-mechanics (QM) methods that can access the electronic structure of materials and the mechanistic details of sodiation/desodiation at the nanoscale, allowing for a fundamental understanding of redox reactions, ion diffusion, as well as the role of defects along the charging/discharging process.18–21 Advanced electronic structure calculations generally require ab initio techniques and the solution of the appropriate Hartree–Fock equation, which is demanding and usually limits the system size. For most problems, density functional theory (DFT) serves the same purpose with lower computational costs. On the other hand, meso-to-macroscopic scale-based phenomena, such as dendritic growth, microstructuring, or degradation processes, can be addressed via molecular mechanics methods, including force-field and coarse-graining techniques.22–26 Notwithstanding the great advances and the broad literature, major efforts are still required to attain full knowledge of either the component material itself or the heterogeneous electrode/electrolyte interface, where complex charge transfer processes take place during battery functioning. With the advent of multiscale modelling, resolving questions over several length and time scales or exploring how microscopic and macroscopic phenomena are interrelated is rapidly emerging.27 The idea of combining atomistic and macroscopic simulations into a multiscale perspective is at the forefront of theoretical investigations in many fields and will drive the upcoming challenges towards realistic modelling of battery materials and their behaviours. Developing sophisticated force fields able to reproduce charge polarization effects, complex reaction pathways and interfacial structuring and dynamics, have the potential to solve generality, accuracy, and reliability issues.28–33 More recently, Machine Learning potentials trained on QM reference data have offered a valuable alternative to classical interatomic potential fitting, and can be used to explore the associated energy surfaces with comparable accuracy.34–37
The upsurging interest for computational-driven design in the energy storage field can be effectively demonstrated by the increasing number of related publications. Many recent reviews discuss the great challenges that the theoretical chemistry community is currently facing, ranging from the importance of preliminary method validation,38 to the key role of dynamic features and ionic conductivity in assessing both electrode and electrolyte development,39,40 as well as the fundamental understanding of electrode–electrolyte complex interfaces, especially for future exploitation of all-solid-state-batteries.41 Whether setting foundations for advancing in multiscale techniques or delivering fundamental knowledge on electroactive materials, QM-based simulations still represent the driving force towards rational design and offer solid and reliable grounds for investigating reaction kinetics, electrochemical potentials, chemical stability, defects chemistry, and adsorption/dissociation energetics.
In this perspective, we provide an overview of recent works from our laboratory on nanostructured electrode materials addressed by first-principles methods. With these examples we offer a general view on the subtle structure–property-function relationships that directly affect the main processes related to battery functioning and that can be exploited to derive original design principles. Provided that appropriate methods must be considered to face specific theoretical challenges, the application of the DFT framework is proven to offer suitable tools for a large variety of material families. The optimal accuracy/computational cost ratio can be achieved by employing the DFT+U scheme to tightly localized d-electrons (e.g., transition metal oxides, Ueff = 3.3 eV for Ti and Ueff = 4.0 eV for Mn, Ni, Fe and Ru, see Sections 2.1 and 3, respectively) in order to correct the large self-interaction error (SIE),42–45 or the a posteriori DFT-D correction to account for key van der Waals (vdW) interactions in interfaces (Section 2.1) and layered structures (Section 3).46–49 Application of DFT-based state-of-the-art computational protocols is shown to provide insightful details on relevant topics: Na+ intercalation in nanostructured anodes and the related effects of morphology and external electric field (Section 2); charge compensation in high-energy cathodes and the tuneable activation of reversible anionic oxygen redox chemistry (Section 3). By performing spin-polarized DFT-PBE calculations within the generalized gradient approximation (GGA) with projector-augmented wave (PAW) potentials and plane wave (PW) basis sets,50,51 reliable models for solid-state crystalline nanoelectrodes can be obtained with affordable computational efforts (forces accuracy for geometry relaxation: 0.03 eV Å−1; energy accuracy: 10−5 eV). Kinetic energy cutoff and k-points sampling schemes are determined via convergence tests to ensure converged energies within 3 meV f.u.−1. Dipole corrections are applied to slab models when considering surface structures so as to avoid long-range polarization from the periodic images along the c-direction (see Sections 2.1 and 2.2).52 By deriving readily computable descriptors that can be directly compared to experimental data, the reported case studies shed light on the electrochemical behaviour of promising NIB systems and drive future strategies for effective tuning of functional materials.
2. NIB anodes: hybrid and nanostructured materials
In the development of solid-state anodes for Na-ion batteries, the most important requirement is represented by the crystalline structure and its mechanical response to a significant stress, i.e., the Na+ intercalation. The lattice should feature suitable host sites for the large Na+, and the crystalline network must be robust enough to retain its shape upon subsequent Na+ insertion/extraction.53 Anode materials should also exhibit oxidation potentials as close as possible to 0 V vs. Na+/Na. In view of developing high energy density batteries, materials research is confined to those families of negative electrodes which allow sodiation/desodiation at few tenths of volts vs. Na+/Na (e.g., carbon-based materials, metal oxides, alloys).11,54–56 However, the operation of most negative electrodes in the low voltage range may be coupled to electrolyte decomposition and metal plating, disturbing both cycle life and safety. Development of highly stable and durable anode materials usually calls for the need of functionally engineered and protective Solid Electrolyte Interphase (SEI) layers.57,58 The scientific literature in this field has been recently enriched with computational modelling and insights from ab initio simulations. The large variety of proposed materials basically differ for the sodiation/desodiation mechanism. Whether they undergo insertion, conversion, or intercalation processes, the atomistic perspective can supply reliable and affordable models to describe the underlying mechanisms and understand the crucial features. From a general perspective, the anodes exploration is mainly motivated by the ineffective intercalation of Na+ into state-of-the-art graphite, which has led to a broad range of systems, including carbonaceous materials, Na-binary alloys, or conversion reaction anodes. As the limiting factor for the unfavourable intercalation, the weak Na-graphite binding can be effectively overcome by ensuring larger interlayer spacing in hard or soft carbons,59 but also via introduction of various point defects into carbon scaffolds, such as mono-vacancy, divacancy, and Stone–Wales defects.60 The first-principles predictions of voltage profiles and structural evolution upon sodiation have enabled the screening of promising Na-binary alloys with both Group-14 and Group-15 element compounds, such as c-NaxSn, a-NaxGe, a-NaxSi and Na–P species.61,62 By unveiling complex reaction pathways, computational studies have also assisted the development of tricky MaXb phases (M = Sn, Sb; X = O, S, Se). While allowing high specific capacity, these materials usually undergo severe volume expansion upon cycling which still limits their practical applications.53 Recently, hybrid and nanostructured materials have attracted increasing consideration as NIB anode applications owing to tuneable shape, morphology and composition that can give the electrodes boosted sodium storage performance. In the following, we present a few representative studies on emerging anode materials, which have recently exemplified the key role of computational-driven design.2.1 Sodiation process in intercalation anodes: the key role of migration mechanisms
Na+ uptake and storage at the anode interface can occur via adsorption of a Na cation on the surface, followed by its migration through the lattice. Thus, the adsorption energy can be easily calculated as:| Eads = EOUTNa@host − Ehost − ENa | (1) |
| Eins = EINNa@host − Ehost − ENa | (2) |
| Emigr = ENaTS − EOUT/INNa@host | (3) |
In the context of NIB anodes, many research efforts are focused on the applications of carbonaceous materials as sustainable and electroactive systems. Given the successful employment of graphite anodes in LIBs, great attention has been paid to disordered hard carbons or graphite-like soft carbons, exposing a porous surface area with a more appropriate layered structure for Na+ uptake and storage.65 The reported sodiation activity is generally good, but some improving strategies can be pointed out thanks to first-principles studies. For example, Tsai et al. have highlighted the role of vacancy defects in favouring the Na intercalation capability thanks to the enhanced Na+-vacancy ionic binding interactions.60 Alloy formation represents another possible route, especially when enabled by the use of low-cost silicon-based materials exhibiting very high specific capacity (954 mA h g−1).66 Huge volume variations usually represent the main drawbacks, but they are minimized in an NaxSi24 allotrope that cycles in a single-phase regime without any nucleation, as unveiled from DFT investigations.67 Migration analysis performed with CI-NEB has also identified the constrained relaxation of the eight-member silicon ring as the limiting factor in Na mobility when moving from a dilute to concentrated regime.67 Few works are also dedicated to germanium based alloys, where ab initio molecular dynamics simulations have reported the full amorphization occurring after earlier Na clustering at low sodiation as the main driving force for enhanced diffusivity compared to crystalline samples.68 With silicon-based materials often suffering from unbearable volume change, a combination with more robust C-based materials has appeared as a promising solution. Sodium migration along the z-direction in silicon–carbide (Si–C) exhibits a minimum energy barrier compared to other lattice directions, which can be further lowered via vacancy introduction.69 As reported by Dhillon et al., numerical simulations can also be insightful: the capacity fading in silicon–graphite composite electrodes seems to be induced more by Si cracking upon cycling rather than the SEI layer growth, and this effect can be prevented by varying the ratio of graphite and silicon accordingly.70 Application of C-based materials is also key in organic batteries, where DFT methods have been applied to predict crystalline structures or redox mechanistic details.71 Graphene also represents a highly pursued material in the battery field, especially in combination with other systems, as electron buffer and robust mechanical support.72 Creating hybrid interfaces to 2D transition metal dichalcogenides (TMDCs) with tuneable interlayer spacing could provide the anode material with the desired intercalation structure for Na ions.73 Fabrication of MoS2/graphene anodes via easy and low-cost processes has led to high-quality and efficient materials, but dissecting the role of each component or the interface still represents a crucial point.55,74 Wang et al. showed how interconnected 3D carbon networks in MoS2/C superstructures are responsible for improving electron transport and Na+ diffusion, while retarding the volumetric strain effect of MoS2.75 In a recent study from our group, we addressed the effects of MoS2 phases on Na intercalation and migration properties.76 Our dispersion-corrected DFT analysis showed that both 3R- and 1T-MoS2/graphene result in electronically conductive heterostructures featuring a graphene-to-MoS2 charge transfer, which would make the MoS2 more prone to interact with the intercalating Na ion.76 Among the multitude of intercalation sites, the overall adsorption energies suggest stronger Na–MoS2 interaction for the 1T case, which correlates with the increased stability of this phase when exfoliated in the presence of alkali metals.77 By considering migration pathways within the interlayer spacing, Na can move along the x direction, where the S atoms pointing toward the interlayer spacing seem to form an appropriate diffusion channel, with the reaction coordinate being the Na–Na distance after each Na jump, i.e., ξ (see Fig. 1). Sodium migration in MoS2/graphene heterostructures has been extensively addressed, either in bulk or freestanding MoS2, graphene sheets, as well as on graphene-supported MoS2 monolayers.78–82 Our results allowed us to conclude that the interlayer mechanism exhibits the lowest barrier, thus representing the more convenient option for Na mobility (from our results: Emigr ∼0.17–0.22 eV for 3R-MoS2/graphene and ∼0.08 to ∼0.70 eV for 1T-MoS2/graphene, calculated according to eqn (3)). The diffusion mechanism has been also coupled to the enlargement of the interlayer spacing occurring upon Na+ passage from the minimum- to the highest-energy structure, and the effect is more relevant in the 1T phase (i.e., from 3.11 Å to 3.70 Å, vs. from 3.35 Å to 3.76 Å in the 3R phase).
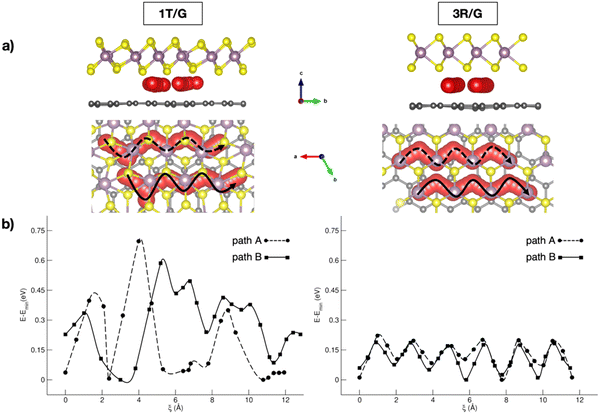 | ||
| Fig. 1 (a) Side and top views of Na migration pathways through 1T- and 3R-MoS2/G interfaces; (b) corresponding energetics computed with the CI-NEB method at the PBE-D3BJ level of theory. Reproduced from ref. 76 [A. Massaro et al., J. Phys. Chem. C, 2021, 125, 2276–2286]. Copyright 2021 American Chemical Society.76 | ||
In the development of 2D-hybrid systems, understanding the role of possible polymorphs, interlayer spacing or interfacial features in determining the overall electrochemical performance of MoS2/graphene-based electrodes can be crucial. With migration mechanisms at the 2D heterojunction being unveiled from first principles, experimental works can set up specific synthesis pathways (e.g., phase-selected and defects-engineering syntheses) and preparation procedures (e.g., interlayer expanded interfaces) toward more functional products.83–85
Titanium oxides are also capable of reversibly intercalating Na at low redox potentials. Starting from the structural lithium analogue, the rock salt-type Na2Ti3O7 has been proposed as NIB anode.86 Computational studies have compared Li2Ti3O7 and Na2Ti3O7 performances in terms of lattice evolution upon lithiation/sodiation. The difference in intercalation potentials (∼0.7 V) can be ascribed to different ionic sizes and polarizing features, leading to different stabilization or volumetric effects.87 Still, the self-discharge phenomena observed for Na2Ti3O7-based devices has been attributed to a large electrostatic repulsion computed for the discharged state, i.e., Na4Ti3O7, leading to structural instability and an increase in the Gibbs free energy.88 TiO2 is a versatile functional material with several applications, ranging from solar cells to photocatalysis and batteries. In the form of anatase, TiO2 shows comparable performances to graphitic materials in LIBs, such as high reversible theoretical capacity (335 mA h g−1), low volume variation upon cycling (less than 4%), and improved safety thanks to the structural robustness and high working potential.89 However, the performances of anatase nanoparticles (NPs) as negative electrodes in NIBs seem to depend on the exposed surfaces, the (100) and (001) facets being much more effective than the most stable (101) surface.54 Yang et al. have tried to explain the surface-dependent activities by means of bare adsorption properties, but the predicted trend did not match the observed activities.90 The simple Na–TiO2 coverage is not a complete nor reliable model for this kind of interface, where each surface acts as a Na+ insertion site exhibiting pseudocapacitive behaviour.54 In a recent work by our group, Na+ insertion through the (101), (100) and (001) TiO2 anatase surfaces has been addressed to prove the mechanism and the origin of observed selectivity toward Na+ uptake.91 Sodium migration can be defined as occurring between adsorption sites lying on top of surfaces and insertion sites in the subsurface layer along the [010] Na+ diffusion channel (see Fig. 2).92 The spatial coordinate along a migration pathway, ξ, is given by the Na–Na distance between two contiguous points acting as possible interstitial sites for ion accommodation and lying along suitable-sized diffusion channels. Sodium moves along a given direction in the lattice, passes across the alternating Ti–O motif, and then enters the cavity in the subsurface along the [010] diffusion channel. Migration analysis derived by the CI-NEB approach revealed that the (001) surface exhibits the lowest energy barrier in both forward and backward directions (i.e., OUT/IN Emigr, calculated according to eqn (3)), suggesting that Na migration will be more likely to occur at this termination compared to (100) and (101).
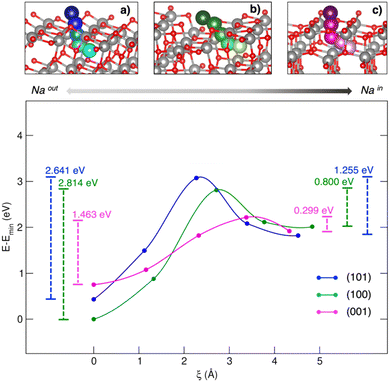 | ||
| Fig. 2 Minimum energy paths (top) and corresponding energetics (bottom) for Na migration through the (a) (101)-, (b) (100)- and (c) (001)-TiO2 anatase surfaces. Energy barriers calculated from eqn (3) for the out/in migration are reported, respectively, at the left- and right-hand sides of the graph. Reproduced from ref. 91 [A. Massaro et al., Nanoscale Adv., 2020, 2, 2745] with permission from the Royal Society of Chemistry.91 | ||
The need for morphology-controlled production of TiO2-based electrodes was already established in recent literature,54,90,92 and is still feeding this research topic.93 Having reliable surface models to describe sodiation at anatase interfaces is essential to provide insightful details on possible elements (e.g., exposed surfaces, contact area, point defects) that may affect the Na+ storage mechanism.
2.2 New frontiers towards realistic simulations: the effects of an applied electric field
The studies reviewed so far highlighted the key role of theory in unveiling determining factors towards sodiation mechanisms of nanostructured anode materials. However, achieving accurate predictions by means of reliable models still represents a major challenge in computational chemistry applied to energy storage. On one hand, simple models allow to gain interesting insights with little computational efforts, but they might be too far from the real device and other relevant information may not be detected. One example is given by the description of the sodiation process under electric field control. The battery operation takes place in a certain voltage range, under the passage of an electric current. A realistic model should therefore not neglect the effect of an electric bias applied to the materials under investigation, in order to overcome possible misinterpretations of thermodynamics and kinetics predicted by conventional DFT approaches encompassing 0-K, in-vacuum and equilibrium conditions. Although many field-related properties, including contact potentials or interfacial electric fields across SEI films, would require the quantitative application of such pioneering methodologies, the qualitative association of field polarization to specific processes can already provide new insights and pave innovative routes into this fundamental research area.94,95 In this context, we have addressed the electric field effects on Na intercalation energetics as well as on structural and electronic properties of anatase surfaces.96 The electric field is simulated in the direction perpendicular to the surface models by adding a sawtooth-like electrostatic potential to the bare ionic potential.97 Positive and negative polarization can be considered, depending on whether the field lies in the same or opposite direction of the z-axis, thus giving a positive or negative slope, respectively. As illustrated in Fig. 3, insertion energies are essentially unchanged with the applied field, and minor structural modifications may be due to the high screening effects exerted by the surface layer. However, the field polarization does affect adsorption values and alters the IN–OUT gap. In particular, the positive field enlarges the energy gap for all the explored surfaces, while the negative one results in smaller differences (blue and red lines, respectively, in Fig. 3). Positive/negative directions lead to opposite effects, stabilizing the NaOUT sites further/closer to the surface and promoting the oxidation/reduction of Ti sublattice.96 Field polarization can therefore be thought as the bias direction that is present during battery cycling and accounts for the desodiation/sodiation of the anodic electrode upon discharge/charge (e.g., the negative one favouring Na intercalation and leading to the reduction of Ti sublattice is representative of sodiation reaction upon charging). Thanks to the inclusion of electric field effects into DFT simulations, the theoretical investigations on electrode interfaces can make significant steps forward in modelling in operando conditions, thus improving the current understanding of electrochemical reactions at NIB electrodes.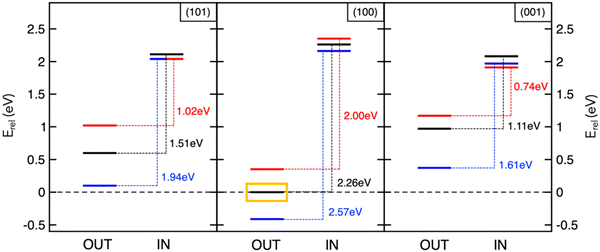 | ||
Fig. 3 Insertion and adsorption energetics for NaIN and NaOUT states at TiO2 surfaces calculated at the PBE+U level of theory. All the energy values, Erel, refer to Na-adsorbed on the (100) surface with zero-field (yellow box). Colour code: zero-field (black lines), positive field, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) × 103 = 5 Ha (blue lines), and negative field, × 103 = 5 Ha (blue lines), and negative field, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) × 103 = −5 Ha (red lines). Reproduced from ref. 96 [F. Fasulo et al., J. Mater. Res., 2022, 37, 3216–3226]. Copyright © 2022, The Authors.96 × 103 = −5 Ha (red lines). Reproduced from ref. 96 [F. Fasulo et al., J. Mater. Res., 2022, 37, 3216–3226]. Copyright © 2022, The Authors.96 | ||
The screening and predictive power of computational modelling can lead to high-impact outcomes that can drive the rational design of efficient materials. For example, further analysis performed in these case studies reveals that the Na storage activity in MoS2/graphene heterostructures and TiO2 anatase nanoparticles is ascribed to the intrinsic structural features of the electrodes. Na+ migration barriers at the MoS2/graphene interlayer spacing are associated to variations in the Na–S coordination when the transition state is reached, the effect being more relevant for the 1T phase compared to the 3R counterpart.76 The single jump is more likely to occur when Na is further from sulphur atoms, thus the local structuring affects the sodium diffusion mechanism. Introducing S vacancies or tuning and nanoengineering the morphology of the MoS2 phase can lead to promising design strategies aiming to reduce the Na–S hindering effects and enhance the overall mobility. Still, structural modifications occurring in the anatase surfaces upon Na migration can account for the different activities.91 The size of the surface lattice window, i.e., the minimum accessible area that Na+ should cross to enter the TiO2 crystalline structure, at the transition state (NaTS), provides a direct measure of the steric hindrance that the migrating Na encounters along its path. This quantity can be calculated straightforwardly from the shortest Ti–Ti distance at the transition state structure (NaTS).91 Defined this way, this descriptor inversely correlates with the barrier heights: the largest lattice window is associated to the lowest migration barrier for the (001) surface (see Table 1). As a matter of fact, the surface lattice windows get larger upon the effect of the negative field. Preferential use of (001)-containing NPs can be exploited to develop more efficient anatase-based NIB devices.
| System | a min (zero-field) |
a
min (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) × 103 = 5 Ha) × 103 = 5 Ha) |
a
min (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) × 103 = −5 Ha) × 103 = −5 Ha) |
|---|---|---|---|
| (101)-TiO2 | 8.60 | 8.58 | 8.64 |
| (100)-TiO2 | 8.71 | 8.68 | 8.73 |
| (001)-TiO2 | 15.14 | 14.83 | 15.14 |
Notwithstanding these insightful outcomes, the rational design of efficient electrodes should not disregard the role of interfaces and the underlying processes: from charge transfer to migration/diffusion properties and interphase formation, up to the interfacial stability over the entire battery lifetime. It is widely recognized that almost all fundamental properties cannot be ascribed to the sum of the single components. Today, the interest in interface studies is rising from both theoretical and experimental communities, as established by an increasing number of scientific reports.95,98 However, major computational challenges still need to be confronted to gain a full description of interfacial processes that usually occur across multiple lengths/timescales.57,99 Herein, we have reported a preliminary attempt to include electric fields into the simulation environment, which would represent a viable way to consider more realistic electrochemical interfaces and the underlying modifications under electric field control.96 The development of a unified workflow that intimately combines different techniques will be critical to enable this paradigm shift in battery design.
3. NIB cathodes: high-energy layered oxides
The development of high-energy, cheap, and structurally stable NIB positive electrodes operating at voltage values in the order of 4.5 V (or even above) represents a Grand Challenge because it is the cathode that mainly affects the battery performance and manufacturing costs. Polyanion materials, organic compounds and layered oxides undoubtedly represent the mostly investigated systems, whose peculiar features responsible for Na ordering, diffusion, and phase transformation, have been recently addressed and unveiled by computational studies. The ab initio determination of Na migration channels and the effect of antisite defects has enabled the optimization of efficient NaxFePO4 and NaxMnPO4 olivine structures.100,101 By means of GGA+U methods, incorporation of highly electronegative F ions into phosphate-based materials has been shown to enhance the cathode voltage, and also lead to a robust crystalline lattice with facile 2D Na diffusion pathways.102 Pioneering AIMD and NEB simulations on V-based fluorophosphates have then unveiled the interplay of Na and anion sublattice disordering as well as TM mixing to facilitate Na diffusivity within Na3V2(PO4)2F3 (NVPF) systems.103,104 Recent works have been devoted to heavy metal-free organic compounds, which would meet sustainability and environmental friendliness requirements. Theoretical challenges in the investigation of these materials (i.e., disodium rhodizonate, benzoquinone derivatives, polyaniline (PANI), and tetracyanoethylene (TCNE)) include the subtle atomistic structure predictions.105–107 The emergence of layered transition-metal oxides, NaxTMO2 (0 < x < 1), dates to the wide employment of LiCoO2 in pioneering LIB prototypes.108 However, the simple replacement with NaCoO2 is impracticable due to critical phase transformations occurring upon desodiation, and the replacement with Mn- or Fe-based compounds also occurred for sustainability purposes.109,110 The strong synergy of computational work with experimental studies drives major advances in the design of layered oxides as high-energy NIB cathodes, aiming to explore new classes of functional compounds while gaining a fundamental understanding that underpins applied research.111As in Li counterparts, the crystalline structure of NaxTMO2 alternates planar layers of alkali metal ions and edge-sharing TMO6 octahedra, where Na ions can easily move in and out upon cycling.112 Among many polymorphs differing for stacking and internal symmetry, P2 and O3 (prismatic/octahedral sites for Na ions and 2/3 TMO2-layers in the unit cell) phases are the most interesting for battery applications, showing different specific capacities, structural stability, and rate performances.113 The charge/discharge operation can be considered as the shuttling of a certain fraction of Na ions, the driving force being the difference in the sodium chemical potential in the two electrodes. During discharge, the cathode material (low sodium chemical potential) is electrochemically reduced by intercalating Na+ from the electrolyte and taking up electrons from an external circuit; simultaneously, the anode material (high sodium chemical potential) is oxidised. The overall reaction for a cell comprising a sodium transition-metal oxide intercalation cathode with NaxTMO2 composition and a Na metal anode would be:
| Nax1TMO2 ⇄ Nax2TMO2 + (x1 − x2)Na | (4) |
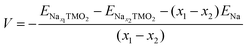 | (5) |
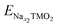 and ENax1TMO2 are the total energies of NaχTMO2 at, respectively, x2 and x1 Na composition (x1 > x2), and ENa is the total energy of one sodium atom inside the Na metal bcc unit cell.63 The ratio and chemical nature of TM composition sensibly affect the phase stability and structural retention during subsequent Na insertion/extraction from the layered lattice.110
and ENax1TMO2 are the total energies of NaχTMO2 at, respectively, x2 and x1 Na composition (x1 > x2), and ENa is the total energy of one sodium atom inside the Na metal bcc unit cell.63 The ratio and chemical nature of TM composition sensibly affect the phase stability and structural retention during subsequent Na insertion/extraction from the layered lattice.110
3.1 Charge compensation mechanisms upon desodiation unveiled from first principles
The electrochemical behaviour also depends on the involved TM redox couples, as the cathode sodiation/desodiation is compensated by the reversible reduction/oxidation of TM ions. How the chemical composition at the TM site determines the physical-chemical properties as well as the electrochemical response is decisive for the performance, but very challenging to predict.115 Great efforts can be found in recent literature, where computationally derived descriptors serve as useful tools to predict the main properties from the chemical structure. One example is the cationic potential postulated by Zhao et al., able to capture the key interactions of layered materials and make it possible to predict the stacking structures and the functional properties.116 By employing DFT calculations to derive the average voltage, volume change and Na ion mobility, the screening method developed by Zhang et al. demonstrates how most promising candidates can be selected from the materials project database.117 The vital role of theoretical investigations is also attested by the new insights gained in understanding the anionic redox activity, i.e., the charge being stored not only by the TM cations but also by the oxide sublattice. This represents a new highly pursued paradigm for research and development of advanced cathode materials, pushing the theoretical specific capacity beyond the fixed limits of TM redox potentials. Whether anionic-redox active materials can accomplish a fully reversible process or undergo O2 loss remains an open question. Which factors can drive the stabilization of oxygen electron holes and preserve the reversible activity upon subsequent cycling? In many Li-rich oxides with O3 stacking, O2 release has often been associated with TM migration from the TMO2 layer to the alkali metal one. DFT calculations performed by Wang et al. have shown that this kind of interlayer migration can safely be excluded in the O3-NaLi1/3Mn2/3O2 phase.118 While Mn cations are greatly stabilized in the interlayer space of pure-Li phases, the presence of Na+ in the alkali layer imposes a too large c parameter, and Mn migration from the metallic to the alkali layer is therefore less favoured. Li+ displacement towards the alkali layer upon first Na+ deinsertion promotes the switching from inter- to intra-layer migration of Mn cations, preventing any voltage fade.118 Anionic redox mechanisms can be intertwined, especially when electrochemical cycling leads to phase transformation. Vergnet et al. have unveiled the voltage hysteresis of NaxMg1/3Mn2/3O2 from first principles, by revealing the competition between a reductive coupling mechanism occurring in P stacking, which is quite reversible, and a disproportionation of oxygen network into peroxo-like pairs and oxo-like atoms in the O stacking, inducing migrations that facilitate oxygen release and entail structural instability.119 The first-cycle voltage hysteresis has also been associated to superstructural ordering in Na0.75[Li0.25Mn0.75]O2, where the most present honeycomb superstructure is lost on charging due to Mn migration that changes the coordination around O2− and lowers the voltage on discharge.120 As supported by DFT investigations, the ribbon superstructure in Na0.6[Li0.2Mn0.8]O2 inhibits manganese disorder and promotes stable electron holes on O2−, hence suppressing O2 formation and voltage hysteresis.120 Ben Yahia et al. have used the electron localization function as a holistic tool to locate the oxygen lone pairs in the structure and follow their participation in the redox activity of layered oxides.121 They propose the charge-transfer gap as the pertinent observable to quantify the amount of extra capacity achievable in charge and its reversibility in discharge. The idea of electron localization around oxygen ions is also present in the work by Zhao et al., where it is shown to be favoured by Ti substitution leading to facilitated charge-transfer reaction for oxygen redox.122 Clearly, the analysis of electronic structure can establish the energy levels positioning and allow the evaluation of several redox mechanisms. In early-TM-based oxides, O 2p states lie well below the TM d states, and the TMs mainly undertake the burden of the redox reaction. As going from early to late transition metals, the increased electronegativity enables larger overlapping between TM d and O p states, allowing the oxygen electron density to directly participate in the charge compensation.123 In Li-rich oxides, i.e., the alkali ion being present in both the alkali and TM layers, the O 2p orbitals overlap with the Li 2s orbitals and form Li+–O–Li+ interactions. The ionic nature of these interactions places the nonbonding O 2p states at the top of the valence band, which engage in anionic redox activity.124 Maitra et al. reported that the presence of excess alkali metal is not necessary to trigger oxygen based processes, which can also take place in Na2/3[Mg0.28Mn0.72]O2 displaying Mg ions in the TM layer.125 Charge compensation occurring along desodiation can be unveiled from electronic structure analysis performed as a function of Na content. Fig. 4 shows the trend of magnetization in each element sublattice for NaxNi0.25Mn0.68O2, where the Mn4+ oxidation state is essentially retained, while desodiation induces Ni2+ →Ni3+ and then →Ni4+ oxidation (Fig. 4a and b, respectively), in agreement with the literature.126,127 The interested reader may be redirected to our previous work, where the oxidation trends are also confirmed by the TMO6 octahedral distortion, with constant Mn–O pattern and shortening of Ni–O bonds along desodiation being associated to Jahn–Teller like effects.128 The PDOS reported in Fig. 4c suggests a strong hybridization of TM d states with O p ones, leading to the highly covalent character of the TM–O bond, which would explain the resulting charge values far from the ionic limit (see Fig. 4d). However, a net variation of oxygen charge is still evident, and the formation of electron holes on oxygen atoms can also be evinced from the increased magnetization to ∼0.3 μB at xNa = 0.25 and up to ∼0.5 μB at xNa = 0.125. As also reported by Zhao et al. for the closely related Na10−xLiNi3Mn8O24 layered oxide, electron extraction would take place from Ni 3d states upon charge, and O 2p states start to participate at high desodiation degrees.129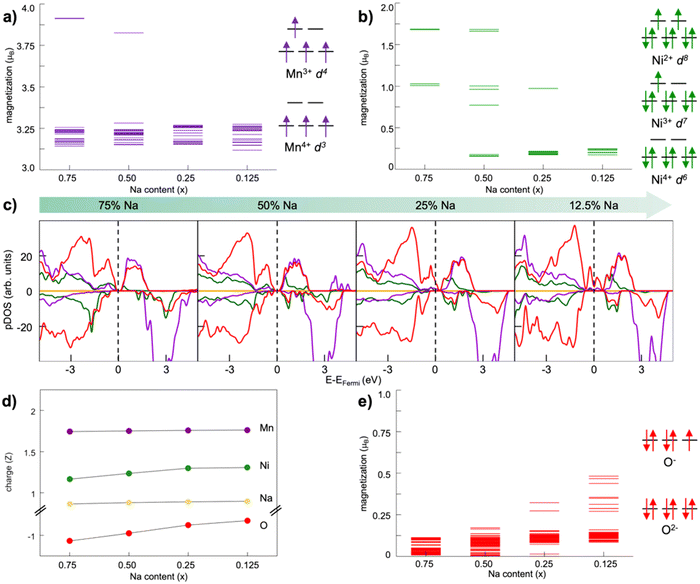 | ||
| Fig. 4 Electronic structure analysis of NaxNi0.25Mn0.68O2 as a function of Na content: net magnetic moments on Mn (a) and Ni (b) species, with the corresponding electronic configuration on the side; (c) atom- and angular momentum-pDOS computed at the PBE+U(-D3BJ) level of theory; (d) Bader charge analysis reported as the average charge for each element; (e) net magnetic moment on O atoms with corresponding electronic configuration on the side. Colour code: Na s states, yellow; Mn d states, purple; Ni d states, green; O p states, red. Reproduced from ref. 128 [A. Massaro et al., ACS Energy Lett., 2021, 6, 2470–2480]. Copyright 2021 American Chemical Society.128 | ||
3.2 The subtle balance between high voltage and reversible capacity: the importance of anionic redox chemistry
Oxygen redox activity can involve dimerization reactions, as experimentally observed but also computationally demonstrated.123,130–132 Herein, the stabilization of oxygen dimers is key to endorse reversibility, and is shown to be managed via covalent TM substitutions.123,130,131 For example, the surface lattice densification following oxygen release in Na2/3Ni1/3Mn2/3O2 and associated to large irreversible capacity loss was shown to be suppressed by Fe substitution.133 The formation of dioxygen species at high voltage has been addressed in our group for the Mn-deficient phase of P2-type NaxNi0.25Mn0.68O2 layered oxides, where rational TM doping has been implemented at the Ni site.128,134,135 The use of TM-defective oxides has attracted great consideration as a viable strategy to activate the anionic redox and thus enhance the specific capacity of layered oxides due to the emergence of nonbonding O 2p states.136 However, the presence of a TM vacancy in the bulk lattice can represent a suitable site to accommodate the reactive oxygen species resulting from uncontrolled anionic redox. In principle, oxygen atoms can move from their regular positions in the crystalline lattice and form partially oxidized species (i.e., peroxo-, superoxo-like) which can be accommodated near the Mn vacancy. The corresponding formation energy of the TM–O2–TM intermediate, i.e., the dioxygen binding to nearby TM atoms, can be computed as:| ΔE = ETM–O2–TM − ENaxTMO2 | (6) |
 | ||
| Fig. 5 Dioxygen formation in NaxNi0.25Mn0.68O2: (top) top-view of A–D structures and (bottom) dioxygen formation energetics identified at (a) xNa = 0.25 and (b) xNa = 0.125. Colour code: Ni, green; Mn, violet; O (lattice position), red; O (dioxygen position), orange; the yellow circles highlight the initial positions before dioxygen formation. Only atoms around the dioxygen complex are shown for clarity. Reproduced from ref. 128 [A. Massaro et al., ACS Energy Lett., 2021, 6, 2470–2480]. Copyright 2021 American Chemical Society.128 | ||
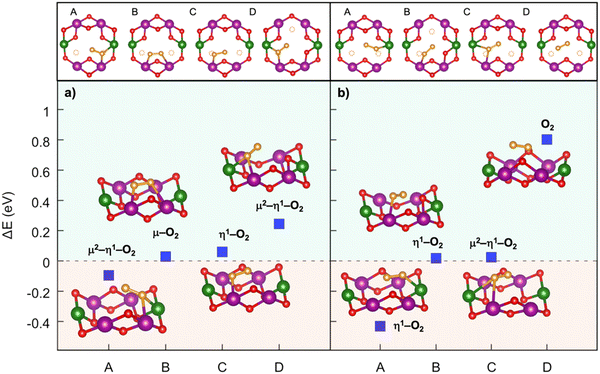
Implementing a stronger covalent nature for the TM–O bond via tailored substitution at the Ni site can represent an effective design strategy for reversible high-energy cathodes. Starting from promising evidence in the literature, Fe- and Ru-doping at the Ni site can be investigated.133,139 On one hand, recent reports on Fe-doped NaxTMO2 cathodes show enhanced and reversible specific capacities that are imputable to oxygen redox with no detection of gaseous O2.133 On the other hand, the presence of Ru in Li-rich materials is known to accomplish the reversible access of oxygen redox: the electronic signatures of reversible O–O coupling in Li2−xRuO3 represent direct evidence of lattice oxygen redox activated at high voltage, and the oxygen dimerization mechanism in Ru-doped Li2TMO3 is shown to be hampered compared to other TM doping.140–142 While Fe-containing oxides would also meet the low-cost and sustainability requirements,110 it is crucial to balance the amount of Ru employed with the overall possible benefits. High cycle stability has also been reported for Na-rich Na2RuO3, where not only the honeycomb superstructure ordering, but also the presence of Ru plays a direct role in suppressing O2 release.143 From these considerations, dioxygen formation has also been addressed in NaxFe0.125Ni0.125Mn0.68O2 and NaxRu0.125Ni0.125Mn0.68O2 at low Na contents (see Fig. 6). The dimerization leads to superoxide species (dO–O ∼1.26–1.37 Å for Fe-doped and 1.28–1.32 Å for Ru-doped) binding the TM atoms in bridging or binuclear bridging coordination modes. At xNa = 0.125, the NaxFe0.125Ni0.125Mn0.68O2 cathode exhibits the most stable superoxide (ΔE = −0.197 eV) formed via breaking of the Ni–O bond. Panel b of Fig. 6 highlights the role of Ru in dioxygen formation, which can only be unfolded at xNa = 0.25 as lower Na compositions are tricky to model and predict.139 Dimerization via Ru–O bond breaking is the most unlikely mechanism, leading to the highest-energy Mn–O2–Ni configuration with ΔE = 3.283 eV and to the unfeasible Mn–O2–Mn that actually restore back the strong Ru–O bond to form the same Mn–O2–Ru structure with ΔE = 1.732 eV. Conversely to the undoped NaxNi0.25Mn0.68O2, the release of molecular O2 is not predicted for the NaxFe0.125Ni0.125Mn0.68O2 and NaxRu0.125Ni0.125Mn0.68O2, thus proving the crucial role played by Fe and Ru in stabilizing the partially oxidized oxygen sublattice. The rather small amount of Fe/Ru doping seems to introduce the essential mild TM–O bond strengths that prevent the O2 evolution while still enabling the activation of anionic redox processes via the formation of potentially reversible superoxide species. In this way, not only extra specific capacity can be achieved, but it can also be recovered upon subsequent charge/discharge cycles since O2 release is suppressed or at least reduced.
 | ||
| Fig. 6 Formation of dioxygen species in the Mn-deficient site of (a) Na1/4Fe1/8Ni1/8Mn3/4−yO2 and (b) Na1/4Ru1/8Ni1/8Mn3/4−yO2. Corresponding formation energy, ΔE, computed according to eqn (3) at PBE+U(-D3BJ) are also reported. Colour code as in Fig. 5, O atoms at dioxygen positions are depicted in brown, Fe in blue and Ru in cyan. Reproduced from ref. 134 [A. Massaro et al., J. Am. Ceram. Soc., 2023, 106, 109–119]. Copyright ©2000–2022 by John Wiley & Sons, Inc.134 Reproduced from ref. 135 [A. Massaro et al., ACS Appl. Energy Mater., 2022, 5(9), 10721–10730]. Copyright 2022 American Chemical Society.135 | ||
The determination of dioxygen migration barriers may be relevant to obtain insightful predictions on the fate of oxygen evolution and assess the lattice role in activating and controlling the oxygen redox at the bulk state. However, multiple reaction pathways arising from such complex chemical frameworks (NaxTMO2, TM = Mn, Ni; Mn, Ni, Fe; Mn, Ni, Ru) lead to highly demanding calculations which will be addressed in the future. It is worth mentioning that comparison with more accurate hybrid-DFT methods would be recommended due to the poor GGA-PBE prediction on O2 energy, and the interested reader is referred to the dedicated benchmark studies.118,123,128
3.3 Design principles towards highly effective cathodes: predicting oxygen evolution
The mechanism underlying dioxygen formation is sensitive to the chemical environment (e.g., metal atoms that are involved upon breaking and formation of TM–O bonds). Indeed, very different outcomes are obtained with Ni-, Ni/Fe- and Ni/Ru-containing TM oxides. The intense debate in the literature on activation and control of oxygen-based redox in layered NaxTMO2 seems to agree in identifying the TM–O bond strength as a key factor which tuning strategies may be referred to. This property can be easily quantified in terms of oxygen vacancy formation energies: the lower the formation energy of a given VO, the easier the tendency to break the involved chemical bonds. In a layered NaxTMO2, the reaction leading to the removal of one oxygen atom and thus to an O-defective material can be written as: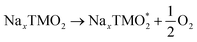 | (7) |
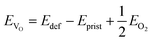 | (8) |
| xNa | VO(2c) Mn/Mn | VO(2c) Mn/Ni | VO(3c) Mn/Mn | VO(3c) Mn/Ni |
|---|---|---|---|---|
| 0.75 | 1.866 | 2.623 | 3.204 | 3.443 |
| 0.50 | 1.944 | 1.447 | 2.865 | 2.858 |
| 0.25 | 1.515 | 1.079 | 2.454 | 2.587 |
| 0.125 | 1.077 | 0.114 | 2.537 | 2.390 |
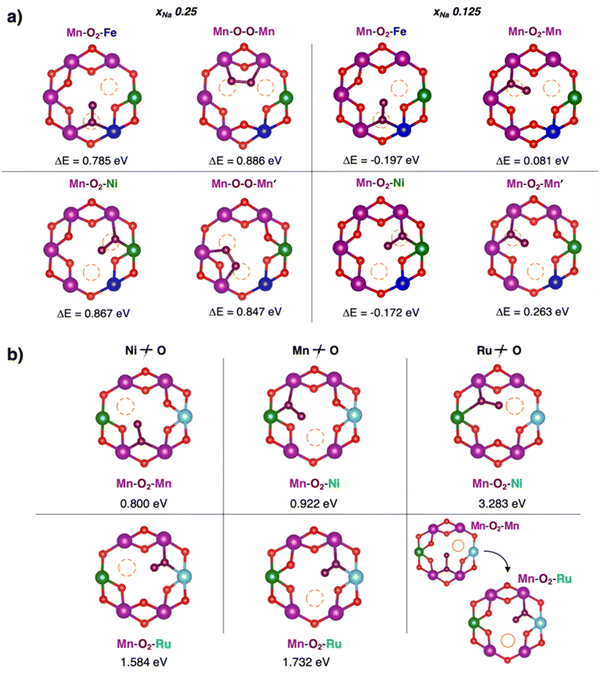
Different kinds of twofold and threefold coordinated oxygen vacancies are then compared for the undoped material, NaxNi0.25Mn0.68O2, and the two doped ones, NaxFe0.125Ni0.125Mn0.68O2 and NaxRu0.125Ni0.125Mn0.68O2, at χNa = 0.25 (see Table 3). Formation energies for VO(2c) exhibit an altered trend: besides the Mn/Ni configuration showing the lowest EVO values in all materials, the effect of Ru doping is opposite compared to Fe, leading to EVO (Mn/Ru) > EVO (Mn). While Fe doping introduces mild TM–O covalency conditions, the presence of Ru atoms results in a significant strengthening of the chemical bond. The doping effects on the VO(3c) are more intertwined: removal of an oxygen atom is more difficult not only from Ru-, but also from Ni-containing configurations (EVO (Mn/Ru, Mn/Ni) > EVO (Mn)). On the other hand, Fe-doping always results in lowering the formation energies. In the most heterogenous site (i.e., Mn/Ni/Ru), Ru and Ni seem to play a synergic effect that results in a higher EVO compared to EVO (Mn). Conversely, the EVO for Mn/Fe and Mn/Ni/Fe in NaxFe0.125Ni0.125Mn0.68O2 are always lower than Mn and Mn/Ni ones, suggesting that the opposite effect of Ru doping compared to Fe is even exerted in the stabilization of the oxide moiety in a Ni-containing site.
| VO(2c) | Mn | Mn/Ni | Mn/Fe | Mn/Ru |
|---|---|---|---|---|
| NNMO | 1.515 | 1.079 | — | — |
| NFNMO | 1.587 | 1.152 | 1.397 | — |
| NRNMO | 1.404 | 1.101 | — | 2.498 |
| VO(3c) | Mn | Mn/Ni | Mn/Fe | Mn/Ru | Mn/Ni/Fe | Mn/Ni/Ru |
|---|---|---|---|---|---|---|
| NNMO | 2.454 | 2.587 | — | — | — | — |
| NFNMO | 2.635 | 2.335 | 1.899 | — | 1.634 | — |
| NRNMO | 2.435 | 3.328 | — | 3.121 | — | 2.983 |
We should recall that similar dopants (i.e., Mn, Ni, Fe, and Ru) have been extensively investigated in LIB counterparts and are currently sought after for next-generation K-ion batteries (KIBs).147–149 A superior performance has been reported for Mn- and Fe-rich layered oxides, which would also meet the sustainability requirements necessary for post-lithium technologies. Nickel incorporation is always beneficial to the overall energy density, thanks to the decreased Jahn-Teller distortion within the dominant Mn sublattice, while the presence of Ru has also been associated to improved structural support.147–149 Research on layered oxides has taken great advantage from earlier efforts and discoveries as LIB cathodes, granting the rational development of novel positive electrodes on a fast-track. Fundamental understanding of structural retention, phase evolution, charge compensation mechanisms, reversible capacity, and high-voltage behaviour in these materials has endorsed significant remarks that are widely applicable to either Na- or K-based counterparts.
These new insights into anionic redox activity highlight simple descriptors able to predict the oxygen evolution from a certain structure and the critical state of charge for irreversible material degradation. The charge compensation mechanism driven by partially oxidized oxygen atoms and suggested by experiments is unfolded by means of readily computable quantities, such as oxygen vacancy formation and TM–O2 coordination energy. These findings can be used to prevent O2 release and improve the efficiency of high-energy cathodes able to recover the extra specific capacity upon subsequent cycling.
The broad theoretical literature on layered oxides is closely intertwined with experimental investigations. On one hand, the in-depth understanding of structural evolution and anionic redox is effectively enabled by atomistic simulations and electronic structure methods. On the other hand, direct connection to experimental data is required to ascertain a reliable description of complex and intricate chemical features evolving upon the electrochemical sodiation/desodiation. After appropriate validation with experiments, our theoretical remarks on NaxNi0.25Mn0.68O2, NaxFe0.125Ni0.125Mn0.68O2, and NaxRu0.125Ni0.125Mn0.68O2 shed light on charge compensation mechanisms upon desodiation and anionic redox processes that are directly related to the electrochemical behaviour detected in the experiments, thus enriching the theoretical investigation with great predictive power.126,127,129,133,139 As proved by the publications trend in the field, this kind of analysis has empowered the rational design of specific TM compositions, the introduction of functional point defects (e.g., metal vacancy, TM doping), or voltage-controlled cycling.150–154
4. Conclusions and perspectives
This perspective article aims at providing an overview on the crucial role of computational chemistry and QM-based simulations in describing nanostructured electrode materials that are relevant for Na-ion battery applications. By accessing electronic structure and sodiation/desodiation mechanistic details at the nanoscale, QM-based methods enable the fundamental understanding of redox reactions, ion diffusion, and the role of defects along the charging/discharging process. Whether setting foundations for advancing multiscale techniques or delivering fundamental knowledge on electroactive materials, DFT simulations represent a powerful predictive tool towards new rational design strategies and offer an atomistic outlook for investigating reaction kinetics, electrochemical potentials, chemical stability, defects chemistry, and adsorption/dissociation energetics.We have briefly illustrated how the recent literature in the field of Na-ion batteries has been enriched with design principles derived from first-principles theoretical investigations. State-of-the-art computational tools are shown to unveil new details on relevant topics, highlighting key features in nanostructured electrode materials that directly affect the sodiation/desodiation mechanisms.
Na+ adsorption, intercalation and migration mechanisms are dissected for several nanostructured anodes: surface morphology and sodium radius, binding strength and steric hinderance are all intertwined features to take appropriately into account in order to obtain a conclusive picture of NIB electrode functioning mechanisms. The inclusion of a sawtooth-like potential has been proven to be a useful tool to efficiently describe how the electric field can control the Na+ electrode interactions and paves the route towards realistic simulations of in operando conditions.
Charge compensation in high-energy layered oxides can be unfolded to outline tuneable activation of reversible anionic-redox active cathodes. More labile TM–O bonds undergo preferential cleavage towards superoxide formation and can be responsible for the full release of molecular oxygen, which can be suppressed by increasing the TM–O covalency.
Overall, our results contribute to shed light on the electrochemical behaviour of promising NIB systems and can drive future strategies for an effective tuning of heterogeneous functional materials. While explaining experimental observations and showing to what extent the key Na migration, charge compensation, anionic redox chemistry, etc., are reliably addressed by first-principles calculations, these findings and the identification of readily computable structural descriptors can be instrumental for the rational design and fast development of novel electrodes. Moreover, the described methodology can be extended to similar systems and set solid foundations for multiscale frameworks able to integrate systems and processes across several scales of space and time.
Over the last two decades, the accuracy and robustness of ab initio methods have enabled the in-depth understanding of complex electrochemical behaviors at the atomistic level. The huge impact of computer power in chemistry and energy related fields has been rapidly growing, up to the point that many technical challenges are overcome, and even automated simulations can be supplied with the advent of data mining and machine learning techniques. Notwithstanding these advances, every DFT calculation requires input structure models, and any computation becomes meaningless with no conception of the relevant material phases or invalid assumptions about the atomic structure. Although thermodynamically stable phases can be generally discovered, it is still challenging to predict metastable phases that may be present under operating conditions, such as nanostructures, polymorphs, or disordered phases. The eventual lack of information on the material structural evolution prevents the possibility of making quantitative predictions, thus hampering the computational design of entirely new materials. So far, most of the first-principles methods in battery research have been focused on crystalline solids, but the need for reliable models of non-crystalline solid-electrolyte interfaces is rapidly emerging as a key aspect to unveil many other battery features. The simulation of such complex structures typically requires large length scales that may be accessible by means of non-conventional multiscale methodologies beyond first principles. Still, major efforts should drive the full comprehension of complex phenomena occurring at heterogeneous electrochemical interfaces. Tricky reactivity, charge and mass transport processes may span different time scales and involve species with intrinsically different chemical natures (i.e., metals, radicals). Great steps forward in ab initio modelling should definitely deal with these new challenges and the upcoming demand of gaining an integrated, unique theoretical perspective on – as real as possible – material models.
A fundamental understanding of battery functioning mechanisms will strongly benefit from upscaled-computational analysis, in view of the close cooperation between theory and experiments as unavoidable driving forces to foster innovation and production of much needed highly performing NIB devices.
Conflicts of interest
The authors declare no conflicts of interests.Acknowledgements
The authors acknowledge European Union (FSE, PON Ricerca e Innovazione 2014–2020, Azione I.1 “Dottorati Innovativi con caratterizzazione Industriale”), for funding a PhD grant to Arianna Massaro. Part of this work was carried out within the activities “Ricerca Sistema Elettrico” funded through contributions to research and development by the Italian Ministry of Economic Development. The computing resources and the related technical support used for this work have been provided by CRESCO/ENEAGRID High Performance Computing infrastructure and its staff;155 CRESCO/ENEAGRID High Performance Computing infrastructure is funded by ENEA, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development and by Italian and European research programs, see: http://www.cresco.enea.it/english for further information.References
- J. B. Goodenough and K.-S. Park, The Li-Ion Rechargeable Battery: A Perspective, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Challenges for Rechargeable Li Batteries, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- B. Nykvist and M. Nilsson, Rapidly Falling Costs of Battery Packs for Electric Vehicles, Nat. Clim. Change, 2015, 5, 329–332 CrossRef.
- D. Larcher and J. M. Tarascon, Towards greener and more sustainable batteries for electrical energy storage, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- G. E. Blomgren, The Development and Future of Lithium Ion Batteries, J. Electrochem. Soc., 2017, 164, A5019–A5025 CrossRef CAS.
- K. M. Abraham, How Comparable Are Sodium-Ion Batteries to Lithium-Ion Counterparts?, ACS Energy Lett., 2020, 5, 3544–3547 CrossRef CAS.
- P. K. Nayak, L. Yang, W. Brehm and P. Adelhelm, From Lithium-Ion to Sodium-Ion Batteries: Advantages, Challenges, and Surprises, Angew. Chem., Int. Ed., 2018, 57, 102–120 CrossRef CAS PubMed.
- K. Chayambuka, G. Mulder, D. L. Danilov and P. H. L. Notten, Sodium-Ion Battery Materials and Electrochemical Properties Reviewed, Adv. Energy Mater., 2018, 8, 1800079 CrossRef.
- Y. Huang, Y. Zheng, X. Li, F. Adams, W. Luo, Y. Huang and L. Hu, Electrode Materials of Sodium-Ion Batteries toward Practical Application, ACS Energy Lett., 2018, 3, 1604–1612 CrossRef CAS.
- J. Y. Hwang, S. T. Myung and Y. K. Sun, Sodium-ion batteries: Present and future, Chem. Soc. Rev., 2017, 46, 3529–3614 RSC.
- Y. Fang, X.-Y. Yu and X. W. Lou, Nanostructured Electrode Materials for Advanced Sodium-Ion Batteries, Matter, 2019, 1, 90–114 CrossRef.
- P. G. Bruce, B. Scrosati and J. M. Tarascon, Nanomaterials for rechargeable lithium batteries, Angew. Chem., Int. Ed., 2008, 47, 2930–2946 CrossRef CAS PubMed.
- M. C. Masedi, P. E. Ngoepe and H. M. Sithole, Beyond lithium-ion batteries: A computational study on Na-S and Na-O batteries, IOP Conf. Ser. Mater. Sci. Eng., 2017, 169, 012001 CrossRef.
- R. Jayan and M. M. Islam, Mechanistic Insights into Interactions of Polysulfides at VS2 Interfaces in Na–S Batteries: A DFT Study, ACS Appl. Mater. Interfaces, 2021, 13, 35848–35855 CrossRef CAS PubMed.
- T. Kaewmaraya, T. Hussain, R. Umer, Z. Hu and X. S. Zhao, Efficient suppression of the shuttle effect in Na–S batteries with an As2 S3 anchoring monolayer, Phys. Chem. Chem. Phys., 2020, 22, 27300–27307 RSC.
- R. Jayan and M. M. Islam, Single-Atom Catalysts for Improved Cathode Performance in Na–S Batteries: A Density Functional Theory (DFT) Study, J. Phys. Chem. C, 2021, 125, 4458–4467 CrossRef CAS.
- Z. Zheng, J. Jiang, H. Guo, C. Li, K. Konstantinov, Q. Gu and J. Wang, Tuning NaO2 formation and decomposition routes with nitrogen-doped nanofibers for low overpotential Na-O2 batteries, Nano Energy, 2021, 81, 105529 CrossRef CAS.
- L. M. Morgan, M. P. Mercer, A. Bhandari, C. Peng, M. M. Islam, H. Yang, J. Holland, S. W. Coles, R. Sharpe, A. Walsh, B. J. Morgan, D. Kramer, M. S. Islam, H. E. Hoster, J. S. Edge and C.-K. Skylaris, Pushing the boundaries of lithium battery research with atomistic modelling on different scales, Prog. Energy, 2022, 4, 012002 CrossRef.
- H. Euchner and A. Groß, Atomistic modeling of Li- and post-Li-ion batteries, Phys. Rev. Mater., 2022, 6, 040302 CrossRef CAS.
- J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Unlocking the Potential of Cation-Disordered Oxides for Rechargeable Lithium Batteries, Science, 2014, 343, 519–522 CrossRef CAS PubMed.
- G. Åvall, J. Mindemark, D. Brandell and P. Johansson, Sodium-Ion Battery Electrolytes: Modeling and Simulations, Adv. Energy Mater., 2018, 8, 1703036 CrossRef.
- Z.-T. Sun and S.-H. Bo, Understanding electro-mechanical-thermal coupling in solid-state lithium metal batteries via phase-field modeling, J. Mater. Res., 2022, 37, 3130–3145 CrossRef CAS.
- T. Shi, Q. Tu, Y. Tian, Y. Xiao, L. J. Miara, O. Kononova and G. Ceder, High Active Material Loading in All-Solid-State Battery Electrode via Particle Size Optimization, Adv. Energy Mater., 2020, 10, 1902881 CrossRef CAS.
- J. M. Reniers, G. Mulder and D. A. Howey, Review and Performance Comparison of Mechanical-Chemical Degradation Models for Lithium-Ion Batteries, J. Electrochem. Soc., 2019, 166, A3189–A3200 CrossRef.
- C. D. Parke, L. Teo, D. T. Schwartz and V. R. Subramanian, Progress on continuum modeling of lithium–sulfur batteries, Sustainable Energy Fuels, 2021, 5, 5946–5966 RSC.
- J. Popovic, D. Brandell, S. Ohno, K. B. Hatzell, J. Zheng and Y.-Y. Hu, Polymer-based hybrid battery electrolytes: theoretical insights, recent advances and challenges, J. Mater. Chem. A, 2021, 9, 6050–6069 RSC.
- R. P. Carvalho, C. F. N. Marchiori, C. M. Araujo and D. Brandell, Redox Polymers for Energy and Nanomedicine, The Royal Society of Chemistry, 2020, pp. 93–136 Search PubMed.
- O. Borodin, G. D. Smith, R. Bandyopadhyaya and O. Byutner, Molecular Dynamics Study of the Influence of Solid Interfaces on Poly(ethylene oxide) Structure and Dynamics, Macromolecules, 2003, 36, 7873–7883 CrossRef CAS.
- O. Borodin and G. D. Smith, Development of Many−Body Polarizable Force Fields for Li-Battery Applications: 2. LiTFSI-Doped Oligoether, Polyether, and Carbonate-Based Electrolytes, J. Phys. Chem. B, 2006, 110, 6293–6299 CrossRef CAS PubMed.
- O. N. Starovoytov, Development of a Polarizable Force Field for Molecular Dynamics Simulations of Lithium-Ion Battery Electrolytes: Sulfone-Based Solvents and Lithium Salts, J. Phys. Chem. B, 2021, 125, 11242–11255 CrossRef CAS PubMed.
- A. Massaro, J. Avila, K. Goloviznina, I. Rivalta, C. Gerbaldi, M. Pavone, M. F. Costa Gomes and A. A. H. Padua, Sodium diffusion in ionic liquid-based electrolytes for Na-ion batteries: the effect of polarizable force fields, Phys. Chem. Chem. Phys., 2020, 22, 20114–20122 RSC.
- Z. Shi, J. Zhou and R. Li, Application of Reaction Force Field Molecular Dynamics in Lithium Batteries, Front. Chem., 2021, 8, 634379 CrossRef PubMed.
- T. C. Lourenço, M. Ebadi, D. Brandell, J. L. F. Da Silva and L. T. Costa, Interfacial Structures in Ionic Liquid-Based Ternary Electrolytes for Lithium-Metal Batteries: A Molecular Dynamics Study, J. Phys. Chem. B, 2020, 124, 9648–9657 CrossRef PubMed.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- J. Behler and M. Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- H. Guo, Q. Wang, A. Stuke, A. Urban and N. Artrith, Accelerated Atomistic Modeling of Solid-State Battery Materials With Machine Learning, Front. Energy Res., 2021, 9, 695902 CrossRef.
- V. L. Deringer, Modelling and understanding battery materials with machine-learning-driven atomistic simulations, J. Phys. Energy, 2020, 2, 041003 CrossRef CAS.
- Q. He, B. Yu, Z. Li and Y. Zhao, Density Functional Theory for Battery Materials, Energy Environ. Mater., 2019, 2, 264–279 CrossRef CAS.
- X. Li, X. Chen, Q. Bai, Y. Mo and Y. Zhu, From atomistic modeling to materials design: computation-driven material development in lithium-ion batteries, Sci. China: Chem., 2023, 1–15 Search PubMed.
- D. A. Aksyonov, A. O. Boev, S. S. Fedotov and A. M. Abakumov, Computational insights into ionic conductivity of transition metal electrode materials for metal-ion batteries - A review, Solid State Ionics, 2023, 393, 116170 CrossRef CAS.
- S. Zhang, J. Ma, S. Dong and G. Cui, Designing All-Solid-State Batteries by Theoretical Computation: A Review, Electrochem. Energy Rev., 2023, 6, 4 CrossRef.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- S. A. Tolba, K. M. Gameel, B. A. Ali, H. A. Almossalami and N. K. Allam, Density Functional Calculations - Recent Progresses of Theory and Application, InTech, 2018, pp. 3–30 Search PubMed.
- S. Lutfalla, V. Shapovalov and A. T. Bell, Calibration of the DFT/GGA+U Method for Determination of Reduction Energies for Transition and Rare Earth Metal Oxides of Ti, V, Mo, and Ce, J. Chem. Theory Comput., 2011, 7, 2218–2223 CrossRef CAS PubMed.
- L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA+U framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- V. Barone, M. Casarin, D. Forrer, M. Pavone, M. Sambi and A. Vittadini, Role and effective treatment of dispersive forces in materials: Polyethylene and graphite crystals as test cases, J. Comput. Chem., 2009, 30, 934–939 CrossRef CAS PubMed.
- A. Pecoraro, E. Schiavo, P. Maddalena, A. B. Muñoz-García and M. Pavone, Structural and electronic properties of defective 2D transition metal dichalcogenide heterostructures, J. Comput. Chem., 2020, 41, 1946–1955 CrossRef CAS PubMed.
- A. B. Muñoz-García, A. Massaro and M. Pavone, Ab initio study of PbCr(1−x)SxO4 solid solution: an inside look at Van Gogh Yellow degradation, Chem. Sci., 2016, 7, 4197–4203 RSC.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. Neugebauer and M. Scheffler, Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111), Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080 CrossRef CAS PubMed.
- V. L. Chevrier and G. Ceder, Challenges for Na-ion Negative Electrodes, J. Electrochem. Soc., 2011, 158, A1011 CrossRef CAS.
- G. Longoni, R. L. Pena Cabrera, S. Polizzi, M. D’Arienzo, C. M. Mari, Y. Cui and R. Ruffo, Shape-Controlled TiO2 Nanocrystals for Na-Ion Battery Electrodes: The Role of Different Exposed Crystal Facets on the Electrochemical Properties, Nano Lett., 2017, 17, 992–1000 CrossRef CAS PubMed.
- L. David, R. Bhandavat and G. Singh, MoS2/graphene composite paper for sodium-ion battery electrodes, ACS Nano, 2014, 8, 1759–1770 CrossRef CAS PubMed.
- W. Lu, Z. Wang and S. Zhong, Sodium-ion battery technology: Advanced anodes, cathodes and electrolytes, J. Phys. Conf. Ser., 2021, 2109, 012004 CrossRef.
- F. Fasulo, A. B. Muñoz-García, A. Massaro, O. Crescenzi, C. Huang and M. Pavone, Vinylene carbonate reactivity at lithium metal surface: first-principles insights into the early steps of SEI formation, J. Mater. Chem. A, 2023, 11, 5660–5669 RSC.
- E. Peled and S. Menkin, Review—SEI: Past, Present and Future, J. Electrochem. Soc., 2017, 164, A1703–A1719 CrossRef CAS.
- Y. Cao, L. Xiao, M. L. Sushko, W. Wang, B. Schwenzer, J. Xiao, Z. Nie, L. V. Saraf, Z. Yang and J. Liu, Sodium Ion Insertion in Hollow Carbon Nanowires for Battery Applications, Nano Lett., 2012, 12, 3783–3787 CrossRef CAS PubMed.
- P.-C. Tsai, S.-C. Chung, S.-K. Lin and A. Yamada, Ab initio study of sodium intercalation into disordered carbon, J. Mater. Chem. A, 2015, 3, 9763–9768 RSC.
- C.-Y. Chou, M. Lee and G. S. Hwang, A Comparative First-Principles Study on Sodiation of Silicon, Germanium, and Tin for Sodium-Ion Batteries, J. Phys. Chem. C, 2015, 119, 14843–14850 CrossRef CAS.
- M. Mayo, K. J. Griffith, C. J. Pickard and A. J. Morris, Ab Initio Study of Phosphorus Anodes for Lithium- and Sodium-Ion Batteries, Chem. Mater., 2016, 28, 2011–2021 CrossRef CAS.
- Q. Bai, L. Yang, H. Chen and Y. Mo, Computational Studies of Electrode Materials in Sodium-Ion Batteries, Adv. Energy Mater., 2018, 8, 1702998 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- E. Irisarri, A. Ponrouch and M. R. Palacin, Review—Hard Carbon Negative Electrode Materials for Sodium-Ion Batteries, J. Electrochem. Soc., 2015, 162, A2476–A2482 CrossRef CAS.
- M. N. Obrovac and V. L. Chevrier, Alloy Negative Electrodes for Li-Ion Batteries, Chem. Rev., 2014, 114, 11444–11502 CrossRef CAS PubMed.
- U. Arrieta, N. A. Katcho, O. Arcelus and J. Carrasco, First-principles study of sodium intercalation in crystalline NaxSi24 (0 ≤ x ≤ 4) as anode material for na-ion batteries, Sci. Rep., 2017, 7, 1–8 CrossRef CAS PubMed.
- V. Sharma, K. Ghatak and D. Datta, Amorphous germanium as a promising anode material for sodium ion batteries: a first principle study, J. Mater. Sci., 2018, 53, 14423–14434 CrossRef CAS.
- A. Majid, K. Hussain, S. Ud-Din Khan and S. Ud-Din Khan, First principles study of SiC as the anode in sodium ion batteries, New J. Chem., 2020, 44, 8910–8921 RSC.
- S. Dhillon, G. Hernández, N. P. Wagner, A. M. Svensson and D. Brandell, Modelling capacity fade in silicon–graphite composite electrodes for lithium-ion batteries, Electrochim. Acta, 2021, 377, 138067 CrossRef CAS.
- R. P. Carvalho, C. F. N. Marchiori, V.-A. Oltean, S. Renault, T. Willhammar, C. Pay Gómez, C. M. Araujo and D. Brandell, Structure–property relationships in organic battery anode materials: exploring redox reactions in crystalline Na- and Li-benzene diacrylate using combined crystallography and density functional theory calculations, Mater. Adv., 2021, 2, 1024–1034 RSC.
- Y. Lu, Y. Lu, Z. Niu and J. Chen, Graphene-Based Nanomaterials for Sodium-Ion Batteries, Adv. Energy Mater., 2018, 8, 1–21 Search PubMed.
- J. Shuai, H. D. Yoo, Y. Liang, Y. Li, Y. Yao and L. C. Grabow, Density functional theory study of Li, Na, and Mg intercalation and diffusion in MoS2 with controlled interlayer spacing, Mater. Res. Express, 2016, 3, 1–8 CrossRef.
- X. Xie, Z. Ao, D. Su, J. Zhang and G. Wang, MoS2/Graphene Composite Anodes with Enhanced Performance for Sodium-Ion Batteries: The Role of the Two-Dimensional Heterointerface, Adv. Funct. Mater., 2015, 25, 1393–1403 CrossRef CAS.
- L. Wang, H. Zhang, Y. Wang, C. Qian, Q. Dong, C. Deng, D. Jiang, M. Shu, S. Pan and S. Zhang, Unleashing ultra-fast sodium ion storage mechanisms in interface-engineered monolayer MoS2/C interoverlapped superstructure with robust charge transfer networks, J. Mater. Chem. A, 2020, 8, 15002–15011 RSC.
- A. Massaro, A. Pecoraro, A. Muñoz-García and M. Pavone, First-Principles Study of Na Intercalation and Diffusion Mechanisms at 2D MoS2/Graphene Interfaces, J. Phys. Chem. C, 2021, 125, 2276–2286 CrossRef CAS PubMed.
- D. Sun, D. Huang, H. Wang, G.-L. Xu, X. Zhang, R. Zhang, Y. Tang, D. Abd EI-Hady, W. Alshitari, A. Saad AL-Bogami, K. Amine and M. Shao, 1T MoS2 nanosheets with extraordinary sodium storage properties via thermal-driven ion intercalation assisted exfoliation of bulky MoS2, Nano Energy, 2019, 61, 361–369 CrossRef CAS.
- J. Su, Y. Pei, Z. Yang and X. Wang, Ab initio study of graphene-like monolayer molybdenum disulfide as a promising anode material for rechargeable sodium ion batteries, RSC Adv., 2014, 4, 43183–43188 RSC.
- G. Barik and S. Pal, Defect Induced Performance Enhancement of Monolayer MoS2 for Li- and Na-Ion Batteries, J. Phys. Chem. C, 2019, 123, 21852–21865 CrossRef CAS.
- E. Olsson, G. Chai, M. Dove and Q. Cai, Adsorption and migration of alkali metals (Li, Na, and K) on pristine and defective graphene surfaces, Nanoscale, 2019, 11, 5274–5284 RSC.
- J. Shuai, H. D. Yoo, Y. Liang, Y. Li, Y. Yao and L. C. Grabow, Density functional theory study of Li, Na, and Mg intercalation and diffusion in MoS2 with controlled interlayer spacing, Mater. Res. Express, 2016, 3, 064001 CrossRef.
- D. Sun, D. Ye, P. Liu, Y. Tang, J. Guo, L. Wang and H. Wang, MoS2/Graphene Nanosheets from Commercial Bulky MoS2 and Graphite as Anode Materials for High Rate Sodium-Ion Batteries, Adv. Energy Mater., 2018, 8, 1702383 CrossRef.
- M. K. Singh, J. Pati, D. Seth, J. Prasad, M. Agarwal, M. A. Haider, J.-K. Chang and R. S. Dhaka, Diffusion mechanism and electrochemical investigation of 1T phase Al–MoS2@rGO nano-composite as a high-performance anode for sodium-ion batteries, Chem. Eng. J., 2023, 454, 140140 CrossRef CAS.
- J. Xiao, J. Zhou, L.-N. Chen and J. Chen, Na transport in bilayer MoS2 and MoS2-WS2 heterojunction with S vacancy defect: First-principles study, AIP Adv., 2022, 12, 65218 CrossRef CAS.
- J. Wang, X. Zheng, Y. Dong, L. Chen, L. Chen and W. He, Reactant conversion–intercalation strategy toward interlayer-expanded MoS 2 microflowers with superior supercapacitor performance, Dalton Trans., 2023, 52, 4537–4547 RSC.
- K. Chiba, N. Kijima, Y. Takahashi, Y. Idemoto and J. Akimoto, Synthesis, structure, and electrochemical Li-ion intercalation properties of Li2Ti3O7 with Na2Ti3O7-type layered structure, Solid State Ionics, 2008, 178, 1725–1730 CrossRef CAS.
- G. Rousse, M. E. Arroyo-de Dompablo, P. Senguttuvan, A. Ponrouch, J.-M. Tarascon and M. R. Palacín, Rationalization of Intercalation Potential and Redox Mechanism for A2Ti3O7 (A = Li, Na), Chem. Mater., 2013, 25, 4946–4956 CrossRef CAS.
- J. Xu, C. Ma, M. Balasubramanian and Y. S. Meng, Understanding Na2Ti3O7 as an ultra-low voltage anode material for a Na-ion battery, Chem. Commun., 2014, 50, 12564–12567 RSC.
- L. Wu, D. Bresser, D. Buchholz, G. A. Giffin, C. R. Castro, A. Ochel and S. Passerini, Unfolding the Mechanism of Sodium Insertion in Anatase TiO2 Nanoparticles, Adv. Energy Mater., 2015, 5, 1401142 CrossRef.
- X. Yang, C. Wang, Y. Yang, Y. Zhang, X. Jia, J. Chen and X. Ji, Anatase TiO2 nanocubes for fast and durable sodium ion battery anodes, J. Mater. Chem. A, 2015, 3, 8800–8807 RSC.
- A. Massaro, A. B. Muñoz-García, P. Maddalena, F. Bella, G. Meligrana, C. Gerbaldi and M. Pavone, First-principles study of Na insertion at TiO2 anatase surfaces: new hints for Na-ion battery design, Nanoscale Adv., 2020, 2, 2745–2751 RSC.
- F. Bella, A. B. Muñoz-García, G. Meligrana, A. Lamberti, M. Destro, M. Pavone and C. Gerbaldi, Unveiling the controversial mechanism of reversible Na storage in TiO2 nanotube arrays: Amorphous versus anatase TiO2, Nano Res., 2017, 10, 2891–2903 CrossRef CAS.
- Z. Bayhan, G. Huang, J. Yin, X. Xu, Y. Lei, Z. Liu and H. N. Alshareef, Two-Dimensional TiO 2 /TiS 2 Hybrid Nanosheet Anodes for High-Rate Sodium-Ion Batteries, ACS Appl. Energy Mater., 2021, 4, 8721–8727 CrossRef CAS.
- K. Leung, L. C. Merrill and K. L. Harrison, Galvanic Corrosion and Electric Field in Lithium Anode Passivation Films: Effects on Self-Discharge, J. Phys. Chem. C, 2022, 126, 8565–8580 CrossRef CAS.
- K. Leung, DFT modelling of explicit solid–solid interfaces in batteries: methods and challenges, Phys. Chem. Chem. Phys., 2020, 22, 10412–10425 RSC.
- F. Fasulo, A. Massaro, A. B. Muñoz-García and M. Pavone, Na uptake at TiO2 anatase surfaces under electric field control: A first-principles study, J. Mater. Res., 2022, 37, 3216–3226 CrossRef CAS.
- S. Selçuk and A. Selloni, Influence of external electric fields on oxygen vacancies at the anatase (101) surface, J. Chem. Phys., 2014, 141, 084705 CrossRef PubMed.
- D. Atkins, E. Ayerbe, A. Benayad, F. G. Capone, E. Capria, I. E. Castelli, I. Cekic-Laskovic, R. Ciria, L. Dudy, K. Edström, M. R. Johnson, H. Li, J. M. G. Lastra, M. L. De Souza, V. Meunier, M. Morcrette, H. Reichert, P. Simon, J.-P. Rueff, J. Sottmann, W. Wenzel and A. Grimaud, Understanding Battery Interfaces by Combined Characterization and Simulation Approaches: Challenges and Perspectives, Adv. Energy Mater., 2022, 12, 2102687 CrossRef CAS.
- A. Pecoraro, F. Fasulo, M. Pavone and A. B. Muñoz-García, First-principles study of interfacial features and charge dynamics between spiro-MeOTAD and photoactive lead halide perovskites, Chem. Commun., 2023, 59, 5055–5058 RSC.
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Voltage, stability and diffusion barrier differences between sodium-ion and lithium-ion intercalation materials, Energy Environ. Sci., 2011, 4, 3680 RSC.
- R. Tripathi, S. M. Wood, M. S. Islam and L. F. Nazar, Na-ion mobility in layered Na2FePO4F and olivine Na[Fe,Mn]PO4, Energy Environ. Sci., 2013, 6, 2257 RSC.
- Y. Zheng, P. Zhang, S. Q. Wu, Y. H. Wen, Z. Z. Zhu and Y. Yang, First-Principles Investigations on the Na2MnPO4F as a Cathode Material for Na-Ion Batteries, J. Electrochem. Soc., 2013, 160, A927–A932 CrossRef CAS.
- S. T. Dacek, W. D. Richards, D. A. Kitchaev and G. Ceder, Structure and Dynamics of Fluorophosphate Na-Ion Battery Cathodes, Chem. Mater., 2016, 28, 5450–5460 CrossRef CAS.
- I. L. Matts, S. Dacek, T. K. Pietrzak, R. Malik and G. Ceder, Explaining Performance-Limiting Mechanisms in Fluorophosphate Na-Ion Battery Cathodes through Inactive Transition-Metal Mixing and First-Principles Mobility Calculations, Chem. Mater., 2015, 27, 6008–6015 CrossRef CAS.
- T. Yamashita, H. Momida and T. Oguchi, Crystal structure predictions of Na C6O6 for sodium-ion batteries: First-principles calculations with an evolutionary algorithm, Electrochim. Acta, 2016, 195, 1–8 CrossRef CAS.
- Y. Chen, J. Lüder, M.-F. Ng, M. Sullivan and S. Manzhos, Polyaniline and CN-functionalized polyaniline as organic cathodes for lithium and sodium ion batteries: a combined molecular dynamics and density functional tight binding study in solid state, Phys. Chem. Chem. Phys., 2018, 20, 232–237 RSC.
- Y. Chen and S. Manzhos, A comparative computational study of lithium and sodium insertion into van der Waals and covalent tetracyanoethylene (TCNE)-based crystals as promising materials for organic lithium and sodium ion batteries, Phys. Chem. Chem. Phys., 2016, 18, 8874–8880 RSC.
- Y. Zhang, R. Zhang and Y. Huang, Air-Stable NaxTMO2 Cathodes for Sodium Storage, Front. Chem., 2019, 7, 335 CrossRef CAS PubMed.
- R. Berthelot, D. Carlier and C. Delmas, Electrochemical investigation of the P2–NaxCoO2 phase diagram, Nat. Mater., 2011, 10, 74–80 CrossRef CAS PubMed.
- N. Yabuuchi and S. Komaba, Recent research progress on iron- and manganese-based positive electrode materials for rechargeable sodium batteries, Sci. Technol. Adv. Mater., 2014, 15, 043501 CrossRef CAS PubMed.
- M. S. Islam and C. A. J. Fisher, Lithium and sodium battery cathode materials: computational insights into voltage, diffusion and nanostructural properties, Chem. Soc. Rev., 2014, 43, 185–204 RSC.
- C. Delmas, C. Fouassier and P. Hagenmuller, Structural classification and properties of the layered oxides, Phys. B + C, 1980, 99, 81–85 CrossRef CAS.
- N. A. Katcho, J. Carrasco, D. Saurel, E. Gonzalo, M. Han, F. Aguesse and T. Rojo, Origins of Bistability and Na Ion Mobility Difference in P2- and O3-Na2/3Fe2/3Mn1/3O2 Cathode Polymorphs, Adv. Energy Mater., 2017, 7, 1601477 CrossRef.
- A. Urban, D.-H. Seo and G. Ceder, Computational understanding of Li-ion batteries, npj Comput. Mater., 2016, 2, 16002 CrossRef CAS.
- R. J. Clément, P. G. Bruce and C. P. Grey, Review—Manganese-Based P2-Type Transition Metal Oxides as Sodium-Ion Battery Cathode Materials, J. Electrochem. Soc., 2015, 162, A2589–A2604 CrossRef.
- C. Zhao, Q. Wang, Z. Yao, J. Wang, B. Sánchez-Lengeling, F. Ding, X. Qi, Y. Lu, X. Bai, B. Li, H. Li, A. Aspuru-Guzik, X. Huang, C. Delmas, M. Wagemaker, L. Chen and Y.-S. Hu, Rational design of layered oxide materials for sodium-ion batteries, Science, 2020, 370, 708–711 CrossRef CAS PubMed.
- X. Zhang, Z. Zhang, S. Yao, A. Chen, X. Zhao and Z. Zhou, An effective method to screen sodium-based layered materials for sodium ion batteries, npj Comput. Mater., 2018, 4, 13 CrossRef.
- Q. Wang, S. Mariyappan, G. Rousse, A. V. Morozov, B. Porcheron, R. Dedryvère, J. Wu, W. Yang, L. Zhang, M. Chakir, M. Avdeev, M. Deschamps, Y.-S. Yu, J. Cabana, M.-L. Doublet, A. M. Abakumov and J.-M. Tarascon, Unlocking anionic redox activity in O3-type sodium 3d layered oxides via Li substitution, Nat. Mater., 2021, 20, 353–361 CrossRef CAS PubMed.
- J. Vergnet, M. Saubanère, M.-L. Doublet and J.-M. Tarascon, The Structural Stability of P2-Layered Na-Based Electrodes during Anionic Redox, Joule, 2020, 4, 420–434 CrossRef CAS.
- R. A. House, U. Maitra, M. A. Pérez-Osorio, J. G. Lozano, L. Jin, J. W. Somerville, L. C. Duda, A. Nag, A. Walters, K. J. Zhou, M. R. Roberts and P. G. Bruce, Superstructure control of first-cycle voltage hysteresis in oxygen-redox cathodes, Nature, 2020, 577, 502–508 CrossRef CAS PubMed.
- M. Ben Yahia, J. Vergnet, M. Saubanère and M.-L. Doublet, Unified picture of anionic redox in Li/Na-ion batteries, Nat. Mater., 2019, 18, 496–502 CrossRef CAS PubMed.
- C. Zhao, Z. Yao, J. Wang, Y. Lu, X. Bai, A. Aspuru-Guzik, L. Chen and Y.-S. Hu, Ti Substitution Facilitating Oxygen Oxidation in Na2/3Mg1/3Ti1/6Mn1/2O2 Cathode, Chem, 2019, 5, 2913–2925 CAS.
- M. Saubanère, E. McCalla, J. M. Tarascon and M. L. Doublet, The intriguing question of anionic redox in high-energy density cathodes for Li-ion batteries, Energy Environ. Sci., 2016, 9, 984–991 RSC.
- D.-H. Seo, J. Lee, A. Urban, R. Malik, S. Kang and G. Ceder, The structural and chemical origin of the oxygen redox activity in layered and cation-disordered Li-excess cathode materials, Nat. Chem., 2016, 8, 692–697 CrossRef CAS PubMed.
- U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Pérez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Oxygen redox chemistry without excess alkali-metal ions in Na2/3[Mg0.28Mn0.72]O2, Nat. Chem., 2018, 10, 288–295 CrossRef CAS PubMed.
- C. Ma, J. Alvarado, J. Xu, R. J. Clément, M. Kodur, W. Tong, C. P. Grey and Y. S. Meng, Exploring Oxygen Activity in the High Energy P2-Type Na0.78Ni0.23Mn0.69O2 Cathode Material for Na-Ion Batteries, J. Am. Chem. Soc., 2017, 139, 4835–4845 CrossRef CAS PubMed.
- T. Risthaus, D. Zhou, X. Cao, X. He, B. Qiu, J. Wang, L. Zhang, Z. Liu, E. Paillard, G. Schumacher, M. Winter and J. Li, A high-capacity P2 Na2/3Ni1/3Mn2/3O2 cathode material for sodium ion batteries with oxygen activity, J. Power Sources, 2018, 395, 16–24 CrossRef CAS.
- A. Massaro, A. B. Muñoz-García, P. P. Prosini, C. Gerbaldi and M. Pavone, Unveiling Oxygen Redox Activity in P2-Type NaxNi0.25Mn0.68O2 High-Energy Cathode for Na-Ion Batteries, ACS Energy Lett., 2021, 6, 2470–2480 CrossRef CAS.
- C. Zhao, Z. Yao, Q. Wang, H. Li, J. Wang, M. Liu, S. Ganapathy, Y. Lu, J. Cabana, B. Li, X. Bai, A. Aspuru-Guzik, M. Wagemaker, L. Chen and Y.-S. Hu, Revealing High Na-Content P2-Type Layered Oxides as Advanced Sodium-Ion Cathodes, J. Am. Chem. Soc., 2020, 142, 5742–5750 CrossRef CAS PubMed.
- M. Sathiya, G. Rousse, K. Ramesha, C. P. Laisa, H. Vezin, M. T. Sougrati, M.-L. Doublet, D. Foix, D. Gonbeau, W. Walker, A. S. Prakash, M. Ben Hassine, L. Dupont and J.-M. Tarascon, Reversible anionic redox chemistry in high-capacity layered-oxide electrodes, Nat. Mater., 2013, 12, 827–835 CrossRef CAS PubMed.
- J. Hong, W. E. Gent, P. Xiao, K. Lim, D. H. Seo, J. Wu, P. M. Csernica, C. J. Takacs, D. Nordlund, C. J. Sun, K. H. Stone, D. Passarello, W. Yang, D. Prendergast, G. Ceder, M. F. Toney and W. C. Chueh, Metal–oxygen decoordination stabilizes anion redox in Li-rich oxides, Nat. Mater., 2019, 18, 256–265 CrossRef CAS PubMed.
- E. McCalla, A. M. Abakumov, M. Saubanere, D. Foix, E. J. Berg, G. Rousse, M.-L. Doublet, D. Gonbeau, P. Novak, G. Van Tendeloo, R. Dominko and J.-M. Tarascon, Visualization of O–O peroxo-like dimers in high-capacity layered oxides for Li-ion batteries, Science, 2015, 350, 1516–1521 CrossRef CAS PubMed.
- Y. Zhang, M. Wu, J. Ma, G. Wei, Y. Ling, R. Zhang and Y. Huang, Revisiting the Na2/3Ni1/3Mn2/3O2 Cathode: Oxygen Redox Chemistry and Oxygen Release Suppression, ACS Cent. Sci., 2020, 6, 232–240 CrossRef CAS PubMed.
- A. Massaro, A. Langella, A. B. Muñoz-García and M. Pavone, First-principles insights on anion redox activity in NaxFe1/8Ni1/8Mn3/4O2: Toward efficient high-energy cathodes for Na-ion batteries, J. Am. Ceram. Soc., 2023, 106, 109–119 CrossRef CAS.
- A. Massaro, A. Langella, C. Gerbaldi, G. Antonio Elia, A. B. Muñoz-García and M. Pavone, Ru-Doping of P2-NaxMn0.75Ni0.25O2-Layered Oxides for High-Energy Na-Ion Battery Cathodes: First-Principles Insights on Activation and Control of Reversible Oxide Redox Chemistry, ACS Appl. Energy Mater., 2022, 5, 10721–10730 CrossRef CAS.
- Q. Shen, Y. Liu, X. Zhao, J. Jin, Y. Wang, S. Li, P. Li, X. Qu and L. Jiao, Transition-Metal Vacancy Manufacturing and Sodium-Site Doping Enable a High-Performance Layered Oxide Cathode through Cationic and Anionic Redox Chemistry, Adv. Funct. Mater., 2021, 2106923 CrossRef CAS.
- C. J. Cramer, W. B. Tolman, K. H. Theopold and A. L. Rheingold, Variable character of O–O and M-O bonding in side-on (η2) 1:1 metal complexes of O2, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3635–3640 CrossRef CAS PubMed.
- L. E. Sutton and H. J. M. Bowen, Tables of Interatomic Distances and Configuration in Molecules and Ions, The Chemical Society, London, Special edn, 1958 Search PubMed.
- Q. Wang, K. Jiang, Y. Feng, S. Chu, X. Zhang, P. Wang, S. Guo and H. Zhou, P2-Type Layered Na0.75Ni1/3Ru1/6Mn 1/2O2 Cathode Material with Excellent Rate Performance for Sodium-Ion Batteries, ACS Appl. Mater. Interfaces, 2020, 12, 39056–39062 CrossRef CAS PubMed.
- N. Kiziltas-Yavuz, A. Bhaskar, D. Dixon, M. Yavuz, K. Nikolowski, L. Lu, R.-A. Eichel and H. Ehrenberg, Improving the rate capability of high voltage lithium-ion battery cathode material LiNi0.5Mn1.5O4 by ruthenium doping, J. Power Sources, 2014, 267, 533–541 CrossRef CAS.
- Y. Yu, P. Karayaylali, S. H. Nowak, L. Giordano, M. Gauthier, W. Hong, R. Kou, Q. Li, J. Vinson, T. Kroll, D. Sokaras, C. J. Sun, N. Charles, F. Maglia, R. Jung and Y. Shao-Horn, Revealing Electronic Signatures of Lattice Oxygen Redox in Lithium Ruthenates and Implications for High-Energy Li-Ion Battery Material Designs, Chem. Mater., 2019, 31, 7864–7876 CrossRef CAS PubMed.
- N. Charles, Y. Yu, L. Giordano, R. Jung, F. Maglia and Y. Shao-Horn, Toward Establishing Electronic and Phononic Signatures of Reversible Lattice Oxygen Oxidation in Lithium Transition Metal Oxides For Li-Ion Batteries, Chem. Mater., 2020, 32, 5502–5514 CrossRef CAS.
- B. Mortemard De Boisse, G. Liu, J. Ma, S. I. Nishimura, S. C. Chung, H. Kiuchi, Y. Harada, J. Kikkawa, Y. Kobayashi, M. Okubo and A. Yamada, Intermediate honeycomb ordering to trigger oxygen redox chemistry in layered battery electrode, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- M. Pavone, A. B. Muñoz-García, A. M. Ritzmann and E. A. Carter, First-principles study of lanthanum strontium manganite: Insights into electronic structure and oxygen vacancy formation, J. Phys. Chem. C, 2014, 118, 13346–13356 CrossRef CAS.
- A. M. Ritzmann, A. B. Muñoz-García, M. Pavone, J. A. Keith and E. A. Carter, Ab Initio DFT+U Analysis of Oxygen Vacancy Formation and Migration in La1−xSrxFeO3−δ (x = 0, 0.25, 0.50), Chem. Mater., 2013, 25, 3011–3019 CrossRef CAS.
- P. Yan, J. Zheng, Z.-K. Tang, A. Devaraj, G. Chen, K. Amine, J.-G. Zhang, L.-M. Liu and C. Wang, Injection of oxygen vacancies in the bulk lattice of layered cathodes, Nat. Nanotechnol., 2019, 14, 602–608 CrossRef CAS PubMed.
- Y. Xie, Y. Jin and L. Xiang, Li-rich layered oxides: Structure, capacity and voltage fading mechanisms and solving strategies, Particuology, 2022, 61, 1–10 CrossRef CAS.
- C. Delmas, D. Carlier and M. Guignard, The Layered Oxides in Lithium and Sodium-Ion Batteries: A Solid-State Chemistry Approach, Adv. Energy Mater., 2021, 11, 2001201 CrossRef CAS.
- M. G. T. Nathan, H. Yu, G. Kim, J. Kim, J. S. Cho, J. Kim and J.-K. Kim, Recent Advances in Layered Metal-Oxide Cathodes for Application in Potassium-Ion Batteries, Adv. Sci., 2022, 9, 2105882 CrossRef CAS PubMed.
- N. Voronina, M.-Y. Shin, H. Kim, N. Yaqoob, O. Guillon, S. H. Song, H. Kim, H.-D. Lim, H.-G. Jung, Y. Kim, H. Lee, K.-S. Lee, K. Yazawa, K. Gotoh, P. Kaghazchi and S.-T. Myung, Hysteresis-Suppressed Reversible Oxygen-Redox Cathodes for Sodium-Ion Batteries, Adv. Energy Mater., 2022, 12, 2103939 CrossRef CAS.
- L. Yang, R. Chen, Z. Liu, Y. Gao, X. Wang, Z. Wang and L. Chen, Configuration-dependent anionic redox in cathode materials, Battery Energy, 2022, 1, 20210015 CrossRef CAS.
- X.-L. Li, C. Ma and Y.-N. Zhou, Transition Metal Vacancy in Layered Cathode Materials for Sodium-Ion Batteries, Chem. – Eur. J., 2023, 29, e202203586 CrossRef CAS PubMed.
- J. Feng, S. Luo, M. Sun, J. Cong, S. Yan, Q. Wang, Y. Zhang, X. Liu, W. Mu and P. Hou, Investigation of Ti-substitution and MnPO4 coating effects on structural and electrochemical properties of P2-Na0.67TixNi0.33Mn0.67−xO2 cathode materials, Appl. Surf. Sci., 2022, 600, 154147 CrossRef CAS.
- J. Feng, S. Luo, J. Cong, K. Li, S. Yan, Q. Wang, Y. Zhang, X. Liu, X. Lei and P. Hou, Synthesis and electrochemical properties of Co-free P2/O3 biphasic Na1−xLixNi0.33Mn0.67O2 cathode material for sodium-ion batteries, J. Electroanal. Chem., 2022, 916, 116378 CrossRef CAS.
- G. Ponti, F. Palombi, D. Abate, F. Ambrosino, G. Aprea, T. Bastianelli, F. Beone, R. Bertini, G. Bracco, M. Caporicci, B. Calosso, M. Chinnici, A. Colavincenzo, A. Cucurullo, P. Dangelo, M. De Rosa, P. De Michele, A. Funel, G. Furini, D. Giammattei, S. Giusepponi, R. Guadagni, G. Guarnieri, A. Italiano, S. Magagnino, A. Mariano, G. Mencuccini, C. Mercuri, S. Migliori, P. Ornelli, S. Pecoraro, A. Perozziello, S. Pierattini, S. Podda, F. Poggi, A. Quintiliani, A. Rocchi, C. Scio, F. Simoni and A. Vita, in 2014 International Conference on High Performance Computing & Simulation (HPCS), IEEE, 2014, pp. 1030–1033.
| This journal is © the Owner Societies 2023 |
