Electronic effects in the dissociative ionisation of pyrene clusters

Abstract

We present a combined experimental and theoretical study on the dissociative ionisation of clusters of pyrene. We measured the experimental appearance energies in the photon energy range 7.2–12.0 eV of the fragments formed from neutral monomer loss for clusters up to the hexamer. The results obtained show a deviation from statistical dissociation. From electronic structure calculations, we suggest that the role of excited states must be considered in the interpretation of experimental results, even in these relatively large systems. Non-statistical effects in the dissociative ionization process of polycyclic aromatic hydrocarbon (PAH) clusters may have an impact on the assessment of mechanisms determining the stability of these clusters in astrophysical environments.

---

1. Introduction

The existence of neutral or cationic polycyclic aromatic hydrocarbons (PAHs) in astrophysical environments has been proposed for several decades based on the observation of aromatic infrared band (AIB) emission^1,2 and diffuse interstellar bands.³ The former result from excitation by vacuum ultraviolet (VUV) photons up to energies of 13.6 eV. The absorption of VUV photons also controls the charge state and survival of these species in astrophysical environments.⁴ Analysis of the evolution of the AIBs as a function of the physical conditions revealed the probable production of free PAHs from very small grains during VUV processing, leading to the proposal that PAH clusters could be present.^5,6 Models have therefore been developed to quantify the stability of PAH clusters in photodissociation regions (PDRs) associated with star- and planet-forming regions.^7–9 These models use statistical evaporation rates to quantify photodissociation for neutral PAH clusters. None of these models consider cationic clusters, even though they are likely involved in these regions due to the low ionisation energy¹⁰ and the high ionisation cross-section of their neutral precursors.

Theoretical studies have shown that ionisation increases the binding energy of clusters,^11,12 which may favour the survival of ionised clusters compared to their neutral counterparts. Recent experimental and theoretical data on thermal evaporation and collision induced dissociation of pyrene cluster cations confirmed the stabilisation of the cationic clusters with respect to the neutral species through charge resonance.^13,14 On the other hand, the absorption of a single VUV photon by neutral clusters can lead to both ionisation and dissociation via a dissociative ionisation process. While this process has been studied for a number of neutral PAHs,^15,16 data are lacking for PAH clusters. It has been discussed in a number of articles that PAH clusters, if present in PDRs, are likely to be present in UV-protected parts of clouds and subsequently exposed to VUV irradiation.^6,7 In this context, obtaining information on the interaction of PAH clusters with VUV photons is critical for modelling their evolution in astrophysical environments.

In this work, we have prepared pyrene neutral clusters in a molecular beam by adiabatic cooling and we applied double imaging photoelectron photoion coincidence techniques to detect and quantify cluster fragmentation after photoionisation using tuneable synchrotron light in the VUV range. The obtained experimental results present trends that deviate from statistical dissociation. Interpretation of the experimental results is provided via the determination and analysis of the excited potential energy surfaces (PES) in reduced dimensionality within the framework of the Density Functional based Tight Binding Configuration Interaction scheme (DFTB-CI).¹⁷ This approach allows the description of the electronic structure of molecular cation clusters, and has been successfully used in combination with experimental studies of the ionisation of pyrene and coronene clusters,¹⁰ the thermal evaporation and collision induced dissociation of pyrene cluster cations,^13,14 and the photo-absorption spectrum of pyrene dimer cations.¹⁸ We describe here how the topology of the PES of the accessible excited states can rationalize the observed experimental trends.

2. Methodology

2.1. Experimental methods

Experiments were performed at the permanent molecular beam endstation SAPHIRS,¹⁹ situated in one of the monochromatised branches of the VUV beamline DESIRS,²⁰ at the French national synchrotron facility SOLEIL. Pyrene (purity ≥ 98% from Fluka) was placed into an in-vacuum stainless-steel oven and the reservoir heated at a temperature of 180 °C. The top part of the oven was kept 50 °C hotter to avoid condensation on the nozzle. The resulting vapor was mixed with 1.2 bars of argon and expanded through a 50 μm nozzle. The temperature and expansion conditions were chosen to optimise the formation of small clusters. The molecular beam traversed a 2 mm skimmer and entered the ionisation chamber where it crossed the synchrotron beam at a right angle. Under similar expansion conditions internal temperatures in the range 100–300 K have been previously estimated for pyrene.¹⁰

The electrons and ions produced were continuously accelerated in opposite directions by a 35 V cm⁻¹ electric field and detected in coincidence inside the Delicious III spectrometer,²¹ by means of a velocity map imaging (VMI) spectrometer²² and a Wiley–McLaren-based 3D momentum imager. Photoelectron images, and therefore the photoelectron spectra and angular distributions (PADs), can be correlated to a specific mass and cation velocity. Under these conditions, the ion energy resolution is estimated to be 3.5 meV, which is equivalent to a translational energy of 40 K.

The undulator-based beamline DESIRS delivered linearly polarised radiation with an associated electric vector parallel to the molecular beam. The monochromator was configured with the low dispersion 200 grooves per mm grating and the photon flux was optimised to avoid saturation of the detectors, leading to photon resolutions of 13 meV to 3 meV in the 7.2 eV to 12.0 eV energy range considered here. A gas filter located upstream the monochromator was filled with 0.12 mbars of xenon to remove second order radiation and ensure spectral purity at the sample.²³

2.2. Computational methods

The selected quantum chemical methodology must describe correctly charge and excitation resonances between the different units while conserving a low computational cost to deal with the large number of electronic and nuclear degrees of freedom in PAH clusters. Wavefunction type methods such as multireference configuration interaction (MRCI) or complete active space second order perturbation theory (CAS-PT2) are, in principle, able to deal with such charge/excitation resonance, but are too computationally demanding. Density functional methods (DFT) present a better computational efficiency but they are affected, in their standard formulation, by the self-interaction problem, which may hinder their ability to properly describe the PES of resonant-charge systems. Following the previous work of Wu and Van Voorhis²⁴ at the DFT level, we have developed the DFTB-CI method,¹⁷ which combines the DFT based tight-binding (TB) scheme, an approximated DFT method,^25,26 with a configuration interaction CI scheme.²⁴ In this approach, and for a cluster of N units, a set of N DFTB calculations are performed constraining the charge to be localised on each monomer unit. The corresponding wavefunctions {φ_k}_k=1,N are built as Slater determinants of the DFTB molecular orbitals. A non-orthogonal CI is then achieved in the basis of those N wavefunctions, delivering the final energies E_m and eigenvectors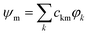 . In this original version, the eigenvectors correspond to all possibilities of delocalising the hole over the cluster structure. In the present work, DFTB-CI has been used with this version for global optimisation of cluster ion geometries.

Not only the ground electronic state, but also charge-transfer excited states can be reached with the DFTB-CI scheme. In addition, we have extended the CI to include localised excitations from the constrained basis functions,²⁷ with only the lowest energetic excitations being considered, i.e., those corresponding to the spin allowed excitation of one electron from a doubly occupied orbital p to the HOMO orbital h, where both p and h are essentially localised on the molecule bearing the charge in configuration k:

φ ^p→h _k = a⁺_pa_hφ_k; p,h∈k

From comparison with ab initio CAS-PT2 calculations, this scheme was found to be relevant to describe the lowest electronic excited states of the benzene, naphthalene and pyrene dimer cations,²⁷ and further proved its ability to describe the ground and electronic excited potential surfaces of these dimer cations throughout important reaction paths, which is still difficult to achieve with TDDFT today.

Dispersion contributions were included using a damped empirical pairwise-additive description for all calculations, either standard DFTB for neutral clusters or DFTB-CI for ions.²⁸ All calculations used the MAT Slater Koster parameters²⁹ and the Charge Model 3 correction of atomic charges, which were shown to provide a better account of the balance between repulsion, electrostatics and dispersion forces for molecular clusters.²⁸

The global optimisation process was reported in a previous work³⁰ and involves a multischeme method with the following steps: (i) a parallel tempering Monte Carlo simulation was first achieved with the rigid molecule approximation and a simplified version of the DFTB-CI scheme in which the CI matrix elements have been parameterized; (ii) a sample of 2000 low energy structures was retained and relaxed within a final all-atom conjugated gradient optimisation process at the DFTB or DFTB-CI level for neutral and cationic clusters, respectively. The full process was repeated to determine the lowest energy isomers for each size and charge state. This process allowed us to determine the energetic properties of the various neutral and ionized clusters. Note that the calculated energy differences discussed in the following do not include the zero-point vibrational energies, the intermolecular modes being quite weak.¹⁴

3. Experimental results

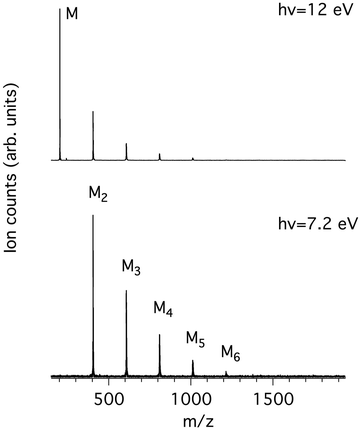
Fig. 1 shows the mass spectra of pyrene obtained at the lowest and highest photon energies considered in this work, 7.2 and 12.0 eV. The low photon energy limit was chosen by considering both previously measured ionisation energies of pyrene clusters¹⁰ and calculated binding energies of cationic clusters³⁰ that give values in the 0.8–1.1 eV range. Therefore, dissociative ionisation is not expected to happen below 7.2 eV even for the largest studied clusters (n = 6, see Table 1). Note that the adiabatic ionisation energy (IE_a) of pyrene was experimentally reported at 7.4256 eV³¹ using the zero kinetic energy (ZEKE) technique and therefore the energy of 7.2 eV is expected to be below the ionisation energy of pyrene monomer in our experiment. Note also that, in our energy range, we do not expect to see masses lighter than the monomer, since the first cationic fragment (m/z 201) due to the loss of H has an appearance energy (AE) of at least 16.6 eV in the μsec time scale of our ion acceleration region.^32,33

Fig. 1 Time-of-Flight mass spectra measured for photon energies of 7.2 eV (bottom) and 12 eV (top).

Table 1 Observed ionisation energies for the parent cation, IE M_n, obtained from ref. 10, and for the loss of a neutral monomer by dissociative ionisation, AE M⁺_n−1 from this work. The AE values were determined from Fig. 5 by two different methods: (i) the first point out of the baseline and (ii) an exponential fit to the onset. The mean values are presented in the AE column and are consistent with an error bar of 100 meV. Observed bond dissociation energies, D^obs M⁺_n are given as AE M⁺_n−1 − IE M_n. Theoretical values of the vertical (IE_v) and adiabatic (IE_a) ionisation energies, the minimal energy E(d + i) to observe dissociative ionisation from the most stable isomer, as well as the bond dissociation energies (D_e = E(d + i) − IE_a) are taken from ref. 30. All units are in eV

Mn	Experiment			Theory
	IE Mn	AE M^+n−1	D ^obs M^+n	IEa/IEv	E(d + i)	D e
n = 2	6.95	8.6	1.65	6.91/7.19	7.98	1.08
n = 3	6.75	7.9	1.15	6.64/6.98	7.43	0.79
n = 4	6.68	7.7	1.02	6.47/6.85	7.35	0.88
n = 5	6.67	7.8	1.13	6.44/6.79	7.30	0.86
n = 6	6.77	8.0	1.23	6.44/6.84	7.32	0.88

---

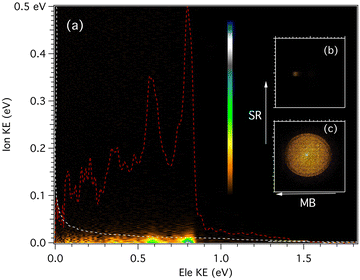
For each of the masses, an electron/ion kinetic energy correlation diagram can be obtained for all photon energies, such as the one pictured in Fig. 2 for the m/z 202 mass recorded at 9.0 eV. From these data, we can extract the photoelectron spectroscopy for a given range of cation translational energies, or the ion kinetic energy release distribution (KERD) for a given vibronic state. The corresponding electron and ion coincident images are also shown in Fig. 2. From the ion image of m/z 202, the velocity along the molecular beam direction was measured to be nearly 650 m sec⁻¹, which corresponds to a beam translational temperature of 94 K assuming a pure argon expansion.

Fig. 2 (a) Kinetic energy correlation diagram for m/z 202 recorded at hν = 9.0 eV, i.e., the intensity matrix representing the number of coincidence events vs. ion and electron kinetic energies. Two possible projections of the matrix are also plotted, the photoelectron spectrum (red dashed line), and the ion KERD (white dashed line). (b) Mass-selected ion and (c) photoelectron images. The molecular beam (MB) velocity is obtained from the lateral displacement of the ion images visible in panel (b). SR = synchrotron radiation.

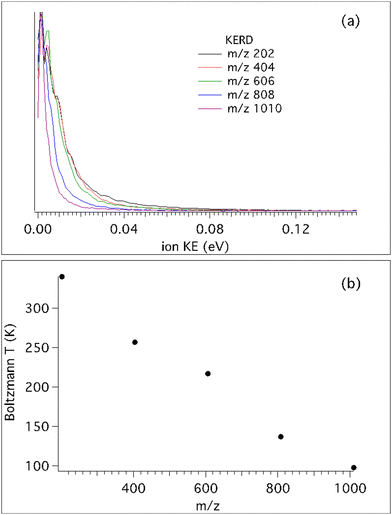
Fig. 3 shows the KERDs and fitted Boltzmann temperatures of the different clusters at a photon energy of 7.2 eV. Note that for the monomer mass m/z 202, the photon energy corresponds to 7.5 eV since its IE_a is higher, at 7.43 eV. It is interesting to note that for the heaviest cation, m/z 1010, the Boltzmann temperature extracted from its KERD perfectly matches the beam translational temperature. But as the number of moieties decreases, the temperature steadily, almost linearly, increases. It is generally assumed that translational cooling inside the molecular beam is most efficient when the molecular mass is similar to that of the carrier gas, so inhomogeneous cooling will not explain this behaviour. Moreover, all clusters present the exact same molecular beam velocity, so the translational temperature difference must be explained by fragmentation processes, either by neutral evaporation in the molecular beam, by dissociative ionisation, or a combination of both. The former has no dependence on the photon energy so that pure dissociative ionisation processes can be observed by measuring the KERD variation as a function of photon energy.

Fig. 3 (a) Ion KERDs up to the pentamer measured at a photon energy of 7.2 eV, except for the monomer which was acquired at 7.5 eV. (b) Translational temperatures extracted from (a) assuming a Boltzmann energy distribution.

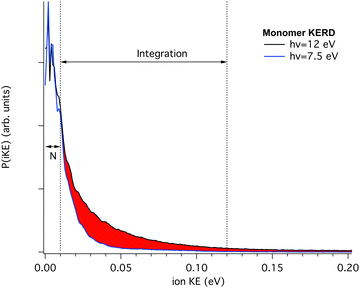
Therefore, we have recorded the KERD of masses up to the pentamer as a function of photon energy. As seen in Fig. 3, neutral clusters possess an initial translational energy due to cascading evaporation processes which, as mentioned above, is independent of the photon energy. Here we will assume that at the lowest photon energy there is no translational component from dissociative ionisation, i.e. that the dissociative ionisation channels are not yet open. In this way, for each mass, and by comparison with their coldest (narrowest) KERD, the signal from dissociative ionisation can be extracted as a function of photon energy, as depicted in Fig. 4 for the case of the m/z 202 channel and hν = 12.0 eV.

Fig. 4 KERDs for m/z 202 recorded at the lowest (7.5 eV) and highest (12.0 eV) photon energy. Assuming that the former belongs only to parent monomer ions, the amount of dissociative ionisation contributing to the m/z 202 channel can be estimated by previous subtraction (after normalisation using the area delimited by N) of the “cold” KERD. The percentage of fragmentation is then given by the red area, divided over the total distribution.

The percentage of dissociative ionisation estimated by comparison with the coldest KERD is displayed in Fig. 5 as a function of photon energy for the channels up to the pentamer. Note that for clusters, the coldest KERD is assumed to be the one at 7.2 eV, while for the monomer it is 7.5 eV.

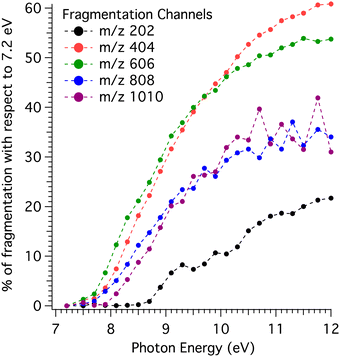Fig. 5 Percentage of dissociative ionisation for the different mass channels obtained via the method outlined in Fig. 4, i.e., by comparison with the KERDs measured at 7.2 eV (7.5 eV for the m/z 202 channel).

The fragmentation behaviour shown in Fig. 5 is remarkable: first, the monomer channel is clearly apart from the rest in terms of fragmentation onset (∼8.7 eV), with the higher mass channels’ onsets concentrated in a region between 7.7 and 7.9 eV (see derived values in Table 1). In addition, the amount of fragmentation in the monomer channel calculated from the method in Fig. 4 is significantly lower. Second, there is some structure in the monomer channel, with several peaks appearing in the curve shown in Fig. 5.

4. Discussion

The presence of a baseline in the fragmentation curves presented in Fig. 5, particularly for the monomer channel, supports the assumption that, at the lowest photon energy, the temperatures measured in Fig. 3b are those of the nascent clusters, and correlate only with fragmentation processes within the neutral clusters via evaporation. A sequential evaporation scenario is consistent with increasing translational temperatures for smaller neutral clusters down to the monomer M_x → M_x−1 + M;⋯;M₂ → M + M, since most of the translational energy will be transferred to the monomer by momentum conservation during the evaporation process.

With increasing photon energy, the excess energy deposited in the cationic cluster will lead to fragmentation (dissociative ionisation), and the appearance of the onsets observed in Fig. 5. Since clusters have lower ionisation energies relative to the monomer,¹⁰ we expect the first appearance threshold to correspond to the ejection of a neutral monomer, with the charge localised onto the largest fragment 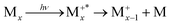. For example, in Fig. 5, only the dimer would contribute to the monomer cation channel through dissociative ionisation. To support this assumption, we also extracted the state selected fragmentation yield in the monomer cation channel, i.e. coincident with slow electrons. The amount of excess energy deposited into the cationic cluster is given by E_int = hv − IE_a − KE_ele. Therefore, selecting the ions correlated to slow electrons (KE_ele∼0) leaves the ions within a well-defined internal state. In this way, the fragmentation becomes state-selected³⁴ and the structures observed in Fig. 5 will be accentuated. Fig. 6 shows the result of this treatment where only ions having electrons with KE_ele < 300 meV are considered. The threshold photoelectron spectrum of the nascent dimer, recorded by only considering photoelectrons in coincidence with cold ions,¹⁰ is also shown for comparison.

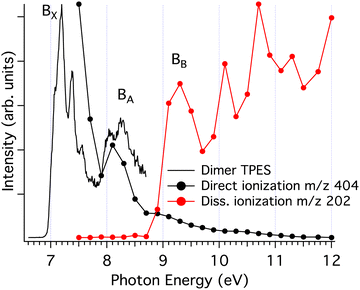Fig. 6 Threshold photoelectron spectrum showing the vibronic states of the pyrene dimer¹⁰ (black curve). The black circles show the threshold photoelectron signal corresponding to direct ionisation of the parent dimer with an energy resolution of 300 meV, obtained by considering only ions having very low translational energies (<20 meV). The red circles show the threshold photoelectron signal corresponding to dissociative ionisation into the monomer channel, obtained with an energy resolution of 300 meV. The experimental bands, B, relevant for the discussion have been labelled.

There is a correlation between the disappearance of the dimer signal (bound dimer states), and the appearance of the signal in the monomer fragment channel, which can be attributed to dissociative dimer states. This reinforces our assumption that the fragmentation of cluster cations proceeds via the loss of a single neutral monomer moiety.³⁰

In principle, we could estimate the dissociation energy (D₀) of the cationic clusters as D₀(M⁺_n) = AE_0K(M⁺_n−1) − IE_a(M⁺_n), assuming a barrierless reaction as observed theoretically in the case of the pyrene dimer (see Fig. 7a). For larger clusters a barrier to the evaporation of a neutral monomer is not expected in view of their published π-stack structures. However, the AE values we can experimentally derive (see Table 1) for the n − 1 fragments are expected to be different from those at 0 K due to statistical kinetic shifts from slow fragmentation rates close to the appearance threshold and to initial thermal energy of the neutral clusters that are expected to shift the AE values to respectively higher and lower energies.^34,35 Therefore we cannot derive precise dissociation energies from our measurements and will refer to observed dissociation energies henceforth.

Fig. 7 Cuts of the PESs for the ground and excited states of plane-parallel pyrene dimer cation along two modes: (a) the breathing mode with a fixed twist angle of 48° (b) the twist mode with a fixed interplane distance of 3.2 Å. The values of 3.2 Å and 48° were chosen as they correspond to the optimised values obtained for a plane-parallel neutral dimer. The points 0 to 7 identify the ground state and the seven lowest excited states and are positioned at the neutral optimised geometry coordinates. The zero of the energy scale corresponds to the first dissociation limit converging to one neutral plus one cationic pyrene unit, both in the ground electronic state. The state crossing points have been named from A to H.

In Table 1, we also report the computed values for the vertical ionisation energy (IE_v), IE_a and the minimal energy E(d + i) to observe ionisation followed by dissociation from the most stable neutral cluster isomer 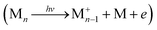, i.e. the energy of the dissociation limit at 0 K without considering possible barriers. From this table, it appears that the observed ionisation energies are between the calculated IE_v and IE_a values of the most stable isomers. It has been shown that under our experimental conditions, isomers at higher energies than the most stable one can be thermally populated and taking this effect into account leads to a better agreement between the calculated and experimental IE values.¹⁰ We can see In Table 1 that the values of the observed dissociation energy D^obs(M⁺_n) are larger than the calculated D_e values for all the considered sizes. Thermal effects such as the population of less stable isomers, or the accumulation of thermal energy in the neutral, would not improve this divergence since they would lead to decreasing values. On the other hand, fragmentation rates which are slower than the experimental analysis window could be invoked to shift the values of AE and therefore of D^obs to higher energies. The corresponding shift ΔE is commonly named as the kinetic shift. As an example, our experimental window to detect fragmentation is 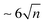μsec and if the fragment detection limit is placed at a molar fraction of 0.01, detection of fragmentation from the dimer cation (n = 2) is only possible in our spectrometer for rate constants larger than ∼10³ s⁻¹ as easily derived from first-order kinetics. Because the rate constant increases with the excess energy deposited in the cation the fragmentation will eventually be fast enough to be detected at ΔE = AE − AE_0K, where ΔE depends on the experimental timescale with respect to the fragmentation rate and the detection limit. The statistical description of the rate constant implies that the kinetic shift increases with the size of the system³⁶ because the rate depends on the ratio between the number of ways that the excess energy can be distributed into transitional modes that lead to fragmentation, and the density of states in the parent ion. In other words, the larger the system the more time it will take for the excess energy to be channelled into the transitional modes and indeed this has been shown to be the case for PAHs too.^16,37 Therefore, with increasing cluster size we would expect the observed dissociation energies to drift to higher values. However, Table 1 shows an unexpected behaviour, with values of D^obs(M⁺_n) remaining almost constant for n > 2 similarly to the theoretical D_e values. On the contrary, the value of D^obs is significantly higher for the dimer, as is the difference between observed and theoretical values. This can be partly due to the larger dissociation energy of the dimer cation by ∼0.3 eV compared to the larger clusters as derived in threshold collision induced dissociation experiments and consistently with theoretical calculations using the DFTB-CI scheme.¹³ However, this cannot fully explain the 0.5 eV relative stability of the pyrene dimer parent ion with respect to the trimer taking into consideration statistical redistribution of the excess energy amongst all internal modes in both systems. All these observations suggest that non-statistical effects play a role in the dissociative ionisation of pyrene clusters in which the excess energy is trapped into electronic excitation instead of being distributed into the rovibrational modes of the cation ground state.

The above proposal calls for an evaluation of the role of excited states in the relaxation and fragmentation of these clusters, the study of which appears challenging. A number of studies do exist in the case of prototype systems such as rare gas clusters due to the relevance of the Diatomics-In-Molecules approach–see for instance ref. 38–41 and references therein. In relatively small aromatic compounds and PAH cation monomers, the theoretical description of energy relaxation and conversion in electronic excited states has been investigated by several groups,^42–51 analysing the role of conical intersections and the efficiency of non-adiabatic transitions and vibrational redistribution. However, theoretical studies on excited states of PAH clusters ions are sparse^17,27,52 due to the large number of electronic and nuclear degrees of freedom. Total electronic-to-vibrational conversion would lead to a hot ground state from which statistical fragmentation then takes place on a given timescale.^15,53,54 Given the aforementioned disagreement of our experimental data with such statistical behaviour, we report here a topological analysis of the ground and excited states electronic PES in reduced dimensionality for the dimer.

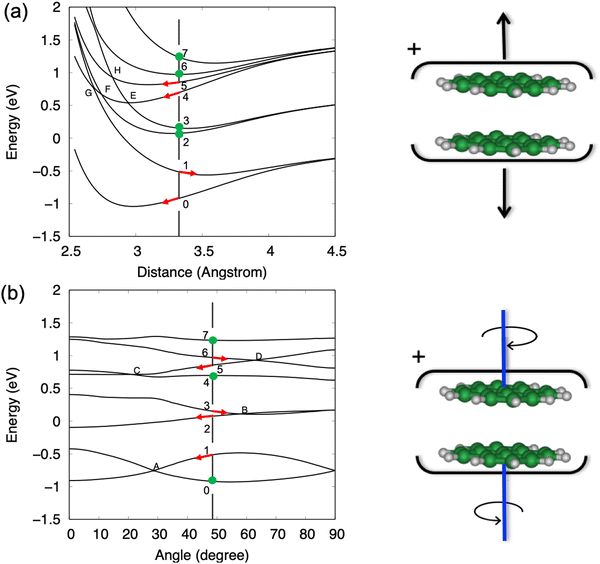
To calculate the PESs of the pyrene dimer cation, the two PAH units are kept frozen, plane parallel, and the centres of mass on top of each other. Exploration of the PESs is then limited to two intermolecular modes, namely the breathing mode and the twist mode, with only the former leading to dissociation. Note that the twist mode consists of two molecules pivoting on top of each other and does not involve global rotation of the cluster. The full 2D PES plots for the ground state and the seven lowest excited states can be found in Fig. S1 (ESI†) of the supplementary information. Fig. 7 shows cuts of the PESs obtained at the equilibrium coordinates of the plane-parallel neutral dimer, i.e., a distance of 3.3 Å and an angle of 48° between the in-plane axis of the two pyrene units. Note that energy bands above 10 eV are not addressed as the DFTB-CI description of these energetic excited states becomes less accurate.²⁷

In Fig. 7a, we identify four pairs of states converging at infinite distance onto one neutral molecule and one cation, with the cation being in its ground state, and first, second or third electronically excited states. As the intermolecular distance decreases, these pairs split due to charge/excitation resonance, but there is no coupling between states of the same pair because symmetry is preserved along this coordinate. The situation is different when the cluster undergoes a relative rotation of the two units, as shown in Fig. 7b, because the symmetry breaking allows coupling between modes and the splitting can fall to zero as it happens, for example, at point A for the ground state and the first excited state.

The calculations lead to the assignment of the first three experimental bands on the photoelectron spectrum of the dimer shown in Fig. 6, to ionisation to the ground state and first excited state of the cation for the B_X band at 7.1–7.5 eV, to the second and third excited states for the B_A band at 8.0–8.6 eV, and to the group formed by the fourth to seventh excited states for the B_B band at 9.0–9.7 eV. Energetically, the B_X band lies below the calculated first dissociation limit, which is consistent with the experimental data where no fragmentation is observed in this energy region. However, the B_A band should lead to fragmentation based on thermochemical arguments alone since the second and third excited states lie above the first dissociation limit. A reason for the unexpected stability can be found in Fig. 7, where the gradient along the dissociation coordinate in these states is rather small at the neutral equilibrium geometry (points 2 and 3 in Fig. 7a), so the system will progress along the twist coordinate (points 2 and 3 in Fig. 7b). In other words, a sufficient excess energy would be immediately dissipated in relative rotation of the units and direct fragmentation would be avoided. Only indirect (also called statistical) fragmentation would remain possible, eventually in competition with other relaxation processes such as radiative cooling, but on a much longer timescale, i.e. longer than the experimental timescale. Note that the third excited state evolves towards the second one through a crossing point (point B in Fig. 7b), conferring more energy to the rotation.

A different behaviour is observed for the states constituting the B_B band. Indeed, the gradient for the fourth electronically excited state is strong along the dissociation coordinate (point 4 in Fig. 7a). The system can then evolve to the third excited state through a crossing point (point E in Fig. 7a) transferring 0.54 eV (energy difference between points 3 and 4) to the breathing mode. Although further evolution from this point will transfer energy to the rotation as seen for B_A band, the system will likely have enough energy stored in the breathing mode for rapid dissociation. A similar behaviour would be expected if relaxation occurs through the crossing point F and even more efficient dissociation would be expected if the first excited state is reached at the point G. Similar arguments apply to dissociation from the fifth or sixth states since they can reach the fourth state by relative rotation of the units as seen in Fig. 7b. Note that fragmentation from the B_B band to the second dissociation limit is now energetically available.

To summarise this attempt to interpret the first three bands, it appears that (i) the B_x band corresponds to absorption in the ground state or in the first excited state of the cationic dimer for which the system does not have enough energy to dissociate, (ii) the B_A band corresponds to absorption in the second or third excited states. The system has enough energy to dissociate but part of this energy is initially given to the non-dissociative twist mode, preventing rapid dissociation. Therefore, in this case, the kinetic shift is not given solely by statistical arguments but arises from electronic effects hindering the reaction. Finally, (iii) the BB band corresponds to absorption in the fourth and higher excited states, for which a significant part of the energy is initially given to the breathing mode, promoting rapid dissociation. One should note that rotational coupling, not considered in the present analysis, is also likely to reduce reaction yields or to increase reaction delays, as documented in simpler systems.^55,56

5. Conclusion

We measured the appearance energies of fragments from dissociative ionisation of pyrene clusters formed in a molecular beam expansion. We were able to distinguish these fragmentation processes from direct ionisation by measuring the ion KERDs in coincidence with photoelectron spectroscopy using a double imaging photoelectron photoion coincidence techniques. We observe that in the molecular beam, the larger clusters experience fragmentation and evaporate single monomer units. This cluster population is then ionised with synchrotron radiation at different photon energies and the amount of dissociative ionisation in all observed mass channels is recorded.

The comparison between the calculated and observed cation stability towards neutral monomer evaporation highlights a non-statistical behaviour: the difference between the corresponding dissociation energies does not increase with the size of the cluster, as would be expected due to the increased kinetic shift when the number of oscillators increases. The calculations show that the energetics and topology of the excited state PESs play an important role on the energy flow and stability of the cationic clusters and could explain the increased stability observed for the pyrene dimer cation. The extended DFTB-CI provides a description not only of the charge transfer states, but also of the locally excited states, but the present theoretical interpretation only concerns the early-stage evolution after excitation, and is restricted to two inter-molecular modes, starting from the lowest energy structure of the dimer. Various aspects such as structural excitation and account of low energy isomers, consideration of the other intermolecular and intramolecular degrees of freedom, dynamical effects such as rotational coupling and non-adiabatic transitions, have not been treated in the present study. Nevertheless, although non-adiabatic dynamics combined with DFTB-CI requires computational developments which are not yet available, the present work emphasizes the role of excited states in the VUV induced photo-fragmentation process, which will incite further theoretical advances. Finally, the present study throws a word of caution against the systematic use of statistical methods only to model the fragmentation of PAH clusters. This is particularly true in the case of dissociative ionisation upon VUV irradiation, as studied in this work, a key process for the evolution of PAH clusters in PDRs that may be revealed by the observations from the James Webb Space Observatory.⁵⁷

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the DESIRS beamline team, in particular to J.-F. Gil for his technical assistance on the SAPHIRS set-up, and to the SOLEIL general staff for running the facility and granting beamtime under project 20130628. We acknowledge the financial support of the Agence Nationale de la Recherche through the GASPARIM project Gas-phase PAH research for the interstellar medium (ANR-10-BLAN-0501) and the use of computing resources offered by the CALMIP supercomputing centre (allocation 2015-P0059). L. D. and C. J. acknowledge support from the European Research Council under grant ERC-2013- Syg-610256-NANOCOSMOS.

References

1. A. Leger and J. L. Puget, Identification of the unidentified IR emission features of interstellar dust, Astron. Astrophys., 1984, 137, L5.
2. L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Polycyclic aromatic hydrocarbons and the unidentified infrared emission bands - Auto exhaust along the Milky Way, Astrophys. J., 1985, 290, L25.
3. F. Salama, G. A. Galazutdinov, J. Krełowski, L. Biennier and Y. Beletsky, et al., Polycyclic aromatic hydrocarbons and the diffuse interstellar bands: a survey, Astrophys. J., 2011, 728, 154.
4. J. Montillaud, C. Joblin and D. Toublanc, Evolution of polycyclic aromatic hydrocarbons in photodissociation regions, Astron. Astrophys., 2013, 552, A15.
5. M. Rapacioli, C. Joblin and P. Boissel, Spectroscopy of polycyclic aromatic hydrocarbons and very small grains in photodissociation regions, Astron. Astrophys., 2005, 429, 193.
6. P. Pilleri, J. Montillaud, O. Berné and C. Joblin, Evaporating very small grains as tracers of the UV radiation field in photo-dissociation regions, Astron. Astrophys., 2012, 542, A69.
7. M. Rapacioli, F. Calvo, C. Joblin, P. Parneix and D. Toublanc, et al., Formation and destruction of polycyclic aromatic hydrocarbon clusters in the interstellar medium, Astron. Astrophys., 2006, 460, 519.
8. J. Montillaud and C. Joblin, Absolute evaporation rates of non-rotating neutral polycyclic aromatic hydrocarbon clusters, Astron. Astrophys., 2014, 567, A45.
9. K. Lange, C. Dominik and A. G. G. M. Tielens, Stability of polycyclic aromatic hydrocarbon clusters in protoplanetary discs, Astron. Astrophys., 2021, 653, A21.
10. C. Joblin, L. Dontot, G. A. Garcia, F. Spiegelman and M. Rapacioli, et al., Size Effect in the Ionization Energy of PAH Clusters, J. Phys. Chem. Lett., 2017, 8, 3697.
11. M. Rapacioli and F. Spiegelman, Modelling singly ionized coronene clusters, Eur. Phys. J. D, 2009, 52, 55.
12. Y. M. Rhee, T. J. Lee, M. S. Gudipati, L. J. Allamandola and M. Head-Gordon, Charged polycyclic aromatic hydrocarbon clusters and the galactic extended red emission, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 5274.
13. S. Zamith, J. M. L’Hermite, L. Dontot, L. Zheng and M. Rapacioli, et al., Threshold collision induced dissociation of pyrene cluster cations, J. Chem. Phys., 2020, 153, 054311.
14. S. Zamith, M. C. Ji, J. M. L’Hermite, C. Joblin and L. Dontot, et al., Thermal evaporation of pyrene clusters, J. Chem. Phys., 2019, 151, 194303.
15. H. W. Jochims, E. Ruhl, H. Baumgartel, S. Tobita and S. Leach, Size effects on dissociation rates of polycyclic aromatic hydrocarbon cations - laboratory studies and astrophysical implications, Astrophys. J., 1994, 420, 307.
16. B. West, S. Rodriguez Castillo, A. Sit, S. Mohamad and B. Lowe, et al., Unimolecular reaction energies for polycyclic aromatic hydrocarbon ions, Phys. Chem. Chem. Phys., 2018, 20, 7195.
17. M. Rapacioli, F. Spiegelman, A. Scemama and A. Mirtschink, Modeling Charge Resonance in Cationic Molecular Clusters: Combining DFT-Tight Binding with Configuration Interaction, J. Chem. Theory Comput., 2011, 7, 44.
18. J. Bernard, A. Al-Mogeeth, S. Martin, G. Montagne and C. Joblin, et al., Experimental and theoretical study of photo-dissociation spectroscopy of pyrene dimer radical cations stored in a compact electrostatic ion storage ring, Phys. Chem. Chem. Phys., 2021, 23, 6017.
19. X. Tang, G. A. Garcia, J.-F. Gil and L. Nahon, Vacuum upgrade and enhanced performances of the double imaging electron/ion coincidence end-station at the VUV beamline DESIRS, Rev. Sci. Instrum., 2015, 86, 123108.
20. L. Nahon, N. de Oliveira, G. A. Garcia, J.-F. Gil and B. Pilette, et al., DESIRS: a state-of-the-art VUV beamline featuring high resolution and variable polarization for spectroscopy and dichroism at SOLEIL, J. Synchrotron Radiat., 2012, 19, 508.
21. G. A. Garcia, B. K. C. de Miranda, M. Tia, S. Daly and L. Nahon, DELICIOUS III: A multipurpose double imaging particle coincidence spectrometer for gas phase vacuum ultraviolet photodynamics studies, Rev. Sci. Instrum., 2013, 84, 053112.
22. A. T. J. B. Eppink and D. H. Parker, Velocity map imaging of ions and electrons using electrostatic lenses: Application in photoelectron and photofragment ion imaging of molecular oxygen, Rev. Sci. Instrum., 1997, 68, 3477.
23. B. Mercier, M. Compin, C. Prevost, G. Bellec and R. Thissen, et al., Experimental and theoretical study of a differentially pumped absorption gas cell used as a low energy-pass filter in the vacuum ultraviolet photon energy range, J. Vac. Sci. Technol., A, 2000, 18, 2533.
24. Q. Wu, B. Kaduk and T. Van Voorhis, Constrained density functional theory based configuration interaction improves the prediction of reaction barrier heights, J. Chem. Phys., 2009, 130, 034109.
25. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner and M. Haugk, et al., Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260.
26. D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947.
27. L. Dontot, N. Suaud, M. Rapacioli and F. Spiegelman, An extended DFTB-CI model for charge-transfer excited states in cationic molecular clusters: model studies versus ab initio calculations in small PAH clusters, Phys. Chem. Chem. Phys., 2016, 18, 3545.
28. M. Rapacioli, F. Spiegelman, D. Talbi, T. Mineva and A. Goursot, et al., Correction for dispersion and Coulombic interactions in molecular clusters with density functional derived methods: application to polycyclic aromatic hydrocarbon clusters, J. Chem. Phys., 2009, 130, 244304.
29. J. Frenzel, A. F. Oliveira, N. Jardillier, T. Heine and G. Seifert, Semi-relativistic, self-consistent charge Slater-Koster tables for density-functional based tight-binding (DFTB) for materials science simulations, TU-Dresden, 2004.
30. L. Dontot, F. Spiegelman and M. Rapacioli, Structures and Energetics of Neutral and Cationic Pyrene Clusters, J. Phys. Chem. A, 2019, 123, 9531.
31. J. Zhang, F. Han and W. Kong, Zero Kinetic Energy Photoelectron Spectroscopy of Pyrene, J. Phys. Chem. A, 2010, 114, 11117.
32. J. Zhen, S. R. Castillo, C. Joblin, G. Mulas and H. Sabbah, et al., VUV photo-processing of PAH cations: quantitative study on the ionization versus fragmentation processes, Astrophys. J., 2016, 822, 113.
33. B. West, F. Useli-Bacchitta, H. Sabbah, V. Blanchet and A. Bodi, et al., Photodissociation of Pyrene Cations: Structure and Energetics from C16H10+ to C14+ and Almost Everything in Between, J. Phys. Chem. A, 2014, 118, 7824.
34. T. Baer and W. L. Hase, Unimolecular reaction dynamics: theory and experiments, Oxford University Press, New York, 1996.
35. B. Sztaray, A. Bodi and T. Baer, Modeling unimolecular reactions in photoelectron photoion coincidence experiments, J. Mass Spectrom., 2010, 45, 1233.
36. C. Lifshitz, Time-resolved appearance energies, breakdown graphs, and mass spectra: The elusive “kinetic shift”, Mass Spectrom. Rev., 1982, 1, 309.
37. Y. Ling, Y. Gotkis and C. Lifshitz, Time-dependent mass spectra and breakdown graphs. 18. pyrene, Eur. J. Mass Spectrom., 1995, 1, 41.
38. R. Kalus, I. Janeček and F. X. Gadéa, Non-adiabatic dynamics combining Ehrenfest, decoherence, and multiscale approaches applied to ionic rare-gas clusters photodissociation, post-ionization fragmentation, and collisions, Comput. Theor. Chem., 2019, 1153, 54.
39. D. Bonhommeau, N. Halberstadt and U. Buck, Fragmentation of rare-gas clusters ionized by electron impact: new theoretical developments and comparison with experiments, Int. Rev. Phys. Chem., 2007, 26, 353.
40. F. Calvo, D. Bonhommeau and P. Parneix, Multiscale dynamics of cluster fragmentation, Phys. Rev. Lett., 2007, 99, 083401.
41. M. Amarouche, G. Durand and J. P. Malrieu, Structure and stability of Xe_n⁺ clusters, J. Chem. Phys., 1988, 88, 1010.
42. E. Posenitskiy, M. Rapacioli, D. Lemoine and F. Spiegelman, Theoretical investigation of the electronic relaxation in highly excited chrysene and tetracene: The effect of armchair vs. zigzag edge, J. Chem. Phys., 2020, 152, 074306.
43. E. Posenitskiy, M. Rapacioli, B. Lepetit, D. Lemoine and F. Spiegelman, Non-adiabatic molecular dynamics investigation of the size dependence of the electronic relaxation in polyacenes, Phys. Chem. Chem. Phys., 2019, 21, 12139.
44. A. Marciniak, V. Despré, T. Barillot, A. Rouzée and M. C. E. Galbraith, et al., XUV excitation followed by ultrafast non-adiabatic relaxation in PAH molecules as a femto-astrochemistry experiment, Nat. Commun., 2015, 6, 7909.
45. S. Ghanta, V. S. Reddy and S. Mahapatra, Theoretical study of electronically excited radical cations of naphthalene and anthracene as archetypal models for astrophysical observations. Part I. Static aspects, Phys. Chem. Chem. Phys., 2011, 13, 14523.
46. S. Ghanta, V. S. Reddy and S. Mahapatra, Theoretical study of the electronically excited radical cations of naphthalene and anthracene as archetypal models for astrophysical observations. Part II. Dynamics consequences, Phys. Chem. Chem. Phys., 2011, 13, 14531.
47. S. N. Reddy and S. Mahapatra, Theoretical study on molecules of interstellar interest. I. Radical cation of noncompact polycyclic aromatic hydrocarbons, J. Phys. Chem. A, 2013, 117, 8737.
48. V. S. Reddy, S. Ghanta and S. Mahapatra, First principles quantum dynamical investigation provides evidence for the role of polycyclic aromatic hydrocarbon radical cations in interstellar physics, Phys. Rev. Lett., 2010, 104, 111102.
49. A. M. Tokmachev, M. Boggio-Pasqua, D. Mendive-Tapia, M. J. Bearpark and M. A. Robb, Fluorescence of the perylene radical cation and an inaccessible D(0)/D(1) conical intersection: An MMVB, RASSCF, and TD-DFT computational study, J. Chem. Phys., 2010, 132, 044306.
50. A. M. Tokmachev, M. Boggio-Pasqua, M. J. Bearpark and M. A. Robb, Photostability via Sloped Conical Intersections: A Computational Study of the Pyrene Radical Cation, J. Phys. Chem. A, 2008, 112, 10881.
51. K. F. Hall, M. Boggio-Pasqua, M. J. Bearpark and M. A. Robb, Photostability via sloped conical intersections: a computational study of the excited states of the naphthalene radical cation, J. Phys. Chem. A, 2006, 110, 13591.
52. B. Bouvier, V. Brenner, P. Millié and J.-M. Soudan, A Model Potential Approach to Charge Resonance Phenomena in Aromatic Cluster Ions, J. Phys. Chem. A, 2002, 106, 10326.
53. O. Braitbart, E. Castellucci, G. Dujardin and S. Leach, Radiationless transitions in excited electronic states of the benzene cation in the gas phase, J. Phys. Chem., 1983, 87, 4799.
54. E. Ruehl, S. D. Price and S. Leach, Single and double photoionization processes in naphthalene between 8 and 35 eV, J. Phys. Chem., 1989, 93, 6312.
55. E. K. Anderson, A. F. Schmidt-May, P. K. Najeeb, G. Eklund and K. C. Chartkunchand, et al., Spontaneous Electron Emission from Hot Silver Dimer Anions: Breakdown of the Born-Oppenheimer Approximation, Phys. Rev. Lett., 2020, 124, 173001.
56. L. Krim, P. Qiu, N. Halberstadt, B. Soep and J. P. Visticot, Femtosecond Chemistry, Wiley-VCH Verlag GmbH, Weinheim, Germany, 1994, pp. 433–447.
57. O. Berné, É. Habart, E. Peeters, A. Abergel and E. A. Bergin, et al., PDRs4All: A JWST Early Release Science Program on Radiative Feedback from Massive Stars, Publ. Astron. Soc. Pac., 2022, 134, 054301.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05679h

---