Branching ratios in the dissociative photoionization of iodomethane by photoelectron photoion coincidence
Andras
Bodi
 *a,
Arnar
Hafliðason
*a,
Arnar
Hafliðason
 b and
Ágúst
Kvaran
b and
Ágúst
Kvaran
 b
b
aLaboratory for Synchrotron Radiation and Femtochemistry, Paul Scherrer Institute, 5232 Villigen, Switzerland. E-mail: andras.boedi@psi.ch
bScience Institute, University of Iceland, Dunhagi 3, 107 Reykjavík, Iceland
First published on 20th February 2023
Abstract
Iodomethane yields ten fragment ions after valence photoionization, in part by multiple dissociation pathways for each, thanks to a plethora of electronic states available in the parent ion as well as in the fragments. The comprehensive breakdown diagram from 11 eV to the double ionization onset, i.e., 26.7 eV, is recorded at high resolution using double imaging photoelectron photoion coincidence spectroscopy with synchrotron vacuum ultraviolet radiation. Based on fragment ion groupings, the changing branching ratios between these groups and between fragment ions within each group, as well as ancillary thermochemistry, we provide an overview of the dissociation pathways at play. Statistical and impulsive dissociations are identified using kinetic energy release analysis. Finally, a newly observed regime change is discussed in double ionization, whereby coincident H+ + I+ formation dominates over a 4 eV photon energy range, outcompeting the normally prevailing CH3+ + I+ channel.
Introduction
As pointed out by Das et al.,1 iodomethane (methyl iodide) is one of the most studied molecules when it comes to ionization, dissociative ionization, or probing the evolution of excited neutrals using time-resolved spectroscopic techniques. Precisely because iodomethane is considered a spectroscopic benchmark system, new experimental techniques, such as ion imaging and velocity map imaging, were also first demonstrated with CH3I as a sample.2,3 True to form, the first imaging photoelectron photoion coincidence (iPEPICO) work on CH3I at the VUV beamline of the Swiss Light Source yielded the iodomethane dissociative photoionization (DPI) threshold to the methyl cation more than a decade ago.4 We will now briefly review recent works on iodomethane before discussing the motivation to revisit CH3I valence photoionization.The photoelectron spectrum of iodomethane was recorded by Holland et al.5 using synchrotron radiation at a photon energy of 85 eV in the 9–28 eV energy range. Together with XUV results,6,7 this showed that iodomethane cannot be core ionized below 50 eV. In addition to the threshold photoelectron spectrum up to 21 eV, Locht et al. also reported iodomethane photoabsorption and photoionization mass spectra.8 Besides the abundantly discussed CH3+/° and I°/+ fragments, they also provided data on the CH2I+ and CH2+ fragment ions and how autoionization contributes to the TPES and influences the dissociative ionization mechanism.
Resonant multiphoton ionization experiments with cation velocity map imaging and time-of-flight mass analysis revealed three pathways after resonant absorption in the 6.9–8.7 eV energy range, followed by the absorption of a further photon. The first leads to dissociation to the excited Rydberg manifold of the iodine atom and a ground-state methyl radical. Alternatively, autoionization to the ground ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) + state of CH3I+ may eventually yield CH3+ and a ground or excited state iodine atom, or, third, a CH3+ + I− ion pair can be formed.9
+ state of CH3I+ may eventually yield CH3+ and a ground or excited state iodine atom, or, third, a CH3+ + I− ion pair can be formed.9
Photoelectron photoelectron double coincidence measurements (PEPECO) provide complete information of the electron energy distributions in single photon double ionization10 as well as the double ionization spectrum, i.e., the electron–electron coincidence signal as a function of double ionization energy.11 Such measurements provided invaluable input to support the theoretical treatment of photoionization to unveil electronic decay reactions.12 Photoion photoion double coincidence (PIPICO) measures branching ratios in the decay of double charged cations, as shown by Masuoka and Koyano for fluoromethane.13 Eland highlighted the photoelectron photoion photoion triple coincidence (PEPIPICO) technique with filtered HeII radiation to obtain initial momentum and angular information on the one neutral and two charged fragments of several doubly charged cations, including iodomethane.14 When considering CH3X compounds with substituents more abundant in space than iodine, such charge separation processes after double ionization can also have astrochemical relevance in X-ray radiation fields.15
Studies on the valence states of the iodomethane cation and analogue compounds are, nonetheless, comparatively rare.16–18 Powis studied dissociative photoionization branching ratios and kinetic energy distributions by PEPICO in the energy range of the Ã+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2A1 and
2A1 and ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2E cation states of CH3I+ and proposed that state-selected, i.e., nonstatistical, fragmentation mechanisms are at play.19 Tsai et al. employed threshold PEPICO and reported appearance energies for bromo- and iodomethanes.20 The 0 K threshold energy to CH3+ + I was found to be 12.25 ± 0.03 eV, apparently confirmed by a later, high-resolution molecular beam pulsed-field ionization (PFI-)PEPICO work by Song et al. as 12.269 ± 0.003 eV.21 Later, Lee and Kim could bracket the threshold energy by exciting the iodomethane cation to discreet vibrational states of the Ã+ cation electronic state.22 The DPI threshold was thus established to lie between 12.235 and 12.251 eV using action spectroscopy, outside the error bar of the PFI-PEPICO measurement. This discrepancy motivated the first iodomethane iPEPICO study at the VUV beamline of the Swiss Light Source more than a decade ago.4 The onset energy:
2E cation states of CH3I+ and proposed that state-selected, i.e., nonstatistical, fragmentation mechanisms are at play.19 Tsai et al. employed threshold PEPICO and reported appearance energies for bromo- and iodomethanes.20 The 0 K threshold energy to CH3+ + I was found to be 12.25 ± 0.03 eV, apparently confirmed by a later, high-resolution molecular beam pulsed-field ionization (PFI-)PEPICO work by Song et al. as 12.269 ± 0.003 eV.21 Later, Lee and Kim could bracket the threshold energy by exciting the iodomethane cation to discreet vibrational states of the Ã+ cation electronic state.22 The DPI threshold was thus established to lie between 12.235 and 12.251 eV using action spectroscopy, outside the error bar of the PFI-PEPICO measurement. This discrepancy motivated the first iodomethane iPEPICO study at the VUV beamline of the Swiss Light Source more than a decade ago.4 The onset energy:
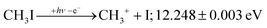 | (1) |
This iPEPICO experiment yielded a well-resolved CH3I breakdown diagram,4 which showed that resonant ionization into the vibrational progression of the Ã+ state resulted in a narrow CH3I+ internal energy distribution. Thus, rotationally excited neutrals have a lower threshold ionization cross section in resonance. In contrast, the apparent parent ion internal energy distribution corresponded to slightly higher than room temperature off resonance, i.e., between the vibrational peaks in the photoelectron spectrum. Rotational excitation was therefore suggested to promote internal conversion of the prompt high-n Rydberg states, belonging to the Ã+ manifold, to neutral dissociative valence states. Thus, the autoionization of predominantly rotationally cold neutrals was responsible for the narrower internal energy distribution in resonance. This can be contrasted with the proposed PFI-PEPICO dissociation mechanism, in which long-lived Rydberg states were postulated to dissociate, followed by autoionization of the Rydberg fragment, i.e., delayed ion formation after fragmentation.23
Cation fragmentation rates, fractional product abundances and excess energy distributions can be modelled in a statistical framework including parallel and sequential fragmentation steps.24 This often yields new and accurate thermochemistry with the help of the ion cycle.25 Furthermore, discrepancies between the statistical prediction and the experimental observation can shine light on non-statistical behavior. Halogen atom loss is ubiquitous in halogen-containing organics, and is often driven by a conical intersection with a seam leading to a repulsive region of the lower-lying state.26 Truly isolated-state behavior, i.e., disjunct statistical dissociation regimes were reported in tetrafluoroethylene.27 A further, somewhat surprising phenomenon is that impulsive, non-statistical dissociation can be followed by a statistical regime in the energy range of excited cation states,28,29 or when impulsive behavior is constrained to a single excited state only.30
PEPICO spectroscopy is not only an emerging analytical tool,31,32 but it reveals the ionization mechanism, the character of the prompt cation state and its coupling to the lower-lying states. This has motivated us to revisit the iodomethane DPI, focusing on high-energy processes. Iodomethane only has two types of covalent bonds (C–I and C–H) making its fragmentation apparently one of the simplest one to study. Breaking these bonds in the cation represents four fragmentation channels, depending on the location of the charge, which are effectively reduced to three at lower energies because of the comparatively high ionization energy of the hydrogen atom at 13.60 eV:33
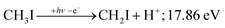 | (2) |
However, as will be shown later, the wealth of fragmentation channels as well as excited parent and fragment electronic states mean that the iodomethane cation fragmentation dynamics is driven by a very rich photochemistry.
Experimental
Iodomethane (99%) was purchased from Sigma-Aldrich and used as received. Photoionization experiments were conducted at the VUV beamline of the Swiss Light Source using the CRF-PEPICO endstation.40,41 The sample was introduced into the ionization chamber at room temperature using a needle valve through a Teflon tube at a pressure of 2 × 10−6 mbar. Bending magnet synchrotron radiation was collimated, dispersed by a 1200 grooves per mm laminar grating and focused in a rare gas filter42 on a 200 μm exit slit. When using photon energies below 21.5 eV, the differentially pumped gas filter was filled with 10 mbar of neon over an effective optical length of 10 cm to suppress the higher order radiation of the grating. In experiments above this energy, the higher order radiation is expected to account for less than 5–10% of the photon flux. The monochromatized light entered the interaction chamber and ionized the sample in a 2 × 2 mm2 spot. The photoelectrons and -ions were extracted by a constant, 260 V cm−1 electric field and detected using fast, position-sensitive Roentdek DLD40 delay-line detectors in delayed coincidence in velocity map imaging and, for the cations, first order space focusing43 conditions. Threshold electrons are, thus, focused onto a small spot in the center of the detector. By subtracting the hot electron contribution, i.e., the signal due to kinetic electrons without any initial off-axis momentum component and also imaged onto this spot, we obtain threshold photoionization mass spectra as well as the corresponding mass-selected cation velocity map images.44 Dissociation rate constants commensurate with the ion residence time in the acceleration region, on the range of μs, show up as asymmetric peaks in the TOF mass spectrum.24 In the absence of such peaks, iodomethane cation fragmentation processes are all fast on the experimental time scale and none of the precursor ions is metastable.Computational
While the thermochemistry of most species is well known, density functional calculations were needed to establish the dissociative ionization thresholds of CHI+ and CI+ formation. These were carried out using the ωB97X-D functional45,46 with the aug-cc-pVTZ-PP basis set and effective core potential on iodine47,48 as well as the PBE0 functional49 with the def2-TZVPPD basis set.47,50,51 The basis sets were obtained from the Basis Set Exchange,52 and the calculations carried out using Gaussian 16.53 The PBE0 and ωB97X-D results agreed generally well. However, the energy threshold to C+ + I + H2 + H formation, known to be 21.73 eV (see Table 1), was better reproduced by ωB97X-D (22.11 eV) than by PBE0 (22.43 eV). Therefore, we also report ωB97X-D values for the CHI+ + H2 and CI+ + H2 + H formation thresholds as 12.92 and 16.46 eV, respectively. For completeness, the analogous PBE0 results were 12.93 and 16.50 eV. These ωB97X-D results, partly in combination with the known H2 bond energy (Table 1), were used to obtain the threshold energies of reactions (11) and (14), involving CHI+, as well as (15) and (16), involving CI+ (see below). The intramolecular H atom transfer (H-transfer) path from CH3I+ to CH2IH+ in HI(+) elimination was also explored using the B3LYP functional,54,55 and the methyl cation was calculated using the G4 method.56 Furthermore, the breakdown diagram of the CHn+ group of species was modelled in terms of statistical theory, relying on the known thermochemical thresholds and B3LYP-calculated harmonic frequencies to obtain densities of states for the excess energy redistribution.24 Finally, the character of the excited CH3I+ electronic states is generally known from the literature, but some insights, such as the H-transfer reaction energy curve, demanded a computational treatment. We carried out equation of motion (for ionization energies) with coupled cluster singles and doubles, EOM-(IP-)CCSD,57 calculations with singlet and triplet neutral as well as doublet cation references and the 6-311G(d,p) basis set58,59 with Q-Chem 4.360 to provide additional insights.| ΔfH⊖0K | ± | Ref.a | |
|---|---|---|---|
| (kJ mol−1) | |||
| a Computed based on the G4 and ae-EOM-IP-CCSD/cc-pVQZ//G4 calculated T0–S0 energy difference in CH3+. b Estimated based on the average of the ae-EOM-IP-CCSD/cc-pVQZ computed S1–T0 energy gap of 0.42 and 0.36 eV at the neutral and T0 triplet cation geometries, respectively. 1 eV = 96.485 kJ mol−1. | |||
| CH3I | 22.76 | 0.30 | 4 |
CH3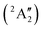 |
149.866 | 0.055 | 34 |
CH3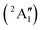 |
699 | 34 and 35 | |
CH3+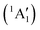 |
1099.339 | 0.050 | 34 |
| CH3+ (3E′) | 1440 | Calc’d hereina | |
| CH3+ (1E′) | 1478 | Calc'd hereinb | |
| I (2P3/2) | 107.157 | 0.002 | 34 |
| I* (2P1/2) | 198.109 | 0.002 | 34 and 36 |
| I** (2[2]5/2) | 760.716 | 0.002 | 34 and 36 |
| I+ (3P2) | 1115.549 | 0.006 | 34 |
| I+ (3P0) | 1192.683 | 0.006 | 34 and 37 |
| I+ (3P1) | 1200.327 | 34 and 37 | |
| I+ (1D2) | 1279.763 | 34 and 37 | |
| I+ (1S0) | 1468.463 | 34 and 37 | |
| CH2 T0 | 391.06 | 0.10 | 34 |
| CH2 S0 | 428.72 | 0.11 | 34 |
| CH2+ | 1393.19 | 0.11 | 34 |
| CH | 592.825 | 0.097 | 34 |
| CH+ | 1619.755 | 0.052 | 34 |
| C | 711.398 | 0.045 | 34 |
| C+ | 1797.851 | 0.052 | 34 |
| H | 216.034 | 0.000 | 34 |
| HI | 28.646 | 0.036 | 34 |
| HI+ | 1030.7 | 0.1 | 34 and 38 |
| CH2I | 219.9 | 4.7 | 39 and 40 |
| CH2I+ | 1023.9 | 4.4 | 39 |
Results and discussion
Overall breakdown diagram
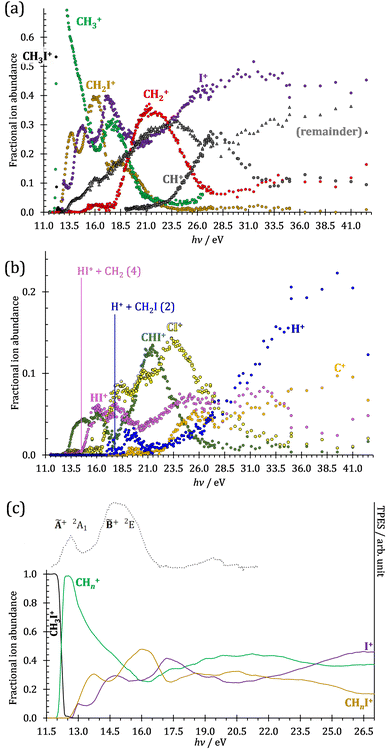
The iodomethane breakdown diagram, i.e., the fractional parent and fragment ion abundances in threshold photoionization, is shown in Fig. 1(a) and (b) in the 11–43 eV photon energy range. Statistical branching ratios correspond to smoothly changing rate constant ratios in parallel processes and to monotonously changing internal energy integrals in sequential ones.24 It is immediately evident that the shape of most breakdown curves is irreconcilable with a statistical fragmentation mechanism.As mentioned before, four fragment ions are conceivable by simple bond breaking of the two non-equivalent covalent bonds, C–H and C–I, in the iodomethane cation, and the sequential fragmentation steps can normally be assigned to the initial fragmentation step unequivocally. The main reason for this is that the C–I bond is stronger in CH2I+ than the C–H bond at 4.88 vs. 4.65 eV, respectively (ωB97X-D results). Consequently, sequential H losses are more likely from the primary CH3+ and CH2I+ fragment ions, while I+ and H+ represent a dead end in the dissociation mechanism.
Before grouping the fragment ions according to the primary step, we consider HI or HI+ formation. According to B3LYP/aug-cc-pVTZ-PP calculations as well as EOM-IP-CCSD/def2-TZVPPD energies along the B3LYP path, H transfer to I can take place over a barrier of 2.15 and 2.54 eV in the cation ground state, i.e., at 11.99 and 12.38 eV, respectively. EOM-IP-CCSD calculations also suggest that H-transfer is associated with a higher barrier and may even be monotonously uphill in the excited cation electronic states. Afterwards, the C–I bond can be broken in CH2IH+ to yield either HI+ + CH2 or HI + CH2+:
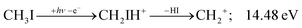 | (3) |
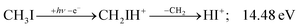 | (4) |
Another minor channel corresponds to charge localization on H+ after C–H bond breaking, at a thermochemical threshold of 17.86 eV, reaction (2). The proton signal in threshold photoionization is negligible up to ca. 18.75 eV, after which it represents a minor channel of 2–5% abundance. Its dynamic rise after 27 eV is due to double ionization (see below).
Fragment ion groups
The CHn+, CHnI+ and I+ fragment ion channels’ fractional abundance is plotted in Fig. 1(c) between 11.5 and 27.0 eV. Single ionization dominates in this energy range. The three groups are energetically allowed above: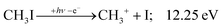 | (1) |
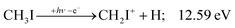 | (5) |
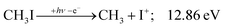 | (6) |
Thereafter, the branching ratios stay in the 0.2–0.4 range in the 15.0–23.5 eV photon energy range. Isolated-state behavior is often recognizable as a correlation between the TPES, characteristic of the initial electronic state of the prompt parent ion, and the breakdown curves, describing the fragmentation of the parent ion. Such correlations are not immediately obvious in the breakdown diagram. Instead, there are multiple photon energy ranges between 13 and 20 eV, in which the I+ abundance increases while that of the CHnI+ channels decreases and vice versa. The CHn+ group may remain unaffected from these oscillations if the branching of the reactive flux towards CHn+ takes place first after ionization, followed by the fluctuating branching ratios towards the I+ and CHnI+ channels. Furthermore, based on the sudden rise of the I+ and CHnI+ channels, followed by a relatively smooth plateau, the competition between them cannot be described as the ratio of smoothly changing statistical rate constants and is nonstatistical instead. CH3+ + I formation has long been associated with the ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) + ground state. This implies that the CHn+ group abundance represents a good approximation of the reactive flux reaching the ground electronic state close to its Franck–Condon point prior to dissociation.
+ ground state. This implies that the CHn+ group abundance represents a good approximation of the reactive flux reaching the ground electronic state close to its Franck–Condon point prior to dissociation.
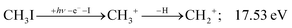 | (7) |
The methylidyne cation, CH+, signal is already visible below the I + 2 H threshold:
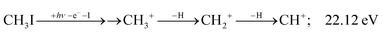 | (8) |
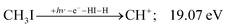 | (9) |
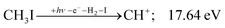 | (10) |
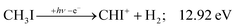 | (11) |
The steeply rising part of the CH+ breakdown curve is observed above 22 eV, consistent with the thermochemical limit of (8). The carbon cation is barely accessible in the plotted energy range by sequential I and H atom losses:
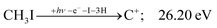 | (12) |
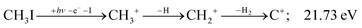 | (13) |
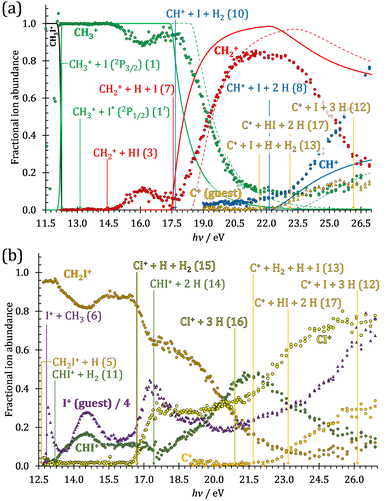 | ||
| Fig. 2 Fractional ion abundances within the (a) CHn+ and (b) CHnI+ fragment ion groups as a function of photon energy. In (a), the statistical model for I and consecutive H loss dissociations is shown as continuous and dashed lines with the latter assuming excited iodine atom formation in the first step and a 0.94 eV higher threshold (see text for details). The relevant thermochemical thresholds to dissociative ionization are shown. C+ in (a) and I+ in (b) are guest signals and not part of the groups (see text). Their branching ratio is shown relative to the total CHn+ and CHnI+ group signals, respectively. For DPI thresholds, see the reactions as referenced, with ancillary thermochemical data in Table 1. | ||
However, molecular hydrogen loss is probably associated with a tighter transition state and is quickly outcompeted by H atom loss with an associated loose transition state. This steep rise of the CH+ breakdown curve correlates poorly with the rise of the C+ signal making them unlikely parallel channels. Thus, we conclude that CH+ is stable up to 26 eV and CH2+ is likely to be only a minor contributor to C+ by H2 loss and C+ primarily belongs to the CHnI+ group of fragment ions.
We have constructed an ab initio statistical model24 describing the sequential I + H + H losses yielding methyl, methylidene, and, finally, methylidyne fragment ions based on the known thermochemical thresholds (Table 1) and harmonic state functions based on B3LYP vibrational analysis. The results are shown as continuous and dashed curves in Fig. 2(a). Mukhtar et al. and Powis studied the fragment ion kinetic energies in different experiments, and both proposed excited iodine (2P1/2) atom formation from the ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) + state of CH3I+:19,61
+ state of CH3I+:19,61
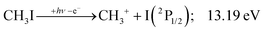 | (1′) |
This would mean that 91 kJ mol−1 excess energy is carried away by the iodine atom in the form of electronic excitation energy, and the CH2+ breakdown curve is in effect shifted to higher photon energies by 0.94 eV. As seen in Fig. 2(a), the experimental breakdown curve rises at the ground-state dissociative ionization energy to CH2+ + H + I. However, it does so less steeply than predicted by the statistical model and crosses the dashed, CH2+ + H + I* model curve at around 20 eV. Thus, although ground-state iodine atoms are formed at the onset of the CH2+ signal, the shape of the breakdown curve also suggests the involvement of the 2P1/2 state of iodine at higher energies. Kinetic energy release analysis will provide further insights below. When we turn to the CH+ breakdown curve, we see the opposite effect, i.e., the experimental abundances are higher than the ones predicted even by the ground-state statistical model. This suggests that some excess energy is trapped in the fragment ion and instead of being released as kinetic energy, it is available for sequential dissociation. This implies that the methyl cation is formed in its electronic excited state, either in the S11E′ or in the T03E′ states, e.g.,
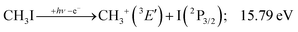 | (1′′) |
Because of the large geometry relaxation, the 5 eV gap to the first excited state band in the methyl photoelectron spectrum represents only an upper bound to the excitation energy.62 Indeed, the triplet–singlet gap of the methyl cation is calculated to be 3.54 eV (G4 result as used in the threshold to (1′′)). Taking into account the well-known methyl ionization energy of 9.838 eV,63 this yields the adiabatic ionization energy to the triplet state as 13.38 eV, cf. 14.76 eV for the vertical transition.62 Dyke et al. suggested that the S1Ã+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E′ methyl cation state was responsible for the 16.10 eV peak in the photoelectron spectrum.62 Our EOM calculations yield an S1–T0 gap of 0.42 eV at the neutral geometry and 0.36 eV at the T0 geometry. Thus, the singlet Ã+ peak likely overlaps with the triplet peak and the feature at 16.10 eV corresponds to the S2 state. The formation of an excited methyl cation traps 3.5–4.0 eV internal energy and makes it available for sequential dissociation. Excited methylene cation formation may have a similar if smaller effect in promoting CH+ formation. Another peculiar aspect of the CHn+ group is the persisting methyl cation signal even above 22 eV photon energy, still clearly below the double ionization threshold, but at energies where the statistical model predicts that almost all CH3+ primary fragments have enough internal energy to yield CH2+. A tentative explanation for the lingering methyl cation signal could be the formation of superexcited 2[2]5/2 I atoms, which stabilizes the methyl cation by 6.77 eV:36
1E′ methyl cation state was responsible for the 16.10 eV peak in the photoelectron spectrum.62 Our EOM calculations yield an S1–T0 gap of 0.42 eV at the neutral geometry and 0.36 eV at the T0 geometry. Thus, the singlet Ã+ peak likely overlaps with the triplet peak and the feature at 16.10 eV corresponds to the S2 state. The formation of an excited methyl cation traps 3.5–4.0 eV internal energy and makes it available for sequential dissociation. Excited methylene cation formation may have a similar if smaller effect in promoting CH+ formation. Another peculiar aspect of the CHn+ group is the persisting methyl cation signal even above 22 eV photon energy, still clearly below the double ionization threshold, but at energies where the statistical model predicts that almost all CH3+ primary fragments have enough internal energy to yield CH2+. A tentative explanation for the lingering methyl cation signal could be the formation of superexcited 2[2]5/2 I atoms, which stabilizes the methyl cation by 6.77 eV:36
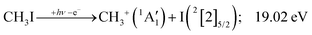 | (1′′′) |
More insights will be revealed by kinetic energy release analysis below.
The iodomethyl cation (CH2I+) has been proposed to be a fragmentation product of the ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2E parent ion state. However, we see CH2I+ earlier, already slightly above its thermochemical onset at 12.59 eV (5). Indeed, EOM calculations suggest that the ground-state CH2I+ + H products also correlate with the CH3I+
2E parent ion state. However, we see CH2I+ earlier, already slightly above its thermochemical onset at 12.59 eV (5). Indeed, EOM calculations suggest that the ground-state CH2I+ + H products also correlate with the CH3I+![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) + state. However, as discussed above, the competition between C–I and C–H bond breaking is not statistical on the ground-state potential energy surface. Similar to the non-statistical competition observed in oxygenated organics,67 a likely explanation is that the conditions and the nuclear geometry at the time of internal conversion determine the branching ratio between the two bond breaking processes: when the kinetic energy in the C–H coordinate is high enough, fragmentation occurs before intramolecular vibrational relaxation could take place and the C–H bond breaks instead of the statistically preferred C–I bond rupture.
+ state. However, as discussed above, the competition between C–I and C–H bond breaking is not statistical on the ground-state potential energy surface. Similar to the non-statistical competition observed in oxygenated organics,67 a likely explanation is that the conditions and the nuclear geometry at the time of internal conversion determine the branching ratio between the two bond breaking processes: when the kinetic energy in the C–H coordinate is high enough, fragmentation occurs before intramolecular vibrational relaxation could take place and the C–H bond breaks instead of the statistically preferred C–I bond rupture.
Similar to the CH2+ onset in the CHn+ group, CHI+ rises much below the calculated threshold to CHI+ + 2H formation:
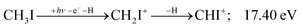 | (14) |
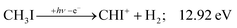 | (11) |
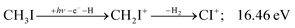 | (15) |
Sharma et al. observed CI+ in the absence of CHI+,65 which led them to conclude that the precursor ion for CI+ is CH2I+. Although we never observe CI+ in the absence of CHI+, we agree with their conclusion based on the correlation between the CH2I+ and CI+ breakdown curves. However, there is intriguing dynamics at play. The onset of CI+ is accompanied by a precipitous drop in the CH2I+ signal, but once the CI+ branching ratio reaches ca. 30% in the CHnI+ group at ca. 17.50 eV (Fig. 2(b)), it flatlines. (i) As this is a sequential dissociation, one may assume two classes of CH2I+ fragment ions: one, which accounts for about a third of the CH2I+ population and is likely to lose molecular hydrogen and yield CI+, as well as one, which accounts for ca. two thirds of the CH2I+ population and is more prone to atomic H loss when fragmenting further. (ii) Considering the 0.94 eV gap between the thermochemical threshold of (14) and (15) and the likely tight H2-loss transition state, (14) is likely competitive once energetically allowed. This suggests that only CH2I+ intermediates formed with sufficient internal energy to lose H2 but still below the H-loss threshold will lose molecular hydrogen. Based on (i) and (ii), one can envisage two CH2I+ formation mechanisms, one leading to a sharp internal energy distribution with less kinetic energy release and one with much kinetic energy lost and a broad internal energy distribution. On the one hand, it is possible for most of the first mechanism to suddenly yield CH2I+ fragments in the H2–H energy gap as the photon energy is increased, thereby contributing to the sudden rise in the CI+ signal. On the other hand, a smaller fraction of the CH2I+ population with broad internal energy distribution will only ever land in this gap. If CH3I+ dissociates on the ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) + surface and about one third of the CH2I+ is formed in an electronic excited state, the trapped excess excitation energy will lead to less kinetic energy release and more energy available for sequential fragmentation, accounting for the first class of CH2I+ intermediates. Two thirds of the CH2I+ signal is due to CH3I+ dissociating on the ground electronic state, which yields a broader internal energy distribution at overall lower internal energies. As the photon energy is increased above 17.5 eV, the internal energy distribution of CH2I+ intermediates of the first class shifts to higher energies but broadens simultaneously, as well, leading to less CI+ and more CHI+ signal, but this effect is counteracted by the increasing population of the CH2I+ intermediates of the second class having enough internal energy to lose H2 but not enough to lose H. Finally, above 21 eV, the sequential loss of three hydrogen atoms becomes feasible:
+ surface and about one third of the CH2I+ is formed in an electronic excited state, the trapped excess excitation energy will lead to less kinetic energy release and more energy available for sequential fragmentation, accounting for the first class of CH2I+ intermediates. Two thirds of the CH2I+ signal is due to CH3I+ dissociating on the ground electronic state, which yields a broader internal energy distribution at overall lower internal energies. As the photon energy is increased above 17.5 eV, the internal energy distribution of CH2I+ intermediates of the first class shifts to higher energies but broadens simultaneously, as well, leading to less CI+ and more CHI+ signal, but this effect is counteracted by the increasing population of the CH2I+ intermediates of the second class having enough internal energy to lose H2 but not enough to lose H. Finally, above 21 eV, the sequential loss of three hydrogen atoms becomes feasible:
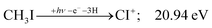 | (16) |
At this energy, the CI+ abundance starts to rise with a coincident drop in the CHI+ abundance, indicating that the sequential loss of three hydrogen atoms is a competitive process.
The carbon cation signal starts to rise at 22 eV, much below the 26.20 eV threshold to atomic fragments (12). The energy is even below the threshold to the formation of HI + 2 H neutrals:
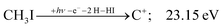 | (17) |
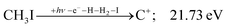 | (13) |
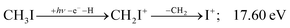 | (18) |
Therefore, I+ fragment ions may also be a product of the CHnI+ group above this energy. Nonetheless, because of the approximately constant I+ signal between 18.5 and 23 eV, it appears likely that I+ is dominantly the result of C–I bond breaking in the parent ion CH3I+ up to 20 eV.
Kinetic energy release analysis
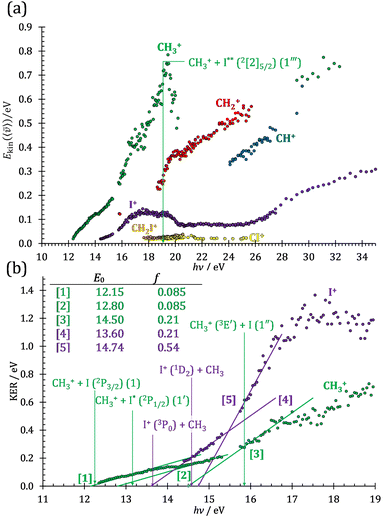
As discussed by Powis,19 kinetic energy release distributions (KERD) offer insights into the fragmentation dynamics, which are inaccessible otherwise. Instead of analyzing the total cation signal per m/z channel, we focus on threshold ionization here, i.e., on the same ionization signal as used to plot the breakdown diagrams in Fig. 1 and 2. Maintaining energy selection by threshold ionization means that the signal levels are lower, sometimes only 1000 ionization events in an m/z channel. This means that plotting projected 1D momentum distributions based on the velocity map images is out of reach.68 Still, the average radius of the mass-selected ion image yields the average ion velocity in the detector plane. Assuming an angularly isotropic distribution, the fragment ion kinetic energies can, thus, be determined at their mean velocity as a function of photon energy (Fig. 3(a)). As expected, they rise significantly with increasing photon energies, with two notable exceptions: the methyl cation KE drops above 19 eV, and the I+ KE drops starting at somewhat higher photon energies, above ca. 19.5 eV. While the relative drop in kinetic energies is similar in magnitude in the two cases, the underlying reason is different. The drop in the methyl cation kinetic energies coincides with the lingering methyl cation signal in the breakdown diagram, suggesting lower internal energy methyl cation fragments after C–I bond breaking. It is seen here that this energy is not released as kinetic energy. Consequently, it must be carried away by the leaving neutral iodine atom. Indeed, the thermochemical threshold to 2[2]5/2 I formation lies at 19.02 eV (1′′′), right at the onset of the drop in methyl cation kinetic energies. Superexcited I** formation has also been observed in the two-photon excitation of molecular iodine followed by one-photon ionization and autoionization in multiphoton ionization experiments.69 As discussed in the CHnI+ section, the iodine cation may also be the fragmentation product of CH2I+ above 17.60 eV (18). Most excess energy is available in the first dissociation step and the kinetic energy release will overwhelmingly affect the leaving neutral hydrogen atom in this case. Thus, the drop in the I+ kinetic energies is brought about by I+ also being a sequential fragmentation product. Alternatively, iodine cation formation in an electronic excited state may also contribute to decreasing KER in I+ formation (see Table 1).While the kinetic energy at the mean velocity equals the mean kinetic energy for a monoenergetic distribution, the former is ca. 20% lower for a Maxwell–Boltzmann velocity distribution. Nonetheless, the conservation of momentum and the effect of the thermal kinetic energy on the apparent fragment kinetic energies can be taken into account as described previously41 to obtain the kinetic energy release in threshold ionization at the mean fragment velocities, as plotted as a function of photon energy for the primary fragments CH3+ and I+ in Fig. 3(b). The linear sections are extrapolated to obtain approximate onset energies and the fraction of the excess energy released as kinetic energy.70 Note that the KER factor gives the fraction of the excess energy released at the mean fragment ion velocity, which may underestimate the average KER depending on the shape of the KER distribution, as described above. The smooth extrapolation nevertheless suggests that the shape of the KER distribution is conserved when the photon energy changes, and, thus, the extrapolated thresholds are not affected. These results also highlight changes in the fragmentation dynamics yielding CH3+ or I+. Three distinct dissociation regimes are seen for CH3+ and two for I+ formation below 17 eV.
The first two methyl cation regimes extrapolate to 12.15 and 12.80 eV threshold with the same slope, i.e., KER factor f = 0.085. This can be compared with the established thresholds to ground and excited-state iodine loss of 12.25 (1) and 13.19 eV (1′), respectively. The 0.1 eV difference for the (1) threshold is entirely due to the uncertainty in the KER extrapolation, but the almost 0.4 eV discrepancy for (1′) likely indicates that, in addition to significant I* formation in the ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) + band of CH3I+,19 ground-state I formation is non-negligible throughout, as also suggested by the statistical analysis of the breakdown diagram. The third regime, setting in at 15.5 eV, extrapolates to 14.50 eV with a much higher KER factor of f = 0.21. Superexcited I** production is only energetically allowed above 19.02 eV (see above). However, triplet CH3+ production (1′′) is energetically allowed above 15.79 eV (Table 1), and correlates with the dissociative
+ band of CH3I+,19 ground-state I formation is non-negligible throughout, as also suggested by the statistical analysis of the breakdown diagram. The third regime, setting in at 15.5 eV, extrapolates to 14.50 eV with a much higher KER factor of f = 0.21. Superexcited I** production is only energetically allowed above 19.02 eV (see above). However, triplet CH3+ production (1′′) is energetically allowed above 15.79 eV (Table 1), and correlates with the dissociative ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) + cation state, accounting for the rise in the KER factor.17 Again, the ca. 1.3 eV discrepancy between the known, 15.79 eV onset and the extrapolation result at 14.50 eV confirm the co-existence of impulsive and statistical dissociations in this energy range.
+ cation state, accounting for the rise in the KER factor.17 Again, the ca. 1.3 eV discrepancy between the known, 15.79 eV onset and the extrapolation result at 14.50 eV confirm the co-existence of impulsive and statistical dissociations in this energy range.
KER extrapolation overestimates the iodine cation onset significantly, pointing towards 13.60 eV, which corresponds to the threshold energy for the 3P0 and 3P1 I+ formation (13.66 and 13.74 eV, respectively) instead of the ground electronic state at 12.86 eV. Unfortunately, the I+ signal levels do not allow for KER insights closer to the dissociation limit, but the KER factor in the 14.25–15.25 eV range is eerily similar to that for CH3+ formation above 16 eV, indicative of an, at least in part, impulsive dissociation. The I+ KER factor then jumps to 0.54 between 15.5 and 16.5 eV photon energy with an apparent onset of 14.74 eV, which is not too dissimilar to the singlet 1D2 I+ formation threshold at 14.56 eV. This is indicative of an even lower lifetime and impulsive dissociation with weaker vibrational coupling to the reaction coordinate in this energy range. The threshold to excited methyl radical (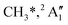 ) formation lies at 18.55 eV, which does not appear to play a role in the KER trends or in the breakdown curves.
) formation lies at 18.55 eV, which does not appear to play a role in the KER trends or in the breakdown curves.
Double ionization channels
Profiting from the flexible coincidence definition based on the recorded electron and ion detection times and positions,41 PEPICO data processing also permits a tentative discussion of the double ionization channels by way of PEPIPICO detection. There are, however, a few limitations, which preclude a complete analysis. First, contrary to magnetic bottle detection,71,72 velocity map imaging does not separate the coincident electrons in time to detect them both. This could be circumvented by analyzing only PIPICO data, i.e., by relying on the time-of-flight difference to assign the cation masses. However, because of the dominance of single ionization events throughout, PIPICO data are more burdened with false coincidence background and the double ionization signal is close to the detection limit. Second, the detector VMI range is limited at 2 eV at the extraction field used, which is expected to be less than the methyl cation kinetic energies formed after Coulomb explosion. Thus, a part of the ion signal is lost. Third, the beamline only delivers high harmonic free radiation up to the neon ionization energy at 21.5 eV.42 The high harmonic contamination of the VUV light is nevertheless expected to be small, as also seen in the smoothly changing fractional ion abundances below and above the neon absorption edge. Thus, the PEPIPICO branching ratios, as plotted in Fig. 4 above the double ionization threshold of 26.67 eV,11 only represent a potentially biased snapshot of the double ionization processes compared with more complete and better adapted methods to studying double ionization.73,74 The doubly charged CH3I2+ could not be observed, and it is evident in Fig. 4 that the Coulomb explosion follows three dynamic regimes in the 27–50 eV energy range. The I+ + CH3+ channel dominates at low and at high energies, whereas the I+ + H+ channel takes over in the intermediate energy region at 39 ± 2 eV. Furthermore, the I+ + CH+, I+ + C+ and H+ + CHnI+ channels also peak in this energy range, albeit in a less pronounced way. This is unexpected, as the double ionization spectrum is rather flat and featureless in this energy region.11 Sun and Yan addressed the fragmentation of CH3I2+ computationally,75 but they did not consider the I+ + H+ channel. Dujardin et al. observed it, although they did not see evidence for large changes in its branching ratio,76 which suggests two possible reasons: either only the kinetic energy release in H+ drops in this energy range, enhancing our collection efficiency, or our higher collection efficiencies for slow electrons ensure some degree of internal energy selection, which allows us to detect this transient change in the branching ratios. The discussion of the reason and the mechanism for these branching ratio changes lies beyond the scope of this work, which only serves to illustrate the potential use of coincidence detection in a simple TOF setup to report newly observed phenomena in double ionization.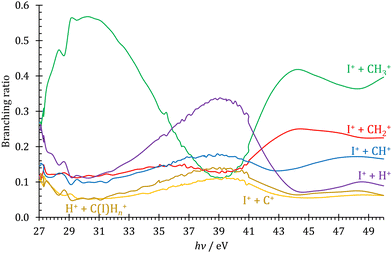 | ||
| Fig. 4 Double ionization branching ratios plotted for the observed ion pairs as detected by PEPIPICO in the 27–50 eV photon energy range. | ||
Conclusions
Dissociative ionization branching ratios have been recorded for iodomethane from the ionization energy up to 43 eV. The breakdown diagram exhibits numerous fragment ions in this energy range and the most important ones aside from I+ could be clustered into the CHn+ and CHnI+ groups. Based on the correlation between these groups, we discuss the role of the parent ion electronic states driving the fragmentation. The breakdown curves and literature or calculated dissociative ionization energies establish the dissociation mechanism and afford novel insights into the flow of the reactive flux. These insights are further augmented by the analysis of the cation kinetic energies, which provide evidence of superexcited iodine atom formation. A drop in the iodine cation kinetic energy release above 19 eV evidences its production in sequential dissociation from CH2I+ group. The fact that there is a dynamic competition between fragment ion groups with CH2I+ dominating the breakdown diagram around 16 eV emphasizes the importance of detecting all fragment ions to obtain a complete picture of the fragmentation dynamics. PEPIPICO data analysis also offers insights into double ionization processes above 27 eV. The fragmentation branching ratios generally favor CH3+ + I+ production, but the H+ + I+ channel was found to be dominant in the 37–41 eV photon energy range.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Experiments were carried out at the VUV beamline of the Swiss Light Source of the Paul Scherrer Institute. The financial support of the University Research Fund, University of Iceland and the Icelandic Research Fund (Grant No. 184693-052) is gratefully acknowledged. The authors wish to thank Patrick Ascher for technical support.References
- S. Das, P. Sharma and R. K. Vatsa, J. Photochem. Photobiol., C, 2017, 33, 27–53 CrossRef CAS.
- D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- A. Bodi, N. S. Shuman and T. Baer, Phys. Chem. Chem. Phys., 2009, 11, 11013–11021 RSC.
- D. M. P. Holland, I. Powis, G. Öhrwall, L. Karlsson and W. von Niessen, Chem. Phys., 2006, 326, 535–550 CrossRef CAS.
- A. R. Attar, A. Bhattacherjee and S. R. Leone, J. Phys. Chem. Lett., 2015, 6, 5072–5077 CrossRef CAS PubMed.
- L. Drescher, M. C. Galbraith, G. Reitsma, J. Dura, N. Zhavoronkov, S. Patchkovskii, M. J. Vrakking and J. Mikosch, J. Chem. Phys., 2016, 145, 011101 CrossRef CAS PubMed.
- R. Locht, D. Dehareng, K. Hottmann, H. W. Jochims, H. Baumgärtel and B. Leyh, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 105101 CrossRef.
- K. Matthiasson, G. Koumarianou, M. X. Jiang, P. Glodic, P. C. Samartzis and A. Kvaran, Phys. Chem. Chem. Phys., 2020, 22, 4984–4992 RSC.
- A. Pilcher-Clayton and J. H. D. Eland, J. Electron Spectrosc. Relat. Phenom., 2005, 142, 313–317 CrossRef CAS.
- A. Hult Roos, J. H. D. Eland, D. Koulentianos, R. J. Squibb, L. Karlsson and R. Feifel, Chem. Phys., 2017, 491, 42–47 CrossRef CAS.
- M. Pernpointner, J. P. Zobel, E. Fasshauer and A. N. Sil, Chem. Phys., 2012, 407, 39–45 CrossRef CAS.
- T. Masuoka and I. Koyano, J. Chem. Phys., 1991, 95, 1619–1627 CrossRef CAS.
- J. H. D. Eland, Mol. Phys., 1987, 61, 725–745 CrossRef CAS.
- E. Ruhl, S. D. Price, S. Leach and J. H. D. Eland, Int. J. Mass Spectrom. Ion Processes, 1990, 97, 175–201 CrossRef CAS.
- M. Kawasaki, H. Sato, T. Kikuchi, S. Kobayashi and T. Arikawa, J. Chem. Phys., 1987, 87, 5739–5745 CrossRef CAS.
- S. Marggi Poullain, D. V. Chicharro, J. Gonzalez-Vazquez, L. Rubio-Lago and L. Banares, Phys. Chem. Chem. Phys., 2017, 19, 7886–7896 RSC.
- S. H. Gardiner, T. N. Karsili, M. L. Lipciuc, E. Wilman, M. N. Ashfold and C. Vallance, Phys. Chem. Chem. Phys., 2014, 16, 2167–2178 RSC.
- I. Powis, Chem. Phys., 1983, 74, 421–432 CrossRef CAS.
- B. P. Tsal, T. Baer, A. S. Werner and S. F. Lin, J. Phys. Chem., 2002, 79, 570–574 CrossRef.
- Y. Song, X. M. Qian, K. C. Lau, C. Y. Ng, J. Liu and W. Chen, J. Chem. Phys., 2001, 115, 4095–4104 CrossRef CAS.
- M. Lee and M. S. Kim, J. Chem. Phys., 2007, 127, 124313 CrossRef PubMed.
- K.-M. Weitzel, G. K. Jarvis, M. Malow, T. Baer, Y. Song and C. Ng, Phys. Rev. Lett., 2001, 86, 3526–3529 CrossRef CAS PubMed.
- B. Sztáray, A. Bodi and T. Baer, J. Mass Spectrom., 2010, 45, 1233–1245 CrossRef PubMed.
- T. Baer and R. P. Tuckett, Phys. Chem. Chem. Phys., 2017, 19, 9698–9723 RSC.
- J. Harvey, P. Hemberger, A. Bodi and R. P. Tuckett, J. Chem. Phys., 2013, 138, 124301 CrossRef PubMed.
- J. Harvey, A. Bodi, R. P. Tuckett and B. Sztáray, Phys. Chem. Chem. Phys., 2012, 14, 3935 RSC.
- J. Harvey, R. P. Tuckett and A. Bodi, Phys. Chem. Chem. Phys., 2014, 16, 20492–20499 RSC.
- A. Bodi, P. Hemberger and R. P. Tuckett, Phys. Chem. Chem. Phys., 2017, 19, 30173–30180 RSC.
- K. Voronova, K. G. Torma, J. P. Kercher, A. Bodi and B. Sztáray, Int. J. Mass Spectrom., 2019, 438, 63–71 CrossRef CAS.
- P. Hemberger, A. Bodi, T. Bierkandt, M. Köhler, D. Kaczmarek and T. Kasper, Energy Fuels, 2021, 35, 16265–16302 CrossRef CAS.
- P. Hemberger, J. A. van Bokhoven, J. Pérez-Ramírez and A. Bodi, Catal. Sci. Technol., 2020, 10, 1975–1990 RSC.
- J. E. Burtness, NIST Chemistry WebBook, NIST Standard Reference Database Number 69, https://webbook.nist.gov/chemistry/, accessed 2022-06-01.
- B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.122r of the Thermochemical Network, https://atct.anl.gov/, accessed 2022-06-01, 2021.
- A. Zanchet, L. Banares, M. L. Senent and A. Garcia-Vela, Phys. Chem. Chem. Phys., 2016, 18, 33195–33203 RSC.
- E. Luc-Koenig, C. Morillon and J. Vergès, Phys. Scr., 1975, 12, 199–219 CrossRef CAS.
- W. C. Martin and C. H. Corliss, J. Res. Natl. Bur. Stand., Sect. A, 1960, 64A, 443–479 CrossRef PubMed.
- J. H. D. Eland and J. Berkowitz, J. Chem. Phys., 1977, 67, 5034–5039 CrossRef CAS.
- A. F. Lago, J. P. Kercher, A. Bödi, B. Sztáray, B. Miller, D. Wurzelmann and T. Baer, J. Phys. Chem. A, 2005, 109, 1802–1809 CrossRef CAS PubMed.
- B. Sztáray, K. Voronova, K. G. Torma, K. J. Covert, A. Bodi, P. Hemberger, T. Gerber and D. L. Osborn, J. Chem. Phys., 2017, 147, 013944 CrossRef PubMed.
- A. Bodi, P. Hemberger, T. Gerber and B. Sztaray, Rev. Sci. Instrum., 2012, 83, 083105 CrossRef PubMed.
- M. Johnson, A. Bodi, L. Schulz and T. Gerber, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 610, 597–603 CrossRef CAS.
- W. C. Wiley and I. H. McLaren, Rev. Sci. Instrum., 1955, 26, 1150–1157 CrossRef CAS.
- B. Sztáray and T. Baer, Rev. Sci. Instrum., 2003, 74, 3763–3768 CrossRef.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113 CrossRef CAS.
- K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 2002, 98, 11623–11627 CrossRef.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 84108 CrossRef PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- M. N. Glukhovtsev, A. Pross, M. P. McGrath and L. Radom, J. Chem. Phys., 1995, 103, 1878–1885 CrossRef CAS.
- Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O'Neill, R. A. DiStasio, R. C. Lochan, T. Wang, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. Van Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonett, J. E. Subotnik, H. L. Woodcock, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 3172–3191 RSC.
- E. S. Mukhtar, I. W. Griffiths, F. M. Harris and J. H. Beynon, Int. J. Mass Spectrom. Ion Phys., 1982, 42, 77–90 CrossRef CAS.
- J. Dyke, N. Jonathan, E. Lee and A. Morris, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1385–1396 RSC.
- J. A. Blush, P. Chen, R. T. Wiedmann and M. G. White, J. Chem. Phys., 1993, 98, 3557–3559 CrossRef CAS.
- J. H. D. Eland, R. Frey, A. Kuestler, H. Schulte and B. Brehm, Int. J. Mass Spectrom. Ion Phys., 1976, 22, 155–170 CrossRef CAS.
- P. Sharma, R. K. Vatsa, B. N. Rajasekhar, N. C. Das, T. K. Ghanty and S. K. Kulshreshtha, Rapid Commun. Mass Spectrom., 2005, 19, 1522–1528 CrossRef CAS PubMed.
- I. Antonov, K. Voronova, M. W. Chen, B. Sztaray, P. Hemberger, A. Bodi, D. L. Osborn and L. Sheps, J. Phys. Chem. A, 2019, 123, 5472–5490 CrossRef CAS PubMed.
- A. Giustini, M. Winfough, J. Czekner, B. Sztaray, G. Meloni and A. Bodi, J. Phys. Chem. A, 2021, 125, 10711–10724 CrossRef CAS PubMed.
- P. Hemberger, X. Wu, Z. Pan and A. Bodi, J. Phys. Chem. A, 2022, 126, 2196–2210 CrossRef CAS PubMed.
- A. Hafliðason, M.-X. Jiang and Á. Kvaran, Chem. Phys., 2021, 541, 111016 CrossRef.
- A. Bodi, P. Hemberger and R. P. Tuckett, J. Phys. Chem. A, 2021, 125, 2601–2611 CrossRef CAS PubMed.
- A. Matsuda, M. Fushitani, C. M. Tseng, Y. Hikosaka, J. H. Eland and A. Hishikawa, Rev. Sci. Instrum., 2011, 82, 103105 CrossRef PubMed.
- J. H. D. Eland, J. Electron. Spectrosc. Relat. Phenom., 2005, 144–147, 1145–1150 CrossRef CAS.
- T. Arion and U. Hergenhahn, J. Electron. Spectrosc. Relat. Phenom., 2015, 200, 222–231 CrossRef CAS.
- J. H. D. Eland and R. Feifel, Chem. Phys., 2006, 327, 85–90 CrossRef CAS.
- Q.-X. Sun and B. Yan, Acta Phys. Sin., 2017, 66, 093101 CrossRef.
- G. Dujardin, L. Hellner, D. Winkoun and M. J. Besnard, Chem. Phys., 1986, 105, 291–299 CrossRef CAS.
| This journal is © the Owner Societies 2023 |