Square planar Pd(II)/oximate complexes as ‘metalloligands’ for the directional assembly of 4f-metal ions: a new family of {Ln₂Pd} (Ln = lanthanide) clusters exhibiting slow magnetization relaxation

Abstract

A relatively unexplored approach in heterometallic chemistry of transition metals and lanthanides has been developed toward the controlled synthesis of a new family of linear heterotrinuclear Ln(III)–Pd(II)–Ln(III) complexes with the general formula [Ln₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂]·[Pd(pao)₂]₄, where Ln^III = Dy^III (2), Gd^III (3), Er^III (4) and Yb^III (5). This strategy was based on the diamagnetic ‘metalloligand’ [Pd(pao)₂] (1), where pao⁻ is the anion of 2-pyridinealdoxime, containing two dangling oximate O-atoms which were trans to each other and available for binding with oxophilic lanthanide ions. Because of their trans-configuration, the [Pd(pao)₂] ‘metalloligand’ was able to direct the binding of two {Ln(NO₃)₃(MeOH)(H₂O)} units on opposite sites, thus yielding the reported trinuclear {Ln–Pd–Ln} clusters. Complexes 2–5 constitute a new family of trinuclear heterometallic {Ln₂Pd} species, and they represent the first examples of a directional assembly approach towards the coordination of 4f-metal ions. Compounds 2 and 5 exhibit out-of-phase signals under applied dc fields of 300 and 2000 Oe, respectively, characteristics of the slow magnetization relaxation, albeit with very small energy barriers for the magnetization reversal. This was due to the combined onset of fast quantum tunneling and the weak crystal field effects induced by the coordinated ligands. The combined results highlight the potential of using the ‘metal complexes as ligands’ method to deliberately prepare heterometallic Pd^II–Ln^III complexes with unique structural and interesting physicochemical (magnetic, optical, catalytic) properties.

---

1. Introduction

More than three decades ago, a significant breakthrough in the research fields of inorganic chemistry and molecular magnetism occurred when researchers discovered that a coordination complex known as {Mn₁₂} could retain its magnetization for extended periods at liquid helium temperatures. This discovery marked the introduction of Single-Molecule Magnets (SMMs),¹ a group of molecules characterized by a large ground state spin (S) and an Ising-type (or easy-axis) magnetoanisotropy, resulting from a negative zero-field splitting parameter (D). The combined presence of S and D leads to an effective energy barrier (U_eff) for magnetization reversal. SMMs are superparamagnetic-type materials, where magnetization relaxes slowly below a specific blocking temperature (T_B), and the phenomenon can be observed through the appearance of out-of-phase ac magnetic susceptibility signals and magnetic hysteresis loops.² Scientists are currently investigating SMMs due to their potential applications in quantum computing, spintronics, magnetic resonance imaging (MRI), and various other fields of science and technology related to information processing and data storage.³

Compelling evidence has highlighted the paramount importance of single-ion anisotropy in the design of SMMs with substantial energy barriers for magnetization reversal.⁴ A pivotal moment in this understanding occurred in 2003 when researchers recognized SMM behavior in mononuclear [Ln^III(pc)₂]⁻ complexes featuring trivalent lanthanide ions (Ln^III = Tb^III, Dy^III; pc²⁻ = dianion of phthalocyanine).⁵ Subsequently, significant emphasis was placed on the synthesis and investigation of SMMs based on mononuclear, dinuclear, and polynuclear Ln^III compounds.⁶ A groundbreaking recent development in this field resulted from the synthesis and study of [(Cp^iPr5)Dy(Cp*)]⁺ (Cp^iPr5 = penta-iso-propylcyclopentadienyl, Cp* = pentamethylcyclopentadienyl). This complex behaves as an SMM with a record blocking temperature of 80 K, which is above the landmark temperature of 77 K (the boiling point of liquid nitrogen).⁷ The SMM behavior observed in mononuclear Ln^III complexes is attributed to the substantial anisotropy of individual ions, arising from strong spin–orbit coupling and the effects of the coordinated ligands on the overall crystal field.⁸ The Dy^III-based SMMs dominate the field; the Dy^III is a Kramers ion characterized by an odd number of 4f electrons and has always a bistable ground state.⁹ The intrinsic quadrupole moment approximation of f-orbitals classifies lanthanide ions into oblate, prolate, or spherical shapes based on their electron density distribution. This classification makes it easier to introduce anisotropy in these ions, particularly when compared to transition metals.^6d Although f-electrons are deeply embedded in the core shell, the ligand field can still have a partial influence on their energies, affecting their magnetic properties. This means that by adjusting the ligand field, it is possible to explore the magnetic dynamics by modulating the f-electron cloud.¹⁰

In the pursuit of SMMs with enhanced properties, various attempts have focused on the synthesis of heterometallic compounds featuring both paramagnetic 4f- and diamagnetic 3d-metal ions, with a particular emphasis on Zn^II and low-spin Co^III ions.¹¹ The primary objective is the stabilization of the electronic ground state with the largest m_J and the increase of the energy gap between the ground and the first excited m_J states of the anisotropic lanthanide ion(s). The presence of diamagnetic metal ions influences the electron density distribution of coordinating ligands by inducing polarization effects, thus affecting the strength of the crystal field.^11a Studies have shown that the presence of diamagnetic 3d-metal ions results in an increased negative charge on the oxygen donor atoms of the bridging ligands. This leads to larger energy gaps between the m_J states, resulting in higher U_eff values and the weakening (or even suppression) of quantum tunneling of magnetization (QTM) as a relaxation process.¹²

The focus has predominantly been on first-row transition metals (3d), primarily because they are more manageable, both experimentally and theoretically, compared to their 4d counterparts. A key distinction between 3d- and the heavier 4d-metal ions is the more extended valence orbitals of the latter. Among the 4d-block elements, it has been demonstrated that diamagnetic transition metal ions, such as the electron-deficient d⁸ Pd^II, can donate electron density to a lanthanide center, implying significant modifications on the magnetic properties of the resulting heterometallic Pd^II/Ln^III compounds.¹³ Because of the tendency of the heavy Pd^II ion to form square planar geometries, the coordinated ligands should be able to satisfy these needs and facilitate the formation of stable species. A recent search in the Cambridge Crystallographic Data Centre (CCDC) revealed limited examples of non-organometallic Pd^II/Ln^III coordination compounds. The majority of these involve carboxylate or thiocarboxylate ions as ligands, along with structures incorporating phosphines, arsenates, and derivatives of pyridine and pyrimidine.^13,14 All of these complexes have been prepared via self-assembly synthetic routes using metal precursors and various ligand ‘blends’.

On the other hand, the ‘metal complexes as ligands’ strategy (often referred to as ‘metalloligands’) has been frequently employed in heterometallic chemistry of various metal ions.¹⁵ This synthetic route offers distinct advantages when compared to the commonly used self-assembly method. It enables more precise control over the reaction's progress and the resulting products. This modular approach facilitates the synthesis of larger molecules by combining mononuclear or dinuclear complexes with suitable polynucleating ligands capable of binding with different metal centers. In this work, the aim was to obtain heterotrinuclear Pd^II/Ln^III complexes with a particular Ln–Pd–Ln configuration (Fig. 1), using ‘end-capping’ ligands for the Ln^III ions and a central ‘metalloligand’ with bridging capabilities.

Fig. 1 Schematic representation for the targeted synthesis of heterotrimetallic complexes with the Ln–Pd–Ln configuration by using the appropriate ‘metalloligands’ and ‘end-capping’ ligands.

To this direction, mononuclear metal oximate complexes appear to be promising building blocks.¹⁶ Our research group and others have conducted extensive studies in the field of coordination chemistry with ligands belonging to the family of 2-pyridyl oximes. These ligands can be described as ‘compartmentalized’ due to their affinity for binding ‘soft’ 3d-metal ions, such as Ni^II and Cu^II, through their N-donor atoms, and ‘hard’ 4f-metal ions through their O-donor(s), following the HSAB (Hard and Soft Acids and Bases) model.^16,17

In our quest to explore the Pd^II/Ln^III chemistry with this group of ligands, we directed our synthetic efforts toward the simplest member of the 2-pyridyl oxime family, known as 2-pyridinealdoxime (paoH, Fig. 2). In addition to yielding a plethora of structurally and magnetically intriguing homometallic 3d- and heterometallic 3d/3d′- and 3d/4f-metal complexes through self-assembly processes,¹⁸ paoH has gained recognition for its exceptional utility as a part of ‘metalloligands’. Upon deprotonation, pao⁻ ligation seems capable of stabilizing square planar complexes via the pyridine and oximate N-atoms, while the unbound, ‘free’ oximate O-atom would bridge neighboring metal ions.^19,20 This observation made us to suspect that such {Pd(oximate)₂} species might have the potential to act as ‘metalloligands’, exploiting the nucleophilicity of the oximate anion and its ability to coordinate with oxophilic Ln^III ions.

Fig. 2 Structural formula and abbreviation of the organic ligand 2-pyridinealdoxime (paoH) used in this study. The red and blue coloration illustrates the ‘hard’ O- and the ‘soft’ N-donor atoms, respectively.

We report herein the high-yield synthesis and use of the mononuclear [Pd(pao)₂] (1) ‘metalloligand’, bearing two trans oximate O-atoms readily available for binding to 4f-metal ions on opposite sides, for the isolation of a new family of [Ln₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂]·[Pd(pao)₂]₄ (Ln^III = Dy (2), Gd (3), Er (4), Yb (5)) complexes with a linear Ln–Pd–Ln conformation and additional co-crystallized [Pd(pao)₂] units forming supramolecular stacks. Complexes 2 and 5 exhibit slow magnetization relaxation upon application of an external dc field.

2. Experimental section

a. Materials, physical and spectroscopic measurements

All manipulations were performed under aerobic conditions using materials (reagent grade) and solvents as received unless otherwise noted. Elemental analyses (C, H, and N) were performed by the University of Patras microanalytical service. Infrared (IR) spectra (4000–400 cm⁻¹) were recorded in the solid state using a PerkinElmer 16 PC spectrometer with samples prepared as KBr pellets. Electrospray ionization (ESI) mass spectra (MS) were taken on a Bruker HCT Ultra mass spectrometer from a solution of complex 1 prepared in MeCN. Variable-temperature direct and alternating current (dc and ac, respectively) magnetic susceptibility studies were performed at the temperature range 1.9–300 K using a Quantum Design MPMS XL-7 SQUID magnetometer equipped with a 7 T magnet. Diamagnetic corrections were applied to the observed paramagnetic susceptibility using Pascal's constants.²¹

b. Synthesis of [Pd(pao)₂] (1)

To a stirred, colorless solution of paoH (0.05 g, 0.30 mmol) and Et₃N (42 μL, 0.30 mmol) in solvent MeOH (15 mL) was added solid PdCl₂ (0.03 g, 0.15 mmol). The resulting yellow slurry was refluxed for 6 h, during which time all the PdCl₂ solid dissolved and the color of the solution remained yellow. The solution was then filtered, and the filtrate was allowed to evaporate slowly at room temperature. After two days, X-ray quality well-formed yellow needle-shaped crystals of 1·2H₂O appeared, and these were collected by filtration, and washed with cold MeOH (2 × 2 mL) and Et₂O (2 × 5 mL). The yield was 90% (based on the organic chelate available). Upon dryness (under vacuum) the crystalline solid was analyzed as 1. Anal. calc. for C₁₂H₁₀PdN₄O₂ (found values in parentheses): C 41.34% (41.37%), H 2.89% (2.94%) and N 16.07% (16.01%). Selected IR data (KBr, cm⁻¹): v = 1668 (w), 1603 (m), 1510 (s), 1478 (m), 1424 (w), 1334 (s), 1248 (s), 1177 (m), 1151 (w), 1037 (w), 895 (w) 835 (m), 777 (w), 681 (w), 656 (w), 573 (w), 525 (w), 486 (w), 432 (m).

c. Synthesis of [Dy₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂]·[Pd(pao)₂]₄ (2)

To a stirred, clear yellow solution of the [Pd(pao)₂] precursor (0.03 g, 0.10 mmol) in a solvent mixture comprising MeOH/MeCN (15 mL, 1 : 2 v/v) was added solid Dy(NO₃)₃·5H₂O (0.09 g, 0.20 mmol). The resulting yellow slurry was refluxed for 4 h, during which time all solids were dissolved and the color of the solution turned light orange. The solution was then filtered, and the filtrate was allowed to evaporate slowly at room temperature. After four days, X-ray quality orange needle-shaped crystals of 2 appeared, and these were collected by filtration, washed with cold MeCN (2 × 2 mL) and Et₂O (2 × 5 mL), and dried in air. The yield was 30% (based on the total available Dy). The crystalline solid was analyzed as 2. Anal. calc. for C₆₂H₆₂Dy₂Pd₅N₂₆O₃₂ (found values in parentheses): C 29.31% (29.42%), H 2.46% (2.53%) and N 14.34% (14.22%). Selected IR data (KBr, cm⁻¹): v = 1608 (s), 1517 (m), 1487 (m), 1434 (m), 1384 (s), 1349 (m), 1249 (s), 1182 (m), 1156 (w), 1030 (w), 902 (w) 835 (w), 770 (m), 682 (w), 662 (w), 575 (w), 527 (w), 431 (w).

d. Synthesis of [Gd₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂]·[Pd(pao)₂]₄ (3), [Er₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂]·[Pd(pao)₂]₄ (4) and [Yb₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂]·[Pd(pao)₂]₄ (5)

X-ray quality crystals of complexes 3–5 were prepared in the same manner as complex 2 but using Gd(NO₃)₃·5H₂O (0.09 g, 0.20 mmol), Er(NO₃)₃·5H₂O (0.09 g, 0.20 mmol), and Yb(NO₃)₃·5H₂O (0.09 g, 0.20 mmol) as the lanthanide sources. The crystals were collected by filtration, washed with cold MeCN (2 × 2 mL) and Et₂O (2 × 5 mL), and dried under in air; the yields were: 28% (3), 32% (4), and 25% (5). We have further confirmed the identities of 3–5 by (i) IR spectroscopic comparison with the authentic, single-crystalline sample of 2 (Fig. S2†), and (ii) elemental analyses. Anal. calc. for 3 (found values in parentheses): C 29.44% (29.53%), H 2.47% (2.56%) and N 14.39% (14.28%). Anal. calc. for 4 (found values in parentheses): C 29.20% (29.11%), H 2.45% (2.32%) and N 14.28% (14.39%). Anal. calc. for 5 (found values in parentheses): C 29.07% (29.19%), H 2.44% (2.54%) and N 14.22% (14.11%).

e. Single-crystal X-ray crystallography

Yellow single-crystals of complex 1 (0.32 × 0.19 × 0.05 mm) and orange single-crystals of the family of complexes 2–5 (0.41 × 0.19 × 0.14 mm for 2; 0.45 × 0.08 × 0.07 mm for 3; 0.40 × 0.08 × 0.08 mm for 4; 0.43 × 0.09 × 0.06 mm for 5), were taken directly from the mother liquor and immediately cooled at 160(2) K. X-ray diffraction data were collected on a Rigaku R-AXIS SPIDER Image Plate diffractometer using graphite-monochromated MoKα (λ = 0.71073 Å) radiation. Data collection (ω-scans) and processing (cell refinement, data reduction, and empirical absorption correction) were performed using the CrystalClear program package.²² The structures of 1–5 were solved by direct methods using SHELXS ver. 2013/1,²³ and refined by full-matrix least-squares techniques on F² with SHELXL ver. 2014/6.²⁴ All H atoms in the structures of 1–5 were introduced at calculated positions and refined as riding on their respective bonded atoms. All non-H atoms were refined anisotropically. It is important to mention that, in all structures, the ligand pao⁻ is disordered over two positions. Specifically in 1, the pao⁻ ligand occupies two positions with occupancies 0.581(5) and 0.489(5), respectively. In the structures of 2–5, the pao⁻ ligand in the {Ln₂Pd} heterometallic unit also occupies two positions with occupancies 0.705(5) and 0.295(5) in 2, 0.707(8) and 0.293(8) in 3, 0.635(7) and 0.365(7) in 4, and 0.60(1) and 0.40(1) in 5. Moreover, in the structures of 2–5, the coordinated pao⁻ ligand to one of the [Pd(pao)₂] units, defined by Pd2, also occupies two positions with occupancies 0.544(4) and 0.456(5) in 2, 0.537(7) and 0.463(7) in 3, 0.560(6) and 0.440(6) in 4, and 0.553(9) and 0.447(9) in 5. The discussion of the above disordered parts of the structures 1–5 is important for the comprehensive structural analysis and description of the supramolecular properties of these complexes (vide infra).

Various figures of all structures were created, using Diamond 3 and Mercury software packages.²⁵ The unit cell parameters, structure solution, and refinement details of the monomeric 1 and the heterometallic complexes 2–5 are summarized in Table S1.† Further crystallographic details of compounds 1–5 can be found in the corresponding CIF files provided in the ESI.†

3. Results and discussion

a. Synthetic comments and IR spectra

The most challenging step towards the preparation of the targeted heterometallic compounds has been the synthesis of a suitable ‘metalloligand’ which would bear free O-binding sites and simultaneously retain its solid-state structure in solution. Square planar palladium(II) complexes (d⁸, diamagnetic) bearing chelating ligands are both thermodynamically stable and kinetically inert, rendering themselves as ideal ‘metalloligands’ and fruitful building blocks for the synthesis of new compounds with interesting architectures and properties. Hence, from the reaction between PdCl₂, paoH and Et₃N in a 1 : 2 : 2 molar ratio, in solvent MeOH, under refluxing conditions to enhance the solubility of the PdCl₂ starting material, we came across the yellow crystalline mononuclear compound [Pd(pao)₂] (1) in excellent yields (∼90%). The general formation of 1 is summarized by the following stoichiometric eqn (1):

Positive (+) ion ES-MS studies were conducted to investigate the stability of 1 in MeCN, a solvent which is widely used for the synthesis of heterometallic transition metal/lanthanide complexes.¹¹ Indeed, complex 1 proved to preserve its structure in solution with a single, high-intensity ion signal located at 349.6 m/z and corresponding to the single-charged [Pd(pao)(paoH)]⁺ species (Fig. 3). The trans-arrangement of the free oximate O-atoms prompted us to carry out structure-directing reactions of 1 with two equivalents of different lanthanide(III) precursors, aiming at the preparation of {Ln–Pd–Ln} compounds.

Fig. 3 Positive ion ES-MS spectrum of 1 in MeCN.

Indeed, from the 1 : 2 general reaction between 1 and Ln(NO₃)₃·5H₂O (Ln^III = Dy^III, Gd^III, Er^III, Yb^III) in MeOH/MeCN under refluxing conditions, an orange-colored solution was obtained, from which orange crystals of the mixed-complex [Ln₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂]·[Pd(pao)₂]₄ (Ln = Dy^III (2); Gd^III (3); Er^III (4); Yb^III (5)) were formed in yields ranging from 25–35% depending on the lanthanide ion. The general formation of complexes 2–5 is summarized by the following stoichiometric eqn (2).

Complexes 2–5 are stable and crystalline solids at room temperature and non-sensitive toward air and moisture. It is noteworthy to mention that in our hands it has not been possible to isolate the same crystalline compounds 2–5 from one-pot reactions between PdX₂ (X⁻ = various anions), Ln(NO₃)₃·5H₂O and ligand paoH, under different conditions, solvents and external bases. It appears that the heterometallic complexes 2–5 can only be prepared in pure and crystalline forms by using complex 1 as the ‘metalloligand’ and Ln(NO₃)₃·5H₂O as a dual provider of Ln^III ions and NO₃⁻ ancillary groups (vide infra). For the preparation of 2–5, the choice of the reaction solvent mixture has been proved crucial for their crystallization and the formation of single-crystals; in the absence of either MeOH or MeCN, we have been unable to identify any heterometallic compound, contrariwise homometallic [PdCl₂(paoH)₂] complex was readily formed.²⁶ Surprisingly, the heterometallic complexes 2–5 co-crystallize with four monomeric [Pd(pao)₂] units (vide infra); that has been chemically unexpected given the fact that the crystalline 2–5 can be obtained only through the 1 : 2 reactions between the corresponding ‘metalloligand’ and the lanthanide precursors. When the stoichiometric 5 : 2 reactions between [Pd(pao)₂] and Ln(NO₃)₃·5H₂O were carried out, the ‘metalloligand’ has been the sole isolated product in all cases and by all chemical means. It is likely that the supramolecular packing of [Pd(pao)₂] units facilitates the stabilization of the crystal lattice and eventually the formation of the mixed heterometallic–homometallic complexes.

The IR spectra of complexes 1–5 are presented in Fig. S1 and S2.† Complexes 2–5 are isostructural, and therefore only the IR spectrum of 2 will be discussed as a representative example. The presence of coordinated aqua and methanol ligands is confirmed by the appearance of a broad IR band centered at 3382 cm⁻¹; the broad character of this band is indicative of hydrogen bonding interactions, as it turned out later by crystallographic studies. The IR spectrum of 2 shows the characteristic bands of bidentate chelating nitrato ligands. The bands at 1487 and 1249 cm⁻¹ are assigned to the ν₁(A₁)[ν(N=O)] and ν₅(B₂)[ν_as(NO₂)] modes,²⁷ the former probably overlapped with an aromatic stretch. The large separation (238 cm⁻¹) of the two stretching nitrato modes indicates the bidentate character of these groups.²⁷ The spectrum exhibits a medium intensity band at 1384 cm⁻¹, characteristic of the ν₃(E′)[ν_d(NO)] mode of the ionic nitrate with D_3h symmetry.²⁷ Such species do not exist in the crystal structure of the neutral compound 2. This is not unusual in IR spectroscopy of coordination compounds, and it can be rationalized in terms of a partial replacement of nitrato groups by bromides from the excess KBr that was used for the preparation of the IR pellet, thus producing ionic nitrates (KNO₃);²⁸ this solid-state replacement is facilitated by the employed hydraulic pressure. The IR spectrum of complex 2 also revealed the in-plane deformation band of the 2-pyridyl ring of the pao⁻ ligands in the range ∼770–682 cm⁻¹, thus confirming the participation of the ring's nitrogen atom in coordination.²⁹ Several bands appear in 1609 cm⁻¹ and in the ∼1517–1349 cm⁻¹ range, assigned to contributions from the v(C=N) vibrations and the stretching vibrations of the aromatic rings of pao⁻ groups, respectively. The ν(N–O) band of the oximate group is situated at 1156 cm⁻¹ and can be attributed to the increased presence of double bond character (N=O) in the electronic structure of the oximate group, resulting from the deprotonation and coordination of the oximate O-atom. As a result, the ν(NO) vibration shifts to higher wavenumbers in the complexes that include deprotonated and coordinated oximate groups in comparison to the unbound, neutral ligands.³⁰

b. Description of structures

Due to the similarities in the crystal structures of complexes 2–5, only the structural features of heterometallic 2 will be discussed in detail as a representative example. Selected interatomic distances and angles for complexes 1 and 2 are listed in Tables S2 and S3,† respectively. Complexes 2–5 are crystal lattice solvate-free, while compound 1 crystallizes with two H₂O solvate molecules.

Complex 1 crystallizes in the centrosymmetric space group P2₁/a. The asymmetric unit of 1 contains half of the [Pd(pao)₂]·2H₂O units. The complex possesses a center of symmetry and the Pd atoms are located at the center of symmetry (Fig. 4a). The pao⁻ ligands are disordered over two orientations (Fig. S3†). The Pd^II ion is four-coordinate in a square planar environment consisting of four N-atoms derived from the two bidentate chelating pao⁻ ligands (Fig. 4a), as confirmed by the Pd^II–N bond distances and the N–Pd–N bond angles (Table S2†). The two coordinated pao⁻ ligands are trans to each other. Both disordered sites of the pao⁻ ligands display the same coordination mode around the Pd^II center.

Fig. 4 Partially labeled representation of the molecular structures of (a) the ‘metalloligand’ 1 and (b) the heterotrinuclear {Dy₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂} unit of complex 2. All H atoms are omitted for clarity. Color scheme: Pd^II, magenta; Dy^III, yellow; O, red; N, blue; C, gray. Symmetry operation for the primed atoms: (′): −x, 2 − y, 2 − z for 1 and (′): −x, −y, 1 − z for 2.

In the structure of 1·2H₂O, intramolecular and intermolecular hydrogen bonds are observed (Fig. S3 and Table S5†) for both orientations A and B of the coordinated pao⁻ ligands. The [Pd(pao)₂]·2H₂O complexes with pao⁻ ligands in orientation A form chains along c axis through C5A–H5A⋯O1Aⁱⁱ hydrogen bonding interactions (Fig. S4a, Table S5,† symmetry code (ii): x, y, z − 1), while those in orientation B form similar H bonds through the C1B–H1B⋯O1Bⁱⁱⁱ interactions (Fig. S4b, Table S5,† symmetry code (iii): −x, −y + 2, −z + 1). The stacking of coordination compounds through phenyl-chelate ring interactions is observed in several square planar transition metal complexes.³¹ Fig. S5† represents the stacking of complexes along a-axis with the distance of the average planes of neighboring complexes being 3.37(1) Å for orientation A, a result that indicates that the pyridine rings favor also this type of stacking. Hence, the [Pd(pao)₂] square planar complexes belong to fraction-2 of five-member chelating ring with fused 6-membered aromatic rings, i.e. the pyridine rings in this case.^31c A parameter used to characterize this type of stacking is the difference of the distance of the centroids of the two pyridine rings with the distance of the centroid of the pyridine ring with the centroid of the chelate ring, represented by the symbol Δ (Δ = 0.736(1) Å). This positive value of Δ indicates a phenyl-chelate interaction type;^31c however, in the case of 1 this interaction is a phenyl-metal type (inset of Fig. S5,† for orientations A and B). For orientation B, the distance of the average planes is 3.62(7) Å and Δ value is 0.912(1) Å. The complexes stacked along a-axis interact through C5A–H5A⋯O1A or C1B–H1B⋯O1B hydrogen bonds, thus forming layers parallel to the [010] planes which lie at the bottom or top (and in the middle) of the cell (Fig. S6†). Among these layers, zig-zag chains of lattice water molecules are formed through O1W–H1WB⋯O1W^vi hydrogen bonds (Table S5,† symmetry code: (vi): x + 1/2, −y + 3/2, z), which also assist in building the 3-D architecture of the structure; these interaction serve to further link complexes belonging to neighboring layers through the O1W–H1WA⋯O1A (or C1B–H1B⋯O1B) hydrogen bonds (Table S5†).

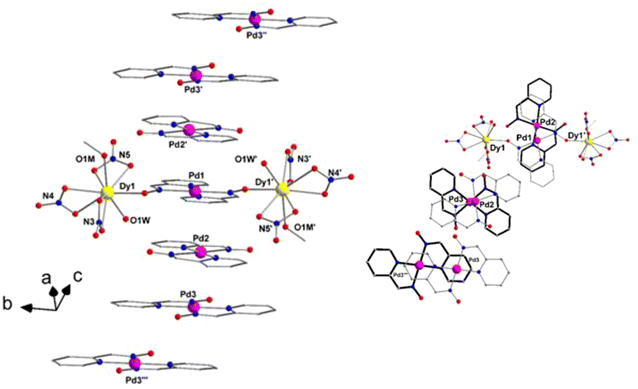
Compounds 2–5 crystalize in the triclinic P1̄ centrosymmetric space group; given that all four structures are isomorphous, only the structure of 2 (Fig. 4b) will be described in detail. The asymmetric unit of the cell contains half of the formula unit {[Dy₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂]·[Pd*(pao)₂]₂·[Pd**(pao)₂]₂}, where Pd, Pd* and Pd** represent symmetry-independent Pd^II atoms and they correspond to the atoms labeled as Pd1, Pd2 and Pd3, respectively, in the following discussion. Thus, the structure of 2 included three types of complexes and they will be described separately. The structure of the complex [Dy₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂] (2A) is shown in Fig. 4b and S7a.† Pd1 atom is located at a center of symmetry and the pao⁻ ligands are also disordered as in 1. Pd2 and Pd3 occupy the same coordination environment as in 1, thus forming square planar co-complexes 2B and 2C, respectively, within the structure of 2. Although, Pd2 occupies a general position, the two symmetry-independent pao⁻ chelates are disordered over positions “A” and “B” (Fig. S7b†). On the other hand, Pd3 also occupies a general position albeit in this case the two symmetry-independent pao⁻ ligands are ordered (Fig. S7c†).

The heterotrinuclear centrosymmetric {Dy₂Pd} unit can be described as a perfectly linear array of two external Dy^III (Dy1, Dy1′) and a central Pd^II ions (Dy1–Pd1–Dy1′ angle = 180°), linked together through the oximate O-atoms (O1A, O1A′) of the {Pd(pao)₂} ‘metalloligand’. Thus, the pao⁻ ligands act as tridentate chelating and bridging, adopting the η¹:η¹:η¹:μ coordination mode, with the ‘hard’ oximate O-atoms binding to the oxophilic Dy^III atoms. Peripheral ligation about the two symmetry-related Dy^III atoms is provided by six bidentate chelating NO₃⁻ groups, and two terminally bound aqua (O1W, O1W′), and two monodentate MeOH (O1M, O1M′) solvate molecules. The intramolecular Dy1⋯Dy1′ separation in 2 is 10.560 Å, presaging negligible magnetic interactions between the paramagnetic centers.

The Dy1 (and its symmetry-related Dy1′) atom is bound to nine O-donor atoms. One of them (O1A) belongs to the deprotonated oximate groups of the {Pd(pao)₂} subunit, six oxygen atoms (O2, O3, O5, O6, O8, O9) belong to the three bidentate chelating nitrato groups, while the remaining two oxygen atoms belong to the terminal MeOH (O1M) and H₂O (O1W) molecules. The Dy–O1A bond (2.282 Å) is the shortest among all Dy–O bond lengths (Table S3†), in accordance with similar separations in Dy–O_oximate complexes.³⁰ The coordination geometry of Dy1 center was determined by the Continuous Shape Measures (CShM) approach of the SHAPE program,³² which allows one to numerically evaluate by how much a particular polyhedron deviates from the ideal shape (Table S4†). Thus, the coordination geometry of Dy1 (and Dy1′) in 2 (Fig. 5) can be described as distorted muffin (CShM value = 2.43) with the second closest polyhedron being that of capped square antiprism (CShM value = 2.57). The basal trigonal plane of the muffin is formed by O5, O6, and O8 atoms, while the equatorial pentagonal plane is made of O1M, O2, O9, O1W, and O3, and the oximate O1A atom occupies the vertex of the muffin.

Fig. 5 The distorted muffin coordination polyhedron of Dy1 (and Dy1′) in 2 with the corresponding atom labeling. The white thin lines define the vertices of the ideal polyhedron. Color scheme: Dy^III, yellow; O, red.

From a supramolecular perspective, there are hydrogen bonding interactions between the dangling oximate O-atoms as acceptors (O21A and O41) of the [Pd(pao)₂] co-crystallized units and the O–H groups of the coordinated MeOH and H₂O molecules as donors. Their dimensions are: O1W⋯O21A = 2.629 Å, O1W⋯O41 = 2.598 Å and O1M⋯O11A = 2.603 Å. These interactions serve to hold together the trinuclear {Dy₂Pd} cluster with the [Pd(pao)₂] units. Further intermolecular hydrogen bonds between molecules belonging to neighboring stacks of pentads stabilize the 3-D supramolecular structure of 2.

In the crystal lattice, complexes 2A, 2B and 2C are stacked in groups of five as shown in Fig. 6, along the [101] direction. Complex 2A is located at the middle of the stack and since the {Dy₂Pd} unit possesses a center of symmetry, 2B and 2C, which are placed below and above the central unit, are also related by center of symmetry and indicated by Pd2, Pd3 and Pd2′, Pd3′ in Fig. 6. The stacking of complexes extends along both directions of [101] through their overlap with Pd3′′ and Pd3′′′ containing complexes that belong to neighboring pentads (Fig. 6). The planar {Pd(pao)₂} units within 2 belong also to fraction-2 as in the case of 1. The type of stacking between 2A and 2B, and 2B and 2C, are of phenyl-chelate interaction (Fig. 6, right) with Δ values of 0.433(1) and 0.906(1) Å, respectively.^31c The angle between the planes of 2A and 2B is 1.3(3)° and between 2B and 2C is 2.0(2)°. The distance of Pd1 from the mean plane of 2B is 3.297(1) Å and that of Pd2 from 2C is 3.264(1) Å. Complexes containing Pd3 and Pd3′′′ atoms are centrosymmetrically-related, and they overlap in a pyridine-metal interaction with a Δ value of 1.061(1) Å and a distance of 3.351(4) Å along the planes.

Fig. 6 (left) Group of five complexes featuring Pd1, Pd2, Pd3 and their centrosymmetric analogues, Pd2′ and Pd3′, stacked along the [101] crystallographic direction. (right) Representations of the overlap of complexes 2A, 2b and 2C with each other. Symmetry codes (′): −x, −y, 1 − z; (′′): 1 + x, y, 1 + z; (′′′): −1 − x, −y, −z.

Finally, complexes 2–5 represent rare examples of discrete, non-polymeric, heterometallic compounds with a Ln^III–M^II–Ln^III linear conformation,³³ and they constitute the only family of linear {Ln₂Pd} complexes reported to date. The only other related example is the complex [Dy₂Pd{(py)₂CNO}₂(hfac)₆], where (py)₂CNOH is the ligand di-2-pyridyl ketoxime and hfacH is 1,1,1,5,5,5-hexafluoropentane-2,4-dione, reported by Okazawa, Ishida and coworkers.³⁴ In that case, the terminal Dy^III ions are 8-coordinate with distorted square antiprismatic geometries.

c. Magnetic studies

Direct current (dc) magnetic susceptibility (χ_M) data on analytically pure, microcrystalline samples of 2–5 were collected in the 2–300 K temperature range under an applied magnetic field of 0.1 T. The data are plotted as χ_MT products vs. T in Fig. 7. From a magnetism perspective, complexes 2–5 can be viewed as “homodinuclear” lanthanide(III) species, provided that square planar Pd(II) is diamagnetic. Note that the very long intramolecular Ln⋯Ln distances in 2–5 preclude the consideration of any significant magnetic interactions between the metal centers. The room temperature χ_MT values for compounds 2 (28.32 cm³ K mol⁻¹), 3 (15.38 cm³ K mol⁻¹), 4 (22.31 cm³ K mol⁻¹) and 5 (5.05 cm³ K mol⁻¹) are in excellent agreement with the expected values of 28.34, 15.76, 22.96 and 5.14 cm³ K mol⁻¹, for two Dy^III (⁶H_15/2, free ion; S = 5/2, L = 5, g_J = 4/3; χ_MT = 14.17 cm³ K mol⁻¹), Gd^III (⁸S_7/2, free ion; S = 7/2, L = 0, g_J = 2; χ_MT = 7.88 cm³ K mol⁻¹), Er^III (⁴I_15/2, free ion; S = 3/2, L = 6, g_J = 6/5; χ_MT = 11.48 cm³ K mol⁻¹) and Yb^III (²F_7/2, free ion; S = 1/2, L = 3, g_J = 8/7; χ_MT = 2.57 cm³ K mol⁻¹) noninteracting ions, respectively.³⁵ Upon cooling, the χ_MT products of complexes 2, 4 and 5 decrease slowly in the 300–50 K temperature range and then more rapidly reaching the values of 23.39 (2), 13.31 (4) and 3.22 (5) cm³ K mol⁻¹ at 2.0 K, while the χ_MT product of the isotropic complex 3 remains almost constant at the entire temperature regime. The observed decrease of the χ_MT products is mostly due to the depopulation of the m_J sublevels of the ground J state of the anisotropic Ln^III ions.³⁶ The χ_MT versus T data for 3 were fit to an isotropic 1-J model that accounts for the long pathway Gd⋯Gd interaction (solid line in Fig. 7). The best-fit parameters were: J = −0.0012(3) cm⁻¹ and g = 1.98(2), thus corroborating the negligible magnetic interactions between the metal centers.

Fig. 7 Plots of χ_MT vs. T for complexes 2–5 in a 0.1 T dc field. The solid pink line is the fit of the data for the isotropic Gd^III-analogue; see the text for the fit parameters.

The field dependence of the magnetization at 1.9, 3 and 5 K, for the magnetically more prominent complexes 2, 4 and 5, shows a relatively rapid increase at low fields without reaching saturation at ∼7 T, which indicates the presence of magnetic anisotropy (Fig. 8). Furthermore, the magnetization values of 2, 4 and 5 at 7 T are ∼10, 12 and 2.5Nμ_B, respectively, much lower than the expected values for two (n = 2) Dy^III (M_S/Nμ_B = ng_JJ = 20Nμ_B), Er^III (M_S/Nμ_B = ng_JJ = 18Nμ_B) and Yb^III (M_S/Nμ_B = ng_JJ = 8Nμ_B) ions, which is due to crystal field effects that induce magnetic anisotropy. For complex 3, the magnetization value at 7 T is 13.7Nμ_B, very close to the theoretical value for two isotropic Gd^III ions (M_S/Nμ_B = ng_JJ = 14Nμ_B) (Fig. S8†).

Fig. 8 Plots of magnetization (M) vs. field (H) for complexes 2, 4 and 5 at three different low temperatures. The solid lines are guides for the eye only.

The presence of anisotropic Ln^III atoms prompted us to explore the magnetic dynamics of compounds 2, 4 and 5, which comprise either oblate (Dy^III) or prolate (Er^III, Yb^III) metal ions with dissimilar distribution of the f-electron density. Our goal was to determine whether these compounds exhibit (or not) slow relaxation of magnetization due to the electrostatic interactions of the crystal field (CF) with the oblate/prolate type electron density of the lanthanide ions. According to this electrostatic model, the oblate ions, having a strong axial CF below and above the xy basal plane, stabilize the largest m_J and maximize the uniaxial anisotropy. However, the prolate ions favor the equatorial coordination geometry to minimize the charge repulsion with the axial electron density.

Hence, we initially conducted alternating current (ac) magnetic susceptibility measurements without an applied dc field, using a 3.5 G ac field oscillating at various frequencies within the temperature range of 2–40 K. One common observation across all compounds was the total absence of frequency dependent signals in the out-of-phase susceptibilities vs. T plots. However, by analyzing the dc field dependence of the at 997 Hz and 1.9 K for compounds 2 (Fig. S9†) and 5 (Fig. S10†), we were able to identify dc fields of 300 and 2000 Oe, which could be suitable (optimum fields) for quenching the operative quantum tunnelling of the magnetization (QTM), a relaxation pathway responsible for the fast magnetization reversal of SMMs at low temperatures. Therefore, we carried out ac studies in the presence of the external dc fields.

Indeed, the appearance of frequency dependent tails of ac signals, in the out-of-phase susceptibilities vs. T plots for 2 (Fig. 9a) under a 300 Oe applied dc field, at temperatures below ∼6 K, indicates the onset of magnetization relaxation and weak SMM behavior. These tails of signals suggest that QTM is still the dominant relaxation mechanism, implying a small effective energy barrier (U_eff). Given the absence of peaks in the vs. T plots, we determined the SMM parameters by assuming that the magnetization relaxation follows a Debye process with only one characteristic time, allowing us to apply the Kramers–Kronig equations,^37,38 resulting in the combined eqn (3), where ω is the angular frequency, τ₀ is the pre-exponential factor, and k_B is the Boltzmann's constant.

ln(χ′′/χ′) = ln(ωτ₀) + U_eff/k_BT (3)

Fig. 9 (a) Temperature dependence of the out-of-phase ac magnetic susceptibility under a 300 Oe applied dc field for complex 2, measured in a 3.5 G ac field oscillating at the indicated frequencies. The solid lines are guides only. (b) Debye plots of complex 2 for the indicated ac frequencies. The solid lines correspond to the fit of the data by applying the Kramers–Kronig eqn (3).

Using eqn (3), we derived the best-fit parameters for compound 2 (Fig. 9b), which gave: U_eff = ∼6.9(1) K and τ₀ = 1.6(1) × 10⁻⁶ s. These values are consistent with the expected properties of a fast-relaxing SMM.¹¹ The resulting energy barrier is quite small, indicating that a thermally assisted Orbach process is unlikely to be the operative mechanism for the magnetization reversal in 2.³⁹

Under a 2000 Oe applied dc field, complex 5 displays frequency dependent in-phase (Fig. S11†) and out-of-phase (Fig. 10a) signals below 3.0 K, thus suggesting the presence of slow relaxation of the magnetization consistent with a field-induced SMM behavior.⁴⁰ The Cole–Cole plots of 5 were fitted at the low temperature regime using a generalized Debye model (Fig. S12†), and the obtained α parameters were found in the range of 0.08–0.13, indicating a relatively narrow distribution of relaxation times, which agrees with the presence of one predominant relaxation processes.³⁸ To determine the temperature dependence of relaxation times (τ) and construct an Arrhenius-type plot, we fitted the data including only the Orbach relaxation mechanism (Fig. 10b); no reasonable values were obtained by fitting the data including Raman and QTM relaxation processes. The data in the temperature range of 1.9 to 3.0 K were analyzed using the following eqn (4):

τ⁻¹ = τ₀⁻¹ exp(−U_eff/k_BT) (4)

where τ⁻¹ defines the relaxation rate and the term τ₀⁻¹ exp(−U_eff/k_BT) corresponds to the Orbach process, in which τ₀ is the pre-exponential factor, k_BT is the thermal energy, and U_eff is the effective energy barrier for the magnetization reversal. As the thermally assisted Orbach process dominates, the relaxation time has an exponential dependence on temperature (linear region), giving a U_eff value of ∼6.0 K as well as a τ₀ value of 1.9 × 10⁻⁵ s.

Fig. 10 (a) Frequency dependence of the out-of-phase 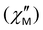ac magnetic susceptibility under a 2000 Oe applied dc field for complex 5, measured in a 3.5 G ac field over the temperature range 1.9–3.5 K. Solid lines represent fits to the data in the frequency range 10–1500 Hz. (b) Arrhenius-type plot of ln(τ) vs. 1/T for complex 5, under a 2000 Oe applied dc field. The solid red line corresponds to the fit of the data by applying eqn (4).

Although there are many {Yb₂} complexes exhibiting field-induced relaxation of magnetization,⁴¹ complex 5 is the first example of a slow-relaxing magnetic species in which the Yb^III ions are separated by such a long-distance spacer, i.e. the ‘metalloligand’ {Pd(pao)₂}.

4. Conclusions

In summary, this work has demonstrated the effectiveness of the ‘metal complexes as ligands’ approach as a successful route for the controlled synthesis of new heterometallic Pd^II/Ln^III complexes with targeted nuclearities and topologies. By utilizing the [Pd(pao)₂] building block (pao⁻ = anion of 2-pyridinealdoxime), we unveiled the coordination of the two dangling, trans oximate, O-atoms of pao⁻ ligands with various Ln^III ions, which led to a new family of linear compounds with the general formula [Ln₂Pd(pao)₂(NO₃)₆(MeOH)₂(H₂O)₂]·[Pd(pao)₂]₄, where Ln^III = Dy (2), Gd (3), Er (4), Yb (5). Compounds 2–5 constitute the only family of {Ln₂Pd} molecular species reported to date. Apart from their structural (and supramolecular) interest, compounds 2 and 5 also display field-induced slow magnetization relaxation under applied dc fields of 300 and 2000 Oe, respectively. However, this is accompanied by relatively low energy barriers for the magnetization reversal due to the fast tunneling mechanism and the weak crystal field effects from the coordinated ligands which constitute the ‘muffin’-like polyhedron of the Ln^III ions.

We are currently trying to expand this synthetic route to various {Pd(oximate)₂} ‘metalloligands’ with either trans or cis unbound oximate O-atoms in an attempt to direct not only the nuclearity (trimers or dimers) and dimensionality (0-D or 1/2-D) of the resulting heterometallic products but also the coordination of the negatively charged oximate O-atoms towards the desired axial or equatorial site (depending on the oblate or prolate Ln^III ion).

Data availability

The data supporting this article has been included as part of the ESI.† Crystallographic data for 1–5 have been deposited at the Cambridge Crystallographic Data Centre (CCDC) under 2385399 (1), 2385400 (2), 2385401 (3), 2385402 (4), and 2385403 (5).†

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The research work was supported by the Hellenic Foundation for Research and Innovation (HFRI) under the 3^rd Call for HFRI PhD Fellowships (Fellowship Number: 5618).

References

1. R. Sessoli, H. Tsai, A. R. Schake, S. Wang, J. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804.
2. R. Sessoli, D. Gatteschi and J. Villain, in Molecular Nanomagnets, Oxford University Press, Oxford, UK, 2006.
3. (a) B. Zhou, R. Tao, S. Q. Shen and J. Q. Liang, Phys. Rev. A, 2002, 66, 010301; (b) J. Tejada, E. M. Chudnovsky, E. del Barco, J. M. Hernandez and T. P. Spiller, Nanotechnology, 2001, 12, 181–186; (c) M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M. A. Arrio, E. Otero, L. Joly, J. C. Cezar, A. Cornia and R. Sessoli, Nature, 2010, 468, 417–421; (d) M. Bottrill, L. Kwok and N. J. Long, Chem. Soc. Rev., 2006, 35, 557–571.
4. M. Nakano and H. Oshio, Chem. Soc. Rev., 2011, 40, 3239.
5. N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694.
6. (a) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110; (b) P. Zhang, Y. N. Guo and J. Tang, Coord. Chem. Rev., 2013, 257, 1728; (c) P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2015, 44, 3923; (d) S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655.
7. F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403.
8. L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092.
9. Y. N. Guo, G. F. Xu, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 9953.
10. N. Ishikawa, M. Sugita, T. Okubo, N. Takana, T. Iino and Y. Kaizu, Inorg. Chem., 2003, 42, 2440–2446.
11. (a) A. Chakraborty, J. Goura, P. Kalita, A. Swain, G. Rajaraman and V. Chandrasekhar, Dalton Trans., 2018, 47, 8841–8864; (b) N. C. Anastasiadis, C. D. Polyzou, G. E. Kostakis, V. Bekiari, Y. Lan, S. P. Perlepes, K. F. Konidaris and A. K. Powell, Dalton Trans., 2015, 44, 19791–19795; (c) A. S. Armenis, V. Vipanchi, K. N. Pantelis, L. Cunha-Silva, K. R. Vignesh, D. I. Alexandropoulos and Th. C. Stamatatos, Chem. – Eur. J., 2023, e202302337.
12. (a) A. Upadhyay, S. K. Singh, C. Das, R. Mondol, S. K. Langley, K. S. Murray, G. Rajaraman and M. Shanmugam, Chem. Commun., 2014, 50, 8838–8841; (b) I. Oyarzabal, J. Ruiz, J. M. Seco, M. Evangelisti, A. Camon, E. Ruiz, D. Aravena and E. Colacio, Chem. – Eur. J., 2014, 20, 14262–14269; (c) A. Upadhyay, C. Das, S. Vaidya, S. K. Singh, T. Gupta, R. Mondol, S. K. Langley, K. S. Murray, G. Rajaraman and M. Shanmugam, Chem. – Eur. J., 2017, 23, 4903–4916.
13. (a) M. A. Sørensen, H. Weihe, M. G. Vinum, J. S. Mortensen, L. H. Doerrerb and J. Bendix, Chem. Sci., 2017, 8, 3566; (b) D. C. Izuogu, T. Yoshida, H. Zhang, G. Cosquer, K. Katoh, S. Ogata, M. Hasegawa, H. Nojiri, M. Damjanovic, W. Wernsdorfer, T. Uruga, T. Ina, B. K. Breedlove and M. Yamashita, Chem. – Eur. J., 2018, 24, 9285–9294; (c) D. Chukwuma Izuogu, T. Yoshida, G. Cosquer, J. N. Asegbeloyin, H. Zhang, A. J. W. Thom and M. Yamashita, Chem. – Eur. J., 2020, 26, 6036–6049; (d) M. Karbowiak, C. Rudowicz and T. Ishida, Inorg. Chem., 2013, 52, 13199–13206.
14. (a) D. Osypiuk, B. Cristóvão and L. Mazur, J. Mol. Struct., 2022, 1261, 132924; (b) Z. G. Lin, L. Y. Fan, A. Kondinski, N. Vankova, T. Heine, B. K. Chen, A. Haider, B. Wang, U. Kortz and C. W. Hu, Inorg. Chem., 2016, 55, 7811–7813; (c) S. L. Huang, A. Q. Jiab and G. X. Jin, Chem. Commun., 2013, 49, 2403–2405; (d) M. Barsukova, N. V. Izarova, R. N. Biboum, B. Keita, L. Nadjo, V. Ramachandran, N. S. Dalal, N. S. Antonova, J. J. Carb, J. M. Poblet and U. Kortz, Chem. – Eur. J., 2010, 16, 9076–9085; (e) B. Miroslaw, B. Cristóvão and Z. Hnatejko, Molecules, 2018, 23, 2423; (f) S. E. Nefedov, N. Y. Kozitsyna, M. N. Vargaftik and I. I. Moiseev, Polyhedron, 2009, 28, 172–180; (g) Z. Wang, L. P. Zhou, T. H. Zhao, L. X. Cai, X. Q. Guo, P. F. Duan and Q. F. Sun, Inorg. Chem., 2018, 57, 7982–7992; (h) M. B. Stuckart, N. V. Izarova, R. A. Barrett, Z. Wang, J. van Tol, H. W. Kroto, N. S. Dalal, P. J. Lozano, J. J. Carbó, J. M. Poblet, M. S. von Gernler, T. Drewello, P. de Oliveira, B. Keita and U. Kortz, Inorg. Chem., 2012, 51, 13214–13228; (i) L. You, W. Zhu, S. Wang, G. Xiong, F. Ding, B. Ren, I. Dragutan, V. Dragutan and Y. Sun, Polyhedron, 2016, 115, 47–53; (j) F. Volcker, F. M. Muck, K. D. Vogiatzis, K. Fink and P. W. Roesky, Chem. Commun., 2015, 51, 11761; (k) J. A. R. Navarro and J. M. Salas, Chem. Commun., 2000, 235–236; (l) L. X. You, L. X. Cui, B. B. Zhao, G. Xiong, F. Ding, B. Y. Ren, Z. L. Shi, I. Dragutan, V. Dragutan and Y. G. Sun, Dalton Trans., 2018, 47, 8755; (m) Z. Lang, P. Yang, Z. Lin, L. Yan, M. X. Li, J. J. Carbo, U. Kortz and J. M. Poblet, Chem. Sci., 2017, 8, 7862.
15. G. Kumar and R. Gupta, Chem. Soc. Rev., 2013, 42, 9403.
16. P. Chaudhuri, Coord. Chem. Rev., 2003, 243, 143.
17. C. J. Milios, Th. C. Stamatatos and S. P. Perlepes, Polyhedron, 2006, 25, 134–194.
18. (a) M. Murugesu, K. A. Abboud and G. Christou, Polyhedron, 2004, 23, 2779–2788; (b) C. D. Polyzou, Z. G. Lada, A. Terzis, C. P. Raptopoulou, V. Psycharis and S. P. Perlepes, Polyhedron, 2014, 79, 29–36; (c) Th. C. Stamatatos, K. A. Abboud, S. P. Perlepes and G. Christou, Dalton Trans., 2007, 3861–3863; (d) K. F. Konidaris, E. Katsoulakou, M. Kaplanis, V. Bekiari, A. Terzis, C. P. Raptopoulou, E. M. Zoupa and S. P. Perlepes, Dalton Trans., 2010, 39, 4492–4494; (e) S. Zhang, L. Zhen, B. Xu, R. Inglis, K. Li, W. Chen, Y. Zhang, K. F. Konidaris, S. P. Perlepes, E. K. Brechin and Y. Li, Dalton Trans., 2010, 39, 3563–3571; (f) C. M. Liu, D. Q. Zhang and D. B. Zhu, RSC Adv., 2014, 4, 53870; (g) D. I. Alexandropoulos, C. Papatriantafyllopoulou, G. Aromi, O. Roubeau, S. J. Teat, S. P. Perlepes, G. Christou and Th. C. Stamatatos, Inorg. Chem., 2010, 49, 3962–3964; (h) C. Papatriantafyllopoulou, Th. C. Stamatatos, C. G. Efthymiou, L. C. Silva, F. A. A. Paz, S. P. Perlepes and G. Christou, Inorg. Chem., 2010, 49, 9743–9745.
19. (a) S. Khanra, B. Biswas, C. Golze, B. Buchner, V. Kataev, T. Weyhermuller and P. Chaudhuri, Dalton Trans., 2007, 481–487; (b) C. D. Polyzou, E. S. Koumousi, Z. G. Lada, C. P. Raptopoulou, V. Psycharis, M. Rouzières, A. C. Tsipis, C. Mathonière, R. Clérac and S. P. Perlepes, Dalton Trans., 2017, 46, 14812; (c) P. Chaudhuri, T. Weyhermüller, R. Wagner, S. Khanra, B. Biswas, E. Bothe and E. Bill, Inorg. Chem., 2007, 46, 9003–9016.
20. (a) K. W. Nordquest, D. W. Phelps, W. F. Little and D. J. Hodgson, J. Am. Chem. Soc., 1976, 98(5), 1104–1107; (b) A. A. Torabi, A. SoudoziI and R. Welter, Z. Kristallogr. - New Cryst. Struct., 2007, 222, 197–198; (c) K. Ha, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2012, 68, m176–m177.
21. G. A. Bain and J. F. J. Berry, Chem. Educ., 2008, 85, 532.
22. CrystalClear, Rigaku/MSC Inc., The Woodlands, Texas, 2005.
23. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122.
24. G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8.
25. (a) K. Brandenburg, DIAMOND, Release 3. 1f, Crystal Impact GbR, Bonn, Germany, 2008, p. 389; (b) I. J. Bruno, J. C. Cole, P. R. Edgington, M. K. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, MERCURY, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 389.
26. K. Ha, Crystal structure of dichloro(2-pyridinealdoxime-κ²N,N′)palladium(II), PdCl₂(C₆H₆N₂O), Z. Kristallogr., 2011, 226, 525–526.
27. K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Wiley, New York, 4th edn, 1986, pp. 254–257.
28. G. J. Kleywegt, W. G. R. Wiesmeijer, G. J. van Driel, W. L. Driessen, J. Reedijk and J. H. Noordik, J. Chem. Soc., Dalton Trans., 1985, 2177.
29. A. B. P. Lever and E. Mantovani, Inorg. Chem., 1971, 10, 817.
30. (a) C. D. Polyzou, H. Nikolaou, C. Papatriantafyllopoulou, V. Phycharis, A. Terzis, C. P. Raptopoulou, A. Escuer and S. P. Perlepes, Dalton Trans., 2012, 41, 13755; (b) Th. C. Stamatatos, E. Katsoulakou, A. Terzis, C. P. Raptopoulou, R. E. P. Winpenny and S. P. Perlepes, Polyhedron, 2009, 28, 1638; (c) Th. C. Stamatatos, A. Escuer, K. A. Abboud, C. P. Raptopoulou, S. P. Perlepes and G. Christou, Inorg. Chem., 2008, 47, 11825–11838.
31. (a) D. N. Sredojevic, Z. D. Tomic and S. D. Zaric, Cent. Eur. J. Chem., 2007, 5, 20–31; (b) Z. D. Tomic, D. N. Sredojevic and S. D. Zaric, Cryst. Growth Des., 2006, 6, 29–31; (c) D. N. Sredojevic, D. Z. Vojislavljevic, Z. D. Tomic and S. D. Zaric, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 261–265.
32. M. Llunell, D. Casanova, J. Girera, P. Alemany and S. Alvarez, SHAPE, Version 2.0, Universitat de Barcelona, Barcelona, Spain, 2010.
33. (a) F. Mori, T. Nyui, T. Ishida, T. Nogami, K.-Y. Choi and H. Nojiri, J. Am. Chem. Soc., 2006, 128, 1440–1441; (b) A. Okazawa, R. Watanabe, M. Nezu, T. Shimada, S. Yoshii, H. Nojiri and T. Ishida, Chem. Lett., 2010, 39, 1331–1332; (c) J. McGuire, B. Wilson, J. McAllister, H. N. Miras, C. Wilson, S. Sproules and J. H. Farnaby, Dalton Trans., 2019, 48, 5491–5495; (d) X. Zhu, W.-K. Wong, J. Guo, W.-Y. Wong and J.-P. Zhang, Eur. J. Inorg. Chem., 2008, 3515–3523; (e) T. Sanada, T. Suzuki and S. Kaizaki, J. Chem. Soc., Dalton Trans., 1998, 959–965.
34. A. Okazawa, H. Nojiri, T. Ishida and N. Kojima, Polyhedron, 2011, 30, 3140–3144.
35. G. G. Morgan and I. A. Kuhne, Practical Approaches to Biological Inorganic Chemistry (Second Edition): Molecular magnetochemistry, Chapter 3, School of Chemistry, University College Dublin, Dublin, Ireland, 2020.
36. J. L. Liu, Y. C. Chen and M. L. Tong, Chem. Soc. Rev., 2018, 47, 2431.
37. (a) M. Grahl, J. Kotzler and I. Sessler, J. Magn. Magn. Mater., 1990, 90–91, 187–188; (b) J. Bartolomé, G. Filoti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014430–014446.
38. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351.
39. Y. N. Guo, G. F. Xu, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 9953–9963.
40. S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669.
41. (a) P.-H. Lin, W.-B. Sun, Y.-M. Tian, P.-F. Yan, L. Ungur, L. F. Chibotaru and M. Murugesu, Dalton Trans., 2012, 41, 12349–12352; (b) W.-B. Chen, L. Zhong, Y.-J. Zhong, Y.-Q. Zhang, S. Gao and W. Dong, Inorg. Chem. Front., 2020, 7, 3136–3145; (c) A. Mondal and S. Konar, Chem. – Eur. J., 2021, 27, 3449–3456; (d) B. Lefeuvre, J. Flores Gonzalez, F. Gendron, V. Dorcet, F. Riobé, V. Cherkasov, O. Maury, B. Le Guennic, O. Cador, V. Kuropatov and F. Pointillart, Molecules, 2020, 25, 492; (e) A. Gorczyński, D. Marcinkowski, M. Kubicki, M. Löffler, M. Korabik, M. Karbowiak, P. Wiśniewski, C. Rudowicz and V. Patroniak, Inorg. Chem. Front., 2018, 5, 605–618; (f) T.-Q. Liu, P.-F. Yan, F. Luan, Y.-X. Li, J.-W. Sun, C. Chen, F. Yang, H. Chen, X.-Y. Zou and G.-M. Li, Inorg. Chem., 2015, 54, 221–228; (g) G. Brunet, R. Marin, M.-J. Monk, U. Resch-Genger, D. A. Gálico, F. A. Sigoli, E. A. Suturina, E. Hemmer and M. Murugesu, Chem. Sci., 2019, 10, 6799–6808; (h) B. Lefeuvre, J. Flores Gonzalez, C. A. Mattei, V. Dorcet, O. Cador and F. Pointillart, Inorganics, 2021, 9, 50; (i) A. Mondal and S. Konar, Dalton Trans., 2021, 50, 13666–13670.

---

Footnote

† Electronic supplementary information (ESI) available: Crystal data and refinement parameters, structural data (tables and figures), spectroscopic and additional magnetism figures for complexes 1–5. CCDC 2385399 (1), 2385400 (2), 2385401 (3), 2385402 (4), and 2385403 (5). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt02691h

---