Open Access Article
Open Access ArticleCoalescence-induced shape transformations in Pd and AuPd clusters
Diana
Nelli
 *,
Edoardo
Dighero
and
Riccardo
Ferrando
*,
Edoardo
Dighero
and
Riccardo
Ferrando
 *
*
Dipartimento di Fisica, Università di Genova, Via Dodecaneso 33, 16146 Genova, Italy. E-mail: diana.nelli@edu.unige.it; riccardo.ferrando@unige.it
First published on 27th September 2024
Abstract
The coalescence of pure Pd and Pd-rich AuPd nanoparticles is studied by molecular dynamics simulations. The collision of icosahedral nanoparticles with face-centered-cubic truncated octahedral ones is considered. These structures are considered because they have been experimentally shown to be the most stable for AuPd nanoalloys and for pure Pd clusters. The final structures of the coalescence process are determined depending on the composition of the initial colliding units, which heavily influences the structure of the final outcome. The key mechanisms at the atomic level of coalescence processes are analysed, revealing the peculiar types of collective atomic rearrangements that enable the transformation of an icosahedron into a sequence of close packed planes and, conversely, the transformation of a series of close packed planes into icosahedral shells.
1 Introduction
Coalescence is a phenomenon which takes place very often in the formation processes of nanoparticles, both in the gas phase and in liquid environments.1–8 In coalescence, two or more clusters collide, attach to each other and progressively fuse to form a larger aggregate. This process takes place through different stages4,9 in which the coalescing units progressively lose their identity to form a final structure which may evolve towards thermodynamic equilibrium. However, in many cases the aggregate remains kinetically trapped into non-equilibrium structures10 often presenting elongated and/or irregular shapes.Traditionally, synthesis processes aimed at avoiding coalescence, because it increases both the polydispersity of the samples and the number of particles with uncontrolled irregular shapes. More recently, there have been several efforts aiming at controlling coalescence in order to use this phenomenon as a tool for the formation of nanoparticles with specific structures and properties.3–5,8 From this point of view, computer simulations of coalescence9 are very useful, because they give the possibility of analysing the relevant mechanisms with atomic resolution. Molecular dynamics (MD) simulations are particularly well suited to this task, as they reproduce atomic trajectories step by step in a realistic manner. For this reason, coalescence is intensely studied by MD simulations in the recent literature, especially for what concerns metallic nanoparticles.1,3,4,7,10–18
Despite these efforts, there are several aspects of coalescence that have yet to be studied. In particular, there are few studies of the coalescence of multi-twin particles, and particularly of icosahedra (IH). These structures are very commonly observed in pure and binary metallic clusters and nanoparticles,19–22 especially for relatively small sizes where they are expected to be energetically favourable,23 and therefore they may become the dominant structures in experimental samples. The few studies involving the coalescence of icosahedra focus on the collision of two icosahedra,12 while the collisions of icosahedra with other common structures, such as the face-centred-cubic (FCC) truncated octahedra (of which the cuboctahedron (CO) is a special case), are much less studied. The study of IH ↔ FCC collisions is indeed very important, because both structures can be present in the same experimental samples.
From this point of view, pure Pd and Pd-rich AuPd nanoparticles are very interesting. In fact, recent experimental results21 have shown that both FCC and IH structures can be grown in gas-phase magnetron sputtering experiments, and that they coexist (with different relative abundances) in the same pure Pd and AuPd nanoparticle samples. The experimental observation of a large number of particles, combined with theoretical free energy calculations, have demonstrated that the relative stability of FCC and IH geometric motifs can be tuned by varying the composition of the nanoparticles.21 For pure Pd nanoparticles, FCC structures are the most energetically favourable, and are therefore dominant in experimental samples, while IH structures are less common. For compositions close to 25 at% Au, IH structures become more favourable, and therefore more abundant, than FCC ones. IH ↔ FCC collisions may occur in both cases, but the coalescence process is expected to exhibit different traits due to the opposite stability of the colliding IH and FCC units.
In this article we study the coalescence of pure Pd nanoparticles and of AuPd nanoalloys by means of MD simulations, colliding a FCC and an IH structure. The scope of our simulations is to relate the composition of the initial colliding units with the geometric motif of the resulting nanoparticle after coalescence, and to unravel the key atomic-level mechanisms of the coalescence process.
2 Model and methods
The coalescence of Pd and AuPd nanoparticles is simulated by MD. In the simulations, the equations of motion of each atom are solved numerically by employing the velocity Verlet algorithm,24 with a time step of 5 fs. The interaction between atoms is modelled by a potential developed on the basis of the second-moment approximation to the tight-binding model,25–27 which is commonly referred to as SMATB, Gupta or Rosato–Guillopé–Legrand (RGL) potential. The analytical form and the parameters of the SMATB potential for Au–Au, Au–Pd and Pd–Pd interactions can be found in ref. 28. This potential has been favourably tested against ab initio DFT calculations.28 Moreover, its predictions are in good agreement with experimental observations of Pd and AuPd nanoparticles; specifically, the model is able to reproduce the reversal in the stability of the FCC and IH motifs while tuning the Au content in Pd-rich AuPd nanoparticles.21We simulate the coalescence of two nanoparticles almost equal in size, but with different geometric structures. In the first case, a FCC truncated octahedron (TO) of 140 atoms collides with an IH of 147 atoms; in the second case, larger nanoparticles are considered (a 314-atom TO and a 309-atom IH). The sizes of the colliding units and of the final products after coalescence are within the size range of the nanoparticles observed in the experiments of ref. 21. All nanoparticles are perfectly symmetric and defect-free. For both cases, two compositions are considered, namely pure Pd and intermixed Au–Pd. Such compositions are chosen because they are representative of different stability trends: in pure Pd nanoparticles, the TO is more energetically favourable than the IH motif; in alloyed AuPd nanoparticles, for some compositions, the opposite holds. In our AuPd nanoparticles, the Au content is in the range 19–20%; at this composition, the IH is more energetically favourable, and the energy difference between the two motifs is close to maximum.21
In the starting configurations of the MD simulations, the two nanoparticles are placed closed to each other (3–4 Å apart), with zero relative velocity and random orientation. The collision is solely due to the attractive forces between atoms of the two particles, and always happens within few simulation steps.
In all simulations, the temperature is kept constant by the Andersen thermostat.24,29 Three temperatures are simulated for each size: 550, 600 and 650 K for the TO140 ↔ IH147 coalescence; 650, 700 and 750 K for TO314 ↔ IH309. In all cases, the simulated temperatures are well below the melting temperatures of the corresponding isolated coalescing clusters. In fact, we have verified by heating simulations that smaller and larger coalescing units melt in the ranges 720–780 K and 830–890 K, respectively. We have chosen two different temperature ranges for the collisions of smaller and larger units in order to obtain evolution time scales of the same order of magnitude in both cases. For this purpose, a good reference is the temperature difference between the melting of the colliding units and the coalescence simulations. For each composition and temperature, 10 independent simulations are performed, with different mutual orientations of the colliding clusters. Some examples of initial configurations are shown in Fig. 1. All simulations are at least 1 μs long; some simulations are prolonged up to 5 μs.
In the case of AuPd nanoparticles, the optimal arrangement of Au atoms within the structure is found by the basin Hopping algorithm.30 Only exchange moves of Au–Pd pairs are employed, while the geometric structure is kept fixed. For both TO and IH geometries, the best placement of Au atoms is in the nanoparticle surface, as found in previous calculations and experiments.21 Such optimised structures are the colliding units of our MD simulations (see Fig. 1(b and d)).
3 Results
3.1 Structural motifs at the end of the coalescence process
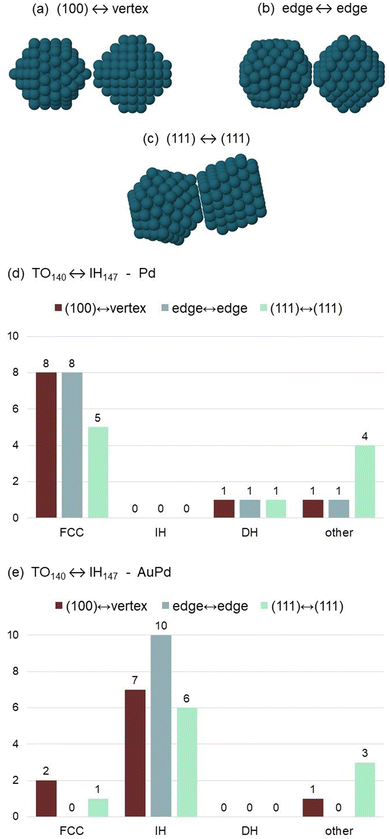
We observe the outcome of the coalescence process after 1 μs, in order to check whether and to what extent the final geometric motif depends on the composition of the colliding units. Results are summarised in Fig. 2. Even though the two initial colliding units are FCC and IH, three possible types of structures are produced in the coalescence process, i.e. FCC, IH and decahedral (DH) particles. FCC particles are made of closed-packed atomic planes. Among those, we count also particles with stacking defects, such as twin planes, extended regions in hexagonal-closed-packed (hcp) stacking or islands in stacking fault on the nanoparticles surface; such defects are indeed present in almost all FCC final structures. IH nanoparticles have incomplete icosahedral structure, characterised by the presence of 6 five-fold symmetry axes converging to the same icosahedral center. In DH structures, a single five-fold symmetry axis is present, either in the central or, more frequently, in the peripheral region of the nanoparticle.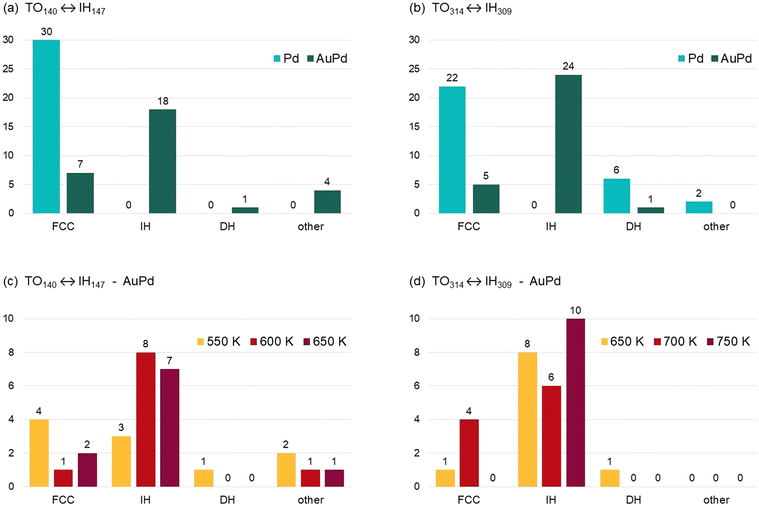 | ||
| Fig. 2 Frequency of the different structural motifs, namely crystalline (FCC), noncrystalline icosahedral (IH) and decahedral (DH) motifs, at the end of the (a) TO140 ↔ IH147 and (b) TO314 ↔ IH309 coalescence simulations, for both pure Pd and ∼20% Au compositions. “Other” structures include bi- and tri-decahedra, i.e. with 2 or 3 converging five-fold symmetry axes,10,31 and kinetically-trapped configurations in which the initial subunits are still well-distinguishable. (c and d) Frequency of the different structural motifs in the AuPd cases, for the three simulation temperatures. | ||
In Fig. 2(a) we show the frequency of the different motifs at the end of the TO140 ↔ IH147 coalescence process. Here we consider all simulations, regardless of the temperature, for a total of 30 final structures for each composition (Pd or AuPd). In the case of pure Pd nanoparticles, all simulations end with a structure of FCC type. In the case of AuPd nanoparticles, all geometric motifs are observed, with the predominance of the IH one (18/30 simulations). The same behaviour is found in the coalescence of larger nanoparticles (Fig. 2(b)): when pure Pd clusters collide, the most frequent final structural motif is the FCC (22/30 simulations), whereas IH structures are not formed in any simulation; on the other hand, the most frequent outcomes of the coalescence of AuPd cluster are IH structures (24/30 simulations), and few FCC structures are found. In all cases, the frequency of the DH motif is very low, as also expected from the observation of few DH structures in the experimental samples.21
In Fig. 2(c and d) we report the frequencies of the different final motifs in the AuPd cases, for the three simulation temperatures. The IH motif is dominant at all temperatures, with the sole exception of TO140 ↔ IH147, 550 K, where however FCC and IH structures are in close competition (4 FCC and 3 IH structures). Our data suggest that the coalesced aggregate is more likely to evolve towards the IH motif if the temperature at which the coalescence process takes place is quite high. Previous calculations have shown that entropic contributions, mainly due to the vibrational term of the free energy, tend to further stabilise IH structures for increasing temperature, with respect to FCC ones.21
Finally, we check whether the outcome of the coalescence does depend on the mutual orientation of the two colliding units. We consider the TO140 ↔ IH147 process, and we simulate three different well-defined mutual orientations, with different initial contact areas, as displayed in Fig. 3(a–c): in the first case, a vertex of the IH is aligned with a truncation of the TO, i.e. with a 2 × 2 facet of (100) type (small contact area); in the second case, the edges of the two units are aligned, i.e. parallel and separated by ∼3 Å (intermediate contact area); in the third case, the (111) facets are aligned (large contact area). The simulations are performed at 650 K, for both compositions (pure Pd and AuPd) of the colliding nanoparticles. For each orientation and composition 10 independent simulations are performed. Results are summarised in the histograms of Fig. 3(d and e).
When pure Pd nanoparticles collide, the IH motif is never observed in the final structure, for any initial orientation. The FCC motif is the most frequent. For the (111) ↔ (111) initial orientation, DH and bi-decahedral (DH2) structures10,11 (here classified as “other”) become more frequent; DH2 structures are expected to evolve towards DH ones, by the elimination of one of the two converging five-fold symmetry axes, so that IH structures are not expected to form even on longer time scales. On the other hand, coalescence simulations of AuPd nanoparticles reveal that, for all initial orientations, the IH final motif is the most frequent, thus confirming the results obtained for random initial orientations.
The results in Fig. 3 demonstrate that the final outcome of the coalescence process is determined by the composition of the colliding units (either Pd or AuPd), while the initial mutual orientation plays a minor role.
In summary, the outcome of the TO ↔ IH coalesce process strongly depends on the composition of the initial clusters, and it reflects the relative stability of the two initial motifs. In the case of pure Pd particles, for which the TO is more energetically favourable than the IH, the coalesced nanoparticles evolves towards a FCC structure, by the elimination of all five-fold symmetry axes of the IH subunit. The coalescence of AuPd nanoparticles very often leads to the formation of an IH structure, with well-developed five-fold symmetry axes converging to the same point, which in most cases is off-centered because at the end of the simulation the structure is still elongated or asymmetric.
Due to this composition-dependent behaviour, the AuPd system is the ideal platform for investigating the coalescence of TO and IH nanoparticles. We can study different coalescence processes, with different final outcomes. Such processes occur for the same sizes of the coalescing units and at the same temperatures, the only difference being the composition of the cluster surfaces; a comparison of the evolution mechanisms and of the typical time scales is therefore possible and straightforward. These evolution mechanisms will be analysed in the following sections.
3.2 Evolution towards the FCC motif and IH ↔ CO transformation
Here we focus on coalescence processes in which the final structure is of FCC type. In such processes, we observe the elimination of the five-fold symmetry axes belonging to the IH colliding unit, while the number of parallel close-packed planes increases during the simulation. This behaviour can be efficiently visualised by the analysis of the local environment of the atoms of the coalescing particle, through the Common Neighbour Analysis (CNA).32 The CNA assigns to each pair of nearest neighbors a signature that depends on their local environment (based on the number and disposition of the common nearest-neighbours of the pair). Here, following the scheme of ref. 33, we classify each atom with the signatures calculated with all the pairs formed with all its nearest neighbours. As such, we are able to visualise atoms with either FCC or IH local environment, and monitor their number during the simulation.In Fig. 4 we show two representative simulations ending up with the FCC structural motif, in the TO140 ↔ IH147 case (Fig. 4(a–c)) and in the TO314 ↔ IH309 one (Fig. 4(d–f)). In both cases, the colliding particles are made of Pd atoms. The coalescence of AuPd nanoparticles (when resulting in a FCC structure) occurs via the same mechanism. In Fig. 4(a and d) we plot the number of IH and FCC atoms in the first stage of the process. Here, IH atoms are those that, according to the CNA, belong either to a specific fivefold-symmetry axis or to the center of the icosahedron, to which different axes converge. FCC atoms are those belonging to closed-packed planes with local fcc stacking. In both cases, only internal atoms are considered, since surface atoms are associated with different sets of CNA signatures. In Fig. 4(b and e) we show some snapshots from the coalescence simulations. In Fig. 4(c and f) the same snapshots are shown, but atoms are coloured according to their local environment: atoms in closed packed planes are coloured in light blue (here also surface atoms are considered and coloured in the same way); IH atoms and icosahedral vertices on the surface are coloured in orange; finally, we use different colours for closed-packed planes with different stacking (pink for inner planes with local hcp stacking, yellow for surface planes in stacking fault), in order to monitor the formation of stacking defects during the simulation; atoms with other local environment are displayed as small spheres.
For both sizes, the number of IH atoms begins to decrease from the very first steps of the simulation. Soon after the collision, many of the five-fold symmetry axes disappear due to the partial disordering of the IH subunit, in the region coming into contact with the TO cluster. On the other hand, the TO subunits keeps the initial symmetry; in the TO314 ↔ IH309 case, we observe the formation of an inner twin plane. Then, the number of IH atoms gradually decreases and, correspondingly, the number of FCC atoms increases. Closed-packed planes form in the initially disordered contact region, parallel to the TO planes. The FCC symmetry gradually propagates into the IH subunit, that still present five-fold symmetry axes in the region opposite to the TO.
A second stage of the process can be identified, in which the number of IH atoms suddenly goes to zero, and, at the same time, the number of FCC atoms largely increases. All the remaining fivefold axes are eliminated, and the coalesced aggregate achieves overall FCC symmetry, without disordered regions. Such process usually leads to the formations of stacking defects, which resemble those formed in the coalescence of two TO clusters, and evolve in the same way.4 At the end of the simulation, the aggregate is rather compact (higher compactness is achieved for higher simulation temperatures) but still presents some stacking defects in the central region. Stacking defects in the nanoparticle surface are more easily eliminated.
Let us now focus on the sudden transformation of the IH subunit. The shape and symmetry of the aggregates before and after the transformation can be seen in Fig. 4(b and c) (snapshots taken at 40 and 50 ps) and in Fig. 4(e and f) (snapshots taken at 150 and 200 ps). Before the transformation, the aggregate appears as a IH fragment connected to a larger FCC region. The IH part has converging five-fold symmetry axes and triangular (111) surface facets. After the transformation, the initially IH subunit becomes FCC, and it presents both (111) and (100) facets. Specifically, it is a fragment of a cuboctahedron (CO), i.e. a TO with deep truncations.34 The transformation, which is shown from another perspective in Fig. 5, is an example of the well known diamond–square (DS) transformation. The vertex of the IH fragment become the vertex of the CO fragment after the transformation; pairs of triangular (111) facets (of overall diamond shape) of the IH transform into single square (100) facets of the CO, from which the name of the transformation. The process is sudden, i.e. it occurs without intermediate steps by the concerted displacement of all atoms in the fragment; in our simulations, it is completed within 0.1 ps. The FCC region on the opposite side is not involved in the transformation, and retains its original shape.
 | ||
| Fig. 5 Coalesced aggregate before and after the diamond–square transformation. (a) A fragment of the 147-atom IH transforms into the corresponding fragment of the CO of the same size. Snapshots are taken from the same simulation as in Fig. 4(a–c). (b) Same as in (a), but the transforming subunit is a fragment of the 309-atom IH. Snapshots are taken from the same simulation as in Fig. 4(d–f). | ||
The transformation from the CO to the IH, suggested by the same magic numbers of the two structures, has first been theoretically described by Mackay,35 and it has been observed in several MD simulations of metal clusters.36–42 It occurs via the square–diamond transformation (the reverse of the DS transformation), in which the square facets of the CO transform into pairs of triangular icosahedral facets. If the cluster is sufficiently small, the transformation occurs in one step, without intermediate local minima.40 The IH → CO transformation via the DS mechanism has only been observed in metadynamics simulations,41,43 in which the dynamics is altered by the addition of a bias potential in order to enhance barrier crossings and direct the evolution towards the desired configuration. Up to now, it had never been observed in unbiased MD simulations of metal clusters. Though the two structures are connected by a simple geometric transformation, it is unlikely that the CO spontaneously forms during the evolution of a free IH cluster, because the IH → CO transformation would require the formation of 6 large, high-energy (100) facets; typically, the evolution from the IH to the FCC symmetry takes place via different routes, ending up with TO structures with a more favourable (100)/(111) surface facet ratio.
In our case, the formation of the CO symmetry is enhanced compared to the case of the evolution of a free cluster, for two main reasons. First, the IH fragment is in contact with an extended FCC region, which facilitates a direct IH → FCC transformation, without intermediate disordered, decahedral or poly-decahedral configurations; indeed, soon after the transformation, the atomic planes of the newly formed CO are aligned with those in the FCC region. Second, since only a CO fragment must be formed, the number of atoms in (100) facets is not that large. We note that the DS transformation always occurs when the IH part is quite small, whereas in the initial stage the IH → FCC symmetry evolution proceeds gradually by the formation of more and more FCC atoms in the contact region.
The achievement of the FCC symmetry is a rather complex process, never occurring in the same way in different independent simulations. Different stacking defects may form in the first stage of the evolution, and the size of the IH fragment that transforms into the CO is quite variable. As such, the time at which the shape transformation is completed is strongly simulation-dependent. In Fig. 6 we have collected all IH → CO transformation times, in both pure Pd and AuPd cases. We can identify some trends. On average, the transformation time decreases for increasing temperature and, for fixed temperature, it increases with nanoparticle size. In the coalescence of AuPd nanoparticles, the IH → CO transformation requires longer times, due to the higher stability of the IH motif in this case. Finally, we note that, in all cases, the transformation time is considerably shorter than the 1 μs duration of the simulations. In the pure Pd cases, even at the lowest temperatures, the transformation is always accomplished within few ns.
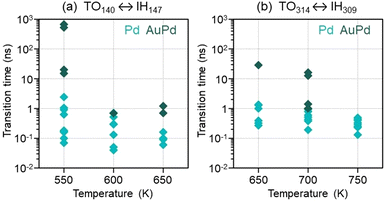 | ||
| Fig. 6 IH → CO transformation times, as found in the different independent simulations of (a) TO140 ↔ IH147 and (b) TO314 ↔ IH309 coalescence processes. | ||
It is meaningful to compare the IH → CO transformation times of Fig. 6 with the lifetime of isolated Pd IH147 and IH309 clusters. To this end, we let them evolve at the higher temperatures employed in the coalescence simulations, i.e. 650 K for IH147 and 750 K for IH309. For each structure, we perform three independent 1 μs-long MD simulations. We find that, in all cases, the cluster retains the IH symmetry to the end of the simulation. We recall, in pure Pd clusters, the lowest-energy structural motif is the FCC; therefore IH clusters are expected to evolve towards more favourable FCC structures. Our simulations show that, though energetically unfavourable, isolated IH structures are metastable. Their lifetime is likely to exceed 1 μs at the (quite high) simulation temperatures, and it is expected to be even longer at lower temperature. On the other hand, when colliding with TO clusters, the stability of IH structures is considerably reduced, their lifetime decreasing by at least three orders of magnitude.
In simulations ending up with the DH motif, the evolution of the coalesced aggregate closely resemble that of Fig. 4: initially, parallel closed-packed planes propagate within the region of the IH subunit, which gradually looses its five-fold symmetry axes; then, by a sudden process of collective character, the IH fragment transform into a DH, with a single peripheral five-fold symmetry axis. This kind of IH → DH transformation is described, for example, in ref. 43. Evolution times are in the same range as those of the IH → CO transformation.
3.3 Evolution towards the IH motif and TO → IH transformation
Here we consider coalescence simulations ending up with an IH fragment. Unlike the previous case, the five-fold symmetry axes of the IH colliding cluster do not disappear, but some of them are progressively elongated through multiple collective processes coupled with the diffusion and rearrangement of surface atoms. The mechanism is quite complex, and independent simulations exhibit rather different behaviours. Here we try to elucidate the main features of such mechanism, with the help of Fig. 7. In the figure, we show two simulations of the coalescence of AuPd nanoparticles, in the case of the smaller (Fig. 7(a–d)) and larger colliding units (Fig. 7(e–h)), to track the evolution of the symmetry, we monitor the number of atoms with different local environments, and visualise them in some representative snapshots.In the graph of Fig. 7(a and e), we can see that the number of IH atoms increases during the simulations and, conversely, the number of FCC atoms decreases. In this case, we do not observe any abrupt changes in the number of IH atoms, meaning that the evolution of the coalesced aggregate proceeds quite regularly, without sudden shape transformations. We note that the increase of IH atoms is not regular: they slightly decrease in the very first part of the simulations, then increase up to a maximum value, from which they begin to decrease and eventually stabilise around a final value, considerably larger than the initial one. In Fig. 7(c and g) we can observe IH atoms in some simulation snapshots. The initial drop is due to the shortening of some five-fold symmetry axes in the contact region, which then reform and become longer. At the end of this stage, we observe one or two fivefold-symmetry axes prolonged within the region of the TO subunit. Then, new five-fold symmetry axes appear in the TO region, which do not converge to the center of the IH subunit. The number and length of such non-converging axes are highly variable from simulation to simulation. In some cases, a single axis develops (see for example Fig. 7(g), 220 ns); in many simulations we observe the formation of 2 or 3 non-converging axes in the TO region, which typically adopt a peculiar tetrahedral arrangement44 (see Fig. 7(c), 200 ns). In the subsequent stage of the evolution, all non-converging five-fold symmetry axes disappear. The resulting aggregate is still quite elongated, with few prolonged fivefold-symmetry axes on one side. The nanoparticle gradually becomes more compact, and, by the end of the simulation, other five-fold symmetry axes are prolonged.
In Fig. 7(d and h) we can observe in detail the mechanism by which the initial five-fold symmetry axes are prolonged within the TO region. The first step of the mechanism consists in the alignment and shift of the atomic planes of the TO subunits, resulting in the formation of one plane in local hcp stacking (marked in pink in the figure). Such planes are the extensions of the hcp planes of the IH subunit, each one including two five-fold symmetry axes at its borders (see Fig. 7(d), 1 ns). In this way, some atoms (marked in yellow in the figure) are placed on the extension of the five-fold symmetry axes; however, they do not exhibit full five-fold symmetry due to the lack of first neighbours on one side. The symmetry is achieved when atoms or islands on the cluster surface diffuse towards the growing axes, surrounding them.
Due to the complexity of the mechanism and to the absence of sudden shape transformations, it is difficult to identify well-defined times for the completion of the FCC → IH evolution. We can say that, in the cases of Fig. 7, the transformation is completed well before the 1 μs. The same hold for all other simulations ending up with the IH motif. In some of the simulations at the lowest temperatures, non-converging five-fold symmetry axes are still present in the final structure. However, also in these cases, we can say that TO subunit has lost its FCC character. Again, we compare the results of the coalescence simulations with the evolution of isolated AuPd TO140 and TO314 clusters, performed by MD at the 650 K and 750 K, respectively. In the AuPd case, TO clusters are expected to evolve towards the more energetically favourable IH motif. However, such evolution is never observed in the 1 μs timescale of our simulations, thus revealing the metastable character of AuPd TO structures.
As in the case of pure Pd IH clusters, AuPd TO clusters are energetically unfavourable, but their lifetime is quite long (>1 μs) even at high temperatures. However, when such metastable structures collide and coalesce with a cluster presenting a more favourable structural motif, their lifetime is drastically reduced.
Finally, we mention an alternative evolution pathway towards the IH motif, which is found in some of the TO140 ↔ IH147, simulations. In this pathway, the TO passes through an intermediate disordered configuration, and transforms into a IH147 structure, with a well-defined icosahedral center. After the transformation, the coalesced aggregate has two icosahedral centers, such as in the coalescence of two IH subunits.12 The newly formed IH usually presents incomplete five-fold symmetry axes and surface defects, and it is therefore less stable compared to the original IH subunits. During the simulation, it gradually looses the IH symmetry; when the icosahedral center is eliminated, the evolution proceeds as in the case of Fig. 7.
3.4 TO and IH atomic mobility during coalescence
In the previous sections, we have seen that the final outcome of the TO ↔ IH coalescence process is dictated by the most energetically favourable (and therefore the most stable) of the two colliding clusters, namely the TO in the pure Pd case and the IH in the AuPd one. The less stable cluster transforms to adapt to the symmetry of the most stable one, which, at least in the first part of the evolution, retains its original shape. The TO ↔ IH coalescence therefore appears as a highly asymmetric process, in which atoms of the different subunits behave rather differently.In order to better highlight such asymmetric character, we monitor the mobility of atoms initially belonging to the two colliding clusters. We do not consider atoms that, initially, are in the cluster surfaces. The diffusion of surface atoms is much faster compared to that of internal atoms, therefore they are expected to move quite freely on the surface of the aggregate soon after the collision, when the symmetry of the two subunits is still unchanged. To track inherent shape and symmetry transformations, it is better to focus on inner atoms, and to neglect the effect of the much more mobile surface ones. Atoms belonging to the inner part of the TO and of the IH clusters before the collision are listed; the number of nearest-neighbours bonds (NB) among atoms of the two groups is monitored during the coalescence simulations.
In Fig. 8, we show the behaviour of two simulations in which the final structure is FCC (the same as in Fig. 4). In Fig. 8(a, b and d, e) we plot the evolution of NB for both the TO and the IH; specifically, we plot the difference ΔNB between the number of bonds counted during the simulation and that before the collision. In Fig. 8(a and d) we focus on the first stage of the coalescence process, up to the IH → CO transformation; in Fig. 8(b and e) we show the evolution of ΔNB for the whole duration of the simulation. The plots in Fig. 8(a and d) show that, from the initial collision to the shape transformation of the IH fragment, atoms of the TO are not involved in the coalescence process. On the contrary, the number of bonds within the IH largely decreases. After the IH → CO transformation, the drop in ΔNB stops, due to the higher stability of the newly-formed CO fragment. On a longer timescale, ΔNB decreases for both subunits, meaning that, at this stage, also atoms of the TO are involved in the reshaping of the coalesced aggregate (see Fig. 8(b and e)). In Fig. 8(c and f) snapshots of the simulations are shown. Atoms of the two groups have different colours, in order to visualise their inter-diffusion. Up to the completion of the IH → CO transformation, TO inner atoms exactly retain their original shape; only after the transformation, some atoms begin to diffuse.
 | ||
| Fig. 8 Mobility of TO and IH inner atoms in two representative simulations ending up with the FCC structural motif. (a–c) TO140 ↔ IH147, pure Pd composition, 600 K. (d–f) TO314 ↔ IH309, pure Pd composition, 700 K. Simulations are the same as in Fig. 4. (a and d) Evolution of ΔNB in the first part of the simulation, up to the IH → CO transformation. (b and e) Evolution of ΔNB during the whole simulation. The simulation in (b) has been prolonged up to 5 μs. (c and f) Snapshots of the simulations, in which atoms are coloured according to their position before the collision: brown – atoms initially belonging to the inner part of the TO; green – atoms initially belonging to the inner part of the IH. All other atoms are displayed as small spheres. | ||
In Fig. 9, the same plot and atom visualisation are shown for two simulations ending up with the IH motif (the same as in Fig. 7). In this case, IH inner atoms keep a perfect icosahedral symmetry in the first part of the simulation, while TO inner atoms change shape and begin to diffuse around the IH subunit. Later on, also some IH inner atoms are involved in the process, but most of them retain their initial positions, so that the original IH is still well-distinguishable.
 | ||
| Fig. 9 Mobility of TO and IH inner atoms in two representative simulations ending up with the IH structural motif. (a and b) TO140 ↔ IH147, AuPd composition, 650 K. (c and d) TO314 ↔ IH309, AuPd composition, 750 K. Simulations are the same as in Fig. 4. (a and c) Evolution of ΔNB during the whole simulation. (b and d) Snapshots of the simulations, in which atoms are coloured according to their position before the collision: brown – atoms initially belonging to the inner part of the TO; green – atoms initially belonging to the inner part of the IH. All other atoms are displayed as small spheres. | ||
4 Discussion and conclusions
In this article, we have investigated the coalescence of two metal nanoparticles with different geometric shapes and symmetries: the crystalline truncated octahedron and the multiply-twinned non-crystalline icosahedron. The AuPd system has been chosen due to recent experimental results, showing that FCC and IH structures coexist in the same sample. Moreover, according to the nanoparticle composition, either the FCC or the IH motif is more energetically favourable in the size range of our colliding clusters. Our simulations show that the coalescence process is deeply influenced by the relative stability of the two units. The most stable cluster (i.e. the TO in the pure Pd case and the IH in the AuPd one) dictates the final structural motif of the coalesced aggregate. On the other hand, the least stable cluster is the most involved in the coalescence process: its atoms are much more subjected to inter-diffusion and are responsible of the achievement of an overall compact shape. The least stable cluster loses its initial symmetry to adapt to the most stable one, via non-trivial shape transformations induced by coalescence, that our atomic-scale molecular dynamics simulations have been able to detect. The typical time scales of such transformation are considerably shorter that the lifetime of the isolated clusters at the same temperatures. As such, we introduce the concept of stability upon coalescence, which is much reduced compared to the inherent stability of isolated clusters. This effect may play some role in the synthesis of metal nanoparticles. At the beginning of the synthesis process, clusters of different competing structures can form. If coalescence is negligible, the clusters are likely to grow within the initial motif and, due to their inherent stability, even the lowest-energy motifs could be observed in the final sample. However, if coalescence events occur during the synthesis process, clusters of the least stable motif are likely to transform, so that the frequency of such motif in the final population would be lower. We note that, traditionally, coalescence is believed to solely produce highly defected and elongated out-of-equilibrium structures. Here we have shown that it can be employed in the opposite way, i.e. to eliminate metastable out-of-equilibrium geometric motifs for producing structural homogenous nanoparticle samples.Data availability
Our own molecular dynamics code used for all simulations is available at https://doi.org/10.5281/zenodo.13172429.The data presented in the article are available at https://doi.org/10.5281/zenodo.13173730.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support under the National Recovery and Resilience Plan (NRRP), Mission 4, Component 2, Investment 1.1, Call for tender No. 104 published on 2.2.2022 by the Italian Ministry of University and Research (MUR), funded by the European Union – NextGenerationEU – Project Title PINENUT – CUP D53D23002340006 – Grant Assignment Decree No. 957 adopted on 30/06/2023 by the Italian Ministry of University and Research (MUR). The authors thank Dr Chloé Minnai for useful discussion.References
- T. H. Lim, D. McCarthy, S. C. Hendy, K. J. Stevens, S. A. Brown and R. D. Tilley, ACS Nano, 2009, 3, 3809–3813 CrossRef CAS.
- P. Lu, M. Chandross, T. J. Boyle, B. G. Clark and P. Vianco, APL Mater., 2014, 2, 022107 CrossRef.
- P. Grammatikopoulos, J. Kioseoglou, A. Galea, J. Vernieres, M. Benelmekki, R. E. Diaz and M. Sowwan, Nanoscale, 2016, 8, 9780–9790 RSC.
- D. Nelli, M. Cerbelaud, R. Ferrando and C. Minnai, Nanoscale Adv., 2021, 3, 836–846 RSC.
- W. Dachraoui, M. I. Bodnarchuk and R. Erni, ACS Nano, 2022, 16, 14198–14209 CrossRef CAS PubMed.
- F. M. Alcorn, M. Chattoraj, R. M. van der Veen and P. K. Jain, J. Phys. Chem. C, 2023, 127, 16538–16544 CrossRef CAS.
- J. Liu, W. Lv, Y. Mou, C. Chen and Y. Kang, J. Mater. Res. Technol., 2023, 27, 2490–2507 CrossRef CAS.
- L. Gu, W. Yuan, Y. Yang, Y. Shen, C. An and W. Xi, Nano Lett., 2024, 24, 5618–5624 CrossRef CAS.
- P. Grammatikopoulos, M. Sowwan and J. Kioseoglou, Adv. Theory Simul., 2019, 2, 1900013 CrossRef.
- D. Nelli, G. Rossi, Z. Wang, R. E. Palmer and R. Ferrando, Nanoscale, 2020, 12, 7688–7699 RSC.
- M. M. Mariscal, S. A. Dassie and E. P. M. Leiva, J. Chem. Phys., 2005, 123, 184505 CrossRef PubMed.
- J. Antúnez-García, S. Mejía-Rosales, E. Pérez-Tijerina, J. M. Montejano-Carrizales and M. José-Yacamán, Materials, 2011, 4, 368–379 CrossRef PubMed.
- S. A. Paz, E. P. M. Leiva, J. Jellinek and M. M. Mariscal, J. Chem. Phys., 2012, 134, 094701 CrossRef.
- P. Grammatikopoulos, C. Cassidy, V. Singh and M. Sowwan, Sci. Rep., 2014, 4, 5779 CrossRef CAS.
- Y. Tang, Y. Shi, Y. Cao, Z. Zhang, X. Duan and X. Zhou, Mol. Catal., 2023, 551, 113634 CrossRef CAS.
- J. Kim and H. Chung, J. Mater. Sci. Technol., 2024, 184, 64–74 CrossRef CAS.
- P. Grammatikopoulos and E. Toulkeridou, J. Aerosol Sci., 2024, 179, 106356 CrossRef CAS.
- S. Zinzani and F. Baletto, Phys. Chem. Chem. Phys., 2024, 26, 21965–21973 RSC.
- Z. W. Wang and R. E. Palmer, Phys. Rev. Lett., 2012, 108, 245502 CrossRef CAS.
- M. R. Langille, J. Zhang, M. L. Personick, S. Li and C. A. Mirkin, Science, 2012, 337, 954–957 CrossRef CAS PubMed.
- D. Nelli, C. Roncaglia, R. Ferrando and C. Minnai, J. Phys. Chem. Lett., 2021, 12, 4609–4615 CrossRef CAS.
- D. Nelli, C. Roncaglia, R. Ferrando, Z. Kataya, Y. Garreau, A. Coati, C. Andreazza-Vignolle and P. Andreazza, Nanoscale, 2023, 15, 18891–18900 RSC.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371–423 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon, Oxford, 1987 Search PubMed.
- F. Cyrot-Lackmann and F. Ducastelle, Phys. Rev. B: Solid State, 1971, 4, 2406–2412 CrossRef.
- R. P. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6265 CrossRef CAS.
- V. Rosato, M. Guillopé and B. Legrand, Philos. Mag. A, 1989, 59, 321 CrossRef.
- F. Pittaway, L. O. Paz-Borbón, R. L. Johnston, H. Arslan, R. Ferrando, C. Mottet, G. Barcaro and F. Fortunelli, J. Phys. Chem. C, 2009, 113, 9141–9152 CrossRef CAS.
- F. Baletto, C. Mottet and R. Ferrando, Surf. Sci., 2000, 446, 31–45 CrossRef CAS.
- G. Rossi and R. Ferrando, J. Phys.: Condens. Matter, 2009, 21, 084208 CrossRef CAS.
- G. Rossi and R. Ferrando, Nanotechnology, 2007, 7, 225706 CrossRef.
- D. Faken and H. Jónsson, Comput. Mater. Sci., 1994, 2, 279 CrossRef CAS.
- C. Roncaglia and R. Ferrando, J. Chem. Inf. Model., 2023, 63, 459–473 CrossRef CAS.
- R. Ferrando, Structure and Properties of Nanoalloys, Elsevier, 2016 Search PubMed.
- A. L. Mackay, Acta Crystallogr., 1962, 15, 916–918 CrossRef CAS.
- T. Li, S. Lee, S. Han and G. Wang, Phys. Lett. A, 2002, 300, 86–92 CrossRef CAS.
- Z. Zhang, W. Hu and S. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125443 CrossRef.
- F. Y. Chen and R. L. Johnston, Acta Mater., 2008, 56, 2374–2380 CrossRef CAS.
- B. Cheng and A. H. W. Ngan, J. Chem. Phys., 2013, 138, 164314 CrossRef.
- K. Rossi, L. Pavan, Y. Soon and F. Baletto, Eur. Phys. J. B, 2018, 91, 33 CrossRef.
- F. Baletto, J. Phys.: Condens. Matter, 2019, 31, 113001 CrossRef PubMed.
- P. N. Plessow, Phys. Chem. Chem. Phys., 2020, 22, 12939–12945 RSC.
- L. Pavan, K. Rossi and F. Baletto, J. Chem. Phys., 2015, 143, 184304 CrossRef CAS PubMed.
- G. Rossi and R. Ferrando, Nanotechnology, 2007, 18, 225706 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |