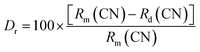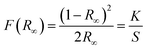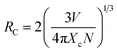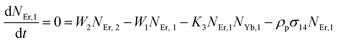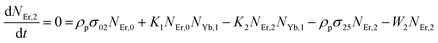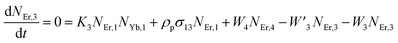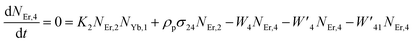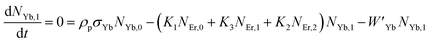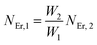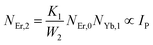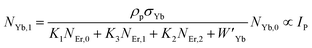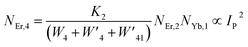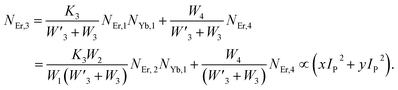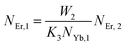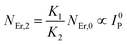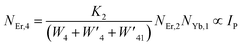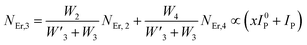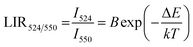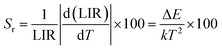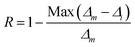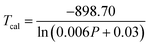DOI:
10.1039/D3RA02126B
(Paper)
RSC Adv., 2023,
13, 21096-21104
Spectroscopic in-depths of upconverting NaZr2(PO4)3 phosphors for LIR-based thermometry
Received
31st March 2023
, Accepted 25th June 2023
First published on 12th July 2023
Abstract
This study employed solid-state synthesis to develop the green emitting Er3+-Yb3+:NaZr2(PO4)3, NASICON material. Using Rietveld refinement, the crystallographic variables of the synthesized phosphors were precisely calculated. The upconverting phenomenon was seen with naked eye when exposed to 980 nm laser radiation. The intermediate excited state dependency on the unusual photon number dependence on the green and red emission has been understood using the steady-state rate law equations. Further, the temperature sensing performances with good repeatability were compared with different laser densities, and it was found that the prepared phosphors could be an ideal material for upconverting and temperature sensing applications.
1. Introduction
The search for suitable energy materials for fuel cells and rechargeable batteries has gained attention in recent years because of the limitation of non-conventional sources and rapid decrement of inexpensive oil. Lithium-ion batteries show potential application as an energy storage system in portable and wearable electronic devices.1–3 Lithium-ion batteries face several shortcomings, including high cost, limited energy densities, the low abundance of lithium, and low efficient recycling.3–5 Again, in lithium batteries, liquid electrolytes, such as LiClO4 dissolved in propylene carbonate, are used, which impart several disadvantages, such as device failure due to electrode corrosion, limited operating temperature range, and unsuitable shapes.6 Thus, it is important to select a solid electrolyte in order to avoid the above-mentioned problems. Currently, research is focused on sodium-ion rechargeable batteries, which can operate at room temperature, owing to their low cost, the natural abundance of sodium, and wide geographical distributions.3–5 The sodium superionic conductor (NASICON) compounds with the structure Na[Ge, Ti, Zr]2(PO4)3 are studied by researchers since the early 60s owing to their unique structure for sodium-ion batteries. NASICON materials possess several interesting features, such as high ionic conductivity at room temperature or elevated temperature, high thermal stability, low thermal expansion coefficient, resistance to radiation damage, low solubility in water, large surface area, and capability to accommodate ions. These properties of NASICON compounds suggest their suitability in various industrial applications, such as in gas sensors, fuel cells, rechargeable batteries, and nuclear waste immobilization.7,8 NaZr2(PO4)3 is an interesting NASICON-type anode material that consists of PO4 tetrahedra sharing a corner with ZrO6 octahedra and linked to the three-dimensionally interstitial space where the alkali and alkaline-earth metal ions can partially occupy. The open and strongly bonded structure makes possible the fast movement i.e., the high mobility of the Na+ ions tunnelling through polyhedra chain (O3ZrO3(Na)ZrO3O3).9–11 In order to synthesize thermally stable efficient luminescent materials, the incorporation of the f-block element in the NASICON structure has been carried out by several researchers. The downconversion luminescence study based on the lanthanide doped (Eu2+, Sm3+) NASICON materials has been reported for a broad range of applications, including white light emitting diodes (WLEDs).10,12 The upconversion (UC) emission characteristics of the NASICON materials can also be studied by choosing suitable dopant ions.13,14 Er3+ ions are widely used as dopant ions owing to their large number of ladder-like energy levels, high emission lifetime, and two thermally coupled levels (TCLs), which result in intense green emission. Although Er3+ ions have a direct energy level corresponding to the 980 nm excitation, Yb3+ ions are used as sensitizers owing to their broad absorption cross-section compared to that of Er3+ ions.15,16 The temperature sensing study is very popular in recent days to monitor the most important physical parameter ‘Temperature’. The accurate temperature detection of inaccessible objects and intracellular cells is very difficult with the contact thermometry method. The non-contact temperature measurement is very essential in the field of coal mines, oil refiners, medical diagnosis, metallurgical, food manipulation, and testing.16,17 In non-contact thermometry, the temperature is measured depending on optical parameters such as luminescence intensity ratio (LIR), luminescence lifetime, emission bandwidth, and peak wavelength. The LIR technique is the most used technique among researchers as it is insensitive to the external environment such as pressure, and light source, whereas other optical techniques strongly depend on the atmosphere.17,18 The energy difference between levels 2H11/2 and 4S3/2 of Er3+ ions is ∼780 cm−1, which lies in TCL's energy gap range. The LIR of the 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2 levels thus can be used for the optical thermometry study.
In this work, the upconversion (UC) luminescence and temperature sensing behaviour using the luminescence intensity ratio technique of Er3+-Yb3+:NaZr2(PO4)3 phosphors were investigated under 980 nm laser radiation. The structural, optical, and electrochemical properties of the generated phosphors were also investigated.
2. Experimental details
2.1. Synthesis of materials
Er3+-Yb3+:NaZr2(PO4)3 NASICON material has been prepared by the solid-state reaction technique. The starting reagents to prepare the host material are sodium carbonate (Na2CO3), zirconium dioxide (ZrO2), and sodium dihydrogen phosphate (NH4H2PO4), which follows the reaction given as,| | |
Na2CO3 + 4ZrO2 + 6NH4H2PO4 = 2NaZr2(PO4)3 + CO2 + 6NH3 + 9H2O
| (1) |
For doping Er3+ and Yb3+ ions into the host material, erbium oxide (Er2O3) and ytterbium oxide (Yb2O3) were taken. Er3+ ions were doped by varying different concentrations from 1 mol% to 9 mol% and after optimizing Er3+ ions, Yb3+ ions were incorporated by varying the concentration from 1 mol% to 15 mol%. The weighed starting materials were taken in an agate mortar and ground for 2 h with the help of acetone and kept in a muffle furnace at 400 °C for 1 h and again annealed at 1200 °C for 4 h.
2.2. Characterization techniques
X-ray diffraction (XRD) patterns of the prepared NASICON materials were obtained using a Bruker DA advance X-ray diffractometer equipped with Cu-Kα radiation (λ = 1.5406 Å). The surface morphology of the prepared phosphors was studied by field emission scanning electron microscopy (FESEM) Supra 55 with an air lock chamber. The Raman spectra of the synthesised phosphors were recorded at room temperature by using a Renishaw Raman spectrometer fitted with an argon ion laser at 514.5 nm. The FT-IR spectra of the prepared phosphors were obtained using a Perkin-Elmer spectrum-2 spectrophotometer. The UV-Vis-NIR double-beam spectrophotometer from Agilent's Cary-5000 series was used to record the diffuse reflectance spectra. The UC emission spectra of all developed phosphors were recorded on a Princeton Acton SP 2300 triple turret grating monochromator with a photomultiplier tube. The samples were placed within a tiny handmade heater that was controlled using a varivolt and monitored by a k-type thermocouple to conduct the temperature dependence study.
3. Results and discussion
3.1. Structural and morphological analysis
The XRD pattern was recorded to confirm the formation of the crystalline phase of the Er3+-Yb3+:NaZr2(PO4)3 phosphors in the range of 10–80° at room temperature {Fig. 1(a)}. In the diffraction pattern, the Bragg peaks well matched with those from the ICSD pattern 98-000-9546, which has a hexagonal structure with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c and space group #167. The maximum intensity peak in the XRD pattern was observed at ∼20.2° corresponding to the (1 1 0) Bragg plane, whereas the other main diffraction peaks were seen at ∼14.02°, ∼19.5°, ∼23.4°, ∼28.2°, ∼31.1°, ∼35.3°, ∼47.8°, and ∼55.2° refers to the (0 1 2), (1 0 4), (1 1 3), (0 2 4), (1 1 6), (0 3 0), (2 2 6), and (1 4 0) diffraction planes, respectively. Some small impurity peaks have been observed in the diffraction pattern, which correspond to zirconium diphosphate (ZrP2O7) and erbium phosphate (ErPO4) denoted in the figures as ‘*’ and ‘♦’, matching the standard ICSD patterns 98-002-4854 and 98-016-7090, respectively having cubic (Pa
c and space group #167. The maximum intensity peak in the XRD pattern was observed at ∼20.2° corresponding to the (1 1 0) Bragg plane, whereas the other main diffraction peaks were seen at ∼14.02°, ∼19.5°, ∼23.4°, ∼28.2°, ∼31.1°, ∼35.3°, ∼47.8°, and ∼55.2° refers to the (0 1 2), (1 0 4), (1 1 3), (0 2 4), (1 1 6), (0 3 0), (2 2 6), and (1 4 0) diffraction planes, respectively. Some small impurity peaks have been observed in the diffraction pattern, which correspond to zirconium diphosphate (ZrP2O7) and erbium phosphate (ErPO4) denoted in the figures as ‘*’ and ‘♦’, matching the standard ICSD patterns 98-002-4854 and 98-016-7090, respectively having cubic (Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) and tetragonal (I41/amd) phases. The impurity peaks appear in very small intensities, thus, they may not have any significant impact on the structural, optical, and conducting properties.19 The ionic radii of Na+, Zr4+, P5+, Er3+, and Yb3+ ions are 102 pm, 72 pm, 38 pm, 89 pm, and 86.8 pm, respectively. To validate the substitution of doped ions in the possible ion site present in the host materials, the acceptable ionic radii percentage difference (Dr) was calculated using the formula given as,19,20
) and tetragonal (I41/amd) phases. The impurity peaks appear in very small intensities, thus, they may not have any significant impact on the structural, optical, and conducting properties.19 The ionic radii of Na+, Zr4+, P5+, Er3+, and Yb3+ ions are 102 pm, 72 pm, 38 pm, 89 pm, and 86.8 pm, respectively. To validate the substitution of doped ions in the possible ion site present in the host materials, the acceptable ionic radii percentage difference (Dr) was calculated using the formula given as,19,20| |
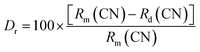 | (2) |
where, Rm(CN) and Rd(CN) represent the ionic radii of the host cation and the doped ion, respectively. The calculated values of Dr are 12.7% and 14.9% (less than 30%) for Er3+ and Yb3+ ions, respectively, to be doped in the Na+ ion site suggesting successful doping of dopant ions. Further, to establish the phase purity of the prepared phosphors, Rietveld refinement of the XRD patterns of the undoped and doped NaZr2(PO4)3 phosphors using FullProf software was carried out. Fig. 1(b) depicts the refinement profile of Er3+-Yb3+:NaZr2(PO4)3 phosphors and the refined parameters with the quantification of the impurity phases of the prepared phosphors are summarized in Table 1.
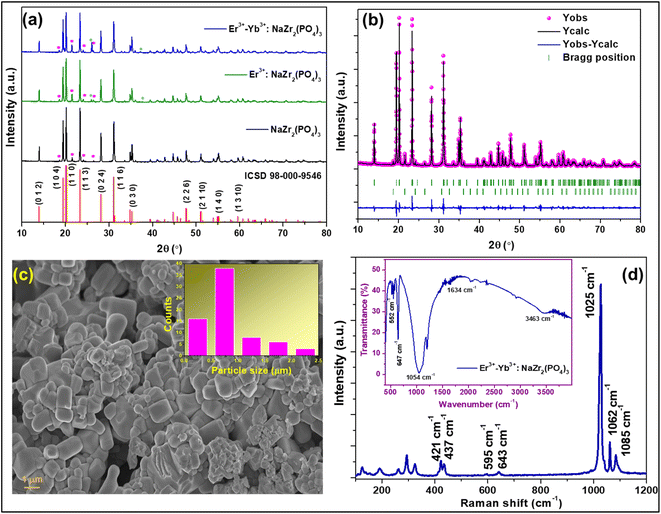 |
| | Fig. 1 X-ray diffraction patterns of (a) NaZr2(PO4)3, 7 mol% Er3+:NaZr2(PO4)3, and 7 mol% Er3+-10 mol% Yb3+:NaZr2(PO4)3 phosphors, (b) Rietveld refinement pattern of 7 mol% Er3+-10 mol% Yb3+:NaZr2(PO4)3 phosphors, (c) FESEM image of 7 mol% Er3+-10 mol% Yb3+:NaZr2(PO4)3 phosphors, (d) Raman spectrum (inset: FT-IR spectrum) of the 7 mol% Er3+-10 mol% Yb3+:NaZr2(PO4)3 phosphors. | |
Table 1 Quantitative Rietveld refinement parameters of NaZr2(PO4)3 phosphors
| Samples |
Phase |
Rp |
Rwp |
Rexp |
χ2 |
Cell parameters (Å) |
Cell volume (Å3) |
Quantification |
| NaZr2(PO4) |
Hexagonal |
11.3 |
11.3 |
5.78 |
3.73 |
a = 8.80018(6), b = 8.80018(6), c = 22.7601(3) |
1526.47(2) |
96.2(2)% |
| Cubic |
a = 8.2439(3), b = 8.2439(3), c = 8.2439(3) |
560.28(4) |
3.78(7)% |
| Er3+:NaZr2(PO4)3 |
Hexagonal |
11.4 |
11.2 |
6.25 |
3.20 |
a = 8.80849(8), b = 8.80849(8), c = 22.7793(3) |
1530.64(3) |
91.9(2)% |
| Cubic |
a = 8.2615(2), b = 8.2615(2), c = 8.2615(2) |
563.88(3) |
7.15(8)% |
| Tetragonal |
a = 6.8620(6), b = 6.8620(6), c = 6.012(1) |
283.09(8) |
0.90(3)% |
| Er3+-Yb3+:NaZr2(PO4)3 |
Hexagonal |
11.8 |
12.2 |
6.11 |
3.98 |
a = 8.8094(1), b = 8.8094(1), c = 22.7772(4) |
1530.85(3) |
88.6(8)% |
| Cubic |
a = 8.2744(3), b = 8.2744(3), c = 8.2744(3) |
566.51(3) |
5.9(5)% |
| Tetragonal |
a = 6.8369(2), b = 6.8369(2), c = 5.9873(5) |
279.87(2) |
5.4(1)% |
In order to examine the surface morphology of Er3+-Yb3+:NaZr2(PO4)3 phosphors FESEM analysis was carried out (Fig. 1(c)). The images showed that the prepared phosphors were agglomerated and the particles had different sizes. From the Gaussian distribution depicted in Fig. 1(c) inset, it has been estimated that the size of most of the particles was in the 500–600 nm range.
3.2. Raman and FTIR analysis
To investigate the structures of the molecules present in the prepared phosphors, vibrational spectroscopic tools such as Raman and Fourier transform infrared (FTIR) spectroscopy were utilized. The Raman spectrum of the prepared NASICON materials was recorded in the range of 100–1200 cm−1 as shown in Fig. 1(d). The spectra consisted of several bands in the range between 320–1089 cm−1, which are ascribed to the PO43− internal vibration whereas the bands arising in the range 100–300 cm−1 are referred to the external modes such as lattice phonon modes, and the translational vibrations and liberations (pseudo-rotations) of the polyhedral.20,21 The most intense Raman band was observed at ∼1025 cm−1, which can be assigned to symmetric stretching (ν1) vibration, and the bands at ∼1062 cm−1 and ∼1085 cm−1 are due to the asymmetric stretching (ν3) vibration of PO43−. The other low intense Raman bands arising at ∼595 cm−1 and ∼643 cm−1 are corresponding to the asymmetric bending (ν4) and that at ∼421 cm−1 and ∼437 cm−1 are due to the symmetric bending (ν2) vibration of PO43−.
The FTIR spectrum of the Er3+-Yb3+:NaZr2(PO4)3 phosphor was recorded to record the vibrational bonds from in material {inset: Fig. 1(d)}. The broad absorption band peaking at ∼1054 cm−1 is due to asymmetric stretching (ν3) of P–O tetrahedra. The peaks in the range 520–650 cm−1 arise due to the asymmetric bending mode (ν4) and below this symmetric bending mode (ν2) of the PO43− group is responsible. The vibrational bands at ∼1634 cm−1 and 3463 cm−1 are due to the O–H bond present in the material.21 The intensity of these impurity bands appears very low in the FTIR spectrum, which represents the better emission intensity of the present phosphor material.
3.3. Spectroscopic investigation
Diffuse reflectance spectra for all synthesized phosphors at room temperature were monitored in the UV-vis-NIR range to study the absorption characteristics of the materials. Fig. 2(a) shows the DRS data for both undoped and co-doped NaZr2(PO4)3 phosphors in the range from 200 to 900 nm, with a step size of 0.5 nm. The BaSO4 powder was adopted as a reference for baseline correction. While the host lattice has been attributed to the broad peak that appears between 200 and 350 nm, the sharp band that appears after this wavelength is caused by f–f transitions from rare-earth ions. The transitions responsible for the peaks at 380, 408, 454, 490, 524, 546, 654, and 799 nm are 4I15/2 → 4G11/2, 4I15/2 → 2H9/2, 4I15/2 → 4F3/2, 4I15/2 → 4F7/2, 4I15/2 → 2H11/2, 4I15/2 → 4S3/2, 4I15/2 → 4F9/2, 4I15/2 → 4I9/2, respectively.22 The DRS spectra, in addition to recognising the peaks, assist in determining the optical bandgap of the synthesized phosphors. The Kubelka–Munk equation was employed to analyse the DRS spectra in order to evaluate the optical bandgap of the phosphor:23| |
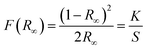 | (3) |
| | |
[F(R∞)hυ]2 = C(hυ − Eg)n
| (4) |
where K and S stand for the absorption and scattering coefficients, respectively, and hv is the input photon energy; F(R∞) is the Kubelka–Munk function; R is the diffuse reflectance of the phosphor; The n value determines the type of optical transition, with n = 1 denoting direct allowed transitions, n = 2 denoting non-metallic materials, n = 3 denoting directly prohibited transitions, n = 4 denoting indirect allowed transitions, and n = 6 denoting indirect forbidden transitions.24 Eg in eV represents the optical band gap. Here, n = 1 produced the best match. The optical bandgaps for NaZr2(PO4)3, Er3+:NaZr2(PO4)3, and Er3+-Yb3+:NaZr2(PO4)3 phosphors were calculated to be 4.5 eV, 4.53 eV, and 4.53 eV, respectively. The minute change in the optical bandgap due to the incorporation of Er3+ and Yb3+ ions could be a result due to the Moss–Burstein effect.
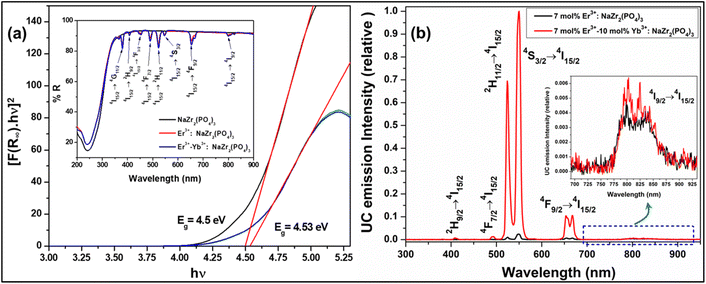 |
| | Fig. 2 (a) Tauc plot of Er3+/Er3+-Yb3+:NaZr2(PO4)3 phosphors, (inset: diffuse reflectance spectra of 7 mol% Er3+ and 7 mol% Er3+-10 mol% Yb3+:NaZr2(PO4)3 phosphors. (b) UC emission spectra of 7 mol% Er3+-10 mol% Yb3+:NaZr2(PO4)3 phosphors and the inset shows the enlarged spectra of (804, 824) nm peak. | |
The frequency UC emission spectra of the optimized Er3+/Er3+-Yb3+:NaZr2(PO4)3, NASICON phosphors recorded in the range 450–850 nm are displayed in Fig. 2(b). The UC spectrum of Er3+:NaZr2(PO4)3 phosphors exhibit prominent green and red emission bands peaking at ∼524 nm, ∼550 nm, and ∼(654, 668) nm corresponding to the 2H11/2 → 4I15/2, 4S3/2 → 4I15/2, 4F9/2 → 4I15/2 and 4F7/2 → 4I15/2 transitions of Er3+ ions, respectively. Also, a weak blue band at ∼490 nm and a NIR band in the range 800–830 nm have been noticed [inset of Fig. 2(b)] corresponding to the 4F7/2 → 4I15/2 and 4I9/2 → 4I15/2 transitions of Er3+ ions, respectively. The codoping of Yb3+ ions in the Er3+:NaZr2(PO4)3 phosphors results in intensity enhancement of all the emission bands. In the optimized 7 mol% Er3+-10 mol% Yb3+:NaZr2(PO4)3 phosphors the green, red, and blue emission band intensities increase ∼87, ∼28, and ∼2 times, respectively, in comparison to the optimized 7 mol% Er3+:NaZr2(PO4)3 phosphors. The significant enhancement in the Er3+-Yb3+ codoped phosphors is due to the energy transfer from Yb3+ ions to Er3+ ions, which refers to the broad absorption cross-section of Yb3+ ions. It can be noted that blue emission intensity does not notably enhance as in the case of green and red emission bands. Thus, the possibility of cooperative energy transfer is ruled out. However, beyond the optimized concentration of dopant ions, the UC emission intensity decreases due to the concentration quenching effect. The concentration quenching phenomenon of the dopant ions occurs because of the non-radiative energy transfer or the cross-relaxation processes between the two neighbouring dopant ions. With the increase of the dopant ion concentrations, the distance between two adjacent dopant ions decreases, which in turn increases the possibility of non-radiative energy transfer. Thus, the energy transfer mechanism occurring between the dopant ions can be analyzed by calculating the critical distance (Rc) between two same adjacent dopant ions with the help of Blasse's equation given as,25
| |
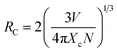 | (5) |
where ‘
V’ is the unit cell volume, ‘
Xc’ refers to the critical concentration of dopant ions, and ‘
N’ is the number of available crystallographic sites occupied by the dopant ions in the unit cell (
N = 6). In the case of optimized Er
3+ and Yb
3+ phosphors, the values of
Rc were calculated to be ∼19.09 Å and ∼14.21 Å, respectively, which are larger than 5 Å. According to Van-Uitert's law, the exchange interaction is not accountable for the energy transfer in the present case rather the
Rc value suggests multipolar interactions between the dopant ions is responsible for the energy transfer process.
Furthermore, when the laser pump power density of the 980 nm laser excitation increases, it has been observed that the UC emission spectra of Er3+-Yb3+:NaZr2(PO4)3 phosphors show a higher increment rate in the ∼524 nm band compared to the ∼550 nm as the pump power increases, which in turn increases the luminescence intensity ratio (LIR) of these two thermally coupled levels (TCLs) of Er3+ ions. The LIR enhancement with the variation of pump power suggests the temperature generation in the phosphor material, which indicates the suitability of the present phosphor in temperature-sensing applications.
Initially, a 980 nm photon is absorbed by an Er3+ ion and promoted to the 4I11/2 level from the ground state 4I15/2 via the ground state absorption (GSA) process. The excited ions at the 4I11/2 level relax non-radiatively to the 4I13/2 level, and through the process of excited state absorption (ESA), the ions in the 4I11/2 and 4I13/2 states are further excited to the 4F7/2 and 4F9/2 states, respectively. The emission at 494 nm can be caused by the radiative transition between 4F7/2 and 4I15/2. Also, the 4F9/2 state was employed to populate the 2H9/2 state by an ESA process, yielding a peak at 409 nm. The multiphonon relaxation from the 4F7/2 state populates the thermally coupled levels, i.e., 2H11/2 and 4S3/2, which then radiatively relax to the ground state. As a result, photons in the green region are observed at 524 nm and 550 nm, associated with the 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2 transitions, respectively. The peak in the red region at 654 and 668 nm can be attributed to the Stark sublevels of the 4F9/2 → 4I15/2 transitions. A small peak in the NIR range of about 804 nm and 824 nm is responsible for the Stark splitting of the 4I9/2 → 4I15/2 transition, as shown in the inset of Fig. 2(b). In the case of Er3+-Yb3+ co-doped phosphors, UC emission was observed by the ET process in addition to GSA and ESA. Because of the GSA and ET from the Yb3+ ions, the population of excited Er3+ ions in the 4I11/2 state for the Er3+-Yb3+ co-doped system is dominant over the Er3+ doped systems. The energy transfer processes that populate the 4I11/2, 4F9/2, 4F7/2, and 2H9/2 states are given as follows.
| ET1: 2F5/2 (Yb3+) + 4I15/2 (Er3+) →2F7/2 (Yb3+) + 4I11/2 (Er3+) |
| ET2: 2F5/2 (Yb3+) + 4I11/2 (Er3+) →2F7/2 (Yb3+) + 4F7/2 (Er3+) |
| ET3: 2F5/2 (Yb3+) + 4I13/2 (Er3+) →2F7/2 (Yb3+) + 4F9/2 (Er3+) |
| ET4: 2F5/2 (Yb3+) + 4F9/2 (Er3+) →2F7/2 (Yb3+) + 2H9/2 (Er3+) |
Moreover, using the steady-state rate equations, the depopulation rates of different metastable states with different pump photon densities could be estimated theoretically as,
| |
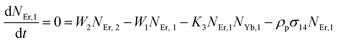 | (6) |
| |
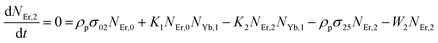 | (7) |
| |
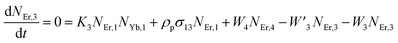 | (8) |
| |
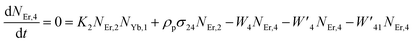 | (9) |
| |
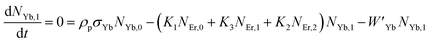 | (10) |
The population densities for Er
3+ ions at the
4I
15/2,
4I
13/2,
4I
11/2,
4F
9/2 and (
4S
3/2,
2H
11/2) levels, are denoted by
NEr,k (
k = 0, 1, 2, 3, 4) whereas
NYb,0 and
NYb,1 represent the population densities for Yb
3+ ions at the
2F
7/2 and
2F
5/2 levels, respectively.
K1,
K2, and
K3 indicate the corresponding energy transfer rates of ET-1, ET-2, and ET-3.
W1,
W2,
W3 and
W4 represents the non-radiative decay rates of the
4I
13/2,
4I
11/2,
4F
9/2 and (
2H
11/2,
4S
3/2) levels, respectively.
W′
3,
W′
4 and
W′
41 defines radiative decay rates of the
4F
9/2,
4S
3/2, and
2H
11/2 levels, respectively. Whereas, the radiative decay rate of
2F
5/2 of the Yb
3+ ion is represented by
W′
Yb. Whereas
σYb stands for the absorption cross-section between Yb
3+ ions at levels
2F
7/2 and
2F
5/2,
σij stands for the absorption cross-section between Er
3+ ions at the
ith and
jth levels.
ρp denotes the pump power density at 980 nm. Since the absorption cross-section of Er
3+ ions is lower than that of Yb
3+ ions, it may be believed that processes such as GSA and ESA had a minimal role in filling the metastable states and can thus be neglected.
The non-radiative linear decays from the 4I11/2 and 4I13/2 levels dominate ET-2 and ET-3 from Yb3+ ions to Er3+ ions at low pump power densities. The energy transfer rates from eqn (6) and (7) can thus be ignored. Thus,
| |
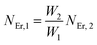 | (11) |
| |
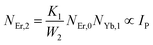 | (12) |
and
eqn (10) can be rewritten as,
| |
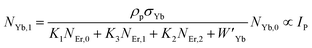 | (13) |
Eqn (11) and (12) may be used to modify eqn (8) and (9), giving the result
| |
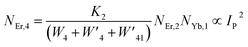 | (14) |
| |
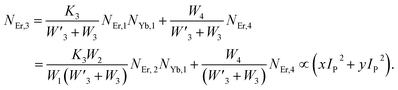 | (15) |
The populations associated with the green and red emissions are represented by eqn (14) and (15), respectively. As can be seen, the populations at each level are quadratic, meaning that two photons are needed to fill levels 2H11/2, 4S3/2, and 4F9/2. It could be assumed that the ET processes must eliminate the non-radiative losses at the 4I11/2 and 4I13/2 levels as the pump power density steadily increases. Thus, by leaving out the variables −W1NEr,1 and −W2NEr,2, eqn (6) and (7) may be simplified as follows:
| |
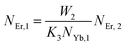 | (16) |
| |
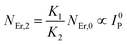 | (17) |
| |
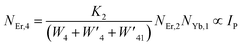 | (18) |
| |
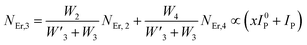 | (19) |
From eqn (18), it can be seen that the population associated with the green emitting level is proportional to a single-photon absorption. Eqn (19), whose first term is independent of the pump photon and second term suggests a single-photon absorption, reflecting the red emission at the same time. According to the above observation, ET-2 becomes efficient at higher pump power densities, non-radiative processes grow quickly, and finally the saturation effect results.
To verify the above theoretical assumptions, the UC emission was measured utilising a range of laser pump power density ranges (980 nm). According to previous studies, the relationship between the input pump power density (p) and the UC emission intensity (IUC) is non-linear, with IUC ∝ IPn.26 The number of infrared (IR) pump photons necessary to reach specific levels in order to produce UC emission depends on the value of “n” in this equation. Fig. 3(b) displays the double logarithmic plot between IUC and Ppump, with “n” calculated from the slope values. The calculated photon number for the 494 nm, 524 nm, 550 nm, 654 nm, and ∼668 nm are found to be 2.04, 1.67, 1.17, 1.18, and 1.12, respectively, which confirmed the involvement of the two photons for the green and red UC emission bands. However, the slope values tended to decrease at higher pump power densities. The results obtained from the double logarithmic plot suggest that for the green emission, the slope value is nearer to 2, but, for the red emission, it approaches 1. This could be understood by comparing the depletion mechanism of the intermediate state responsible for the UC luminescence. According to Pollnau et al., when the linear decay of the intermediate state is the dominant depletion mechanism, IUC ∝ IP2, whereas, IUC ∝ IP1 when the upconversion (e.g., ESA and ET) becomes the primary depletion mechanism.27 The intermediate states for the green and red emissions in the Er3+-doped phosphors are 4I11/2 and 4I13/2, respectively. Upconversion emerges as the primary depletion mechanism of 4I13/2 because the linear decay rate of the 4I11/2 level is relatively higher than that of the 4I13/2 level. As a result, the green emission has a larger slope value than the red emission. Due to the large concentration of Er3+ and Yb3+ ions in Er3+-Yb3+:NaZr2(PO4)3 phosphors, the ET rates between the dopants would increase the efficiency of upconversion from the intermediate state to the emitting state, hence elevating the significance of upconversion. As a result, the slope of the UCL shifts from quadratic to linear.28
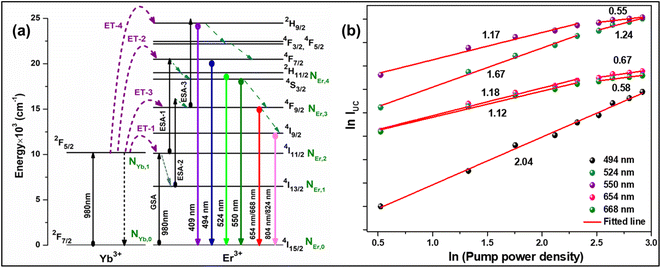 |
| | Fig. 3 (a) Energy level diagram of Er3+-Yb3+ codoped system, (b) ln–ln plot of UC emission intensity and laser pump power density. | |
3.4. Temperature sensing behaviour
The temperature-dependent UC emission spectra of Er3+-Yb3+:NaZr2(PO4)3 phosphors were recorded in the temperature range 303–573 K under 980 nm excitation with fixed laser pump power. To study the LIR variation based on the green TCLs of Er3+ ions with temperature variation the emission spectra have been recorded in the wavelength range 510–570 nm. The overall green emission intensity decreases with the increase in temperature without any change in the band position, which is due to an increase in non-radiative relaxation rate and electron–phonon coupling within the sample. It is noticeable that with the increase of temperature, the rate of decrement in UC emission intensity corresponding to the 2H11/2 → 4I15/2 transition is higher than that for the 4S3/2 → 4I15/2 transition, which results in the LIR increment of these TCLs. The LIR variation with temperature can be described by the Boltzmann distribution, which follows the equation,29| |
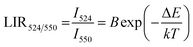 | (20) |
where, I524 and I550 represents the integrated intensities of the 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2 transitions, respectively, B is the proportionality constant, ΔE is the energy separation between two thermally coupled levels, k and T are the Boltzmann's constant and absolute temperature, respectively. To examine the temperature sensing performance of the prepared phosphors, first, the pump power density was fixed to 5.78 W cm−2, and the LIR change was monitored with the elevation temperature. For Er3+-Yb3+:NaZr2(PO4)3 phosphors, the LIR varies from 0.43 to 1.47 as the temperature varies from 303 K to 573 K.
By fitting the experimental data according to eqn (20), we obtained the temperature sensing parameter, ΔE/k = 780.54{Fig. 4(a)}. The values of ‘B’ and ‘ΔE’ were found to be 5.70 and 542.48 cm−1, respectively, for the Er3+-Yb3+:NaZr2(PO4)3 phosphors. However, the impact of laser power density may induce a heating effect which hinders the temperature sensing performance. To further verify the effect of laser-induced heating, we have monitored the temperature sensing performance at a lower pump power density, i.e., at 3.76 W cm−2. As can be seen from Fig. 4(b), the temperature sensing parameter enhances to 898.70 with the change in LIR from 0.37 to 1.41 on varying the temperature from 303 to 573 K. Moreover, to quantify the temperature sensing performance of Er3+-Yb3+:NaZr2(PO4)3 phosphors, the sensitivity was calculated. The relative sensor sensitivity (Sr) is a crucial parameter to validate the phosphor material as a temperature-sensing probe. The relative sensor sensitivity (Sr) can be defined as,30
| |
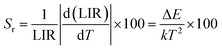 | (21) |
where all terms have their usual meanings. The maximum value of
Sr for Er
3+-Yb
3+:NaZr
2(PO
4)
3 phosphors was obtained as 0.98% K
−1 at 303 K for 3.76 W cm
−2 of pump power density. In
Table 2, we have compared the temperature sensing sensitivity of the present work with other reported works and we have found the Er
3+-Yb
3+:NaZr
2(PO
4)
3 phosphors could be utilized for temperature sensing applications.
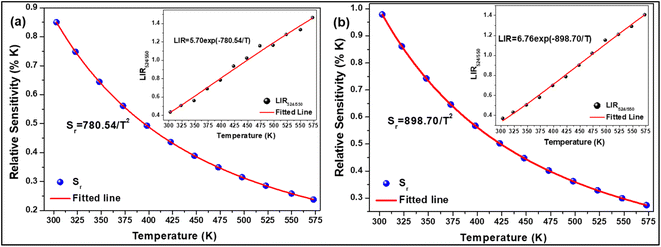 |
| | Fig. 4 Relative sensitivity (LIR524/550 variation) as a function of temperature at (a) 3.76 W cm−2, (b) 5.78 W cm−2 of 7 mol% Er3+-10 mol% Yb3+:NaZr2(PO4)3 phosphors. | |
Table 2 Summary of the 2H11/2, 4S3/2 → 4I15/2 TCLs-based temperature sensing performance of different Er3+ and Er3+-Yb3+ codoped materials excited under 980 nm laser
| Doped phosphors |
Temperature range (K) |
Maximum Sr (% K−1) |
Ref. |
| Er3+-Yb3+:NaYF4 |
223–403 |
0.36% K−1 at 300 K |
33 |
| Er3+-Yb3+:Gd2O3 phosphor |
300–900 |
0.39% K−1 at 300 K |
34 |
| Er3+:SrSnO3 |
294–372 |
0.997% K−1 at 294 K |
35 |
| Er3+-Yb3+:Na2GdMg2(VO4)3 phosphors |
303–573 |
0.976% K−1 at 303 K |
36 |
| Er3+-Yb3+:NaZr2(PO4)3 phosphors |
303–573 |
0.98% K−1 at 303 K |
Present work |
| Er3+-Yb3+:Ba3La(PO4)3 |
298–498 |
1.17% K−1 at 298 K |
37 |
| Er3+-Yb3+:NaBiF4 nanoparticle |
303–483 |
1.24% K−1 at 303 K |
38 |
To verify the reproducibility of the experiment, we monitored the LIR change for 3 different cycles in the temperature range from 303–573 K and computed the repeatability (R) as,31
| |
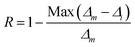 | (22) |
Here
Δm states the mean LIR value for 3 cycles and
Δi states the LIR value at temperature
T. After calculating the
R-value, we obtained that it was ∼96% at 303 and 423 K and 93% at 573 K {
Fig. 5(a)}. The Er
3+-Yb
3+:NaZr
2(PO
4)
3 phosphors not only have good sensitivity at low pump power density, but they could also convert some of the absorbed NIR excitations to heat at higher pump power. The inset of
Fig. 5(b) shows that the LIR grows linearly with the pump power (
P), resulting in the equation,
32By comparing
eqn (23) to
eqn (20), the temperature was determined as
| |
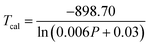 | (24) |
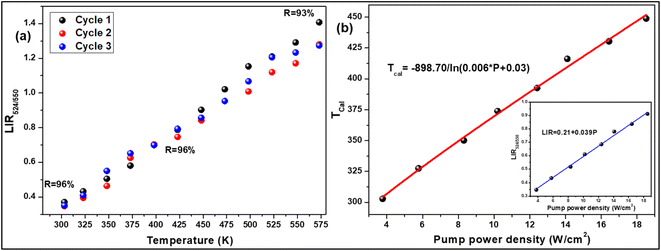 |
| | Fig. 5 (a) Repeatability of LIR from 300 K to 573 K for 3 cycles, (b) a plot of calculated temperatures vs. pump power densities (inset: LIR vs. pump power densities) for 7 mol% Er3+-10 mol% Yb3+:NaZr2(PO4)3 phosphors. | |
According to the above equation, each pump photon has a unique temperature associated with it that is produced by non-radiative relaxation from the higher energy levels (Fig. 5(b)). According to earlier research, applications such as photothermal treatment require temperatures between 315 and 318 K to kill cancer cells.32 Hence, it can be claimed that the criteria may be satisfied by varying the laser pump power between 4.81 and 4.96 W cm−2.
4. Conclusion
In conclusion, a series of NaZr2(PO4)3 UC green phosphors doped with Er3+ and Yb3+ ions were synthesised by a solid-state-reaction approach. The Rietveld refinement of XRD profiles offered structural insight into the phases present in the phosphors, and the acquired crystal structure parameters demonstrate that the predicted model is the best fit for the refinement. Raman spectroscopy was used to validate various lattice vibrations. The prepared phosphors have a non-uniform shape, which may be seen in the microstructure. The co-doping of Yb3+ ions considerably enhanced the UC green emission, which corresponded to the 2H11/2, 4S3/2 → 4I15/2 transition of Er3+ ions, and about 87-fold enhancement was observed at 10 mol% Yb3+ doping concentration. The energy-level diagram for UC was examined in depth using steady-state rate law equations. In the temperature dependence UC study, the maximum Sr values for the optimised phosphor were determined to be 0.98% K−1 at 303 K for 3.76 W cm−2 of pump power density using the LIR method. As a result of the enhanced UC luminescence and temperature sensing capability, the produced phosphor is a promising contender in the area of optical thermometry.
Conflicts of interest
There is no conflict of interest.
Acknowledgements
The authors would like to thank IIT (ISM) Dhanbad for providing the research fund and experimental facilities.
References
- R. Rajagopalan, Z. Zhang, Y. Tang, C. Jia, X. Ji and H. Wang, Energy Storage Mater., 2021, 34, 171–193 CrossRef.
- Y. Zhao, Z. Wei, Q. Pang, Y. Wei, Y. Cai, Q. Fu, F. Du, A. Sarapulova, H. Ehrenberg, B. Liu and G. Chen, ACS Appl. Mater. Interfaces, 2017, 9, 4709–4718 CrossRef CAS PubMed.
- S. Yu, Z. Liu, H. Tempel, H. Kungl and R. A. Eichel, J. Mater. Chem. A, 2018, 6, 18304–18317 RSC.
- Z. Deng, T. P. Mishra, E. Mahayoni, Q. Ma, A. J. K. Tieu, O. Guillon, J. N. Chotard, V. Seznec, A. K. Cheetham, C. Masquelier and G. S. Gautam, Nat. Commun., 2022, 13, 4470 CrossRef CAS PubMed.
- S. Chen, C. Wu, L. Shen, C. Zhu, Y. Huang, K. Xi, J. Maier and Y. Yu, Adv. Mater., 2017, 29, 1700431 CrossRef.
- N. Anantharamulu, K. Koteswara Rao, G. Rambabu, B. Vijaya Kumar, V. Radha and M. Vithal, J. Mater. Sci., 2011, 46, 2821–2837 CrossRef CAS.
- C. Li, R. Li, K. Liu, R. Si, Z. Zhang and Y. S. Hu, Interdiscip. Mater., 2022, 1, 396–416 CrossRef.
- X. Lu, S. Wang, R. Xiao, S. Shi, H. Li and L. Chen, Nano Energy, 2017, 41, 626–633 CrossRef CAS.
- B. Ouyang, J. Wang, T. He, C. J. Bartel, H. Huo, Y. Wang, V. Lacivita, H. Kim and G. Ceder, Nat. Commun., 2021, 12, 5752 CrossRef CAS PubMed.
- B. Glorieux, V. Jubera, A. I. Orlova, A. E. Kanunov, A. Garcia, C. Pallier and T. A. Oleneva, Inorg. Mater., 2013, 49, 82–88 CrossRef CAS.
- Y. Liu, C. Sun, Y. Li, H. Jin and Y. Zhao, Energy Storage Mater., 2023, 57, 69–80 CrossRef.
- L. Alcaraz, J. Isasi, C. Díaz-Guerra, M. Peiteado and A. C. Caballero, J. Phys. D: Appl. Phys., 2016, 49, 115501 CrossRef.
- S. Zhao, W. Liu, X. Xue, Y. Yang, Z. Zhao, Y. Wang and B. Zhou, RSC Adv., 2016, 6, 81542–81551 RSC.
- A. I. Orlova, A. E. Kanunov, E. N. Gorshkova, A. N. Shushunov, S. N. Pleskova, E. R. Mikheeva, D. O. Savinykh and E. S. Leonov, Inorg. Mater., 2013, 49, 89–94 CrossRef CAS.
- W. Lu, J. Zhang and J. Shi, J. Mate. Sci. Mater. Electron., 2019, 30, 17780–17786 CrossRef CAS.
- L. Peng, Q. Meng and W. Sun, RSC Adv., 2019, 9, 2581–2590 RSC.
- Y. Zhang, H. Jia, X. He, Y. Zheng, R. Bai and H. Liu, J. Lumin., 2021, 236, 118111 CrossRef CAS.
- W. Ran, H. M. Noh, S. H. Park, B. C. Choi, J. H. Kim, J. H. Jeong and J. Shi, Dalton Trans., 2019, 48, 11382–11390 RSC.
- U. Ahmadu, T. Salkus, A. O. MusaandK and U. Isah, Open J. Phys. Chem., 2011, 94, 1 Search PubMed.
- K. Kamali, T. R. Ravindran, C. Ravi, Y. Sorb, N. Subramanian and A. K. Arora, Phys. Rev. B, 2012, 86, 144301 CrossRef.
- Z. H. Wang, D. Y. Xie, B. H. Yuan, X. S. Liu, W. B. Song, B. Yuan and E. J. Liang, Adv. Mater. Res., 2011, 415–417, 1023 Search PubMed.
- M. Prasad and V. K. Rai, Methods Appl. Fluoresc., 2022, 10, 034004 CrossRef PubMed.
- P. Chen, M. M. Murshed, M. Fischer, T. Frederichs and M. Gesing, Inorg. Chem., 2020, 59, 18214–18224 CrossRef CAS PubMed.
- S. Som, A. K. Kunti, V. Kumar, V. Kumar, S. Dutta, M. Chowdhury, S. K. Sharma, J. J. Terblans and H. C. Swart, J. Appl. Phys., 2014, 115, 193101 CrossRef.
- S. Pattnaik and V. K. Rai, Methods Appl. Fluoresc., 2022, 10, 034002 CrossRef PubMed.
- S. Pattnaik, M. Mondal, L. Mukhopadhyay, S. Basak, V. K. Rai, R. Giri and V. Singh, New J. Chem., 2022, 46, 10897–10906 RSC.
- M. Pollnau, D. R. Gamelin, S. R. Lüthi, H. U. Güdel and M. P. Hehlen, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3337–3346 CrossRef CAS.
- Y. Lei, H. Song, L. Yang, L. Yu, Z. Liu, G. Pan, X. Bai and L. Fan, J. Chem. Phys., 2005, 123, 174710 CrossRef PubMed.
- L. Mukhopadhyay and V. K. Rai, J. Alloys Compd., 2021, 878, 160351 CrossRef CAS.
- R. S. Monika, R. S. Yadav, A. Bahadur and S. B. Rai, RSC Adv, 2019, 9, 40092–40108 RSC.
- Y. Jiang, Y. Tong, S. Chen, W. Zhang, F. Hu, R. Wei and H. Guo, Chem. Eng. J., 2021, 413, 127470 CrossRef CAS.
- M. Runowski, P. Woźny, N. Stopikowska, I. R. Martín, V. Lavín and S. Lis, ACS Appl. Mater. Interfaces, 2020, 12, 43933–43941 CrossRef CAS PubMed.
- B. Dong, R. N. Hua, B. S. Cao, Z. P. Li, Y. Y. He, Z. Y. Zhang and O. S. Wolfbeis, Phys. Chem. Chem. Phys., 2014, 16, 20009–20012 RSC.
- S. K. Singh, K. Kumar and S. B. Rai, Er3+/Yb3+codoped Gd2O3 nanophosphor for optical thermometry, Sens. Actuators A, 2009, 149, 16–20 CrossRef CAS.
- E. Cortés-Adasme, M. Vega, I. R. Martin and J. Llanos, RSC Adv., 2017, 7, 46796–46802 RSC.
- L. Li, Y. Tong, J. Chen, Y. Chen, G. Abbas Ashraf, L. Chen, T. Pang and H. Guo, J. Am. Ceram. Soc., 2022, 105, 384–391 CrossRef CAS.
- J. Cao, J. Zhang and X. Li, Appl. Opt., 2018, 57, 1345–1350 CrossRef CAS.
- P. Du, L. Luo, X. Huang and J. S. Yu, J. Colloid Interface Sci., 2018, 514, 172–181 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a and
Vineet Kumar Rai
a and
Vineet Kumar Rai *a
*a
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c and space group #167. The maximum intensity peak in the XRD pattern was observed at ∼20.2° corresponding to the (1 1 0) Bragg plane, whereas the other main diffraction peaks were seen at ∼14.02°, ∼19.5°, ∼23.4°, ∼28.2°, ∼31.1°, ∼35.3°, ∼47.8°, and ∼55.2° refers to the (0 1 2), (1 0 4), (1 1 3), (0 2 4), (1 1 6), (0 3 0), (2 2 6), and (1 4 0) diffraction planes, respectively. Some small impurity peaks have been observed in the diffraction pattern, which correspond to zirconium diphosphate (ZrP2O7) and erbium phosphate (ErPO4) denoted in the figures as ‘*’ and ‘♦’, matching the standard ICSD patterns 98-002-4854 and 98-016-7090, respectively having cubic (Pa
c and space group #167. The maximum intensity peak in the XRD pattern was observed at ∼20.2° corresponding to the (1 1 0) Bragg plane, whereas the other main diffraction peaks were seen at ∼14.02°, ∼19.5°, ∼23.4°, ∼28.2°, ∼31.1°, ∼35.3°, ∼47.8°, and ∼55.2° refers to the (0 1 2), (1 0 4), (1 1 3), (0 2 4), (1 1 6), (0 3 0), (2 2 6), and (1 4 0) diffraction planes, respectively. Some small impurity peaks have been observed in the diffraction pattern, which correspond to zirconium diphosphate (ZrP2O7) and erbium phosphate (ErPO4) denoted in the figures as ‘*’ and ‘♦’, matching the standard ICSD patterns 98-002-4854 and 98-016-7090, respectively having cubic (Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) and tetragonal (I41/amd) phases. The impurity peaks appear in very small intensities, thus, they may not have any significant impact on the structural, optical, and conducting properties.19 The ionic radii of Na+, Zr4+, P5+, Er3+, and Yb3+ ions are 102 pm, 72 pm, 38 pm, 89 pm, and 86.8 pm, respectively. To validate the substitution of doped ions in the possible ion site present in the host materials, the acceptable ionic radii percentage difference (Dr) was calculated using the formula given as,19,20
) and tetragonal (I41/amd) phases. The impurity peaks appear in very small intensities, thus, they may not have any significant impact on the structural, optical, and conducting properties.19 The ionic radii of Na+, Zr4+, P5+, Er3+, and Yb3+ ions are 102 pm, 72 pm, 38 pm, 89 pm, and 86.8 pm, respectively. To validate the substitution of doped ions in the possible ion site present in the host materials, the acceptable ionic radii percentage difference (Dr) was calculated using the formula given as,19,20