Open Access Article
Open Access ArticleExceptional ultrafast nonlinear optical response of functionalized silicon nanosheets†
Michalis
Stavrou‡
 ab,
Amelie M.
Mühlbach‡
ab,
Amelie M.
Mühlbach‡
 c,
Vasilios
Arapakis
c,
Vasilios
Arapakis
 ab,
Elisabeth
Groß
ab,
Elisabeth
Groß
 c,
Tim
Kratky
d,
Sebastian
Günther
c,
Tim
Kratky
d,
Sebastian
Günther
 d,
Bernhard
Rieger
d,
Bernhard
Rieger
 *c and
Stelios
Couris
*c and
Stelios
Couris
 *ab
*ab
aDepartment of Physics, University of Patras, 265 04 Patras, Greece. E-mail: couris@upatras.gr
bFoundation for Research and Technology Hellas-Institute of Chemical Engineering Sciences (FORTH/ICE-HT), 26504 Rio-Patras, Greece. E-mail: couris@iceht.forth.gr
cWacker-Chair of Macromolecular Chemistry, Department of Chemistry, TUM School of Natural Sciences, Technical University of Munich, Lichtenbergstraße 4, 85748 Garching, Germany. E-mail: rieger@tum.de
dPhysical Chemistry with Focus on Catalysis, Department of Chemistry, TUM School of Natural Sciences, Technical University of Munich, Lichtenbergstraße 4, 85748 Garching, Germany
First published on 9th October 2023
Abstract
The present work reports on the ultrafast saturable absorption (SA), optical limiting (OL), and the nonlinear refractive response of hydride-terminated silicon nanosheets (SiNS-H) differently functionalized with styrene and tert-butyl methacrylate (tBuMA), namely, SiNS-styrene and SiNS-tBuMA, using 50 fs, 400 nm and 70 fs, 800 nm laser pulses. SiNS-styrene and SiNS-tBuMA exhibit dramatically enhanced nonlinear optical (NLO) responses compared to SiNS-H, with their absorptive nonlinearity strongly dependent on the laser excitation wavelength. More specifically, the studied functionalized SiNSs reveal strong SA behavior under 400 nm laser excitation, with NLO absorption coefficients, saturable intensities, and modulation depths comparable to various two-dimensional (2D) materials, known to exhibit strong SA, such as graphene, black phosphorous (BP), some transition metal dichalcogenides (TMDs), and some MXenes. On the other hand, under 800 nm laser excitation, SiNS-styrene and SiNS-tBuMA show highly efficient OL performance with OL onset values of about 0.0045 and 0.0065 J cm−2, respectively, which are significantly lower than those of other 2D nanostructures. In addition, it is shown that both SiNS samples have great potential in already existing Si-based optoelectronic devices for optical-switching applications since they exhibit very strong NLO refraction comparable to that of bulk Si. The results of the present work demonstrate that the chemical functionalization of SiNSs provides a highly efficient strategy for the preparation of 2D Si-based nanostructures with enhanced NLO response in view of several optoelectronic and photonic applications, such as OL, SA, and all-optical switching.
1. Introduction
In the last few years, graphene, the archetype of two-dimensional (2D) materials, has stimulated substantial scientific interest in fundamental research and technological development due to its unique structure and striking physicochemical properties.1–3 Besides the experimental discovery of graphene,1 more graphene-like 2D systems, such as Xenes and Xanes (where X = silic, german, etc.),4–6 transition metal dichalcogenides (e.g., MoS2, WS2, MoSe2, WSe2),7,8 hexagonal boron nitride,9 MXenes (e.g., transition metal carbides and nitrides),10 black phosphorus,11 and 2D perovskites12,13 have been synthesized. Among them, silicon nanosheets have attracted considerable attention due to their expected compatibility with the current Si-based nanotechnology. Silicon nanosheets are differentiated between the graphene analog silicene, which consists of mixed sp2/sp3-hybridized silicon atoms,14 and the analog of hydrogen-terminated graphene, so-called silicane, with sp3-hybridized silicon atoms.15 As the sp3-hybridization is favored for silicon,16 silicene is unstable and thus only epitaxially grown on substrates, e.g., Ag(111) or Ir(111).17–22 The more stable silicane (hydrogen-terminated silicene, SiNS-H) is prepared by the deintercalation of calcium cations from the Zintl phase calcium disilicide (CaSi2) with concentrated hydrochloric acid at low temperatures.6 SiNS-H exhibit unique electronic, mechanical, and optical properties. According to theoretical studies, SiNS-H is a semiconducting material23 with a strain-tunable band gap,24,25 while its atomic configuration determines whether the band gap is direct or indirect.26 Experimental results showed that the material exhibits photoluminescence with an emission maximum at approximately 500 nm (ref. 27) and a superior nonlinear optical (NLO) response compared to graphene.28–30 As-prepared SiNS-H can be functionalized, e.g., via radical-induced hydrosilylation reactions with unsaturated compounds.27,31 Surface functionalization might influence the optoelectronic properties32–34 and prevent the nanosheets from stacking and oxidation.34Recently, it was reported that the chemical functionalization of SiNS-H with unsaturated compounds like 1-dodecene is a powerful tool to enhance the NLO response compared to SiNS-H.28–30 In particular, it was demonstrated that 1-dodecene functionalized SiNS-H, namely SiNS-dodecene, exhibits very strong saturable absorption (SA) and self-focusing behavior, promoting the high potential of SiNSs for optoelectronic and photonic applications as saturable absorbers and optical switchers. Based on these previous studies, the present work investigates the NLO responses of SiNSs functionalized with two different organic moieties. As functionalization was achieved via hydrosilylation reactions, unsaturated compounds were used. Therefore, the vinyl compounds styrene and tert-butyl methacrylate (tBuMA) were chosen as functionalization agents to prepare SiNS-styrene and SiNS-tBuMA. The aromatic phenethyl group, which is introduced to SiNS in the case of the functionalization with styrene, is slightly electron-donating and nonpolar. The tBuMA moiety, on the other hand, has a polar tert-butyl ester group and is slightly electron-withdrawing. To study the influence of these functional groups on the NLO response, the ultrafast NLO absorption and refraction of these SiNS samples were investigated using Z-scan and pump–probe Optical Kerr Effect (OKE) techniques with fs laser pulses at 400 and 800 nm. Furthermore, although the optical limiting (OL) efficiency of various graphene-based nanostructures (associated with their strong reverse saturable absorption (RSA)) has been demonstrated,35–40 similar studies on the OL performance of SiNSs have been scarce, limiting the scope of their potential applications. In that view, to the best of our knowledge, the present work is the first attempt to shed light on the OL performance of SiNSs. For that purpose, the OL performance of SiNS-tBuMA and SiNS-styrene, respectively, was studied using the Z-scan technique under fs laser irradiation. The findings of the current work suggest functionalized SiNSs as highly promising candidates for optical limiting and saturable absorption applications (depending on the excitation conditions), as well as ultrafast all-optical switching devices.
2. Experimental
2.1. General information
All reactants and reagents were purchased from Sigma-Aldrich or TCI. Unless stated otherwise, they were used without further purification. Styrene and tBuMA were passed through an alumina column and stored under argon atmosphere. Acetone was distilled, passed through a column containing activated alumina and 3 Å molecular sieves, and kept under argon atmosphere. Toluene was dried with an MBraun solvent purification system, MB SPS-800, whereby argon was used as inert gas. It was stored on 3 Å molecular sieves under argon atmosphere. Ethyl acetate was distilled and stored under argon atmosphere on 4 Å molecular sieves. Benzene was stored under argon atmosphere on 4 Å molecular sieves.2.2. Synthesis and functionalization of SiNS-H
2.3. Characterization of SiNSs
Fourier-transform infrared spectroscopy (FT-IR) measurements of the powdery SiNS-H and functionalized SiNSs were conducted on a nitrogen-cooled Bruker Vertex 70A spectroscope on an attenuated total reflection module.Raman spectra were acquired with a Renishaw inVia Raman spectrometer with a Leica DM/LM microscope and a 785 nm laser as the excitation source. A 50× objective was used to focus the laser beam onto a spot on the sample's surface.
Thermogravimetric analysis (TGA) was performed inside an argon-filled glove box on a Netzsch TG 209 F 1 Libra instrument with a heating rate of 10 °C min−1 from 20–700 °C under an argon flow of 20 mL min−1.
Photoluminescence spectroscopy (PL) was performed with an AVANTES AVA-Spec 2048 spectroradiometer coupled with the 365 nm light source Prizmatix (LED Current controller) and an Avantes CUV-FL-UV/VIS cuvette holder. Measurements were taken from toluene dispersions in a quartz glass cuvette (40 × 10 × 1 mm) and recorded with a 90° angle between the light source and spectrometer.
Samples for atomic force microscopy (AFM) were prepared from toluene dispersions drop-casted onto polished Si/SiO2 substrates inside an argon-filled glove box. AFM measurements were recorded on a Bruker Veeco Dimension V with TAP190DLC tips in tapping mode with a scan rate of 0.5 Hz.
Scanning electron microscope (SEM) images were collected on a JEOL JSM 7500F at an accelerating voltage of 1 kV. SEM samples were prepared under argon atmosphere by depositing a droplet of diluted dispersions in toluene onto a clean silicon wafer.
Transmission electron microscopy (TEM) was performed on a JEOL JEM 1400 plus microscope at an accelerating voltage of 120 kV. Samples were drop-casted from a toluene dispersion onto a carbon-coated 300 mesh copper grid (obtained from Quantifoil) inside an argon-filled glove box.
X-ray photoelectron spectra were recorded on a Leybold-Heraeus LHS 10 spectrometer using a non-monochromatized Mg Kα source (1253.6 eV). SiNS powder samples were pressed into cavities of a stainless-steel sample holder. Sample preparation and transfer into the XPS spectrometer were carried out under argon atmosphere. The analyzer was operated at a constant pass energy of 100 eV leading to an energy resolution with a full width at half-maximum (FWHM) of ∼1.1 eV. The energy scale of the spectra was corrected for sample charging by using the C 1s main signal (aliphatic/aromatic carbon at 284.5 eV).41 All spectra were recorded in an ultra-high vacuum chamber at a pressure below 5 × 10−8 mbar. Core level spectra were deconvoluted using Voigt functions after linear background subtraction.
2.4. Sample preparation for Z-scan and OKE measurements
Due to the strong oxophilicity of silicon, the dispersions of SiNS samples in toluene were prepared in an argon bag and were kept under argon atmosphere. The dispersions were left to rest for one day to avoid any sedimentation of the samples during the Z-scan and OKE measurements. For the experiments, a part of the supernatant was transferred to 1 mm thick quartz cells tightly sealed to prevent oxidation of the SiNSs. The concentrations of these dispersions were determined through TGA measurements. The UV-Vis-NIR absorption spectra of the dispersions were checked regularly before and after the NLO measurement for any oxidation/sedimentation by a JASCO V-670 double-beam spectrophotometer.2.5. Z-scan measurements
The third-order NLO response (i.e., NLO absorption and refraction) of SiNS-tBuMA and SiNS-styrene was investigated using the Z-scan technique.42 According to this technique, the normalized transmittance of a sample being exposed to variable laser intensities as it moves along the propagation direction (z-axis) of a focused laser beam is monitored by two different experimental configurations, the so-called “Open-Aperture” (OA) and “Closed-Aperture” (CA) Z-scans. In the former transmission measurement (i.e., the OA Z-scan), the laser beam transmitted through the sample is totally collected by a lens and measured by a detector (e.g., by a photomultiplier or a photodiode). Simultaneously, in the latter transmission measurement (i.e., the CA Z-scan), only a part of the transmitted laser beam is measured after it has passed through a narrow aperture placed in the far field of the focusing lens in front of the detector. The obtained OA and CA Z-scan recordings allow the determination of the nonlinear absorption coefficient β and the nonlinear refractive index parameter γ′, respectively. In presence of non-negligible NLO absorption, the CA Z-scan is usually divided by the corresponding OA Z-scan to remove the effect of the NLO absorption, thus yielding the so-called “divided” Z-scan. In this case, the “divided” Z-scan allows the determination of the nonlinear refractive index parameter γ′.In general, the OA Z-scan recordings can either present a transmission minimum or maximum at the focal plane, i.e., at z = 0, corresponding to reverse saturable absorption (RSA, β > 0) or saturable absorption (SA, β < 0), respectively. Correspondingly, the presence of a pre-focal transmission minimum (valley) followed by a post-focal maximum (peak), or vice versa, in the “divided” Z-scan denotes self-focusing (γ′ > 0) or self-defocusing (γ′ < 0), respectively.
For the determination of the values of β and γ′, the experimental OA and “divided” Z-scan curves are fitted with eqn (1) and (2), respectively:
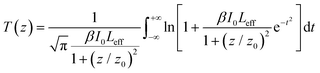 | (1) |
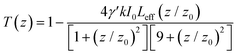 | (2) |
Then, using the nonlinear absorption coefficient β and the nonlinear refractive parameter γ′, the real and the imaginary part of the third order susceptibility χ(3) can be deduced following eqn (3) and (4):
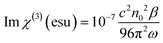 | (3) |
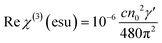 | (4) |
Since these parameters are concentration-dependent quantities, to facilitate comparisons, the corresponding figures of merit (FOM) for the imaginary and real parts of the third-order susceptibility, defined as |Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/α0| and |Re
χ(3)/α0| and |Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/α0|, respectively, are used.
χ(3)/α0|, respectively, are used.
For the Z-scan measurements, a CPA mode-locked Ti:sapphire laser system (Trident X, Amplitude Technologies) operating at 800 nm (70 fs), and at its second harmonic (SHG) at 400 nm (50 fs) at a repetition rate of 10 Hz was employed. The laser beam was focused into the samples by a 20 cm focal length quartz lens, while its spot radius at the focus was determined by a CCD camera, and was found to be ∼20 and ∼25 μm for the 400 and 800 nm laser outputs, respectively. Different concentrations of the SiNS-styrene and SiNS-tBuMA dispersions (i.e., ranging from 0.03 to 0.1 mg mL−1) were prepared for the Z-scan experiments. The measurements were performed under various incident laser intensities ranging from 128 to 896 GW cm−2.
The laser beam intensity, I0, was calculated using the relation I = 2E/πw02τ, where E is the laser energy, measured by a joulemeter; w0 is the beam waist of the laser beam at the focal plane, measured with a CCD camera; and τ is the laser pulse duration obtained from the respective autocorrelation measurements.
2.6. Optical limiting measurements
The optical limiting (OL) performance of the SiNS samples was assessed at 800 nm using the OA Z-scan recordings obtained from the Z-scan experiments. For that purpose, the input fluence Fin(z) at each z-position was determined considering the beam radius r(z) at each z-position and the incident laser energy Ein through eqn (5):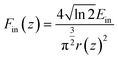 | (5) |
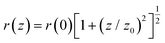 | (6) |
Then, the output fluence Fout(z) was calculated through the following relation:
| Fout(z) = Eine−α0LeffT(z) | (7) |
2.7. OKE measurements
Besides the Z-scan measurements, Optical Kerr Effect (OKE) measurements were also performed.43 OKE is a pump–probe technique that, in addition to measuring the magnitude of the third-order nonlinear susceptibility χ(3), can also provide its temporal evolution. According to this technique, the laser beam is split into two parts, an intense pump and a weak probe beam, with an intensity ratio of about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The former induces a birefringence in the sample, which is detected by the probe beam. After following different optical paths through a Mach–Zehnder type interferometer, the two beams are spatially overlapped and focused into the sample with a 20 cm focal length quartz lens. One of the arms of the interferometer is equipped with a stepper motor, allowing for the insertion of a controllable temporal delay between the pump and probe beams and/or their temporal overlapping. Both beams, which are linearly polarized, are set to have a phase difference of 45°. The transmitted probe beam becomes elliptically polarized when the time delay is near zero. Then, it passes through a Glan-Thompson analyzer whose optical axis is set to be perpendicular to the initial probe beam polarization. The probe beam is then measured using a detector, and the third-order susceptibility χ(3) is determined by comparison with a reference material using eqn (8):
1. The former induces a birefringence in the sample, which is detected by the probe beam. After following different optical paths through a Mach–Zehnder type interferometer, the two beams are spatially overlapped and focused into the sample with a 20 cm focal length quartz lens. One of the arms of the interferometer is equipped with a stepper motor, allowing for the insertion of a controllable temporal delay between the pump and probe beams and/or their temporal overlapping. Both beams, which are linearly polarized, are set to have a phase difference of 45°. The transmitted probe beam becomes elliptically polarized when the time delay is near zero. Then, it passes through a Glan-Thompson analyzer whose optical axis is set to be perpendicular to the initial probe beam polarization. The probe beam is then measured using a detector, and the third-order susceptibility χ(3) is determined by comparison with a reference material using eqn (8):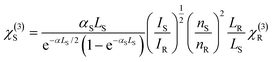 | (8) |
The OKE measurements were performed at 800 and 400 nm, using the same laser system employed for the Z-scan experiments. The beam radii at the focal plane were determined to be ∼25 and ∼20 μm for the 800 and 400 nm, respectively.
All OKE measurements were conducted using lower concentrations (e.g., up to 0.05 mg mL−1) than those used for the Z-scan experiments to minimize the absorption of the OKE signal by the sample.
3. Results and discussion
The successful preparation and functionalization of SiNS-H were proven by FT-IR and Raman spectroscopy (cf. spectra in Fig. S1–S3†). As the IR and Raman spectra of functionalized SiNSs show the characteristic Si–H stretching vibration band at approximately 2100 cm−1, functionalization is not complete. SiNS-H, SiNS-styrene, and SiNS-tBuMA exhibit Raman bands at 495, 635, and 730 cm−1, assigned to Si–Si and Si–H vibration modes, respectively. Additional bands in the Raman spectrum of SiNS-styrene at 1000, 1030, in a range from 1150 to 1200, 1580, and 1600 cm−1, representing aromatic C–H and C–C modes, indicate successful functionalization. Further, the absence of the vinyl C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching band at 1630 cm−1 implies that styrene is covalently attached to the SiNSs. Similar to SiNS-tBuMA, the absence of the vinyl C
C stretching band at 1630 cm−1 implies that styrene is covalently attached to the SiNSs. Similar to SiNS-tBuMA, the absence of the vinyl C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching band at 1640 cm−1 confirms the successful surface capping. Moreover, characteristic bands of the C
C stretching band at 1640 cm−1 confirms the successful surface capping. Moreover, characteristic bands of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode and the C–H deformation mode of the tert-butyl group at 1725 and 1455 cm−1 are observed, respectively. Complementary information was provided by FTIR spectroscopy. Bands assigned to aromatic (1600 and 2970 to 3110 cm−1) and aliphatic signals (905, 1380 to 1510, and 2805 to 2955 cm−1) are present next to the Si–H signal at 2100 cm−1, and bands of oxidized Si at 800 and 1065 cm−1 in the spectrum of SiNS-styrene (Fig. S1†). The FTIR spectrum of SiNS-tBuMA (Fig. S2†) exhibits aliphatic signals (1340 to 1510 and 2855 to 3040 cm−1), bands of C
O stretching mode and the C–H deformation mode of the tert-butyl group at 1725 and 1455 cm−1 are observed, respectively. Complementary information was provided by FTIR spectroscopy. Bands assigned to aromatic (1600 and 2970 to 3110 cm−1) and aliphatic signals (905, 1380 to 1510, and 2805 to 2955 cm−1) are present next to the Si–H signal at 2100 cm−1, and bands of oxidized Si at 800 and 1065 cm−1 in the spectrum of SiNS-styrene (Fig. S1†). The FTIR spectrum of SiNS-tBuMA (Fig. S2†) exhibits aliphatic signals (1340 to 1510 and 2855 to 3040 cm−1), bands of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (1720 cm−1), and C–O stretching vibration (1135 cm−1) besides the Si–H signal at 2100 cm−1. Vinylic C
O (1720 cm−1), and C–O stretching vibration (1135 cm−1) besides the Si–H signal at 2100 cm−1. Vinylic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C modes of the ligands are not present after functionalization with styrene and tBuMA, confirming the results obtained by Raman spectroscopy. Incomplete functionalization is further confirmed by TGA measurements of SiNS-styrene and SiNS-tBuMA (cf. Fig. S4†), as the obtained mass losses are lower than expected for completely functionalized SiNSs. The estimated surface coverages are 30% and 31% for SiNS-tBuMA and SiNS-styrene, respectively.
C modes of the ligands are not present after functionalization with styrene and tBuMA, confirming the results obtained by Raman spectroscopy. Incomplete functionalization is further confirmed by TGA measurements of SiNS-styrene and SiNS-tBuMA (cf. Fig. S4†), as the obtained mass losses are lower than expected for completely functionalized SiNSs. The estimated surface coverages are 30% and 31% for SiNS-tBuMA and SiNS-styrene, respectively.
AFM characterization provides information about the thickness of SiNS samples. The profile height of SiNS-tBuMA is 4 nm, while for SiNS-styrene, it is approximately 2 nm (cf. AFM images in Fig. S5†). Both values are in good agreement with literature values of other functionalized SiNSs.33,44–46 SEM and TEM images (Fig. S6 and S7†) reveal more information regarding the morphology of SiNS-styrene and SiNS-tBuMA. Fig. S6 and S7† show representative SEM and TEM images of the SiNS samples. According to these images, SiNS-styrene and SiNS-tBuMA are nanosheets with irregular shapes and inhomogeneous lateral sizes. Lateral nanosheet dimensions of up to 25 μm and 20 μm were found for SiNS-styrene and SiNs-tBuMA, respectively (cf. SEM images in Fig. S6(c) and (e)†). Instead of monolayers, mainly stacks of several sheets were present, indicating a tendency towards agglomeration. It is important to note that the characterization of the solid SiNSs via SEM, TEM, and AFM does not represent the SiNSs in toluene dispersion used for Z-scan and OKE measurements, as agglomeration is probably favored in the dry state.
PL spectra (Fig. S8†) of both functionalized SiNSs show an emission maximum at approximately 500 nm, independent of their surface group, which is in accordance with previously reported PL maxima.27,31
XPS data were acquired for both types of functionalized SiNSs. Fig. 1 displays the fitted C 1s and Si 2p spectra scaled to the same total Si 2p peak intensity. The data prove the successful functionalization of the nanosheets. The C 1s peak is deconvoluted with three species at a binding energy of 288.3, 286.2, and 284.5 eV. The first two species can be assigned to the carboxylic C and C–O–C bond present in tBuMA in accordance with the literature,47 and the last species to aliphatic/aromatic carbon. Note that the relative peak intensities of the first two species with respect to the aliphatic carbon of 0.16 match the expected ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 of tBuMA.
6 of tBuMA.
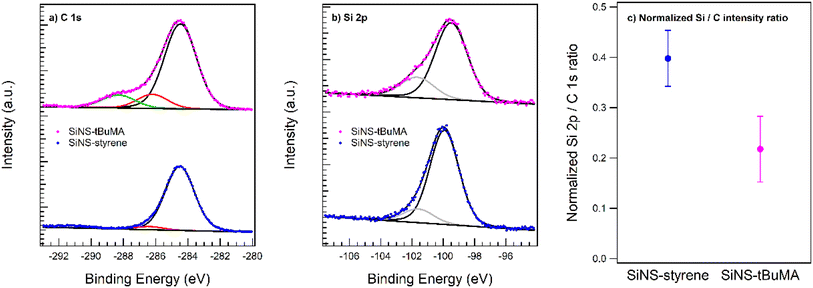 | ||
| Fig. 1 XPS spectra of the (a) C 1s and (b) Si 2p core levels of SiNS-tBuMA and SiNS-styrene. (c) Normalized Si 2p/C 1s ratio reflecting the atomic surface composition. | ||
In the case of SiNS-styrene, essentially only the 284.5 eV species is observed as expected for the styrene functionalization. The minority species at 286.4 eV is tentatively attributed to the carbon atom through which the ligand is attached to the SiNS. Note that the small peak at ∼291 eV, omitted from the peak fitting, resembles a known π–π* excitation feature of aromatic systems such as styrene.48
The Si 2p data underline the picture of a pristine SiNS on which the respective ligand was attached. This is indicated by the main Si(0) component between 99.5 and 99.9 eV binding energy in accordance with the literature and a slightly shifted component at 101.6–101.7 eV, which is tentatively assigned to the anchoring Si atom of the ligand.49,50 The AFM data proves the SiNS in a flat-lying geometry on the support with a tBuMA layer about twice as thick as the styrene functionalization layer around the nanosheet. The different apparent thickness of the functionalization layers is also reflected in the relative Si 2p/C 1s peak intensities, which are displayed in Fig. 1(c). The integrated peak intensities are normalized to the photoionization cross section and the transfer function of the analyzer so that the ratio reflects the atomic ratio of the functionalized SiNSs. The value of 0.4 for the SiNS-styrene sample matches the fraction of 30% of silicon atoms in SiNS to which eight carbon atoms of the styrene ligand are attached when neglecting any photoelectron attenuation due to the styrene layer for the emitted Si 2p photoelectrons. However, the about 1 nm thick layer (functionalization on both sides of the silicon nanosheet) will induce a signal damping of the Si 2p core level emission. With an effective attenuation length between 10 and 30 Å, an attenuation of a factor of about 2 perfectly matches the styrene coverage of ∼15% on either side of the sheet as obtained by TGA.51 Accordingly, due to the doubling of the functionalization layer thickness in case of tBuMA, a further Si 2p damping by another factor of 2 is readily observed. Note that the given error bars rather represent the uncertainties of the sample cleanliness regarding the presence of carbon sources other than the ligand species that may occur during sample preparation.
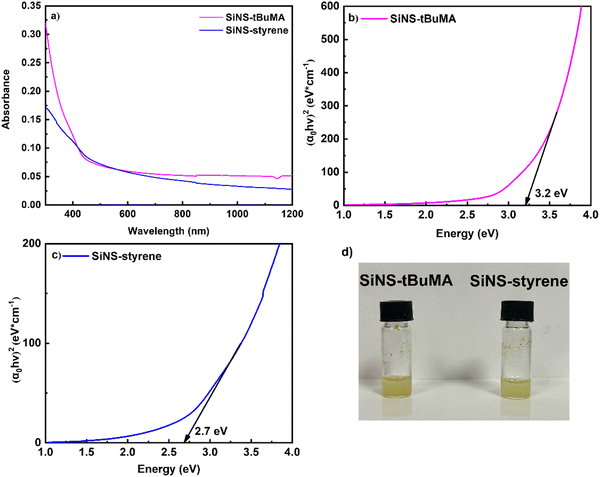
Fig. 2(a) presents some representative UV-Vis-NIR absorption spectra of SiNS-tBuMA and SiNS-styrene dispersions (after having subtracted any toluene absorption), all corresponding to the same concentration of 0.1 mg mL−1. As shown in this figure, the optical absorption spectra of both SiNSs exhibit an absorption peak around 300 nm, attributed to the excitation of carriers from occupied σ to unoccupied σ* states.52 Based on the Tauc plot method,53 the optical band gap energies of SiNS-tBuMA and SiNS-styrene for direct interband transitions were estimated to be approximately 3.2 and 2.7 eV, respectively, as shown in Fig. 2(b and c). Absorption measurements performed on tBuMA and styrene revealed negligible absorption in the spectral region of interest.
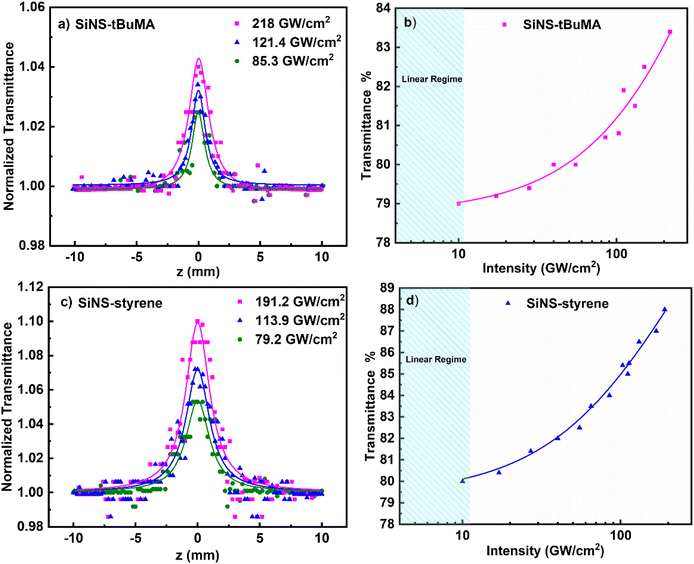
In Fig. 3(a and c) some OA Z-scans of SiNS-tBuMA and SiNS-styrene toluene dispersions (0.1 mg mL−1) are presented, obtained under 50 fs, 400 nm laser excitation using different laser intensities. All dispersions had a linear absorption coefficient α0 of ∼2.55 cm−1 at 400 nm. The solid lines correspond to the best fit of the experimental OA Z-scan data points (solid points) by eqn (1). Since the neat solvent (i.e., toluene) exhibited some NLO absorption for incident laser intensities above 250 GW cm−2, for simplicity, the OA Z-scans shown in this figure correspond to measurements performed at lower laser intensities, where solvent did not contribute. As can be seen, all OA Z-scans present a transmission maximum at the focal plane, indicating saturable absorption (SA) behavior (i.e., β < 0), increasing with the laser intensity. By fitting these OA Z-scans with eqn (1), the average values of the nonlinear absorption coefficient β of the SiNS-tBuMA and SiNS-styrene dispersions at different laser intensities were determined to be about (−8.3 ± 0.8) × 10−15 and (−17 ± 2) × 10−15 m W−1, respectively. The variation of the transmittance at the focal plane (i.e., under maximum laser intensity) of SiNS-tBuMA and SiNS-styrene with the laser intensity is presented in Fig. 3(b and d), respectively. As can be seen from Fig. S9a,† the β values of both SiNSs obtained at different laser intensities remain practically unchanged within the experimental error, suggesting the absence of any saturation effects and/or higher-order nonlinearities.
According to the typical model for saturable absorption for one-photon absorption (1PA),54 the intensity-dependent transmittance of a material can be described by the following relation:
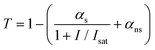 | (9) |
In Fig. 4 the processes contributing to the NLO absorption of the studied SiNSs are shown schematically. Since the estimated band gap energies of SiNS-styrene and SiNS-tBuMA are about 2.7 and 3.2 eV, respectively, 1PA-related transitions from the valence to the conduction band can readily occur under 400 nm (i.e., 3.1 eV) laser excitation (Fig. 4(a and b)). Thus, electrons from the valence band of SiNSs can be directly promoted to higher energy states lying in the conduction band under sufficient laser intensity. From there, after an ultrashort relaxation time, the photogenerated electron–hole pairs cool down to form a Fermi–Dirac distribution.60 As the sample approaches the focal plane, the interband transitions become more efficient due to the sufficiently higher laser intensity leading to the depletion of all the empty band states. As a result, further excitation of carriers is impeded due to the Pauli exclusion principle, giving rise to the manifestation of SA behavior.
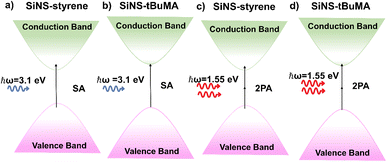 | ||
| Fig. 4 Schematic representation of the processes contributing to the NLO absorption of SiNS-styrene and SiNS-tBuMA under (a, b) 400 and (c, d) 800 nm laser excitation. | ||
In Fig. 5(a and b) some representative OA Z-scans of SiNS-tBuMA and SiNS-styrene dispersions are shown, obtained under 70 fs, 800 nm laser excitation, using different laser intensities. All dispersions had a linear absorbance α0 of 1 cm−1 at 800 nm. Since the solvent exhibited some NLO absorption for intensities higher than 400 GW cm−2, for simplicity, the shown OA Z-scans correspond to laser intensities up to 384.9 GW cm−2, thus providing the sign of the NLO absorption of the SiNS samples straightforwardly. As shown from these scans, both SiNSs exhibited a decrease in their linear transmittance close to the focal plane, indicating reverse saturable absorption (RSA, β > 0). This behavior is opposite to the SA behavior observed under 400 nm excitation, indicating the dependence of the NLO absorption of the SiNSs on the excitation wavelength. In general, the RSA behavior of 2D nanostructures can be attributed to different NLO processes, such as two-photon absorption (2PA), excited state absorption (ESA), free carrier absorption (FCA), and nonlinear scattering (NLS). In the present case, since the excitation wavelength at 800 nm corresponds to a photon energy of 1.55 eV, it implies that the band gap of both SiNSs can be bridged by two photons (Fig. 4(c and d)). Therefore, it is reasonable to assume that the observed RSA of SiNS-tBuMA and SiNS-styrene is due to a 2PA process. From the fitting of the OA Z-scans in Fig. 5(a and b) with eqn (1), the nonlinear absorption coefficients β of SiNS-tBuMA and SiNS-styrene were calculated. The average values of β for the 0.1 mg mL−1 dispersions (corresponding to a linear absorption coefficient α0 of about 1 cm−1) of SiNS-tBuMA and SiNS-styrene were calculated to be about (165 ± 20) × 10−15 and (203 ± 9) × 10−15 m W−1, respectively. An intensity-independent nonlinear absorption coefficient β was also observed for all other studied concentrations (see, e.g., Fig. S9b†), suggesting that 2PA should be the dominant process contributing to the RSA behavior.61 This can be explained by taking into account that 2PA is a weak nonlinear process as virtual states are involved, resulting in negligible ground state depletion. Thus, an intensity-independent nonlinear absorption coefficient β is expected. Finally, it is worth noting that the contribution of ESA, FCA, and NLS to the NLO response of SiNSs should be considered negligible, as they usually become operational under ns laser excitation.62,63
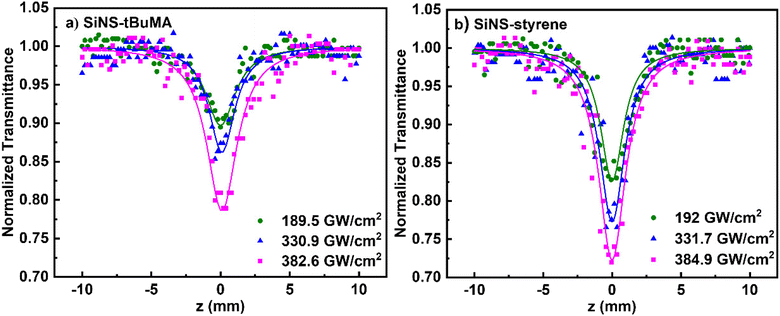 | ||
| Fig. 5 OA Z-scans of (a) SiNS-tBuMA and (b) SiNS-styrene dispersions under different laser intensities at 800 nm. All dispersions had a linear absorption coefficient α0 of about 1 cm−1. | ||
In Table S2,† the determined values of the nonlinear absorption coefficients β of SiNS-tBuMA and SiNS-styrene (0.1 mg mL−1 dispersions, 800 nm laser excitation) are presented and compared with those of other 2D nanomaterials, also exhibiting 2PA under similar experimental conditions.64–68 As seen from the FOM values, SiNS-tBuMA and SiNS-styrene reveal comparable and even larger NLO absorption than the other 2D nanomaterials of Table S2.† It is worth noting that the large β values of both SiNS render them very promising candidates for optical limiting (OL) devices aiming to protect the human retina, sensitive optical sensors, etc., from accidental exposure to high-power laser radiations.
In general, an OL material exhibits high linear transmittance for low incident laser intensity/fluence, following the Beer–Lambert law, while its transmittance decreases at high incident laser intensity, deviating from this law. The laser intensity at which this deviation occurs is referred to as the optical limiting onset (OLon) and is usually employed to characterize the efficiency of an OL material. Fig. 6 presents the OL action of SiNS-styrene and SiNS-tBuMA toluene dispersions under 70 fs, 800 nm laser irradiation, with a concentration of 0.1 mg mL−1. The dotted straight lines correspond to the samples’ linear transmittance, which was about ∼90% at 800 nm, while the solid lines connecting the experimental data points guide the eye. As shown, the OLon values of the SiNS-styrene and SiNS-tBuMA dispersions were determined to be ∼0.0045 and ∼0.0065 J cm−2, respectively, which are much lower than those of other 2D materials previously reported.63,65,69–71
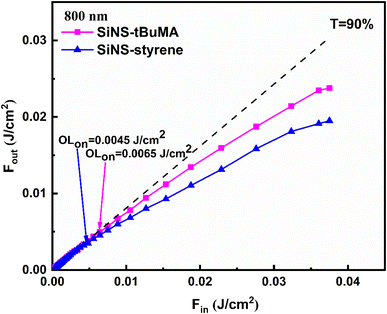 | ||
| Fig. 6 Optical limiting performance of SiNS-tBuMA and SiNS-styrene dispersions under 70 fs, 800 nm laser irradiation. The linear transmittance of the samples at 800 nm was ∼90%. | ||
Concerning the NLO refraction of the studied SiNSs, some representative “divided” Z-scans are presented in Fig. 7, obtained under 50 fs, 400 nm, and 70 fs, 800 nm laser excitation. The concentration of all dispersions was 0.1 mg mL−1. Since the solvent toluene exhibited sizeable NLO refraction under all laser intensities, its NLO response was also measured under the same experimental conditions and considered for determining the sign and the magnitude of the nonlinear refractive index parameter γ′ of the SiNS. “Divided” Z-scans of toluene exhibited a valley–peak configuration under both excitation wavelengths, indicating self-focusing behavior (i.e., γ′ > 0), similar to the “divided” Z-scans of the SiNSs dispersions. However, the ΔTp–v values of the dispersions were found to increase with SiNSs’ concentration, suggesting that the SiNSs and toluene possess the same sign of the nonlinear refractive index parameter γ′. It is reminded that the ΔTp–v parameter is defined as the difference of the normalized transmittance between the valley and the peak of a “divided” Z-scan. From the fitting of the experimental “divided” Z-scans with eqn (2), the nonlinear refractive index parameters γ′ of SiNS-tBuMA and SiNS-styrene, after subtracting toluene contribution, were determined to be about (6.0 ± 0.9) × 10−21 and (15.7 ± 2.0) × 10−21 m2 W−1 at 400 nm, respectively, and about (33.4 ± 5.0) × 10−21 and (74.0 ± 8.0) × 10−21 m2 W−1 at 800 nm. The origin of the NLO refraction of the studied SiNSs under fs laser irradiation is attributed to the instantaneous bound electronic response (Kerr nonlinearity) since other NLO refraction-related processes, such as free carrier refraction, become operational over longer timescales.72,73 In addition, the contribution of thermal lensing to the observed NLO refraction should be excluded since low repetition rate excitation is used (i.e., 10 Hz).
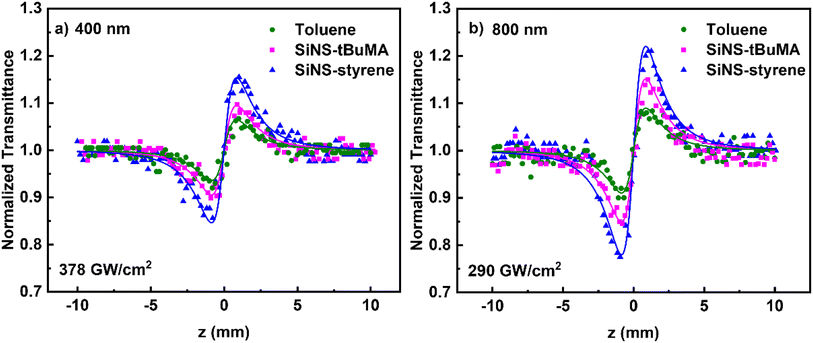 | ||
| Fig. 7 “Divided” Z-scans of 0.1 mg mL−1 SiNS-tBuMA and SiNS-styrene dispersions in toluene, under (a) 50 fs, 400 and (b) 70 fs, 800 nm laser excitation. | ||
Next, the results of the investigation of the NLO response of the SiNSs dispersions by the OKE technique are presented. First, the dependence of the OKE signal on the pump beam intensity is presented in Fig. 8(a and b), for toluene and some SiNS-tBuMA and SiNS-styrene dispersions (0.05 mg mL−1) under 50 fs, 400 nm and 70 fs, 800 nm laser excitation. The intensity of the probe beam was kept constant at 100 and 80 GW cm−2, at 400 and 800 nm, respectively, while the intensity of the pump beam was varied. In all cases, the OKE signals were found to exhibit a quadratic dependence on the pump laser intensity, as expected for third-order optical nonlinearities according to the literature for OKE technique.43 For the analysis of the OKE data, toluene was used as reference material, with its Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) values being (11.4 ± 1.0) × 10−16 and (74.3 ± 6.0) × 10−16 esu at 400 and 800 nm, respectively, having been determined by Z-scan measurements. Then, the values of the real part of the third-order susceptibility, Re
χ(3) values being (11.4 ± 1.0) × 10−16 and (74.3 ± 6.0) × 10−16 esu at 400 and 800 nm, respectively, having been determined by Z-scan measurements. Then, the values of the real part of the third-order susceptibility, Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3), of the SiNS-tBuMA and SiNS-styrene dispersions were calculated to be about (3.8 ± 0.4) × 10−16 and (8.0 ± 1.0) × 10−16 esu under 400 nm excitation, respectively, and about (24 ± 2.0) × 10−16 and (38 ± 4.0) × 10−16 esu under 800 nm excitation.
χ(3), of the SiNS-tBuMA and SiNS-styrene dispersions were calculated to be about (3.8 ± 0.4) × 10−16 and (8.0 ± 1.0) × 10−16 esu under 400 nm excitation, respectively, and about (24 ± 2.0) × 10−16 and (38 ± 4.0) × 10−16 esu under 800 nm excitation.
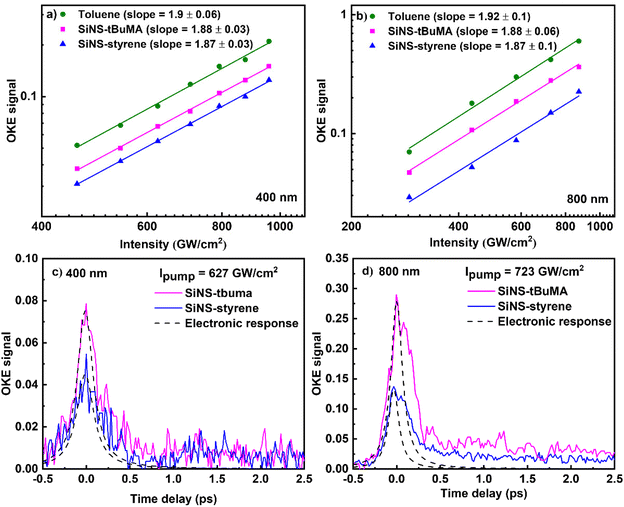 | ||
| Fig. 8 Dependence of the OKE signal on the pump beam intensity and its temporal evolution at (a, c) 400 nm and (b, d) 800 nm. | ||
The time evolution of the OKE signals of the SiNS dispersions is presented in Fig. 8(c and d). The first peak (on the left) at zero-time delay corresponds to the instantaneous electronic response. This peak has been fitted with a Gaussian-type function to provide the laser pulse autocorrelation profile. The adjacent smaller peak corresponds to the molecular reorientation contribution to the OKE signal. It is followed by an exponential-like decay revealing the relaxation of the system towards equilibrium and the relaxation of hot carriers of SiNSs towards the bottom of valence and conduction bands after laser excitation. However, the accurate estimation of the carriers’ relaxation time is difficult because of the interference of the different contributions to the Kerr signal arising from both the solvent and the SiNSs. At this point, it should be added that from the analysis of the autocorrelation traces of the laser pulses in front of the OKE experimental setup, their duration was estimated to be ∼120 and ∼270 fs for the 400 and 800 nm laser beams, respectively, i.e., much longer than the 50 and 70 fs pulse durations measured in front of the Z-scan setup. This temporal broadening is most probably attributed to dispersion effects and other nonlinear optical effects (as e.g., self-phase modulation (SPM)), occurring during the propagation of the laser beam through the different optical components.
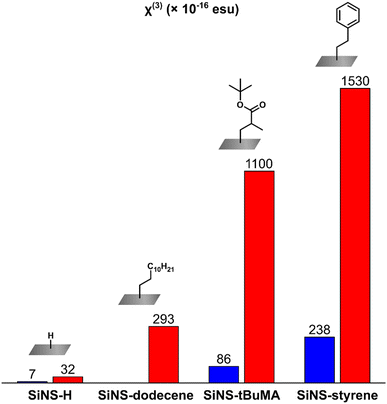
The determined values of the NLO parameters (i.e., the nonlinear absorption coefficient β, the nonlinear refractive index parameter γ′, and the third-order susceptibility χ(3) along with its real and imaginary parts) of SiNS-tBuMA and SiNS-styrene, are summarized in Table 1. To facilitate comparisons, all values of this table refer to a concentration of 1 mg mL−1 (i.e., they have been normalized by the concentration) after considering all the concentrations measured by the Z-scan and OKE techniques presented in Tables S4 and S5.† For completeness of the present study and comparison purposes, the corresponding NLO parameters of the non-functionalized SiNS-H (see also Fig. S10†) and SiNS-dodecene,29 obtained from Z-scan experiments, are also included in Table 1.
| λ (nm) | Sample | Z-scan | OKE | ||||
|---|---|---|---|---|---|---|---|
| β (× 10−15 m W−1) | γ′ (× 10−21 m2 W−1) | Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) (× 10−16 esu) χ(3) (× 10−16 esu) |
Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) (× 10−16 esu) χ(3) (× 10−16 esu) |
|χ|(3) (× 10−16 esu) | Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) (× 10−16 esu) χ(3) (× 10−16 esu) |
||
| a Values are taken from ref. 29. | |||||||
| 400 | Toluene | 24.6 ± 2.0 | 8.0 ± 0.8 | 7.2 ± 0.6 | 11.4 ± 1.0 | 13.5 ± 1.0 | 11.4 ± 1.0 |
| SiNS-H | −5.6 ± 0.3 | 4.9 ± 0.9 | −1.5 ± 0.1 | 7.0 ± 1.0 | 7.2 ± 1.0 | 5.3 ± 0.4 | |
| SiNS-tBuMA | −79.5 ± 10 | 57.7 ± 8.0 | −23.3 ± 3.0 | 82.3 ± 11.0 | 85.5 ± 11.0 | 73.2 ± 8.0 | |
| SiNS-styrene | −177 ± 20 | 162.5 ± 18.0 | −51.8 ± 6.0 | 231.8 ± 26.0 | 237.5 ± 27.0 | 170 ± 20 | |
| 800 | Toluene | 53.8 ± 4.0 | 52.1 ± 4.0 | 30.7 ± 2.0 | 74.3 ± 6.0 | 80.4 ± 6.0 | 74.3 ± 6.0 |
| SiNS-H | — | 22 ± 4 | — | 32 ± 6 | 32 ± 6 | 30 ± 3 | |
| SiNS-dodecenea | −400.0 ± 61.0 | 133.0 ± 6.0 | −225.0 ± 34.0 | 189.0 ± 9.0 | 293.0 ± 35.0 | N/A | |
| SiNS-tBuMA | 1661.0 ± 200.0 | 331.8 ± 38.0 | 947.4 ± 114.0 | 472.9 ± 54.0 | 1100.0 ± 126.0 | 458.3 ± 36.0 | |
| SiNS-styrene | 1968.0 ± 90.0 | 728.7 ± 72.0 | 1122.4 ± 51.0 | 1039.5 ± 102.0 | 1530.0 ± 114.0 | 853.1 ± 70.0 | |
As can be seen from Table 1, the functionalization of SiNS-H has a significant effect on the third-order NLO response of these SiNSs, leading to an exceptional enhancement of both the NLO absorption and refraction, opening up new possibilities for their implementation in high-performance optoelectronic and photonic devices. In more detail, the third-order susceptibilities χ(3) of SiNS-tBuMA and SiNS-styrene obtained from the Z-scan measurements under 800 nm laser excitation, were found to be ∼35 and ∼50 times larger than that of SiNS-H and ∼5 times larger than that of SiNS-dodecene. Similarly, in the case of 400 nm laser excitation, the third-order susceptibilities χ(3) of SiNS-tBuMA and SiNS-styrene exhibited a ∼12 and ∼33 times enhancement compared to SiNS-H. At this point, it should be emphasized that since the NLO responses of neat tBuMA and styrene, measured under similar excitation conditions, were found to be negligible, the enhanced NLO responses of SiNS-tBuMA and SiNS-styrene can be undoubtedly attributed to the functionalization of the SiNSs. The above results are schematically presented in Fig. 9. Comparing the NLO response of the two functionalized SiNSs, SiNS-styrene exhibits ∼1.5 and ∼3 times larger third-order susceptibilities χ(3) than SiNS-tBuMA under 800 and 400 nm laser excitation, respectively. The difference in the NLO responses of SiNS-styrene and SiNS-tBuMA is due to the different nature of the two functional groups, which can act as electron-donors/acceptors,74,75 similarly to what has been reported elsewhere e.g., for graphene.76 So, since the NLO response of SiNS-styrene was found to be stronger than that of SiNS-tBuMA, it could be reasonably assumed that the charge transfer between the styrene group and the SiNS is more efficient compared to that occurring in the case of the tBuMA group.
Concerning the NLO absorptive response of the investigated SiNSs, it has to be highlighted that the chemical functionalization of SiNS-H with tBuMA and styrene gives rise to a very strong NLO absorption, as shown in Table 1. So, while SiNS-H exhibits insignificant NLO absorption under 800 nm laser excitation (i.e., practically zero nonlinear absorption coefficient β (or Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3))), SiNS-tBuMA and SiNS-styrene have very large β values, i.e., (1661 ± 200) and (1968 ± 90) × 10−15 m W−1 after what the β value of SiNS-styrene is the largest one. Similar findings were observed under 400 nm laser excitation, where SiNS-tBuMA and SiNS-styrene possess ∼15 and ∼32 times larger β values than SiNS-H, with the styrene functionalized SiNSs featuring the largest value. More importantly, both functionalized SiNSs were found to show reverse saturable absorption (i.e., β > 0) under 800 nm excitation and saturable absorption (i.e., β < 0) under 400 nm excitation. This sign alternation of the NLO absorption is particularly interesting for photonic applications. Thus, the studied SiNSs can be employed as optical limiters or saturable absorbers by selecting the appropriate excitation wavelength.
χ(3))), SiNS-tBuMA and SiNS-styrene have very large β values, i.e., (1661 ± 200) and (1968 ± 90) × 10−15 m W−1 after what the β value of SiNS-styrene is the largest one. Similar findings were observed under 400 nm laser excitation, where SiNS-tBuMA and SiNS-styrene possess ∼15 and ∼32 times larger β values than SiNS-H, with the styrene functionalized SiNSs featuring the largest value. More importantly, both functionalized SiNSs were found to show reverse saturable absorption (i.e., β > 0) under 800 nm excitation and saturable absorption (i.e., β < 0) under 400 nm excitation. This sign alternation of the NLO absorption is particularly interesting for photonic applications. Thus, the studied SiNSs can be employed as optical limiters or saturable absorbers by selecting the appropriate excitation wavelength.
Similar trends to those found for the NLO absorption of the functionalized SiNSs were observed for their NLO refractive properties. So, under 800 nm laser excitation, the nonlinear refractive index parameters γ′ (or Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)) of SiNS-tBuMA and SiNS-styrene were found to be enhanced by ∼15 and ∼33 times compared to that of SiNS-H, while under 400 nm excitation, a similar enhancement was found, i.e., ∼12 and ∼33 times that of SiNS-H. In all cases, the styrene functionalized SiNSs exhibited the largest NLO refractive index parameter γ′. At this point, it is important to add that the results of the Re
χ(3)) of SiNS-tBuMA and SiNS-styrene were found to be enhanced by ∼15 and ∼33 times compared to that of SiNS-H, while under 400 nm excitation, a similar enhancement was found, i.e., ∼12 and ∼33 times that of SiNS-H. In all cases, the styrene functionalized SiNSs exhibited the largest NLO refractive index parameter γ′. At this point, it is important to add that the results of the Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) of SiNSs determined from the OKE measurements are in excellent agreement with those obtained from the Z-scan experiments (see also Table 1), confirming the observed trends. So, SiNS-styrene exhibits larger (i.e., almost double) Re
χ(3) of SiNSs determined from the OKE measurements are in excellent agreement with those obtained from the Z-scan experiments (see also Table 1), confirming the observed trends. So, SiNS-styrene exhibits larger (i.e., almost double) Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) values than SiNS-tBuMA, at both excitation wavelengths. In addition, the Re
χ(3) values than SiNS-tBuMA, at both excitation wavelengths. In addition, the Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) values of SiNS-tBuMA and SiNS-styrene were ∼15 and ∼30 times larger than that of SiNS-H at both excitation conditions.
χ(3) values of SiNS-tBuMA and SiNS-styrene were ∼15 and ∼30 times larger than that of SiNS-H at both excitation conditions.
It is worth noting that the NLO refractive response of the present SiNSs is among the stronger ones for 2D nanostructures. This is shown in Table S6,† where the NLO parameters of the studied SiNSs, i.e., γ′, Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3), and the corresponding figure of merit FOM, i.e., the Re
χ(3), and the corresponding figure of merit FOM, i.e., the Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) normalized by the linear absorption, are compared to those of some other 2D materials recently reported in the literature, as, e.g., graphene, TMDs, BP, and MXenes.57,59,77,78 The NLO refractive responses of SiNS-styrene and SiNS-tBuMA are significantly stronger than those of the materials above. Finally, it is helpful to add that since the NLO refraction of both SiNSs is comparable to that of bulk Si (i.e., ∼10−19 m2 W−1 under 800 nm laser excitation),79–82 they can also be considered as promising candidates for ultrafast all-optical switching applications in the Si-based photonic industry.
χ(3) normalized by the linear absorption, are compared to those of some other 2D materials recently reported in the literature, as, e.g., graphene, TMDs, BP, and MXenes.57,59,77,78 The NLO refractive responses of SiNS-styrene and SiNS-tBuMA are significantly stronger than those of the materials above. Finally, it is helpful to add that since the NLO refraction of both SiNSs is comparable to that of bulk Si (i.e., ∼10−19 m2 W−1 under 800 nm laser excitation),79–82 they can also be considered as promising candidates for ultrafast all-optical switching applications in the Si-based photonic industry.
4. Conclusions
In the present work, the ultrafast NLO response (NLO absorption and refraction) of two functionalized silicon nanosheets, namely SiNS-styrene and SiNS-tBuMA, was studied using fs laser excitation at 800 and 400 nm. For the determination of the different nonlinear optical parameters, two experimental techniques were employed, namely Z-scan and OKE techniques. Both SiNSs were found to exhibit very strong NLO responses significantly enhanced compared to pristine SiNS-H, demonstrating the importance of chemical functionalization for improving and tailoring the NLO response of SiNSs in view of several potential optoelectronic and photonic applications. In addition to their large optical nonlinearities, the present SiNSs were found to present wavelength-dependent NLO absorptive response, exhibiting reverse saturable absorption (RSA) at 800 nm and saturable absorption nm at 400 nm, thus enlarging the range of their potential applications for optical limiting or as saturable absorbers, respectively. Concerning the NLO refraction, both SiNSs presented strong self-focusing, rendering them promising candidates for optical switching applications. Notably, the present functionalized SiNSs possess significantly better NLO absorption and refraction than several other 2D nanostructures reported so far. Future research will focus on the introduction of further functional groups to SiNSs in order to systematically explore the influence of the functionalization on the NLO response.83 The above findings demonstrate that chemical functionalization and the choice of laser excitation conditions can be efficiently used for the enhancement and the custom-made modification of the NLO properties of SiNSs in view of high-performance optoelectronic and photonic devices.Author contributions
A. M. and E. G. prepared and characterized the samples; T. K. and S. G. performed the XPS measurements and evaluation; M. S. and V. A. performed the nonlinear optical experiments and data analysis; M. S., A. M., V. A., E. G., T. K., and S. G. wrote the initial manuscript; S. C. and B. R. conceptualized the study, supervised the work, review and editing the final draft, and acquired funding; all authors have read and agreed to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the help of Sabine Zeitz and Thomas Fässler for providing the starting material CaSi2, Sabrina Artmeier for performing AFM, Philipp Weingarten for TEM measurements, and Dr Carsten Troll and Dr Sergei Vagin for SEM. Michalis Stavrou acknowledges support from the Hellenic Foundation for Research and Innovation (HFRI) under the HFRI PhD Fellowship grant (number: 83656). Elisabeth Groß and Amelie M. Mühlbach thank the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for funding (project number 245845833) within International Research Training Group IRTG 2022 – Alberta Technical University of Munich School for Functional Hybrid Materials (ATUMS). Support within IGSSE is greatly appreciated.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- L. Wang, I. Meric, P. Y. Huang, Q. Gao, Y. Gao, H. Tran, T. Taniguchi, K. Watanabe, L. M. Campos, D. A. Muller, J. Guo, P. Kim, J. Hone, K. L. Shepard and C. R. Dean, Science, 2013, 342, 614–617 CrossRef CAS PubMed.
- G. X. Ni, L. Wang, M. D. Goldflam, M. Wagner, Z. Fei, A. S. McLeod, M. K. Liu, F. Keilmann, B. Özyilmaz, A. H. Castro Neto, J. Hone, M. M. Fogler and D. N. Basov, Nat. Photonics, 2016, 10, 244–247 CrossRef CAS.
- A. Molle, J. Goldberger, M. Houssa, Y. Xu, S. C. Zhang and D. Akinwande, Nat. Mater., 2017, 16, 163–169 CrossRef CAS PubMed.
- E. Bianco, S. Butler, S. Jiang, O. D. Restrepo, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 4414–4421 CrossRef CAS PubMed.
- S. Yamanaka, H. Matsu-ura and M. Ishikawa, Mater. Res. Bull., 1996, 31, 307–316 CrossRef CAS.
- A. A. Tedstone, D. J. Lewis and P. O'Brien, Chem. Mater., 2016, 28, 1965–1974 CrossRef CAS.
- R. Lv, J. A. Robinson, R. E. Schaak, D. Sun, Y. Sun, T. E. Mallouk and M. Terrones, Acc. Chem. Res., 2015, 48, 56–64 CrossRef CAS PubMed.
- K. K. Kim, A. Hsu, X. Jia, S. M. Kim, Y. Shi, M. Hofmann, D. Nezich, J. F. Rodriguez-Nieva, M. Dresselhaus, T. Palacios and J. Kong, Nano Lett., 2012, 12, 161–166 CrossRef PubMed.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2013, 26, 992–1005 CrossRef PubMed.
- H. Liu, Y. Du, Y. Deng and P. D. Ye, Chem. Soc. Rev., 2015, 44, 2732–2743 RSC.
- Z. Cheng and J. Lin, CrystEngComm, 2010, 12, 2646–2662 RSC.
- L. Dou, A. B. Wong, Y. Yu, M. Lai, N. Kornienko, S. W. Eaton, A. Fu, C. G. Bischak, J. Ma, T. Ding, N. S. Ginsberg, L.-W. Wang, A. Paul Alivisatos and P. Yang, Science, 2015, 349, 1518–1521 CrossRef CAS PubMed.
- Y. Yamada-Takamura and R. Friedlein, Sci. Technol. Adv. Mater., 2014, 15, 064404 CrossRef PubMed.
- H. Okamoto, Y. Sugiyama and H. Nakano, Chem. – Eur. J., 2011, 17, 9864–9887 CrossRef CAS PubMed.
- U. Röthlisberger, W. Andreoni and M. Parrinello, Phys. Rev. Lett., 1994, 72, 665–668 CrossRef PubMed.
- P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Phys. Rev. Lett., 2012, 108, 155501 CrossRef PubMed.
- C. L. Lin, R. Arafune, K. Kawahara, N. Tsukahara, E. Minamitani, Y. Kim, N. Takagi and M. Kawai, Appl. Phys. Express, 2012, 5, 045802 CrossRef.
- D. Chiappe, C. Grazianetti, G. Tallarida, M. Fanciulli and A. Molle, Adv. Mater., 2012, 24, 5088–5093 CrossRef CAS PubMed.
- A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang and Y. Yamada-Takamura, Phys. Rev. Lett., 2012, 108, 245501 CrossRef PubMed.
- B. Lalmi, H. Oughaddou, H. Enriquez, A. Kara, S. Vizzini, B. Ealet and B. Aufray, Appl. Phys. Lett., 2010, 97, 223109 CrossRef.
- L. Meng, Y. Wang, L. Zhang, S. Du, R. Wu, L. Li, Y. Zhang, G. Li, H. Zhou, W. A. Hofer and H.-J. Gao, Nano Lett., 2013, 13, 685–690 CrossRef CAS PubMed.
- G. G. Guzmán-Verri and L. C. Lew Yan Voon, J. Phys.: Condens. Matter, 2011, 23, 145502 CrossRef PubMed.
- O. D. Restrepo, R. Mishra, J. E. Goldberger and W. Windl, J. Appl. Phys., 2014, 115, 033711 CrossRef.
- C. Zhang, A. De Sarkar and R.-Q. Zhang, J. Phys. Chem. C, 2011, 115, 23682–23687 CrossRef CAS.
- M. Houssa, G. Pourtois, M. M. Heyns, V. V. Afanas'ev and A. Stesmans, J. Electrochem. Soc., 2011, 158, H107–H110 CrossRef CAS.
- T. Helbich, A. Lyuleeva, I. M. D. Höhlein, P. Marx, L. M. Scherf, J. Kehrle, T. F. Fässler, P. Lugli and B. Rieger, Chem. – Eur. J., 2016, 22, 6194–6198 CrossRef CAS PubMed.
- M. Stavrou, I. Papadakis, A. Stathis, M. J. Kloberg, J. Mock, T. Kratky, S. Günther, B. Rieger, M. Becherer, A. Lyuleeva-Husemann and S. Couris, J. Phys. Chem. Lett., 2021, 12, 815–821 CrossRef CAS PubMed.
- A. Stathis, M. Stavrou, I. Papadakis, J. Mock, M. J. Kloberg, M. Becherer, A. Lyuleeva-Husemann and S. Couris, J. Phys. Chem. C, 2021, 125, 18510–18516 CrossRef CAS.
- M. Stavrou, A. Stathis, I. Papadakis, A. Lyuleeva-Husemann, E. Koudoumas and S. Couris, Nanomaterials, 2022, 12, 90 CrossRef CAS PubMed.
- T. Helbich, A. Lyuleeva, T. Ludwig, L. M. Scherf, T. F. Fässler, P. Lugli and P. Rieger, Adv. Funct. Mater., 2016, 26, 6711–6718 CrossRef CAS.
- M. J. S. Spencer, T. Morishita, M. Mikami, I. K. Snook, Y. Sugiyama and H. Nakano, Phys. Chem. Chem. Phys., 2011, 13, 15418–15422 RSC.
- H. Okamoto, Y. Kumai, Y. Sugiyama, T. Mitsuoka, K. Nakanishi, T. Ohta, H. Nozaki, S. Yamaguchi, S. Shirai and H. Nakano, J. Am. Chem. Soc., 2010, 132, 2710–2718 CrossRef CAS PubMed.
- Y. Sugiyama, H. Okamoto, T. Mitsuoka, T. Morikawa, K. Nakanishi, T. Ohta and H. Nakano, J. Am. Chem. Soc., 2010, 132, 5946–5947 CrossRef CAS PubMed.
- M. Stavrou, D. Panáček, A. Bakandritsos and S. Couris, J. Phys. Chem. C, 2022, 126, 14339–14345 CrossRef CAS.
- M. Stavrou, I. Papadakis, S. Bawari, T. N. Narayanan and S. Couris, J. Phys. Chem. C, 2021, 125, 16075–16085 CrossRef CAS.
- M. Stavrou, N. Chazapis, E. Nikoli, R. Arenal, N. Tagmatarchis and S. Couris, ACS Appl. Nano Mater., 2022, 5, 16674–16686 CrossRef CAS.
- A. Wang, L. Long, W. Zhao, Y. Song, M. G. Humphrey, M. P. Cifuentes, X. Wu, Y. Fu, D. Zhang, X. Li and C. Zhang, Carbon, 2013, 53, 327–338 CrossRef CAS.
- J. Zhu, Y. Li, Y. Chen, J. Wang, B. Zhang, J. Zhang and W. J. Blau, Carbon, 2011, 49, 1900–1905 CrossRef CAS.
- K. Mondal, S. Biswas, A. Pramanik, D. Banerjee, V. R. Soma, A. K. Chaudhary and P. Kumbhakar, Appl. Surf. Sci., 2022, 578, 151966 CrossRef CAS.
- K. L. Smith and K. M. Black, J. Vac. Sci. Technol., A, 1984, 2, 744–747 CrossRef CAS.
- M. Sheik-bahae, A. A. Said and E. W. Van Stryland, Opt. Lett., 1989, 14, 955–957 CrossRef CAS PubMed.
- P. P. Ho and R. R. Alfano, Phys. Rev. A, 1979, 20, 2170–2187 CrossRef CAS.
- A. Lyuleeva, T. Helbich, B. Rieger and P. Lugli, J. Phys. D: Appl. Phys., 2017, 50, 135106 CrossRef.
- H. Nakano, M. Nakano, K. Nakanishi, D. Tanaka, Y. Sugiyama, T. Ikuno, H. Okamoto and T. Ohta, J. Am. Chem. Soc., 2012, 134, 5452–5455 CrossRef CAS PubMed.
- T. Helbich, M. J. Kloberg, R. Sinelnikov, A. Lyuleeva, J. G. C. Veinot and B. Rieger, Nanoscale, 2017, 9, 7739–7744 RSC.
- A. A. Qaiser and M. M. Hyland, Mater. Sci. Forum, 2010, 657, 35–45 CAS.
- C. Enkvist, S. Lunell, B. Sjögren, P. A. Brühwiler and S. Svensson, J. Chem. Phys., 1995, 103, 6333–6342 CrossRef CAS.
- A. A. Galuska, J. C. Uht and N. Marquez, J. Vac. Sci. Technol., A, 1988, 6, 110–122 CrossRef CAS.
- M. Dasog, Z. Yang, S. Regli, T. M. Atkins, A. Faramus, M. P. Singh, E. Muthuswamy, S. M. Kauzlarich, R. D. Tilley and J. G. C. Veinot, ACS Nano, 2013, 7, 2676–2685 CrossRef CAS PubMed.
- W. H. Gries, Surf. Interface Anal., 1996, 24, 38–50 CrossRef CAS.
- S. Chowdhury and D. A. Jana, Rep. Prog. Phys., 2016, 79, 126501 CrossRef PubMed.
- J. Tauc, Mater. Res., 1968, 1, 37–46 Search PubMed.
- E. Garmire, IEEE J. Sel. Top. Quantum Electron., 2000, 6, 1094–1110 CAS.
- K. Wang, Y. Feng, C. Chang, J. Zhan, C. Wang, Q. Zhao, J. N. Coleman, L. Zhang, W. J. Blau and J. Wang, Nanoscale, 2014, 6, 10530–10535 RSC.
- C. Lu, C. Quan, K. Si, X. Xu, C. He, Q. Zhao, Y. Zhan and X. Xu, Appl. Surf. Sci., 2019, 479, 1161–1168 CrossRef CAS.
- K. Wang, J. Wang, J. Fan, M. Lotya, A. O'Neill, D. Fox, Y. Feng, X. Zhang, B. Jiang, Q. Zhao, H. Zhang, J. N. Coleman, L. Zhang and W. J. Blau, ACS Nano, 2013, 7, 9260–9267 CrossRef CAS PubMed.
- S. B. Lu, L. L. Miao, Z. N. Guo, X. Qi, C. J. Zhao, H. Zhang, S. C. Wen, D. Y. Tang and D. Y. Fan, Opt. Express, 2015, 23, 11183–11194 CrossRef CAS PubMed.
- X. Jiang, S. Liu, W. Liang, S. Luo, Z. He, Y. Ge, H. Wang, R. Cao, F. Zhang, Q. Wen, J. Li, Q. Bao, D. Fan and H. Zhang, Laser Photonics Rev., 2017, 12, 1700229 CrossRef.
- E. Cinquanta, G. Fratesi, S. dal Conte, C. Grazianetti, F. Scotognella, S. Stagira, C. Vozzi, G. Onida and A. Molle, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 165427 CrossRef.
- M. Rumi and J. W. Perry, Adv. Opt. Photonics, 2010, 2, 451–518 CrossRef CAS.
- D. N. Christodoulides, I. C. Khoo, G. J. Salamo, G. I. Stegeman and E. W. Van Stryland, Adv. Opt. Photonics, 2010, 2, 60–200 CrossRef CAS.
- J. Wang, Y. Hernandez, M. Lotya, J. N. Coleman and W. J. Blau, Adv. Mater., 2009, 21, 2430–2435 CrossRef CAS.
- L. Ran, Z. Chai, Y. Gao, W. Wu, Q. Chang and D. Kong, Curr. Appl. Phys., 2016, 16, 985–988 CrossRef.
- X. F. Jiang, L. Polavarapu, S. T. Neo, T. Venkatesan and Q. H. Xu, J. Phys. Chem. Lett., 2012, 3, 785–790 CrossRef CAS PubMed.
- G. Wang, D. Bennett, C. (John) Zhang, C. Ó. Coileáin, M. Liang, N. McEvoy, J. J. Wang, J. Wang, K. Wang, V. Nicolosi and W. J. Blau, Adv. Opt. Mater., 2020, 8, 1902021 CrossRef CAS.
- M. Maldonado, M. L. da Silva Neto, P. G. Vianna, H. B. Ribeiro, V. O. Gordo, I. C. Carvalho, L. de S. Menezes, C. B. de Araújo, C. J. S. de Matos, L. Seixas, A. M. Jawaid, R. Busch, A. J. Ritter, R. A. Vaia and A. S. L. Gomes, J. Phys. Chem. C, 2020, 124, 15425–15433 CrossRef CAS.
- C. Lu, M. Luo, Y. Ge, Y. Huang, Q. Zhao, Y. Zhou and X. Xu, ACS Appl. Mater. Interfaces, 2021, 14, 2390–2400 CrossRef PubMed.
- N. Dong, Y. Li, Y. Feng, S. Zhang, X. Zhang, C. Chang, J. Fan, L. Zhang and J. Wang, Sci. Rep., 2015, 5, 14646 CrossRef CAS PubMed.
- J. Huang, N. Dong, S. Zhang, Z. Sun, W. Zhang and J. Wang, ACS Photonics, 2017, 4, 3063–3070 CrossRef CAS.
- W. Shen, J. Hu, T. Ma, J. Wang, Y. Wei, Y. Zhang, J. Wu and J. Chen, Electron. Mater. Lett., 2021, 17, 521–531 CrossRef CAS.
- R. L. Sutherland, D. G. McLean and S. Kirkpatrick, Handbook of Nonlinear Optics, Marcel Dekker, New York & Basel, 2003 Search PubMed.
- A. A. Said, M. Sheik-Bahae, D. J. Hagan, T. H. Wei, J. Wang, J. Young and E. W. Van Stryland, J. Opt. Soc. Am. B, 1992, 9, 405–414 CrossRef CAS.
- S. Srichan, D. Chan-Seng and J. F. Lutz, ACS Macro Lett., 2012, 1, 589–592 CrossRef CAS PubMed.
- R. Goseki, Y. Matsuo and A. Hirao, Polym. Chem., 2018, 9, 834–844 RSC.
- B. Das, R. Voggu, C. S. Rout and C. N. R. Rao, Chem. Commun., 2008, 5155–5157 RSC.
- M. Stavrou, I. Dalamaras, N. Karampitsos and S. Couris, J. Phys. Chem. C, 2020, 124, 27241–27249 CrossRef CAS.
- Y. Xu, F. Jiang, Y. Ge, Z. Guo, Z. Zeng, Q.-H. Xu, H. Zhang, X.-F. Yu and D. Fan, J. Mater. Chem. C, 2017, 5, 3007–3013 RSC.
- M. Dinu, F. Quochi and H. Garcia, Appl. Phys. Lett., 2003, 82, 2954–2956 CrossRef CAS.
- A. D. Bristow, N. Rotenberg and H. M. van Driel, Appl. Phys. Lett., 2007, 90, 191104 CrossRef.
- R. Wu, J. Collins, L. T. Canham and A. Kaplan, Appl. Sci., 2018, 8, 1810 CrossRef.
- S. Tzortzakis, L. Sudrie, M. Franco, B. Prade, A. Mysyrowicz, A. Couairon and L. Bergé, Phys. Rev. Lett., 2001, 87, 213902 CrossRef CAS PubMed.
- M. Stavrou, A. M. Mühlbach, B. Rieger and S. Couris, in preparation.
Footnotes |
| † Electronic supplementary information (ESI) available: FT-IR and Raman spectra, TGA measurements and calculation of surface coverages, AFM, SEM, and TEM images, PL spectra, intensity-dependent nonlinear absorption coefficients, “divided” Z-scans of SiNS-H, purity of SiNS-styrene and SiNS-tBuMA, comparisons of NLO parameters with other 2D materials, NLO parameters of dispersions with different concentrations. See DOI: https://doi.org/10.1039/d3nr03497f |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |