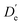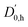Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Subtle hydrogen bond preference and dual Franck–Condon activity – the interesting pairing of 2-naphthol with anisole†
Arman
Nejad
 *a,
Ariel F.
Pérez Mellor‡
*a,
Ariel F.
Pérez Mellor‡
 b,
Manuel
Lange
b,
Manuel
Lange
 a,
Ivan
Alata
b,
Anne
Zehnacker
a,
Ivan
Alata
b,
Anne
Zehnacker
 b and
Martin A.
Suhm
b and
Martin A.
Suhm
 a
a
aInstitute of Physical Chemistry, Georg-August University of Göttingen, Tammannstraße 6, 37077 Göttingen, Germany. E-mail: anejad@gwdg.de; msuhm@gwdg.de
bInstitut des Sciences Moléculaires d'Orsay (ISMO), CNRS, Université Paris-Saclay, 91405 Orsay, France. E-mail: anne.zehnacker-rentien@universite-paris-saclay.fr
First published on 31st March 2023
Abstract
The hydrogen-bonded complexes between 2-naphthol (or β-naphthol) and anisole are explored by detecting their IR absorption in the OH stretching range as well as their UV absorption by means of laser-induced fluorescence and resonance-enhanced two-photon UV ionisation. For the more stable cis and the metastable trans conformations of the OH group in 2-naphthol, hydrogen bonding to the oxygen atom of anisole is consistently detected in different supersonic jet expansions. Alternative hydrogen bonding to the aromatic ring of anisole remains elusive, although the majority of state-of-the-art hybrid DFT functionals with London dispersion correction and – less surprisingly – MP2 wavefunction theory predict it to be slightly more stable at zero-point level, unless three-body dispersion correction is added to the B3LYP-D3(BJ) approach. This changes at the CCSD(T) level, which forecasts an energy advantage of 1–3 kJ mol−1 for the classical hydrogen bond arrangement even after including (DFT) zero-point energy contributions. The UV and IR spectra of the cis complex exhibit clear evidence for intensity redistribution of the primary OH stretch oscillator to combination states with the same low-frequency intermolecular bending mode by Franck–Condon-type vertical excitation mechanisms. This rare case of dual (vibronic and vibrational) Franck–Condon activity of a low-frequency mode invites future studies of homologues where aromatic ring docking of the OH group may be further stabilised, e.g. through anisole ring methylation.
1 Introduction
The spectroscopic study of hydrogen-bonded complexes in the gas phase is a mature field, where different spectral regions and different detection techniques lead to a fruitful synergy and powerful conclusions.1–13 When two multifunctional molecules form a weakly bound complex, there are two interesting structural aspects which lend themselves to closer experimental investigation, because they can provide quantum chemical methods with suitable reference points. One is the ground state preference for one over other structural arrangements of the complex in the competition of intermolecular forces. It is addressed by the concept of intermolecular energy balances,14–16 where systems are picked for being ambivalent in terms of two different arrangements of their constituents.17–24 The other aspect is the influence of molecular excitation of the components on this structural arrangement of the complex, due to the coupling of intramolecular degrees of freedom with intermolecular ones. This leads to the phenomenon of Franck–Condon effects in electronic and – less frequently observed in neutral complexes – vibrational spectroscopy of molecular aggregates.25–30In this work, we argue that the complex between 2-naphthol and anisole (Fig. 1) is a particularly interesting and challenging case of an intermolecular energy balance and of a dual Franck–Condon effect. It is a rare case where even rather high-level electronic structure calculations supplemented by (harmonic) vibrational zero-point energy correction remain ambiguous about the global minimum structure. Only at the highest level, one can confidently conclude that the detectable structure is the energetically winning structure in a very subtle competition. The 2-naphthol-anisole complex is also a rare case where apparently the same slow intermolecular vibrational mode is demonstrated to be excited together with electronic or together with a suitable high-frequency vibrational excitation. This again reflects the sensitivity of the molecular complex structure to internal excitation, and thus the strongly competing character of different intermolecular forces in determining this structure.
 | ||
| Fig. 1 Schematic Lewis structures of anisole (A) and conformational isomers of 2-naphthol (2N). The cis isomer is the global minimum conformation of 2-naphthol. | ||
2 Experimental and computational methods
2.1 FTIR jet spectroscopy
To obtain the FTIR jet spectra, two different versions of the heatable “popcorn-jet” setup were used (hereafter referred to as “old”19 and “new”31). In both cases, a stream of helium (Linde, 99.996%) was first seeded with anisole (Fluka, 99%) molecules in a saturator tempered to 0–20 °C (273–293 K) and then led into a 69 L reservoir at a stagnation pressure of 1.5 bar. Afterwards, the gas mixture was directed through a heatable chamber which contained the less volatile 2-naphthol (Merck, 99%), deposited on molecular sieve and heated to 115–120 °C (388–393 K), and was enclosed by two individually heatable poppet valves. The gas mixture was subsequently expanded in pulses through a slit nozzle. Further details on the measurement conditions can be found in the ESI.† In the old setup (spectra (i), (ii), (a), and (b) in Fig. 3), a straight double 0.5 × 10 mm2 slit nozzle was used with a pulse length of 316 ms and an opening pressure of the poppet valves of 690 mbar. The new setup (spectra (c) and (d) in Fig. 3) features an individually heatable single 162° angled 0.2 × 60 mm2 slit nozzle with a shortened pulse length of 200 ms and a reduced opening pressure of 350 mbar. In both versions of the setup, a 3.6 m3 buffer volume that is permanently evacuated by three consecutive vacuum pumps with a total pumping speed of 500 m3 h−1 ensured a sufficiently low background pressure during expansions. The FTIR spectra (in both versions one double-sided interferogram scan per pulse) were recorded perpendicular to the expansion direction by a Bruker IFS 66 v/S spectrometer containing a ceramic glower as light source, a KBr beamsplitter and CaF2 optics. A resolution of 2 cm−1 was achieved.In ref. 31, the main advantages of the new setup and differences to the previous setup have already been discussed in detail. The comparison of spectra recorded with the old (a and b) and new (c and d) setup in Fig. 3 nicely illustrates the overall signal enhancement achieved through the increased absorption path length in combination with the reduced opening pressure of the poppet valves. In essence, the new setup can produce more useful spectra despite the shortened pulse length and the partially lower temperature and thus lower substance concentration.
2.2 UV and IR-UV jet spectroscopy
Anisole (Sigma-Aldrich, 99.7%) and 2-naphthol (Sigma-Aldrich, 99%) were purchased and used without further purification. The supersonic expansion was obtained by expanding helium at a pressure of 4 bar through a 200 μm pulsed nozzle (General Valve). The carrier gas was seeded with 2-naphthol heated at 120 °C (393 K) and room-temperature anisole. Mass-resolved S1 ← S0 spectra were obtained by one-colour resonance-enhanced multiphoton ionisation (1c-REMPI). Molecules were excited by a tunable frequency-doubled dye laser (Sirah 0.02 cm−1 resolution) that was pumped by a Nd:YAG laser (Quanta Ray, Spectra Physics). The ions were detected by a microchannel plate detector (RM Jordan, 25 mm) mounted on top of a 1 m linear time-of-flight mass spectrometer (RM Jordan, Wiley-McLaren type). Fluorescence excitation spectra were obtained by collecting the fluorescence by a two-mirror system composed of a toroidal mirror and a rotating planar mirror. The emitted light was focused on the entrance slit of a 25 cm monochromator (Huet M25) used under broadband conditions (∼20 nm resolution) and was detected by a photomultiplier tube (PMT, Hamamatsu R2059).10 The ion or the PMT signal was averaged by an oscilloscope (Lecroy wavesurfer) and processed through a personal computer.The vibrational spectra were obtained resorting to the IR-UV double resonance technique,2 using either ion or fluorescence detection.32–35 To this end, two counter-propagating lasers were focused by a 500 mm focal length lens on the cold region of the supersonic expansion. The UV laser wavelength was fixed on a transition of a given conformer, while the IR laser was scanned in the region of the O–H and C–H stretch modes. An active baseline subtraction procedure was used to monitor the IR absorption by measuring the signal difference produced by successive UV laser pulses (one without and one with the IR laser present). The tunable IR source was a tabletop IR Optical Parametric Oscillator/Amplifier (OPO/OPA, LaserVision) with 3 cm−1 resolution. The synchronisation between the lasers was performed by a computer-controlled home-made gate generator.
The IR-UV spectra were calibrated in the wavenumber domain against an atmospheric water reference using a linear calibration function ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) cal = 0.98677
cal = 0.98677![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) + 55.37389 cm−1. To convert from air to vacuum, the calibrated wavenumbers were subsequently divided by n = 1.000273 which is valid between 2.5 and 3.0 μm (from https://refractiveindex.info/, based on ref. 36). To convert the UV spectra into the wavenumber domain (
+ 55.37389 cm−1. To convert from air to vacuum, the calibrated wavenumbers were subsequently divided by n = 1.000273 which is valid between 2.5 and 3.0 μm (from https://refractiveindex.info/, based on ref. 36). To convert the UV spectra into the wavenumber domain (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) −1 = nλ), we used n = 1 + 0.05792105·(238.0185 − [λ/μm]−2)−1 + 0.00167917·(57.362 − [λ/μm]−2)−1 (from https://refractiveindex.info/, based on ref. 37).
−1 = nλ), we used n = 1 + 0.05792105·(238.0185 − [λ/μm]−2)−1 + 0.00167917·(57.362 − [λ/μm]−2)−1 (from https://refractiveindex.info/, based on ref. 37).
2.3 Conformer searches
Informed by the structures of related anisole complexes with aliphatic or aromatic hydroxy compounds (ref. 20, 21 and unpublished data), chemical intuition was used to generate different start structures and explore the conformational landscape of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex between cis/trans-2-naphthol and anisole. Initial geometries were constructed with GaussView and pre-optimised with Gaussian 09 Rev. D.0138 at the B97-D/TZVP level.39,40 Unique configurations that remained after pre-optimisation were subsequently optimised at the B3LYP-D3abc (BJ)/def2-TZVP level with TURBOMOLE 7.0.41–43 The absence of imaginary harmonic frequencies was taken as an indication for a (local) minimum on the multi-dimensional potential energy surface.
1 complex between cis/trans-2-naphthol and anisole. Initial geometries were constructed with GaussView and pre-optimised with Gaussian 09 Rev. D.0138 at the B97-D/TZVP level.39,40 Unique configurations that remained after pre-optimisation were subsequently optimised at the B3LYP-D3abc (BJ)/def2-TZVP level with TURBOMOLE 7.0.41–43 The absence of imaginary harmonic frequencies was taken as an indication for a (local) minimum on the multi-dimensional potential energy surface.
To independently check that no relevant structures were missed, we utilised the CREST program (Conformer-Rotamer Ensemble Sampling Tool).44,45 Using the recommended “-nci” option for non-covalently bound complexes, the four geometries from Fig. 2 were provided as initial start structures and the resulting configurations (within E − Emin ≤ 25.1 kJ mol−1) were again optimised at the B3LYP-D3abc(BJ)/def2-TZVP level, this time using ORCA 5.0.3.46–48 Rewardingly, this second search did not reveal any new relevant structures. For consistency, all final DFT geometries utilised in this work were re-optimised with ORCA 5.0.3.
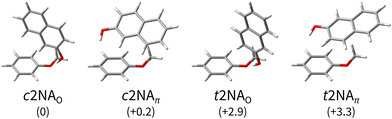 | ||
Fig. 2 Computed minimum-energy structures of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes between 2-naphthol (2N) and anisole (A). The 2-naphthol either forms a directional hydrogen bond with a lone pair of the anisole oxygen (O) or a distorted hydrogen bond with the electron-rich benzene ring, in favour of increased dispersion interaction between 2N and A (π). The complexes are sorted by their harmonically zero-point-corrected relative energies (in kJ mol−1), as predicted at the B3LYP-D3abc(BJ)/def2-QZVP level (Table 1). 1 complexes between 2-naphthol (2N) and anisole (A). The 2-naphthol either forms a directional hydrogen bond with a lone pair of the anisole oxygen (O) or a distorted hydrogen bond with the electron-rich benzene ring, in favour of increased dispersion interaction between 2N and A (π). The complexes are sorted by their harmonically zero-point-corrected relative energies (in kJ mol−1), as predicted at the B3LYP-D3abc(BJ)/def2-QZVP level (Table 1). | ||
2.4 Employed density functionals
Density functional theory (DFT) results presented throughout this work, such as geometries, energies, and vibrational properties, were computed with two hybrid functionals, B3LYP49,50 and PBE0,51 using the so-called Karlsruhe basis sets (def2-XVP; X = S, TZ, QZ).52 In all cases, Grimme's two-body dispersion correction (D3; optionally with Axilrod–Teller–Muto three-body dispersion D3abc) and Becke–Johnson damping (BJ) were included.53,54 Throughout all DFT geometry optimisation (“VeryTightOpt”) and analytic harmonic frequency calculations (“Freq Mass2016”), very strict thresholds were used (“DefGrid3 VeryTightSCF NoRI NoCosX”).46–482.5 DLPNO and PNO single-point energy calculations
To obtain more accurate relative energy predictions beyond dispersion-corrected DFT, we used DFT-optimised reference geometries to compute frozen-core single-point electronic energies at the second-order Møller–Plesset (MP2 and its spin-component-scaled variant SCS-MP255) and the coupled-cluster singles, doubles, perturbative triples (CCSD(T)) level.To expedite the calculations and achieve near-convergence with respect to the one-particle basis, their local (pair natural orbitals, PNO) and explicitly correlated (F12) variants were used,56,57 as implemented in MOLPRO 2021.358,59 and ORCA 5.0.3.47,48 The PNO implementation in ORCA is referred to as DLPNO which stands for “domain based local pair natural orbital”.
Strict thresholds ensured minimal errors on the relative energies due to the localisation approximations (“DomOpt = Tight PairOpt = Tight” for Molpro; “TightSCF TightPNO” for ORCA). In these correlated calculations, Dunning's augmented correlation-consistent basis sets (aug-cc-pVXZ; aVXZ) and their non-augmented F12 (cc-pVXZ-F12; VXZ-F12) variants by Peterson et al. were utilised from aVDZ up to VQZ-F12.60,61
3 Survey of the conformational landscape
There are two stable conformers of 2-naphthol (Fig. 1), t2N and c2N, which are separated by a barrier of ∼15 kJ mol−1 (from the lower-energy c2N well) with a relative energy difference of ∼2 kJ mol−1. These values are computational predictions at the B3LYP-D3(BJ)/def2-TZVP level, including harmonic zero-point vibrational corrections, that were recently published by Hazrah et al.62 The relative energy between c2N and t2N has been estimated to be ∼1.7 kJ mol−1,63 although this value must be taken with caution. (Prior, Hollas and bin Hussein estimated a similar value,64 providing error bars of ±0.6 kJ mol−1.) To the best of our knowledge, no experimental value of the barrier has been published so far.In view of the high interconversion barrier between t2N and c2N and the relatively small cis–trans energy difference that leads to significant amounts of the higher-energy t2N conformer in the stagnation region, one may argue that there is no major complexation-assisted trans–cis relaxation during expansion (vide infra), thus leading to the formation of c2NA and t2NA complexes according to the monomeric free energy difference at the stagnation temperature. We, therefore, define the dissociation energy D′ as
| D′[x2NA] = E[A] + E[x2N] − E[x2NA] ∀x ∈ {c,t} | (1) |
As expected,20,21 there are two main bonding motifs predicted by the calculations (Fig. 2): one hinge-like structure where a rather directional, ‘classical’ O–H⋯O hydrogen bond between 2N and a lone pair of the anisole oxygen atom is formed (2NAO) and one where a distorted O–H⋯π hydrogen bond to the benzene ring of anisole is realised along with increased dispersion interactions between the molecular planes (2NAπ). Other 2NA conformers found in the conformer search that are within a few kJ mol−1 above the minimum exhibit these two bonding motifs where only the relative 2N and A orientations slightly differ. Other than in the anisole or 1-naphthol homodimers,11,65 the π−π stacked motif is predicted to be unfavourable in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 2NA complex; the conformer searches did not yield a stable conformation. For the moment, we note that the hydrogen bond preference, π or oxygen lone pair, sensitively depends on the employed density functional, basis set, and inclusion of three-body dispersion (abc). These effects are quantified in more detail later (Section 6).
1 2NA complex; the conformer searches did not yield a stable conformation. For the moment, we note that the hydrogen bond preference, π or oxygen lone pair, sensitively depends on the employed density functional, basis set, and inclusion of three-body dispersion (abc). These effects are quantified in more detail later (Section 6).
At the B3LYP-D3abc(BJ)/def2-QZVP level, both bonding motifs are predicted to be very close in energy, well within 1 kJ mol−1. We would, therefore, anticipate to observe at least four signals in the OH stretching spectra that correspond to c2NAO, c2NAπ, t2NAO, and t2NAπ. Their key electronic and (double harmonic) vibrational OH stretching properties at this level are summarised in Table 1. Based on the computed harmonic complexation shifts of the OH stretch, we anticipate to be able to easily distinguish between all four complexes via their spectroscopic signature in the OH stretching range (Table 1).
4 Analysis of the jet-cooled OH stretching spectra
4.1 FTIR spectra
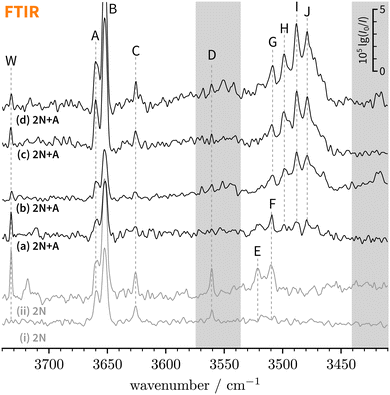 | ||
| Fig. 3 FTIR decadic absorbance spectra (lg(I0/I)) of bare 2-naphthol expansions (i and ii, grey) and 2-naphthol and anisole co-expansions (a–d, black) with varying concentrations and water content. An extended version covering a broader spectral range can be found in the ESI† (Fig. S1). The overall signal enhancement from traces (a)–(d) illustrates the extended absorption path length in the new setup.31 Note that bands F and G partially overlap (see Section 4.1.2). | ||
E and F clearly correspond to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 2-naphthol hydrates as they are absent in spectrum (i) which has the lowest water concentration – the extent of water contamination can be assessed by the ro-vibrational lines of the antisymmetric water stretching vibration, labelled “W”.67 The vibrational signatures of 2-naphthol hydrates were previously characterised by Schütz et al.68 and Matsumoto et al.66 and the new band centres agree within the experimental resolution with previously reported values (cf.Table 2).
1 2-naphthol hydrates as they are absent in spectrum (i) which has the lowest water concentration – the extent of water contamination can be assessed by the ro-vibrational lines of the antisymmetric water stretching vibration, labelled “W”.67 The vibrational signatures of 2-naphthol hydrates were previously characterised by Schütz et al.68 and Matsumoto et al.66 and the new band centres agree within the experimental resolution with previously reported values (cf.Table 2).
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0, in cm−1) of 2-naphthol monomers and clusters (2N), 2-naphthol hydrates (2NW), and 2-naphthol-anisole complexes (2NA). Note that bands F and G partially overlap (see Section 4.1.2)
0, in cm−1) of 2-naphthol monomers and clusters (2N), 2-naphthol hydrates (2NW), and 2-naphthol-anisole complexes (2NA). Note that bands F and G partially overlap (see Section 4.1.2)
| FTIR | IR-UV | IR-UV | Assignment | |
|---|---|---|---|---|
| Label |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0
0
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0
0
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0 (ref. 66)
0 (ref. 66) |
|
| A | 3659 | 3660 | 3661 | t2N |
| B | 3652 | 3653 | 3654 | c2N |
| C | 3626 | (2N)2 | ||
| D | 3560 | (2N)≥3 | ||
| E | 3521 | 3523 | t2NW | |
| F | 3510 | 3512 | c2NW | |
| G | 3509 | 3509 | c2NAO | |
| H | 3498 | 3499 | c2NAO | |
| I | 3488 | 3489 | c2NAO | |
| 3486 | t2NAO | |||
| J | 3479 | 3479 | t2NAO | |
Lastly, C and D can be ascribed to clusters of 2-naphthol; on the basis of their scaling behaviour with increased 2-naphthol concentration (see ESI,† Fig. S1(iii)), we ascribe C to a homodimer whereas D corresponds to a larger, presumably trimeric, cluster. To the best of our knowledge, vacuum-isolated clusters of 2-naphthol have so far not been spectroscopically investigated. The comparably small red-shift of C indicates that no classical hydrogen bond is formed. Explorative quantum chemical searches of the conformational landscape (not shown) further indicate dominant π−π contributions to the binding energy, quite similar to the experimentally-characterised homodimers of 1-naphthol11,69 and 2-naphthalenethiol,70 a heavier homologue of 2N. We refrain from assigning C to a particular dimeric 2N conformer which is not possible based on vibrational frequencies alone.11
It is worth mentioning that under similar conditions, only traces of the higher-energy rotamer are observed in the jet-cooled FTIR OH stretching spectrum of 1-naphthol.23 This can be ascribed to the nearly two-fold smaller cis–trans energy difference in 2-naphthol62 which leads to a higher initial population of the higher-energy rotamer than in 1-naphthol.
Turning now to mixed complexes, the question of relative abundance and visibility of t and c isomers arises. Assuming the same abundance ratio as for monomers, the c isomers will dominate. Anisole as a binding partner does not switch this energetic preference but rather seems to enhance it somewhat (Table 1). Based on spectral intensities in Table 1, O-bound isomers will generally be more visible than π-bound isomers. We thus do not expect to observe t2NAπ which is predicted somewhere between bands C and D. However, the OH stretch of t2NAO is predicted to considerably gain in intensity relative to t2N. Furthermore, it is consistently predicted to be 1.6–2 times more visible than that of c2NAO (all twelve combinations of B3LYP, PBE0, D3(BJ), D3abc(BJ), def2-SVP, def2-TZVP, def2-QZVP). Thus, we would anticipate to also observe t2NAO with a relative t2NAO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c2NAO intensity ratio between 2
c2NAO intensity ratio between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 1
3 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, if complexation-induced trans–cis relaxation is negligible. The latter assumption may not hold quantitatively. The energy freed upon complexation is in principle enough to induce thermal isomerisation even in a supersonic jet expansion.16,74,75 Such processes are still poorly understood, unlike corresponding laser-induced processes.76,77 Therefore, partial relaxation of t2NAO to the further solvent-stabilised c2NAO should not be strictly ruled out but is unlikely to be quantitative.
3, if complexation-induced trans–cis relaxation is negligible. The latter assumption may not hold quantitatively. The energy freed upon complexation is in principle enough to induce thermal isomerisation even in a supersonic jet expansion.16,74,75 Such processes are still poorly understood, unlike corresponding laser-induced processes.76,77 Therefore, partial relaxation of t2NAO to the further solvent-stabilised c2NAO should not be strictly ruled out but is unlikely to be quantitative.
Overall, there are three main new absorption regions that correspond to mixed 2-naphthol-anisole clusters in Fig. 3(a–d). They are highlighted through two grey bars and the white space in-between. The main absorption feature in-between is observed even in the lowest-concentrated spectrum (a) whereas the features in the grey bars seem to be correlated. Because the signals on the right (near 3400 cm−1) appearing in higher-concentration spectra (b) and (d) are likely due to trimeric or larger aggregates, this could also be the case on the left (near 3550 cm−1), close to D marking 2N homocluster traces, where c2NAπ would be expected at low intensity. The same applies to the even less abundant and visible t2NAπ, which is expected near 3600 cm−1. In search of π-bound 2NA complexes, we tried to optimise the expansion conditions to maximise the new signals around D (left grey bar) while keeping the formation of trimers or higher clusters minimal (right grey bar), which proved to be difficult. All in all, one can at best derive upper bounds for π-bound 2NA complexes in the FTIR jet spectra and these bounds will not be very tight due to the smaller IR visibility of π-bound 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes in the OH stretching region (Table 1). We return to the analysis in Section 6 and focus on the more conclusive O-bound absorption features in-between the grey bars for the remainder of this section.
1 complexes in the OH stretching region (Table 1). We return to the analysis in Section 6 and focus on the more conclusive O-bound absorption features in-between the grey bars for the remainder of this section.
Within the broad absorption around 3500 cm−1, which roughly spans 60 cm−1, there are several distinguishable peaks that we label G–J. Due to the presence of water impurities in the jet spectra, one might argue that G is not a new 2-naphthol-anisole band but actually a 2-naphthol hydrate signal (F, see Table 2). This is to a large extent the case for spectrum (a) but not (b) which displays only negligible amounts of water. By extension, this argument applies to spectra (c) and (d) where G, H, and I exhibit a similar intensity scaling ratio as in (b). Similarly, we can exclude anisole hydrates as possible origins.78 While the overall broad absorption may well include contributions from trimeric or larger 2-naphthol-anisole clusters, we are cautiously optimistic that peaks H–J correspond to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes as they persist in spectrum (a). Therefore, this argument similarly applies to G. On the basis of the computed complexation shifts of different 2NA conformers (Table 1) and known shifts of similar O–H⋯O hydroxy compound-anisole 1
1 complexes as they persist in spectrum (a). Therefore, this argument similarly applies to G. On the basis of the computed complexation shifts of different 2NA conformers (Table 1) and known shifts of similar O–H⋯O hydroxy compound-anisole 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes (phenol −174 and 1-naphthol −197 cm−1, ref. 23), G–J are plausible candidates for c2NAO and t2NAO. But if this were the case, we would at most expect two signals in this spectral region and not four or more.
1 complexes (phenol −174 and 1-naphthol −197 cm−1, ref. 23), G–J are plausible candidates for c2NAO and t2NAO. But if this were the case, we would at most expect two signals in this spectral region and not four or more.
Left with three plausible explanations to account for the excessive number of persistent absorption features in Fig. 3(a–d) – conformational richness of 2NA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, larger clusters, or spectral transitions beyond the standard double harmonic oscillator selection rules –, we recorded jet-cooled conformer- and mass-selective IR-UV double-resonance spectra to gain clarity. In view of the last possibility, it should be noted that the absorption features near D exhibit a similarly regular pattern of near-evenly spaced bands.
1 complexes, larger clusters, or spectral transitions beyond the standard double harmonic oscillator selection rules –, we recorded jet-cooled conformer- and mass-selective IR-UV double-resonance spectra to gain clarity. In view of the last possibility, it should be noted that the absorption features near D exhibit a similarly regular pattern of near-evenly spaced bands.
4.2 REMPI and IR-UV spectra
4.3 The 2-naphthol-anisole spectrum
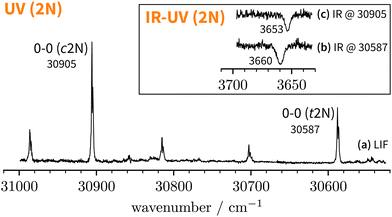
Since the UV spectrum of the 2-naphthol-anisole complex had not been measured before, we first explored the UV region using mass detection (REMPI), then switching to fluorescence detection (LIF). The one-colour REMPI spectrum obtained by monitoring the 2NA mass channel is shown in Fig. 5.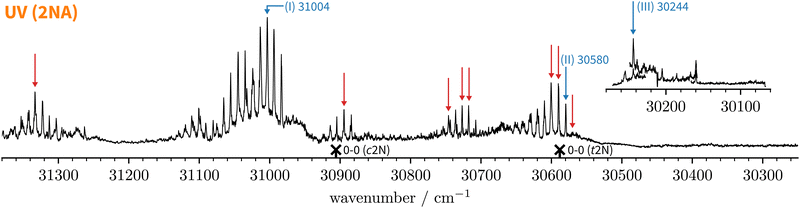 | ||
Fig. 5 Normalised one-colour REMPI spectrum of the jet-cooled co-expansion of 2-naphthol and anisole monitored at the 2NA mass channel (252 amu). The 0-0 band positions of the S1 ← S0 transitions of c2N and t2N are shown for reference (crosses). The normalised LIF spectrum below 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 cm−1 is shown as an inset. Blue arrows mark selected S1 ← S0 transitions where IR-UV double-resonance spectra were recorded (see Fig. 6). Red arrows mark all S1 ← S0 bands that were checked to exhibit the same IR spectrum as bands (I) and (II). 280 cm−1 is shown as an inset. Blue arrows mark selected S1 ← S0 transitions where IR-UV double-resonance spectra were recorded (see Fig. 6). Red arrows mark all S1 ← S0 bands that were checked to exhibit the same IR spectrum as bands (I) and (II). | ||
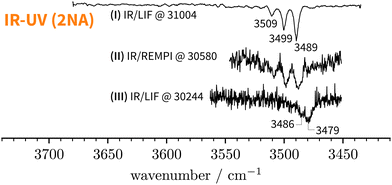
Starting above 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, the REMPI spectrum exhibits several UV band systems. All the main electronic band systems exhibit a vibronic Franck–Condon progression built on a 10 cm−1 mode. By probing these UV band systems – blue arrows (I and II) and red arrows in Fig. 5 – with IR-UV double-resonance spectroscopy, it was revealed that all observed band systems correspond to only one conformer. The IR-UV spectra of this species are shown in Fig. 6. (II) was measured using mass detection and (I) using fluorescence detection to improve the signal-to-noise ratio. These spectra clearly exhibit three IR bands, at 3489, 3499, and 3509 cm−1, which are again separated by 10 cm−1. The three band centres match the FTIR band positions of I, H, and G, respectively (cf.Table 2).
500 cm−1, the REMPI spectrum exhibits several UV band systems. All the main electronic band systems exhibit a vibronic Franck–Condon progression built on a 10 cm−1 mode. By probing these UV band systems – blue arrows (I and II) and red arrows in Fig. 5 – with IR-UV double-resonance spectroscopy, it was revealed that all observed band systems correspond to only one conformer. The IR-UV spectra of this species are shown in Fig. 6. (II) was measured using mass detection and (I) using fluorescence detection to improve the signal-to-noise ratio. These spectra clearly exhibit three IR bands, at 3489, 3499, and 3509 cm−1, which are again separated by 10 cm−1. The three band centres match the FTIR band positions of I, H, and G, respectively (cf.Table 2).
 | ||
| Fig. 6 IR-UV double-resonance spectra at selected S1 ← S0 transitions of 2NA (see Fig. 5). | ||
The conformer-selectivity of IR-UV double-resonance spectroscopy only leaves two possible explanations for the two surplus bands. Either the measured ion intensity corresponds to ionic 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 2-naphthol-anisole complexes that fragmented from larger clusters or the neutral 1
1 2-naphthol-anisole complexes that fragmented from larger clusters or the neutral 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex gives rise to more than one IR signal in the OH stretching range due to anharmonic effects. The former can be excluded for two main reasons. First, the preceding analysis of the FTIR spectra makes a mixed trimeric, let alone tetrameric, assignment for these three IR bands highly unlikely. Second, if more than one 2-naphthol were in the complex, we would either expect at least one band near(er) to the OH stretching band of bare 2-naphthol due to weaker O–H⋯π hydrogen bonds (or dangling OH groups) or at least one much more shifted IR band due to cooperativity effects since all OH groups would form O–H⋯O hydrogen bonds.
1 complex gives rise to more than one IR signal in the OH stretching range due to anharmonic effects. The former can be excluded for two main reasons. First, the preceding analysis of the FTIR spectra makes a mixed trimeric, let alone tetrameric, assignment for these three IR bands highly unlikely. Second, if more than one 2-naphthol were in the complex, we would either expect at least one band near(er) to the OH stretching band of bare 2-naphthol due to weaker O–H⋯π hydrogen bonds (or dangling OH groups) or at least one much more shifted IR band due to cooperativity effects since all OH groups would form O–H⋯O hydrogen bonds.
With the main UV band systems in Fig. 5 assigned to 2NA, we can determine the relative orientation of the 2-naphthol hydroxy group (cis or trans) and the hydrogen bond motif (O–H⋯O or O–H⋯π) based on the UV and IR-UV spectra alone. This facilitates the discrimination of the four predicted 2NA complexes purely experimentally (Fig. 2). The magnitude of the OH stretch shift upon complexation is indicative of an O–H⋯O hydrogen bond and quantitatively matches previously measured complexation shifts of phenol-anisole and 1-naphthol-anisole.23 Based on the complexation-induced UV shift, we can discriminate between c2NAO and t2NAO as the electronic S1 ← S0 transition is a much more sensitive probe to the 2-naphthol conformation (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 and 30
905 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587 cm−1) than the OH stretch fundamental in the S0 state (3653 and 3660 cm−1). The several vibronic Franck–Condon progressions in Fig. 5 complicate a precise assignment of the 0-0 band origin which we approximately locate at 30
587 cm−1) than the OH stretch fundamental in the S0 state (3653 and 3660 cm−1). The several vibronic Franck–Condon progressions in Fig. 5 complicate a precise assignment of the 0-0 band origin which we approximately locate at 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 550 cm−1. If we assign it to c2NAO, the resulting UV shift relative to c2N is approximately −350 cm−1. If referenced to t2N instead, the shift is about −50 cm−1. The suspected assignment to c2NAO can be confirmed by comparing to the UV shifts of 1
550 cm−1. If we assign it to c2NAO, the resulting UV shift relative to c2N is approximately −350 cm−1. If referenced to t2N instead, the shift is about −50 cm−1. The suspected assignment to c2NAO can be confirmed by comparing to the UV shifts of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes with a similar connectivity and bonding motif. The UV shift of anisole-phenol82 amounts to −352 cm−1 and 1
1 complexes with a similar connectivity and bonding motif. The UV shift of anisole-phenol82 amounts to −352 cm−1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrates66 of cis- and trans-2-naphthol exhibit similar shifts of −371 and −332 cm−1. Even the π−π stacked 1-naphthol69 and anisole83 homodimers show similarly large red shifts. This purely experimental assignment to c2NAO is in agreement with quantum chemical calculations that predict this conformer to be the global minimum structure (Table 1). It is worth noting that the observed vibrational spacing of 10 cm−1 in the electronic ground state (Fig. 6) effectively matches the UV fine structure of several observed Franck–Condon bands in the first excited electronic state (Fig. 5), indicating that the potential of the involved intermolecular vibrational mode is similar in the S0 and S1 states and rather harmonic.
1 hydrates66 of cis- and trans-2-naphthol exhibit similar shifts of −371 and −332 cm−1. Even the π−π stacked 1-naphthol69 and anisole83 homodimers show similarly large red shifts. This purely experimental assignment to c2NAO is in agreement with quantum chemical calculations that predict this conformer to be the global minimum structure (Table 1). It is worth noting that the observed vibrational spacing of 10 cm−1 in the electronic ground state (Fig. 6) effectively matches the UV fine structure of several observed Franck–Condon bands in the first excited electronic state (Fig. 5), indicating that the potential of the involved intermolecular vibrational mode is similar in the S0 and S1 states and rather harmonic.
To summarise, the overwhelming majority of observed UV signals in the jet-cooled REMPI spectrum (Fig. 5) correspond to c2NAO. By employing size- and conformer-selective IR-UV spectroscopy, we could confirm that the FTIR bands G, H, and I all correspond to c2NAO. We did not find evidence for the c2NAπ complex, which is predicted by harmonically zero-point-corrected DFT to be near-isoenergetic, leaving the origins of the FTIR absorption features around D (left grey panel in Fig. 3) unclear. The absence of π-bound 2NA conformers in the UV spectra is not a conclusive proof of their absence in the jet expansion but could be attributed to rapid isomerisation to c2NAO, rapid dissociation, or – rather unlikely – very small UV absorption cross sections.
Lastly, we must address the assignment of the FTIR band J at 3479 cm−1 which, based on its high intensity and scaling behaviour, most likely corresponds to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. t2NAO is the obvious choice. Based on the complexation-induced UV shift of c2NAO, the 0-0 band of t2NAO is expected around 30
1 complex. t2NAO is the obvious choice. Based on the complexation-induced UV shift of c2NAO, the 0-0 band of t2NAO is expected around 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1. The REMPI spectrum in Fig. 5, however, does not provide evidence for a t2NA complex. This is probably due to the fact that the photon energy is too low for ionising the complex below ∼30
250 cm−1. The REMPI spectrum in Fig. 5, however, does not provide evidence for a t2NA complex. This is probably due to the fact that the photon energy is too low for ionising the complex below ∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. Indeed, the ionisation energy of bare 2-naphthol is 63
500 cm−1. Indeed, the ionisation energy of bare 2-naphthol is 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 for c2N and 63
670 for c2N and 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 189 cm−1 for t2N.63 Even if one considers the decrease of the ionisation energy upon complexation, it is possible that at 30
189 cm−1 for t2N.63 Even if one considers the decrease of the ionisation energy upon complexation, it is possible that at 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 – the low-energy limit of the UV spectrum obtained by REMPI –, the photon energy is not sufficient for ionising the system. Therefore, we recorded the S1 ← S0 spectrum in the same region using LIF. Normalised LIF spectra that cover the relevant spectral range are shown as an inset in Fig. 5. We measured the IR-UV double-resonance spectrum by setting the probe on the UV band at 30
300 cm−1 – the low-energy limit of the UV spectrum obtained by REMPI –, the photon energy is not sufficient for ionising the system. Therefore, we recorded the S1 ← S0 spectrum in the same region using LIF. Normalised LIF spectra that cover the relevant spectral range are shown as an inset in Fig. 5. We measured the IR-UV double-resonance spectrum by setting the probe on the UV band at 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 244 cm−1 which is shown in Fig. 6(III). The OH stretching band exhibits a broad dip that appears to consist of several overlapping bands with a ‘maximum’ at 3479 cm−1. The band centre is in very good agreement with the FTIR band centre of J. Moreover, it appears that the perturbations in c2NAO that give rise to additional IR bands are similarly present in t2NAO, albeit with a decreased splitting. The third member in the progression is not well resolved in Fig. 6(III) but appears to be roughly centred at 3493 cm−1. Indeed, there is an additional peak between the FTIR bands H and I at 3495 cm−1 close to the noise level which can best be seen in Fig. 3(a) and (c), providing further evidence that also t2NAO gives rise to (at least) three IR bands in the OH stretching range.
244 cm−1 which is shown in Fig. 6(III). The OH stretching band exhibits a broad dip that appears to consist of several overlapping bands with a ‘maximum’ at 3479 cm−1. The band centre is in very good agreement with the FTIR band centre of J. Moreover, it appears that the perturbations in c2NAO that give rise to additional IR bands are similarly present in t2NAO, albeit with a decreased splitting. The third member in the progression is not well resolved in Fig. 6(III) but appears to be roughly centred at 3493 cm−1. Indeed, there is an additional peak between the FTIR bands H and I at 3495 cm−1 close to the noise level which can best be seen in Fig. 3(a) and (c), providing further evidence that also t2NAO gives rise to (at least) three IR bands in the OH stretching range.
5 The split OH stretching band of c2NAO
The experimental analysis in the preceding section unequivocally showed that the OH stretch fundamental of c2NAO in the electronic ground state is split into three (possibly more but less visible) evenly spaced (i.e. within the resolution uncertainty) bands at 3488, 3498, and 3509 cm−1 with decreasing intensity. The similarity of the IR-UV and FTIR intensity pattern rules out hot band interpretations. In increasing wavenumber, we assign them to νOH – the pure OH stretch fundamental –, νOH+νinter, and νOH+2νinter. νinter is an intermolecular vibrational mode with a fundamental wavenumber of approximately 10 cm−1 which is promoted by OH stretch excitation in the same way in which it is promoted by electronic excitation (Fig. 5), namely structural change along the mode in higher-energy states of the complex.Based on the experimental separation of 10 cm−1, the harmonic wavenumber of a suitable vibrational coupling partner should ideally be slightly larger than 10 cm−1 to leave room for some (diagonal) anharmonicity. To get a feeling for the numerical sensitivity of the low-frequency vibrations, we compared several different DFT calculations (all eight combinations of B3LYP, PBE0, D3(BJ), D3abc(BJ), def2-TZVP, def2-QZVP). Very strict SCF and geometry optimisation thresholds and large DFT grids ensured numerical stability (see Section 2.4). In all these calculations, two intermolecular normal modes are consistently predicted below 20 cm−1, which we label ν101 and ν102 following the nomenclature by Herzberg.84Fig. 7 shows that the second-lowest vibration (ν101, 11–14 cm−1) is a plausible candidate as it modulates the O–H⋯O hydrogen bond angle in a seesaw-like movement of the anisole.85 This hydrogen bond angle, in turn, will likely be stiffened when the OH stretch is excited and gains in dipole moment. As a result, OH stretch intensity is redistributed to the intermolecular combination bands in a vibrational Franck–Condon fashion.25–30 In first approximation, the total intensity of this progression should be compared to the harmonic intensity predicted for the OH stretch. In the adiabatic picture, the intensity pattern can be rationalised through the squared wavefunction overlap of different ninter states – the ‘slow’ mode – between the adiabatic nOH = 0 and nOH = 1 potentials which take the roles of the ground and excited electronic Born–Oppenheimer potentials in vibronic Franck–Condon theory. Dropping the adiabatic approximation in combination with realistic electric dipole surfaces may introduce further effects.86 Studies along the lines of ref. 30, where only the relevant vibrational degrees of freedom are retained, could provide instructive insights into the vibrational couplings, complementing the adiabatic picture.
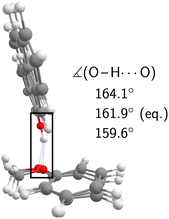 | ||
| Fig. 7 Equilibrium geometry of c2NAO at the B3LYP-D3abc(BJ)/def2-QZVP level superimposed with normal mode displacements in opposing directions along ν101 which modulates the O–H⋯O angle. | ||
6 To π or not to π?
The preceding analysis of the FTIR and IR-UV spectra showed that the O–H⋯O-bound 2NA complex is formed in the jet expansions and in both conformers, c2NAO and t2NAO, the S0 OH stretch fundamental is found to exhibit a Franck–Condon-like progression.It remains to be addressed if the π-bound 2NA complex is formed in the FTIR jet expansion but perhaps concealed by other spectral contributions. For this purpose, we will investigate experimental uncertainty and computational error sources in the following.
6.1 Assessment of experimental uncertainty sources
There are essentially three uncertainties, preventing the accurate FTIR estimation of a reliable c2NAπ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c2NAO concentration ratio.
c2NAO concentration ratio.
Firstly, the three OH stretch bands of c2NAO are superimposed by other absorption features, most notably the J band, preventing the determination of reliable experimental band integrals.
Secondly, and most importantly, it is unclear where c2NAπ is spectrally located. Moreover, in view of the previously confirmed Franck–Condon-like progression in c2NAO and t2NAO, this begs the question if similarly the already weakly IR-active OH stretch of c2NAπ is affected. Indeed, we noted earlier that the band system around D in Fig. 3(b) could plausibly correspond to c2NAπ. By closely comparing the scaling behaviour of bands C and D from spectrum (a) through to (c), we can infer that the absorption feature at 3561 cm−1 in spectrum (b) only partially corresponds to a 2-naphthol homodimer (band D). Its spacing to the two neighbouring bands at 3570 and 3552 cm−1 is about 9 cm−1. A similar vibrational Franck–Condon progression in c2NAπ thus appears feasible.
Thirdly, even if reliable band integrals of c2NAπ and c2NAO could be obtained, there is a sizeable variation in their predicted band strength ratio from 0.21 to 0.47 (all eight combinations of B3LYP, PBE0, D3(BJ), D3abc(BJ), def2-TZVP, def2-QZVP), emphasising the low and erratic visibility of the π conformer. It is particularly noteworthy that with B3LYP-D3, the band strength in the π conformer decreases by roughly 30% once subtle three-body terms are added to the two-body dispersion. Calculations with and without three-body dispersion on the respective other optimised geometry show that these are entirely geometric effects.
Depending on the computational method for band strengths and the assumed spectral spread of the c2NAπ contribution, its non-observation could still be consistent with a slight excess over c2NAO in the FTIR-probed expansions. However, a trace role of c2NAπ in relation to c2NAO is at least as likely, considering its non-observation by all explored spectral techniques. Because the driving force of hydrogen bond isomerisation is weak and the barrier rather broad, it is difficult to say whether a subtle energy penalty will result in substantial depopulation by simple carrier gas collisions or more elaborate mechanisms.16,74,75
6.2 Assessment of computational error sources
The key property we wish to obtain from quantum chemistry is the vibrational zero-point-corrected relative energy ΔEπ–O0 which consists of a purely electronic (ΔEπ–Oe) and zero-point vibrational contribtion (ΔZPVEπ–O). For positive relative energies, the O–H⋯O hydrogen bonding motif is energetically preferred.Starting with the relative harmonic ZPVE, the data in the ESI† (Table S1) show that this quantity quickly converges with respect to the basis set size. The impact of three-body dispersion and the density functional are of the order of a few 100 J mol−1. Harmonic zero-point vibrational effects persistently predict the relative stabilisation of the π over the oxygen bonding site in the 2NA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. Until now, we have completely omitted vibrational anharmonicity, by assuming ΔE0 ≈ ΔE0,h. To lowest-order, anharmonic contributions to the ZPVE can be approximated using second-order vibrational perturbation theory.87–89 The results (not shown) are not reliable due to a multitude of large-amplitude vibrations leading to imaginary anharmonic fundamentals. We do not expect the anharmonic ZPVE corrections to dominate the harmonic ones. Based on the harmonic DFT predictions in Table S1 (ESI†), we estimate a generous error bar of ±0.5 kJ mol−1 to account for the missing vibrational anharmonicity, yielding a best estimate of ΔZPVEπ–O = −(1.0 ± 0.5) kJ mol−1.
1 complex. Until now, we have completely omitted vibrational anharmonicity, by assuming ΔE0 ≈ ΔE0,h. To lowest-order, anharmonic contributions to the ZPVE can be approximated using second-order vibrational perturbation theory.87–89 The results (not shown) are not reliable due to a multitude of large-amplitude vibrations leading to imaginary anharmonic fundamentals. We do not expect the anharmonic ZPVE corrections to dominate the harmonic ones. Based on the harmonic DFT predictions in Table S1 (ESI†), we estimate a generous error bar of ±0.5 kJ mol−1 to account for the missing vibrational anharmonicity, yielding a best estimate of ΔZPVEπ–O = −(1.0 ± 0.5) kJ mol−1.
Remaining in the realm of harmonic DFT, we can study the impact of the basis size, the choice of exchange-correlation functional, and inclusion of three-body dispersion on ΔEπ–O0,h. The main results are visualised in Fig. 8, a more complete list of data can be found in the ESI† (Table S1). Starting from our initial method in the centre, i.e. B3LYP-D3abc(BJ)/def2-QZVP, the vertical deviation reflects the basis set error, the deviation to the left the impact of three-body dispersion, and the deviation to the right the influence of the exchange–correlation functional when using PBE0 instead. Both, the change from PBE0 to B3LYP and inclusion of three-body dispersion lead to a relative destabilisation of the π hydrogen bond acceptor site which agrees with the primary experimental interpretation. While the trend of the DFT calculations weakly points towards c2NAO being more stable, even at the B3LYP-D3abc(BJ)/def2-QZVP level, only a 0.2 kJ mol−1 harmonically zero-point-corrected preference of O over π is predicted.
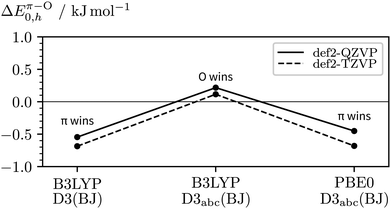 | ||
| Fig. 8 Impact of the basis size, exchange–correlation functional, and inclusion of three-body dispersion on the relative stabilities of c2NAO and c2NAπ (ΔEπ–O0,h). | ||
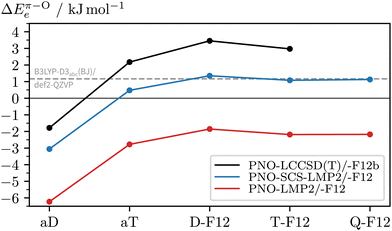
To see if there are significant electron correlation errors at the DFT-D3 level, we lastly consult PNO-coupled-cluster. As geometry optimisations are too expensive, the single-point energies are computed using the DFT equilibrium geometries. In the absence of microwave data (or other structural information) on the 2NA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, one can only speculate which DFT geometry is closest to the experimental one. One can also compare a posteriori which method gives geometries with the lowest PNO energy and should, therefore, be used in the PNO-LCCSD(T)-F12b/VDZ-F12 calculations (see Table S2, ESI†). Out of all optimised c2NAO geometries included in Fig. 8, B3LYP-D3abc(BJ)/def2-TZVP is closest to the ‘true’ coupled-cluster minimum, closely followed by B3LYP-D3abc(BJ)/def2-QZVP (+0.1 kJ mol−1) whereas the PBE0-D3abc(BJ)/def2-TZVP geometry is already 1.7 kJ mol−1 higher in energy, providing further evidence that B3LYP is structurally more reliable than PBE0 for this system. Remarkably, when instead comparing the relative energies (ΔEπ–Oe), PNO-LCCSD(T)-F12b/VDZ-F12 is found to be relatively insensitive to the reference geometry with deviations of the order of a few 100 J mol−1, the main error source being the geometry of c2NAπ. In Fig. 9, the basis set convergence of ΔEπ–Oe is examined for Møller–Plesset and coupled-cluster predictions. Additional PNO data, including dissociation energies, are reported in the ESI† (Table S2). Fig. 9 shows two things. Firstly, PNO-LCCSD(T)-F12b/VDZ-F12 unambiguously favours c2NAO over c2NAπ. The F12 approximation errors are insignificant and relative electronic energies between 3.2 and 3.5 kJ mol−1 are obtained with Molpro's PNO-LCCSD(T)-F12a and -F12b and ORCA's DLPNO-CCSD(T)-F12 and -F12D when using the VDZ-F12 basis. Secondly, PNO-LMP2 consistently overestimates the π binding site due to its well-known overestimation of dispersion effects. PNO-SCS-LMP2 significantly improves upon PNO-LMP2 but the converged relative energies are not an improvement over B3LYP-D3abc(BJ)/def2-QZVP. Inspection of the absolute complex stabilities, i.e. the dissociation energies (Tables S1 and S2, ESI†), reveals that the main deviations between PNO-LCCSD(T) and the investigated DFT-D3 functionals arise from an overestimation of the binding energy of the π-bound complex by the latter, even when three-body dispersion is included. Informed by the parallel LMP2/SCS-LMP2 basis set progression in Fig. 9, we expect a stabilisation of the O binding site slightly below 3 kJ mol−1 at the PNO-LCCSD(T) basis set limit.
1 complex, one can only speculate which DFT geometry is closest to the experimental one. One can also compare a posteriori which method gives geometries with the lowest PNO energy and should, therefore, be used in the PNO-LCCSD(T)-F12b/VDZ-F12 calculations (see Table S2, ESI†). Out of all optimised c2NAO geometries included in Fig. 8, B3LYP-D3abc(BJ)/def2-TZVP is closest to the ‘true’ coupled-cluster minimum, closely followed by B3LYP-D3abc(BJ)/def2-QZVP (+0.1 kJ mol−1) whereas the PBE0-D3abc(BJ)/def2-TZVP geometry is already 1.7 kJ mol−1 higher in energy, providing further evidence that B3LYP is structurally more reliable than PBE0 for this system. Remarkably, when instead comparing the relative energies (ΔEπ–Oe), PNO-LCCSD(T)-F12b/VDZ-F12 is found to be relatively insensitive to the reference geometry with deviations of the order of a few 100 J mol−1, the main error source being the geometry of c2NAπ. In Fig. 9, the basis set convergence of ΔEπ–Oe is examined for Møller–Plesset and coupled-cluster predictions. Additional PNO data, including dissociation energies, are reported in the ESI† (Table S2). Fig. 9 shows two things. Firstly, PNO-LCCSD(T)-F12b/VDZ-F12 unambiguously favours c2NAO over c2NAπ. The F12 approximation errors are insignificant and relative electronic energies between 3.2 and 3.5 kJ mol−1 are obtained with Molpro's PNO-LCCSD(T)-F12a and -F12b and ORCA's DLPNO-CCSD(T)-F12 and -F12D when using the VDZ-F12 basis. Secondly, PNO-LMP2 consistently overestimates the π binding site due to its well-known overestimation of dispersion effects. PNO-SCS-LMP2 significantly improves upon PNO-LMP2 but the converged relative energies are not an improvement over B3LYP-D3abc(BJ)/def2-QZVP. Inspection of the absolute complex stabilities, i.e. the dissociation energies (Tables S1 and S2, ESI†), reveals that the main deviations between PNO-LCCSD(T) and the investigated DFT-D3 functionals arise from an overestimation of the binding energy of the π-bound complex by the latter, even when three-body dispersion is included. Informed by the parallel LMP2/SCS-LMP2 basis set progression in Fig. 9, we expect a stabilisation of the O binding site slightly below 3 kJ mol−1 at the PNO-LCCSD(T) basis set limit.
Based on the estimates for the relative electronic and zero-point vibrational energies, we arrive at 1.0–3.0 kJ mol−1 for the predicted total stabilisation of c2NAO over c2NAπ at T = 0 K. It should be noted that we have entirely neglected calculated temperature effects, e.g. by comparing rigid-rotor-harmonic-oscillator Gibbs free energies ΔGπ–ORRHO,73 which are inconclusive and highly erratic. Furthermore, the complexes are believed to form and still interconvert at relatively low temperatures, other than monomers with high interconversion barriers from the start of the expansion.
7 Conclusions
When 2-naphthol complexes anisole, the orientation of its OH group may either be cis or trans and it may either form a hydrogen bond to the ether group or to the π system of anisole. Because the barrier between cis and trans is high, it is not easily overcome in a supersonic jet expansion. Experimental evidence presented in this work by FTIR and IR-UV spectroscopies is consistent with a partially frozen distribution. The hydrogen bond preference of the complex is more interesting and has been explored in this work by a combination of experimental and theoretical methods. It results from a balance of hydrogen bonding and less directional London dispersion forces between the two aromatic ring systems. Experimentally, the question has to remain open because of the strong π hydrogen bond distortion and thus weak IR intensity and because of an interesting dynamical feature in the vibrational spectrum of at least one of the isomers. We unambiguously showed that OH stretching excitation of cis-2-naphthol bound to the ether group leads to such a large change in the preferred complex geometry that it is accompanied in about 50% of all vertical transitions by the simultaneous excitation of a global scaffold vibration, which is three orders of magnitude slower. Such a Franck–Condon-type progression based on the adiabatic separation of fast and slow degrees of freedom is less frequently observed in vibrational spectroscopy than in electronic spectroscopy. However, it seems to be characteristic of the interaction between a phenol-containing molecule and an ether.27–29 For the present system, ring methylation of the anisole, as a means to stabilise the π binding site21 and to modulate the Franck–Condon progressions, appears particularly promising in view of some exploratory quantum chemical calculations.The experimental elusiveness of the π-bonded structure has triggered theoretical investigations which are indeed diverse and thus educational in terms of the quality of electronic structure methods in describing hydrogen bonds to different sites in a molecule. Popular dispersion-corrected density functional calculations close to the basis set limit with important harmonic zero-point vibrational energy corrections predict an almost perfect energy balance between the competing isomers where even three-body dispersion corrections or different hybrid density functionals switch the sign of the energy sequence. Basis-set converged wavefunction methods also span the entire range from clear π-favouring (MP2) over undecided (SCS-MP2) to clearly ether-favouring (CCSD(T)) coordination. Direct detection of the π-bound conformation by a structural method11,12 may add further insight to this subtle and demanding intermolecular energy balance. It could turn this complex into a true benchmark for electronic structure theory, in addition to its here demonstrated role as a case of vibrational excitation-induced structural change which leads to a vibrational Franck–Condon-like progression detected by both direct absorption and size- as well as conformation-selective spectroscopies.
Author contributions
Conceptualisation: AN, AZ, MAS; formal analysis: AN; funding acquisition: AZ, MAS; investigation: AN, AFPM, ML, IA; supervision: AZ, MAS; visualisation: AN; writing – original draft: AN (lead), ML, AZ, MAS; writing – review & editing: AN, AZ, MAS.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This cooperative work was supported by a France-Germany scientist exchange program by Campus France and the Deutscher Akademischer Austauschdienst (DAAD, German Academic Exchange Service) – Grant No. 37586TL (PROCOPE) and 57315059 (PPP). The topic was inspired by research projects funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Grant No. 271107160/SPP1807 (priority program on London dispersion interactions) and 389479699/GRK2455 (research training group on experimental benchmarking). Computational support includes a Göttingen chemistry computer cluster (DFG Grant No. 405832858). AN acknowledges funding by the DAAD to conduct measurements in Orsay and GRK2455 start-up funding to complete the analysis. ML acknowledges SPP1807 funding to improve the IR spectra. Discussions with and help from Dr Anja Poblotzki on the IR absorption spectroscopy and Dr Valéria Lepère on the UV/IR-UV measurements are gratefully acknowledged.Notes and references
- G. V. Hartland, B. F. Henson, V. A. Venturo and P. M. Felker, Ionization-loss stimulated Raman spectroscopy of jet-cooled hydrogen-bonded complexes containing phenols, J. Phys. Chem., 1992, 96, 1164–1173 CrossRef CAS.
- R. N. Pribble and T. S. Zwier, Size-Specific Infrared Spectra of Benzene-(H2O)n Clusters (n = 1 through 7): Evidence for Noncyclic (H2O)n Structures, Science, 1994, 265, 75–79 CrossRef CAS PubMed.
- H. W. Rohrs, C. T. Wickham-Jones, G. B. Ellison, D. Berry and B. M. Argrow, Fourier transform infrared absorption spectroscopy of jet-cooled radicals, Rev. Sci. Instrum., 1995, 66, 2430–2441 CrossRef CAS.
- T. Watanabe, T. Ebata, S. Tanabe and N. Mikami, Size-selected vibrational spectra of phenol-(H2O)n (n = 1–4) clusters observed by IR-UV double resonance and stimulated Raman-UV double resonance spectroscopies, J. Chem. Phys., 1996, 105, 408–419 CrossRef.
- H. G. Kjaergaard, D. L. Howard, D. P. Schofield, T. W. Robinson, S.-I. Ishiuchi and M. Fujii, OH- and CH-Stretching Overtone Spectra of Catechol, J. Phys. Chem. A, 2002, 106, 258–266 CrossRef CAS.
- G. Tejeda, J. M. Fernández, S. Montero, D. Blume and J. P. Toennies, Raman Spectroscopy of Small Para-H2 Clusters Formed in Cryogenic Free Jets, Phys. Rev. Lett., 2004, 92, 223401 CrossRef CAS PubMed.
- M. Hippler, L. Oeltjen and M. Quack, High-Resolution Continuous-Wave-Diode Laser Cavity Ring-Down Spectroscopy of the Hydrogen Fluoride Dimer in a Pulsed Slit Jet Expansion: Two Components of the N = 2 Triad near 1.3 μm, J. Phys. Chem. A, 2007, 111, 12659–12668 CrossRef CAS PubMed.
- M. A. Suhm and F. Kollipost, Femtisecond single-mole infrared spectroscopy of molecular clusters, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721 RSC.
- A. Potapov and P. Asselin, High-resolution jet spectroscopy of weakly bound binary complexes involving water, Int. Rev. Phys. Chem., 2014, 33, 275–300 Search PubMed.
- S. Peukert, M. Kijak, J. Ostapko, J. Sepioł, C. Le Bris, A. Zehnacker-Rentien, M. Gil and J. Waluk, Supersonic jet spectroscopy of parent hemiporphycene: structural assignment and vibrational analysis for S0 and S1 electronic states, J. Chem. Phys., 2018, 149, 134307 CrossRef PubMed.
- N. A. Seifert, A. S. Hazrah and W. Jäger, The 1-Naphthol Dimer and Its Surprising Preference for π–π Stacking over Hydrogen Bonding, J. Phys. Chem. Lett., 2019, 10, 2836–2841 CrossRef CAS PubMed.
- M. Juanes, R. T. Saragi, W. Caminati and A. Lesarri, The Hydrogen Bond and Beyond: Perspectives for Rotational Investigations of Non-Covalent Interactions, Chem. – Eur. J., 2019, 25, 11402–11411 CrossRef CAS PubMed.
- E. Gloaguen, M. Mons, K. Schwing and M. Gerhards, Neutral Peptides in the Gas Phase: Conformation and Aggregation Issues, Chem. Rev., 2020, 120, 12490–12562 CrossRef CAS PubMed.
- D. Scuderi, K. Le Barbu-Debus and A. Zehnacker, The role of weak hydrogen bonds in chiral recognition, Phys. Chem. Chem. Phys., 2011, 13, 17916–17929 RSC.
- A. Poblotzki, H. C. Gottschalk and M. A. Suhm, Tipping the Scales: Spectroscopic Tools for Intermolecular Energy Balances, J. Phys. Chem. Lett., 2017, 8, 5656–5665 CrossRef CAS PubMed.
- M. Lange, E. Sennert and M. A. Suhm, London Dispersion-Assisted Low-Temperature Gas Phase Synthesis of Hydrogen Bond-Inserted Complexes, Synlett, 2022, 33, 2004–2008 CrossRef CAS.
- N. Seurre, J. Sepioł, K. Le Barbu-Debus, F. Lahmani and A. Zehnacker-Rentien, The role of chirality in the competition between inter and intramolecular hydrogen bonds: jet-cooled van der Waals complexes of (±)2-naphthyl-1-ethanol with (±)1-amino-2-propanol and (±)2-amino-1-butanol, Phys. Chem. Chem. Phys., 2004, 6, 2867–2877 RSC.
- N. Borho, M. A. Suhm, K. Le Barbu-Debus and A. Zehnacker, Intra- vs. intermolecular hydrogen bonding: dimers of alpha-hydroxyesters with methanol, Phys. Chem. Chem. Phys., 2006, 8, 4449–4460 RSC.
- J. Altnöder, A. Bouchet, J. J. Lee, K. E. Otto, M. A. Suhm and A. Zehnacker-Rentien, Chirality-dependent balance between hydrogen bonding and London dispersion in isolated (±)-1-indanol clusters, Phys. Chem. Chem. Phys., 2013, 15, 10167–10180 RSC.
- M. Heger, J. Altnöder, A. Poblotzki and M. A. Suhm, To π or not to π – how does methanol dock onto anisole?, Phys. Chem. Chem. Phys., 2015, 17, 13045–13052 RSC.
- H. C. Gottschalk, J. Altnöder, M. Heger and M. A. Suhm, Control over the Hydrogen-Bond Docking Site in Anisole by Ring Methylation, Angew. Chem., Int. Ed., 2016, 55, 1921–1924 CrossRef CAS PubMed.
- F. BenNasr, A. Pérez-Mellor, I. Alata, V. Lepere, N.-E. Jaïdane and A. Zehnacker, Stereochemistry-dependent hydrogen bonds stabilise stacked conformations in jet-cooled cyclic dipeptides: (LD) vs. (LL) cyclo tyrosine-tyrosine, Faraday Discuss., 2018, 212, 399–419 RSC.
- A. Poblotzki, Intermolecular energy scales based on aromatic ethers and alcohols, Niedersächsische Staats- und Universitätsbibliothek Göttingen, Göttingen, 2019 DOI:10.53846/goediss-7629.
- C. Zimmermann, A. C. Dorst and M. A. Suhm, Raising the benchmark potential of a simple alcohol-ketone intermolecular balance, Phys. Chem. Chem. Phys., 2023, 25, 384–391 RSC.
- F. Lahmani, M. Broquier and A. Zehnacker-Rentien, The o-cyanophenol dimer as studied by laser-induced fluorescence and IR fluorescence dip spectroscopy: a study of a symmetrical double hydrogen bond, Chem. Phys. Lett., 2002, 354, 337–348 CrossRef CAS.
- R. Wugt Larsen, P. Zielke and M. A. Suhm, Hydrogen-bonded OH stretching modes of methanol clusters: a combined IR and Raman isotopomer study, J. Chem. Phys., 2007, 126, 194307 CrossRef PubMed.
- R. Kusaka, Y. Inokuchi, T. Haino and T. Ebata, Structures of (3n-Crown-n)-Phenol (n = 4, 5, 6, 8) Host-Guest Complexes: Formation of a Uniquely Stable Complex for n = 6 via Collective Intermolecular Interaction, J. Phys. Chem. Lett., 2012, 3, 1414–1420 CrossRef CAS PubMed.
- A. V. Zabuga, M. Z. Kamrath and T. R. Rizzo, Franck–Condon-like Progressions in Infrared Spectra of Biological Molecules, J. Phys. Chem. A, 2015, 119, 10494–10501 CrossRef CAS PubMed.
- K. Hirata, Y. Mori, S.-I. Ishiuchi, M. Fujii and A. Zehnacker, Chiral discrimination between tyrosine and β-cyclodextrin revealed by cryogenic ion trap infrared spectroscopy, Phys. Chem. Chem. Phys., 2020, 22, 24887–24894 RSC.
- E. L. Sibert III, K. N. Blodgett and T. S. Zwier, Spectroscopic Manifestations of Indirect Vibrational State Mixing: Novel Anharmonic Effects on a Prereactive H Atom Transfer Surface, J. Phys. Chem. A, 2021, 125, 7318–7330 CrossRef PubMed.
- B. Hartwig, M. Lange, A. Poblotzki, R. Medel, A. Zehnacker and M. A. Suhm, The reduced cohesion of homoconfigurational 1,2-diols, Phys. Chem. Chem. Phys., 2020, 22, 1122–1136 RSC.
- K. Le Barbu-Debus, F. Lahmani, A. Zehnacker-Rentien, N. Guchhait, S. S. Panja and T. Chakraborty, Fluorescence spectroscopy of jet-cooled chiral (±)-indan-1-ol and its cluster with (±)-methyl- and ethyl-lactate, J. Chem. Phys., 2006, 125, 174305 CrossRef PubMed.
- K. Le Barbu-Debus, M. Broquier, A. Mahjoub and A. Zehnacker-Rentien, Chiral recognition in jet-cooled complexes of (1R,2S)-(+)-cis-1-amino-2-indanol and methyl lactate: on the importance of the CH⋯π interaction, Phys. Chem. Chem. Phys., 2009, 11, 7589–7598 RSC.
- A. Sen, A. Bouchet, V. Lepère, K. Le Barbu-Debus, D. Scuderi, F. Piuzzi and A. Zehnacker-Rentien, Conformational Analysis of Quinine and Its Pseudo Enantiomer Quinidine: A Combined Jet-Cooled Spectroscopy and Vibrational Circular Dichroism Study, J. Phys. Chem. A, 2012, 116, 8334–8344 CrossRef CAS PubMed.
- A. Mahjoub, A. Chakraborty, V. Lepere, K. Le Barbu-Debus, N. Guchhait and A. Zehnacker, Chirality-dependent hydrogen bond direction in jet-cooled (S)-1,2,3,4-tetrahydro-3-isoquinoline methanol (THIQM): IR-ion dip vibrational spectroscopy of the neutral and the ion, Phys. Chem. Chem. Phys., 2009, 11, 5160–5169 RSC.
- R. J. Mathar, Refractive index of humid air in the infrared: model fits, J. Opt. A: Pure Appl. Opt., 2007, 9, 470–476 CrossRef CAS.
- P. E. Ciddor, Refractive index of air: new equations for the visible and near infrared, Appl. Opt., 1996, 35, 1566–1573 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Electronic structure calculations on workstation computers: the program system Turbomole, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Turbomole, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, TURBOMOLE: modular program suite for ab initio quantum-chemical and condensed-matter simulations, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- S. Grimme, Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Software update: the ORCA program system-Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: the PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, Improved second-order Møller-Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, Communication: an improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)], J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- Q. Ma and H.-J. Werner, Explicitly correlated local coupled-cluster methods using pair natural orbitals, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1371 Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general-purpose quantum chemistry program package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller III, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, The Molpro quantum chemistry package, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- K. A. Peterson, T. B. Adler and H.-J. Werner, Systematically convergent basis sets for explicitly correlated wavefunctions: the atoms H, He, B–Ne, and Al–Ar, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- A. S. Hazrah, S. Nanayakkara, N. A. Seifert, E. Kraka and W. Jäger, Structural study of 1- and 2-naphthol: new insights into the non-covalent H-H interaction in cis-1-naphthol, Phys. Chem. Chem. Phys., 2022, 24, 3722–3732 RSC.
- C. Lakshminarayan, J. M. Smith and J. L. Knee, Laser photoelectron spectroscopy of 1- and 2-naphthol: relative stability of the cis and trans cation rotamers, Chem. Phys. Lett., 1991, 182, 656–662 CrossRef CAS.
- J. M. Hollas and M. Z. bin Hussein, Evidence for two rotational isomers of 1-naphthol and 2-naphthol from their gas-phase electronic absorption spectra, J. Mol. Spectrosc., 1988, 127, 497–508 CrossRef CAS.
- G. Pietraperzia, M. Pasquini, N. Schiccheri, G. Piani, M. Becucci, E. Castellucci, M. Biczysko, J. Bloino and V. Barone, The Gas Phase Anisole Dimer: A Combined High-Resolution Spectroscopy and Computational Study of a Stacked Molecular System, J. Phys. Chem. A, 2009, 113, 14343–14351 CrossRef CAS PubMed.
- Y. Matsumoto, T. Ebata and N. Mikami, Characterizations of the hydrogen-bond structures of 2-naphthol-(H2O)n (n = 0 − 3 and 5) clusters by infrared-ultraviolet double-resonance spectroscopy, J. Chem. Phys., 1998, 109, 6303–6311 CrossRef CAS.
- T. Furtenbacher, R. Tóbiás, J. Tennyson, O. L. Polyansky, A. A. Kyuberis, R. I. Ovsyannikov, N. F. Zobov and A. G. Császár, The W2020 Database of Validated Rovibrational Experimental Transitions and Empirical Energy Levels of Water Isotopologues. II. H217O and H218O with an Update to H216O, J. Phys. Chem. Ref. Data, 2020, 49, 043103 CrossRef CAS.
- M. Schütz, T. Bürgi, S. Leutwyler and T. Fischer, Intermolecular bonding and vibrations of 2-naphthol·H2O (D2O), J. Chem. Phys., 1993, 99, 1469–1481 CrossRef.
- M. Saeki, S.-I. Ishiuchi, M. Sakai and M. Fujii, Structure of the Jet-Cooled 1-Naphthol Dimer Studied by IR Dip Spectroscopy: cooperation between the π–π Interaction and the Hydrogen Bonding, J. Phys. Chem. A, 2007, 111, 1001–1005 CrossRef CAS PubMed.
- R. T. Saragi, C. Calabrese, M. Juanes, R. Pinacho, J. E. Rubio, C. Pérez and A. Lesarri, π-Stacking Isomerism in Polycyclic Aromatic Hydrocarbons: The 2-Naphthalenethiol Dimer, J. Phys. Chem. Lett., 2023, 14, 207–213 CrossRef CAS PubMed.
- The OH stretch of t2N is predicted to be 1.3 times more visible than that of c2N (Table 1). Rewardingly, this relative band strength ratio is very robust with respect to variations of the harmonic DFT calculations (all twelve combinations of B3LYP, PBE0, D3(BJ), D3abc(BJ), def2-SVP, def2-TZVP, def2-QZVP). Using the band intensity ratio from Table 1 and experimental band integrals of A and B, we can estimate a t2N
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c2N concentration ratio of 1
c2N concentration ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.3–1
3.3–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.2, depending on the integration method.
4.2, depending on the integration method. - This value is composed of an estimate of the basis set limit CCSD(T) electronic energy (2.4; basis set progression of PNO-LCCSD(T) with DFT geometries) and different DFT-D3 zero-point vibrational (−0.2 ± 0.2; VPT2) and thermal corrections (−0.4 ± 0.2; rigid-rotor-harmonic-oscillator Gibbs free energy at roughly 400 K).
- S. Grimme, Supramolecular Binding Thermodynamics by Dispersion-Corrected Density Functional Theory, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- U. Erlekam, M. Frankowski, G. von Helden and G. Meijer, Cold collisions catalyse conformational conversion, Phys. Chem. Chem. Phys., 2007, 9, 3786–3789 RSC.
- W. Y. Sohn, M. Kim, S.-S. Kim, Y. D. Park and H. Kang, Solvent-assisted conformational isomerization and the conformationally-pure REMPI spectrum of 3-aminophenol, Phys. Chem. Chem. Phys., 2011, 13, 7037–7042 RSC.
- T. Ebata, K. Kouyama and N. Mikami, IR induced cis↔ trans isomerization of 2-naphthol: catalytic role of hydrogen-bond in the photoinduced isomerization, J. Chem. Phys., 2003, 119, 2947–2950 CrossRef CAS.
- K. Kouyama, M. Miyazaki, N. Mikami and T. Ebata, IR laser manipulation of cis ↔ trans isomerization of 2-naphthol and its hydrogen-bonded clusters, J. Chem. Phys., 2006, 124, 054315 CrossRef PubMed.
- B. Reimann, K. Buchhold, H.-D. Barth, B. Brutschy, P. Tarakeshwar and K. S. Kim, Anisole-(H2O)n (n = 1–3) complexes: an experimental and theoretical investigation of the modulation of optimal structures, binding energies, and vibrational spectra in both the ground and first excited states, J. Chem. Phys., 2002, 117, 8805–8822 CrossRef CAS.
- A. Oikawa, H. Abe, N. Mikami and M. Ito, Rotational isomers of meta-substituted phenols and β-naphthol studied by electronic spectra in supersonic free jets, J. Phys. Chem., 1984, 88, 5180–5186 CrossRef CAS.
- J. R. Johnson, K. D. Jordan, D. F. Plusquellic and D. W. Pratt, High resolution S1 ← S0 fluoescence excitation spectra of the 1- and 2-hydroxynaphthalenes. Distinguishing the cis and trans rotamers, J. Chem. Phys., 1990, 93, 2258–2273 CrossRef CAS.
- Y. Matsumoto, T. Ebata and N. Mikami, Structures and vibrations of 2-naphthol-(NH3)n (n = 1–3) hydrogen-bonded clusters investigated by IR-UV double-resonance spectroscopy, J. Mol. Struct., 2000, 552, 257–271 CrossRef CAS.
- G. Pietraperzia, M. Pasquini, F. Mazzoni, G. Piani, M. Becucci, M. Biczysko, D. Michalski, J. Bloino and V. Barone, Noncovalent Interactions in the Gas Phase: The Anisole-Phenol Complex, J. Phys. Chem. A, 2011, 115, 9603–9611 CrossRef CAS PubMed.
- N. Schiccheri, M. Pasquini, G. Piani, G. Pietraperzia, M. Becucci, M. Biczysko, J. Bloino and V. Barone, Integrated experimental and computational spectroscopy study on π-stacking interaction: the anisole dimer, Phys. Chem. Chem. Phys., 2010, 12, 13547–13554 RSC.
- G. Herzberg, Molecular spectra and molecular structure. II. Infrared and Raman spectra of polyatomic molecules, Van Nostrand Reinhold Company, New York, 1st edn, 1945 Search PubMed.
- The normal mode displacements of ν102, 10-12 cm−1, similarly modulate the hydrogen bond angle but the movement more resembles a hindered rotation of 2N perpendicular to the anisole plane. But, at this stage, we cannot rule out its involvement.
- E. Vogt, R. M. Huchmala, C. V. Jensen, M. A. Boyer, J. Wallberg, A. S. Hansen, A. Kjærsgaard, M. I. Lester, A. B. McCoy and H. G. Kjaergaard, Coupling of torsion and OH-stretching in tert-butyl hydroperoxide. II. The OH-stretching fundamental and overtone spectra, J. Chem. Phys., 2021, 154, 164307 CrossRef CAS PubMed.
- M. S. Schuurman, W. D. Allen, P. von Ragué Schleyer and H. F. Schaefer III, The highly anharmonic BH5 potential energy surface characterized in the ab initio limit, J. Chem. Phys., 2005, 122, 104302 CrossRef PubMed.
- S. V. Krasnoshchekov, E. V. Isayeva and N. F. Stepanov, Criteria for first- and second-order vibrational resonances and correct evaluation of the Darling-Dennison resonance coefficients using the canonical Van Vleck perturbation theory, J. Chem. Phys., 2014, 141, 234114 CrossRef PubMed.
- M. Mendolicchio, J. Bloino and V. Barone, General Perturb-Then-Diagonalize Model for the Vibrational Frequencies and Intensities of Molecules Belonging to Abelian and Non-Abelian Symmetry Groups, J. Chem. Theory Comput., 2021, 17, 4332–4358 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental and computational background information for Fig. 3 (Fig. S1) and Fig. 8 and 9 (Tables S1 and S2). See DOI: https://doi.org/10.1039/d3cp00160a |
| ‡ Current affiliation: Department of Physical Chemistry, University of Geneva, 30 Quai Ernest-Ansermet, 1211 Geneva 4, Switzerland. |
| This journal is © the Owner Societies 2023 |