The effect of dissolved chlorides on the photocatalytic degradation properties of titania in wastewater treatment

Abstract

We investigate the effect of chlorides on the photocatalytic degradation of phenol by titania polymorphs (anatase and rutile). We demonstrate how solubilised chlorides can affect the hydroxyl radical formation on both polymorphs with an overall effect on their photodegradative activity. Initially, the photocatalytic activity of anatase and rutile for phenol degradation is investigated in both standard water and brines. With anatase, a significant reduction of the phenol conversion rate is observed (from a pseudo-first-order rate constant k = 5.3 × 10⁻³ min⁻¹ to k = 3.5 × 10⁻³ min⁻¹). In contrast, the presence of solubilised chlorides results in enhancement of rutile activity under the same reaction conditions (from 2.3 × 10⁻³ min⁻¹ to 4.8 × 10⁻³ min⁻¹). Periodic DFT methods are extensively employed and we show that after the generation of charge separation in the modelled titania systems, adsorbed chlorides are the preferential site for partial hole localisation, although small energy differences are computed between partially localised hole densities over adsorbed chloride or hydroxyl. Moreover, chlorides can reduce or inhibit the ability of r-TiO₂ (110) and a-TiO₂ (101) systems to localise polarons in the slab structure. These results indicate that both mechanisms – hole scavenging and the inhibition of hole localisation – can be the origin of the effect of chlorides on photocatalytic activity of both titania polymorphs. These results provide fundamental insight into the photocatalytic properties of titania polymorphs and elucidate the effect of adsorbed anions over radical formation and oxidative decomposition of organic pollutants.

---

1. Introduction

Dissolved organic compounds are one of the main components of polluted wastewater. They can originate from non-biodegradable pesticides, pharmaceuticals, and food additives, amongst other industrial compounds and by-products.^1–3 Extensive work has been undertaken during the last decades to eliminate these contaminants prior to reutilisation or the return of the effluent to nature.^4,5 In this context, the photodegradation of organic pollutants by heterogeneous catalysts under visible-UV light has shown very promising results for oxidation and mineralisation of such organic materials, with the additional benefit of eliminating the need to use hazardous materials, such as hypochlorite, peroxide, and ozone, in these processes.⁶

Titania-based photocatalytic materials have been widely employed in such applications and are currently considered to be one of the most effective materials for environmental applications.¹ In addition to its photocatalytic properties, TiO₂ is low-cost, has high chemical and biological stability, and low toxicity, all of which make the material ideal for wastewater treatment.^1,7 Although TiO₂ has shown promise in the degradation of organic compounds dissolved in standard water solutions, the performance of such photocatalysts was observed to decrease drastically when investigating wastewater solutions containing a high content of dissolved salts.^8,9 This depletion of titania's photoactivity is often attributed to blockage of surface sites, impeding the adsorption of hydroxyl anions and formation of hydroxyl radicals, or, hole trapping/scavenging, inhibiting the formation of active radicals responsible for the oxidation of organic pollutants.⁸

Conversely, the opposite effect has also been reported when halide anions were present in a wide range of experimental conditions. Pre-treatment of titania catalysts by HF or HCl, for instance, have been demonstrated to enhance the decomposition rate of organic derivatives such as benzene, phenol, and toluene,^10,11 and the HCl pre-treated systems were shown to be active for the decomposition of branched aromatics.¹¹ A similar enhancement was reported for the photodecomposition of Reactive Brilliant Orange K–R in NaCl solutions,¹² during the decomposition of halogenated organic derivatives (perchloroethylene),¹³ and after chlorination of titania surface by CHCl₃ decomposition or HCl impregnation.^14,15 Although these distinct observations of depletion/enhancement of activity seem contradictory, in principle they could be rationalized by comparison of the distinct chemical system and reaction conditions employed in each case (pH, substrate, hydrogenation of the catalyst surface, etc.) Nevertheless, there is a need for a more thorough appraisal and rationalisation of the halide effect over the degradative photocatalytic activity of titania, which can be key for the proposal of new mitigation approaches for reduced photoactivity performance of TiO₂-based catalysts in contaminated waters.

In this work, we compare periodic DFT based calculations of the potential role of solubilised chlorides on the photocatalytic activity of anatase and rutile with the experimentally observed effect of chlorides on the photocatalytic activity of the two TiO₂ polymorphs for phenol decomposition. Blockage of surface sites and changes in the polaronic self-trapping ability of the different titania surfaces by adsorbed chlorides are considered in detail.

2. Methodology

Materials

All chemical reagents were used without further purification, which are listed as follows; titanium(IV) oxide-anatase (99.8%, SA: 9 m² g⁻¹, Merck), titanium(IV) oxide-rutile (99.99%, SA: 4 m² g⁻¹, Merck), sodium chloride (analytical grade reagent, Fisher Scientific), acetonitrile (HPLC grade, Fisher Scientific) and 1,4-benzoquinone (standard reference material, Aldrich).

Photocatalysis experiments

The effect of chloride ions on the photocatalytic activity of anatase and rutile photocatalysts was evaluated in a batch reactor using phenol as the model organic compound.¹⁶ In a typical experiment, phenol (60 mg L⁻¹, 110 mL) was mixed with the selected photocatalytic powder (1 g L⁻¹) and all experiments performed under stirring in a double-walled open-top reactor coated with aluminium foil paper. Before illumination, the photocatalyst-phenol solution was stirred in the dark for 30 min to achieve an absorption–desorption equilibrium. The photocatalyst-phenol solution was irradiated with light for 4 h under constant stirring using a 300 W Xe arc lamp (1000 W m⁻²). During the reaction, 2 mL sample aliquots were withdrawn at specific time intervals, diluted and then centrifuged to remove the photocatalyst. Analysis for residual phenol and intermediate species formed during the reaction was performed by high-performance liquid chromatography (HPLC) and UV-Vis spectroscopy. HPLC analysis was performed on an Agilent Technologies 1200 series instrument, equipped with an Agilent C18 column, using a stepwise gradient elution mode with a mixture of acidified water (phosphoric acid) and acetonitrile as the mobile phase. The temperature of the Agilent C18 column was maintained at 30 °C during analysis. To prepare the hypersaline brines, NaCl (100 g L⁻¹ Cl⁻) was added to the reaction mixture while the phenol (60 mg L⁻¹) and photocatalyst (1 g L⁻¹) concentrations were maintained.

Computational methods

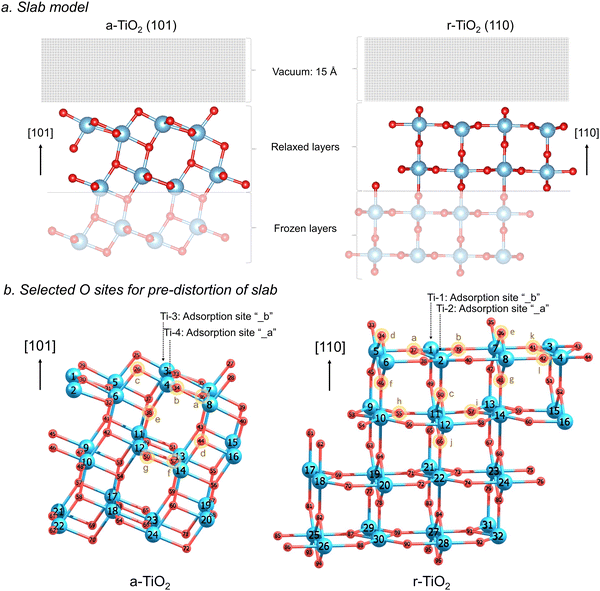
All calculations were performed using the Vienna ab initio simulation package (VASP)^17–20 within the framework of periodic density functional theory (DFT). The electronic structure of all the systems modelled employed the RPBE²¹ functional combined with Grimme's semiclassical D3 dispersion correction^22,23 and Coulomb repulsive interaction (U = 4.5 eV) for the d orbitals of Ti, in accordance with preliminary evaluation of the relative stability of the titania polymorphs investigated²⁴ (Fig. S1, ESI†) and evaluation of the effect of distinct U values (U = 2.5 eV, 4.5 eV, and 6 eV) on the charge localisation in these systems (Table S1 and Fig. S2, S3, ESI†). The electron–ionic core interaction was represented by the projector-augmented-wave (PAW) potentials^25,26 and the cut-off energy was selected after extensive benchmarking and set to 550 eV (Fig. S5 and S6, ESI†). The Ti 3d³4s¹ and O 2s²2p⁴ orbitals were explicitly included as valence electrons. Brillouin zone sampling was performed using the Monkhorst-Pack scheme with a k-point grid of 7 × 7 × 1 together with a Gaussian smearing broadening of 0.02 eV. Forces and electronic SCF convergence were set at 10⁻² eV Å⁻¹ and 10⁻⁵ eV, respectively. Dipole corrections were additionally used during all calculations, according to the method by Makov & Payne²⁷ and Neugebauer & Scheffler.²⁸ The optimized lattice constants obtained at this level of theory were used in this work to construct the investigated surface models.

The most stable surfaces of anatase and rutile were selected for this investigation, namely a-TiO₂ (101) and r-TiO₂ (110). The slab model for a-TiO₂ (101) surface used a 2 × 1 × 3 supercell containing 24 titanium and 48 oxygen atoms, whereas for r-TiO₂ (110), a 2 × 2 × 4 supercell containing 32 titanium and 64 oxygen atoms was used. In a-TiO₂ (101) model, the 8 top titanium ions and 20 oxygen ions were allowed to relax, whereas for r-TiO₂ (110) model, 16 top titanium ions and 32 oxygen ions were allowed to relax (see illustration in Fig. 1a). A vacuum gap of 15 Å in the z direction was added to the surface in order to avoid undesired interactions with slab images.

Fig. 1 Slab models used for r-TiO₂ (110) and a-TiO₂ (101) surface simulations (a) and selected O sites considered in the pre-distortion of r-TiO₂ (110) and a-TiO₂ (101) ionic structures (b). Alternative adsorption sites and number label of each atom are additionally shown.

In order to simulate excited state electronic structures, the difference between electron spins up and down was set to 2 (N = 2), formally resulting in a triplet state. For simulation of anionic species (OH⁻ and/or Cl⁻) adsorbed on the investigated surface, one excess electron was added to the system. In these cases, a neutralizing background charge was assumed to compensate the resulting negative charge over the slab. For the hole- and excess electron-containing electronic structures, one electron was removed or added, respectively, to the system. Similarly, a neutralizing background charge is assumed and the difference between electron spins up and down was set to 1 (N = 1), formally resulting in a doublet state. It is worth noting, however, the well-known limitations to this methodology due to divergence of Coulomb energy when distinct vacuum widths are inserted between slab images.^29,30 Nevertheless, alternative tests performed in the presence of counterions in order to avoid the use of charged slabs resulted in unrealistic solutions of the electronic structure of the systems studied. More details are given in Tables S2–S4 and Fig. S8, in the ESI.† Therefore, utilisation of neutralizing background charge was chosen as a more appropriate approach to investigate self-trapping of polarons in this work.

For all simulations involving the triplet state (N = 2), or hole and electron-containing structures (N = 1), the ionic structure of the surfaces underwent pre-optimisations to produce local lattice distortions around selected oxygen sites, facilitating the formation of a O⁻–Ti³⁺ charge localised systems within the slab model employed in our calculations. Such pre-distortion of the ionic structure was performed by temporarily replacing one oxygen atom by one fluorine atom in a selected lattice site (Fig. 1b) and allowing the ions around it to relax. The lower charge of the fluorine/fluoride results in an outward relaxation of the surrounding titanium ions and thereby produces an appropriate geometry for charge localisation when the oxygen atom was returned to the structure. The procedure follows an approach developed by Grau-Crespo et al. for localising electrons in CeO₂.^31,32 Twelve distinct pre-distortions of lattice sites were considered for all calculations involving r-TiO₂ (110), and seven for a-TiO₂ (101), as illustrated in Fig. 1b. Additional tests of pre-distortion around Ti sites were conducted (Fig. S9 and S10, ESI†) by temporarily replacing one titanium by a scandium atom, leading to results very similar to those obtained for structures with biased O sites.

3. Results and discussion

3.1 Photocatalytic oxidation of phenol in standard water and brine solutions: anatase and rutile activities

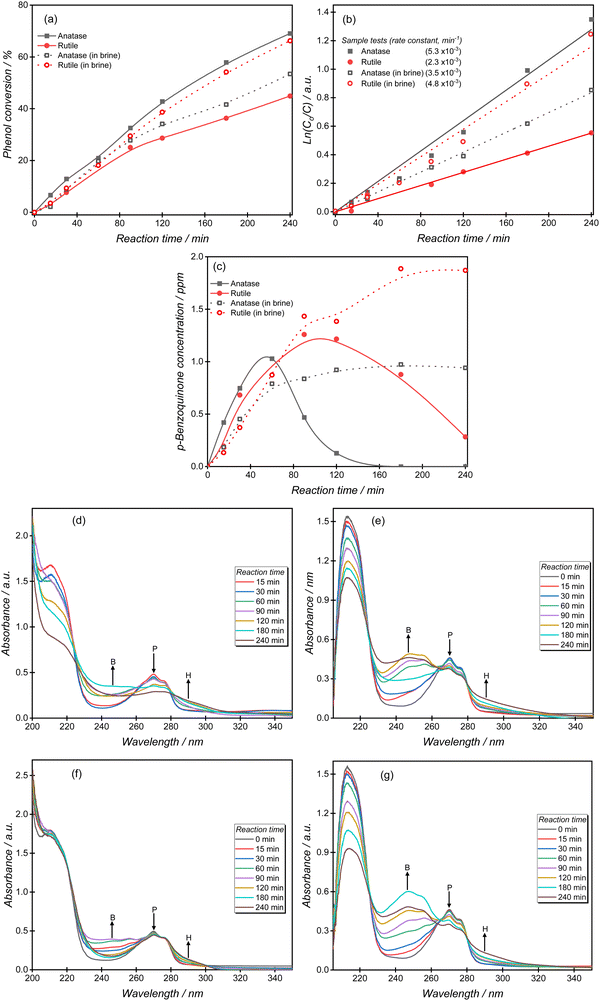
The photocatalytic oxidation of phenol is an attractive reaction to compare catalyst structure and reaction conditions, because of the relatively rapid rate and reproducibility of results. The phenol oxidation reaction is approximately twice as fast over anatase than rutile, with a pseudo-first-order rate constant of 5.3 × 10⁻³ min⁻¹ calculated for the anatase reaction (Fig. 2a and b). In the presence of chloride ions, the rate of phenol oxidation over the anatase surface decreased significantly giving an apparent first-order rate constant k of 3.5 × 10⁻³ min⁻¹, Fig. 2a and b. A very different effect was observed over rutile however, with the photocatalytic activity in brines accelerated by a factor of more than two, with the pseudo-first-order rate constant increasing from 2.3 × 10⁻³ min⁻¹ to 4.8 × 10⁻³ min⁻¹. In contrast to some other reported systems,^9,33–36 the higher phenol oxidation rates observed in brines over rutile suggests that there are alternative reaction pathways offered by the presence of chlorine radicals.

Fig. 2 (a) Experimental comparison of the effect of chlorides [100 g L⁻¹ Cl⁻] on the photocatalytic oxidation of phenol over rutile and anatase catalysts as analysed by HPLC, (b) corresponding degradation kinetics, and (c) production of the p-benzoquinone intermediate. Representative UV-Vis spectroscopy data measured during the photocatalytic experiments over (d) anatase in water, (e) anatase in brine, (f) rutile in water and (g) rutile in brine are shown. The peaks denoted B, P and H represent absorption peak positions for p-benzoquinone, phenol and hydroquinone.

To study the chloride effect on reaction intermediates, we monitored the formation and subsequent oxidation of p-benzoquinone (BQ), a primary phenol oxidation product. Over the anatase surface, BQ achieves a maximum concentration of 1 ppm after 60 min and then declines until it is undetectable by HPLC analysis at the end of the reaction (Fig. 2c). BQ production over rutile follows a similar trend but a steady decline in total concentration is observed due to the slower degradation kinetics over this TiO₂ polymorph. The brine experiments resulted in a constantly high BQ concentration; an effect attributed to a reduced generation of reactive oxygen species. Notably higher BQ concentrations were measured over rutile than anatase, consistent with the phenol oxidation trend observed in brine solutions.

It is generally accepted that phenol degradation occurs via the initial hydroxylation of the aromatic ring to form benzoquinone, hydroquinone and catechol, followed by aromatic ring opening to produce short-chain aliphatic acids such as maleic acid, formic acid and oxalic acid, which are subsequently mineralized to carbon dioxide and water.^37–40Fig. 2d–g shows the transformation of phenol over anatase and rutile comparing experiments performed in water or in brines. For experiments performed in water, the phenol absorption peaks (210, 270 nm) decreased significantly over anatase relative to rutile, in agreement with many studies about the superior photo-activity of anatase. During these experiments the intensities of both p-benzoquinone (246 nm) and hydroquinone (288 nm) increased, with the former intermediate gradually decreasing as the reaction progressed. Several differences were noted when the reactions were performed in brines. First, the phenol peak decreased significantly over rutile indicating an unusually improved phenol degradation compared to experiments performed in aqueous solutions. Secondly, higher p-benzoquinone signal intensities were observed over both TiO₂ polymorphs indicating the accumulation of the intermediate as the reaction progressed. The UV-Vis spectra agree with the HPLC results discussed earlier.

In any of these cases, the effect of chlorides can originate from interference with the OH radical generation during UV irradiation. In an aqueous medium, after the photogeneration of charge carriers in the system, hydroxyl radicals can be expected to be generated via two mechanisms: (i) from H₂O₂ decomposition produced after O₂ reacts with an electron in the conduction band, forming solubilised hydroxyl radicals, and, (ii) from concerted H₂O deprotonation/oxidation by a hole in the valence band, generating adsorbed hydroxyl radicals (OH˙_ads).⁵ In principle, chlorides could interfere with both mechanisms; however, the latter is considered to be the most relevant pathway for the degradation of organic molecules, and it was selected for further evaluation by DFT methods.^5,41 Nevertheless, the many complex processes expected to occur in solution could also have a key role in the rationalisation of the chloride effect. However, they will be explored in a future investigation.

Chloride interference in OH˙_ads generation has been proposed to occur by at least two mechanisms, blockage of surface sites and/or hole trapping/scavenging.⁸ In the following subsection, we describe an investigation of the competitive adsorption of Cl⁻ and OH⁻ anions over two titania model surfaces – a-TiO₂ (101) and r-TiO₂ (110). Subsequently, the self-trapping ability of Cl⁻ and OH⁻ containing systems is analysed.

3.2 Competitive adsorption of chloride and hydroxyl anions over a-TiO₂ (101) and r-TiO₂ (110)

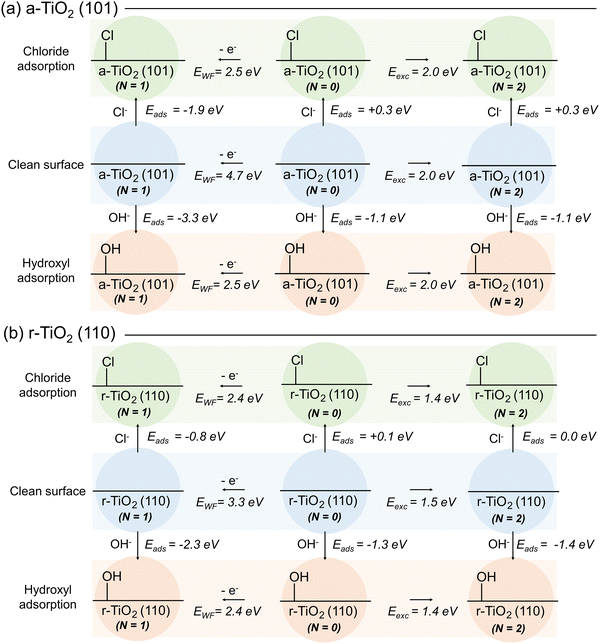
The role of competitive adsorption of chloride and hydroxyl anions over model titania systems was initially investigated by DFT methods. For this, we took into consideration three distinct electronic states of these systems: (i) the ground (singlet) state, identified in Fig. 3 as N = 0, (in which N is the difference between electron with spin up and down in the system); (ii) the excited (triplet, N = 2) state and the doublet state (N = 1) for hole-containing structures. For each of these cases, the adsorption energy (E_ads) of chloride and hydroxyl anions was computed considering a-TiO₂ (101) and r-TiO₂ (110) surfaces (Fig. 3a and b, respectively). Additionally, the excitation energy (E_exc) for the triplet state was calculated as the energy difference between the ground and excited state structure, and the work function (E_WF) was computed as the energy difference between ground state and the hole-containing structure (Fig. 3). Although the computed work function and excitation energies may diverge from experimental values, comparisons made at the same theory level can still provide relevant insights into the trends of these systems. Limitations of these methods with regard to the intrinsic aspects of the electronic structure are well known, including the ambiguities about the reference energy in periodic methods, and alternative approaches may be required for computing values directly comparable to experiment.⁴² However, such limitations should only have a small effect on the comparative analysis in this and the following subsections.

Fig. 3 Calculated adsorption energies (E_ads) of hydroxyl and chloride over (a) a-TiO₂ (101) and (b) r-TiO₂ (110). Calculated work function and excitation energies (E_WF and E_exc, respectively) for each hydroxyl- and chloride-containing system are additionally shown.

For all cases presented in Fig. 3, the adsorption of chlorides is less energetically favourable than the adsorption of hydroxyl anions, regardless of surface or the electronic state of the system. Whilst the calculated adsorption energies of the chloride vary between −1.9 and +0.3 eV, for the hydroxyl anion the values range between −3.3 and −1.1 eV. These results indicate that the putative competitive adsorption of chloride and hydroxyl anion would result in the latter being favoured, at least over the surfaces selected for this investigation. Such a behaviour suggests that inhibition of oxidative photoactivity of titania catalysts by blockage of adsorption sites by chlorides is unlikely to occur. Arguably, competitive adsorption over ground state surface would be better described if the calculated adsorption energies of water molecules and chloride were compared, instead. However, the E_ads for water calculated at the same level of theory are similar to that of hydroxyl anions: −1.1 and −1.0 eV over a-TiO₂ (101) and r-TiO₂ (110), respectively (Fig. S11, ESI†). Once again, these results confirm that adsorption of the hydroxyl anion (or water itself) is still favoured in chloride-containing aqueous solutions. Nevertheless, these results do not eliminate the possibility of small amounts of chloride being adsorbed over the surface of the photocatalyst and acting as hole scavengers, as previously suggested.^8,9 To investigate such a possibility, in the next stage of this work, we compare the ability of such systems to self-trap holes and electrons in their structure.

3.3 Charge localisation on clean, hydroxylated, and chlorinated surfaces

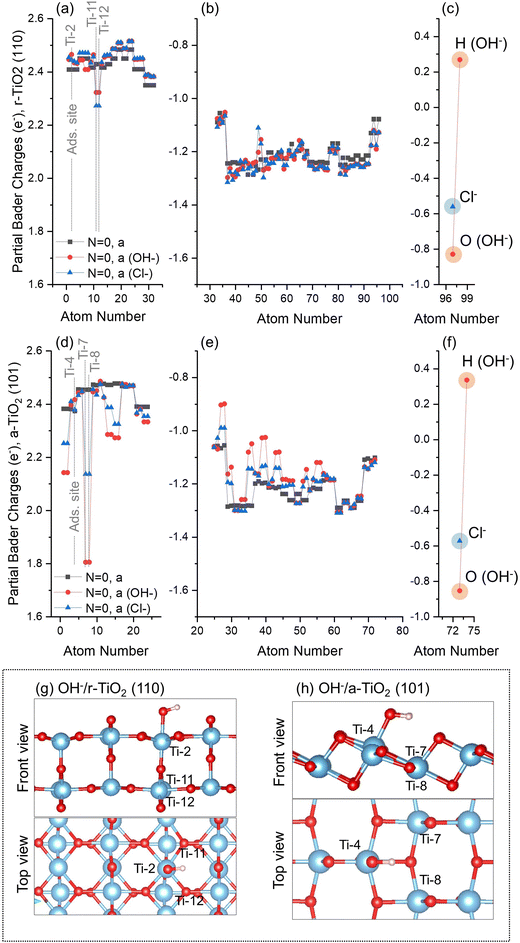
This stage of our investigation was divided into four steps: investigation of atomic charges in a-TiO₂ (101) and r-TiO₂ (110) surfaces, before and after adsorption of hydroxyl and chloride anions (Subsection 3.3.a); Investigation of atomic charges over surface atoms of clean a-TiO₂ (101) and r-TiO₂ (110) surfaces when simulating ground state and triplet states, as well as hole-containing and excess electron-containing electronic structures (Subsection 3.3.b); the variation of atomic charges in hydroxyl- and chloride-containing surfaces (Subsections 3.3.c and 3.3.d) when considering triplet states and hole-containing electronic structures; and, finally, the co-adsorption of hydroxyl and chloride anions over a-TiO₂ (101) and r-TiO₂ (110) surfaces (Subsection 3.3.e).

3.3.a. Charges in ground state (singlet) electronic structure of hydroxyl- and chloride-containing surfaces. Partial Bader charges were initially calculated for a-TiO₂ (101) and r-TiO₂ (110) surfaces, before and after adsorption of hydroxyl and chloride anions. Fig. 4 presents the charges over Ti (Fig. 4a and d) and O (Fig. 4b and e) ions, as well as the charges over the adsorbates (Fig. 4c and f). The clean r-TiO₂ (110) surface showed partial Bader charges over Ti cations varying between +2.3e and +2.5e (Fig. 4a), whereas a-TiO₂ (101) has partial charges varying between +2.4e and +2.5e (Fig. 4d). For O anions, these values varied between −1.3e and −1.0e for both clean r-TiO₂ (110) (Fig. 4b) and a-TiO₂ (101) (Fig. 4e).

Fig. 4 Partial Bader charges for ground state (singlet, N = 0) electronic structure of clean, hydroxyl-, and chloride-containing (a–c) r-TiO₂ (110) and (d–f) a-TiO₂ (101) surfaces. Charges over Ti ions (a and d), O ions (b and e), and absorbates (c and f) are individually presented. Inserts show representative example of adsorbate-containing surface (g: OH⁻/r-TiO₂ (110); h: OH⁻/a-TiO₂ (101)). Atom numbers refer to labels defined in the methodology section.

After adsorption of hydroxyl or chloride anions, the charges over surface atoms of r-TiO₂ (110) remain roughly unchanged, including the adsorption site Ti-2 (Fig. 4a and g). The only exceptions are the cations Ti-11 and Ti-12 located below the adsorption sites of r-TiO₂ (110) (Fig. 4g), which have a slight reduction of their positive charges when compared to the case of the clean surface (Δq ∼ −0.15e). Similar behaviour was observed for a-TiO₂ (101) (Fig. 4d); however, in this case the cations with larger charge variation after adsorption of hydroxyl or chloride anions were Ti-7 and Ti-8 (see Fig. 4h), with computed Δq of −0.65e for OH⁻/a-TiO₂ (101) and −0.31e for Cl⁻/a-TiO₂ (101) when compared to the clean surface.

No significant differences are observed between the calculated charges of hydroxyl or chloride on the surfaces of the two polymorphs (Fig. 4c and f). Adsorbed Cl and O(H) atoms on r-TiO₂ (110) have partial charges of −0.56e and −0.83e, respectively (Fig. 4c). On a-TiO₂ (101) these species have charges of −0.57e and −0.86e for Cl and O(H) atoms, respectively (Fig. 4f). For the adsorbed hydroxyl anion, the total charges of this group are −0.57e for r-TiO₂ (110) and −0.52e for a-TiO₂ (101).

Overall, only small variations of charge were computed for a-TiO₂ (101) and r-TiO₂ (110) surfaces after adsorption of chloride or hydroxyl anions. The most significant changes occurred at surface and subsurface Ti sites neighbouring the adsorption site in a-TiO₂ (101) and r-TiO₂ (110), respectively. Additionally, charges over adsorbates were comparable for both polymorphs, varying between −0.57e and −0.57e for chloride and from −0.57e to −0.52e for hydroxyl anion.

3.3.b. Simulating photoexcitation in clean surfaces. For the simulation of the triplet state (N = 2) and the hole-, and electron-containing structures (N = 1), local pre-distortion of the ionic structure was used to facilitate charge localisation (as discussed in the Methodology Section). In most cases, however, full optimisation of the pre-distorted structures led to the same (or very similar) optimised structures, with energy differences smaller than 0.1 eV and delocalised charges. Two or three distinct structures were obtained when considering a triplet state or excess electron-containing electronic structure of clean r-TiO₂ (110) and a-TiO₂ (101) as shown in Fig. 5. Such structures had different energies due to their different charge distributions and associated lattice distortion. As can be seen, for instance, in Fig. 5a and b, whilst “N = 1 electron, a” shows a significant increase in electron density at Ti-32, no significant charge localisation was computed for “N = 1 electron, d” (conversely, it presents delocalised charges only). The computed energies of the two structures are different and both structures were kept in the discussion. Other possible local pre-distortions are not reported as they resulted in structures identical to those mentioned above. The same will be seen later for OH⁻/r-TiO₂ (110), in Fig. 6a and b.

Fig. 5 Partial Bader charges over (a and b) r-TiO₂ (110) and (c and d) a-TiO₂ (101) surfaces when considering the ground state (N = 0, a) electronic structure, as well as triplet state (N = 2, a and c), hole-containing (N = 1 hole, a), and excess electron-containing electronic structures (N = 1 electron, a–c). Charges over Ti ions (a and c) and O ions (b and d) are individually presented. The relative energy (E_rel.) of each obtained structure is given in parentheses. Atom numbers refer to labels defined in the methodology section.

Fig. 6 Partial Bader charges over (a–c) OH⁻/r-TiO₂ (110) and (d–f) OH⁻/a-TiO₂ (101) surfaces when considering the ground state (N = 0, a; and N = 0, a (OH⁻)) of the electronic structure, as well as triplet state (N = 2 b_b (OH⁻) and N = 2 c_b (OH⁻)) and hole-containing electronic structure (N = 1 hole, a, (OH⁻)). Charges of respective clean surfaces are given for comparison. Charges over Ti ions (a and d), O ions (b and e), and adsorbate (c–f) are individually presented. The relative energy (E_rel.) of each structure is given in parentheses. Atom numbers refer to labels defined in the methodology section.

For the hole-containing structure, only one ionic structure was obtained for both cases and no significant charge localisation was observed over the O atoms of TiO₂ systems. Similar behaviour was observed regarding hole localisation when considering triplet state systems, which is consistent with previous investigations using DFT hybrid functional (HSE06 and PBE0-TC-LRC) and ab initio embedded cluster approaches,^43–46 in which hole trapping is not observed for r-TiO₂ (110) systems, except in the presence of adsorbed/dissociated water or hydroxyl species on the surface of the catalyst. Such behaviour is also the case here, as will be further discussed in Subsection 3. 3.c. For a-TiO₂ (101), on the other hand, previous investigations have shown this system as capable of hole trapping.^43,47–53 In our approach, however, such hole trapping could only be observed when in the presence of hydroxyl species (see Subsection 3.3.c) – similar behaviour to that observed for rutile.

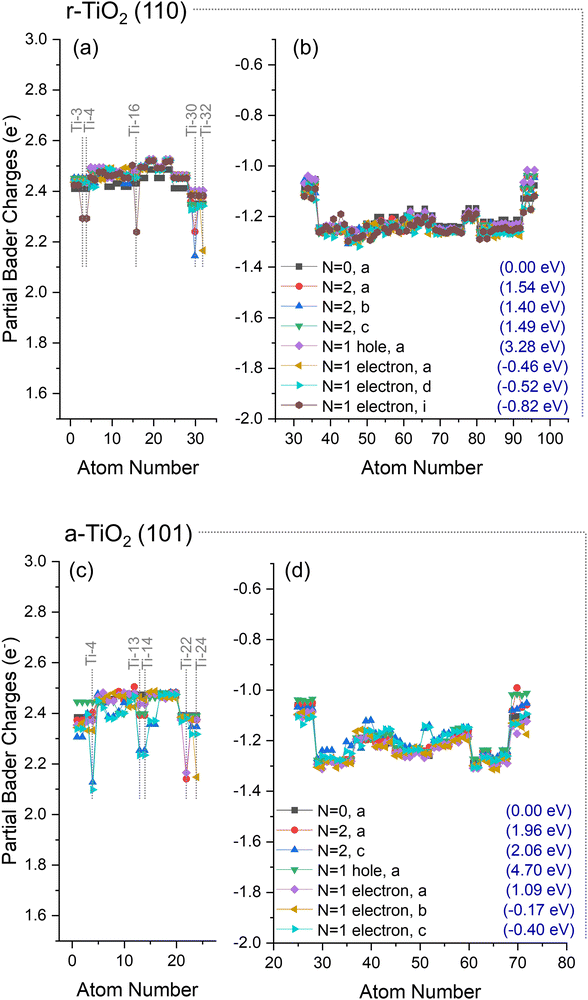
A slight increase of the electron density over Ti cations was observed for rutile at Ti-32 (N = 1 electron, a, Fig. 5a), Ti-30 (N = 2, a and b, Fig. 5a), or simultaneously over Ti-3, Ti-4, and Ti-16 (N = 1 electron, i, Fig. 5a). Ti-32 and Ti-30 are 5-fold titanium ions localised at the bottom of the slab (Fig. 1), whereas Ti-3 and Ti-4 are localised at the surface and directly over Ti-16 (Fig. 1). Such observations are consistent with previous investigations, in which electron trapping in r-TiO₂ (110) systems was reported to occur either in the subsurface or surface of the catalyst, with only small energy differences between these possibilities.^{5,43,47,54–61}

For anatase, the most significant electron localisations were observed at Ti-22 (N = 2, a, and, N = 1 electron, a, Fig. 5c), Ti-24 (N = 1 electron, b, Fig. 5c), and simultaneously over Ti-13, Ti-14, and Ti-4 (N = 2, c, and, N = 1 electron, c, Fig. 5c). Ti-22 and Ti-24 are 5-fold titanium ions localised at the bottom of the slab (Fig. 1), whereas Ti-4 is localised at the surface, and sites Ti-13 and Ti-14 are localised in the subsurface directly below Ti-4 (Fig. 1). Previous work has proposed that only in the presence of water molecules, a-TiO₂ (101) systems would be able to trap electrons.^43,47,49,55 However, as discussed above, at least five distinct structures with partial localisation of electrons in clean anatase were identified.

These results show that no hole localisation is found when clean r-TiO₂ (110) and a-TiO₂ (101) surfaces are considered. However, distinct electron localisations were obtained for both systems at surface and subsurface Ti sites, not requiring the presence of adsorbates. Next, the changes in the polaronic self-trapping ability of r-TiO₂ (110) and a-TiO₂ (101) surfaces due to adsorbed anionic species are investigated.

3.3.c. Simulating photoexcitation in hydroxyl-containing surfaces. Similar to the approach used for the clean surfaces, pre-distortion of hydroxyl- and chloride-containing surfaces was also used to facilitate charge localisation (as discussed in the Methodology Section). For these cases, two distinct adsorption sites were considered for each surface (Fig. 1), resulting in 24 pre-distorted structures for all calculations involving r-TiO₂ (110), and 14 pre-distorted structures for a-TiO₂ (101). The results for the distinct structures obtained for OH⁻/r-TiO₂ (110) and (b) OH⁻/a-TiO₂ (101) systems after full optimisation are shown in Fig. 6. Calculations using chloride-containing surfaces are discussed in the next subsection.

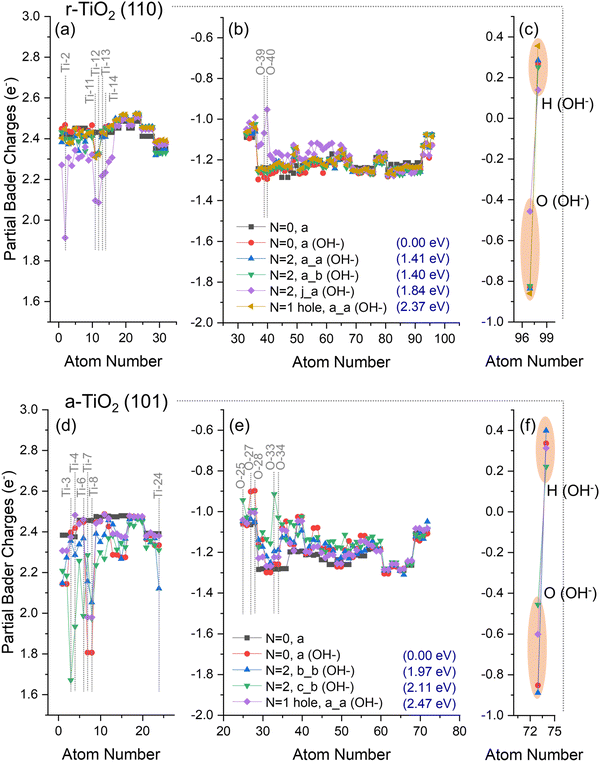
No significant hole or electron localisation was observed for OH⁻/r-TiO₂ (110) systems, except for the triplet state “N = 2, j_a (OH⁻)” (Fig. 6a–c), which exhibited significant charge variation over both titanium (Ti-11 and Ti-12: Δq = −0.24e; Ti-13 and Ti-14: Δq = −0.21e; and Ti-2: Δq = −0.56e, Fig. 6a) and oxygen ions (O-39: Δq = +0.2e; O-40: Δq = +0.3e, Fig. 6b) when compared to ground state OH⁻/r-TiO₂ (110) system (N = 0, a, Fig. 4a). Ti-11, Ti12, Ti-13, and Ti-14 are located at the subsurface of the slab, whereas Ti-2 is the hydroxyl adsorption site in the “N = 2, j_a (OH⁻)” system (Fig. 1). Charges over the O(H) atom of the absorbate were roughly the same in most of the alternative structures considered for OH⁻/r-TiO₂ (110), with partial Bader charges circa −0.8e. The only exception was, again, “N = 2, j_a (OH⁻)” structure (Fig. 6c), which showed a significant reduction of electron density over the O atom of the hydroxyl, with a calculated partial charge of −0.46e. When charges over both O and H atoms of the adsorbate are summed up, the hydroxyl total charge for “N = 2, j_a (OH⁻)” is −0.3e, which represents a Δq ∼ +0.2e if compared to the ground state OH⁻/r-TiO₂ (110) system (N = 0, a, Fig. 4c). For all the other cases considered here, the total charge of the hydroxyl varied between −0.6e and −0.5e, revealing no significant charge variation when compared to the ground state system.

Similarly, no significant hole localisation was observed over O ions in the surface of OH⁻/a-TiO₂ (101) systems (Fig. 6e). In this case, the largest decrease of electron density over O ions was observed for O-25, O-33, O-34 (Δq = +0.1e, +0.2e, and +0.3e). Moreover, only the triplet states in OH⁻/a-TiO₂ (101) systems led to partial electron localisation over Ti ions (Ti-3: Δq = −0.7e; Ti-24: Δq = −0.2e; Ti-6: Δq = −0.4e; and Ti-4: Δq = −0.5e). Ti-4 and Ti-3 are adsorption sites considered for “N = 2, b_b (OH⁻)” and N = 2, c_b (OH⁻), respectively; Ti-6 is next to the adsorption site on the surface; and Ti-24 is located at the bottom of the slab. For Ti-7 and Ti-8 (both neighbouring the adsorption sites on the surface) a charge reduction was computed over these ions when compared to ground state OH⁻/a-TiO2 (101) system (N = 0 (OH⁻), a, Fig. 4f): Ti-7, Δq = 0.2–0.5e; Ti-8, Δq = 0.2e. Considering the charge of the O atom of the absorbate, a partial charge of −0.46e was obtained for “N = 2, c_b (OH⁻)” structure, −0.60e for the hole-containing structure (N = 1 hole, a), and partial Bader charges circa −0.8e over O(H) atom for all other cases. When the total charge over the hydroxyl was calculated, these values were −0.2e for “N = 2, c_b (OH⁻)”, −0.3e for hole-containing structure (N = 1 hole, a), and −0.5e for all other cases. For these first two cases, this represents a reduction of the calculated charges of Δq ∼ 0.2–0.3e if compared to the ground state system.

Analysis of the energy differences between the structures obtained can give insight into the thermodynamic aspect of photogenerated charges.⁶² When compared to the ground state energy of OH⁻/r-TiO₂ (110), the energy cost to form the triplet state structures a_a, a_b, and j_b (Fig. 6a–c) was 1.41, 1.40, and 1.84 eV, respectively. The same analysis reveals a higher energy cost for forming the triplet states structures b_b and c_b (1.97 and 2.11 eV, Fig. 6d–f) from ground state OH⁻/a-TiO₂ (101), as would be expected due to the intrinsic differences in band gap energy for these polymorphs.⁶³ The calculated energy cost to form the triplet state structures in the clean surfaces varied between 1.40–1.54 eV and 1.96–2.06 eV for a-TiO₂ (101) and r-TiO₂ (110), respectively.

Despite these observations, it is well known that formation of adsorbed hydroxyl radicals over rutile has a higher energy barrier than over anatase.⁶⁴ Geng et al. investigated the photoinduced water dissociation on a-TiO₂ (101) surface by laser surface photolysis technique.⁶⁴ The authors showed that at high water coverages, the water dissociation on r-TiO₂ (110) is largely inhibited by the strong hydrogen bonding network between solvent molecules, whereas the same process over a-TiO₂ (101) is considerably more efficient due to the much weaker interactions between these molecules.⁵⁰ The same effect can be expected to occur under the reaction conditions tested here (Subsection 3.1) since anatase presents a higher rate of phenol degradation than rutile.

3.3.d. Simulating photoexcitation in chloride-containing surfaces. When the same methodology is applied to the systems containing a chloride ion, the ability of r-TiO₂ (110) to localise charges in the surface was significantly reduced. As can be seen in Fig. 7a–c, only one ionic structure could be obtained for hole-containing and triplet state systems, and no significant changes in the charges are observed compared to the ground state Cl⁻/r-TiO₂ (110) system. For example, one of the largest changes in charge observed here was at Ti-2, which showed Δq ∼ −0.1e, much smaller than the variations computed in OH⁻/r-TiO₂ (Δq = −0.56e, Fig. 6). However, for the adsorbate in Cl⁻/r-TiO₂ (110), the charges over the chloride are −0.6e and −0.5e for singlet (N = 0, a_a (Cl⁻)) and triplet (N = 2, a_a (Cl⁻)) state systems, respectively, whereas the hole-containing structure (N = 1 hole, a_a (Cl⁻)) has a charge of −0.37e over the Cl atom (Fig. 7c). Unlike the hole-containing OH⁻/r-TiO₂ (110) structure (Fig. 6c), in this case the hole density over the adsorbate was significantly increased when going from the ground state to a hole-containing Cl⁻/r-TiO₂ (110) system.

Fig. 7 Partial Bader charges over (a–c) Cl⁻/r-TiO₂ (110) and (d–f) Cl⁻/a-TiO₂ (101) surfaces when considering the ground state (N = 0, a, and, N = 0, a (Cl⁻)) of the electronic structure, as well as triplet state (N = 2, a_a (Cl⁻), N = 2, e_a (Cl⁻), N = 2, e_b (Cl⁻)) and hole-containing (N = 2, a_a (Cl⁻)) electronic structure. Charges of respective clean surfaces are given for comparison. Charges over Ti ions (a and d), O ions (b and e), and adsorbate (c–f) are individually presented. The relative energy (E_rel.) of each structure is given in parentheses. Atom numbers refer to labels defined in the methodology section.

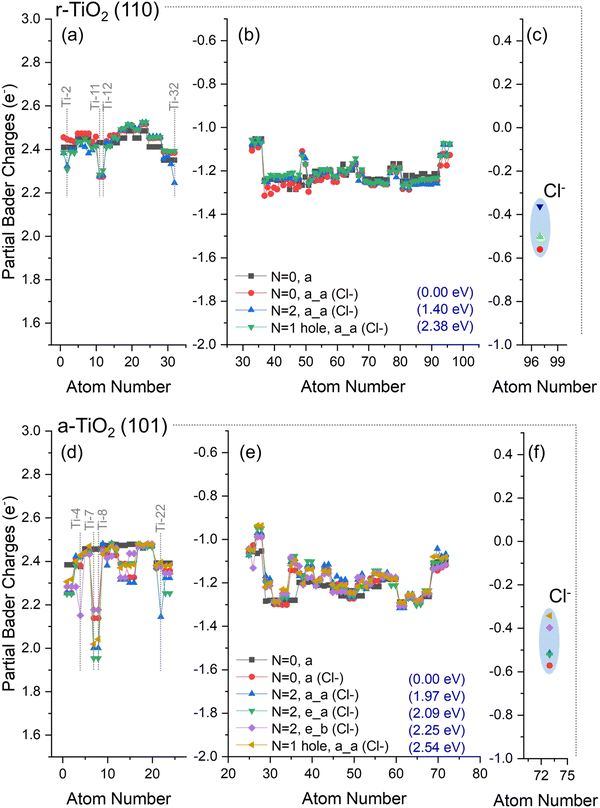
For calculations using Cl⁻/a-TiO₂ (101), three distinct structures for triplet state configurations were obtained (N = 2, a_a (Cl⁻), N = 2, e_a (Cl⁻), and N = 2, e_b (Cl⁻), Fig. 7e); however, the magnitudes of the localised charges over the surface atoms were significantly reduced when compared to the results from OH⁻/a-TiO₂ (101) (Fig. 6e). The hole-containing system (N = 1 hole, a_a (Cl⁻)) gave a partial Bader charge for the Cl atom of −0.34e, whereas the triplet “e–b” structure had a charge of −0.40e. For all other cases, the charge over Cl atom varied between −0.6e and −0.5e.

These results show that the presence of chloride over r-TiO₂ (110) and a-TiO₂ (101) reduces the ability of these systems to localise charges in their structure when compared to hydroxylated surfaces, indicating a chloride induced destabilisation of separated charges in titania and, consequently, a reduction in the formation of adsorbed hydroxyl radicals could be expected. In contrast, partial hole localisation over adsorbed chloride is highly favoured, confirming the hole sink character of this species. Although such observations can be used to rationalise the decrease of activity of anatase in brines, it does not explain why rutile activity was enhanced under the same conditions (Subsection 3.1). This point will be further discussed in the following subsection.

For Cl⁻/r-TiO₂ (110), the energy difference between triplet and ground state structures was 1.40 eV (Fig. 7a–c), whereas for Cl⁻/a-TiO₂ (101) this difference ranged between 1.97–2.25 eV (Fig. 7d–f). Interestingly, the energy to form triplet states structures from ground state titania in chloride-containing systems was similar to that of hydroxyl-containing systems for both anatase and rutile (Fig. 6). Consequently, the stability of adsorbed hydroxyl and chloride radicals are predicted to be comparable in both titania phases. This result is also confirmed when co-adsorption of hydroxyl and chloride anions is considered, as will be discussed next.

3.3.e. Simulating holes in co-adsorbed hydroxyl- and chloride-containing surfaces. In the final stage of this study, we investigated the hole self-trapping ability of r-TiO₂ (110) and a-TiO₂ (101) systems when both hydroxyl and chloride anions were co-adsorbed (Fig. 8a and b). Following the approach used in the previous subsections, local lattice distortion around O sites was used in order to facilitate the charge density localisation, allowing one and two partially localised holes to be created in the electronic structure of these systems.

Fig. 8 Hydroxyl and chloride anions co-adsorption over r-TiO₂ (110) and a-TiO₂ (101) surfaces (a and b) and charges over hydroxyl and chloride when considering one (a.i and b.i) and two hole-containing structures (a.ii and b.ii). Computed charges in singlet (ground) state OH⁻,Cl⁻/r-TiO₂ (110) and OH⁻,Cl⁻/a-TiO₂ (101) are also given for comparison.

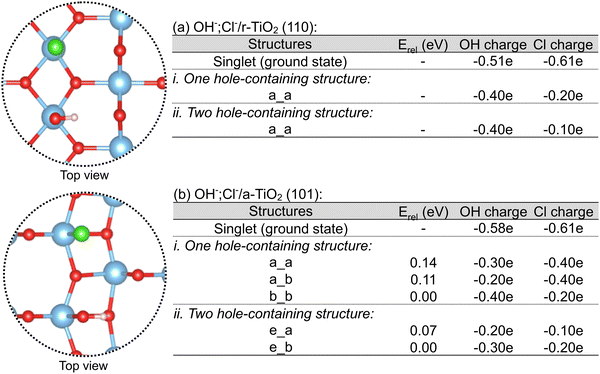
As shown in Fig. 8a, only one distinct structure was obtained for rutile in each of these cases, in which the hole density over chloride was always larger than that of the co-adsorbed hydroxyl. Additionally, when these charges are compared to the singlet (ground state) OH⁻,Cl⁻/r-TiO₂ (110) system, it is clear that there is a larger reduction of electron density (or increase of hole density) over chloride than over hydroxyl when holes are added to the electronic structure. For anatase, three and two distinct structures were obtained for the calculation considering one and two hole-containing structures (Fig. 8b), respectively. The most stable structures were those in which chloride bears higher hole density than hydroxyl. However, the calculated energy differences are small, ranging between 0.07 and 0.14 eV. Such a small difference suggests that adsorbed hydroxyl and chlorine radicals have comparable stabilities, as proposed in Subsection 3.3 d.

It is worth noting, however, that the formation of adsorbed hydroxyl radicals over titania is not thermodynamically, but kinetically controlled. As proposed by Geng et al.,⁶⁴ the energy barrier for forming adsorbed hydroxyl radical derives from the energy cost for concerted deprotonation and oxidation of adsorbed water molecules. These authors showed that rutile presents a high energy barrier for adsorbed hydroxyl radical formation, caused by the inhibition of proton transfer due to a strong hydrogen bonding network between solvent molecules, resulting in lower activity.⁶⁴ The same effect is not observed for a-TiO₂ (101), as weaker interactions between solvent molecules are expected.⁶⁴ This factor is one of a number of possible justifications for the distinct photocatalytic activities of anatase and rutile previously published^5,41,64–69 and, as mentioned in Subsection 3.2 c it is in agreement with our experimental results (Subsection 3.1). In contrast, formation of adsorbed chlorine radicals from chloride is a much simpler process and would not be hindered by solvent molecules. The energy cost for forming such a species can be expected to be very similar to that of creating charge separation in the system, as estimated in Fig. 7. In this case Cl˙/r-TiO₂ (110) could be formed at a lower energy cost than Cl˙/a-TiO₂ (101). In other words, rutile requires a higher energy to form an adsorbed hydroxyl radical than anatase; however, formation of adsorbed chlorine radical from adsorbed chloride could be kinetically favoured. This is a key observation to rationalise the enhancement of the photocatalytic activity of rutile in brines.

It has been reported by different authors that chloride radicals can decompose branched aromatics but would be ineffective for non-branched aromatic decomposition due to the endothermicity of this reaction, which was confirmed by Lewandowski et al. for hydrogen abstraction from benzene.¹¹ Interestingly, the slight endothermicity of hydrogen abstraction from phenol by chlorine radicals is a strong indicator that it could be surmounted due to the exothermicity of the overall degradation process.

All these factors lead us to hypothesise that the enhancement of the photocatalytic activity of rutile in brine could be due to the low concentration of adsorbed hydroxyl radicals formed in standard water and the relative higher surface concentration of adsorbed chlorine radicals in brine. In both polymorphs, adsorbed chlorides will act as hole scavengers (as shown by an increase of hole density over chlorides in contrast to hydroxyl) and by inhibition of charge localisation (as demonstrated by there being only one solution for the hole-containing structure, despite the multiple preliminary lattice distortion considered here). However, formation of adsorbed chlorine radicals over anatase would inhibit the formation of a hydroxyl radical rich surface, whereas for rutile a hydroxyl radical poor surface would be replaced by one with a relative high chlorine radical concentration. Although chlorine is slightly less reactive than hydroxyl radicals, the overall effect would still be an increase in the activity of this photocatalyst. These observations are in agreement with the observed changes in phenol degradation rate observed for these polymorphs in brine, as described in Subsection 3.1. It is worth mentioning, however, that future investigations will be required to confirm the proposed mechanism, in which kinetic effects for the formation of radicals should be taken in consideration, as well as their reactivity towards the target model molecule.

4. Summary and conclusions

In summary, we have investigated the changes in the photocatalytic activity of two titania polymorphs (anatase and rutile) during phenol degradation in standard water and brines. Under such conditions, we observed a significant reduction of the phenol conversion rate over anatase but an enhancement of rutile activity under the same reaction conditions. The origin of such diverging effects was investigated by periodic DFT methods, comparing the possibility of competitive adsorption of hydroxyl and chloride, as well as analysing the polaronic self-trapping ability of these systems.

Our calculations of adsorption at a-TiO₂ (101) and r-TiO₂ (110) surfaces showed that regardless of the model surface or its electronic state, adsorption of the hydroxyl anion is always more favourable than the chloride. Therefore, inhibition of oxidative photoactivity of these systems by blockage of surface sites is unlikely to occur. Nevertheless, the chloride might still be adsorbed in small amounts, resulting in the observed changes of titania activity.

The ability of chlorides to act as hole scavengers was also investigated. According to our approach, a-TiO₂ (101) and r-TiO₂ (110) systems are unable to localise holes in the absence of adsorbates. On the other hand, weak electron localisation was observed for both surfaces when considering triplet states or excess electrons in these systems. For the hydroxylated surfaces, OH⁻/r-TiO₂ (110) and OH⁻/a-TiO₂ (101), hole localisation was observed mainly on the hydroxyl, but also in the surrounding surface oxygen. Electron localisation was also present in both hydroxylated surfaces when considering triplet states; however, this effect was more significant in anatase than rutile.

Chlorinated surfaces – Cl⁻/r-TiO₂ (110) and Cl⁻/a-TiO₂ (101) – showed a significant reduction in their ability to localise holes and electrons, when compared to the hydroxylated system. For rutile, only delocalised charges were obtained during our calculations, except when the hole-containing electronic structure was considered, in which case the adsorbed chloride showed an increase in its hole density. When anatase was investigated, although distinct structures were found as solutions for the triplet state structure, the localisation of electron density to Ti ions was less significant than that observed for the hydroxylated surface. Additionally, partial hole localisation was also observed at the adsorbed chloride over a-TiO₂ (101). Overall, our results indicate that adsorbed chlorides are the preferred hole traps, even in the presence of co-adsorbed hydroxyl. Moreover, this anion can reduce or inhibit the ability of r-TiO₂ (110) and a-TiO₂ (101) systems to localise polarons in its structure. These results indicate that both mechanisms – hole scavenging and the inhibition of hole localisation – can lead to the observed chloride effect on titania photocatalytic activity. Interestingly, while the formation of adsorbed chlorines on anatase results in a reduction of its activity, the phenol decomposition rate over rutile is proposed to be enhanced due to its higher energy barrier to form adsorbed hydroxyl radicals in standard water and more facile adsorbed chlorines formation in brines. As noted, although chlorines are less reactive than hydroxyl radicals towards phenol degradation, the high concentration of the former in brines and low concentration of the latter in standard water could result in an overall increase of the observed activity of this polymorph.

Overall, our results reveal a decrease of anatase activity in brine, originating from hole scavenging and inhibition of hole localisation cause by adsorbed chlorides. Conversely, rutile exhibited an enhancement of phenol conversion rate in brine, which we hypothesise to occur due to high energy barriers for formation of hydroxyl radicals over rutile with a more facile formation of chlorine radicals, and phenol degradation being initiated by reaction of chlorine radicals. Nevertheless, further investigation of the energy barriers for the formation of radicals and their reactivity towards the target model molecule will be required to confirm the proposed Cl⁻ effect over rutile photoactivity. These findings provide fundamental insights into the photocatalytic properties of titania polymorphs and associated mechanisms for radical formation and oxidative decomposition of organic pollutants.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work used the computing facilities provided by ARCCA at Cardiff University (HPC Wales), GW4 Isambard ‘‘Phase 2’’ – ARM XC50 at Bristol University, and Cirrus UK National Tier-2 HPC Service at EPCC (https://www.cirrus.ac.uk) funded by the University of Edinburgh and EPSRC (EP/P020267/1). Additionally, via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431), this work used the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk) and the UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/T022213). UK Catalysis Hub is kindly thanked for resources and support provided via our membership of the UK Catalysis Hub Consortium and funded by EPSRC grant: EP/R026939/1, EP/R026815/1, EP/R026645/1, EP/R027129/1. XP spectra in the SI were acquired by EPSRC National Facility for Photoelectron Spectroscopy (HarwellXPS), operated by Cardiff University and UCL under contract number PR16195.

References

1. S. Kanan, M. A. Moyet, R. B. Arthur and H. H. Patterson, Catal. Rev.: Sci. Eng., 2020, 62, 1–65.
2. D. Kanakaraju, B. D. Glass and M. Oelgemöller, J. Environ. Manage., 2018, 219, 189–207.
3. D. J. Lapworth, N. Baran, M. E. Stuart and R. S. Ward, Environ. Pollut., 2012, 163, 287–303.
4. Q. Guo, Z. Ma, C. Zhou, Z. Ren and X. Yang, Chem. Rev., 2019, 119, 11020–11041.
5. Q. Guo, C. Zhou, Z. Ma and X. Yang, Adv. Mater., 2019, 31, 1–26.
6. C. McCullagh, N. Skillen, M. Adams and P. K. J. Robertson, J. Chem. Technol. Biotechnol., 2011, 86, 1002–1017.
7. D. Friedmann, C. Mendive and D. Bahnemann, Appl. Catal., B, 2010, 99, 398–406.
8. M. Krivec, R. Dillert, D. W. Bahnemann, A. Mehle, J. Štrancar and G. Dražić, Phys. Chem. Chem. Phys., 2014, 16, 14867–14873.
9. E. Bouleghlimat, D. Bethell and P. R. Davies, Chemosphere, 2020, 251, 126469.
10. C. Minero, G. Mariella, V. Maurino, D. Vione and E. Pelizzetti, Langmuir, 2000, 16, 8964–8972.
11. M. Lewandowski and D. F. Ollis, J. Catal., 2003, 217, 38–46.
12. W. Zhang, T. An, M. Cui, G. Sheng and J. Fu, J. Chem. Technol. Biotechnol., 2005, 80, 223–229.
13. N. Petit, A. Bouzaza, D. Wolbert, P. Petit and J. Dussaud, Catal. Today, 2007, 124, 266–272.
14. R. Yuan, T. Chen, E. Fei, J. Lin, Z. Ding, J. Long, Z. Zhang, X. Fu, P. Liu, L. Wu and X. Wang, ACS Catal., 2011, 1, 200–206.
15. R. Yuan, S. Fan, H. Zhou, Z. Ding, S. Lin, Z. Li, Z. Zhang, C. Xu, L. Wu, X. Wang and X. Fu, Angew. Chem., Int. Ed., 2013, 52, 1035–1039.
16. G. J. Hutchings, P. R. Davies, S. Pattisson, T. E. Davies, D. J. Morgan and M. W. Dlamini, Catal. Commun., 2022, 169, 106480.
17. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
18. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
19. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
20. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
21. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
22. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
23. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
24. D. Mahlberg, S. Sakong, K. Forster-Tonigold and A. Groß, J. Chem. Theory Comput., 2019, 15, 3250–3259.
25. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
26. D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
27. G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022.
28. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080.
29. C. Freysoldt, J. Neugebauer and C. G. Van De Walle, Phys. Rev. Lett., 2009, 102, 1–4.
30. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
31. N. C. Hernández, R. Grau-Crespo, N. H. De Leeuw and J. F. Sanz, Phys. Chem. Chem. Phys., 2009, 11, 5246–5252.
32. M. M. Branda, N. J. Castellani, R. Grau-Crespo, N. H. De Leeuw, N. C. Hernandez, J. F. Sanz, K. M. Neyman and F. Illas, J. Chem. Phys., 2009, 131, 094702.
33. Y. Nosaka and A. Nosaka, ACS Energy Lett., 2016, 1, 356–359.
34. B. Tryba, M. Toyoda, A. W. Morawski, R. Nonaka and M. Inagaki, Appl. Catal., B, 2007, 71, 163–168.
35. H. Park, H. Kim, G. Moon and W. Choi, Energy Environ. Sci., 2016, 9, 411–433.
36. W. Kim, T. Tachikawa, G. Moon, T. Majima and W. Choi, Angew. Chem., Int. Ed., 2014, 53, 14036–14041.
37. C. Prasse, B. Ford, D. K. Nomura and D. L. Sedlak, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2311–2316.
38. R. Alnaizy and A. Akgerman, Adv. Environ. Res., 2000, 4, 233–244.
39. G. Darabdhara, P. K. Boruah, P. Borthakur, N. Hussain, M. R. Das, T. Ahamad, S. M. Alshehri, V. Malgras, K. C. W. Wu and Y. Yamauchi, Nanoscale, 2016, 8, 8276–8287.
40. R. Su, R. Tiruvalam, Q. He, N. Dimitratos, L. Kesavan, C. Hammond, J. A. Lopez-Sanchez, R. Bechstein, C. J. Kiely, G. J. Hutchings and F. Besenbacher, ACS Nano, 2012, 6, 6284–6292.
41. Y. Nam, J. H. Lim, K. C. Ko and J. Y. Lee, J. Mater. Chem. A, 2019, 7, 13833–13859.
42. D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798–801.
43. A. R. Elmaslmane, M. B. Watkins and K. P. McKenna, J. Chem. Theory Comput., 2018, 14, 3740–3751.
44. D. Wang, H. Wang and P. Hu, Phys. Chem. Chem. Phys., 2015, 17, 1549–1555.
45. S. Kerisit, N. Aaron Deskins, K. M. Rosso and M. Dupais, J. Phys. Chem. C, 2008, 112, 7678–7688.
46. V. Shapovalov, E. V. Stefanovich and T. N. Truong, Surf. Sci., 2002, 498, 1–6.
47. J. J. Carey and K. P. McKenna, J. Phys. Chem. C, 2018, 122, 27540–27553.
48. J. J. Carey, J. A. Quirk and K. P. McKenna, J. Phys. Chem. C, 2021, 125, 12441–12450.
49. C. Di Valentin and A. Selloni, J. Phys. Chem. Lett., 2011, 2, 2223–2228.
50. N. M. Dimitrijevic, Z. V. Saponjic, B. M. Rabatic, O. G. Poluektov and T. Rajh, J. Phys. Chem. C, 2007, 111, 14597–14601.
51. J. M. Coronado, A. Javier Maira, A. Martínez-Arias, J. C. Conesa and J. Soria, J. Photochem. Photobiol. A Chem., 2002, 150, 213–221.
52. T. Berger, M. Sterrer, O. Diwald, E. Knözinger, D. Panayotov, T. L. Thompson and J. T. Yates, J. Phys. Chem. B, 2005, 109, 6061–6068.
53. T. Berger, M. Sterrer, O. Diwald and E. Knözinger, Chem. Phys. Chem., 2005, 6, 2104–2112.
54. S. K. Wallace and K. P. Mckenna, J. Phys. Chem. C, 2015, 119, 1913–1920.
55. S. Selcuk and A. Selloni, Nat. Mater., 2016, 15, 1107–1112.
56. C. C. Mercado, F. J. Knorr, J. L. McHale, S. M. Usmani, A. S. Ichimura and L. V. Saraf, J. Phys. Chem. C, 2012, 116, 10796–10804.
57. M. Chiesa, M. C. Paganini, S. Livraghi and E. Giamello, Phys. Chem. Chem. Phys., 2013, 15, 9435–9447.
58. P. Zawadzki, J. Phys. Chem. C, 2013, 117, 8647–8651.
59. M. Setvin, X. Hao, B. Daniel, J. Pavelec, Z. Novotny, G. S. Parkinson, M. Schmid, G. Kresse, C. Franchini and U. Diebold, Angew. Chem., Int. Ed., 2014, 53, 4714–4716.
60. N. A. Deskins, R. Rousseau and M. Dupuis, J. Phys. Chem. C, 2009, 113, 14583–14586.
61. C. J. Calzado, N. C. Hernández and J. F. Sanz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 1–10.
62. G. Di Liberto, S. Tosoni and G. Pacchioni, Phys. Chem. Chem. Phys., 2019, 21, 21497–21505.
63. J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919–9986.
64. Z. Geng, X. Chen, W. Yang, Q. Guo, C. Xu, D. Dai and X. Yang, J. Phys. Chem. C, 2016, 120, 26807–26813.
65. S. Tan, H. Feng, Y. Ji, Y. Wang, J. Zhao, A. Zhao, B. Wang, Y. Luo, J. Yang and J. G. Hou, J. Am. Chem. Soc., 2012, 134, 9978–9985.
66. A. Migani and L. Blancafort, J. Am. Chem. Soc., 2017, 139, 11845–11856.
67. Y. Ji, B. Wang and Y. Luo, J. Phys. Chem. C, 2014, 118, 21457–21462.
68. A. Y. Ahmed, T. A. Kandiel, T. Oekermann, C. Günnemann and D. Bahnemann, ACS Appl. Energy Mater., 2019, 2, 5308–5318.
69. T. Luttrell, S. Halpegamage, J. Tao, A. Kramer, E. Sutter and M. Batzill, Sci. Rep., 2015, 4, 1–8.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03140j

---