Harnessing osmotic swelling stress for robust hydrogel actuators
Xitao
He
ab,
Jie
Zhu
b and
Canhui
Yang
 *ab
*ab
aShenzhen Key Laboratory of Soft Mechanics & Smart Manufacturing, Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, 518055, P. R. China. E-mail: yangch@sustech.edu.cn
bSoft Mechanics Lab, Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, 518055, P. R. China
First published on 30th June 2022
Abstract
The volumetric expansion of hydrogels driven by osmotic swelling stress has enabled hydrogel actuators for myriad applications. However, most existing studies disregard optimizing the osmotic swelling stress for powerful actuation and simply utilize the osmotic swelling stress to trigger certain modes of actuation. In this work, we probe the osmotic swelling stress of hydrogels using polyacrylamide as a model system. We design and perform constrained swelling experiments to measure the osmotic swelling stresses at different levels of constraint and compare the results to the theoretical predictions based on the Flory–Huggins model. We optimize the osmotic swelling properties by tuning the constituents and structures of the hydrogel and achieve an enhancement of the magnitude of actuation stress from ∼180 kPa to ∼400 kPa. As a proof of concept, we demonstrate a robust hydrogel jack that can lift a weight 2000 times its own weight by harnessing the high osmotic swelling stress. The feasibility and limits of harnessing the osmotic swelling stress of hydrogels for actuation are discussed.
Introduction
Submerged in water, a hydrogel often tends to imbibe water and swell. The imbibition of water is driven by the osmotic pressure difference between the interior of the hydrogel and the surrounding aqueous environment, in response to various external stimuli such as solvent,1 ions,2 temperature,3 pH,4 electric field,5 magnetic field,6 and light.7 The swelling causes a hydrogel to expand its volume, enabling soft hydrogel actuators for applications as diverse as soft machines,8 soft robotics,9 tunable optics,10 smart microvalves,11 biomedicine,12 and artificial muscles.13As a hydrogel swells, the osmotic pressure decreases, and the polymer network of the hydrogel is stretched, exerting elastic restoring stress. The resultant of the osmotic pressure and the elastic restoring stress determines the apparent swelling stress, which is essentially the driving force for hydrogel actuators.14 As such, the magnitude of the osmotic swelling stress of a hydrogel actuator predominately depends on the extent of swelling. Osmotic pressure can be very large, and the osmotic swelling stress, in principle, can be as large as the osmotic pressure, so long as the polymer network of the hydrogel is entropic and barely deformed.15 Salient examples of large osmotic swelling stress comprise the expansion of wooden wedges after absorbing water, which might have allowed the ancient Egyptians to mine megaliths,16 and the growth of plant roots that destroys rocks. In synthetic hydrogels, osmotic stress of 45 MPa has been realized using poly(N-isopropyl acrylamide) hydrogel.17 Very recently, it has been reported that robust actuators of actuating stress on the order of 1 MPa can be achieved using hydrogels by invoking the turgor pressure.18 Nevertheless, most existing studies so far have overlooked the optimization of the actuating stress and simply utilize the osmotic swelling stress to trigger certain modes of actuation.19 Quantifying the osmotic swelling stress is of great importance for the applications of hydrogel actuators, for instance, to make the utmost of the osmotic pressure and to construct the force-stroke relationship,20 which is crucial information for an actuator in practice,21,22 but the paucity of such quantification persists to date.
In this work, we fill the paucity by quantifying the osmotic swelling stress of hydrogels using polyacrylamide as a model material. We design a constrained swelling test to measure the osmotic swelling stress, characterized by the blocking stress, and compare the experimental results to the theoretical predictions derived from the Flory–Huggins model. Subsequently, we optimize the osmotic swelling properties, including the magnitude of osmotic swelling stress and the swelling kinetics, by varying the components and structures of the polyacrylamide hydrogel. We obtain osmotic swelling stress ∼400 kPa and a characteristic response time of about 3.6 minutes for a 500 μm thick sample. Using the optimized version, we demonstrate the use of a hydrogel actuator as a robust hydrogel jack that can lift a weight 2000 times its own weight. We enclose the current study by discussing the design space and the lift efficiency of hydrogel actuators.
Results and discussion
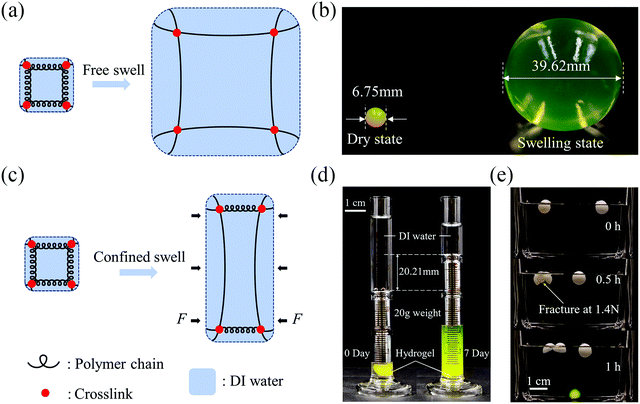
We first examine the swelling behaviors of hydrogels with/without constraint. Take a covalently crosslinked single-network hydrogel as an example. Recall that the free energy of a hydrogel results from two molecular processes: stretching the polymer network and mixing the polymers and the water molecules, and can be described as W = Ws + Wm, where Ws accounts for the strain energy due to stretching and Wm accounts for mixing.23 When a hydrogel undergoes free swelling (Fig. 1(a)), water molecules migrate into the polymer network due to the osmotic pressure, resulting in the uniform extension of the polymer chains in all directions. The absorption of water lessens the osmotic pressure. The stretch of polymer chains induces elastic restoring stress due to entropy and exposes more polymer segments for mixing. The osmotic pressure facilitates while the entropic elasticity prohibits the inward water migration. The equilibrium state is reached once the osmotic pressure balances with the elastic restoring stress. We illustrate the free swelling of the hydrogel by soaking a dry sodium polyacrylate hydrogel ball in deionized water. After swelling, the volume of the ball expands more than 200 times (Fig. 1(b)). Note that the mechanical strength of the hydrogel will deteriorate with swelling, due to the dilution of the polymer chains by water, and the fragile hydrogel might fracture during swelling.Unlike free swelling, when a hydrogel undergoes confined swelling, the polymer chains can only extend in the unconfined direction whereas a blocking force will be exerted in the confined direction to prevent swelling (Fig. 1(c)). The blocking force, the resultant of the osmotic swelling stress determined by the difference between the osmotic pressure and the elastic restoring stress, can be manipulated for actuation. We demonstrate the osmotic swelling stress using two simple examples. In one example, we put a dry sodium polyacrylate hydrogel ball into a 5 ml measuring cylinder, place a 20 g weight on it, and then add deionized water. Because of the constraint of the measuring cylinder, the hydrogel ball can only swell in the vertical direction after it reaches the boundary of the inner wall. After 7 days, the lifting height of the weight plateaus at about 20.21 mm, corresponding to a swelling ratio of the hydrogel of ∼9 (Fig. 1(d)). The 20 g weight corresponds to the nominal compressive stress of about 2.5 kPa, which apparently is not adequate to completely block the swelling of the hydrogel. In another example, we wrap the hydrogel ball with a paraffin shell drilled with holes at both ends. The swelling of the hydrogel ball renders hoop stress to break the paraffin shell, whose strength is measured to be about 12.4 kPa, while the paraffin shell without hydrogel remains intact (Fig. 1(e)).
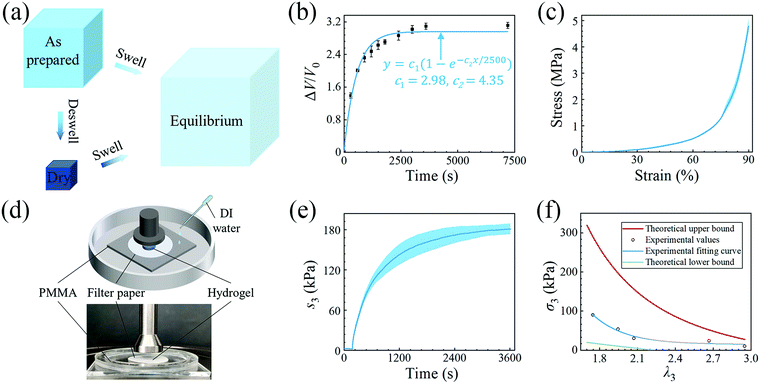
We then quantitatively characterize the swelling using polyacrylamide (PAAM) hydrogel. We synthesize a PAAM hydrogel with ∼75% water, by weight, as the reference. Briefly, 3.6 g acrylamide is dissolved in 10 ml deionized water, followed by adding 400 μl of 0.1 mol L−1N,N′ methylene bis(acrylamide), and 400 μl of 0.1 mol L−1 α-ketoglutaric acid as the crosslinker and the initiator, respectively. Because the amounts of the crosslinker and the initiator are tiny, their weights are neglected and only the weights of monomer and water are accounted for. After homogeneous mixing and defoaming, the precursor is injected into a glass mold with a 500 μm thick spacer and cured under UV light for 1 hour. As shown in Fig. 2(a), at the as-prepared state, the PAAM network can be regarded as swollen with an isotropic stretch of λ0 with respect to the dry state. After swelling to the equilibrium state, the PAAM network has stretches of λ1/λ0, λ2/λ0, and λ3/λ0 with respect to the as-prepared state and λ1, λ2, and λ3 with respect to the dry state. Although the PAAM network must be stress-free at the as-prepared state, we will determine the state of the hydrogel by taking the dry state as the datum in the following sections.
We conduct free swelling for the PAAM hydrogel and measure the volume ratio ΔV/V0, where ΔV is the difference between the volume at the current state V and the volume at the as-prepared state V0, as a function of time (Fig. 2(b)). Assuming that the total volume of hydrogel is equal to the sum of the volume of the dry PAAM network, Vdry, and the volume of water, we measure the mass of the hydrogel and calculate the volume at the current state as
| V = Vdry + (mH − mp)/ρw | (1) |
Since free swelling is generally insufficient in generating large actuation force,18,20 we improve the osmotic swelling stress using constraints. We design an experimental setup for measurement (Fig. 2(d)). We prepare the hydrogel sample into a 10 mm diameter disc, place it on a piece of 15 mm diameter filter paper, and then on a piece of acrylate sheet inside a container. The top surface of the hydrogel sample is contacted by the 20 mm diameter loading head of a mechanical testing machine (INSTRON 5966). A preload of 0.2 N is applied to guarantee intimate contact between the loading head and the hydrogel and then the position of the loading head is held. After that, deionized water is infused into the container to swell the hydrogel. The filter paper is porous, allowing the hydrogel to swell as if its bottom surface were free. The swelling of the hydrogel is blocked by the loading head. The force recorded by the machine is normalized by the area of the hydrogel measured at the as-prepared state and plotted against time in Fig. 2(e). After saturation in about 1 hour, the maximum osmotic swelling stress, i.e. blocking stress, of ∼180 kPa is obtained. When the blocking force supplied by the loading head is reduced, the hydrogel pushes the loading head upward by a distance before reaching equilibrium, increasing the stretch in the vertical direction. We vary the blocking force and obtain the true block stress as a function of λ3 (hollow circles in Fig. 2(f)). The true block stress is calculated based on the measurement of the area of the sample after the experiment. The experimental data are fitted to the following formular:24σ = 1058(λ3−1)4.47.
We observe that the area of the hydrogel increases considerably after the experiment, implying that the filter paper does not constrain the deformation of the hydrogel in lateral directions, i.e. λ1 ≠ λ0, λ2 ≠ λ0. Recall that the chemo-mechanical behaviors of the hydrogel can be described by invoking the theory of an ideal elastomeric gel, whereby the equations of state of the swelling hydrogel can be written as20
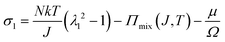 | (2) |
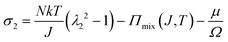 | (3) |
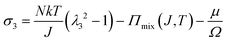 | (4) |
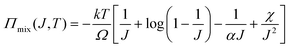 | (5) |
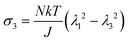 | (6) |
The upper bound (red curve in Fig. 2(f)) is obtained based on eqn (4) and (5) when the lateral deformation is completely constrained, i.e. λ1 = λ2 = λ0. The experimental data fall in-between the green and red curves, implying a certain degree of in-plane constraint, which is presumably caused by the friction at the interfaces. Indeed, we measure the friction coefficient between the hydrogel and a steel indenter to be 0.29 using a rheometer.26 Although a reliable friction coefficient between the hydrogel and the filter paper is difficult to measure, it should be larger because of the rougher surface. Additionally, it should be noted that we have used the Flory–Huggins model, which assumes dilute solution,27 without any modification, which, however, has long been proven feasible in describing the behaviors of hydrogels.14
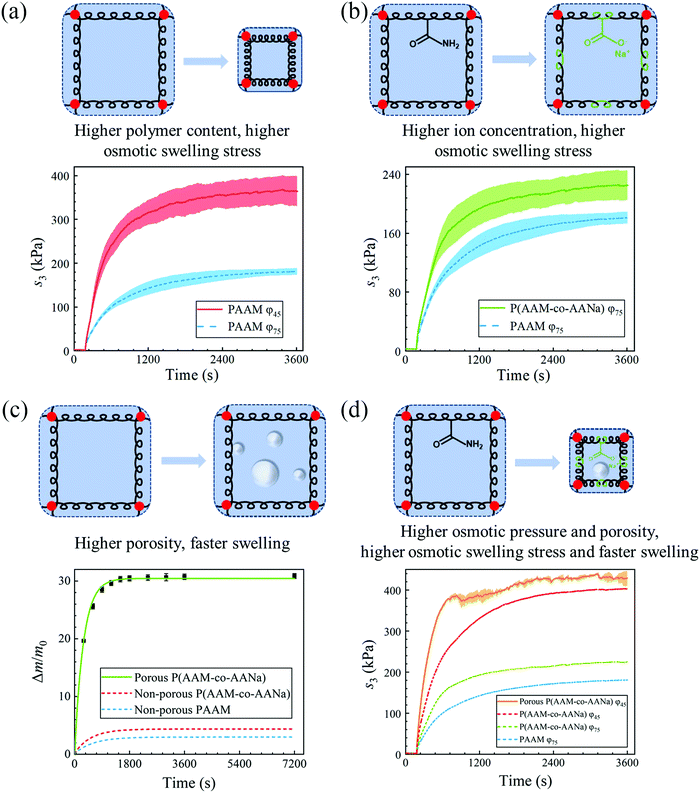
Now that we have quantitatively measured the osmotic swelling stress of PAAM hydrogel containing 75% water, next we try to optimize its osmotic swelling properties. One conspicuous way is to increase the osmotic pressure of the hydrogel. We do so by two methods. First, we increase the polymer content by dehydrating the as-prepared hydrogel sample to 45% water content (Fig. 3(a)). Deswelling does not induce elastic restoring stress since the relaxed polymer chains in the as-prepared state remain relaxed after dehydration,28 yet it causes an increment in the shear modulus of the hydrogel since the number of polymer chains per unit volume is enlarged. As expected, the saturated nominal osmotic swelling stress escalates, to ∼364 kPa, which corresponds to an improvement of more than 100% compared to that of the as-prepared hydrogel. Second, we increase the ion concentration by replacing one-quarter of the acrylamide monomers with sodium acrylate while keeping the same water content. The copolymerization yields poly(acrylamide-co-sodium acrylate) (P(AAM-co-AANa)) (Fig. 3(b)), and the saturated nominal osmotic swelling stress increases from ∼180 kPa to ∼225 kPa accordingly.
Apart from the magnitude of the osmotic swelling stress, the response speed can be pivotal for hydrogel actuators and sometimes even becomes the primary concern.29 The osmotic swelling of hydrogel is accomplished by the diffusion of water through the polymer network, an intrinsically slow molecular process. We assuaged this issue by imparting the hydrogel matrix with bubbles, which are generated from the reaction of acrylic acid and sodium bicarbonate within the precursor of the hydrogel before curing. The time for reaching (1 − e−1) equilibrium swelling, referred to as the time constant, is shortened from ∼10 minutes for the non-porous PAAM hydrogel to ∼5 minutes for the porous P(AAM-co-AANa) hydrogel (Fig. 3(c)). In addition, the porous P(AAM-co-AANa) hydrogel possesses a much larger swelling ratio, ∼31, with respect to the mass of the as-prepared state, and ∼170, with respect to the mass of the dry polymer. The large swelling ratio is ascribed to the reduction of effective stiffness due to the presence of pores on one hand, and to the uptake of water due to the filling of the pores on the other hand. Note that the swelling ratio here is represented by weight, since the expansion of the volume of the pores from an empty state to water-filled state confounds the swelling ratio of the porous hydrogel. The residual sodium acrylate will dissociate fully into sodium ions and acrylate ions to increase the ion concentration, which expedites the swelling process. To exclude this confounding effect, we also synthesize non-porous P(AAM-co-AANa) hydrogel containing the same amount of sodium acrylate and measure its swelling ratio as a function of time. It can be seen from Fig. 3(c) that, whereas the swelling ratio increases a bit, the swelling speed only changes slightly. Within the first-order linear paradigm, we estimate the time constant to be ∼9 minutes. Based on the preceding results, we further synthesize a porous P(AAM-co-AANa) hydrogel with 45% water and achieve the highest osmotic swelling stress, ∼400 kPa, with the shortest swelling time, ∼3.6 minutes, for the stress to increase from the addition of deionized water to (1 − e−1) × 100% of the maximum value (Fig. 3(d)). Also plotted for comparison is the nominal stress–time curves of non-porous PAAM hydrogels with 75% water and non-porous P(AAM-co-AANa) hydrogel with 75% and 45% water. According to eqn (4), assuming that the chemical potential of water is zero and the temperature is constant, the osmotic swelling stress at a given swelling ratio will be larger when the shear modulus of the hydrogel is smaller. The porous P(AAM-co-AANa) hydrogel has a smaller modulus than that of the non-porous P(AAM-co-AANa) hydrogel, so that its osmotic swelling stress is higher.
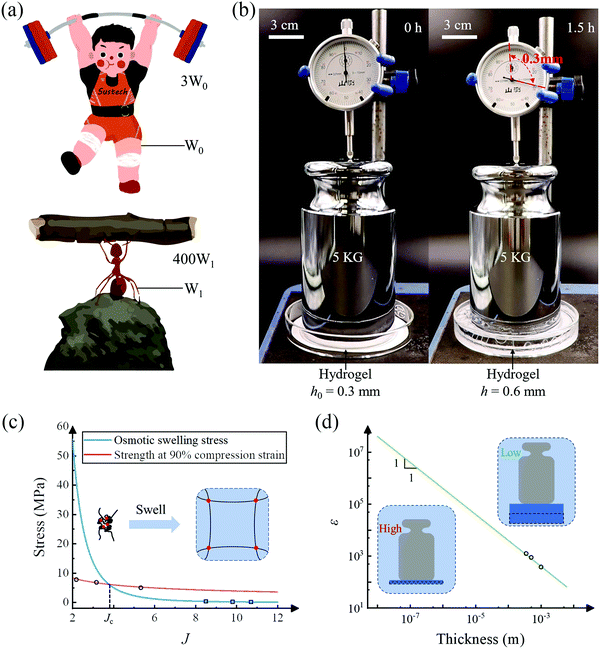
One of the major working modes of hydrogel actuators is to displace an object by a certain distance. Such an operation resembles the scenario of weightlifting. In nature, a weightlifter can at most lift a barbell about three times his/her weight, and the natural Hercules, ants, can lift an object as large as about 400 times their own weight (Fig. 4(a)). For hydrogel actuators, we define a successful lift as elevating a weight by a distance not less than the thickness of the hydrogel and the lift efficiency as the weight lifted divided by the weight of the hydrogel. We prepare a piece of 0.3 mm thick porous P(AAM-co-AANa) hydrogel containing 45% water and put on it a 5 kg weight, whose top surface is connected to a micrometer (Fig. 4(b)). After swelling in water for 1.5 hours, the hydrogel functions like a jack that successfully lifts the weight by 0.3 mm, corresponding to a lift efficiency of 2000. A hydrogel actuator can be a robust hydrogel jack.
As mentioned before, the osmotic swelling stress of a hydrogel is the competing resultant of the osmotic pressure and the elastic restoring stress of the polymer network. Whereas the osmotic pressure can approach infinite theoretically, refer to eqn (5), the mechanical strength of the polymer network is finite. In this sense, the osmotic swelling stress is bottlenecked by the strength of the hydrogel. According to the Flory–Huggins theory,23 both the osmotic pressure and the mechanical strength decrease with the swelling ratio J. In the constrained swelling experiment, the maximum blocking stress is obtained by completely blocking the swelling of the as-prepared/dehydrated sample in the vertical direction. The elastic restoring stress at the as-prepared/dehydrated state is zero such that the maximum blocking stress equates to the osmotic pressure if the lateral deformations are completely restricted.18 Consequently, for a hydrogel of decent mechanical strength, there exists a critical swelling ratio Jc, above which the strength is larger than the osmotic swelling stress and the hydrogel actuator will operate reliably (Fig. 4(c)). Taking the non-porous PAAM hydrogel as an example, we measure the osmotic swelling stresses at 75%, 60%, and 45% water contents and fit the data (hollow squares) through y1 = 602.7x−3.447. On the other hand, we also measure the strength of the hydrogels at 90% uniaxial compression strain and fit the data (hollow circles) through y2 = 11.51x−0.4792. The stress level at 90% uniaxial compression strain is purposely taken as the strength for the sake of the safety of the testing machine. Note here that the strength is measured at the as-prepared state while the osmotic swelling stress is measured at the swollen state. The strength is higher than the osmotic swelling stress after swelling and the hydrogel maintains integrity as observed in the experiments. A critical swelling ratio of Jc = 3.73 is obtained.
We define the lift efficiency (ε) of a hydrogel actuator as the ratio of the maximum mass it can lift (at least by a height of its thickness) over its mass: ε = σ/ρgh, where ρ and h are the density and the thickness of the hydrogel, and g is the gravitational acceleration. We extrapolate the blue curve in Fig. 2(f) and obtain a lift efficiency of ε ≈ 1000 for the 500 μm thick non-porous PAAM hydrogel, corresponding to the middle hollow circle in Fig. 4(d). We also test the lifting efficiency of 350 μm and 1000 μm thick PAAM hydrogels and the experimental results are in good agreement with the prediction. Since the output force, namely the result of osmotic swelling stress, is independent of the thickness whilst the lift efficiency is inversely proportional to the thickness, one can anticipate that the theoretical maximum of lift efficiency is achieved when the thickness of the hydrogel actuator levels off to the mesh size of the polymer network. Depending on the constituents, the mesh size of a hydrogel typically ranges from 10–100 nm.30 In this sense, the lift efficiency on the order of 1000 we have accomplished using hundreds of micrometers thick hydrogel is far from optimal.
It should be pointed out that, throughout the experiments, we have used the single-network PAAM hydrogel which has limited mechanical strength. When the osmotic swelling swell is set by the strength, hydrogels of higher strength are ready to be chosen, such as double-network hydrogels,31–33 nanofiber-reinforced hydrogels,34 and topological hydrogels.35 For the promotion of swelling kinetics, connected pores36 or microchannels via freeze-casting37 can be constructed within the hydrogel matrix. Nonetheless, careful attention should be paid since introducing voids into the matrix generally compromises the mechanical properties.
Conclusions
In conclusion, we have investigated the osmotic swelling stress of hydrogels by taking the PAAM hydrogel as the specific embodiment. Compared to previous studies invoking the osmotic swelling stress simply for actuation demonstrations, the emphasis of this work is placed on optimizing the magnitude of the osmotic swelling stress. Several strategies for optimizations are proposed and validated experimentally. A robust hydrogel jack that can lift a weight 2000 times its own weight is achieved.Harnessing the osmotic swelling stress of hydrogels has enormous practical meaning. For example, instead of the qualitative trial and error demonstrations, which are often time-consuming and expensive, quantitative design and optimization allow for the efficient tailoring and programming of hydrogel actuators and hydrogel soft robots.8,9 As another example, the capability of hydrogel actuators has not been exploited fully.18 There is much room for fabricating robust hydrogel actuators of large payloads and large output force. Furthermore, the escalation of the lift efficiency with the decline of the thickness signifies the miniaturization of hydrogel actuators for small-scale hydrogel-based microactuators and microrobots such as microlenses10 and drug vehicles.38 It is envisioned that more innovative hydrogel actuators will be designed and fabricated to fulfill extreme tasks that were previously inaccessible by pushing the limits of hydrogels.
Author contributions
X. H. and C. Y. conceived the idea and designed the study. X. H. prepared the samples and conducted the tests. X. H., J. Z., and C. Y. analyzed and interpreted the results. X. H. and C. Y. wrote the manuscript with inputs from all authors. C. Y. supervised the study.Conflicts of interest
The authors declare that there are no conflicts of interest.Acknowledgements
The work at the Southern University of Science and Technology is supported by the Natural Science Foundation of Guangdong Province (2214050008118), the Stable Support Plan Program of Shenzhen Natural Science Fund Grant (K21326303), and the Science, Technology and Innovation Commission of Shenzhen Municipality under grant no. ZDSYS20210623092005017.References
- J.-F. Louf, N. B. Lu, M. G. O’Connell, H. J. Cho and S. S. Datta, Sci. Adv., 2021, 7, eabd2711 CrossRef PubMed.
- V. Kozlovskaya, E. Kharlampieva, M. L. Mansfield and S. A. Sukhishvili, Chem. Mater., 2006, 18, 328–336 CrossRef CAS.
- J. Zheng, P. Xiao, X. Le, W. Lu, P. Theato, C. Ma, B. Du, J. Zhang, Y. Huang and T. Chen, J. Mater. Chem. C, 2018, 6, 1320–1327 RSC.
- R. Marcombe, S. Cai, W. Hong, X. Zhao, Y. Lapusta and Z. Suo, Soft Matter, 2010, 6, 784–793 RSC.
- D. Morales, E. Palleau, M. D. Dickey and O. D. Velev, Soft Matter, 2014, 10, 1337–1348 RSC.
- H. Haider, C. H. Yang, W. J. Zheng, J. H. Yang, M. X. Wang, S. Yang, M. Zrínyi, Y. Osada, Z. Suo and Q. Zhang, Soft Matter, 2015, 11, 8253–8261 RSC.
- S.-L. Xiang, Y.-X. Su, H. Yin, C. Li and M.-Q. Zhu, Nano Energy, 2021, 85, 105965 CrossRef CAS.
- X. Liu, J. Liu, S. Lin and X. Zhao, Mater. Today, 2020, 36, 102–124 CrossRef CAS.
- Y. Lee, W. J. Song and J.-Y. Sun, Mater. Today Phys., 2020, 100258 CrossRef.
- L. Dong, A. K. Agarwal, D. J. Beebe and H. Jiang, Nature, 2006, 442, 551–554 CrossRef CAS PubMed.
- D. J. Beebe, J. S. Moore, J. M. Bauer, Q. Yu, R. H. Liu, C. Devadoss and B.-H. Jo, Nature, 2000, 404, 588–590 CrossRef CAS PubMed.
- H. Qin, T. Zhang, N. Li, H.-P. Cong and S.-H. Yu, Nat. Commun., 2019, 10, 2202 CrossRef PubMed.
- N. Park and J. Kim, Adv. Intell. Syst., 2020, 2, 1900135 CrossRef.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, J. Mech. Phys. Solids, 2008, 56, 1779–1793 CrossRef CAS.
- Q. Liu and Z. Suo, Extreme Mech. Lett., 2016, 7, 27–33 CrossRef.
- D. A. Stocks, Experiments in Egyptian archaeology: stoneworking technology in ancient Egypt, Routledge, 2013 Search PubMed.
- S. Juodkazis, N. Mukai, R. Wakaki, A. Yamaguchi, S. Matsuo and H. Misawa, Nature, 2000, 408, 178–181 CrossRef CAS PubMed.
- H. Na, Y.-W. Kang, C. S. Park, S. Jung, H.-Y. Kim and J.-Y. Sun, Science, 2022, 376, 301–307 CrossRef CAS PubMed.
- X. Le, W. Lu, J. Zhang and T. Chen, Adv. Sci., 2019, 6, 1801584 CrossRef PubMed.
- W. R. K. Illeperuma, J.-Y. Sun, Z. Suo and J. J. Vlassak, Soft Matter, 2013, 9, 8504–8511 RSC.
- G. M. Spinks, L. Liu, G. G. Wallace and D. Zhou, Adv. Funct. Mater., 2002, 12, 437–440 CrossRef CAS.
- R. Kornbluh, R. Pelrine, J. Eckerle and J. Joseph, 1998.
- P. Flory and J. Rehner, Chem. Phys., 1943, 11, 521–526 CAS.
- Y. Lou, A. Robisson, S. Cai and Z. Suo, J. Appl. Phys., 2012, 112, 034906 CrossRef.
- J. Li, Y. Hu, J. J. Vlassak and Z. Suo, Soft Matter, 2012, 8, 8121–8128 RSC.
- J. P. Gong, G. Kagata and Y. Osada, J. Phys. Chem. B, 1999, 103, 6007–6014 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- Z. Li, Z. Liu, T. Y. Ng and P. Sharma, Extreme Mech. Lett., 2020, 35, 100617 CrossRef.
- M. Li, X. Wang, B. Dong and M. Sitti, Nat. Commun., 2020, 11, 1–10 CrossRef PubMed.
- C. Yang and Z. Suo, Nat. Rev. Mater., 2018, 3, 125 CrossRef CAS.
- J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Adv. Mater., 2003, 15, 1155–1158 CrossRef CAS.
- J. Y. Sun, X. Zhao, W. R. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed.
- C. H. Yang, M. X. Wang, H. Haider, J. H. Yang, J.-Y. Sun, Y. M. Chen, J. Zhou and Z. Suo, ACS Appl. Mater. Interfaces, 2013, 5, 10418–10422 CrossRef CAS PubMed.
- J. Ni, S. Lin, Z. Qin, D. Veysset, X. Liu, Y. Sun, A. J. Hsieh, R. Radovitzky, K. A. Nelson and X. Zhao, Matter, 2021, 4, 1919–1934 CrossRef CAS.
- C. Liu, N. Morimoto, L. Jiang, S. Kawahara, T. Noritomi, H. Yokoyama, K. Mayumi and K. Ito, Science, 2021, 372, 1078–1081 CrossRef CAS PubMed.
- Z. Wu, P. Zhang, H. Zhang, X. Li, Y. He, P. Qin and C. Yang, J. Hazard. Mater., 2022, 421, 126754 CrossRef CAS PubMed.
- Y. Alsaid, S. Wu, D. Wu, Y. Du, L. Shi, R. Khodambashi, R. Rico, M. Hua, Y. Yan and Y. Zhao, Adv. Mater., 2021, 33, 2008235 CrossRef CAS PubMed.
- J. Li and D. J. Mooney, Nat. Rev. Mater., 2016, 1, 1–17 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |