Open Access Article
Open Access ArticleGraph-convolutional neural networks for (QM)ML/MM molecular dynamics simulations†
Albert
Hofstetter
 ,
Lennard
Böselt
,
Lennard
Böselt
 and
Sereina
Riniker
and
Sereina
Riniker
 *
*
Laboratory of Physical Chemistry, ETH Zürich, Vladimir-Prelog-Weg 2, 8093 Zürich, Switzerland. E-mail: sriniker@ethz.ch; Tel: +41 44 633 42 39
First published on 15th September 2022
Abstract
To accurately study the chemical reactions in the condensed phase or within enzymes, both quantum-mechanical description and sufficient configurational sampling are required to reach converged estimates. Here, quantum mechanics/molecular mechanics (QM/MM) molecular dynamics (MD) simulations play an important role, providing QM accuracy for the region of interest at a decreased computational cost. However, QM/MM simulations are still too expensive to study large systems on longer time scales. Recently, machine learning (ML) models have been proposed to replace the QM description. The main limitation of these models lies in the accurate description of long-range interactions present in condensed-phase systems. To overcome this issue, a recent workflow has been introduced combining a semi-empirical method (i.e. density functional tight binding (DFTB)) and a high-dimensional neural network potential (HDNNP) in a Δ-learning scheme. This approach has been shown to be capable of correctly incorporating long-range interactions within a cutoff of 1.4 nm. One of the promising alternative approaches to efficiently take long-range effects into account is the development of graph-convolutional neural networks (GCNNs) for the prediction of the potential-energy surface. In this work, we investigate the use of GCNN models – with and without a Δ-learning scheme – for (QM)ML/MM MD simulations. We show that the Δ-learning approach using a GCNN and DFTB as a baseline achieves competitive performance on our benchmarking set of solutes and chemical reactions in water. This method is additionally validated by performing prospective (QM)ML/MM MD simulations of retinoic acid in water and S-adenoslymethionine interacting with cytosine in water. The results indicate that the Δ-learning GCNN model is a valuable alternative for the (QM)ML/MM MD simulations of condensed-phase systems.
1 Introduction
A key goal of computational chemistry is the molecular level understanding of chemical reactions in solution and enzymes. For this, the free-energy change (rather than the change in potential energy) during a reaction process is the central property. To calculate free-energy differences, molecular dynamics (MD) simulations from tens of picoseconds to hundreds of nanoseconds are typically required to obtain sufficiently converged results. While classical force fields can be used for MD simulations of condensed-phase systems over long time scales,1,2 higher level quantum-mechanical (QM) methods are required for an accurate description of molecular interactions and chemical reactions. Unfortunately, QM calculations are much more computationally intensive, limiting the accessible time and spatial scales.In order to overcome this bottleneck, the combined QM and molecular mechanical (QM/MM) approach provides a QM description of the region of interest (QM zone) coupled with a realistic modelling of the long-range interactions of the surrounding condensed-phase system (MM zone).3–6 The interaction between the zones is then calculated based on either mechanical constraints (i.e., a “mechanical embedding” scheme) or electronic perturbations (i.e., an “electrostatic embedding” scheme). Generally, the electrostatic embedding scheme has been shown to be more accurate and it is currently the gold standard for QM/MM simulations.5,7–10 In the QM/MM scheme, the QM zone requires electronic structure calculations at each time step and is thus the computational bottleneck. While the computational costs of QM/MM MD simulations are reduced compared to full ab initio simulations, the accessible time and spatial scales are still not sufficient for most free-energy calculations. This issue can be partially circumvented by using semi-empirical methods to describe the QM zone.9,11,12 However, this reduces not only the computational cost but also the achievable accuracy. An alternative is to use machine-learned (ML) potentials to describe the QM zone.
In recent years, there have been major advances in the development of ML models trained to reproduce the potential-energy surface (PES) of chemical systems.13–28 For small-to-medium sized compounds in the gas phase or in periodic materials, state-of-the-art ML models have been shown to achieve chemical accuracy, for both the predicted energies and forces.20–24,29 However, condensed-phase systems pose an additional challenge to ML models due to the typically large number of involved atoms, element types, and rotatable bonds without any exploitable symmetries, and important long-range interactions and non-local charge transfer. In particular, the long-range interactions and the non-local charge transfer currently limit the established ML methods, as these often rely on local descriptors and are thus unable to take global changes in the electronic structure into account.26,30,31 There are two main approaches to overcome this locality dependence of the descriptors used in the current ML models. Either non-local information transfer is incorporated directly in the ML models26,30–32 or ML methods are combined with a fast or semi-empirical QM method with an explicit treatment of long-range interactions in a Δ-learning scheme.33–36 The Δ-learning approach has already been shown to be promising for the (QM)ML/MM MD simulations of condensed-phase systems.34–36
Next to the descriptor-based approaches, there has also been a lot of development on message passing approaches trained to reproduce the PES of QM systems.22,23,37–39 These graph networks typically use dense layers of neural networks as non-linear functions for the message passing convolutions and are thus known as graph-convolutional neural networks (GCNNs). One of the main advantages of GCNNs compared to descriptor-based ML models is that no specialized descriptors have to be developed for chemical systems. Instead, this is achieved directly through the graph-convolutional layers. A further advantage is that through iterative message passing operations more distant information is taken into account and thus the local dependence of descriptor based models can be (partially) avoided. However, each consecutive convolution substantially increases the model size. Thus, in practice, long-range contributions are terminated at a certain cutoff and global changes in the electronic structure are not considered. To address this issue, the total energy can be separated into a short-range electrostatic term and a long-range electrostatic term, for which a GCNN is used to predict atomic charges.23,31 Furthermore, long-range charge transfer and global changes in the electronic structure may be taken into account by including a global state or a self-attention mechanism in the message passing operation.23,31,32,40
In this work, we assess the applicability of GCNNs to reproduce the PES of condensed-phase systems and their use in (QM)ML/MM MD simulations. For this, we validate a GCNN model with and without a Δ-learning scheme on different molecular systems in water and compare it with the previously developed high-dimensional neural network potentials (HDNNPs),34,41 which use the same Δ-learning scheme with DFTB42,43 as the baseline method. In the Theory section, we briefly describe the relevant concepts behind the QM/MM approach as well as the GCNNs. In the Methods section, we describe the setup used for the QM/MM simulations, the implemented GCNN architecture as well as the training setup. In the Results section, we evaluate different GCNN models, including different global information transfer schemes, with different (QM)ML/MM and training setups. Finally, we compare the resulting GCNN model with the previous HDNNP model.34
2 Theory
2.1 QM/MM scheme
QM/MM is a multi-scale approach, which incorporates a QM zone within a larger MM zone describing the condensed-phase system.3–6 This enables the accurate calculation of the region of interest coupled with a realistic modelling of long-range interactions with the surrounding environment. The main challenge here is how to describe the interaction between these two different zones. In order to calculate the total energy (EQM/MM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) )) of the combined QM/MM system, an additive or subtractive scheme can be chosen. In the more prominent additive scheme, the total energy (EQM/MM(
)) of the combined QM/MM system, an additive or subtractive scheme can be chosen. In the more prominent additive scheme, the total energy (EQM/MM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) )) is described as the sum of the energy of the QM subsystem (EQM(
)) is described as the sum of the energy of the QM subsystem (EQM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) QM)) and the MM subsystem (EMM(
QM)) and the MM subsystem (EMM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) MM)) plus the electrostatic (EelQM-MM(
MM)) plus the electrostatic (EelQM-MM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) )) and short-range van der Waals interactions (EvdWQM-MM(
)) and short-range van der Waals interactions (EvdWQM-MM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) )) between the two subsystems.
)) between the two subsystems.EQM/MM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ) = EQM( ) = EQM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) QM) + EMM( QM) + EMM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) MM) + EelQM-MM( MM) + EelQM-MM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ) + EvdWQM-MM( ) + EvdWQM-MM(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ) ) | (1) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) referring to all nuclei in the system, and
referring to all nuclei in the system, and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) QM and
QM and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) MM referring to the nuclei of the QM and MM zones, respectively. In the additive scheme, the interaction terms between the QM and MM zones are described either via a mechanical or an electrostatic embedding scheme,7 where the latter scheme has been shown to be more accurate.5 For this, two Hamiltonians are introduced in the QM calculation. In atomic units, ĤelQM–MM is given as
MM referring to the nuclei of the QM and MM zones, respectively. In the additive scheme, the interaction terms between the QM and MM zones are described either via a mechanical or an electrostatic embedding scheme,7 where the latter scheme has been shown to be more accurate.5 For this, two Hamiltonians are introduced in the QM calculation. In atomic units, ĤelQM–MM is given as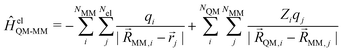 | (2) |
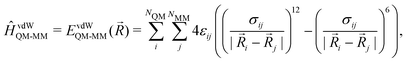 | (3) |
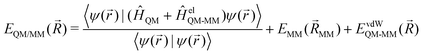 | (4) |
2.2 Graph-convolutional neural networks
In our description of graph-convolutional neural networks (GCNNs) or message passing neural networks, we follow the notations used by ref. 39 and 45. Here, GCNNs are permutation-invariant ML models that operate on the graph structured data. In the present work, atoms are represented as nodes ν and interactions between atoms are represented as edges e, whereby only interactions up to a certain cutoff Redge are considered as edges. Note that we will refer to two different cutoffs throughout the manuscript. Rc is the cutoff used in the QM/MM scheme, and the summations in eqn (2) and (3) run over all partial charges within Rc. Redge, on the other hand, is the cutoff used for the edge definition in the GCNNs. The GCNNs contain consecutive graph-convolutional layers, where each layer consists of an edge or message update operation (eqn (5)), an aggregation operation (eqn (6)), and a node update operation (eqn (7)). Considering a graph G = (V,E) with nodes νi ∈ V and edges eij ∈ E, message passing can be defined as follows:| mij = ϕe(hli,hlj,aij) | (5) |
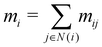 | (6) |
| hl+1i = ϕh(hli,mi). | (7) |
3 Methods
3.1 Systems
To allow a direct comparison, the same systems as in ref. 34 were investigated. For the validation of different GCNN models and training setups, we used two single-solute systems with different MM cutoff radii (Rc): (i) benzene in water, and (ii) uracil in water. For the comparison to the previous HDNNP model,34 we used the largest single-solute system (retionic acid in water), and two chemical reactions in water (constrained close to the transition state): (i) the second-order nucleophilic substitution (SN2) reaction of CH3Cl with Cl-, and (ii) the reaction of S-adenosylmethionate (SAM) with cytosine. We investigated the accuracy of the different models in training/validation/test splits and the performance in a prospective (QM)ML/MM MD simulation. The data sets are freely available on https://www.research-collection.ethz.ch/handle/20.500.11850/512374.3.2 General computational details
All QM/MM and (QM)ML/MM MD simulations were performed using the GROMOS software package47,48 interfaced to DFTB+/19.242,43 and ORCA/4.2.0.49 All structures used in the training, validation and test sets were taken from ref. 34 (available at https://www.research-collection.ethz.ch/handle/20.500.11850/512374). These come from QM/MM MD trajectories, where the first 70% of the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames were considered to be the training set, the following 20% constitute the validation set, and the last 10% are taken as the test set. The computational details of the (QM)ML/MM simulations are provided in ref. 34. Note that a MM cutoff radius of Rc = 0.6 nm was used for benzene in water, while Rc = 1.4 nm was used for all other systems. The GCNNs were implemented using Tensorflow/keras.50 The models were trained in Python and then exported to the C++ GROMOS code as described in ref. 34 for the HDNNPs.
000 frames were considered to be the training set, the following 20% constitute the validation set, and the last 10% are taken as the test set. The computational details of the (QM)ML/MM simulations are provided in ref. 34. Note that a MM cutoff radius of Rc = 0.6 nm was used for benzene in water, while Rc = 1.4 nm was used for all other systems. The GCNNs were implemented using Tensorflow/keras.50 The models were trained in Python and then exported to the C++ GROMOS code as described in ref. 34 for the HDNNPs.
For the validation of the different GCNN models, we compare both the full-QM learning task and the Δ-learning scheme. For the full-QM learning task, we use the GCNN models to directly predict the DFT49 energies and forces, whereas DFTB42,43 is used as the baseline method in the Δ-learning scheme and the GCNN models predicts the difference between the DFT and DFTB properties. After the initial validation and comparison of the two learning tasks, we continue only with the Δ-learning approach throughout the remainder of the study.
3.3 (QM)ML/MM MD simulations
For retionic acid in water and the SAM/cytosine transition state in water, we performed (QM)ML/MM MD simulations using the trained GCNN models with the Δ-learning setup. To ensure comparability, we used the same MD and DFTB settings as in ref. 34. The time step was set to 0.5 fs, the temperature was set to T = 298 K, and the pressure was set to 1 bar. For the SAM/cytosine system, we set the force constant for the position restraints to 2000 kJ mol−1 nm−2. All point charges within the cutoff radius Rc = 1.4 nm were included in an electrostatic embedding scheme in the QM(ML) computation. The selected solvent atoms beyond the cutoff were included to avoid the bond-breaking and creation of artificial charges. Long-range electrostatic interactions beyond Rc were included using a reaction-field method.51 Note that the reaction field acts only on the MM particles. As starting coordinates for the prospective simulations, we used the last snapshot from the test set (which originated from the initial QM/MM MD trajectory). The simulations were performed for 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps for retionic acid in water and 110
000 steps for retionic acid in water and 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps for the SAM/cytosine transition state in water.
000 steps for the SAM/cytosine transition state in water.
3.4 GCNN architectures
The basic building blocks of the GCNN are so-called dense layers. They take an input vector x ∈ Rnin and return an output vector y ∈ Rnout according to the transformation| y = Wx + b. | (8) |
![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) and positions
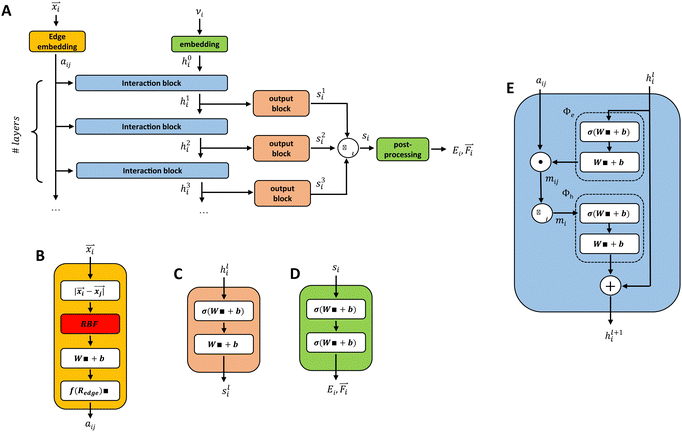
and positions ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i ∈ R3. We evaluate four different GCNN architectures with different global information transfer schemes. An overview of the basic network architecture is given in Fig. 1A. In the following sections, this architecture is referred to as the GCNN model.
i ∈ R3. We evaluate four different GCNN architectures with different global information transfer schemes. An overview of the basic network architecture is given in Fig. 1A. In the following sections, this architecture is referred to as the GCNN model.
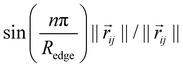 as proposed by Klicpera et al.38 Additionally, we apply a cosine cutoff to the filters,41 which ensures continuous behavior when an atom enters or leaves the cutoff sphere.
as proposed by Klicpera et al.38 Additionally, we apply a cosine cutoff to the filters,41 which ensures continuous behavior when an atom enters or leaves the cutoff sphere.
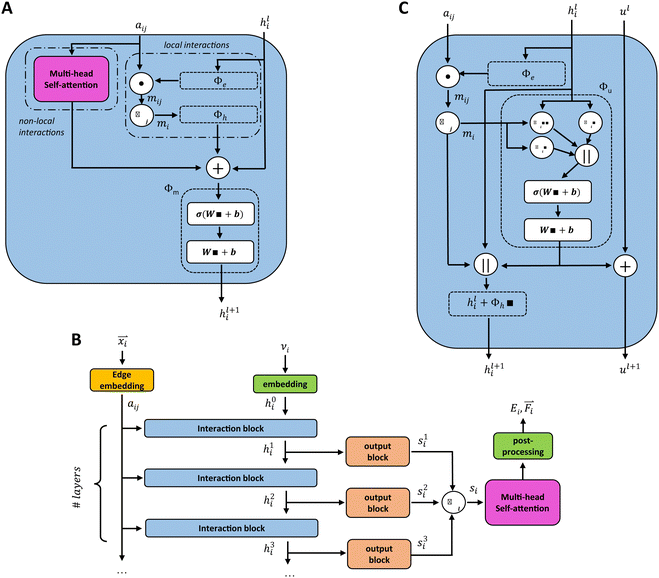
Unke et al.31 introduced a GCNN model, which takes into account non-local effects and charge transfer. They achieved this by introducing non-local interactions using a self-attention layer.40,53 An attention layer maps a matrix X ∈ RT×nin of query (Q) tokens T to nout dimensions using a matrix Y ∈ RT×nin of key (K) tokens T′ as follows:
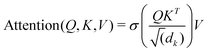 | (9) |
| Q = XWQ, K = YWk, V = YWV. | (10) |
| MultiAttention = {Attention0|Attention1|…|AttentionNheads}Wmulti, | (11) |
We introduce the multi-head self-attention layer at two different stages in our basic GCNN architecture: (i) within the interaction block (Fig. 2A) as described in ref. 31, and (ii) after at the end of the model (Fig. 2B). This way we can investigate the effect of repeating the global information transfer within each message passing update as compared to a single transfer step using the final atom features. In the following sections, these models are referred to as the “interaction GCNN” and “attention GCNN”.
A different GCNN architecture, which considers global information transfer, has been reported by Chen et al.32 Here, the authors introduce a global state ul into the message passing operation. We adapted this idea by changing the message update step (eqn (7)) to
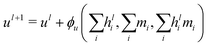 | (12) |
| hl+1 = hl + ϕh(hli,mi,ul+1), | (13) |
3.5 Training setup
We implemented the four different GCNN model architectures using Tensorflow/keras. The models were trained using the Adam optimizer54 with an exponentially decaying learning rate ([initial learning-rate, decay steps, and decay rate] = [1e−3, 5e3, and 0.96]). The Adam optimizer is one of the most well-established methods for the training of neural network models. It is based on a stochastic gradient descent optimizer that uses an adaptive estimation of the first and second-order moments. The models were trained for up to 2000 epochs (or until convergence) using a batch sampling of 2–32, depending on the memory requirements of the models and systems. Note that the models were trained using Tensorflow 2.7.0, but the models were saved using Tensorflow 1.15 for the integration with the GROMOS C++ code (as described in ref. 34 for the HDNNPs).As a loss function, we used the weighted mean-squared-error (MSE) of the energies and forces
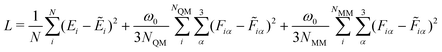 | (14) |
4 Results and discussion
In order to evaluate the different model architectures and parametrizations as well as the training setup, the two simplest test systems from ref. 34, i.e., benzene in water and uracil in water, were used with the same training/validation/test split as in the original publication. The use case here is that the training set is generated from a short initial MD simulation, from which the energies and forces of the subsequent MD steps can be predicted. In the first step, we evaluated the full-QM learning task and a Δ-learning scheme with DFTB42,43 as the baseline for the different GCNN architectures. The Δ-learning scheme simplifies the learning task, and we adopted the same approach as used in ref. 34 for the HDNNPs. For the basic setup of our GCNN model, 128 features per dense layer (nf), five interaction blocks, and Redge = 0.5 nm were used. For the multi-head self-attention models, we used four heads with nk = 32. Finally, we compare the best GCNN model with the previous HDNNP model in ref. 34 for all five test systems: (i) benzene in water, (ii) uracil in water, (iii) retionic acid in water, (iv) (close to) the transition state of the SN2 reaction of CH3Cl with Cl- in water, and (v) (close to) the transition state of SAM with cytosine in water. Note that, for the parametrization and evaluation of the GCNN models and training procedure, we solely used the training and validation sets. The test sets were only taken for the comparison between the final GCNN model with the previous HDNNP model.4.1 Model architectures
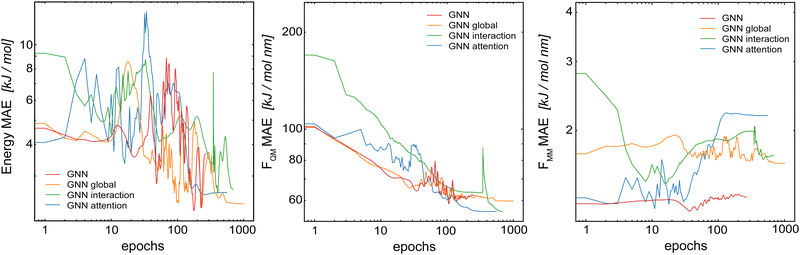
In the first step, we compared the different model architectures in order to evaluate how the global transfer schemes influence the inclusion of the long-range information directly into the model. For this, four different GCNN models were trained: (a) a basic GCNN model, (b) a GCNN model including multi-head self-attention at the post-processing stage (labeled as the “attention GCNN”), (c) a GCNN model including multi-head self-attention in the interaction layers (labeled as the “interaction GCNN”), and (d) a GCNN model including a global state (labeled as the “global GCNN”). The two test systems consist of benzene (apolar molecule) in water with a short MM cutoff radius of Rc = 0.6 nm, and uracil (polar molecule) in water with a longer Rc = 1.4 nm.Table 1 shows the mean absolute error (MAE) of the different model architectures for the validation sets of benzene in water and uracil in water. When the models were trained on the full QM energies and forces, we observe for benzene that all models achieve a similar accuracy on the energies, while the basic GCNN outperforms the other architectures for the forces (FQM and FMM). When using the Δ-learning scheme, the accuracy is generally improved, with similar performances of the different architectures (Table 1). Only the interaction GCNN model has a significantly higher MAE for both the energies and the forces. For uracil, we observe similar trends as for benzene (Table 1). Again, no large differences are observed between the models for both the “full QM” and the Δ-learning setup (Fig. 3). In contrast to benzene, also the interaction GCNN models achieve a similar accuracy compared to the other models.
| GCNN model | Full QM | Δ-Learning | ||||
|---|---|---|---|---|---|---|
| E (kJ mol−1) | F QM (kJ mol−1 nm−1) | F MM (kJ mol−1 nm−1) | E (kJ mol−1) | F QM (kJ mol−1 nm−1) | F MM (kJ mol−1 nm−1) | |
| Benzene | ||||||
| Basic | 2.7 | 48.7 | 8.3 | 1.0 | 22.9 | 3.5 |
| Global | 2.4 | 54.1 | 8.9 | 1.0 | 22.7 | 3.8 |
| Interaction | 2.7 | 52.8 | 9.7 | 3.9 | 36.2 | 7.3 |
| Attention | 2.7 | 61.7 | 10.0 | 1.2 | 23.7 | 4.2 |
| Uracil | ||||||
| Basic | 7.3 | 135.2 | 5.8 | 2.2 | 60.2 | 1.3 |
| Global | 8.1 | 129.7 | 6.4 | 2.3 | 59.8 | 1.7 |
| Interaction | 8.0 | 138.4 | 4.4 | 2.6 | 55.5 | 1.6 |
| Attention | 7.4 | 134.9 | 7.3 | 2.5 | 55.5 | 1.4 |
As observed for HDNNPs in ref. 34, the use of a Δ-learning scheme with DFTB as the baseline method reduces the prediction error by about two folds. This is also the case for the GCNN models containing global information. This indicates that the Δ-learning approach is more suited to incorporate the long-range interactions. A reason for this could be that while the GCNNs containing global information can in theory learn long-range interactions, the large number of MM atoms present leads to an exponential increase in possible system configurations. This in turn requires a huge number of training data points in order to accurately capture the long-range interactions. If the size of the training set is limited to a practically useful number (as done here), the training set is evidently not large enough to achieve the desired accuracy.
In conclusion, the Δ-learning scheme leads to a clear and consistent performance improvement, whereas no large differences are observed between the four different GCNN architectures for both test systems. While the improved GCNN models can reach a slightly lower MAE than the basic GCNN model for some setups, these improvements do not justify their increased model complexity and the subsequently higher computational requirements. For comparison, the basic GCNN model has around 710![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tunable parameters, while the global GCNN model has around 1
000 tunable parameters, while the global GCNN model has around 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 parameters (870
000 parameters (870![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in the interaction GCNN and 840
000 in the interaction GCNN and 840![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in the attention GCNN). In addition, the interaction GCNN and attention GCNN models require dot products of the query (Q ∈ Rnin×nk) and key (K ∈ Rnin×nk) matrices, which are computationally expensive (although the costs can be reduced through the use of multi-head self-attention and nout = nk < nin). For these reasons, we decided to focus on the basic GCNN model and the Δ-learning scheme in the following.
000 in the attention GCNN). In addition, the interaction GCNN and attention GCNN models require dot products of the query (Q ∈ Rnin×nk) and key (K ∈ Rnin×nk) matrices, which are computationally expensive (although the costs can be reduced through the use of multi-head self-attention and nout = nk < nin). For these reasons, we decided to focus on the basic GCNN model and the Δ-learning scheme in the following.
4.2 Model parametrization
For the basic GCNN architecture, we explored different model parametrizations: an edge-cutoff value (Redge) from 0.3 to 0.6 nm, a number of features per dense layer (nf) from 32 to 256, and a model depth (i.e., number of interaction blocks) from 2 to 8. The edge-cutoff value and the model depth directly influence the contributions from long-range interactions, as they both determine (directly and indirectly) the distance up to which atoms contribute to the message update function. The number of features per dense layer, on the other hand, determines the maximum possible complexity of each message update function.Fig. 4 shows the influence of the edge-cutoff value (Redge) on the model performance for the Δ-learning GCNN model of uracil in water. For the energy, the error is the lowest for a Redge of 0.5 nm. For both force terms (FQM and FMM), however, smaller Redge values of 0.4 nm and 0.3 nm, respectively, give the lowest errors. Note that, for both the energy and the force terms, the error increases again for larger Redge values. The reason for this could be that larger cutoffs are connected with an increase in possible system configurations, requiring in turn more training data points. If the same training set is used, overfitting might occur. For benzene in water, a different trend is observed. Here, a large Redge of 0.6 nm still leads to an improvement in the MAE of the forces (Table 2). This is especially interesting as a different MM cutoff radius is used in the reference QM/MM calculations of benzene and uracil (Rc = 0.6 nm and 1.4 nm, respectively). A reason could be that the reduced MM cutoff radius (Rc) leads to a smaller configuration space in the MM-region and thus a GCNN model with a larger Redge is able to sufficiently learn the important contributions.
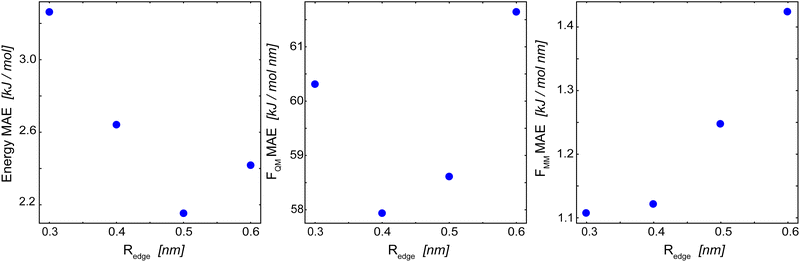 | ||
| Fig. 4 Influence of Redge on the mean absolute error (MAE) of the Δ-learning basic GCNN model for uracil in water. (left): MAE of the energies in the QM zone. (middle): MAE of the forces on the QM particles. (right): MAE of the forces on the MM particles from the QM zone. The numerical values are given in Table 2. | ||
| R edge (nm) | Δ-Learning | ||
|---|---|---|---|
| E (kJ mol−1) | F QM (kJ mol−1 nm−1) | F MM (kJ mol−1 nm−1) | |
| Benzene | |||
| 0.3 | 2.4 | 27.8 | 5.5 |
| 0.4 | 1.3 | 23.7 | 4.2 |
| 0.5 | 1.0 | 22.9 | 3.5 |
| 0.6 | 1.1 | 21.0 | 3.1 |
| Uracil | |||
| 0.3 | 3.3 | 60.4 | 1.1 |
| 0.4 | 2.6 | 59.2 | 1.1 |
| 0.5 | 2.2 | 60.2 | 1.3 |
| 0.6 | 2.4 | 62.9 | 1.5 |
For the model depth, we observe a similar trend as for the edge-cutoff value. Namely that including the information about further distant nodes (atoms) is not always beneficial for the model performance (Table S1 in the ESI†). For the test system uracil in water, the MAE of both the energies and forces is lowest at around 2–4 interaction layers, while up to 6–8 interaction layers are required for the benzene in water test system. The results for the number of features per dense layer (nf) are given in Table S2 in the ESI.† In general, a higher number of features per dense layer does not lead to a lower error, with convergence at around 64 features per dense layer for uracil in water. For the test system of benzene in water, on the other hand, a more complex model leads again to a decrease in the errors.
4.3 Loss contribution of the forces
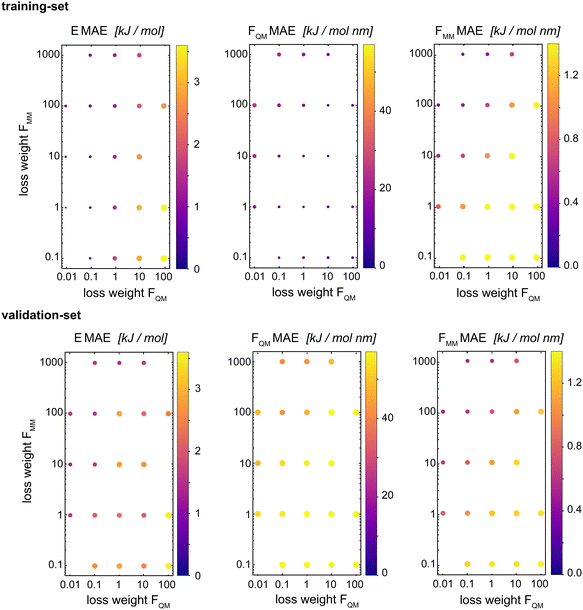
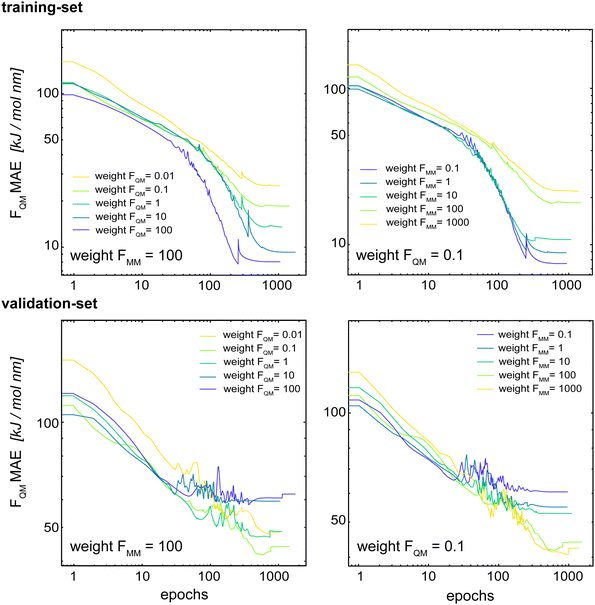
Böselt et al.34 showed that the relative weighting of the different loss terms (energy loss, FQM loss, and FMM loss) can have a significant influence on the prediction accuracy. Thus, we systematically trained and evaluated GCNN models by varying the relative loss weightings (wE, wFQM, and wFMM). We decided to keep wE constant at 1.0, while changing FQM from 0.001 to 100 and FMM from 0.1 to 1000.Fig. 5 shows the MAE on the training and validation set of the basic GCNN model with the Δ-learning scheme for the test system of uracil in water when varying wFQM and wFMM. For the training set, we observe the expected behaviour, i.e. the error on FQM decreases when the weight wFQM is increased and the same for FMM with wFMM. Interestingly, the results on the validation set are different. While the error on FMM still decreases with increasing wFMM as expected (the bottom right panel in Fig. 5), the MAE on FQM is the smallest for low wFQM and high wFMM (the bottom middle panel in Fig. 5). This observation is further illustrated in Fig. 6, which shows the learning curves for FQM in the training and validation sets (corresponding to the horizontal line at wFMM = 100 and the vertical line at wFQM = 0.1 in the bottom middle panel in Fig. 5).
For the training set, the learning curves show again the expected dependence with FQM and FMM, respectively (top panels in Fig. 6). However, for the validation set, the lowest error of FQM is observed with wFQM = 0.1 and not with wFQM = 100. In general, a relative weighting of 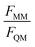 around 100–1000 results in the lowest MAE of FQM. Higher relative wFQM values seem to result in over-fitting of FQM. Thus, for the final GCNN model, we use the following relative loss weights: wE = 1, wFQM = 0.1, and wFMM = 10. Note that the same observations were made for the Δ-learning GCNN model with benzene in water (Fig. S1 and S2 in the ESI†).
around 100–1000 results in the lowest MAE of FQM. Higher relative wFQM values seem to result in over-fitting of FQM. Thus, for the final GCNN model, we use the following relative loss weights: wE = 1, wFQM = 0.1, and wFMM = 10. Note that the same observations were made for the Δ-learning GCNN model with benzene in water (Fig. S1 and S2 in the ESI†).
4.4 Neighborhood reduction
The main increase in computational requirements for the GCNN models (especially memory requirements when using GPUs during the batched training procedure) comes from the growing number of edges with an increasing size of the edge-cutoff (Redge). For example, Redge = 0.4 nm leads to around 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 edges for one of the uracil in water snapshots, while Redge = 0.5 nm already leads to around 38
000 edges for one of the uracil in water snapshots, while Redge = 0.5 nm already leads to around 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 edges. Therefore, we investigated whether the number of edges can be reduced using different neighborhood schemes, without decreasing the model performance. To limit the number of edges around each atom, we explored the k-nearest-neighbour55 method with eight (KNN-8) and twelve (KNN-12) neighbours, and the Voronoi–Dirichlet polyhedra (VD).56,57 With the same Redge = 0.5 nm, KNN-8 leads to around 12
000 edges. Therefore, we investigated whether the number of edges can be reduced using different neighborhood schemes, without decreasing the model performance. To limit the number of edges around each atom, we explored the k-nearest-neighbour55 method with eight (KNN-8) and twelve (KNN-12) neighbours, and the Voronoi–Dirichlet polyhedra (VD).56,57 With the same Redge = 0.5 nm, KNN-8 leads to around 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 edges for a uracil in water snapshot, KNN-12 to around 18
000 edges for a uracil in water snapshot, KNN-12 to around 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 edges, and VD to around 11
000 edges, and VD to around 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 edges. Thus, the memory requirement for the GCNN model is drastically reduced by all these approaches.
000 edges. Thus, the memory requirement for the GCNN model is drastically reduced by all these approaches.
For the following results, we used the same settings for the GCNN models, i.e., Redge = 0.5 nm, nf = 128 with five interaction layers, and loss weightings of wE = 1.0, wFQM = 0.1, and wFMM = 10. Fig. 7 shows the learning curves on the validation set of the Δ-learning GCNN model for the test system uracil in water. While the MAE on the energies is largely unaffected (within the fluctuations of the error) by the choice of the neighborhood scheme (KNN-12 being the closest to the complete model), the errors on the force terms (FQM and FMM) increase substantially with all neighborhood schemes compared to the complete model. The same trends are also observed for the Δ-learning model of benzene in water (Table S3 in the ESI†).
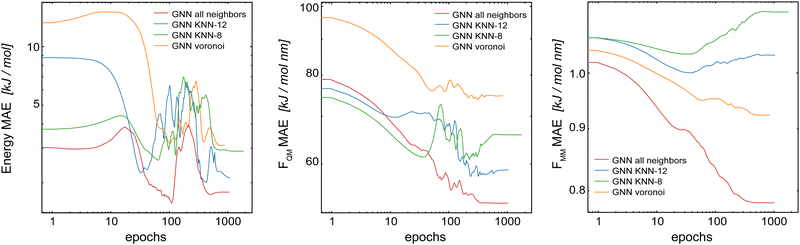 | ||
| Fig. 7 Learning curves on the validation set of the Δ-learning GCNN model when using different neighborhood selection schemes. The test system uracil in water was used. | ||
4.5 Data set ordering
The split into training/validation/test sets was chosen with the future application in MD simulations in mind. The idea is that a short initial QM/MM MD run of the target system can be used as the training set for subsequent longer (QM)ML/MM MD simulations. To mimic this, the first 70% of the frame from the initial QM/MM trajectory was taken as the training set, the following 20% as the validation set and the final 10% as the test set.34 This leads to a time-based ordering of the frames within the training set. Here, we investigate if this correlated ordering has an effect on the model performance. For this, we compared five models trained with the same training set but using a different frame ordering within the set: (i) original time-based ordering from the MD simulation, (ii–iv) random-ordering using three different random number seeds, and (v) a farthest-point sampling (fps) as described in the ESI.† For all models, we used Redge = 0.5 nm, nf = 128 with five interaction layers, and loss weightings of wE = 1.0, wFQM = 0.1, and wFMM = 10.Fig. 8 shows the learning curves for the training and validation sets of the basic GCNN model with the Δ-learning scheme trained with different orderings of the data points in the training set. First, the results clearly show that the order of the training data points does indeed affect the model performance. For all three properties (energies and forces), the error for the training set is clearly smallest with the fps-ordering (orange line) or MD-ordering (purple line). Interestingly, using an fps-ordering of the training data points results in a higher MAE for the validation set, indicating that the fps-ordering leads to an over-fitting of the model for this setup. The situation is different for the MD-ordering, which leads to comparable results on the validation set as the random-ordering, except for FQM. Here, the accuracy is between the random and the fps-ordering. For the test system of benzene in water (Fig. S3 in the ESI†), the same trends are observed for fps-ordering on the training and validation sets, while the MD-ordering shows again a comparable accuracy as the random-orderings for both the training and the validation sets. However, in all cases, the random-orderings converge earlier (at around 1000 epochs) compared to the MD-ordering (around 2000 epochs). Thus, using a random-ordering of the MD frames in the training set seems to be beneficial by reducing the training costs and potentially increasing robustness.
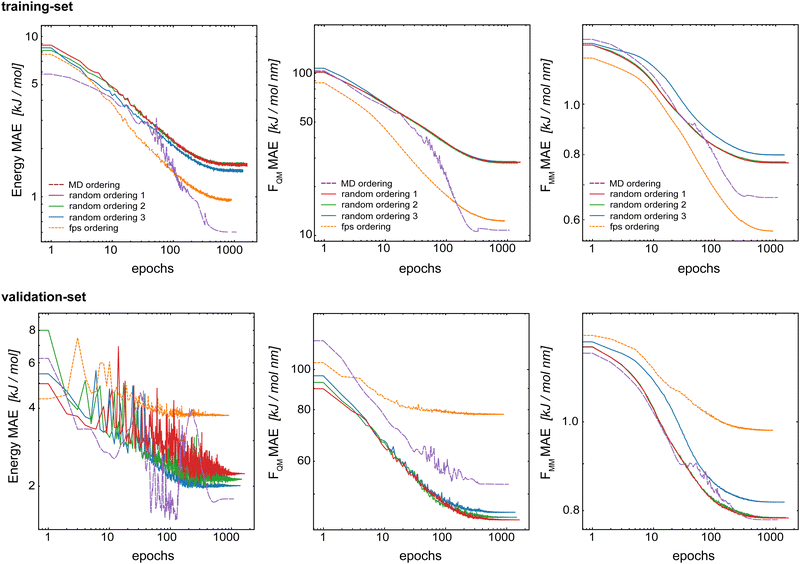 | ||
| Fig. 8 Learning curves for the training set (top) and validation set (bottom) when varying the order of the data points in the training set. The Δ-learning GCNN for uracil in water is shown. | ||
4.6 Comparison to HDNNPs
As a final evaluation, we compare the GCNN models with the previously developed HDNNPs,34,41 which use the same Δ-learning scheme with DFTB42,43 as the baseline, for all five test systems: (i) benzene in water, (ii) uracil in water, (iii) retionic acid in water, (iv) (close to) the transition state of the SN2 reaction of CH3Cl with Cl- in water, and (v) (close to) the transition state of SAM with cytosine in water. The model performance is compared on the training set (7000 frames), validation set (2000 frames), and test set (1000 frames). Note that the models were solely developed using the training and validation sets, and are only evaluated on the test set at this stage. Furthermore, hyperparameters were only tuned on the two test systems benzene and uracil in water. For all models, we used Redge = 0.5 nm, nf = 128 with four (systems i and ii) or five (systems iii–v) interaction layers, and loss weightings of wE = 1.0, wFQM = 0.1, and wFMM = 10.Fig. 9 compares the learning curves and final MAE between the HDNNP and the GCNN models for benzene in (top panels) and uracil in water (bottom panels). For both systems, the learning curves for the GCNN validation and test sets show a very similar performance. This indicates that the models are not overfitted and are able to generalize to new data points within the same MD trajectory. For the HDNNP models, we observe a similar behaviour. However, the MAE values for the test set of benzene in water are consistently above the MAE for the validation set. For this system, we can directly compare the effect of the training set size between the HDNNP and GCNN models. While both models show a similar MAE for small training set sizes, the GCNN model outperforms the HDNNP model when all training data points are used. A possible reason for this observation is that the GCNN model has to learn the descriptor for the atomic environments and would thus profit from a larger training set. This is also indicated by the fact that the learning curves of the GCNN models are still continuously decreasing even at 7000 training structures. For the system of uracil in water, the final MAE values are comparable for all models. Here, we note that the benzene test system has a shorter MM-cutoff radius (Rc), which might simplify the learning task and thus a similar behaviour might be observed for uracil at a larger training set size.
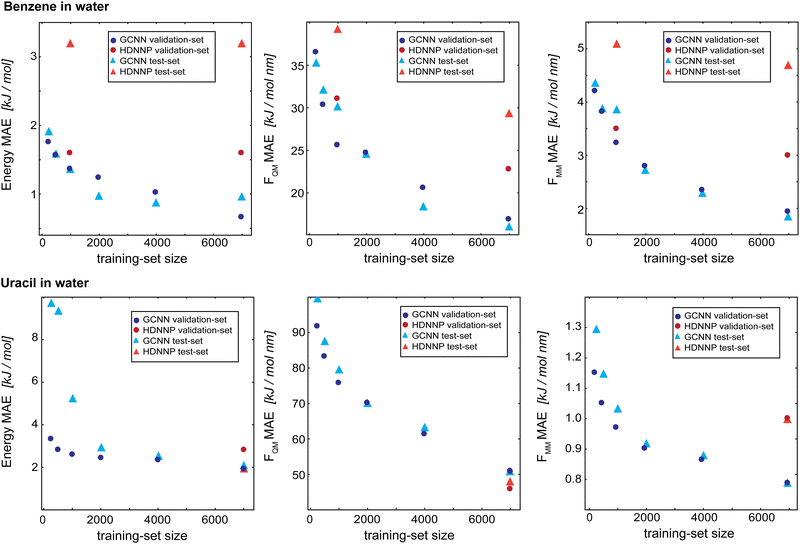 | ||
| Fig. 9 Learning curves as a function of the training-set size of the Δ-learning models for benzene in water (top) and uracil in water (bottom). The dark blue circles show the GCNN validation MAE, the dark red circles show the HDNNP validation MAE, the light blue triangles show the GCNN test MAE, and the light red triangles show the HDNN test MAE. The numerical values are given in Table 3. | ||
Table 3 shows the MAE values on the training, validation, and test sets for all five test systems. Overall, the GCNN models perform similar or slightly better than the HDNNP models. A major exception to this is the SAM/cyt in water system. Here, the GCNN model reaches the same accuracy as the HDNNP model on the training set, but the MAE on the validation and test set is two to five times higher than with the HDNNP model. This may be because the GCNN models were parametrized and benchmarked on the simpler systems (i.e., benzene and uracil in water) and there is less transferability of the hyperparameters than that with the HDNNP.
| System | HDNNP | GCNN | ||||
|---|---|---|---|---|---|---|
| E (kJ mol−1) | F QM (kJ mol−1 nm−1) | F MM (kJ mol−1 nm−1) | E (kJ mol−1) | F QM (kJ mol−1 nm−1) | F MM (kJ mol−1 nm−1) | |
| Benzene | 1.8/1.6/3.2 | 23.7/22.8/29.4 | 3.5/3.0/4.7 | 0.4/0.7/0.7 | 8.6/14.7/15.3 | 1.3/1.9/2.0 |
| Uracil | 1.2/2.8/2.0 | 34.3/45.9/48.1 | 1.1/1.0/1.0 | 0.8/1.9/2.1 | 14.1/51.0/51.0 | 0.7/0.8/0.8 |
| Chloroform | 1.8/1.7/2.2 | 24.9/29.5/30.7 | 1.0/1.0/1.0 | 0.5/1.1/1.2 | 5.3/21.4/22.1 | 0.5/0.6/0.6 |
| Retionic acid | 3.9/4.4/— | 43.8/44.8/— | 1.1/1.1/— | 0.6/4.4/4.4 | 20.5/37.0/37.0 | 0.7/0.9/0.9 |
| SAM/cyt | 6.3/8.5/— | 74.8/74.6/— | 2.3/2.3/— | 5.6/21.1/28.8 | 79.7/130.4/130.4 | 11.9/12.0/12.2 |
Up to this point, we have evaluated the performance of the GCNN models in terms of the MAE on reasonable validation and test sets. Böselt et al.34 have already emphasized that it is important to test a ML model for the intended application, which in our case are (QM)ML/MM MD simulations. While rare outliers get averaged in the MAE assessment, they might be less tolerable in an actual simulation, where the results of the next step depend directly on the results of the previous step. For this reason, it is crucial to test the performance of the developed (QM)ML/MM models in a prospective MD simulation. We performed therefore (QM)ML/MM MD simulations using the Δ-learning GCNN model for the two test systems with larger conformational flexibility as in ref. 34: (i) retinoic acid and (ii) (close to) the transition state of SAM with cytosine in water. Note that the models were only trained on the initial 7000 steps of the QM/MM MD simulations and no adaptive re-training during the (QM)ML/MM production runs was performed. Shen and Yang35 have shown that adaptive neural networks can use on-the-fly corrections of the model to further improve the model performance. However, this comes with an increase in the training cost of the model and changing energies/forces (i.e., the estimated properties of a configuration may not be the same at the beginning versus the end of the simulation).
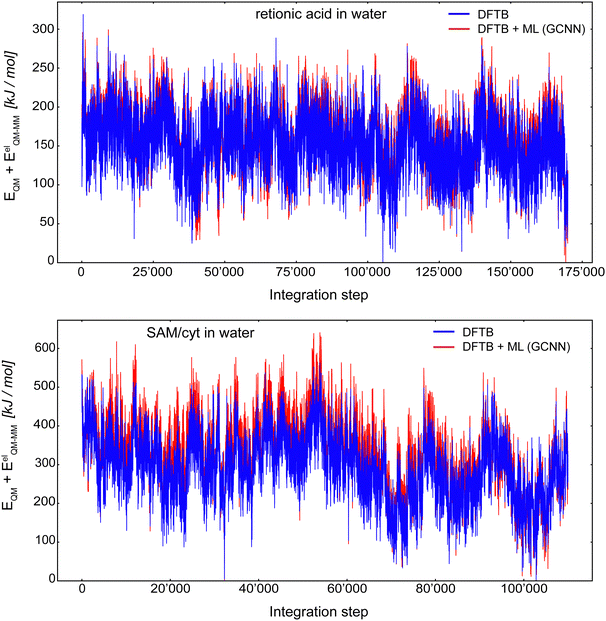
Fig. 10 shows the MD energy (EQM + EelQM–MM) trajectories for retionic acid in water (top panel) and SAM/cyt in water (bottom panel) using an integration step of 0.5 fs. The (QM)ML/MM MD simulation of retionic acid in water was carried out for 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 consecutive steps, while the simulation of SAM/cyt in water was performed for 110
000 consecutive steps, while the simulation of SAM/cyt in water was performed for 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 consecutive steps. For both systems, the first 200 steps were discarded as equilibration. Thus, it was possible to propagate these systems stably using the Δ-learning GCNN model based on a fraction of the otherwise required QM/MM MD simulation steps. For both systems, the energy fluctuations during the (QM)ML/MM MD simulation were comparable to the ones with the Δ-learning HDNNP model: For retionic acid, σDFTB+GCNN = 37.1 kJ mol−1 and σDFTB+HDNNP = 55.2 kJ mol−1, and for SAM/cyt, σDFTB+GCNN = 94.9 kJ mol−1 and σDFTB+HDNNP = 73.3 kJ mol−1. Of course, the possibility that in a longer simulation an ill-represented structure may be encountered cannot be fully excluded. Interestingly, even though the accuracy of the GCNN model on the validation/test sets of the SAM/cyt in water was considerably lower than that with the HDNNP model, we still observe a stable and robust simulation over 110
000 consecutive steps. For both systems, the first 200 steps were discarded as equilibration. Thus, it was possible to propagate these systems stably using the Δ-learning GCNN model based on a fraction of the otherwise required QM/MM MD simulation steps. For both systems, the energy fluctuations during the (QM)ML/MM MD simulation were comparable to the ones with the Δ-learning HDNNP model: For retionic acid, σDFTB+GCNN = 37.1 kJ mol−1 and σDFTB+HDNNP = 55.2 kJ mol−1, and for SAM/cyt, σDFTB+GCNN = 94.9 kJ mol−1 and σDFTB+HDNNP = 73.3 kJ mol−1. Of course, the possibility that in a longer simulation an ill-represented structure may be encountered cannot be fully excluded. Interestingly, even though the accuracy of the GCNN model on the validation/test sets of the SAM/cyt in water was considerably lower than that with the HDNNP model, we still observe a stable and robust simulation over 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (QM)ML/MM MD steps based solely on the initial 7000 QM/MM MD simulation steps.
000 (QM)ML/MM MD steps based solely on the initial 7000 QM/MM MD simulation steps.
5 Conclusion
In this work, we investigated the use of GCNN models in (QM)ML/MM MD simulations for condensed-phase systems with DFT accuracy for the QM subsystem, and compared the results with the previously developed HDNNPs for the same systems. In the first step, we evaluated different GCNN architectures capable of incorporating long-range effects, with and without a Δ-learning scheme. While no large improvements could be found with the more complex GCNN architectures, the Δ-learning GCNN using DFTB as the baseline yielded the most accurate description of the energies and forces. Based on these observations, we focused on the basic GCNN with Δ-learning for the remainder of the study. Next, we assessed the influence of different parameters on the performance of the GCNN models. Here, we found that the inclusion and the correct weighting of the QM and MM gradients in the loss function were crucial to improve the model performance. Interestingly, we observed that increasing the loss weights of the QM gradients does not lead to an improved accuracy when predicting them due to overfitting. Instead, the relative loss weights of wE = 1, wFQM = 0.1 and wFMM = 10 provided the model with the best ability to generalize new data points.In order to reduce the computational requirements of the GCNN models, we also investigated different neighborhood reduction schemes in the creation of the GCNN edges. While these schemes decrease indeed the computational costs without significantly affecting the accuracy of the QM energies, the performance on the QM and MM forces is clearly worse. Thus, we do not recommend using these schemes in (QM)ML/MM MD simulations, as the predicted forces are directly used to propagate the system in time.
An interesting observation was made regarding the order of the data points in the training set. In order to mimic the future application, the training set was chosen as the first 70% of frames from a QM/MM trajectory. This leads to a time-based ordering of the training data points. When using a random ordering of the training set (without changing the actual training/validation/test split!), a similar model performance was reached, but the random ordering converges faster and thus leads to a reduction in the required training time.
Finally, we compared the Δ-learning HDNNP and Δ-learning GCNN models with each other for five different test systems in water. While both models perform at a similar accuracy, the GCNN model reaches slightly lower MAE values for most of the five test systems. The Δ-learning GCNN model can also be used to perform stable (QM)/ML/MM MD simulations as the corresponding HDNNP model. However, the two model types differ drastically in their architecture and come with advantages and disadvantages, which should be considered when choosing an adequate model for a (QM)ML/MM simulation. The symmetry functions in HDNNPs include a cosine term for all the inter-atomic angles within an atomic environment, which results in a computational scaling of O(N3), where N is the combined number of atoms in the QM and MM environments. The GCNN model, on the other hand, only depends on the edge-update operations to describe the atomic environments resulting in a computational scaling of O(N2). Note that, by using a finite cutoff for the atomic environments and edge-update operations, the scaling can be reduced to O(N(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N)2) and O(N
N)2) and O(N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N), respectively. Additionally, the number of angle terms in the HDNNP symmetry functions scales exponentially with the number of element types (which can be partially resolved by introducing weighted symmetry functions), whereas the GCNN atom types are encoded directly in an embedding vector and do not directly change the scaling of the model. Another important difference is that HDNNPs are based upon individual neural-network potentials (NNPs) for each atomic environment, whose evaluation can be easily distributed over multiple GPUs and the memory requirement for each individual NNP does not increase drastically with the increasing QM or MM system size. However, in contrast, GCNNs are based upon iterative and overlapping message passing operations and thus, a distributed evaluation is not as straightforward. Additionally, for each message passing operation within the GCNN graph, all edges have to be transformed using a dense layer. Therefore, the memory requirement for the GCNN evaluation scales as O(Ne·nf), where Ne is the number of edges. This means that the memory increases with the increasing QM or MM system size. Note that this can be critical when using a batched training procedure on a GPU.
N), respectively. Additionally, the number of angle terms in the HDNNP symmetry functions scales exponentially with the number of element types (which can be partially resolved by introducing weighted symmetry functions), whereas the GCNN atom types are encoded directly in an embedding vector and do not directly change the scaling of the model. Another important difference is that HDNNPs are based upon individual neural-network potentials (NNPs) for each atomic environment, whose evaluation can be easily distributed over multiple GPUs and the memory requirement for each individual NNP does not increase drastically with the increasing QM or MM system size. However, in contrast, GCNNs are based upon iterative and overlapping message passing operations and thus, a distributed evaluation is not as straightforward. Additionally, for each message passing operation within the GCNN graph, all edges have to be transformed using a dense layer. Therefore, the memory requirement for the GCNN evaluation scales as O(Ne·nf), where Ne is the number of edges. This means that the memory increases with the increasing QM or MM system size. Note that this can be critical when using a batched training procedure on a GPU.
In summary, the HDNNP based Δ-learning (QM)ML/MM setup appears to be best suited for condensed-phase systems with a limited number of different element types in the QM zone and the surrounding MM zone. Examples are the reactions of organic molecules in a solvent – similar to the five test systems investigated in this paper – or reactions at the interface of a mono-atomic surface. In these cases, the limited number of symmetry functions and the parallelizability over multiple GPUs/CPUs favor the HDNNP setup. On the other hand, the GCNN based Δ-learning (QM)ML/MM setup is most useful for condensed-phase systems with a larger number of element types, as the model scaling of the GCNN is much less affected by the number of element types than the HDNNP. Examples are the reactions within the active site of a metalloenzyme, proteins with covalently bound or interacting ligands, reactions involving organometallic catalysts, or reactions catalyzed at the interface of a poly-atomic surface.
Data and software availability
All structures used in the training, validation and test sets were taken from ref. 34 (freely available at https://www.research-collection.ethz.ch/handle/20.500.11850/512374). The GCNNs were implemented using Tensorflow/keras.50 The models were trained in Python and then exported to the C++ GROMOS code as described in ref. 34 for the HDNNPs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Moritz Thürlemann for the helpful discussions about GCNNs and HDNNPs, and Felix Pultar for his help in debugging the (QM)ML/MM code and the insightful discussions. The calculations were carried out on the high-performance cluster Euler of ETH Zurich.References
- S. Riniker, J. Chem. Inf. Model., 2018, 58, 565–578 CrossRef CAS.
- P. S. Nerenberg and T. Head-Gordon, Curr. Opin. Struct. Biol., 2018, 49, 129–138 CrossRef CAS PubMed.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS.
- A. J. Mulholland, P. D. Lyne and M. Karplus, J. Am. Chem. Soc., 2000, 122, 534–535 CrossRef CAS.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- G. Groenhof, Methods Mol. Biol., 2013, 924, 43–66 CrossRef CAS PubMed.
- H. Lin and D. G. Truhlar, Theor. Chem. Acc., 2007, 117, 185–199 Search PubMed.
- C. Panosetti, A. Engelmann, L. Nemec, K. Reuter and J. T. Margraf, J. Chem. Theory Comput., 2020, 16, 2181–2191 CrossRef CAS.
- E. Brunk and U. Röthlisberger, Chem. Rev., 2015, 115, 6217–6263 CrossRef CAS PubMed.
- L. W. Chung, W. M. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H. B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS PubMed.
- A. S. Christensen, T. Kubař, Q. Cui and M. Elstner, Chem. Rev., 2016, 116, 5301–5337 CrossRef CAS PubMed.
- J. J. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- M. Rupp, A. Tkatchenko, K.-R. R. Müller and O. A. Von Lilienfeld, Phys. Rev. Lett., 2012, 108, 1–5 CrossRef PubMed.
- J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955 RSC.
- K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. von Lilienfeld, A. Tkatchenko and K. R. Müller, J. Chem. Theory Comput., 2013, 9, 3404–3419 CrossRef CAS PubMed.
- S. Lorenz, A. Groß and M. Scheffler, Chem. Phys. Lett., 2004, 395, 210–215 CrossRef CAS.
- J. Behler, J. Phys.: Condens. Matter, 2014, 26, 183001 CrossRef CAS PubMed.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733 CrossRef.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- A. Grisafi, J. Nigam and M. Ceriotti, Chem. Sci., 2021, 12, 2078–2090 RSC.
- K. T. Schütt, P. J. Kindermans, H. E. Sauceda, S. Chmiela, A. Tkatchenko and K. R. Müller, Adv. Neural Inf. Process. Syst., 2017, 991–1001 Search PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS.
- D. P. Kovács, C. Van Der Oord, J. Kucera, A. E. A. Allen, D. J. Cole, C. Ortner and G. Csányi, J. Chem. Theory Comput., 2021, 17, 7696–7711 CrossRef PubMed.
- V. Zaverkin and J. Kästner, J. Chem. Theory Comput., 2020, 16, 5410–5421 CrossRef CAS PubMed.
- T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Nat. Commun., 2021, 12, 398 CrossRef CAS PubMed.
- Z. Li, J. R. Kermode and A. De Vita, Phys. Rev. Lett., 2015, 114, 1–5 Search PubMed.
- B. Anderson, T. S. Hy and R. Kondor, Adv. Neural Inf. Process. Syst., 2019, 32, 14537–14546 Search PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS.
- A. Grisafi and M. Ceriotti, J. Chem. Phys., 2019, 151, 204105 CrossRef PubMed.
- O. T. Unke, S. Chmiela, M. Gastegger, K. T. Schütt, H. E. Sauceda and K.-R. Müller, Nat. Commun., 2021, 12, 7273 CrossRef CAS PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- L. Böselt, M. Thürlemann and S. Riniker, J. Chem. Theory Comput., 2021, 17, 2641–2658 CrossRef.
- L. Shen and W. Yang, J. Chem. Theory Comput., 2018, 14, 1442–1455 CrossRef CAS PubMed.
- J. Zeng, T. J. Giese, S. Ekesan and D. M. York, J. Chem. Theory Comput., 2021, 17, 6993–7009 CrossRef CAS PubMed.
- K. T. Schütt, O. T. Unke and M. Gastegger, Proceedings of the 38th International Conference on Machine Learning, 2021, vol. 139, pp. 9377–9388.
- J. Klicpera, J. Groß and S. Günnemann, 2020, arXiv:2003.03123.
- V. G. Satorras, E. Hoogeboom and M. Welling, 2021, arXiv:2102.09844.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser and I. Polosukhin, Adv. Neural Inf. Process. Syst., 2017, 5999–6009 Search PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- M. Elstner, Theor. Chem. Acc., 2006, 116, 316–325 Search PubMed.
- B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitric, A. Dominguez, S. Ehlert, M. Elstner, T. Van Der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Åezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101 CrossRef CAS PubMed.
- R. E. Bulo, B. Ensing, J. Sikkema and L. Visscher, J. Chem. Theory Comput., 2009, 5, 2212–2221 CrossRef CAS.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, 34th International Conference on Machine Learning, ICML 2017, 2017, vol. 3, pp. 2053–2070.
- G. Corso, L. Cavalleri, D. Beaini, P. Liò and P. Velickovic, Adv. Neural Inf. Process. Syst., 2020, 33, 13260–13271 Search PubMed.
- N. Schmid, C. D. Christ, M. Christen, A. P. Eichenberger and W. F. van Gunsteren, Comput. Phys. Commun., 2012, 183, 890–903 CrossRef CAS.
- K. Meier, N. Schmid and W. F. V. Gunsteren, J. Comput. Chem., 2012, 33, 2108–2117 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 4–9 Search PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015 Search PubMed.
- I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459 CrossRef CAS.
- P. Ramachandran, B. Zoph and Q. V. Le, 2017, arXiv:1710.05941.
- J.-b Cordonnier and A. Loukas, 2020, arXiv:2006.16362.
- D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, 2017 Search PubMed.
- E. Fix and J. L. Hodges, Int. Stat. Rev., 1989, 57, 238 CrossRef.
- P. Niggli, XXIV. Die topologische Strukturanalyse. I.
- V. A. Blatov, Crystal. Rev., 2004, 10, 249–318 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures and tables for the validation with the test system benzene in water (PDF). See DOI: https://doi.org/10.1039/d2cp02931f |
| This journal is © the Owner Societies 2022 |