Open Access Article
Open Access ArticleU2N@Ih(7)-C80: fullerene cage encapsulating an unsymmetrical U(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) U(V) cluster†
U(V) cluster†
Xiaomeng
Li‡
a,
Yannick
Roselló‡
 b,
Yang-Rong
Yao‡
c,
Jiaxin
Zhuang
a,
Xingxing
Zhang
a,
Antonio
Rodríguez-Fortea
b,
Yang-Rong
Yao‡
c,
Jiaxin
Zhuang
a,
Xingxing
Zhang
a,
Antonio
Rodríguez-Fortea
 b,
Coen
de Graaf
b,
Coen
de Graaf
 bd,
Luis
Echegoyen
bd,
Luis
Echegoyen
 c,
Josep M.
Poblet
c,
Josep M.
Poblet
 b and
Ning
Chen
b and
Ning
Chen
 *a
*a
aCollege of Chemistry, Chemical Engineering and Materials Science, Soochow University, Suzhou, Jiangsu 215123, P. R. China. E-mail: chenning@suda.edu.cn
bDepartament de Química Física i Inorgànica, Universitat Rovira i Virgili, 43007, Tarragona, Spain
cDepartment of Chemistry, University of Texas at El Paso, 500 West University Avenue, El Paso, Texas 79968, USA
dICREA, Passeig Lluís Companys 23, Barcelona, Spain
First published on 27th October 2020
Abstract
For the first time, an actinide nitride clusterfullerene, U2N@Ih(7)-C80, is synthesized and fully characterized by X-ray single crystallography and multiple spectroscopic methods. U2N@Ih(7)-C80 is by far the first endohedral fullerene that violates the well-established tri-metallic nitride template for nitride clusterfullerenes. The novel U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U cluster features two U
U cluster features two U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds with uneven bond distances of 2.058(3) Å and 1.943(3) Å, leading to a rare unsymmetrical structure for the dinuclear nitride motif. The combined experimental and theoretical investigations suggest that the two uranium ions show different oxidation states of +4 and +5. Quantum-chemical investigation further reveals that the f1/f2 population dominantly induces a distortion of the U
N bonds with uneven bond distances of 2.058(3) Å and 1.943(3) Å, leading to a rare unsymmetrical structure for the dinuclear nitride motif. The combined experimental and theoretical investigations suggest that the two uranium ions show different oxidation states of +4 and +5. Quantum-chemical investigation further reveals that the f1/f2 population dominantly induces a distortion of the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U cluster, which leads to the unsymmetrical structure. A comparative study of U2X@C80 (X = C, N and O) reveals that the U–X interaction in U
U cluster, which leads to the unsymmetrical structure. A comparative study of U2X@C80 (X = C, N and O) reveals that the U–X interaction in U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U clusters can hardly be seen as being formed by classical multiple bonds, but is more like an anionic central ion Xq− with biased overlaps with the two metal ions, which decrease as the electronegativity of X increases. This study not only demonstrates the unique bonding variety of actinide clusters stabilized by fullerene cages, showing different bonding from that observed for the lanthanide analogs, it also reveals the electronic structure of the U
U clusters can hardly be seen as being formed by classical multiple bonds, but is more like an anionic central ion Xq− with biased overlaps with the two metal ions, which decrease as the electronegativity of X increases. This study not only demonstrates the unique bonding variety of actinide clusters stabilized by fullerene cages, showing different bonding from that observed for the lanthanide analogs, it also reveals the electronic structure of the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U clusters (X = C, N and O), which are of fundamental significance to understanding these actinide bonding motifs.
U clusters (X = C, N and O), which are of fundamental significance to understanding these actinide bonding motifs.
Introduction
The investigation of uranium nitride chemistry has long been a topic of interest due to the remarkable potential of uranium nitride complexes as new generation ceramic nuclear fuels and as candidates for the nitride transfer reaction and activation of unreactive small molecules like N2, H2, CO, CO2 and CS2 and even C–H bonds.1–7 More fundamentally, studying molecular uranium nitride complexes is essential to establishing a thorough understanding of the 5f and 6d orbital participation in multiple actinide–ligand bonds.8–12 To date, most of the reported uranium nitride bonding motifs have been stabilized by multiple chelating ligands.Our recent research shows that the fullerene cage is an ideal nano-container to capture and stabilize novel actinide metallic clusters, which makes them accessible for detailed bonding and structural analysis.13–15 These novel bonding motifs, which are important for fundamental actinide element chemistry studies, show remarkable uniqueness compared to those of their lanthanide analogs, due to the peculiar electronic structure and flexible oxidation states of actinide metal ions.
On the other hand, the first reported and most studied clusterfullerenes so far are the nitride clusterfullerenes (NCFs). Despite the diversity of the metals encapsulated in the nitride cluster, all of this family unexceptionally follows the tri-metallic nitride template (TNT), proposed in the study of Sc3N@C80, the first reported NCF.16–18 This template is rationalized by the inherent electronic features of the metallic species. Metals of subgroup III like Sc, Y and the lanthanides, when combined with nitrogen, result in an [M3N]6+ unit, which transfers six electrons stabilizing specific fullerene cages to form [M3N]6+@[C2n]6−.19–21 This template applies for all the NCFs discovered to date and has become the structural model for all NCF studies during the past few decades.
Encouraged by the recent advances made in actinide fullerenes,13–15,22–25 we further expanded our exploration to the NCFs. Herein, for the first time, we report the successful synthesis and full characterization of U2N@Ih(7)-C80, an unexpected dimetallic nitride clusterfullerene which violates the long standing TNT stoichiometry. In particular, the structural and theoretical analysis revealed the bonding nature of the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U cluster, a notably unsymmetrical dinuclear nitride with two uneven U
U cluster, a notably unsymmetrical dinuclear nitride with two uneven U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds, induced by the f1/f2 population. Furthermore, a systematic study of U2X (X = C, N, O) was carried out in this study to reveal the nature of these actinide bonding motifs.
N bonds, induced by the f1/f2 population. Furthermore, a systematic study of U2X (X = C, N, O) was carried out in this study to reveal the nature of these actinide bonding motifs.
Results and discussion
Preparation and purification
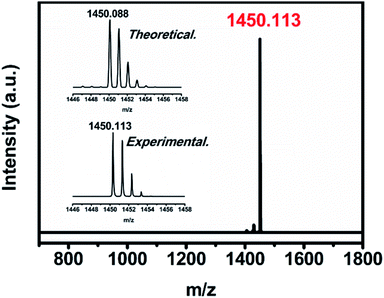
The uranium-based endohedral fullerenes were synthesized by a modified Krätschmer–Huffman DC arc-discharge method26 and separated by a high-performance liquid chromatography (HPLC) procedure (see the ESI†); the purity of U2N@C80 was confirmed by the observation of a sole peak at 1450 m/z in the MALDI-TOF mass spectrum, and the observed isotopic distribution agrees well with the theoretical calculation (see Fig. 1).Single crystal X-ray diffraction study
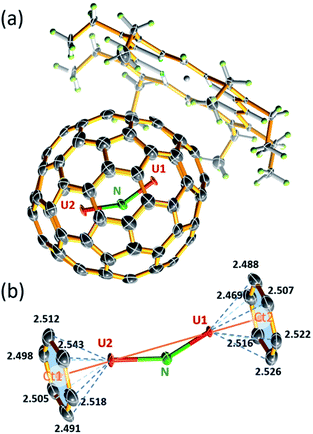
The molecular structure of U2N@Ih(7)-C80 was unambiguously determined by single-crystal X-ray diffraction analysis. Black crystal blocks of U2N@Ih(7)-C80·[NiII–OEP] (OEP = 2,3,7,8,12,13,17,18-octaethylporphyrin dianion) were obtained by slow diffusion of a benzene solution of NiII–OEP into a CS2 solution of U2N@C80. The crystallographic analysis shows that the structure crystallized in the P21/c (no. 14) space group (see Fig. 2a). In this cocrystal, both the fullerene cage and the central N atom are fully ordered. Two major sites of the two U atoms have a common dominant occupancy of 0.86 (Fig. S3†).The two dominant U atoms are located over two parallel hexagons in the Ih(7)-C80 cage (Fig. 2b). The shortest U-cage distances range from 2.491(5) to 2.543(5) Å for U1 and from 2.448(4) to 2.526(4) Å for U2, respectively, similar to those observed for U2C@Ih(7)-C80.15 The U⋯U distance of 3.864 Å is slightly longer than those observed in U2C@Ih(7)-C80 (ref. 15) and U2C2@Ih(7)-C80,14 but notably shorter than that in U2C2@D3h(5)-C78 (ref. 14) (see Table 1). Moreover, the U1 to U2 line coincides with the C2 axis (Ct1–Ct2 axis, Fig. 2b) of the Ih(7)-C80 cage with a very small angle of 2.1°. Such a metal-cage configuration is very close to those of U2C@Ih(7)-C80 and U2@Ih(7)-C80.13,15 These results suggest that, despite the major differences between the bonding motifs of U2N, U2C and U2, the position of the U atoms inside the fullerene cages is overwhelmingly dominated by the cage structure of Ih(7)-C80, rather than the configuration of the uranium metallic clusters themselves. The different uranium-nonmetal bonds are formed only by the variation of the positions of the nonmetal ions between the two uranium ions.
The most interesting feature of this novel actinide clusterfullerene is the encaged U2N cluster, which, to the best of our knowledge, represents the first observation of a stabilized bimetallic uranium nitride cluster. Neither theoretical nor experimental studies have ever proposed such a structure. Moreover, this observation changes the established ‘trimetallic nitride template (TNT)’, in which all the nitride clusters contain three metal ions bonded to a central N atom.16–18 The stabilization of this unique uranium nitride cluster proves that the combination of the unique electronic structures of actinides and the special chemical environment inside the fullerene cage leads to the stabilization of novel actinide clusters, which do not resemble their lanthanide analogs or the bonding motifs currently accessible by conventional synthetic methods.
The encaged U2N cluster presents a bent configuration, with a UNU angle of 150.0(2)°. Such a significant torsion of the U2N cluster is notably different from the linear configuration of the conventional chelate UNU complexes, such as [{((Me3Si)2N)2U(THF)}2(μ-N)]7 and [(μ-N) (U(NtBuAr)3)2],1 in which the UNU units adopt a linear configuration. Nevertheless, bent U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U moieties were also observed in the recent reports by Mazzanti et al. and Liddle et al., with UNU angles ranging from ca. 160–168°.11,12 Selected examples are presented in Table 2. Compared to these complexes, the UNU angle of 150° in U2N@Ih(7)-C80 appears to be more bent, likely the result of the steric effect of the encapsulation by the fullerene cage. Moreover, different from the symmetric structure of U
U moieties were also observed in the recent reports by Mazzanti et al. and Liddle et al., with UNU angles ranging from ca. 160–168°.11,12 Selected examples are presented in Table 2. Compared to these complexes, the UNU angle of 150° in U2N@Ih(7)-C80 appears to be more bent, likely the result of the steric effect of the encapsulation by the fullerene cage. Moreover, different from the symmetric structure of U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U in U2C@Ih(7)-C80, the U2N cluster is notably unsymmetrical with two uneven U–N bonds. The longer bond distance of 2.058(3) Å for U2–N is commonly observed in the chelated UNU complexes, as shown in Table 2. The shorter U1–N bond distance of 1.943(3) Å is, however, among the shortest U
U in U2C@Ih(7)-C80, the U2N cluster is notably unsymmetrical with two uneven U–N bonds. The longer bond distance of 2.058(3) Å for U2–N is commonly observed in the chelated UNU complexes, as shown in Table 2. The shorter U1–N bond distance of 1.943(3) Å is, however, among the shortest U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond distances reported so far.3,4,27–36 The U2N cluster exhibits a dramatic difference of over 0.11 Å between the two U
N bond distances reported so far.3,4,27–36 The U2N cluster exhibits a dramatic difference of over 0.11 Å between the two U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds.
N bonds.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U and N
U and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U
U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N complexes
N complexes
| Compound | U–N bonds (Å) | U–N–U bond angle (°) | Oxidation states of uranium | Ref. |
|---|---|---|---|---|
| U2N@Ih(7)-C80 | 1.943/2.058 | 150.0 | IV/V | This work |
| [{((Me3Si)2N)2U(THF)}2(μ-N)] | 2.063 | 180 | III/IV | 7 |
| [(μ-N)(U(NtBuAr)3)2] | 2.0625 | 180 | IV/V | 1 |
| Cs2[{U(OSi(OtBu)3)3}2(μ-N)] | 2.099/2.081 | 169.1 | III/IV | 4 |
(C5Me5)2U{![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N[P(SiMe3) (Mes)]}[ N[P(SiMe3) (Mes)]}[![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(SiMe3)] N(SiMe3)] |
1.952/2.001 | — | VI | 37 |
| [Na(dme)3][((Me3Si)2N)3U(μ-N)U(N(SiMe3)2)(OSi(OtBu)3)] | 2.055/2.066 | 168.4 | IV/IV | 11 |
| [{((Me3Si)2N)3U}2(μ-N)] | 2.080/2.150 | 179.4 | IV/V | 11 |
| [{U(TrenDMBS)}2(μ-N)] | 2.081/2.136 | 161.2 | IV/V | 12 |
In effect, to facilitate a (U2)9+N3−@(Ih(7)-C80)6− model to effectively stabilize the fullerene cage, different oxidation states of IV and V of the two uranium ions can be well rationalized. Thus U1 with a shorter U–N bond of 1.943 Å can be assigned to U(V) and U2 with a longer U–N bond of 2.058 Å can be assigned to U(IV). This conclusion was confirmed by theoretical calculations and X-ray absorption analyses (see below). As summarized in Table 2, unsymmetrical U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U bonding motifs containing U ions with different oxidation states, stabilized by chelating ligands, have been reported. In particular, the U
U bonding motifs containing U ions with different oxidation states, stabilized by chelating ligands, have been reported. In particular, the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U bonding motif found inside the C80 cage, though with a slightly shorter U
U bonding motif found inside the C80 cage, though with a slightly shorter U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond length, resembles that of the recently reported [{((Me3Si)2N)3U}2(μ-N)], which possesses a similar U(IV)
N bond length, resembles that of the recently reported [{((Me3Si)2N)3U}2(μ-N)], which possesses a similar U(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U(V) core.11 In this study, Mazzanti et al. investigated a series of molecular uranium complexes and found that, in these compounds, the ligand significantly affects the bonding and the resulting metric parameters of the U
U(V) core.11 In this study, Mazzanti et al. investigated a series of molecular uranium complexes and found that, in these compounds, the ligand significantly affects the bonding and the resulting metric parameters of the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U core, and the uneven bond lengths of U
U core, and the uneven bond lengths of U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U are the result of the localized valences.11 Thus, in the present case, the C80 fullerene cage likely functions as a special spherical ligand, which creates a coordination environment to stabilize the reactive U
U are the result of the localized valences.11 Thus, in the present case, the C80 fullerene cage likely functions as a special spherical ligand, which creates a coordination environment to stabilize the reactive U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U moiety and imposes a significant influence on the U–N bonding, resulting in the varied oxidation states of U and the unsymmetrical U–N bond lengths.
U moiety and imposes a significant influence on the U–N bonding, resulting in the varied oxidation states of U and the unsymmetrical U–N bond lengths.
Spectroscopic characterization: UV-vis-NIR, IR and Raman spectra
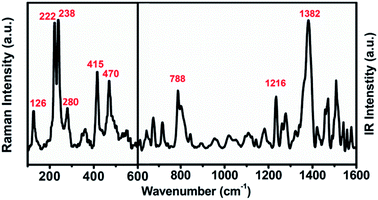
The UV-vis-NIR absorption spectrum of U2N@Ih(7)-C80 (see Fig. S2†) is largely featureless except for minor absorption peaks at 446 nm and 680 nm. The absorption onset is measured at about 1350 nm and the optical band gap is determined to be 0.92 eV, which is typical for Ih(7)-C80 cage based EMFs and similar to those observed for U2C@Ih(7)-C80 and U2@Ih(7)-C80.13,15,18The molecular vibrational features of U2N@Ih(7)-C80 are shown in Fig. 3. The vibrations between 600 cm−1 and 220 cm−1 of the Raman spectrum, which reflect the vibration modes of the carbon cage, show high similarity to those of the previously reported EMFs with the Ih(7)-C80 cage,13,15 in agreement with the structural determination of the X-ray diffraction analysis. In the lower-wavenumber range, weaker features at 126 cm−1 and 280 cm−1 are observed, which can be assigned to the Raman-active UNU cluster modes (see Table S3† for a more detailed assignment), resembling those of the UCU modes of U2C@Ih(7)-C80 (126 cm−1 and 277 cm−1).15 In the IR spectrum, typical characteristics for Ih(7)-C80 based EMFs, major overlapping bands around 1380 cm−1 and the featureless gap between 1100 and 900 cm−1, are observed.15,38 The UNU unsymmetrical stretching mode can be assigned to the major peak of 788 cm−1, slightly shifted from 785 cm−1 for U2C@Ih(7)-C80.15
Theoretical analysis of the non-symmetric U2N unit within a fullerene
DFT and CASSCF calculations were performed to rationalize the electronic structure of U2N@Ih(7)-C80. The geometry of the clusterfullerene was optimized at the DFT PBE0 level, reproducing well the X-ray unsymmetrical form of the encapsulated cluster, even though the asymmetry is somewhat larger for the DFT structure. While the experimental bond lengths for U1–N and U2–N are 1.943 and 2.058 Å, the corresponding computed values are 1.911 and 2.113 Å, respectively. The computed angle for U1–N–U2 of 155° is slightly larger than the experimental value of 150.2° (Table 3). As stated above, this situation is different from what was reported for U2C@C80, in which the two U–C bonds were described by two equal double bonds.15 The main difference between the two clusterfullerenes is that while in the carbide the two U atoms are in oxidation state V, in the nitride clusterfullerene the spin density distribution clearly confirms that it is a mixed valence species with U1 and U2 in formal oxidation states V and IV, respectively (Table 3 and Fig. S4†). To corroborate the DFT results we have also performed CASSCF calculations on the overall molecule, which clearly confirm the mixed valence nature of U2N@Ih(7)-C80.| System | Bond lengtha | Anglea | Mayer BIb | Spin densityc | BEd | ||||
|---|---|---|---|---|---|---|---|---|---|
| U1–X | U2–X | U1–X–U2 | U1–X | U2–X | U1 | U2 | X | X | |
| a All bond lengths are given in angstroms; X-ray values for U2X@Ih(7)-C80 in parentheses. b Mayer bond indices. c Mulliken spin density. d Energy in eV associated with the process U2@Ih(7)-C80 + X → U2X@Ih(7)-C80. e Computed structure for the U2N fragment. | |||||||||
| U2N@Ih(7)-C80 | 1.913 (1.943) | 2.113 (2.058) | 155.5 (150.2) | 1.707 | 0.942 | 1.093 | 2.081 | −0.113 | −8.35 |
| U2N@Ih(7)-C80+ | 2.000 | 2.000 | 177.0 | 1.304 | 1.303 | 1.138 | 1.138 | −0.107 | |
| U2Ne | 2.029 | 2.033 | 120.5 | 1.396 | 1.371 | 4.634 | 4.652 | −0.286 | |
| U2O@Ih(7)-C80 | 2.067 | 2.067 | 148.0 | 0.768 | 0.771 | 2.094 | 2.094 | −0.087 | −11.08 |
| U2C@Ih(7)-C80 | 2.032 (2.033) | 2.032 (2.028) | 143.9 (142.9) | 1.528 | 1.528 | 1.134 | 1.134 | −0.130 | −8.89 |
| U2C@Ih(7)-C80 (non-symmetric) | 1.876 | 2.192 | 149.6 | 2.097 | 0.955 | 0.071 | 2.034 | −0.062 | −8.50 |
To better understand the asymmetry of U2N, we have compared the bond lengths, bond angles and Mulliken spin densities for U2N@Ih(7)-C80 and [U2N@Ih(7)-C80]+, which is isoelectronic to U2C@Ih(7)-C80. It is very illustrative to see that while in the oxidized form of the internal cluster with two formal U(f1) ions, the UNU unit exhibits a symmetric arrangement; for the neutral form, the f1/f2 population induces a distortion of the cluster. This could be attributed to the repulsion between non-bonding f electrons and bonding U–N electrons, which is higher for the uranium atom with two f electrons. Because the uranium atoms in the homologous U2O@Ih(7)-C80 endohedral fullerene are in oxidation state IV, the U2O unit again exhibits a symmetric arrangement. Interestingly, for U2C@Ih(7)-C80, we have been able to obtain a symmetric (f1/f1) and an unsymmetrical (f0/f2) form, confirming the relevance of the number of f electrons in the distortion of the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U unit within a fullerene (Table 3). We have also analysed the molecular electrostatic potential (MEP) for U2N@Ih(7)-C80, which suggests a non-homogeneous charge distribution over the cage with a more negative region of the MEP in the equatorial belt between the two U atoms (Fig. 5). In spite of the different formal oxidation states of the two metal atoms, the electrostatic potential values for the two regions near the two U ions are very similar and less negative than those of the belt (see the ESI† for more details).
U unit within a fullerene (Table 3). We have also analysed the molecular electrostatic potential (MEP) for U2N@Ih(7)-C80, which suggests a non-homogeneous charge distribution over the cage with a more negative region of the MEP in the equatorial belt between the two U atoms (Fig. 5). In spite of the different formal oxidation states of the two metal atoms, the electrostatic potential values for the two regions near the two U ions are very similar and less negative than those of the belt (see the ESI† for more details).
The formal enclosure of a N atom in U2@C80 to give U2N@C80 is a thermodynamically favorable process with an energy gain of 8.35 eV, which can be associated primarily with the formation of two new U–N bonds. Similar energies are involved in the encapsulation of an extra C atom to give the homologous carbide (−8.89 eV) and even somewhat higher energy for the oxide (−11.08 eV). It is worth mentioning that the addition of a third uranium atom to give U3N@C80 is also an exothermic process involving more than −10 eV. The U3N within C80 is not planar (Fig. 4b), similar to what was reported for the biggest lanthanide ions.16,39,40 The absence of classical trimetallic nitrides in the mass spectra is probably not related to an energetic factor, but rather to a lower capacity of U3N to act as an effective template during the endofullerene formation.
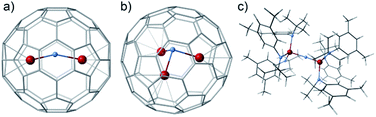 | ||
| Fig. 4 Several PBE0 computed structures containing U2N or U3N cores. (a) U2N@C80; (b) U3N@C80 and (c) (μ-N)(U(NtBuAr)3)2. | ||
Bonding in the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) X
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) U cores
U cores
The neutral UNU molecule has 17 valence electrons with a bonding pattern that could be represented by the two bonding forms U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[N with combining macron]](https://www.rsc.org/images/entities/char_004e_0304.gif) –U ↔ U–
–U ↔ U–![[N with combining macron]](https://www.rsc.org/images/entities/char_004e_0304.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U. In this hypothetical molecule, the two U atoms have a total of nine electrons that do not contribute to the two U–N bonds. As expected, this molecule shows a bent form with a bond angle of 120.5°. When encapsulated inside the fullerene, six electrons are transferred from the cluster to the fullerene and therefore only three f electrons remain in U atoms as non-bonding electrons. Because of the U⋯U repulsion the computed bond angle increases up to 150°. In addition to the two bonding patterns represented above, we can foresee other forms in which the central atom acts formally with a positive charge U
U. In this hypothetical molecule, the two U atoms have a total of nine electrons that do not contribute to the two U–N bonds. As expected, this molecule shows a bent form with a bond angle of 120.5°. When encapsulated inside the fullerene, six electrons are transferred from the cluster to the fullerene and therefore only three f electrons remain in U atoms as non-bonding electrons. Because of the U⋯U repulsion the computed bond angle increases up to 150°. In addition to the two bonding patterns represented above, we can foresee other forms in which the central atom acts formally with a positive charge U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U ↔ U
U ↔ U![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–U ↔ U–N
N–U ↔ U–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) U or carrying a formal negative charge as in
U or carrying a formal negative charge as in 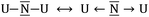 . Because of the higher electronegativity of N with respect to U, it is expected that the most ionic forms will strongly compete with the bonding forms exhibiting multiple bonds. Indeed, the observed U–N–U angle between 180 and 120 degrees underlines the presence of the competition between the two limit forms: the ones dominated by the multiple uranium–nitrogen bonds and the ones dominated by the higher electronegativity of the central atom. This conflict is solved by the formation of polarized σ and π bonds as already proposed for the homologous U2C core inside C80 and analyzed for the model system C7H7UCUC7H7 using CASSCF calculations.15
. Because of the higher electronegativity of N with respect to U, it is expected that the most ionic forms will strongly compete with the bonding forms exhibiting multiple bonds. Indeed, the observed U–N–U angle between 180 and 120 degrees underlines the presence of the competition between the two limit forms: the ones dominated by the multiple uranium–nitrogen bonds and the ones dominated by the higher electronegativity of the central atom. This conflict is solved by the formation of polarized σ and π bonds as already proposed for the homologous U2C core inside C80 and analyzed for the model system C7H7UCUC7H7 using CASSCF calculations.15
To gain a better understanding of the bonding in U2X cores, we have analyzed the series U2X@C80, with X= C, N and O, using localized molecular orbitals (MOs). The Boys–Foster localization method is able to entirely separate MOs localized on U2X from those localized/delocalized over the carbon cage (Fig. 6) and recover the four orbitals involved in bonding, which are schematically represented in Scheme 1. In all these systems, there are two sigma and two pi orbitals formed by d–f hybrid orbitals of U and s and p orbitals of N. The atomic percentages are compiled in Table S2.† As expected, the occupied orbitals with the highest energies for U2N@C80 correspond to three non-bonding f electrons localized on uranium atoms, which are in an energy range between −8.52 and −7.15 eV, while the two orbitals with π-overlap are found at −13.11 eV and at −12.54 eV. Much deeper, we find the two σ U–N orbitals that have significant contributions from the lone pair of N. Localized MOs for U2C@C80 and U2O@C80 are essentially identical to those of U2N@C80. Pipek–Mezey localized orbitals show an analogous qualitative interpretation (see Fig. S11†). The main differences or peculiarities can be summarized as follows: (1) the energy of MOs contributing to U–X bonds is very sensitive to the electronegativity of the central atom, being much deeper for the oxide; (2) the π-type bonding orbitals are somewhat more extended when X = C and more compact when X = O; (3) the sigma-type orbitals are rather similar for the nitride, carbide and oxide and (4) population analysis reveals that the contribution of the valence orbitals of X to the bond increases as the electronegativity of the bridging atom increases, going from about 60% for the carbide up to more than 80% for the oxide (Table S2†), with the nitride somewhere in between these two. The Mayer bond indices (BIs) compiled in Table 3 underline that the nature of the bond changes with the bridging ion and with the oxidation states of the two U atoms. The U–X BIs significantly decrease when going from C (1.53) to O (0.77) because of the polarization of the involved orbitals, which would be in line with a significant increase of the contribution of the resonance form 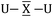 for the metal oxide. Similarly, the rather different BIs of 1.71 and 0.94 found for U(V)–N and U(IV)–N bonds suggest that the U
for the metal oxide. Similarly, the rather different BIs of 1.71 and 0.94 found for U(V)–N and U(IV)–N bonds suggest that the U![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N–U form has a non-negligible participation in these mixed-valence nitrides.
N–U form has a non-negligible participation in these mixed-valence nitrides.
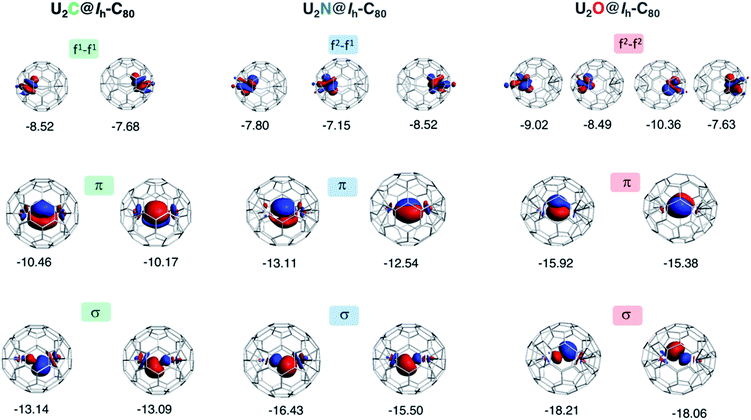 | ||
Fig. 6 Localized (Boys–Foster) MOs for U2X@C80 with X = C, N and O. MOs relevant to bonding in the U2X moiety are represented. The orbital energies (in eV) of non-bonding f electrons of U do not depend significantly on X, but π and σ orbitals are much more sensitive to the central atom. The modest multiple bond nature of U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X interaction decreases further as electronegativity of X increases. Orbital compositions are given in Table S2.† X interaction decreases further as electronegativity of X increases. Orbital compositions are given in Table S2.† | ||
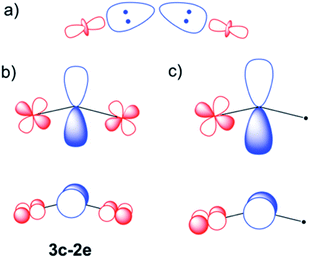 | ||
Scheme 1 σ (a) and π (b and c) U–N–U interactions are represented schematically. In a metal ligand formulation, in which the U atoms are in formal oxidation states IV and V ( ), the high electron density on the central ion is back donated through π overlaps. This can be done with two 3-center-2e orbitals (b) or also via a triple bond in the unsymmetrical form (c). Orbital contributions are similar for 6d and 5f atomic uranium orbitals (Table S2†), but only d orbitals have been represented for simplicity. ), the high electron density on the central ion is back donated through π overlaps. This can be done with two 3-center-2e orbitals (b) or also via a triple bond in the unsymmetrical form (c). Orbital contributions are similar for 6d and 5f atomic uranium orbitals (Table S2†), but only d orbitals have been represented for simplicity. | ||
As mentioned above, CASSCF calculations have allowed us to confirm the mixed valence nature of the endohedral fullerene. Another important result from the CASSCF calculations is that it was not possible to include any U–N orbital with π-overlap in the active space. In all the attempts, these orbitals remain strictly doubly occupied and replaced by other non-bonding U (d or f) orbitals. As found at DFT level, these CASSCF π-like orbitals have a small contribution from the f and d orbitals of U. This confirms that the bond can be seen as a N3− ligand with some π donation to uranium atoms, which is somewhat stronger for U5+. Selected CASSCF-MOs are given in Fig. S6.†
U2N bonding in organometallic complexes
Finally, we have explored U–N bonding in a series of bimetallic uranium nitride complexes possessing a linear U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U core.1 X-ray analysis of [(μ-N)(U(NtBuAr)3)2]n with n = −1, 0 and +1, shows that the U2N unit exhibits a linear arrangement in all three oxidation states of U atoms; f2–f2 (IV–IV), f2–f1 (IV–V) and f1–f1 (V–V), i.e. for the anion, neutral complex and cation, respectively. Geometry optimizations reproduce very well the experimental structures for the cationic and anionic forms (Table 4). Nevertheless, the computed structure for the neutral complex (Fig. 4c) shows a distortion of the U2N core, similar to that observed inside the fullerene, with long and short U–N bond lengths of 2.179 and 1.919 Å, in contrast with the symmetric arrangement observed in the X-ray structure.1 To evaluate if the discrepancy between experiments and calculations could come from the DFT treatment, we have performed CASPT2 calculations for the model system U2N(NH2)6, reproducing almost exactly the asymmetry obtained for the real system (Table 4). At the CASPT2 level a symmetric structure with bond lengths equal to 2.027 Å was found to be about 10 kcal mol−1 higher in energy than the unsymmetrical one. CASPT2 energy analysis confirmed the presence of two electronic states with U4+–N–U5+ and U5+–N–U4+ distributions (Fig. S7†). Given the high energy of the symmetric form and the very small interaction between the two electronic states, a dynamic transformation between the two forms seems unlikely. Therefore, it could be that what one observes in experiments is a disordered phase with a 50–50 population of the two unsymmetrical possibilities. The CASSCF MOs for U2N(NH2)6 show that bonding in the U2N core is essentially similar to that described for endohedral fullerenes (Fig. S8 and S9†).
U core.1 X-ray analysis of [(μ-N)(U(NtBuAr)3)2]n with n = −1, 0 and +1, shows that the U2N unit exhibits a linear arrangement in all three oxidation states of U atoms; f2–f2 (IV–IV), f2–f1 (IV–V) and f1–f1 (V–V), i.e. for the anion, neutral complex and cation, respectively. Geometry optimizations reproduce very well the experimental structures for the cationic and anionic forms (Table 4). Nevertheless, the computed structure for the neutral complex (Fig. 4c) shows a distortion of the U2N core, similar to that observed inside the fullerene, with long and short U–N bond lengths of 2.179 and 1.919 Å, in contrast with the symmetric arrangement observed in the X-ray structure.1 To evaluate if the discrepancy between experiments and calculations could come from the DFT treatment, we have performed CASPT2 calculations for the model system U2N(NH2)6, reproducing almost exactly the asymmetry obtained for the real system (Table 4). At the CASPT2 level a symmetric structure with bond lengths equal to 2.027 Å was found to be about 10 kcal mol−1 higher in energy than the unsymmetrical one. CASPT2 energy analysis confirmed the presence of two electronic states with U4+–N–U5+ and U5+–N–U4+ distributions (Fig. S7†). Given the high energy of the symmetric form and the very small interaction between the two electronic states, a dynamic transformation between the two forms seems unlikely. Therefore, it could be that what one observes in experiments is a disordered phase with a 50–50 population of the two unsymmetrical possibilities. The CASSCF MOs for U2N(NH2)6 show that bonding in the U2N core is essentially similar to that described for endohedral fullerenes (Fig. S8 and S9†).
| System | Method | U–Na | U–N–U | Mayer BIb | Spin densityc | |
|---|---|---|---|---|---|---|
| U–N | U | N | ||||
| a Distance and angles are in angstroms and degrees. b Mayer bond indices. c Mulliken spin density. | ||||||
| Neutral | X-ray | 2.065 | 180 | |||
| Neutral | PBE0 | 1.919/2.179 | 176.7 | 1.877/0.543 | 1.221/2.160 | −0.13 |
| Cation | X-ray | 2.047/2.051 | 180 | |||
| Cation | PBE0 | 2.020/2.036 | 178.6 | 1.335/1.326 | 1.211/1.241 | −0.11 |
| Anion | X-ray | 2.062/2.080 | 175 | |||
| Anion | PBE0 | 2.045/2.046 | 178.9 | 1.314/1.313 | 2.155/2.156 | −0.14 |
| Neutral | CASPT2 | 1.879/2.179 | 180 | 1.025/1.988 | −0.03 | |
Pyykkö and Atsumi predicted from the sum of U and N radii a bond length of 1.94 Å for a U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond.41 Nevertheless, U–N bond distances reported for some U imido complexes (U
N bond.41 Nevertheless, U–N bond distances reported for some U imido complexes (U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–R) display values as short as 1.89 Å,36 even 1.85 Å.42,43 DFT calculations for several uranium bis(imido) complexes demonstrated that U–N interactions must be seen as a slightly polarized triple bond.41 Given that the existence of more or less polarized triple bonds is possible in many uranium–nitride complexes, and in concomitance with the unpaired number of f electrons in U2N-containing systems, we believe that the asymmetry of the U2N unit is inherent in all these mixed-valence systems.
N–R) display values as short as 1.89 Å,36 even 1.85 Å.42,43 DFT calculations for several uranium bis(imido) complexes demonstrated that U–N interactions must be seen as a slightly polarized triple bond.41 Given that the existence of more or less polarized triple bonds is possible in many uranium–nitride complexes, and in concomitance with the unpaired number of f electrons in U2N-containing systems, we believe that the asymmetry of the U2N unit is inherent in all these mixed-valence systems.
X-ray absorption spectrum of U2N@ U2N@Ih(7)-C80
The X-ray absorption spectrum (XAS) of U2N@Ih(7)-C80 is shown in Fig. 7. Notably, the white line peak energy of U2N@Ih(7)-C80 lies between those observed for U(V)2C@Ih(7)-C80 and U(III)2@C80. A closer look shows that the white line of U2N@C80 is much closer to that of U(V)2C@Ih(7)-C80 than to that of U(III)2@Ih(7)-C80, indicating a higher average oxidation state than IV. This observation agrees well with the IV/V oxidation states assigned by the structural and theoretical analysis above. However, the spectrum of U2N@Ih(7)-C80 does not show split white line peaks for different oxidation states of U. A similar phenomenon was observed for uranium-based compounds with varied oxidation states.44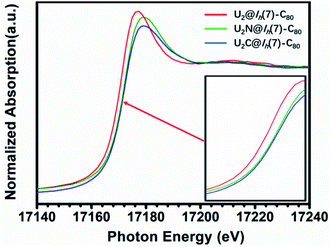 | ||
| Fig. 7 U L3-edge XAS spectra of U2N@C80 as compared to those of U2@C80 and U2C@C80. The inset is the absorption edges magnified for a clearer observation. | ||
Electrochemical studies
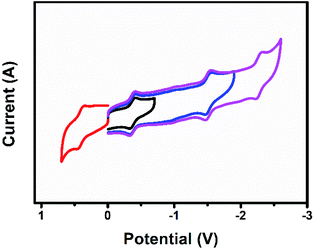
Fig. 8 shows the cyclic voltammogram of U2N@Ih(7)-C80. The first reduction and oxidation potentials of U2N@Ih(7)-C80 are −0.38 V and +0.40 V, respectively, which are slightly different from those of U2C@Ih(7)-C80 (−0.41 V and +0.42 V, respectively), and the electrochemical gap for U2N@Ih(7)-C80 is 0.78 V, narrower than that of U2C@Ih(7)-C80 by 0.05 V (Table 5).15 The substitution of C with N within the cluster exerts a significant impact on the energies of some MOs. However, the changes in the energies of 5f orbitals are significantly smaller. This explains the relatively small differences observed in the first oxidation and reduction potentials between U2N@Ih(7)-C80 and U2C@Ih(7)-C80. Similarly, we can predict a greater influence on the redox properties of the clusterfullerene when C is replaced by O.On the other hand, the electrochemical behavior of U2N@Ih(7)-C80 presents a notable difference compared to the chelated analogue [(μ-N)[U(NtBuAr)3]2].1 The first oxidation and reduction potentials of [(μ-N)(U(NtBuAr)3)2] are measured at −0.64 V and −1.69 V, resulting in an electrochemical gap of 1.05 V, dramatically larger than that for U2N@Ih(7)-C80. These results indicate that the coordination environment also exerts great influence on the electrochemical properties of the central UNU group and on the frontier MOs of the entire molecule. Indeed, stronger metal–ligand interactions in the chelated [(μ-N)(U(NtBuAr)3)2] complex result in higher frontier orbital energies for this complex compared to those of endohedral fullerenes (see Fig. S10†), justifying the shifts observed in the redox potentials. In these systems the first oxidation and reduction involve U(f) orbitals.
Conclusions
In summary, for the first time, a uranium nitride clusterfullerene, U2N@Ih(7)-C80, was synthesized and fully characterized by X-ray crystallography, UV-vis-NIR spectroscopy, Raman spectroscopy, Fourier transform infrared absorption spectroscopy, X-ray absorption spectroscopy and cyclic voltammetry. This is the first example of a dimetallic nitride clusterfullerene, changing the traditional composition of the trimetallic nitride clusterfullerenes. Moreover, the novel U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U cluster features two U
U cluster features two U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds with uneven bond distances of 2.058(3) Å and 1.943(3) Å, leading to a rare unsymmetrical structure. Theoretical investigation further revealed that, while U
N bonds with uneven bond distances of 2.058(3) Å and 1.943(3) Å, leading to a rare unsymmetrical structure. Theoretical investigation further revealed that, while U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U exhibits a symmetric arrangement for the oxidized form of the internal cluster with two formal U(f1) ions, in the neutral form, the f1/f2 population induces a distortion of the U
U exhibits a symmetric arrangement for the oxidized form of the internal cluster with two formal U(f1) ions, in the neutral form, the f1/f2 population induces a distortion of the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U cluster, which leads to this unsymmetrical structure.
U cluster, which leads to this unsymmetrical structure.
Systematic computational studies for U2X@C80 (X = C, N and O) and for other organometallic complexes further revealed that U–X bonding in these molecules can be described as a polarized U–X interaction and, depending on the number of U(f) electrons, the U2X core can be unsymmetrical. Formally, the bonding in U2X can be represented as U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U; however, it is important to underline that the U–X interaction can hardly be seen as being formed by classical multiple bonds, but is more like an anionic central ion Xq− with biased π overlaps with the two metal ions, which decrease as the electronegativity of X increases.
U; however, it is important to underline that the U–X interaction can hardly be seen as being formed by classical multiple bonds, but is more like an anionic central ion Xq− with biased π overlaps with the two metal ions, which decrease as the electronegativity of X increases.
This study shows the unique bonding variety for actinide clusters stabilized by fullerene cages. More importantly, the stabilization of the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U cluster enables us to reveal the electronic structure of U
U cluster enables us to reveal the electronic structure of U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X
X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U clusters (X= C, N and O), which is of fundamental significance to understanding actinide bonding motifs.
U clusters (X= C, N and O), which is of fundamental significance to understanding actinide bonding motifs.
Experimental section
Synthesis and isolation of U2N@C80
The carbon soot-containing uranium EMFs were produced by the direct current arc discharge method. The graphite rods, packed with U3O8 and graphite powders (1.27 g of U3O8 powder and 1.62 g of graphite powder per rod, molar ratio of U/C = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30), were vaporized in the arcing chamber under a 200 torr helium atmosphere with 1 torr NH3. The soot collected was refluxed in CS2 under an argon atmosphere for 24 h. The separation and purification of U2N@C80 were achieved by multistage HPLC procedures. Totally, 100 rods were vaporized and ca. 4.0 g crude fullerene extract was obtained (ca. 40 mg per rod), out of which ca. 0.1 mg U2N@Ih(7)-C80 was finally isolated. Multiple HPLC columns, including Buckyprep-M (25 × 250 mm, Cosmosil, Nacalai Tesque Inc.), Buckyprep-D (10 × 250 mm, Cosmosil, Nacalai Tesque, Japan) and Buckyprep (10 × 250 mm, Cosmosil, Nacalai Tesque, Japan), were utilized in the procedures (further details are described in the ESI†).
30), were vaporized in the arcing chamber under a 200 torr helium atmosphere with 1 torr NH3. The soot collected was refluxed in CS2 under an argon atmosphere for 24 h. The separation and purification of U2N@C80 were achieved by multistage HPLC procedures. Totally, 100 rods were vaporized and ca. 4.0 g crude fullerene extract was obtained (ca. 40 mg per rod), out of which ca. 0.1 mg U2N@Ih(7)-C80 was finally isolated. Multiple HPLC columns, including Buckyprep-M (25 × 250 mm, Cosmosil, Nacalai Tesque Inc.), Buckyprep-D (10 × 250 mm, Cosmosil, Nacalai Tesque, Japan) and Buckyprep (10 × 250 mm, Cosmosil, Nacalai Tesque, Japan), were utilized in the procedures (further details are described in the ESI†).
Spectroscopic and electrochemical studies
A positive-ion mode laser desorption/ionization time-of-flight mass-spectrometer (Bruker, Germany) was employed for mass characterization. The UV-vis-NIR spectra of the purified U2N@C80 were measured in CS2 solution with a Cary 5000 UV-vis-NIR spectrophotometer (Agilent, U.S.). The Raman spectra were obtained using a Horiba Lab RAM HR Evolution Raman spectrometer using a laser at 633 nm. The micro Fourier transform infrared spectra were obtained at room temperature using a Vertex 70 spectrometer (Bruker, Germany) with a resolution of 4 cm−1. For the IR and Raman measurements, the samples were drop-coated on aluminized paper and a quartz plate, respectively. The residual CS2 was eliminated in a drying chamber in a vacuum at 40 °C.Cyclic voltammetry (CV) was conducted in o-dichlorobenzene using a CHI-660E instrument. A conventional three-electrode cell consisting of a platinum counter-electrode, a glassy carbon working electrode, and a silver reference electrode was used for the measurement. (n-Bu)4NPF6 (0.05 M) was used as the supporting electrolyte. CV was measured at a scan rate of 100 mV s−1.
X-ray crystallographic study
The black-block crystals of U2N@C80 were obtained by slow diffusion of a carbon disulfide solution of the target sample into a benzene solution of [NiII·(OEP)]. The single-crystal X-ray data of U2N@C80 were collected at 100 K using synchrotron radiation (0.77484 Å) with a MX300-HE CCD detector at beamline BL17B of the Shanghai Synchrotron Radiation Facility (SSRF), and the X-ray diffraction data of U2N@C80 were collected on a diffractometer (APEX II; Bruker Analytik GmbH) equipped with a CCD collector. The multiscan method was used for absorption correction. The structures were solved using direct methods45 and refined on F2 using full-matrix least-squares using the SHELXL2015 crystallographic software package.46 Hydrogen atoms were inserted at calculated positions and constrained with isotropic thermal parameters.Crystal data for U2N@Ih(7)-C80·[NiII–(OEP)]·1.5C6H6·CS2: Mr = 2235.62, 0.18 mm × 0.15 mm × 0.12 mm, monoclinic, P21/c (no. 14), a = 17.6663(2) Å, b = 16.9578(2) Å, c = 26.7308(3) Å, α = 90°, β = 106.76°, γ = 90°, V = 7667.84 (15) Å3, Z = 4, ρcalcd = 1.937 g cm−3, μ(Cu Kα) = 2.575 mm−1, θ = 1.570–28.574, T = 100 K, R1 = 0.0393, wR2 = 0.0993 for all data; R1 = 0.0379, wR2 = 0.0979 for 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 reflections (I > 2.0σ(I)) with 1305 parameters. Goodness-of-fit indicator 1.035. Maximum residual electron density 1.688 e Å−3.
730 reflections (I > 2.0σ(I)) with 1305 parameters. Goodness-of-fit indicator 1.035. Maximum residual electron density 1.688 e Å−3.
The crystallographic data for this structure have been deposited at the Cambridge Crystallographic Data Centre (CCDC) with the deposition number 2010986.
Computational details
DFT calculations were carried out with the ADF 2017 package47 using PBE0 exchange-correlation functionals in combination with Slater TZP basis set quality.48,49 Frozen cores were described by means of single Slater functions, consisting of shell 1s for C, N and O and of 1s to 5d for U. Scalar relativistic corrections were included by means of the ZORA formalism. Dispersion corrections by Grimme were also included.50 The vibrational frequencies and Raman/IR spectra were calculated with the Gaussian 16 code51 using the PBE0 functional, the Stuttgart–Dresden pseudopotential for U and 6-31G(d,p) basis for C and N.Single point CASSCF calculations were performed for the U2N@C80 system and for some other models using PBE0 geometries with OpenMolcas.52 Scalar relativistic effects were taken into account with the Douglas–Kroll–Hess Hamiltonian.53 ANO-RCC basis sets were used to expand the orbitals of the system, U (9s, 8p, 7d, 5f, 2g, 1h), N (3s, 2p, 1d), C (3s, 2p).
A data set collection of the computational results is available in the ioChem-BD repository and can be accessed viahttps://doi.org/10.19061/iochem-bd-2-42.54
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We cordially thank Prof. Fangfang Li (Huazhong University of Science and Technology) for the help with X-ray crystal structure characterization and Prof. Eugen Schwarz (Tsinghua University) for the discussions on the theoretical analysis. We also thank beamline BL11B and BL17B of the Shanghai Synchrotron Radiation Facility for the XAS and X-ray single crystal structure tests and Dr Duo Zhang (Soochow University) for technical support. N. C. thanks the National Science Foundation China (NSFC 91961109 and 51302178) and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD). J. M. P. and C. d. G. thank the Spanish Ministry of Science (grants CTQ2017-87269-P and CTQ2017-83566-P), the Generalitat de Catalunya (grant 2017SGR629) and the URV for support. J. M. P. also thanks the ICREA foundation for an ICREA ACADEMIA award. L. E. thanks the Robert A. Welch Foundation for an endowed chair (grant AH-0033) and the US National Science Foundation (grant CHE-1801317) for generous financial support.Notes and references
- A. R. Fox, P. L. Arnold and C. C. Cummins, Uranium−Nitrogen Multiple Bonding: Isostructural Anionic, Neutral, and Cationic Uranium Nitride Complexes Featuring a Linear U
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U Core, J. Am. Chem. Soc., 2010, 132, 3250–3251 CrossRef CAS.
U Core, J. Am. Chem. Soc., 2010, 132, 3250–3251 CrossRef CAS. - M. Falcone, L. Barluzzi, J. Andrez, F. Fadaei Tirani, I. Zivkovic, A. Fabrizio, C. Corminboeuf, K. Severin and M. Mazzanti, The role of bridging ligands in dinitrogen reduction and functionalization by uranium multimetallic complexes, Nat. Chem., 2019, 11, 154–160 CrossRef CAS.
- M. Falcone, L. Chatelain, R. Scopelliti, I. Živković and M. Mazzanti, Nitrogen reduction and functionalization by a multimetallic uranium nitride complex, Nature, 2017, 547, 332 CAS.
- L. Chatelain, R. Scopelliti and M. Mazzanti, Synthesis and Structure of Nitride-Bridged Uranium(III) Complexes, J. Am. Chem. Soc., 2016, 138, 1784–1787 CAS.
- M. Falcone, L. Chatelain and M. Mazzanti, Nucleophilic Reactivity of a Nitride-Bridged Diuranium(IV) Complex: CO2 and CS2 Functionalization, Angew. Chem., Int. Ed., 2016, 55, 4074–4078 CAS.
- S. M. Mansell, N. Kaltsoyannis and P. L. Arnold, Small Molecule Activation by Uranium Tris(aryloxides): Experimental and Computational Studies of Binding of N2, Coupling of CO, and Deoxygenation Insertion of CO2 under Ambient Conditions, J. Am. Chem. Soc., 2011, 133, 9036–9051 CrossRef CAS.
- C. T. Palumbo, R. Scopelliti, I. Zivkovic and M. Mazzanti, C–H Bond Activation by an Isolated Dinuclear U(III)/U(IV) Nitride, J. Am. Chem. Soc., 2020, 142, 3149–3157 CrossRef CAS.
- D. M. King and S. T. Liddle, Progress in molecular uranium-nitride chemistry, Coord. Chem. Rev., 2014, 266–267, 2–15 CrossRef CAS.
- T. W. Hayton, Recent developments in actinide–ligand multiple bonding, Chem. Commun., 2013, 49, 2956–2973 RSC.
- D. M. King, F. Tuna, E. J. L. McInnes, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Synthesis and Structure of a Terminal Uranium Nitride Complex, Science, 2012, 337, 717 CrossRef CAS.
- C. T. Palumbo, L. Barluzzi, R. Scopelliti, I. Zivkovic, A. Fabrizio, C. Corminboeuf and M. Mazzanti, Tuning the structure, reactivity and magnetic communication of nitride-bridged uranium complexes with the ancillary ligands, Chem. Sci., 2019, 10, 8840–8849 RSC.
- J. Du, D. M. King, L. Chatelain, E. Lu, F. Tuna, E. J. L. McInnes, A. J. Wooles, L. Maron and S. T. Liddle, Thorium- and uranium-azide reductions: a transient dithorium-nitride versus isolable diuranium-nitrides, Chem. Sci., 2019, 10, 3738–3745 RSC.
- X. Zhang, Y. Wang, R. Morales-Martínez, J. Zhong, C. de Graaf, A. Rodríguez-Fortea, J. M. Poblet, L. Echegoyen, L. Feng and N. Chen, U2@Ih(7)-C80: Crystallographic Characterization of a Long-Sought Dimetallic Actinide Endohedral Fullerene, J. Am. Chem. Soc., 2018, 140, 3907–3915 CrossRef CAS.
- J. Zhuang, L. Abella, D.-C. Sergentu, Y.-R. Yao, M. Jin, W. Yang, X. Zhang, X. Li, D. Zhang, Y. Zhao, X. Li, S. Wang, L. Echegoyen, J. Autschbach and N. Chen, Diuranium(IV) Carbide Cluster U2C2 Stabilized Inside Fullerene Cages, J. Am. Chem. Soc., 2019, 141, 20249–20260 CrossRef CAS.
- X. Zhang, W. Li, L. Feng, X. Chen, A. Hansen, S. Grimme, S. Fortier, D.-C. Sergentu, T. J. Duignan, J. Autschbach, S. Wang, Y. Wang, G. Velkos, A. A. Popov, N. Aghdassi, S. Duhm, X. Li, J. Li, L. Echegoyen, W. H. E. Schwarz and N. Chen, A diuranium carbide cluster stabilized inside a C80 fullerene cage, Nat. Commun., 2018, 9, 2753 CrossRef.
- A. A. Popov, S. Yang and L. Dunsch, Endohedral Fullerenes, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS.
- S. Yang, T. Wei and F. Jin, When metal clusters meet carbon cages: endohedral clusterfullerenes, Chem. Soc. Rev., 2017, 46, 5005–5058 RSC.
- S. Stevenson, G. Rice, T. Glass, K. Harich, F. Cromer, M. R. Jordan, J. Craft, E. Hadju, R. Bible, M. M. Olmstead, K. Maitra, A. J. Fisher, A. L. Balch and H. C. Dorn, Small-bandgap endohedral metallofullerenes in high yield and purity, Nature, 1999, 401, 55–57 CrossRef CAS.
- J. M. Campanera, C. Bo and J. M. Poblet, General Rule for the Stabilization of Fullerene Cages Encapsulating Trimetallic Nitride Templates, Angew. Chem., Int. Ed., 2005, 44, 7230–7233 CrossRef CAS.
- M. N. Chaur, R. Valencia, A. Rodríguez-Fortea, J. M. Poblet and L. Echegoyen, Trimetallic Nitride Endohedral Fullerenes: Experimental and Theoretical Evidence for the M3N6+@C2n6− model, Angew. Chem., Int. Ed., 2009, 48, 1425–1428 CrossRef CAS.
- R. Valencia, A. Rodríguez-Fortea, A. Clotet, C. de Graaf, M. N. Chaur, L. Echegoyen and J. M. Poblet, Electronic Structure and Redox Properties of Metal Nitride Endohedral Fullerenes M3N@C2n (M=Sc, Y, La, and Gd; 2n=80, 84, 88, 92, 96), Chem.–Eur. J., 2009, 15, 10997–11009 CrossRef CAS.
- W. Cai, C.-H. Chen, N. Chen and L. Echegoyen, Fullerenes as Nanocontainers That Stabilize Unique Actinide Species Inside: Structures, Formation, and Reactivity, Acc. Chem. Res., 2019, 52, 1824–1833 CrossRef CAS.
- X. Li, Y.-R. Yao, W. Yang, J. Zhuang, L. Echegoyen and N. Chen, Crystallographic and spectroscopic characterization of a mixed actinide–lanthanide carbide cluster stabilized inside an Ih(7)-C80 fullerene cage, Chem. Commun., 2020, 56, 3867–3870 RSC.
- Y.-X. Zhao, K. Yuan, M.-Y. Li, M. Ehara and X. Zhao, In-Depth Theoretical Probe into Novel Mixed-Metal Uranium-Based Endohedral Clusterfullerenes Sc2UX@Ih(31924)-C80 (X = C, N), Inorg. Chem., 2019, 58, 10769–10777 CrossRef CAS.
- Y. Li, L. Yang, Z. Li, Q. Hou, L. Li and P. Jin, U2C Unit in Fullerenes: Robust Multicenter Bonds with a Cluster Shape Controlled by Cage Size and Charge Transfer, Inorg. Chem., 2019, 58, 10648–10655 CrossRef CAS.
- W. Krätschmer, L. D. Lamb, K. Fostiropoulos and D. R. Huffman, Solid C60: a new form of carbon, Nature, 1990, 347, 354–358 CrossRef.
- J. G. Brennan and R. A. Andersen, Electron-transfer reactions of trivalent uranium. Preparation and structure of the uranium metallocene compounds (MeC5H4)3U:NPh and [(MeC5H4)3U]2[μ-η1,. η2-PhNCO], J. Am. Chem. Soc., 1985, 107, 514–516 CrossRef CAS.
- C. R. Graves and J. L. Kiplinger, Pentavalent uranium chemistry-synthetic pursuit of a rare oxidation state, Cheminform, 2009, 3831–3853 CAS.
- C. R. Graves, P. Yang, S. A. Kozimor, A. E. Vaughn, D. L. Clark, S. D. Conradson, E. J. Schelter, B. L. Scott, J. D. Thompson and P. J. Hay, Organometallic Uranium(V)-Imido Halide Complexes: From Synthesis to Electronic Structure and Bonding, J. Am. Chem. Soc., 2008, 130, 5272–5285 CrossRef CAS.
- O. P. Lam, S. M. Franke, H. Nakai, F. W. Heinemann and W. Hieringer, Observation of the inverse trans influence (ITI) in a uranium(V) imide coordination complex: an experimental study and theoretical evaluation, Inorg. Chem., 2012, 51, 6190–6199 CrossRef CAS.
- S. C. Bart, C. Anthon, F. W. Heinemann, E. Bill, N. M. Edelstein and K. Meyer, Carbon Dioxide Activation with Sterically Pressured Mid- and High-Valent Uranium Complexes, J. Am. Chem. Soc., 2008, 130, 12536–12546 CrossRef CAS.
- A. Zalkin, J. G. Brennan and R. A. Andersen, Tris[bis(trimethylsilyl)amido](trimethylsilylimido)uranium(V), Acta Crystallogr., 1988, C44, 1553–1554 CAS.
- I. Castrorodriguez and K. Meyer, Engendering a Reactive Uranium(III) Center with a Single Pocket for Reactivity: A Combined Synthetic, Spectroscopic, and Computational Study, Teratology, 2003, 45, 383–391 Search PubMed.
- R. E. Jilek, L. P. Spencer, R. A. Lewis, B. L. Scott, T. W. Hayton and J. M. Boncella, A Direct Route to Bis(imido)uranium(V) Halides via Metathesis of Uranium Tetrachloride, J. Am. Chem. Soc., 2012, 134, 9876–9878 CrossRef CAS.
- P. L. Spencer, J. E. Schelter, P. Yang, L. R. Gdula and L. B. Scott, Cation–Cation Interactions, Magnetic Communication, and Reactivity of the Pentavalent Uranium Ion [U(N-tBu)2]+, Angew. Chem., Int. Ed., 2009, 121, 3853–3856 CrossRef.
- C. Camp, J. Pécaut and M. Mazzanti, Tuning Uranium–Nitrogen Multiple Bond Formation with Ancillary Siloxide Ligands, J. Am. Chem. Soc., 2013, 135, 12101–12111 CrossRef CAS.
- R. J. Ward, P. Rungthanaphatsophon, I. d. Rosal, S. P. Kelley and J. R. Walensky, Divergent uranium- versus phosphorus-based reduction of Me3SiN3 with steric modification of phosphido ligands, Chem. Sci., 2020, 11, 5830–5835 RSC.
- S. Yang, A. Popov, M. Kalbac and L. Dunsch, The Isomers of Gadolinium Scandium Nitride Clusterfullerenes GdxSc3−xN@C80 (x=1, 2) and Their Influence on Cluster Structure, Chem.–Eur. J., 2008, 14, 2084–2092 CrossRef CAS.
- M. N. Chaur, X. Aparicio-Anglès, B. Q. Mercado, B. Elliott, A. Rodríguez-Fortea, A. Clotet, M. M. Olmstead, A. L. Balch, J. M. Poblet and L. Echegoyen, Structural and Electrochemical Property Correlations of Metallic Nitride Endohedral Metallofullerenes, J. Phys. Chem. C, 2010, 114, 13003–13009 CrossRef CAS.
- X. Aparicio-Anglès, N. Alegret, A. Clotet, A. Rodríguez-Fortea and J. M. Poblet, Endohedral Metallofullerenes Containing Lanthanides: A Robust Yet Simple Computational Approach, J. Phys. Chem. C, 2013, 117, 12916–12921 CrossRef.
- P. Pyykkö and M. Atsumi, Molecular Double-Bond Covalent Radii for Elements Li–E112, Chem.–Eur. J., 2009, 15, 12770–12779 CrossRef.
- C. J. Burns, W. H. Smith, J. C. Huffman and A. P. Sattelberger, Uranium(VI) organoimido complexes, J. Am. Chem. Soc., 1990, 112, 3237–3239 CrossRef CAS.
- T. W. Hayton, J. M. Boncella, B. L. Scott, E. R. Batista and P. J. Hay, Synthesis and Reactivity of the Imido Analogues of the Uranyl Ion, J. Am. Chem. Soc., 2006, 128, 10549–10559 CrossRef CAS.
- G. Leinders, R. Bes, K. O. Kvashnina and M. Verwerft, Local Structure in U(IV) and U(V) Environments: The Case of U3O7, Inorg. Chem., 2020, 59, 4576–4587 CrossRef CAS.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Adamo and V. Barone, Towards reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6169 CrossRef CAS.
- M. Ernzenhof and G. E. Scuseria, Assessment of the Perdew-Burke-Ernzenhof exchange-correlation functional, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Jr Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, Molcas 8: new capabilities for multiconfigurational quantum chemical calculations across the periodic table, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS.
- B. A. Hess, Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748 CrossRef CAS.
- M. Álvarez-Moreno, C. de Graaf, N. López, F. Maseras, J. M. Poblet and C. Bo, Managing the Computational Chemistry Big Data Problem: The ioChem-BD Platform, J. Chem. Inf. Model., 2015, 55, 95–103 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2010986. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc04677a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |