Understanding the multiscale self-assembly of metal–organic polyhedra towards functionally graded porous gels

Abstract

Spatial heterogeneity and gradients within porous materials are key for controlling their mechanical properties and mass/energy transport, both in biological and synthetic materials. However, it is still challenging to induce such complexity in well-defined microporous materials such as crystalline metal–organic frameworks (MOFs). Here we show a method to generate a continuous gradient of porosity over multiple length scales by taking advantage of the amorphous nature of supramolecular polymers based on metal–organic polyhedra (MOPs). First, we use time-resolved dynamic light scattering (TRDLS) to elucidate the mechanism of hierarchical self-assembly of MOPs into colloidal gels and to understand the relationship between the MOP concentrations and the architecture of the resulting colloidal networks. These features directly impact the viscoelastic response of the gels and their mechanical strength. We then show that gradients of stiffness and porosity can be created within the gel by applying centrifugal force at the point of colloidal aggregation. These results with the creation of asymmetric and graded pore configuration in soft materials could lead to the emergence of advanced properties that are coupled to asymmetric molecule/ion transport as seen in biological systems.

---

Introduction

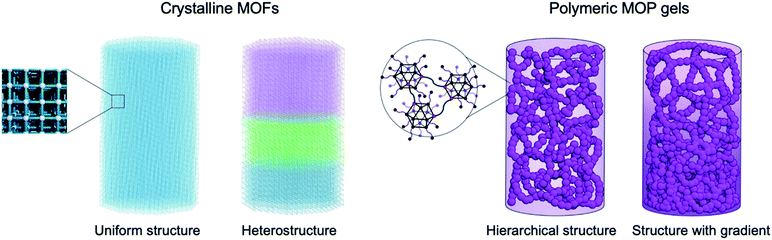
Natural organisms often have hierarchical structures spanning multiple length scales that present heterogeneities or gradients – in this way it is possible for complex functions to emerge from a relatively limited set of building blocks.^1,2 The spatial distribution of biological materials particularly affects local mechanical properties, with continuous gradients tuning the stiffness;³ for instance, the combination of rigidity and flexibility found in squid sucker ring teeth arises from a gradient in porous materials made from supramolecular networks of semi-crystalline proteins.⁴ Inspired by biological systems, synthetic materials with such gradients have been designated as functionally graded materials (FGM),⁵ and porous materials containing gradients can give unique mechanical properties and permeability, with applications in various fields from tissue engineering⁶ to the aerospace industry.⁷ In most cases, the fabrication procedures to engineer porosity have been limited to top-down approaches including microfluidics⁸ or 3D printing technologies;⁹ indeed, inducing gradients of porosity over the mesoporous and microporous regimes remains a challenge.

Recent developments in metal–organic frameworks (MOFs) or covalent-organic frameworks (COFs) allow us to finely tune the size and shape of micropores;^10,11 however, because of the crystalline nature of the materials there are only a few methods that could potentially induce gradients in the porosity. One method is to use post-synthetic ligand exchange to change the pore size by introducing longer ligands, thus creating larger pores than those found in the parent MOF structure.¹² In this case the resulting materials intrinsically possess a core–shell configuration such that this method leads only to radial gradients. Another approach is to build up the MOF structure from a substrate using layer-by-layer methods,¹³ which allows for hybridizing several MOFs but with sharp interfaces, rather than continuous and gradual changes of function. While there are also several synthetic strategies to use nano-sized crystalline MOFs as building blocks to obtain hierarchical superstructures over the mesoscopic and macroscopic scale, most focus on localizing the assembly of metal ions and organic linkers, meaning that there is no general strategy to generate a graded distribution of the material.¹⁴ We believe that induction of porosity gradients can be a new way to increase the complexity of materials based on MOFs, adding to recently described approaches to this trend in the field, which include MOFs with multiple components,^15,16 hierarchical architectures,^17,18 and disordered structures.^19,20

Very recently we used metal–organic polyhedra (MOPs), which are discrete molecules self-assembled from organic linkers and metal clusters and are recognized as potentially the smallest porous unit, to introduce a new class of microporous material. This material was synthesized by simply assembling pre-synthesized MOP molecules [Rh₂(bdc-C₁₂)₂]₁₂ (C₁₂RhMOP; bdc-C₁₂ = 5-dodecoxybenzene-1,3-dicarboxylate) with the ditopic linker, 1,4-bis(imidazole-1-ylmethyl)benzene (bix) by coordination-driven supramolecular polymerization.²¹ The resulting amorphous MOP network is shaped into colloidal particles at the mesoscale, followed by connecting particles leading to the formation of macroscale colloidal gels. This structural hierarchy is spontaneously generated during the self-assembly process. Hence, we envisaged that by revealing the individual steps underlying the multistep assembly, one could then influence specific stages of the polymerization by applying external stimuli and thus induce functional gradients in the porous gels. This feature distinguishes it from other MOF-based gel materials, in which the formation of gels is usually induced by controlling specific reaction conditions (e.g. pH, temperature, solvent, use of surfactants, or concentration of reagents).^22–24 However, the solution-phase techniques that are often used to elucidate the molecular self-assembly mechanisms of gels, such as NMR,²⁵ rheology,²⁶ or light scattering,²⁷ are ineffective due to the low solubility of MOFs.

Here we show that detailed evaluation of the hierarchical self-assembly process of MOPs is an essential step to then create continuous gradients of porosities and mechanical properties within the colloidal gels. First, we reveal the correlation of the gel formation with the resulting macroscopic architecture using time-resolved dynamic light scattering (TRDLS) techniques, and the effect on the mechanical properties of the gels. TRDLS can be used to gain insight into (i) the dynamics of the self-assembly near the gelation threshold (t_g); (ii) the mechanism of gelation; and (iii) the final architecture of the supramolecular gel based on C₁₂RhMOP. Finally, we show that applying centrifugal force only at the onset of colloidal aggregation leads to the formation of the density gradient of colloidal networks, which induces the gradual change of mechanical properties.

Results and discussion

In order to induce gradients of porosities over the microporous and mesoporous regimes, initial design of materials is essential. As summarized in Fig. 1, metal–organic materials can be categorized into four distinct configurations from the viewpoint of gradients. As discussed above, heterostructured MOFs with sharp chemical interfaces can be created in crystalline MOFs by stepwise framework growth.¹³ On the other hand, colloidal gel materials based on MOPs possess continuous networks of hierarchical colloidal structures. By controlling the mesoscale assembly of colloids, we have an opportunity to induce non-uniform colloidal architectures, leading to graded porosities. First, we investigate the hierarchical assembly process of MOPs into polymers.

Fig. 1 Illustration of structural complexity in porous materials. Crystalline MOF materials provide uniform pore distributions throughout the entire material due to their crystallinity. Layer-by-layer growth methods allow for the fabrication of heterostructured MOFs with sharp interfaces. On the other hand, amorphous porous materials composed of polymeric MOP gels intrinsically generate more complex hierarchical structures, thanks to the formation of colloidal particles based on MOP polymerization; the particles are then linked to form colloidal architectures. This study further induces a gradient in the distribution of the colloidal particles to synthesize functionally graded porous materials.

Study of the gel formation dynamics

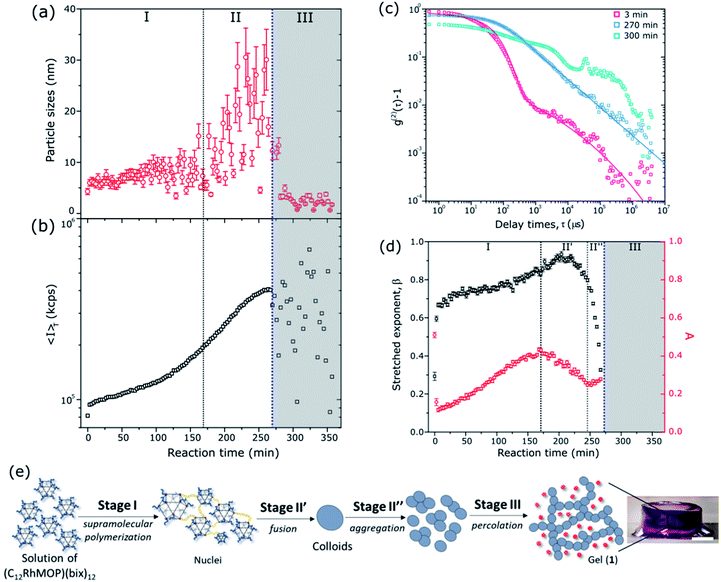
We previously reported that the coordination reaction between C₁₂RhMOP and bix in DMF produces a supramolecular coordination polymer, leading to gel formation.²¹ In order to monitor the formation of the colloidal gel, the kinetics of the polymerization reaction must be controlled: this is achieved by isolation of a kinetically trapped cage molecule in which each of the twelve exohedral axial sites of the dirhodium clusters are coordinated by a bix molecule in a monodentate fashion, giving a composition of (C₁₂RhMOP)(bix)₁₂. Because the π* → σ* transition at the Rh–Rh bond is sensitive to axial coordination, UV-visible spectroscopy can be used to reveal the coordination of 12 equivalents of bix molecules to C₁₂RhMOP, inducing a shift of the absorption maximum from 593 to 553 nm (Fig. S2a†) due to the ligand exchange reaction of DMF for bix at the Rh axial site.

The long dodecoxy chains functionalizing the surface of the cage molecule improve their solubility, and allow their solution phase dynamics to be monitored using spectroscopic techniques.^28,29 The size of the discrete MOP is ca. 3 nm, and therefore detectable by dynamic light scattering (DLS) measurements. These characteristics allow us to follow the hierarchical self-assembly process that occurs during gelation with in situ monitoring of the scattering elements. DLS analysis gives a particle size for the kinetically trapped MOP (C₁₂RhMOP)(bix)₁₂ of 3.2 ± 1.4 nm (Fig. S2b†). Supramolecular polymerization is induced by heating the solution of (C₁₂RhMOP)(bix)₁₂ at 80 °C, driving the coordination equilibrium toward dissociation of bix and creating a vacant axial site, which can be occupied by a bix ligand attached to a neighboring kinetically trapped MOP. Indeed, this reaction resulted in the formation of a gel (1) over the course of several hours. The self-assembly process was followed by TRDLS; Fig. 2a shows the evolution of particle size as a function of time for an initial MOP concentration of 0.93 mM. Once polymerization begins, the system hierarchically assembles into colloidal particles as observed in the TRDLS measurements, where a steep increase in particle size occurs during stage II to reach a maximum of 30.5 ± 4.5 nm after 250 minutes. As the infinite coordination network forms and immobilizes the DMF solvent molecules, the general mobility of the particles is frozen due to topological constraints and the diffusion becomes null, rendering reliable measurement of the particle size impossible (represented as the gray region, stage III). Rather than following particle size evolution, changes in the time-averaged scattering intensity, I_T, can give a clearer indication of sol–gel transitions as shown in Fig. 2b.^30,31 Indeed, the plot of I_T as a function of time shows that random fluctuations appear at 270 min, corresponding to the onset of the gelation point (t_g). These changes in the particle size and the I_T are characteristic of the loss of ergodicity and homogeneity that occurs upon gelation.^32,33

Fig. 2 Time-resolved dynamic light scattering experiments (TRDLS) to elucidate the mechanism of hierarchical self-assembly of MOPs into colloidal gels. TRDLS measurement during the supramolecular polymerization of (C₁₂RhMOP)(bix)₁₂ at 80 °C at a concentration of 0.93 mM, showing (a) the particle size evolution and (b) the time-averaged scattering intensity. (c) Log–log plot of the intensity–time correlation function (ICF) for different reaction times during the supramolecular polymerization reaction at a concentration of 0.93 mM. The solid lines represent the fitted ICF using a stretched exponential and power-law function for the solution state (at 3 min) and gel threshold (270 min) respectively. The ICF, beyond the gel point, is shown in cyan (300 min). (d) Variation of the fraction of the fast diffusion mode (A) and stretched exponent (β) as a function of the reaction time. The gelation threshold is represented by the blue dotted line. The gray region highlights the effect of the frozen mobility of particles due to gel formation on the DLS response. The fraction of the fast diffusion mode (A) and stretched exponent (β) are fitted parameters obtained from (d). (e) Proposed mechanism for the supramolecular polymerization of the kinetically trapped phase into a colloidal gel. The scale bar is 0.5 cm.

Mechanism of gelation

Each DLS measurement recorded during the gelation has an associated time-averaged intensity correlation function (ICF), g⁽²⁾(τ) − 1, that is derived from the time dependence of the decay in scattered light by a randomly diffusing object.^32,34 Because the diffusion will depend on the nature of the particles in solution, the analysis of the ICF can give insight into the gelation mechanism of 1. Fig. 2c shows the ICF at three stages of the gelation process, for t = 3, 270 and 300 min, i.e. at the beginning of the reaction, at t_g, and beyond the gelation point, respectively. In the solution regime (pregel, 0 < t < 270), the ICF can be fitted as a sum of single and stretched exponentials (eqn (1)):

g⁽²⁾(τ) − 1 = σ₁²{Ae^(−τ/τ_f) + (1 − A)e^{−(τ/τ_s)β}}² (1)

where σ₁² is the initial amplitude of the ICF, A is the fraction of the fast diffusion mode, β is the stretched exponent, and τ_f and τ_s are the relaxation times of the fast and slow components, respectively.³⁴ Here, β reflects the distribution of relaxation times of the slow mode,³⁵ and τ_f is inversely proportional to the diffusion D (see ESI† for further details). The two-step relaxation observed at 3 min (Fig. 2c) is attributed to the combination of a fast mode due to translational diffusion of the MOP cages with a slow mode attributed to the stretched dodecoxy chains on the isophthalate linker. In order to confirm the appearance of the slow mode, the temperature dependence of ICF of the pristine C₁₂RhMOP was measured (Fig. S3a†). Similar to what is observed for polymer chains grafted on spherical particles,^36,37 at room temperature the ICF of the solubilized C₁₂RhMOP in DMF shows only a monotonic decay without the slow mode, which is attributed to the compacted dodecoxy chain (Fig. S3a†). On the other hand, increasing the temperature of the C₁₂RhMOP solution to 80 °C leads to the appearance of the slow relaxation mode stemmed from the collective motion of thermally agitated chains extended away from the MOP (Fig. S3a†). The same trend is observed for the kinetically trapped phase, (C₁₂RhMOP)(bix)_12, at 25 and 80 °C (Fig. S3b†). This indicates that the appearance of the slow mode relies on a thermal effect.

Fig. 2d shows the variation with time of A and β obtained from the fits of the ICF of the pregel sample using eqn (1). At the beginning of the reaction at 80 °C, the low A value reflects the large contribution of the slow mode as discussed above. With continuous heating the A value increases, which implies that the fast relaxation mode becomes the dominant factor. We attribute this change to the closer proximity of the MOPs caused by polymerization, which hinders the stretched alkyl chains and therefore quenches the slow mode associated with isolated MOPs. During this reaction time, the increase in particle size is only a few nanometers (growth from ∼5 to ∼10 nm as shown in Fig. 2a) and is ascribed to nuclei formation (oligomer formation) as (C₁₂RhMOP)(bix)₁₂ are linked to each other by the bix molecules (stage I) during supramolecular polymerization. At t = 168 min the value of A begins to decrease as another slow diffusion mode starts to contribute, caused by the loss of mobility of the nuclei as they fuse into colloidal particles and behave as local oscillators (stage II′). As shown in Fig. S4,† the ICF shows that this slow mode (t = 249 min) is different from the one at the stage I (t = 3 min): the shape of exponential decay is more stretched at stage II′ compared to the two-step decay seen at stage I. In addition, the slow relaxation mode, τ_s, enters a plateau around 150 μs during stage I and starts to increase in stage II (Fig. S5,†τ_s = 526 μs at the end of stage II′ at t = 249 min). Meanwhile, β shows a continuous increase towards unity, indicating a lower distribution of the relaxation times;³⁵ we propose that this reflects the formation of colloidal particles of uniform size and hence similar relaxation times (stage I and II′), as supported by subsequent SEM measurements (see below). After 249 min, the colloidal particles begin to aggregate and form the premise of the gel network that will be assembled at the gelation threshold (t_g = 270 min). Finally, as the colloids randomly aggregate, the distribution of relaxation times of the particles increases, shown by the decrease in β (stage II′′).³⁵ This decrease indicates the wider size distribution of colloidal aggregates.

From these data, we propose the mechanism shown in Fig. 2e. First, heating pushes the coordination equilibrium between MOP and bix towards dissociation, creating a vacant site to be occupied by a free imidazole moiety of bix attached to neighboring (C₁₂RhMOP)(bix)₁₂ molecules. As the supramolecular polymerization progresses, the MOPs self-assemble into small nuclei, which cause the initial slow growth in particle size shown in Fig. 2a (stage I). Stage II′ occurs when the nuclei fuse into colloidal particles driving (i) a faster increase in the particle size, (ii) a decrease in the fraction of the fast diffusion, A, (Fig. 2d) and (iii) a lower size-distribution of colloidal particles with reaching their maximum size. Beyond this point, attractive interactions drive the aggregation of the colloidal particles (stage II′′).^38,39 On the surface of the particles many monodentate bix molecules are immobilized, which helps to keep the particles within short proximity of each other. The simultaneous removal of those bix molecules from the surface induces the exposure of reaction sites, leading to the linkage of colloidal particles by the Rh–bix coordination bonds. Finally, the aggregates form a percolating elastic network spanning the liquid medium, yielding the supramolecular gel (stage III). The ¹H NMR experiments on the digested gels revealed the composition of the gel to be (C₁₂RhMOP)(bix)_9.7, indicating that there are also monodentate bix incorporated in the gels.

Architecture and mechanical properties of the colloidal gel

The mechanical properties of a gel, such as its viscoelasticity, are governed by the network architecture,^40,41 which is in turn defined by (i) the correlation length ξ, which reflects the evolution of the density of the network during the reaction time in the solution phase (Fig. S1†);^35,42,43 and (ii) the degree of branching n, which is determined at the sol–gel transition.^44,45ξ is obtained from eqn (1) as it is directly related to the diffusion D through the Stokes–Einstein equation (see the ESI† for details). The value for ξ was observed to only diverge just before gelation (Fig. S6†). At the gelation threshold the characteristic correlation length, ξ*, is expected to be a measure of the density of the network of the gel and is estimated to be 113 ± 3 nm. Meanwhile, the degree of branching, n, can be obtained from eqn (2), which reflects the change of the ICF shape from a stretched exponential to a power-law function at t_g due to the transition from sol to gel.^46,47 Macroscopic quantities and physical properties characterizing a system follow a power law behavior when the critical point is approached in agreement with the prediction of the theory of critical phenomena.^46,48 Indeed, at the gelation threshold the ICF can no longer be fitted by the eqn (1), but instead by the sum of a single exponential and power-law according to eqn (2):

g⁽²⁾(τ) − 1 = σ₁²{Ae^(−τ/τ_f) + (1 − A)(1 + τ/τ*)^(n−1)/2}² (2)

where τ* is the characteristic time where the power-law behavior begins and the power-law exponent n is related to the degree of branching.⁴⁴ Beyond the gelation point, the appearance of nonergodicity and the decrease in the magnitude of the fluctuations of the scattering elements are reflected by the appearance of small amplitude variations in the ICF, which makes the fitting of the ICF with eqn (2) more difficult (Fig. 2c, 300 min).

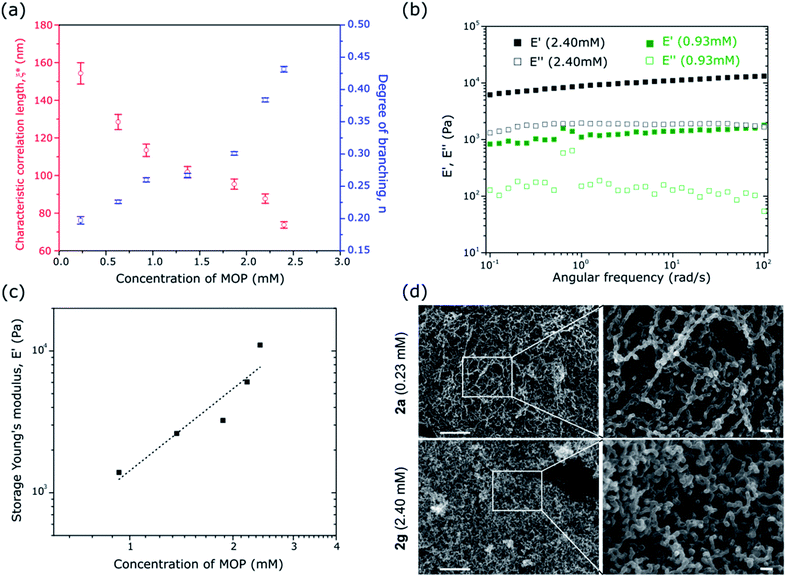
To understand how the correlation length and the degree of branching affect the structure and mechanical properties of our system, gels with initial C₁₂RhMOP concentrations of 0.23, 0.63, 0.93, 1.37, 1.83, 2.20 and 2.40 mM (1a, 1b, 1c, 1d, 1e, 1f and 1g, respectively) were prepared. The dynamics of gel formation at each concentration were followed using TRDLS (Fig. S7–S10†) to extract ξ* and n by fitting the equations described above. Increasing the MOP concentration of the gels induces an increase of the degree of branching and a decrease in the correlation length. This tendency means that the connectivity and density of the network of colloidal particles increase with increasing the concentration of MOPs (Fig. 3a).

Fig. 3 Relationship between the MOP concentrations and the resulting colloidal network architectures on the viscoelastic response of the gels and its mechanical strength. Effect of the concentration of MOPs on (a) the characteristic correlation length (ξ*) and degree of branching (n) for the gels 1a–g obtained from the fitted ICF using a stretched exponential and power-law functions. (b) Storage and loss Young's modulus, E′ and E′′ respectively, for gels prepared with concentration of MOP of 2.40 (1g, black) and 0.93 mM (1c, green). The measurements were performed at a fixed strain amplitude (1%) within the linear viscoelastic regime. The lower concentration gels 1a and 1b were too weak to sustain the applied strain and to be measured. (c) Effect of the MOP concentration on the storage Young's modulus (E′) of the gels at 10 rad s⁻¹. (d) FE-SEM images of the aerogels 2a (0.23 mM) and 2g (2.40 mM). The right part images are magnification of the corresponding white square. The scale bars for lower and highest magnification are 1 μm and 100 nm, respectively.

Changes in the gel architecture should affect the viscoelasticity of soft matter. To elucidate the mechanical properties of 1a–g, the fully matured gel samples were characterized by dynamic mechanical analysis using a rheometer with compression geometry to determine the resistance to elastic deformation (stiffness). Measurements of the storage and loss Young's modulus, E′ and E′′, respectively, were carried out as a function of the oscillatory deformation frequency ω, at a fixed strain amplitude (1%) within the linear viscoelastic regime. At 10 rad s⁻¹, for a gel concentration of 2.40 mM, E′ and E′′ are 11.0 × 10³ and 1.9 × 10³ Pa, respectively, while at a concentration of 0.93 mM those values are 1.4 × 10³ and 0.1 × 10³ Pa, respectively (Fig. 3b). These values are similar to those found for soft tissues, cells, gelatine or agarose and PVA gels (0.5–70 × 10³ Pa) but smaller than those found in silicone rubber (500–5000 × 10³ Pa) or cartilage (∼1 × 10⁶ Pa) and bone (1–10 × 10⁹ Pa). Over the entire frequency range, these values are essentially constant and E′ is approximately one order magnitude higher than E′′. The samples are confirmed as behaving as elastic solids (full data set shown in Fig. S11;† the lower concentration gels 1a and 1b were too weak to sustain the applied strain and to be measured).^49–51Fig. 3c shows the evolution of the storage Young's modulus E′, at ω = 10 rad s⁻¹, as a function of the MOP concentration in the gel. As the MOP concentration increases, E′ increases almost exponentially indicating mechanically stronger gels. The macroscopic behavior of the gels is directly correlated to the change in the gel architecture.⁵² Higher degrees of branching and shorter correlation lengths in the colloidal network result in the formation of stiffer gels.

Aerogel structure and porosity

The gels of 1a–g were converted to the corresponding aerogel forms of 2a–g, after solvent exchange and supercritical CO₂ treatment, for field emission scanning electron microscopy (FESEM) and gas adsorption measurements. The FESEM images of the aerogel with the lowest (2a: 0.23 mM) and highest (2g: 2.40 mM) C₁₂RhMOP concentrations (Fig. 3d) show distinct features corresponding to the observations made from the evolution of the correlation length and the degree of branching with the concentration. Indeed, Fig. 3d shows almost linear chains of colloidal particles forming a light network structure for 2a. In contrast, the network is denser and built from more highly interconnected particles in the case of 2g. The statistical analysis of the size distribution of colloidal particles in the network revealed that the concentration did not strongly influence the size (38.0 ± 8.4 nm for 2a and 34.4 ± 7.4 nm for 2g), which correspond to the sizes derived from TRDLS measurements (Fig. S12†) and imply that the number of particles rather than the size of the particles increases with concentration.

N₂ and CO₂ sorption experiments subsequent to activation at 120 °C for 12 h, performed on aerogels of 2a–g at 77 K and 195 K, respectively, show that the intrinsic porosity of the MOP cages is still accessible even after assembly into 3D colloidal networks (Fig. S13†). In addition, the maximum CO₂ uptakes remain within a similar range of 60–72 cm³ g⁻¹ at P/P₀ = 0.95 for all of the aerogels (Fig. S13a†), higher than the bulk powder of pristine C₁₂RhMOP (46.01 cm³ g⁻¹ as previously reported²¹). The fact that there is no significant change to the sorption properties among the samples prepared with different MOP concentrations is attributed to the similar size of colloidal particles in the network observed by FESEM. However, increasing the concentration of MOPs causes a slight decrease in the N₂ uptake at P/P₀ = 0.95, which is ascribed to the increased density of the aerogel networks leading to a reduction in the macroporosity (Fig. S13b†).

Functionally graded porous material

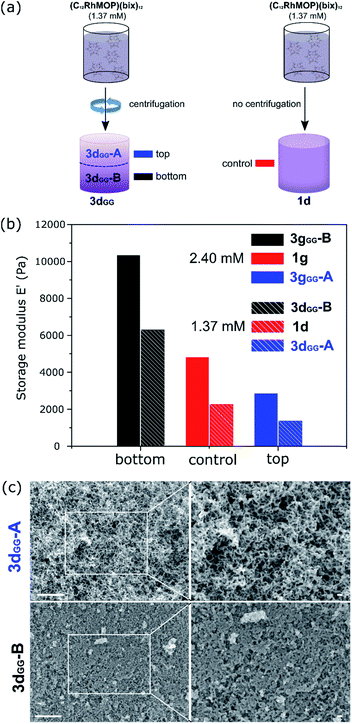
Understanding the correlation between the mechanism of gel formation and the resulting network structure is fundamental to then be able to increase complexity at the macroscale by, for example, creating gradients of properties within the material. It is known that colloidal gels compact under their own weight with aging due to gravity, ultimately leading to the collapse of the structure.^53,54 However, it has been shown for depletion gels that before collapse, gradients can be created by using gravitational stress to compress the gel.⁵⁵ Given that centrifugation has been used to create gradients in polyvinylpyrrolidone-coated silica nanoparticles⁵⁶ and to tune the compressive yield response of suspended particles,⁵⁷ we hypothesized that it could be used to modify the mechanical properties of colloidal gels containing MOPs.

From the analysis of the TRDLS measurements, we concluded that the mechanical properties of the gels are dictated during stage II′′, when the correlation length and degree of branching are determined. We then supposed it ought to be possible to increase the complexity of the system over longer length scales by perturbing this out-of-equilibrium stage. Thus, we used TRDLS to monitor the evolution of the diffusion coefficient D of a gelating solution at 80 °C at a concentration of 1.37 mM of C₁₂RhMOP. When the diffusion coefficient reached a value of 7.82 μm² s⁻¹, corresponding to the maximum particle size reached (Fig. S14a†), the sample was centrifuged for 5 minutes at 3500 rpm at room temperature, before further heating at 80 °C to continue gelation, yielding the gradient gel 3d_GG. The gradient gel was sliced into two parts, 3d_GG-A and 3d_GG-B, the top and bottom parts, respectively, as shown in Fig. 4a. The rheology measurements of these two parts were carried out, together with a control experiment, which was not centrifuged (1d) (Fig. S15†). 3d_GG-B has an increased storage modulus (6.0 × 10³ Pa), compared to the control experiment (2.0 × 10³ Pa). In contrast, the top part 3d_GG-A presents a lower storage modulus E′ (1.0 × 10³ Pa) as shown in Fig. 4b. The difference in stiffness between the top and bottom parts suggests the creation of a gradient of network density in 3d_GG. The FESEM images support this claim as a less dense network of colloidal particles is observed for the gel formed at the top compared to the gel formed at the bottom (Fig. 4c). The same trend was observed for a sample with an initial MOP concentration of 2.40 mM for 3g_GG (Fig. S14b† for TRDLS analysis, Fig. 4b for the rheology experiments and Fig. S16† for the FESEM images). In order to clarify the importance of the time at which the centrifugal force is applied, a control experiment was performed on a 1.37 mM (C₁₂RhMOP)(bix)₁₂ solution following a similar protocol as described above. The only difference is that the sample was centrifuged in the early stage of the supramolecular polymerization reaction (stage I, t = 60 min), when colloidal particles have not yet formed. The FESEM images of the top (3neg_GG-A) and bottom (3neg_GG-B) part of the aerogel samples show no difference in their network structures (Fig. S17†). In addition, a partial sedimentation of the sample occurred during the centrifugation step. The FESEM images show a dense material with no specific network structure (Fig. S18†), which highlights the importance of understanding the mechanism of hierarchical self-assembling processes as a first step towards functionally graded soft materials.

Fig. 4 Creation of a gradients of stiffness and porosity within the gel by applying centrifugal force at the specific moment of colloidal aggregation. (a) Gelation of the (C₁₂RhMOP)(bix)₁₂ solution (1.37 mM) prepared by applying centrifugal force during the beginning of stage II′′ corresponding to the onset of colloidal aggregation. The sample was centrifuged for 5 minutes at 3500 rpm at room temperature, and then heating at 80 °C was continued for gelation to proceed, yielding the gradient gel 3d_GG. The sample was cut into two equal parts for further dynamic mechanical analysis. The same gelation procedure was performed without centrifugation, which serve as control experiment (1d). (b) Histogram of the storage modulus E′ at 10 rad s⁻¹ of the bottom (3g_GG-B, black and 3d_GG-B, black stripes) and top part (3g_GG-B, blue and 3d_GG-B, blue stripes) of 2.40 and 1.37 mM MOP-based gel prepared using centrifugation method to create a concentration gradient. For comparison the same gel was prepared without applying centrifugation as reference (red). (c) FE-SEM images of the top (3d_GG-A) and bottom part (3d_GG-B) of 3d_GG (1.37 mM) MOP-based aerogels prepared using centrifugation method. The scale bars for lower and highest magnification are 1 μm and 100 nm, respectively.

Conclusions

In this work, we have shown that the use of TRDLS gives us a better understanding of the mechanism underlying the assembly of colloidal gels formed from porous building blocks, in this case MOPs. TRDLS measurements can be used to determine features of the network and its formation, such as the correlation length between the particles, the degree of branching, and the duration of the distinct stages of polymerization. These analyses show the initial formation of nuclei from the linking of a few MOPs during stage I, which further fuse into colloidal particles with approximately the size of 35 nm during the stage II′. The duration of stage I and II′ depend on the concentration of MOPs because the supramolecular polymerization reaction is the main kinetic factor directing the formation of colloidal particles. On the other hand, the duration of stage II′′, which corresponds to the time necessary for the colloidal particles to aggregate before reaching the gelation point, is almost constant for all of the samples with different concentrations. However, stage II′′ affects the architecture of the colloidal network. A higher concentration of MOPs in the gel leads to an increase in the density and the degree of branching of colloidal backbone. This last stage is critical for the determination of the macroscopic behavior of the gel system such as the mechanical strength as demonstrated by the increase of stiffness with concentration. From this understanding, we demonstrated the fabrication of functionally graded porous gels using centrifugation during stage II′′. The gradual change of viscoelasticity in the resulting gels, determined by rheology experiments, is explained by the density gradient of colloidal networks formed with the gravitational stress applied during centrifugation. Such functionally graded materials, which possess a property gradient within a material, in particular, asymmetric configuration of porosities, could lead to the emergence of advanced materials functions such as separation, catalysis and energy storage, which can be related to the controlled transport of molecules/ions as seen in biomimetic systems.^58–60

Experimental

Materials

All chemical reagents and solvents were purchased (Wako, Japan) and used without further purification. The detailed protocols for ligand and crosslinker synthesis can be found elsewhere.²¹

Gels characterization

The rheological measurements of the gels were made using a stress-controlled AR-G2 (TA Instruments, New Castle, DE, USA) rheometer. The measurements were conducted with a 1% strain amplitude that was well inside the linear regime. Gelation was performed in a syringe during the night before rheological measurement in order to minimize solvent evaporation. After the reaction, the gel was removed from the syringe and viscoelastic properties directly measured.

The hydrodynamic diameter (R_H), collective diffusion (D), time-averaged autocorrelation function (ICF) and scattering intensity (I_T) were measured using time-resolved dynamic light scattering (TRDLS) performed on a Zetasizer Nano ZS instrument (Malvern Instruments, Malvern, UK). The light source was a HeNe laser working at λ = 633 nm. The observations were made at the backscattering angle θ = 173°. The time dependence of R_H, D_,I_T and ICF, during gelation process of solution 1a, 1b, 1c, 1d, 1e, 1f, 1g was evaluated at 80 ± 0.5 °C for 360 min. Every 3 min, the data of 10 independent measurements over 12 s were averaged. Note that the data thus obtained represent time-averaged characteristics where only one position of the sample is probed. After gelation, the system becomes nonergodic and the ICF becomes dependent upon the sample position. However, when using long enough data collection time, a relative spatial homogeneity just after the gelation threshold can be assumed by considering the heterogeneities to be partially frozen-in and having still some mobility.³³

Aerogels characterization

N₂ and CO₂ gas sorption isotherms of the aerogels 2a–g were recorded on a BELSORP-mini volumetric adsorption instrument from BEL Japan Inc. at 77 K and 195 K respectively. Prior to gas sorption measurement, the samples were activated at 120 °C for 12 h. Specific surface areas were determined using the Brunauer, Emmett, and Teller (BET) method applied on a linear portion of the N₂ adsorption isotherm below P/P₀ = 0.3, with R > 0.999 and C > 0.⁶¹

Aerogel samples were observed using a field-emission scanning electron microscope (FE-SEM) with a JEOL Model JSM-7001F4 system operating at 10 kV and 5 mA current. ¹H-NMR spectra were recorded on a Bruker Biospin DRX-600 (600 MHz) spectrometer. For ¹H-NMR analysis, 5–10 mg of aerogel samples were digested in a mixture of DMSO-d₆ (750 μl) and DCl (50 μl). The mixture was heated at 100 °C overnight to obtain a yellow solution.

Synthesis of C₁₂RhMOP

The cuboctahedral MOP cage was synthesized as reported previously.^21,62

Synthesis of the kinetically trapped phase, (C₁₂RhMOP)(bix)₁₂

The metastable state of the MOP was synthesized by solubilizing C₁₂RhMOP in 1.5 mL of DMF at 80 °C. The solution was added to 12 mol. eq. of 1,4-bis(imidazole-1-ylmethyl)benzene (bix) in 1.5 mL at 80 °C followed by a rapid cooling to room temperature which formed isolated MOP molecules with the composition of (C₁₂RhMOP)(bix)₁₂. Seven solutions with different MOP concentration were prepared ((C₁₂RhMOP)(bix)₁₂: 0.23/0.67/0.93/1.37/1.83/2.20/2.40 mM).

Synthesis of supramolecular colloidal gel (1)

The gel was formed by putting 3 mL of the kinetically trapped phase, (C₁₂RhMOP)(bix)₁₂, into a plastic syringe from which the top part was cut in order to remove easily the gel for rheology measurement. The solution was kept in the oven at 80 °C for 12 h to give 1, a supramolecular colloidal gel. Seven gels were prepared using one of the solutions with a MOP “gelator” concentration of 0.23, 0.67, 0.93, 1.37, 1.83, 2.20 and 2.40 mM to give 1a, 1b, 1c, 1d, 1e, 1f and 1g respectively.

Aerogel preparation (2)

The gel samples were exchanged with fresh acetone for 3 days. The supercritical CO₂ drying process of the gels, to form the aerogels, was carried out on a SCLEAD-2BD autoclave (KISCO) using super-critical CO₂ at 14 MPa and 50 °C to give 2a, 2b, 2c, 2d, 2e, 2f and 2g.

Gradient gel preparation (3)

TRDLS was used to monitor the evolution of the diffusion coefficient D of a gelating solution at 80 °C at a concentration of 1.37 mM and 2.40 mM of (C₁₂RhMOP)(bix)₁₂. When the diffusion coefficient reached a value of 7.8 μm² s⁻¹, corresponding to the maximum particle size reached, the sample was centrifuged for 5 minutes at 3500 rpm at room temperature, and then heating at 80 °C was continued for gelation to proceed, yielding the gradient gel 3d_GG and 3g_GG, respectively.

Conflicts of interest

The authors declare that they have no competing financial interests.

Acknowledgements

This work was supported by JSPS KAKENHI grant number 19H04575 (Coordination Asymmetry). The authors thank the iCeMS Analysis Center for access to analytical instruments. We would like to thanks Prof. T. Norisuye (Kyoto Institute of Technology) for fruitful discussion and Mr Shun Tokuda (Kyoto University) for his help with drawing the Fig. 1.

Notes and references

1. R. Lakes, Nature, 1993, 361, 511–515.
2. M. Eder, S. Amini and P. Fratzl, Science, 2018, 362, 543.
3. Z. Liu, M. A. Meyers, Z. Zhang and R. O. Ritchie, Prog. Mater. Sci., 2017, 88, 467–498.
4. A. Miserez, J. C. Weaver, P. B. Pedersen, T. Schneeberk, R. T. Hanlon, D. Kisailus and H. Birkedal, Adv. Mater., 2009, 21, 401–406.
5. Y. Miyamoto, W. A. Kaysser, B. H. Rabin, A. Kawasaki and R. G. Ford, Functionally Graded Materials: Design, Processing and Applications, Springer, US, 2013.
6. D. Kokkinis, F. Bouville and A. R. Studart, Adv. Mater., 2018, 30, 1705808.
7. J. Hohe, V. Hardenacke, V. Fascio, Y. Girard, J. Baumeister, K. Stöbener, J. Weise, D. Lehmhus, S. Pattofatto, H. Zeng, H. Zhao, V. Calbucci, F. Rustichelli and F. Fiori, Mater. Des., 2012, 39, 20–32.
8. M. Costantini, J. Jaroszewicz, Ł. Kozoń, K. Szlązak, W. Święszkowski, P. Garstecki, C. Stubenrauch, A. Barbetta and J. Guzowski, Angew. Chem., Int. Ed., 2019, 58, 7620–7625.
9. X. Kuang, J. Wu, K. Chen, Z. Zhao, Z. Ding, F. Hu, D. Fang and H. J. Qi, Sci. Adv., 2019, 5, eaav5790.
10. A. P. Côté, A. I. Benin, N. W. Ockwig, M. Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166.
11. S. T. Meek, J. A. Greathouse and M. D. Allendorf, Adv. Mater., 2011, 23, 249–267.
12. C. Liu, C. Zeng, T.-Y. Luo, A. D. Merg, R. Jin and N. L. Rosi, J. Am. Chem. Soc., 2016, 138, 12045–12048.
13. O. Shekhah, K. Hirai, H. Wang, H. Uehara, M. Kondo, S. Diring, D. Zacher, R. A. Fischer, O. Sakata, S. Kitagawa, S. Furukawa and C. Wöll, Dalton Trans., 2011, 40, 4954–4958.
14. S. Furukawa, J. Reboul, S. Diring, K. Sumida and S. Kitagawa, Chem. Soc. Rev., 2014, 43, 5700–5734.
15. H. Deng, C. J. Doonan, H. Furukawa, R. B. Ferreira, J. Towne, C. B. Knobler, B. Wang and O. M. Yaghi, Science, 2010, 327, 846.
16. T.-Y. Zhou, B. Auer, S. J. Lee and S. G. Telfer, J. Am. Chem. Soc., 2019, 141, 1577–1582.
17. J. Reboul, S. Furukawa, N. Horike, M. Tsotsalas, K. Hirai, H. Uehara, M. Kondo, N. Louvain, O. Sakata and S. Kitagawa, Nat. Mater., 2012, 11, 717–723.
18. C. Avci, I. Imaz, A. Carné-Sánchez, J. A. Pariente, N. Tasios, J. Pérez-Carvajal, M. I. Alonso, A. Blanco, M. Dijkstra, C. López and D. Maspoch, Nat. Chem., 2018, 10, 78–84.
19. W. Chen, S. Horike, D. Umeyama, N. Ogiwara, T. Itakura, C. Tassel, Y. Goto, H. Kageyama and S. Kitagawa, Angew. Chem., Int. Ed., 2016, 55, 5195–5200.
20. L. Longley, S. M. Collins, C. Zhou, G. J. Smales, S. E. Norman, N. J. Brownbill, C. W. Ashling, P. A. Chater, R. Tovey, C.-B. Schönlieb, T. F. Headen, N. J. Terrill, Y. Yue, A. J. Smith, F. Blanc, D. A. Keen, P. A. Midgley and T. D. Bennett, Nat. Commun., 2018, 9, 2135.
21. A. Carné-Sánchez, G. A. Craig, P. Larpent, T. Hirose, M. Higuchi, S. Kitagawa, K. Matsuda, K. Urayama and S. Furukawa, Nat. Commun., 2018, 9, 2506.
22. M. R. Lohe, M. Rose and S. Kaskel, Chem. Commun., 2009, 40, 6056–6058.
23. B. Bueken, N. Van Velthoven, T. Willhammar, T. Stassin, I. Stassen, D. A. Keen, G. V. Baron, J. F. M. Denayer, R. Ameloot, S. Bals, D. De Vos and T. D. Bennett, Chem. Sci., 2017, 8, 3939–3948.
24. B. M. Connolly, M. Aragones-Anglada, J. Gandara-Loe, N. A. Danaf, D. C. Lamb, J. P. Mehta, D. Vulpe, S. Wuttke, J. Silvestre-Albero, P. Z. Moghadam, A. E. H. Wheatley and D. Fairen-Jimenez, Nat. Commun., 2019, 10, 2345.
25. B. Escuder, M. Llusar and J. F. Miravet, J. Org. Chem., 2006, 71, 7747–7752.
26. A. Dawn and H. Kumari, Chem.–Eur. J., 2018, 24, 762–776.
27. F. Gaboriaud, A. Nonat, D. Chaumont and A. Craievich, J. Phys. Chem. B, 1999, 103, 5775–5781.
28. R. W. Larsen, J. Am. Chem. Soc., 2008, 130, 11246–11247.
29. N. Hosono, M. Gochomori, R. Matsuda, H. Sato and S. Kitagawa, J. Am. Chem. Soc., 2016, 138, 6525–6531.
30. M. Kroon, G. H. Wegdam and R. Sprik, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6541–6550.
31. T. Suzuki, H. Endo, N. Osaka and M. Shibayama, Langmuir, 2009, 25, 8824–8832.
32. P. N. Pusey and W. Van Megen, Phys. A, 1989, 157, 705–741.
33. A. B. Rodd, D. E. Dunstan, D. V. Boger, J. Schmidt and W. Burchard, Macromolecules, 2001, 34, 3339–3352.
34. M. Shibayama and T. Norisuye, Bull. Chem. Soc. Jpn., 2002, 75, 641–659.
35. H. Asai, K. Nishi, T. Hiroi, K. Fujii, T. Sakai and M. Shibayama, Polymer, 2013, 54, 1160–1166.
36. C. Yang, J. N. Kizhakkedathu, D. E. Brooks, F. Jin and C. Wu, J. Phys. Chem. B, 2004, 108, 18479–18484.
37. P. S. Mohanty, S. Nöjd, K. van Gruijthuijsen, J. J. Crassous, M. Obiols-Rabasa, R. Schweins, A. Stradner and P. Schurtenberger, Sci. Rep., 2017, 7, 1487.
38. F. Sciortino, S. V. Buldyrev, C. De Michele, G. Foffi, N. Ghofraniha, E. La Nave, A. Moreno, S. Mossa, I. Saika-Voivod, P. Tartaglia and E. Zaccarelli, Comput. Phys. Commun., 2005, 169, 166–171.
39. E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101.
40. C. J. Rueb and C. F. Zukoski, J. Rheol., 1997, 41, 197–218.
41. E. D. Gado and W. Kob, Europhys. Lett., 2005, 72, 1032–1038.
42. A. Onuki, J. Non-Cryst. Solids, 1994, 172–174, 1151–1157.
43. S. Seiffert, Prog. Polym. Sci., 2017, 66, 1–21.
44. T. Norisuye, M. Inoue, M. Shibayama, R. Tamaki and Y. Chujo, Macromolecules, 2000, 33, 900–905.
45. R. Liu, X. Gao and W. Oppermann, Polymer, 2006, 47, 8488–8494.
46. J. E. Martin and J. P. Wilcoxon, Phys. Rev. Lett., 1988, 61, 373–376.
47. T. Norisuye, M. Shibayama, R. Tamaki and Y. Chujo, Macromolecules, 1999, 32, 1528–1533.
48. P. G. De Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, NY, 1979.
49. S. B. Ross-Murphy, Polym. Gels Networks, 1994, 2, 229–237.
50. J. R. Stokes and W. J. Frith, Soft Matter, 2008, 4, 1133–1140.
51. S. Minami, D. Suzuki and K. Urayama, Curr. Opin. Colloid Interface Sci., 2019, 43, 113–124.
52. T. Fujii, T. Yano, H. Kumagai and O. Miyawaki, Biosci., Biotechnol., Biochem., 2000, 64, 1618–1622.
53. S. Manley, J. M. Skotheim, L. Mahadevan and D. A. Weitz, Phys. Rev. Lett., 2005, 94, 218302.
54. P. Padmanabhan and R. Zia, Soft Matter, 2018, 14, 3265–3287.
55. J. J. Liétor-Santos, C. Kim, P. J. Lu, A. Fernández-Nieves and D. A. Weitz, Eur. Phys. J. E, 2009, 28, 159–164.
56. H. Pertoft, T. C. Laurent, T. Låås and L. Kågedal, Anal. Biochem., 1978, 88, 271–282.
57. K. T. Miller, R. M. Melant and C. F. Zukoski, J. Am. Ceram. Soc., 1996, 79, 2545–2556.
58. M. Tagliazucchi and I. Szleifer, Mater. Today, 2015, 18, 131–142.
59. H. Zhang, Y. Tian and L. Jiang, Nano Today, 2016, 11, 61–81.
60. H. Yang, H. Wu, Z. Yao, B. Shi, Z. Xu, X. Cheng, F. Pan, G. Liu, Z. Jiang and X. Cao, J. Mater. Chem. A, 2018, 6, 583–591.
61. J. Rouquerol, P. Llewellyn and F. Rouquerol, Stud. Surf. Sci. Catal., 2007, 160, 49–56.
62. S. Furukawa, N. Horike, M. Kondo, Y. Hijikata, A. Carné-Sánchez, P. Larpent, N. Louvain, S. Diring, H. Sato, R. Matsuda, R. Kawano and S. Kitagawa, Inorg. Chem., 2016, 55, 10843–10846.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc04543k

---