Excited-state hydrogen atom abstraction initiates the photochemistry of β-2′-deoxycytidine

Abstract

Understanding the effects of ultraviolet radiation on nucleotides in solution is an important step towards a comprehensive description of the photochemistry of nucleic acids and their constituents. Apart from having implications for mutagenesis and DNA photoprotection mechanisms, the photochemistry of cytidines is a central element in UV-assisted syntheses of pyrimidine nucleotides under prebiotically plausible conditions. In this contribution, we present UV-irradiation experiments of β-2′-deoxycytidine in aqueous solution involving H–D exchange followed by NMR spectroscopic analysis of the photoproducts. We further elucidate the outcome of these experiments by means of high-level quantum chemical calculations. In particular, we show that prolonged UV-irradiation of cytidine may lead to H–C1′ hydrogen atom abstraction by the carbonyl oxygen atom of cytosine. This process may enable photoanomerisation and nucleobase loss, two previously unexplained photoreactions observed in pyrimidine nucleotides.

---

1 Introduction

The photochemistry and photophysics of nucleic acids and their constituents has attracted appreciable interest in recent years. Besides mechanistic studies on UV-induced mutagenic processes^1–4 and the photochemical origins of life,^5–10 a lot of effort has been put into understanding ultrafast photodeactivation pathways of DNA and RNA nucleobases (adenine, guanine, cytosine, thymine and uracil). Both spectroscopic and theoretical techniques have been employed to investigate radiationless deexcitation of purine and pyrimidine bases as well as the Watson–Crick base pairs.^11–18 Although the photostability of isolated nucleobases seems to be well-understood, the proposed mechanisms are not necessarily transferable to the wider context of poly- and oligo-nucleotides. Recent findings confirm that the photochemistry of nucleobases may be significantly altered due to stacking interactions. In particular, UV-irradiation of single and double strands rich in adenine leads to the formation of long-lived and photostable excimers with much longer lifetimes than the isolated adenine molecule.^19,20

Separate nucleotides and nucleosides also evince distinct photochemical behavior to their respective nucleobases. For instance, results of resonant two-photon ionization studies indicate a much shorter excited-state lifetime of adenosine in comparison to adenine.^21,22 This might be caused by the accessibility of a significantly more efficient radiationless deactivation channel in the nucleoside. Tuna et al. attributed these observations to the presence of intramolecular O5′–H⋯N3 hydrogen bonds between the ribose and adenine moieties.²³ Excited-state forward–backward proton transfer along the intramolecular hydrogen bond might effectively dissipate the excess energy of UV-excited adenosine.²³ These results support the hypothesis that sugars could directly modulate the photochemistry of nucleotides via interactions with the chromophore (i.e. nucleobase). It is also becoming evident that with the increasing complexity of target compounds, often only combined experimental-theoretical studies allow the unambiguous determination of plausible photodeactivation mechanisms.

UV-irradiation plays a fundamental role in the final step of prebiotically plausible synthesis of pyrimidine nucleotides reported by Powner and co-workers.²⁴ Prolonged exposure of the product mixture to ultraviolet light resulted in the destruction of the biologically irrelevant stereoisomers of cytidine and uridine, while the biologically important forms of the pyrimidine nucleotides remained nearly intact.²⁴

Besides providing a prebiotically highly plausible route towards pyrimidine nucleotides, this latter work offered a valuable insight into the complex photochemistry which could have taken place on the early Earth parallel to the synthesis of the building blocks of the first genetic molecules. The most prominent photoreactions reported in this work were the formation of oxazolidinone, photoanomerisation and nucleobase loss.^9,10,24,25 A low yield of photoanomerisation was also observed in an earlier prebiotic synthesis of nucleotides performed by Sanchez and Orgel.²⁶ Nevertheless, the mechanisms of these processes have not yet been comprehensively discussed.

In this article, we focus on the photoanomerisation and nucleobase loss reactions of UV-irradiated β-2′-deoxycytidine (β-dC), a model reaction which was also studied in ref. 9. This molecule was selected for the purpose of our studies since the absence of the 2′-OH group prevents the photochemical formation of oxazolidinone derivatives, and thus allows us to concentrate on the photoanomerisation and nucleobase loss. We present a joint experimental/computational analysis of the photochemistry of this molecule including irradiation and H–D exchange experiments, NMR spectroscopic analysis, quantum chemical calculations of potential-energy (PE) surfaces and characterization of conical intersections. In particular, we discuss regioselective and anomer-selective deuterium incorporation from the solvent which indicates the possible reaction mechanisms.

2 Results and discussion

Irradiation of C6-deuterated β-dC rules out the possibility of [1,3]-hydrogen shift

UV-irradiation experiments of different phosphorylated and non-phosphorylated cytidines were recently published by some of us.^9,10,24,25Fig. 1 shows the yields of the products formed through the 72 h irradiation of β-dC in H₂O.⁹ Ultraviolet irradiation of cytosine nucleosides in aqueous solution leads to the reversible formation of photohydrates and subsequent partial deamination to yield the respective uridine analogs.^27–29 In addition, and besides photoanomerisation, variable amounts of bare cytosine, uracil and oxazolidinone are formed (the latter when the 2′-OH group is present in the substrate). Revisiting the previous work by Sanchez and Orgel,²⁶ a tentative reaction mechanism was proposed for the photoanomerisation of α-cytidine into β-cytidine based on the formation of iminium ions (A and B) prone to intramolecular [1,3]-sigmatropic rearrangement (Fig. 1b).⁹

Fig. 1 (a) Photoproducts of the 72 h irradiation of β-2′-deoxycytidine described in ref. 9; (b) scheme showing [1,3]-sigmatropic rearrangement that was proposed as the mechanism explaining photoanomerisation of β-ribocytidine in ref. 9.

With the aim of investigating the suggested mechanism, we decided to irradiate β-dC selectively labeled with deuterium at the C(6) position of the nucleobase (see the ESI† for more details), which would allow for the easy tracking of the proposed [1,3]-hydrogen shift by ¹H NMR spectroscopy. Irradiation of [6-D]-β-dC for 44 h resulted in the formation of its α anomer in 15% yield, along with 8% of the deaminated product, α-dU. To our surprise, the deuterium atom at the C(6) position remained in place, and the corresponding C1′ hydrogens did not exhibit any isotopic exchange. Furthermore, the H–C(5) signals of the free bases cytosine (7%) and uracil (3%) were also singlets, proving that no deuterium shift occurred during glycosidic C–N bond cleavage (see Fig. S3 in the ESI† for the respective NMR spectrum). These results forced us to search for alternative pathways for the photoanomerisation of cytosine nucleosides.

Irradiation of β-dC in D₂O solution leads to anomer-selective deuterium incorporation from the solvent

Given the valuable information that can be extracted from H–D isotopic exchange, we decided to reinvestigate the photochemistry of β-dC using D₂O as the solvent. The UV-irradiation was carried out for 44 h, and afterwards the products were examined for any deuterium incorporation from the solvent. The ¹H-NMR spectrum of the resulting product mixture is presented in Fig. 2. Two distinct sets of signals at 6.13 and 6.16 ppm correspond to α-dC and α-dU, produced in 9% and 5% yields, respectively. Interestingly, after the integration of the signals, we observed a considerable difference between the H–C(6) and H–C1′ peaks for α-dC and α-dU (see Fig. 4 for the atom numbering). More precisely, H–C1′ peaks for the α-anomers represented only 20% of the integral for H–C(6) peaks. This indicates partial, but not complete, deuterium incorporation from the solvent at the C1′ position of the sugar ring. Apart from this, partial deuteration was also observed at the C(5) position of the nucleobase moiety. The latter finding was presumably due to photohydration and it is most probably not involved in photoanomerisation and nucleobase loss reactions.

Fig. 2 ¹H-NMR analysis of the products of the 44 h UV-irradiation of β-dC in D₂O. No H–C(5) was detectable because of the exchange with D under irradiation conditions; integration of α-dC–H–C1′ amounts to around 20% of the integration of α-dC–H–C(6).

A potential explanation for the partial deuteration at the C1′ position of the deoxyribose fragment is an interrupted Norrish type II reaction mechanism, in which photoexcitation to the nπ* state localized at the carbonyl group of cytosine leads to H–C1′ hydrogen atom abstraction (see Fig. 3). The intermediate formed in this photoreaction may readily undergo inversion of the C1′ stereogenic center. Because the hydrogen–deuterium exchange of the nucleobase enol thus produced can be expected to be extremely rapid, the reaction should lead to both α- and β-anomers deuterated at H–C1′.

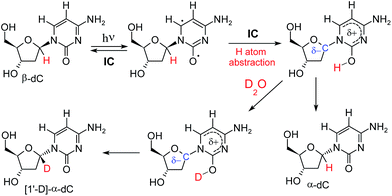Fig. 3 Proposed mechanism that explains photoanomerisation of β-dC with partial incorporation of deuterium at H–C1′. The electronic structure of the H–C1′ hydrogen atom abstraction intermediate (shown in the top right corner) is discussed later in the text and in the ESI.†

Although this mechanism could explain why only partial deuteration was encountered at the C1′ position, it cannot be definitely confirmed without performing any additional experiments or simulations, particularly since the above considerations entail two major uncertainties. First of all, it is well established that Norrish type II reactions are usually initiated by the abstraction of a γ-hydrogen atom with respect to the reactive carbonyl group.³⁰ In this case, H–C2′ abstraction should be at least feasible (if not dominant), however, no deuteration was detected at this position by ¹H-NMR analysis. Secondly, assuming that this mechanism took place, one would also expect some H–C1′ deuteration of β-dC, although this was not detected (H–C1′ deuteration was observed only in the case of the α-anomer).

In order to confirm the validity of the proposed variation of the Norrish type II mechanism, the two issues mentioned above needed clarification. It was already pointed out that the spatial positioning of the carbonyl group may impose hydrogen atom abstraction at an unusual site.^30–32 Thus, if this mechanism is true for β-dC photoanomerisation, the lowest energy conformers should somehow prevent H–C2′ abstraction and simultaneously enable H–C1′ abstraction. The anomer-selective deuteration in the C1′ position could be promoted by higher stability of α-configured intermediates, directly after the hydrogen atom abstraction. Indeed we have found that the β-configured intermediates formed after the H–C1′ atom abstraction are thermodynamically less stable in bulk water. In the next section we discuss these two phenomena and we provide thorough theoretical analysis of the proposed reaction channels.

Some theoretical insights into the photochemistry of β-dC were already published by Zgierski and Alavi.³³ The authors concluded that the substitution of cytosine with deoxyribose should not have a significant impact on the electronic relaxation mechanism.³³ In contrast, picosecond and sub-picosecond time-resolved spectroscopic experiments used to investigate the photodynamics of β-dC reveal that the substitution with 2′-deoxyribose has a significant effect on the excited-state lifetime and probably on the photochemical reactivity.^34–37 Considering this lack of agreement, we decided to investigate in detail the role of the sugar in the photochemistry of β-dC and its implications in the proposed interrupted Norrish II type photoanomerisation mechanism, by means of quantum-chemical calculations.

β-dC may adopt either a C2′-endo or a C3′-endo conformation in bulk water

We have considered two conformers of β-dC that were proposed to be the lowest-energy conformers according to gas phase ab initio calculations,^38,39 molecular dynamics simulations with explicit water molecules⁴⁰ and NMR data obtained at 278 K in aqueous solution.⁴¹ Both of the conformers exhibit an anti orientation of cytosine with respect to 2′-deoxyribose, and C–H⋯O interactions form between the nucleobase and the O5′ oxygen atom.^42,43 The only difference between these conformers is the arrangement of the furanose ring: C2′-endo denoted S (for South) and C3′-endo denoted N (for North) (see Fig. 4 for the schematic representation of these conformers). The S conformer was found to be more stable in aqueous solution than the N conformer,^40,41 whereas the opposite was found in the gas phase.³⁸ Gibbs free energy calculations performed using the Kohn–Sham density functional theory with a M06-2X functional and a C-PCM implicit solvent model were consistent with those findings (ΔG^PCM_S–N = 0.9 kJ mol⁻¹ and ΔG^gas_S–N = −3.7 kJ mol⁻¹). Therefore, considering these results and the aforementioned NMR data measured between 278 K and 358 K, the S conformer should constitute approximately 60% of β-dC in solution.⁴¹ The remaining part of β-dC in solution should mainly correspond to the N conformer. The preference of the S conformer can also be explained in terms of the strong gauche stereoelectronic effect of the O4′–C4′–C3′–O3′ fragment which is present in 2′-deoxyribonucleosides and shifts the N⇌S equilibrium towards the S form.⁴⁴ The gauche effect is partially compensated for by the relatively weaker anomeric effect of cytosine.⁴⁴ Consequently, only a slight excess of the S conformer is observed in aqueous solution.

Fig. 4 Schematic representation of the two most stable conformers of β-dC, considered in the theoretical investigations. The atom numbering presented above is used throughout the manuscript.

The equilibrium ground-state geometry of the S conformer is characterized by a very short distance between the carbonyl oxygen atom of cytosine and the H–C1′ hydrogen atom (2.26 Å). On the contrary, the accessible H–C2′ atom is 3.99 Å away from this carbonyl oxygen atom. In the case of the N conformer, the distance between this oxygen atom and the H–C2′ atom is much shorter (2.69 Å), but H–C1′ still remains the nearest hydrogen atom (2.38 Å) that could be potentially abstracted after the photoexcitation. Thus, the conformational positioning of the carbonyl group of cytosine with respect to the various H–C bonds could already partially explain the preferential H–C1′ abstraction.

The minimum of the S₁ state of β-dC is of nπ* character

The vertical excitation energies computed at the CC2 level show that the lowest-lying excited singlet state of β-dC is of ππ* character. This is the most intense transition which is responsible for the absorption of this molecule in the UV-B spectral range (see Table 1). The nπ* state that is significantly involved in the photodeactivation mechanisms of cytosine is the S₂ state, which lies approximately 0.3 eV above the optically bright ππ* state. These results are consistent for both the S and N conformers and are comparable to the vertical excitation energies calculated for cytosine.⁴⁵

Table 1 CC2 vertical excitation energies (in eV) of both β-dC conformers, computed assuming the ground-state minimum energy structures optimized at the M06-2X/6-311++G(2d,2p) level

State/transition		E exc/[eV]	f osc	λ/[nm]
S conformer of β-dC; CC2/cc-pVTZ
S1	ππ*	4.72	0.124	262.7
S2	nπ*	5.07	3.20 × 10^−3	244.5
S3	nπ*	5.44	5.65 × 10^−3	227.9
N conformer of β-dC; CC2/cc-pVTZ
S1	ππ*	4.79	0.120	258.8
S2	nπ*	5.11	1.83 × 10^−3	242.6
S3	nπ*	5.54	1.73 × 10^−2	223.8

---

We have optimized the geometries of the lowest excited singlet state structures at the CASSCF level. Similarly as in the case of cytosine the minimum of the S₁ state is of nπ* character.⁴⁵ This state is of biradical character with unpaired electrons localized on the C6 carbon atom and on the carbonyl oxygen atom (see Fig. 3). This is reflected by slight pyramidalization of the C6 atom and elongation of the C=O bond. Interestingly, the distances between the carbonyl oxygen atom and the H–C1′ hydrogen atom amount to approximately 2.20 Å in the minima on S₁ PE surfaces of both the considered conformers. In contrast, the H–C2′ atom is much more distant from the carbonyl oxygen atom: 4.44 Å and 3.80 Å in the S and N conformers respectively. In the light of the above structural data, photoinduced γ-hydrogen atom abstraction seems rather improbable.

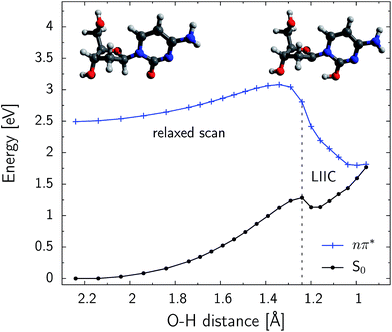
Excited-state hydrogen atom abstraction is possible at the C1′ position

Fig. 5 shows the PE profile for the H–C1′ hydrogen atom abstraction in the S conformer of β-dC. The reaction path is generally ascending until the C=O⋯H–C1′ distance reaches 1.35 Å. Further shortening of this contact rapidly decreases the energy of the nπ* state. The respective ground-state energy is systematically increased along the reaction coordinate and the S₁ and S₀ PE surfaces nearly intersect for distances shorter than 1.0 Å. The S₁/S₀ conical intersection is separated from the minimum of the nπ* (S₁) state by an energy barrier of 0.59 eV (56.9 kJ mol⁻¹). This indicates that the predicted quantum yield of hydrogen atom abstraction might be rather low, particularly since it could be largely outcompeted by the effective ring-puckering processes responsible for the photostability of cytosine.^45–47 Nevertheless, the photodynamics starts in the Franck–Condon region of photoexcited β-dC, which is higher in energy than the intersection seam responsible for the hydrogen atom abstraction. The excess energy gained after the UV-excitation is easily redistributed into vibrational degrees of freedom. Consequently, the modest energy barrier found for this process can be overcome and a fraction of photoexcitation events might lead to the photoproducts reported in our experiments. The shallow minimum, present on the ground-state PE surface for C=O⋯H–C1′ distances close to 1.2 Å, indicates that a short-lived intermediate may be formed after this conical intersection is reached.

Fig. 5 Relaxed PE scan along the C=O⋯H–C1′ distance, performed at the SA4-CASSCF(10,8)/cc-pVDZ level of theory. The S conformer of β-dC was considered. The initial and final points represent the minimum of the S₁ state and the optimized minimum-energy conical intersection respectively. These structures are also shown in the top left-hand and top right-hand corners of the graph. The final six structures before the optimized conical intersection geometry were obtained by LIIC (linear interpolation in internal coordinates). A single-point CASPT2 energy correction was calculated at every point of the PE profile.

We have performed an analogous relaxed scan along the C=O⋯H–C2′ distance, in order to investigate the possibility of hydrogen atom abstraction in the γ-position. However, shortening of this distance to up to 1.20 Å does not lead to a state crossing and the S₁ hypersurface is over 1.0 eV above the electronic ground-state. We also did not locate the conical intersection related to this process, and the optimizations drove the geometry to another region on the PE surface. These results are consistent with our findings that no deuteration is observed at the C2′ position. Therefore, the possibility of γ-hydrogen abstraction in β-dC can be practically ruled out.

To further characterize the photoinduced H–C1′ atom abstraction, we have optimized the respective conical intersection at the CASSCF level. The length of the newly formed O–H bond amounts to merely 0.95 Å in the case of the optimized minimum-energy conical intersection (MECI) geometry. The remaining structural parameters do not differ significantly from the equilibrium of the S₁ state. Single point CASPT2 calculations performed at the located stationary points show that the MECI structure is lower in energy than the S₁ minimum (by approximately 0.8 eV). Thus, once UV-excited β-dC lands in the vicinity of this conical intersection, the probability of escaping to a different region of the nπ* hypersurface is rather low.

The branching space coordinates provide additional information about possible evolution of the system after the non-adiabatic transition to the electronic ground state. These lift the electronic state degeneracy and consequently, define the conical intersection. Yarkony defined these coordinates as the energy difference gradient (g) and non-adiabatic coupling (h) vectors.^48,49 In the case of the aforementioned MECI, the g vector is predominantly composed of in-plane vibrations of the cytosine ring and stretching of the O–H bond formed after the H–C1′ atom abstraction. In other words, if the photoreaction proceeds along the g vector, the hydrogen atom may be immediately returned to its initial C1′ position simultaneously with the redistribution of the π bond structure in cytosine, thus yielding β-dC as the final photoproduct (see Fig. 6a). In this scenario the initial form of the irradiated molecule (β-dC) is preserved. The h vector is composed of several modes responsible for the puckering of the cytosine ring and for the rotation of the hydroxyl group formed after the hydrogen atom abstraction (see Fig. 6b). The rotating hydroxyl group may form a hydrogen bond with a nearby water molecule yielding a relatively stable ground-state intermediate. At the same time, the C1′ carbon atom after hydrogen atom abstraction enables free interconversion between the α- and β-anomers.

Fig. 6 Optimized geometries of relevant stationary points: (a) and (b) present the g and h vectors, respectively, displayed on the CASSCF optimized geometry of the minimum-energy S₁/S₀ conical intersection of the S conformer of β-dC; the g and h vectors point in the directions of possible photoproducts; (c) is the lowest energy conformer of the ground-state intermediate formed after H–C1′ atom abstraction, optimized at the M06-2X level (note the α-configuration of the N-glycosidic bond); (d) is the lowest energy conformer of the deprotonated intermediate that could be formed during the H–D exchange reaction, optimized at the M06-2X/6-311++G(2d,2p) level (again, note the α-configuration of the N-glycosidic bond).

Regardless of the direction of the photoreaction, analysis of the CASSCF wave function reveals that the respective photoproducts have closed-shell electronic structures. Although the hydrogen atom abstraction occurs on the hypersurface of a biradicalic electronically excited state, the subsequent non-adiabatic transition to the electronic ground state results in the redistribution of the electronic structure. More precisely, the ground-state intermediates after H–C1′ hydrogen atom abstraction are of closed-shell character with substantial charge-transfer (see Fig. 3 for a schematic representation and Fig. S1 and S2 in the ESI† for more details). According to electron population analysis of these intermediates, approximately 0.8 electrons are transferred from the nucleobase to the sugar moiety. In the next few paragraphs we will discuss the Gibbs free energy (ΔG^PCM) differences between various conformers of the H–C1′ hydrogen atom abstraction intermediate, based on the results of M06-2X/6-311++G(2d,2p) calculations, assuming the C-PCM model of bulk water.

H–C1′ atom abstraction intermediates are more stable in the α-configuration

Owing to pyramidalization of the C1′ carbon atom, the H–C1′ atom abstraction intermediates of dC may adopt an α- or a β-configuration. Right after the hydrogen atom abstraction, both the S and N conformers of dC will be in the β-configuration. However, the α-configured conformers are thermodynamically more stable in both cases. In particular, the α-S C1′ hydrogen atom abstraction intermediate (Fig. 6c) is more stable by 24.8 and 30.4 kJ mol⁻¹ than the β-S and β-N conformers, respectively (cf.Table 2). The α-N H–C1′ atom abstraction intermediate is slightly higher in energy, but it is still more stable than the β-configured conformers. In consequence, the α-configuration of the intermediate should be preferred after the hydrogen atom abstraction. If this compound exchanges the H–O(2) proton to deuteron in D₂O solution, only the α-anomers of the final photoproducts should be deuterated at H–C1′ after the reverse reaction.

Table 2 Relative Gibbs free energy values (in kJ mol⁻¹) of the H–C1′ hydrogen atom abstraction intermediates calculated with respect to the lowest energy conformer at the M06-2X/6-311++G(2d,2p) level assuming the C-PCM model of bulk water

α-C1′-endo	α-S	β-S	α-N	β-N
a Optimization of the α-N intermediate after the O–H bond dissociation converged to the α-C1′-endo conformer, thus, their respective energies are identical. b Optimization of the β-N intermediate after the O–H bond dissociation converged to the β-S conformer, thus, their respective energies are identical.
Neutral intermediates before the O–H group dissociation
12.0	0.0	24.8	17.8	30.4
Intermediates after the O–H bond dissociation
0.0^a	0.1	17.6^b	0.0^a	17.6^b

---

H–D exchange of the photochemically-created hydroxyl group of cytosine would first require the proton to be transferred to the nearby D₂O molecule. Thus, we have also considered different conformers of the negatively charged intermediates after such a proton transfer to the nearby solvent molecule. Similarly as in the previous case, the α-configured negatively charged conformers are more stable than the β-configured intermediates (by over 17.0 kJ mol⁻¹). The lowest-energy conformer presented in Fig. 6d, has a very strong O5′–H⋯C1′ interaction (approximately 1.84 Å). This indicates that a considerable part of the negative charge is centered on the C1′ carbon atom and that the 5′-hydroxyl group acts to stabilize the intermediate in the α-configuration. It is worth noting that this intermediate has an unusual arrangement of the sugar ring that enables this interaction, namely the C1′-endo conformation. The respective α-S negatively charged intermediate is almost isoenergetic with the C1′-endo conformer.

H–C1′ atom abstraction intermediates might undergo nucleobase loss reaction

To elucidate the reasons for the relatively high yield of nucleobase loss, we reconsidered the lowest-energy direct product of the photochemical H–C1′ abstraction (α-S conformer). Rupture of the N-glycosidic bond of this moiety might result in the formation of the enol form of cytosine and a carbene of 2′-deoxyribose (see Fig. 7). The corresponding activation free energy ΔG amounts to 10.8 kJ mol⁻¹. According to this estimate, the considered reaction path has a remarkably low energetic barrier, and it might explain the presence of bare cytosine in the product mixture after 44 h of UV-irradiation. Since the N-glycosidic bond is in the α–β position with respect to the carbonyl group, this reaction strikingly resembles the classic Norrish type II cleavage.^30,50 In fact, the only difference is the position at which hydrogen atom abstraction occurs (the β-position in the case of cytidine, instead of the γ-position in the regular Norrish type II reaction).^30,50

Fig. 7 Rupture of the N-glycosidic bond in the H–C1′ atom abstraction intermediate leads to the formation of the enol form of cytosine, which could explain its presence among the photoproducts.

3 Conclusions

In this article we emphasize the role of deoxyribose in the photochemistry of 2′-deoxycytidine. In particular, we elucidate the mechanisms of photoanomerisation and nucleobase loss reactions that were reported in several previous works describing plausible origins of nucleotides on early Earth.^9,10,24,25 We performed UV-irradiation experiments in D₂O solution followed by the analysis of the NMR spectra of the photoproducts. The experiment resulted in partial deuteration (approximately 80%) at the H–C1′ position of the α-anomer of dC. We further explained this phenomenon on the basis of quantum chemical calculations and we showed that the main photoproducts can be formed after the photoinduced H–C1′ hydrogen atom abstraction. In particular, our findings imply that similarly as in adenosine,²³ the sugar subunit is responsible for a significant part of the photochemistry of cytidine.

The conical intersection responsible for the H–C1′ atom abstraction is separated from the S₁ minimum by a modest energetic barrier. Thus, a rather low quantum yield of H–C1′ atom abstraction is expected. This is confirmed by relatively long irradiation periods that are necessary to generate the resulting photoproducts. Potentially competitive γ-hydrogen atom abstraction was ruled out by both experiment (no deuteration at H–C2′) and computations (no respective conical intersection). Therefore, the above-mentioned mechanism can be referred to as an interrupted variation of the Norrish type II reaction.

After the abstraction of the H–C1′ hydrogen atom, anomerisation to the α-configured intermediates is an exergonic process. Consequently, the reverse proton transfer in the ground-state H–C1′ hydrogen atom abstraction intermediate might exclusively occur after the β to α anomerisation. If the photochemically-created hydroxyl group of cytosine undergoes H–D exchange, only the α-anomers of dC can be deuterated. This explains the anomer-selective deuteration of α-dC observed in our experiment. Finally, the intermediate may also readily undergo nucleobase loss reaction, if no reverse-protonation of the C1′ carbon atom occurs.

Although we elucidated part of the photoreactions mentioned in several articles that describe plausible origins of pyrimidine nucleotides,^9,10,24,25 there are still a number of questions that should be addressed in future works related to this topic. First of all, some additional insights could be provided by non-adiabatic molecular dynamics simulations. However, such a study needs to be carefully designed considering the system size and the excited-state lifetime predicted by experiments.³⁵ Furthermore, the presence of the 2′-hydroxyl group in ribocytidine and additional phosphorylation might enable interactions which are absent in dC. Since these factors may significantly alter the photochemistry of cytosine nucleosides, more experimental and theoretical insights are necessary in order to fully understand their photochemistry.

4 Methodology

Experimental section

Synthesis of [6-D]-β-dC. The deuterated β-dC was prepared by a modification of the reported procedure⁵¹ giving rise to selective deuteration of the C(6) and C(5) positions at levels of 97% and 85%, respectively. Since the H–C(5) proton is readily exchanged under irradiation conditions anyway, its deuteration did not present any problems.

General procedure for photochemical reactions. β-dC (30 mg, 0.13 mmol) was dissolved in D₂O (5 mL) and the pH adjusted to 6.5 using degassed 1 M HCl and a Russell RL150 pH meter. The solution was purged with N₂ for 10 min and then, with a continuous stream of N₂ bubbling through the solution to agitate it, irradiated with an unfiltered Hg lamp (254 nm, cooled to 15 °C by a quartz water jacket). After 44 h of irradiation, the solution was heated at 90 °C for 40 h, lyophilized, and the residue re-dissolved in D₂O (0.75 mL). ¹H NMR spectra were then acquired before and after spiking the sample with authentic standards of β-dC, β-dU, α-dC and α-dU.

Computational methods

All the stationary points on the ground-state PE surface were located using the Kohn–Sham formulation of Density Functional Theory (KS-DFT). The M06-2X functional was chosen, due to its performance in computing thermodynamic properties.^52,53 These ground-state calculations were carried out using the 6-311++G(2d,2p) basis set. In order to account for the solvent screening effects exerted by bulk water we used the conductor-like polarizable continuum model (C-PCM) as implemented in the Gaussian 09 code.^54–56

Vertical excitation energies of β-dC were calculated at the CC2/cc-pVTZ level. Optimizations of S₁ minima, conical intersection and relaxed scans were performed using the SA-CASSCF/cc-pVDZ method. A single-point CASPT2 energy correction was computed where appropriate in order to account for dynamic electron correlation.

The CC2 calculations were performed using the TURBOMOLE 6.3 package,^57,58 whereas the constrained CASSCF optimizations and the CASPT2 calculations were done using the MOLCAS 7.8 package.^59,60 The CASSCF optimizations of conical intersections were performed with the COLUMBUS 7.0 program package.^61,62 All the KS-DFT calculations reported in this study were performed using the Gaussian 09 quantum chemistry package.⁶³

More details regarding the experimental procedures and computational methods are specified in the ESI.†

Acknowledgements

We thank Dr Holger Kruse for reading and commenting on the manuscript. This work was supported by the Grant Agency of the Czech Republic (grant no. 14-12010S) to J.E.S. and a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wrocław University of Technology to R.W.G. Financial support from the project “CEITEC – Central European Institute of Technology” (CZ.1.05/1.1.00/02.0068) from the European Regional Development Fund is gratefully acknowledged.

References

1. W. J. Schreier, T. E. Schrader, F. O. Koller, P. Gilch, C. E. Crespo-Hernández, V. N. Swaminathan, T. Carell, W. Zinth and B. Kohler, Science, 2007, 315, 625–629.
2. S. Yuan, W. Zhang, L. Liu, Y. Dou, W. Fang and G. V. Lo, J. Phys. Chem. A, 2011, 115, 13291–13297.
3. M. C. Cuquerella, V. Lhiaubet-Vallet, F. Bosca and M. A. Miranda, Chem. Sci., 2011, 2, 1219–1232.
4. K. Haiser, B. P. Fingerhut, K. Heil, A. Glas, T. T. Herzog, B. M. Pilles, W. J. Schreier, W. Zinth, R. de Vivie-Riedle and T. Carell, Angew. Chem., Int. Ed., 2012, 51, 408–411.
5. H. L. Barks, R. Buckley, G. A. Grieves, E. Di Mauro, N. V. Hud and T. M. Orlando, ChemBioChem, 2010, 11, 1240–1243.
6. R. Szabla, D. Tuna, R. W. Góra, J. Šponer, A. L. Sobolewski and W. Domcke, J. Phys. Chem. Lett., 2013, 4, 2785–2788.
7. E. Boulanger, A. Anoop, D. Nachtigallova, W. Thiel and M. Barbatti, Angew. Chem., Int. Ed., 2013, 125, 8158–8161.
8. R. Szabla, R. W. Góra, J. Šponer and J. E. Šponer, Chem.–Eur. J., 2014, 20, 2515–2521.
9. M. W. Powner, C. Anastasi, M. A. Crowe, A. L. Parkes, J. Raftery and J. D. Sutherland, ChemBioChem, 2007, 8, 1170–1179.
10. M. W. Powner and J. D. Sutherland, ChemBioChem, 2008, 9, 2386–2387.
11. A. L. Sobolewski and W. Domcke, Europhys. News, 2006, 37, 20–23.
12. M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 21453–21458.
13. K. Kleinermanns, D. Nachtigallová and M. S. de Vries, Int. Rev. Phys. Chem., 2013, 32, 308–342.
14. C. Canuel, M. Mons, F. Piuzzi, B. Tardivel, I. Dimicoli and M. Elhanine, J. Chem. Phys., 2005, 122, 074316.
15. M. S. de Vries and P. Hobza, Annu. Rev. Phys. Chem., 2007, 58, 585–612.
16. C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2020.
17. H. Saigusa, J. Photochem. Photobiol., C, 2006, 7, 197–210.
18. R. Weinkauf, J.-P. Schermann, M. S. d. Vries and K. Kleinermanns, Eur. Phys. J. D, 2002, 20, 309–316.
19. C. E. Crespo-Hernández and B. Kohler, J. Phys. Chem. B, 2004, 108, 11182–11188.
20. C. E. Crespo-Hernández, B. Cohen and B. Kohler, Nature, 2005, 436, 1141–1144.
21. E. Nir and M. S. de Vries, Int. J. Mass Spectrom., 2002, 219, 133–138.
22. H. Asami, K. Yagi, M. Ohba, S.-H. Urashima and H. Saigusa, Chem. Phys., 2013, 419, 84–89.
23. D. Tuna, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2014, 118, 122–127.
24. M. W. Powner, B. Gerland and J. D. Sutherland, Nature, 2009, 459, 239–242.
25. M. Powner, J. Sutherland and J. Szostak, Synlett, 2011, 1956–1964.
26. R. A. Sanchez and L. E. Orgel, J. Mol. Biol., 1970, 47, 531–543.
27. G. Deboer, O. Klinghoffer and H. E. Johns, Biochim. Biophys. Acta, 1970, 213, 253–268.
28. F.-T. Liu and N. C. Yang, Biochemistry, 1978, 17, 4877–4885.
29. H. E. Johns, J. C. LeBlanc and K. B. Freeman, J. Mol. Biol., 1965, 13, 849–861.
30. T. Bach and J. Hehn, Angew. Chem., Int. Ed., 2011, 50, 1000–1045.
31. B. Makino, M. Kawai, K. Kito, H. Yamamura and Y. Butsugan, Tetrahedron, 1995, 51, 12529–12538.
32. P. De Mayo and R. Suau, J. Am. Chem. Soc., 1974, 96, 6807–6809.
33. M. Z. Zgierski and S. Alavi, Chem. Phys. Lett., 2006, 426, 398–404.
34. P. M. Keane, M. Wojdyla, G. W. Doorley, G. W. Watson, I. P. Clark, G. M. Greetham, A. W. Parker, M. Towrie, J. M. Kelly and S. J. Quinn, J. Am. Chem. Soc., 2011, 133, 4212–4215.
35. S. Quinn, G. W. Doorley, G. W. Watson, A. J. Cowan, M. W. George, A. W. Parker, K. L. Ronayne, M. Towrie and J. M. Kelly, Chem. Commun., 2007, 2130–2132.
36. P. M. Keane, M. Wojdyla, G. W. Doorley, J. M. Kelly, I. P. Clark, A. W. Parker, G. M. Greetham, M. Towrie, L. M. Magno and S. J. Quinn, Phys. Chem. Chem. Phys., 2012, 14, 6307–6311.
37. A. S. Chatterley, C. W. West, V. G. Stavros and J. R. R. Verlet, Chem. Sci., 2014, 5, 3963–3975.
38. A. Hocquet, N. Leulliot and M. Ghomi, J. Phys. Chem. B, 2000, 104, 4560–4568.
39. O. V. Shishkin, A. Pelmenschikov, D. M. Hovorun and J. Leszczynski, J. Mol. Struct., 2000, 526, 329–341.
40. N. Foloppe and L. Nilsson, J. Phys. Chem. B, 2005, 109, 9119–9131.
41. J. Plavec, C. Thibaudeau and J. Chattopadhyaya, Pure Appl. Chem., 1996, 68, 2137–2144.
42. A. Hocquet and M. Ghomi, Phys. Chem. Chem. Phys., 2000, 2, 5351–5353.
43. A. Hocquet, Phys. Chem. Chem. Phys., 2001, 3, 3192–3199.
44. J. Plavec, W. Tong and J. Chattopadhyaya, J. Am. Chem. Soc., 1993, 115, 9734–9746.
45. M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová and H. Lischka, Phys. Chem. Chem. Phys., 2011, 13, 6145–6155.
46. J. González-Vázquez and L. González, ChemPhysChem, 2010, 11, 3617–3624.
47. S. Mai, P. Marquetand, M. Richter, J. González-Vázquez and L. González, ChemPhysChem, 2013, 14, 2920–2931.
48. D. R. Yarkony, Rev. Mod. Phys., 1996, 68, 985–1013.
49. D. R. Yarkony, Acc. Chem. Res., 1998, 31, 511–518.
50. A. Henne and H. Fischer, Angew. Chem., Int. Ed. Engl., 1976, 15, 435.
51. J. A. Rabi and J. J. Fox, J. Am. Chem. Soc., 1973, 95, 1628–1632.
52. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
53. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
54. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
55. G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110.
56. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
57. C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161.
58. TURBOMOLE v6.3 2011, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, 2011, http://www.turbomole.com.
59. G. Karlström, R. Lindh, P.-A. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239.
60. F. Aquilante, L. De Vico, N. Ferre, G. Ghigo, P.-A. Malmqvist, P. Neogrady, T. B. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andres, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247.
61. H. Lischka, T. Müller, P. G. Szalay, I. Shavitt, R. M. Pitzer and R. Shepard, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 191–199.
62. H. Lischka, R. Shepard, I. Shavitt, R. M. Pitzer, M. Dallos, T. Müller, P. G. Szalay, F. B. Brown, R. Ahlrichs, H. J. Böhm, A. Chang, D. C. Comeau, R. Gdanitz, H. Dachsel, C. Ehrhardt, M. Ernzerhof, P. Höchtl, S. Irle, G. Kedziora, T. Kovar, V. Parasuk, M. J. M. Pepper, P. Scharf, H. Schiffer, M. Schindler, M. Schüler, M. Seth, E. A. Stahlberg, J.-G. Zhao, S. Yabushita, Z. Zhang, M. Barbatti, S. Matsika, M. Schuurmann, D. R. Yarkony, S. R. Brozell, E. V. Beck, J.-P. Blaudeau, M. Ruckenbauer, B. Sellner, F. Plasser and J. J. Szymczak, COLUMBUS, release 7.0 2012, an ab initio electronic structure program, 2012, http://www.univie.ac.at/columbus.
63. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision C.01, Gaussian Inc., Wallingford CT, 2009.

---

Footnote

† Electronic supplementary information (ESI) available: Including relevant preliminary results as well as illustrations and geometrical parameters of selected structures. See DOI: 10.1039/c4sc03761h

---