The effect of ring sizes and alkali metal cations on interaction energy, charge transfer and nonlinear optical properties of crown ether derivatives†
Ying Gao,
Rong-Lin Zhong,
Hong-Liang Xu*,
Shi-Ling Sun and
Zhong-Min Su*
Institute of Functional Material Chemistry, Faculty of Chemistry, Northeast Normal University, Changchun 130024, Jilin, People's Republic of China. E-mail: hlxu@nenu.edu.cn; zmsu@nenu.edu.cn
First published on 23rd March 2015
Abstract
In 2003, a novel compound 2 containing the benzo-15-crown-5 moiety was synthesized and described. In the present work, we have designed two compounds 1 (benzo-12-crown-4) and 3 (benzo-18-crown-6) on the basis of compound 2. Further, nine configurations N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) are designed by the compounds 1, 2 and 3 complexing alkali metal cations. Density functional calculation is performed to investigate the effect of ring size and the nature of the alkali metal cations on the interaction energy, charge transfer and nonlinear optical properties. The results indicate that the interaction energy of N*M depends on both the ring size and the nature of the alkali metal cations. Moreover, the amount of net charge transfer is related to the diameters of the alkali metal cations. In addition, the calculated nonlinear optical properties reveal that compound 2 has the largest first hyperpolarizability among the three compounds 1, 2 and 3. However, the alkali metal cations give rise to different effects on the nonlinear optical properties. Significantly, the order of the first hyperpolarizability can be explained by the transition energy and the dipole moment variation within the two-state approximation.
1. Introduction
Crown ethers are kinds of heterocycle that are cyclic oligomers of dioxane.1 In 1967, Pedersen initially reported the synthesis and complexing properties of crown ethers.2,3 Since then, considerable attention4–8 has been focused on synthesizing functional crown compounds due to their widespread applications in mediating ion transport,9 the ability of molecular assembly10,11 and developing advanced analytical methods12 and so on.13,14 Besides that, one significant feature of the crown compound is the versatile range of interactions with alkali metal cations.15,16 Moreover, the structures of crown ethers have enormous varieties.17 For example, the variation of ring sizes,18 the oxygen atoms in the ring is replaced with nitrogen and sulfur heteroatoms,19–21 the substituents of different functional groups in crown ether.6 Due to the structural flexibilities, thousands of crown compounds have been synthesized for specific goals. A novel compound 2 (Scheme 1) has been synthesized by condensation of 2,3,3-trimethylindolenine with substituted benzaldehydes in the presence of NaOMe in DMSO.22 Significantly, the compound 2 has the characteristic of chromo-fluoro probe for alkali and alkaline-earth cations.8On the other hand, numerous researches have been subjected to search for excellent nonlinear optical (NLO) materials because of the board applications in frequency doubling of low power diode lasers, electro-optic modulation, optical signal processing, imaging enhancements and frequency upconversion lasing.23 The accurate experimental determination of the NLO characteristics is difficult to measure.24 Hence, the reliable theoretical predictions of NLO properties are particularly valuable and serve as an increasingly important companion to experimental investigations.25 In general, the NLO properties of molecules originate from the hyperpolarizability concerned with the response of electronic changes to the oscillating applied electric field of a laser beam. The large first hyperpolarizability value requires that the molecule is noncentrosymmetric and possesses π-conjugated bridge with electron donor (D) and acceptor (A) substituents.25 Based on the D–π–A model, a variety of molecules have been designed to search for good NLO material candidates.26 In addition, some other factors are considered, such as the effect of the knot number on the structure and the first hyperpolarizability27 and the effect of shapes on (hyper)polarizability.28 Recently, the size-dependent effect on the structure and electro-optical properties of Möbius Cyclacenes has been studied.29 On the other hand, numerous valuable papers have demonstrated that the alkali doping can significantly enhance the NLO response of studied systems.30–37
Inspired by our previous papers and the advantages of crown compounds (the structural flexibility and the interaction with alkali metal cations), we intend to investigate the effect of the ring sizes and the nature of alkali metal cations on the NLO properties. Firstly, based on the synthesized compound 2, the compounds 1 and 3 are designed. The difference among compounds 1, 2 and 3 is the number of oxygen atoms in crown moiety which is four, five and six, respectively. Secondly, nine configurations N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) are designed by the compounds 1, 2 and 3 complexing alkali metal cations. And, the geometrical parameters and a series of properties including interaction energy, extended charge decomposition, NLO and charge transfer analysis, were discussed.
2. Computational details
In present work, all calculations were performed with the Gaussian 09 program.38 The geometry optimizations were carried out at B3LYP/6-31G* for compounds 1, 2 and 3 and the N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) configurations. To understand the bonding and electronic properties of the studied configurations, the atoms in molecules (AIM) analysis39 was performed. The charge density (ρ(r)) and the Laplacian of charge density (∇2ρ(r)) of the (3, −1) at the bond critical points (BCPs), where the electron density becomes a minimum along the bond path, were discussed. Additionally, the interaction energy (Eint) was calculated at BHandHLYP/6-311+G**. In order to avoid the basis set superposition error (BSSE), the counterpoise (CP) corrections were used to calculate all Eint values.40,41 According to the method, the Eint is calculated with the following equation.| Eint = −(EN*M(Xab) − EN(Xab) − EM(Xab)) | (1) |
The mean dipole moment (μ0) and polarizability (α0) can be defined as follows.
| μ0 = (μx2 + μy2 + μz2)1/2 | (2) |
 | (3) |
The first hyperpolarizability (β0) is according to the following equation.
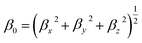 | (4) |
 | (5) |
The Multiwfn package45 was used to carry out the atoms in molecules analysis, charge decomposition analysis, extended charge decomposition analysis, and charge transfer analysis based on the optimized wave functions.
3. Results and discussion
3.1 Optimized geometries and atoms in molecules analysis
The compound 2 has been synthesized, and the compounds 1 and 3 are designed in theory (Fig. 1). When the compounds 1, 2 and 3 complexing alkali metal cations, nine configurations N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) are constructed. All optimized geometries are shown in Fig. 2. The selected geometrical parameters are collected in Table 1, and the definition of atom numbering used in Table 1 is presented in Fig. 2. The detailed O–O and O–M (M = Li+, Na+ and K+) distances are tabulated in Table S1,† and Table 1 gives the average O–O and O–M (M = Li+, Na+ and K+) distances. We can see that the average O–O distance of compound 1 is 3.840 Å. In 1*Li+, the compound 1 distorts seriously because the diameter of Li+ is too small to fit the ring size of compound 1. Thus, the average O–O distance (3.556 Å) of 1*Li+ is 0.284 Å shorter than that of pristine compound 1. For the Na+ and K+, the ring size of compound 1 is too small, resulting in the Na+ and K+ running away the planar of the crown ether and locating on the upper of the crown ether ring. Thus, the average O–O distances (3.852 Å for 1*Na+ and 3.918 Å for 1*K+) of both 1*Na+ and 1*K+ are longer than that of the pristine compound 1. For compound 2, the ring size is enough large for the diameters of Li+, Na+ and K+. Thus, the alkali metal cations locate on the center of the crown ether. Meanwhile, in 2*M, the structure of the pristine compound 2 leads to a distortion. It is proved by the evidence that the distances of average O–O (4.483 Å) of the pristine compound 2 is longer than those of 2*M (M = Li+, Na+ and K+). For compound 3, the ring size is quite large for the alkali metal cations, and the average O–O distance (5.670 Å) of the pristine compound 3 is longer than those of 3*M (M = Li+, Na+ and K+). However, the average O–O distance (3.716 Å) of 3*Li is much shorter than that of the pristine compound 3 compared with 3*Na and 3*K. That is the fact that the ring size of the pristine compound 3 is too large for Li+, resulting in a noticeable distortion of the structure. The average O–M (M = Li+, Na+ and K+) distances are considered, and it is found that the variation of average O–M distances is independent of the ring sizes of compounds 1, 2 and 3. The data listed in Table 1 indicate that the average O–M distances of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) increase with increasing the diameters of alkali metal cations. | ||
| Fig. 1 Atom numbering used in describing the geometrical parameters. Color code: carbon (yellow), oxygen (red), nitrogen (purple). The hydrogen atoms are omitted for clarity. | ||
 | ||
| Fig. 2 Optimized structures of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+). All hydrogen atoms are omitted for clarify. | ||
| Average O–O (Å) | Average O–M (Å) | Average ρb (au) | Average ∇2ρb (au) | |
|---|---|---|---|---|
| a Average O–O = (O1–O3 + O2–O4)/2 for 1 and 1*M (M = Li+, Na+ and K+) average O–O = (O2–O4 + O1–O4 + O2–O5 + O3–O5 + O1–O3)/5 for 2 and 2*M (M = Li+, Na+ and K+) average O–O = (O3–O6 + O1–O4 + O2–O5)/3 for 3 and 3*M (M = Li+, Na+ and K+) average O–M = (O1–M + O2–M + O3–M + O4–M)/4 for 1*M (M = Li+, Na+ and K+) average O–M = (O1–M + O2–M + O3–M + O4–M + O5–M)/5 for 2*M (M = Li+, Na+ and K+) average O–M = (O1–M + O2–M + O3–M + O4–M + O5–M + O6–M)/6 for 3*M (M = Li+, Na+ and K+). | ||||
| 1 | 3.840 | |||
| 1*Li+ | 3.556 | 2.281 | 0.0328 | 0.2430 |
| 1*Na+ | 3.852 | 2.662 | 0.0213 | 0.1313 |
| 1*K+ | 3.918 | 3.056 | 0.0139 | 0.0615 |
| 2 | 4.483 | |||
| 2*Li+ | 4.193 | 2.206 | 0.0114 | 0.0885 |
| 2*Na+ | 4.374 | 2.305 | 0.0174 | 0.1348 |
| 2*K+ | 4.419 | 2.702 | 0.0143 | 0.0794 |
| 3 | 5.670 | |||
| 3*Li+ | 3.716 | 2.155 | 0.0149 | 0.0942 |
| 3*Na+ | 5.262 | 2.635 | 0.0098 | 0.0525 |
| 3*K+ | 5.463 | 2.752 | 0.0164 | 0.0697 |
In order to gain greater insight into the nature of O–M (M = Li+, Na+ and K+) interaction, the atoms in molecules (AIM) analysis was performed using the result at B3LYP/6-31G*. In the AIM analysis, the parameters of electron density (ρ) and Laplacian of the electron density (∇2ρ) are discussed. The data of ρ and ∇2ρ values at BCPs are listed in Table 1. The ρ value at a BCP correlates with the strength of an atomic interaction.46 The ρ values of 1*M (M = Li+, Na+ and K+) have a range from 0.0139 to 0.0328, and the 1*Li has the largest ρ value. From Table 1, it can be seen that the ρ values of 2*M (M = Li+, Na+ and K+) range from 0.0114 to 0.0174 with 2*Na+ possessing the largest ρ value. While, for 3*M (M = Li+, Na+ and K+), the range of ρ values is from 0.0098 to 0.0164, and the ρ value of 3*K+ is the largest. According to the analysis of ρ values, it can be concluded that the compounds 1, 2 and 3 are favourable for binding the Li+, Na+ and K+, respectively. The ∇2ρ value represents the curvature of the electron density in three-dimensional space at the BCP of O–M interaction.46 As for the ∇2ρ value, the negative ∇2ρ value suggests the shared electron (covalent) interaction, while the positive ∇2ρ value indicates the closed-shell (electrostatic) interaction. The ∇2ρ values of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) listed in Table 1 are all positive, suggesting that the O–M (M = Li+, Na+ and K+) interaction has a dominant electrostatic character.
3.2 Interaction energy and extended charge decomposition analysis
In this section, we consider the ring sizes and the nature of alkali metal cations (Li+, Na+ and K+) effect on the interaction energy (Eint) of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+). The Eint values of studied configurations were calculated at BHandHLYP/6-311+G** level. The corresponding Eint values are displayed in Table 2 and plotted in Fig. 3.| 1*Li+ | 1*Na+ | 1*K+ | |
|---|---|---|---|
| Eint (kcal mol−1) | 100.0 | 67.11 | 45.47 |
| 2*Li+ | 2*Na+ | 2*K+ | |
| Eint (kcal mol−1) | 114.0 | 87.88 | 62.18 |
| 3*Li+ | 3*Na+ | 3*K+ | |
| Eint (kcal mol−1) | 130.5 | 94.22 | 74.89 |
 | ||
| Fig. 3 Interaction energy (Eint) and extend charge decomposition analysis (ECDA) of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+). | ||
Firstly, we consider the effect of the ring sizes of compounds 1, 2 and 3 on Eint values. Taking the N*Li+ (N = 1, 2 and 3) as an example, the Eint values are in the following order 3*Li+ (130.5) > 2*Li+ (114.0) > 1*Li+ (100.0 kcal mol−1). As with the N*Na+ (N = 1, 2 and 3) and N*K+ (N = 1, 2 and 3), the variations of Eint values are consistent with that of N*Li+ (N = 1, 2 and 3). From the data given in Table 2, such conclusion is obtained that the Eint values of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) enhance as the ring sizes increase irrespective of the alkali metal cations. Secondly, the effect of alkali metal cations (Li+, Na+ and K+) on Eint is considered. When the alkali metal cations (Li+, Na+ and K+) complexing respectively compounds 1, 2 and 3, the variations of Eint values show the same trend. For example, the Eint values of 1*M (M = Li+, Na+ and K+) are in the order: 1*Li+ (100.0) > 1*Na+ (67.11) > 1*K+ (45.47 kcal mol−1). The Eint values of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) decrease as the diameters of alkali metal cations increase irrespective of the ring sizes of the compounds 1, 2 and 3. Consequently, the Eint values of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) depend on both the ring sizes and the nature of alkali metal cations.
Dapprich and Frenking have proposed that the charge decomposition analysis (CDA) method which is used to quantify the charge donation and back donation between fragments in a complex to achieve charge equilibrium. The difference between the total number of donation and back donation is regarded as the net charge transfer. When two fragments are combined to form a bond, there are two types of electronic interactions that will affect the compositions of the molecule orbital of the complex. One is the charge transfer (CT) from the donor to the acceptor, and the other is electronic polarization (PL) of one fragment in the presence of another.43 Broadly speaking, the CDA method considers both CT and PL effects, which is not correct in term of analyzing the amount of the net charge transfer. Later, the extended charge decomposition analysis (ECDA) method is proposed, in which the PL effect is excluded in the calculation of the amount of the net charge transfer. Therefore, the amount of charge transfer with CDA and ECDA methods are not consistent, but the results obtained with ECDA method are more reasonable. However, in the CDA, the charge transfer can be decomposed to the orbital contribution of complex. While, the ECDA method only reveals how many charge are transferred between two fragments. The number of net charge transfer from A to B can be obtained according to: CT(A → B) − CT(B → A) = [PL(A) + CT(A → B)] − [PL(A) + CT(B → A)].47 Fig. 3 plots the variation of the net charge transfer obtained by ECDA method as a function of configurations. As seen from Table 3, the amount of the net charge transfer obtained by CDA method is different from that obtained by ECDA method. According to the previous papers, we only discuss the results obtained by ECDA method. For 1*M (M = Li+, Na+ and K+), it is noting that the amount of the net charge transfer is in the order of 1*Li+ (0.4689) > 1*Na+ (0.3255) > 1*K+ (0.1864 au). The net charge transfer of the 2*M (M = Li+, Na+ and K+) and 3*M (M = Li+, Na+ and K+) is the same to that of 1*M (M = Li+, Na+ and K+). Thus, the amount of the net charge transfer of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) decrease as the diameters of the alkali metal cations increase. Moreover, the variation of the amount of the net charge transfer is consistent with that of the interaction energy.
| CDA | ECDA | |
|---|---|---|
| 1*Li+ | 0.3416 | 0.4689 |
| 1*Na+ | 0.2475 | 0.3255 |
| 1*K+ | 0.1461 | 0.1864 |
| 2*Li+ | 0.3287 | 0.4361 |
| 2*Na+ | 0.3141 | 0.4018 |
| 2*K+ | 0.2055 | 0.2577 |
| 3*Li+ | 0.3281 | 0.4668 |
| 3*Na+ | 0.3379 | 0.4254 |
| 3*K+ | 0.2377 | 0.2998 |
3.3 Linear and nonlinear optical properties
The difference among compounds 1, 2 and 3 is the ring sizes, and we initially investigate the effect of ring sizes on the linear and nonlinear optical properties. To confirm the accuracy of results, we choose three methods (BHandHLYP, CAM-B3LYP and M06-2X) to calculate the linear and nonlinear optical properties of compounds 1, 2 and 3. The data of dipole moment (μ0), polarizability (α0) and first hyperpolarizability (β0) are listed in Table 4. Meanwhile, Fig. 4 depicts the variation of μ0, α0 and β0 values as the function of the compounds 1, 2 and 3 using three methods. From Fig. 4, it is clear that the results of three methods agree broadly, showing the same trend. However, three parameters show different variations. For example, the order of μ0 values is 3 > 2 > 1, indicating that the μ0 values enhance with increasing the ring sizes. The variation of α0 values is in accordance with that of μ0 values. However, the variation of β0 values is in the following order: 2 > 3 > 1.| 1 | 2 | 3 | ||
|---|---|---|---|---|
| BH and HLYP | μ0 | 1.010 | 1.491 | 2.039 |
| α0 | 306.8 | 339.7 | 364.9 | |
| βx | −907.5 | −2049 | −1974 | |
| βy | −22.67 | 274.7 | 286.3 | |
| βz | 1.592 | 175.4 | 265.0 | |
| β0 | 907.8 | 2075 | 2012 | |
| M062X | μ0 | 0.9554 | 1.452 | 1.965 |
| α0 | 309.6 | 343.6 | 369.6 | |
| βx | −1204 | −2486 | −2388 | |
| βy | 63.07 | 399.8 | 426.9 | |
| βz | −6.463 | 196.5 | 310.3 | |
| β0 | 1205 | 2525 | 2446 | |
| Cam-B3LYP | μ0 | 0.9731 | 1.488 | 2.002 |
| α0 | 308.5 | 342.4 | 368.2 | |
| βx | −1181 | −2413 | −2337 | |
| βy | 41.93 | 371.0 | 393.5 | |
| βz | −4.081 | 194.7 | 304.4 | |
| β0 | 1182 | 2449 | 2389 |
It is well-known that the original reason of the difference of the β0 values is able to be explained within the two-state approximation: larger β0 values are concerned with smaller excitation energies. Considering the computational cost and time, the crucial transition energy (ΔE) is calculated using BHandHLYP method. From Fig. 4, we can see that the variation of ΔE values is in the order: 1 > 3 > 2. The variation of β0 values is inversely proportional to that of ΔE values. Therefore, the transition energy is the major factor in producing the difference of the first hyperpolarizability within the two-state approximation.
The effect of alkali metal cations on the linear and nonlinear optical properties of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) was studied. In the former part, it has been concluded that the three methods obtain the similar linear and nonlinear optical properties. Thus, taking the computational cost and time into account, the linear and nonlinear optical properties of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) were calculated using BHandHLYP method. In the following section, we discuss the effect of the nature of alkali metal cations (Li+, Na+ and K+) on the linear and nonlinear optical properties of compounds 1, 2 and 3. The corresponding data are listed in Table 5. Fig. 5–7 illustrate the relationship between the μ0, α0, β0 and ΔE values and configurations.
| μ0 | α0 | βx | βy | βz | β0 | |
|---|---|---|---|---|---|---|
| 1*Li+ | 7.464 | 312.4 | 3847 | −733.0 | 10.02 | 3916 |
| 1*Na+ | 7.236 | 309.8 | 3305 | −688.6 | −179.4 | 3381 |
| 1*K+ | 7.451 | 313.7 | −3111 | −677.9 | 117.7 | 3187 |
| 2*Li+ | 7.624 | 337.4 | 2337 | −609.1 | −72.10 | 2416 |
| 2*Na+ | 7.269 | 338.4 | 2423 | −639.6 | −75.03 | 2508 |
| 2*K+ | 7.301 | 342.1 | 2295 | −611.7 | −162.0 | 2381 |
| 3*Li+ | 6.812 | 357.8 | 2443 | −555.6 | −271.4 | 2520 |
| 3*Na+ | 7.293 | 364.2 | 1602 | −528.9 | −122.1 | 1692 |
| 3*K+ | 6.687 | 367.3 | 1666 | −562.2 | −139.9 | 1763 |
 | ||
| Fig. 5 Dipole moment (μ0), polarizability (α0), first hyperpolarizability (β0) and transition energy (ΔE) of 1*M (M = Li+, Na+ and K+). | ||
 | ||
| Fig. 6 Dipole moment (μ0), polarizability (α0), first hyperpolarizability (β0) and transition energy (ΔE) of 2*M (M = Li+, Na+ and K+). | ||
 | ||
| Fig. 7 Dipole moment (μ0), polarizability (α0), first hyperpolarizability (β0) and transition energy (ΔE) of 3*M (M = Li+, Na+ and K+). | ||
For 1*M (M = Li+, Na+, K+), the μ0 values are in the order: 1*Li+ > 1*K+ > 1*Na+, and the α0 values are in the sequence 1*K+ > 1*Li+ > 1*Na+. However, the β0 values increase as decreasing the diameters of alkali metal cations with the order: 1*Li+ > 1*Na+ > 1*K+. Therefore, when compound 1 complexing alkali metal cations, the 1*Li+ has the largest μ0 value and β0 value, and the 1*K+ has the largest α0 value. Furthermore, the variation of ΔE values is in the order: 1*K+ > 1*Na+ > 1*Li+, which is inversely proportional to that of β0 values. As expected, the difference of β0 values is well explained within the two-state approximation.
For 2*M (M = Li+, Na+ and K+), the μ0 values are in the order of 2*Li+ > 2*K+ > 2*Na+. The α0 values are in the sequence 2*K+ > 2*Na+ > 2*Li+. While, the 2*Na+ has the largest β0 value, and the 2*K+ has the smallest β0 value with the order of 2*Na+ > 2*Li+ > 2*K+. Moreover, the ΔE values decrease on moving along the series 2*K+ → 2*Li+ → 2*Na+, which is inversely proportional to that of β0 values.
For 3*M (M = Li+, Na+ and K+), the μ0 values are in the order of 3*Na+ > 3*Li+ > 3*K+, and the α0 values enhance with increasing the diameters of alkali metal cations with the sequence 3*K+ > 3*Na+ > 3*Li+. On the other hand, the β0 values are in the series of configurations with 3*Li+ > 3*K+ > 3*Na+, which is inversely proportional to that of ΔE values with the order of 3*Na+ > 3*K+ > 3*Li+.
The transition properties of studied configurations were calculated using BHandHLYP method, and the data are shown in Table 6. The crucial transition state is selected based on the excited state with the largest oscillate strength (f0). As can be seen from Table 6, the f0 values of compounds 1, 2 and 3 are in a small range from 1.290 to 1.378. When the compounds 1, 2 and 3 complexing alkali metal cations (Li+, Na+, K+), the f0 values of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) become smaller approximately 1.100–1.200. Significantly, the crucial transition state of compounds 1, 2 and 3 and N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) is all the first excited state. Moreover, the first excited state is dominated by HOMO → LUMO or HOMO → LUMO + 1. For 1*Na and 1*K, the first excited state is dominated by HOMO → LUMO + 1. In particular, the first excited state of 2*K include two transitions, which are HOMO → LUMO and HOMO → LUMO + 1. The rest configurations are all HOMO → LUMO. The UV-vis spectra of compounds 1, 2 and 3 and N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) are depicted in Fig. 8. From Fig. 8, it is noticeable that the spectra of compounds 1, 2 and 3 are similar, and their maximum absorption wavelengths are almost the same. Moreover, the maximum absorption wavelength originates from the transition from the first excited state to the ground state. When the compounds 1, 2 and 3 complexing alkali metal cations, the maximum absorption wavelengths of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) induce a small red-shift compared with compounds 1, 2 and 3. Meanwhile, the absorption intensities of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) corresponding the maximum absorption wavelength are lower than those of compounds 1, 2 and 3. To gain greater insight into the red-shift, the HOMO and LUMO levels are calculated and tabulated in Table 6. It can be seen that the complexing alkali metal cations cause significant reduction of both HOMO and LUMO levels. Moreover, the Egap values are in a decrease after compounds 1, 2 and 3 complexing alkali metal cations. On the other hand, relevant ref. 8 has reported that the reduced charge transfer for the first electronic transition produces the hypsochromic shifts when complexing metal cation. Further, we continue to analyze the electronic excited-states in the following section. Gavin in Table 7, the transferred charge (qCT) values of compounds 1, 2 and 3 are 0.427, 0.450 and 0.450 au, respectively. Compared to the qCT values of compounds 1, 2 and 3, it is noteworthy that the transferred charge between the first excited state and the ground state has a significant increase when complexing alkali metal cations. As a result, the both decreased Egap values and transferred charge are predicted to the reason of the red-shift when compounds 1, 2 and 3 complexing alkali metal cations.
| Oscillate strength | Transition energy (eV) | Wavelength (nm) | Crucial transition | HOMO (eV) | LUMO (eV) | Egap (eV) | |
|---|---|---|---|---|---|---|---|
| 1 | 1.290 | 3.800 | 326.3 | HOMO → LUMO | −6.270 | −0.740 | 5.530 |
| 1*Li+ | 1.120 | 3.607 | 343.7 | HOMO → LUMO | −8.380 | −3.160 | 5.220 |
| 1*Na+ | 1.111 | 3.635 | 341.1 | HOMO → LUMO + 1 | −8.340 | −3.210 | 5.130 |
| 1*K+ | 1.125 | 3.650 | 339.7 | HOMO → LUMO + 1 | −8.270 | −3.290 | 4.980 |
| 2 | 1.373 | 3.749 | 330.8 | HOMO → LUMO | −5.990 | −0.550 | 5.440 |
| 2*Li+ | 1.178 | 3.692 | 335.8 | HOMO → LUMO | −8.170 | −2.810 | 5.360 |
| 2*Na+ | 1.174 | 3.686 | 336.4 | HOMO → LUMO | −8.190 | −2.840 | 5.350 |
| 2*K+ | 1.177 | 3.699 | 335.2 | HOMO → LUMO | −8.130 | −2.780 | 5.350 |
| 3 | 1.378 | 3.753 | 330.3 | HOMO → LUMO + 1 | −6.010 | −0.560 | 5.450 |
| HOMO → LUMO | |||||||
| 3*Li+ | 1.185 | 3.698 | 335.2 | HOMO → LUMO | −8.160 | −2.780 | 5.380 |
| 3*Na+ | 1.216 | 3.730 | 332.4 | HOMO → LUMO | −8.010 | −2.590 | 5.420 |
| 3*K+ | 1.208 | 3.723 | 333.0 | HOMO → LUMO | −8.060 | −2.650 | 5.410 |
| Transferred charge (au) | Distance of CT (Å) | Dipole moment variation (Debye) | H index (Å) | |
|---|---|---|---|---|
| 1 | 0.427 | 0.152 | 0.313 | 3.598 |
| 1*Li+ | 0.593 | 2.825 | 8.048 | 4.004 |
| 1*Na+ | 0.577 | 2.708 | 7.506 | 3.948 |
| 1*K+ | 0.566 | 2.656 | 7.224 | 3.949 |
| 2 | 0.450 | 0.828 | 1.789 | 3.783 |
| 2*Li+ | 0.541 | 2.459 | 6.390 | 3.967 |
| 2*Na+ | 0.544 | 2.468 | 6.494 | 3.978 |
| 2*K+ | 0.536 | 2.426 | 6.247 | 3.978 |
| 3 | 0.450 | 0.766 | 1.655 | 3.824 |
| 3*Li+ | 0.549 | 2.470 | 6.511 | 4.048 |
| 3*Na+ | 0.511 | 2.186 | 5.363 | 3.947 |
| 3*K+ | 0.516 | 2.221 | 5.504 | 3.963 |
3.4 Charge transfer indexes
From the transition properties analysis, we can conclude that the crucial transition state of all studied configurations is the first excited state. In the following part, we analyze the electronic excited-states (ES) using both density difference plots representing an electronic transition with a single picture, and Le Bahers' model quantifying the charge transfer (CT) nature of the ES.48,49 Firstly, the difference in density between the first excited state and the ground state is shown in Fig. 9. For all studied configurations, the charge transfer occurs in the chain which is independent of the crown ether ring and the nature of alkali metal cations. Moreover, it can be found clearly alternating regions of electron density gain and loss for all studied configurations. In order to provide a more detailed feature of the ES of studied configurations, we analyze the CT parameters including the CT distance (DCT), the transferred charge (qCT) and the dipole moment variation (μCT). The computed CT indexes are listed in Table 7. Corresponding illustrations are shown in Fig. 10–13. As can be seen from Table 7, the DCT values are in the order 2 (0.828) > 3 (0.766) > 1 (0.152 Å). Meanwhile, the μCT values of compounds 1, 2 and 3 going from 2 → 3 → 1 induce a decrease from 1.789 → 1.655 → 0.313 Debye. The variations of qCT, DCT, and μCT are in accordance with that of β0 values. It has been reported that the difference of β0 values can be explained well within the two-state approximation. In the equation, the β0 value is inversely proportional to the ΔE value, and the β0 value is proportional to the μCT value. As a consequence, the calculated μCT values explain perfectly the variation of β0 value of compounds 1, 2 and 3. | ||
| Fig. 10 Transferred charge (qCT), charge transfer distance (DCT), dipole moment variation (μCT) and first hyperpolarizability (β0) of compounds 1, 2 and 3. | ||
 | ||
| Fig. 11 Transferred charge (qCT), charge transfer distance (DCT), dipole moment variation (μCT) and first hyperpolarizability (β0) of 1*M (M = Li+, Na+ and K+). | ||
 | ||
| Fig. 12 Transferred charge (qCT), charge transfer distance (DCT), dipole moment variation (μCT) and first hyperpolarizability (β0) of 2*M (M = Li+, Na+ and K+). | ||
 | ||
| Fig. 13 Transferred charge (qCT), charge transfer distance (DCT), dipole moment variation (μCT) and first hyperpolarizability (β0) of 3*M (M = Li+, Na+ and K+). | ||
In the following section, we continue to discuss the CT indexes of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) shown in Table 7. For 1*M (M = Li+, Na+ and K+), the variations of qCT (0.566–0.593 au), DCT (2.656–2.825 Å) and μCT (7.224–8.048 Debye) values show the same trend which is in the order of 1*Li+ > 1*Na+ > 1*K+. As expected, the variation of μCT values of 1*M (M = Li+, Na+ and K+) is proportional to that of β0 values.
For 2*M (M = Li+, Na+ and K+), the largest qCT (0.544 au), DCT (2.468 Å) and μCT (6.494 Debye) amplitude appear when complexing Na+, and the smallest qCT (0.536 au), DCT (2.426 Å) and μCT (6.247 Debye) values appear when complexing K+. The variation of qCT, DCT and μCT values are in the order of 2*Na+ > 2*Li+ > 2*K+, which is in a good agreement with that of β0 values.
For 3*M (M = Li+, Na+ and K+), the qCT values are in the order of 3*Li+ (0.549) > 3*K+ (0.516) > 3*Na+ (0.511 au), and the DCT values are in the sequence of 3*Li+ (2.470) > 3*K+ (2.221) > 3*Na+ (2.186 Å), and the order of μCT values is 3*Li+ (6.511) > 3*K+ (5.504) > 3*Na+ (5.363 Debye). It is worthwhile that the qCT, DCT and μCT values display the same variation. Moreover, that variation is in good line with that of β0 values. Therefore, the difference of β0 values of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) is well explained by the μCT values within the two-state approximation.
To visualize the overlap between the regions of density depletion and increment, the centroids of charge have been used. On one hand, it is much easier to recognize the donor an acceptor moieties. On the other hand, it is clear to display the overlap between the regions of density depletion and increment. Fig. 14 depicts the centroids of respective density depletion and increment of all studied configurations, and it is evidenced clearly that an overlap between the regions of density depletion and increment. The H index is defined as the overlap between the centroids of charge representing the zones of increase and decrease of electron density on excitation. In general, if H > DCT, there is an overlap between the regions of density depletion and increment. From Table 7, for all studied configurations, the H values are larger than the DCT values. As a result, there is an overlap between the regions of density depletion and increment on excitation from the first excitation state to the ground state, which is in accordance with the conclusion given in Fig. 14.
 | ||
| Fig. 14 Centroids of respective charge, and the light blue (dark blue) regions correspond to decrease (increase) of the electron density. | ||
4. Conclusions
In summary, we have designed compounds 1 and 3 based on the synthesized compound 2. The difference among three compounds is the ring sizes of crown moiety. The crown moiety of compounds 1, 2 and 3 has four, five and six O atoms, respectively. The calculated nonlinear optical properties of compounds 1, 2 and 3 using three methods indicate that the compound 2 has the largest first hyperpolarizability magnitude. Further, we calculated a series of properties of nine configurations constructed by compounds 1, 2 and 3 complexing alkali metal cations (Li+, Na+ and K+). The conclusions are as followed.(1) The atoms in molecules analysis indicates that the compounds 1, 2 and 3 are favourable for binding the Li+, Na+ and K+, and the O–M (M = Li+, Na+ and K+) interaction has a dominant electrostatic character.
(2) The Eint values of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) increase as the ring sizes increase, and decrease as the diameters of alkali metal cations increase. The amount of the net charge transfer of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) decrease with increasing the diameters of the alkali metal cations.
(3) The alkali metal cations produce different influences on the nonlinear optical properties. For compounds 1*M (M = Li+, Na+, K+), the 1*Li+ has the largest μ0 and β0 values, and 1*K+ has the largest α0 value. However, for 2*M (M = Li+, Na+, K+), the μ0 value of 2*Li+, the α0 value of 2*K+ and the β0 value of 2*Na+ are the largest. The cases are very different from the 3*M (M = Li+, Na+ and K+), with 3*Na+, 3*K+ and 3*Li+ possessing the largest μ0, α0 and β0 values, respectively.
(4) From the transition properties analysis, it is concluded that the crucial excited state of studied configurations is all the first excited state. The variations of qCT, DCT and μCT values of 1*M (M = Li+, Na+ and K+) are in the order of 1*Li+ > 1* Na+ > 1*K+. The variations of qCT, DCT and μCT values of 2*M (M = Li+, Na+ and K+) are in the sequence 2*Na+ > 2*Li+ > 2*K+. The variations of qCT, DCT and μCT values of 3*M (M = Li+, Na+ and K+) is in the order 3*Li+ > 3*K+ > 3*Na+. Moreover, the variations of β0 values of N*M (N = 1, 2 and 3; M = Li+, Na+ and K+) are proportional to those of their ΔE values, and inversely proportional to that of those of their μCT values.
(6) The H values and the illustration of centroids of respective density depletion and increment suggest that there is an overlap between the regions of density depletion and increment on excitation from the first excitation state to the ground state.
Acknowledgements
The authors gratefully acknowledge financial support from National Science Foundation of China (NSFC) (21003019, 21473026), the Science and Technology Development Planning of Jilin Province (201201062 and 20140101046JC), the Computing Center of Jilin Province provided essential support and H.-L.X. acknowledges support from the Hong Kong Scholars Program. And Project funded by China Postdoctoral Science Foundation 2014M560227).References
- G. W. Gokel, W. M. Leevy and M. E. Weber, Chem. Rev., 2004, 104, 2723–2750 CrossRef CAS PubMed.
- C. J. Pedersen, J. Am. Chem. Soc., 1967, 89, 2495–2496 CrossRef CAS.
- C. J. Pedersen, Angew. Chem., Int. Ed. Engl., 1988, 27, 1021–1027 CrossRef.
- P. B. Armentrout, C. A. Austin and M. T. Rodgers, J. Phys. Chem. A, 2014, 118, 8088–8097 CrossRef CAS PubMed.
- S. Nishihara, T. Akutagawa, D. Sato, S. Takeda, S.-i. Noro and T. Nakamura, Chem.–Asian J., 2007, 2, 1083–1090 CrossRef CAS PubMed.
- S. P. Gromov, S. N. Dmitrieva, A. I. Vedernikov, N. A. Kurchavov, L. G. Kuz'mina, S. K. Sazonov, Y. A. Strelenko, M. V. Alfimov, J. A. K. Howard and E. N. Ushakov, J. Org. Chem., 2013, 78, 9834–9847 CrossRef CAS PubMed.
- J. Motoyoshiya, T. Tanaka, M. Kuroe and Y. Nishii, J. Org. Chem., 2008, 74, 1014–1018 CrossRef PubMed.
- O. A. Fedorova, Y. V. Fedorov, E. N. Andryukhina, S. P. Gromov, M. V. Alfimov and R. Lapouyade, Org. Lett., 2003, 5, 4533–4535 CrossRef CAS PubMed.
- J.-M. Lehn, Angew. Chem., Int. Ed. Engl., 1988, 27, 89–112 CrossRef.
- H. Tsukube, Coord. Chem. Rev., 1996, 148, 1–17 CrossRef CAS.
- Y.-H. Luo, S.-W. Ge, W.-T. Song and B.-W. Sun, New J. Chem., 2014, 38, 723–729 RSC.
- J. W. Grate, R. Strebin, J. Janata, O. Egorov and J. Ruzicka, Anal. Chem., 1996, 68, 333–340 CrossRef CAS.
- E. P. Horwitz, M. L. Dietz and D. E. Fisher, Solvent Extr. Ion Exch., 1991, 9, 1–25 CrossRef CAS.
- R. Chiarizia, E. P. Horwitz and M. L. Dietz, Solvent Extr. Ion Exch., 1992, 10, 337–361 CrossRef CAS.
- J. W. Steed, Coord. Chem. Rev., 2001, 215, 171–221 CrossRef CAS.
- G. W. Gokel, L. J. Barbour, R. Ferdani and J. Hu, Acc. Chem. Res., 2002, 35, 878–886 CrossRef CAS PubMed.
- K. E. Krakowiak, J. S. Bradshaw and D. J. Zamecka-Krakowiak, Chem. Rev., 1989, 89, 929–972 CrossRef CAS.
- A. I. Vedernikov, E. N. Ushakov, L. G. Kuz'mina, A. V. Churakov, Y. A. Strelenko, M. Wörner, A. M. Braun, J. A. K. Howard, M. V. Alfimov and S. P. Gromov, J. Phys. Org. Chem., 2010, 23, 195–206 CAS.
- S. Cooper and S. Rawle, In Bioinorganic Chemistry, Springer Berlin Heidelberg, 1990, vol. 72, pp. 1–72 Search PubMed.
- S. R. Cooper, Acc. Chem. Res., 1988, 21, 141–146 CrossRef CAS.
- S. N. Dmitrieva, N. I. Sidorenko, N. A. Kurchavov, A. I. Vedernikov, A. Y. Freidzon, L. G. Kuz'mina, A. K. Buryak, T. y. M. Buslaeva, A. A. Bagatur'yants, Y. A. Strelenko, J. A. K. Howard and S. P. Gromov, Inorg. Chem., 2011, 50, 7500–7510 CrossRef CAS PubMed.
- O. A. Fedorova, E. N. Andryukhina and S. P. Gromov, Synthesis, 2003, 2003, 0371–0374 CrossRef PubMed.
- A. J. Garza, O. I. Osman, A. M. Asiri and G. E. Scuseria, J. Phys. Chem. B, 2015, 119, 1202–1212 CrossRef CAS PubMed.
- D. P. Shelton and J. E. Rice, Chem. Rev., 1994, 94, 3–29 CrossRef CAS.
- B. J. Coe and R. A. Pilkington, J. Phys. Chem. A, 2014, 118, 2253–2268 CrossRef CAS PubMed.
- R. L. Zhong, H. L. Xu, Z. M. Su, Z. R. Li, S. L. Sun and Y. Q. Qiu, ChemPhysChem, 2012, 13, 2349–2353 CrossRef CAS PubMed.
- H. L. Xu, Z. R. Li, Z. M. Su, S. Muhammad, F. L. Gu and K. Harigaya, J. Phys. Chem. C, 2009, 113, 15380–15383 CAS.
- H. L. Xu, Z. R. Li, F. F. Wang, D. Wu, K. Harigaya and F. L. Gu, Chem. Phys. Lett., 2008, 454, 323–326 CrossRef CAS PubMed.
- Y. Gao, H.-L. Xu, R.-L. Zhong, S.-L. Sun and Z.-M. Su, J. Mol. Model., 2014, 20, 1–7 CAS.
- Y. Gao, S.-L. Sun, H.-L. Xu and Z.-M. Su, Chem. Phys. Lett., 2014, 600, 123–127 CrossRef CAS PubMed.
- Y. Gao, S.-L. Sun, H.-L. Xu, L. Zhao and Z.-M. Su, RSC Adv., 2014, 4, 24433–24438 RSC.
- W. Chen, Z.-R. Li, D. Wu, Y. Li, C.-C. Sun, F. L. Gu and Y. Aoki, J. Am. Chem. Soc., 2006, 128, 1072–1073 CrossRef CAS PubMed.
- W. Chen, Z.-R. Li, D. Wu, Y. Li, C.-C. Sun and F. L. Gu, J. Am. Chem. Soc., 2005, 127, 10977–10981 CrossRef CAS PubMed.
- S. Muhammad, H. Xu, Y. Liao, Y. Kan and Z. Su, J. Am. Chem. Soc., 2009, 131, 11833–11840 CrossRef CAS PubMed.
- H.-L. Xu, Z.-R. Li, D. Wu, B.-Q. Wang, Y. Li, F. L. Gu and Y. Aoki, J. Am. Chem. Soc., 2007, 129, 2967–2970 CrossRef CAS PubMed.
- H.-L. Xu, Z.-R. Li, D. Wu, F. Ma, Z.-J. Li and F. L. Gu, J. Phys. Chem. C, 2009, 113, 4984–4986 CAS.
- H. L. Xu, Z. R. Li, D. Wu, F. Ma and Z. J. Li, J. Phys. Chem. C, 2009, 113, 4984–4986 CAS.
- M. J. Frisch, et al., Gaussian 09, revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- R. Sumathi, S. D. Peyerimhoff and D. Sengupta, J. Phys. Chem. A, 1999, 103, 772–778 CrossRef CAS.
- S. Dapprich and G. Frenking, J. Phys. Chem., 1995, 99, 9352–9362 CrossRef CAS.
- S. I. Gorelsky, S. Ghosh and E. I. Solomon, J. Am. Chem. Soc., 2006, 128, 278–290 CrossRef CAS PubMed.
- M. Nakano, R. Kishi, T. Nitta, T. Kubo, K. Nakasuji, K. Kamada, K. Ohta, B. Champagne, E. Botek and K. Yamaguchi, J. Phys. Chem. A, 2005, 109, 885–891 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. Iwaoka, H. Komatsu, T. Katsuda and S. Tomoda, J. Am. Chem. Soc., 2004, 126, 5309–5317 CrossRef CAS PubMed.
- X. Yang, Y. Liang, S. Ding, S. Li, Z. Chai and D. Wang, Inorg. Chem., 2014, 53, 7848–7860 CrossRef CAS PubMed.
- T. Le Bahers, C. Adamo and I. Ciofini, J. Chem. Theory Comput., 2011, 7, 2498–2506 CrossRef CAS.
- D. Jacquemin, T. L. Bahers, C. Adamo and I. Ciofini, Phys. Chem. Chem. Phys., 2012, 14, 5383–5388 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra01145k |
| This journal is © The Royal Society of Chemistry 2015 |




